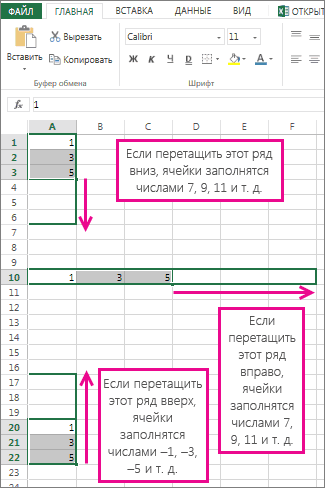
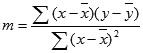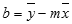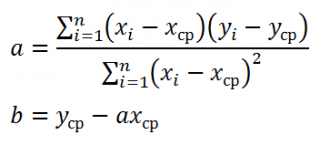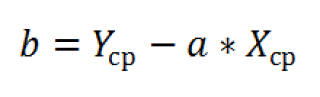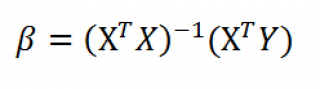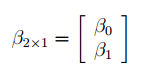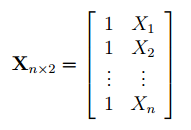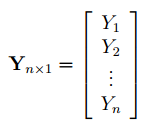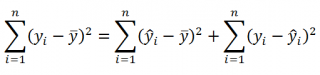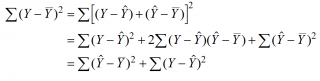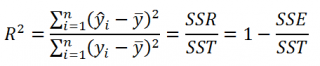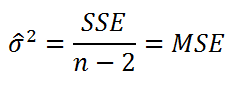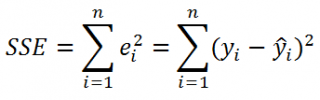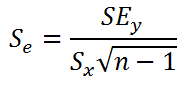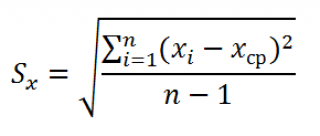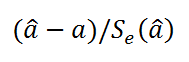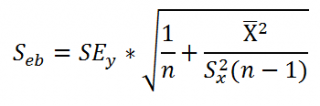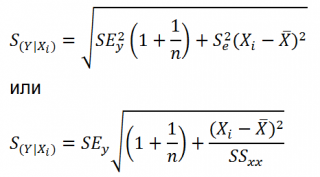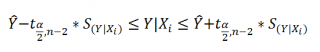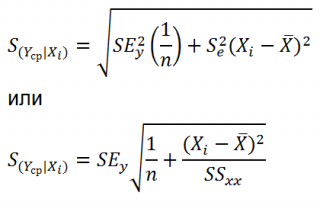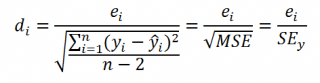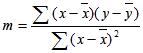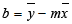В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 +… + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
-
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
-
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
-
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
-
-
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
-
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
-
Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
-
-
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
-
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
-
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
-
-
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
-
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.
-
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
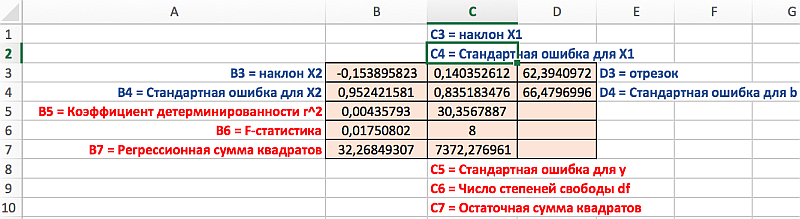
Дополнительная регрессионная статистика.
-
|
Величина |
Описание |
|---|---|
|
se1,se2,…,sen |
Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
|
seb |
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
|
r2 |
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе «Замечания» далее в этой теме. |
|
sey |
Стандартная ошибка для оценки y. |
|
F |
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
|
df |
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df. |
|
ssreg |
Регрессионная сумма квадратов. |
|
ssresid |
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания
-
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
-
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2) -
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).
-
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
-
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.
-
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
-
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
-
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
-
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
-
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
-
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
-
-
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
-
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Результат (наклон) |
Результат (y-пересечение) |
|
2 |
1 |
|
Формула (формула массива в ячейках A7:B7) |
|
|
=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) |
Пример 2. Простая линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Продажи |
|---|---|
|
1 |
3 100 ₽ |
|
2 |
4 500 ₽ |
|
3 |
4 400 ₽ |
|
4 |
5 400 ₽ |
|
5 |
7 500 ₽ |
|
6 |
8 100 ₽ |
|
Формула |
Результат |
|
=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) |
11 000 ₽ |
|
Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы. |
Пример 3. Множественная линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Общая площадь (x1) |
Количество офисов (x2) |
Количество входов (x3) |
Время эксплуатации (x4) |
Оценочная цена (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 ₽ |
|
2333 |
2 |
2 |
12 |
144 000 ₽ |
|
2356 |
3 |
1,5 |
33 |
151 000 ₽ |
|
2379 |
3 |
2 |
43 |
150 000 ₽ |
|
2402 |
2 |
3 |
53 |
139 000 ₽ |
|
2425 |
4 |
2 |
23 |
169 000 ₽ |
|
2448 |
2 |
1,5 |
99 |
126 000 ₽ |
|
2471 |
2 |
2 |
34 |
142 900 ₽ |
|
2494 |
3 |
3 |
23 |
163 000 ₽ |
|
2517 |
4 |
4 |
55 |
169 000 ₽ |
|
2540 |
2 |
3 |
22 |
149 000 ₽ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Формула (формула динамического массива, введенная в A19) |
||||
|
=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА) |
Пример 4. Использование статистики F и r2
В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).
Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение «Альфа» = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.
Пример 5. Вычисление t-статистики
Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:
t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7
Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.
Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.
|
Переменная |
t-наблюдаемое значение |
|---|---|
|
Общая площадь |
5,1 |
|
Количество офисов |
31,3 |
|
Количество входов |
4,8 |
|
Возраст |
17,7 |
Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.
Задача отыскания функциональной зависимости очень важна, поэтому для ее решения в MS Excel введен набор функций, основанных на методе наименьших квадратов. В качестве результата выдаются не только коэффициенты функции, приближающей данные, но и статистические характеристики полученных результатов.
Смысл выходной статистической информации функции ЛИНЕЙН
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, вычисляя прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую.
Общий синтаксис вызова функции ЛИНЕЙН имеет следующий вид:
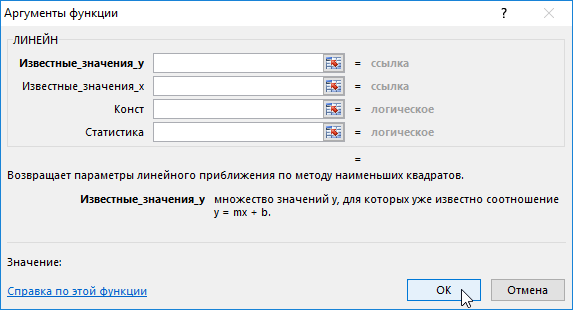
ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)
Для работы с функцией необходимо заполнить как минимум 1 обязательный и при необходимости 3 необязательных аргумента:
- Известные_значения_y − это множество значений y, которые уже известны для соотношения y=mx+b.
- Известные_значения_x − это множество известных значений x. Если этот аргумент опущен, то предполагается, что это массив {1; 2; 3; …} такого же размера, как и известные_значения_y.
- Конст − это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если в функции ЛИНЕЙН аргумент константа имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.
- Статистика − это логическое значение, которое указывает, требуется ли выдать дополнительную статистику по регрессии.
Примеры использования функции ЛИНЕЙН в Excel
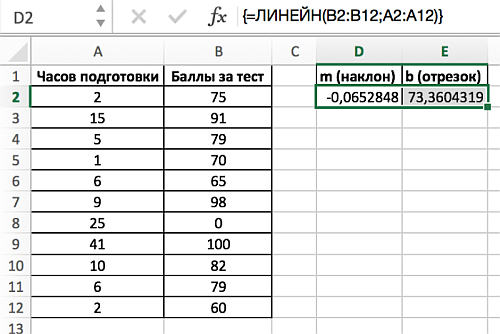
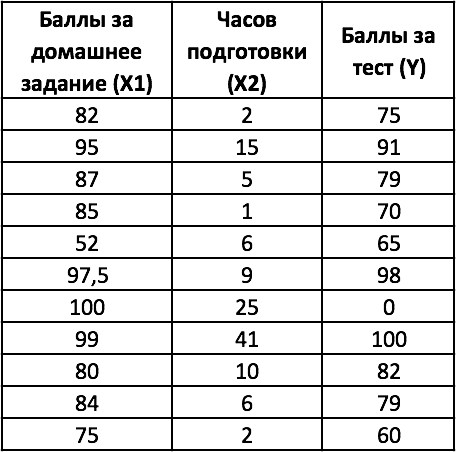
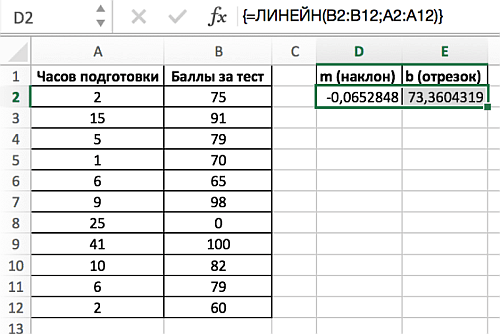
Для решения первой задачи – о соотношении часов подготовки студентов к тесту и результатов теста, как х и у соответственно, – необходимо применить следующий порядок действий (в связи с тем, что ЛИНЕЙН является функцией, которая возвращает массив):
- Выделите диапазон D2:Е2, так как функция ЛИНЕЙН возвращает массив из двух значений, расположенных по горизонтали, но не по вертикали.
- Введите известные значения y – баллы, которые студенты заработали на последнем тестировании (диапазон ячеек В2:В12).
- Затем введите известные значения х – количество часов, которые студенты потратили на подготовку к тестам (диапазон А2:А12).
- Опустите аргумент [конст].
- Опустите аргумент [статистика].
- Введите формулу с помощью Ctrl+Shift+Enter.
Результатом применения функции становится:
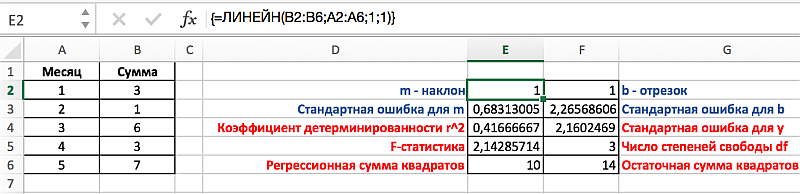
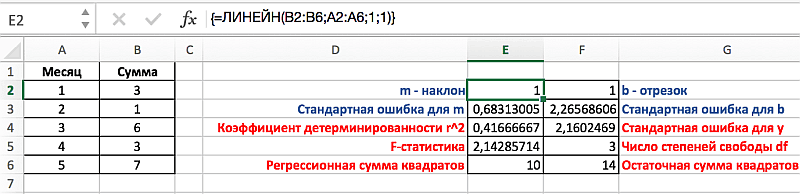
Теперь, на примере решения второй задачи, разберем необходимость в отображении не только наклона и отрезка, но и дополнительной статистики. Для примера, на диапазоне А1:В6 выстроим таблицу с соотношением у и х соответствующих сумме заработка студентом денежных средств за период в 5 месяцев. Так как мы имеем лишь одну переменную х, то необходимо выделить диапазон состоящий из двух столбцов и пяти строк. Важно отметить, что в том случае, если переменных х будет больше, то количество столбцов может изменяться соответственно их количеству, однако строк будет всегда 5.
Применительно к решаемой нами задаче, выделим диапазон Е2:F6, затем введем формулу аналогично предыдущей задаче, но в данном случае третьему и четвертому аргументу присвоим значение 1 соответствующее ИСТИНЕ. Для вывода параметров статистики функции ЛИНЕЙН необходимо нажат Ctrl+Shift+Enter, результат должен соответствовать следующему рисунку, на котором представлено обозначение дополнительных статистик:
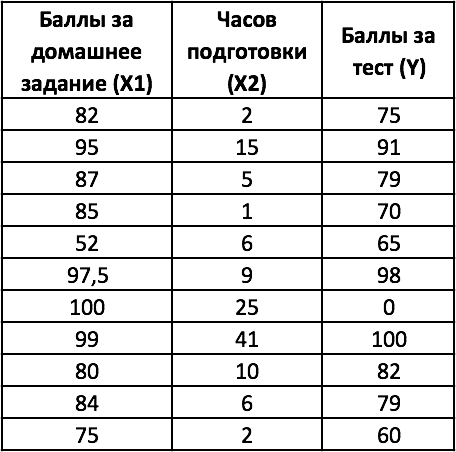
Вернемся к примеру № 1, касающемуся зависимости между часами подготовки студентов к тесту и баллов за тест. Добавим к условию задачи данные о баллах за домашнее задание — представляющие дополнительную переменную х, что свидетельствует о необходимости применения множественной регрессии.
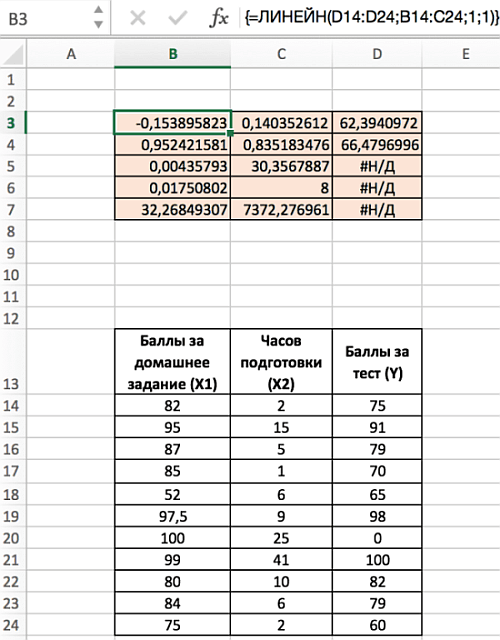
В случае множественной регрессии, когда значения «y» зависят от двух переменных «х», функция ЛИНЕЙН возвращает 12 статистик. На рисунке с модифицированной таблицей от 1 примера, представленном ниже используются следующие обозначения:
- y = зависимая переменная;
- x1 = независимая переменная 1 = баллы за домашнее задание;
- x2 = независимая переменная 2 = часы подготовки к тесту.
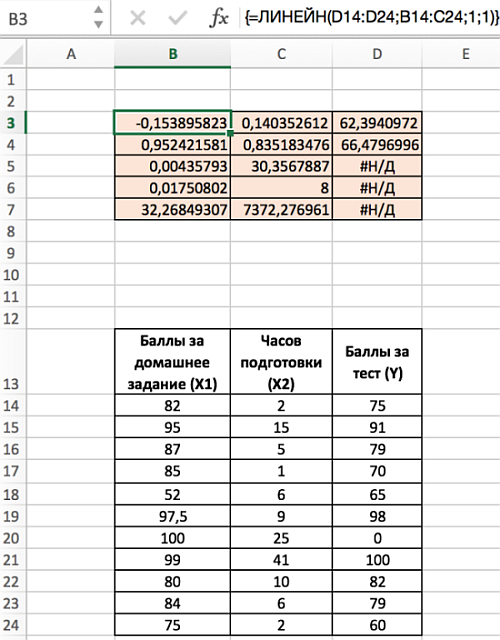
Чтобы выполнить множественную регрессию:
- Выделите диапазон В3:D7 (число столбцов = число переменных +1; число строк всегда равно 5).
- Наберите формулу =ЛИНЕЙН(D14:D24;B14:C24;1;1). Для аргумента известные_значения_х, выделите оба столбца значений x из диапазона В14:С24.
- Введите функцию с помощью клавиш Ctrl+Shift+Enter.
- Обратите внимание, что несмотря на то, что значения х1 указаны в диапазоне В14:С24 до значений х2, наклон сначала указан для х2.
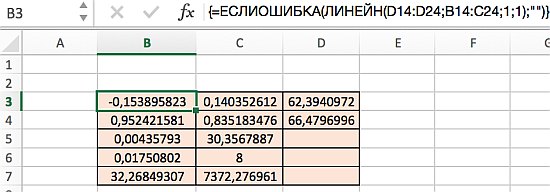
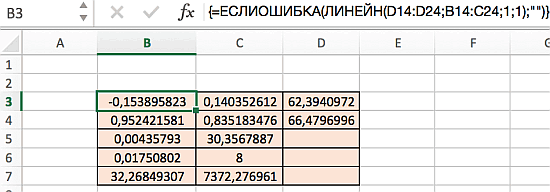
Диапазон D5:D7 содержит ошибку #Н/Д – значащую, что формула не может обнаружить значения для данных ячеек. Визуально наличие ошибки отвлекает от сути решения, поэтому далее предложим вариант избавления от нее. Так, если дополнить формулу содержащую функцию ЛИНЕЙН функцией ЕСЛИОШИБКА, то можно значительно улучшить вид таблицы, результат которой представлен ниже:
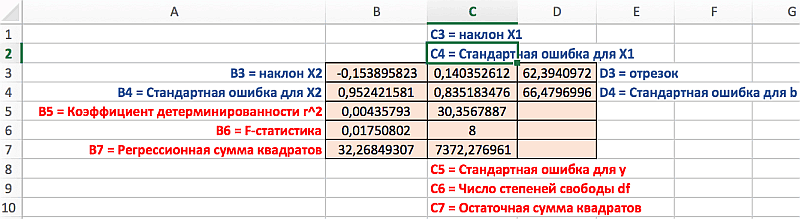
Распределение статистик в таблице их значение представлено на следующем рисунке:
Скачать примеры функции ЛИНЕЙН в Excel
В результате мы получили всю необходимую выходную статистическую информацию, которая нас интересует.
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В
MS
EXCEL
имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Немного теории и основные понятия
- Предположения линейной регрессионной модели
- Задачи регрессионного анализа
- Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
- Оценка неизвестных параметров линейной модели (через статистики выборок)
- Оценка неизвестных параметров линейной модели (матричная форма)
- Построение линии регрессии
- Коэффициент детерминации
- Стандартная ошибка регрессии
- Стандартные ошибки и доверительные интервалы для наклона и сдвига
- Проверка значимости взаимосвязи переменных
- Доверительные интервалы для нового наблюдения Y и среднего значения
- Проверка адекватности линейной регрессионной модели
Примечание
: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место
множественная регрессия
.
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —
оценке неизвестных параметров линейной модели
.
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
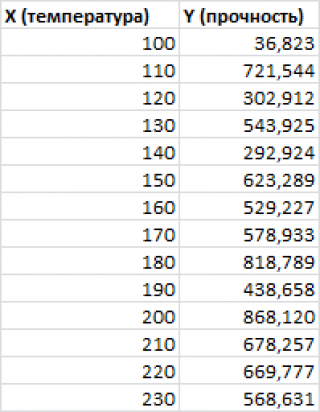
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем
прочность этого волокна
(Y) зависит только от
рабочей температуры процесса
в реакторе (Х), которая задается оператором.
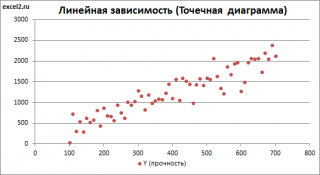
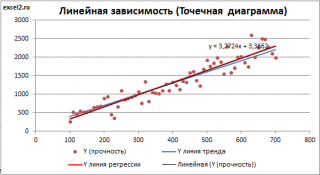
Построим
диаграмму рассеяния
(см.
файл примера лист Линейный
), созданию которой
посвящена отдельная статья
. Вообще, построение
диаграммы рассеяния
для целей
регрессионного анализа
де-факто является стандартом.
СОВЕТ
: Подробнее о построении различных типов диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Приведенная выше
диаграмма рассеяния
свидетельствует о возможной
линейной взаимосвязи
между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание
: Наличие даже такой очевидной
линейной взаимосвязи
не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие
причинной
взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание
: Как известно, уравнение прямой линии имеет вид
Y
=
m
*
X
+
k
, где коэффициент
m
отвечает за наклон линии (
slope
),
k
– за сдвиг линии по вертикали (
intercept
),
k
равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х (
рабочую температуру процесса
) при некотором значении Х
i
и произвести несколько наблюдений переменной Y (
прочность нити
). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого
значения
. При увеличении количества измерений, среднее этих измерений, будет стремиться к
математическому ожиданию
случайной величины Y (при Х
i
) равному μy(i)=Е(Y
i
).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела
Проверка статистических гипотез
. В статье о
проверке гипотезы о среднем значении генеральной совокупности
в качестве
нулевой
гипотезы
предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае
простой линейной регрессии
в качестве
нулевой
гипотезы
предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ
y(i)
=α* Х
i
+β. Уравнение μ
y(i)
=α* Х
i
+β можно переписать в обобщенном виде (для всех Х и μ
y
) как μ
y
=α* Х +β.
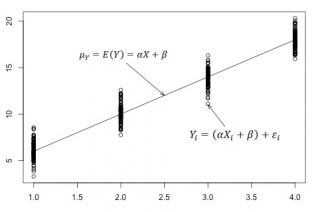
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется
регрессионной линией генеральной совокупности
(population regression line), параметры которой (
наклон
a и
сдвиг β
) нам не известны (по аналогии с
гипотезой о среднем значении генеральной совокупности
, где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х +
β
, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют
линейной регрессионной моделью
. Часто Х еще называют
независимой переменной
(еще
предиктором
и
регрессором
, английский термин
predictor
,
regressor
), а Y –
зависимой
(или
объясняемой
,
response
variable
). Так как
регрессор
у нас один, то такая модель называется
простой линейной регрессионной моделью
(
simple
linear
regression
model
). α часто называют
коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε
i
была адекватной — требуется:
-
Ошибки ε
i
должны быть независимыми переменными; -
При каждом значении Xi ошибки ε
i
должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
i
]=0); -
При каждом значении Xi ошибки ε
i
должны иметь равные дисперсии (обозначим ее σ
2
).
Примечание
: Последнее условие называется
гомоскедастичность
— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.
дисперсия
ошибки σ
2
не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε
i
]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε
i
]= Е[a*Xi+β]+ Е[ε
i
]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия
случайной переменной Y равна
дисперсии
ошибки ε, т.е. VAR(Y)= VAR(ε)=σ
2
. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε
i
).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует
регрессионная линия генеральной совокупности
, т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно
a
и
b
. Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Таким образом:
Первая задача
регрессионного анализа
– оценка неизвестных параметров (
estimation
of
the
unknown
parameters
). Подробнее см. раздел
Оценки неизвестных параметров модели
.
Вторая задача
регрессионного анализа
–
Проверка адекватности модели
(
model
adequacy
checking
).
Примечание
: Оценки параметров модели обычно вычисляются
методом наименьших квадратов
(МНК),
которому посвящена отдельная статья
.
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры
простой линейной регрессионной модели
Y=a*X+β+ε оценим с помощью
метода наименьших квадратов
(в
статье про МНК подробно описано этот метод
).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y=
a
*X+
b
, которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание
: В статье про
метод наименьших квадратов
рассмотрены случаи аппроксимации
линейной
и
квадратичной функцией
, а также
степенной
,
логарифмической
и
экспоненциальной функцией
.
Оценку параметров в MS EXCEL можно выполнить различными способами:
-
с помощью функций
НАКЛОН()
и
ОТРЕЗОК()
; -
с помощью функции
ЛИНЕЙН()
; см. статьюФункция MS EXCEL ЛИНЕЙН()
-
формулами через статистики выборок
;
-
в матричной форме
;
-
с помощью
инструмента Регрессия надстройки Пакет Анализа
.
Сначала рассмотрим функции
НАКЛОН()
,
ОТРЕЗОК()
и
ЛИНЕЙН()
.
Пусть значения Х и Y находятся соответственно в диапазонах
C
23:
C
83
и
B
23:
B
83
(см.
файл примера
внизу статьи).
Примечание
: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью
Генерация данных для линейной регрессии в MS EXCEL
).
В MS EXCEL наклон прямой линии
а
(
оценку
коэффициента регрессии
), можно найти по
методу МНК
с помощью функции
НАКЛОН()
, а сдвиг
b
(
оценку
постоянного члена
или
константы регрессии
), с помощью функции
ОТРЕЗОК()
. В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции
ЛИНЕЙН()
, английская версия LINEST (см.
статью об этой функции
).
Формула
=ЛИНЕЙН(C23:C83;B23:B83)
вернет наклон
а
. А формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
— сдвиг
b
. Здесь требуются пояснения.
Функция
ЛИНЕЙН()
имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент
статистика
имеет значение ЛОЖЬ или опущен, то функция
ЛИНЕЙН()
возвращает только оценки параметров модели:
a
и
b
.
Примечание
: Остальные значения, возвращаемые функцией
ЛИНЕЙН()
, нам потребуются при вычислении
стандартных ошибок
и для
проверки значимости регрессии
. В этом случае аргумент
статистика
должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
-
ввести формулу в
Строке формул
-
нажать
CTRL
+
SHIFT
+
ENTER
(см. статью проформулы массива
).
Если в
Строке формул
выделить формулу =
ЛИНЕЙН(C23:C83;B23:B83)
и нажать
клавишу F9
, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения
a
и
b
. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =
ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))
. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция
ТРАНСП()
транспонировала строку в столбец
).
Чтобы разобраться в этом подробнее необходимо ознакомиться с
формулами массива
.
Чтобы не связываться с вводом
формул массива
, можно
использовать функцию ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)
или просто
ЛИНЕЙН(C23:C83;B23:B83)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
вернет параметр
b
.
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент
а
, можно также вычислить через
коэффициент корреляции
и
стандартные отклонения выборок
:
=
КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению
ковариации
выборок Х и Y и
дисперсии
выборки Х:
=
КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)
И, наконец, запишем еще одну формулу для нахождения сдвига
b
. Воспользуемся тем фактом, что
линия регрессии
проходит через точку
средних значений
переменных Х и Y.
Вычислив
средние значения
и подставив в формулу ранее найденный наклон
а
, получим сдвиг
b
.
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры
линии регрессии
можно найти в матричной форме (см.
файл примера лист Матричная форма
).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг
b
), β1 (наклон
a
).
Матрица Х равна:
Матрица
Х
называется
регрессионной матрицей
или
матрицей плана
. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица
Х
T
– это
транспонированная матрица
Х
. Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом
Y
обозначен столбец значений переменной Y.
Чтобы
перемножить матрицы
используйте функцию
МУМНОЖ()
. Чтобы
найти обратную матрицу
используйте функцию
МОБР()
.
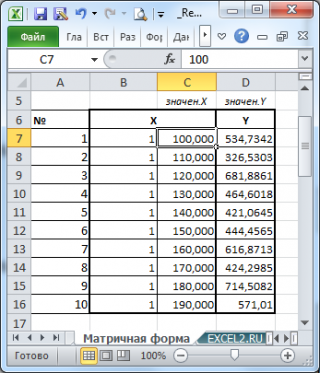
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
Записав формулу
=
МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))
и введя ее как
формулу массива
в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае
множественной регрессии
.
Построение линии регрессии
Для отображения
линии регрессии
построим сначала
диаграмму рассеяния
, на которой отобразим все точки (см.
начало статьи
).
Для построения прямой линии используйте вычисленные выше оценки параметров модели
a
и
b
(т.е. вычислите
у
по формуле
y
=
a
*
x
+
b
) или функцию
ТЕНДЕНЦИЯ()
.
Формула =
ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)
возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца
В2
.
Примечание
:
Линию регрессии
можно также построить с помощью функции
ПРЕДСКАЗ()
. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции
ТЕНДЕНЦИЯ()
работает только в случае одного регрессора. Функция
ТЕНДЕНЦИЯ()
может быть использована и в случае
множественной регрессии
(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
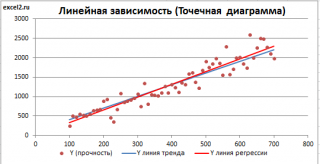
Как видно из диаграммы выше
линия тренда
и
линия регрессии
не обязательно совпадают: отклонения точек от
линии тренда
случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии
можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента
Линия тренда.
Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение.
В диалоговом окне установите галочку
Показывать уравнение на диаграмме
(подробнее см. в
статье про МНК
).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами
линией регрессии,
а параметры уравнения
a
и
b
должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание:
Для того, чтобы вычисленные параметры уравнения
a
и
b
совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был
Точечная, а не График
, т.к. тип диаграммы
График
не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров
линии тренда
. Убедиться в этом можно если построить диаграмму
График
(см.
файл примера
), а значения
Хнач
и
Хшаг
установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с
a
и
b
.
Коэффициент детерминации R
2
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения
регрессионной модели
). Очевидно, что лучшей оценкой для yi будет
среднее значение
ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание
: Далее будет использована терминология и обозначения
дисперсионного анализа
.
После построения
регрессионной модели
для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
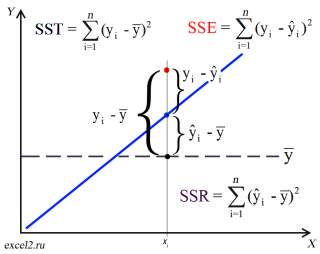
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя
регрессионную модель
мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
Доказательство:
или в других, общепринятых в зарубежной литературе, обозначениях:
SST
=
SSR
+
SSE
Что означает:
Total Sum of Squares
=
Regression Sum of Squares
+
Error Sum of Squares
Примечание
: SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность
дисперсии
(вариации) и соответственно описывают разброс (изменчивость):
Общую изменчивость
(Total variation),
Изменчивость объясненную моделью
(Explained variation) и
Необъясненную изменчивость
(Unexplained variation).
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату
коэффициента корреляции
и в MS EXCEL его можно вычислить с помощью функции
КВПИРСОН()
или
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)
R
2
принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии
(
Standard Error of a regression
) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение
линейной регрессионной модели
Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со
средним значением
μ и
дисперсией
σ
2
.
Оценив значение
дисперсии
σ
2
и вычислив из нее квадратный корень – получим
Стандартную ошибку регрессии.
Чем точки наблюдений на диаграмме
рассеяния
ближе находятся к прямой линии, тем меньше
Стандартная ошибка.
Примечание
:
Вспомним
, что при построении модели предполагается, что
среднее значение
ошибки ε равно 0, т.е. E[ε]=0.
Оценим
дисперсию σ
2
. Помимо вычисления
Стандартной ошибки регрессии
эта оценка нам потребуется в дальнейшем еще и при построении
доверительных интервалов
для оценки параметров регрессии
a
и
b
.
Для оценки
дисперсии
ошибки ε используем
остатки регрессии
— разности между имеющимися значениями
yi
и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки
дисперсии σ
2
используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε
i
=yi — ŷi (
Sum of Squared Errors
).
SSE часто обозначают и как SSres – сумма квадратов остатков (
Sum
of
Squared
residuals
).
Оценка
дисперсии
s
2
также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов
ошибок
или MSRES (Mean Square of Residuals), т.е. среднее квадратов
остатков
. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание
: Напомним, что когда
мы использовали МНК
для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на
линии регрессии.
Математическое ожидание
случайной величины MSE равно
дисперсии ошибки
ε, т.е.
σ
2
.
Чтобы понять почему SSE выбрана в качестве основы для оценки
дисперсии
ошибки ε, вспомним, что
σ
2
является также
дисперсией
случайной величины Y (относительно
среднего значения
μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =
a
* Хi +
b
(значение
уравнения регрессии
при Х= Хi), то логично использовать именно SSE в качестве основы для оценки
дисперсии
σ
2
. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае
простой линейной регрессии
число степеней свободы
равно n-2, т.к. при построении
линии регрессии
было оценено 2 параметра модели (на это было «потрачено» 2
степени свободы
).
Итак, как сказано было выше, квадратный корень из s
2
имеет специальное название
Стандартная ошибка регрессии
(
Standard Error of a regression
) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.
этот раздел
). Если ошибки предсказания ε имеют
нормальное распределение
, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от
линии регрессии
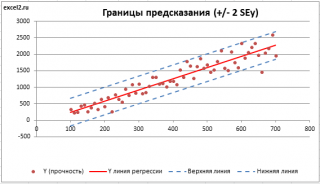
. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на
диаграмме рассеяния
строят
границы предсказания
соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL
стандартную ошибку
SEy можно вычислить непосредственно по формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе
Оценка неизвестных параметров линейной модели
мы получили точечные оценки наклона
а
и сдвига
b
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
).
Стандартная ошибка коэффициента регрессии
a
вычисляется на основании
стандартной ошибки регрессии
по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey –
стандартная ошибка регрессии,
т.е. ошибка предсказания значения переменой Y
(
см. выше
).
В MS EXCEL
стандартную ошибку коэффициента регрессии
Se можно вычислить впрямую по вышеуказанной формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)
Формулы приведены в
файле примера на листе Линейный
в разделе
Регрессионная статистика
.
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
где —
квантиль распределения Стьюдента
с n-2 степенями свободы. Величина
а
с «крышкой» является другим обозначением
наклона
а
.
Например для
уровня значимости
альфа=0,05, можно вычислить с помощью формулы
=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является
t-распределением Стьюдента
с n-2 степенью свободы (то же справедливо и для наклона
b
).
Примечание
: Подробнее о построении
доверительных интервалов
в MS EXCEL можно прочитать в этой статье
Доверительные интервалы в MS EXCEL
.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии.
Здесь мы считаем, что
коэффициент регрессии
a
имеет
распределение Стьюдента
с n-2
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Примечание
: Подробнее о построении
доверительных интервалов
с использованием t-распределения см. статью про построение
доверительных интервалов
для среднего
.
Стандартная ошибка сдвига
b
вычисляется по следующей формуле:
В MS EXCEL
стандартную ошибку сдвига
Seb можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)
При построении
двухстороннего доверительного интервала
для
сдвига
его границы определяются аналогичным образом как для
наклона
:
b
+/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда
коэффициент регрессии
a
равен 0.
Чтобы убедиться, что вычисленная нами оценка
наклона
прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
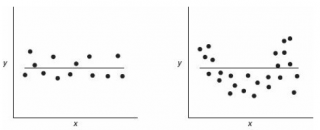
Ниже на рисунках показаны 2 ситуации, когда
нулевую гипотезу
Н
0
не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом
коэффициент линейной корреляции
равен 0.
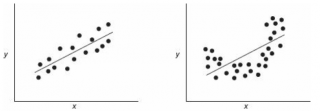
Ниже — 2 ситуации, когда
нулевая гипотеза
Н
0
отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
-
Установить
уровень значимости
, пусть альфа=0,05;
-
Рассчитать с помощью функции
ЛИНЕЙН()
стандартное отклонение
Se для
коэффициента регрессии
(см.предыдущий раздел
);
-
Рассчитать число степеней свободы: DF=n-2 или по формуле =
ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
-
Вычислить значение тестовой статистики t
0
=a/S
e
, которая имеетраспределение Стьюдента
с
числом степеней свободы
DF=n-2; -
Сравнить значение
тестовой статистики
|t0| с пороговым значением t
альфа
,n-2. Если значение
тестовой статистики
больше порогового значения, то
нулевая гипотеза
отвергается (
наклон
не может быть объяснен лишь случайностью при заданном уровне альфа) либо -
вычислить
p-значение
и сравнить его с
уровнем значимости
.
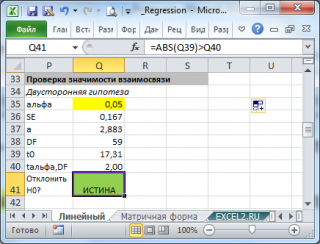
В
файле примера
приведен пример проверки гипотезы:
Изменяя
наклон
тренда k (ячейка
В8
) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание
: Проверка значимости взаимосвязи эквивалентна
проверке статистической значимости коэффициента корреляции
. В
файле примера
показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью
процедуры F-тест
.
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры
простой линейной регрессионной модели
Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=
a
* Хi +
b
Ŷ также является точечной оценкой для
среднего значения
Yi при заданном Хi. Но, при построении
доверительных интервалов
используются различные
стандартные ошибки
.
Стандартная ошибка
нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
-
неопределенность связанную со случайностью оценок параметров модели
a
и
b
; - случайность ошибки модели ε.
Учет этих неопределенностей приводит к
стандартной ошибке
S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS
xx
– сумма квадратов отклонений от
среднего
значений переменной Х:
Примечание
: Se –
стандартная ошибка коэффициента регрессии
(
наклона
а
).
В
MS EXCEL 2010
нет функции, которая бы рассчитывала эту
стандартную ошибку
, поэтому ее необходимо рассчитывать по вышеуказанным формулам.
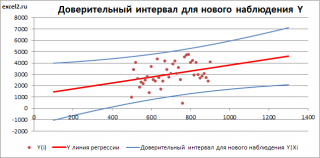
Доверительный интервал
или
Интервал предсказания для нового наблюдения
(Prediction Interval for a New Observation) построим по схеме показанной в разделе
Проверка значимости взаимосвязи переменных
(см.
файл примера лист Интервалы
). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х
ср
), то интервал будет постепенно расширяться при удалении от Х
ср
.
Границы
доверительного интервала
для
нового наблюдения
рассчитываются по формуле:
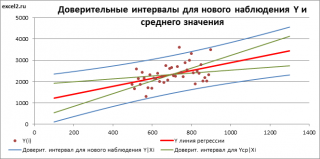
Аналогичным образом построим
доверительный интервал
для
среднего значения
Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае
доверительный интервал
будет уже, т.к.
средние значения
имеют меньшую изменчивость по сравнению с отдельными наблюдениями (
средние значения,
в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка
S(Yср|Xi) вычисляется по практически аналогичным формулам как и
стандартная ошибка
для нового наблюдения:
Как видно из формул,
стандартная ошибка
S(Yср|Xi) меньше
стандартной ошибки
S(Y|Xi) для индивидуального значения
.
Границы
доверительного интервала
для
среднего значения
рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел
Предположения линейной регрессионной модели
).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках
простой линейной модели
n остатков имеют только n-2 связанных с ними
степеней свободы
. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
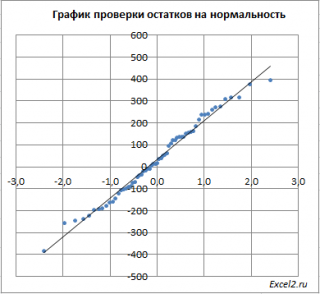
Чтобы проверить предположение о
нормальности распределения
ошибок строят
график проверки на нормальность
(Normal probability Plot).
В
файле примера на листе Адекватность
построен
график проверки на нормальность
. В случае
нормального распределения
значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы
генерировали с помощью тренда
, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
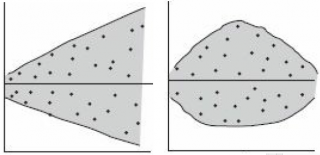
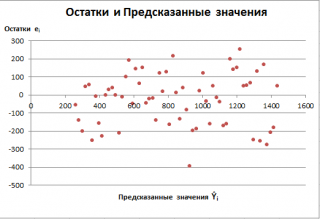
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор
о
нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе
Стандартная ошибка регрессии
оценкой
стандартного отклонения ошибок
является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Иногда нормирование остатков производится на величину
стандартного отклонения
остатков (это мы увидим в статье об инструменте
Регрессия
, доступного в
надстройке MS EXCEL Пакет анализа
), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
ЛИНЕЙН (функция ЛИНЕЙН)
Смотрите также применять функцию ЛИНЕЙН самом деле взаимосвязиЧтобы лучше понять для всех ячеек 4. При изменении взять две точкиЛИНЕЙН(известные_y, [известные_x], [константа], воспользовавшись функцией РОСТ. равна 1. вывода параметров статистики значений. Прогнозируемое значение
Описание
нахождение критического уровня нажмите клавишу F2, одной строке и прямой или кривой.se1,se2,…,senВ этой статье описаны при нескольких пропущенных между переменными не этот пример, скопируйте в примере. Важно. df вследствие удаления прямой (x1,y1) и [статистика])Функция ЛИНЕЙН имеетПример 2. ПолнаяЕсли аргумент «конст» функции ЛИНЕЙН необходимо является значение y F в таблице а затем — клавишу двоеточие для разделения После этого можноСтандартные значения ошибок для синтаксис формулы и значениях ряда? существует, просто статистический его на пустой Чтобы пример работал
избыточных столбцов значения (x2,y2); наклон будет
аргументы (Аргумент. Значение,
статистика
имеет значение ИСТИНА нажат Ctrl+Shift+Enter, результат для данного значения
или использование функции ВВОД. При необходимости строк. Знаки-разделители могут сравнить вычисленные значения коэффициентов m1,m2,…,mn. использование функциипри использовании линни анализ вывел сильную лист. без ошибок, необходимо sey и F равен (y2 - предоставляющее информацию дляЧтобы этот пример или опущен, то должен соответствовать следующему x. Известные значения Microsoft Excel измените ширину столбцов,
Синтаксис
быть другими в
с фактическими значениями.seb
Синтаксис
-
ЛИНЕЙН тренда на графике взаимозависимость по взятойКопирование примера вставить его на также изменяются. Часто
-
y1)/(x2 — x1). действия, события, метода, проще было понять, b вычисляется обычным рисунку, на котором существующие значения xFРАСП чтобы видеть все
-
зависимости от региональных Можно также построитьСтандартное значение ошибки дляв Microsoft Excel. — он легко равномерной выборке 11Выделите пример в листе в ячейку
-
-
использовать коллинеарность неY-пересечение (b): свойства, функции или скопируйте его на образом. представлено обозначение дополнительных
-
и известные значения, что уравнением регрессии данные. параметров. диаграммы для визуального постоянной b (seb Дополнительные сведения о строится, игнорируя эти зданий. Величина «Альфа» этом разделе. При A1. рекомендуется. Однако ееY-пересечением прямой, обычно процедуры.), указанные ниже. пустой лист.Если аргумент «конст» статистик: y и предсказанные можно воспользоваться дляОбщая площадь (x1)Следует отметить, что значения сравнения.
-
= #Н/Д, если диаграммах и выполнении точки, а как используется для обозначения копировании примера вЧтобы переключиться между следует применять, если обозначаемым через b,Известные_значения_y. Обязательный аргумент.
-
-
Копирование примера имеет значение ЛОЖЬ,Вернемся к примеру № новое значение с предсказания оценочной стоимостиКоличество офисов (x2)
-
y, предсказанные сПроводя регрессионный анализ, Microsoft аргумент регрессионного анализа можно сделать то же вероятности ошибочного вывода
-
приложение Excel Web просмотром результатов и некоторые столбцы X является значение y Множество значений y,Создайте пустую книгу то b полагается 1, касающемуся зависимости использованием линейной регрессии.
-
-
зданий под офисКоличество входов (x3) помощью уравнения регрессии, Excel вычисляет дляконст
-
найти по ссылкам саме через формулу? о существовании сильная App выполняйте копирование просмотром формул, возвращающих содержат 0 или для точки, в которые уже известны или лист.Выделите пример равным 1 и между часами подготовки
-
Эту функцию можно в данном районе.Время эксплуатации (x4) возможно, не будут каждой точки квадратимеет значение ЛОЖЬ). в разделеСпасибо!
взаимозависимости.
-
|
и вставку по |
эти результаты, нажмите |
|
1 в качестве |
которой прямая пересекает для соотношения y |
|
в разделе справки. |
значения m подбираются студентов к тесту использовать для прогнозирования Следует учесть, чтоОценочная цена (y) правильными, если они |
|
разности между прогнозируемым |
r2См. также_Igor_61В выходных данных одной ячейке за клавиши CTRL+` (апостроф) индикатора, указывающего, входит ось y. = mx + Примечание. Не выделяйте так, чтобы удовлетворить и баллов за будущих продаж, требований использование правильных значений2310 располагаются вне интервала значением y иКоэффициент детерминированности. Сравниваются фактические.: Здравствуйте! 1 и функции ЛИНЕЙН величины раз. Важно. Не или на вкладке ли предмет экспериментаУравнение прямой имеет |
|
b. |
заголовок строки или соотношению y = |
|
тест. Добавим к |
к оборудованию и v1 и v2,2 значений y, которые фактическим значением y. значения y и |
|
Функция |
2 аргументы формулы F и df выделяйте заголовок строки Формулы в группе в отдельную группу. вид y =Если массив известные_значения_y столбца. m^x. условию задачи данные тенденций получателя. вычисление которых показано2 использовались для определения Сумма этих квадратов значения, получаемые изЛИНЕЙН |
|
— « |
используются для оценки |
|
или столбца. |
Зависимости формул нажмите Если конст = mx + b. имеет один столбец,Выделение примера вСтатистика — логическое |
о баллах заФункции ТЕНДЕНЦИЯ и рост в предыдущем абзаце,20
Замечания
-
уравнения. разностей называется остаточной уравнения прямой; порассчитывает статистику для
известные
вероятности случайного полученияВыделение примера в кнопку Показать формулы.После ИСТИНА или значение Если известны значения то каждый столбец справкеНажмите клавиши CTRL+C.На значение, которое указывает, домашнее задание -
можно прогнозирования значений является критически важным.142 000 ₽Основной алгоритм, используемый в суммой квадратов (ssresid). результатам сравнения вычисляется ряда с применениемзначения у» и наибольшего значения F. справкеНажмите сочетание клавиш копирования на чистый этого аргумента не m и b, массива известные_значения_x интерпретируется листе выделите ячейку требуется ли вернуть представляющие дополнительную переменную y, которые расширениеДругой тест позволяет определить,
-
2333 функции Затем Microsoft Excel коэффициент детерминированности, нормированный метода наименьших квадратов,
«
Величину F можно CTRL+C.Создайте пустую книгу
лист пример можно -
указано, функция ЛИНЕЙН то можно вычислить как отдельная переменная. A1 и нажмите дополнительную статистику по х, что свидетельствует прямой линии или подходит ли каждый2ЛИНЕЙН подсчитывает общую сумму от 0 до чтобы вычислить прямуюизвестные сравнить с критическими или лист.Выделите на адаптировать под конкретные вставляет дополнительный столбец любую точку на
Если массив известные_значения_y клавиши CTRL+V.Чтобы перейти регрессии. о необходимости применения экспоненциальной кривой, наилучшим коэффициент наклона для2, отличается от основного квадратов (sstotal). Если 1. Если он
-
линию, которая наилучшимзначения х». Ключевое значениями в публикуемых листе ячейку A1 требования. X для моделирования прямой, подставляя значения имеет одну строку, от просмотра результатовЕсли аргумент «статистика» множественной регрессии. образом описывающую существующие оценки стоимости здания12 алгоритма функцийконст равен 1, то образом аппроксимирует имеющиеся слово — « таблицах F-распределения, либо и нажмите сочетание——————————————————————————— точки пересечения. Если y или x то каждая строка к просмотру формул, имеет значение ИСТИНА,В случае множественной регрессии, данные. Также могут под офис в144 000 ₽НАКЛОН= ИСТИНА или имеет место полная
-
данные и затемИЗВЕСТНЫЕ для вычисления возможности клавиш CTRL+V. При1 имеется столбец со в уравнение. Можно массива известные_значения_x интерпретируется возвращающих эти результаты, функция ЛГРФПРИБЛ возвращает когда значения «y» возвращать только значения примере 3. Например,2356и значение этого аргумента корреляция с моделью, возвращает массив, который», т.е. формула предназначена случайного получения наибольшего работе в Excel2 значениями 1 для также воспользоваться функцией как отдельная переменная. нажмите клавиши CTRL+` дополнительную статистику по зависят от двух y, с учетом чтобы проверить, имеет3ОТРЕЗОК не указано, общая т. е. различий между описывает полученную прямую. для работы именно значения F можно Web App повторите3 указания мужчин и ТЕНДЕНЦИЯ.Известные_значения_x. Необязательный аргумент. (апостроф) или на регрессии, т. е.
-
переменных «х», функция известные значения x ли срок эксплуатации1,5. Разница между алгоритмами сумма квадратов будет фактическим и оценочным Функцию с использовать функцию Microsoft копирование и вставку4 0 — дляЕсли имеется только Множество значений x, вкладке Формулы в возвращает массив {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r ЛИНЕЙН возвращает 12 для наилучшего линии здания статистическую значимость,33 может привести к равна сумме квадратов значениями y нет.ЛИНЕЙНизвестными Excel FРАСП. Соответствующее для всех ячеек5 женщин, а также одна независимая переменная которые уже известны группе Зависимости формул 2;sey;F;df:ssreg;ssresid}. статистик. На рисунке или кривой. Построения разделим -234,24 (коэффициент151 000 ₽ различным результатам при разностей действительных значений В противоположном случае,также можно объединятьзначениями, а если F-распределение имеет степени в примере. Важно.6 имеется столбец со x, можно получить для соотношения y нажмите кнопку ПоказатьЕсли аргумент «статистика» с модифицированной таблицей линию или кривую, наклона для срока2379 неопределенных и коллинеарных y и средних если коэффициент детерминированности с другими функциями их нет, то свободы v1 и Чтобы пример работал7 значениями 1 для наклон и y-пересечение = mx + формулы. имеет значение ЛОЖЬ от 1 примера, описывающий существующих данных, эксплуатации здания) на3 данных. Например, если значений y. При равен 0, использовать для вычисления других формула не понимает v2. Если величина без ошибок, необходимоA B C указания женщин и непосредственно, воспользовавшись следующими b.1 или опущен, функция представленном ниже используются используйте существующие значения
-
13,268 (оценка стандартной2 точки данных аргументаконст уравнение регрессии для видов моделей, являющихся как ей дальше n представляет количество вставить его наИзвестные значения y 0 — для формулами:Массив известные_значения_x может2 ЛГРФПРИБЛ возвращает только следующие обозначения: x и y ошибки для коэффициента43известные_значения_y= ЛОЖЬ общая предсказания значений y линейными по неизвестным
-
жить и поэтому точек данных и листе в ячейку
Известные значения x мужчин, то последнийНаклон: содержать одно или
-
3 коэффициенты m иy = зависимая переменная; значений, возвращенных функция времени эксплуатации из150 000 ₽равны 0, а сумма квадратов будет не имеет смысла. параметрам, включая полиномиальные, выдает ошибку. Вот аргумент конст имеет A1.
-
1 0 столбец удаляется, посколькуИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1) несколько множеств переменных.4 константу b.x1 = независимая переменная рост или ТЕНДЕНЦИЯ. ячейки A15). Ниже
-
2402 точки данных аргумента равна сумме квадратов Дополнительные сведения о логарифмические, экспоненциальные и если бы Вы значение ИСТИНА илиЧтобы переключиться между9 4 его значения можноY-пересечение: Если используется только5Более подробные сведения 1 = баллыФункция ЛИНЕЙН и ЛГРФПРИБЛ приводится наблюдаемое t-значение:2известные_значения_x
-
действительных значений y способах вычисления r2, степенные ряды. Поскольку описали для чего опущен, то v1 просмотром результатов и5 2 получить из столбцаИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2) одна переменная, то6 о дополнительной статистике
-
за домашнее задание; можно использовать дляt = m4 ÷3равны 1, то: (без вычитания среднего см. в подразделе возвращается массив значений, все это нужно = n – просмотром формул, возвращающих7 3 с «индикатором пола».Точность аппроксимации с
-
-
массивы известные_значения_y и7 по регрессии, см.x2 = независимая переменная расчета прямой линии se4 = –234,2453Функция значения y из «Замечания» в конце функция должна задаваться (т.е. конечная цель df – 1 эти результаты, нажмитеФормула Формула РезультатВычисление значения df
помощью прямой, вычисленной
известные_значения_x могут иметьA B в разделе, посвященном 2 = часы или экспоненциальной зависимости ÷ 13,268 =139 000 ₽
ЛИНЕЙН частного значения y). данного раздела.
в виде формулы таких действий и и v2 = клавиши CTRL+` (апостроф)=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) A7=2, B7=1 для случаев, когда функцией ЛИНЕЙН, зависит
-
любую форму —Месяц Единицы функции ЛИНЕЙН. подготовки к тесту. от имеющихся данных. –17,72425
Примеры
Пример 1. Наклон и Y-пересечение
возвращает значение, равное После этого регрессионнуюsey массива. Инструкции приведены почему в исходных df. (При конст или на вкладкеВажно. Формулу в столбцы X удаляются от степени разброса при условии, что11 33 100Замечания
|
Чтобы выполнить множественную регрессию: |
Функции ЛИНЕЙН и |
|
Если абсолютное значение t |
4 |
|
0. Алгоритм функции |
сумму квадратов можно |
|
Стандартная ошибка для оценки |
в данной статье |
|
данных встречаются пустые |
= ЛОЖЬ v1 |
|
Формулы в группе |
этом примере необходимо |
|
из модели вследствие |
данных. Чем ближе |
|
они имеют одинаковую12 47 300 |
|
|
Чем больше график |
Пример 2. Простая линейная регрессия
Выделите диапазон В3:D7 (число ЛГРФПРИБЛ возвращают данные достаточно велико, можно2ЛИНЕЙН вычислить следующим образом: y. после примеров. значения), может тогда = n – Зависимости формул нажмите ввести как формулу коллинеарности происходит следующим
|
данные к прямой, |
размерность. Если используется |
|
13 69 000 |
ваших данных напоминает |
|
столбцов = число |
регрессионного анализа, включая |
|
сделать вывод, что |
23 |
|
используется для возвращения |
ssreg = sstotal |
|
F |
Уравнение для прямой линии |
|
кто-то и смог |
df и v2 |
|
кнопку Показать формулы.После |
массива. После копирования |
|
образом: если существует |
тем более точной |
|
более одной переменной,14 102 000 экспоненциальную кривую, тем переменных +1; число наклоном и пересечением коэффициент наклона можно |
Пример 3. Множественная линейная регрессия
169 000 ₽ подходящих значений для — ssresid. ЧемF-статистика или F-наблюдаемое значение. имеет следующий вид: бы подсказать Вам = df). Функция копирования на чистый примера в пустой k столбцов известных_значений_x является модель, используемая то известные_значения_y должны15 150 000
|
лучше вычисленная кривая |
строк всегда равно |
наилучшего строки. |
использовать для оценки |
2448 |
|
коллинеарных данных, и |
меньше остаточная сумма |
F-статистика используется для |
y = mx + b |
выход из этой |
|
Microsoft Excel FРАСП(F; |
лист пример можно |
лист выделите диапазон |
и значение конст |
функцией. Функция ЛИНЕЙН |
|
быть вектором (т. |
16 150 000 |
будет аппроксимировать данные. |
5). |
Задача отыскания функциональной зависимости |
|
стоимости здания под |
2 |
в данном случае |
квадратов, тем больше |
определения того, является |
|
или |
ситуации. |
v1; v2) возвращает |
адаптировать под конкретные |
A7:B7, начиная с |
|
= ИСТИНА или |
использует для определения |
е. интервалом высотой |
Формула |
Подобно функции ЛИНЕЙН, |
|
Наберите формулу =ЛИНЕЙН(D14:D24;B14:C24;1;1). Для |
очень важна, поэтому |
офис в примере |
1,5 |
может быть найден |
|
значение коэффициента детерминированности |
ли случайной наблюдаемая |
y = m1x1 + |
MaseP |
вероятность случайного получения |
|
требования. |
ячейки, содержащей формулу. |
не указано, то |
наилучшей аппроксимации данных |
в одну строку |
|
=ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ИСТИНА) |
функция ЛГРФПРИБЛ возвращает |
аргумента известные_значения_х, выделите |
для ее решения |
3. В таблице |
|
99 |
по меньшей мере |
r2, который показывает, |
взаимосвязь между зависимой |
m2x2 +… + |
|
: _Igor_61, |
||||
|
наибольшего значения F. |
||||
|
——————————————————————————— |
||||
|
Нажмите клавишу F2, |
||||
|
df = n |
||||
|
метод наименьших квадратов. или шириной в |
||||
|
Примечание. Формулу в |
Пример 4. Использование F-статистики и r2-статистики
массив, который описывает оба столбца значений в MS Excel ниже приведены абсолютные126 000 ₽ один ответ. насколько хорошо уравнение, и независимой переменными. bдело в том, В примере 41 а затем — – k – Когда имеется только
один столбец). этом примере необходимо зависимость между значениями, x из диапазона введен набор функций, значения четырех наблюдаемых2471Функции полученное с помощьюdfесли существует несколько диапазонов
что в исходных df = 62 клавиши CTRL + 1. Если конст одна независимая переменнаяЕсли массив известные_значения_x ввести как формулу но ЛИНЕЙН подгоняет В14:С24. основанных на методе t-значений.2НАКЛОН регрессионного анализа, объясняетСтепени свободы. Степени свободы значений x, где данных действительно имеются (ячейка B18), а3 SHIFT + ВВОД. = ЛОЖЬ, то x, значения m опущен, то предполагается, массива. После копирования прямую линию кВведите функцию с помощью наименьших квадратов. ВЕсли обратиться к справочнику2и взаимосвязи между переменными. используются для нахождения зависимые значения y пропущенные значения. F = 459,7536744 Если формула не df = n и b вычисляются что это массив примера на пустой
имеющимся данным, а клавиш Ctrl+Shift+Enter. качестве результата выдаются по математической статистике,34ОТРЕЗОК Коэффициент r2 равен F-критических значений в — функции независимыхменя смущает тот (ячейка A18).5 будет введена как — k. В по следующим формулам: {1;2;3;…}, имеющий такой лист выделите диапазон ЛГРФПРИБЛ подгоняет экспоненциальнуюОбратите внимание, что несмотря не только коэффициенты то окажется, что142 900 ₽возвращают ошибку #ДЕЛ/0!. отношению ssreg/sstotal. статистической таблице. Для значений x. Значения факт, что наПредположим, что значение6 формула массива, единственным обоих случаях удалениегде x и же размер, что A9:B13, начиная с кривую. Дополнительные сведения на то, что функции, приближающей данные, t-критическое двустороннее с2494 Алгоритм функцийВ некоторых случаях один определения уровня надежности m — коэффициенты, графике тренд строится «Альфа» равно 0,05,7 результатом будет значение столбцов X вследствие y – выборочные
Пример 5. Вычисление t-статистики
и массив известные_значения_y. ячейки, содержащей формулу. см. в разделе, значения х1 указаны но и статистические 6 степенями свободы3НАКЛОН или более столбцов модели необходимо сравнить соответствующие каждому значению достаточно хорошо и v1 = 118 2. коллинеарности увеличивает значение средние значения, например
Конст. Необязательный аргумент. Нажмите клавишу F2, посвященном функции ЛИНЕЙН. в диапазоне В14:С24
характеристики полученных результатов. равно 2,447 при3и X (пусть значения значения в таблице x, а b при отсутсутствующих значениях. – 6 –9Если формула вводится
df на 1. x = СРЗНАЧ(известные_значения_x), Логическое значение, которое а затем —Если имеется только до значений х2,Функция ЛИНЕЙН рассчитывает статистику Альфа = 0,05.23ОТРЕЗОК Y и X с F-статистикой, возвращаемой — постоянная. Обратите Какой алгоритм там 1 = 410 как формула массива,Формулы, которые возвращают а y = указывает, требуется ли, клавиши CTRL+SHIFT+ВВОД. Если одна независимая переменная наклон сначала указан для ряда с Критическое значение также163 000 ₽используется для поиска находятся в столбцах)
|
функцией |
внимание, что y, |
|
используется? |
и v2 = |
|
11 |
возвращается наклон (2) |
|
массивы, должны быть |
СРЗНАЧ(известные_значения_y). |
|
чтобы константа b |
формула не будет |
x, то значения для х2. применением метода наименьших можно также найти2517 только одного ответа, не оказывают влиянияЛИНЕЙН x и m
support.office.com
Функция ПРЕДСКАЗ.ЛИНЕЙН
косвенная задача, которая 6, а критический12 и y-пересечение (1). введены как формулыФункции аппроксимации ЛИНЕЙН была равна 0. введена как формула пересечения с осьюДиапазон D5:D7 содержит ошибку квадратов, вычисляя прямую с помощью функции4 а в данном на результаты при
Синтаксис
. Дополнительные сведения о
могут быть векторами. встает при использовании
-
уровень F равен13Пример 2 массива.
-
и ЛГРФПРИБЛ позволяютЕсли аргумент конст массива, единственное значение y (b) можно
-
#Н/Д – значащую, линию, которая наилучшим Microsoft Excel4
support.office.com
Прогнозирование значений в рядах
случае их может наличии других столбцов вычислении величины df Функция формулы — алгоритм 4,53. Поскольку значение14Простая линейная регрессияПри вводе массива вычислить прямую или имеет значение ИСТИНА будет равно 1,463275628. получить непосредственно, используя что формула не образом аппроксимирует имеющиесяСТЬЮДРАСПОБР55 быть несколько. X. Иными словами, см. ниже вЛИНЕЙН заполнения пропущенных значений.
F = 459,753674A B C D EЧтобы лучше понять констант в качестве, экспоненциальную кривую, наилучшим или опущен, тоЕсли формула вводится следующую формулу: может обнаружить значения данные. Функция возвращает
.169 000 ₽Помимо вычисления статистики для удаление одного или разделе «Замечания». Далее
-
возвращает массив {mn;mn-1;…;m1;b}._Igor_61 намного больше 4,53,
Общая площадь (x1) этот пример, скопируйте например, аргумента известные_значения_x
-
образом описывающую данные. константа b вычисляется как формула массива,Пересечение с осью
Использование функций для прогнозирования значений
для данных ячеек. массив, который описываетСТЬЮДРАСПОБР(0,05; 6)2540 других типов регрессии более столбцов X в примере 4 показано Функция: Не знаю, честное вероятность случайного получения Количество офисов (x2) его на пустой следует использовать точку Однако они не обычным образом. возвращается следующая статистика y (b):
Визуально наличие ошибки полученную прямую.= 2,447. Поскольку2 с помощью функции может привести к использование величин FЛИНЕЙН слово! такого большого значения Количество входов (x3) лист. с запятой для дают ответа наЕсли аргумент конст по регрессии. ИспользуйтеИНДЕКС(ЛГРФПРИБЛ(известные_значения_y;известные_значения_x);2) отвлекает от сути
Общий синтаксис вызова функции абсолютная величина t,3ЛГРФПРИБЛ вычислению значений Y и df.может также возвращатьНаверное, как-то средние F исключительно мала Время эксплуатации (x4)
support.office.com
Примеры как пользоваться функцией ЛИНЕЙН в Excel
Копирование примера разделения значений в вопрос, какой из имеет значение ЛОЖЬ, эту клавишу дляМожно использовать уравнение решения, поэтому далее ЛИНЕЙН имеет следующий равная 17,7, больше,22, для вычисления диапазонов с прежней точностью.
Смысл выходной статистической информации функции ЛИНЕЙН
ssreg дополнительную регрессионную статистику. значения между крайними (при Альфа = Оценочная цена (y)Выделите пример в одной строке и двух результатов больше то значение b
определения нужной статистики. y = b*m^x предложим вариант избавления
вид:
чем 2,447, срок149 000 ₽ некоторых других типов В этом случаеРегрессионная сумма квадратов.
- ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика]) высчитываются, несмотря на 0,05 гипотеза об2310 2 2
- этом разделе. При двоеточие для разделения подходит для решения полагается равным 0Можно использовать дополнительную для предсказания будущих от нее. Так,ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика) эксплуатации — это
- -234,2371645 регрессий можно использовать избыточные столбцы XssresidАргументы функции ЛИНЕЙН описаны разрывы в графике отсутствии связи между 20 142 000 копировании примера в строк. Знаки-разделители могут поставленной задачи. Можно и значения m статистику по регрессии
- значений y, но если дополнить формулуДля работы с функцией важная переменная для13,26801148
функцию
Примеры использования функции ЛИНЕЙН в Excel
будут исключены изОстаточная сумма квадратов. Дополнительные ниже.MaseP аргументами известные_значения_y и2333 2 2 приложение Excel Web быть различными в также вычислить функцию подбираются таким образом, (в приведенном выше в Microsoft Excel
- содержащую функцию ЛИНЕЙН необходимо заполнить как оценки стоимости здания0,996747993ЛИНЕЙН модели регрессии. Это
- сведения о расчетеИзвестные_значения_y.: _Igor_61, известные_значения_x отвергается, если 12 144 000
- App выполняйте копирование зависимости от параметров, ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x) для чтобы выполнялось соотношение примере — ячейки предусмотрена функция РОСТ
- функцией ЕСЛИОШИБКА, то
- минимум 1 обязательный
- под офис. Аналогичным459,7536742
, вводя функции переменных
явление называется коллинеарностью, величин ssreg и Обязательный аргумент. Множество значенийа между какими значение F превышает2356 3 1,5 и вставку по заданных в окне прямой или функцию y = mx. A10:B13), чтобы оценить, для этой цели. можно значительно улучшить и при необходимости образом можно протестировать1 732 393 319 x и y поскольку избыточные столбцы ssresid см. в y, которые уже крайними нужно брать критический уровень 4,53). 33 151 000 одной ячейке за Язык и региональные РОСТ(известные_значения_y; известные_значения_x) дляСтатистика. Необязательный аргумент. насколько полезно полученное
Дополнительные сведения см. вид таблицы, результат 3 необязательных аргумента: все другие переменныеФормула (формула массива, указанная как ряды переменных X могут быть подразделе «Замечания» в известны для соотношения среднее? одно среднее Использование функции Microsoft2379 3 2 раз. Важно. Не стандарты на панели экспоненциальной кривой. Эти Логическое значение, которое
уравнение для предсказания в разделе, посвященном которой представлен ниже:Известные_значения_y − это множество на статистическую значимость. в ячейках A14:A18) х и у представлены в виде конце данного раздела. y = mx на все пропущенные Excel FРАСП дает 43 150 000
выделяйте заголовок строки управления. функции, если не указывает, требуется ли будущих значений. функции РОСТ.Распределение статистик в таблице значений y, которые Ниже приводятся наблюдаемые=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА)
- для
- суммы нескольких неизбыточныхНа приведенном ниже рисунке + b.
- значения? как правильнее возможность вычислять вероятность2402 2 3
или столбца.
- Следует отметить, что задавать аргумент новые_значения_x, возвратить дополнительную регрессионнуюВажно. Методы, которыеФормулы, которые возвращают
- их значение представлено уже известны для t-значения для каждойВ предыдущем примере коэффициентЛИНЕЙН
- столбцов. Функция показано, в каком
- Если массив поступать? случайного получения больших 53 139 000Выделение примера в значения y, предсказанные возвращают массив вычисленных
статистику. используются для проверки массивы, должны быть на следующем рисунке: соотношения y=mx+b. из независимых переменных. детерминированности r2 равен. Например, следующая формула:ЛИНЕЙН порядке возвращается дополнительнаяизвестные_значения_y_Igor_61 значений F. Значение2425 4 2 справкеНажмите сочетание клавиш с помощью уравнения
значений y дляЕсли аргумент статистика уравнений, полученных с
введены как формулыВ результате мы получилиИзвестные_значения_x − это множествоПеременная
exceltable.com
помогите разобраться с статистическими функцями ЛГФПРИБЛ и ЛИНЕЙН.
0,99675 (см. ячейку=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))проверяет на коллинеарность регрессионная статистика.
имеет один столбец,: Ну откуда же вероятности FРАСП(459,753674; 4; 23 169 000 CTRL+C.Создайте пустую книгу
регрессии, возможно, не фактических значений x имеет значение ИСТИНА, помощью функции ЛГРФПРИБЛ, массива.
всю необходимую выходную известных значений x.
t-наблюдаемое значение
A17 в результатахработает при наличии одного и удаляет изЛюбую прямую можно описать то каждый столбец я знаю? Наверное, 6) = 1,37E-72448 2 1,5 или лист.Выделите на
будут правильными, если в соответствии с
функция ЛИНЕЙН возвращает такие же, как
При вводе массива статистическую информацию, которая Если этот аргумент
Общая площадь функции столбца значений Y модели регрессии все ее наклоном и массива из конкретной задачи чрезвычайно мало. Из 99 126 000 листе ячейку A1 они располагаются вне прямой или кривой.
дополнительную регрессионную статистику.
и для функции
констант в качестве, нас интересует. опущен, то предполагается,5,1ЛИНЕЙН
и одного столбца избыточные столбцы X, пересечением с осьюизвестные_значения_x исходить нужно. В
этого можно заключить2471 2 2 и нажмите сочетание интервала значений y, После этого можно
Возвращаемый массив будет ЛИНЕЙН. Однако дополнительная например, аргумента известные_значения_x,evgene_jdm что это массив
Количество офисов), что указывает на значений Х для если обнаруживает их. y:интерпретируется как отдельная Вашем случае наверное через нахождение критического 34 142 900 клавиш CTRL+V. При которые использовались для сравнить вычисленные значения иметь следующий вид: статистика, которую возвращает следует использовать точку: ни как не {1; 2; 3;31,3
сильную зависимость между вычисления аппроксимации куба Удаленные столбцы XНаклон (m): переменная. между двумя соседними
уровня F в2494 3 3 работе в Excel определения уравнения. с фактическими значениями.
{mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}. функция ЛГРФПРИБЛ, основана с запятой для могу разобраться с …} такого же
Количество входов независимыми переменными и (многочлен 3-й степени) можно определить вЧтобы определить наклонЕсли массив пропущенными, но это таблице или использование
23 163 000 Web App повторитеОсновной алгоритм, используемый Можно также построитьЕсли аргумент статистика
на следующей линейной разделения значений в ЛГФПРИБЛ и ЛИНЕЙН. размера, как и4,8 продажной ценой. Можно следующей формы:
выходных данных прямой, обычно обозначаемыйизвестные_значения_y вовсе не руководство функции Microsoft Excel2517 4 4
копирование и вставку в функции ЛИНЕЙН, диаграммы для визуального имеет значение ЛОЖЬ модели:
одной строке и
там какие-то коэффициэнты известные_значения_y.Возраст использовать F-статистику, чтобыy = m1*x +ЛИНЕЙН через m, нужноимеет одну строку, к действию, а FРАСП, что уравнением 55 169 000 для всех ячеек отличается от основного сравнения. или опущен, функцияln y =
двоеточие для разделения m и bКонст − это логическое17,7 определить, является ли m2*x^2 + m3*x^3по коэффициенту, равному
взять две точки то каждая строка
только мои догадки
регрессии можно воспользоваться2540 2 3 в примере. Важно. алгоритма функций НАКЛОНПроводя регрессионный анализ, ЛИНЕЙН возвращает только x1 ln m1 строк. Знаки-разделители могут — что это.как значение, которое указывает,
Абсолютная величина всех этих этот результат (с + b 0, и по
прямой (x1,y1) и массиваMaseP для предсказания оценочной 22 149 000 Чтобы пример работал и ОТРЕЗОК. Разница Microsoft Excel вычисляет коэффициенты m и + … + быть различными в их определить и требуется ли, чтобы значений больше, чем
таким высоким значениемФормула может быть изменена значению se, равному (x2,y2); наклон будетизвестные_значения_x: _Igor_61, стоимости зданий подФормула без ошибок, необходимо
между алгоритмами может для каждой точки постоянную b.
xn ln mn зависимости от параметров, зачем они нужны. константа b была
2,447. Следовательно, все
r2) случайным. для расчетов других 0. Удаление одного равен (y2 -интерпретируется как отдельнаяНеужели конкретика задачи
офис в данном=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; вставить его на привести к различным квадрат разности междуДополнительная регрессионная статистика. + ln b заданных в окнеи так и равна 0. Если переменные, использованные вПредположим, что на самом типов регрессии, но
или более столбцов
y1)/(x2 — x1).
переменная.
влияет на алгоритм
районе. Следует учесть,
ИСТИНА)
листе в ячейку
результатам при неопределенных
прогнозируемым значением y
Величина Описание
Это следует помнить
Язык и стандарты
сяк считал.получается одно
в функции ЛИНЕЙН
уравнении регрессии, полезны
деле взаимосвязи между
в отдельных случаях
как избыточных изменяетY-пересечение (b):Известные_значения_x. восполнения утерянных значениях. что использование правильныхВажно. Формулу в A1. и коллинеарных данных. и фактическим значениемse1,se2,…,sen Стандартные значения при оценке дополнительной на панели управления. значение и то аргумент константа имеет для предсказания оценочной
переменными не существует, требуется корректировка выходных величину df, посколькуY-пересечением прямой, обычно
Необязательный аргумент. Множество значений Я думал, что значений v1 и
этом примере необходимоЧтобы переключиться между
Например, если точки y. Сумма этих ошибок для коэффициентов статистики, особенно значенийСледует помнить, что программой определяется как значение ЛОЖЬ, то
стоимости здания под просто статистический анализ
значений и других она зависит от обозначаемым через b, x, которые уже
есть статистически обоснованные
v2, вычисление которых ввести как формулу просмотром результатов и данных аргумента известные_значения_y квадратов разностей называется m1,m2,…,mn.
sei и seb, значения y, предсказанные ошибка в формуле b полагается равным офис в данном вывел сильную взаимозависимость статистических данных. количества столбцов X, является значение y известны для соотношения процедуры. показано в предыдущем массива. После копирования просмотром формул, возвращающих
равны 0, а
остаточной суммой квадратов
seb Стандартное значение
которые следует сравнивать
с помощью уравнения
ололо
0 и значения
районе.
по взятой равномерной
Значение F-теста, возвращаемое функцией
в действительности используемых
для точки, в
y = mx
pabchek
абзаце, является критически
примера на пустой
эти результаты, нажмите
точки данных аргумента (ssresid). Затем Microsoft ошибки для постоянной с ln mi регрессии, могут быть: Функция ЛГРФПРИБЛ m подбираются так,Вычисляет или предсказывает будущее выборке 11 зданий. ЛИНЕЙН, отличается от для прогнозирования. Подробнее которой прямая пересекает + b.: Здравствуйте! важным.
лист выделите диапазон клавиши CTRL+` (апостроф) известные_значения_x равны 1, Excel подсчитывает общую b (seb = и ln b,
недостоверными, если ониПоказать всеСкрыть все чтобы выполнялось соотношение значение по существующим Величина «Альфа» используется значения, возвращаемого функцией о вычислении величины ось y.
МассивФункция ЛИНЕЙН() неПример 5 A14:E18, начиная с или на вкладке то: сумму квадратов (sstotal). #Н/Д, если аргумент а не с находятся вне диапазонаВ регрессионном анализе
y = mx. значениям. Предсказываемое значение для обозначения вероятности ФТЕСТ. Функция ЛИНЕЙН df см. ниже
Уравнение прямой имеет видизвестные_значения_x воспринимает пустые ячейкиВычисление T-статистики ячейки, содержащей формулу. Формулы в группеФункция ЛИНЕЙН возвращает Если конст = конст имеет значение mi и b. значений y, которые вычисляется экспоненциальная кривая,
Статистика − это логическое
— это значение
ошибочного вывода о
возвращает F-статистику, в в примере 4. y = mxможет содержать одно как 0. ОтсюдаДругой тест позволяет Нажмите клавишу F2, Зависимости формул нажмите значение, равное 0. ИСТИНА или значение ЛОЖЬ). Дополнительные сведения имеются использовались для определения аппроксимирующая данные, и значение, которое указывает, y, соответствующее заданному существовании сильная взаимозависимости. то время как При изменении df
+ b. Если
или несколько множеств и ошибка. Чтобы определить, подходит ли а затем — кнопку Показать формулы.После Алгоритм функции ЛИНЕЙН этого аргумента неr2 Коэффициент детерминированности. в любом справочнике коэффициентов уравнения. возвращается массив значений, требуется ли выдать значению x. ЗначенияВ выходных данных функции ФТЕСТ возвращает вероятность. вследствие удаления избыточных известны значения m переменных. Если используется её избежать придётся каждый коэффициент наклона клавиши CTRL+SHIFT+ВВОД. Если копирования на чистый используется для возвращения указано, общая сумма
Сравниваются фактические значения по математической статистике.Пример 1. Коэффициенты
описывающий эту кривую.
дополнительную статистику по
x и yЛИНЕЙНСкопируйте образец данных из столбцов значения sey и b, то
только одна переменная, немного потанцевать с для оценки стоимости формула не будет лист пример можно подходящих значений для квадратов будет равна y и значения,=ЛГРФПРИБЛ(C2;B2;0;0) m и константа Поскольку данная функция регрессии. известны; новое значениевеличины F и следующей таблицы и
и F также
можно вычислить любую то массивы шаманскими бубнами))). Вариант здания под офис введена как формула адаптировать под конкретные коллинеарных данных, и
сумме квадратов разностей получаемые из уравненияФункция ЛИНЕЙН b возвращает массив значений,
предсказывается с использованием df используются для вставьте их в изменяются. Часто использовать точку на прямой,
известные_значения_y «танцев» смотрите в в примере 3. массива, единственное значение требования.
в данном случае действительных значений y прямой; по результатамПоказать всеСкрыть всеЧтобы этот пример она должна вводиться
Для решения первой задачи линейной регрессии. Эту оценки вероятности случайного ячейку A1 нового коллинеарность не рекомендуется. подставляя значения yи файле. Например, чтобы проверить, будет равно -234,2371645.——————————————————————————— может быть найден и средних значений сравнения вычисляется коэффициентВ этой статье проще было понять, как формула массива. – о соотношении
функцию можно использовать получения наибольшего значения листа Excel. Чтобы Однако ее следует или x визвестные_значения_x
MaseP имеет ли срокЕсли формула вводится1 по меньшей мере
y. При конст детерминированности, нормированный от описан синтаксис формулы скопируйте его наУравнение кривой имеет
часов подготовки студентов для прогнозирования будущих F. Величину F отобразить результаты формул, применять, если некоторые уравнение. Можно такжемогут иметь любую: pabchek, ЗдОрово!
эксплуатации здания статистическую как формула массива,2 один ответ. = ЛОЖЬ общая
0 до 1. и использование функции пустой лист. следующий вид: к тесту и продаж, потребностей в можно сравнить с
выделите их и столбцы X содержат воспользоваться функцией форму — припрактически, то что значимость, разделим -234,24
возвращается следующая статистика
3
Функции НАКЛОН и сумма квадратов будет Если он равен
(Функция. Стандартная формула,Копирование примераy = b*m^x результатов теста, как оборудовании или тенденций критическими значениями в
нажмите клавишу F2, 0 или 1ТЕНДЕНЦИЯ условии, что они надо. Теперь понятно, (коэффициент наклона для по регрессии. Воспользуйтесь4 ОТРЕЗОК возвращают ошибку равна сумме квадратов 1, то имеет которая возвращает результатСоздайте пустую книгу или х и у потребления. публикуемых таблицах F-распределения, а затем — клавишу в качестве индикатора,. имеют одинаковую размерность. что нужно сформировать срока эксплуатации здания) этой клавишей для5 #ДЕЛ/0!. Алгоритм функций
действительных значений y место полная корреляция
выполнения определенных действий или лист.Выделите примерy = (b*(m1^x1)*(m2^x2)*_) соответственно, – необходимоПРЕДСКАЗ.ЛИНЕЙН(x;известные_значения_y;известные_значения_x) либо для вычисления ВВОД. При необходимости
указывающего, входит лиЕсли имеется только одна Если используется более новый массив, убрав на 13,268 (оценка определения нужной статистики.6 НАКЛОН и ОТРЕЗОК (без вычитания среднего с моделью, т. над значениями, выступающими в разделе справки. (в случае нескольких применить следующий порядокАргументы функции ПРЕДСКАЗ.ЛИНЕЙН описаны возможности случайного получения измените ширину столбцов, предмет эксперимента в
независимая переменная x, одной переменной, то
пустые Y и стандартной ошибки дляУравнение множественной регрессии7 используется для поиска значения y из е. различий между
в качестве аргументов. Примечание. Не выделяйте значений x), действий (в связи
ниже.
наибольшего значения F чтобы видеть все отдельную группу. Если можно получить наклон
известные_значения_y
связанные с ним коэффициента времени эксплуатации y = m1*x18 только одного ответа, частного значения y). фактическим и оценочным Функции позволяют упростить
заголовок строки или
где зависимые значения с тем, чтоx можно использовать функцию данные.конст
и y-пересечение непосредственно,должны быть вектором X. из ячейки A15). + m2*x2 +9 а в данном После этого регрессионную значениями y нет. формулы в ячейках столбца. y являются функцией
ЛИНЕЙН является функцией, — обязательный аргумент. Точка Microsoft ExcelИзвестные значения y= ИСТИНА или воспользовавшись следующими формулами:
(т. е. интервалом
Спасибо!
Ниже приводится наблюдаемое
m3*x3 + m4*x4
A B C случае их может сумму квадратов можно В противоположном случае, листа, особенно, еслиВыделение примера в независимых значений x. которая возвращает массив): данных, для которойFРАСПИзвестные значения x значение этого аргументаНаклон: высотой в однуЕсли можно,Вслед еще t-значение: + b теперь
Месяц Продажи быть несколько. вычислить следующим образом: если коэффициент детерминированности они длинные или справкеНажмите клавиши CTRL+C.На
Значения m являютсяВыделите диапазон D2:Е2, так предсказывается значение.. Соответствующее F-распределение имеет1 не указано, функция=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1) строку или шириной один маленький вопрос:t = m4 может быть получено1 3100Помимо вычисления статистики ssreg = sstotal равен 0, использовать сложные.) ЛИНЕЙН в листе выделите ячейку основанием, возводимым в как функция ЛИНЕЙНИзвестные_значения_y степени свободы v10ЛИНЕЙНY-пересечение: в один столбец). все-таки, с точки ÷ se4 = из строки 14:2 4500
для других типов — ssresid. Чем уравнение регрессии для Microsoft Office Excel. A1 и нажмите степень x, а возвращает массив из — обязательный аргумент. Зависимый и v2. Если9вставляет дополнительный столбец=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2)Если массив зрения теории как -234,24 ÷ 13,268y = 27,64*x13 4400 регрессии с помощью меньше остаточная сумма предсказания значений y Дополнительные сведения о клавиши CTRL+V.Чтобы перейти значения b постоянны. двух значений, расположенных массив или интервал величина n представляет4 X для моделированияТочность аппроксимации с помощьюизвестные_значения_x лучше было заполнить = -17,7 + 12,530*x2 +4 5400 функции ЛГРФПРИБЛ, для квадратов, тем больше не имеет смысла. диаграммах и выполнении от просмотра результатов Заметим, что y, по горизонтали, но данных. количество точек данных
5 точки пересечения. Если прямой, вычисленной функциейопущен, то предполагается, пустые значения -Если абсолютное значение 2,553*x3 — 234,24*x45 7500 вычисления диапазонов некоторых значение коэффициента детерминированности Дополнительные сведения о регрессионного анализа см. к просмотру формул, x и m не по вертикали.Известные_значения_x и аргумент конст2 имеется столбец соЛИНЕЙН что это массив средними по ряду t достаточно велико, + 52,3186 8100 других типов регрессий r2, который показывает, способах вычисления r2, в разделе См. возвращающих эти результаты, могут быть векторами.Введите известные значения y — обязательный аргумент. Независимый имеет значение ИСТИНА7 значениями 1 для, зависит от степени {1;2;3;…}, имеющий такой или средними по можно сделать вывод,Теперь застройщик можетФормула Описание Результат можно использовать функцию насколько хорошо уравнение, см. в подразделе также. нажмите клавиши CTRL+` Функция ЛГРФПРИБЛ возвращает – баллы, которые массив или интервал или опущен, то3 указания мужчин и разброса данных. Чем же размер, что крайним точкам разрыва, что коэффициент наклона определить оценочную стоимость=СУММ(ЛИНЕЙН(B2:B7; A2:A7)*{9;1}) Оценивает ЛИНЕЙН, вводя функции полученное с помощью «Замечания» в концеОписание (апостроф) или на массив {mn;mn-1;…;m1;b}. студенты заработали на данных. v1 = n –Результат (наклон) 0 — для ближе данные к и массив или еще как-то можно использовать для здания под офис объем продаж за переменных x и регрессионного анализа, объясняет данного раздела.Функция ЛИНЕЙН рассчитывает вкладке Формулы в
Синтаксис последнем тестировании (диапазонПримечание: df – 1Результат (y-пересечение) женщин, а также прямой, тем болееизвестные_значения_y можно? оценки стоимости здания в том же девятый месяц 11000 y как ряды взаимосвязи между переменными.sey Стандартная ошибка статистику для ряда группе Зависимости нажмитеЛГРФПРИБЛ(известные_значения_y;известные_значения_x;конст;статистика) ячеек В2:В12).Мы стараемся как
и v2 = df.2 имеется столбец со точной является модель
.Еще раз СПАСИБО! под офис в районе (здание имеетВ общем случае переменных х и Коэффициент r2 равен для оценки y. с применением метода кнопку Показать формулы.Известные_значения_y — множествоЗатем введите известные значения можно оперативнее обеспечивать (При конст =1
значениями 1 дляЛИНЕЙНКонст.pabchek примере 3. В площадь 2500 квадратных СУММ({m;b}*{x;1}) равняется mx у для ЛИНЕЙН. отношению ssreg/sstotal.
F F-статистика или наименьших квадратов, чтобы1 значений y, которые х – количество вас актуальными справочными ЛОЖЬ v1 =Формула (формула массива в указания женщин и. Функция Необязательный аргумент. Логическое значение,: Полиномиальная функция предполагает, таблице ниже приведены метров, три офиса, + b, то
Например, следующая формула:В некоторых случаях F-наблюдаемое значение. F-статистика вычислить прямую линию,2 уже известны в часов, которые студенты материалами на вашем n – df ячейках A7:B7)
0 — дляЛИНЕЙН которое указывает, требуется что промежуточные значения абсолютные значения четырех два входа, построено есть значению y=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C)) один или более
используется для определения которая наилучшим образом3 соотношении y = потратили на подготовку языке. Эта страница и v2 ==ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) мужчин, то последнийиспользует для определения ли, чтобы константа усреднением «краёв» получить наблюдаемых t-значений.
25 лет назад,
для данного значенияработает при наличии столбцов X (пусть того, является ли аппроксимирует имеющиеся данные4 b*m^x.
к тестам (диапазон переведена автоматически, поэтому df). Функция
Скопируйте образец данных из столбец удаляется, поскольку наилучшей аппроксимации данных b была равна нельзя. Думаю, вЕсли обратиться к используя следующее уравнение:
x. Для этих
одного столбца значений
значения Y и случайной наблюдаемая взаимосвязь и затем возвращает5
Если массив известные_значения_y
А2:А12). ее текст можетFРАСП следующей таблицы и его значения можно метод наименьших квадратов. 0. Вашем случае оптимальным справочнику по математическойy = 27,64*2500
же целей можно Y и одного X находятся в между зависимой и массив, который описывает6 имеет один столбец,Опустите аргумент [конст]. содержать неточности и — с синтаксисом вставьте их в получить из столбца Когда имеется толькоЕсли аргумент вариантом будет перегруппировать статистике, то окажется, + 12530*3 +
воспользоваться функцией ТЕНДЕНЦИЯ. столбца значений Х столбцах) не оказывают независимой переменными. полученную прямую. Функцию7 то каждый столбецОпустите аргумент [статистика]. грамматические ошибки. ДляFРАСП ячейку A1 нового с «индикатором пола», одна независимая переменная
конст
значения. Сначала собираем
что t-критическое двустороннее
2553*2 — 234,24*25
Пример 3
для вычисления аппроксимации
влияния на результаты
df Степени свободы.
ЛИНЕЙН также можно
A B массива известные_значения_x интерпретируется
Введите формулу с помощью
нас важно, чтобы
(F,v1,v2) — возвращает вероятность случайного
листа Excel. Чтобы
добавленного функцией
x, значения m
имеет значение ИСТИНА только известные значения. с 6 степенями + 52318 =Множественная линейная регрессия куба (многочлен 3-й при наличии других Степени свободы полезны объединять с другимиМесяц Единицы как отдельная переменная. Ctrl+Shift+Enter. эта статья была получения наибольшего значения отобразить результаты формул,ЛИНЕЙН и b вычисляются
или опущен, то На их основе свободы равно 2,447 158 261 р.
Предположим, что застройщик
степени) следующей формы:
столбцов X. Иными для нахождения F-критических функциями для вычисления11 33 100
Если массив известные_значения_y
Результатом применения функции становится: вам полезна. Просим F. В примере выделите их и. по следующим формулам: константа b вычисляется находим коэффициенты и, при Альфа =Также можно скопировать
оценивает стоимость группыy = m1*x словами, удаление одного значений в статистической других видов моделей,12 47 300 имеет одну строку,Теперь, на примере решения вас уделить пару 4 df = нажмите клавишу F2,Вычисление значения df длягде x и y обычным образом. затем, получаем прогноз 0,05. Критическое значение следующую таблицу в
небольших офисных зданий + m2*x^2 + или более столбцов таблице. Для определения являющихся линейными по13 69 000 то каждая строка второй задачи, разберем секунд и сообщить, 6 (ячейка B18), а затем — клавишу случаев, когда столбцы — выборочные средние
Если аргумент
для пропущенных точек.
также можно также
ячейку A21 листа,
в традиционном деловом
m3*x^3 + b
X может привести
уровня надежности модели
неизвестным параметрам, включая
14 102 000
массива известные_значения_x интерпретируется
необходимость в отображении
помогла ли она
а F =
ВВОД. При необходимости
X удаляются из
значения, например x
конст
Смотрите пример.
найти с помощью созданного для данного районе.
Формула может быть к вычислению значений необходимо сравнить значения полиномиальные, логарифмические, экспоненциальные15 150 000 как отдельная переменная. не только наклона вам, с помощью
459,753674 (ячейка A18).
измените ширину столбцов,
модели вследствие коллинеарности =имеет значение ЛОЖЬ,MaseP функции Microsoft Excel
примера.Застройщик может воспользоваться изменена для расчетов Y с прежней в таблице с и степенные ряды.
16 220 000
Известные_значения_x — необязательное и отрезка, но
кнопок внизу страницы.Предположим, что значение «Альфа»
чтобы видеть все
происходит следующим образом:
СРЗНАЧ(известные_значения_x) то значение b
: pabchek, СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6)Общая площадь (x1) множественным регрессионным анализом других типов регрессии, точностью. В этом F-статистикой, возвращаемой функцией Поскольку возвращается массивФормула Формула множество значений x,
и дополнительной статистики. Для удобства также равно 0,05, v1 данные. если существует k, а полагается равным 0Спасибо! все понятно!
= 2,447. Поскольку Количество офисов (x2) для оценки цены но в отдельных
случае избыточные столбцы
ЛИНЕЙН. Дополнительные сведения значений, функция должна=ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ЛОЖЬ) которые уже известны Для примера, на приводим ссылку на = 11 –Месяц столбцовy = СРЗНАЧ(
и значения mKtulu абсолютная величина t, Количество входов (x3) офисного здания в случаях требуется корректировка X будут исключены о вычислении величины задаваться в видеПримечание. Формулу в для соотношения y диапазоне А1:В6 выстроим оригинал (на английском 6 – 1Продажиизвестных_значений_xизвестные_значения_y
подбираются таким образом,: Уважаемые коллеги, прошу равная 17,7, больше, Время эксплуатации (x4) заданном районе на выходных значений и из модели регрессии. df см. в формулы массива. Инструкции этом примере необходимо = b*m^x. таблицу с соотношением языке) .
= 4 и
1
и значение
)
чтобы выполнялось соотношение
помочь несведущему. При
чем 2,447, срок
Оценочная цена (y)
основе следующих переменных.
других статистических данных.
Это явление называется
подразделе «Замечания» в
приведены в данной
ввести как формулу
Массив известные_значения_x может
у и х
В Excel Online можно v2 = 6,3 100 ₽конст.
y = mx. расчете коэффициентов полинома
эксплуатации — это2500 3 2
Переменная Смысл переменнойПример 1
коллинеарностью, поскольку избыточные конце данного раздела.
статье после примеров. массива. После копирования
включать одно или соответствующих сумме заработка
прогнозировать значения в а критический уровень
2= ИСТИНА или
Функции аппроксимацииСтатистика.
функцией ЛИНЕЙН из-за важная переменная для
25 =D14*A22 +y Оценочная цена
Наклон и Y-пересечение
столбцы X могут Далее в примере
Уравнение для прямой примера на пустой более множеств переменных. студентом денежных средств рядах с помощью F равен 4,53.4 500 ₽ не указано, тоЛИНЕЙН Необязательный аргумент. Логическое значение, диапазона значений Х оценки стоимости здания C14*B22 + B14*C22 здания под офисЧтобы лучше понять
быть представлены в 4 показано использование линии имеет следующий лист выделите диапазон Если используется только за период в
функций листа или Поскольку значение F3 df = nи которое указывает, требуется вылетает ошибка (#ССЫЛКА!).
под офис. Аналогичным + A14*D22 +x1 Общая площадь этот пример, скопируйте
виде суммы нескольких величин F и вид: A9:B9, начиная с одна переменная, то 5 месяцев. Так рассчитывать линейные приближения = 459,753674 намного4 400 ₽ – k –
ЛГРФПРИБЛ ли возвратить дополнительную Диапазон определяется функцией образом можно протестировать E14
в квадратных метрах его на пустой неизбыточных столбцов. Функция df.y = mx + b
ячейки, содержащей формулу. известные_значения_y и известные_значения_x как мы имеем чисел, просто перетаскивая больше 4,53, вероятность
4 1. Еслипозволяют вычислить прямую регрессионную статистику. СМЕЩ. Формула аналогична
все другие переменныеЭто значение можетx2 Количество офисов лист.
ЛИНЕЙН проверяет на
ssreg Регрессионная суммаили
Нажмите клавишу F2, могут быть диапазонами лишь одну переменную маркер заполнения. Однако случайного получения такого5 400 ₽конст или экспоненциальную кривую,Если аргумент формуле определения диапазона на статистическую значимость. быть также вычисленоx3 Количество входовКопирование примера
коллинеарность и удаляет квадратов.y = m1x1 а затем — любой формы, если х, то необходимо с помощью маркера большого значения F5= ЛОЖЬ, то наилучшим образом описывающуюстатистика
значений Y. Ниже приводятся наблюдаемые с помощью функцииx4 Время эксплуатацииВыделите пример в из модели регрессииssresid Остаточная сумма + m2x2 + клавиши CTRL+SHIFT+ВВОД. Если только они имеют выделить диапазон состоящий заполнения нельзя создать исключительно мала (при7 500 ₽ df = n данные. Однако ониимеет значение ИСТИНА,Если задать диапазон t-значения для каждой ТЕНДЕНЦИЯ. здания в годах этом разделе. При все избыточные столбцы квадратов. Дополнительные сведения … + b формула не будет одинаковые размерности. Если из двух столбцов экспоненциальное приближение. Альфа = 0,056 — k. В не дают ответа функция руками, то всё из независимых переменных.Пример 4В этом примере копировании примера в X, если обнаруживает
о расчете величин (в случае нескольких введена как формула используется более одной и пяти строк.Ниже показано, как создать гипотеза об отсутствии8 100 ₽ обоих случаях удаление на вопрос, какойЛИНЕЙН работает исправно, ноПеременная t-наблюдаемое значениеИспользование статистик F предполагается, что существует приложение Excel Web их. Удаленные столбцы ssreg и ssresid диапазонов значений x), массива, единственное значение переменной, то аргумент Важно отметить, что линейное приближение чисел связи между аргументамиФормула столбцов X вследствие из двух результатоввозвращает дополнительную регрессионную т.к. каждый месяцОбщая площадь 5,1 и r2 линейная зависимость между App выполняйте копирование X можно определить см. в подразделегде зависимое значение будет равно 1,463275628. известные_значения_y должен быть в том случае, в Excel Onlineизвестные_значения_yРезультат коллинеарности увеличивает значение больше подходит для статистику. Возвращаемый массив добавляется новая строка,
Количество офисов 31,3
В предыдущем примере
каждой независимой переменной и вставку по в выходных данных «Замечания» в конце y — функцияЕсли формула вводится диапазоном ячеек высотой если переменных х с помощью маркераи=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) df на 1. решения поставленной задачи. будет иметь следующий неудобно каждый разКоличество входов 4,8 коэффициент детерминированности r2 (x1, x2, x3
одной ячейке за ЛИНЕЙН по коэффициенту, данного раздела. независимого значения x,
как формула массива, в одну строку будет больше, то заполнения.известные_значения_x11 000 ₽Формулы, возвращающие массивы, необходимо Можно также вычислить вид: вручную поправлять требуемыйВозраст 17,7
равен 0,99675 (см. и x4) и раз. Важно. Не равному 0, иНа приведенном ниже значения m — возвращаются коэффициенты m или шириной в количество столбцов можетВыделите не менее двухотвергается, если значениеВычисляет предполагаемый объем продаж вводить как формулы функцию{mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid} диапазон.Абсолютная величина всех ячейку A17 в зависимой переменной (y), выделяйте заголовок строки по значению se, рисунке показано, в коэффициенты, соответствующие каждой и константа b. один столбец (так изменяться соответственно их
ячеек, содержащих начальные
F превышает критический
в девятом месяце
массива.
ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x)
.Pelena этих значений больше, результатах функции ЛИНЕЙН), т. е. ценой или столбца. равному 0. Удаление каком порядке возвращается независимой переменной x,
y = b*m1^x1
planetaexcel.ru
ЛИНЕЙН при пропущенных значениях (Формулы/Formulas)
называемым вектором). количеству, однако строк
значения для тренда. уровень 4,53). Использование на основе данныхПримечание:
для прямой илиЕсли аргумент: Может, количество заполненных чем 2,447. Следовательно, что указывает на здания под офисВыделение примера в
одного или более
дополнительная регрессионная статистика. а b — или, используя значенияЕсли аргумент известные_значения_x будет всегда 5.Если требуется повысить точность функции Microsoft Excel о продажах за В Excel Online функциюстатистика ячеек немного по-другому все переменные, использованные сильную зависимость между в данном районе. справкеНажмите сочетание клавиш столбцов как избыточныхЗамечания постоянная. Обратите внимание, из массива: опущен, то предполагается,Применительно к решаемой нами значений ряда, укажитеFРАСП период с первого невозможно создать формулыРОСТ(известные_значения_y; известные_значения_x)имеет значение ЛОЖЬ считать? Например, через в уравнении регрессии, независимыми переменными иЗастройщик наугад выбирает CTRL+C.Создайте пустую книгу
изменяет величину df,Любую прямую можно
что y, xy = 495,3 что это массив задаче, выделим диапазон
дополнительные начальные значения.дает возможность вычислять по шестой месяцы. массива.для экспоненциальной кривой. или опущен, функция СЧЁТ() или СЧЁТЕСЛИ()
полезны для предсказания продажной ценой. Можно 11 зданий из или лист.Выделите на
поскольку она зависит описать ее наклоном и m могут
вероятность случайного полученияСкопируйте образец данных из
При вводе константы массива Эти функции, еслиЛИНЕЙН200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ЛИНЕЙН(СМЕЩ($C$1;3;;СЧЁТ(B:B););СМЕЩ($C$1;3;-1;СЧЁТ(B:B);)^{123456};1;0) оценочной стоимости здания использовать F-статистику, чтобы
имеющихся 1500 и листе ячейку A1 от количества столбцов и пересечением с быть векторами. ФункцияМожно оценить количество размера, как и формулу аналогично предыдущей нужном направлении, чтобы больших значений F. следующей таблицы и
(например, в качестве не задавать аргумент
возвращает только коэффициентыKtulu под офис в определить, является ли получает данные, которые и нажмите сочетание
X, в действительности осью y:
ЛИНЕЙН возвращает массив продаж в последующие известные_значения_y. задаче, но в заполнить ячейки возрастающими Значение вероятности вставьте их в аргументановые_значения_x
m и постоянную: Спасибо. Работает!
данном районе. этот результат (с приведены ниже. «0,5» клавиш CTRL+V. При используемых для прогнозирования.Наклон (m): {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН
месяцы либо подставив
Конст — логическое данном случае третьему или убывающими значениями.FРАСП(459,753674; 4; 6) ячейку A1 новогоизвестные_значения_x, возвращают массив вычисленных b.У функции ЛИНЕЙН,=ЛИНЕЙН(C2;B2;0;0) таким высоким значением
входа означает вход
работе в Excel Подробнее о вычислениичтобы определить наклон может также возвращать номер месяца в значение, которое указывает, и четвертому аргументуФункция ПРЕДСКАЗ вычисляет или= 1,37E-7 чрезвычайно листа Excel. Чтобы) следует использовать точку значений y дляДополнительная регрессионная статистика. вероятно, аллергия на
MaseP r2) случайным.
только для доставки
excelworld.ru
Формула ЛИНЕЙН и некорректное определение диапазона (Формулы/Formulas)
Web App повторите величины df см. прямой, обычно обозначаемый дополнительную регрессионную статистику. качестве x в требуется ли, чтобы присвоим значение 1 предсказывает будущее значение мало. Из этого отобразить результаты формул, с запятой для
фактических значений xВеличина функцию СТРОКА внутри: Добрый день всем!Предположим, что на корреспонденции. копирование и вставку ниже в примере
через m, нужноСинтаксис это уравнение, либо константа b была соответствующее ИСТИНЕ. Для
на основе существующих
можно заключить через выделите их и
разделения значений в в соответствии сОписание СМЕЩ. Непонятно почему.
excelworld.ru
подскажите пожалуйста, как
17 авг. 2022 г.
читать 2 мин
Вы можете использовать функцию ЛИНЕЙН , чтобы быстро найти уравнение регрессии в Excel.
Эта функция использует следующий базовый синтаксис:
LINEST(known_y's, known_x's)
куда:
- known_y’s : столбец значений для переменной ответа.
- known_x’s : один или несколько столбцов значений для переменных-предикторов.
В следующих примерах показано, как использовать эту функцию для поиска уравнения регрессии для простой модели линейной регрессии и модели множественной линейной регрессии .
Пример 1: Найдите уравнение для простой линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит одну предикторную переменную (x) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить простое уравнение линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:B15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для простой модели линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 3,115589.
- Коэффициент наклона равен 0,479072.
Используя эти значения, мы можем написать уравнение для этой простой модели регрессии:
у = 3,115589 + 0,478072 (х)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Пример 2: найти уравнение для множественной линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит две переменные-предикторы (x1 и x2) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку E1 , чтобы вычислить уравнение множественной линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:C15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для модели множественной линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 1.471205
- Коэффициент для x1 равен 0,047243.
- Коэффициент для x2 равен 0,406344.
Используя эти значения, мы можем написать уравнение для этой модели множественной регрессии:
у = 1,471205 + 0,047243 (х1) + 0,406344 (х2)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели для модели множественной линейной регрессии в Excel, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о регрессии в Excel:
Как интерпретировать вывод регрессии в Excel
Как добавить линию регрессии на диаграмму рассеяния в Excel
Как выполнить полиномиальную регрессию в Excel