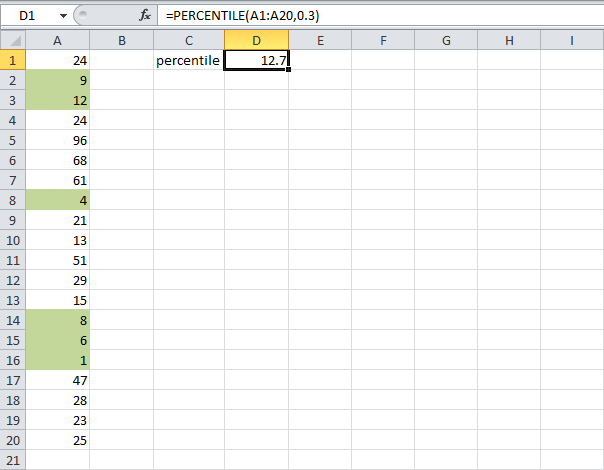
Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в
MS
EXCEL
.
Понятие
Квантиля
основано на определении
Функции распределения
. Поэтому, перед изучением
Квантилей
рекомендуем освежить в памяти понятия из статьи
Функция распределения вероятности
.
Содержание статьи:
- Определение
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
- Квантили F-распределения
- Квантили распределения Вейбулла
- Квантили экспоненциального распределения
Сначала дадим формальное определение
квантиля,
затем приведем примеры их вычисления в MS EXCEL.
Определение
Пусть случайная величина
X
, имеет
функцию распределения
F
(
x
).
α-квантилем
(
альфа-
квантиль,
x
a
,
квантиль
порядка
α, нижний
α-
квантиль
) называют решение уравнения
x
a
=F
-1
(α), где
α
— вероятность, что случайная величина х примет значение меньшее или равное x
a
, т.е. Р(х<= x
a
)=
α.
Из определения ясно, что нахождение
квантиля
распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении
функции распределения
мы находим вероятность
α,
зная x
a
, то при нахождении
квантиля
мы, наоборот, ищем
x
a
зная
α
.
Чтобы пояснить определение, используем график функции
стандартного нормального распределения
(см.
файл примера Лист Определение
):
Примечание
: О построении графиков в MS EXCEL можно прочитать статью
Основные типы диаграмм в MS EXCEL
.
Например, с помощью графика вычислим 0,21-ю
квантиль
, т.е. такое значение случайной величины, что Р(X<=x
0,21
)=0,21.
Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с
функцией распределения
. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я
квантиль
равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная
стандартному нормальному закону,
примет значение
меньше
-0,81, равна 0,21 (21%).
Примечание
: При вычислении
квантилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Точное значение
квантиля
в нашем случае можно найти с помощью формулы
=НОРМ.СТ.ОБР(0,21)
СОВЕТ
: Процедура вычисления
квантилей
имеет много общего с вычислением
процентилей
выборки
(см. статью
Процентили в MS EXCEL
).
Квантили специальных видов
Часто используются
Квантили
специальных видов:
-
процентили
x
p/100
, p=1, 2, 3, …, 99 -
квартили
x
p/4
, p=1, 2, 3 -
медиана
x
1/2
В качестве примера вычислим
медиану (0,5-квантиль)
логнормального распределения
LnN(0;1) (см.
файл примера лист Медиана
).
Это можно сделать с помощью формулы
=ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей
стандартного нормального распределения
возникает при
проверке статистических гипотез
и при
построении доверительных интервалов.
Примечание
: Про
проверку статистических гипотез
см. статью
Проверка статистических гипотез в MS EXCEL
. Про
построение доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.
В данных задачах часто используется специальная терминология:
Нижний квантиль уровня
альфа
(
α
percentage point)
;
Верхний квантиль уровня альфа (upper
α
percentage point)
;
Двусторонние квантили уровня
альфа
.
Нижний квантиль уровня альфа
— это обычный
α-квантиль.
Чтобы пояснить название «
нижний» квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
(см.
файл примера лист Квантили
).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше
α-квантиля
. Из определения
квантиля
эта вероятность равна
α
. Из графика
функции распределения
становится понятно, откуда происходит название »
нижний квантиль» —
выделенная область расположена в нижней части графика.
Для
α=0,05,
нижний 0,05-квантиль
стандартного нормального распределения
равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при
проверке гипотез
и построении
доверительных интервалов
чаще используется «верхний»
α-квантиль.
Покажем почему.
Верхним
α
—
квантилем
называют такое значение x
α
, для которого вероятность, того что случайная величина X примет значение
больше или равное
x
α
равна
альфа:
P(X>= x
α
)=
α
. Из определения понятно, что
верхний альфа
—
квантиль
любого распределения равен
нижнему (1-
α)
—
квантилю.
А для распределений, у которых
функция плотности распределения
является четной функцией,
верхний
α
—
квантиль
равен
нижнему
α
—
квантилю
со знаком минус
.
Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для
α=0,05,
верхний 0,05-квантиль
стандартного нормального распределения
равен 1,645. Т.к.
функция плотности вероятности
стандартного нормального
распределения
является четной функцией, то вычисления в MS EXCEL
верхнего квантиля
можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие
верхний
α
—
квантиль?
Только из соображения удобства, т.к. он при
α<0,5
всегда положительный (в случае
стандартного нормального
распределения
). А при проверке гипотез
α
равно
уровню значимости
, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре
проверки гипотез
пришлось бы записывать условие отклонения
нулевой гипотезы
μ>μ
0
как Z
0
>Z
1-
α
, подразумевая, что Z
1-
α
–
обычный
квантиль
порядка
1-
α
(или как Z
0
>-Z
α
). C верхнем квантилем эта запись выглядит проще Z
0
>Z
α
.
Примечание
: Z
0
— значение
тестовой статистики
, вычисленное на основе
выборки
. Подробнее см. статью
Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)
.
Чтобы пояснить название «
верхний»
квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
для
α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше
верхнего 0,05-квантиля
, т.е.
больше
значения 1,645. Эта вероятность равна 0,05.
На графике
плотности вероятности
площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика
функции распределения
становится понятно, откуда происходит название «верхний»
квантиль
—
выделенная область расположена в верхней части графика. Если Z
0
больше
верхнего квантиля
, т.е. попадает в выделенную область, то
нулевая гипотеза
отклоняется.
Также при
проверке двухсторонних гипотез
и построении соответствующих
доверительных интервалов
иногда используется понятие «двусторонний»
α-квантиль.
В этом случае условие отклонения
нулевой гипотезы
звучит как |Z
0
|>Z
α
/2
, где Z
α
/2
–
верхний
α/2-квантиль
. Чтобы не писать
верхний
α/2-квантиль
, для удобства используют «двусторонний»
α-квантиль.
Почему двусторонний? Как и в предыдущих случаях, построим график
плотности вероятности стандартного нормального распределения
и график
функции распределения
.
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение
между
нижним квантилем уровня α
/2 и
верхним квантилем
уровня α
/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
0
попадает в одну из выделенных областей, то
нулевая гипотеза
отклоняется.
Вычислить
двусторонний
0,05
—
квантиль
это можно с помощью формул MS EXCEL:
=НОРМ.СТ.ОБР(1-0,05/2)
или
=-НОРМ.СТ.ОБР(0,05/2)
Другими словами,
двусторонние α-квантили
задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Аналогичным образом
квантили
вычисляются и для
распределения Стьюдента
. Например, вычислять
верхний
α/2-
квантиль
распределения Стьюдента с
n
-1 степенью свободы
требуется, если проводится
проверка двухсторонней гипотезы
о
среднем значении
распределения при
неизвестной
дисперсии
(
см. эту статью
).
Для
верхних квантилей
распределения Стьюдента
часто используется запись t
α/2,n-1
. Если такая запись встретилась в статье про
проверку гипотез
или про построение
доверительного интервала
, то это именно
верхний квантиль
.
Примечание
:
Функция плотности вероятности распределения Стьюдента
, как и
стандартного нормального распределения
, является четной функцией.
Чтобы вычислить в MS EXCEL
верхний
0,05/2
—
квантиль
для t-распределения с 10 степенями свободы (или тоже самое
двусторонний
0,05-квантиль
), необходимо записать формулу
=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)
или
=СТЬЮДРАСПОБР(0,05; 10)
или
=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)
или
=-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е.
двусторонний квантиль
.
Квантили распределения ХИ-квадрат
Вычислять
квантили
распределения ХИ-квадрат
с
n
-1 степенью свободы
требуется, если проводится
проверка гипотезы
о
дисперсии нормального распределения
(см. статью
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
).
При
проверке таких гипотез
также используются
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
распределения
ХИ
2
: χ
2
α/2,n-1
и
χ
2
1-
α/2,n-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
, где используется
стандартное нормальное распределение
или
t-распределение
?
Дело в том, что в отличие от
стандартного нормального распределения
и
распределения Стьюдента
, плотность распределения
ХИ
2
не является четной (симметричной относительно оси х). У него все
квантили
больше 0, поэтому
верхний альфа-квантиль
не равен
нижнему (1-альфа)-квантилю
или по-другому:
верхний альфа-квантиль
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2
—
квантиль
для
ХИ
2
-распределения
с
числом степеней свободы
10, т.е.
χ
2
0,05/2,n-1
, необходимо в MS EXCEL записать формулу
=ХИ2.ОБР.ПХ(0,05/2; 10)
или
=ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Чтобы вычислить
верхний
(1-0,05/2)-
квантиль
при том же
числе степеней свободы
, т.е.
χ
2
1-0,05/2,n-1
и необходимо записать формулу
=ХИ2.ОБР.ПХ(1-0,05/2; 10)
или
=ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Квантили F-распределения
Вычислять
квантили
распределения Фишера
с
n
1
-1 и
n
2
-1 степенями свободы
требуется, если проводится
проверка гипотезы
о равенстве
дисперсий двух нормальных распределений
(см. статью
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
).
При
проверке таких гипотез
используются, как правило,
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
F
-распределения:
F
α/2,n1-1,
n
2
-1
и
F
1-α/2,n1-1,
n
2
-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
? Причина та же, что и для распределения ХИ
2
– плотность
F-распределения
не является четной
.
Эти
квантили
нельзя выразить один через другой как для
стандартного нормального распределения
.
Верхний альфа-квантиль
F
-распределения
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2-квантиль
для
F
-распределения
с
числом степеней свободы
10 и 12, необходимо записать формулу
=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)
Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Квантили распределения Вейбулла
Иногда
обратная функция распределения
может быть представлена в явном виде с помощью элементарных функций, например как для
распределения Вейбулла
. Напомним, что функция этого распределения задается следующей формулой:
После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p
—
квантиль.
Суть от этого не меняется.
Это и есть обратная функция, которая позволяет вычислить
P
—
квантиль
(
p
—
quantile
). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
p
(вероятность того, что случайная величина Х примет значение меньше или равное х
p
равна P).
Квантили экспоненциального распределения
Задача
:
Случайная величина имеет
экспоненциальное распределение
:
Требуется выразить
p
-квантиль
x
p
через параметр распределения λ и заданную вероятность
p
.
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p-квантиль
. Суть от этого не меняется.
Решение
: Вспоминаем, что
p
-квантиль
– это такое значение x
p
случайной величины X, для которого P(X<=x
p
)=
p
. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
p
равна
p
. Запишем это утверждение с помощью формулы:
По сути, мы записали
функцию вероятности экспоненциального распределения
: F(x
p
)=
p
.
Из определения
квантиля
следует, что для его нахождения нам потребуется
обратная функция распределения
.
Проинтегрировав вышеуказанное выражение, получим:
Используя это уравнение, выразим x
p
через λ и вероятность
p
.
Конечно, явно выразить
обратную функцию распределения
можно не для всех
функций распределений
.
Функция КВАРТИЛЬ в Excel используется для расчета квартиля диапазона числовых данных и возвращает соответствующее числовое значение.
Функция КВАРТИЛЬ.ВКЛ вычисляет на основе указанной процентили в качестве второго аргумента функции. Полностью соответствует первой функции. Последняя используется в Excel 2007 и более ранних версиях и оставлена для совместимости.
Функция КВАРТИЛЬ.ИСКЛ используется для расчета квартили диапазона числовых значений на основе известной процентили, за исключением граничных значений (минимального и максимального значения в диапазоне).
Квартили используются для распределения диапазона чисел на четыре равные части:
- Первый квартиль является числом из диапазона исследуемых значений, которое делит данный диапазон на две части так, что около 25% данного диапазона являются числами, которые меньше первого квартиля, а остальные (75%) – больше. Рассматриваемые функции могут возвращать результат интерполяции двух соседних значений из диапазона.
- Второй квартиль эквивалентен медиане выборки (исследуемого числового диапазона), то есть числовому значению, которое делит диапазон на две части: 50% чисел меньше медианы, остальные 50% чисел больше медианы. Так, запись =КВАРТИЛЬ.ВКЛ(A1:A10;2) возвращает значение, эквивалентное результату вычисления функции =МЕДИАНА(A1:A10), при условии, что ячейки из диапазона A1:A10 содержат числовые значения.
- Третий квартиль – числовое значение, делящее диапазон на две части, в первой из которой содержатся 75% чисел диапазона, которые меньше полученного значения, а во второй (25%) – больше.
Функция КВАРТИЛЬ.ВКЛ может быть использована не только для определения медианы выборки (второго квартиля), а и нахождения минимального и максимального значений соответственно. При работе с большими диапазонами чисел для подобных расчетов рекомендуется использовать функции МИН и МАКС соответственно.
Существует несколько алгоритмов расчета квартилей. Все рассмотренные функции используют следующую формулу:
Qp=(1-(x-i)∙Ai+(x-i)∙A(i+1), где:
- Qp – p-й квантиль (является частным случаем квантиля);
- x – индекс квантиля;
- i – индекс элемента из выборки;
- A1,A2…Ai – элементы выборки, отсортированной по возрастанию значений.
Для расчета индекса квантиля (x) функция КВАРТИЛЬ.ВКЛ используют формулу:
x=(n-1)p, где n – количество элементов в диапазоне.
Функция КВАРТИЛЬ.ИСКЛ использует формулу x=(n+1)p.
В Excel принято так, что первые выше указанные 2 функции используют метод N-1-интерполяцию, а третья функция – N+1-интерполяцию.
Примеры использования функций КВАРТИЛЬ в Excel
Пример 1. В столбце таблицы содержится числовая последовательность. Определить число, которое делит последовательность на 2 части, 25% первой – числа меньше полученного значения, а 75% — больше. Использовать N+1-интерполяцию.
Вид таблицы данных:
Для определения 1-го квартиля используем функцию:
Описание аргументов:
- A2:A15 – диапазон ячеек с исследуемыми числами;
- 1 – номер вычисляемого квартиля.
Полученный результат:
Проверим утверждение о том, что второй квартиль соответствует медиане выборке. Определим 2-й по формуле:
Вычислим медиану:
=МЕДИАНА(A2:A15)
Полученные значения совпадают:
В результате расчетов мы получили первый, второй квартили и медиану для исходного диапазона чисел.
Статистический анализ роста доли дохода в Excel за период
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:
Определим 3-й по формуле:
Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;»<«&B15)/СЧЁТ(B2:B13)
Полученные результаты:
Анализ статистики случайно сгенерированных чисел в Excel
Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
=СЛУЧМЕЖДУ(0;1000)
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:
Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:
Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Особенности использования функций расчета квартиля в Excel
Все рассматриваемые функции имеют одни и те же аргументы:
=КВАРТИЛЬ(массив;часть)
Описание аргументов:
- массив – обязательный аргумент, принимающий константу массива или ссылку на диапазон ячеек с числовыми значениями, для которых будет рассчитан требуемый квартиль;
- часть – обязательный аргумент, принимающий числовые значения, указывающие номер возвращаемого квартиля. В зависимости от используемой функции, может принимать числа из диапазонов:
- От 0 до 4 (КВАРТИЛЬ.ВКЛ), при этом числа 0 и 1 характеризуют минимальное и максимальное значения из исследуемого диапазона соответственно. Число 1 соответствует 1-й квартили, 2 – медиане, 3 – 3-й квартили.
- От 1 до 3 (функция КВАРТИЛЬ.ИСКЛ), соответствующие 1-й, 2-й и 3-й квартилям.
Примечания:
- Все рассматриваемые функции не учитывают имена и текстовые строки, которые не могут быть преобразованы к числам, логические значения и пустые ячейки. Ячейки, содержащие значение 0 (нуль), в расчет включаются.
- Если в качестве первого аргумента функций передан пустой массив или ссылка на диапазон пустых значений, все функции вернут код ошибки #ЧИСЛО!.
- Если в качестве второго аргумента функций было передано нецелое число из диапазона допустимых значений, дробная часть будет усечена.
- Если второй аргумент задан числом, взятым из вне диапазона допустимых значений, в результате вычислений будет возвращен код ошибки #ЧИСЛО!.
Содержание
- Доверительный интервал для оценки дисперсии в EXCEL
- Задача
- Функция распределения и плотность вероятности в EXCEL
- Генеральная совокупность и случайная величина
- Функция распределения
- Непрерывные распределения и плотность вероятности
- Вычисление плотности вероятности с использованием функций MS EXCEL
- Вычисление вероятностей с использованием функций MS EXCEL
- Обратная функция распределения (Inverse Distribution Function)
Доверительный интервал для оценки дисперсии в EXCEL
history 27 ноября 2016 г.
Построим доверительный интервал для оценки дисперсии случайной величины, распределенной по нормальному закону, в MS EXCEL .
Построение доверительного интервала для оценки среднего приведено в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL . Процедура построения доверительного интервала для оценки дисперсии имеет много общего с процедурой для оценки среднего , поэтому в этой статье она изложена менее подробно, чем в указанной статье.
Формулировка задачи. Предположим, что из генеральной совокупности имеющей нормальное распределение с неизвестным средним значением μ и неизвестной дисперсией σ 2 взята выборка размера n. Необходимо на основании этой выборки оценить дисперсию распределения и построить доверительный интервал .
Примечание : Построение доверительного интервала для оценки среднего относительно нечувствительно к отклонению генеральной совокупности от нормального закона . А вот при построении доверительного интервала для оценки дисперсии требование нормальности является строгим.
СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:
В качестве точечной оценкой дисперсии распределения, из которого взята выборка , используют Дисперсию выборки s 2 .
Также, перед процедурой проверки гипотезы , исследователь устанавливает требуемый уровень значимости – это допустимая для данной задачи ошибка первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна ( уровень значимости обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01)
В статье про ХИ2-распределение показано, что выборочное распределение статистики y=(n-1) s 2 /σ 2 , имеет ХИ2-распределение с n-1 степенью свободы.
Воспользуемся этим свойством и построим двухсторонний доверительный интервал для оценки дисперсии :
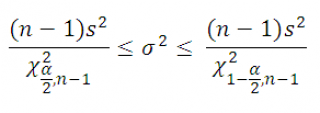
Примечание : В файле примера на листе Квантили показан расчет квантилей для распределения ХИ2 . На рисунке выделена область соответствующая уровню доверия 95%, которая ограничена верхним и нижним квантилем . Обратите внимание, что в отличие от нормального и t-распределения распределение ХИ2 несимметрично, поэтому для двустороннего доверительного интервала потребуется вычислить два квантиля , значения которых будут отличаться.
Примечание : Доверительный интервал для стандартного отклонения может быть получен путем извлечения квадратного корня из вышеуказанного выражения.
В файле примера на листе 2х сторонний создана форма для расчета и построения двухстороннего доверительного интервала .
Для построения односторонних доверительных интервалов используйте нижеследующие выражения:
Задача
В следующей задаче найдем верхний односторонний доверительный интервал для дисперсии .
Автоматический аппарат заполняет емкости с растворителем. Предполагается, что объемы налитой жидкости в емкостях распределены по нормальному закону . Если разброс значений объемов будет слишком велик, то значительная часть емкостей будет существенно переполнена или не заполнена. Для оценки дисперсии в качестве выборки взято 20 наполненных жидкостью емкостей. На основе выборки была вычислена дисперсия выборки s 2 , которая составила 0,0153 (литров 2 ). Принято решение оценить верхний уровень дисперсии с уровнем доверия 95%.
Для решения задачи воспользуемся выражением
Сначала найдем верхний (1-α)-квантиль (или равный ему нижний α-квантиль ) ХИ2-распределения с n-1 степенью свободы при у ровне значимости α равном 1-0,95=0,05. Это можно сделать в MS EXCEL по формулам: =ХИ2.ОБР.ПХ(1-0,05; 20-1) или =ХИ2.ОБР(0,05; 20-1)
В результате получим верхний доверительный интервал для дисперсии: σ 2 файле примера на листе 1 сторонний .
СОВЕТ : О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
Источник
Функция распределения и плотность вероятности в EXCEL
history 13 октября 2016 г.
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта ]]> www.excel2.ru ]]> . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL .
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):
В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x 1 Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
Непрерывные распределения и плотность вероятности
В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой функции плотности распределения p(x) . Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF) .
Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution ) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.
Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что плотность распределения является производной от функции распределения , т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения ).
Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.
Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.
Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.
Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .
Обратная функция распределения вычисляет квантили распределения , которые используются, например, при построении доверительных интервалов . Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения . В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Содержание
- Медиана и квартили
- Математическое описание
- Среднее значение
- Отклонение от среднего
- Квантиль
- Построение интервалов
- Двусторонний доверительный интервал
- Первый квартиль
- Третий квартиль
- Квартили непрерывного распределения
- Квартили в MS EXCEL
- Моменты случайной величины
- Статистический анализ роста доли дохода в Excel за период
- Анализ статистики случайно сгенерированных чисел в Excel
- Расчет квартилей в R и SAS
- Расчет децилей для дискретного ряда
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
Квантили нормального распределения
Основная статья: Медиана (статистика)
- 0,25-квантиль называется первым (или нижним) квартилем (от лат. quarta — четверть);
- 0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым квартилем
- 0,75-квантиль называется третьим (или верхним) квартилем.
Интерквартильным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями. Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.
Математическое описание
Смотря на закон распределения, мы можем понять, какова вероятность того или иного события, можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести в математически обоснованное утверждение.
Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении – это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:
(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Момент степени k:
(5) νk = E(Xk)
Центральный момент степени k:
(6) μk = E[X – E(X)]k
Среднее значение
Среднее значение (μ) закона распределения – это математическое ожидание случайной величины (случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 114 | 115 | 52 | 52 | 24 | 13 | 30 |
| Таблица 1. Количество посетителей в час |
График 1. Количество посетителей в час
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (114 • 0 + 115 • 1 + 52 • 2 + 52 • 3 + 24 • 4 + 13 • 5 + 30 • 6) / 400 = 716/400 = 1.79
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.29 + 1 • 0.29 + 2 • 0.13 + 3 • 0.13 + 4 • 0.06 + 5 • 0.03 + 6 • 0.08 = 1.79 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.79 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 28.5 | 28.8 | 13 | 13 | 6 | 3.3 | 7.5 |
| Таблица 2. Закон распределения количества посетителей |
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы использовать в качестве меры удалённости “разность” между средним и случайными величинами:
(7) xi – μ
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц между величинами и средним значением:
(8) (xi – μ)2
Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:
(9) σ2 = E[(X – E(X))2] Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда: (10) σ2 = E[(X – E(X))2] = ∑[(Xi – μ)2]/n Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi – μ)2]/n]
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
σ = √(∑(x-μ)2/n) = √{[(90 – 99.95)2 + (91 – 99.95)2 + (92 – 99.95)2 + (93 – 99.95)2 + (94 – 99.95)2 + (95 – 99.95)2 + (96 – 99.95)2 + (97 – 99.95)2 + (98 – 99.95)2 + (99 – 99.95)2 + (100 – 99.95)2 + (101 – 99.95)2 + (102 – 99.95)2 + (103 – 99.95)2 + (104 – 99.95)2 + (105 – 99.95)2 + (106 – 99.95)2 + (107 – 99.95)2 + (108 – 99.95)2 + (109 – 99.95)2 + (110 – 99.95)2]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.: квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%. На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
- 2-квантиль – медиана
- 4-квантиль – квартиль
- 10-квантиль – дециль
- 100-квантиль – перцентиль
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям, и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например, интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов: односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область“
Первый квартиль
Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5
Третий квартиль
Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5
Квартили непрерывного распределения
Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй – F(х) =0,5, а третий F(х) =0,75.
Примечание : Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .
Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана (2-й квартиль ) вычисляется по формуле e μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.
Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e μ .
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .
При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .
Моменты случайной величины
Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.
#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.
#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.
#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:

#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.

Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.
Статистический анализ роста доли дохода в Excel за период
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:

Определим 3-й по формуле:


Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;”<“&B15)/СЧЁТ(B2:B13)
Полученные результаты:

Анализ статистики случайно сгенерированных чисел в Excel
Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
=СЛУЧМЕЖДУ(0;1000)
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:

Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:

Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Расчет квартилей в R и SAS
Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R!). Квантиль при i-м методе расчета:
где i – номер метода, 1 ≤ i ≤ 9, (j–m)/n ≤ p < (j–m+1)/n, хj – j-ый порядковый элемент упорядоченного ряда, n – размер выборки, γ является функцией двух параметров: j = floor(np + m) и g = np + m – j, где floor – функция возвращающая наибольшее целое, но всё еще меньшее, чем аргумент функции (аналог в Excel – ОКРВНИЗ.МАТ), m – константа, определяемая типом алгоритма расчета квантиля. Если вас интересуют подробности, обратитесь к справочной системе R.
SAS предлгает 5 методов расчета квантилей.
Расчет децилей для дискретного ряда
-
Определяем номер дециля по формуле:
,
-
Если номер дециля – целое число, то значение дециля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру дециля. Например, если номер дециля равен 20, его значение будет равно значению признака с S =20 (накопленной частотой равной 20).
Если номер дециля – нецелое число, то дециль попадает между двумя наблюдениями. Значением дециля будет сумма, состоящая из значения элемента, для которого накопленная частота равна целому значению номера дециля, и указанной части (нецелая часть номера дециля) разности между значением этого элемента и значением следующего элемента.
Например, если номер дециля равна 20,25, дециль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.
Квантили специальных видов
Часто используются Квантили специальных видов:
- процентили x p/100 , p=1, 2, 3, …, 99
- квартили x p/4 , p=1, 2, 3
- медиана x 1/2
В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).
Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.
Примечание : Про проверку статистических гипотез см. статью Проверка статистических гипотез в MS EXCEL . Про построение доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
В данных задачах часто используется специальная терминология:
- Нижний квантиль уровня альфа ( α percentage point)
- Верхний квантиль уровня альфа (upper α percentage point)
- Двусторонние квантили уровня альфа .
Нижний квантиль уровня альфа – это обычный α-квантиль. Чтобы пояснить название « нижний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения (см. файл примера лист Квантили ).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше α-квантиля . Из определения квантиля эта вероятность равна α . Из графика функции распределения становится понятно, откуда происходит название ” нижний квантиль” – выделенная область расположена в нижней части графика.
Для α=0,05, нижний 0,05-квантиль стандартного нормального распределения равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при проверке гипотез и построении доверительных интервалов чаще используется “верхний” α-квантиль. Покажем почему.
Верхним α – квантилем называют такое значение x α , для которого вероятность, того что случайная величина X примет значение больше или равное x α равна альфа: P(X>= x α )= α . Из определения понятно, что верхний альфа – квантиль любого распределения равен нижнему (1- α) – квантилю. А для распределений, у которых функция плотности распределения является четной функцией, верхний α – квантиль равен нижнему α – квантилю со знаком минус . Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие верхний α – квантиль? Только из соображения удобства, т.к. он при α всегда положительный (в случае стандартного нормального распределения ). А при проверке гипотез α равно уровню значимости , который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре проверки гипотез пришлось бы записывать условие отклонения нулевой гипотезы μ>μ 0 как Z 0 >Z 1- α , подразумевая, что Z 1- α – обычный квантиль порядка 1- α (или как Z 0 >-Z α ). C верхнем квантилем эта запись выглядит проще Z 0 >Z α .
Примечание : Z 0 – значение тестовой статистики , вычисленное на основе выборки . Подробнее см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .
Чтобы пояснить название « верхний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения для α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше верхнего 0,05-квантиля , т.е. больше значения 1,645. Эта вероятность равна 0,05.
На графике плотности вероятности площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика функции распределения становится понятно, откуда происходит название “верхний” квантиль – выделенная область расположена в верхней части графика. Если Z 0 больше верхнего квантиля , т.е. попадает в выделенную область, то нулевая гипотеза отклоняется.
Также при проверке двухсторонних гипотез и построении соответствующих доверительных интервалов иногда используется понятие “двусторонний” α-квантиль. В этом случае условие отклонения нулевой гипотезы звучит как |Z 0 |>Z α /2 , где Z α /2 – верхний α/2-квантиль . Чтобы не писать верхний α/2-квантиль , для удобства используют “двусторонний” α-квантиль. Почему двусторонний? Как и в предыдущих случаях, построим график плотности вероятности стандартного нормального распределения и график функции распределения .
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение между нижним квантилем уровня α /2 и верхним квантилем уровня α /2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z 0 попадает в одну из выделенных областей, то нулевая гипотеза отклоняется.
Вычислить двусторонний 0,05 – квантиль это можно с помощью формул MS EXCEL: =НОРМ.СТ.ОБР(1-0,05/2) или =-НОРМ.СТ.ОБР(0,05/2)
Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Аналогичным образом квантили вычисляются и для распределения Стьюдента . Например, вычислять верхний α/2- квантиль распределения Стьюдента с n -1 степенью свободы требуется, если проводится проверка двухсторонней гипотезы о среднем значении распределения при неизвестной дисперсии ( см. эту статью ).
Для верхних квантилей распределения Стьюдента часто используется запись t α/2,n-1 . Если такая запись встретилась в статье про проверку гипотез или про построение доверительного интервала , то это именно верхний квантиль .
Примечание : Функция плотности вероятности распределения Стьюдента , как и стандартного нормального распределения , является четной функцией.
Чтобы вычислить в MS EXCEL верхний 0,05/2 – квантиль для t-распределения с 10 степенями свободы (или тоже самое двусторонний 0,05-квантиль ), необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05; 10) или =СТЬЮДРАСПОБР(0,05; 10) или =СТЬЮДЕНТ.ОБР(1-0,05/2; 10) или =-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е. двусторонний квантиль .
Квантили распределения ХИ-квадрат
Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).
При проверке таких гипотез также используются верхние квантили. Например, при двухсторонней гипотезе требуется вычислить 2 верхних квантиля распределения ХИ 2 : χ 2 α/2,n-1 и χ 2 1- α/2,n-1 . Почему требуется вычислить два квантиля , не один, как при проверке гипотез о среднем , где используется стандартное нормальное распределение или t-распределение ?
Дело в том, что в отличие от стандартного нормального распределения и распределения Стьюдента , плотность распределения ХИ 2 не является четной (симметричной относительно оси х). У него все квантили больше 0, поэтому верхний альфа-квантиль не равен нижнему (1-альфа)-квантилю или по-другому: верхний альфа-квантиль не равен нижнему альфа-квантилю со знаком минус.
Чтобы вычислить верхний 0,05/2 – квантиль для ХИ 2 -распределения с числом степеней свободы 10, т.е. χ 2 0,05/2,n-1 , необходимо в MS EXCEL записать формулу =ХИ2.ОБР.ПХ(0,05/2; 10) или =ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике функции распределения .
Чтобы вычислить верхний (1-0,05/2)- квантиль при том же числе степеней свободы , т.е. χ 2 1-0,05/2,n-1 и необходимо записать формулу =ХИ2.ОБР.ПХ(1-0,05/2; 10) или =ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Источники
- https://dic.academic.ru/dic.nsf/ruwiki/291015
- https://k-tree.ru/articles/statistika/analiz_dannyh/svoistva_raspredeleniia
- https://univer-nn.ru/zadachi-po-statistike-primeri/kvartili-v-statistike/
- https://excel2.ru/articles/kvartili-i-interkvartilnyy-interval-iqr-v-ms-excel
- https://nuancesprog.ru/p/3307/
- https://exceltable.com/funkcii-excel/primery-funkcii-kvartil
- https://baguzin.ru/wp/kvartil-kakie-formuly-rascheta-ispol/
- https://studfile.net/preview/5316597/page:4/
- https://excel2.ru/articles/kvantili-raspredeleniy-ms-excel
Функция КВАРТИЛЬ
Возвращает квартиль множества данных. Квартиль часто используются при анализе продаж для разбиения генеральной совокупности на группы. Например, можно воспользоваться функцией КВАРТИЛЬ, чтобы найти среди всех предприятий 25 процентов наиболее доходных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция КВАРТИЛЬ.ИСКЛ и Функция КВАРТИЛЬ.ВКЛ.
Синтаксис
Аргументы функции КВАРТИЛЬ описаны ниже.
Массив Обязательный. Массив или диапазон ячеек с числовыми значениями, для которых определяется значение квартиля.
Часть Обязательный. Значение, которое требуется вернуть.
Все, рассмотренные в этом разделе инструменты вычисляют значения квантилей как значения функций, обратных соответствующим функциям распределения. Все эти функции – библиотечные функции Excel из группы функций «Статистические»,.
Функция вычисления критических точек распределения Лапласа
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) стандартного нормального распределения.
Функция вычисления критических точек распределения Стьюдента
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения Стьюдента с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
Важно знать, что функция Excel СТЬЮДРАСПОБР( p , k ) возвращает значение t , при котором P (| x | > t ) = p , x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы.
Поэтому решение уравнения в Excel возвращает функция СТЬЮДРАСПОБР( a , n – 1).
Функция вычисления критических точек распределения
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
В Excel функция распределения случайной величины определена нестандартно: F x ( x ) = P ( x > x ). Поэтому для вычисления квантиля вводим в качестве аргумента функции ХИ2ОБР значение вероятности, равное , а для вычисления – .
Excel for Microsoft 365 Excel for Microsoft 365 for Mac Excel for the web Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 for Mac Excel 2016 Excel 2016 for Mac Excel 2013 Excel 2010 Excel 2007 Excel for Mac 2011 Excel Starter 2010 More…Less
Returns the quartile of a data set. Quartiles often are used in sales and survey data to divide populations into groups. For example, you can use QUARTILE to find the top 25 percent of incomes in a population.
Important: This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.
For more information about the new functions, see QUARTILE.EXC function and QUARTILE.INC function.
Syntax
QUARTILE(array,quart)
The QUARTILE function syntax has the following arguments:
-
Array Required. The array or cell range of numeric values for which you want the quartile value.
-
Quart Required. Indicates which value to return.
|
If quart equals |
QUARTILE returns |
|---|---|
|
0 |
Minimum value |
|
1 |
First quartile (25th percentile) |
|
2 |
Median value (50th percentile) |
|
3 |
Third quartile (75th percentile) |
|
4 |
Maximum value |
Remarks
-
If array is empty, QUARTILE returns the #NUM! error value.
-
If quart is not an integer, it is truncated.
-
If quart < 0 or if quart > 4, QUARTILE returns the #NUM! error value.
-
MIN, MEDIAN, and MAX return the same value as QUARTILE when quart is equal to 0 (zero), 2, and 4, respectively.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data |
||
|---|---|---|
|
1 |
||
|
2 |
||
|
4 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
10 |
||
|
12 |
||
|
Formula |
Description (Result) |
R |
|
=QUARTILE(A2:A9,1) |
First quartile (25th percentile) of the data above (3.5) |
3.5 |
Need more help?
Want more options?
Explore subscription benefits, browse training courses, learn how to secure your device, and more.
Communities help you ask and answer questions, give feedback, and hear from experts with rich knowledge.
3 способа расчета полинома в Excel.
Автор: Алексей Батурин.
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax 2 +bx+c (полином второй степени) и y=ax 3 +bx 2 +cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
У полинома второй степени y=ax 2 +bx+c один экстремум (на графике ниже 1 максимум).
У Полинома третьей степени y=ax 3 +bx 2 +cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
Выделяем ряд со значениями и строим график временного ряда.
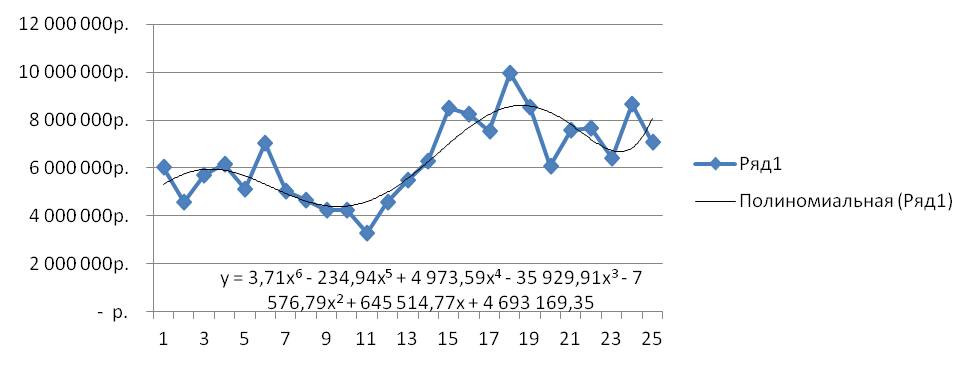
На график добавляем полином 6-й степени.
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
После этого уравнение выводится на график y = 3,7066x 6 — 234,94x 5 + 4973,6x 4 — 35930x 3 — 7576,8x 2 + 645515x + 5E+06 . Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
Получаем следующего вида формулу:
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^ <1:2:3:4:5:6>— для расчета коэффициентов полинома 6-й степени
- ^ <1:2:3:4:5>— для расчета коэффициентов полинома 5-й степени
- ^ <1:2>— для расчета коэффициентов полинома 2-й степени
Получаем формулу следующего вида:
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Множественная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти простую линейную регрессию – прогнозирование на основе значений только одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Множественного регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Множественный регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется множественной регрессией .
Множественная линейная регрессионная модель (Multiple Linear Regression Model) имеет вид Y=β 0 +β 1 *X 1 +β 2 *X 2 +…+β k *X k +ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е. регрессоров . ε — случайная ошибка . Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных линейная модель имеет вид:
Параметры этой модели β i нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β 0 , β 1 , β 2 ) обычно вычисляются методом наименьших квадратов (МНК) , который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Ошибка ε имеет случайную природу и имеет свою функцию распределения со средним значением =0 и дисперсией σ 2 .
Оценки b 1 и b 2 называются коэффициентами регрессии , они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются неизменными .
Сдвиг (intercept) или постоянный член b 0 , определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто сдвиг не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями МНК ).
Вычислив оценки, полученные методом МНК, позволяют прогнозировать значения переменной Y:
Примечание : Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в плоскости регрессии ).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что прочность нити Y зависит от концентрации исходного раствора (Х 1 ) и температуры реакции (Х 2 ), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
В MS EXCEL коэффициенты множественной регрессии удобнее всего вычислить с помощью функции ЛИНЕЙН() . Это сделано в файле примера на листе Коэффициенты . Чтобы вычислить оценки:
- выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2 коэффициента регрессии + величина сдвига = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон С8:Е8 ;
- в Строке формул введите = ЛИНЕЙН(D20:D50;B20:C50) . Предполагается, что в столбце В содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах С и D содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).
- нажмите CTRL+SHIFT+ENTER (т.к. это формула массива ).
В левой ячейке будет рассчитано значение коэффициента регрессии b 2 для переменной Х2, в средней ячейке — значение коэффициента регрессии b 1 для переменной Х1, в правой – сдвиг . Обратите внимание, что порядок вывода коэффициентов регрессии обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент b 2 располагается левее по отношению к b 1 , тогда как значения переменной Х2 располагаются правее значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17 файла примера .
Примечание : В принципе без функции ЛИНЕЙН() можно обойтись, записав альтернативные формулы. Для этого в файле примера на листе Коэффициенты в столбцах I : K вычислены отклонения значений переменных Х 1i , Х 2i , Y i от их средних значений 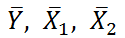
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления коэффициентов регрессии значительно усложняются, поэтому следует использовать матричный подход.
В файле примера на листе Матричная форма выполнены расчеты коэффициентов регрессии с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной формулой массива :
Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b =(X T X) -1 (X T Y) или в другом виде записи b =(X ’ X) -1 (X ’ Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Диаграмма рассеяния
В случае простой линейной регрессии (один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят диаграмму рассеяния (двумерную).
В случае множественной линейной регрессии двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См. файл примера лист Диагр расс (матричная) ).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см. Introduction to linear regression analysis / D . C . Montgomery , E . A . Peck , G . G . Vining , раздел 3.2.5 ), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X i и Y.
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной диаграммы рассеяния . В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно плоскости регрессии , то картину, на мой взгляд, будет проще интерпретировать.
Сравним две матричные диаграммы рассеяния (см. файл примера на листе «Диагр расс (в плоск регрессии)» , построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно провести процедуру F-теста ).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
- Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть среднее и разделить на стандартное отклонение ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со стандартным нормальным распределением , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
- Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти матрицу вращения , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
- Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках Q31:S31 ).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Примечание: В MS EXCEL прогнозное значение Y для заданных Х 1 и Х 2 можно также предсказать с помощью функции ТЕНДЕНЦИЯ() . При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х 1 и Х 2 , а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х 1i и Х 2i ) для выбранного наблюдения i (см. файл примера, лист Коэффициенты, столбец G ). Функция ПРЕДСКАЗ() , использованная нами в простой регрессии, не работает в случае множественной регрессии .
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить доверительный интервал этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае простой линейной регрессии , для построения доверительных интервалов нам потребуется сначала вычислить стандартную ошибку модели (standard error of the model) , которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления стандартной ошибки оценивают дисперсию ошибки ε, т.е. сигма^2 (ее часто обозначают как MS Е либо MSres ) . Затем, вычислив из полученной оценки квадратный корень, получим Стандартную ошибку регрессии (часто обозначают как SEy или sey ).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi ( Sum of Squared Errors ). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае простой множественной регрессии с 2-мя регрессорами число степеней свободы равно n-3, т.к. при построении плоскости регрессии было оценено 3 параметра модели b (т.е. на это было «потрачено» 3 степени свободы ).
В MS EXCEL стандартную ошибку SEy можно вычислить формулы (см. файл примера, лист Статистика ):
Стандартная ошибка нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) – уровень значимости (обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
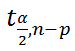
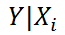
Стандартная ошибка среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе Оценка неизвестных параметров мы получили точечные оценки коэффициентов регрессии . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ) коэффициентов регрессии .
Стандартная ошибка коэффициента регрессии b j (обозначается se ( b j ) ) вычисляется на основании стандартной ошибки по следующей формуле:
где C jj является диагональным элементом матрицы (X ’ X) -1 . Для коэффициента сдвига b 0 индекс j=1 (верхний левый элемент), для b 1 индекс j=2, b 2 индекс j=3 (нижний правый элемент).
SEy – стандартная ошибка регрессии (см. выше ).
В MS EXCEL стандартные ошибки коэффициентов регрессии можно вычислить с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. статью Функция MS EXCEL ЛИНЕЙН() .
Применяя матричный подход стандартные ошибки можно вычислить и через обычные формулы (точнее через формулу массива , см. файл примера лист Статистика ):
= КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где t – это t-значение , которое можно вычислить с помощью формулы = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) для уровня значимости 0,05.
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии b j . Здесь мы считаем, что коэффициент регрессии b j имеет распределение Стьюдента с n-p степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все коэффициенты регрессии β равны 0.
Чтобы убедиться, что вычисленная нами оценка коэффициентов регрессии не обусловлена лишь случайностью (они не случайно отличны от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы Н 1 принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением дисперсионного анализа , использованного нами в случае простой линейной регрессии (F-тест) .
Если нулевая гипотеза справедлива, то тестовая F -статистика имеет F-распределение со степенями свободы k и n — k -1 , т.е. F k, n-k-1 :
Проверку значимости регрессии можно также осуществить через вычисление p -значения . В этом случае вычисляют вероятность того, что случайная величина F примет значение F 0 (это и есть p-значение ), затем сравнивают p-значение с заданным уровнем значимости α (альфа) . Если p-значение больше уровня значимости , то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
В MS EXCEL для проверки гипотезы через p -значение используйте формулу =F.РАСП.ПХ(F 0 ;k;n-k-1) файл примера лист Статистика , где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного уровня значимости F 1-альфа, k, n-k-1 можно вычислить по формуле = F.ОБР(1- альфа;k;n-k-1) или = F.ОБР.ПХ(альфа;k; n-k-1) . Другими словами требуется вычислить верхний альфа- квантиль F -распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F 0 > F 1-альфа, k, n-k-1 мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Надстройка , которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
- задать коэффициенты регрессии ( b );
- задать тренд (вычислить значения Y= b0 +b1 * Х 1 + b2 * Х 2 );
- задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в файле примера, лист Тренд для случая 2-х регрессоров. Там же построены диаграммы рассеяния .
Коэффициент детерминации
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью ( SSR ) / Общая изменчивость ( SST ).
Этот показатель можно вычислить с помощью функции ЛИНЕЙН() :
При добавлении в модель новой объясняющей переменной Х, коэффициент детерминации будет всегда расти. Поэтому, рост коэффициента детерминации не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является нормированный коэффициент детерминации (Adjusted R-squared):
где p – число независимых регрессоров (вычисления см. файл примера лист Статистика ).
Нелинейная регрессия в Excel
Нелинейная регрессия в Excel
Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.
Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.
Основными типами нелинейных регрессий являются:
- полиномиальные (квадратичная, кубическая);
- гиперболическая;
- степенная;
- показательная;
- логарифмическая.
Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.
В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке
На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:
Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax 2 +bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.
Получится заполненная нужными для решения уравнения таблица вида.
Далее посчитаем суммы по каждому столбцу — воспользуемся ∑ в программе Excel.
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=«. Следуем той системе уравнений, которую мы избрали для решения регрессии.
То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.
В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.
Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.
Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.
Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) — «=K22/K21»; b (в ячейке M23) — «=K23/K21»; с (в ячейке M24) — «=K24/K21».
Получим наше искомое уравнение парной квадратичной регрессии:
y=-0,074x 2 +2,151x+6,523
Оценим тесноту линейной связи индексом корреляции.
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24». Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.
Для вычисления сумм (Y-Y усредненное) 2 добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.
В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».
Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.
Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».
Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.
Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки
Если возникнет необходимость, по полученным значениям мы можем построить график.
источники:
http://excel2.ru/articles/mnozhestvennaya-regressiya-v-ms-excel
http://pcandlife.ru/nelineinaya-regressiya-v-excel/
A Q-Q plot, short for “quantile-quantile” plot, is often used to assess whether or not a set of data potentially came from some theoretical distribution. In most cases, this type of plot is used to determine whether or not a set of data follows a normal distribution.
This tutorial explains how to create a Q-Q plot for a set of data in Excel.
Example: Q-Q Plot in Excel
Perform the follow steps to create a Q-Q plot for a set of data.
Step 1: Enter and sort the data.
Enter the following data into one column:
Note that this data is already sorted from smallest to largest. If your data is not already sorted, go to the Data tab along the top ribbon in Excel, then go to the Sort & Filter group, then click the Sort A to Z icon.
Step 2: Find the rank of each data value.
Next, use the following formula to calculate the rank of the first value:
=RANK(A2, $A$2:$A$11, 1)
Copy this formula down to all of the other cells in the column:
Step 3: Find the percentile of each data value.
Next, use the following formula to calculate the percentile of the first value:
=(B2-0.5)/COUNT($B$2:$B$11)
Copy this formula down to all of the other cells in the column:
Step 4: Calculate the z-score for each data value.
Use the following formula to calculate the z-score for the first data value:
=NORM.S.INV(C2)
Copy this formula down to all of the other cells in the column:
Step 5: Create the Q-Q plot.
Copy the original data from column A into column E, then highlight the data in columns D and E.
Along the top ribbon, go to Insert. Within the Charts group, choose Insert Scatter (X, Y) and click the option that says Scatter. This will produce the follow Q-Q plot:
Click the plus sign on the top right-hand corner of the graph and check the box next to Trendline. This will add the following line to the chart:
Feel free to add labels for the title and axes of the graph to make it more aesthetically pleasing:
The way to interpret a Q-Q plot is simple: if the data values fall along a roughly straight line at a 45-degree angle, then the data is normally distributed. We can see in our Q-Q plot above that the data values tend to deviate from the 45-degree line quite a bit, especially on the tail ends, which could be an indication that the data set is not normally distributed.
Although a Q-Q plot isn’t a formal statistical test, it offers an easy way to visually check whether or not a data set is normally distributed.
В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.
Ключевые слова:
безотказная работа, доверительный интервал, испытания, нормальный закон распределения, число отказов.
Определение показателей надёжности необходимо для формулирования требования по надежности к проектируемым устройствам или системам. Показатель надежности — это количественная характеристика одного или нескольких свойств, составляющих надежность объекта [1].
Поскольку отказы и сбои элементов являются случайными событиями, то теория вероятностей и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности должны выбираться из числа показателей, принятых в теории вероятностей [2, с.
13].
Количественные характеристики надежности при нормальном законе распределения отказов могут быть определены из следующих выражений:
(1)
P(t)=
(2)
λ(
)=
(3),
где
нормированная и центрированная функция Лапласа.
Произведем расчет параметров надежности испытаний, проведенных в течение 100 часов на 100 деталях, 34 из которых вышли из строя.
Для построения статистического ряда время испытаний разбивают на интервалы (разряды) и подсчитывают частоту, интенсивность и вероятность отказов, используя выражения (1), (2) и (3). Определяют доверительные интервалы математического ожидания и среднеквадратичного отклонения при нормальном законе распределения отказов и заданном коэффициенте доверия [3, с. 60].
Результаты вычислений представлены в таблице Excel (Таблица 1).
Таблица 1
Результаты расчета основных показателей испытаний
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
5 |
3 |
5 |
2 |
2 |
3 |
3 |
3 |
5 |
3 |
|
|
0,935 |
0,917 |
0,896 |
0,870 |
0,841 |
0,805 |
0,767 |
0,725 |
0,680 |
0,633 |
|
|
0,983 |
0,986 |
0,988 |
0,990 |
0,991 |
0,992 |
0,993 |
0,993 |
0,994 |
0,994 |
|
λн(t) |
1,050 |
1,074 |
1,102 |
1,137 |
1,178 |
1,232 |
1,294 |
1,369 |
1,460 |
1,570 |
|
|
0,064 |
0,082 |
0,103 |
0,129 |
0,158 |
0,194 |
0,232 |
0,274 |
0,319 |
0,366 |
|
|
0,014 |
0,002 |
0,026 |
0,020 |
0,011 |
0,005 |
0,002 |
0,014 |
0,009 |
0,026 |
|
|
0,085065269 |
|||||||||
Листинг фрагмента программы расчета показателей при нормальном законе распределения:
‘Вычислим 43 строку таблицы(45)=============================Рн(t)
СтрокаТаблицы = 45
‘a=(t-Tср)/Сигма
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
a = Abs(Sheets(«ОсновнаяТаблица»).
‘b=Фо
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
If a <= Sheets(«Таблица функции Лапласа»).Cells(2, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(2, 2).Value
GoTo далее
End If
If a >= Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
GoTo далее
End If
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value = a Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
GoTo далее3
End If
If a < Sheets(«Таблица функции Лапласа»).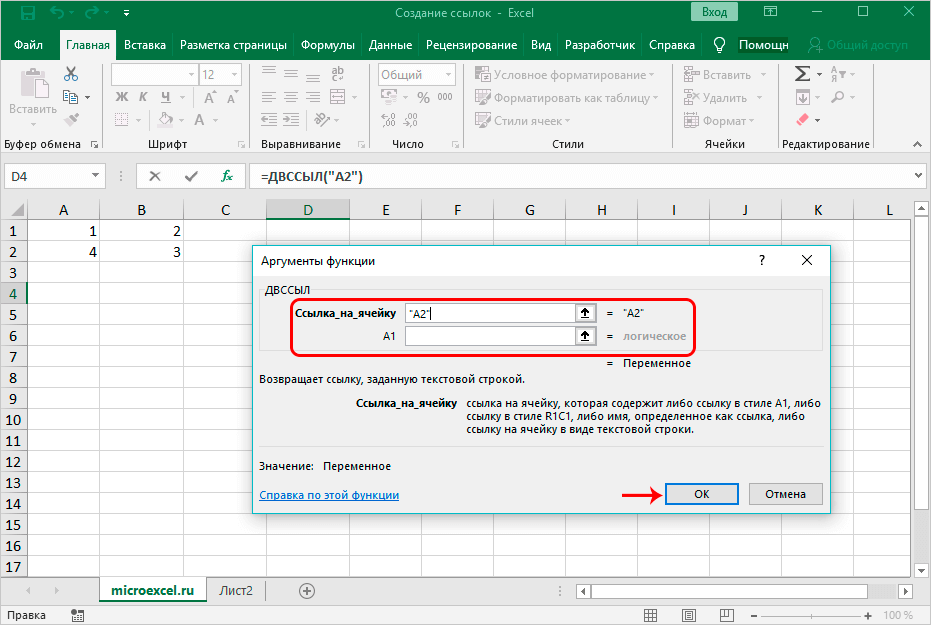
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value — a < a — Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
Else
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
End If
GoTo далее3
End If
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
далее3:
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 0.5 + ф0
Next
‘Вычислим 44 строку таблицы(46)=============================fн(t)
СтрокаТаблицы = 46
СтолбецТаблицы = 4
Pi = Application.WorksheetFunction.Pi
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).
Next
‘Заполним 45 строку таблицы(47)=============================Лямбда н(t)
СтрокаТаблицы = 47
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Sheets(«ОсновнаяТаблица»).Cells(46, n).Value / Sheets(«ОсновнаяТаблица»).Cells(45, n).Value
Next
Для определения доверительного интервала для математического ожидания по таблице квантилей распределения Стьюдента находят квантиль вероятности. Используя выражения (4) и (5) проводят расчеты
(4)
(5)
‘Заполним 30 строку таблицы(32)=============================Tср min
СтрокаТаблицы = 32
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).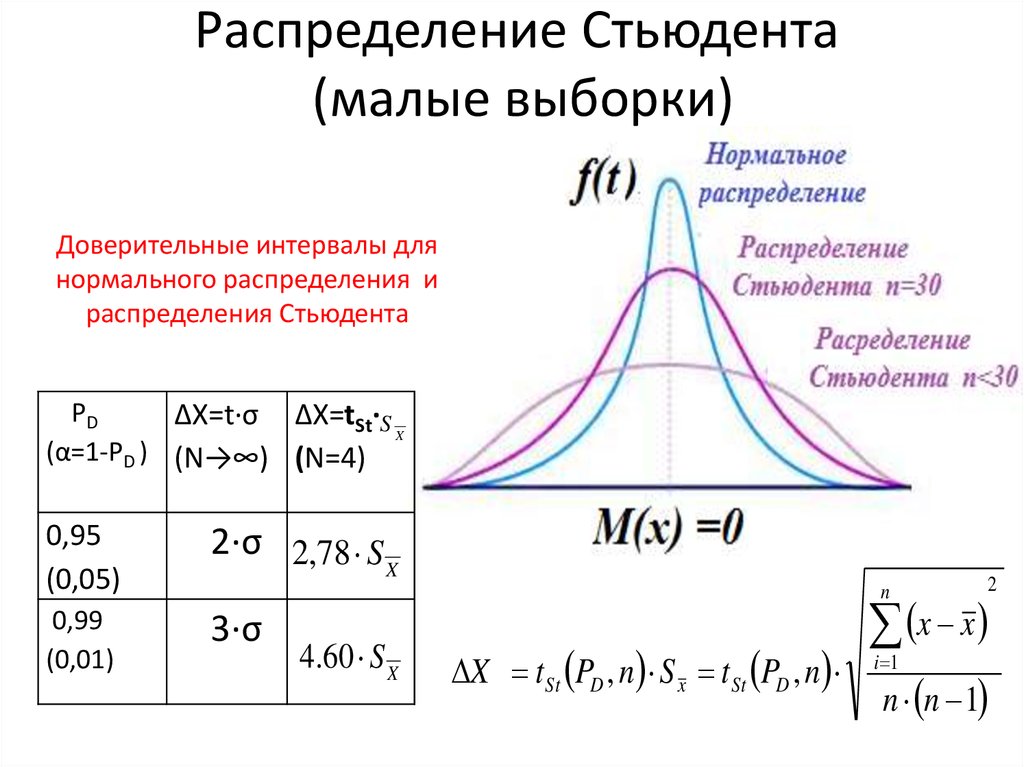
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 31 строку таблицы(33)=============================Tср max
СтрокаТаблицы = 33
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp + Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
|
Тср, min = |
79,29380755 ч. |
|
Тср, max = |
172,43129 ч. |
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей χ
2
– квадрат распределения определяют квантили для заданных вероятностей
P
1
и
P
2
.
|
(0,05) = |
3,32511 |
|
(0,95) = |
16,919 |
‘Заполним 32 строку таблицы(34)=============================X1(0,05)
СтрокаОсновнойТаблицы = 34
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).
СтрокаТабл = 4
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск10:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.05
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск11
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск11
End If
СледующийПоиск11:
СтолбецТаблКвантили = 11
While Sheets(«Квантили распределения хи»).
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск12
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск12
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск12:
x1 = Sheets(«Квантили распределения хи»).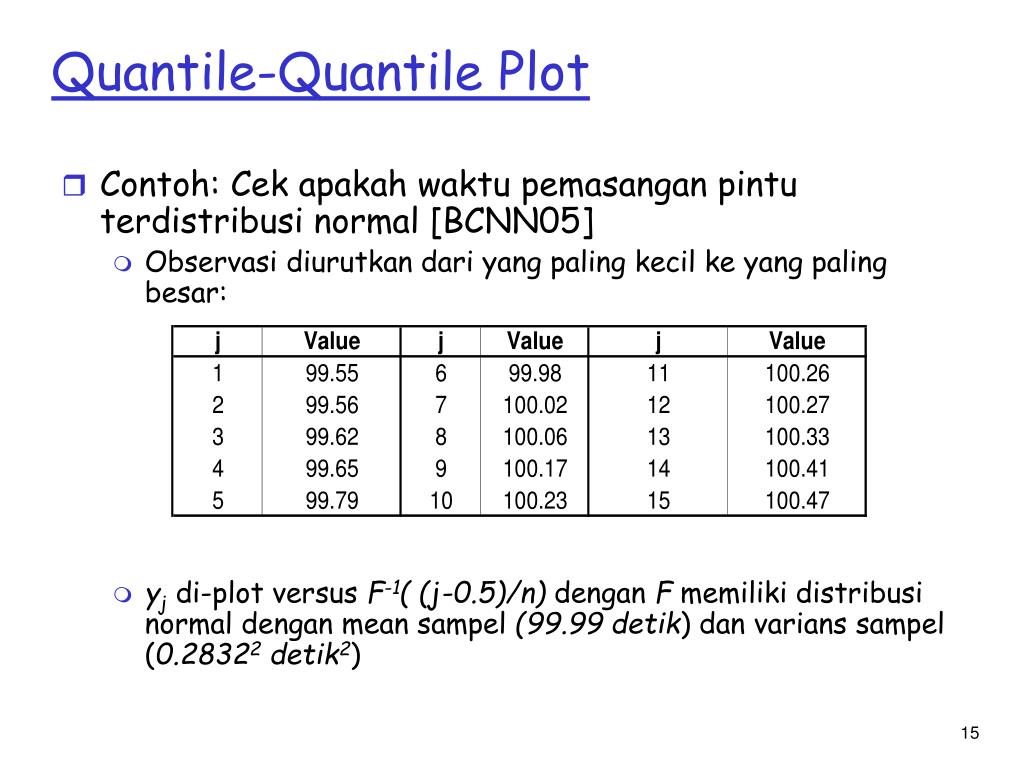
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 33 строку таблицы(35)=============================X2(0,95)
СтрокаОсновнойТаблицы = 35
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск13:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск14
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск14
End If
СледующийПоиск14:
СтолбецТаблКвантили = 2
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск15
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).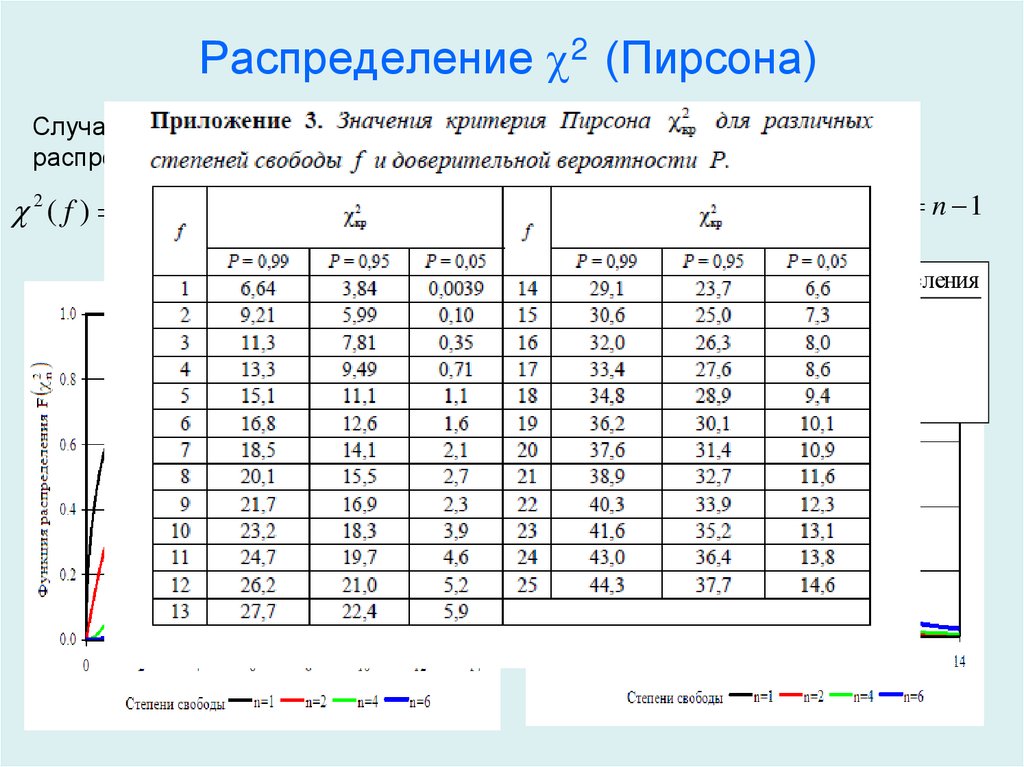
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск15
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск15:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).
Получим минимальное σ
min
и максимальное σ
max
значения среднеквадратического отклонения:
(6)
(7)
‘Заполним 34 строку таблицы(36)=============================Сигма min
СтрокаТаблицы = 36
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(35, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 35 строку таблицы(37)=============================Сигма max
СтрокаТаблицы = 37
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).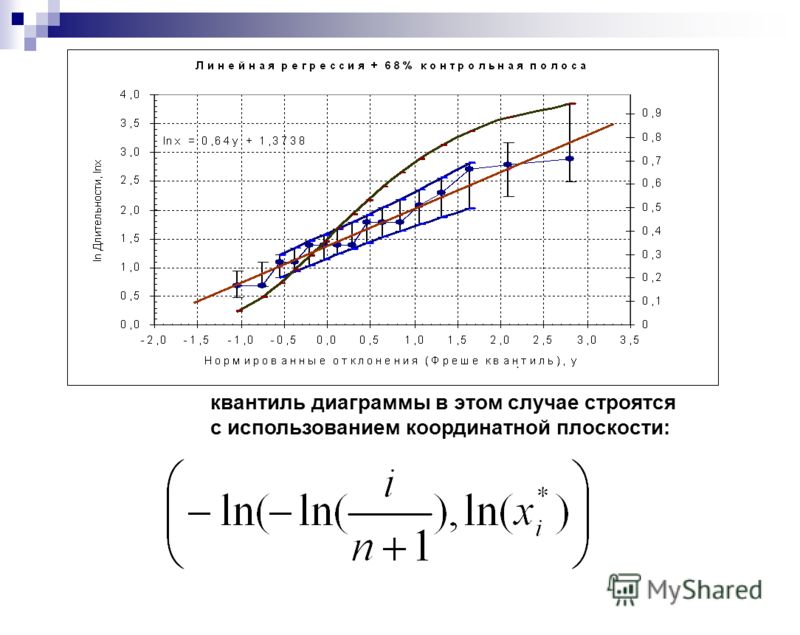
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
Число разрядов, на которые следует группировать статистический ряд, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и часто в нем обнаруживают незакономерные колебания), с другой стороны, оно не должен быть слишком малым (свойства распределения при этом описываются статистическим рядом слишком грубо).
Литература:
-
ГОСТ 27.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
- Федотов, А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск : Изд-во ОмГТУ, 2010 – 64 с.
- Коваленко, В. Н. Надежность устройств железнодорожной автоматики, телемеханики : учеб. пособие / В. Н. Коваленко. – Екатеринбург : Изд-во УрГУПС, 2013. – 87 с.
Основные термины (генерируются автоматически): Таблица функции, строка таблицы, доверительный интервал, Сигма, математическое ожидание, распределение отказов, среднеквадратичное отклонение, статистический ряд, таблица, теория вероятностей.
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ
КОРРЕЛЯЦИИ В ПРОГРАММЕ EXCEL
t-статистика=0,99*(КОРЕНЬ(20-2)/КОРЕНЬ(1-0,99*0,99))=29,7745296027549
Коэффициент корреляции=0,991477169252612
Распределение Стьюдента=2,10092204024104
Расчетное значение t-статистики больше квантиля распределения Стьюдента, следовательно величина коэффициента корреляции является значимой.
2. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ
МЕЖДУ ДВУМЯ ВЕЛИЧИНАМИ
1-ый способ
| a1= 0,5014 | a0= 2,5326 |
| Se1= 0,0155 | Se0= 0,7075 |
| R2= 0,9830 | Se= 0,5561 |
| Se= 0,5561 | n-k-1= 18 |
| QR= 322,4250 | Qe= 5,5670 |
Для проверки адекватности
модели нашли квантиль распределения Фишера Ff. с помощью функции FРАСПОБР
FРАСПОБР=4,4139
Проверили адекватность
построенной модели, используя расчетный уровень значимости (P):
2,18499711496499E-17
2 –й способ
|
а=2,532579627 |
|
в=0,50139175 |
Для данного примера
уравнение модели имеет вид:Y=2,53+0,5X
Проверка адекватности модели выполняется по расчетному уровню значимости P,
указанному в столбце Значимость F.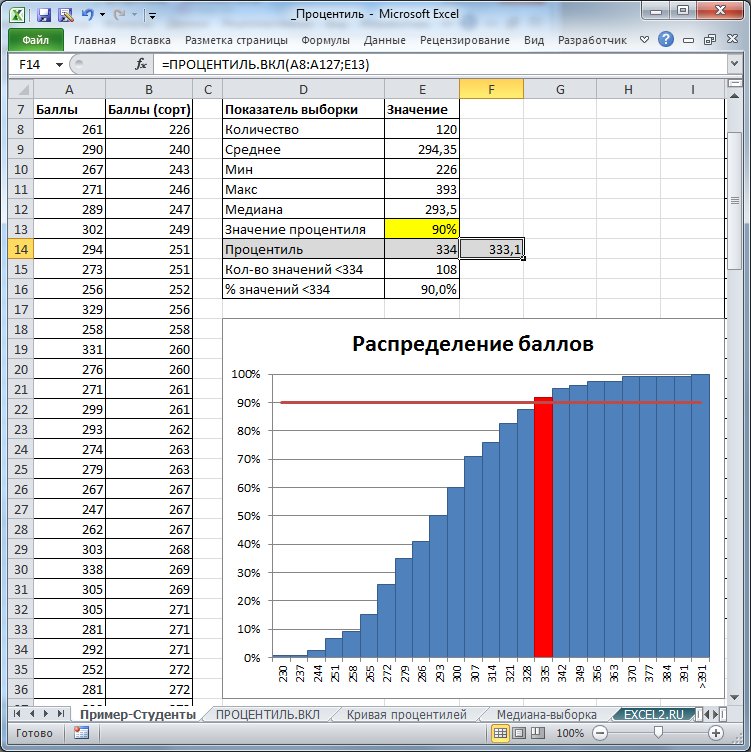
расчетный уровень значимости меньше заданного уровня значимости α =0,05, то модель адекватна.
Проверка статистической значимости коэффициентов модели выполняется по расчетным
уровням значимости P, указанным в столбце P-значение. Если расчетный уровень значимости меньше заданного
уровня значимости α =0,05, то соответствующий
коэффициент модели статистически значим.
Множественный R – коэффициент корреляции. Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями. Для данного примера R= 0,99. Это позволяет сделать
вывод, что качество земли – один из основных факторов, от которого зависит
урожайность зерновых культур.
R-квадрат – коэффициент
детерминации. Он получается возведением в квадрат коэффициента корреляции –
R2=0,98. Он
показывает, что урожайность зерновых культур на 98% зависит от качества почвы,
а на долю других факторов приходится 0,02%.
3-ий способ (графический)
Расчет квантилей или процентилей в Excel
В этом руководстве показано, как вычислять квантили или процентили, связанные с доверительными интервалами, в Excel с помощью программного обеспечения XLSTAT.
Квантиль и процентили
XLSTAT имеет полный инструмент для вычисления квантилей или процентилей, их доверительного интервала и графического представления.
Квантили являются важными статистическими показателями, их легко понять. Квантиль 0,5 — это значение, при котором половина выборки находится ниже, а другая половина — выше. Его еще называют средним. Квантиль называется процентилем, если он основан на шкале от 0 до 100. 0,95-квантиль эквивалентен 95-процентилю и таков, что 95 % выборки ниже его значения, а 5 % выше.
Набор данных для создания квантиля
Набор данных был получен от [Lewis T. and Taylor L.R. (1967). Введение в экспериментальную экологию, Нью-Йорк: Academic Press, Inc. Это касается 237 детей, описанных по полу и росту в сантиметрах (1 см = 0,4 дюйма).
Настройка расчета определенного квантиля
После открытия XLSTAT выберите XLSTAT / Description / Quantiles , или нажмите на соответствующую кнопку панели инструментов «Описание» (см.
После нажатия кнопки появится диалоговое окно Quantile . Выберите данные на листе Excel.
В нашем случае; переменная — это «Высота». Данные должны быть количественными .
Поскольку для переменных был выбран заголовок столбца, необходимо активировать опцию Метки переменных .
Мы выбираем метод оценки по умолчанию ( средневзвешенное значение при x(Np) ) и оба типа доверительных интервалов с доверительной вероятностью 95 % .
Подробную информацию о статистических методах можно найти в справке XLSTAT.
Во вкладке диаграммы выбираем все диаграммы и нас интересует 67-процентиль (две трети детей меньше, а одна треть выше).
Вычисления начинаются после того, как вы нажмете на ОК . Затем будут отображены результаты.
Интерпретация результатов генерации квантилей
В первой таблице показаны некоторые описательные статистические данные о переменной высоты.
Затем отображается значение 67-процентиля. Две трети детей меньше 164,58 см.
Первый график (см. ниже) позволяет нам визуализировать эмпирическую кумулятивную функцию распределения со значением 67-го процентиля.
Вторая и третья диаграммы представляют собой коробчатую диаграмму и диаграмму рассеяния. 67-процентиль отображается синей линией.
Вы также можете использовать подвыборки, например пол можно использовать в качестве групповой переменной. Веса, связанные с наблюдениями, также могут быть включены.
Была ли эта статья полезной?
- Да
- №
Квантиль (квартиль, дециль и процентиль): расчет вручную + Microsoft
Квантиль — важная статистическая концепция, позволяющая разделить данные на равные группы.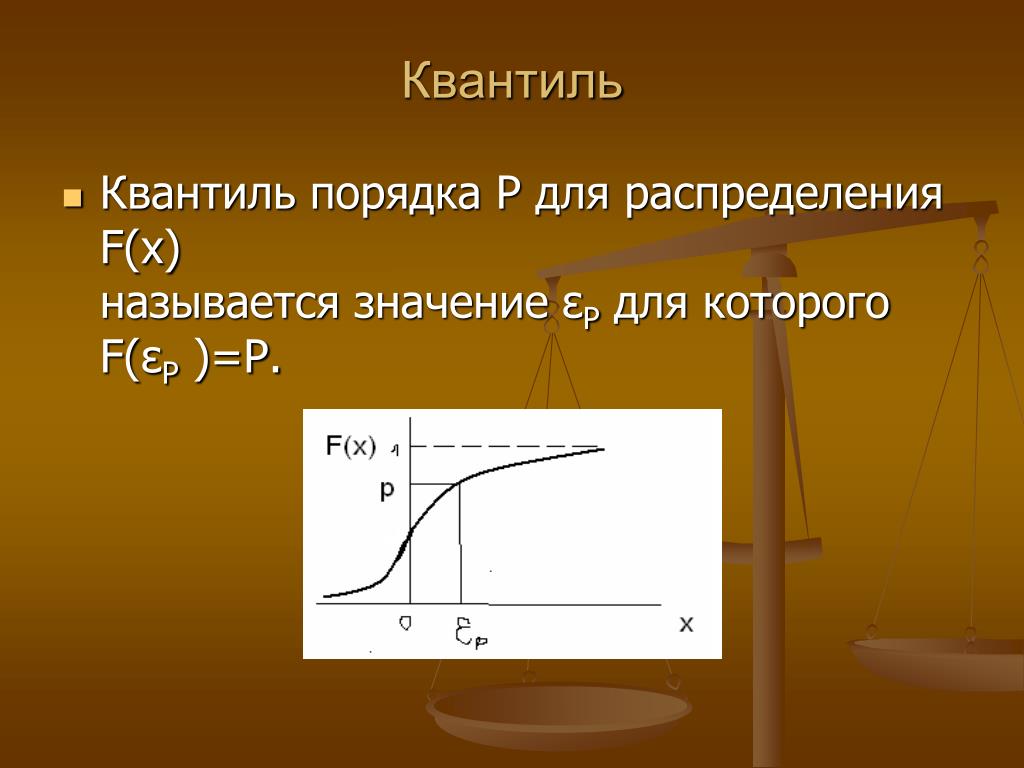
Квантиль
Квантиль — это мера, указывающая значение, ниже которого падает определенная доля наблюдений в группе наблюдений. Квантиль используется в статистике для разделения группы наблюдений на группы одинакового размера. Например, квантиль 0,25 — это значение, ниже которого падают 25% наблюдений; квантиль 0,50 — это значение, ниже которого падает 50%, и так далее. Другим родственным измерением является медиана, которая совпадает с квантилем 0,50, поскольку 50% данных находятся ниже медианы.
Какие общие квантили существуют?
Некоторые распространенные квантили включают:
1. Квартиль
Квартиль — это тип квантиля, который делит группу наблюдений на четыре группы одинакового размера.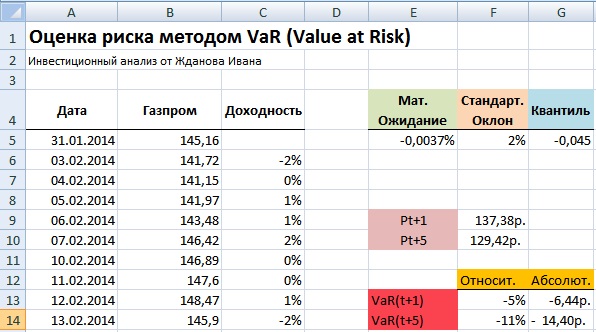
2. Дециль
Дециль – это мера, которая делит группу наблюдений на десять групп одинакового размера. Например, в группе наблюдений первый дециль (D1) — это значение, ниже которого попадают первые 10% наблюдений, второй дециль (D2) — это значение, ниже которого попадают первые 20% наблюдений, и скоро. 9-й дециль (D9) — это значение, ниже которого опускаются последние 10% наблюдений.
3. Процентиль
Процентиль — это мера, указывающая значение, ниже которого находится определенный процент наблюдений в группе наблюдений. Например, в группе наблюдений 20-й процентиль (P20) — это значение, ниже которого опускаются первые 20% наблюдений, 50-й процентиль (P50) — это значение, ниже которого опускаются средние 50% наблюдений, и 95-й процентиль (P95) — это значение, ниже которого падают последние 95% наблюдений.
50-й процентиль также является медианой, вторым квартилем и 5-м децилем.
Процентиль: Расчет вручную / Microsoft Excel
Процентиль — это мера, используемая в статистике для указания значения, ниже которого находится определенный процент наблюдений в группе наблюдений.
Чтобы найти местоположение определенного процентиля, такие программы, как Minitab, Python, R и Excel, используют следующие шаги:
- Расположите наблюдения в порядке возрастания.
- Используйте формулу для определения положения процентиля, чтобы вычислить положение, в котором будет располагаться значение процентиля, используя желаемое значение процентиля и общее количество наблюдений в качестве входных данных. Существует два подхода: EXC (Exclusive) и INC (Inclusive). Процентное положение в подходе EXC определяется формулой (K(N+1)), а положение в подходе INC определяется формулой (K(N-1)+1).
- Если местоположение процентиля является целым числом, значение в этой позиции в упорядоченном списке наблюдений является значением процентиля.
- Если местоположение процентиля не является целым числом, значение процентиля рассчитывается путем вычисления значения на пропорциональной основе между этими двумя числами.
Чтобы найти 65-й процентиль в группе из 8 наблюдений, вы должны сначала расположить наблюдения в порядке возрастания: 8, 9, 12, 22, 23, 33, 55, 61.
Затем вы должны использовать формулу для местоположения процентиля, чтобы вычислить положение, в котором будет расположен 65-й процентиль:
Для ПРОЦЕНТИЛЬ.ИСКЛ рассчитанный ранг равен (K(N+1)).
Расположение в процентиле (с использованием эксклюзивного подхода) = (left(frac{65}{100}right)(8+1)) = 5,85
Поскольку положение в процентиле не является целым числом, 65-й процентиль будет между 5-м пунктом (номер 23) и 6-м пунктом (номер 33) на пропорциональной основе. Это будет (23+0,85(33-23) = 31,5).
Для PERCENTILE.INC (и PERCENTILE) рассчитанный ранг равен (K(N-1)+1).
Расположение в процентах (с использованием инклюзивного подхода) = ((65/100) (8-1)+1) = 5,55
Поскольку местоположение процентиля не является целым числом, 65-й процентиль будет почти посередине между 5-м элементом (число 23) и 6-м элементом (число 33).
Квартиль: пример расчета вручную
Квартиль — это статистическое значение, которое делит набор данных на четыре равные части или четверти. Первый квартиль, также известный как нижний квартиль или Q1, — это значение, которое отделяет самые низкие 25 % данных от остальных. Второй квартиль, также известный как медиана или Q2, представляет собой значение, которое отделяет самые низкие 50% данных от самых высоких 50% данных. Третий квартиль, также известный как верхний квартиль или Q3, — это значение, которое отделяет самые высокие 25% данных от остальных.
Например, если у нас есть следующие числа: 14, 9, 10, 11, 11 и 6, мы можем разделить данные на четыре равные группы, найдя первый, второй и третий квартили.
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Затем нам нужно найти медиану, или Q2, которая является средним значением в наборе данных.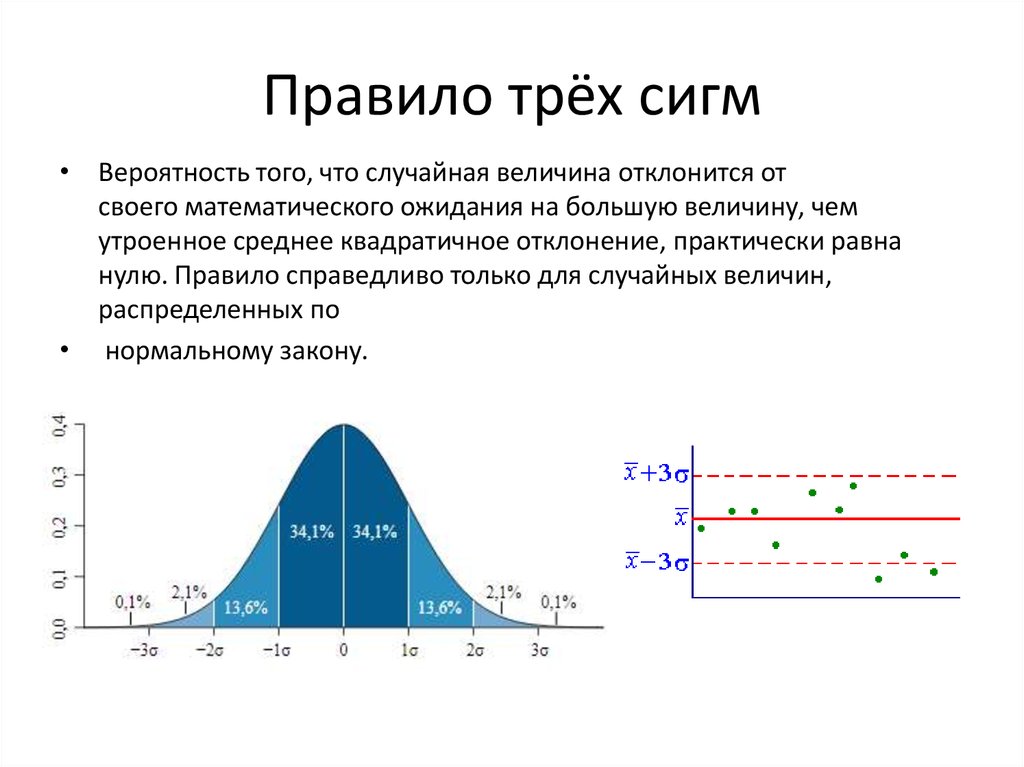
Чтобы найти нижний квартиль или Q1, мы берем медиану значений ниже медианы. В данном случае это будет медиана 9. Чтобы найти верхнюю квартиль или Q3, мы берем медиану значений выше медианы. В данном случае это будет медиана 11, 11 и 14, что равно 11.
Таким образом, для этого набора данных квартили: эти числа расчета квартиля не совпадают с расчетом Excel?
Квартиль Использование Excel:
Для расчета квартилей такие программы, как Microsoft Excel и Minitab, используют метод процентилей, как объяснялось ранее. Q1 рассчитывается как 25-й процентиль, Q2 — как 50-й и Q3 — как 75-й процентиль. Это приводит к тому, что значение квартиля иногда отличается от значения, рассчитанного с использованием обычного ручного метода расчета.
Возьмем тот же пример, который мы использовали ранее в ручном расчете для расчета первого квартиля (Q1).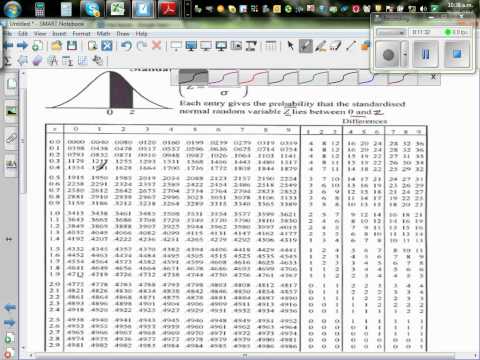
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Вы можете использовать функцию КВАРТИЛЬ.ИСКЛ или КВАРТИЛЬ.ВКЛ. найти квартили набора чисел в Excel.
Quartile.Exc
Для QUARTILE.EXC расчетный ранг равен K*(N+1). Чтобы рассчитать положение Q1 (или 25-го процентиля), подставим в эту формулу соответствующие значения.
Местоположение 1-го квартиля (с использованием эксклюзивного подхода) = (25/100) * (6+1) = 1,75
Поскольку положение процентиля не является целым числом, 1-й квартиль будет между 1-м элементом (номер 6) и 2-м элементом (номер 9) на пропорциональной основе. Получится (6 + (9-6)*0,75) = 8,25.
Использование Minitab: Если вы используете Minitab для расчета Q1, это значение (8,25), которое вы получите в описательной статистике. Minitab использует метод EXC для расчета процентилей и квартилей.
Квартиль.Вкл
Для КВАРТИЛЬ.

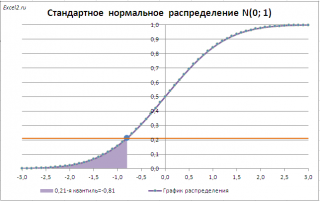
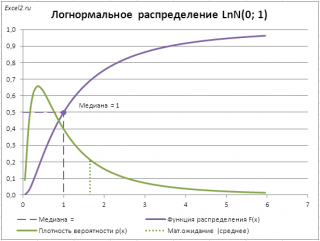
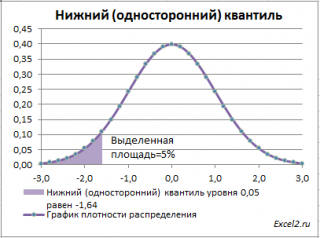
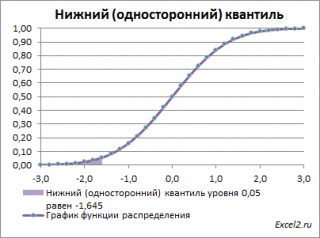
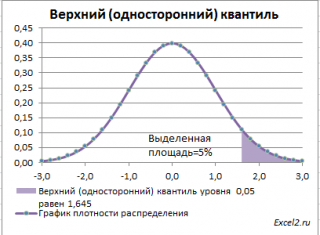
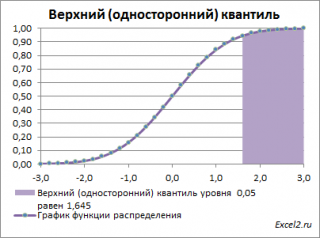
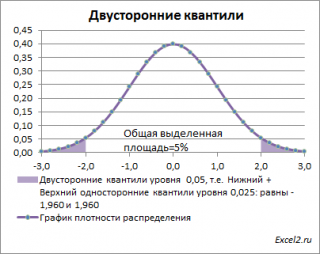
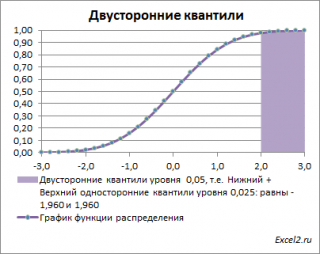
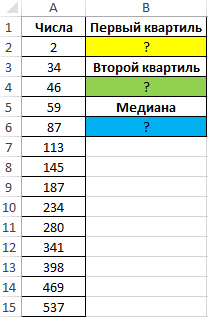
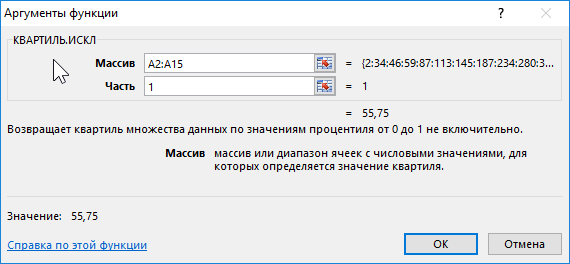
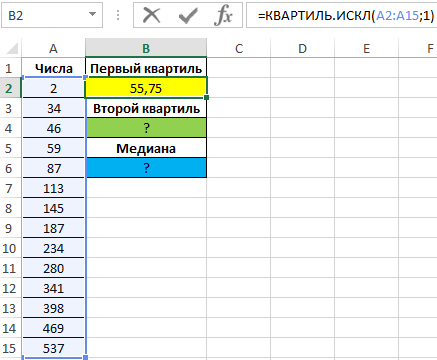
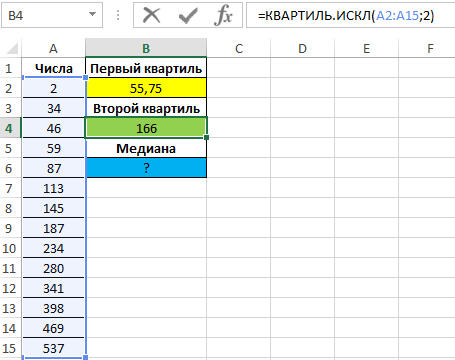
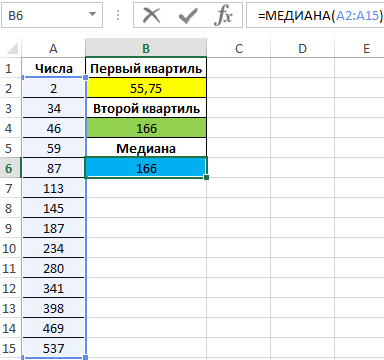
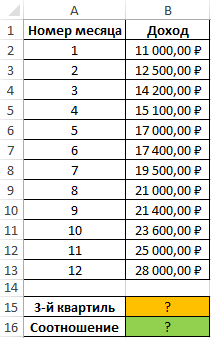
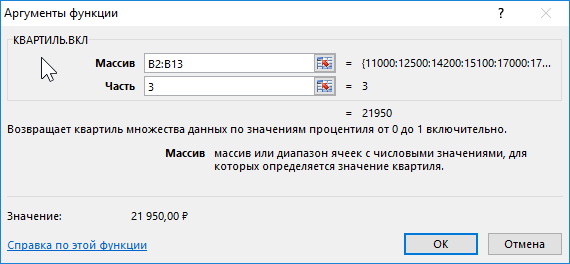
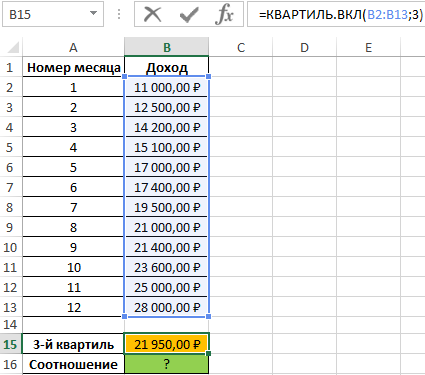
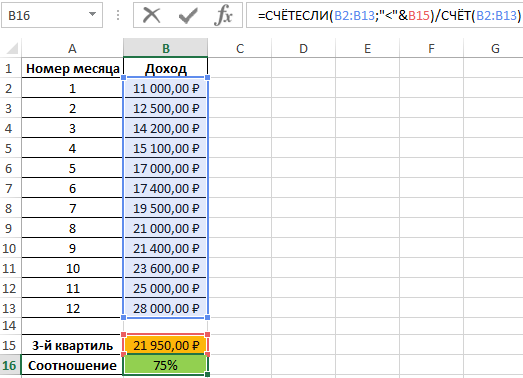
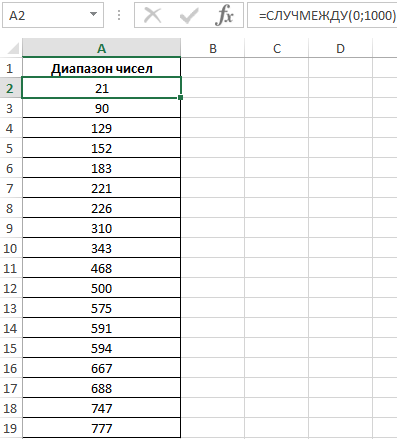
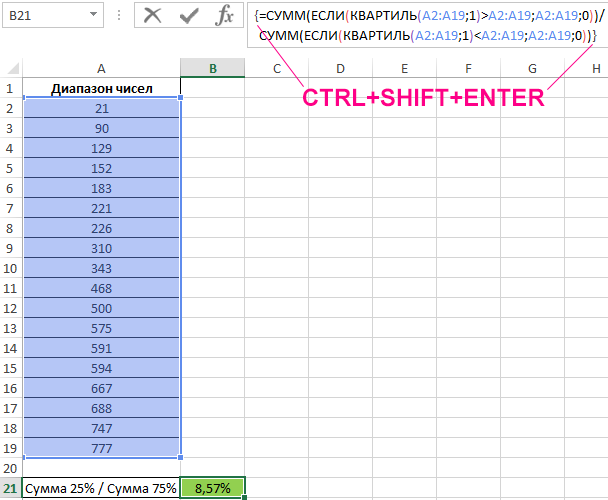
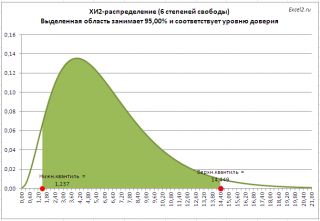
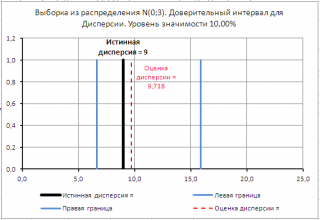
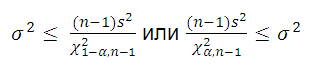
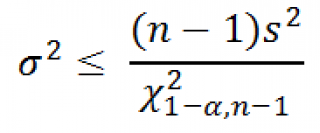
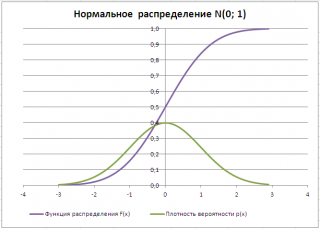
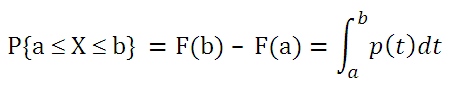
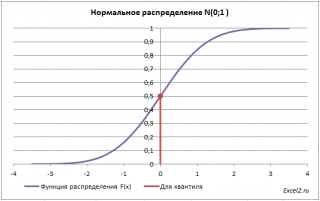
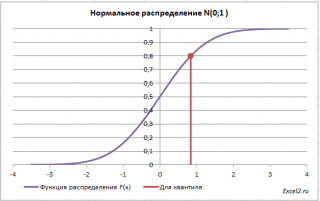



 ,
,












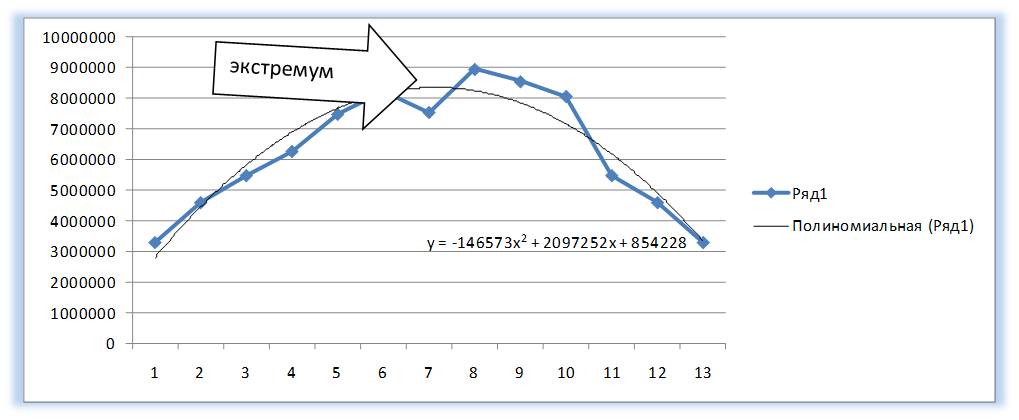
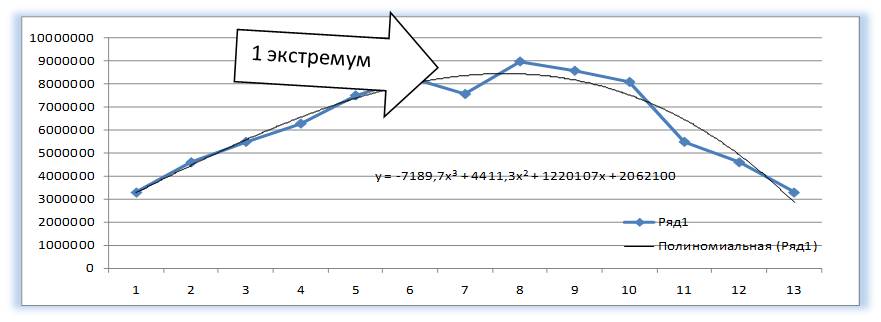
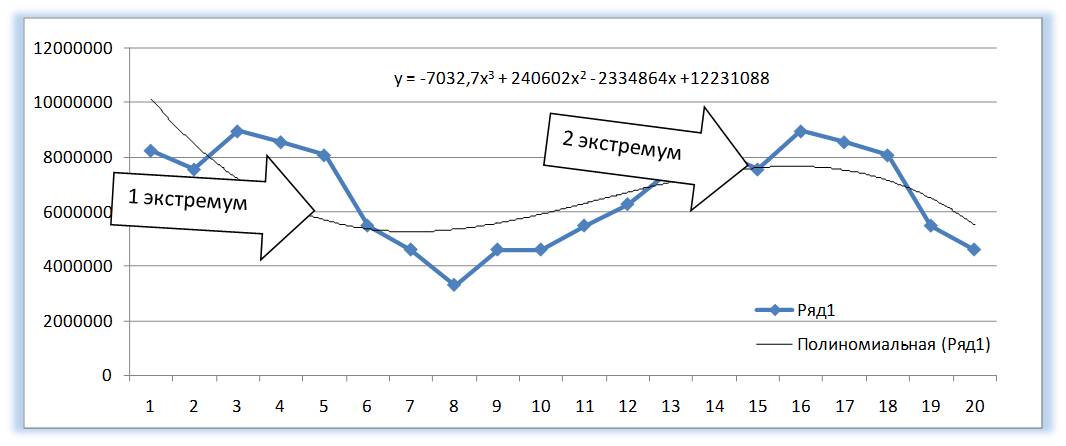
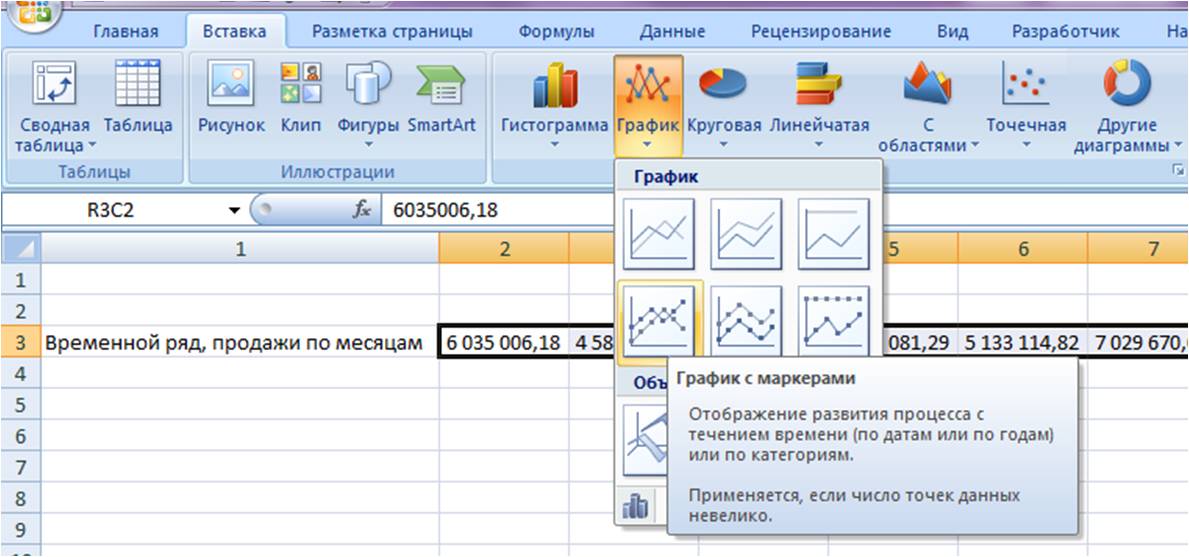
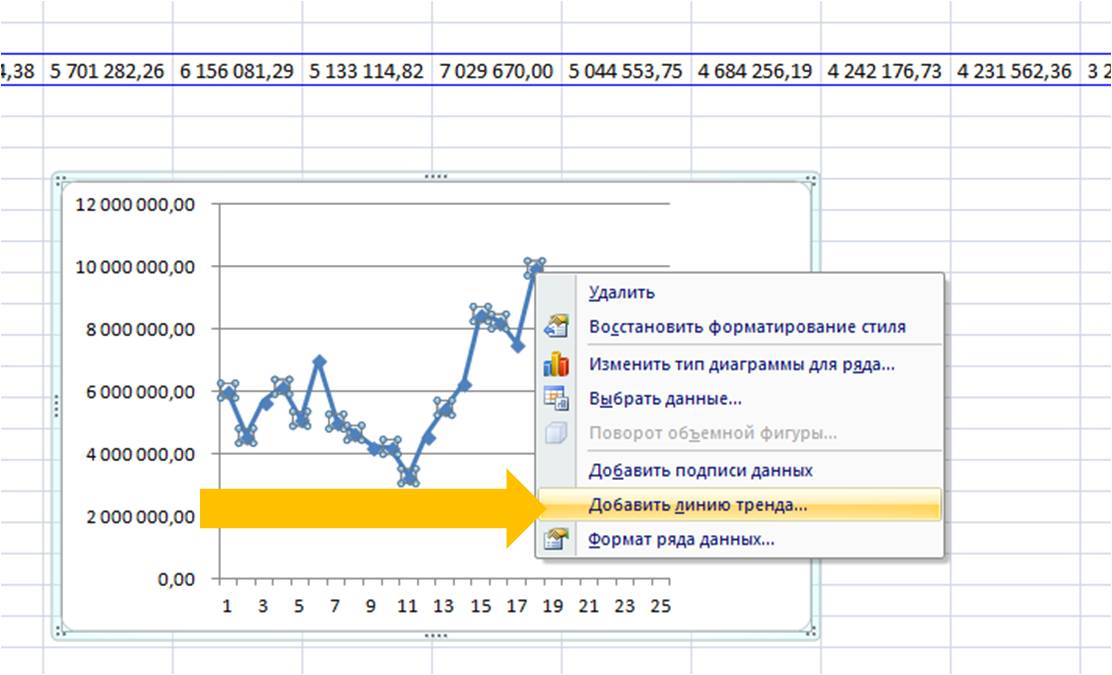
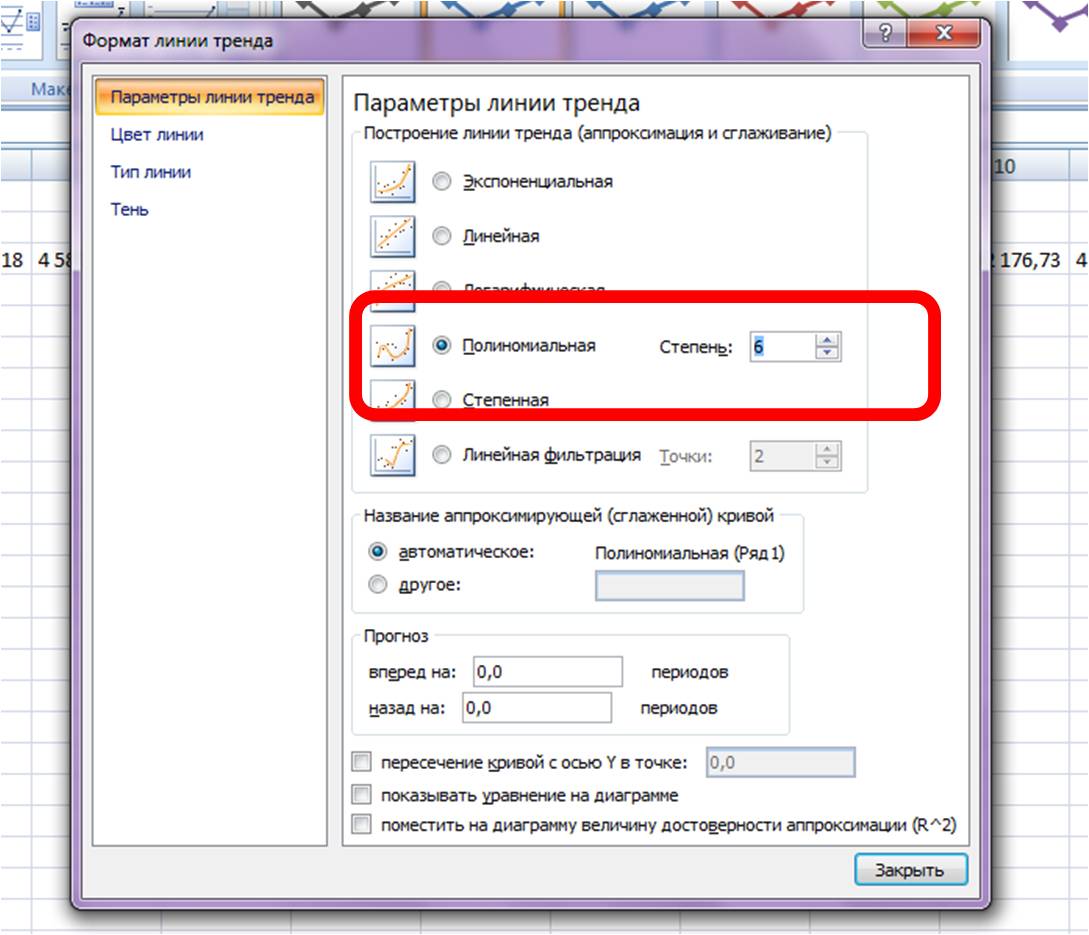
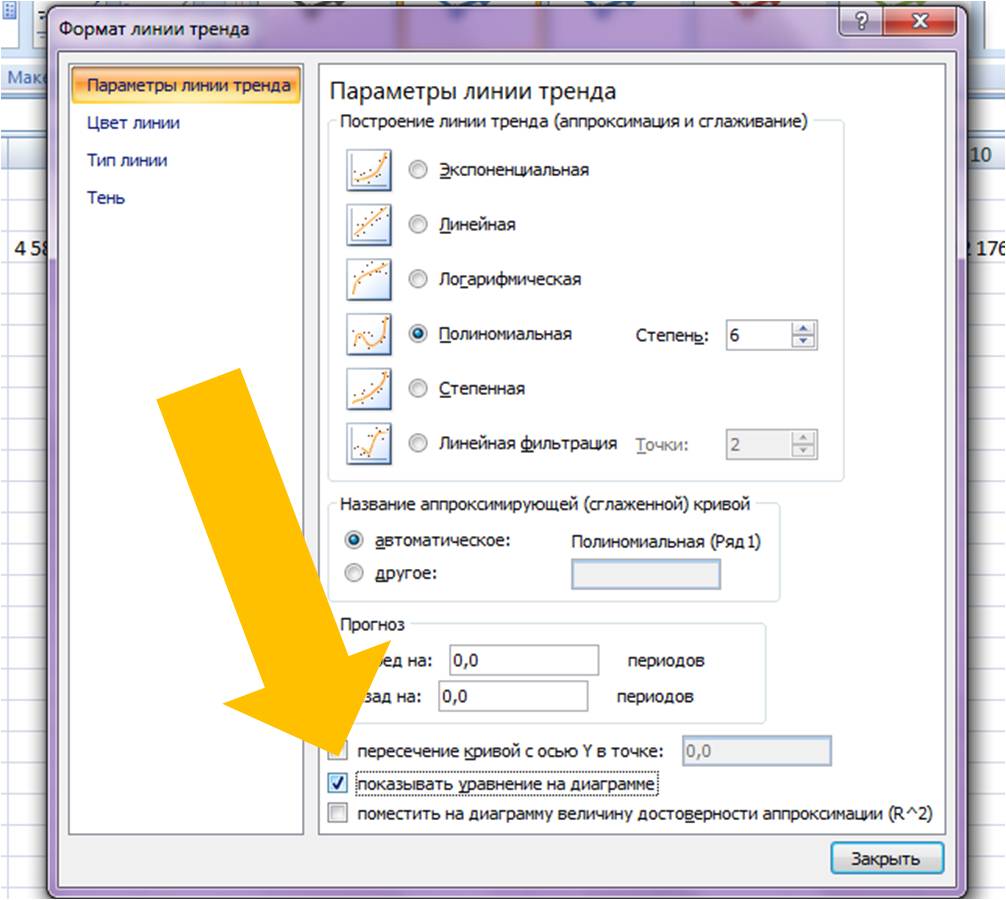
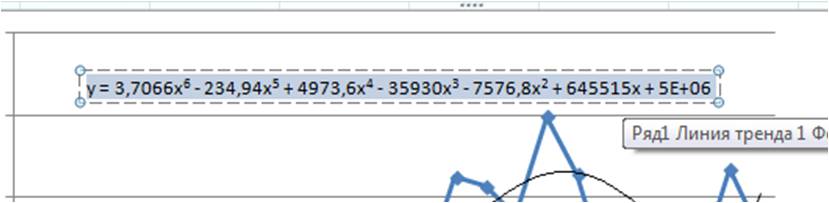
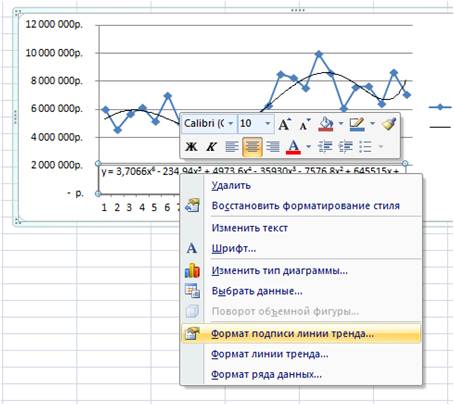
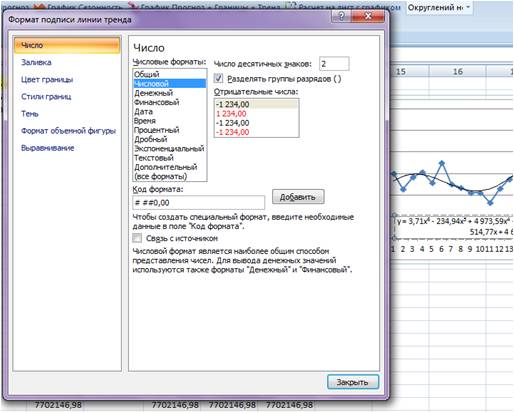


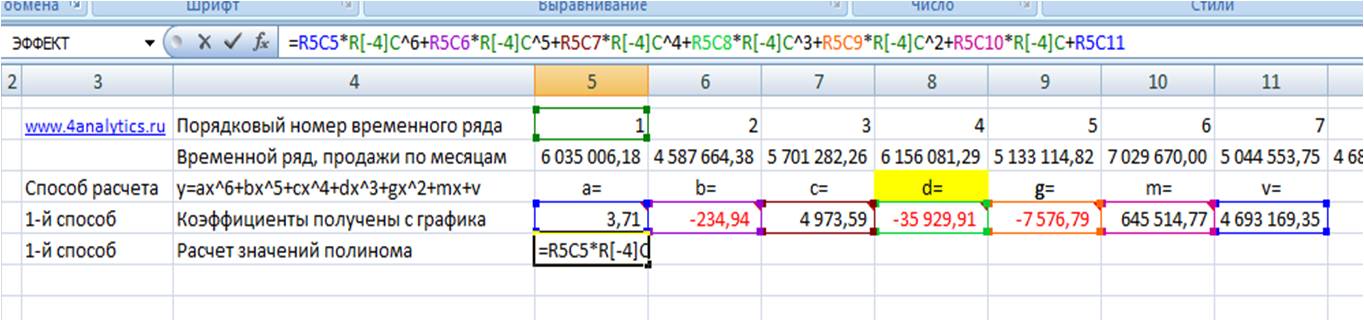
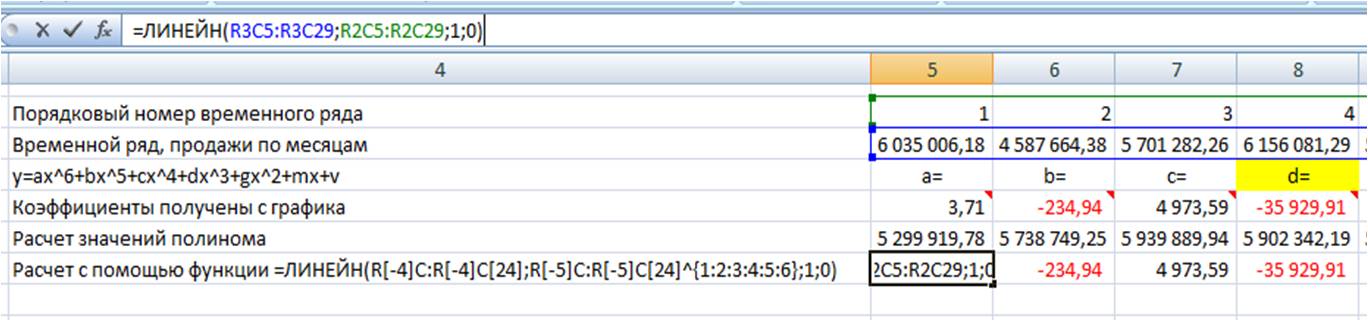
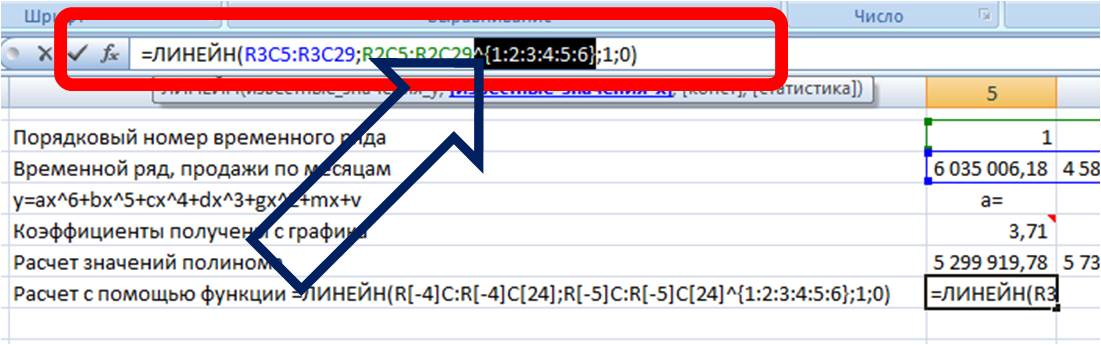

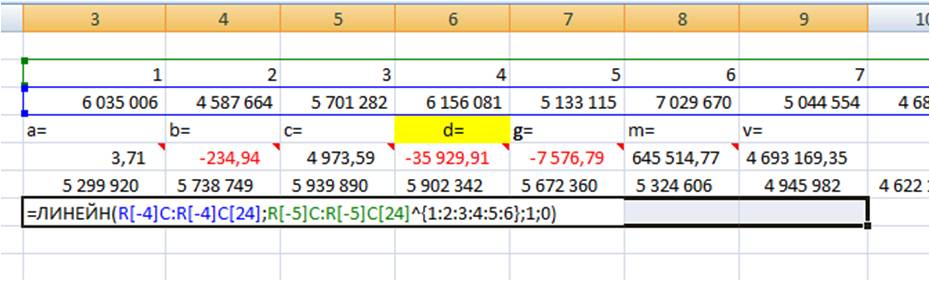

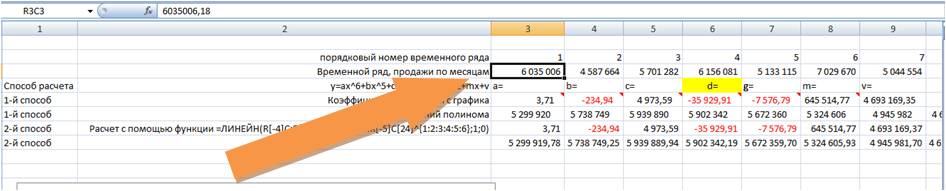
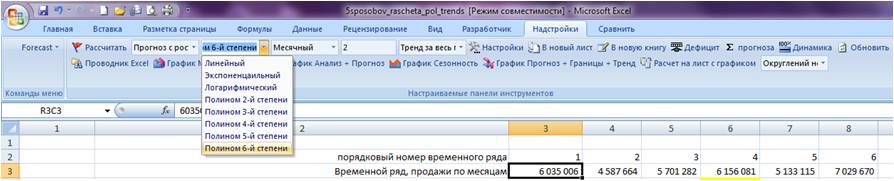
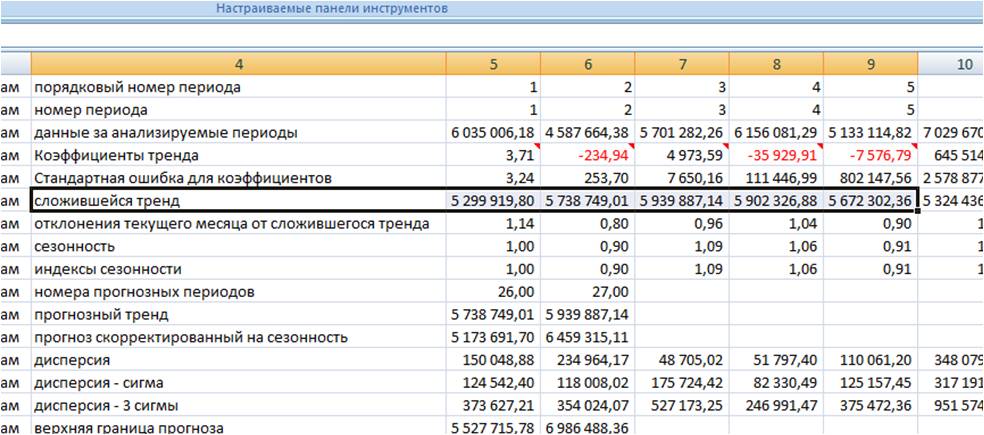

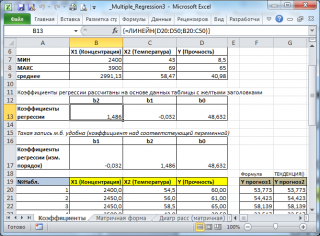
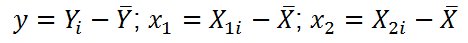
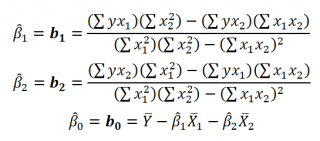
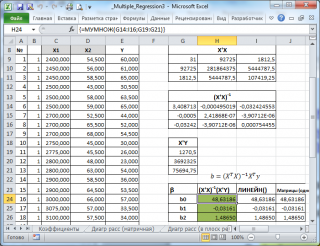
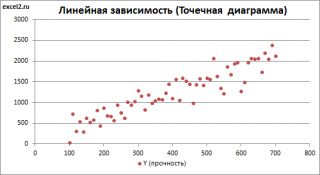
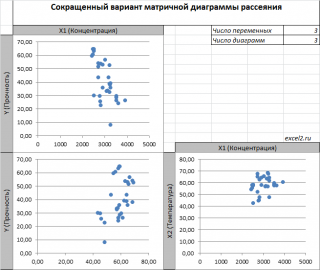

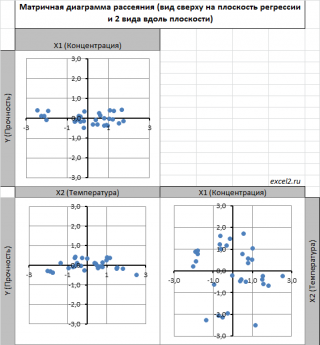
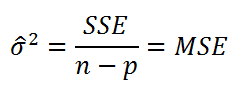
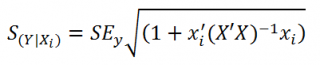
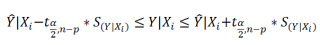
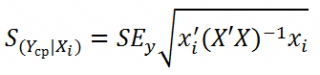
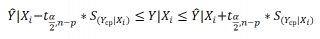
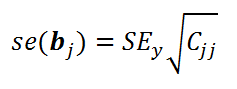
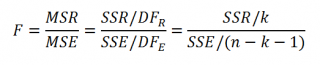
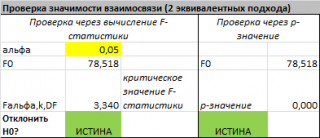
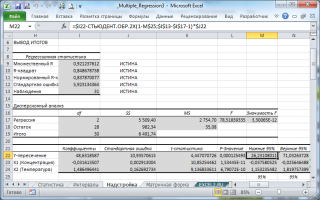
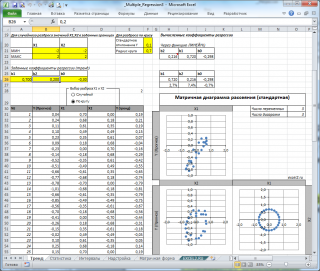
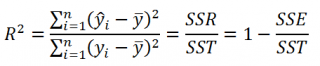
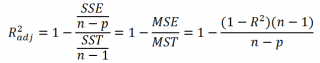


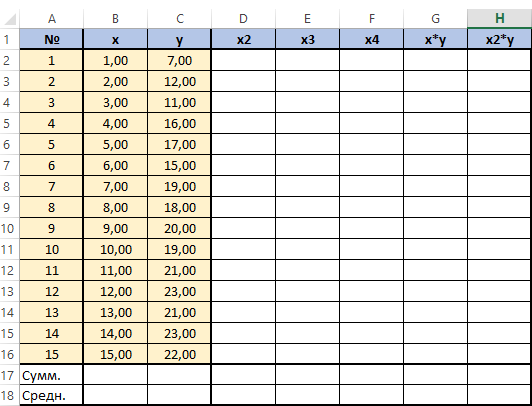
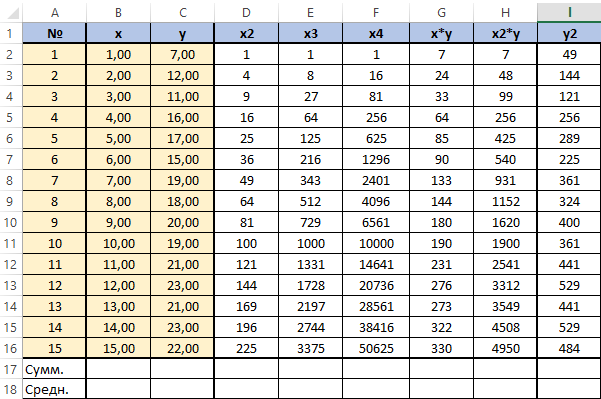
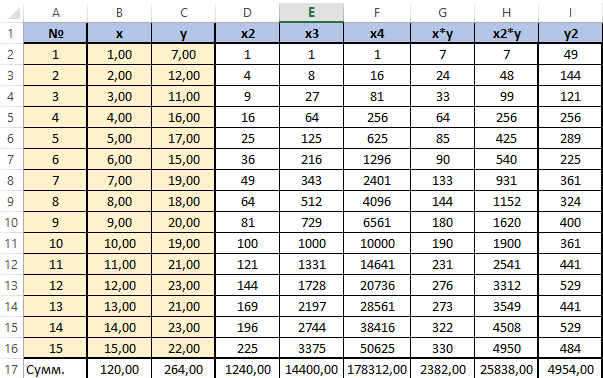
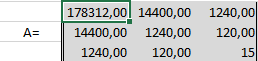

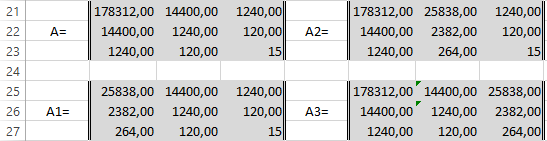


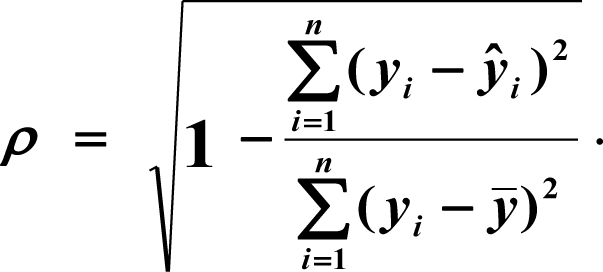
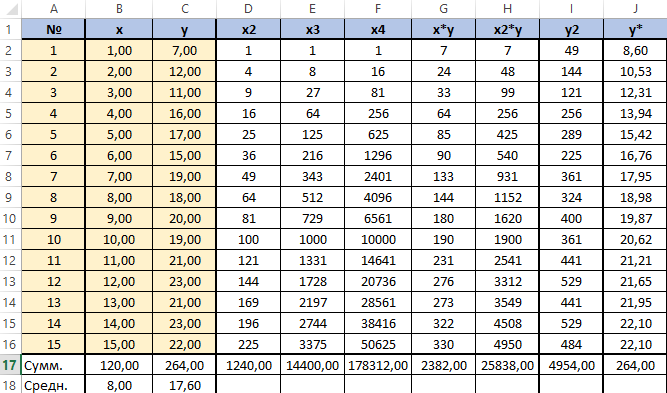
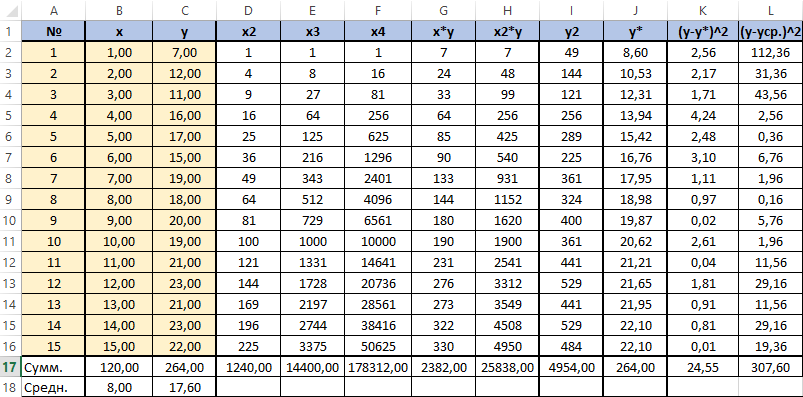
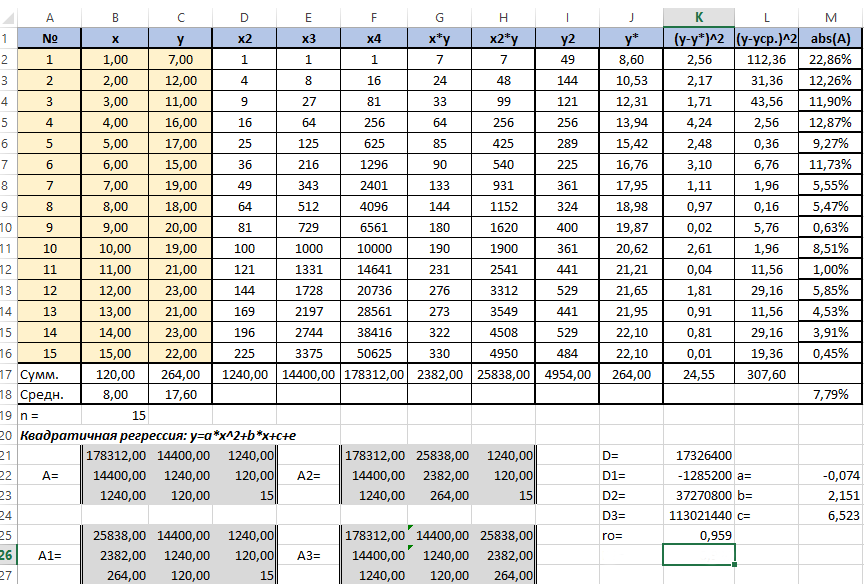
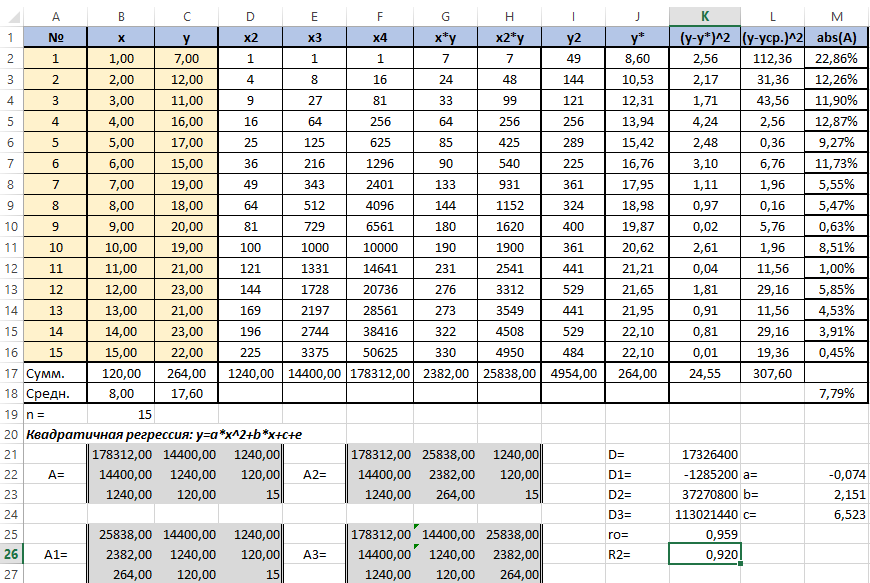











 002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.