Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СУММКВ в Microsoft Excel.
Описание
Возвращает сумму квадратов аргументов.
Синтаксис
СУММКВ(число1;[число2];…)
Аргументы функции СУММКВ описаны ниже.
-
Число1, число2,… Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется сумма квадратов. Вместо аргументов, разделенных точкой с запятой, можно использовать один массив или ссылку на массив.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются числа, логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибки или текст, не преобразуемый в числа, вызывают ошибку.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание (результат) |
Результат |
|
=СУММКВ(3; 4) |
Сумма квадратов чисел 3 и 4 (25) |
25 |
Нужна дополнительная помощь?
Нахождение суммы квадратов в Microsoft Excel может быть повторяющейся задачей. Наиболее очевидная формула требует ввода большого количества данных, хотя есть менее известный вариант, который приведет вас в то же место.
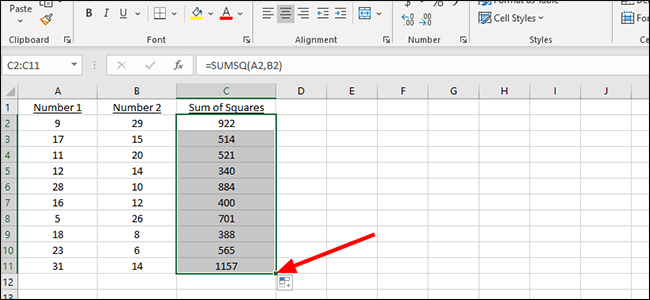
Нахождение суммы квадратов для нескольких ячеек
Начните новый столбец в любом месте электронной таблицы Excel и пометьте его. Здесь мы выведем решение наших квадратов. Квадраты не обязательно должны быть рядом друг с другом, как и секция вывода; это может быть где угодно на странице.
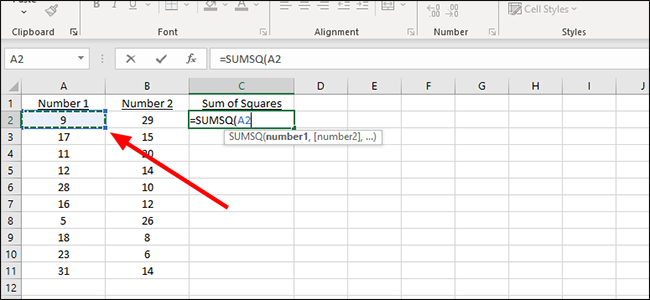
Введите следующую формулу в первую ячейку нового столбца:
=SUMSQ(
Отсюда вы можете вручную добавить буквенно-цифровую комбинацию столбца и строки или просто щелкнуть мышью. Мы будем использовать мышь, которая автоматически заполняет этот раздел формулы ячейкой A2.
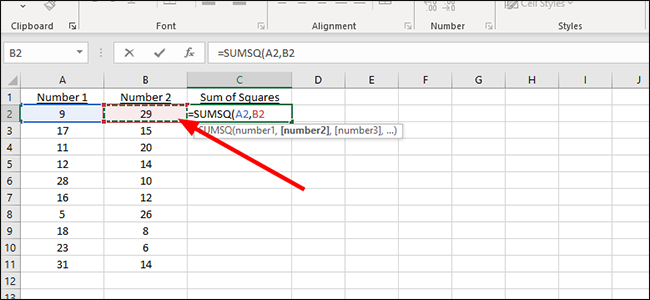
Добавьте запятую, а затем мы добавим следующий номер, на этот раз из B2. Просто введите B2 в формулу или щелкните соответствующую ячейку, чтобы заполнить ее автоматически.
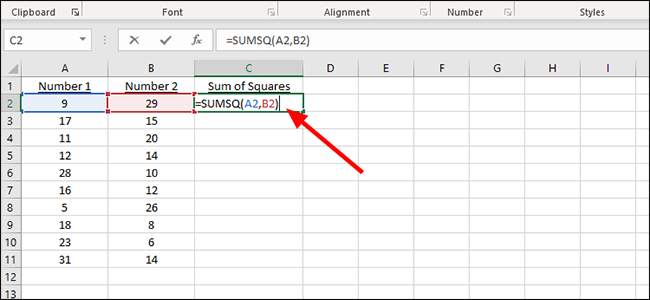
Закройте скобки и нажмите «Enter» на клавиатуре, чтобы отобразить сумму обоих квадратов. В качестве альтернативы, если вы можете продолжить здесь, добавьте дополнительные ячейки, разделив каждую запятую в формуле.
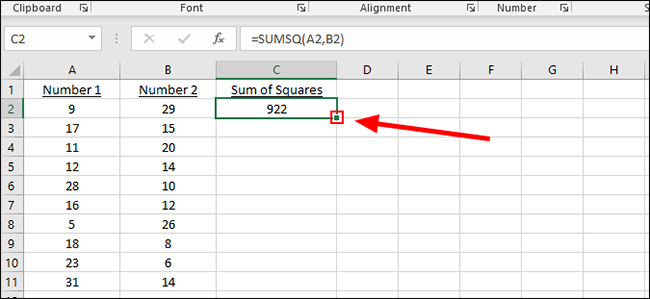
Чтобы применить формулу к дополнительным ячейкам, найдите маленький залитый квадрат в ячейке, содержащей решение нашей первой проблемы. В этом примере это C2.
Щелкните квадрат и перетащите его до последней строки пар чисел, чтобы автоматически сложить сумму остальных квадратов.
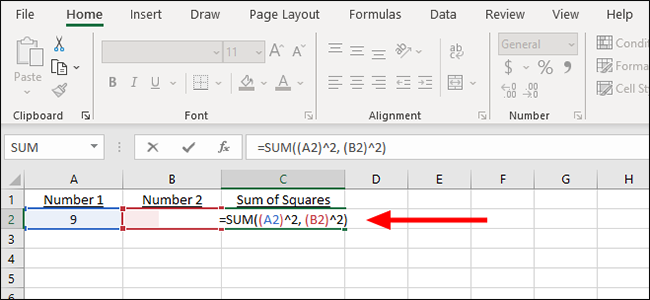
Нахождение суммы квадратов всего для нескольких ячеек
В нашем столбце «Сумма квадратов», который мы создали в предыдущем примере, в данном случае C2, начните вводить следующую формулу:
=SUM((A2)^2,(A3)^2)
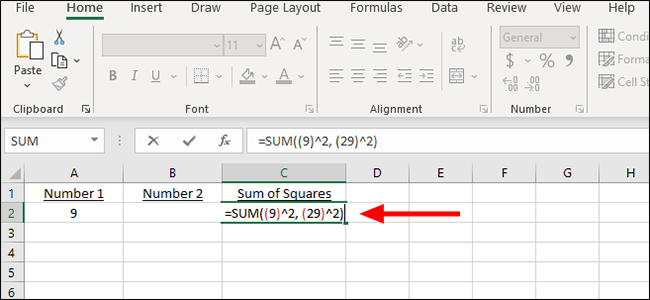
В качестве альтернативы мы можем просто добавить числа вместо ячеек в формулу, так как в любом случае мы попадем в одно и то же место. Эта формула выглядит так:
=SUM((9)^2, (29)^2)
Вы можете изменять эти формулы по мере необходимости, изменяя ячейки, добавляя дополнительные числа или находя сумму квадратов, которых даже нет в вашей книге. И хотя легче следовать приведенному выше руководству, используя формулу SUMSQ, чтобы найти решение для нескольких квадратов, часто проще просто ввести быструю формулу, подобную этой, если вы не будете повторять ее на протяжении всей книги.
Одним из наиболее частых математических действий, применяемых в инженерных и других вычислениях, является возведение числа во вторую степень, которую по-другому называют квадратной. Например, данным способом рассчитывается площадь объекта или фигуры. К сожалению, в программе Excel нет отдельного инструмента, который возводил бы заданное число именно в квадрат. Тем не менее, эту операцию можно выполнить, использовав те же инструменты, которые применяются для возведения в любую другую степень. Давайте выясним, как их следует использовать для вычисления квадрата от заданного числа.
Процедура возведения в квадрат
Как известно, квадрат числа вычисляется его умножением на самого себя. Данные принципы, естественно, лежат в основе вычисления указанного показателя и в Excel. В этой программе возвести число в квадрат можно двумя способами: использовав знак возведения в степень для формул «^» и применив функцию СТЕПЕНЬ. Рассмотрим алгоритм применения данных вариантов на практике, чтобы оценить, какой из них лучше.
Способ 1: возведение с помощью формулы
Прежде всего, рассмотрим самый простой и часто используемый способ возведения во вторую степень в Excel, который предполагает использование формулы с символом «^». При этом, в качестве объекта, который будет возведен в квадрат, можно использовать число или ссылку на ячейку, где данное числовое значение расположено.
Общий вид формулы для возведения в квадрат следующий:
В ней вместо «n» нужно подставить конкретное число, которое следует возвести в квадрат.
Посмотрим, как это работает на конкретных примерах. Для начала возведем в квадрат число, которое будет составной частью формулы.
-
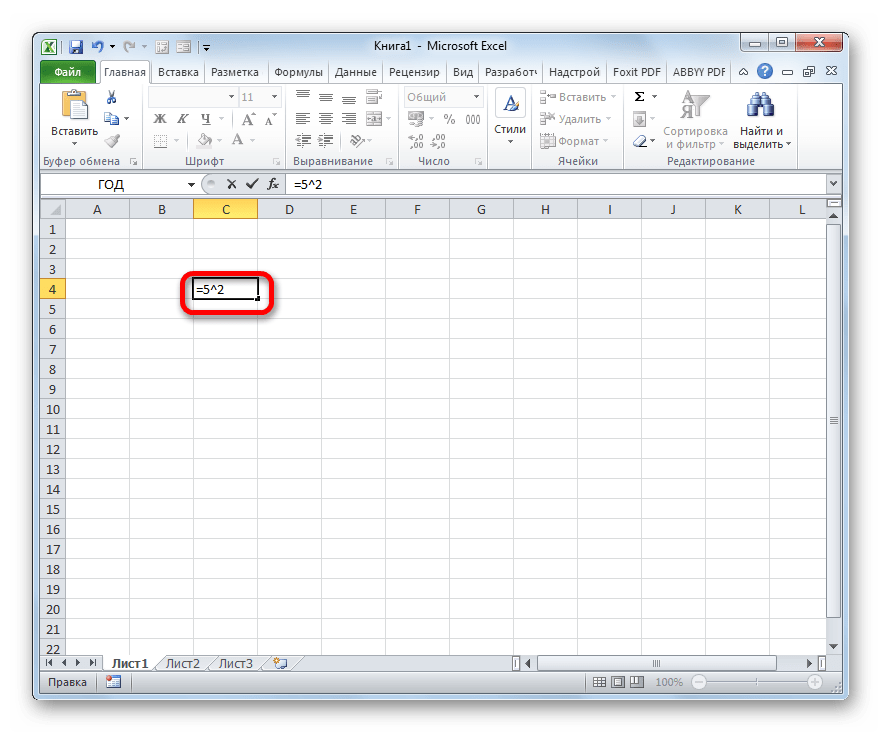
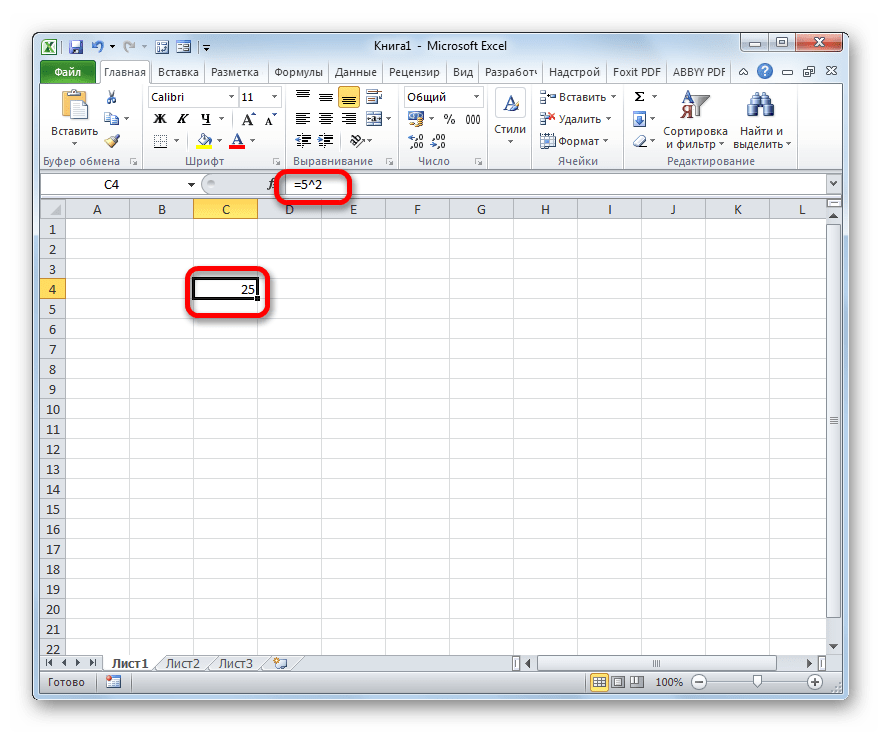
Выделяем ячейку на листе, в которой будет производиться расчет. Ставим в ней знак «=». Потом пишем числовое значение, которое желаем возвести в квадратную степень. Пусть это будет число 5. Далее ставим знак степени. Он представляет собой символ «^» без кавычек. Затем нам следует указать, в какую именно степень нужно произвести возведение. Так как квадрат – это вторая степень, то ставим число «2» без кавычек. В итоге в нашем случае получилась формула:
Теперь давайте посмотрим, как возвести в квадрат значение, которое расположено в другой ячейке.
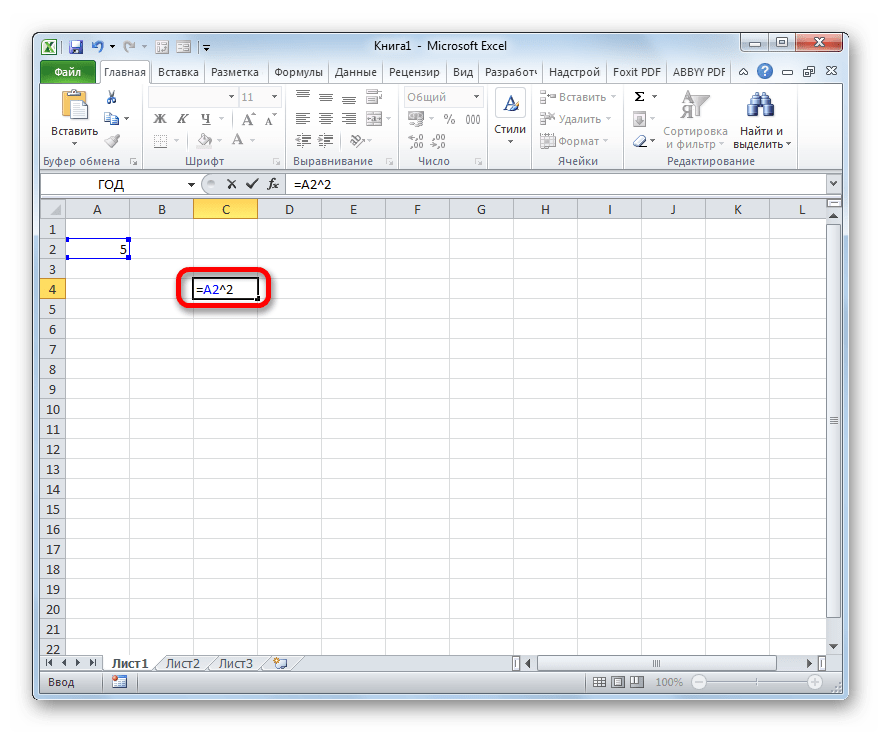
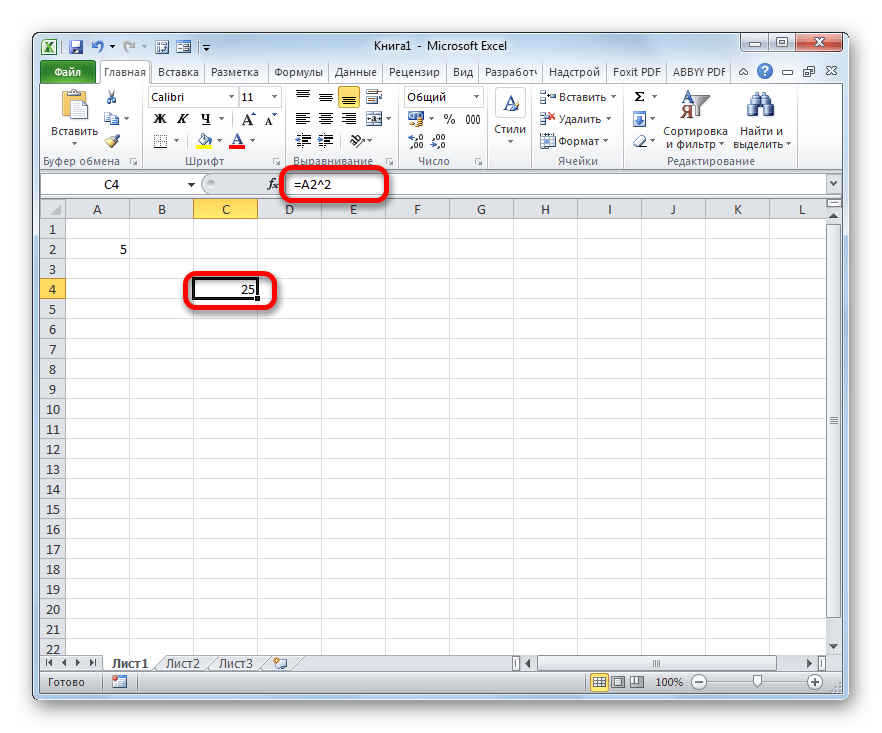
- Устанавливаем знак «равно» (=) в той ячейке, в которой будет выводиться итог подсчета. Далее кликаем по элементу листа, где находится число, которое требуется возвести в квадрат. После этого с клавиатуры набираем выражение «^2». В нашем случае получилась следующая формула:
Способ 2: использование функции СТЕПЕНЬ
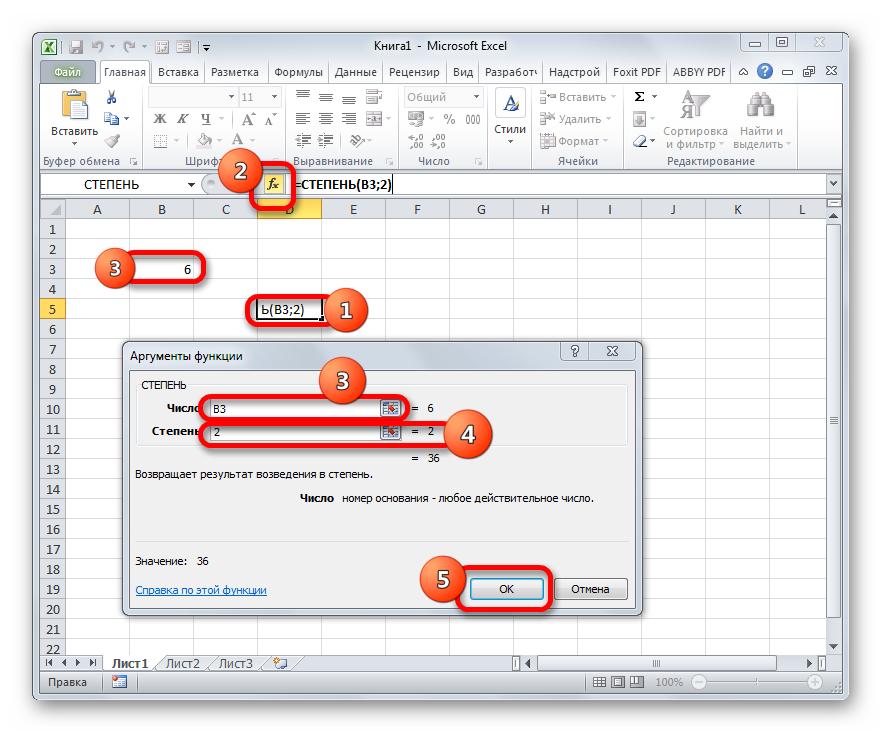
Также для возведения числа в квадрат можно использовать встроенную функцию Excel СТЕПЕНЬ. Данный оператор входит в категорию математических функций и его задачей является возведение определенного числового значения в указанную степень. Синтаксис у функции следующий:
Аргумент «Число» может представлять собой конкретное число или ссылку на элемент листа, где оно расположено.
Аргумент «Степень» указывает на степень, в которую нужно возвести число. Так как перед нами поставлен вопрос возведения в квадрат, то в нашем случае данный аргумент будет равен 2.
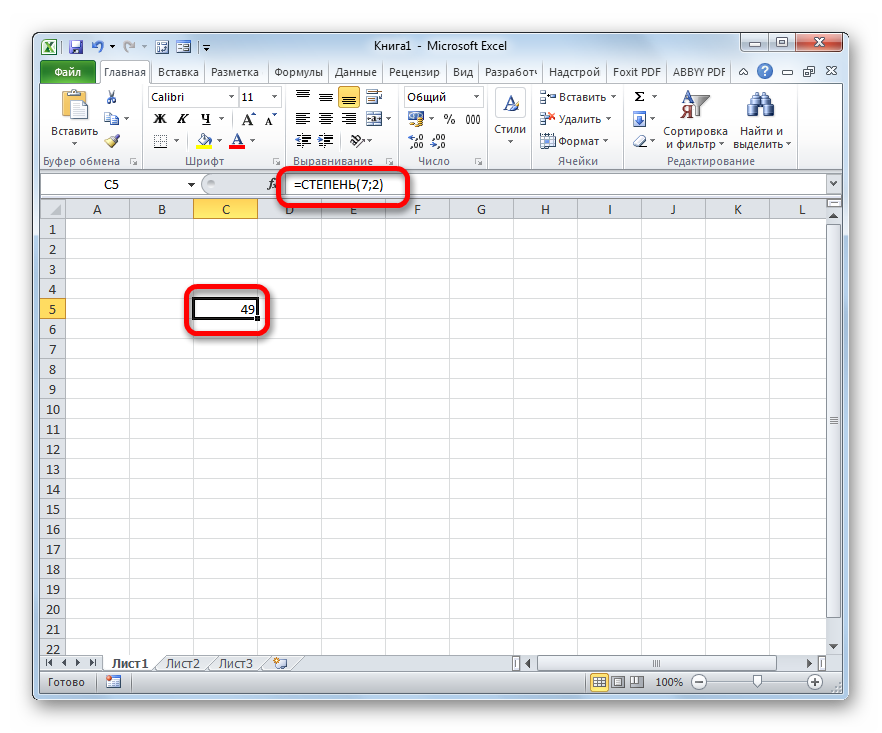
Теперь посмотрим на конкретном примере, как производится возведение в квадрат с помощью оператора СТЕПЕНЬ.
-
Выделяем ячейку, в которую будет выводиться результат расчета. После этого щелкаем по иконке «Вставить функцию». Она располагается слева от строки формул.
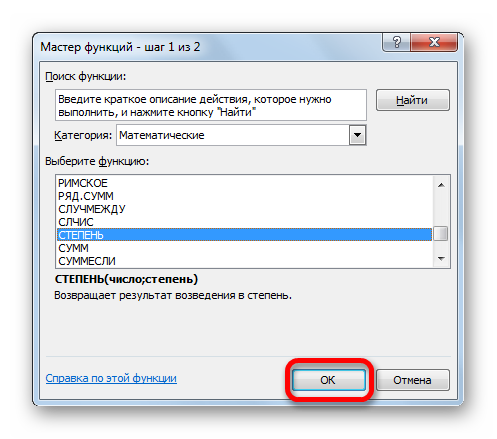
Происходит запуск окошка Мастера функций. Производим переход в нем в категорию «Математические». В раскрывшемся перечне выбираем значение «СТЕПЕНЬ». Затем следует щелкнуть по кнопке «OK».
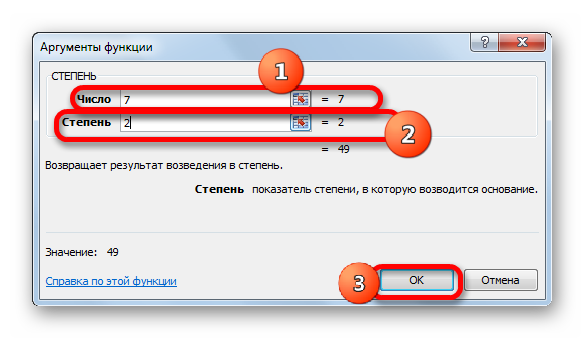
Производится запуск окошка аргументов указанного оператора. Как видим, в нем располагается два поля, соответствующие количеству аргументов у этой математической функции.
В поле «Число» указываем числовое значение, которое следует возвести в квадрат.
В поле «Степень» указываем цифру «2», так как нам нужно произвести возведение именно в квадрат.
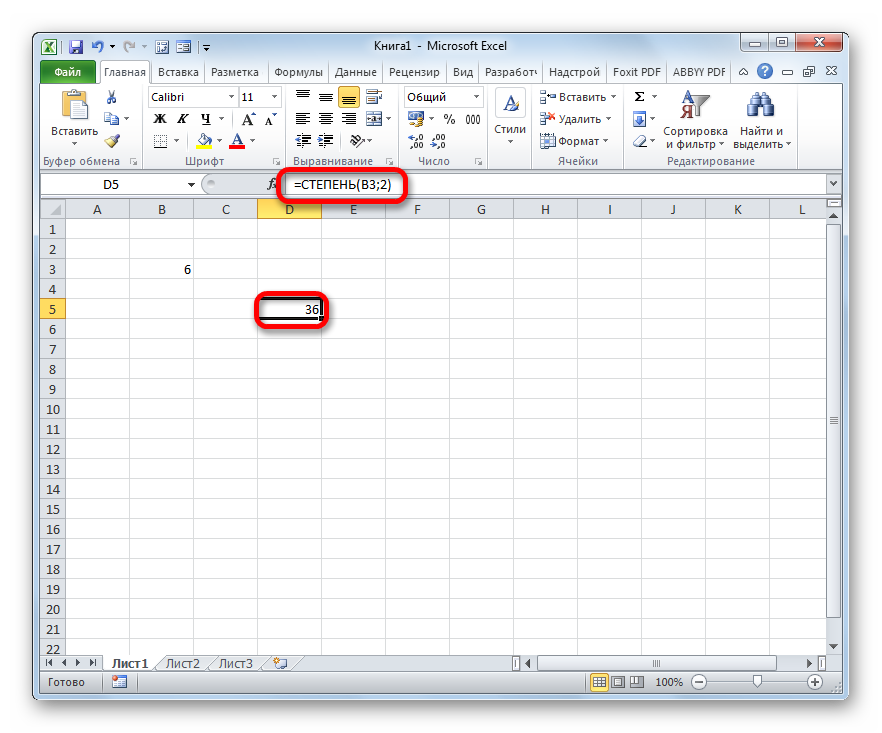
После этого производим щелчок по кнопке «OK» в нижней области окна.
Также для решения поставленной задачи вместо числа в виде аргумента можно использовать ссылку на ячейку, в которой оно расположено.
-
Для этого вызываем окно аргументов вышеуказанной функции тем же способом, которым мы это делали выше. В запустившемся окне в поле «Число» указываем ссылку на ячейку, где расположено числовое значение, которое следует возвести в квадрат. Это можно сделать, просто установив курсор в поле и кликнув левой кнопкой мыши по соответствующему элементу на листе. Адрес тут же отобразится в окне.
В поле «Степень», как и в прошлый раз, ставим цифру «2», после чего щелкаем по кнопке «OK».
Как видим, в Экселе существует два способа возведения числа в квадрат: с помощью символа «^» и с применением встроенной функции. Оба этих варианта также можно применять для возведения числа в любую другую степень, но для вычисления квадрата в обоих случаях нужно указать степень «2». Каждый из указанных способов может производить вычисления, как непосредственно из указанного числового значения, так применив в данных целях ссылку на ячейку, в которой оно располагается. По большому счету, данные варианты практически равнозначны по функциональности, поэтому трудно сказать, какой из них лучше. Тут скорее дело привычки и приоритетов каждого отдельного пользователя, но значительно чаще все-таки используется формула с символом «^».
Отблагодарите автора, поделитесь статьей в социальных сетях.
Довольно часто перед пользователями встает задача – возвести определенное число в квадрат, или, другими словами, во вторую степень. Это может потребоваться для решения инженерных, математических и иных задач.
Несмотря на широкое применение данной математической функции, в том числе, в Excel, специальной формулы, которая позволяет возвести число в квадрат, в программе нет. Однако, есть общая формула для возведения числового значения в степень, с помощью которой можно легко посчитать и квадрат.
Как рассчитывается квадрат числа
Как мы помним из школьной программы, квадрат числа – это число, помноженное на само себя. В Excel для возведения числа в квадрат, разумеется, используется этот же принцип. И для решения этой задачи можно пойти двумя путями: воспользоваться формулой, включающей специальный символ степени “^”, либо применить функцию СТЕПЕНЬ.
Давайте рассмотрим оба метода на практике, чтобы понять, как они реализуются и какой из них проще и удобнее.
Формула для расчета квадрата числа
Этот способ, пожалуй, самый легкий и наиболее часто применяемый для получения квадратной степени числа в Эксель. Для расчета используется формула со специальным знаком “^”.
Сама формула выглядит следующим образом: =n^2.
где n – это число, квадратную степень которого требуется вычислить. Значение этого аргумента можно указать разными способами: в виде конкретного числа, либо указав адрес ячейки, которая содержит требуемое числовое значение.
Теперь давайте попробуем применить формулу на практике. В первом варианте мы пропишем в формуле непосредственно само число, квадратную степень которого необходимо вычислить.
- Для начала определяемся с ячейкой книги, в которой будет отображаться результат вычислений, и отмечаем ее левой кнопкой мыши. Затем пишем в ней формулу, не забывая в самом начале поставить знак “равно” (“=”) . Например, формула “=7^2″ означает, что мы хотим возвести в квадрат число 7. Формулу, кстати, можно прописать и в строке формул, предварительно выделив нужную ячейку.
- После того, как формула набрана, щелкаем клавишу Enter на клавиатуре, чтобы получить требуемый результат.
Теперь давайте рассмотрим второй вариант, в котором вместо конкретного числа в формуле мы укажем адрес ячейки, содержащей нужное число.
- Выбираем ячейку, где будет отображаться результат, и пишем в ней формулу. Как обычно, в начале ставим “=”. Затем щелкаем по ячейке, содержащей число, квадрат которого требуется получить (в нашем случае – это ячейка B3). Далее добавляем символ степени и цифру 2, означающую возведение во вторую степень. В итоге формула выглядит так: “=B3^2“.
- После этого нажимаем Enter для вывода результата в выбранной ячейке с формулой.
Примечание: данная формула применима не только для возведения числа в квадрат, но и в другие степени. В этом случае вместо цифры 2 мы пишем другую желаемую цифру. Например, формула “=4^3” возведет число 4 в третью степень или, другими словами, в куб.
Функция СТЕПЕНЬ для возведения числа в квадрат
В данном случае для нахождения квадрата числа нам поможет специальная функция под названием СТЕПЕНЬ. Эта функция относится к категории математических операторов и выполняет задачу по возведению указанного числа в заданную степень.
Формула данного оператора выглядит так: =СТЕПЕНЬ(число;степень).
Как мы видим, в данной формуле присутствует два аргумента: число и степень.
- “Число” – аргумент, который может быть представлен двумя способами. Можно прописать конкретное число, которое требуется возвести в степень, либо указать адрес ячейки с требуемым числом.
- “Степень” – аргумент, указывающий степень, в которую будет возводиться наше число. Так как мы рассматриваем возведение числа в квадрат, то указываем значение аргумента, равное цифре 2.
Давайте разберем применение функции СТЕПЕНЬ на примерах:
Способ 1. Указываем в качестве значения аргумента «Число» конкретную цифру
- Выбираем ячейку, в которой будем производить расчеты. Затем кликаем по кнопке “Вставить функцию” (с левой стороны от строки формул).
- Откроется окно Мастера функций. Кликаем по текущей категории и выбираем в открывшемся перечне строку “Математические”.
- Теперь нам нужно в предложенном списке функций найти и кликнуть по оператору “СТЕПЕНЬ”. Далее подтверждаем действие нажатием OK.
- Перед нами откроется окно с настройками двух аргументов функции, которое содержит, соответственно, два поля для ввода информации, после заполнения которых жмем кнопку OK.
- в поле “Число” пишем числовое значение, которое требуется возвести в степень
- в поле “Степень” указываем нужную нам степень, в нашем случае – 2.
- В результате проделанных действий мы получим квадрат заданного числа в выбранной ячейке.
Способ 2. Указываем в качестве значения аргумента «Число» адрес ячейки с числом
- Теперь у нас уже есть конкретное числовое значение в отдельно ячейке (в нашем случае – B3). Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”.
- В отличие от первого способа, теперь вместо указания конкретного числа в поле “Число” указываем адрес ячейки, содержащей нужное число. Для этого кликаем сначала по полю аргумента, затем – по нужной ячейке. Значение поля “Степень” так же равно 2.
- Далее нажимаем кнопку OK и получаем результат, как и в первом способе, в ячейке с формулой.
Примечание: Также, как и в случае использования формулы для расчета квадрата числа, функцию СТЕПЕНЬ можно применять для возведения числа в любую степень, указав в значении аргумента “Степень” нужную цифру. Например, чтобы возвести число в куб, пишем цифру 3.
Далее жмем Enter и значение куба указанного числа появится ячейке с фукнцией.
Заключение
Возведение числа в квадрат – пожалуй, самое популярное математическое действие среди всех вычислений, связанных с расчетами различных степеней числовых значений. В Microsoft Excel данное действие можно выполнять двумя способами: с помощью специальной формулы или используя оператор под названием СТЕПЕНЬ.
В этой статье описаны синтаксис формулы и использование функции СУММКВ в Microsoft Excel.
Описание
Возвращает сумму квадратов аргументов.
Синтаксис
Аргументы функции СУММКВ описаны ниже.
Число1, число2. Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется сумма квадратов. Вместо аргументов, разделенных точкой с запятой, можно использовать один массив или ссылку на массив.
Замечания
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются числа, логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибки или текст, не преобразуемый в числа, вызывают ошибку.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Как посчитать сумму квадратов в Excel
Гайд в разделе MS Office Как посчитать сумму квадратов в Excel содержит информацию, советы и подсказки, которые помогут изучить самые важные моменты и тонкости вопроса….
Нахождение суммы квадратов в Microsoft Excel может быть повторяющейся задачей. Самая очевидная формула требует ввода большого количества данных, хотя есть менее известный вариант, который приведет вас в то же место.
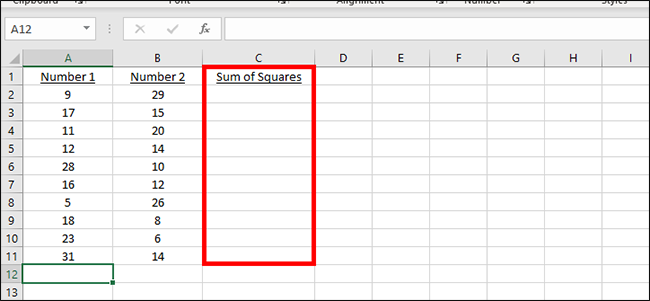
Определение суммы квадратов для нескольких ячеек
Начните новый столбец в любом месте электронной таблицы Excel и обозначьте это. Здесь мы выведем решение наших квадратов. Квадраты не обязательно должны быть рядом друг с другом, как и раздел вывода, он может находиться в любом месте страницы.
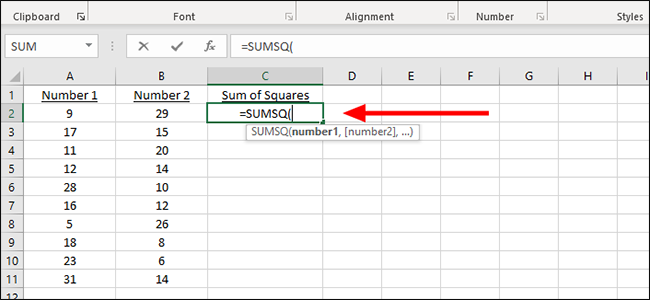
Введите следующую формулу в первая ячейка в новом столбце:
= SUMSQ (
Отсюда вы можете вручную добавить буквенно-цифровую комбинацию столбца и строки или просто щелкнуть по ней с помощью мыши. Мы будем использовать мышь, которая автоматически заполняет этот раздел формулы ячейкой A2.
Добавьте запятую, а затем мы добавим следующее число, на этот раз из B2. Просто введите B2 в формулу или щелкните соответствующую ячейку, чтобы заполнить ее автоматически.
Закройте круглые скобки и нажмите «Enter» на клавиатуре, чтобы отобразить сумму. обоих квадратов. В качестве альтернативы, если вы можете продолжить здесь, добавьте дополнительные ячейки, разделив их запятыми в формуле.
Чтобы применить формулу к дополнительным ячейкам, найдите маленький залитый квадрат в ячейке, которая содержит решение нашей первой проблемы. В этом примере это C2.
Щелкните квадрат и перетащите его до последней строки пар чисел, чтобы автоматически сложить сумму остальных квадратов.
Нахождение суммы квадратов для нескольких ячеек
В нашем столбце «Сумма квадратов», который мы создали в предыдущем примере, в данном случае C2, начните вводить по следующей формуле:
= СУММ ((A2) ^ 2, (A3) ^ 2)
В качестве альтернативы мы можем просто добавить числа вместо ячеек в формула в любом случае приводит нас в одно и то же место. Эта формула выглядит так:
= SUM ((9) ^ 2, (29) ^ 2)
Вы можете изменять эти формулы по мере необходимости, изменяя ячейки , например, добавление дополнительных чисел или поиск суммы квадратов, которых нет даже в вашей книге. И хотя легче следовать приведенному выше руководству, используя формулу SUMSQ, чтобы найти решение для нескольких квадратов, часто проще просто ввести быструю формулу, подобную этой, если вы не будете повторять ее на протяжении всей книги.
Как посчитать сумму квадратов в Excel
Просмотров: 140
Функция СУММКВ возвращает сумму квадратов чисел.
Описание функции СУММКВ
Возвращает сумму квадратов аргументов.
Синтаксис
=СУММКВ(число1; [число2]; …)Аргументы
число1; число2 …
Обязательный аргумент число1, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется сумма квадратов. Вместо аргументов, разделенных точкой с запятой, можно использовать один массив или ссылку на массив.
Замечания
- Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Учитываются числа, логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
- Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
- Аргументы, которые представляют собой значения ошибки или текст, не преобразуемый в числа, вызывают ошибку.
Пример
В этом учебном материале вы узнаете, как использовать Excel функцию СУММКВ с синтаксисом и примерами.
Описание
Microsoft Excel функция СУММКВ возвращает сумму квадратов ряда значений. СУММКВ — это встроенная в Excel функция, относящаяся к категории математических / тригонометрических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию СУММКВ можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции СУММКВ в Microsoft Excel:
СУММКВ(число1;[число2];…)
Аргументы или параметры
- число1;[число2];…
- Серия числовых значений, которые должны быть возведены в квадрат и затем просуммированы. Может быть до 30 значений.
Возвращаемое значение
Функция СУММКВ возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции СУММКВ, чтобы понять, как использовать Excel функцию СУММКВ в качестве функции рабочего листа в Microsoft Excel:
На основании, приведенной выше электронной таблицы Excel, будут возвращены следующие примеры функции СУМСК:
|
=СУММКВ(A1:A2) Результат: 10 =СУММКВ(A1:A2; B1:B2) Результат: 30 =СУММКВ(3; D1:D2) Результат: 83 =СУММКВ(1; 2; 3) Результат: 14 |
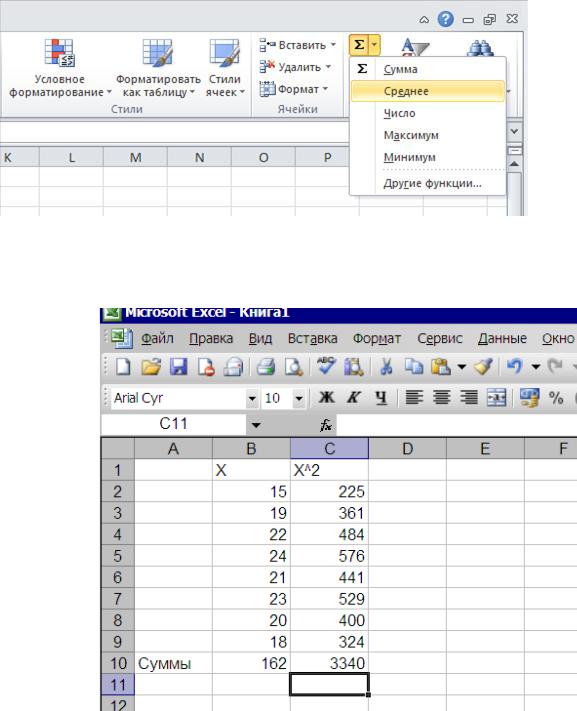
Теперь необходимо определить в ячейке В10 суммы значений Х и в ячейке С10 суммы квадратов Х2. Для определения сумм воспользуемся значком ∑ из строки инструментов и затем последовательно выделим диапазоны ячеек с цифрами по столбцам В2:В9 и С2:С9 (Рис. 2.4 )
Добраться до формулы можно по-разному. Вначале нужно выделить ячейку, в которой будет стоять формула. Саму формулу можно прописать вручную в строке формул либо воспользоваться ее наличием на панели задач – закладка «Главная», справа вверху есть разворачивающаяся кнопка со значком суммы Σ (рис. 2.5) . После вызова формулы в скобках потребуется прописать диапазон данных С2:С9, по которым будет рассчитываться сумма. Сделать это можно мышкой, нажав левую клавишу и протянув по нужному диапазону.
Рис. 2.5. Знак суммирования
В итоге получаем: ∑X= 162 и ∑X2 = 3340 (рис. 2.6. )
Рис. 2.6. Сумма значений Х и сумма квадратов Х2.
11
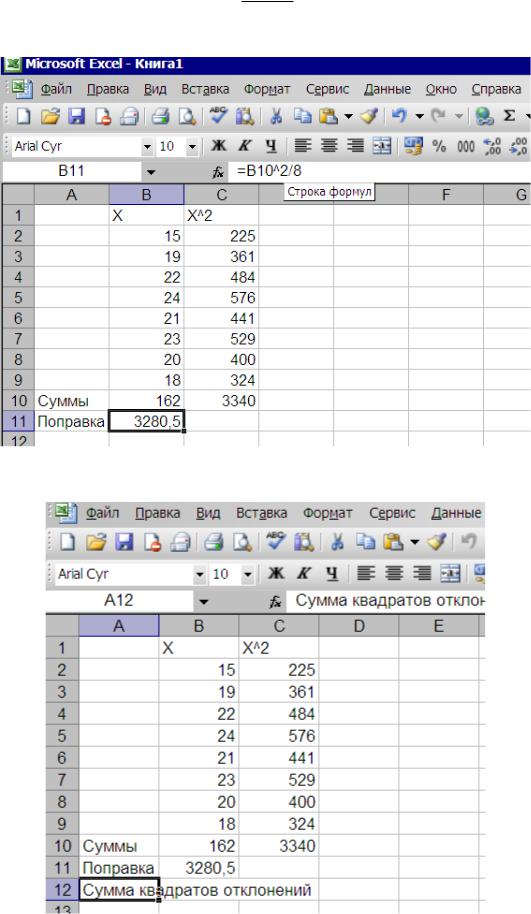
Далее необходимо рассчитать поправку ( С ( X )2 ). Для этого активизируем ячейку В11, . n
затем в строке формул записываем формулу B10^2/8 (рис 2.7. ) и итоге получаем С= 3280,5
Рис. 2.7. Расчет поправки
В строку А12 введем текст «Сумма квадратов отклонений» (рис.2.8. )
Рис.2.8. Текст «Сумма квадратов отклонений» в ячейке А12
12
Несмотря на то, что в каждую отдельную ячейку можно ввести до 32000 символов, после введения больших текстов и перевода курсора в другую ячейку, в первой ячейке видна только часть текста. Поэтому каждую ячейку или столбец можно раздвинуть вправо или сформатировать ячейку, указав на перенос слов. Для того, чтобы расширить ячейку А12, наведите курсор мыши в шапке между столбцами А и В, курсор изменяет форму. Появится значок «прямоугольный крест» Зажмите левую кнопку мыши и, не отпуская ее, переместить курсор вправо, будет изменяться ширина столбца А. (рис.2.9.)
Рис.2.9. Ширина столбца после изменения.
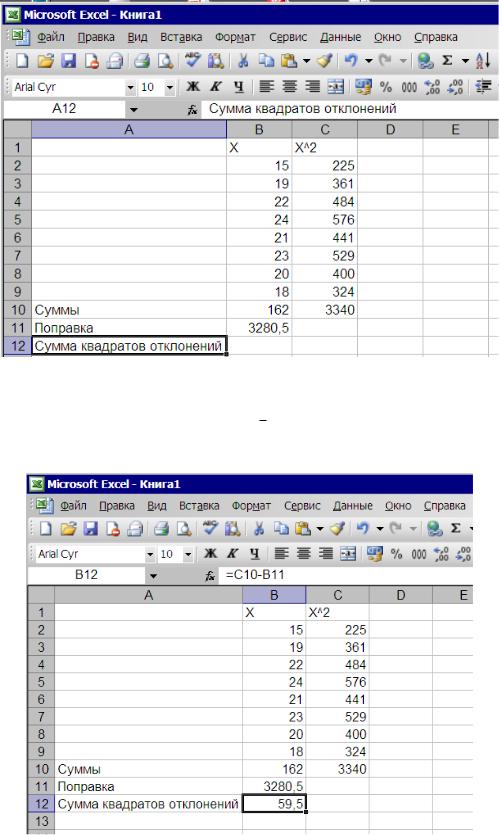
Расчет сумм квадратов отклонений ( X x)2 = X 2 – С = произведем в Excel
следующим образом. В строку формул введем формулу со ссылками: сумма квадратов (С10) – поправка (В11) и в результате получаем сумму квадратов – 59,5 в ячейке В12 (рис.2.10)
Рис. 2.10. Расчет сумм квадратов отклонений
13
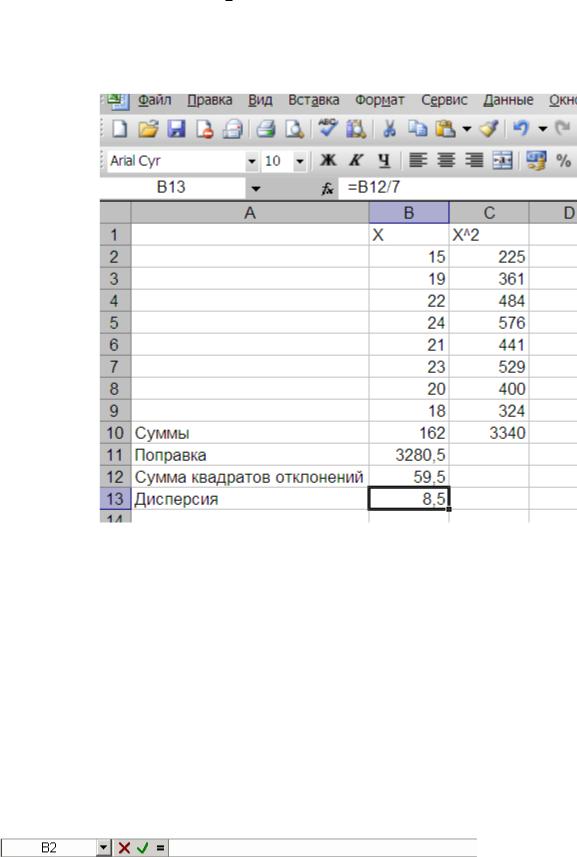
Дисперсия S 2 ( X x)2 . Для расчета дисперсии в строку формул введем формулу n 1
В12/7 и в итоге в ячейке В13 получаем значение дисперсии –8,5 (рис. 2.11.)
Рис.2.11. Расчет дисперсии
2.2. Расчеты с использованием Мастера функций
Выше приведенные методы расчета статистических показателей неудобны, так как для каждого из них необходимо вручную прописывать формулы. Поэтому для удобства работы в программе Excel предусмотрен мастер функций, позволяющий вводить их в полуавтоматическом режиме и практически без ошибок. Многие статистические показатели выборки и параметры генеральной совокупности можно очень быстро определить с помощью функций, тем более что наименование большинства функций совпадает с наименованием статистических показателей.
В Листе 1 файла Книга1 в столбце введем символ Х и значения глубины вспашки по 8-ми точкам. В ячейки с А10 по А17 впишем наименование статистических показателей, которые приведены в работе 1.
Для определения средней выборочной (средняя арифметическая) активизируем ячейку В10 (выделенная ячейка со знаком =), в этой ячейке будут отображаться результаты наших вычислений. Для вызова мастера функций необходимо нажать кнопку Вставка функции на стандартной панели инструментов или на строке формул нажать на «fx».
Появляется контекстное меню «Мастер функций – шаг 1 из 2, в категории выбрать «Статистические» (рис. 2.12. )
14
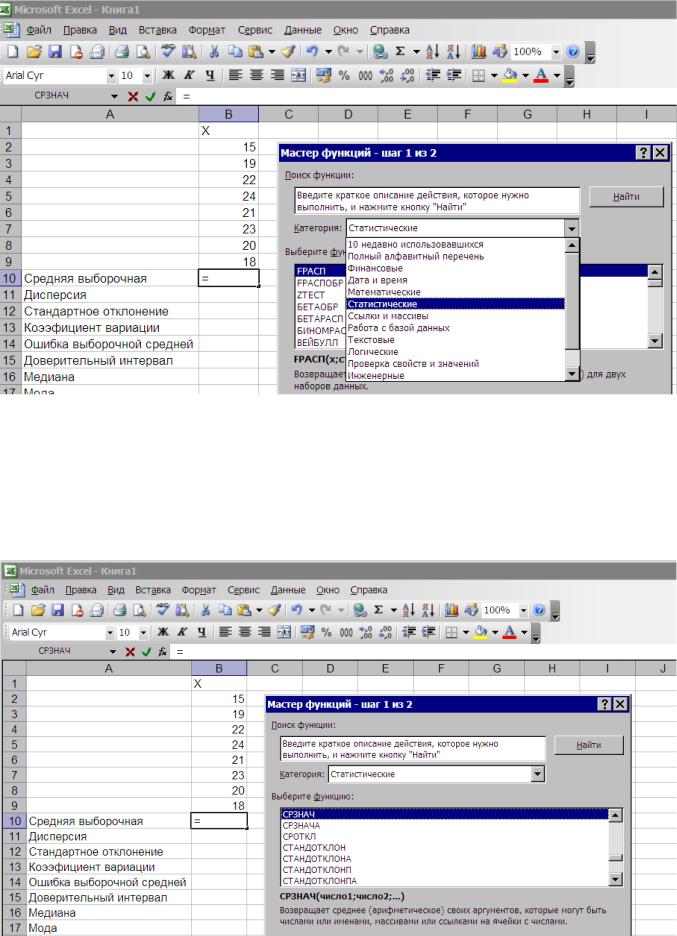
Рис.2.12. Лист с исходными данными и контекстным меню «Мастер функций»
После выбора категории « Статистические».в окне появляется перечень конкретных статистических функций, выбираем СРЗНАЧ, что означает среднюю по выборке (рис. 2.13 ).
Рис. 2.13. Выбор функции СРЗНАЧ
15
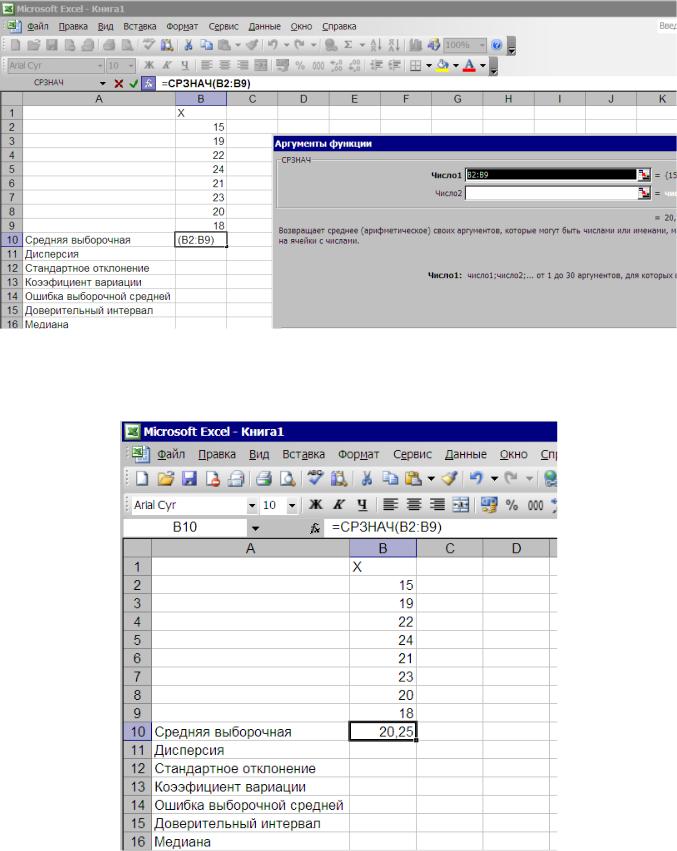
Далее открывается окно для выбора аргументов функции. В поле Число 1 ставим курсор и мышкой выбираем диапазон значений глубины вспашки В2:В9, нажимаем клавишу ОК , в строке формул автоматически появляется наименование функции и диапазон ячеек (=СРЗНАЧ(В2:В9), а в ячейке В10 появляется в скобках этот же диапазон (рис. 2.14. )
Рис. 2.14. Диалоговое окно для выбора аргументов функции.
После нажатия клавиши ОК или щелчка мышки в ячейке В10 появляется значение выборочной средней – средняя глубина вспашки – 20,25 см. (рис. 2.15.)
Рис.2.15. Средняя глубины вспашки – средняя выборочная – 20,25 см.
16
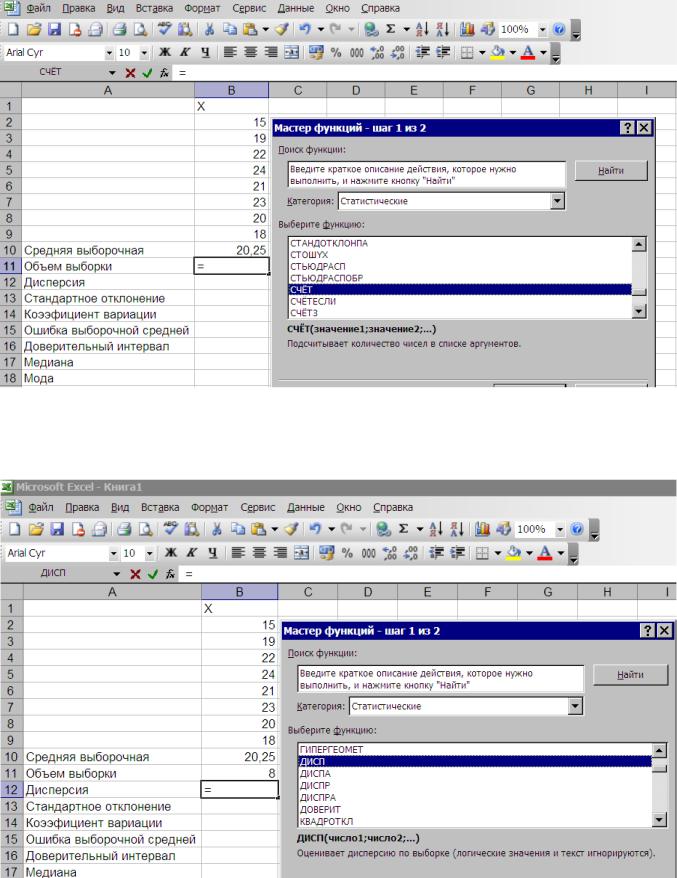
Находим объем выборки (n), который в Мастере функций называется счет (рис. 2.16.)
Рис.2.16. Диалоговое окно для нахождения объема выборки (счет)
Выбираем из списка функций ДИСП – дисперсия для выборки. Обратите внимание на то, что в списке имеется ДИСПР – дисперсия для генеральной совокупности. Для нашего примера необходимо выбрать ДИСП, так как находим дисперсию для выборки (рис. 2.17.).
Рис. 2.17. Диалоговое окно для выбора дисперсии Для расчета дисперсии в поле Число 1 ставим курсор и мышкой выбираем диапазон значений глубины вспашки В2:В9, нажимаем клавишу ОК (рис.2.18)
17
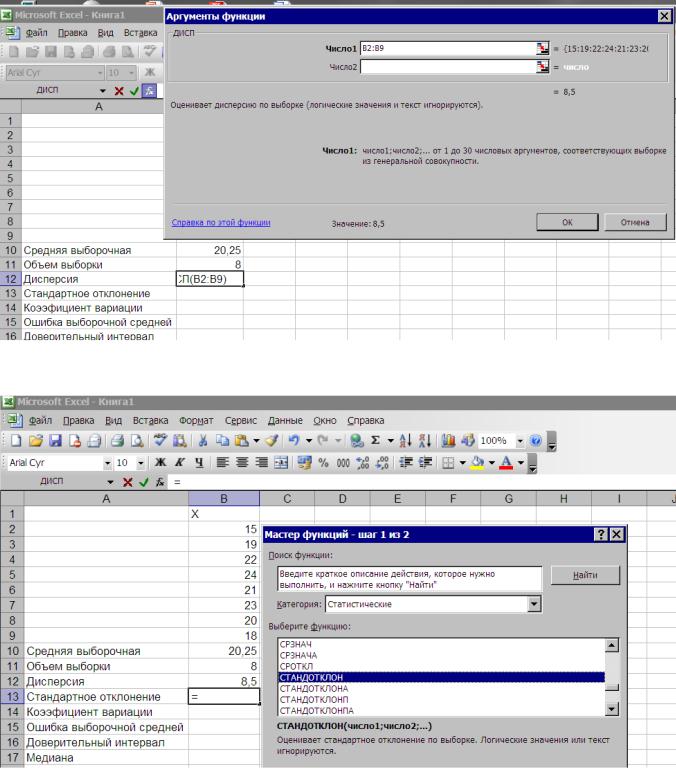
Рис. 2.18. Выбор диапазона ячеек для определения дисперсии Выбираем из списка функций СТАНДОТКЛОН – стандартное отклонение для выборки
(рис. 2.19).
Рис. 2.19. Диалоговое окно для выбора стандартного отклонения
В списке как математических, так и статистических функций нет такой функции с помощью, которой можно рассчитать коэффициент выборки (V), поэтому воспользуемся уже известной процедурой ручного набора формул.
Коэффициент вариации представляет собой отношение стандартного отклонения к выборочной средней, выраженной в %. Выделим ячейку для формулы коэффициента вариации В14, затем в строке формул пропишем формулу со ссылкой на ячейки, где находятся стандартное отклонение и выборочная средняя – (В13/В10*100) (рис. 2.20)
В итоге получаем коэффициент вариации (V) = 14,3974%. 18
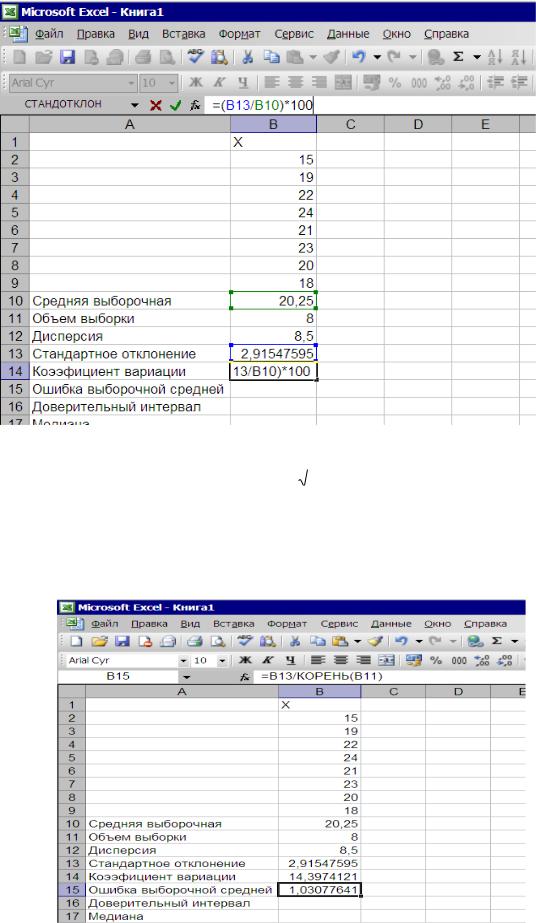
Рис. 2.20. Формула для определения коэффициента вариации
|
Расчет ошибки выборочной средней S |
S |
|||||
|
x |
||||||
|
n |
||||||
Так как в списке функций нет очень важного статистического показателя – ошибки выборочной средней (стандартная ошибка), рассчитаем этот статисческий показатель с помощью формул. Выделим ячейку для размещения формулы и получения готового результата В15 , затем в строке формул сначала вставим символ = и укажем следующую формулу: В13/КОРЕНЬ (В11). В ячейке В13 значение стандартного отклонения, в ячейке В11 – объем выборки. После нажатия на клавишу Enter в ячейке В15 получаем результат – 1,0307764. (рис. 2.21)
Рис. 2.21. Расчет ошибки выборочной средней
19
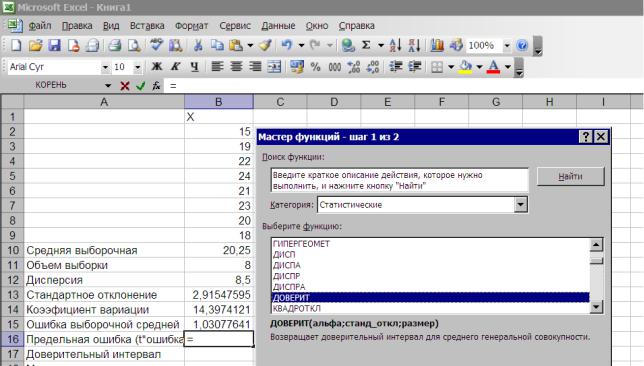
Расчет предельной ошибки выборочной средней для нахождения доверительного интервала генеральной средней. Предельная ошибка выборочной средней представляет собой произведение критерия Стьюдента на ошибку выборочной средней (t 05*Sx ). Значение критерия Стьюдента зависит от числа степеней свободы (n – 1) .
В Мастере функций для нахождения предельной ошибки средней выборочной имеется функция, которая имеет странное название ДОВЕРИТ. Поместим курсор в ячейку В16 . затем из списка статистических функций выберем функцию ДОВЕРИТ (рис. 2.22 ), нажимаем ОК.
Рис. 2.22. Выбор в меню функции ДОВЕРИТ (предельная ошибка средней) В появившемся диалоговом окне вводим:
— в поле Альфа введем уровень значимости – 0,05,
—в поле Станд_откл. – ссылку на ячейку, где находится стандартное отклонение или готовое значение (2,915),
—в поле Размер – объем выборки ( 
После нажатия на клавишу ОК получаем результат – предельная ошибка выборочной средней равна 2,019 (рис. 2.23)
20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #