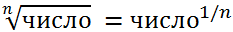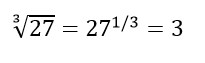Формула корень третьей степени в excel

Изучим особенности извлечения корня в Excel: от квадратного и кубического до произвольного корня n-й степени.

Операция нахождения корня числа широко применима в школьной математике (например, в теореме Пифагора и в поиске решений квадратных уравнений), финансовом анализе, или в быту, при определении длины стороны комнаты или участка зная площадь квадрата.

Квадратный корень вероятно является самым популярным среди всех степеней, вследствие чего в Excel существует стандартная функция позволяющая его найти.

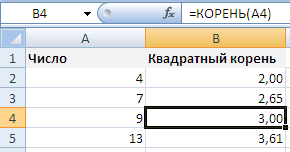
Функция КОРЕНЬ в Excel

КОРЕНЬ(число)
Возвращает значение квадратного корня.

• Число (обязательный аргумент) — число, из которого извлекается квадратный корень.

Обратите внимание, что извлечь корень четной степени (в частности второй) в математике однозначно нельзя.
К примеру, корень из 4 может принимать как положительное значение (+2), так и отрицательное (-2), в связи с этим для четных степеней в Excel для определения знака применяется понятие арифметического корня, значение которого всегда неотрицательно, то есть в примере это число 2.
При работе с данной функцией учитывайте, что если аргумент функции является отрицательным, то в качестве ответа будет возвращена ошибка.
Поэтому найти корень из отрицательных чисел средствами Excel не получится, так как работа с комплексными числами в программе не предусмотрена.

Корень n-й степени в Excel

Для 2-й степени в Excel существует стандартная встроенная функция, но как вычислить корень для степеней большего порядка, в частности, третьей или четвертой степени?
Из школьного курса математики вспомним, что извлечение корня из числа является обратной операцией к возведению числа в степень:

Другими словами, чтобы найти корень n-й степени из числа необходимо возвести данное число в степень 1/n, к примеру, формула КОРЕНЬ эквивалентна возведению в степень 1/2 и т.д.

Примеры

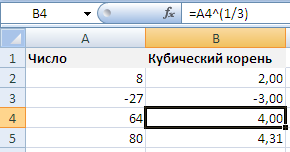
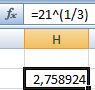
Применим данную формулу для поиска корня 3 степени:

Как видим кубический корень можно извлечь и из отрицательных чисел, и проблемы однозначности при определении знака не стоит.
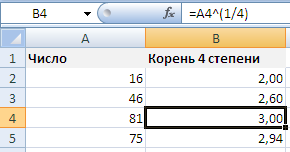
Аналогичные действия производим и для вычисления корня 4 степени:

Вместо математического символа ^ (Shift + 6 на клавиатуре в английской раскладке) можно также использовать функцию СТЕПЕНЬ.

Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!

Для извлечения корня в Excel и возведения числа в степень используются встроенные функции и математические операторы. Рассмотрим на примерах.

Примеры функции КОРЕНЬ в Excel

Встроенная функция КОРЕНЬ возвращает положительное значение квадратного корня. В меню «Функции» она находится в категории «Математические».

Синтаксис функции: =КОРЕНЬ(число).

Единственный и обязательный аргумент представляет собой положительное число, для которого функция вычисляет квадратный корень. Если аргумент имеет отрицательное значение, Excel вернет ошибку #ЧИСЛО!.

В качестве аргумента можно указывать конкретное значение либо ссылку на ячейку с числовым значением.

Рассмотрим примеры.

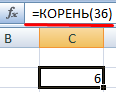
Функция вернула квадратный корень числа 36. Аргумент – определенное значение.

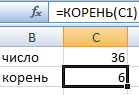
Аргумент функции – ссылка на ячейку с положительным значением 36.

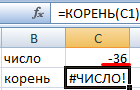
Функция вернула ошибку, т.к. аргумент – ссылка на ячейку с отрицательным значением.

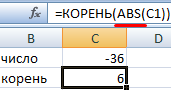
Функция ABS возвращает абсолютное значение числа -36. Ее использование позволило избежать ошибки при извлечении квадратного корня из отрицательного числа.

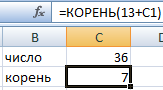
Функция извлекла квадратный корень от суммы 13 и значения ячейки C1.



Функция возведения в степень в Excel

Синтаксис функции: =СТЕПЕНЬ(значение; число). Оба аргумента обязательные.

Значение – любое вещественное числовое значение. Число – показатель степени, в которую нужно возвести заданное значение.

Рассмотрим примеры.

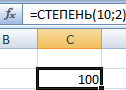
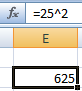
В ячейке C2 – результат возведения числа 10 в квадрат.

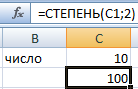
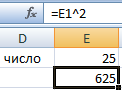
В качестве основания указана ссылка на ячейку с положительным значением 10.

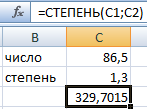
Аргументы функции – ссылки на ячейки с дробными значениями. Результат – число 86,5, возведенное в степень 1,3.

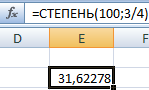
Функция вернула число 100, возведенное к ¾.

Возведение к степени с помощью оператора

Для возведения числа к степени в Excel, можно воспользоваться математическим оператором «^». Для его введения нажать Shift + 6 (с английской раскладкой клавиатуры).

Чтобы Excel воспринимал вводимую информацию как формулу, сначала ставится знак «=». Далее водится цифра, которую нужно возвести в степень. А после значка «^» – значение степени.

Вместо любого значения данной математической формулы можно использовать ссылки на ячейки с цифрами.

Это удобно, если нужно возвести множество значений.

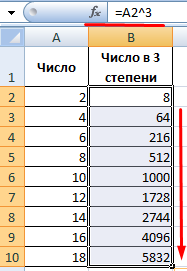
Скопировав формулу на весь столбец, быстро получили результаты возведения чисел в столбце A в третью степень.

Извлечение корней n-й степени

КОРЕНЬ – это функция квадратного корня в Excel. А как извлекать корень 3-й, 4-й и иной степеней?

Вспомним один из математических законов: чтобы извлечь корень n-й степени, необходимо возвести число в степень 1/n.

Например, чтобы извлечь кубический корень, возводим число в степень 1/3.

Воспользуемся формулой для извлечения корней разных степеней в Excel.

Формула вернула значение кубического корня из числа 21. Для возведения в дробную степень использовали оператор «^».

Обратите внимание! Дробная степень пишется в скобках.

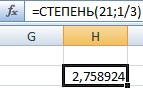
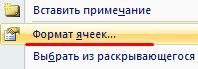
Выполнили ту же задачу, но с использованием функции СТЕПЕНЬ.

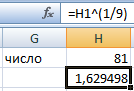
Извлекли корень девятой степени из значения ячейки H1.

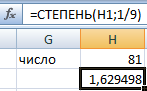
Извлекли корень пятой степени из суммы числа 9 и значения ячейки H1.

Те же математические операции можно выполнить с помощью функции СТЕПЕНЬ:

Таким образом, возвести в степень и извлечь корень n-й степени в Excel можно с помощью одной функции.

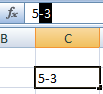
Как написать число в степени

Для корректного отображения числа в степени при демонстрации файла или его печати, необходимо произвести ряд манипуляций:

1. Щелкаем по ячейке с числом правой кнопкой мыши. Выбираем «Формат ячеек» (или нажмите CTRL+1).



2. В открывшемся меню переходим на вкладку «Число». Задаем «Текстовый» формат. Текстовый формат для значения в ячейке можно также задать через панель инструментов («Главная» – «Число»). После установки текстового формата цифра в ячейке становится слева.



3. Рядом с цифрой вводим в ячейку значение со знаком «минус».



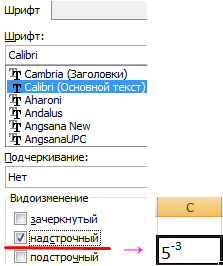
4. Выделяем только значение степени («-3»). Вызываем меню «Формат ячеек». Устанавливаем видоизменение «Надстрочный». И нажимаем ОК.

Получили корректное отображение числа 5 в -3 степени.

Добрый день.

Давненько не писал никаких постов по Word и Excel на страницах блога. И вот, сравнительно не давно, получил довольно интересный вопрос от одного из читателей: «как извлечь корень n-ой степени из числа в Excel». Действительно, насколько я помнил, в Excel есть функция «КОРЕНЬ», но она извлекает только квадратный корень, если нужен корень любой другой степени?

И так…

Кстати, примеры ниже будут работать в Excel 2010-2013 (в остальных версиях их работу я не проверял, и сказать, будет ли работать — не могу).

Как известно из математики, корень любой степени n от числа будет равен возведению в степень этого же числа на 1/n. Чтобы было понятнее это правило, приведу небольшую картинку (см. ниже).

В Excel возвести в степень достаточно просто, для этого используется специальный значок ^ («крышка», обычно такой значок расположен на клавише «6» клавиатуры).

Т.е. чтобы извлечь корень n-ой степени из любого числа (например из 27), формулу нужно записать так:

=27^(1/3)

где 27 — число из которого извлекаем корень;

3 — степень.

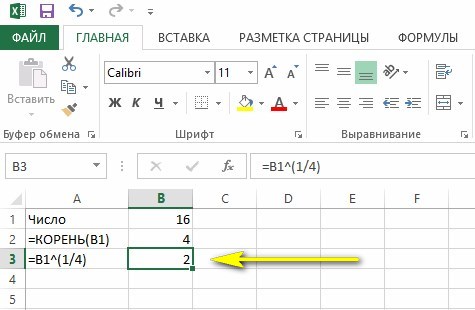
Пример работы ниже на скриншоте.

Кстати, степень можно записывать и сразу в виде десятичного числа. К примеру вместо 1/4, можно записать 0,25, результат будет таким же, а наглядность выше (актуально при длинных формулах и больших расчетах).

На этом все, удачной работы в Excel…

Среди базовых математических вычислений помимо сложения, вычитания, умножения и деления можно выделить возведение в степень и обратное действие – извлечение корня. Давайте посмотрим, каким образом можно выполнить последнее действие в Эксель разными способами.

Метод 1: использование функции КОРЕНЬ

Множество операций в программе реализуется с помощью специальных функций, и извлечение корня – не исключение. В данном случае нам нужен оператор КОРЕНЬ, формула которого выглядит так:

=КОРЕНЬ(число)

Для выполнения расчета достаточно написать данную формулу в любой свободной ячейке (или в строке формул, предварительно выбрав нужную ячейку). Слово “число”, соответственно, меняем на числовое значение, корень которого нужно найти.

Когда все готово, щелкаем клавишу Enter и получаем требуемый результат.

Вместо числа можно, также, указать адрес ячейки, содержащей число.

Указать координаты ячейки можно как вручную, прописав их с помощью клавиш на клавиатуре, так и просто щелкнув по ней, когда курсор находится в положенном месте в формуле.

Вставка формулы через Мастер функций

Воспользоваться формулой для извлечения корня можно через окно вставки функций. Вот, как это делается:

1. Выбрав ячейку, в которой мы хотим выполнить расчеты, щелкаем по кнопке “Вставить функцию” (fx).
2. В окне мастера функций выбираем категорию “Математические”, отмечаем оператор “КОРЕНЬ” и щелкаем OK.
3. Перед нами появится окно с аргументом функции для заполнения. Как и при ручном написании формулы можно указать конкретное число или ссылку на ячейку, содержащую числовое значение. При этом, координаты можно указать, напечатав их с помощью клавиатуры или просто кликнуть по нужному элементу в самой таблице.
4. Щелкнув кнопку OK мы получим результат в ячейке с функцией.

Вставка функции через вкладку “Формулы

1. Встаем в ячейку, в которой хотим произвести вычисления. Щелкаем по кнопке “Математические” в разделе инструментов “Библиотека функций”.
2. Пролистав предложенный перечень находим и кликаем по пункту “КОРЕНЬ”.
3. На экране отобразится уже знакомое окно с аргументом, который нужно заполнить, после чего нажать кнопку OK.

Метод 2: нахождение корня путем возведения в степень

Описанный выше метод позволяет с легкостью извлекать квадратный корень из числа, однако, для кубического уже не подходит. Но и эта задача в Excel реализуема. Для этого числовое значение нужно возвести в дробную степень, где в числителе будет стоять “1”, а в знаменателе – цифра, означающая степень корня (n).

В общем виде, формула выглядит так:

=(Число)^(1/n)

Безусловным преимуществом такого способа является то, что мы можем извлечь корень любой степени, заменив букву “n” в знаменателе дроби на требуемую цифру.

Для начала давайте рассмотрим формулу для извлечения квадратного корня. Она выглядит следующим образом: =(Число)^(1/2).

Соответственно, для расчета кубического корня будет использоваться выражение ниже:

=(Число)^(1/3)

Допустим, нам нужно извлечь кубический корень из числа 27. В этом случае нужно записать в ячейке такую формулу: =27^(1/3).

Нажав Enter, получаем результат вычислений.

Аналогично работе с функцией КОРЕНЬ, вместо конкретного числа можно указать ссылку на ячейку.

Заключение

Таким образом, в Excel можно без особых усилий извлечь корень из любого числа, и сделать это можно разными способами. К тому же, возможности программы позволяют выполнять расчеты для извлечения не только квадратного, но и кубического корня. В редких случаях требуется найти корень n-степени, но и эта задача достаточно просто выполняется в программе.