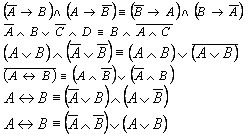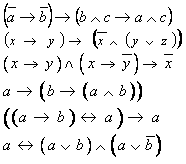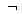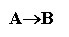В настоящее время применение информационных
технологий становится неотъемлемой частью
образовательного процесса. Компьютер наиболее
полно удовлетворяет дидактическим требованиям и
позволяет адаптировать процесс обучения к
индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в
процесс обучения и диагностики, позволяют
упростить процесс отработки навыков и умений и
оценки знаний учащихся.
В данной работе рассматривается применение
табличного процессора MS Excel при изучении основ
логики.
Существует множество задач, в которых исходные
и результатные данные должны быть представлены в
табличной форме. Электронные таблицы
представляют собой удобный инструмент для
автоматизации таких вычислений. Решения многих
вычислительных задач на ЭВМ, которые раньше
можно было осуществить только путем
программирования, стало возможно реализовать.
Использование математических формул в
электронных таблицах позволяет представить
взаимосвязь между различными параметрами
некоторой реальной системы. Основное свойство
электронных таблиц – мгновенный пересчет формул
при изменении значений входящих в них операндов.
Благодаря этому свойству, таблица представляет
собой удобный инструмент для организации
численного эксперимента:
- подбор параметров,
- прогноз поведения моделируемой системы,
- анализ зависимостей,
- планирование.
В электронных таблицах предусмотрен также
графический режим работы, который дает
возможность графического представления (в виде
графиков, диаграмм) числовой информации,
содержащейся в таблице.
В процессе изучения алгебры логики учащиеся
знакомятся с такими понятиями как: высказывание,
таблицы истинности, логические функции и
логические операции. Алгебра логики является
разделом математической логики, в которой
изучаются методы доказательства истинности (1)
или ложности (0) сложных логических конструкций,
составленных из простых высказываний, на основе
истинности или ложности последних. Для
закрепления полученных знаний возможно
использование табличного процессора MS Excel и его
функций.
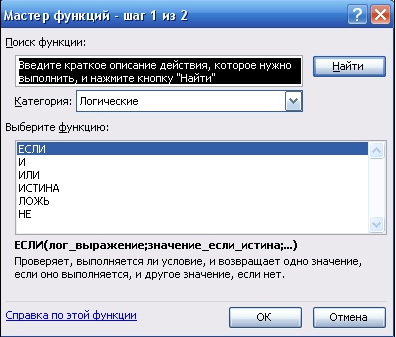
Для реализации функций булевой алгебры
используются логические функции: ЕСЛИ, И, ИЛИ, НЕ,
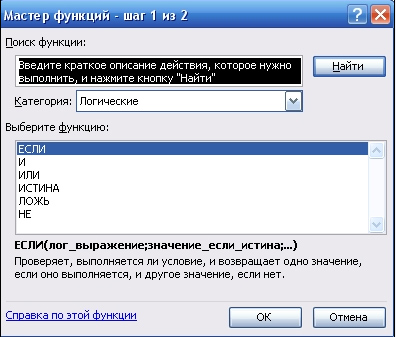
ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel
используется мастер функций (Вставка Функция…), в котором отображается
имя функции, ее описание и аргументы.
Рисунок 1. Окно мастера функций
Первоначально следует создать таблицу
основных логических операций:
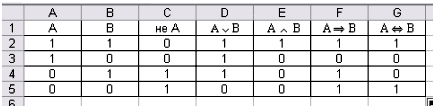
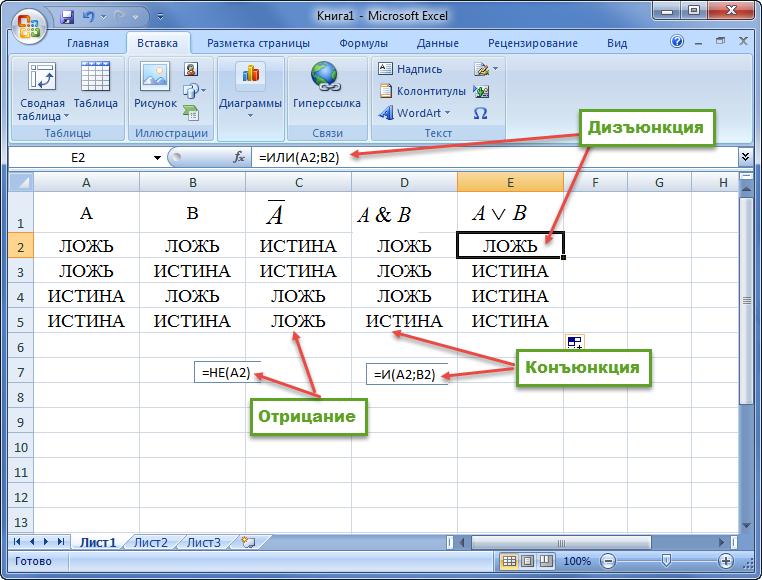
Рисунок 2. Таблица истинности основных
логических операций
При составлении таблицы истинности
используются следующие формулы:
- Инверсия: =ЕСЛИ(A2=1;0;1);
- Дизъюнкция: =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0);
- Конъюнкция: =ЕСЛИ(И(A2=1;B2=1);1;0);
- Импликация: =ЕСЛИ(И(A2=1;B2=0);0;1);
- Эквивалентность: =ЕСЛИ(A2=B2;1;0).
В последующей работе данная таблица может
использоваться учащимися как основа для
выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая
работа.
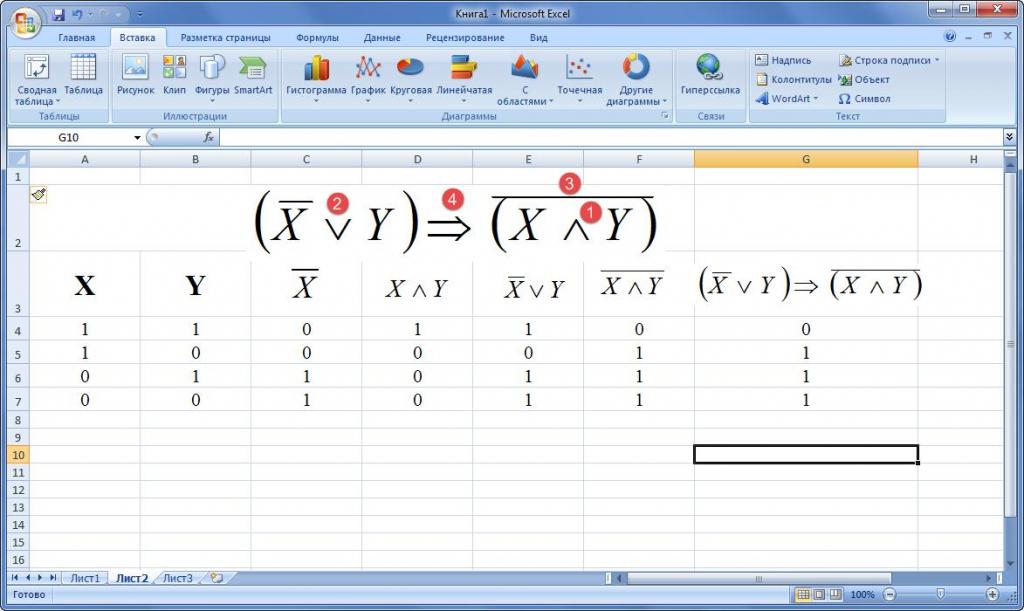
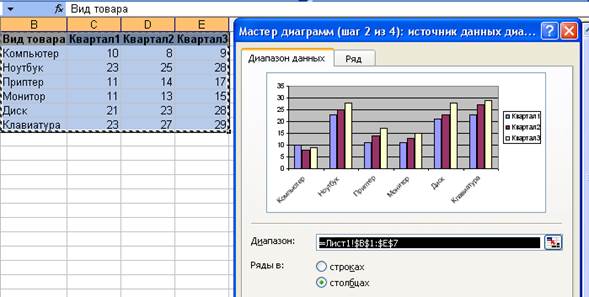
Задание: Построить таблицу истинности для
формулы (A
B
C)
A, используя MS Excel.
Алгоритм:
- Определить количество наборов входных
переменных, по формуле: Q = 2n, где n –
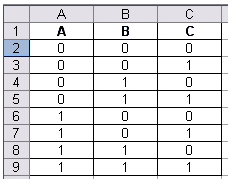
количество переменных. Q = 23 = 8. - Внести в таблицу все наборы входных переменных:
Рисунок 3. Исходные данные
- Определить количество логических операций и
порядок их выполнения:
- Заполнить столбцы результатами выполнения
логических операций в обозначенной
последовательности.
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
в G2: =ЕСЛИ(F2=A2;1;0).
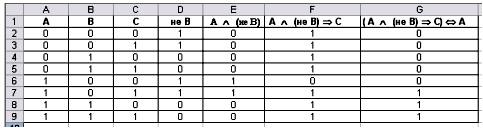
Заполнение остальных строк произвести путем
копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для
закрепления не только материала математической
логики, но и для основ теории вероятностей и
математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности
равносильность формул.
Определить являются ли формулы тавтологиями.
Содержание
- 1 Использование логических функций в Excel
- 2 Логические функции в Excel и примеры решения задач
- 3 Статистические и логические функции в Excel
- 3.1 Логическое следование (импликация).
- 3.2 Логическое равенство (эквивалентность).
- 3.3 Логические законы и правила преобразования логических выражений.
- 4 Глава 5.
- 5 Решение логических задач.
- 6 Глава 6.Логические операции и
- 7 условная функция в электронных таблицах Excel.
- 7.1 Логические выражения.
- 7.2 Составление таблиц истинности с помощью Excel.
- 8 Заключение.
- 9 Библиографический список.
- 10 Приложение.

Вот я, наконец, то и добрался к своим любимым логическим функциям Excel. Признаю, что мне они наиболее ближе и удобнее в использовании нежели другие разделы функций, каюсь грешен, должны же быть и у меня любимчики… А если говорить серьезно, логические функции одни из самых распространённых в использовании функции и самые полезные в работе бухгалтеров, экономистов, да и в принципе любого специалиста финансовых дисциплин.
Основной особенностью этих функций, это проверка данных на соответствие результату «ИСТИНА» или «ЛОЖЬ», то есть когда результат соответствует заданному условию, получаем итог «ИСТИНА» и «ЛОЖЬ», когда условия не выполнены. На самом деле это намного легче понять, чем описать и я думаю, что читая дальше, вы сможете понять логику работы этих функций.
Поскольку хочется написать многое, описать работу и возможности функций в одной статье, это будет чрезмерно много, поэтому, как и в случае с описанием текстовых функций, я разобью информацию о логических функциях на 2 части.
В своем арсенале Excel содержит 7 логических функций, хотя в зависимости от версий их может быть и меньше, и больше. Найти перечень доступных функций вы можете в панели управления на вкладке «Формулы», в блоке «Библиотека функций», нажав кнопку «Логические» с выпадающем перечнем логических функций. Или с помощью мастера функций: 
- Функция ЕСЛИ;
- Функция ИСТИНА;
- Функция ЛОЖЬ;
- Функция НЕ.
Все предоставленные функции достаточны, просты и легки в использовании, и я думаю, у вас не будет никаких затруднений в их реализации и использовании. Главное условие этого я бы выделил только понимание сути и логики исполнения функции и варианты ее применения вы сразу сможете понять.
Функция ЕСЛИ
Сразу скажу это одна из самых классных функций в Excel. Я ее результатами пользуюсь, где нужно и ненужно, а поэтому считаю, что изучить ее возможности необходимо любому уважающему себя человеку, который хочет показать себя как специалист финансовых дисциплин. Несмотря на кажущуюся простоту, возможности этой функции очень удивляют и приятно радуют. Для углублённого изучения ее возможностей вам поможет статья «Как используется функция ЕСЛИ в Excel с несколькими условиями».
Функция ЕСЛИ возвращает один результат в случаях, если аргумент «логическое выражение» при вычислении получает ответ «ИСТИНА» и совсем другой, если ответ «ЛОЖЬ». Функция может содержать до семи логических условий внутри себя для аргумента «_значение если истина_», а для аргумент «_значение если ложь_» умеет выполнять функции или команды дальнейшего действия (к примеру, использование функции ПЕРЕЙТИ).
Синтаксис функции:
=ЕСЛИ(_лог_выражение_,_значение_если_истина_,_значение_если_ложь_), где:
- Логическое выражение – указывается практически любое выражение или значение, которое в процессе вычисления получает значение «ИСТИНА» или «ЛОЖЬ»;
- Значение если истина – это значение, которое будет возвращено, если аргумент «Логическое выражение» получит результат «ИСТИНА». В случае, когда этот аргумент не указан в формуле, возвращается результат «ИСТИНА»;
- Значение если ложь — это значение, которое будет возвращено, если аргумент «Логическое выражение» получит результат «ЛОЖЬ». В случае, когда этот аргумент опущен в формуле, возвращается результат «ЛОЖЬ».
Пример №1:
Рассмотрим усложнённый пример со многими условиями, вложенными в функцию ЕСЛИ. У нас есть персонал, которому в зависимости от стажа работы, производится доплата к ставке заработной платы. Всего будет три доплаты, стаж работы 3 года – 10%, 10 лет – 20% и 20 лет – 30%. Для получения результата и автоматического расчёта доплаты в зависимости от стажа нам нужна формула такого вида:
=ЕСЛИ(C2>=20;»30%»;ЕСЛИ(C2>=10;»20%»;ЕСЛИ(C2>=3;»10%»;»0%»))).

Рассмотрим еще один сложный пример, в котором мы будем определять, и идентифицировать виды банковских карточек по их номерам. Для первого аргумента используем текстовую функцию ЛЕВСИМВ для захвата первых 4 цифр, которые и будут условием определения. Для карты «Visa Electron» установим идентификатор 1234, для карты «Maestro» — 5678 и все остальные карты будут по умолчанию «MasterCard Standard». Теперь собственно формула, которая поможет нам определить результат будет такова:
=ЕСЛИ( ЛЕВСИМВ (B14;4)= «1234»; «Visa Electron»; ЕСЛИ ( ЛЕВСИМВ (B14;4)=»5678»; «Maestro»; «MasterCard Standard»)).

Абсолютно простая логическая функция ИСТИНА, не имеет никаких аргументов и умеет возвращать всего лишь логическое значение «ИСТИНА». Имеет смысл использовать только в связке с другими функциями.
Синтаксис функции:
=ИСТИНА().
Аргументы отсутствуют.

Простая функция ЛОЖЬ аналогична описываемой ранее функции ИСТИНА, но наоборот, умеет возвращать всего лишь логическое значение «ЛОЖЬ» и не имеет никаких аргументов. Её тоже необходимо использовать в тандеме с другими функциями.
Синтаксис функции:
=ЛОЖЬ().
Аргументов нет.

Простая в работе и исполнении логическая функция НЕ умеет только одно, производит замену полученного логического значения своего аргумента на абсолютно противоположный, т.е. он заменяет значение «ЛОЖЬ» на «ИСТИНА» и, наоборот, в другую сторону. Использование функции НЕ, рационально применять в случаях, когда нужна 100%-ная уверенность что некое значение не будет равно некой определённой величине.
Синтаксис функции:
= НЕ(_логическое_значение_), где:
- Логическое значение – это выражение, ссылка на ячейку или значение, которое как результат вычислений дает логическое значение «ИСТИНА» или «ЛОЖЬ». Функция НЕ при получении такого результата меняет его: «ЛОЖЬ» на «ИСТИНА» и «ИСТИНА» на «ЛОЖЬ».
Пример:

А на этом у меня пока всё, жду вас на страницах второй части статьи! Я очень надеюсь, что описанные всех логических функций в Excel в этой части были ёмкими и понятными. Буду очень благодарен за оставленные комментарии, так как это показатель читаемости и вдохновляет на написание новых статей! Делитесь с друзьями, прочитанным и ставьте лайк!
Не забудьте поблагодарить автора!
Богатство приносит не большое состояние, а скромные потребности.
Эпиктет (Epictetus)
Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.
Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.
| Название функции | Значение | Синтаксис | Примечание |
| ИСТИНА | Не имеет аргументов, возвращает логическое значение «ИСТИНА». | =ИСТИНА () | Редко используется в качестве самостоятельной функции. |
| ЛОЖЬ | Не имеет аргументов, возвращает логическое выражение «ЛОЖЬ». | =ЛОЖЬ () | ——-//——- |
| И | Если все заданные аргументы возвращают истинный результат, то функция выдает логическое выражение «ИСТИНА». В случае хотя бы одного ложного логического значения вся функция выдает результат «ЛОЖЬ». | =И (Лог_знач. 1; Лог_знач. 2;…) | Принимает до 255 аргументов в виде условий или ссылок. Обязательным является первый. |
| ИЛИ | Показывает результат «ИСТИНА», если хотя бы один из аргументов является истинным. | =ИЛИ (Лог_знач.1; Лог_знач. 2;…) | ——-//——- |
| НЕ | Меняет логическое значение «ИСТИНА» на противоположное – «ЛОЖЬ». И наоборот. | #ИМЯ? | Обычно сочетается с другими операторами. |
| ЕСЛИ | Проверяет истинность логического выражения и возвращает соответствующий результат. | #ИМЯ? | «Логическое_выражение» при вычислении должно иметь результат «ИСТИНА» или «ЛОЖЬ». |
| ЕСЛИОШИБКА | Если значение первого аргумента истинно, то возвращает сам аргумент. В противном случае – значение второго аргумента. | #ИМЯ? | Оба аргумента обязательны. |
Логические функции в Excel и примеры решения задач
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.
Сформируем таблицу с исходными параметрами:
Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).
Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.
Формула приобретает следующий вид: .
В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.
Для решения используем логические функции ЕСЛИ и ИЛИ: . Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.
При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.
В качестве аргументов можно использовать другие функции. К примеру, математические.
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.
Составим таблицу с исходными данными:
Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».
Введем формулу вида: . Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.
Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.
Статистические и логические функции в Excel
Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.
Работаем с таблицей из предыдущего раздела:
Для решения задачи используем формулу вида: . В логическом выражении «D2
Задача 2. Найти средние продажи в магазинах сети.
Составим таблицу с исходными данными:
Необходимо найти среднее арифметическое для ячеек, значение которых отвечает заданному условию. То есть совместить логическое и статистическое решение.
Чуть ниже таблицы с условием составим табличку для отображения результатов:
Решим задачу с помощью одной функции: . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.
Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.
Задача 3. Найти средние продажи в магазине №1 г. Москва.
Видоизменим таблицу из предыдущего примера:
Нужно выполнить два условия – воспользуемся функцией вида: .
Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.
Скачать примеры логических функций
Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.
Функция учитывает только те значения, которые соответствуют всем заданным условиям.
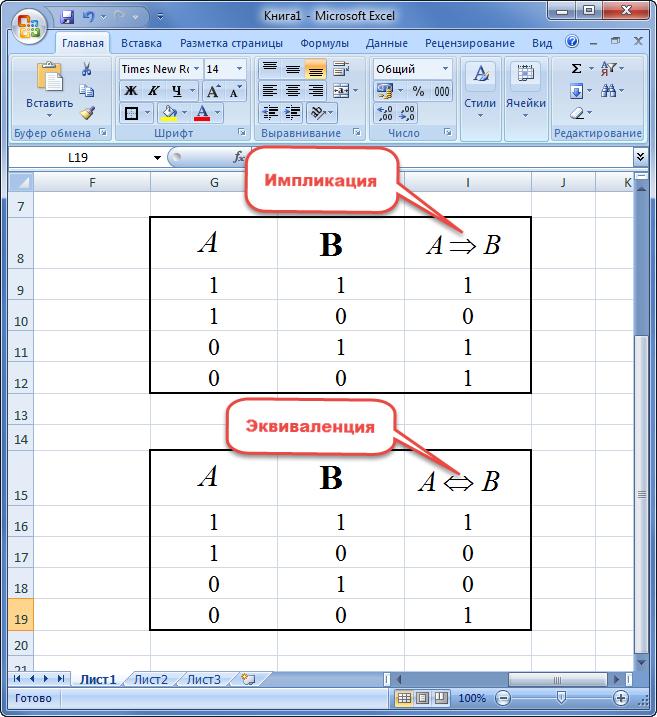
Логическое следование (импликация).
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
Логическая операция импликации «если А то В», обозначается А В и выражается с помощью логической функции F14, которая задается соответствующей таблицей истинности.
Таблица истинности логической функции импликация.
|
A |
B |
F14=A В |
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, т.к. истинны и первое высказывание (предпосылка), и второе высказывание (вывод).
Высказывание «Если число делится на 10, то оно делится на 3» ложно, т. к. из истинной предпосылки делается ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание ложно, то вне зависимости от истинности или ложности второго высказывания составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.
Логическое равенство (эквивалентность).
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…».
Логическая операция эквивалентности «А эквивалентно В» обозначается А~В и выражается с помощью логической функции F10, которая задается соответствующей таблицей истинности.
Таблица истинности логической функции эквивалентности.
|
A |
B |
F10 |
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Рассмотрим, например, два высказывания А= «Компьютер может производить вычисления» и В= «Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности истинно, когда оба высказывания либо истинны, либо ложны.
«Компьютер может производить вычисления тогда и только тогда, когда компьютер включен».
« Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».
Составное высказывание, полученное с помощью операции эквивалентности ложно, когда одно высказывание истинно, а другое — ложно:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».
Логические законы и правила преобразования логических выражений.
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствии с законами логики.
Закон тождества. Всякое высказывание тождественно самому себе:
А=А.
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А- истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:
А&А=0.
Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение истина:
АvА=1.
Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
=
А=А.
Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.
Законы Моргана.
АvВ=А&В.
А&В=АvВ.
Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:
|
Логическое умножение |
Логическое сложение |
|
А&В=В&А |
АvВ=ВvА |
Правило ассоциативности. Если в логическом выражении используются только операция логического умножения или только логического сложения, то можно пренебрегать скобками или произвольно их расставлять:
|
Логическое умножение |
Логическое сложение |
|
(А&В)&С=А&(В&С) |
(АvВ)vС=Аv(ВvС) |
Правило дистрибутивности. В отличии от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
|
Дистрибутивность умножения относительно сложения |
Дистрибутивность сложения относительно умножения |
|
(а*в)+(а*с)=а*(в+с) (А&В)v(А&С)=А&(ВvС) |
(АvВ)&(АvС)=Аv(В&С) |
Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
(А&В)v(А&В).
Воспользуемся правилом дистрибутивности и вынесем за скобки А:
(А&В)v(А&В)=А&(ВvВ).
По закону исключенного третьего ВvВ=1, следовательно:
А&(ВvВ)=А&1=А.
Законы и правила преобразования логических выражений позволяют упростить сложное выражение и, не применяя таблиц истинности, найти ответ при решении задач.
Глава 5.
Решение логических задач.
Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.
Условие задачи.
В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На аудиториях повесили шутливые таблички. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках или обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Решение задачи.
Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:
А — «В первой аудитории находится кабинет информатики»,
В — «Во второй аудитории находится кабинет информатики».
Тогда отрицаниям этих высказываний будут соответствовать:
А — «В первой аудитории находится кабинет физики»,
В — «Во второй аудитории находится кабинет физики».
Высказывание, содержащееся на табличке на первой аудитории, соответствует логическому выражению:
X=АvВ.
Высказывание, содержащееся на табличке на второй аудитории, соответствует логическому выражению:
Y=А.
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные, в соответствии с законом исключенного третьего записывается следующим образом:
(X&Y) v (X&Y)=1.
Подставим вместо X и Y соответствующие формулы:
(X&Y) v (X &Y) = ((A v B)&A) v (A v B) &A.
|
А |
В |
А |
В |
АvВ&А |
АvВ&А |
(АvВ&А)v(АvВ&А) |
Из таблицы истинности можно сделать вывод, что в первой аудитории находится кабинет физики, а во второй- кабинет информатики.
Глава 6.
Логические операции и
условная функция в электронных таблицах Excel.
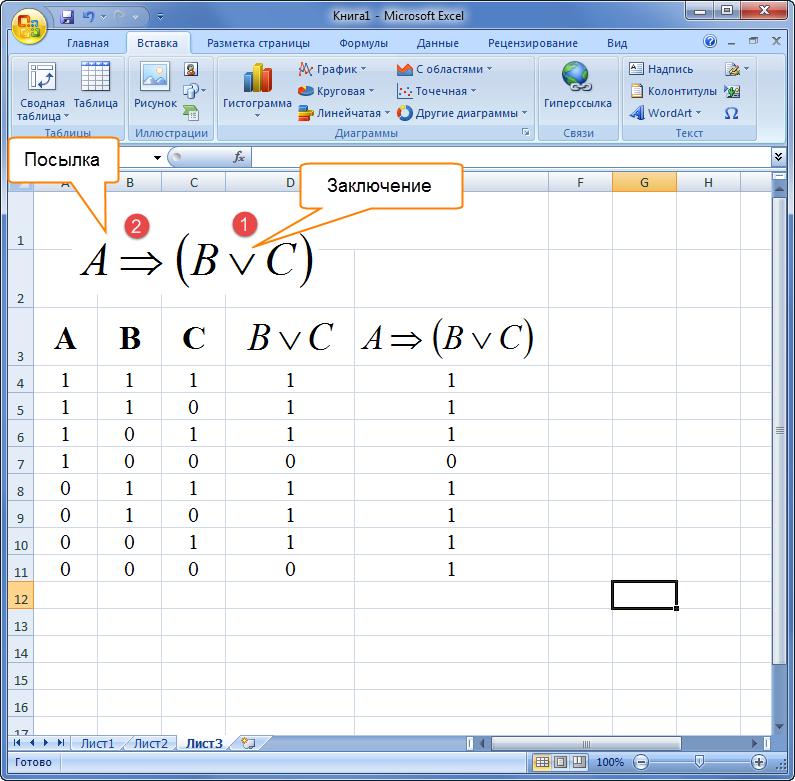
Общий вид условной функции следующий:
ЕСЛИ (, , )
Условие — это логическое выражение, которое может принимать значение ИСТИНА или ЛОЖЬ. и могут быть числами, формулами или текстами.
Условная функция, записанная в ячейку таблицы, выполняется так: если условие истинно, то значение данной ячейки определит , в противном случае -.
Логические выражения.
Логические выражения строятся с помощью операций отношения (, =(больше или равно), =, (не равно)) и логических операций(логическое И, логическое ИЛИ, логическое НЕ). Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ.
Существуют особенности записи логических операций в табличных процессорах: сначала записывается имя логической операции (И, ИЛИ, НЕ), а затем в круглых скобках перечисляются логические операнды.
Составление таблиц истинности с помощью Excel.
Задача 1. Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предложения:
-
Аня пойдет в кино только тогда, когда пойдут Вика и Сергей;
-
Аня и Сергей пойдут в кино вместе или же оба останутся дома;
-
чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино?
Решение. Обозначим простые высказывания:
А — Аня пойдет в кино;
В — Вика пойдет в кино;
С — Сергей пойдет в кино.
Каждое составное высказывание можно выразить в виде формулы – логического выражения.
-
А(В&С)
-
(А&С)v(А&С)
-
СВ
Составим таблицу истинности в Excel.
В каждую колонку введем формулы, которые будут соответствовать логическим операциям. В Excel существуют логические операции «И», «ИЛИ», «НЕ». Для функции логического следования (импликации) воспользуемся условной функцией если (…), то.., а для функции логического равенства (эквивалентности) воспользуемся функцией «равно». В результате в режиме формул наша таблица примет следующий вид:
|
А |
В |
С |
не А |
не С |
В & С |
А(В&С) |
A & C |
(неА)&(неС) |
(A&C)v(неА&неС) |
СВ |
|
=НЕ(A33) |
=НЕ(C33) |
=И(B33;C33) |
=A33=F33 |
=И(A33;C33) |
=И(D33;E33) |
=ИЛИ(H43;I33) |
=C33=B33 |
|||
|
=НЕ(A34) |
=НЕ(C34) |
=И(B34;C34) |
=A34=F34 |
=И(A34;C34) |
=И(D34;E34) |
=ИЛИ(H44;I34) |
=C34=B34 |
|||
|
=НЕ(A35) |
=НЕ(C35) |
=И(B35;C35) |
=A35=F35 |
=И(A35;C35) |
=И(D35;E35) |
=ИЛИ(H45;I35) |
=C35=B35 |
|||
|
=НЕ(A36) |
=НЕ(C36) |
=И(B36;C36) |
=A36=F36 |
=И(A36;C36) |
=И(D36;E36) |
=ИЛИ(H46;I36) |
=C36=B36 |
|||
|
=НЕ(A37) |
=НЕ(C37) |
=И(B37;C37) |
=A37=F37 |
=И(A37;C37) |
=И(D37;E37) |
=ИЛИ(H47;I37) |
=C37=B37 |
|||
|
=НЕ(A38) |
=НЕ(C38) |
=И(B38;C38) |
=A38=F38 |
=И(A38;C38) |
=И(D38;E38) |
=ИЛИ(H48;I38) |
=C38=B38 |
|||
|
=НЕ(A39) |
=НЕ(C39) |
=И(B39;C39) |
=A39=F39 |
=И(A39;C39) |
=И(D39;E39) |
=ИЛИ(H49;I39) |
=C39=B39 |
Введем значения А, В и С в виде «истина» и «ложь», и получим искомый результат:
|
А |
В |
С |
не А |
не С |
В & С |
А(В&С) |
А & С |
(неА)&(неС) |
(A&C)v(неА&неС) |
СВ |
|
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
|
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
|
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
|
ИСТИНА |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
|
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
|
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
|
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
ЛОЖЬ |
Ответ. Т.к. два высказывания должны быть «истина», а одно «ложь», то правильный ответ следующий: Аня и Сергей не пойдут в кино, а пойдет Вика.
Таким образом, электронные таблицы упрощают работу с таблицами истинности и помогают быстрее решать логические задачи.
Заключение.
-
Тема, затронутая в данном реферате, имеет практическое значение. Каждый мыслящий человек должен иметь представление о законах логики. Логика изучает внутреннюю структуру процесса мышления.
-
Логические операции, описанные Аристотелем, помогают решать сложные логические задачи математики и информатики.
-
Применение компьютера при работе над данной темой еще раз подтверждает возможность использования вычислительной техники в различных сферах науки, и жизни человека.
Библиографический список.
-
Информатика. Задачник-практикум. / Под редакцией И. Г. Семакина, Е.К. Хеннера: том. 2. – Москва: Лаборатория Базовых Знаний, 2001.
-
Информатика. Задачник-практикум. / Под редакцией И. Г. Семакина, Е.К. Хеннера: том. 1. – Москва: Лаборатория Базовых Знаний, 2001.
-
Угринович Н.Д. Информатика и информационные технологии. Учебное пособие для 10-11 классов. Углубленный курс. – Москва: Лаборатория Базовых Знаний, 2000.
-
Информатика. Базовый курс. 7-9 классы. – М.: Лаборатория Базовых Знаний, 2001.
-
Шафрин Ю.А. Информационные технологии: В 2 ч. Ч. 2: Офисная технология и информационные системы. – М.: Лаборатория Базовых Знаний, 2001.
-
Вершинин О.Е. За страницами учебника информатики: Кн. Для учащихся 10-11 кл. средней шк.- М.: Просвещение, 1991.
-
Журин А.А. Excel 2000. Для школьников и начинающих пользователей. – М.: «АКВАРИУМ», К.:ГИППВ, — 2000.
Приложение.
Задача 2.
Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша: «Это сосуд греческий и изготовлен в V веке».
Боря: «Это сосуд финский и изготовлен в Ш веке».
Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Задача 3.
В нарушении правил обмена валюты подозревают четыре работника банка – А, В, С и D. Известно, что:
-
Если А нарушил, то и В нарушил правила обмена валюты.
-
Если В нарушил, то и С нарушил или А не нарушал.
-
Если D не нарушил, то А нарушил, а С не нарушал.
-
Если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
Задача 4.
На вопрос, какая завтра будет погода, синоптик ответил:
-
«если не будет ветра, то будет пасмурная погода без дождя»;
-
«если будет дождь, то будет пасмурно и без ветра»;
-
«если будет пасмурная погода, то будет дождь и не будет ветра».
Подумав немного, синоптик уточнил, что его три высказывания можно лаконично записать в виде одного составного высказывания. Сформулируйте его, решив задачу с помощью логических операций.
Задача 5.
Определите, кто из подозреваемых участвовал в преступлении, если известно:
-
Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
-
Если Иванов не участвовал, то Сидоров не участвовал.
Задача 6.
Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:
-
Сергей – первый, Роман – второй;
-
Сергей – второй, Виктор – третий;
-
Леонид – второй, Виктор – четвертый.
Известно, что в каждом ответе только одно утверждение истинно. Как распределились места?
Фев 04 2021
Вроде простая вещь — нужно вычислить результат для нескольких булевых переменных
Читаем основную статью
Компьютер
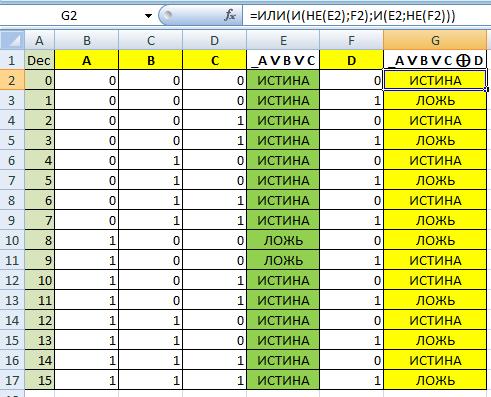
Вроде всё просто. Но вот такой пример вида _A ∨ B ∨ C ⊕ D
Переводим на русский язык (с математического языка) — нужно сделать таблицу истинности для выражения
не A или B или C иск.или D
для всех вариантов переменных A,B.C.D, которые могут принимать значения «Истина» / «Ложь»
Или на английском (для программирования) = not.A.or.B.or.C.xor.D
Задача на булеву алгебру не сложная — но у нас четыре переменных и 16 строк в таблице (да, 24 = 16). А если таких переменных будет 5, то в таблице будет 32 строки.
Но у нас есть Excel (Execute Cell), который прекрасно понимает формулы логики. Достаточно правильно написать формулу для одной строки — и потом мышкой перетащить эту формулу на остальные строки. Готово!
Итак по частям.
Логическая операция это операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логическая связка это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
Логические операции
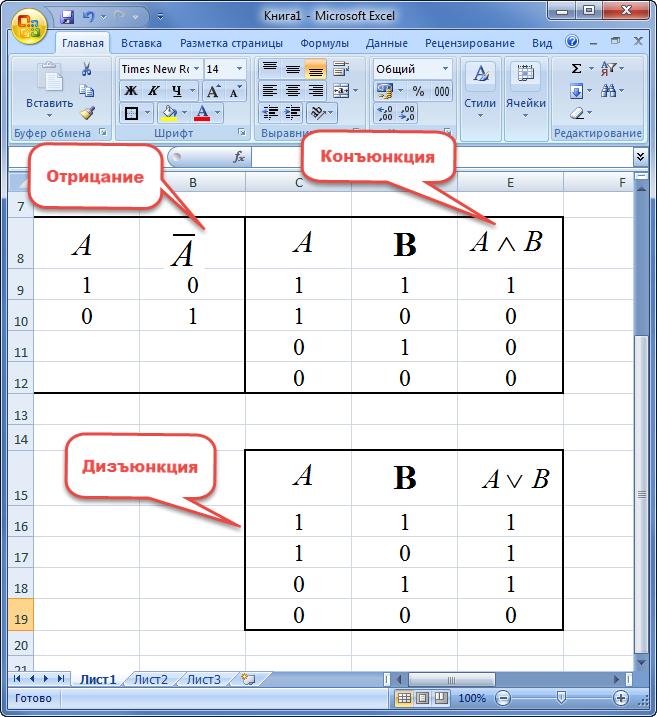
Логическая операция И (Конъюнкция)
Конъюнкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логическое «И», логическое умножение, иногда просто «И»
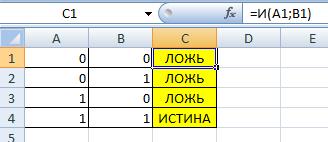
И таблица истинности (AND таблица истинности)
=И(A1;B1)
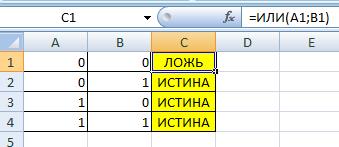
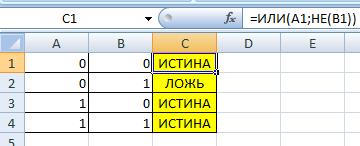
Логическая операция ИЛИ (Дизъюнкция)
Дизъюнкция (от лат. disjunctio — «разобщение») — логическое сложение, логическое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»
ИЛИ таблица истинности (OR таблица истинности)
=ИЛИ(A1;B1)
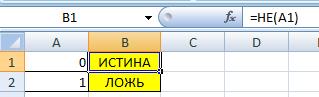
Логическая операция отрицания (Инверсия)
Инверсия (от лат. inversio «переворачивание; перестановка») — отрицание — переворачивание смысла, замена «белого» «чёрным»
НЕ таблица истинности (NOT таблица истинности)
=НЕ(A1)
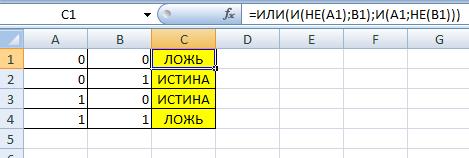
Логическая операция XOR (исключающее ИЛИ)
XOR таблица истинности
В Excel 2007 её нет.
В более современных версиях она есть. Но мы её можем собрать самостоятельно.
=ИЛИ(И(НЕ(A1);B1);И(A1;НЕ(B1)))
Логические связки
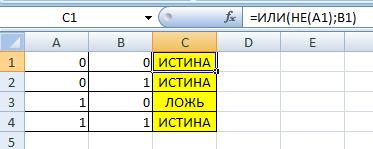
Логическая связка Импликация (прямая)
Логическая связка как A → B
используем аналог _A V B
=ИЛИ(НЕ(A1);B1)
Логическая связка Импликация (обратная)
Логическая связка как A ← B
используем аналог A V _B
=ИЛИ(A1;НЕ(B1))
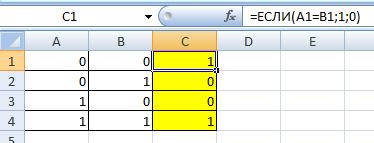
Логическая связка ТОЖДЕСТВО
Используем ЕСЛИ, чтобы логическая связка получилась
=ЕСЛИ(A1=B1;1;0)
или вывод текстом
=ЕСЛИ(A1=B1;"ИСТИНА";"ЛОЖЬ")
Собираем таблицу истинности
Не обязательно собирать всё в одной ячейке. Можно сделать столбцы для промежуточных вычислений.
Для нашего примера _A ∨ B ∨ C ⊕ D
Удобно.
Последние публикации
- Статьи от: Автор
- Рубрика: Блог
- Сортировка: дата публикации по убыванию
Классический вход Windows 7
Публикация 2 года назад
Как это было в Windows XP Для входа в систему нужно указать: пользователь (login)
пароль В Windows 7 сделали по умолчанию стандартный вход в систему Мышкой выбираем пользователя и вводим только пароль (если он установлен). Как вернуть классический вход в систему Windows 7 и зачем это нужно? Для работы на локальной машине — конечно удобнее стандартный вход. А вот если Вы подключаетесь к удаленной машине через RDP — то ввода только пароля недостаточно. Читаем статью RDP — удаленный рабочий стол Большое количество ботов со всего мира подберет Ваш пароль достаточно быстро (в логах будет по 5-10 попыток в секунду). Читаем статью Включаем шифрование…
(Читать полностью…)
Процессоры AMD FX и их «ядра»

Публикация 2 года назад
Немного маркетинга в тему — ядра процессоров AMD FX и ядра процессоров Intel AMD FX (AM3+) — хорошие были процессоры. Но есть нюанс. AMD использовала хитрую терминологию — «ядра» и «модули». Это была вершина маркетинга 
Одно…
(Читать полностью…)
Загадочная «маска подсети» — это просто
Публикация 2 года назад
Многие видели в Windows свойства адаптера сети при ручной настройке Многие даже понимают, что IP-адрес 192.168.1.1 — это запись в десятичной форме 32-х бит адреса IP v4 с разбивкой на оксеты (по 8 бит). Что такое «маска подсети»?
Которая 255.255.255.0. И зачем она нужна? Посмотрим в таком же двоичном виде — легко видеть, что это 24 единицы подряд Это просто так айтишники шутят 
(Читать полностью…)
Вычисляем большие числа

Публикация 2 года назад
Самое известное большое число googol — отсюда собственно название Google 10100 = это 1 единица и 100 нулей Хорошо. А например, 2512 — это сколько? Калькулятор Windows говорит, что это 1,3 * 10154 Тоже неплохо, да и больше чем googol на 54 порядка 
(Читать полностью…)
Как соединить два роутера проводом?
Публикация 3 года назад
Предположим, у нас есть «Главный роутер», который управляем всеми нашими устройствами PC. И еще есть: у «Главного роутера» второй WAN-порт
бесхозный ADSL роутер Простой вопрос — как сделать резервирование интернета? Что бы при отсутствии основного интернета можно было подключить и использовать «Роутер ADSL»? Основная статья про сеть здесь Варианты в лоб: использовать только «Роутер ADSL» — но это придется к нему переподключать все конечные ПК
и сетку Wi-Fi придется перестраивать для переподключения мобильных устройств Нехорошо 
(Читать полностью…)
Как не надо устанавливать SSD M.2

Публикация 3 года назад
Иногда вот такая жесть бывает при установке SSD M.2. Небольшой изгиб, так сказать. Основная статья про M.2 тут Интерфейс NVMe и разъемы M.2 и U.2 Как это получилось? Обычно так бывает при самостоятельной сборке ПК из новых комплектующих. SSD M.2 устанавливается под 45% в разъем на плате и потом прижимается винтиком, которые вкручивается в другой винтик на материнской плате. Но почему этот основной винтик «пенек» может отсутствовать на материнской плате? Вот тут хорошо видно проблему 
или кладет все…
(Читать полностью…)
Как набрать немецкие умляуты (umlaut) на обычной клавиатуре в России?

Публикация 3 года назад
Будем разбираться с немецкими умляутами Делаем свой набор горячих клавиш (hotkey) для умляутов
Самый удобный вариант 
R Alt A
Ä
ä O
Ö
ö U
Ü
ü S
ẞ
ß Здесь символы A, O, U и S — это не буквы, а кнопки на клавиатуре. Как это сделать? Используем программу QuickTextPaste — в ней можно завязать не только отдельные буквы, и целые части текста. Настройки хранятся в C:UsersNameAppDataRoamingQuickTextPasteQuickTextPaste.ini Использование простое: добавляем комбинацию клавиш
…
(Читать полностью…)
Типовое задание № 2
(базовый уровень,
время – 3 мин)
Тема:
Анализ таблиц истинности логических выражений.
Что проверяется:
Умение строить таблицы
истинности и логические схемы.
1.5.1.
Высказывания, логические операции, кванторы, истинность высказывания
1.1.6.
Умение строить модели объектов, систем и процессов в виде таблицы истинности
для логического высказывания
Про обозначения
К
сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной»
математической логике (Ù,Ú,¬), неудобны, интуитивно
непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему
стыду, до сих пор иногда путает Ù и Ú.
Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком
умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+»
(логическое сложение). В разных учебниках используют разные обозначения. К
счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,¬), что еще раз подчеркивает проблему.
Что нужно знать:
условные
обозначения логических операций
¬ A, не
A (отрицание, инверсия)
A Ù B, A и B (логическое
умножение, конъюнкция)
A Ú B, A или B
(логическое сложение, дизъюнкция)
A → B импликация (следование)
A º B
эквивалентность (равносильность)
операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = ¬ A Ú B или в других обозначениях A → B =
иногда для упрощения выражений полезны формулы де Моргана:
¬ (A Ù
B) = ¬ A Ú ¬ B
¬ (A Ú
B) = ¬ A Ù ¬ B
если в выражении нет скобок, сначала выполняются все операции
«НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя –
«эквивалентность»
таблица
истинности выражения определяет его значения при всех возможных комбинациях
исходных данных
если
известна только часть таблицы истинности, соответствующее логическое выражение
однозначно определить нельзя, поскольку частичной таблице могут соответствовать
несколько разных логических выражений (не совпадающих для других вариантов
входных данных);
количество
разных логических функций, удовлетворяющих неполной таблице истинности, равно , где
– число отсутствующих строк; например, полная
таблица истинности выражения с тремя переменными содержит 23=8 строчек, если
заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции,
удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
логическая
сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все
слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение
истинно)
логическое
произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда,
когда все сомножители одновременно равны единице, а в остальных случаях равно 0
(выражение ложно)
логическое
следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка)
истинна, а B (следствие) ложно
эквивалентность
АºB равна 1 тогда и только тогда,
когда оба значения одновременно равны 0 или одновременно равны 1
По материалам К.Ю. Полякова с сайта ЕГЭ по информатике: подготовка к
ЕГЭ-2022 по информатике, разбор задач ЕГЭ-2022 по информатике, материалы для
подготовки к ЕГЭ (kpolyakov.spb.ru)
Решение задач
второго типа в MS Excel
Алгоритм решения
1.
Составить таблицу входных значения, перечисляя все комбинации переменных в
порядке возрастания двоичного кода. Для этого подсчитать n число переменных в
исходном выражении, выписать наборы входных переменных. Количество
наборов входных переменных 2n.
2. Для каждой строки находим логическое решение. Для этого:
·
Подсчитать
общее число логических операций в выражении;
·
Установить последовательность
выполнения логических операций с учетом скобок и приоритетов.
3. Выполнить поиск значения функции,
отсортировать данное значение по искомой части (1 или 0).
4. Сопоставить исходную таблицу и вновь
полученную.
Используемые фукции в MS Excel
|
Операция |
Функция |
|
|
Отрицание |
=НЕ |
=ЕСЛИ(A2=1;0;1) |
|
Дизъюнкция |
=ИЛИ |
=ЕСЛИ(ИЛИ(A2=1;B2=1);1;0) |
|
Конъюнкция |
=И |
=ЕСЛИ(И(A2=1;B2=1);1;0) |
|
Импликация |
=ЕСЛИ(И(A2=1;B2=0);0;1) |
|
|
Эквиваленция |
=ЕСЛИ(A2=B2;1;0) |
Примеры:
1 (Задача 158 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением ¬x Ù y Ù (w ® z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F истинна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |

z, w в том порядке, в котором идут соответствующие им столбцы.
Решение
1.
Подсчитаем количество переменных: x, y, z, w – 4 переменных, следовательно,
ищем количество наборов по формуле: 2n
= 24 = 16 наборов. Заполняем разными возможными вариантами (см.
рисунок)
2.
Определим наборы операций:
1) ¬x
2) (w ®
z)
3) ¬x Ù y Ù
(w ® z)
Ищем
результаты действий.
Результат вычислений Введенные
формулы
Следующий
шаг это отфильтровать значения 1 по столбцу H:
Сопоставим
с условием:

Анализируем:
0
– всегда X 1 – всегда Y 011 – Z 001
— W
|
y |
x |
z |
w |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
Ответ:
YXZW
2(Задача 168 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением
x Ú (¬y
Ú z Ú ¬w) Ù (y Ú ¬z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F ложна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в
котором идут соответствующие им столбцы.

|
W |
X |
Z |
Y |
F |
|
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
Ответ:
WXZY
3(Задача 178 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением (Øz ÚØ
y) ® (x º z). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий
неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F
соответствует каждая из переменных x, y, z.
В
ответе напишите буквы x, y, z в том порядке, в котором
идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких
разделителей между буквами ставить не нужно.
Ответ:
YXZ
4 (Задача 188 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением (w Ù y) Ú ((x ® w) º (y ® z)). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся
строки. Определите, какому столбцу таблицы истинности функции F соответствует
каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
|||
|
1 |
1 |
0 |
||
|
1 |
1 |
1 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
ZWYX
5 (Задача 198 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением
(w ® y) Ù ((x ® z) º (y ® x)). На рисунке приведён частично заполненный фрагмент таблицы
истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу
таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
1 |
||
|
0 |
1 |
1 |
||
|
0 |
1 |
0 |
1 |
1 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
WZXY
Содержание
- Как сделать таблицу истинности в excel?
- Примеры использования логических функций ИСТИНА, ЛОЖЬ и НЕ в Excel
- Как посчитать среднее значение по условию в Excel
- Как получить значение по модулю числа без использования функции ABS
- Таблицы истинности для основных двоичных логических функций
- Порядок выполнения логических операций
- Примеры решения задач
- Построить таблицу истинности в Excel: основные понятия и примеры
- Математическая логика: основные понятия
- Алгоритм реализации вычислений в логических операциях
- Порядок построения табличной формы для логических операндов в Excel
- Построить таблицу истинности в Excel: основные понятия и примеры
- Математическая логика: основные понятия
- Алгоритм реализации вычислений в логических операциях
- Порядок построения табличной формы для логических операндов в Excel
Как сделать таблицу истинности в excel?
Функция ИСТИНА в Excel предназначена для указания логического истинного значения и возвращает его в результате вычислений.
Функция ЛОЖЬ в Excel используется для указания логического ложного значения и возвращает его соответственно.
Функция НЕ в Excel возвращает противоположное указанному логическому значению. Например, запись =НЕ(ИСТИНА) вернет результат ЛОЖЬ.
Примеры использования логических функций ИСТИНА, ЛОЖЬ и НЕ в Excel
Пример 1. В таблице Excel хранятся телефонные номера различных организаций. Звонки на некоторые из них являются бесплатными (с кодом 8800), на остальные – платные по тарифу 1,5 руб/мин. Определить стоимость совершенных звонков.
В столбце «Бесплатный» отобразим логические значения ИСТИНА или ЛОЖЬ по следующему условию: является ли код номера телефона равным «8800»? Введем в ячейку C3 формулу:
- ЛЕВСИМВ(B3;4)=»8800″ – условие проверки равенства первых четырех символов строки указанному значению («8800»).
- Если условие выполняется, функция ИСТИНА() вернет истинное логическое значение;
- Если условие не выполнено, функция ЛОЖЬ() вернет ложное логическое значение.
Аналогично определим является ли звонок бесплатным для остальных номеров. Результат:
Для расчета стоимости используем следующую формулу:
- C3=ИСТИНА() – проверка условия «является ли значение, хранящееся в ячейке C3 равным значению, возвращаемым функцией (логическое истина)?».
- 0- стоимость звонка, если условие выполнено.
- D3*1,5 – стоимость звонка, если условие не выполнено.
Мы получили суммарную стоимость вех совершенных звонков по всем организациям.
Как посчитать среднее значение по условию в Excel
Пример 2. Определить средний балл за экзамен для группы студентов, в составе которой есть студенты, которые его провалили. Так же необходимо получить среднюю оценку успеваемости только лишь для тех студентов, которые сдали экзамен. Оценка студента, не сдавшего экзамен, должна учитываться как 0 (нуль) в формуле для расчета.
Для заполнения столбца «Сдал» используем формулу:
Создадим новый столбец, в который перезапишем оценки при условии, что оценка 2 интерпретируется как 0 с использованием формулы:
Определим средний балл по формуле:
Теперь получим средний балл успеваемости, для студентов, которые допущены к следующим экзаменам. Для этого воспользуемся еще одной логической функцией СРЗНАЧЕСЛИ:
Как получить значение по модулю числа без использования функции ABS
Пример 3. Реализовать алгоритм определения значения модуля числа (абсолютную величину), то есть альтернативный вариант для функции ABS.
Для решения используем формулу массива:
=ЕСЛИ(НЕ(A3:A100, функция НЕ будет возвращать ЛОЖЬ.
Если единственным аргументом функции НЕ является текстовая строка, функция вернет код ошибки #ЗНАЧ!. В вычислительной технике используется специальный логический тип данных (в программировании имеет название «булев» тип или Boolean в честь известного математика Джорджа Буля). Этот тип данных оперирует всего двумя значениями: 1 и 0 (ИСТИНА, ЛОЖЬ). В Excel истинному логическому значению также соответствует число 1, а ложному логическому значению – также числовое значение 0 (нуль). Функции ИСТИНА() и ЛОЖЬ() могут быть введены в любую ячейку или использоваться в формуле и будут интерпретированы в качестве логических значений соответственно. Обе рассмотренные выше функции необходимы для обеспечения совместимости с другими программными продуктами, предназначенными для работы с таблицами. Функция НЕ позволяет расширить возможности функций, предназначенных для выполнения логической проверки. Например, при использовании данной функции в качестве аргумента лог_выражение функции ЕСЛИ, можно обеспечить проверку сразу нескольких условий.
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
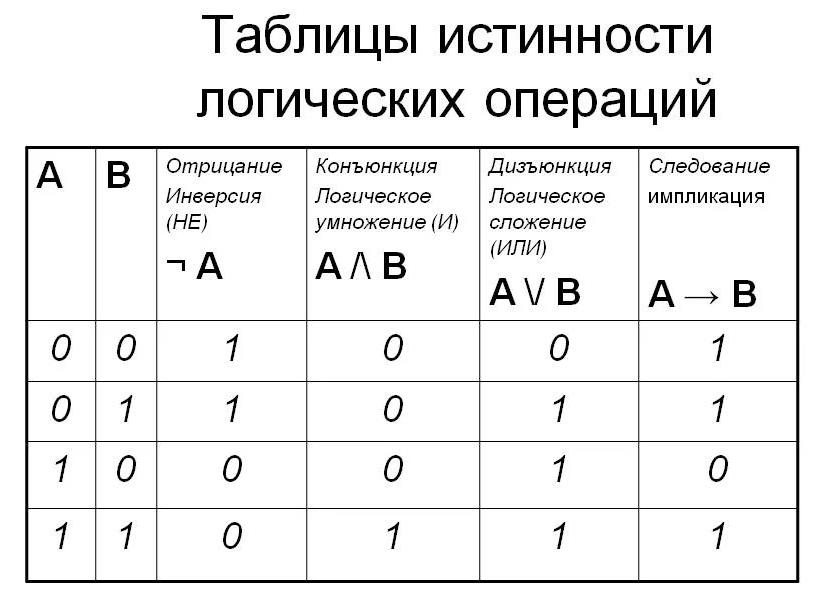
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.


Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
по теме «Построение таблиц истинности с помощью электронных таблиц Excel»
Цель работы: познакомиться с логическими функциями Excel, научиться строить таблицы истинности сложных высказываний.
Порядок выполнения работы.
1.Найдите обозначения логических функций, которые имеются в Excel
2.Используя Мастер функций , начните заполнять таблицу:
Источник
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Источник
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.

Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Источник
Использование MS Excel при изучении математической логики
В настоящее время применение информационных технологий становится неотъемлемой частью образовательного процесса. Компьютер наиболее полно удовлетворяет дидактическим требованиям и позволяет адаптировать процесс обучения к индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в процесс обучения и диагностики, позволяют упростить процесс отработки навыков и умений и оценки знаний учащихся.
В данной работе рассматривается применение табличного процессора MS Excel при изучении основ логики.
Существует множество задач, в которых исходные и результатные данные должны быть представлены в табличной форме. Электронные таблицы представляют собой удобный инструмент для автоматизации таких вычислений. Решения многих вычислительных задач на ЭВМ, которые раньше можно было осуществить только путем программирования, стало возможно реализовать. Использование математических формул в электронных таблицах позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Основное свойство электронных таблиц – мгновенный пересчет формул при изменении значений входящих в них операндов. Благодаря этому свойству, таблица представляет собой удобный инструмент для организации численного эксперимента:
- подбор параметров,
- прогноз поведения моделируемой системы,
- анализ зависимостей,
- планирование.
В электронных таблицах предусмотрен также графический режим работы, который дает возможность графического представления (в виде графиков, диаграмм) числовой информации, содержащейся в таблице.
В процессе изучения алгебры логики учащиеся знакомятся с такими понятиями как: высказывание, таблицы истинности, логические функции и логические операции. Алгебра логики является разделом математической логики, в которой изучаются методы доказательства истинности (1) или ложности (0) сложных логических конструкций, составленных из простых высказываний, на основе истинности или ложности последних. Для закрепления полученных знаний возможно использование табличного процессора MS Excel и его функций.
Для реализации функций булевой алгебры используются логические функции: ЕСЛИ, И, ИЛИ, НЕ, ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel используется мастер функций (Вставка Функция…), в котором отображается имя функции, ее описание и аргументы.
Рисунок 1. Окно мастера функций
Первоначально следует создать таблицу основных логических операций:
Рисунок 2. Таблица истинности основных логических операций
При составлении таблицы истинности используются следующие формулы:
- Инверсия: =ЕСЛИ(A2=1;0;1);
- Дизъюнкция: =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0);
- Конъюнкция: =ЕСЛИ(И(A2=1;B2=1);1;0);
- Импликация: =ЕСЛИ(И(A2=1;B2=0);0;1);
- Эквивалентность: =ЕСЛИ(A2=B2;1;0).
В последующей работе данная таблица может использоваться учащимися как основа для выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая работа.
Задание: Построить таблицу истинности для формулы (A 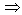

A, используя MS Excel.
Алгоритм:
- Определить количество наборов входных переменных, по формуле: Q = 2 n , где n – количество переменных. Q = 2 3 = 8.
- Внести в таблицу все наборы входных переменных:
Рисунок 3. Исходные данные
- Определить количество логических операций и порядок их выполнения:
- Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
в G2: =ЕСЛИ(F2=A2;1;0).
Заполнение остальных строк произвести путем копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для закрепления не только материала математической логики, но и для основ теории вероятностей и математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности равносильность формул.
Определить являются ли формулы тавтологиями.
Примеры вычислений с использованием стандартных функций
СУММ(А) – функция суммирования, где: А — список от 1 до 30 аргументов суммирования.
СУММЕСЛИ(диапазон; критерий; диапазон_суммирования) – суммирования ячеек диапазона, удовлетворяющих заданным условиям, где:
· диапазон — диапазон адресов вычисляемых ячеек;
· критерий — критерий в виде числа, выражения или текста, определяющего суммируемые ячейки. Например, критерий может быть выражен как 24, «>22»;
· диапазон_суммирования — фактические ячейки для суммирования.
ЕСЛИ(логическое_выражение; значение_если_истина; значение_если_ложь) – проверяет, выполняется ли логическое выражение, если да, то выводит значение если истина, нет – значение если ложь;
Ошибки в формулах Excel.Если формула построена неправильно, Excel формирует соответствующую ошибку, основными причинами появления которых следующие:
· #ЗНАЧ! — используется недопустимый тип аргумента;
· #ДЕЛ/0! — в формуле выполняется деление на ноль;
· #ИМЯ? — Excel не может определить используемое в формуле имя;
· #ССЫЛКА! — используется недопустимая ссылка на ячейку;
· #Н/Д — неопределенные данные, при некорректном определении аргументов функции;
· #ПУСТО! — задано пересечение двух областей, не имеющих общих ячеек.
2.3 Построение диаграмм и графиков в Excel
Наиболее удобным способом создания диаграммы является использование Мастера диаграмм,вызываемый нажатием кнопки Мастер диаграмм 
1. Выбор типа и вида диаграммы.После вызова Мастера диаграммв диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы следует выбрать тип и вид диаграммы. Диалоговое окно имеет две вкладки: Стандартные и Нестандартные. Во вкладке Стандартные расположены стандартные типы диаграмм Excel и их разновидности. Для просмотра внешнего вида выбранной диаграммы следует нажать и удерживать кнопку Просмотр результата. Выбранный тип и вид диаграммы можно будет изменить в последующем при редактировании и оформлении диаграммы.
2. Выбор источника данных.В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать источник данных для диаграммы (рис.4.22), диалоговое окно имеет две вкладки: Диапазон данных и Ряд.
Рис. 4.22. Выбор источника данных диаграммы
Если перед началом создания диаграммы на листе были выделены ячейки с данными, то во вкладке Диапазон данных в поле Диапазон указан диапазон ячеек листа, для которого создается диаграмма, а на листе этот диапазон обведен «бегущим» пунктиром. При необходимости можно очистить поле Диапазон и, не закрывая диалогового окна, на листе выделить другой диапазон ячеек.
Как правило, независимо от размещения данных на листе, Excel правильно выбирает вариант построения рядов данных (по строкам или по столбцам выделенного диапазона) и устанавливает соответствующий переключатель (на строках или на столбцах), имена рядов данных показываются в легенде.
Содержание вкладки Ряд зависит от типа выбранной диаграммы, а также от выбора варианта построения рядов данных.
По окончании работы с источниками данных диаграммы в диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы следует нажать кнопку Далее.
3. Выбор параметров диаграммы.Выполняется на 3-емшаге вокне Мастер диаграмм (шаг 3 из 4 ): параметры диаграммы. На данном шаге мастером предлагается определить заголовок создаваемой диаграммы, использовать линии сетки, включить легенду в любом месте диаграммы, дать имена осям Х и У, определить подписи данных и щелкнуть Далее для перехода на последний четвертый шаг.
4. Размещение диаграммы. Выполняется в окне Мастер Диаграмм (шаг 4 из 4): размещение диаграммы.На этом шаге пользователь определяет, где поместить диаграмму: на текущем рабочем листе или на отдельном листе книги. После нажатия кнопки Готово Excel создаст диаграмму. Затем пользователь может внести изменения данных в исходной таблице, что автоматически отразится на построенной диаграмме.
Определим логические функции:
1) Инверсия (отрицание) — это логическое не.
Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А»
Для обозначения отрицания суждения употребляется символ или– над переменной.
Запись А читается как «не А».
2) Коньюкция — это логическое умножение.
Обозначение: А & В ( АВ, А / В) . Читается так “ А и В “.
3) Дизьюкция — это логическое сложение.
Обозначение: А V В , ( А + В ). Читается так: “ А или В ”.
4) Эквиваленция — это функция тождества.
Она обозначается символами= ,
Выбираем обозначение А = В. («тогда и только тогда»).
Запись А = В читается как «А эквивалентно В».
5) Импликация — это логическое следование.
Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО».
Она обозначается символом->
Читается как «из А следует В»
Обозначение:
Импликация устроена немного сложнее других функций. В импликации существенное значение имеет порядок аргументов. Первый называется посылкой, а второй следствием. Можно сказать, что первое высказывание является как бы причиной второго, а второе как бы вытекает из первого.
Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация 
.
Таблицы истинности:
прямая импликация (от a к b) (материальная импликация, материальный кондиционал)
если , то истинно (1),
«Житейский» смысл импликации. Для более лёгкого понимания смысла прямой импликации и запоминания ее таблицы истинности может пригодиться житейская модель: А — начальник. Он может приказать «работай» (1) или сказать «делай что хочешь» (0). В — подчиненный. Он может работать (1) или бездельничать (0). В таком случае импликация — не что иное, как послушание подчиненного начальнику. По таблице истинности легко проверить, что послушания нет только тогда, когда начальник приказывает работать, а подчиненный бездельничает.
Условная функция. Общий вид условной функции следующий:
Условие — это логическое выражение, которое может принимать значениеИСТИНА илиЛОЖЬ. и могут быть числами, формулами или текстом.
Условная функция, записанная в ячейку таблицы, выполняется так: если условие истинно, то значение данной ячейки определит , в противном случае — .
Логические выражения. Логические выражения строятся с помощью операций отношения ( , = (больше или рано), =, <>(не равно)) и логических операций (логическое И, логическоеИЛИ, логическое отрицаниеНЕ).Результатом вычисления логического выражения являются логические величиныИСТИНА илиЛОЖЬ.
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Использование логических функций в Excel
Табличный редактор Эксель – очень гибкий и мощный инструмент для структурированной работы с данными. Среди большого количества его эффективных инструментов стоит отдельно выделить логические операторы, в основе использования которых лежит признание выражения истинным или ложным. Эти функции эффективно встроены в инструментарий формул и позволяют создавать гибкие условия для различных вычислений или заполнения ячеек на основе логических выражений. В данной статье будут описаны основные используемые функции, а также приведен практический пример использования логических операторов в Excel.
Основные логические функции, используемые в Эксель
Перечень наиболее часто используемых логических операторов можно ограничить следующим набором:
В большинстве случаев их достаточно для построения сложных логических конструкций и задания условий.
Для каждого из указанных выше операторов существуют аргументы (за исключением функций ИСТИНА и ЛОЖЬ) – это могут быть как цифровые или текстовые значения, так и ссылки на данные, содержащиеся в других ячейках.
Операторы ИСТИНА и ЛОЖЬ
Функция ИСТИНА не имеет собственных аргументов и практически всегда используется, как структурный компонент для других логических выражений, так как принимает одно конкретно заданное значение.
Функция ЛОЖЬ, напротив, может принимать любые значения, не являющиеся истинными. Как и ИСТИНА, практически всегда используется, как структурный компонент для других сложных выражений.
Операторы И и ИЛИ
Синтаксис оператора И выглядит следующим образом:
=И(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.
Оператор И используется в качестве элемента-связки для нескольких условий логического выражения. Важно, чтобы все аргументы оператора имели значение ИСТИНА (если в выражении их несколько), в противном случае вся логическая цепочка будет возвращать значение ЛОЖЬ.
Синтаксис оператора ИЛИ:
=ИЛИ(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.
В отличие от И, функция ИЛИ будет возвращать значение ИСТИНА даже в случае, когда хотя бы один из используемых аргументов ему соответствует, а все остальные – ложные.
Оператор НЕ
Синтаксис функции НЕ: =НЕ(лог_значение).
Количество аргументов оператора НЕ – всегда один. Соответственно, результат функции (ИСТИНА/ЛОЖЬ) полностью зависит только от значения аргумента.
Операторы ЕСЛИ и ЕСЛИОШИБКА
Общий синтаксис функции ЕСЛИ представляет собой конструкцию:
=ЕСЛИ(логическое_выражение;значение_если_истина;значение_если-ложь).
Оператор ЕСЛИ используется для построения сложных развернутых логических цепочек. Суть функции – в проверке внесенного в качестве логического выражения условия. Если условие выполняется, и оно истинно, то в качестве результата функции возвращается одно выражение, если же логическое выражение ложно, то в качестве результата функции возвращается другое условие.
Синтаксис оператора ЕСЛИОШИБКА имеет вид:
=ЕСЛИОШИБКА(значение;значение_если_ошибка).
Функция проверяет истинность логического выражения для первого аргумента, и если он соблюдается, то возвращает в качестве результата его значение. Если же выражение ложно, то в качестве результата выдается значение второго аргумента, указанное в функции.
Операторы ЕОШИБКА и ЕПУСТО
Оператор ЕОШИБКА имеет следующую структуру:
=ЕОШИБКА(значение)
Он позволяет осуществить проверку корректности уже заполненных ячеек (одной или диапазона), и, если ячейка некорректно заполнена, возвращает результат ИСТИНА, в противном случае – ЛОЖЬ.
Примеры значений в некорректно заполненных ячейках:
Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.
Формула функции ЕПУСТО выглядит следующим образом:
=ЕПУСТО(значение)
Функционал оператора проверяет ячейку или диапазон ячеек и возвращает ИСТИНА, если в ячейке/диапазоне ячеек нет данных, и ЛОЖЬ, если в ячейке/диапазоне ячеек присутствуют данные. Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.
Практический пример использования логических функций
В примере ниже попробуем частично использовать описанные выше функции для решения задачи, приближенной к реальной ситуации с расчетом премии, зависящей от определенных условий.
В качестве исходных данных – таблица со сведениями о работниках, в которой указан их пол и возраст.
Нам необходимо произвести расчет премии. Ключевые условия, от которых зависит размер премии:
- величина обычной премии, которую получат все сотрудники без исключения – 3 000 руб.;
- сотрудницам женского пола положена повышенная премия – 7 000 руб.;
- молодым сотрудникам (младше 1984 г. рождения) положена повышенная премия – 7 000 руб.;
Выполним необходимые расчеты, используя логические функции.
- Встаем в первую ячейку столбца, в которой хотим посчитать размеры премий и щелкаем кнопку “Вставить функцию” (слева от сроки формул).
- В открывшемся Мастере функций выбираем категорию “Логические”, затем в предложенном перечне операторов кликаем по строке “ЕСЛИ” и жмем OK.
- Теперь нам нужно задать аргументы функции. Так как у нас не одно, а два условия получения повышенной премии, причем нужно, чтобы выполнялось хотя бы одно из них, чтобы задать логическое выражение, воспользуемся функцией ИЛИ. Находясь в поле для ввода значения аргумента “Лог_выражение” кликаем в основной рабочей области книги на небольшую стрелку вниз, расположенную в левой верхней части окна программы, где обычно отображается адрес ячейки. В открывшемся списке функций выбираем оператор ИЛИ, если он представлен в перечне (или можно кликнуть на пункт “Другие функции” и выбрать его в новом окне Мастера функций, как мы изначально сделали для выбора оператора ЕСЛИ).
- Мы переключимся в окно аргументов функци ИЛИ. Здесь задаем наши условия получения премии в 7000 руб.:
- год рождения позже 1984 года;
- пол – женский;
- Теперь обращаем внимание на строку формул. Кликаем в ней на название первоначального оператора ЕСЛИ, чтобы переключиться в аргументы этой функции.
- Заполняем аргументы функции и щелкаем OK:
- в значении “Истина” пишем цифру 7000;
- в значении “Ложь” указываем цифру 3000;
- Результат работы логических операторов отобразится в первой ячейке столбца, которую мы выбрали. Как мы можем видеть, окончательный вид формулы выглядит следующим образом:
=ЕСЛИ(ИЛИ(C2>1984;D2=»жен.»);7000;3000) .
Кстати, вместо использования Мастера функций можно было вручную составить и прописать данную формулу в требуемой ячейке. - Чтобы рассчитать премию для всех сотрудников, воспользуемся Маркером заполнения. Наведем курсор на правый нижний угол ячейки с формулой. После того, как курсор примет форму черного крестика (это и есть Маркер заполнения), зажимаем левую кнопку мыши и протягиваем выделение вниз, до последней ячейки столбца.
- Все готово. Благодаря логическим операторам мы получили заполненные данные для столбца с премиями.
Заключение
Логические операторы используются практически во всех сложных формулах, в которых значение в ячейке зависит от соблюдения одного или нескольких условий и позволяют строить гибкие конструкции, объединяя простые функции и расчеты в одной ячейке. Это дает возможность значительно сократить время на обработку данных и повысить эффективность работы, так как снимает большое количество промежуточных шагов в расчетах и вычислениях.
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.

Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
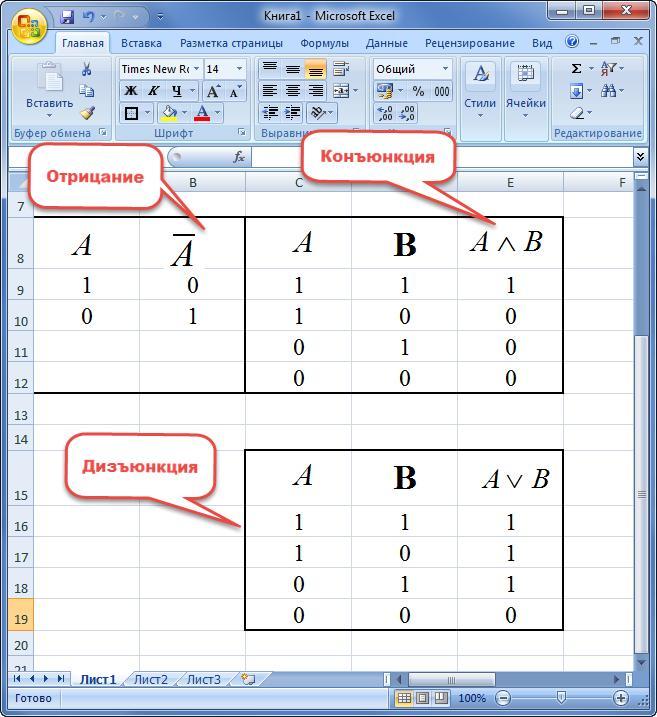
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
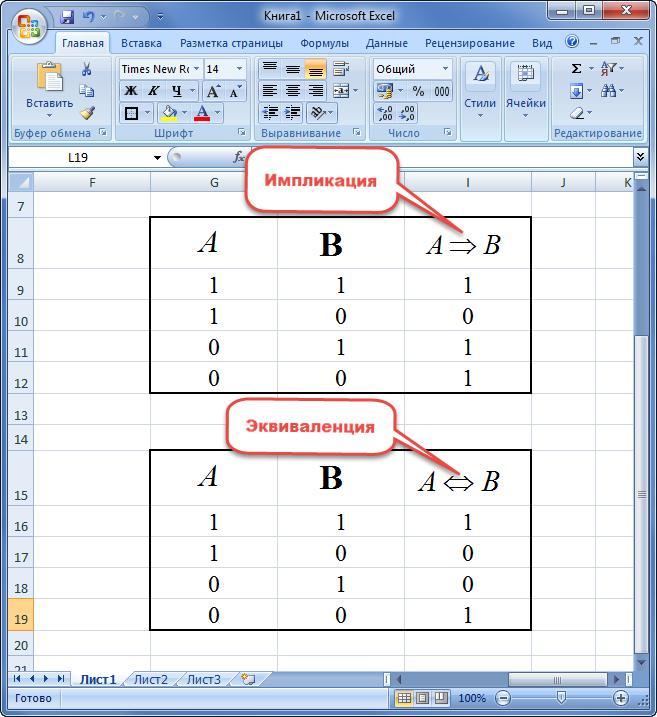
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
- штрих Шеффера;
- стрелка Пирса.
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
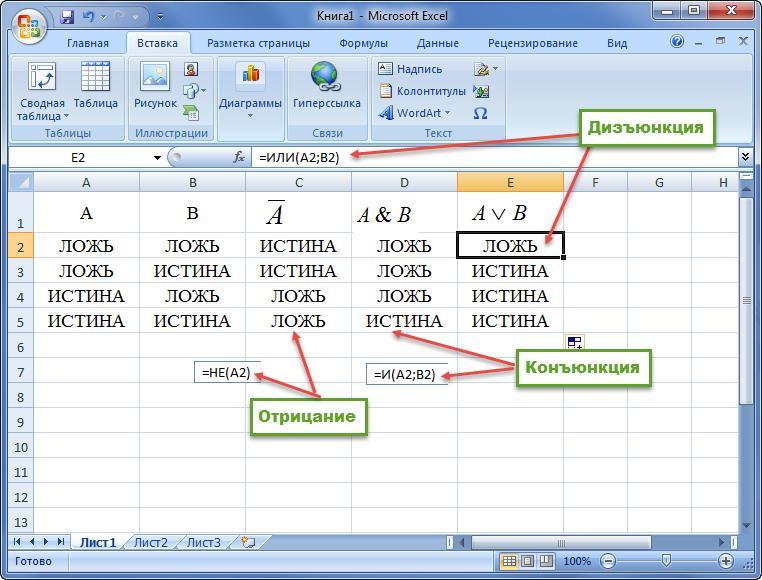
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
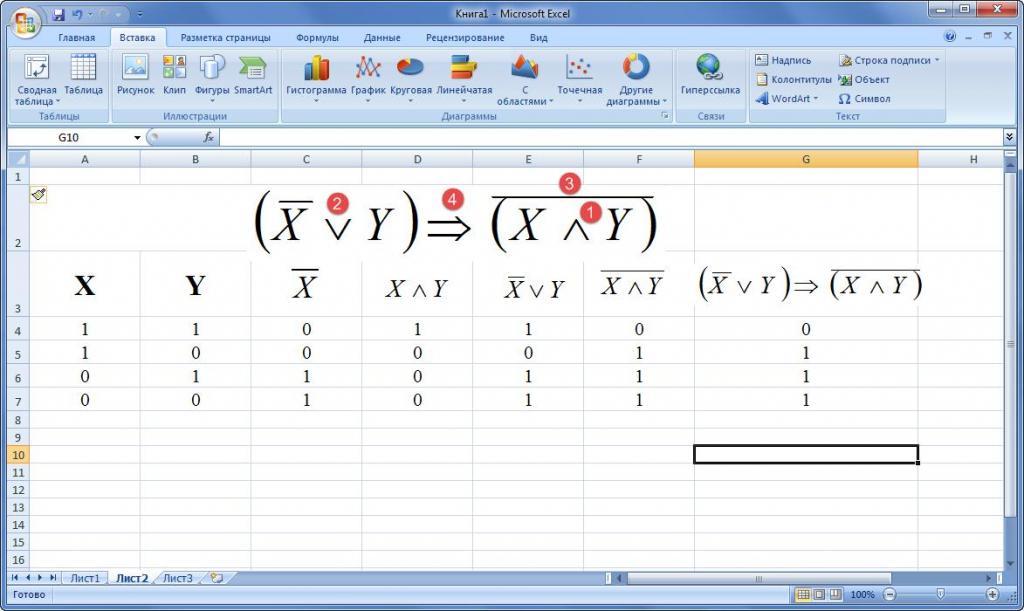
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
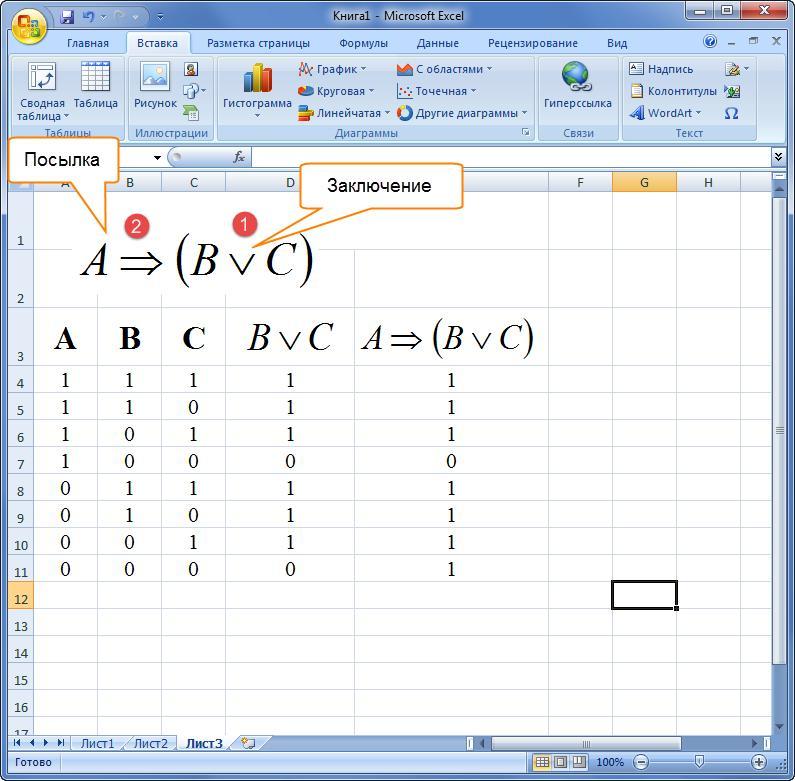
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Автор:
03-12-2018 21:56
Жду ваши вопросы и мнения в комментариях
Оглавление:
- 1 Как сделать импликацию в excel? — Разбираем подробно
- 2 Использование логических функций в Excel
- 3 Логические функции в Excel и примеры решения задач
- 4 Статистические и логические функции в Excel
- 4.1 Логическое следование (импликация).
- 4.2 Логическое равенство (эквивалентность).
- 4.3 Логические законы и правила преобразования логических выражений.
- 5 Глава 5.
- 6 Решение логических задач.
- 7 Глава 6.
Логические операции и - 8 условная функция в электронных таблицах Excel.
- 8.1 Логические выражения.
- 8.2 Составление таблиц истинности с помощью Excel.
- 9 Заключение.
- 10 Библиографический список.
- 11 Приложение.
Доброго времени суток уважаемый читатель!
Вот я, наконец, то и добрался к своим любимым логическим функциям Excel. Признаю, что мне они наиболее ближе и удобнее в использовании нежели другие разделы функций, каюсь грешен, должны же быть и у меня любимчики… А если говорить серьезно, логические функции одни из самых распространённых в использовании функции и самые полезные в работе бухгалтеров, экономистов, да и в принципе любого специалиста финансовых дисциплин.
Основной особенностью этих функций, это проверка данных на соответствие результату «ИСТИНА» или «ЛОЖЬ», то есть когда результат соответствует заданному условию, получаем итог «ИСТИНА» и «ЛОЖЬ», когда условия не выполнены. На самом деле это намного легче понять, чем описать и я думаю, что читая дальше, вы сможете понять логику работы этих функций.
Поскольку хочется написать многое, описать работу и возможности функций в одной статье, это будет чрезмерно много, поэтому, как и в случае с описанием текстовых функций, я разобью информацию о логических функциях на 2 части.
В своем арсенале Excel содержит 7 логических функций, хотя в зависимости от версий их может быть и меньше, и больше. Найти перечень доступных функций вы можете в панели управления на вкладке «Формулы», в блоке «Библиотека функций», нажав кнопку «Логические» с выпадающем перечнем логических функций. Или с помощью мастера функций:
А вот собственно и перечень логических функций, которые мы будем рассматривать в первой части этой статье:
- Функция ЕСЛИ;
- Функция ИСТИНА;
- Функция ЛОЖЬ;
- Функция НЕ.
Все предоставленные функции достаточны, просты и легки в использовании, и я думаю, у вас не будет никаких затруднений в их реализации и использовании. Главное условие этого я бы выделил только понимание сути и логики исполнения функции и варианты ее применения вы сразу сможете понять.
Функция ЕСЛИ
Сразу скажу это одна из самых классных функций в Excel. Я ее результатами пользуюсь, где нужно и ненужно, а поэтому считаю, что изучить ее возможности необходимо любому уважающему себя человеку, который хочет показать себя как специалист финансовых дисциплин. Несмотря на кажущуюся простоту, возможности этой функции очень удивляют и приятно радуют. Для углублённого изучения ее возможностей вам поможет статья «Как используется функция ЕСЛИ в Excel с несколькими условиями».
Функция ЕСЛИ возвращает один результат в случаях, если аргумент «логическое выражение» при вычислении получает ответ «ИСТИНА» и совсем другой, если ответ «ЛОЖЬ». Функция может содержать до семи логических условий внутри себя для аргумента «_значение если истина_», а для аргумент «_значение если ложь_» умеет выполнять функции или команды дальнейшего действия (к примеру, использование функции ПЕРЕЙТИ).
Синтаксис функции:
=ЕСЛИ(_лог_выражение_,_значение_если_истина_,_значение_если_ложь_), где:
- Логическое выражение – указывается практически любое выражение или значение, которое в процессе вычисления получает значение «ИСТИНА» или «ЛОЖЬ»;
- Значение если истина – это значение, которое будет возвращено, если аргумент «Логическое выражение» получит результат «ИСТИНА». В случае, когда этот аргумент не указан в формуле, возвращается результат «ИСТИНА»;
- Значение если ложь — это значение, которое будет возвращено, если аргумент «Логическое выражение» получит результат «ЛОЖЬ». В случае, когда этот аргумент опущен в формуле, возвращается результат «ЛОЖЬ».
Пример №1:
Рассмотрим усложнённый пример со многими условиями, вложенными в функцию ЕСЛИ. У нас есть персонал, которому в зависимости от стажа работы, производится доплата к ставке заработной платы. Всего будет три доплаты, стаж работы 3 года – 10%, 10 лет – 20% и 20 лет – 30%. Для получения результата и автоматического расчёта доплаты в зависимости от стажа нам нужна формула такого вида:
=ЕСЛИ(C2>=20;»30%»;ЕСЛИ(C2>=10;»20%»;ЕСЛИ(C2>=3;»10%»;»0%»))).
Пример №2:
Рассмотрим еще один сложный пример, в котором мы будем определять, и идентифицировать виды банковских карточек по их номерам. Для первого аргумента используем текстовую функцию ЛЕВСИМВ для захвата первых 4 цифр, которые и будут условием определения. Для карты «Visa Electron» установим идентификатор 1234, для карты «Maestro» — 5678 и все остальные карты будут по умолчанию «MasterCard Standard». Теперь собственно формула, которая поможет нам определить результат будет такова:
=ЕСЛИ( ЛЕВСИМВ (B14;4)= «1234»; «Visa Electron»; ЕСЛИ ( ЛЕВСИМВ (B14;4)=»5678»; «Maestro»; «MasterCard Standard»)).
Функция ИСТИНА
Абсолютно простая логическая функция ИСТИНА, не имеет никаких аргументов и умеет возвращать всего лишь логическое значение «ИСТИНА». Имеет смысл использовать только в связке с другими функциями.
Синтаксис функции:
=ИСТИНА().
Аргументы отсутствуют.
Функция ЛОЖЬ
Простая функция ЛОЖЬ аналогична описываемой ранее функции ИСТИНА, но наоборот, умеет возвращать всего лишь логическое значение «ЛОЖЬ» и не имеет никаких аргументов. Её тоже необходимо использовать в тандеме с другими функциями.
Синтаксис функции:
=ЛОЖЬ().
Аргументов нет.
Функция НЕ
Простая в работе и исполнении логическая функция НЕ умеет только одно, производит замену полученного логического значения своего аргумента на абсолютно противоположный, т.е. он заменяет значение «ЛОЖЬ» на «ИСТИНА» и, наоборот, в другую сторону. Использование функции НЕ, рационально применять в случаях, когда нужна 100%-ная уверенность что некое значение не будет равно некой определённой величине.
Синтаксис функции:
= НЕ(_логическое_значение_), где:
- Логическое значение – это выражение, ссылка на ячейку или значение, которое как результат вычислений дает логическое значение «ИСТИНА» или «ЛОЖЬ». Функция НЕ при получении такого результата меняет его: «ЛОЖЬ» на «ИСТИНА» и «ИСТИНА» на «ЛОЖЬ».
Пример:
Обращаю внимание! Все логические функции в своих выражениях используют знаки сравнения «=», «», «=» или «», в результате чего получаются значения «ИСТИНА» и «ЛОЖЬ».
А на этом у меня пока всё, жду вас на страницах второй части статьи! Я очень надеюсь, что описанные всех логических функций в Excel в этой части были ёмкими и понятными. Буду очень благодарен за оставленные комментарии, так как это показатель читаемости и вдохновляет на написание новых статей!
Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.
Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.
Использование логических функций в Excel
Логические функции в Excel и примеры решения задач
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.
Сформируем таблицу с исходными параметрами:
Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).
Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.
Формула приобретает следующий вид: .
В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.
Для решения используем логические функции ЕСЛИ и ИЛИ: . Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.
При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.
В качестве аргументов можно использовать другие функции. К примеру, математические.
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.
Составим таблицу с исходными данными:
Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».
Введем формулу вида: . Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.
Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.
Статистические и логические функции в Excel
Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.
Работаем с таблицей из предыдущего раздела:
Для решения задачи используем формулу вида: . В логическом выражении «D2
Задача 2. Найти средние продажи в магазинах сети.
Составим таблицу с исходными данными:
Необходимо найти среднее арифметическое для ячеек, значение которых отвечает заданному условию. То есть совместить логическое и статистическое решение.
Чуть ниже таблицы с условием составим табличку для отображения результатов:
Решим задачу с помощью одной функции: . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.
Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.
Задача 3. Найти средние продажи в магазине №1 г. Москва.
Видоизменим таблицу из предыдущего примера:
Нужно выполнить два условия – воспользуемся функцией вида: .
Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.
Скачать примеры логических функций
Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.
Функция учитывает только те значения, которые соответствуют всем заданным условиям.
Логическое следование (импликация).
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
Логическая операция импликации «если А то В», обозначается А В и выражается с помощью логической функции F14, которая задается соответствующей таблицей истинности.
Таблица истинности логической функции импликация.
A
B
F14=A В
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, т.к. истинны и первое высказывание (предпосылка), и второе высказывание (вывод).
Высказывание «Если число делится на 10, то оно делится на 3» ложно, т. к. из истинной предпосылки делается ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание ложно, то вне зависимости от истинности или ложности второго высказывания составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.
Логическое равенство (эквивалентность).
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…».
Логическая операция эквивалентности «А эквивалентно В» обозначается А~В и выражается с помощью логической функции F10, которая задается соответствующей таблицей истинности.
Таблица истинности логической функции эквивалентности.
A
B
F10
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Рассмотрим, например, два высказывания А= «Компьютер может производить вычисления» и В= «Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности истинно, когда оба высказывания либо истинны, либо ложны.
«Компьютер может производить вычисления тогда и только тогда, когда компьютер включен».
« Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».
Составное высказывание, полученное с помощью операции эквивалентности ложно, когда одно высказывание истинно, а другое — ложно:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».
Логические законы и правила преобразования логических выражений.
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствии с законами логики.
Закон тождества. Всякое высказывание тождественно самому себе:
А=А.
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А- истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:
А&А=0.
Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение истина:
АvА=1.
Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
=
А=А.
Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.
Законы Моргана.
АvВ=А&В.
А&В=АvВ.
Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:
Логическое умножение
Логическое сложение
А&В=В&А
АvВ=ВvА
Правило ассоциативности. Если в логическом выражении используются только операция логического умножения или только логического сложения, то можно пренебрегать скобками или произвольно их расставлять:
Логическое умножение
Логическое сложение
(А&В)&С=А&(В&С)
(АvВ)vС=Аv(ВvС)
Правило дистрибутивности. В отличии от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
Дистрибутивность умножения относительно сложения
Дистрибутивность сложения относительно умножения
(а*в)+(а*с)=а*(в+с)
(А&В)v(А&С)=А&(ВvС)
(АvВ)&(АvС)=Аv(В&С)
Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
(А&В)v(А&В).
Воспользуемся правилом дистрибутивности и вынесем за скобки А:
(А&В)v(А&В)=А&(ВvВ).
По закону исключенного третьего ВvВ=1, следовательно:
А&(ВvВ)=А&1=А.
Законы и правила преобразования логических выражений позволяют упростить сложное выражение и, не применяя таблиц истинности, найти ответ при решении задач.
Глава 5.
Решение логических задач.
Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.
Условие задачи.
В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На аудиториях повесили шутливые таблички. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках или обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Решение задачи.
Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:
А — «В первой аудитории находится кабинет информатики»,
В — «Во второй аудитории находится кабинет информатики».
Тогда отрицаниям этих высказываний будут соответствовать:
А — «В первой аудитории находится кабинет физики»,
В — «Во второй аудитории находится кабинет физики».
Высказывание, содержащееся на табличке на первой аудитории, соответствует логическому выражению:
X=АvВ.
Высказывание, содержащееся на табличке на второй аудитории, соответствует логическому выражению:
Y=А.
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные, в соответствии с законом исключенного третьего записывается следующим образом:
(X&Y) v (X&Y)=1.
Подставим вместо X и Y соответствующие формулы:
(X&Y) v (X &Y) = ((A v B)&A) v (A v B) &A.
А
В
А
В
АvВ&А
АvВ&А
(АvВ&А)v(АvВ&А)
Из таблицы истинности можно сделать вывод, что в первой аудитории находится кабинет физики, а во второй- кабинет информатики.
Глава 6.
Логические операции и
условная функция в электронных таблицах Excel.
Общий вид условной функции следующий:
ЕСЛИ (, , )
Условие — это логическое выражение, которое может принимать значение ИСТИНА или ЛОЖЬ. и могут быть числами, формулами или текстами.
Условная функция, записанная в ячейку таблицы, выполняется так: если условие истинно, то значение данной ячейки определит , в противном случае -.
Логические выражения.
Логические выражения строятся с помощью операций отношения (, =(больше или равно), =, (не равно)) и логических операций(логическое И, логическое ИЛИ, логическое НЕ). Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ.
Существуют особенности записи логических операций в табличных процессорах: сначала записывается имя логической операции (И, ИЛИ, НЕ), а затем в круглых скобках перечисляются логические операнды.
Составление таблиц истинности с помощью Excel.
Задача 1. Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предложения:
- Аня пойдет в кино только тогда, когда пойдут Вика и Сергей;
- Аня и Сергей пойдут в кино вместе или же оба останутся дома;
- чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино?
Решение. Обозначим простые высказывания:
А — Аня пойдет в кино;
В — Вика пойдет в кино;
С — Сергей пойдет в кино.
Каждое составное высказывание можно выразить в виде формулы – логического выражения.
- А(В&С)
- (А&С)v(А&С)
- СВ
Составим таблицу истинности в Excel.
В каждую колонку введем формулы, которые будут соответствовать логическим операциям. В Excel существуют логические операции «И», «ИЛИ», «НЕ». Для функции логического следования (импликации) воспользуемся условной
| А | В | С | не А | не С | В & С | А(В&С) | A & C | (неА)&(неС) | (A&C)v(неА&неС) | СВ |
| А | В | С | не А | не С | В & С | А(В&С) | A & C | |||
| =НЕ(A33) | =НЕ(C33) | =И(B33;C33) | =A33=F33 | =И(A33;C33) | ||||||
| =НЕ(A34) | =НЕ(C34) | =И(B34;C34) | =A34=F34 | =И(A34;C34) | ||||||
| =НЕ(A35) | =НЕ(C35) | =И(B35;C35) | =A35=F35 | =И(A35;C35) | ||||||
| =НЕ(A36) | =НЕ(C36) | =И(B36;C36) | =A36=F36 | =И(A36;C36) | ||||||
| =НЕ(A37) | =НЕ(C37) | =И(B37;C37) | =A37=F37 | =И(A37;C37) | ||||||
| =НЕ(A38) | =НЕ(C38) | =И(B38;C38) | =A38=F38 | =И(A38;C38) | ||||||
| Введем значения А, В и С в виде «истина» и «ложь», и получим искомый результат: | ||||||||||
| А | В | С | не А | не С | В & С | А(В&С) | А & С | (неА)&(неС) | (A&C)v(неА&неС) | СВ |
| ИСТИНА | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
| ЛОЖЬ | ИСТИНА | ИСТИНА | ИСТИНА | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ИСТИНА |
| ИСТИНА | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА | ЛОЖЬ |
| ИСТИНА | ИСТИНА | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ИСТИНА | ИСТИНА | ЛОЖЬ | ИСТИНА | ИСТИНА |
| ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ИСТИНА |
| ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА | ИСТИНА | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА | ИСТИНА | ЛОЖЬ |
| ЛОЖЬ | ЛОЖЬ | ИСТИНА | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
Ответ. Т.к. два высказывания должны быть «истина», а одно «ложь», то правильный ответ следующий: Аня и Сергей не пойдут в кино, а пойдет Вика.
Таким образом, электронные таблицы упрощают работу с таблицами истинности и помогают быстрее решать логические задачи.
Заключение.
- Тема, затронутая в данном реферате, имеет практическое значение. Каждый мыслящий человек должен иметь представление о законах логики. Логика изучает внутреннюю структуру процесса мышления.
- Логические операции, описанные Аристотелем, помогают решать сложные логические задачи математики и информатики.
- Применение компьютера при работе над данной темой еще раз подтверждает возможность использования вычислительной техники в различных сферах науки, и жизни человека.
Библиографический список.
- Информатика. Задачник-практикум. / Под редакцией И. Г. Семакина, Е.К. Хеннера: том. 2. – Москва: Лаборатория Базовых Знаний, 2001.
- Информатика. Задачник-практикум. / Под редакцией И. Г. Семакина, Е.К. Хеннера: том. 1. – Москва: Лаборатория Базовых Знаний, 2001.
- Угринович Н.Д. Информатика и информационные технологии. Учебное пособие для 10-11 классов. Углубленный курс. – Москва: Лаборатория Базовых Знаний, 2000.
- Информатика. Базовый курс. 7-9 классы. – М.: Лаборатория Базовых Знаний, 2001.
- Шафрин Ю.А. Информационные технологии: В 2 ч. Ч. 2: Офисная технология и информационные системы. – М.: Лаборатория Базовых Знаний, 2001.
- Вершинин О.Е. За страницами учебника информатики: Кн. Для учащихся 10-11 кл. средней шк.- М.: Просвещение, 1991.
- Журин А.А. Excel 2000. Для школьников и начинающих пользователей. – М.: «АКВАРИУМ», К.:ГИППВ, — 2000.
Приложение.
Задача 2.
Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша: «Это сосуд греческий и изготовлен в V веке».
Боря: «Это сосуд финский и изготовлен в Ш веке».
Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Задача 3.
В нарушении правил обмена валюты подозревают четыре работника банка – А, В, С и D. Известно, что:
- Если А нарушил, то и В нарушил правила обмена валюты.
- Если В нарушил, то и С нарушил или А не нарушал.
- Если D не нарушил, то А нарушил, а С не нарушал.
- Если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
Задача 4.
На вопрос, какая завтра будет погода, синоптик ответил:
- «если не будет ветра, то будет пасмурная погода без дождя»;
- «если будет дождь, то будет пасмурно и без ветра»;
- «если будет пасмурная погода, то будет дождь и не будет ветра».
Подумав немного, синоптик уточнил, что его три высказывания можно лаконично записать в виде одного составного высказывания. Сформулируйте его, решив задачу с помощью логических операций.
Задача 5.
Определите, кто из подозреваемых участвовал в преступлении, если известно:
- Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
- Если Иванов не участвовал, то Сидоров не участвовал.
Задача 6.
Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:
- Сергей – первый, Роман – второй;
- Сергей – второй, Виктор – третий;
- Леонид – второй, Виктор – четвертый.
Известно, что в каждом ответе только одно утверждение истинно. Как распределились места?
Did you find apk for android? You can find new Free Android Games and apps.
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
- штрих Шеффера;
- стрелка Пирса.
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.