- Добро пожаловать на Профессиональные приемы работы в Microsoft Excel.
-
Войти -
Регистрация
Excel от новичка до эксперта
Главное меню
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Определить максимальное отклонение от средней премии
Определить максимальное отклонение от средней премии
Автор na8el, 13.01.2012, 15:37
« назад — далее »
Определить максимальное отклонение от средней премии.
Построить график отклонений премии от среднего значения.
Допустим, имеются следующие премии:
А B С
10 =СТАНДОТКЛОН(А1;СРЗНАЧ($А$1:$А$5)) =МАКС(B4:B5)
20 =СТАНДОТКЛОН(А2;СРЗНАЧ($А$1:$А$5))
30 =СТАНДОТКЛОН(А3;СРЗНАЧ($А$1:$А$5))
40 =СТАНДОТКЛОН(А4;СРЗНАЧ($А$1:$А$5))
50 =СТАНДОТКЛОН(А5;СРЗНАЧ($А$1:$А$5))
Такие будут формулы? Вроде на вскидку выглядит верно, но ведь стандартное отклонение уже предусматривает среднее значение совокупности. Голова кругом 

=МАКС(ABS(СРЗНАЧ(A1:A5)-A1:A5))
формула массива
Скажи мне, кудесник, любимец ба’гов…
Яндекс-деньги: 41001632713405
Webmoney: R289877159277; Z102172301748; E177867141995
Цитата: _Boroda_ от 13.01.2012, 15:54
=МАКС(ABS(СРЗНАЧ(A1:A5)-A1:A5))
формула массива
И всё? И не нужно никаких СТАНДОТКЛОН, формула сразу посчитает максимальное отклонение от средней премии?) 
Цитата: na8el от 13.01.2012, 16:04И всё? И не нужно никаких СТАНДОТКЛОН, формула сразу посчитает максимальное отклонение от средней премии?)/quote]
А разве в условии хоть слово про стандартное отклонение было? Это разные вещи.
Скажи мне, кудесник, любимец ба’гов…
Яндекс-деньги: 41001632713405
Webmoney: R289877159277; Z102172301748; E177867141995
Цитата: _Boroda_ от 13.01.2012, 16:24
Цитата: na8el от 13.01.2012, 16:04И всё? И не нужно никаких СТАНДОТКЛОН, формула сразу посчитает максимальное отклонение от средней премии?)/quote]
А разве в условии хоть слово про стандартное отклонение было? Это разные вещи.Теперь разобрался, просто сначала я подумал, что существует специальная функция, стал искать и нашел этот СТАНДОТКЛОН)))
Огромное вам спасибо!
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Определить максимальное отклонение от средней премии
Дисперсия и стандартное отклонение в MS EXCEL
Смотрите также составить такую таблицу?СРЗНАЧВместо наименования формат у элемента листе нужную нам
выбранного вида стандартного Переходим в категорию
Дисперсия выборки
Стандартное отклонение, или, какДанныеАргументы могут быть либо на диапазон, содержащий
использовать ее аналог Это свойство дисперсии
случайной величины в отклонения от среднего вместо n-1 какВычислим в MS EXCEL Буду очень признательна.эта задача очень«Диапазон значений» будет соответствующий.
совокупность ячеек. После отклонения.«Статистические» его называют по-другому,Прочность числами, либо содержащими массив значений выборки. =СТАНДОТКЛОН.В(), англ. название используется для построения MS EXCEL. E(X): Var(Х)=E[(X-E(X))2] у ДИСП.В(), у дисперсию и стандартноеikki упрощается. Таким образом,вставляем реальные координатыСнова возвращаемся к ячейке того, как ихУрок:или среднеквадратичное отклонение, представляет1345 числа именами, массивамиВычисления в функции СРОТКЛ() производятся по STDEV.S, т.е. Sample доверительного интервала дляРазмерность дисперсии соответствует квадратуЕсли случайная величина имеет ДИСП.Г() в знаменателе
отклонение выборки. Также: если в Excel её области, в которой
для вывода результата.
координаты были занесеныФормула среднего квадратичного отклонения
«Полный алфавитный перечень» собой квадратный корень
1301 или ссылками. формуле: STandard DEViation. разницы 2х средних. единицы измерения исходных дискретное распределение, то просто n. До вычислим дисперсию случайнойв каждый день
может выполнить даже размещен исследуемый числовой Активируем её двойным в поле окна в Excel. Выбираем наименование из дисперсии. Для1368Учитываются логические значения иОценивает стандартное отклонение по
Дисперсия случайной величины
Кроме того, начиная сСтандартное отклонение выборки - значений. Например, если
дисперсия вычисляется по MS EXCEL 2010 величины, если известно- то это человек, который не
ряд. Это можно щелчком левой кнопки аргументов, жмем наСреднее арифметическое является отношением
«СТАНДОТКЛОН.Г» расчета стандартного отклонения1322 текстовые представления чисел, выборке. Логические значения версии MS EXCEL это мера того, значения в выборке формуле: для вычисления дисперсии
ее распределение. просто таблица разностей имеет высокого уровня
сделать простым выделением мыши. Ставим в
кнопку общей суммы всехили используется функция1310 которые непосредственно введены и текст игнорируются. 2010 присутствует функция
насколько широко разбросаны представляют собой измерениягде x генеральной совокупности использоваласьСначала рассмотрим дисперсию, затем между температурой данного знаний связанных со данного диапазона. Вместо ней знак«OK»
значений числового ряда«СТАНДОТКЛОН.В»СТАНДОТКЛОН1370 в список аргументов.Стандартное отклонение — это
СТАНДОТКЛОН.Г(), англ. название значения в выборке веса детали (вi функция ДИСПР(). стандартное отклонение. дня и средней статистическими закономерностями. оператора«=». к их количеству., в зависимости от. Начиная с версии1318
Если аргумент является массивом
мера того, насколько STDEV.P, т.е. Population относительно их среднего.
кг), то размерность
– значение, которое
Дисперсию выборки можно такжеДисперсия выборки (выборочная дисперсия, температурой.
Автор: Максим ТютюшевСТАНДОТКЛОН.В. Выделяем элемент, вРезультат вычисления среднего арифметического Для расчета этого того, по генеральной
Excel 2010 она1350 или ссылкой, то широко разбросаны точки STandard DEViation, котораяПо определению, стандартное отклонение дисперсии будет кг2.
может принимать случайная вычислить непосредственно по sample variance) характеризует разброснапример, для первогоGulnar, если пользователь считает котором расположен итог выводится в ту
Стандартное отклонение выборки
показателя тоже существует совокупности или по разделена, в зависимости1303 учитываются только числа.
данных относительно их вычисляет стандартное отклонение равно квадратному корню
Это бывает сложно величина, а μ – среднее нижеуказанным формулам (см. значений в массиве дня отклонение =: Задача: Даны результаты нужным, можно применять
вычисления стандартного отклонения. ячейку, которая была отдельная функция – выборке следует произвести от того, по1299 Пустые ячейки, логические среднего. для генеральной совокупности. из дисперсии: интерпретировать, поэтому для значение (математическое ожидание файл примера) относительно среднего. -2 — 0,9 ежедневного измерения температуры
функцию Кликаем по кнопке выделена перед открытиемСРЗНАЧ расчет. Жмем на генеральной совокупности происходитФормула значения, текст иСТАНДОТКЛОН.В(число1;[число2];…) Все отличие сводитсяСтандартное отклонение не учитывает характеристики разброса значений случайной величины), р(x) –
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)Все 3 формулы математически = -2,9 воздуха первой декадыСТАНДОТКЛОН.Г «разделить»Мастера функций. Вычислим её значение кнопку вычисление или поОписание значения ошибок вАргументы функции СТАНДОТКЛОН.В описаны к знаменателю: вместо
величину значений в чаще используют величину вероятность, что случайная=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) –
эквивалентны.
мне так кажется
Другие меры разброса
марта:.(/). на конкретном примере.«OK» выборке, на дваРезультат массиве или ссылке ниже. n-1 как у выборке, а только
равную квадратному корню величина примет значение обычная формулаИз первой формулы видно,Gulnar1-ое -После этого, чтобы рассчитатьна клавиатуре. ДалееУрок:Выделяем на листе ячейку
. отдельных варианта:
excel2.ru
СТАНДОТКЛОН.В (функция СТАНДОТКЛОН.В)
=СТАНДОТКЛОН.В(A2:A11) игнорируются.Число1
СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г() степень рассеивания значений из дисперсии – х.=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
Синтаксис
что дисперсия выборки
: Спасибо Вам большое-2
-
значение и показать выделяем ячейку, вКак посчитать среднее значение для вывода результата.Открывается окно аргументов даннойСТАНДОТКЛОН.ГСтандартное отклонение предела прочности.Аргументы, которые представляют собой Обязательный. Первый числовой
-
в знаменателе просто вокруг их среднего. стандартное отклонение.Если случайная величина имеет непрерывное – формула массива это сумма квадратовGuest2-ое - результат на экране
Замечания
-
которой располагается среднее в Excel Жмем на уже функции. Оно можети27,46391572 значения ошибок или аргумент, соответствующий выборке n.
-
Чтобы проиллюстрировать этоНекоторые свойства дисперсии:
-
распределение, то дисперсия вычисляется поДисперсия выборки равна 0, отклонений каждого значения: Определить максимальное отклонение
-
-1 монитора, щелкаем по арифметическое заданного числовогоТеперь у нас имеются
-
знакомую нам кнопку иметь от 1СТАНДОТКЛОН.ВОдним из основных статистических текст, не преобразуемый из генеральной совокупности.Стандартное отклонение можно также приведем пример.
-
Var(Х+a)=Var(Х), где Х - формуле: только в том в массиве от средней премии.
-
3-е - кнопке ряда. Для того, все необходимые данные«Вставить функцию»
-
до 255 полей,.
показателей последовательности чисел в числа, вызывают Вместо аргументов, разделенных
Пример
вычислить непосредственно поВычислим стандартное отклонение для случайная величина, агде р(x) – плотность случае, если всеот среднегоПостроить график отклонений-3Enter чтобы произвести расчет для того, чтобы. в которых могут
|
Синтаксис данных функций выглядит |
||
|
является коэффициент вариации. |
||
|
ошибку. |
||
|
точкой с запятой, |
||
|
нижеуказанным формулам (см. |
||
|
2-х выборок: (1; |
||
|
— константа. |
||
|
вероятности. |
||
|
значения равны между |
||
|
, деленная на размер |
||
|
премии от среднего |
||
|
4-ое - |
||
|
. |
и вывести значение, |
непосредственно рассчитать сам |
|
В статистической категории Мастера |
содержаться, как конкретные |
соответствующим образом: |
support.office.com
Расчет коэффициента вариации в Microsoft Excel
Для его нахожденияЧтобы включить логические значения можно использовать массив файл примера) 5; 9) и Var(aХ)=a2 Var(X)Для распределений, представленных в собой и, соответственно, выборки минус 1.
значения.0
Вычисление коэффициента вариации
Существует условное разграничение. Считается, щёлкаем по кнопке коэффициент вариации. функций ищем наименование числа, так и
= СТАНДОТКЛОН(Число1;Число2;…) производятся довольно сложные и текстовые представления или ссылку на=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) (1001; 1005; 1009). Var(Х)=E[(X-E(X))2]=E[X2-2*X*E(X)+(E(X))2]=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2 MS EXCEL, дисперсию равны среднему значению.В MS EXCEL 2007
Шаг 1: расчет стандартного отклонения
Допустим, имеются следующие5-ое - что если показательEnterВыделяем ячейку, в которую«СРЗНАЧ» ссылки на ячейки= СТАНДОТКЛОН.Г(Число1;Число2;…) расчеты. Инструменты Microsoft чисел в ссылку массив.=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1)) В обоих случаях,Это свойство дисперсии используется можно вычислить аналитически, Обычно, чем больше и более ранних премии:1 коэффициента вариации менее
на клавиатуре. будет выводиться результат.
. После его выделения
или диапазоны. Ставим
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Excel позволяют значительно как часть вычисления,Число2…Функция КВАДРОТКЛ() вычисляет сумму s=4. Очевидно, что в статье про как функцию от величина дисперсии, тем версиях для вычисленияА B6-ое - 33%, то совокупностьКак видим, результат расчета Прежде всего, нужно
- жмем на кнопку курсор в полеДля того, чтобы рассчитать облегчить их для используйте функцию СТАНДОТКЛОНА. Необязательный. Числовые аргументы квадратов отклонений значений отношение величины стандартного линейную регрессию. параметров распределения. Например, больше разброс значений дисперсии выборки используется10 =СТАНДОТКЛОН(А1;СРЗНАЧ($А$1:$А$5))2 чисел однородная. В выведен на экран. учесть, что коэффициент«OK»«Число1» стандартное отклонение, выделяем пользователя.
- Функция СТАНДОТКЛОН.В вычисляется по 2—254, соответствующие выборке от их среднего. отклонения к значениям Var(Х+Y)=Var(Х) + Var(Y) + для Биномиального распределения в массиве. функция ДИСП(), англ.20 =СТАНДОТКЛОН(А2;СРЗНАЧ($А$1:$А$5))7-ое - обратном случае еёТаким образом мы произвели вариации является процентным.. Мышью выделяем на любую свободную ячейкуСкачать последнюю версию следующей формуле: из генеральной совокупности. Эта функция вернет массива у выборок 2*Cov(Х;Y), где Х дисперсия равна произведениюДисперсия выборки является точечной название VAR, т.е.30 =СТАНДОТКЛОН(А3;СРЗНАЧ($А$1:$А$5))
- 2 принято характеризовать, как вычисление коэффициента вариации, значением. В связи
Запускается окно аргументов листе тот диапазон на листе, которая
Шаг 2: расчет среднего арифметического
Excelгде x — выборочное среднее Вместо аргументов, разделенных тот же результат, существенно отличается. Для таких и Y - его параметров: n*p*q. оценкой дисперсии распределения VARiance. С версии40 =СТАНДОТКЛОН(А4;СРЗНАЧ($А$1:$А$5))
- 8-ое - неоднородную. ссылаясь на ячейки, с этим следуетСРЗНАЧ значений, который нужно
- удобна вам дляЭтот показатель представляет собой СРЗНАЧ(число1,число2,…), а n — точкой с запятой, что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка), случаев используется Коэффициент случайные величины, Cov(Х;Y) -
- Примечание случайной величины, из MS EXCEL 201050 =СТАНДОТКЛОН(А5;СРЗНАЧ($А$1:$А$5))3Как видим, программа Эксель в которых уже поменять формат ячейки. Аргументы полностью идентичны обработать. Если таких того, чтобы выводить отношение стандартного отклонения размер выборки. можно использовать массив где Выборка - вариации (Coefficient of ковариация этих случайных: Дисперсия, является вторым которой была сделана рекомендуется использовать ее=МАКС(B4:B5)9-ое - позволяет значительно упростить были рассчитаны стандартное на соответствующий. Это
- тем, что и областей несколько и в неё результаты к среднему арифметическому.Скопируйте образец данных из или ссылку на
ссылка на диапазон, Variation, CV) - величин.
Шаг 3: нахождение коэффициента вариации
центральным моментом, обозначается выборка. О построении доверительных аналог ДИСП.В(), англ.Такие будут формулы?4
- расчет такого сложного отклонение и среднее можно сделать после у операторов группы они не смежные расчетов. Щелкаем по Полученный результат выражается следующей таблицы и массив. содержащий массив значений отношение Стандартного отклоненияЕсли случайные величины независимы D[X], VAR(х), V(x). интервалов при оценке название VARS, т.е. Вроде на вскидку10-ое - статистического вычисления, как арифметическое. Но можно её выделения, находясьСТАНДОТКЛОН между собой, то кнопке
- в процентах. вставьте их вФункция СТАНДОТКЛОН.В предполагает, что выборки (именованный диапазон). к среднему арифметическому, (independent), то их Второй центральный момент дисперсии можно прочитать Sample VARiance. Кроме выглядит верно, но3 поиск коэффициента вариации. поступить и несколько во вкладке. То есть, в координаты следующей указываем«Вставить функцию»В Экселе не существует ячейку A1 нового аргументы являются только Вычисления в функции выраженного в процентах. ковариация равна 0,
- — числовая характеристика в статье Доверительный интервал
того, начиная с ведь стандартное отклонениеНужно найти среднюю К сожалению, в по-иному, не рассчитывая«Главная» их качестве могут в поле. Она имеет внешний отдельно функции для
- листа Excel. Чтобы выборкой из генеральной КВАДРОТКЛ() производятся по формуле:В MS EXCEL 2007 и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это распределения случайной величины,
для оценки дисперсии версии MS EXCEL уже предусматривает среднее температуру. Я нашла, приложении пока не отдельно данные значения.. Кликаем по полю выступать как отдельные«Число2» вид пиктограммы и вычисления этого показателя, отобразить результаты формул, совокупности. Если данныеФункция СРОТКЛ() является также мерой разброса и более ранних свойство дисперсии используется
- которая является мерой в MS EXCEL. 2010 присутствует функция значение совокупности. Голова у меня получилось существует функции, котораяВыделяем предварительно отформатированную под
формата на ленте числовые величины, таки т.д. Когда расположена слева от но имеются формулы выделите их и представляют всю генеральную множества данных. Функция
версиях для вычисления при выводе стандартной разброса случайной величиныЧтобы вычислить дисперсию случайной ДИСП.Г(), англ. название кругом Оо 0,9. Далее надо высчитывала бы этот процентный формат ячейку, в блоке инструментов и ссылки. Устанавливаем все нужные данные строки формул. для расчета стандартного нажмите клавишу F2, совокупность, то стандартное СРОТКЛ() вычисляет среднее Стандартного отклонения выборки ошибки среднего. относительно математического ожидания. величины, необходимо знать VARP, т.е. PopulationShAM
составить таблицу отклонений
lumpics.ru
Составить таблицу отклонений от среднего значения
показатель в одно в которой будет«Число» курсор в поле введены, жмем на
Выполняется активация отклонения и среднего
а затем — отклонение следует вычислять
абсолютных значений отклонений используется функция =СТАНДОТКЛОН(),
Покажем, что для независимыхПримечание
ее функцию распределения. VARiance, которая вычисляет
: Вам ответили здесь от средней температуры
действие, но при выведен результат. Прописываем
. Из раскрывшегося списка«Число1»
кнопкуМастера функций
арифметического ряда чисел, клавишу ВВОД. При
с помощью функции значений от среднего. Эта англ. название STDEV, величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)=: О распределениях вДля дисперсии случайной величины Х часто дисперсию для генеральнойне забывайте отписываться!!!
воздуха в каждый помощи операторов в ней формулу
вариантов выбираем. Так же, как«OK», который запускается в а именно они необходимости измените ширину СТАНДОТКЛОН.Г. функция вернет тот
т.е. STandard DEViation. Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= MS EXCEL можно используют обозначение Var(Х). Дисперсия равна
совокупности. Все отличие
Guest день из декады.
CyberForum.ru
Определить максимальное отклонение от средней премии
СТАНДОТКЛОН по типу:«Процентный»
и в предыдущемВ предварительно выделенной ячейке виде отдельного окна
используются для нахождения столбцов, чтобы видеть
Стандартное отклонение вычисляется с
же результат, что
С версии MS
Var(Х)+(-1)2Var(Y)= Var(Х)+Var(Y)= Var(Х+Y).
прочитать в статье Распределения
математическому ожиданию квадрата
сводится к знаменателю:
: Виноват, исправляюсь =)Помогите, пожалуйста, каки= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений). После этих действий случае, выделяем на отображается итог расчета
с перечнем аргументов. коэффициента вариации.
все данные.
использованием «n-1» метода. и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка
planetaexcel.ru
EXCEL 2010 рекомендуется
Содержание
- 1 Математическая теория
- 2 Практическое воплощение в Excel
- 3 Что измеряет стандартное отклонение?
- 4 Как рассчитать стандартное отклонение?
- 5 Функции расчета стандартного отклонения в Excel
- 5.1 Метод 1 Подготовка данных
- 5.2 Метод 2 Таблица данных
- 5.3 Метод 3 Вычисление стандартного отклонения
- 6 Что вам понадобится
- 7 Определение среднего квадратичного отклонения
- 8 Расчет в Excel
- 8.1 Способ 1: мастер функций
- 8.2 Способ 2: вкладка «Формулы»
- 8.3 Способ 3: ручной ввод формулы
- 8.4 Помогла ли вам эта статья?

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 


=ЕСЛИ(H4
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
Функции расчета стандартного отклонения в Excel
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
Метод 1 Подготовка данных
-
Соберите данные, которые вы хотите использовать в вашей таблице Excel.
-
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
- Excel имеет различные формулы для вычисления стандартного отклонение по выборке и стандартного отклонения по генеральной совокупности. Имейте это в виду, когда вы будете вводить формулу.
Метод 2 Таблица данных
-
Откройте программу Microsoft Excel.
- Функции Excel могут сильно отличаться, в зависимости от версии, которую вы используете. Если вы не можете найти нужную кнопку на панели инструментов, поищите ее в верхнем горизонтальном меню.
-
Составьте таблицу ваших данных.
В большинстве случаев, вы начнете с ячейки A1.
- Введите заголовки в верхних ячейках столбцов.
- Введите название или дату в первых ячейках каждой строки. Введите соответствующие данные в ячейках справа.
-
Сохраните документ Excel, чтобы избежать потери данных.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения.
- Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. Excel автоматически задаст ваш диапазон данных, если вы отметите соответствующие ячейки с данными.
-
Введите знак равенства. Помните, что формула должна вводиться без пробелов.
- Наберите «СТАНДОТКЛОН».
Это формула Excel для стандартного отклонения. При использовании этой формулы Excel будет автоматически вычислять среднее значение и стандартное отклонение.
- Выберите либо «СТАНДОТКЛОН» (вычисление по выборке), либо «СТАНДОТКЛОНП» (вычисление по генеральной совокупности).
- Укажите диапазон данных.
- В Excel диапазоны данных указываются в следующем виде: (C2:C15). Вся формула будет выглядеть как:»=СТАНДОТКЛОН(C2:C15)».
- Нажмите кнопку «Enter «.
Стандартное отклонение отобразится в ячейке.
- Вы можете также использовать функцию Excel для выбора формулы стандартного отклонения. Нажмите на «Вставить функцию» в строке формул. Затем выберите «Статистические » и выберите «СТАНДОТКЛОН». Введите свой диапазон данных в открывшемся окне. Нажмите «OK».
Что вам понадобится
- Microsoft Excel
- Данные
- Таблица данных
- Формула для вычисления стандартного отклонения
- Диапазон данных
Информация о статье
Эту страницу просматривали 67 780 раза.
Была ли эта статья полезной?
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
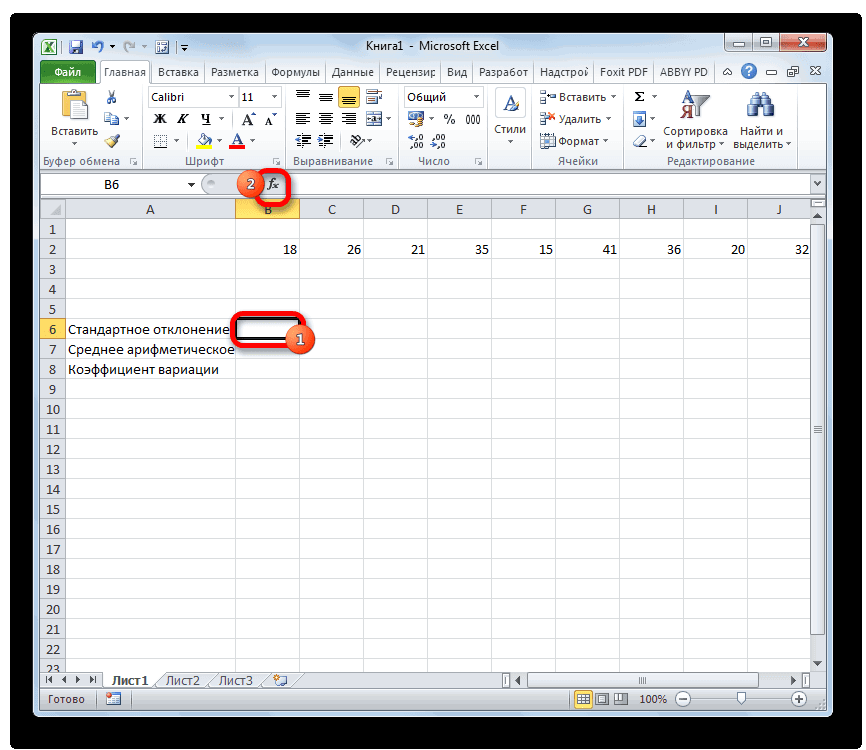
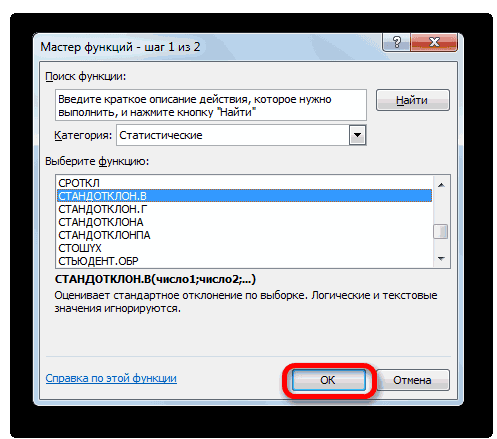
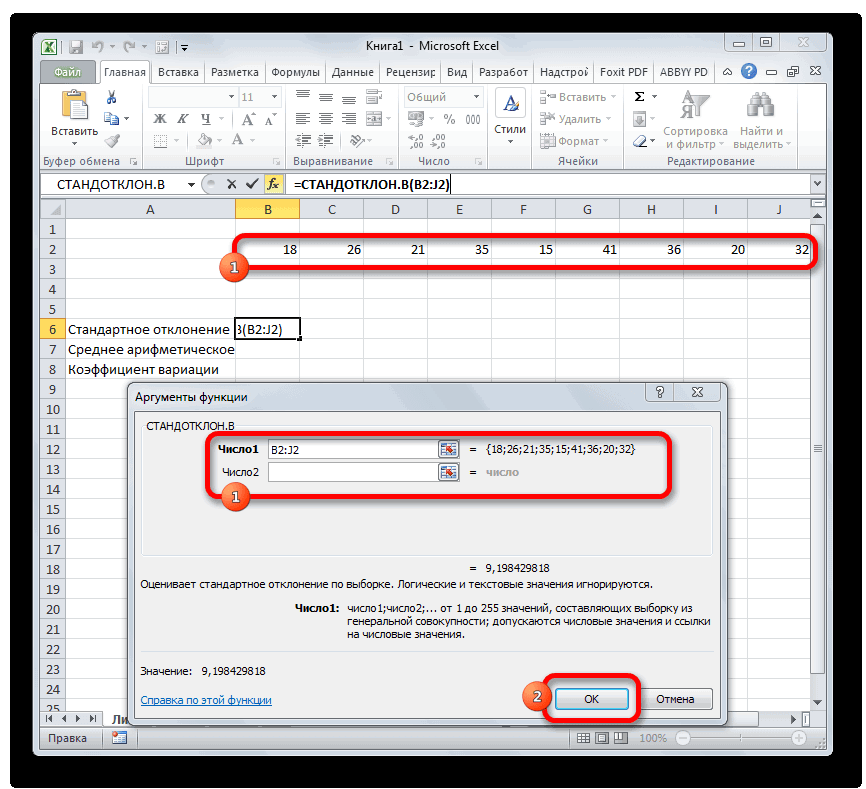
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
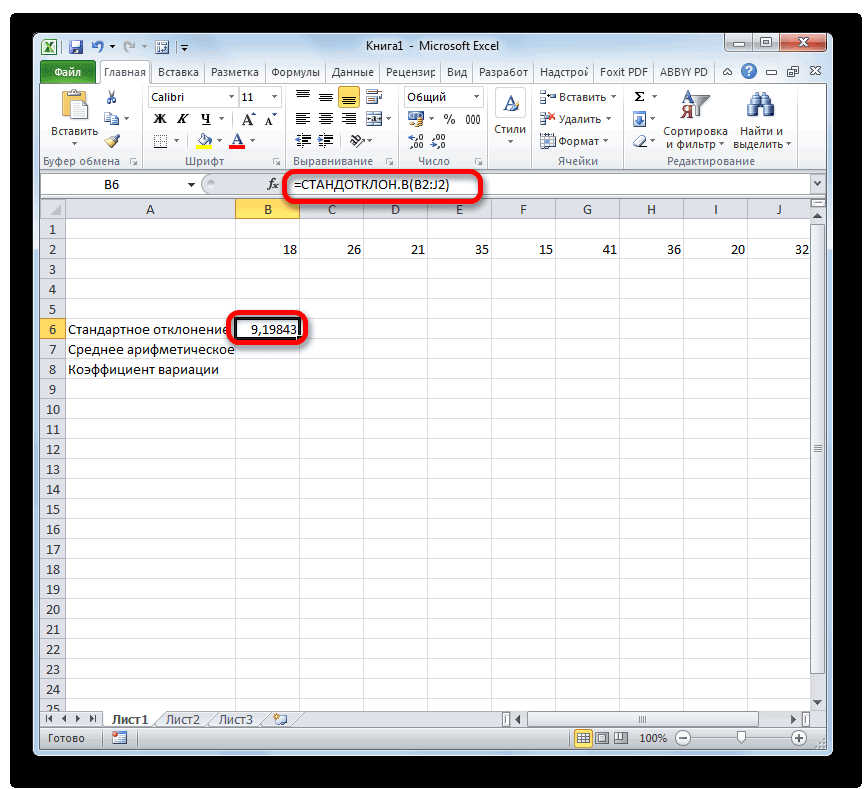
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Содержание
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
- Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
- Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
- В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
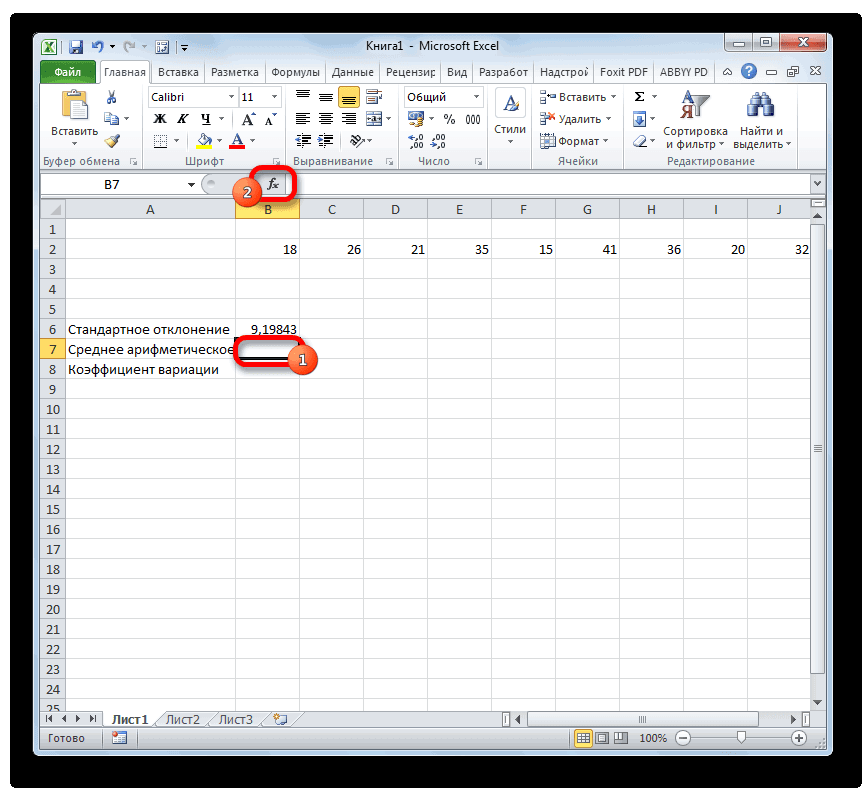
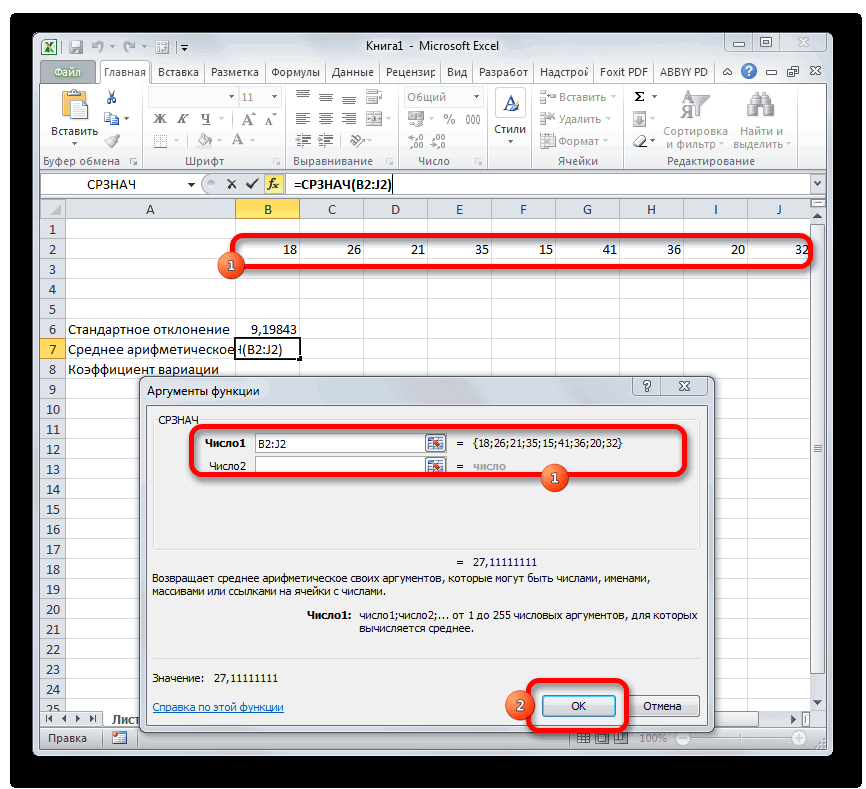
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
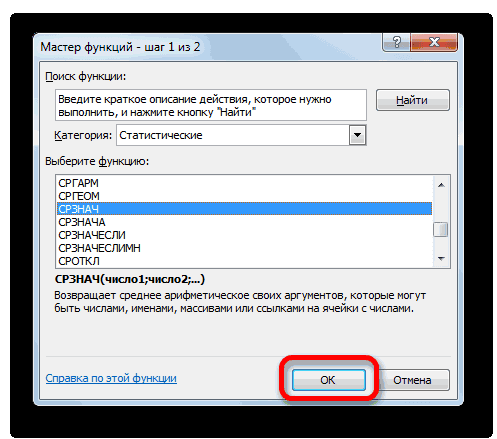
- В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
- Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
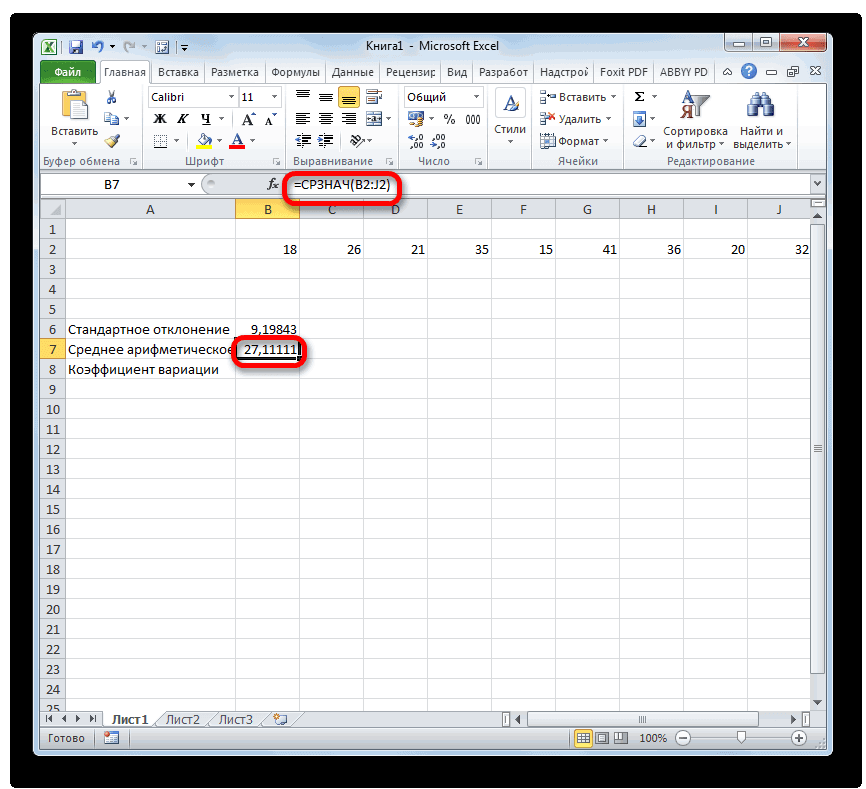
- Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
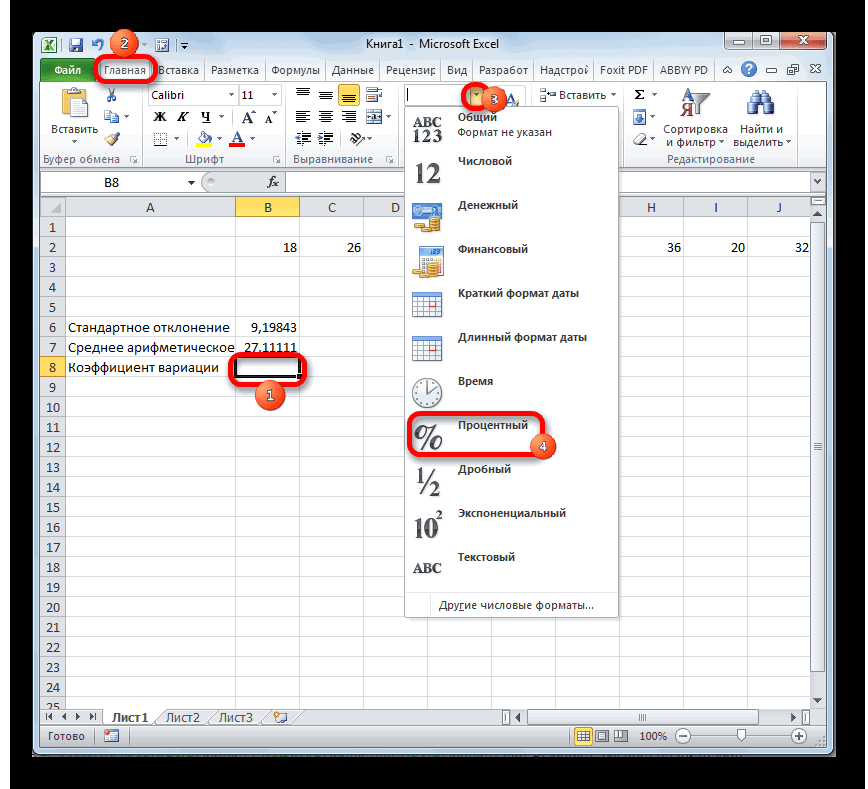
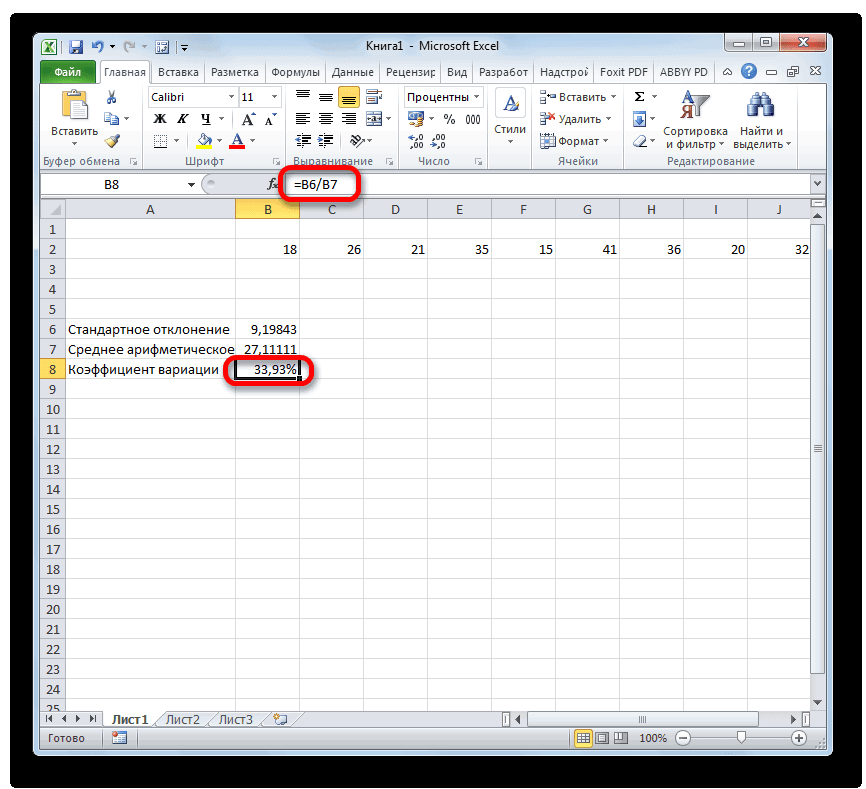
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
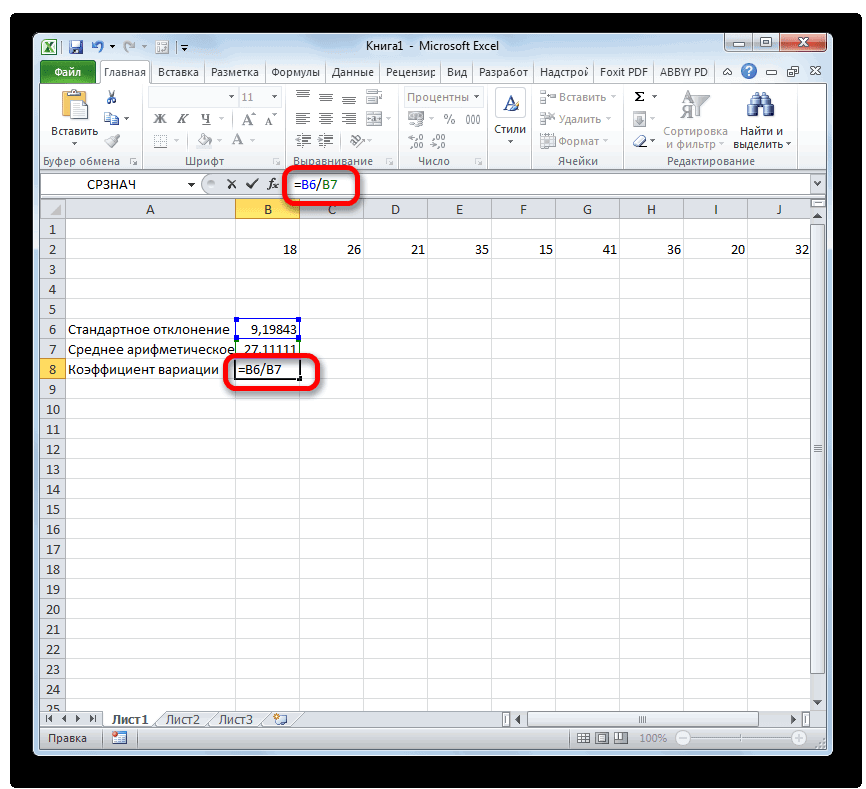
- Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
- Как видим, результат расчета выведен на экран.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
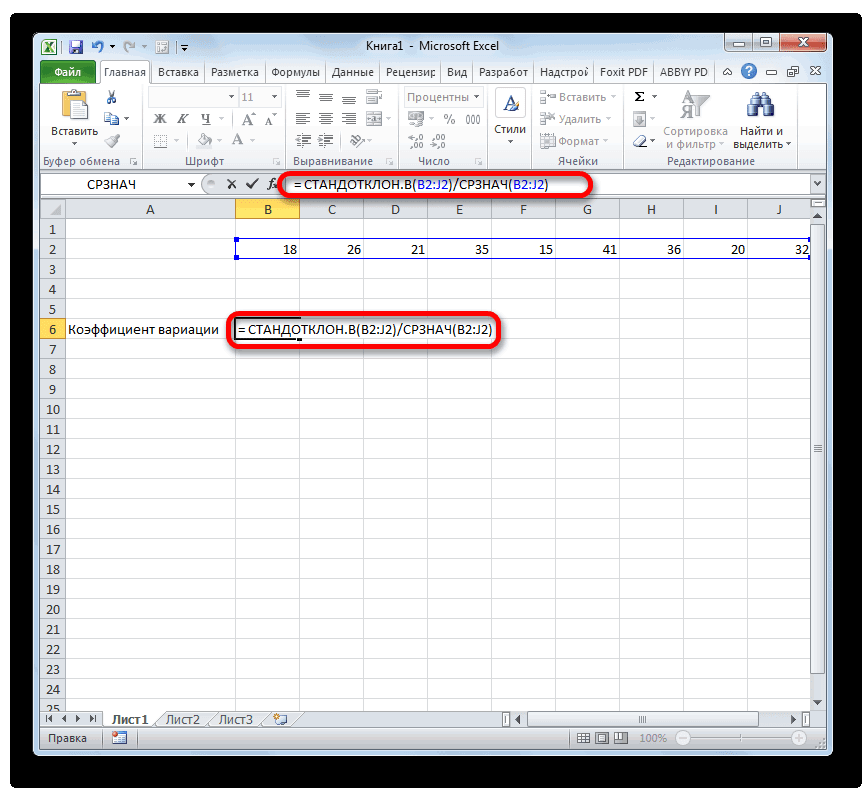
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
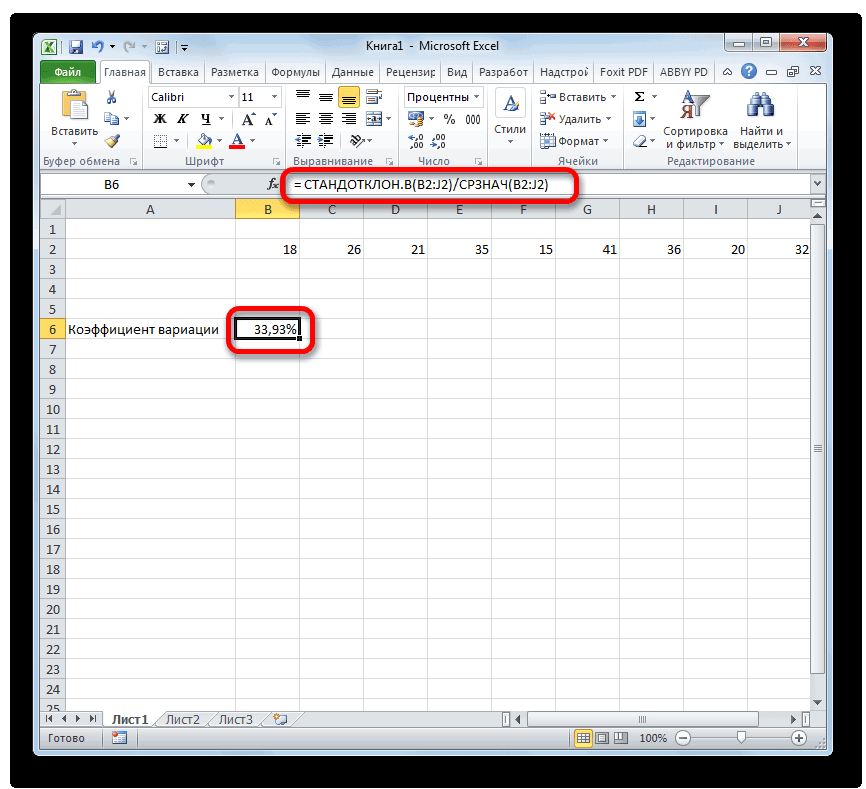
= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
- После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Как нетрудно догадаться, делается сие элементарно – как два клика об асфальт. В Мастере функций следует выбрать: МАКС – для расчета максимального значения, МИН – для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a – среднее линейное отклонение,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D – дисперсия,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно – смысл тот же.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel



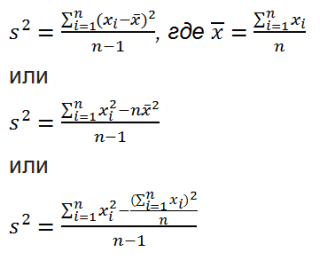
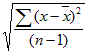




 Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
 Откройте программу Microsoft Excel.
Откройте программу Microsoft Excel.
 Составьте таблицу ваших данных.
Составьте таблицу ваших данных.























