Функция РОСТ используется для расчета прогнозируемого экспоненциального роста на основе принимаемых на вход известных массивов данных X и Y, и возвращает массив значений для зависимой переменной Y на основе полученных новых данных для массива независимой переменной X.
Метод прогнозируемого экспоненциального роста c использованием функции РОСТ
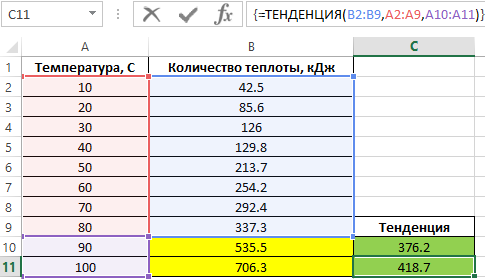
Пример 1. В ходе выполнения лабораторной работы студент должен определить зависимость между температурой количеством теплоты, содержащемся в веществе определенной массы. По условиям задания, необходимо провести 10 опытов, из которых было выполнено 8. Для получения остальных величин студент решил использовать метод прогнозируемого экспоненциального роста.
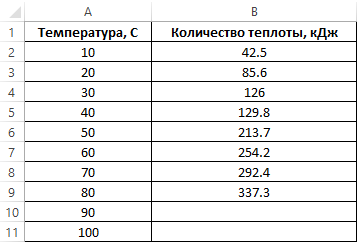
Таблица с исходными данными:
Выделяем диапазон ячеек B10:B11 и используем следующую функцию:
Описание аргументов:
- B2:B9 – диапазон известных значений количества теплоты, полученные в результате проведения опытов;
- A2:A9 – диапазон температур, для которых проводились опыты;
- A10:A11 – диапазон температур, для которых необходимо вычислить предполагаемые значения количества теплоты.
Для ввода формулы используем комбинацию клавиш CTRL+SHIFT+Enter так как формула должна выполняться в массиве. В результате получим:
Визуально заметно явное несоответствие найденных величин диапазону уже известных значений. В Excel существует еще одна функция для прогнозирования на основе известных значений – ТЕНДЕНЦИЯ. Воспользуемся ей и сравним полученные результаты. Для этого выделяем диапазон ячеек C10:C11 и снова в массиве вводим функцию ТЕНДЕНЦИЯ:
Как видно, синтаксические записи функций РОСТ и ТЕНДЕНЦИЯ идентичны, однако они используют различные алгоритмы для вычислений. Для ввода функции ТЕНДЕНЦИЯ снова используем комбинацию клавиш CTRL+SHIFT+Enter. В результате получим:
То есть, в данном примере функция ТЕНДЕНЦИЯ дает более точный прогноз и целесообразно использовать именно ее.
Прогноз эффективности использования рекламного бюджета по функции РОСТ
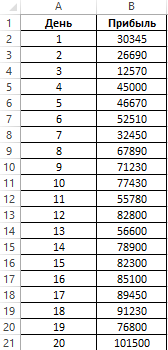
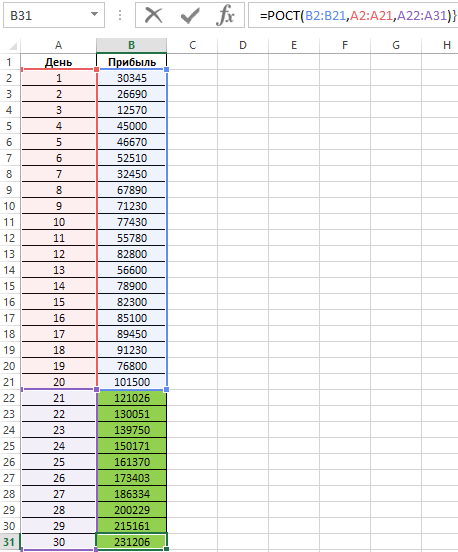
Пример 2. За 10 дней до окончания 30-дневного месяца было решено определить общую прогнозируемую прибыль сети магазинов в месяц на основании имеющихся данных за прошедшие 20 дней, на протяжении которых прибыль за день в целом постоянно увеличивалась благодаря использованию эффективной рекламы. Необходимо рассчитать, превысит ли прибыль значение в 3 млн. рублей.
Исходные данные:
Для решения используем следующую формулу:
=РОСТ(B2:B21;A2:A21;A22:A31)
Описание аргументов:
- B2:B21 – массив известных значений прибыли за день для первых 20 дней;
- A2:A21 – массив дней, для которых размер прибыли уже известен;
- A22:A31 – массив дней, для которых выполняется прогнозирование прибыли.
В результате имеем:
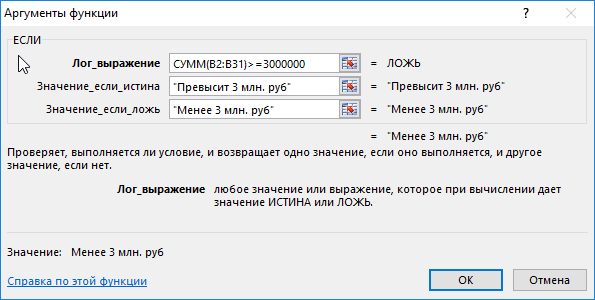
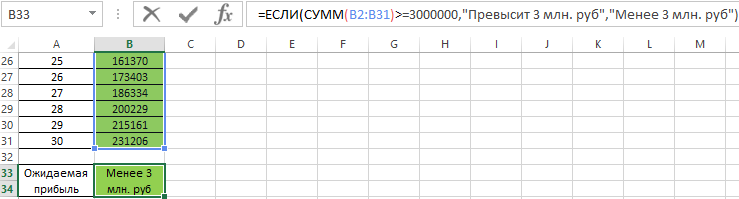
Для получения ответа на поставленный вопрос запишем следующую формулу:
Полученный результат:
Прогноз прибыли за месяц с использованием функции РОСТ в Excel
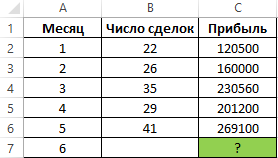
Пример 3. Экономист развивающегося предприятия ведет учет прибыли, при этом в таблице содержатся три вектора данных: месяц, число сделок, общая сумма прибыли. Необходимо спрогнозировать прибыль на следующий месяц при двух условиях:
- Количество сделок будет равно показателю за предыдущий месяц;
- Количество сделок увеличится на 2.
Исходные данные:
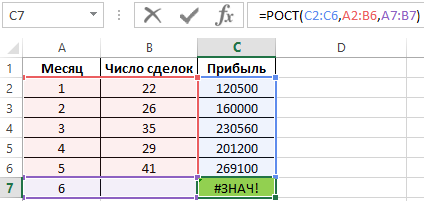
Вводим функцию РОСТ и получаем ошибку #ЗНАЧ!:
Внимание! В данном случае для прогнозирования прибыли будет использовано сочетание двух факторов: номер месяца и число сделок. Поэтому в качестве аргумента [известные_значения_x] необходимо передать диапазон значений A2:B6, а в качестве аргумента [новые_значения_x] – диапазон A7:B7.
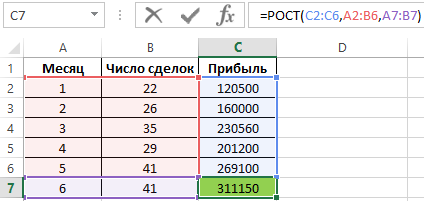
Для определения прибыли при условии, что число сделок составит 41, запишем следующую формулу:
Теперь увеличим количество сделок на 2-е:
Как и ожидалось, прогнозируемая прибыль увеличилась. Пример наглядно демонстрирует, что для увеличения точности предсказания можно использовать 2 и более зависящих друг от друга параметров.
Функция РОСТ в Excel и особенности ее использования
Функция РОСТ имеет следующую синтаксическую запись:
=РОСТ(известные_значения_y;[известные_значения_x];[новые_значения_x];[конст])
Описание аргументов:
- известные_значения_y – массив данных, элементы которого характеризуют значения зависимой переменной y в уравнении y=bkx. Аргумент обязателен для заполнения.
- [известные_значения_x] – массив данных, элементы которого соответствуют известным значениям независимой переменной x в записи y=bkx. Аргумент является необязательным.
- [новые_значения_x] – массив с новыми значениями независимой переменной x, на основе которых функция выполняет расчет новых значений зависимой переменной y. Аргумент необязателен для заполнения.
- [конст] – данные логического типа (ИСТИНА или ЛОЖЬ), определяющие значение константы b в уравнении y=bkx. По умолчанию (если аргумент явно не указан), а также при явном указании логического ИСТИНА, коэффициент b вычисляется обычным способом. Если данный параметр принимает значение ЛОЖЬ, дальнейшие расчеты проводятся для уравнения y=kx, поскольку значение b принимается равным единице.
Примечания 1:
- Элементы массива известные_значения_y должны быть взяты из диапазона положительных чисел. При наличии отрицательных значений или значений, равных 0 (нулю), результатом выполнения функции РОСТ будет код ошибки #ЧИСЛО!.
- В качестве аргумента [известные_значения_x] может быть передано одно либо несколько множеств значений. Размерности множеств, передаваемых в качестве первого и второго аргументов должны совпадать, если используется единственная переменная. При вводе нескольких переменных в качестве аргумента известные_значения_y должен быть передан вектор. В Excel вектором считается интервал значений, высота которого составляет одну строку, либо ширина которого равна только одному столбцу).
- Функция РОСТ интерпретирует каждый столбец или каждую строку массива [известные_значения_x] в качестве отдельной переменной, если массив известные_значения_y содержит только один столбец или только одну строку соответственно.
- Если второй аргумент функции явно не указан, то по умолчанию используется массив данных {1;2;3;…;n}, размерность которого соответствует размерности массива известные_значения_y.
- Массив [новые_значения_x]должен быть аналогичен по своей структуре массиву [известные_значения_x], то есть содержать строку либо столбец для каждого элемента массива известные_значения_y.
- Если третий аргумент рассматриваемой функции явно не указан, считается, что он тождественен значению второго аргумента данной функции. Если второй и третий аргументы опущены, они оба являются массивами типа {1;2;3;…;n} с требованиями, указанными в пункте 4.
- Если массив значений передается в качестве константы массива, по правилам записи массивов в Excel необходимо использовать знак «;» для разделения значений, содержащихся в одной строке, и знак «:» для разделения строк.
Примечания 2:
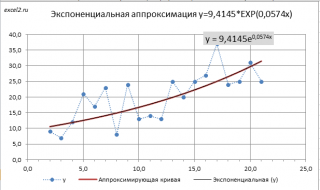
- Функция РОСТ часто используется для аппроксимации (упрощения) значений независимой (x) и зависимой (y) переменных экспоненциальной кривой.
- Данная функция принадлежит к классу формул массивов, поэтому при ее использовании необходимо выделить соответствующее количество ячеек, а после ввода всех требуемых аргументов следует нажать сочетание клавиш Ctrl+Shift+Enter для корректного отображения результатов.
- В качестве функции экспоненциального роста используется уравнение типа y=bkx.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование
в Microsoft Excel.
Описание
Рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих значений x и y. Функцию РОСТ также можно использовать для аппроксимации существующих значений x и y экспоненциальной кривой.
Синтаксис
РОСТ(известные_значения_y;[известные_значения_x];[новые_значения_x];[конст])
Аргументы функции РОСТ описаны ниже.
-
Известные_значения_y — обязательный аргумент. Множество значений y в уравнении y = b*m^x, которые уже известны.
-
Если массив «известные_значения_y» содержит один столбец, каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.
-
Если массив «известные_значения_y» содержит одну строку, каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.
-
Если любое из чисел в known_y 0 или отрицательное, то «РОСТ» возвращает #NUM! значение ошибки #ЗНАЧ!.
-
-
Известные_значения_x Необязательный. Множество значений x, которые могут быть уже известны для соотношения y = b*m^x.
-
Массив известные_значения_x может включать одно или более множеств переменных. Если используется только одна переменная, то аргументы «известные_значения_y» и «известные_значения_x» могут быть диапазонами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то аргумент «известные_значения_y» должен быть вектором (то есть диапазоном высотой в одну строку или шириной в один столбец).
-
Если аргумент «известные_значения_x» опущен, то предполагается, что это массив {1;2;3;…} того же размера, что и «известные_значения_y».
-
-
Новые_значения_x — необязательный аргумент. Новые значения x, для которых функция РОСТ возвращает соответствующие значения y.
-
Аргумент «новые_значения_x» должен содержать столбец (или строку) для каждой независимой переменной, так же как и «известные_значения_x». Таким образом, если «известные_значения_y» — это один столбец, то «известные_значения_x» и «новые_значения_x» должны иметь одинаковое количество столбцов. Если массив «известные_значения_y» состоит из одной строки, столько же строк должно содержаться в массивах «известные_значения_x» и «новые_значения_x».
-
Если аргумент «новые_значения_x» опущен, предполагается, что он совпадает с аргументом «известные_значения_x».
-
Если опущены аргументы «известные_значения_x» и «новые_значения_x», предполагается, что каждый из них представляет собой массив {1;2;3;…} того же размера, что и «известные_значения_y».
-
-
Конст — необязательный аргумент. Логическое значение, которое указывает, должна ли константа b равняться 1.
-
Если аргумент «конст» имеет значение ИСТИНА или опущен, b вычисляется обычным образом.
-
Если аргумент «конст» имеет значение ЛОЖЬ, то предполагается, что b = 1, а значения m подбираются таким образом, чтобы выполнялось равенство y = m^x.
-
Замечания
-
Формулы, возвращающие массивы, необходимо вводить как формулы массивов после того, как будет выделено соответствующее количество ячеек.
-
При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точки с запятой для разделения значений в одной строке и двоеточия для разделения строк.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Единицы |
Формула (соответствующие единицы) |
|
|
11 |
33 100 |
32 618 |
|
|
12 |
47 300 |
47 729 |
|
|
13 |
69 000 |
69 841 |
|
|
14 |
102 000 |
102 197 |
|
|
15 |
150 000 |
149 542 |
|
|
16 |
220 000 |
218 822 |
|
|
Месяц |
Формула (предполагаемые единицы) |
Формулы, использующиеся в вышеприведенном массиве C2:C7 |
|
|
17 |
320 197 |
=РОСТ(B2:B7;A2:A7) |
|
|
18 |
468 536 |
||
|
Формулы, использующиеся в вышеприведенном массиве B9:B10 |
|||
|
=РОСТ(B2:B7;A2:A7;A9:A10) |
Нужна дополнительная помощь?
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной
функции.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным. Основная статья про МНК —
МНК: Метод Наименьших Квадратов в MS EXCEL
.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m
x
=a*(e
ln(m)
)
x
= a*e
x*ln(m)
=a*e
bx
, где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю
линейной зависимости
с помощью замены переменных (см.
файл примера
).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента
a
необходимо выполнить обратное преобразование a=
EXP(A)
.
Примечание
: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы
Линия тренда
(
Экспоненциальная линия тренда
). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью
Основы построения диаграмм в MS EXCEL
.
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больш
и
х по модулю отрицательных чисел) соответствующее значение
y
асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы
Линия тренда.
Если среди значений
y
есть отрицательные, то с помощью инструмента
Линия тренда
экспоненциальную линию тренда построить не удастся.
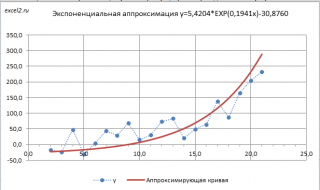
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте
х
значения
y
также будут увеличиваться. В качестве
с
можно взять некую заранее известную нижнюю границу для
y
, ниже которой
у
не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см.
файл примера лист Экспонента2
).
Если при росте
х
значения
y
уменьшаются по экспоненциальной кривой, т.е. a<0 (существует некая верхняя граница
с
для
у
), то к линейному случаю Y=b*x+A свести задачу позволит замена переменных Y=ln(c-y) и A=ln(-a) (см.
файл примера лист Экспонента3
).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции
РОСТ()
, английское название GROWTH.
Синтаксис функции следующий:
РОСТ(
известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст]
)
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент
известные_значения_y
) и на массив значений переменной Х (аргумент
известные_значения_x
). Функция рассчитает прогнозные значения Y для Х, указанных в
аргументе новые_значения_x
. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент
конст
должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений
y
есть отрицательные, то с помощью функции
РОСТ()
аппроксимирующую кривую построить не удастся.
Безусловно, использование функции
РОСТ()
часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции
РОСТ()
вычислить коэффициенты уравнения y=
a
*EXP(
b
*x).
Примечание
: В MS EXCEL имеется специальная функция
ЛГРФПРИБЛ()
, которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент
a
(значение Y в точке Х=0) используйте формулу
=РОСТ(C26:C45;B26:B45;0)
. В диапазонах
C26:C45
и
B26:B45
должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент
b
используйте формулу:
=
LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция
ЛГРФПРИБЛ()
на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты
а
и
m
уравнения y=
a
*
m
^x.
Используя свойство степеней a
mn
=(a
m
)
n
приведем уравнение экспоненциального тренда y=
a
*EXP(
b
*x)=
a
*e
b
*x
=
a
*(e
b
)
x
к виду y=
a
*
m
^x, сделав замену переменной m= e
b
=EXP(
b
).
Чтобы вычислить коэффициенты уравнения y=
a
*EXP(
b
*x) используйте следующие формулы:
=
LN(ЛГРФПРИБЛ(C26:C45;B26:B45))
— коэффициент
b
=
ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2)
— коэффициент
a
Примечание
: Функция
ЛГРФПРИБЛ()
, английское название LOGEST, является
формулой массива, возвращающей несколько значений
. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в
Строке формул
ввести =
ЛГРФПРИБЛ(C26:C45;B26:B45)
, затем для ввода формулы вместо обычного
ENTER
нажать
CTRL
+
SHIFT
+
ENTER
.
Функция
ЛГРФПРИБЛ()
имеет линейный аналог – функцию
ЛИНЕЙН()
, которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (
статистика
) установлен ИСТИНА, то
ЛГРФПРИБЛ()
возвращает регрессионную статистику:
стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов:
SSR
,
SSE
и др.
Примечание
: Особой нужды в функции
ЛГРФПРИБЛ()
нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=
a
*
m
^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=
a
*EXP(
b
*x).
17 авг. 2022 г.
читать 2 мин
Экспоненциальная регрессия — это тип модели регрессии, который можно использовать для моделирования следующих ситуаций:
1. Экспоненциальный рост: рост начинается медленно, а затем стремительно ускоряется без ограничений.
2. Экспоненциальное затухание: затухание начинается быстро, а затем замедляется, приближаясь к нулю.
Уравнение модели экспоненциальной регрессии принимает следующий вид:
у = аб х
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в Excel.
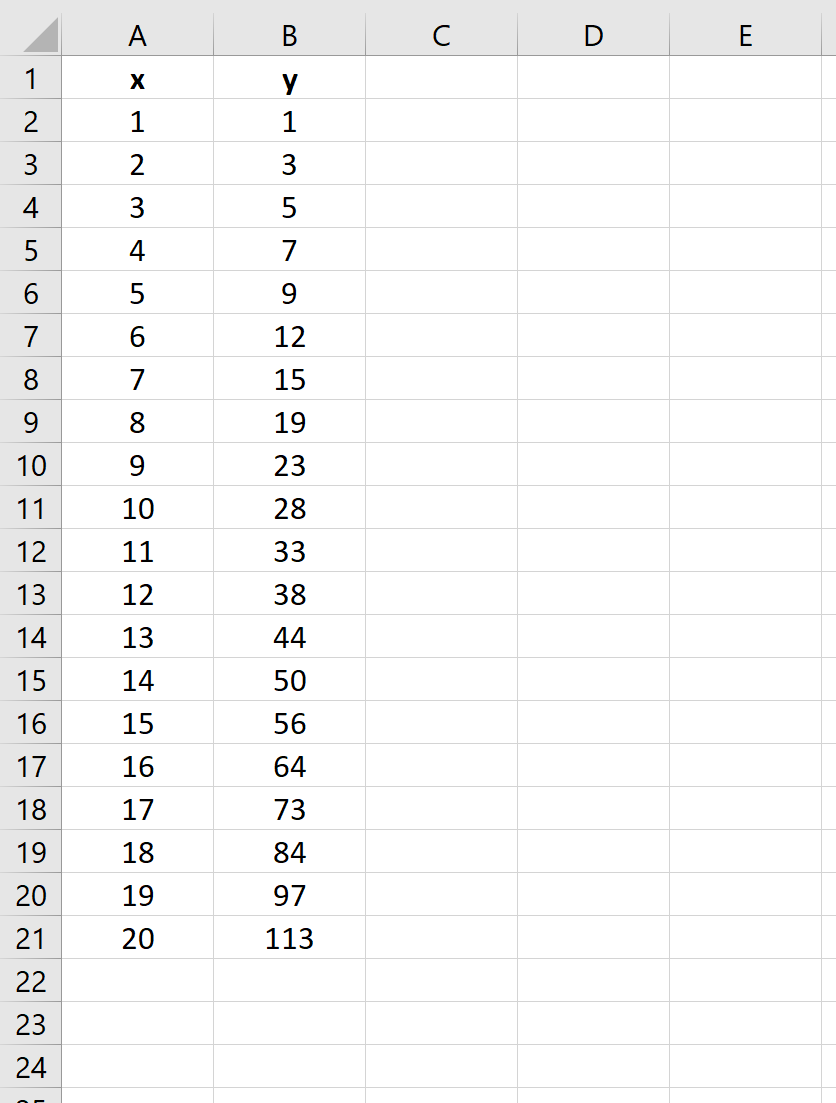
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных, содержащий 20 наблюдений :
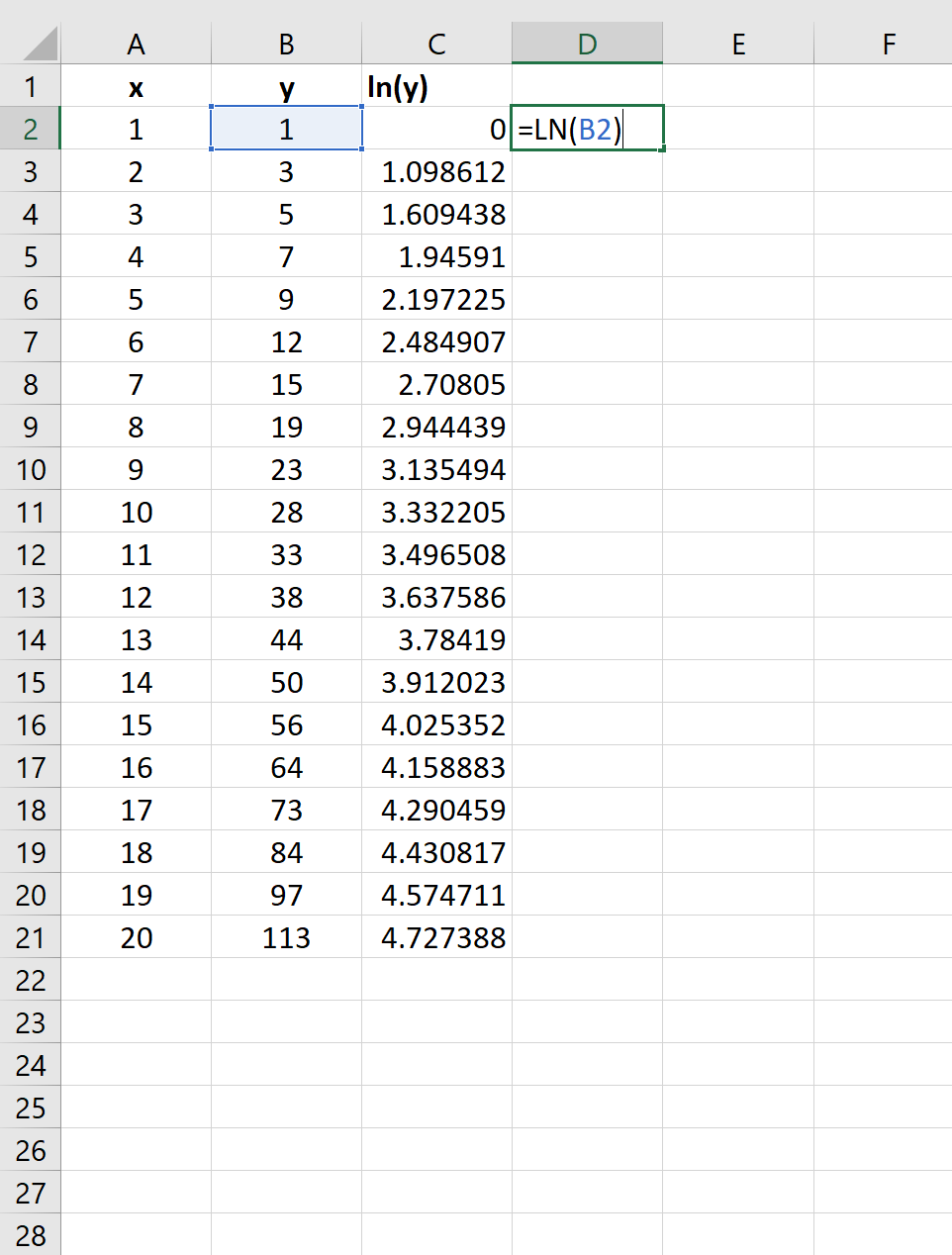
Шаг 2: возьмите натуральный логарифм переменной отклика
Далее нам нужно создать новый столбец, представляющий естественный журнал переменной ответа y :
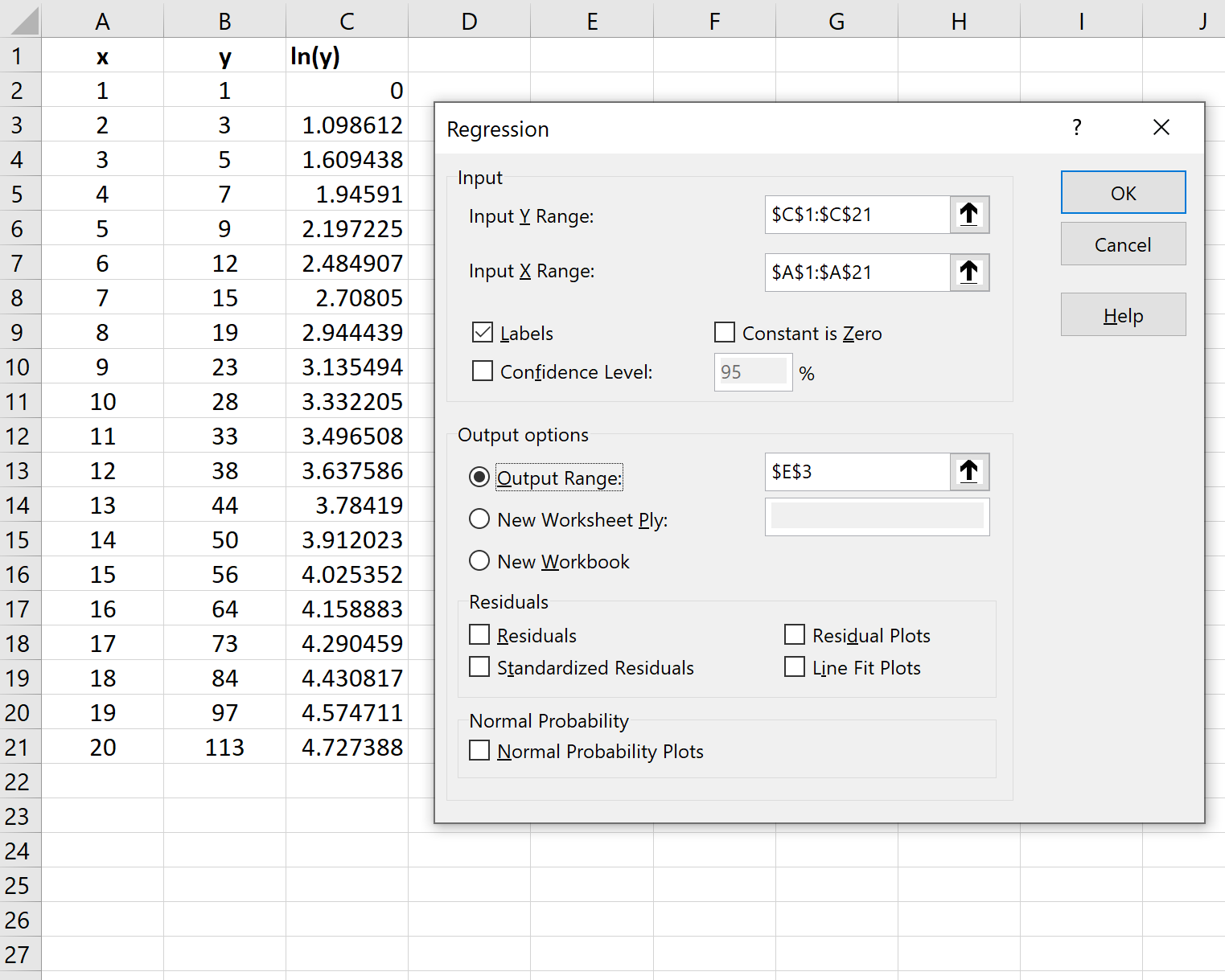
Шаг 3: Подберите модель экспоненциальной регрессии
Далее мы подгоним модель экспоненциальной регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
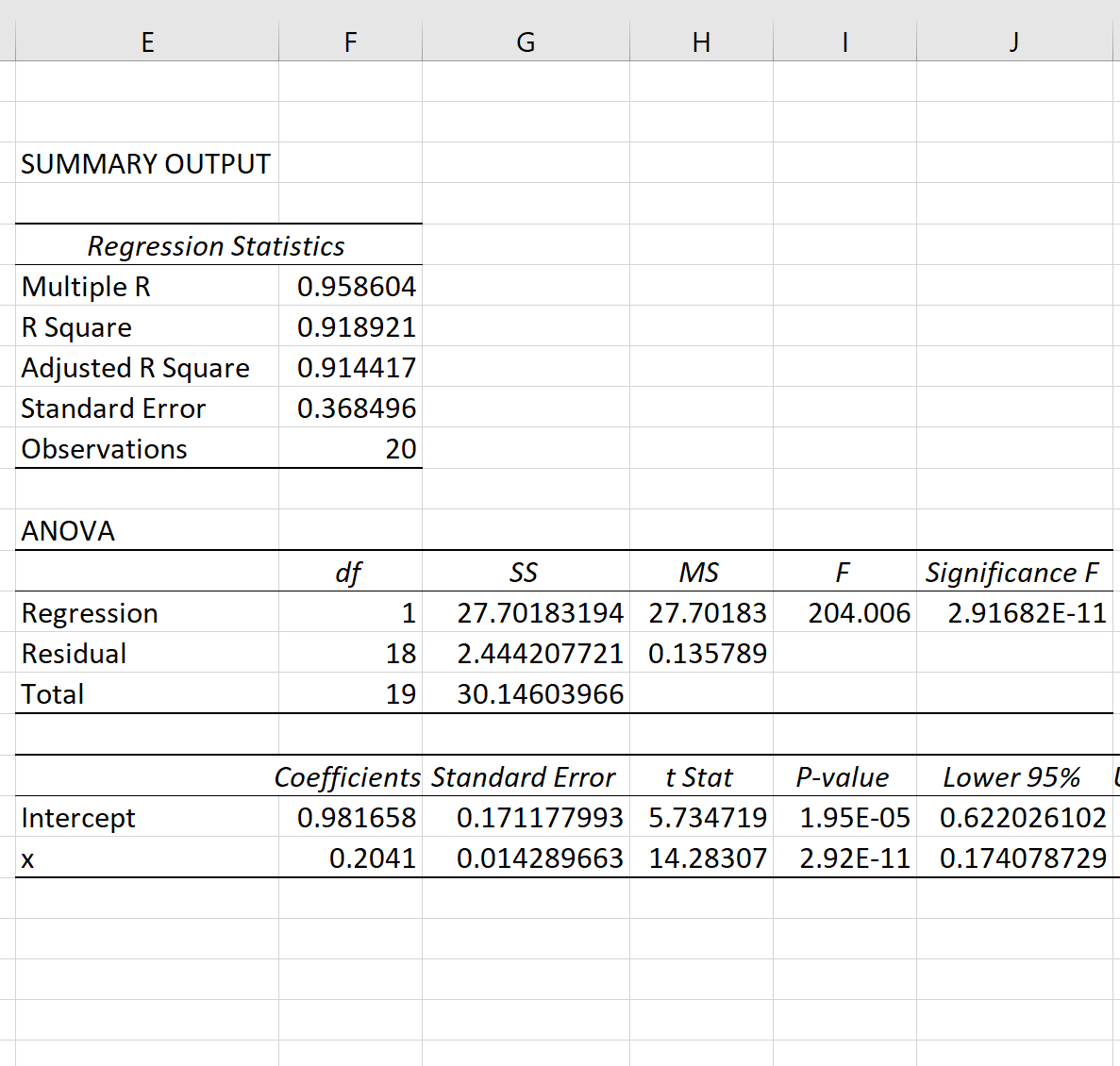
Как только вы нажмете OK , будут показаны результаты модели экспоненциальной регрессии:
Общее значение F модели составляет 204,006, а соответствующее значение p чрезвычайно мало, что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии:
ln(у) = 0,9817 + 0,2041(х)
Применив e к обеим частям, мы можем переписать уравнение как:
у = 2,6689 * 1,2264 х
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 14, то мы можем предсказать, что y будет равно 46,47 :
у = 2,6689 * 1,2264 14 = 46,47
Бонус: не стесняйтесь использовать этот онлайн- калькулятор экспоненциальной регрессии для автоматического вычисления уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Примеры функции РОСТ и прогноз экспоненциального роста в Excel
Функция РОСТ используется для расчета прогнозируемого экспоненциального роста на основе принимаемых на вход известных массивов данных X и Y, и возвращает массив значений для зависимой переменной Y на основе полученных новых данных для массива независимой переменной X.
Метод прогнозируемого экспоненциального роста c использованием функции РОСТ
Пример 1. В ходе выполнения лабораторной работы студент должен определить зависимость между температурой количеством теплоты, содержащемся в веществе определенной массы. По условиям задания, необходимо провести 10 опытов, из которых было выполнено 8. Для получения остальных величин студент решил использовать метод прогнозируемого экспоненциального роста.
Таблица с исходными данными:
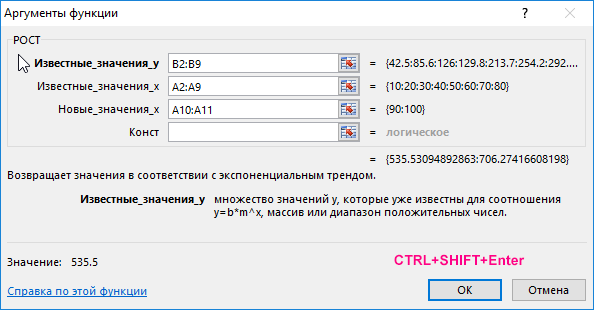
Выделяем диапазон ячеек B10:B11 и используем следующую функцию:
- B2:B9 – диапазон известных значений количества теплоты, полученные в результате проведения опытов;
- A2:A9 – диапазон температур, для которых проводились опыты;
- A10:A11 – диапазон температур, для которых необходимо вычислить предполагаемые значения количества теплоты.
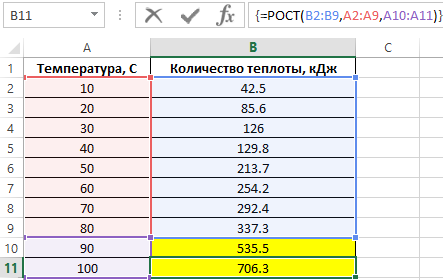
Для ввода формулы используем комбинацию клавиш CTRL+SHIFT+Enter так как формула должна выполняться в массиве. В результате получим:
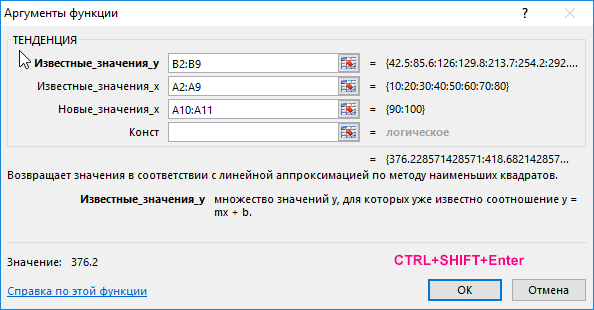
Визуально заметно явное несоответствие найденных величин диапазону уже известных значений. В Excel существует еще одна функция для прогнозирования на основе известных значений – ТЕНДЕНЦИЯ. Воспользуемся ей и сравним полученные результаты. Для этого выделяем диапазон ячеек C10:C11 и снова в массиве вводим функцию ТЕНДЕНЦИЯ:
Как видно, синтаксические записи функций РОСТ и ТЕНДЕНЦИЯ идентичны, однако они используют различные алгоритмы для вычислений. Для ввода функции ТЕНДЕНЦИЯ снова используем комбинацию клавиш CTRL+SHIFT+Enter. В результате получим:
То есть, в данном примере функция ТЕНДЕНЦИЯ дает более точный прогноз и целесообразно использовать именно ее.
Прогноз эффективности использования рекламного бюджета по функции РОСТ
Пример 2. За 10 дней до окончания 30-дневного месяца было решено определить общую прогнозируемую прибыль сети магазинов в месяц на основании имеющихся данных за прошедшие 20 дней, на протяжении которых прибыль за день в целом постоянно увеличивалась благодаря использованию эффективной рекламы. Необходимо рассчитать, превысит ли прибыль значение в 3 млн. рублей.
Для решения используем следующую формулу:
- B2:B21 – массив известных значений прибыли за день для первых 20 дней;
- A2:A21 – массив дней, для которых размер прибыли уже известен;
- A22:A31 – массив дней, для которых выполняется прогнозирование прибыли.
В результате имеем:
Для получения ответа на поставленный вопрос запишем следующую формулу:
=3000000;»Превысит 3 млн. руб»;»Менее 3 млн. руб»)’ class=’formula’>
Прогноз прибыли за месяц с использованием функции РОСТ в Excel
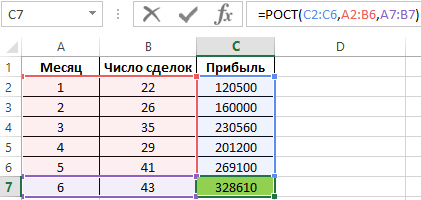
Пример 3. Экономист развивающегося предприятия ведет учет прибыли, при этом в таблице содержатся три вектора данных: месяц, число сделок, общая сумма прибыли. Необходимо спрогнозировать прибыль на следующий месяц при двух условиях:
- Количество сделок будет равно показателю за предыдущий месяц;
- Количество сделок увеличится на 2.
Вводим функцию РОСТ и получаем ошибку #ЗНАЧ!:
Внимание! В данном случае для прогнозирования прибыли будет использовано сочетание двух факторов: номер месяца и число сделок. Поэтому в качестве аргумента [известные_значения_x] необходимо передать диапазон значений A2:B6, а в качестве аргумента [новые_значения_x] – диапазон A7:B7.
Для определения прибыли при условии, что число сделок составит 41, запишем следующую формулу:
Теперь увеличим количество сделок на 2-е:
Как и ожидалось, прогнозируемая прибыль увеличилась. Пример наглядно демонстрирует, что для увеличения точности предсказания можно использовать 2 и более зависящих друг от друга параметров.
Функция РОСТ в Excel и особенности ее использования
Функция РОСТ имеет следующую синтаксическую запись:
- известные_значения_y – массив данных, элементы которого характеризуют значения зависимой переменной y в уравнении y=bkx. Аргумент обязателен для заполнения.
- [известные_значения_x] – массив данных, элементы которого соответствуют известным значениям независимой переменной x в записи y=bkx. Аргумент является необязательным.
- [новые_значения_x] – массив с новыми значениями независимой переменной x, на основе которых функция выполняет расчет новых значений зависимой переменной y. Аргумент необязателен для заполнения.
- [конст] – данные логического типа (ИСТИНА или ЛОЖЬ), определяющие значение константы b в уравнении y=bkx. По умолчанию (если аргумент явно не указан), а также при явном указании логического ИСТИНА, коэффициент b вычисляется обычным способом. Если данный параметр принимает значение ЛОЖЬ, дальнейшие расчеты проводятся для уравнения y=kx, поскольку значение b принимается равным единице.
- Элементы массива известные_значения_y должны быть взяты из диапазона положительных чисел. При наличии отрицательных значений или значений, равных 0 (нулю), результатом выполнения функции РОСТ будет код ошибки #ЧИСЛО!.
- В качестве аргумента [известные_значения_x] может быть передано одно либо несколько множеств значений. Размерности множеств, передаваемых в качестве первого и второго аргументов должны совпадать, если используется единственная переменная. При вводе нескольких переменных в качестве аргумента известные_значения_y должен быть передан вектор. В Excel вектором считается интервал значений, высота которого составляет одну строку, либо ширина которого равна только одному столбцу).
- Функция РОСТ интерпретирует каждый столбец или каждую строку массива [известные_значения_x] в качестве отдельной переменной, если массив известные_значения_y содержит только один столбец или только одну строку соответственно.
- Если второй аргумент функции явно не указан, то по умолчанию используется массив данных <1;2;3;…;n>, размерность которого соответствует размерности массива известные_значения_y.
- Массив [новые_значения_x]должен быть аналогичен по своей структуре массиву [известные_значения_x], то есть содержать строку либо столбец для каждого элемента массива известные_значения_y.
- Если третий аргумент рассматриваемой функции явно не указан, считается, что он тождественен значению второго аргумента данной функции. Если второй и третий аргументы опущены, они оба являются массивами типа <1;2;3;…;n>с требованиями, указанными в пункте 4.
- Если массив значений передается в качестве константы массива, по правилам записи массивов в Excel необходимо использовать знак «;» для разделения значений, содержащихся в одной строке, и знак «:» для разделения строк.
- Функция РОСТ часто используется для аппроксимации (упрощения) значений независимой (x) и зависимой (y) переменных экспоненциальной кривой.
- Данная функция принадлежит к классу формул массивов, поэтому при ее использовании необходимо выделить соответствующее количество ячеек, а после ввода всех требуемых аргументов следует нажать сочетание клавиш Ctrl+Shift+Enter для корректного отображения результатов.
- В качестве функции экспоненциального роста используется уравнение типа y=bkx.
МНК: Экспоненциальная зависимость в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
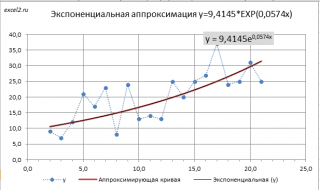
Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
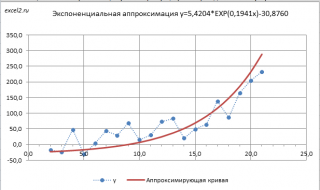
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).
Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание: Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL+SHIFT+ENTER.
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (статистика) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR, SSE и др.
Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).
Функция РОСТ
Дата добавления: 2013-12-23 ; просмотров: 8756 ; Нарушение авторских прав
ПРЕДСКАЗ(х; изв_знач_y; изв_знач_x)
Функция ПРЕДСКАЗ
Прогнозирование с помощью функций
Прогнозирование экономических показателей
Для расчета ожидаемого исполнения бюджета и при составлении проекта бюджета на следующий год используется прогнозирование различных экономических показателей.
В Excel для прогнозирования используются ряд функций (ПРЕДСКАЗ, РОСТ, ТЕНДЕНЦИЯ) и диаграммы.
Функция ПРЕДСКАЗ позволяет сделать прогноз, применяя линейную регрессию диапазона известных данных или массивов (x,y). Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по существующим значениям.
Предсказываемое значение — это y-значение, соответствующее заданному x-значению. Известные значения — это x- и y-значения, а новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для предсказания будущих продаж, потребностей в оборудовании или тенденций потребления.
х — это точка данных, для которой предсказывается значение.
изв_знач_y — это зависимый массив или интервал данных.
изв_знач_x — это независимый массив или интервал данных.
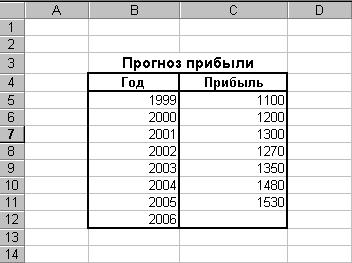
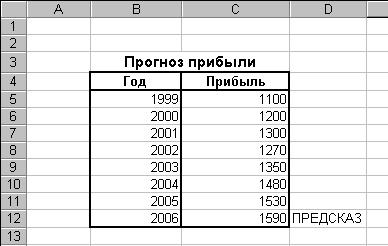
В качестве примера выполним расчет ожидаемой прибыли за 2006 год на основе данных о полученной прибыли в целом за год за 1999-2005 годы, используя функцию ПРЕДСКАЗ (рис. 92).
Рис. 92. Исходные данные для прогнозирования прибыли предприятия
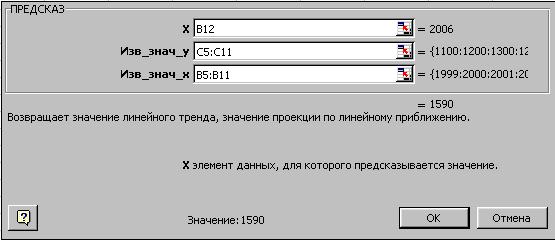
Для расчета прибыли за 2006 год установите курсор в ячейку С12, выберите команду Функция в меню Вставка. В раскрывшемся окне Мастера функций выберите категориюфункцийСтатистическиеи затем вызовите функцию ПРЕДСКАЗ. На экране появится диалоговое окно функции ПРЕДСКАЗ. (рис. 93).
Рис. 93. Окно диалога функции ПРЕДСКАЗ
в появившемся окне введите исходные данные и получите результат (рис. 94).
Рис. 94. Результаты прогнозирования с помощью функции ПРЕДСКАЗ
Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений. Функция рабочего листа РОСТ может применяться также для аппроксимации существующих x- и y-значений экспоненциальной кривой.
РОСТ(изв_знач_y; изв_знач_x; нов_знач_x; константа),
изв_знач_y — это множество значений y, которые уже известны для соотношения y = b*m^x.
изв_знач_x — это необязательное множество значений x, которые уже известны для соотношения y = b*m^x.
нов_знач_x — это новые значения x, для которых РОСТ возвращает соответствующие значения y.
константа — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1.
Если константа имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
Если константа имеет значение ЛОЖЬ, то b полагается равном 1, а значения m подбираются так, чтобы y = m^x.
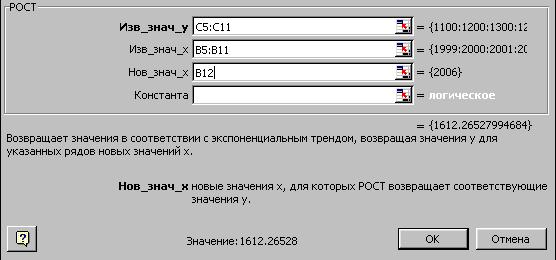
В качестве примера использования этой функции выполним расчет прибыли за 2006 год на основе данных, приведенных на рис. 92.
Установите курсор в ячейку С12, выберите команду Функция в меню Вставка, а затем выберите функцию РОСТ. На экране появится диалоговое окно функции РОСТ (рис. 95).
Рис. 95. Окно диалога функции РОСТ
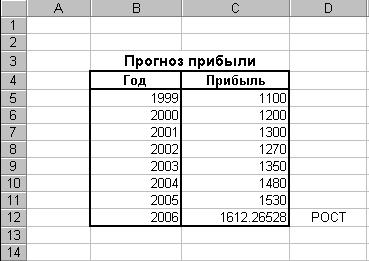
в появившемся окне введите исходные данные и получите результат (рис. 96).
Рис. 96. Результаты прогнозирования с помощью функции РОСТ
РОСТ (функция РОСТ)
В этой статье описаны синтаксис формулы и использование функции РОСТ в Microsoft Excel.
Рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих значений x и y. Функцию РОСТ также можно использовать для аппроксимации существующих значений x и y экспоненциальной кривой.
Аргументы функции РОСТ описаны ниже.
Известные_значения_y — обязательный аргумент. Множество значений y в уравнении y = b*m^x, которые уже известны.
Если массив «известные_значения_y» содержит один столбец, каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.
Если массив «известные_значения_y» содержит одну строку, каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.
Если какие-либо числа в массиве «известные_значения_y» равны 0 или имеют отрицательное значение, функция РОСТ возвращает значение ошибки #ЧИСЛО!.
Известные_значения_x — необязательный аргумент. Множество значений x в уравнении y = b*m^x, которые уже известны.
Массив «известные_значения_x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, множества «известные_значения_y» и «известные_значения_x» могут иметь любую длину, но их размерности должны совпадать. Если используется более одной переменной, аргумент «известные_значения_y» должен быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если аргумент «известные_значения_x» опущен, то предполагается, что это массив <1;2;3;. >того же размера, что и «известные_значения_y».
Новые_значения_x — необязательный аргумент. Новые значения x, для которых функция РОСТ возвращает соответствующие значения y.
Аргумент «новые_значения_x» должен содержать столбец (или строку) для каждой независимой переменной, так же как и «известные_значения_x». Таким образом, если массив «известные_значения_y» состоит из одного столбца, то столько же столбцов должны иметь массивы «известные_значения_x» и «новые_значения_x». Если массив «известные_значения_y» состоит из одной строки, столько же строк должно содержаться в массивах «известные_значения_x» и «новые_значения_x».
Если аргумент «новые_значения_x» опущен, предполагается, что он совпадает с аргументом «известные_значения_x».
Если опущены аргументы «известные_значения_x» и «новые_значения_x», предполагается, что каждый из них представляет собой массив <1;2;3;. >того же размера, что и «известные_значения_y».
Конст — необязательный аргумент. Логическое значение, которое указывает, должна ли константа b равняться 1.
Если аргумент «конст» имеет значение ИСТИНА или опущен, b вычисляется обычным образом.
Если аргумент «конст» имеет значение ЛОЖЬ, то предполагается, что b = 1, а значения m подбираются таким образом, чтобы выполнялось равенство y = m^x.
Формулы, возвращающие массивы, необходимо вводить как формулы массивов после того, как будет выделено соответствующее количество ячеек.
При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точки с запятой для разделения значений в одной строке и двоеточия для разделения строк.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Статистические функции Microsoft Excel: описание, примеры применения
Функция РОСТ()
Функция РОСТ() рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений. Функция рабочего листа РОСТ может применяться также для аппроксимации существующих x- и y-значений экспоненциальной кривой.
РОСТ (известные_значения_y;известные_значения_x;новые_значения_x; конст)
Известные_значения_y — множество значений y, которые уже известны в уравнении
Если массив «известные_значения_y» содержит один столбец, каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.
Если массив «известные_значения_y» содержит одну строку, каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.
Если какие-либо числа в массиве «известные_значения_y» равны 0 или имеют отрицательное значение, функция РОСТ возвращает значение ошибки #ЧИСЛО!. Известные_значения_x — необязательное множество значений x, которые уже известны в уравнении
Массив «известные_значения_x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, множества «известные_значения_y» и «известные_значения_x» могут иметь любую длину, но их размерности должны совпадать. Если используется более одной переменной, аргумент «известные_значения_y» должен быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если аргумент «известные_значения_x» опущен, то предполагается, что это массив <1;2;3;. >того же размера, что и «известные_значения_y».
Новые_значения_x — новые значения x, для которых РОСТ возвращает соответствующие значения y.
Аргумент «новые_значения_x» должен содержать столбец (или строку) для каждой независимой переменной, так же как и «известные_значения_x». Таким образом, если массив «известные_значения_y» состоит из одного столбца, то столько же столбцов должны иметь массивы «известные_значения_x» и «новые_значения_x». Если массив «известные_значения_y» состоит из одной строки, столько же строк должно содержаться в массивах «известные_значения_x» и «новые_значения_x».
Если аргумент «новые_значения_x» опущен, предполагается, что он совпадает с аргументом «известные_значения_x».
Если опущены оба аргумента «известные_значения_x» и «новые_значения_x», то предполагается, что каждый из них представляет собой массив <1;2;3;. >того же размера, что и «известные_значения_y».
Конст — логическое значение, которое указывает, должна ли константа b равняться 1. Если аргумент «конст» имеет значение ИСТИНА или опущен, b вычисляется обычным образом. Если аргумент «конст» имеет значение ЛОЖЬ, то предполагается, что b = 1, а значения m подбираются таким образом, чтобы выполнялось равенство y = m^x.
Замечания Формулы, возвращающие массивы, должны быть введены как формулы массивов после того, как будет выделено соответствующее количество ячеек. При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.