Расчет
численности населения России к 2020-му году
Цель работы:
С помощью электронной таблицы методом
подбора наименьшей абсолютной погрешности определить численность населения
России 2020-м году.
Введение в работу:
F(t)
– функция, выражающая зависимость численности населения России от времени.
Точный вид этой функции не известен, но исследования показали, что ее вид можно
принять таким:
Здесь A и B
– коэффициенты, имеющие свое значение для каждого государства.
Отклонение
теоретического значения F(t)
от данных по переписи населения в статистическом справочнике – это модуль
разности двух чисел: фактического значения и значения, подсчитанного по
указанной выше формуле.
Погрешность
– это максимальное значение отклонения.
Таким образом, цель лабораторной работы заключается
в том, чтобы найти такие коэффициенты A и B,
чтобы погрешность расчетов по нашей формуле по сравнению с известными данными
за прошедшие годы была наименьшей.
Тогда мы сможем воспользоваться формулой с
подобранными коэффициентами для ее экстраполяции, т.е. продления ее действия на
2020-й год, для нахождения искомой величины – численности населения России в
2020-м году.
Выполнение работы:
1. Будем
считать, что у Вас уже создана новая пустая электронная таблица.
2. Здесь
и далее не забывайте делать подписи соответствующих ячеек, как это показано на
рисунках, чтобы было понятно, какие данные в них хранятся.
3. Начнем
с того, что в ячейках A2
и B2
разместим начальные значения коэффициентов A и B,
которые в дальнейшем мы будем подбирать – 100 и 1 соответственно.
4. Подготовим
таблицу справочных данных. Для этого в ячейки А5 и A6
внесем значения годов 2000 и 2001, а в ячейки B5
и B6
значения t – значения 0 и 1.
Остальные значения вплоть до 2006-го года можно получить путем выделения
диапазона A5:B6
и расширения его до ячейки B11
при помощи перетаскивания маркера в правом нижнем углу диапазона.

5. Заполнить
диапазон C5:C11
справочными данными, как показано на рисунке:
6. Ввести
в ячейку D5
формулу, показанную на рисунке:
7. Ввести
в ячейку E5
формулу, показанную на рисунке:
8. Выделите
диапазон D5:E5
и перетаскиванием маркера в нижнем правом углу диапазона расширьте его на все
ячейки вплоть до E11,
чтобы получилась таблица показанная на рисунке:

9. В
ячейку E14
введите следующую формулу, чтобы получился результат, показанный на рисунке:
10. Выделите
диапазон C5:D11
и постройте график. Для этого перейдите на панель «Вставка» и выберите «График
с маркерами» из меню «График».

11. Настроить
график таким образом, чтобы имя первого ряда было «Справочник», а имя
второго – «Население», а в качестве подписей оси X использовались года.
12. Путем
подбора значений A и B в ячейках A2
и B2
добиться, чтобы значение погрешности в ячейке E14
оказалось меньше единицы. Для этого удобно пользоваться графиком.
Необходимо добиться, чтобы график «Население» как можно более точно
соответствовал графику «Справочник».
13. Провести
экстраполяцию. Для этого необходимо занести в ячейки A12
и B12
значения 2020 и 20, а затем скопировать формулу из ячейки D11
в ячейку D12.
Полученное значение
ячейки D12 является искомой
численностью населения России в 2020-м году.
14. Провести
анализ и сделать вывод.
Содержание
- Построение линейной диаграммы в Excel
- Для какой цели используется линейная диаграмма
- Как построить линейную диаграмму в Excel
- Линейчатая диаграмма
- Вычисления по формулам в программе Microsoft Excel. Решение задач
- Расчет относительных величин, используя MS Excel
Построение линейной диаграммы в Excel
С помощью линейной диаграммы пользователь представляет наглядно вариацию, динамику и взаимосвязь. Графически изображение представляет собой последовательность точек, соединенных отрезками прямой в ломаные линии. Как происходит построение линейной диаграммы в Excel.
Для какой цели используется линейная диаграмма
Линейные диаграммы графики целесообразно использовать в следующих ситуациях:
- Динамический ряд имеет достаточно большое количество значений. Непрерывная линия, соединяющая их, подчеркивает непрерывность процесса.
- Нужно показать общую тенденцию развития явления.
- Необходимо в пределах одной геометрической плоскости сравнить несколько динамических рядов.
- В сопоставлении нуждаются не абсолютные значения, а темпы роста явления.
На оси абсцисс, как правило, показывается временная характеристика явления. На оси ординат – значение показателя.
Как построить линейную диаграмму в Excel
С помощью линейного графика в Excel можно быстро сопоставить продажи в компании за определенные промежутки времени, проанализировать баланс, доходы и расходы, значения какого-либо эксперимента и т.п. Рассмотрим на примере как сделать линейную диаграмму в Excel.
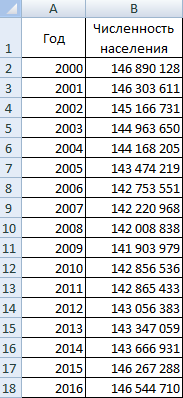
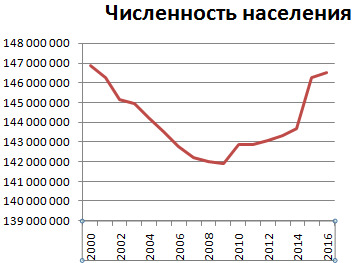
Создадим таблицу в Excel «Численность населения России за 2000-2016 гг.»:
- Все ячейки в колонках должны быть заполнены.
- Данные имеют одинаковый формат.
- В одном столбце – значения одного типа (даты, численность).
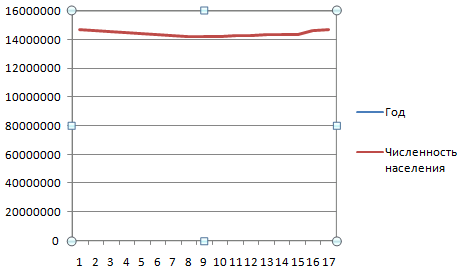
Выделяем всю таблицу, включая заголовки. Переходим на вкладку «Вставка» — в меню «Диаграммы». Выбираем «График».
Можно выбрать «с накоплением», «нормированный», «с маркерами» и т.п. Щелкаем по иконке выбранной разновидности графика левой кнопкой мыши. Получаем:
Такой график нас не устраивает – он построен не совсем правильно. Поэтому щелкаем по области построения, чтобы активировалась вкладка «Работа с диаграммами». Нажимаем кнопку «Выбрать данные».
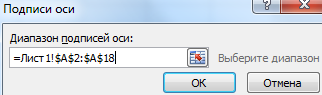
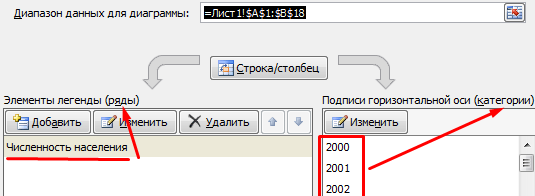
В окне «Выбор источника данных» мы сначала изменим подписи горизонтальной оси.
После нажатия кнопки «Изменить» откроется поле для назначения диапазона подписей. Выбираем столбец с датами.
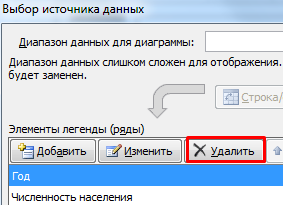
Нажимаем ОК. Программа возвращает нас к диалоговому окну «Выбор источника данных».
В «Элементы легенды» попали данные столбца «Год» и «Численность населения». «Год» удалим.
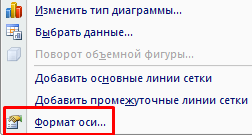
По умолчанию подписи горизонтальной и вертикальной оси принимают горизонтальное направление. Каждое значение года имеет 4 цифры. Они сливаются – и плохо видно. Чтобы изменить их направление, щелкаем правой кнопкой мыши по подписям. Нажимаем кнопку «Формат оси».
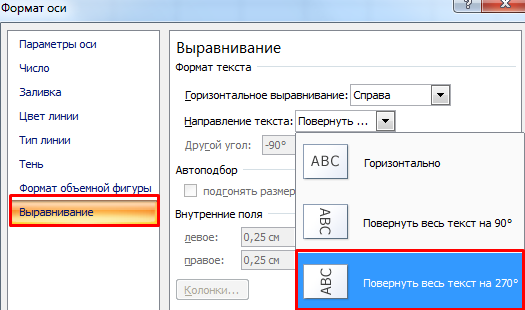
В открывшемся диалоговом окне переходим на вкладку «Выравнивание». Здесь мы можем изменить направление текста.
Получаем график вида:
Построить линейную диаграмму по таблице достаточно просто. Готовые график можно менять (цвет, толщину линии, размер шрифта, подписи и т.п.), используя доступные инструменты на вкладках «Конструктор», «Макет», «Формат».
Линейчатая диаграмма
В Excel 2007 имеется такой тип. По сути, это столбчатая гистограмма, где столбики повернуты горизонтально. Столбчатая гистограмма и линейчатая диаграмма взаимозаменяемы. Они применяются для анализа изменений показателя за определенный промежуток времени.
Каждый столбик (прямоугольник) показывает величину уровня в анализируемом статистическом ряду. Сравниваемые данные имеют одинаковые единицы измерения. Поэтому удается проанализировать рассматриваемый процесс.
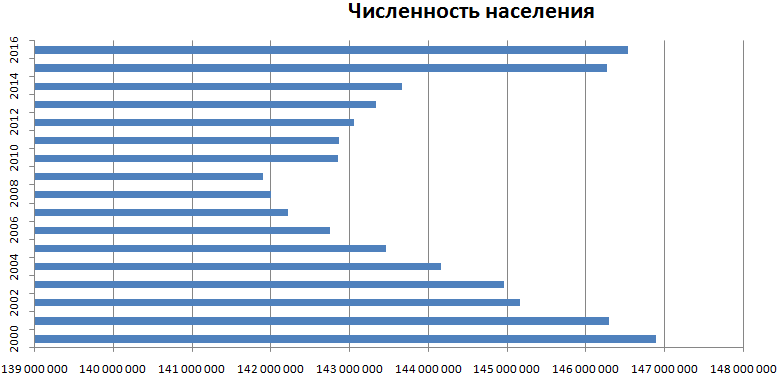
На основе уже имеющихся данных по численности населения построим линейчатую диаграмму.
Обратите внимание: так как столбики имеют горизонтальное направление, диаграмма как будто ложится на бок.
Теперь годы – это подписи вертикальной оси, а численность – горизонтальной. Но при выборе источника данных для диаграммы нужно придерживаться прежнего порядка:
Значения для категорий и рядов должны остаться теми же.
Источник
Вычисления по формулам в программе Microsoft Excel. Решение задач
Решение задач. (9 класс)
Тип урока: обобщения
Цели урока:
- Формирование умений и навыков, носящих в современных условиях общенаучный и общеинтеллектуальный характер.
- Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений.
- Научить школьников применять современное программное обеспечение в решении задач.
Задачи урока:
- Воспитательная — развитие познавательного интереса, воспитание информационной культуры.
- Учебная — изучить и закрепить основные навыки работы с электронными таблицами.
- Развивающая — развитие логического мышления, расширение кругозора.
Оборудование: компьютеры, доска, проектор, карточки для самостоятельной работы
I. Организационный момент.
Проверить готовность класса к уроку, отметить отсутствующих.
II. Этап проверки знаний.
Сегодня мы с вами продолжаем изучать тему «Технология обработки числовой информации в электронных таблицах» и познакомимся с новыми возможностями программы Microsoft Excel. Приложение_4 Но сначала давайте повторим основные понятия, которые будут нужны нам на уроке.
Четверо учащихся выполнят задания, записанные на карточке Приложение_1 . А мы с вами будем работать по цепочке.
Вопросы для повторения:
- Для чего предназначены электронные таблицы? Какова их структура?
- Основные объекты электронных таблиц? Как они определяются?
- Что можно записать в ячейки электронной таблицы?
- Какие форматы данных вы знаете?
- Формулы в электронных таблицах? Правила ее записи?
- Какие виды ссылок существуют и чем они отличаются?
- Какие встроенные функции вы знаете и для чего они нужны?
Затем проверить работу учащихся по карточкам.
III. Этап подготовки учащихся к активному и сознательному усвоению нового материала.
На предыдущих уроках, создавая различные таблицы, мы убедились с вами в том, что электронные таблицы — это удобное средство для обработки большого количества числовой информации. Во всех табличных процессорах имеются встроенные средства, которые помогают производить вычисления значительно быстрее, главная цель научиться обрабатывать числовую информацию рационально.
Рассмотрим такую задачу (Работа1 Вариант1) Приложение_2 :
1. На отрезке [0;2] с шагом 0,2 протабулировать функцию:
| A | B | C | D |
| Шаг | 0,2 | ||
| X | Y | ||
| 0 | =КОРЕНЬ(A3^3+A3+1,5)/(A3+1) | ||
| A3+B1 | =КОРЕНЬ(A4^3+A4+1,5)/(A4+1) | ||
| A4+B1 | =КОРЕНЬ(A5^3+A5+1,5)/(A5+1) | ||
| A5+B1 | =КОРЕНЬ(A6^3+A6+1,5)/(A6+1) |
Получаем: в ячейку А4 вводим формулу =А3+$B$1, а в ячейку В3 = КОРЕНЬ(A3^3+A3+1.5)/(A3+1)
2. Используя набор данных «Территория и население по континентам» (Приложение, №1), составить таблицу и выяснить минимальную и максимальную плотность населения в 1970 году и в 1989 году, суммарную площадь всех континентов.
| A | B | C | D | E | F |
| Территория, млн.кв.км. | Население, млн.чел | Плотность населения, чел. на кв.км. | |||
| 1970 | 1989 | 1970 | 1989 | ||
| Весь мир | 135,8 | 3693 | 5201 | 27 | 38 |
| Европа | 10,5 | 642 | 701 | 61 | 67 |
| Австралия и Океания | 8,5 | 19 | 26 | 2 | 3 |
| Африка | 30,3 | 361 | 628 | 12 | 21 |
| Южная Америка | 17,8 | 190 | 291 | 11 | 16 |
| Северная и Центральная Америка | 24,3 | 320 | 422 | 13 | 17 |
| Азия | 44,4 | 2161 | 3133 | 49 | 71 |
| Минимальная плотность населения: | =МИН(E3:E9) | =МИН(F3:F9) | |||
| Максимальная плотность населения: | =МАКС(E3:E9) | =МАКС(F3:F9) | |||
| Суммарная площадь всех континентов | =СУММ(В3:В9) |
IV. Этап усвоения и закрепления материала.
1. Выполнение индивидуальных работ (15 вариантов). Используется Задачник-практикум Семакин И.Г., Хеннер Е.К. Индивидуальная работа № 1 Варианты: 1-15
Примечание. Класс делится на две группы: одна группа выполняет задание в тетради, а вторая решает задачу на компьютере, затем меняются.
Сохраните файл под именем Работа 1 Вариант (свой)
V. Подведение итогов урока.
1) Оценить работу класса и отдельных учащихся.
2) Домашнее задание:
В тетради подготовить кроссворд по данной теме.
Найти площадь круга и длину окружности, если известен радиус (4 см)
Источник
Расчет относительных величин, используя MS Excel



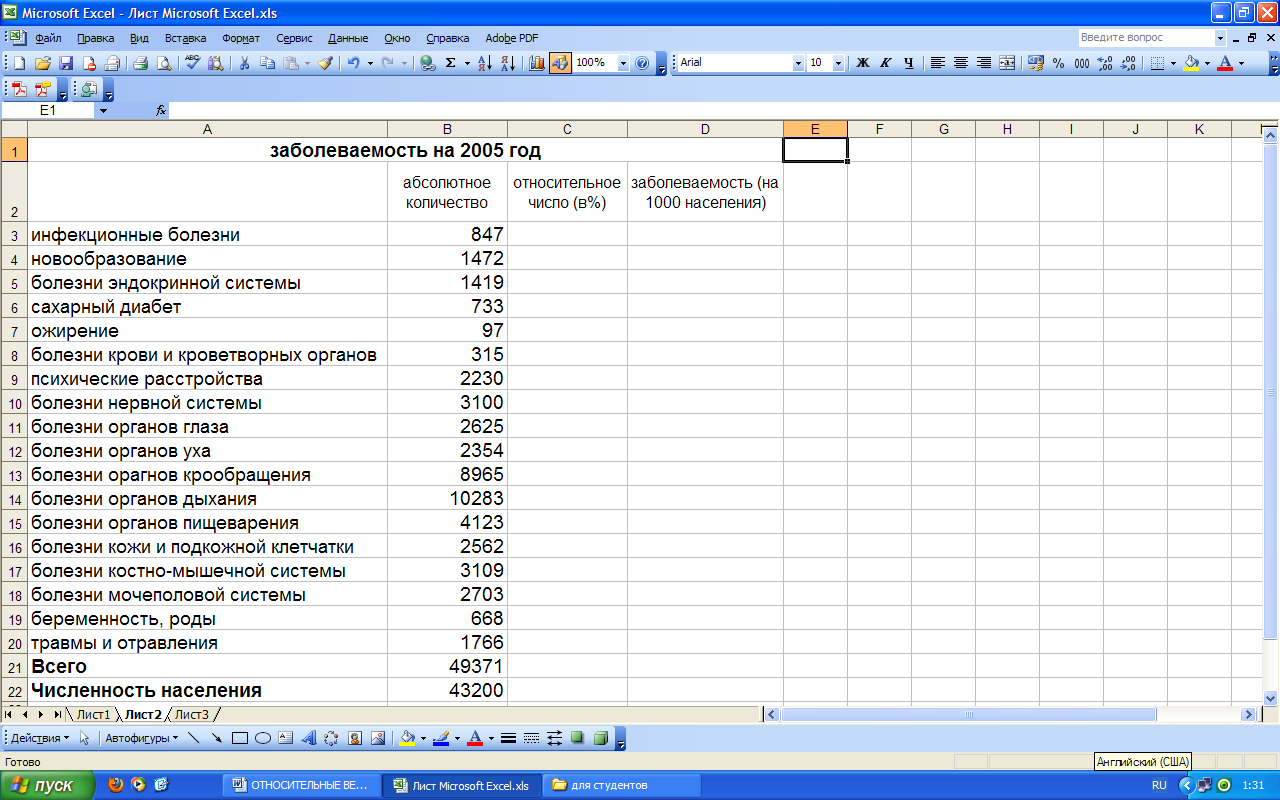
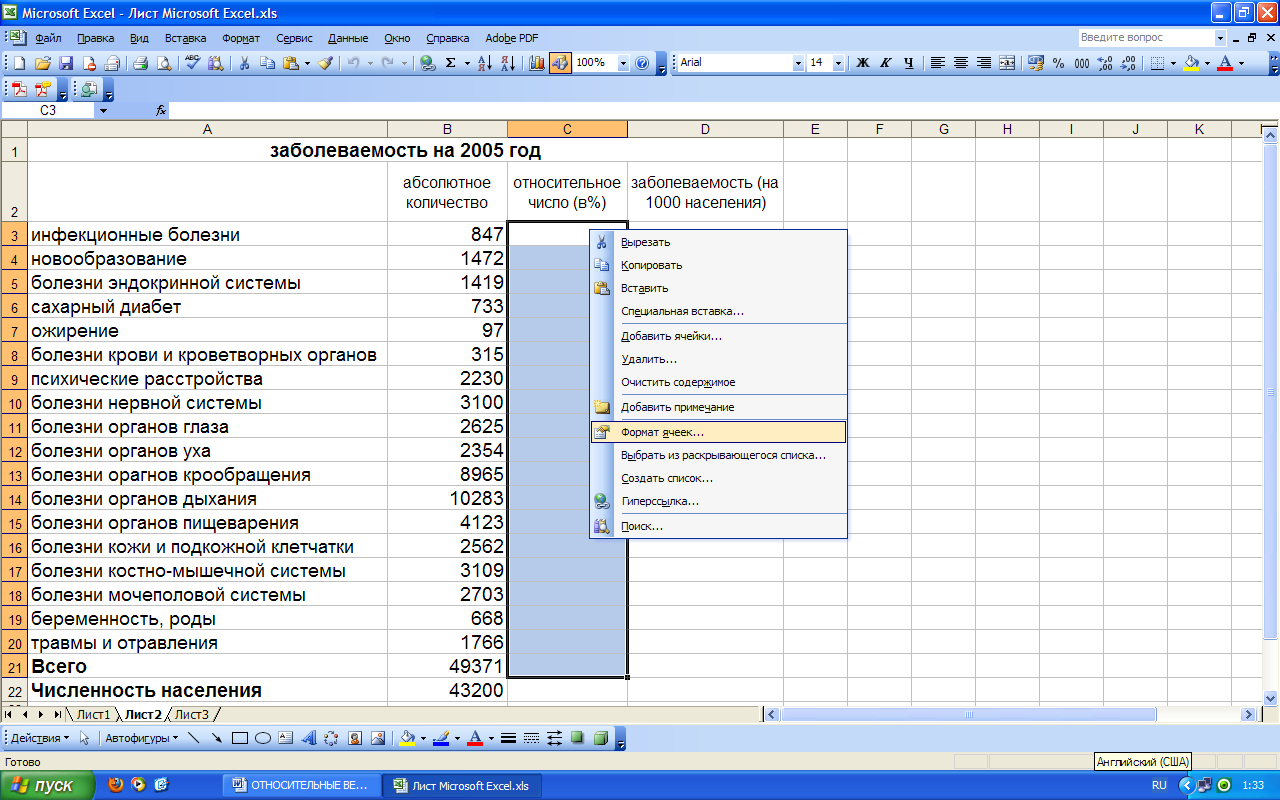
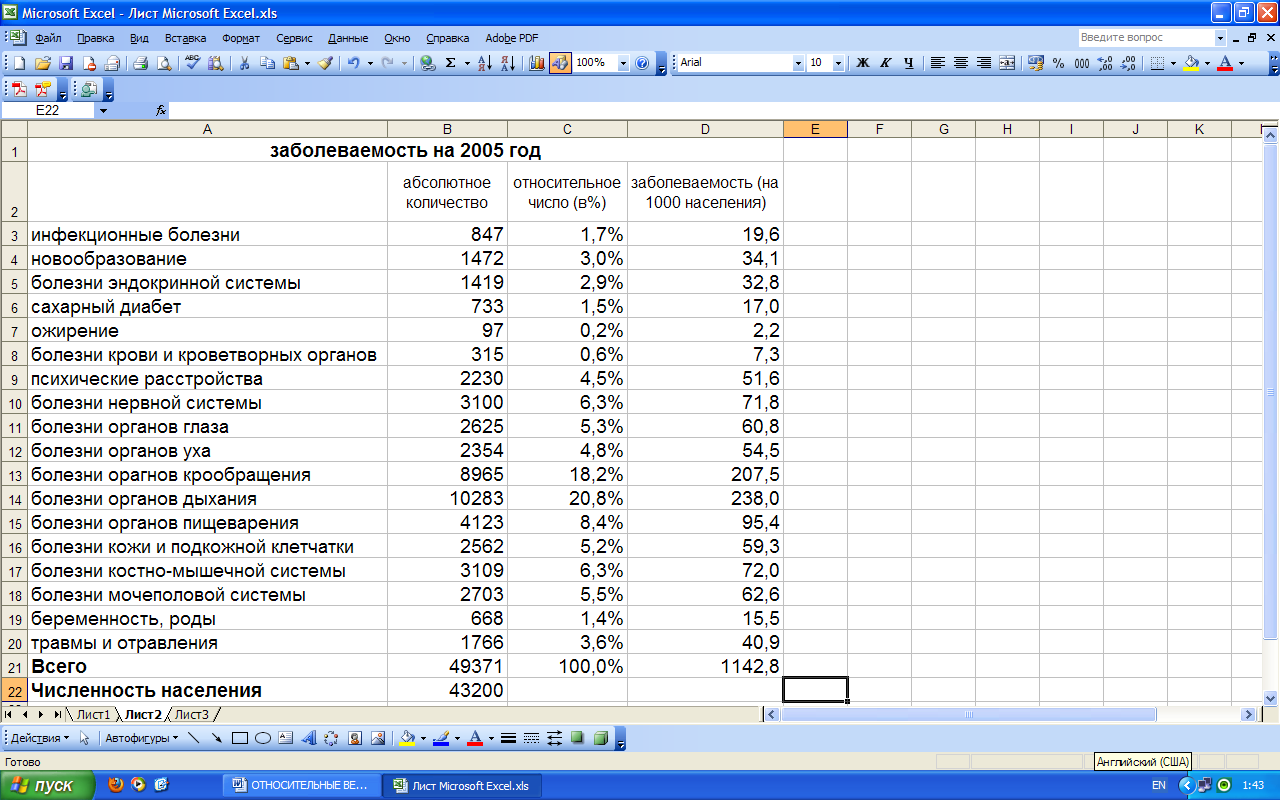
В качестве примера рассмотрим расчет структуры первичной заболеваемости (в %) и первичной заболеваемости (на 1000 населения) сельского административного района в электронных таблицах Excel. после ввода первичных данных – абсолютного количества заболеваний (Рис. 1) – с помощью мыши выделяем ячейки С3:С21 и нажатием на правую кнопку мыши вызываем контекстное меню, в котором выбираем пункт «Формат ячеек» (Рис. 2).
Рис. 1. Таблица с введенными данными количества первичных заболеваний
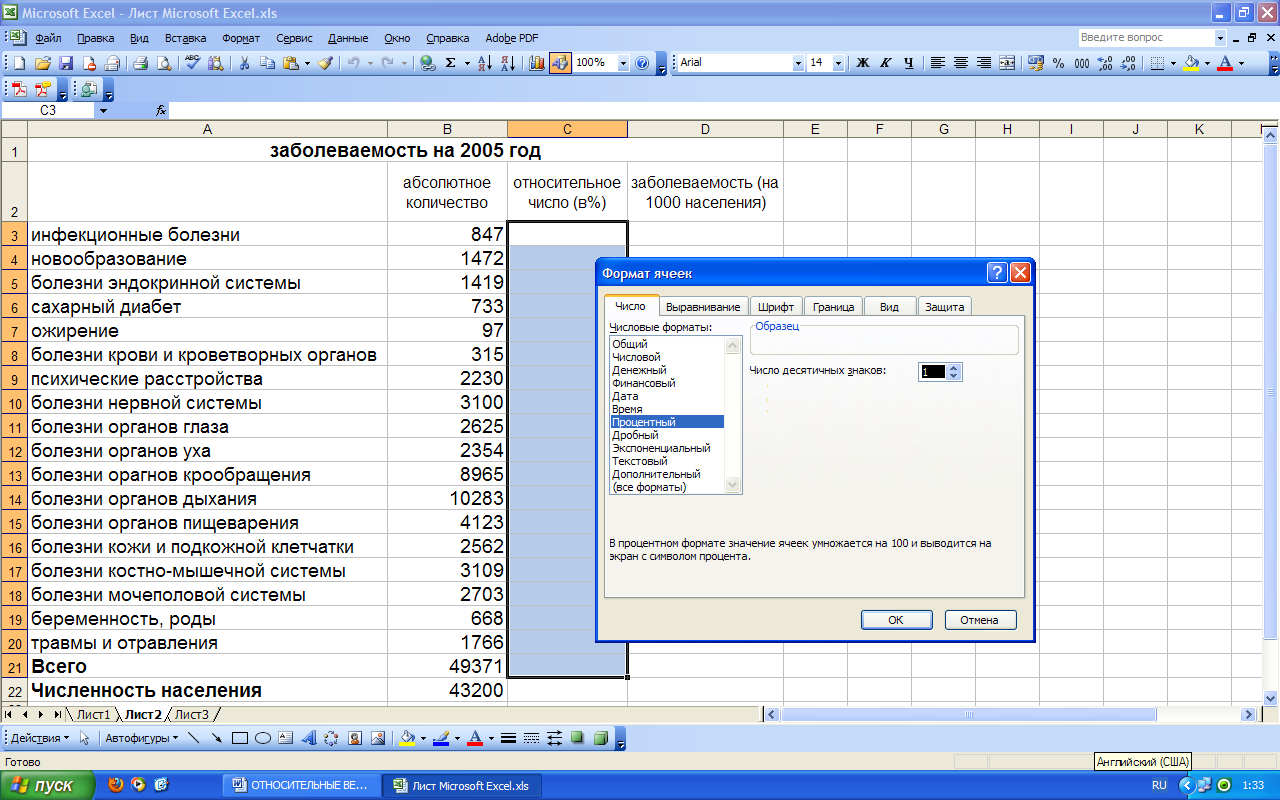
Рис. 2. Выбор пункта «Формат ячеек» в контекстном меню
Далее в подразделе «Число» выбираем процентный формат ячеек и устанавливаем необходимое количество знаков после запятой (Рис. 3), после чего нажимаем кнопку ОК.
Рис. 3. Установка процентного формата ячеек
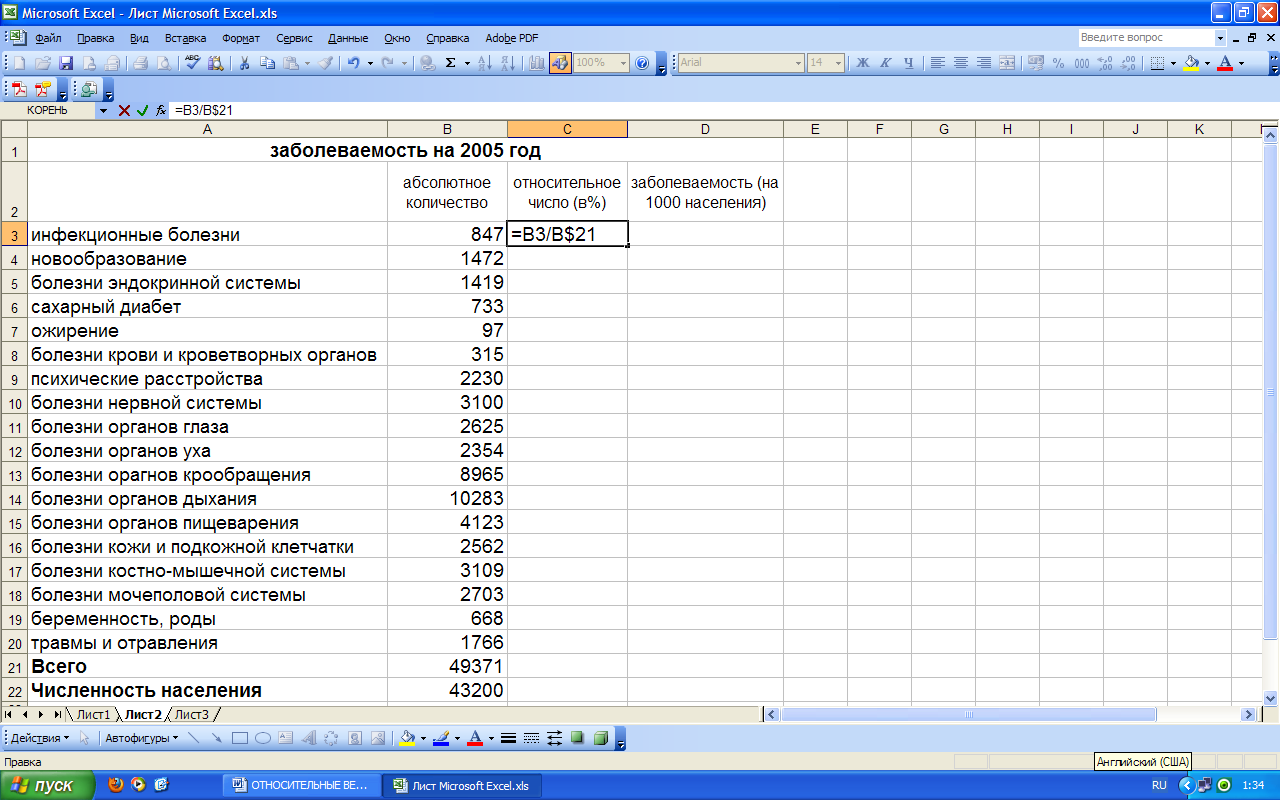
В ячейку С3 вводим формулу деления количества инфекционных болезней на обще количество заболеваний В3/В$21 (знак $ означает неизменный адрес строки) и нажимаем клавишу ввода. В ячейке появляется результат, представляющий процентную (%) долю инфекциооных заболеваний в общем количестве заболеваний (Рис.4).
Рис. 4. Ввод формулы в ячейку
Далее устанавливаем курсор на ячейку С3 с формулой и копируем ее содержимое, вызвав контекстное меню нажатием правой кнопки мыши и выбрав соответствующий пункт. выделяем мышью ячейку С3:С21 и вводим в них скопированную формулу, используя пункт «Вставить» главного меню или контекстного меню, вызванного нажатием правой кнопки мыши. после нажатия клавиши ввода получаем заполненный столбец таблицы с результатами расчета структуры заболеваемости (в %) (экстенсивные показатели).
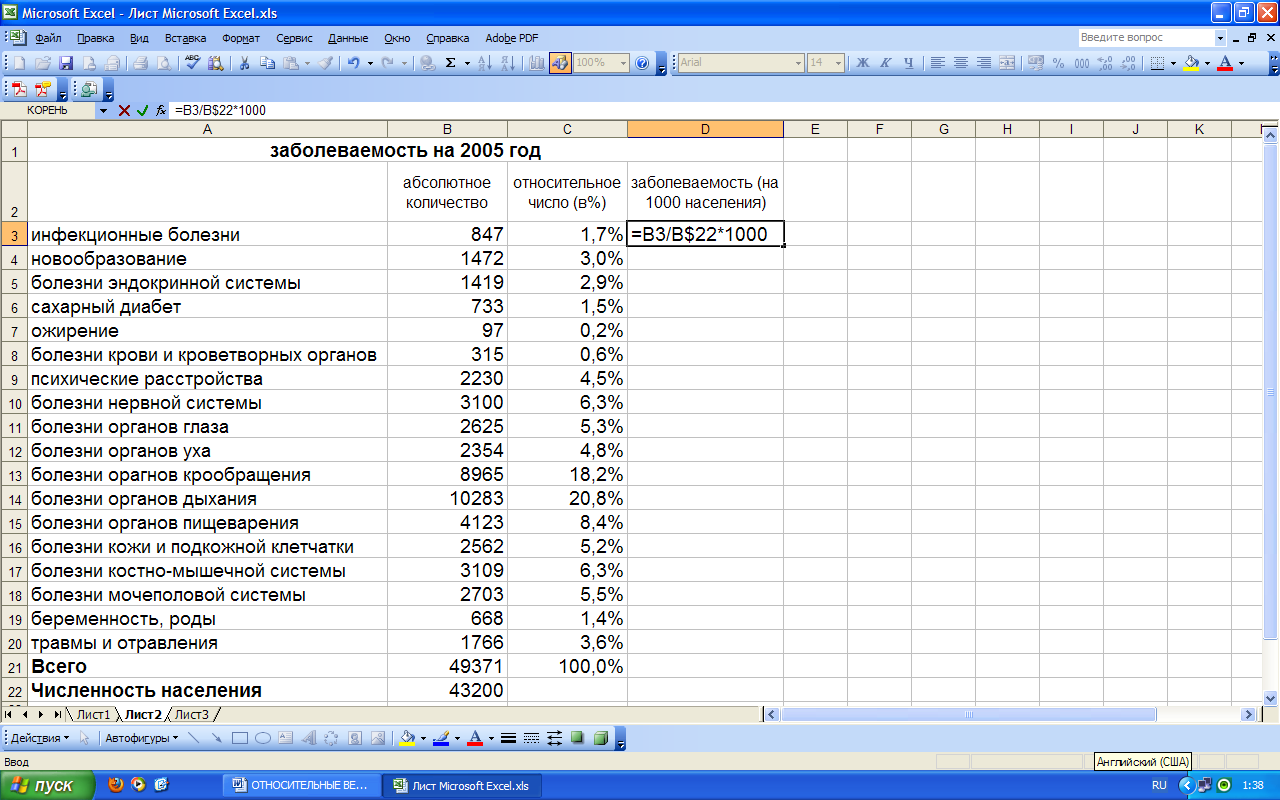
Для расчета интенсивных показателей заболеваемости на 1000 населения выделяем и форматируем ячейки D3:D21 в числовом формате и вводим в ячейку D3 формулу расчета для инфекционных болезней деление абсолютного числа заболеваний на общее число жителей района, умноженное на 1000 (В3/В$22*1000) (Рис. 5).
Рис. 5. Ввод формулы показателя заболеваемости на 1000 населения
Рис. 6. Результаты расчетов показателей заболеваемости
Как это было описано выше, формула копируется в остальные ячейки, что позволяет автоматически получить результаты расчетов (рис. 6).
КОНТРОЛЬНЫЕ ВОПРОСЫ:
· Перечислите виды относительных величин.
· Какие виды диаграмм применяются при графическом изображении структуры статистической совокупности?
· Что следует понимать под «средой», а что под «явлением» при анализе показателя «заболеваемость»?
· Какое правило необходимо соблюдать при расчете удельного веса каждого составляющего элемента всей совокупности в целом?
· Какой показатель отражает увеличение или уменьшение заболеваемости за 10-летний период?
· Какой показатель характеризует частоту явления в среде?
· В чем различия показателей соотношения и интенсивности?
· Какие бывают ошибки при использовании относительных величин?
· Какими данными нужно располагать для расчета интенсивного показателя?
· Какая ошибка допущена в выводе по имеющимся данным в ниже приведенной таблице?
Динамика заболеваемости гриппом в городе Н. за 2010—2011 гг.
| Показатели | 2010 г. | 2011 г. |
| Интенсивные | 30% | 50% |
| Экстенсивные | 20% | 15% |
Вывод. Заболеваемость гриппом в городе Н. в 2011 г. снизилась.
ТЕСТОВЫЕ ЗАДАНИЯ:
Выберите один или несколько правильных ответов:
1. Относительные величины используются для:
а) анализа состояния здоровья населения;
б) анализа качества оказываемой медицинской помощи;
в) анализа эффективности профилактических мероприятий;
г) сравнения абсолютных размеров явления в различных совокупностях;
д) выявления закономерностей изучаемого явления.
2. Интенсивные показатели используются для:
а) сравнения различных совокупностей;
б) характеристики структуры изучаемой совокупности;
в) оценки динамики изучаемого явления;
г) выявления закономерностей в течении различных заболеваний.
3. Показатели соотношения используются для:
а) расчета обеспеченности населения различными видами медицинской помощи (кадры, ЛПУ);
б) расчета частоты возникновения заболеваний;
в) расчета структуры изучаемой совокупности.
4. Экстенсивные показатели используются для:
а) сравнения различных совокупностей;
б) характеристики структуры изучаемого явления;
в) характеристики удельного веса составляющих признаков в изучаемой совокупности.
5. Показатели наглядности применяются для:
а) оценки динамики изучаемого процесса;
б) сравнения размеров признака в изучаемых совокупностях;
в) расчетов обеспеченности населения медицинской помощью;
г) оценки структуры совокупности.
6. Для сопоставления различных совокупностей можно использовать показатели:
а) интенсивные;
б) экстенсивные;
в) наглядности;
г) соотношения.
7. Обеспеченность населения койками — это показатель:
а) интенсивный;
б) наглядности;
в) соотношения;
Г) экстенсивный.
8. Распределение населения города Н. по возрастным группам это показатель:
а) наглядности;
б) соотношения;
в) интенсивный;
г) экстенсивный.
9. Заболеваемость студентов желудочно-кишечными заболеваниями за определенный период (год) — это показатель:
а) экстенсивный;
б) наглядности;
в) соотношения;
г) интенсивный.
СИТУАЦИОННЫЕ ЗАДАЧИ:
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
17 авг. 2022 г.
читать 2 мин
Дисперсия — это способ измерения разброса значений в наборе данных.
Формула для расчета дисперсии населения :
σ 2 = Σ (xi – μ) 2 / N
куда:
- Σ : символ, означающий «сумма».
- μ : Среднее значение населения
- x i : i -й элемент из совокупности
- N : Численность населения
Формула для расчета выборочной дисперсии :
s 2 = Σ (x i – x ) 2 / (n-1)
куда:
- x : выборочное среднее
- x i : i -й элемент из выборки
- n : размер выборки
Мы можем использовать формулы VAR.S() и VAR.P() в Excel, чтобы быстро вычислить выборочную дисперсию и дисперсию генеральной совокупности (соответственно) для заданного набора данных.
В следующих примерах показано, как использовать каждую функцию на практике.
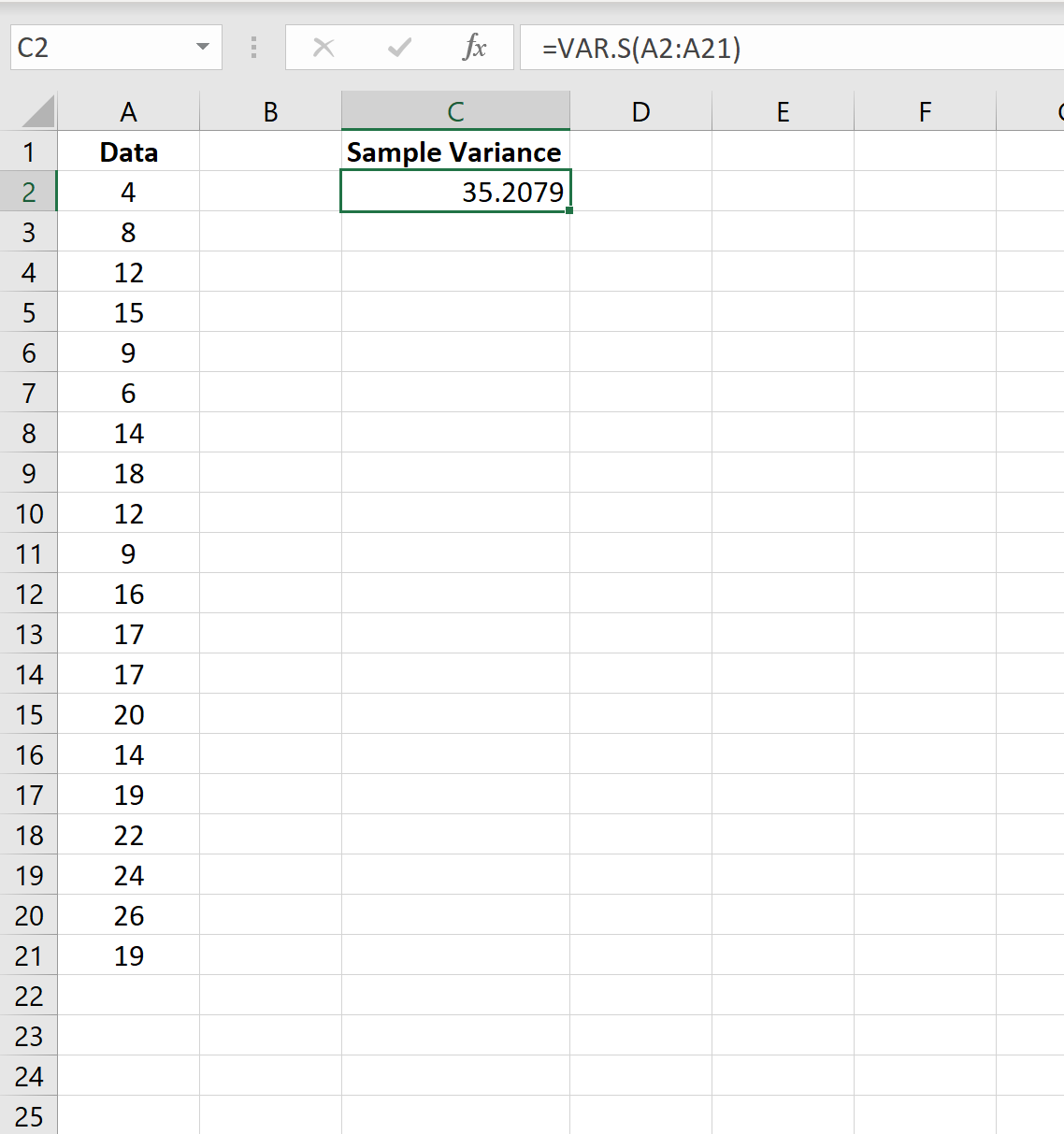
Пример 1: Расчет выборочной дисперсии в Excel
На следующем снимке экрана показано, как использовать функцию VAR.S() для расчета выборочной дисперсии значений в столбце A:
Выборочная дисперсия оказывается равной 35,2079 .
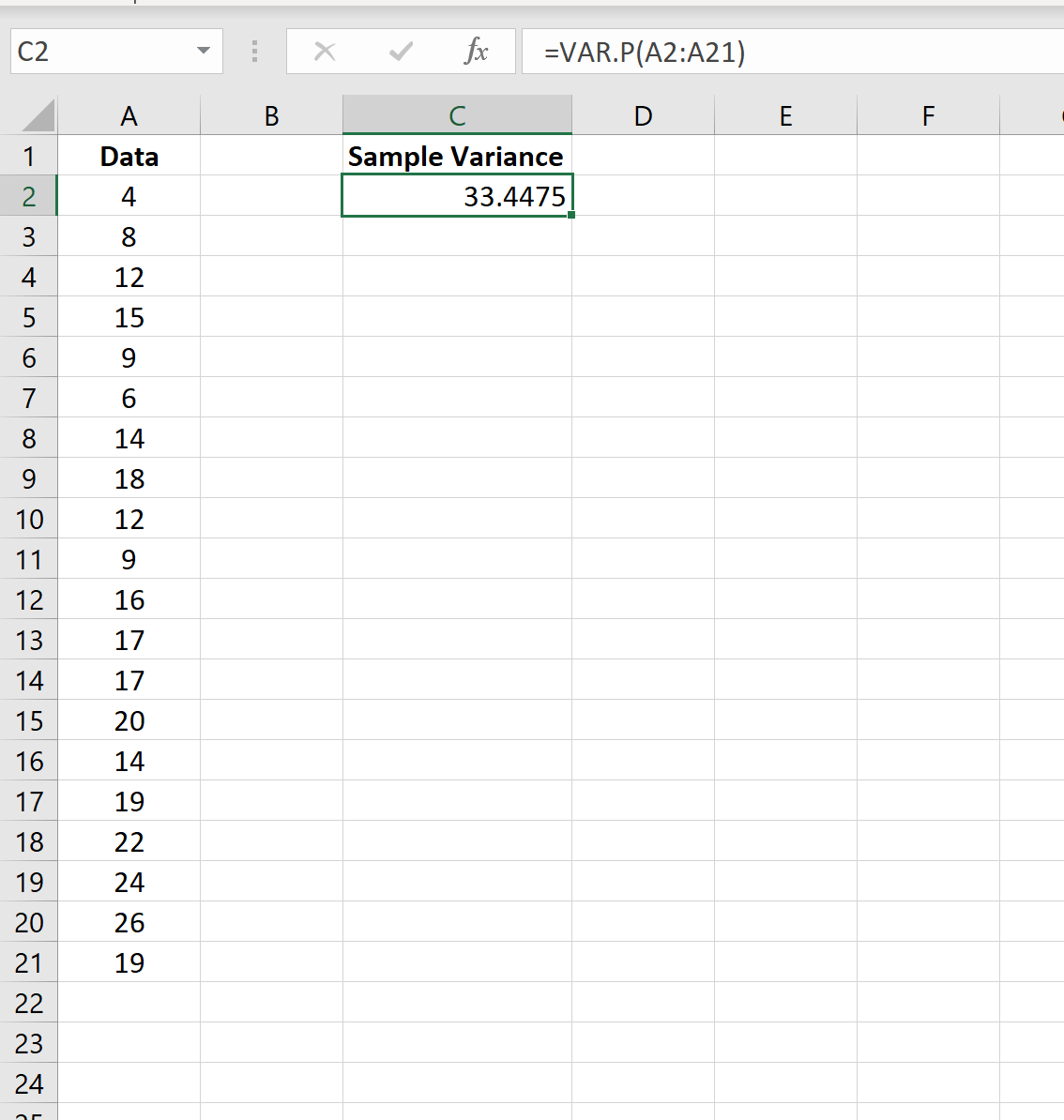
Пример 2: Расчет дисперсии населения в Excel
На следующем снимке экрана показано, как использовать функцию VAR.P() для расчета дисперсии совокупности значений в столбце A:
Дисперсия населения оказывается равной 33,4475 .
Примечания по расчету выборки и дисперсии генеральной совокупности
При расчете дисперсии выборки и генеральной совокупности следует учитывать следующее:
- Вы должны вычислить дисперсию совокупности , когда набор данных, с которым вы работаете, представляет всю совокупность, то есть каждое значение, которое вас интересует.
- Вы должны рассчитать выборочную дисперсию , когда набор данных, с которым вы работаете, представляет собой выборку, взятую из большей интересующей совокупности.
- Выборочная дисперсия набора данных всегда будет больше, чем дисперсия генеральной совокупности для того же набора данных, потому что при расчете дисперсии выборки больше неопределенности, поэтому наша оценка дисперсии будет больше.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать другие показатели спреда в Excel:
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать взвешенное стандартное отклонение в Excel
Как рассчитать коэффициент вариации в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
«Slicing» — это то, где вы назначаете объект производного класса экземпляру базового класса, тем самым теряя часть информации — часть его «нарезана».
Например,
class A {
int foo;
};
class B : public A {
int bar;
};
Итак, объект типа B имеет два элемента данных: foo и bar.
Тогда, если вы должны были написать это:
B b;
A a = b;
Затем информация в b о члене bar теряется в a.
задан player0 24 March 2019 в 16:38
поделиться
Урок №8.
ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННОЙ ТАБЛИЦЫ ДЛЯ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Цель работы:
- научиться использовать электронные таблицы для выбора оптимального решения поставленной задачи и проверки правильности построения математической модели.
Электронная таблица выполняет не только функцию автоматизации вычислений. Она является очень эффективным средством проведения численного моделирования ситуации или объекта, для математического описания которых (т.е. построения математической модели) используется ряд параметров. Часть этих параметров известна, а часть рассчитывается по формулам. Меняя во всевозможных сочетаниях значения исходных параметров, вы будете наблюдать за изменением расчетных параметров и анализировать получаемые результаты. Excel производит такие расчеты быстро и без ошибок, предоставляя в считанные минуты множество вариантов решения поставленной задачи, на основании которых вы выберите наиболее приемлемое. Поиск решения и моделирование — одни из самых мощных инструментов Excel.
В данной работе рассматриваются две задачи.
ЗАДАЧА № 1
Чему будет равна численность населения России в начале третьего тысячелетия?
Сразу ясно, что задачу не решить, если не знать, как со временем будет меняться численность населения России, т.е. необходимо иметь функцию, выражающую зависимость численности населения от времени. Обозначим эту функцию f(t). Но такая функция неизвестна, так как народонаселение зависит от многих факторов: экологии, состояния медицинского обслуживания, морали, права и даже от политической обстановки. Но, общие демографические данные, можно указать общий вид функции f(t).
f(t) = a*eb-1. (1)
где коэффициенты а, b для каждого государства свои; е — основание натурального логарифма.
Эта формула лишь приближенно отражает реальность. Однако слишком большая точность и не нужна. Будет хорошо, если численность населения будет спрогнозирована с точностью до нескольких миллионов.
Как же определить а и b ? Идея состоит в том, что хотя а и b не известны, значение функции f(t) можно получить из статистического справочника. Зная эти данные, можно приближенно подобрать а и b так, чтобы теоретические значения f(t), вычисленные по формуле (1), не сильно отличались от данных справочника (т.е. максимальное отклонение теоретических результатов от фактических данных не должно быть слишком большим). Каждое из отклонений — это модуль разности двух чисел: фактического и соответствующего теоретического значений f(t). Максимальное отклонение называют погрешностью. Необходимо найти такие а и b, чтобы погрешность была наименьшей.
Итак, математическая модель процесса изменения численности населения такова. Предполагается, что:
I) зависимость численности населения от времени выражается формулой f(t) = a*eb-1.
2a =const и b=const, следует считать справедливым лишь для не очень большого промежутка времени (например, 40 лет);
3)значения а и b можно найти с достаточной точностью, минимизировав погрешность.
Исходные данные: сведения из статистического справочника за период с 1960 по 1995 г. (60<=t<=95).
Результаты:
1)значения а и b.
2) численность населения России в 2000 г. (при t=100).
Кроме того, установлена связь между исходными данными и результатами: сначала надо найти а и b, минимизируя погрешность, а затем при этих a и b вычислить значения f(100).
Итак, математическая модель составлена. Использование электронной таблицы освобождает нас от составления программы. Нужно только определенным образом записать в таблицу исходные данные и математические соотношения, входящие в модель. После этого можно начать процесс численного моделирования исследуемой ситуации, т.е. подбор коэффициентов а и b в формуле (1), а затем определение численности населения.
ХОД РАБОТЫ
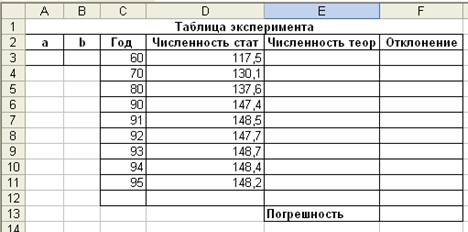
ЗАДАНИЕ 1. Заполните таблицу.
1.1. Сделайте заголовок и заполните шапку таблицы.
1.2. Столбцы А и В отведите под коэффициенты а и b соответственно.
1.3. В столбец С занесите значения t с 1960 г.
1.4. В столбец D занесите взятые из справочника значения численности населения России с I960 г.
ЗАДАНИЕ 2. Подберите значения коэффициентов а и b.
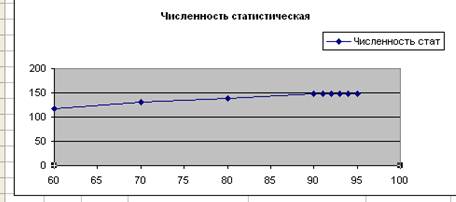
Следующий шаг в решении задачи — это вычисление теоретической численности по формуле (1), в которой не известны значения коэффициентов а и b. Подбор а и b можно произвести в два этапа. Сначала определим их значения приближенно, для чего построим график роста статистической численности и аппроксимируем его. Затем уточним полученные коэффициенты а и b с использованием функции Excel Поиск решения.
2.1.Постройте график типа X-Y по данным таблицы. (Х-годы; Y- статистическая численность).
2.2. Перемасштабируйте оси Х и Y.
Для более наглядного представления данных необходимо перемасштабировать оси.
- Выделите ось X.
- Вызовите контекстно-зависимое меню и выполните команду: Формат оси — Шкала
- Установите минимальное значение X, основную единицу измерения и пересечение с осью У.
- Аналогично Перемасштабируйте ось Y.
2.3. Аппроксимируйте полученную кривую.
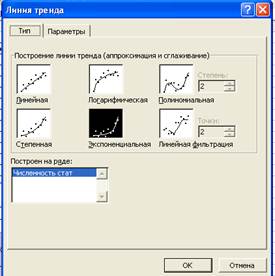
Необходимо статистические данные по численности населения представить на графике плавной кривой (аппроксимировать). Эта кривая называется линией тренда. Для построения линии тренда:
- Выделите линию графика.
- Выполните команду меню Диаграмма Добавить линию тренда или аналогичную команду контекстно-зависимого меню.
Откроется диалог Линия тренда.
- Выберите экспоненциальный тип (см. формулу (1)).
- Выберите в диалоге Линия тренда вкладку Параметры.
- Установите флажок (*) Показывать уравнение на диаграмме и нажмите кнопку ОК.
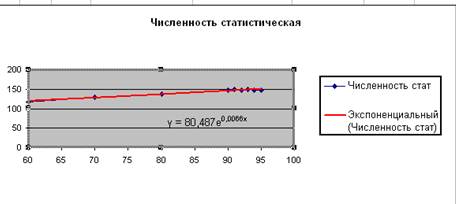
В результате на графике появится линия тренда и уравнение с подобранными коэффициентами а и b.
2.4. Занесите полученные значения коэффициентов а и b в ячейки A3 ВЗ и присвойте им имена:
A3 имя а
ВЗ имя b
Коэффициенты а и b не изменяются с течением времени, это константы, следовательно, при вычислении теоретической численности они должны быть адресованы абсолютно.
ЗАДАНИЕ 3. Вычислите теоретическую численность по формуле(1).
3.1. В ячейку ЕЗ занесите формулу =а *ЕХР(b * СЗ)
3.2.Скопируйте формулу в ячейки Е4:Е11
ЗАДАНИЕ 4. Вычислите отклонение.
Отклонение — это модуль разности теоретических и фактических значений функции f(t)..
4.1. В ячейку F3 занесите формулу =ABS(E3- D3)
4.2. Скопируйте формулу в ячейки F4:F11
ЗАДАНИЕ 5. Вычислите погрешность.
Погрешность — это максимальное отклонение.
В ячейку F:13 введите функцию определения максимального из чисел этого столбца.
ЗАДАНИЕ 6. Подберите значения коэффициентов а и b более точно.
При полученных в результате аппроксимации коэффициентах а и b погрешность уже неплохая (по условию она должна быть в пределах нескольких миллионов). Но коэффициенты а и b можно подобрать более тонко, используя функцию Excel Поиск решения. В отличие от Подбора параметра Поиск решения может для достижения нужного результата изменять или подбирать подходящие значения во многих ячейках.
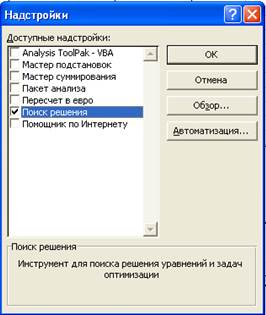
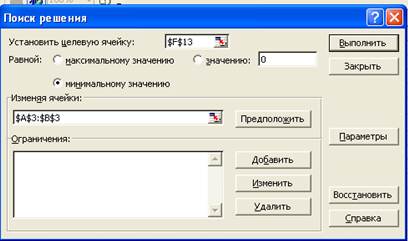
6.1. Выполните команду: Сервис — Поиск решения
Если этого пункта в меню нет, то его следует загрузить, выполнив команду меню Сервис – Настройки.. В открывшемся диалоговом окне следует поставить флажок (*) около дополнения Поиск решения.
6.2. Сделайте необходимые настройки в окне диалога Поиск решения
В поле Установить целевую ячейку укажите адрес ячейки $F$13 (в ней погрешность).
- Установите переключатель(*) минимальному значению
- В поле Изменяя ячейки укажите $А$3:$В$3
В этом поле задаются адреса ячеек, значения которые, будут варьироваться в процессе поиска решения. В нашем случае — это адреса ячеек со значениями a и b.
- Нажните на кнопку <Выполнить>.
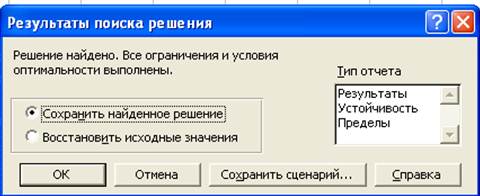
Начнется поиск решения. Так как у нас довольно точные коэффициенты а и b, то поиск займет немного времени. Когда Excel найдет решение, то откроется диалог, представленный на рисунке.
Поиск свелся к текущему решению. Все ограничения выполнены.
- Нажмите на кнопку <ОК>.
Произойдет изменение значений ячеек в соответствии с найденным решением. Обратите внимание, что коэффициенты а и b изменились, а погрешность уменьшилась.
ЗАДАНИЕ 7. Определите численность населения России в 2000 г.
7.1. Подставьте в ячейку С12 число 100, что соответствует 2000 г.
7.2. В Е12 скопируйте формулу из Е11. В ячейке Е12 появится искомое число.
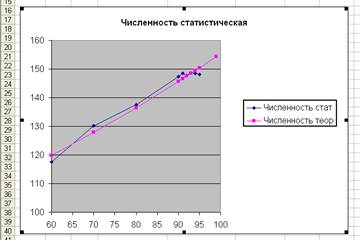
ЗАДАНИЕ 8.Построите на одной диаграмме совмещенные графики роста численности населения на основе статистических и теоретических данных.
8.1.Выделите на построенном графике линию тренда и удалите ее, выполнив команду Очистить контекстно-зависимого меню линии тренда.
8.2. Добавьте в уже построенную диаграмму теоретические данные.
- В таблице эксперимента выделите теоретические данные Е2.Е12.
- Установите указатель мыши на правой границе выделенного блока.
- Нажмите левую кнопку мыши и прибуксируйте данные на диаграмму.
- В появившемся окне сделайте настройку (если это необходимо).
8.3.Оформите диаграмму в соответствии с рисунком, где показан примерный вид графиков.
ЗАДАНИЕ 9. Оформите таблицу на свой вкус (обрамление, заполнение, шрифты).
ЗАДАНИЕ 10. Воспользуйтесь предварительным просмотром печати.
10.1. Разместите диаграмму на одном листе с таблицей.
10.2.Добейтесь хорошего расположения таблицы и диаграммы на листе.
10.3. Снимите сетку.
10 4.Установите верхний колонтитул: Численное моделирование. Работу выполнил <Фамилия и имя>. В нижнем колонтитуле укажите дату и время.
ЗАДАНИЕ 11. Сохраните файл в личном каталоге под именем work 8_1. xls
ЗАДАНИЕ 12. Распечатайте результаты работы на принтере.
ЗАДАНИЕ 13. Проанализировав данные таблицы и графика, сделайте вывод об адекватности предложенной математической модели реальному процессу (т.е. вывод о правильности описания роста населения формулой (1)).
ЗАДАНИЕ 14 (дополнительное).
Самостоятельно попробуйте выбрать для построения линии тренда другие типы, а соответственно и другие формулы для описания математической модели.
Предъявите преподавателю:
- файл work8_l.xls;
- распечатку результатов работы.
ЗАДАЧА № 2
Несколько человек решили организовать видеокафе на 6 столиков по 4 места за каждым. С каждого посетителя будет взиматься плата за сеанс видеофильма и ужин (всем посетителям будет предлагаться один и тот же набор блюд). Администрация города постановила, что плата за вход не должна превышать 5 $. Требуется определить такую входную плату, при которой будет получена наибольшая выручка.
Казалось бы, здесь и решать нечего. Разве не ясно, что чем больше входная плата, тем больше выручка. Вот и ответ: входная плата должна быть 5 $. Очень часто планирующие органы подобным образом и поступают. В нашем случае если сильно увеличить входную плату, то люди перестанут посещать кафе.
Начать надо, как всегда, с построения математической модели. В чем были причины нашей неудачи? Мы предположили, что посещаемость не зависит от входной платы, и получили модель задачи, не соответствующую действительности. Значит, надо предполагать, что посещаемость зависит от входной платы.
Обозначим входную плату через X. Тогда среднее число посетителей видеосалона является функцией от Х. Обозначим эту функцию через Р(Х). В задаче требуется найти такое значение А, при котором выручка, равная произведению входной платы на количество посетителей X* Р(Х), достигает максимума. Если бы функция Р(Х) была известна, то найти требуемый максимум не составило бы особого труда. Но эта функция не известна, поэтому попробуем найти хотя бы общий вид функции. Его можно указать, обобщив опыт работы подобных кафе:
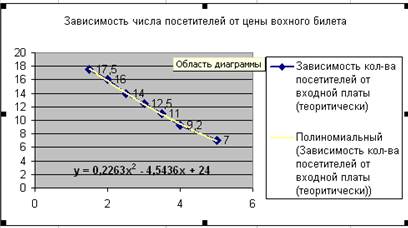
Р(Х) = ах2-bх + с. (2)
Коэффициенты a, b и с для каждого кафе свои. Как же их определить? Проще всего найти значение с. Представьте себе невообразимое — в видеокафе пускают бесплатно (т. е. Х=0). Ясно, что свободных мест не будет. Следовательно, P(0) равно числу мест в кафе. С другой стороны, подставив 0 вместо X, получим Р(0)=с. Значит, с равно количеству мест. В нашем случае с=24 (6 столиков по 4 места за каждым).
Определить а и b так же просто не удается. Справочников по посещаемости видеокафе еще нет. Поэтому здесь требуется эксперимент.
Достаточно открыть кафе и установить на некоторый срок (дней на десять) определенную плату за вход. Среднее число посетителей и даст нам (приближенное!) значение функции. Установив другую плату за вход, найдем приближенное значение Р(Х) при новом X, и так несколько раз.
Зависимость посещаемости от входной платы (на основе экспериментальных данных для конкретного кафе):
|
Входная плата |
Среднее число посетителей сеанса Р(Х) |
|
1 |
20 |
|
1,5 |
17,5 |
|
2 |
16 |
|
2,5 |
14 |
|
3 |
12,4 |
|
3,5 |
11 |
|
4 |
9,2 |
|
5 |
7 |
Пользуясь электронной таблицей, можно подобрать значения а и b способом, аналогичным описанному при решении задачи № 1,т.е. минимизацией погрешности между экспериментальной и теоретической выручкой. Затем можно определить, при какой входной плате выручка будет наибольшей.
ХОД РАБОТЫ:
ЗАДАНИЕ 1. Внимательно ознакомьтесь с постановкой задачи.
На каких предположениях строится математическая модель? Что является исходными данными? Что должно явиться результатом?
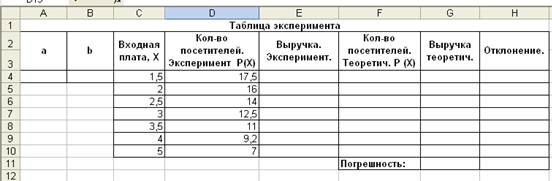
ЗАДАНИЕ 2. Заполните таблицу эксперимента.
2.1. Сделайте заголовок и заполните шапку таблицы.
2.2.Отведите столбцы А и В таблицы соответственно лад коэффициенты а и b.
2.3. В столбец С занесите данные по входной плате.
2.4.В столбец D занесите экспериментальные данные по среднему числу посетителей.
2.5. В столбце Е подсчитайте выручку на основе экспериментальных данных как произведение входной платы на количество посетителей.
ЗАДАНИЕ 3. Подберите приближенное значение коэффициентов а и b.
Подбор коэффициентов а и b выполняется аппроксимацией экспериментальных данных по аналогии с задачей 1.
3.1. Постройте диаграмму типа X-Y по экспериментальным данным.
(X — входная плата, Y- экспериментальные данные по количеству посетителей).=
3.2. Аппроксимируйте полученную кривую. При построении линии тренда следует выбрать полиномиальный тип (см. формулу (2)) и указать Y-пересечение = 24.
3.3. Занесите полученные значения коэффициентов а и b в таблицу.
ЗАДАНИЕ 4. Вычислите теоретическое количество посетителей и теоретическую выручку.
4.1. В столбце F вычислите по формуле (2) теоретическое количество посетителей, причем, как объяснялось выше, С=24.
4.2. В столбце G вычислите теоретическую выручку.
ЗАДАНИЕ 5. Вычислите отклонение между экспериментальной и теоретической выручкой и погрешность.
5.1.В столбце Н вычислите отклонение между экспериментальной и теоретической выручкой (аналогично заданию 4 в задаче 1).
5.2. В свободной ячейке столбца Н определите погрешность
(аналогично заданию 5 в задаче 1).
ЗАДАНИЕ 6. Подберите коэффициенты а и b, стараясь минимизировать погрешность (аналогично заданию 5 в задаче 1).
ЗАДАНИЕ 7. Постройте графики.
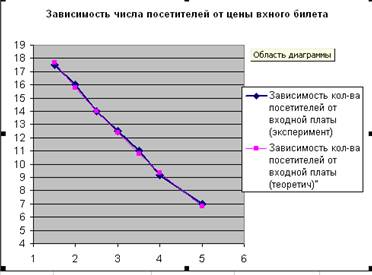
7.1.Постройте на одной диаграмме два графика типа Х-Y (экспериментальный и теоретический) зависимости количества посетителей от входной платы P(Х) (аналогично заданию 8 в задаче 1).
7.2. Разместите диаграмму на одном листе с таблицей и оформите, как показано на рисунке.
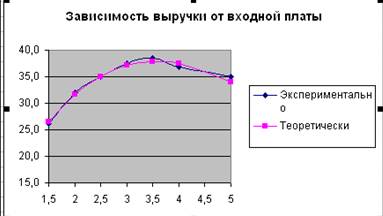
7.3.Постройте на одной диаграмме два графика типа X-Y (экспериментальный и теоретический) зависимости выручки от входной платы X.
7.4. Разместите диаграмму на том же листе и оформите, как показано на рисунке.
ЗАДАНИЕ 8. Определите, при какой входной плате выручка будет максимальна.
Каково среднее число посетителей сеанса при найденной оптимальной входной плате?
ЗАДАНИЕ 9. Оформите таблицу на свой вкус (обрамление, заполнение, шрифты).
ЗАДАНИЕ 10. Воспользуйтесь предварительным просмотром печати.
10.1. Добейтесь хорошего расположения таблицы и двух диаграмм на листе.
10.2. Снимите сетку.
10.3.Установите верхний колонтитул: Численное моделирование. Работу выполнил <Фамилия и имя>. В нижнем колонтитуле укажите дату и время.
ЗАДАНИЕ 11.Сохраните файл в личном каталоге под именем work8_2.xls
ЗАДАНИЕ12. Распечатайте результат работы на принтере.
ЗАДАНИЕ 13. Проанализировав данные таблицы эксперимента и график, сделайте выводы об адекватности предложенной математической модели.
ЗАДАНИЕ 14.(дополнительное) Самостоятельно попробуйте выбрать для построения линии тренда другие типы, а соответственно и другие формулы для описания математической модели.