Построить таблицу
значений периметра и площади прямоугольного
треугольника при изменении длин его
катетов от 1см до 10см с шагом 1см.
Периметр
прямоугольного треугольника вычисляется
по формуле:
где a,b,
— катеты, c
–гипотенуза, которая вычисляется по
формуле:
Площадь прямоугольного
треугольника вычисляется по формуле:
Для решения задачи
построим шапку таблицу:
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
4
Теперь занесем
формулы. В столбец А
занесем значения катета a=1,
в столбец
В – значения
катета b
от 1до 10 с шагом 1.
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
1
1
4
1
2
5
1
3
6
1
4
7
1
5
8
1
6
9
1
7
10
1
8
11
1
9
12
1
10
В ячейку С3
запишем формулу, вычисляющую гипотенузу:
=КОРЕНЬ(А3^2+B3^2),
в ячейку D3
запишем формулу: =A3+B3+C3,
в ячейку
E3
запишем формулу:
=(1/2)*A3*B3
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
1
1
=КОРЕНЬ(А3^2+B3^2)
=A3+B3+C3
=(1/2)*A3*B3
4
1
2
…
12
1
10
Теперь скопируем
формулы третьей строки во все остальные
строки
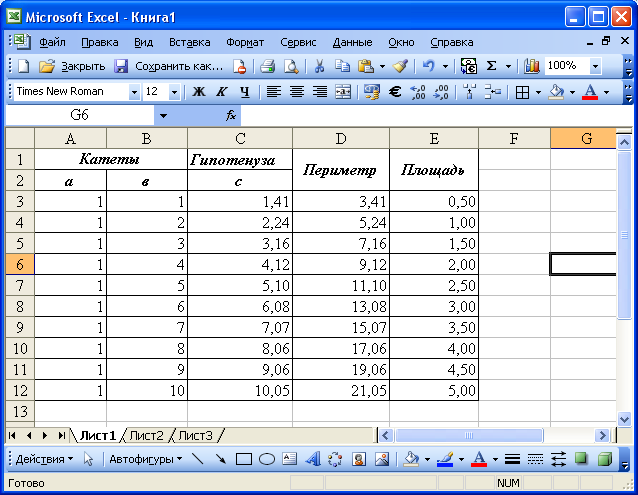
(Рис. 89.). Отформатируем формат
представления чисел до 2 знаков после
запятой.
Заметим, что во
всех формулах используются относительные
адреса ячеек.
Рис. 89. Решение
задачи 2
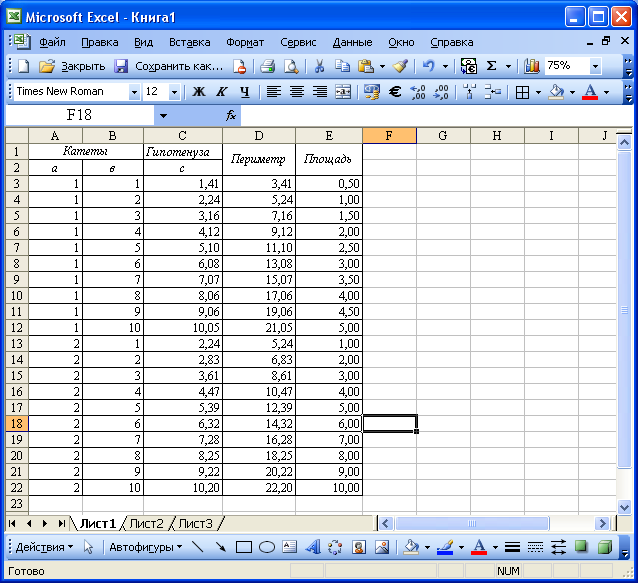
Теперь добавим
строки, в которых катет a
будет равен 2 (Рис. 90.), не забывая копировать
в них формулы.
Рис. 90. Решение
задачи 2 с добавление данных
Так же можно
добавить строки с другими значениями
катета a.
Соседние файлы в предмете Информатика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Расчёт периметра формулой массива |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Для квадрата со стороной a периметр P можно
вычислить с помощью следующих формул
Переходим к
формулам для двух огородов в форме прямоугольников. Обозначим через b меньшую сторону прямоугольника, а через q отношение его сторон (для первого прямоугольника q=2, для второго – q=3).
Тогда формулы для вычисления периметра в случае прямоугольника можно записать
так
Рассмотрим теперь формулы для выбора самого короткого забора вокруг
четырех огородов. Пусть i – порядковый номер огорода, Pi – периметр i — го
огорода, Pmin – искомый минимальный
периметр. Тогда можно написать формулу
Обозначим буквой T – форму огорода с
самым коротким забором и напишем формулу для ее автоматического вычисления
Легко проверить, что условия задачи позволяют выполнить расчеты по
формулам (3.1)-(3.5) и найти решение поставленной задачи.
3.4. Описание решения задачи
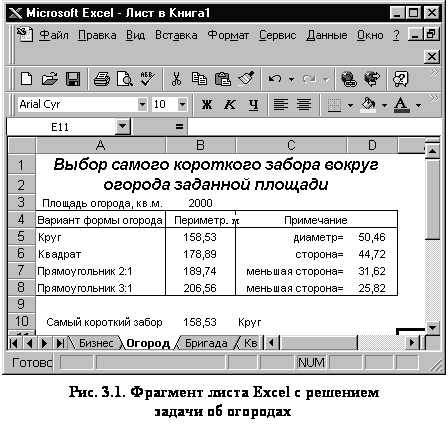
Фрагмент рабочего листа Excel с решением
задачи об огородах (см. рис. 3.1) дает пример возможного оформления результатов
вычислений.
 |
Ввод и форматирование заголовка произведено так, как описано в
задачах о платежной ведомости и об оптимальном бизнесе. Заданная площадь
огородов введена в ячейку B3. Расчеты, связанные с
определением длины заборов вокруг огородов, представлены в табличной форме в
ячейках интервала A4:D8. Первая
колонка таблицы представляет варианты формы огородов. Длина заборов (периметры),
вычисленная по формулам (3.1)-(3.3), видна во втором столбце таблицы.
Вспомогательные величины вычислены в ячейках интервала D5:D8 и вместе с кратким пояснением в ячейках C5:C8 образуют третий столбец таблицы (см. рис. 3.1). Например,
для квадрата в ячейку D6 введена формула =КОРЕНЬ(B3), обеспечивающая вычисление стороны, а в ячейку B6 формула =4*D6 для вычисления
периметра. Копирование этих формул в другие ячейки не производилось, поэтому в
них можно использовать ссылки на ячейки любого типа. Основу указанных двух
формул составляют формулы (3.2) из подраздела 3.3.
Наибольший интерес представляют формулы в ячейках B10
и C10. В ячейку B10 введена
формула =МИН($B$5:$B$8),
реализующая вычисление минимального периметра Pmin
по формуле (3.4). Более сложна формула в ячейке C10
=ЕСЛИ(B5=B10;A5;ЕСЛИ(B6=B10;A6;ЕСЛИ(B7=B10;A7;A8)))
Она реализует выбор варианта формы огорода с минимальным периметром
в точном соответствии с формулой (3.5). Пояснения по использованию логической
функции ЕСЛИ имеются в подразделе 2.4.
3.5. Выводы
Результаты решения задачи соответствуют известному математическому
факту: чем более «правильную» форму имеет плоская фигура заданной площади, тем
меньше ее периметр. Периметры огородов в форме круга, квадрата и двух прямоугольников
(см. рис. 3.1) увеличиваются по мере уклонения их формы от «правильной».
Наименьший периметр 158,53 м имеет огород в форме круга. Наибольший периметр
206,56 м у прямоугольника с отношением сторон 3:1. Следовательно, по
сравнению с круглым огородом забор для второго прямоугольного огорода на
48,03 м длиннее. Соответственно увеличиваются затраты на его
строительство.
На практике круглые огороды не очень распространены. Поэтому из
трех других вариантов формы следует выбрать квадрат, у которого периметр
меньше, чем у остальных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.
-
Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
-
НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
Использование статистических функций
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
СРЗНАЧ
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
МАКС
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
МИН
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.ОДН(число1;число2;…)
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)

Заключение
В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.
Практическая работа
Работа с формулами в Microsoft Excel
-
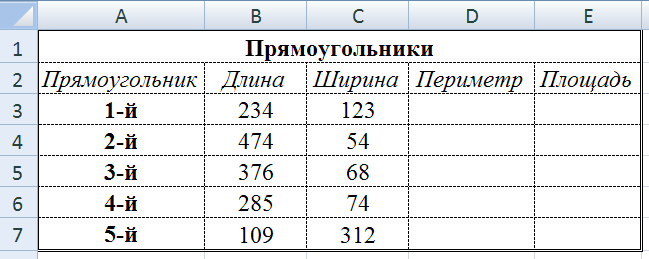
Периметр и площадь прямоугольника.
Создайте структуру таблицы по образцу. С помощью формул вычислите периметр и площадь прямоугольников.
-
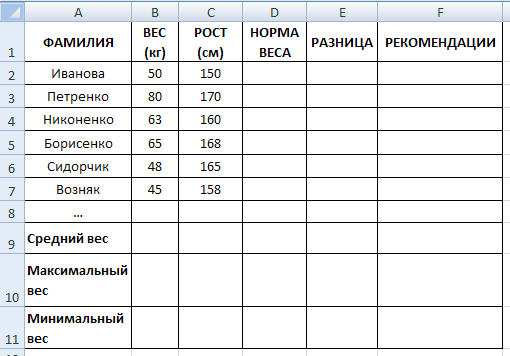
Рост и вес.
Создайте и заполните таблицу, используя формулы.
Норма веса = рост – 110;
Разница = норма веса – вес;
РЕКОМЕНДАЦИИ: если разница между нормой и весом отрицательна — «надо худеть», а положительна — «все хорошо».
=ЕСЛИ(E2
-
Средняя годовая температура.
Создайте структуру таблицы по образцу. С помощью функций вычислите средние годовые значения температур, а так же найдите минимальные и максимальные температуры, зафиксированные на метеостанциях.
-
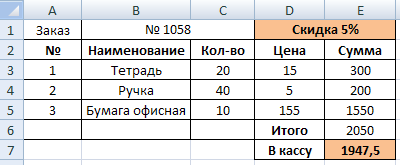
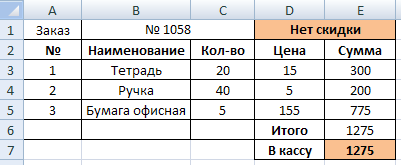
Скидка.
Алгоритм выполнения задания:
-
Создать таблицу, заполнить ячейки столбцов «№», «Наименование», «Кол-во», «Цена» данными.
-
Выполнить расчет столбца «Сумма» =C3*D3 с помощью автозаполнения.
-
Подсчитать итоговую сумму с помощью функции СУММ.
-
В ячейке D1 выбрать функцию ЕСЛИ
-
Если итоговая сумма больше 2000, то скидка 5%,
-
Иначе – нет скидки.
5. Рассчитать сумму «В кассу», с учетом скидки, самостоятельно.