Формула для матрицы excel

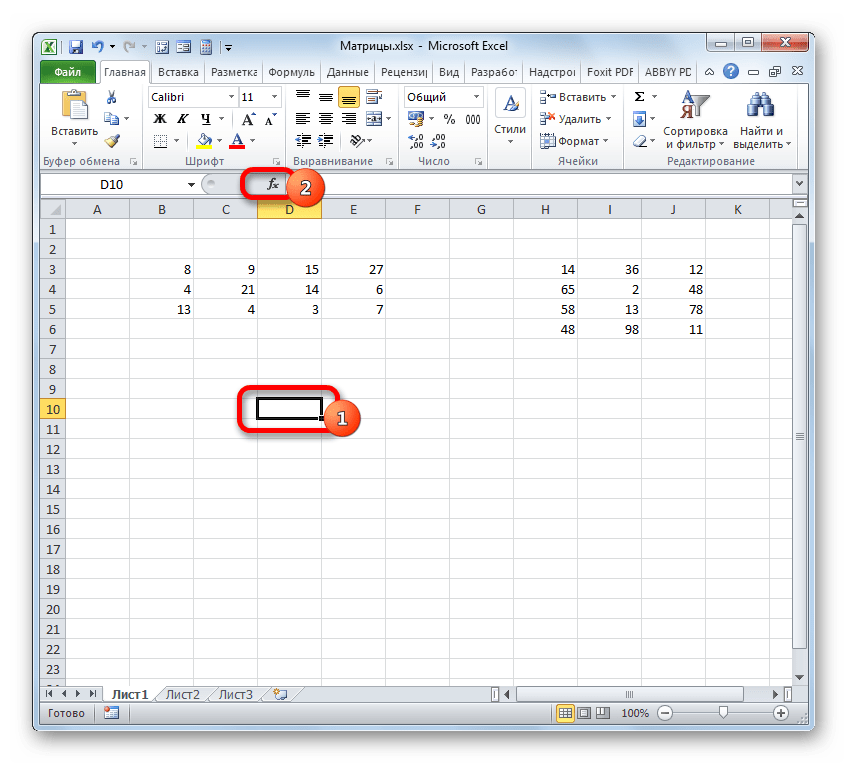
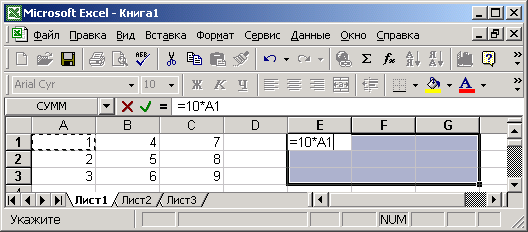
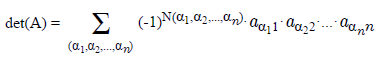В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

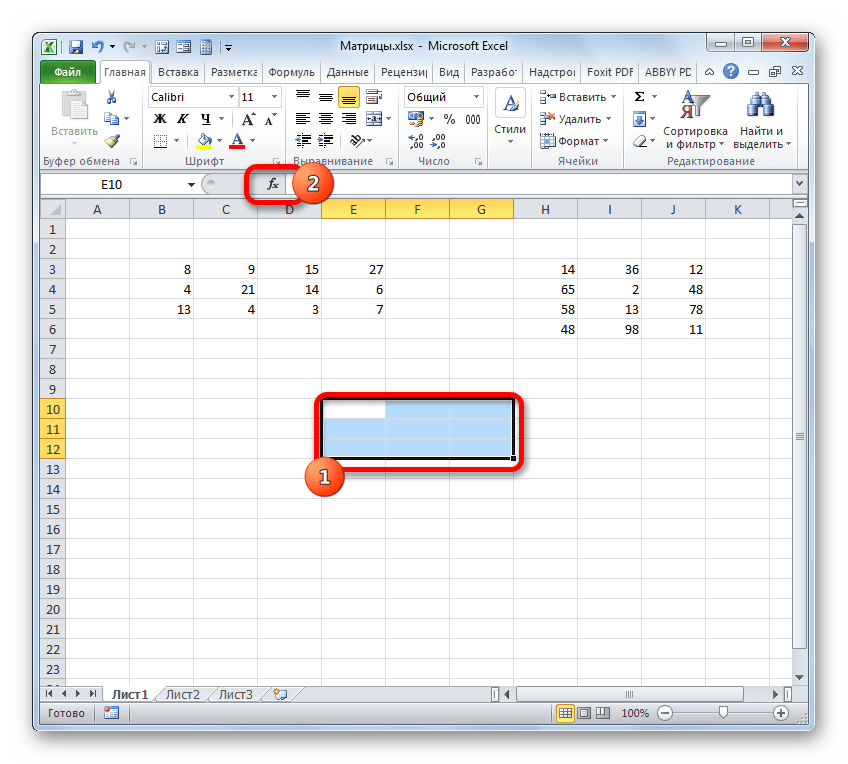
1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

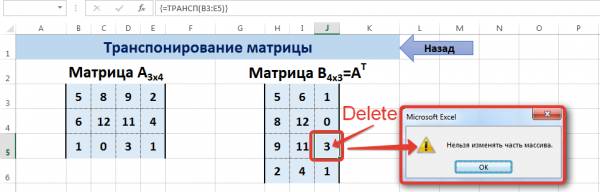
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.



Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

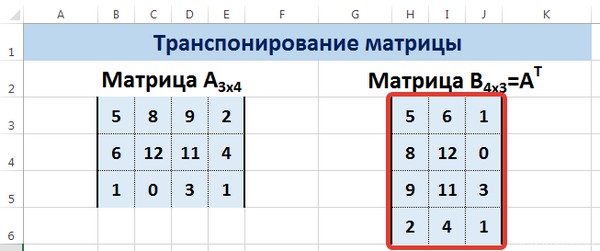
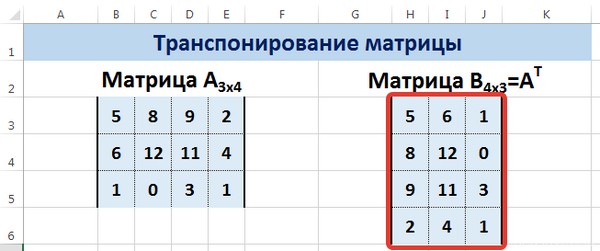
Транспонировать матрицу – поменять строки и столбцы местами.

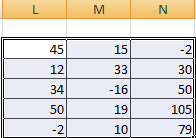
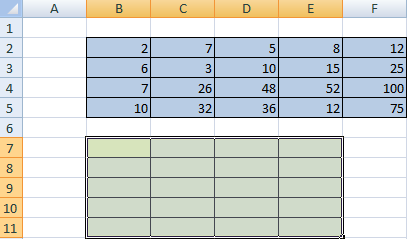
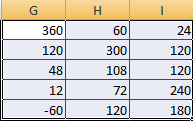
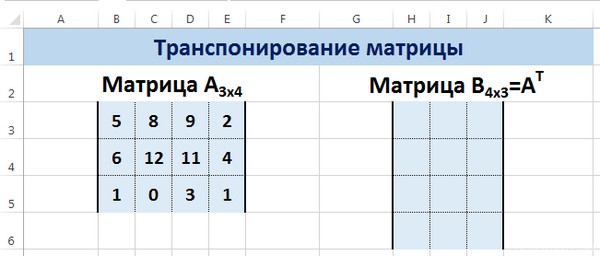
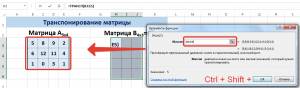
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

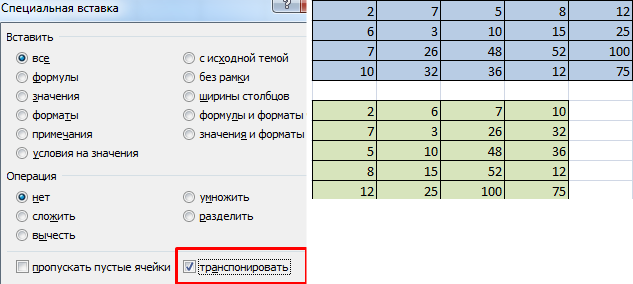
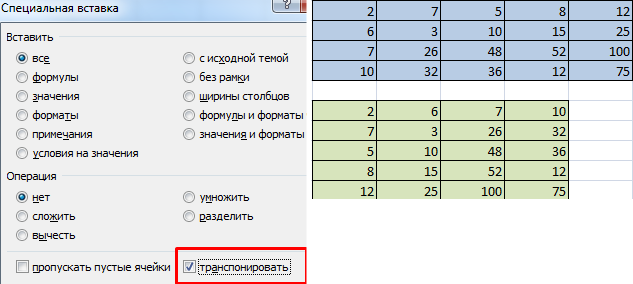
• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.



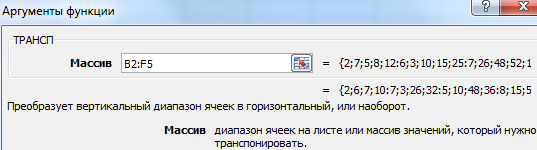
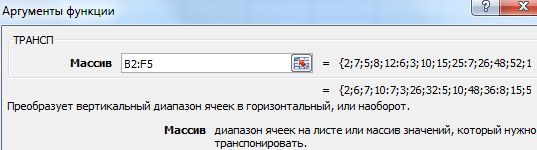
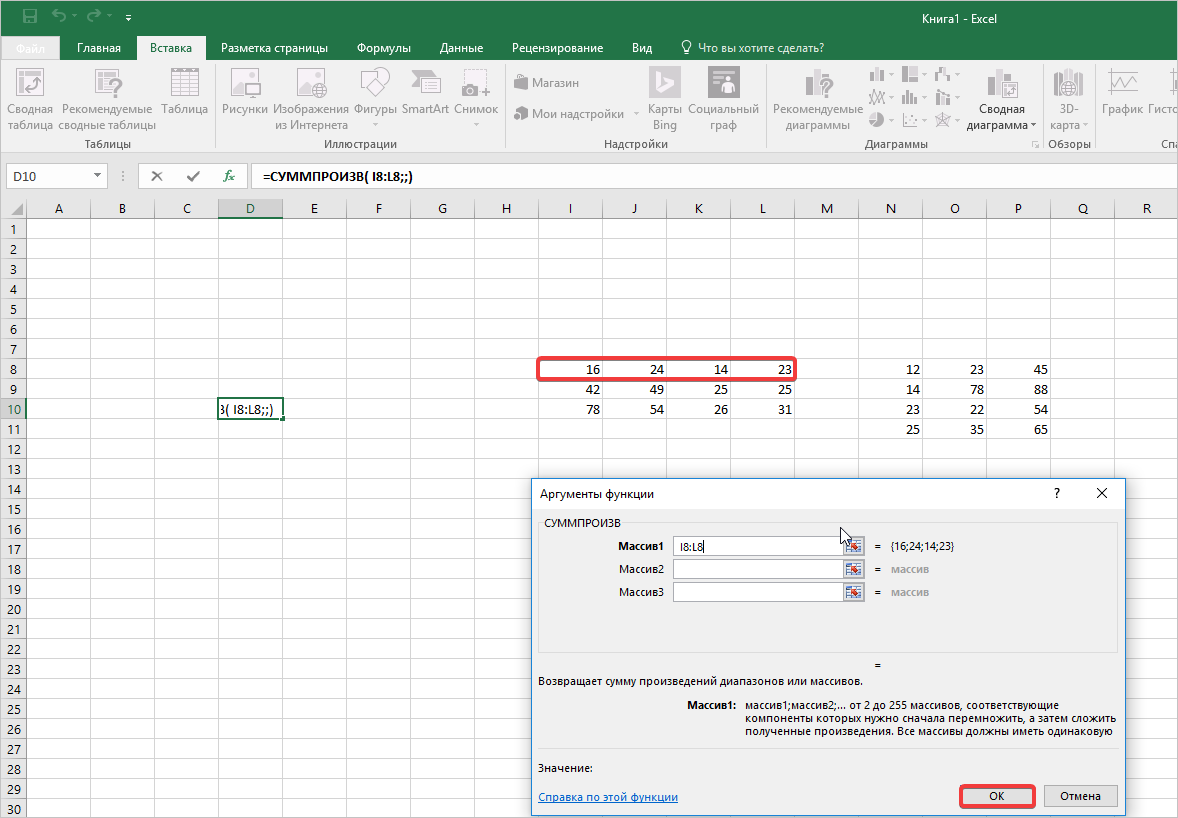
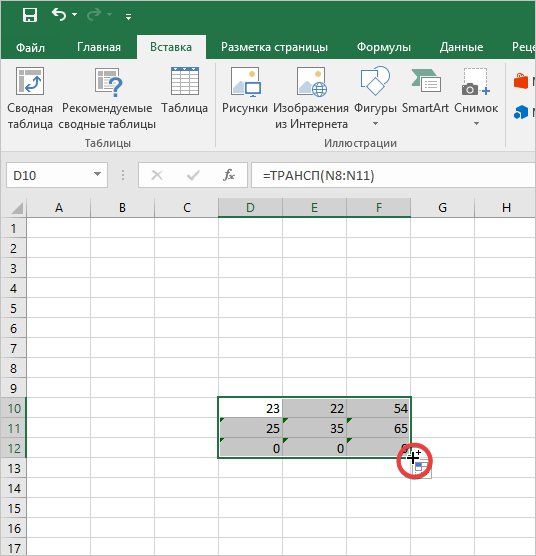
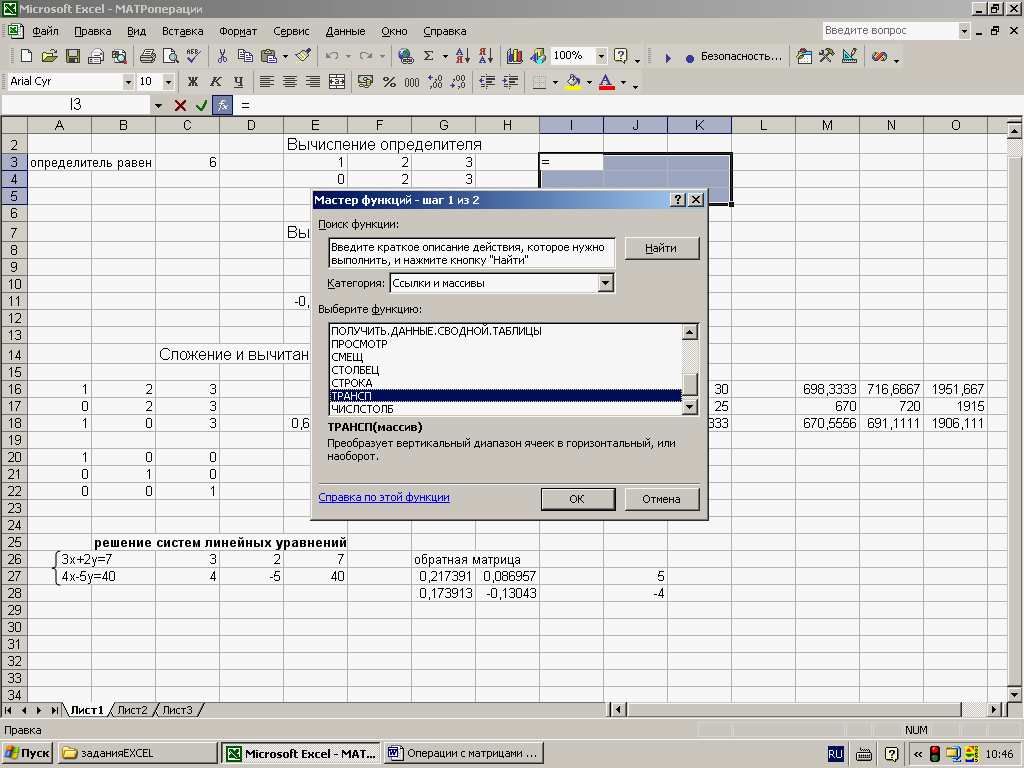
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

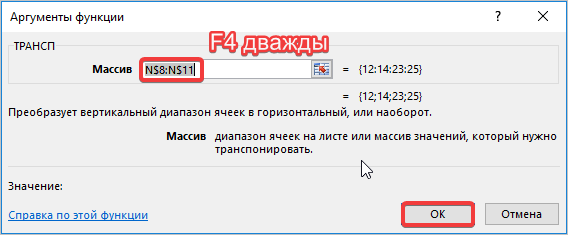
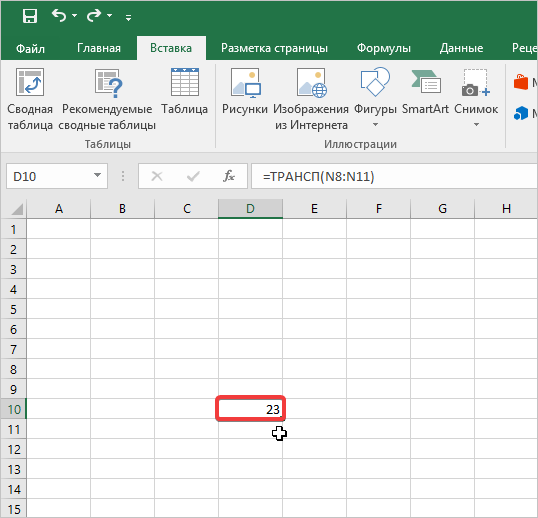
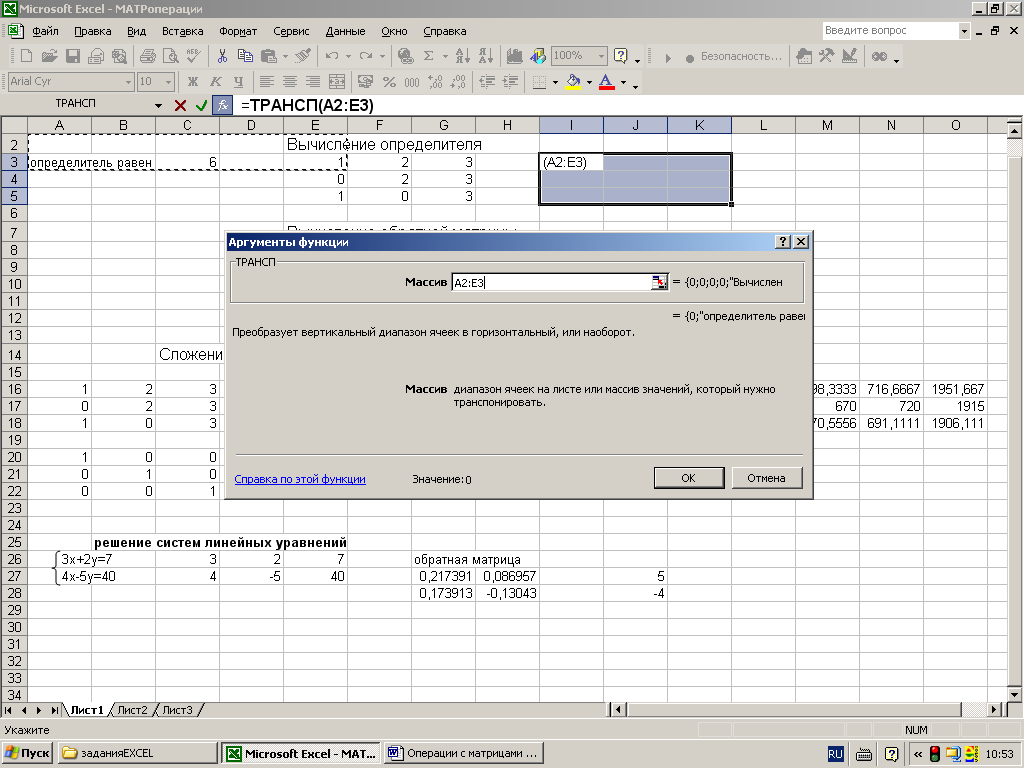
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

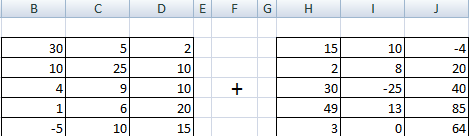
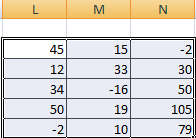
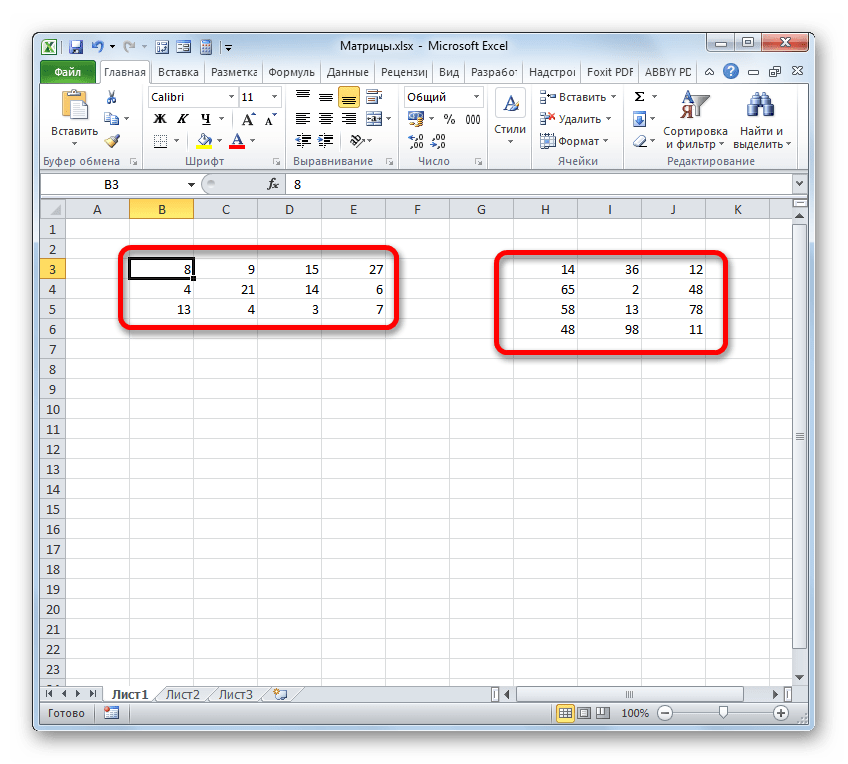
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

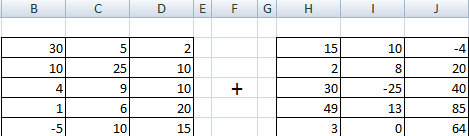
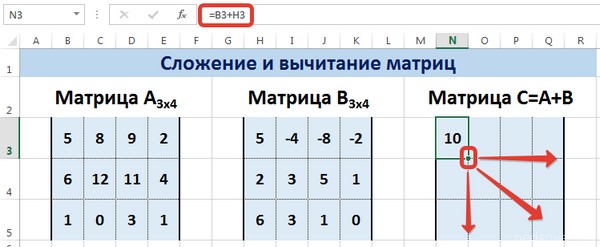
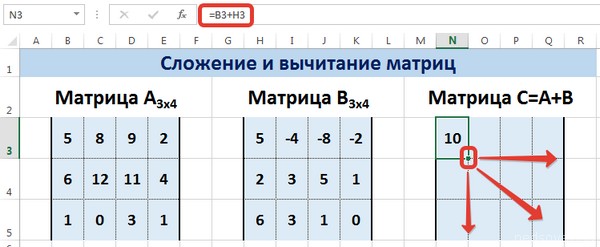
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

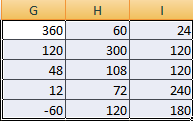
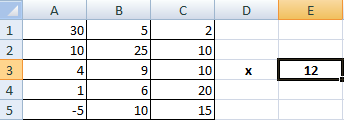
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

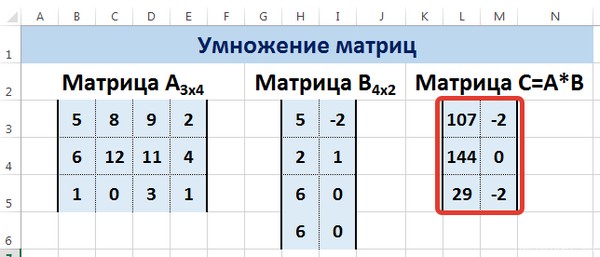
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

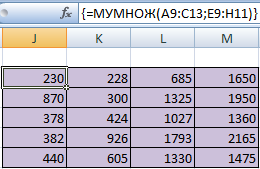
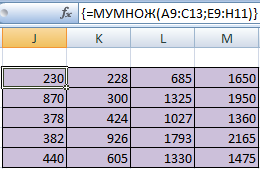
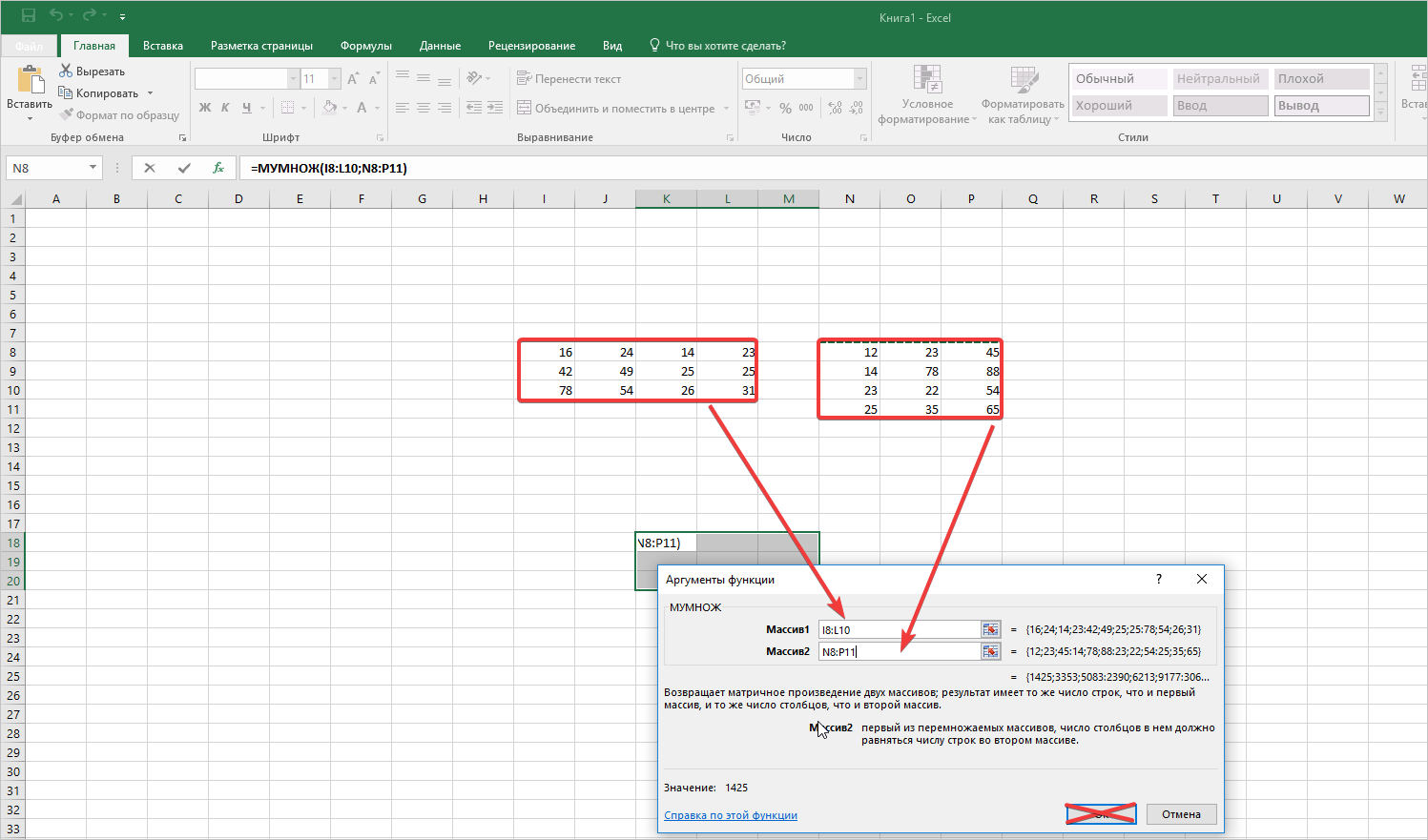
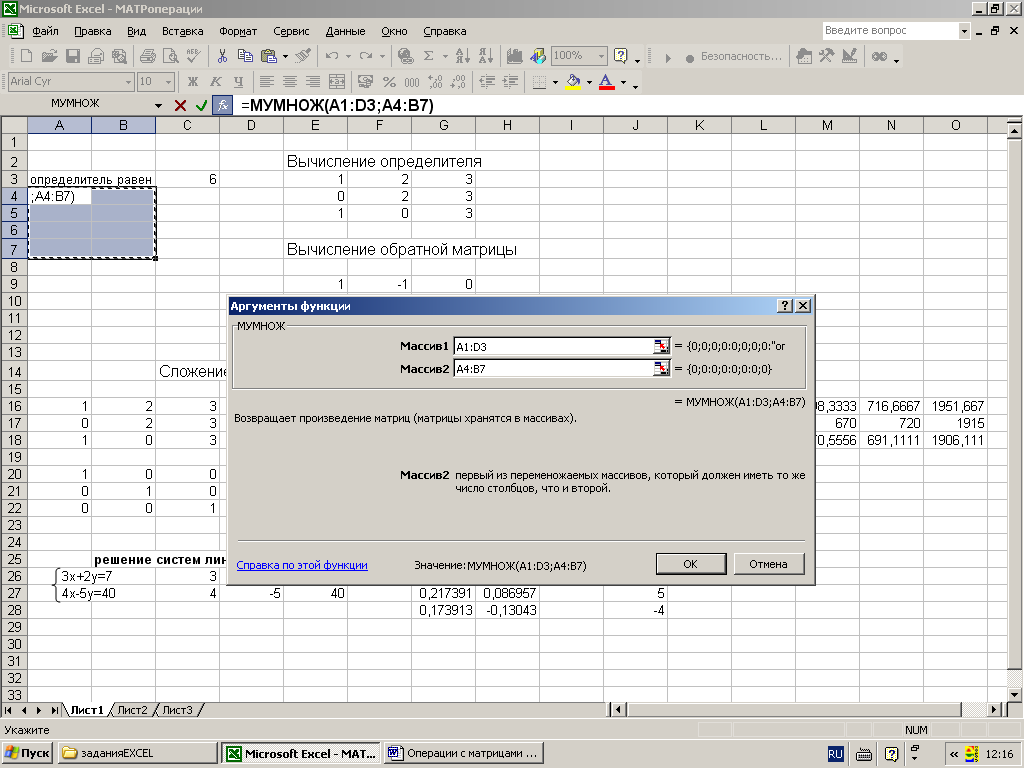
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

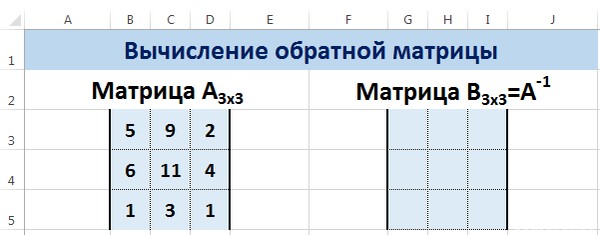
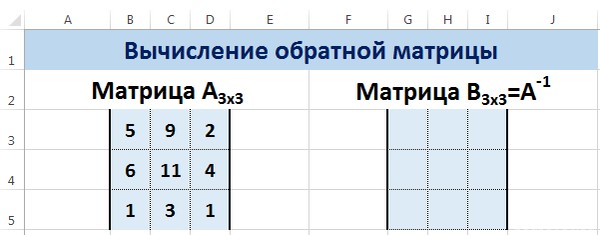
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

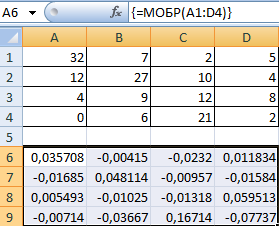
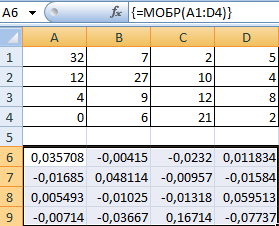
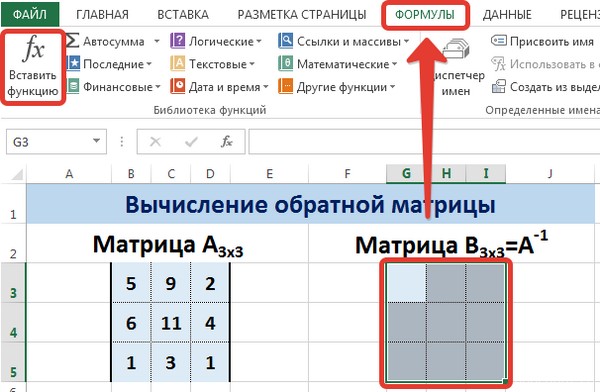
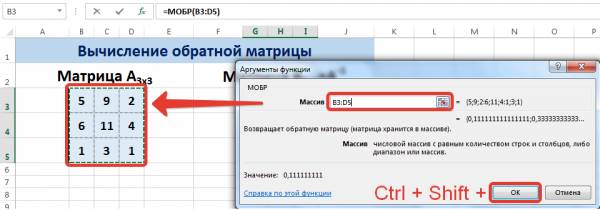
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

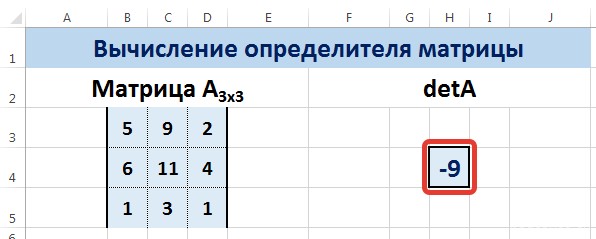
Нахождение определителя матрицы

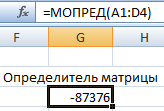
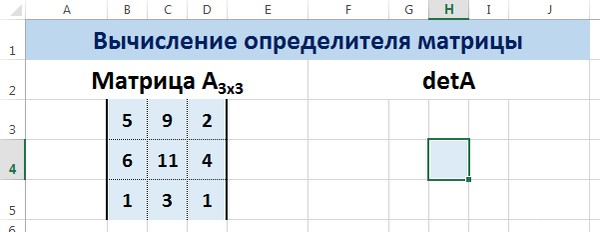
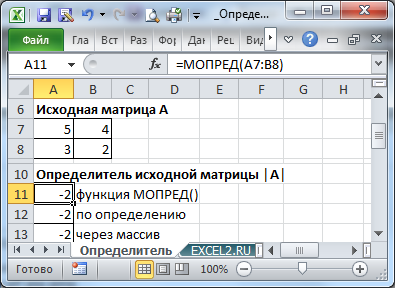
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.

Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу. 

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

1. Выделить набор ячеек, где будут выводиться значения. 
2. Непосредственно введение формулы. 
3. Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием. 

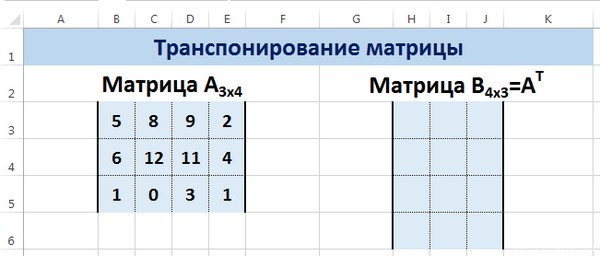
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.

Далее есть несколько методов, как можно осуществить транспонирование. 

Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.

Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.

После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

1. Выделить набор ячеек, отведенных под транспонированную матрицу.
2. Нажать клавишу F2.
3. Нажать на горячие клавиши Ctrl + Shift + Enter.

Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

Сложение

Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.

В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.

=Первый элемент первой матрицы + Первый элемент второй матрицы 

Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.

Умножение

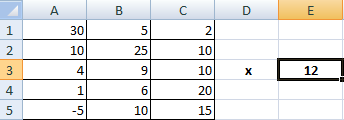
Предположим, у нас есть такая таблица, которую следует умножить на 12.

Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.

При этом важно указывать абсолютные ссылки на ячейки.

Итого, получится такая формула.

=A1*$E$3

Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек. 

Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.

Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.

Обратная матрица

Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.

Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.

Поиск определителя матрицы

Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.

Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)

Несколько примеров

Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.

Умножение и деление

Метод 1

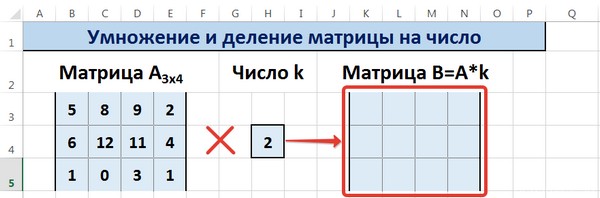
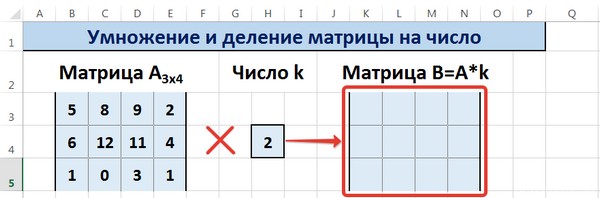
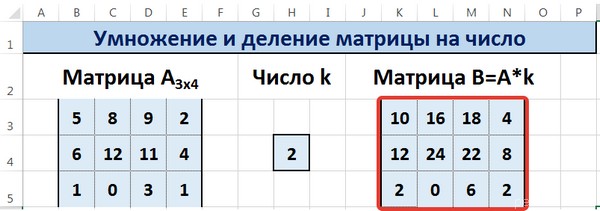
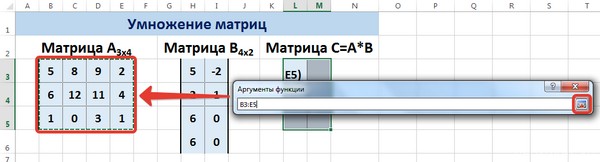
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.

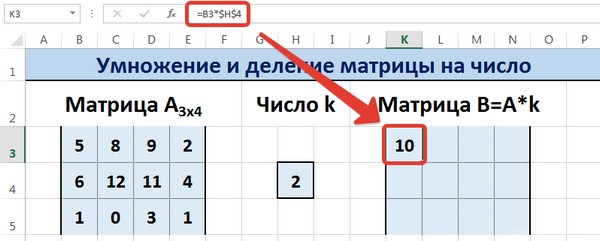
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k. 

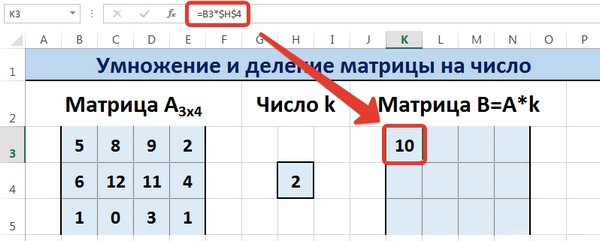
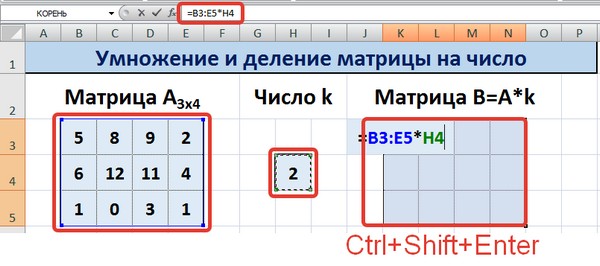
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.

Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.

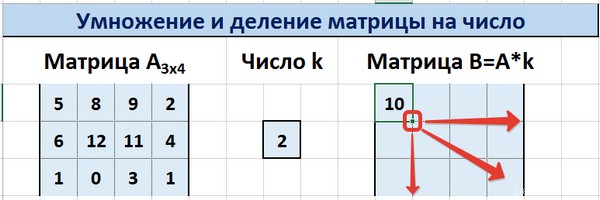
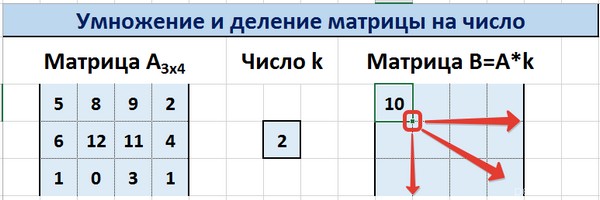
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.

Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.

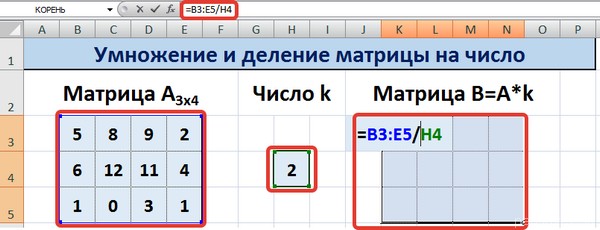
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.

Метод 2

Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.

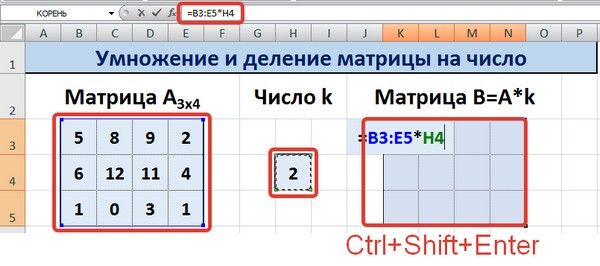
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.

Деление осуществляется аналогичным образом, только знак * нужно заменить на /.

Сложение и вычитание

Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.

Метод 1

Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.

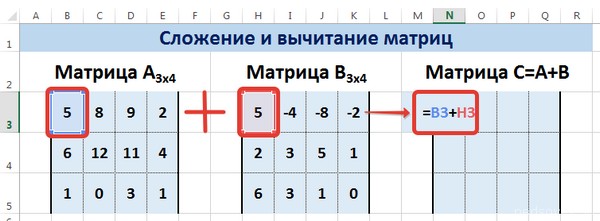
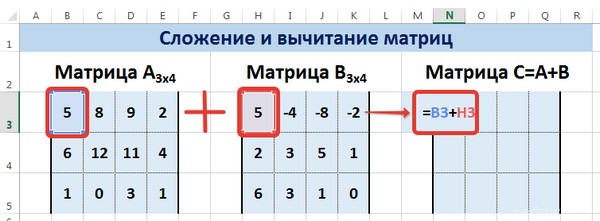
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:

=B3+H3

Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.

Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.

Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.

Метод 2

Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.

Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.

Пример транспонирования матрицы

Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().

Выделяем диапазон для ячеек матрицы АТ.

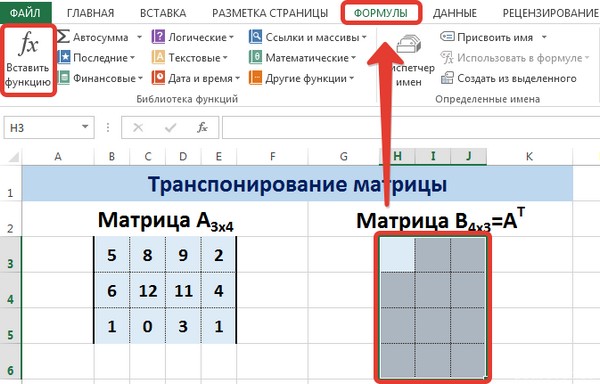
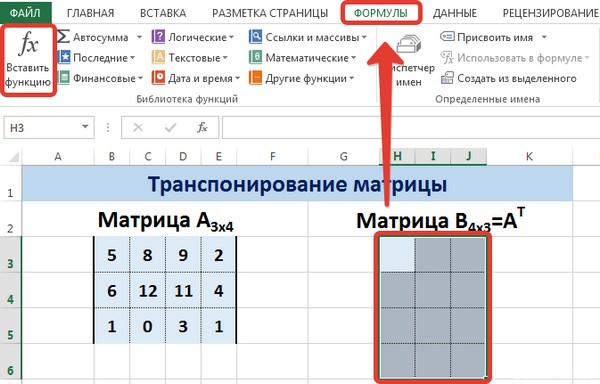
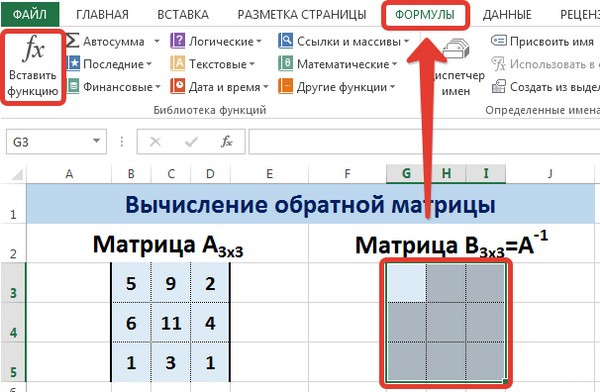
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.

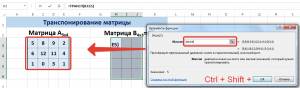
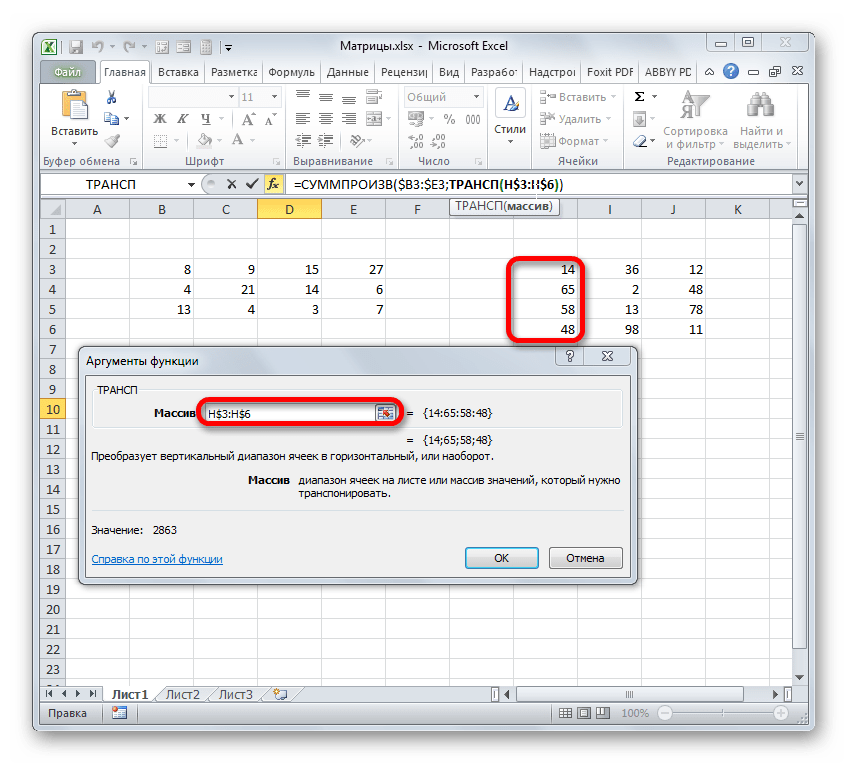
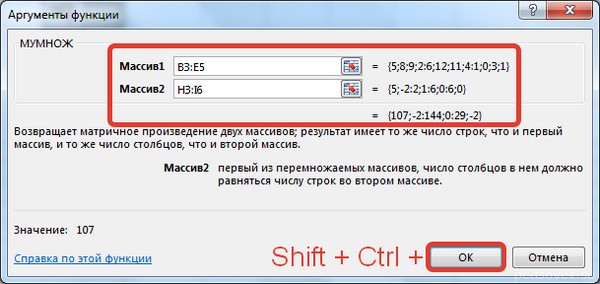
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».

Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.

В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.

Поиск обратной матрицы

Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().

Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».

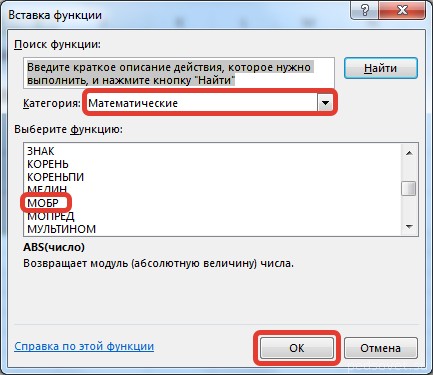
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.

Выводы

Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.

Содержание

• Процедура перемножения матриц
  • Способ 1: функция МУМНОЖ
  • Способ 2: использование составной формулы
• Вопросы и ответы

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.

Процедура перемножения матриц

Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.

Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.

Способ 1: функция МУМНОЖ

Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:

=МУМНОЖ(массив1;массив2)

Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.

Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

1. Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».



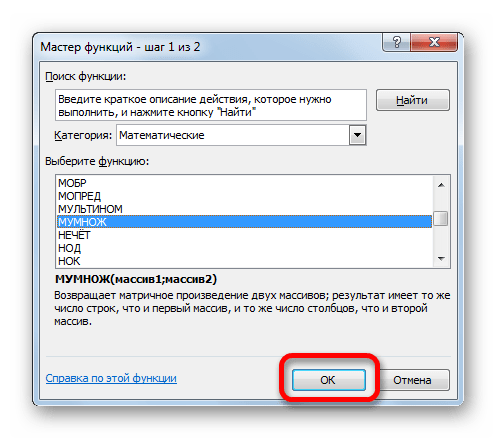
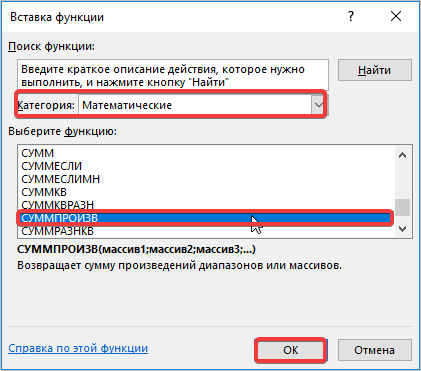
2. Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.



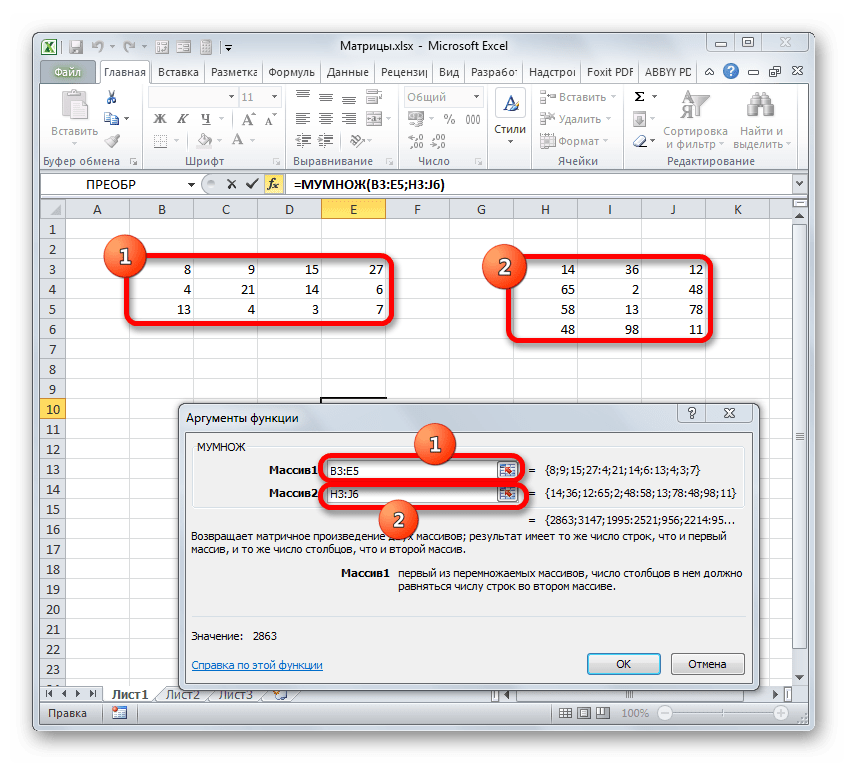
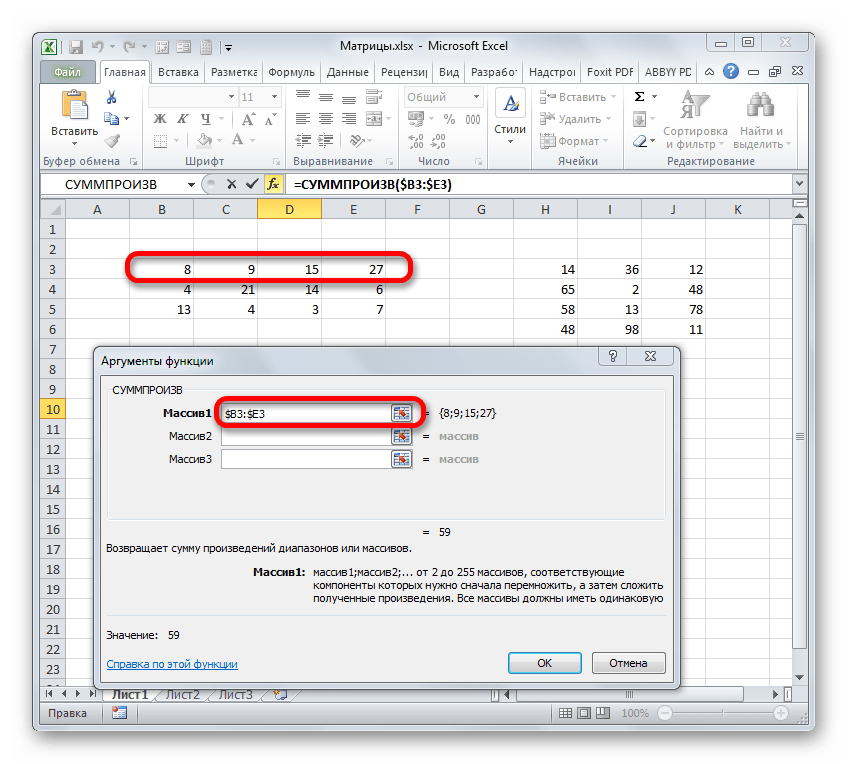
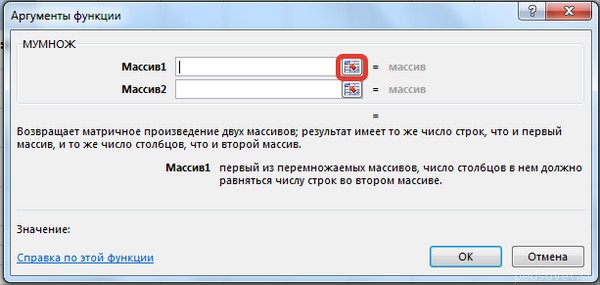
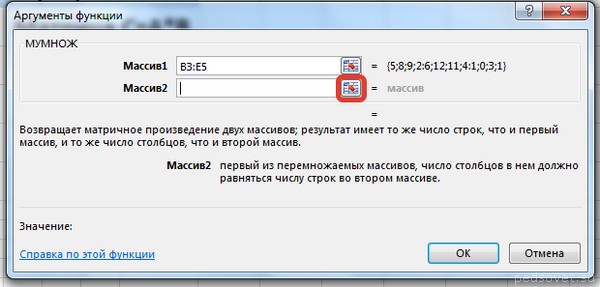
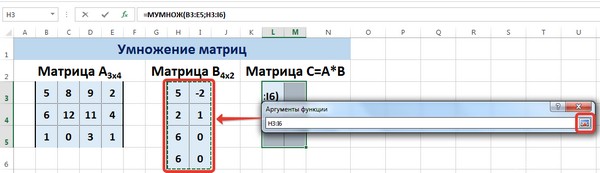
3. Будет выполнен запуск окна аргументов требуемой функции. В этом окне имеется два поля для ввода адресов матричных массивов. Ставим курсор в поле «Массив1» и, зажав левую кнопку мыши, выделяем на листе всю область первой матрицы. После этого её координаты отобразятся в поле. Ставим курсор в поле «Массив2» и аналогичным образом выделяем диапазон второй матрицы.

   После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.



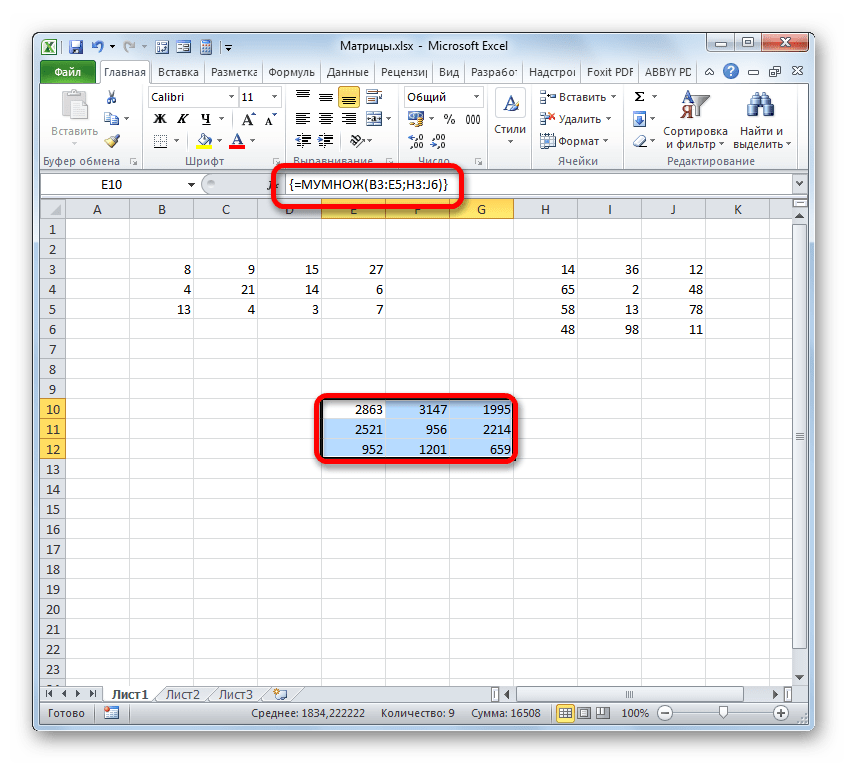
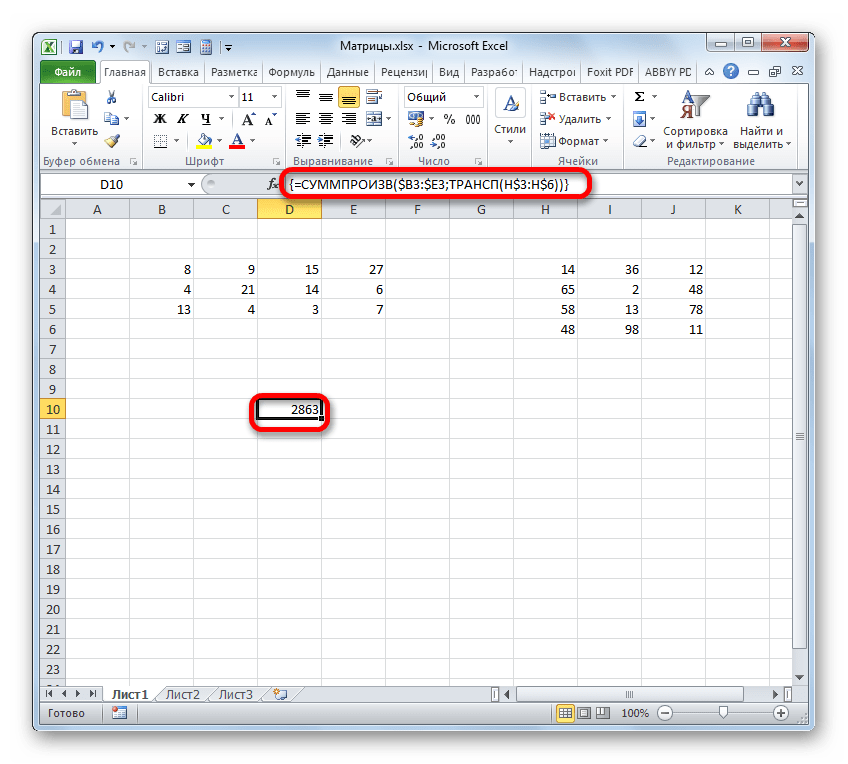
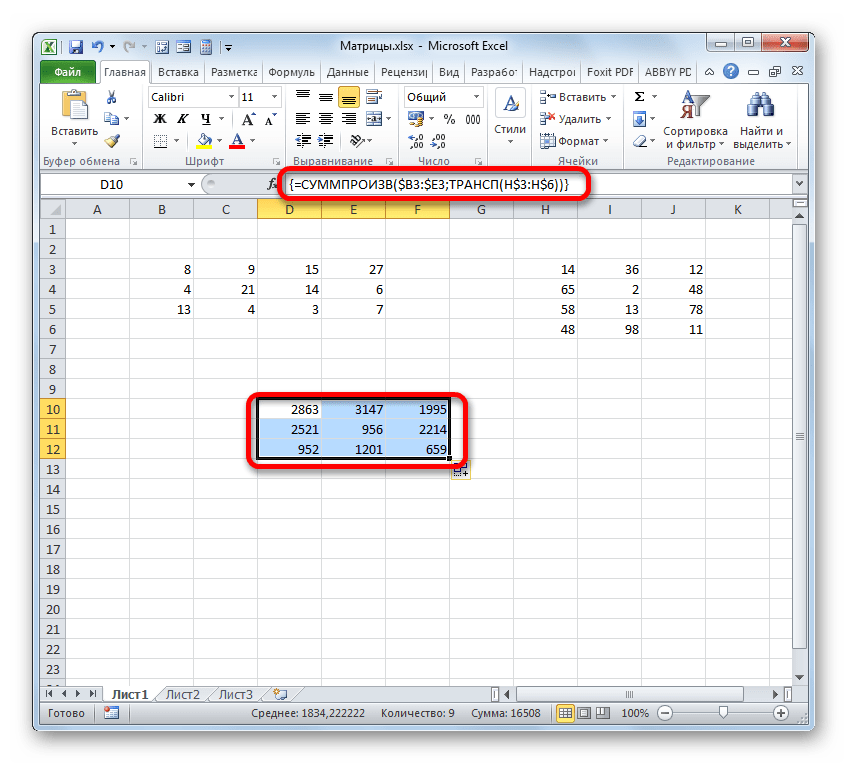
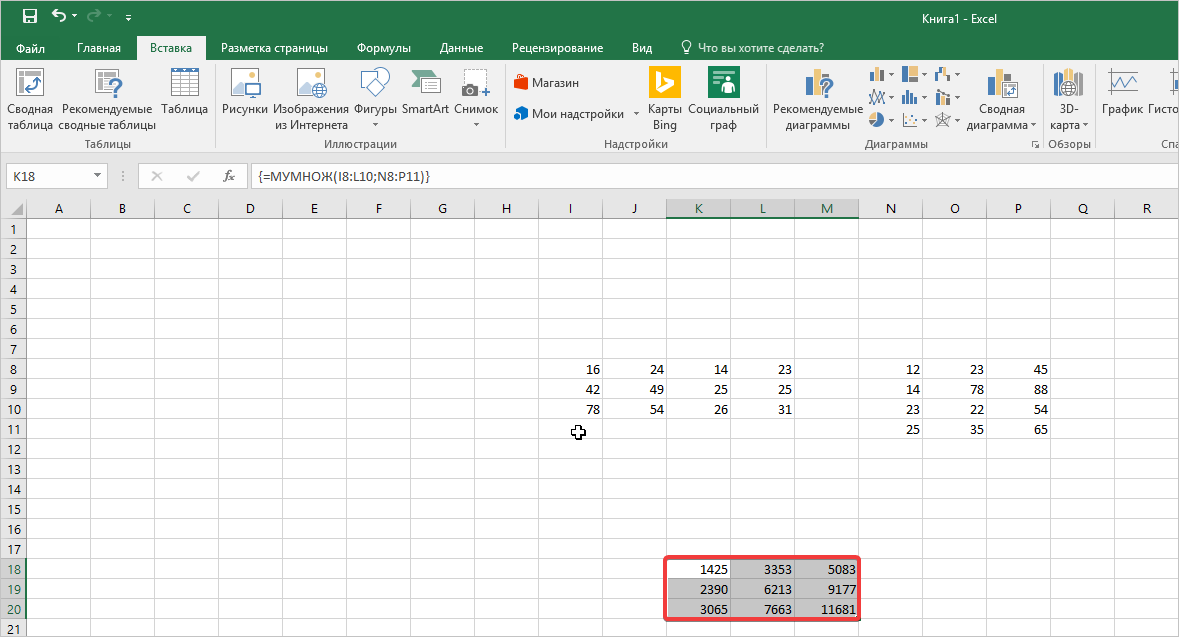
4. Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.

Урок: Функция МУМНОЖ в Экселе

Способ 2: использование составной формулы

Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.

1. На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».



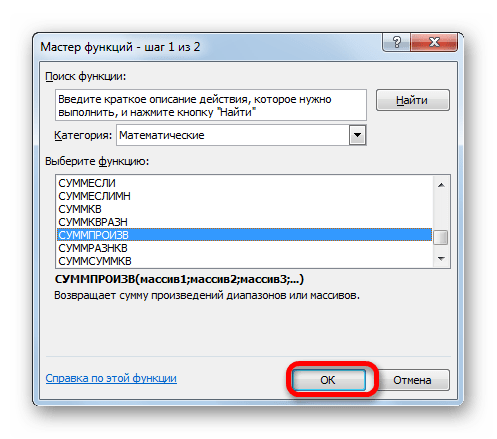
2. Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».



3. Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:

   =СУММПРОИЗВ(массив1;массив2;…)

   В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.

   Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.



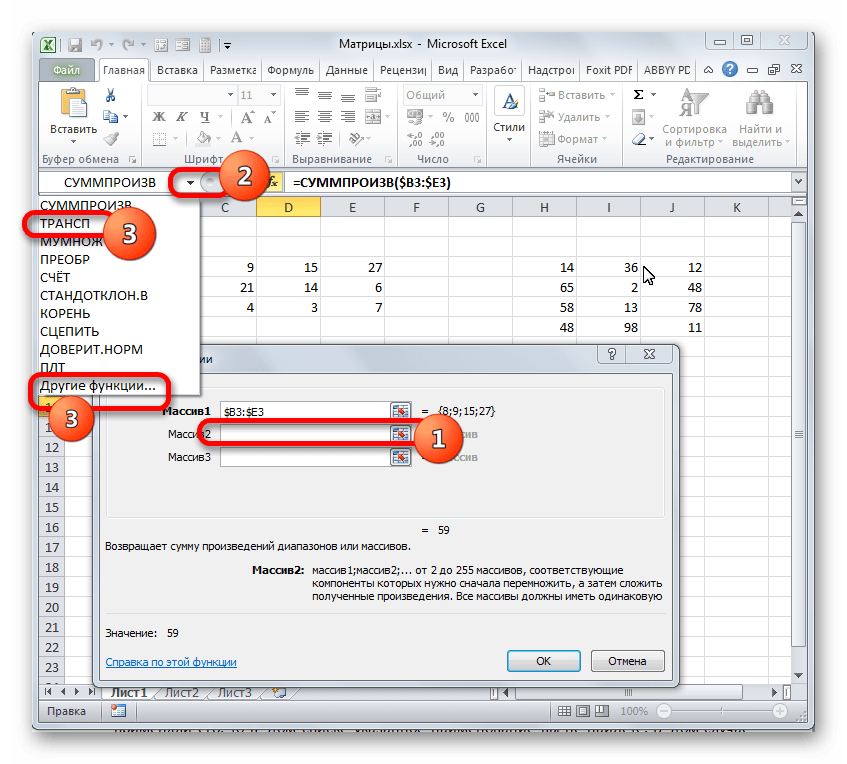
4. После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.

   Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».



5. Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».



6. Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:

   =ТРАНСП(массив)

   То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.

   Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.



7. Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.



8. Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.

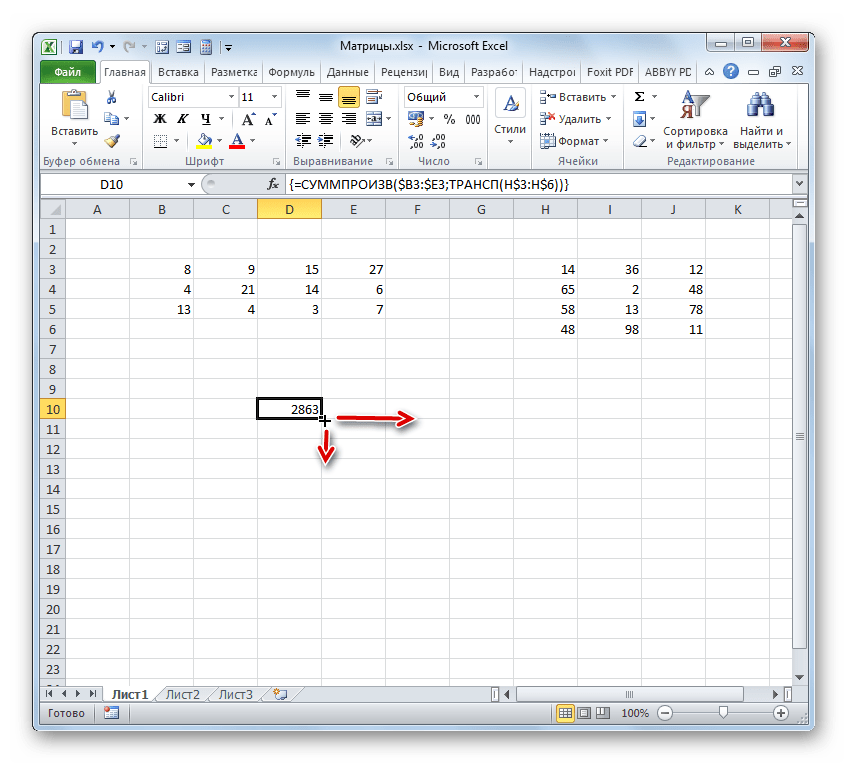
   Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.



9. Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.

Урок: Работа с массивами в Экселе

Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.

Еще статьи по данной теме:

Помогла ли Вам статья?

Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

 

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

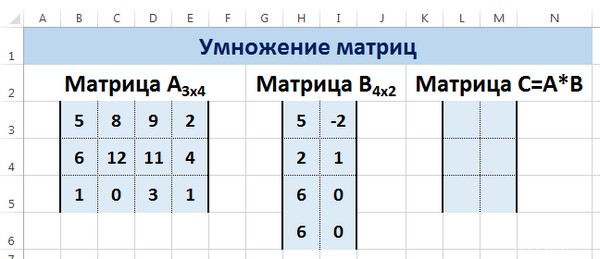
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

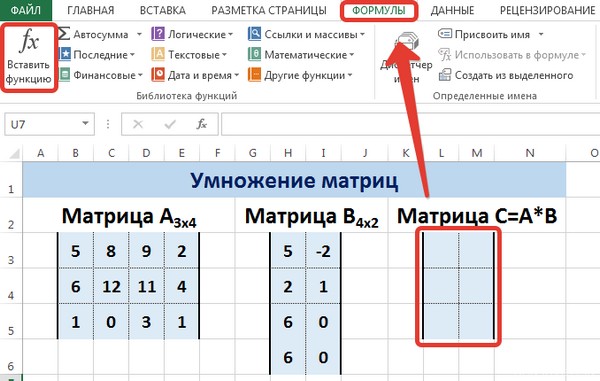
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

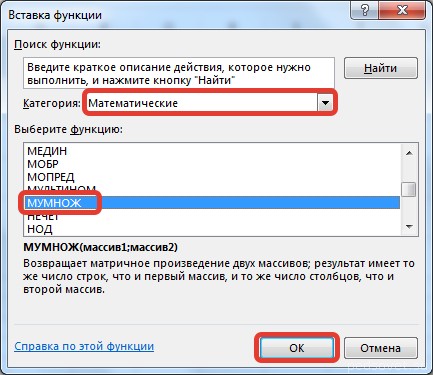
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А^Т.

Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А^Т, причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А^Т.

Нажмите для увеличения

Мы получили транспонированную матрицу.

Нахождение обратной матрицы в Excel

Матрица А^-1 называется обратной для матрицы А, если АžА^-1=А^-1žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А^-1.

Нажмите для увеличения

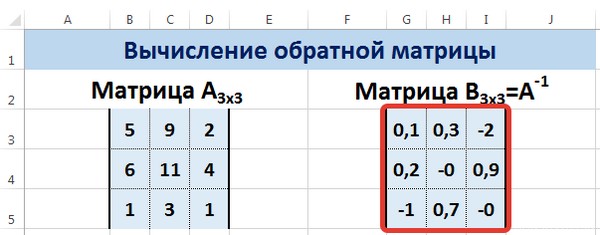
Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

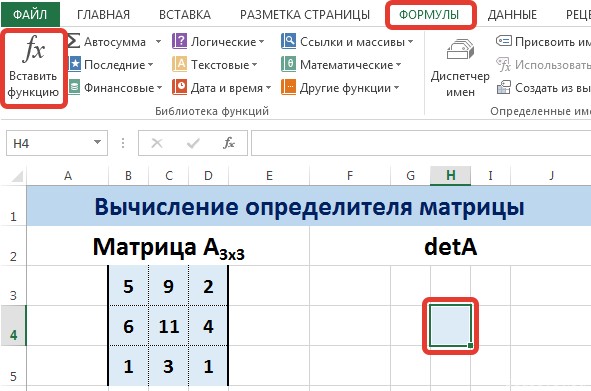
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

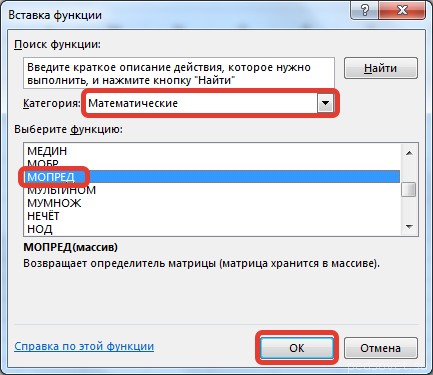
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

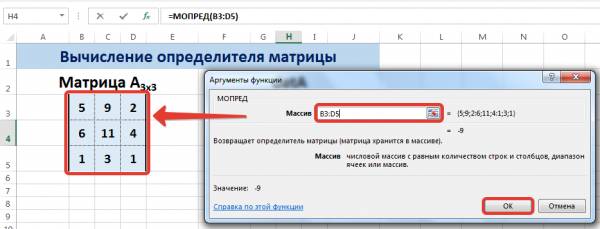
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

Нажмите для увеличения

Мы вычислили определитель матрицы А.

В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

---

Компьютерные пользователи пользуются программой Microsoft Excel не только для создания квартальных и годовых отчетов, но и еще в качестве многофункционального калькулятора. Например, вычислить матрицу в Excel несложно, достаточно лишь правильно использовать поля книги и инструменты.

Как умножить матрицы в Excel

Электронный редактор позволяет нам открыть мощный табличный диапазон утилит и параметров. Благодаря чему мы получаем возможность быстро создавать расчеты. Каждому пользователю известно, что перемножать можно лишь те матрицы, которые имеют одинаковое количество строк и столбцов.

Полезно знать!

Если матрица имеет пустые элементы, то перемножать ее тоже нельзя, поэтому использовать для расчетов в Excel можно не все виды математических условий.

Как пользоваться функцией МУМНОЖ для вычисления матрицы

Функция МУМНОЖ имеет возможность производить перемножение двух матричных массивов. Для этой операции используется специальный синтаксис, в котором недопустимо делать ошибки. Предлагаем на примере рассмотреть, как производится решение матриц в электронной таблице.

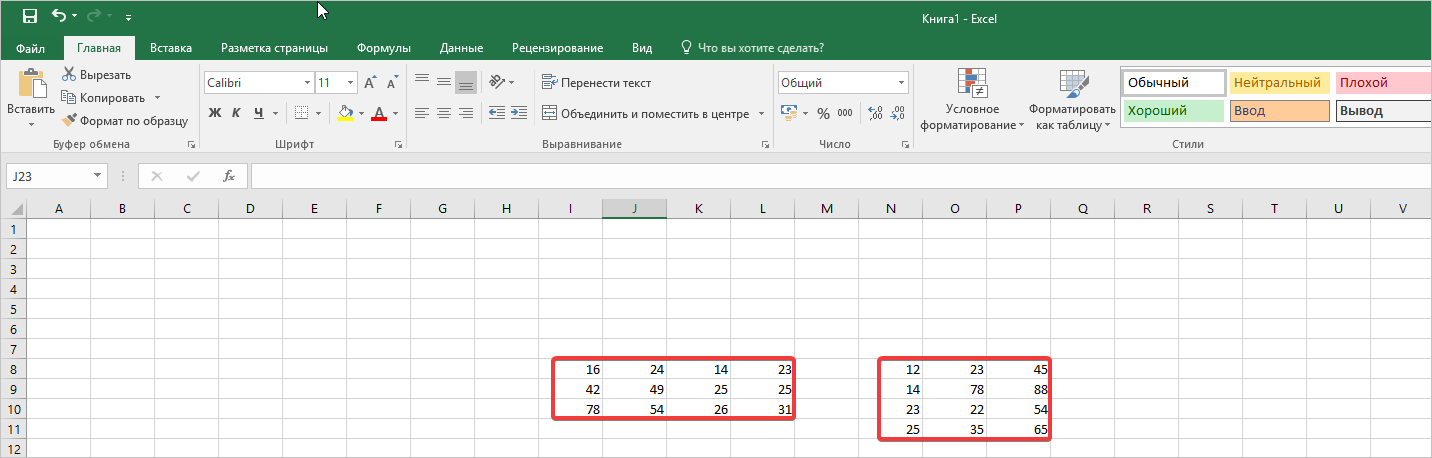
1. Предположим, имеется пример двух матриц. Чтобы их перемножить, их необходимо сначала внести в свободные ячейки листа в Excel.

1. Далее переходим в другую свободную зону. Здесь выделяем диапазон ячеек, который должен вмещать все ответы после перемножения, то есть в нашем случае результат должен занимать три строчки и два столбика. После выделения нажимаем на кнопку «Вставить функцию».

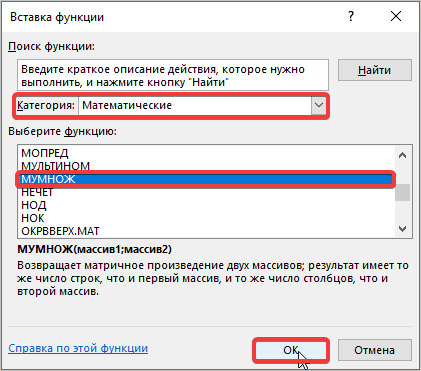
1. Мы попадаем в мастер функций. Здесь в поле «Категория» выбираем «Математические», листаем до середины и находим «МУМНОЖ». Выбираем ее и нажимаем кнопку «ОК».

1. В появившемся окне вводим аргументы массивов. В первый массив прописываем координаты первой матрицы, а во второй — второй, соответственно. Обратите внимание, что в полях проставились адреса этих объектов, затем нажмите комбинацию клавиш Ctrl+Shift+Enter.

Важно!

Перед выводом результата в выделенный диапазон ячеек не нужно нажимать кнопку ОК. Это не даст результата, а только лишь выведет ошибку на экран. Так как здесь формула перемножения массива, необходимо использовать комбинацию кнопок, указанную выше.

Использование сборной формулы для решения

Если по какой-то причине первый вариант перемножения у вас не получился либо считаете его слишком простым, рекомендуем ознакомится с еще одним способом, который послужит дополнительным навыком в работе с матрицами в электронных таблицах.

1. Начнем с выделения одной свободной ячейки на листе. Затем нажимаем кнопку «Вставить функцию».

1. Открывается окно с набором функций, выбираем категорию «Математические», где в нижнем списке находим значение «СУММПРОИЗВ». Нажимаем кнопку ОК.

1. Затем в появившемся окне, где нужно в пустые поля прописать диапазон ячеек, участвующих в вычислениях. В первое поле заносим ссылки на первую строчку первой матрицы.

1. Именно со вторым полем могут возникнуть сложности. Поэтому дочитайте инструкцию до конца. Активируйте поле «Массива 2», затем перейдите к группе функций.

1. Открываем категорию «Ссылки и массивы», затем выбираем функцию «ТРАНСП». Следом нажмите кнопку ОК. Во вновь открывшемся окне в пустое поле вводим диапазон первого столбика второй матрицы.

1. Затем выделите фоном указанные адреса, после чего нажмите два раза клавишу F4. Это поможет проставить знак доллара к цифровым символам, что делает их привязанными. Затем также нажмите комбинацию клавиш Ctrl+Shift+Enter, как в предыдущем способе.

1. Как видим у нас заполнилась только одна ячейка, чтобы изменить это и увидеть расчеты для оставшихся чисел, необходимо активировать маркер автозаполнения. Для этого наведите на правый нижний угол ячейки и протяните на количество строчек и количество столбцов. В нашем случае 3х3.

Таким образом вы можете использовать до двух вариантов работы с матрицами. Однако если необходимо быстро справиться с задачей, следует воспользоваться первым способом.

Введение

Матрица представляет собой комплект ячеек, которые располагаются последовательно одна за другой и отображаются как прямоугольник. Операции с матрицами в Excel выполняются аналогично работе со стандартным диапазоном памяти. Все матрицы обладают отдельным адресом, который записывается так же, как и диапазон. Сначала указывается адрес первой ячейки диапазона, которая располагается вверху в левом углу. Далее записывается адрес последней ячейки, расположенной в нижнем правом углу.

Формулы массива

Матрица, по сути, является массивом и для работы с ними применяются соответствующие формулы. Главным их отличием от стандартных формул считается то, что обычные стандартные формулы могут вывести только одну величину. Чтобы использовать формулы работы с массивами, следует выполнить такой набор операций:

1. Осуществить выделение участка ячеек, куда следует вывести значения.
2. Задать требуемую формулу для вычислений.
3. Нажать клавишный набор Ctrl + Shift +Enter.

По завершению этих процедур в поле для ввода отобразится формула массива. Она отличается от стандартной формулы наличием фигурных скобок. Чтобы отредактировать или удалить формулу работы с массивом, нужно сделать выделение нужного диапазона и выполнить коррекцию. Для редактирования самой матрицы применяются те же комбинации клавиш, что и при её формировании.

Операции с матрицами

Операция замены местами строк и столбцов называется транспонированием. Перед началом этой процедуры, надо выполнить выделение отдельной зоны, имеющей число строк равное числу столбцов преобразуемой матрицы, и то же самое относительно столбцов. Существует два способа выполнения транспонирования. Согласно первому способу надо выполнить следующие действия:

1. Нужно выполнить выделение матрицы и сделать её копию.
2. Выполнить выделение диапазона ячеек для вставки транспонируемого диапазона.
3. Открыть окно «Специальная вставка».
4. Выбрать кнопку «Транспонировать» и нажать ОК.

«Матрица в Excel» 👇

Второй способ заключается в следующем. Нужно выполнить выделение ячейки, находящейся в левом верхнем углу диапазона, выделенного для транспонируемой матрицы. Далее следует открыть диалоговое окно с набором функций и выбрать функцию ТРАНСП.

В качестве параметра функции используется диапазон, соответствующий изначальной матрице. Но после того, как будет нажата клавиша ОК, появится сообщение об ошибке, поскольку вставляемая функция не определена в качестве формулы массива. То есть далее надо сделать следующее:

1. Выполнить выделение комплекта ячеек, предназначенных для транспонируемой матрицы.
2. Нажать кнопку F2.
3. Нажать набор клавиш Ctrl + Shift + Enter.

Основным преимуществом такого способа является то, что транспонированная матрица сразу способна корректировать заложенную в неё информацию, по мере внесения коррекций в исходную матрицу.

Далее рассмотрим операцию сложения. Эта операция допустима только для тех диапазонов, которые имеют одинаковое число компонентов. Иначе говоря, матрицы, подлежащие сложению, обязаны иметь один и тот же размер. Пример представлен на рисунке ниже:

В итоговой матрице необходимо сделать выделение первой ячейки и задать следующую формулу:

= Начальный компонент первой матрицы + Начальный компонент второй матрицы

Затем следует подтвердить задание формулы клавишей Enter и применить функцию авто заполнения (квадрат в нижнем правом углу) для копирования всех величин в новую матрицу. Итог приведён на рисунке ниже:

Далее рассмотрим операцию умножения. Имеется следующая таблица, все элементы которой необходимо умножить на двенадцать:

Суть метода умножения аналогична сложению, но здесь нужно все ячейки матрицы умножить на двенадцать и итог также отразить в отдельной матрице. Необходимо помнить об указании абсолютных ссылок на ячейки. В итоге получаем формулу:

=A1*$E$3

И результирующую матрицу:

Рассмотрим пример перемножения матриц. Это возможно только при соблюдении одного условия. Необходимо, чтобы число строк и столбцов у этих матриц являлось зеркально одинаковым, то есть число столбцов равнялось числу строк.

Для удобства можно выделить диапазон итоговой матрицы. Следует поместить курсор на ячейку в левом верхнем углу и задать следующую формулу:

=МУМНОЖ(А9:С13;Е9:H11).

Далее следует нажать комбинацию клавиш Ctrl + Shift + Enter, чтобы увидеть итог:

Далее рассмотрим пример обратной матрицы. Если матрица (её диапазон) квадратной формы, то есть число ячеек по вертикали равно числу ячеек по горизонтали, то значит, при необходимости, можно определить обратную матрицу. Это можно сделать при помощи функции МОБР. Сначала нужно сделать выделение первой ячейки матрицы, куда будет вставлена обратная матрица. В неё нужно ввести формулу:

=МОБР(A1:A4).

В качестве аргумента нужно указать диапазон, для которого следует сформировать обратную матрицу. Далее нужно использовать комбинацию клавиш Ctrl + Shift + Enter.

Далее рассмотрим нахождение определителя матрицы. Определителем матрицы является число, определяемое для квадратной матрицы по заданной формуле. Для этой цели в программе Excel есть специальная функция МОПРЕД. Необходимо установить курсор на любую ячейку матрицы и задать функцию:

=МОПРЕД(A1:D4).

Далее рассмотрим ещё один пример вычислений. Имеется матрица А, размером три на четыре. Есть, так же, некоторое число k, записанное вне матрицы. Когда будет выполнена операция умножения матрицы на это число, возникнет диапазон величин, который имеет такие же размеры, но все его компоненты умножены на k:

Диапазон B3:E5 является исходной матрицей, подлежащей умножению на число k, расположенному в клетке H4. Итоговая матрица будет располагаться в диапазоне K3:N5. Исходная матрица обозначается как А, а итоговая как В. Итоговая матрица В будет образована умножением матрицы А на величину k. Формула для вычислений записывается в ячейку К3:

=B3*$H$4.

Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.

Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

Синтаксис

МОБР(массив)

Аргументы функции МОБР описаны ниже.

• Массива    Обязательный. Числовой массив с равным количеством строк и столбцов.

Замечания

• Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.

• Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».

• МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.

• Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.

• В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.

	Столбец A	Столбец B
Строка 1	d/(a*d-b*c)	b/(b*c-a*d)
Строка 2	c/(b*c-a*d)	a/(a*d-b*c)

• Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.

• Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.

Примеры

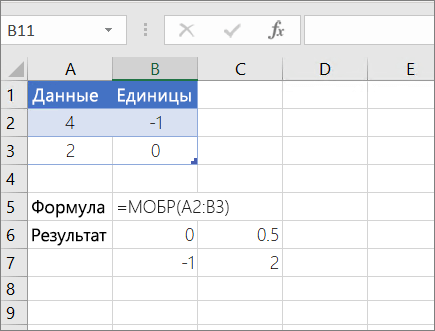
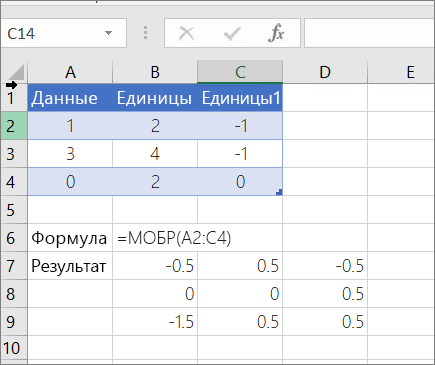
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Вычислим определитель (детерминант) матрицы с помощью функции

МОПРЕД()

или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).

Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.

Для вычисления определителя в MS EXCEL есть специальная функция

МОПРЕД()

. В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см.

файл примера

).

Массив может быть задан не только как интервал ячеек, например

A7:B8

, но и как

массив констант

, например

=МОПРЕД({5;4:3;2})

. Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на

именованный диапазон

.

Для матриц порядка 2 можно определитель можно вычислить без использования функции

МОПРЕД()

. Например, для вышеуказанной матрицы выражение

=A7*B8-B7*A8

вернет тот же результат.

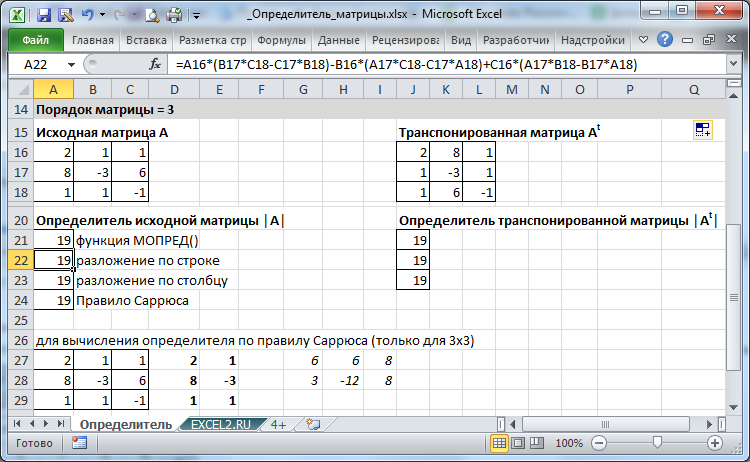
Для матрицы порядка 3, например размещенной в диапазоне

A16:C18

, выражение усложняется

=A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18)

(разложение по строке).

В

файле примера

для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.

Свойства определителя

Теперь о некоторых свойствах определителя (см.

файл примера

):

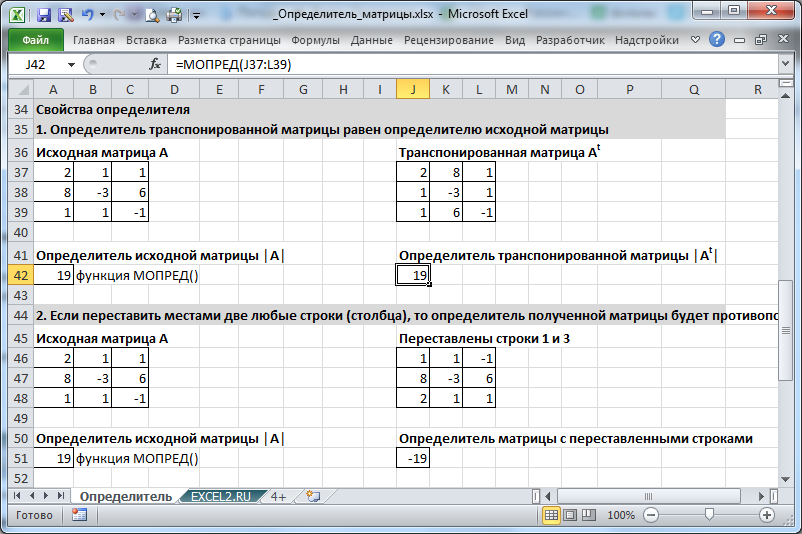
• Определитель

  транспонированной матрицы

  равен определителю исходной матрицы

• 
  Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
  
• 
  Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
  
• 
  Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет
  
  равен определителю исходной матрицы, умноженному на
  
  k
  
• 
  Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
  
• 
  det(А)=1/det(А
  
  ^-1
  
  ), где А
  
  ^-1
  
  —

  матрица обратная

  матрице А (А — квадратная невырожденная матрица).
  

Вычисление определителя матрицы по определению (до 6 порядка включительно)

СОВЕТ

: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция

МОПРЕД()

.

Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции

МОПРЕД()

) придется вспомнить определение:

Определителем квадратной матрицы порядка

n

х

n

является сумма, содержащая

n!

слагаемых (

=ФАКТР(n)

). Каждое слагаемое представляет собой произведение

n

элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы

А

. Перед

k-ым

слагаемым появляется коэффициент

(-1)

, если элементы матрицы

А

в произведении упорядочены по номеру строки, а количество инверсий в

k-ой

перестановке множества номеров столбцов нечетно.

где (

α

₁

,

α

₂

,…,

α

_n

) — перестановка чисел от 1 до

n

, N(

α

₁

,

α

₂

,…,

α

_n

) — число

инверсий в перестановке

, суммирование идёт по всем возможным перестановкам порядка

n

.

Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.

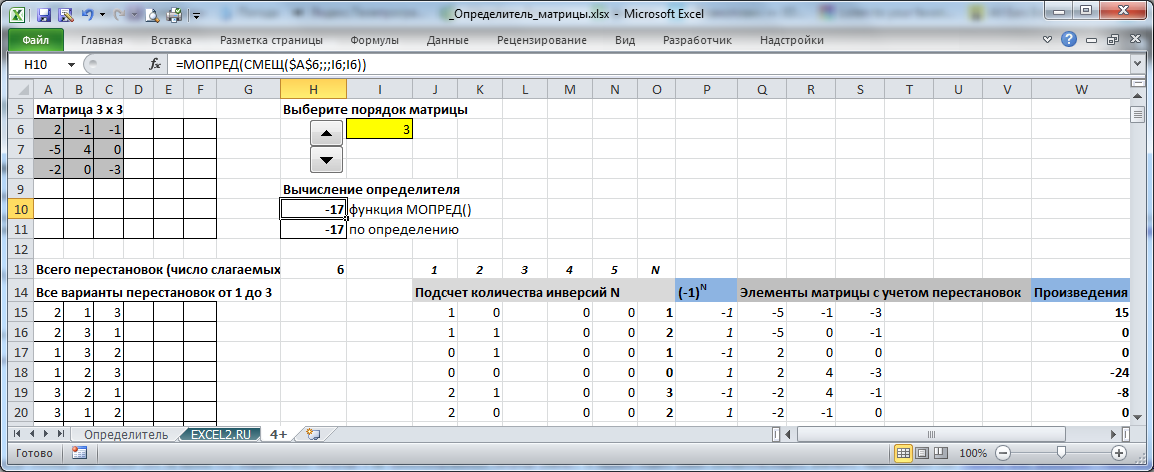
Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:

• а21*а12*а33
• а21*а32*а13
• а11*а32*а23
• а11*а22*а33
• а31*а22*а13
• а31*а12*а23

а21, а12 и т.д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее

транспонированной матрицы

равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).

Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения (

в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы

А

),

а в нашем слагаемом нет элемента из строки 3.

Примечание

: Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок:

(1, 2, 3),

(1, 3, 2),

(2, 3, 1),

(2, 1, 3),

(3, 1, 2),

(3, 2, 1). См. статью

Перестановки без повторений: Комбинаторика в MS EXCEL

Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).

СОВЕТ

: Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье

Перебор всех возможных Перестановок в MS EXCEL

.

Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.

Примечание

:

Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.

Сложив все слагаемые:  (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.

В

файле примера на листе 4+,

и

зменяя порядок матрицы с помощью

элемента управления Счетчик

, можно вычислить определитель матрицы до 6 порядка включительно.

Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования

МОПРЕД()

не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).

РХТУ
им. Д.B.
Менделеева
Кафедра
ИКМ Методическое пособие по изучению
Excel

Операции
с матрицами в Excel

Как и над числами, над матрицами можно
проводить ряд операций, причем в случае
с матрицами некоторые из операций
являются специфическими.

1. Транспонирование.

Транспонированной называется матрица
(A^T), в которой столбцы исходной
матрицы (А) заменяются строками с
соответствующими номерами.

Пример. Пусть в диапазон ячеек А1:Е2
введена матрица размера 2 x
5. Необходимо получить транспонированную
матрицу.

• Выделить указателем мыши при нажатой
  левой кнопке блок ячеек, где будет
  находиться транспонированная матрица.
  В нашем примере блок размера 5 x
  2 в диапазоне А4:В8.

• Нажать на панели инструментов Стандартная
   вставка
  функции.

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категория
  выбрать Ссылки и массивы, а в рабочем
  поле Функция – имя функции ТРАСП
  (рис.1)

рис.1

• Появившееся диалоговое окно ТРАСП
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:Е2 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего, не нажимая кнопку
  ОК, нажать сочетание клавиш CTRL+SHIFT+ENTER
  (рис.2)

• Если транспонированная матрица не
  появилась в заданном диапазоне А4:В8,
  то надо щелкнуть указателем мыши в
  строке формул и повторить нажатие
  клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А4:В8 появится
транспонированная матрица.

Рис.2

1. Вычисление определителя матрицы

Пусть в диапазон А1:С3 введена матрица.
Необходимо вычислить определитель
матрицы

• Табличный курсор поставить в ячейку,
  в которой требуется получить значение
  определителя, например. В А4.

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МОПРЕД.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МОПРЕД
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:С3 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего нажать кнопку ОК.

В ячейке А4 появится значение определителя
матрицы.

1. Нахождение обратной матрицы

Пусть в диапазон А1:С3 введена матрица.
Необходимо в диапазоне А5:С7 получить
обратную матрицу.

• Выделить блок ячеек под обратную
  матрицу (в нашем примере А5:С7)

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МОБР.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МОБР мышью
  отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:С3 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего, не нажимая кнопку
  ОК, нажать сочетание клавиш CTRL+SHIFT+ENTER

• Если обратная матрица не появилась в
  заданном диапазоне А1:С3, то надо щелкнуть
  указателем мыши в строке формул и
  повторить нажатие клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А1:С3 появится
обратная матрица.

1. Сложение и вычитание матриц, умножение
   и деление матрицы на число

Складывать (вычитать) матрицы можно
одного размера. В Excel для
выполнения операция сложения (вычитания)
матриц используются формулы, вводимые
в соответствующие ячейки.

Пример. Пусть матрица А введена в диапазон
А1:С2, а матрица В – в диапазон А4:С5.
Необходимо найти матрицу С, являющуюся
их суммой, в диапазоне Е1:G2.

С = А + В

• Табличный курсор установить в левый
  верхний угол результирующей матрицы
  – ячейку Е1.

• Ввести формулу для вычисления первого
  элемента результирующей матрицы =А1+А4
  (предварительно установить английскую
  раскладку клавиатуры)

• Скопируйте введенную формулу в остальные
  ячейки результирующей матрицы.

В результате в ячейках E1:G2
появится матрица, равная сумме исходных
матриц.

Подобным образом вычисляется разность
матриц, только в формуле вместо знака
+, ставится знак -.

Если необходимо умножить (разделить)
матрицу А на число k, то
формула будет иметь вид =А1*k.

Рис.3

Умножение матриц

Произведение двух матриц определено,
если число столбцов первой матрицы
произведения равно числу строк второй
матрицы произведения.

Пример. Пусть матрица введена в
диапазон A1:D3,
а матрица В – в диапазон А4:В7. Необходимо
найти произведение этих матриц С=А x
В.

• Выделить блок ячеек указателем мыши
  при нажатой левой кнопке под результирующую
  матрицу. Если матрица А имеет размерность
  3 x 4, а матрица В
  имеет размерность 4
  x 3, то результирующая матрица С
  имеет размерность 3
  x 3. Поэтому следует внимательно
  следить, чтобы размерность матрицы С
  в точности соответствовала определению
  произведения двух матриц. Пусть матрица
  С будет размещаться в диапазоне F1:G3.

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МУМНОЖ.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МУМНОЖ
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон первой матрицы
  А1:D3 в рабочее поле Массив1
  (указателем мыши при нажатой левой
  кнопке), а диапазон матрицы В – А4:В7
  ввести в рабочее поле Массив2. После
  чего, не нажимая кнопку ОК, нажать
  сочетание клавиш CTRL+SHIFT+ENTER
  (рис.3)

Рис.4

• Если произведение матриц не появилось
  в заданном диапазоне А1:С3, то надо
  щелкнуть указателем мыши в строке
  формул и повторить нажатие клавиш
  CTRL+SHIFT+ENTER.

В результате в диапазоне F1:G3
появится обратная матрица.

Соседние файлы в папке Excel

• #
• #
• #

  08.01.201420.99 Кб113Excel-таблицы-простые.xls

• #
• #
• #