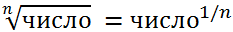Егорова Елена 
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!
Для извлечения корня в Excel и возведения числа в степень используются встроенные функции и математические операторы. Рассмотрим на примерах.
Примеры функции КОРЕНЬ в Excel
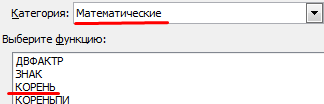
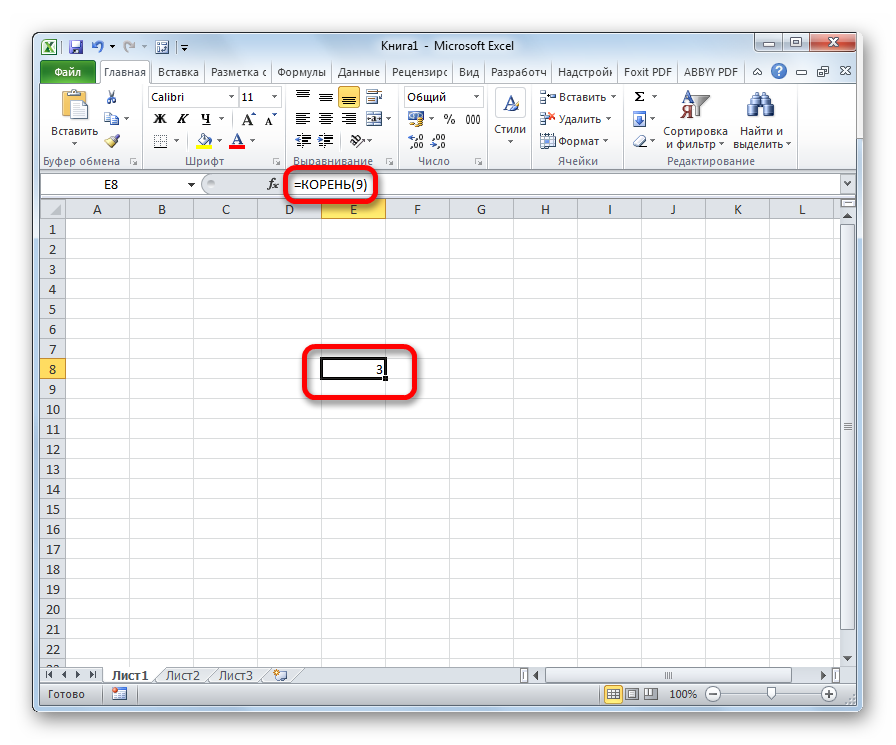
Встроенная функция КОРЕНЬ возвращает положительное значение квадратного корня. В меню «Функции» она находится в категории «Математические».
Синтаксис функции: =КОРЕНЬ(число).
Единственный и обязательный аргумент представляет собой положительное число, для которого функция вычисляет квадратный корень. Если аргумент имеет отрицательное значение, Excel вернет ошибку #ЧИСЛО!.
В качестве аргумента можно указывать конкретное значение либо ссылку на ячейку с числовым значением.
Рассмотрим примеры.
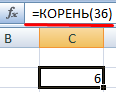
Функция вернула квадратный корень числа 36. Аргумент – определенное значение.
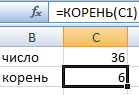
Аргумент функции – ссылка на ячейку с положительным значением 36.
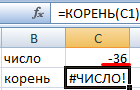
Функция вернула ошибку, т.к. аргумент – ссылка на ячейку с отрицательным значением.
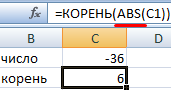
Функция ABS возвращает абсолютное значение числа -36. Ее использование позволило избежать ошибки при извлечении квадратного корня из отрицательного числа.
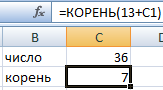
Функция извлекла квадратный корень от суммы 13 и значения ячейки C1.
Функция возведения в степень в Excel
Синтаксис функции: =СТЕПЕНЬ(значение; число). Оба аргумента обязательные.
Значение – любое вещественное числовое значение. Число – показатель степени, в которую нужно возвести заданное значение.
Рассмотрим примеры.
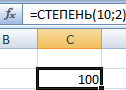
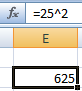
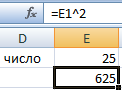
В ячейке C2 – результат возведения числа 10 в квадрат.
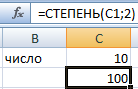
В качестве основания указана ссылка на ячейку с положительным значением 10.
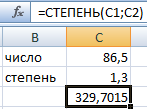
Аргументы функции – ссылки на ячейки с дробными значениями. Результат – число 86,5, возведенное в степень 1,3.
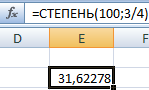
Функция вернула число 100, возведенное к ¾.
Возведение к степени с помощью оператора
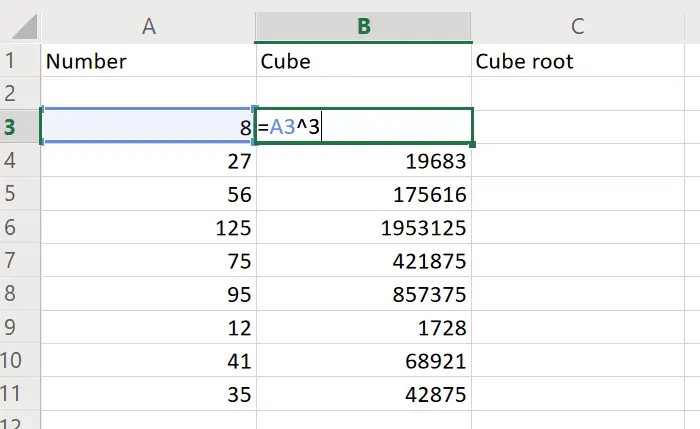
Для возведения числа к степени в Excel, можно воспользоваться математическим оператором «^». Для его введения нажать Shift + 6 (с английской раскладкой клавиатуры).
Чтобы Excel воспринимал вводимую информацию как формулу, сначала ставится знак «=». Далее водится цифра, которую нужно возвести в степень. А после значка «^» – значение степени.
Вместо любого значения данной математической формулы можно использовать ссылки на ячейки с цифрами.
Это удобно, если нужно возвести множество значений.
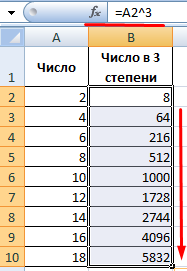
Скопировав формулу на весь столбец, быстро получили результаты возведения чисел в столбце A в третью степень.
Извлечение корней n-й степени
КОРЕНЬ – это функция квадратного корня в Excel. А как извлекать корень 3-й, 4-й и иной степеней?
Вспомним один из математических законов: чтобы извлечь корень n-й степени, необходимо возвести число в степень 1/n.
Например, чтобы извлечь кубический корень, возводим число в степень 1/3.
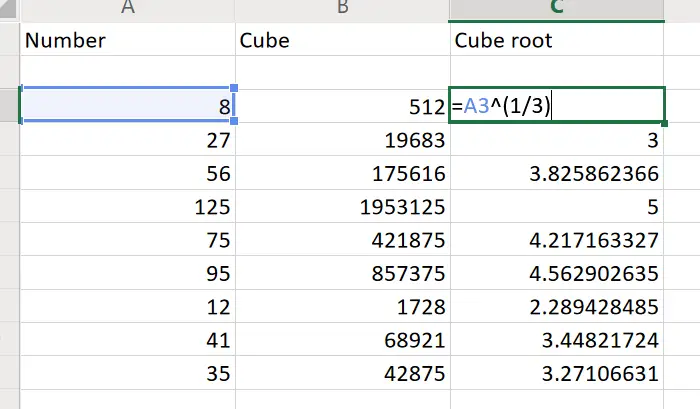
Воспользуемся формулой для извлечения корней разных степеней в Excel.
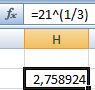
Формула вернула значение кубического корня из числа 21. Для возведения в дробную степень использовали оператор «^».
Обратите внимание! Дробная степень пишется в скобках.
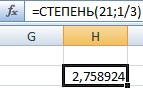
Выполнили ту же задачу, но с использованием функции СТЕПЕНЬ.
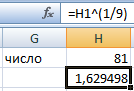
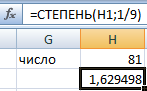
Извлекли корень девятой степени из значения ячейки H1.
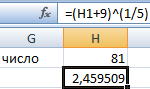
Извлекли корень пятой степени из суммы числа 9 и значения ячейки H1.
Те же математические операции можно выполнить с помощью функции СТЕПЕНЬ:
Таким образом, возвести в степень и извлечь корень n-й степени в Excel можно с помощью одной функции.
Как написать число в степени
Для корректного отображения числа в степени при демонстрации файла или его печати, необходимо произвести ряд манипуляций:
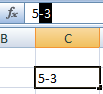
- Щелкаем по ячейке с числом правой кнопкой мыши. Выбираем «Формат ячеек» (или нажмите CTRL+1).
- В открывшемся меню переходим на вкладку «Число». Задаем «Текстовый» формат. Текстовый формат для значения в ячейке можно также задать через панель инструментов («Главная» – «Число»). После установки текстового формата цифра в ячейке становится слева.
- Рядом с цифрой вводим в ячейку значение со знаком «минус».
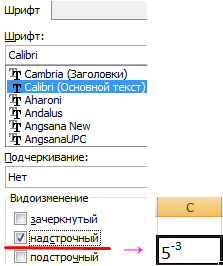
- Выделяем только значение степени («-3»). Вызываем меню «Формат ячеек». Устанавливаем видоизменение «Надстрочный». И нажимаем ОК.
Получили корректное отображение числа 5 в -3 степени.
Среди базовых математических вычислений помимо сложения, вычитания, умножения и деления можно выделить возведение в степень и обратное действие – извлечение корня. Давайте посмотрим, каким образом можно выполнить последнее действие в Эксель разными способами.
- Метод 1: использование функции КОРЕНЬ
- Метод 2: нахождение корня путем возведения в степень
- Заключение
Метод 1: использование функции КОРЕНЬ
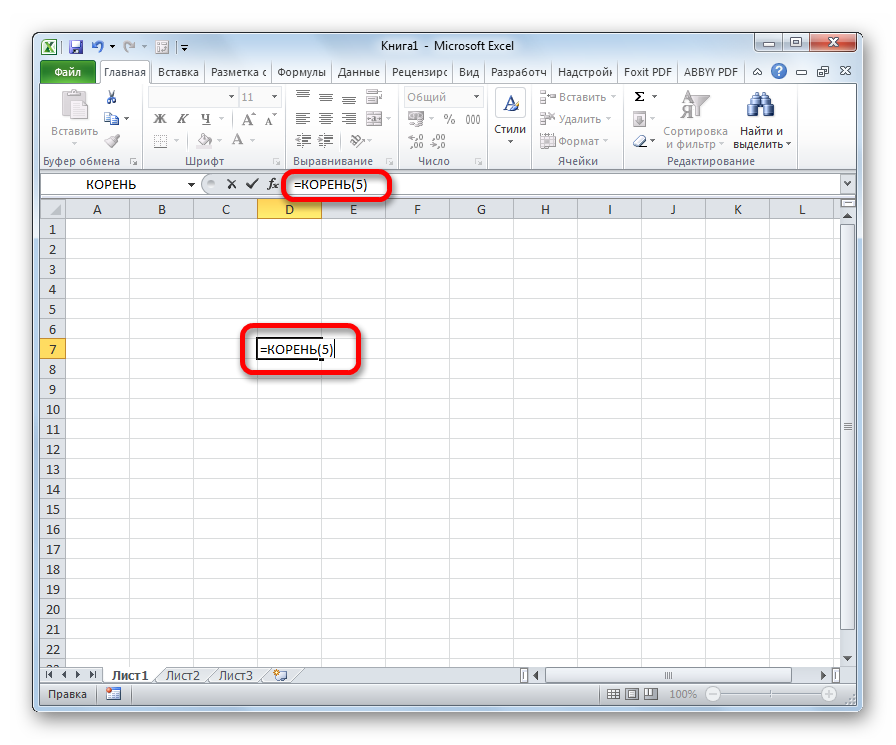
Множество операций в программе реализуется с помощью специальных функций, и извлечение корня – не исключение. В данном случае нам нужен оператор КОРЕНЬ, формула которого выглядит так:
=КОРЕНЬ(число)
Для выполнения расчета достаточно написать данную формулу в любой свободной ячейке (или в строке формул, предварительно выбрав нужную ячейку). Слово “число”, соответственно, меняем на числовое значение, корень которого нужно найти.
Когда все готово, щелкаем клавишу Enter и получаем требуемый результат.
Вместо числа можно, также, указать адрес ячейки, содержащей число.
Указать координаты ячейки можно как вручную, прописав их с помощью клавиш на клавиатуре, так и просто щелкнув по ней, когда курсор находится в положенном месте в формуле.
Вставка формулы через Мастер функций
Воспользоваться формулой для извлечения корня можно через окно вставки функций. Вот, как это делается:
- Выбрав ячейку, в которой мы хотим выполнить расчеты, щелкаем по кнопке “Вставить функцию” (fx).
- В окне мастера функций выбираем категорию “Математические”, отмечаем оператор “КОРЕНЬ” и щелкаем OK.
- Перед нами появится окно с аргументом функции для заполнения. Как и при ручном написании формулы можно указать конкретное число или ссылку на ячейку, содержащую числовое значение. При этом, координаты можно указать, напечатав их с помощью клавиатуры или просто кликнуть по нужному элементу в самой таблице.
- Щелкнув кнопку OK мы получим результат в ячейке с функцией.
Вставка функции через вкладку “Формулы
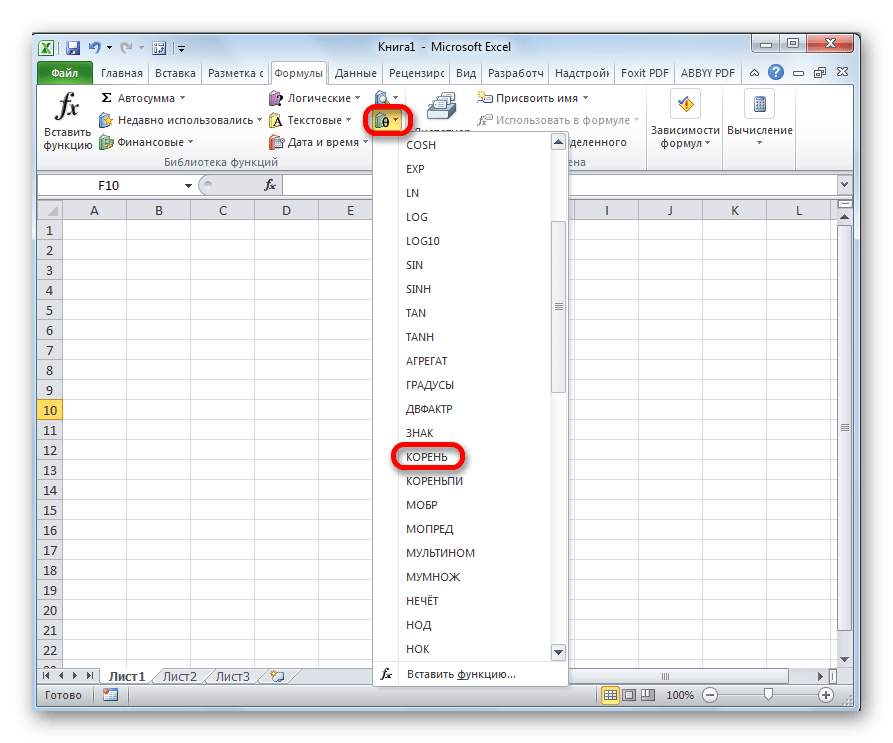
- Встаем в ячейку, в которой хотим произвести вычисления. Щелкаем по кнопке “Математические” в разделе инструментов “Библиотека функций”.
- Пролистав предложенный перечень находим и кликаем по пункту “КОРЕНЬ”.
- На экране отобразится уже знакомое окно с аргументом, который нужно заполнить, после чего нажать кнопку OK.
Метод 2: нахождение корня путем возведения в степень
Описанный выше метод позволяет с легкостью извлекать квадратный корень из числа, однако, для кубического уже не подходит. Но и эта задача в Excel реализуема. Для этого числовое значение нужно возвести в дробную степень, где в числителе будет стоять “1”, а в знаменателе – цифра, означающая степень корня (n).
В общем виде, формула выглядит так:
=(Число)^(1/n)
Безусловным преимуществом такого способа является то, что мы можем извлечь корень любой степени, заменив букву “n” в знаменателе дроби на требуемую цифру.
Для начала давайте рассмотрим формулу для извлечения квадратного корня. Она выглядит следующим образом: =(Число)^(1/2).
Соответственно, для расчета кубического корня будет использоваться выражение ниже:
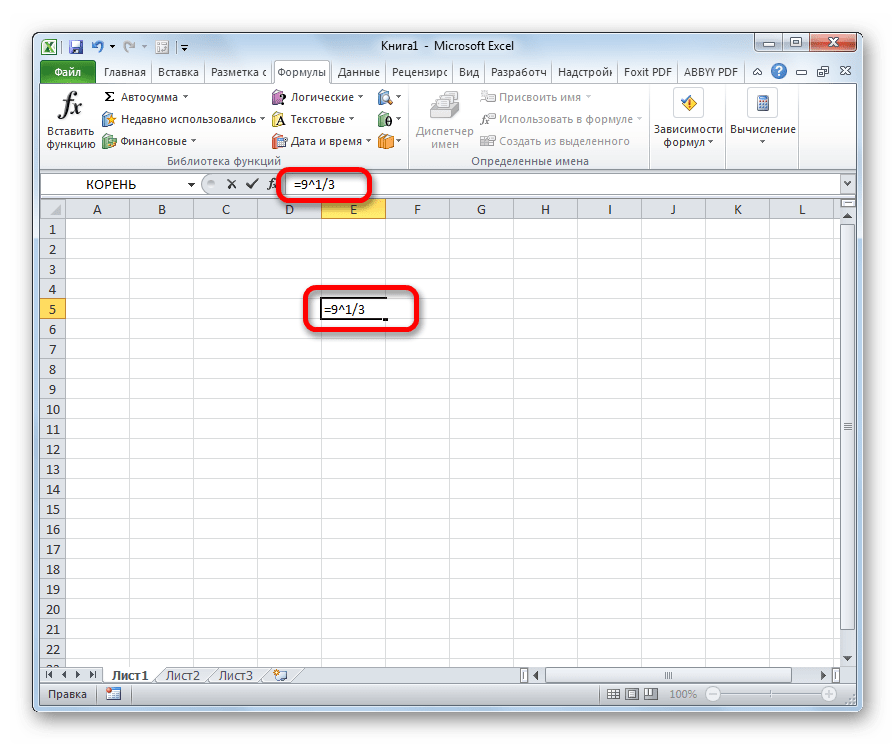
=(Число)^(1/3)
Допустим, нам нужно извлечь кубический корень из числа 27. В этом случае нужно записать в ячейке такую формулу: =27^(1/3).
Нажав Enter, получаем результат вычислений.
Аналогично работе с функцией КОРЕНЬ, вместо конкретного числа можно указать ссылку на ячейку.
Заключение
Таким образом, в Excel можно без особых усилий извлечь корень из любого числа, и сделать это можно разными способами. К тому же, возможности программы позволяют выполнять расчеты для извлечения не только квадратного, но и кубического корня. В редких случаях требуется найти корень n-степени, но и эта задача достаточно просто выполняется в программе.
Содержание
- Способы извлечения
- Способ 1: применение функции
- Способ 2: возведение в степень
- Вопросы и ответы
Извлечение корня из числа является довольно распространенным математическим действием. Оно применяется и для различных расчетов в таблицах. В Microsoft Excel есть несколько способов посчитать данное значение. Давайте подробно рассмотрим различные варианты осуществления подобных расчетов в этой программе.
Способы извлечения
Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.
Способ 1: применение функции
Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.
Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.
Кроме того, можно применить данную формулу через мастер функций.
- Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.
- В открывшемся списке выбираем пункт «КОРЕНЬ». Кликаем по кнопку «OK».
- Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена. Достаточно кликнуть по этой ячейке, чтобы её адрес был внесен в поле. После ввода данных жмем на кнопку «OK».
В итоге в указанной ячейке будет отображаться результат вычислений.
Также функцию можно вызвать через вкладку «Формулы».
- Выделяем ячейку для отображения результата расчета. Переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» на ленте кликаем по кнопке «Математические». В появившемся списке выбираем значение «КОРЕНЬ».
- Открывается окно аргументов. Все дальнейшие действия в точности такие же, как и при действии через кнопку «Вставить функцию».
Способ 2: возведение в степень
Рассчитать кубический корень использование указанного выше варианта не поможет. В этом случае величину нужно возвести в дробную степень. Общий вид формулы для расчета таков:
=(число)^1/3
То есть, формально это даже не извлечение, а возведение величины в степень 1/3. Но данная степень и является корнем кубическим, поэтому именно такое действие в Эксель используется для его получения. В эту формулу вместо конкретного числа также можно вписать координаты ячейки с числовыми данными. Запись производится в любой области листа или в строке формул.
Не стоит думать, что данный способ можно применять только для извлечения кубического корня из числа. Таким же образом можно рассчитать квадратный и любой другой корень. Но только в этом случае придется использовать следующую формулу:
=(число)^1/n
n – это степень возведения.
Таким образом, этот вариант является намного универсальнее, чем использование первого способа.
Как видим, несмотря на то, что в Excel нет специализированной функции для извлечения кубического корня, данное вычисление можно провести, используя возведение в дробную степень, а именно — 1/3. Для извлечения квадратного корня можно воспользоваться специальной функцией, но существует также возможность сделать это путем возведения числа в степень. На этот раз нужно будет возвести в степень 1/2. Пользователь сам должен определить, какой способ вычислений для него удобнее.
Еще статьи по данной теме:
Помогла ли Вам статья?
Нахождение квадратного и кубического корня с помощью функций и формул
При работе с Microsoft Excel вы можете найти квадратный корень из чисел двумя способами. Вы можете использовать функцию, которая уже запрограммирована в формате Excel, которая называется функцией «КОРЕНЬ». И второй метод — это вручную добавить формулу квадратного корня из числа, для которого вы хотите получить значение квадратного корня. Давайте посмотрим, как можно использовать оба метода.
Но прежде чем мы перейдем к тому, как можно работать с обоими методами нахождения квадратного корня из числа, вам необходимо знать основы работы с таблицами Excel. Иногда мы допускаем незначительные ошибки в наших записях в таблице Excel, которые могут дать нам неточные или ожидаемые ответы. Чтобы избежать таких ошибок, необходимо всегда помнить следующие важные основы использования листов Excel. И даже если вы забыли их использовать и обнаружили ошибку, вы можете перепроверить список ниже, чтобы убедиться, что ошибка возникла из-за пропуска этих шагов.
- Знак «=». Знак равенства — самая важная часть формулы. Вы упустите это, и введенная вами формула или функция будет просто отображаться как простой текст. Добавление знака «=» в ячейку перед вводом формулы или функции является частью реализации формулы в этой ячейке.
- Скобки (). Скобки играют очень важную роль в формулах и функциях Excel. Поэтому убедитесь, что вы добавили скобки в свою функцию, поскольку они должны быть добавлены. Для большинства функций скобки обычно содержат значение или номера ячеек, по которым будет реализована формула.
- Наконец, клавиша ввода. Нажмите клавишу ввода после закрытия скобок или заполнения формулы, чтобы наконец сделать функцию функцией.
Важно отметить, что пропуск любого из них не даст вам ответов по существу или даже может привести к ошибке. Так что запомните это.
Способ 1
Функция SQRT в Microsoft Excel
- Откройте лист Excel на пустой странице. Или, если вы уже создали файл данных, откройте его. Основная идея — иметь числа, для которых нужен квадратный корень.
Работа с Microsoft Excel может быть хорошим опытом. Он помогает своим пользователям во многих отношениях.
- Теперь, например, я хочу узнать квадратный корень из числа 7. Я напишу функцию, как показано на рисунке ниже.
= sqrt (число)
Я начну со знака равенства, и после добавления этого значения в ячейку, в которой я хочу отображать квадратный корень значений, я начну набирать «sqrt». Через минуту введите s, список формул начнет появляться в раскрывающемся списке для этой ячейки. Теперь, когда я вижу формулу sqrt, я дважды щелкаю по ней, и она отображается в выбранной ячейке.
Начните вводить функцию
Открывающая скобка появляется автоматически, когда вы дважды щелкаете по формуле, вы добавляете сюда номер / значение ячейки, закрываете скобку и нажимаете ввод.
Двойной щелчок по формуле, которая появляется в раскрывающемся списке ячейки, открывает саму скобку.
После открытой скобки вы вводите либо номер ячейки, либо само число / значение
Добавление числа, для которого вы хотите найти квадратный корень, в скобках функции.
Ответ в обоих случаях будет одним и тем же независимо от того, добавляете ли вы само значение или номер ячейки.
Квадратный корень из числа 7.
Это ваш квадратный корень для 7. Если вы не уверены, следует ли вам добавлять номер ячейки или значение напрямую, я бы посоветовал вам добавить номер ячейки. Потому что существует высокая вероятность того, что вам, возможно, придется внести некоторые изменения в свой лист Excel. Если число в ячейке A2 изменилось, и если вы написали A2 в формуле функций, значение квадратного корня изменится автоматически. В противном случае вам придется вручную изменить значение для каждой ячейки, в которую вы добавили «7» вместо «A2».
Способ 2
Добавление формулы для квадратного корня вручную
Формула, которую вы должны ввести вручную в ячейку для нахождения квадратного корня из числа, выглядит следующим образом:
= число ^ (1/2)
или же
= число ^ 0,5
Вы можете увидеть следующие изображения, чтобы убедиться, как это можно сделать.
= число ^ (1/2) Скобки здесь будут играть очень важную роль, поэтому не перемещайте скобки.
Квадратный корень после добавления формулы вручную = число ^ (1/2)
= число ^ 0,5
квадратный корень, используя = число ^ 0,5
Кубический корень
Чтобы найти корень куба, вы можете вручную ввести = число ^ (1/3). Единственное отличие здесь — число 3. Вы также можете использовать функцию Power, как показано на изображении ниже, чтобы найти кубический корень числа.
Использование функции Power в Excel, чтобы найти Cub Root
Мощность (количество ячеек, мощность)
Ответ на кубический корень.
Download PC Repair Tool to quickly find & fix Windows errors automatically
Finding cubes and cube roots have plenty of real-life applications. They are essential as a part of many mathematical functions. Even more, they are used for estimating the volume of vessels. If you wish to find the cube and cube root of numbers in a cell or a range of cells in Excel, please read through this article.
There is no specific known function for finding the cube or cube root in Excel, so you could use the exponential function instead. That is seemingly the easiest option.
The syntax of the formula for finding the cube of a number in Excel is as follows:
=<first cell with number>^3
Where, <first cell with number> is the first cell in the range of cells from which you start counting the cube for the range of cells.
Eg. Let us consider an example where you have a range of numbers across column A from cell A3 to cell A11. You need the cube of these numbers in the respective columns across column B, from cells B3 to B11. To do so, enter the following formula in cell B3:
=A3^3
When you hit Enter, Excel will return the value of the cube of the number in cell A3 to the cell B3. Then, you can use the Fill function to pull the formula down to cell B11. To do so, click on any cell outside cell B3 (which contains the formula) and then back on it.
This will highlight the Fill function which is represented by a small dot at the right-bottom corner of the selected cell. Now, hover your mouse over that dot, click it, and without releasing the click, pull the formula down to cell B11.
How to find the Cube Root in Excel
The syntax of the formula for finding the cube of a number in Excel is as follows:
=<first cell with number>^(1/3)
Where, <first cell with number> is the first cell in the range of cells from which you start counting the cube for the range of cells.
Eg. Let us consider the previous example and add that you need the list of cube roots in column C, from C3 to C11. So, the formula you would have to enter the following formula in cell C3:
=A3^(1/3)
Hit Enter to get the cube root for the number in cell A3 in cell C3 and then use the Fill function to pull the formula down till cell C11.
Read: How to find the Square and Square Root of a number in Excel.
Hope it helps!
Karan is a B.Tech, with several years of experience as an IT Analyst. He is a passionate Windows user who loves troubleshooting problems and writing about Microsoft technologies.
Автор:
Обновлено: 09.10.2022
Пользователи электронных таблиц широко используют функцию по извлечению корня числа. Поскольку работа с данными обычно требуют обработки больших чисел, считать вручную бывает довольно сложно. В этой статье вы найдете подробный разбор вопроса об извлечении корня любой степени в Excel.
Как извлечь корень любой степени в Excel 2010-2013?
Содержание
- Извлечение квадратного корня
- Извлечение корней 3-ей, 4-ой и других степеней.
- Извлечение корня любой степени с помощью функции
- Извлечение корня любой степени с использованием значка степени «^»
- Примеры записи выражений
- Видео — Как извлечь корень любой степени в Excel
Извлечение квадратного корня
Довольно легкая задача, поскольку в программе присутствует отдельная функция, которую можно взять из перечня. Для этого вам нужно сделать следующее:
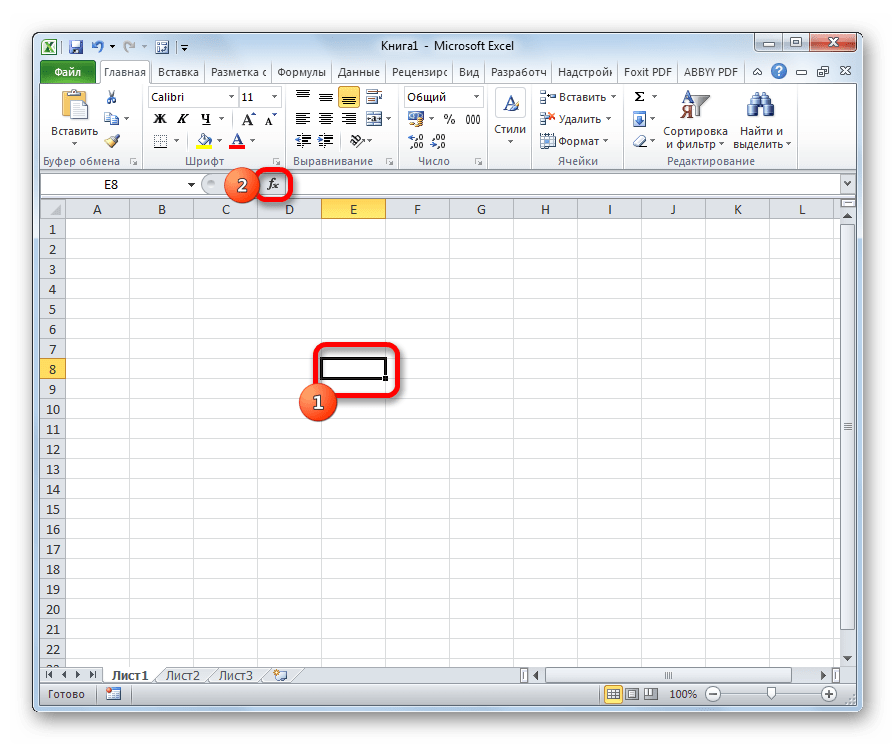
- Выберите ячейку, в которой хотите прописать функцию, кликнув на нее один раз левой кнопкой мыши. Появится черная обводка, оранжевым подсветятся активная строка и столбец, а в адресной ячейке появится имя.
Левой кнопкой мышки щелкаем по нужной ячейке
- Нажмите на кнопку «fx» («Вставить функцию»), которая расположена выше названий столбцов, после адресной ячейки, перед строкой формул.
Щелкаем по кнопке «fx» («Вставить функцию»)
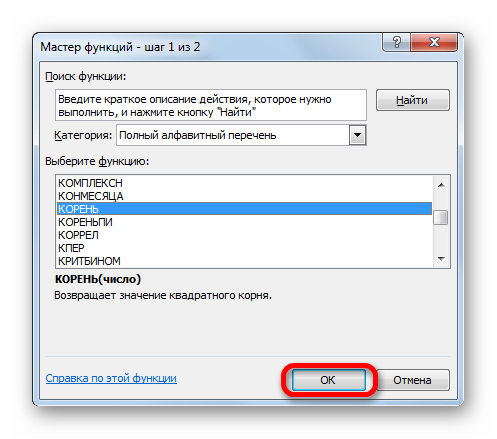
- Появится ниспадающее меню, в котором нужно найти функцию «Корень». Это можно сделать в категории «Математические» или в «Полном алфавитном перечне», прокрутив мышкой меню чуть ниже.
В разделе «Категория» выбираем из списка «Полный алфавитный перечень» или «Математические»
- Выберите пункт «Корень», нажав один раз левой кнопкой мыши, далее – кнопку «ОК».
В окне «Выберите функцию» пролистываем мышкой ниже, находим и выделяем функцию «Корень», нажимаем «ОК»
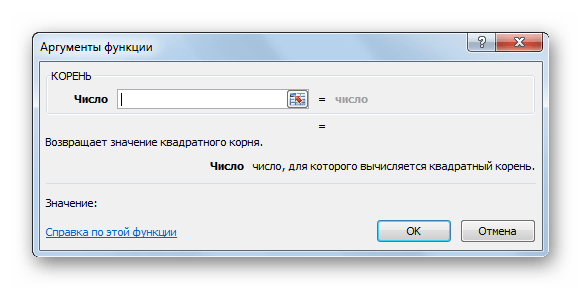
- Появится следующее меню – «Аргументы функции».
Окно «Аргументы функции»
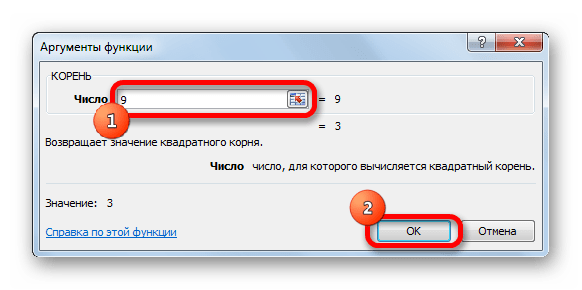
- Введите число или выберите ячейку, в которой заранее было написано данное выражение или формула, для этого один раз кликните левой кнопкой по строке «Число», далее наведите курсор на нужную вам ячейку и нажмите на нее. Имя ячейки будет автоматически забито в строку.
В поле «Число» вводим число, из которого извлекаем квадратный корень
- Нажмите на кнопку «ОК».
Кликаем по кнопке «ОК»
- И все готово, функция посчитала квадратный корень, записав результат в выбранную ячейку.
Посчитанный результат функцией в выбранной ячейке
Читайте подробную инструкцию в нашей новой статье — «Как написать формулу в Excel?Обучение азам работы в Excel».
Существует также возможность извлечь квадратный корень из суммы числа и ячейки (данных, которые забиты в данной ячейке) или двух ячеек, для этого введите значения в строку «Число». Напишите число и кликните один раз по ячейке, программа сама поставит знак сложения.
На заметку! Эту функцию можно вписать и вручную. В строку формул введите следующее выражение: «=КОРЕНЬ(x)», где х – искомое число.
В ячейке вводим значение «=КОРЕНЬ(64)» вручную, нажимаем «Enter»
Извлечение корней 3-ей, 4-ой и других степеней.
Отдельной функции для решения этого выражения в Excel нет. Для извлечения корня n-ой степени необходимо для начала рассмотреть его с математической точки зрения.
Корень n-ой степени равен возведению числа в противоположную степень (1/n). То есть, квадратный корень соответствует числу в степени ½ (или 0.5).
Например:
- корень четвертой степени из 16 равен 16 в степень ¼;
- кубический корень из 64 = 64 в степени 1/3;
Выполнить данное действие в программе электронных таблиц можно двумя способами:
- С помощью функции.
- Используя значок степени «^», ввести выражение вручную.
Извлечение корня любой степени с помощью функции
- Выберите нужную ячейку и кликните на «Вставить функцию» во вкладке «Формулы».
Выделяем ячейку, переходим во вкладку «Формулы», щелкаем по опции «Вставить функцию»
- Раскройте список в пункте «Категория», в категории «Математические» или «Полный алфавитный перечень» найдите функцию «Степень».
В разделе «Категория» выбираем из списка «Полный алфавитный перечень» или «Математические»
Находим и выделяем функцию «Степень», нажимаем «ОК»
- В строке «Число» введите цифру (в нашем случае – это число 64) или имя ячейки, кликнув на нее один раз.
Вводим число в строке «Число»
- В строчке «Степень» напечатайте степень, в которую вы хотите возвести корень (1/3).
В поле «Степень» вводим значение степени, в которую хотим возвести корень
Важно! Для обозначения знака деления необходимо использовать значок «/», а не стандартный знак деления «:».
- Нажмите «ОК», и результат действия появится в изначально выбранной ячейке.
Щелкаем «ОК»
Результат извлечения корня любой степени с помощью функции
Примечание! Наиболее подробную инструкцию с фото по работе с функциями смотри в статье выше.
Извлечение корня любой степени с использованием значка степени «^»
- Выберите ячейку и наведите курсор на строку формул, нажав единожды левой кнопкой мыши.
Щелкаем по ячейке, затем левой кнопкой мышки кликаем по строке формул
- Введите выражение, начиная со знака «=» (тогда программа воспримет текст как математическое выражение), и занесите степень в круглые скобки. В нашем случае: =64^(1/3). Получается, формула имеет общий вид: «Корень n-ой степени из x = x^(1/n)».
Вводим в поле формулу, начиная со знака «=»
- Переключитесь на другую ячейку, кликнув 1 раз левой кнопкой мыши, программа сама выведет результат.
Кликаем левой кнопкой мышки по пустой ячейке, в ячейке с формулой автоматически появится результат
Примечание! Записывать степень можно как дробью, так и десятичным числом. Например, дробь ¼ можно записать как 0,25. Для отделения десятых, сотых, тысячных и так далее разрядов используйте запятую, как принято в математике.
Пример ввода степени десятичным числом
Примеры записи выражений
- «=16^(1/4)» – извлечение корня 4-ой степени из 16;
Результат извлечение корня 4-ой степени из 16
- «=А1^(0,5)» – кубический корень из выражения, записанного в ячейке «А1»;
Результат кубического корня из выражения, записанного в ячейке «А1»
- «=(B1+30)^(1/3)» – извлечение кубического корня из суммы числа 30 и значения ячейки «B1».
Результат извлечения кубического корня из суммы числа 30 и значения ячейки «B1»
Читайте также подробную инструкцию в новой статье — «Как посчитать сумму в EXcel? Как сложить числа в ячейках».
С наглядной пошаговой инструкцией вы можете ознакомиться по видео.
Видео — Как извлечь корень любой степени в Excel
Рекомендуем похожие статьи
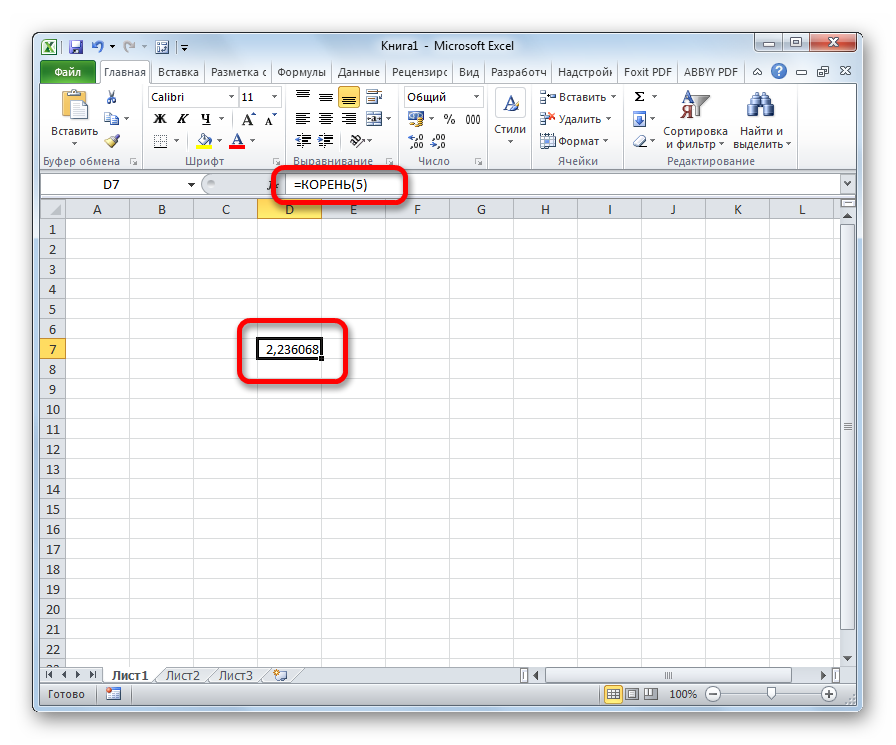
На клавиатуре нет кнопок с написанием квадратного или другого корня, поэтому в Excel создана специальная функция, вводит и вычисляет квадратный корень. Как ей воспользоваться, а также как извлечь корни разных степеней в Excel? Рассмотрим несколько примеров.
Важно! Функции в Excel вводятся в ячейках русскими буквами без пробелов, перед названием функции ставится знак равно =
За квадратный корень отвечает функция КОРЕНЬ(значение). Чтобы воспользоваться ей, нужно в ячейке написать =КОРЕНЬ и без пробелов внутри скобки написать значение, от которого нужно найти квадратный корень.
Для квадратного корня есть своя функция — КОРЕНЬ — а как быть с другими с другими корнями?
Из курса математики известно, что извлечение корня N —степени равно возведению числа в степень 1/ N .
Этой формулой и нужно пользоваться для вычисления корней разных степеней в Excel. Для возведения степени использовать функцию СТЕПЕНЬ(аргумент) или галочку ^ (на английской раскладке SHIFT + 6). Саму дробную степень писать в скобках.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
2007-2022 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.
Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.
Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
- Опубликовать урок
- Опубликовать статью
- Дать объявление
- Подписаться на новости
- Частые вопросы
сервис вебинаров —>
О работе с сайтом
Мы используем cookie.
Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.
При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.
Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены. 
Как найти корни кубического уравнения в эксель
Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).
Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.
Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

|
| Рис. 8. График функции |
Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:
где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).
- В ячейку Хнач (В4) заносим начальное приближение — 5.
- В ячейку Хтекущ (С4) записываем формулу:
=ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)). - В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
- Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
- Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
Рис. 9. Определение начальных установок значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.
2.2. Подбор параметра
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:
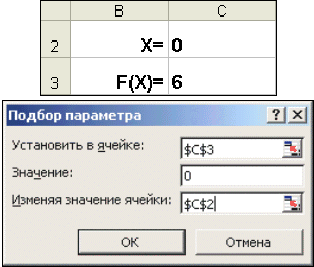
- В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
Рис. 10. Окно диалога Подбор параметра стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
- В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
- После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.
Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):
- В ячейку Х (С2) вводим начальное приближение.
- В ячейку Хi (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
=X-(X^2-5*X+6)/(2*X-5). - В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Хi.
- После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).
Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.
2.3. Поиск решения
Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.
Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:
Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х1, х2, … , хn), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:
- найти максимум целевой функции F(х1, х2, … , хn);
- найти минимум целевой функции F(х1, х2, … , хn);
- добиться того, чтобы целевая функция F(х1, х2, … , хn) имела фиксированное значение: F(х1, х2, … , хn) = a.
Функции G(х1, х2, … , хn) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.
Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.
Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
|
| Рис. 12. Окно диалога Поиск решения |
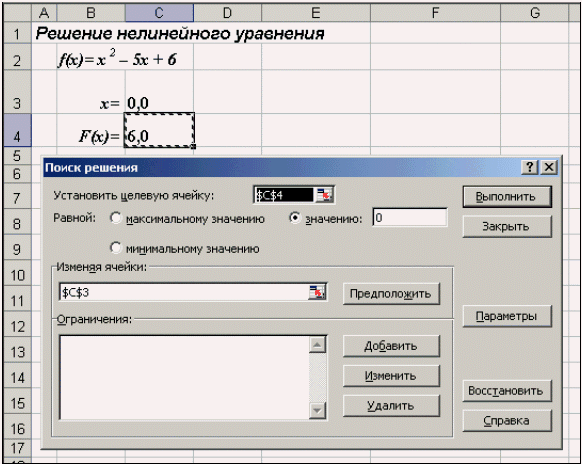
После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:
- в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
- для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
- в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
- в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
- для запуска процесса поиска решения нажать кнопку Выполнить.

|
| Рис. 13. Результаты поиска |
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
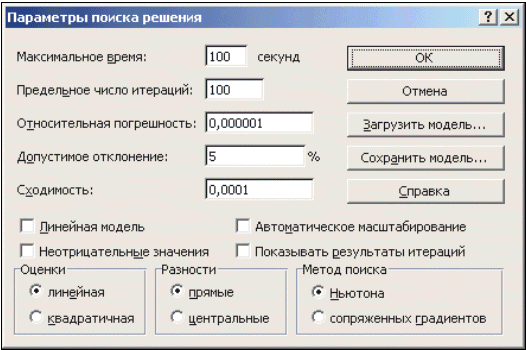
Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):
|
| Рис. 14. Настройка параметров Решателя |
- Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
- Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
- Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
- Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
- Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
- Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
- Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
- Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
- Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
- Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
- Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
- Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Сохранить модель поиска решения можно следующими способами:
- при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
- если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
- еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.
Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.
|
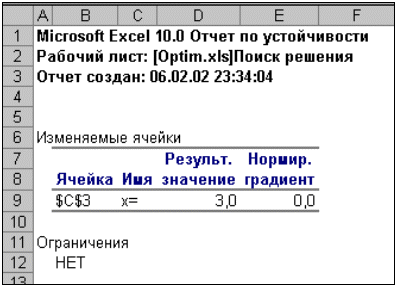
| Рис. 15. Отчет по устойчивости |
Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

|
| Рис. 16. Отчет по результатам |
Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.
Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://old.exponenta.ru/EDUCAT/systemat/pimonov/Equations/gl2.asp
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/