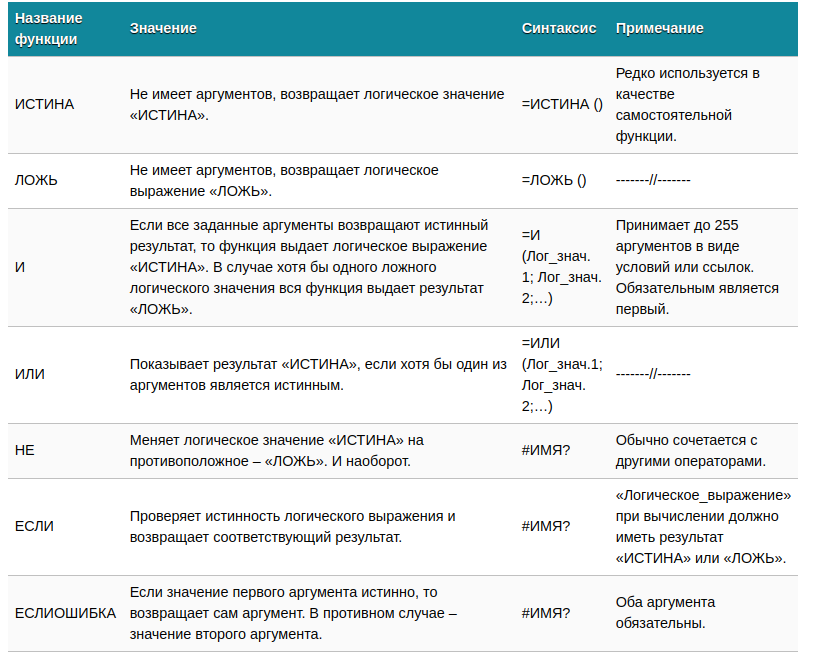
Автор Антон Андронов На чтение 1 мин Опубликовано 30.05.2015
В Excel очень легко создавать практически все виды последовательностей. Например, последовательность Фибоначчи.
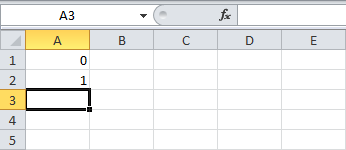
- Первые два числа в последовательности Фибоначчи – 0 и 1.
- Каждое последующее значение можно найти путем сложения двух предыдущих чисел.
- Нажмите на правый нижний угол ячейки A3 и перетащите его вниз.
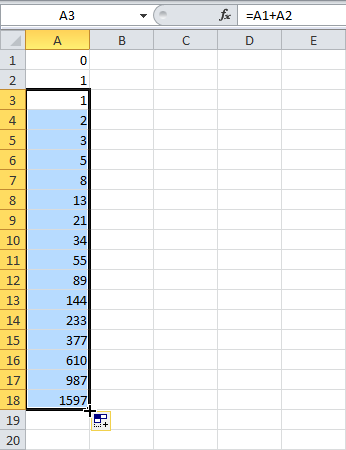
Результат: Последовательность Фибоначчи в Excel:
Оцените качество статьи. Нам важно ваше мнение:
Вам также может понравиться
Работая с таблицами Excel, иногда возникает необходимость
Тем людям, которые регулярно работают с таблицами Excel
Нередко пользователям приходится перенести часть информации
Огромное преимущество электронных таблиц Excel заключается
Пользователю Excel нередко приходится сталкиваться
Excel – одна из лучших программ для аналитика данных.
Время от времени при работе с электронными таблицами
Excel – удивительная программа, дающая возможность
Сейчас век информации. Количество данных, которые людям
Определение процента от числа – довольно частая задача
Excel – невероятно функциональная программа.
Excel – невероятно функциональная программа, позволяющая
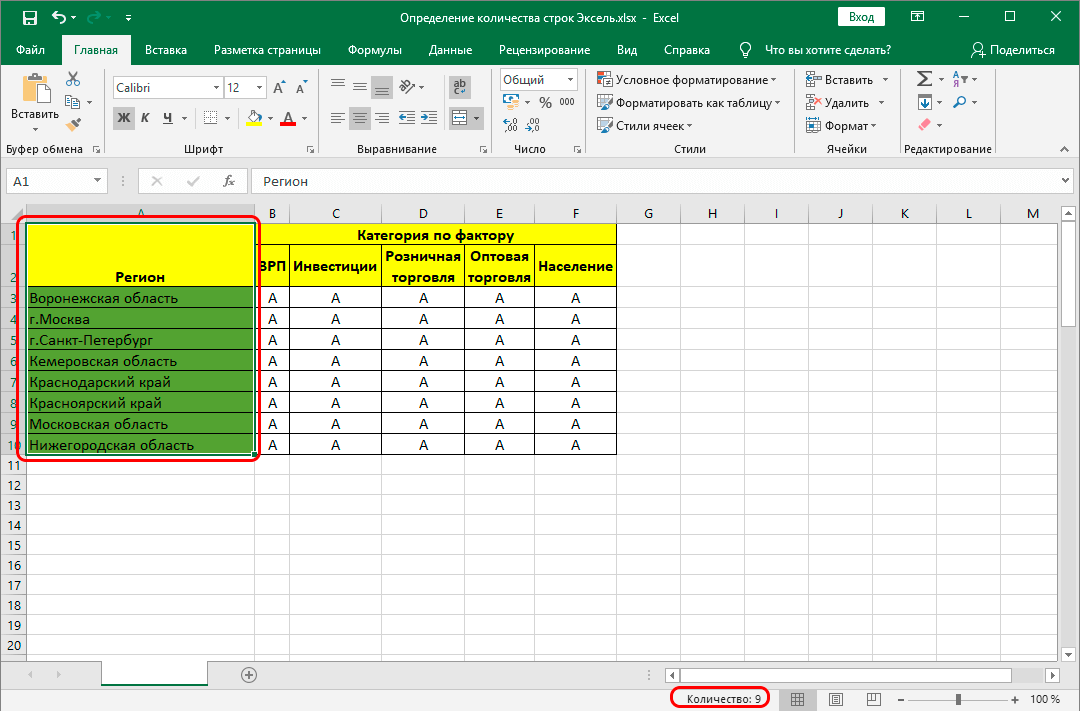
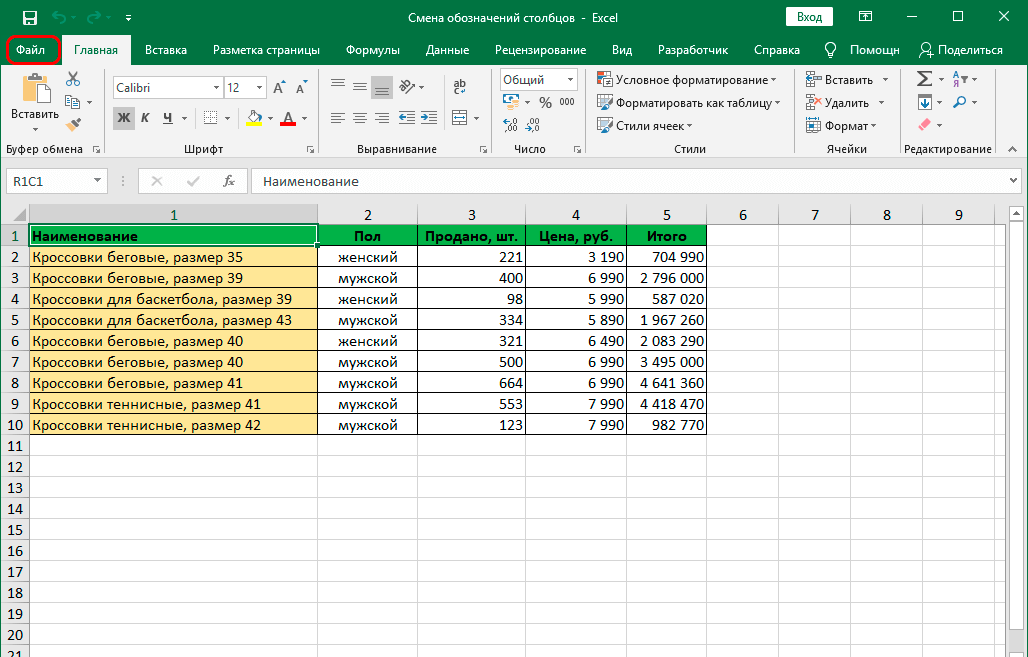
Стандартное обозначение строк в Excel – цифровое.
Набор функций у программы Excel, конечно, поистине огромный.
При работе с Excel могут возникать различные ситуации
Важно понимать, что Excel – это не только программа
Числа Фибоначчи – это последовательность чисел, которая начинается с цифр 0 и 1, а каждое последующее значение является суммой двух предыдущих.
- Формула последовательности Фибоначчи
- Золотое сечение
- Таблица последовательности Фибоначчи
- C-код (Си-код) функции
Формула последовательности Фибоначчи
Например:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Золотое сечение
Соотношение двух последовательных чисел Фибоначчи сходится к золотому сечению:
где φ – это золотое сечение = (1 + √5) / 2 ≈ 1,61803399
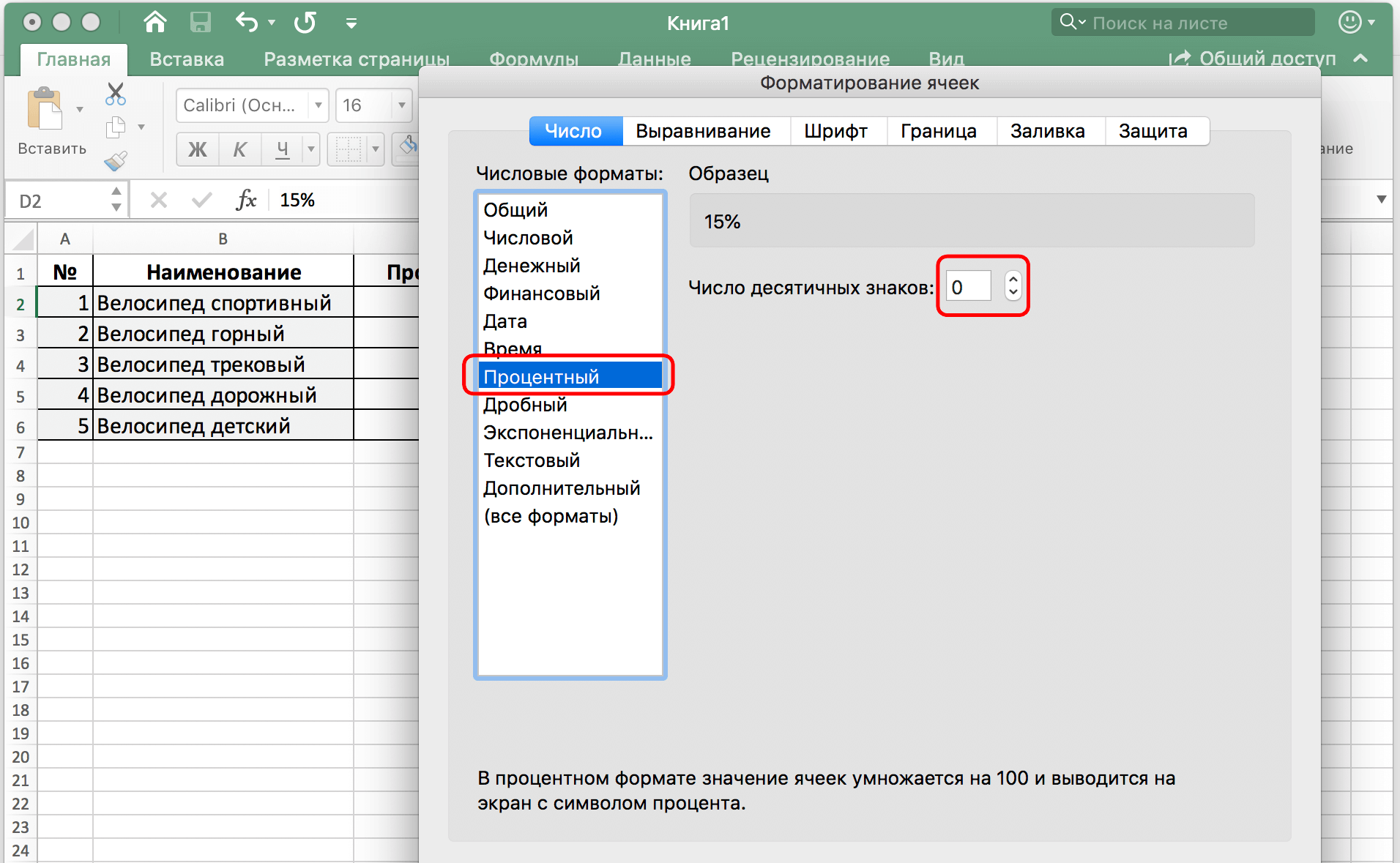
Чаще всего, это значение округляют до 1,618 (или 1,62). А в округленных процентах пропорция выглядит так: 62% и 38 %.
Таблица последовательности Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
microexcel.ru
C-код (Си-код) функции
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n > 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
As with all basic math operations in Excel, if you wish to add two or more numbers, create a formula. Formulas offer a quick way to find the sum of a few digits.
Instructions in this article apply to Excel for Microsoft 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010, Excel 2007, and Excel for Mac.
Excel Formula Syntax
Some important points to remember about Excel formulas:
- Formulas in Excel begin with an equal sign.
- The equal sign is typed into the cell where the answer will appear.
- The addition sign in Excel is the plus symbol.
- Formulas are completed by pressing the Enter key.
Use Cell References in Addition Formulas
In the example data shown below, rows 2 through 4 use a formula that is located in column C to add the data in columns A and B. In row 2, the result is computed using an addition formula, =5+5.
Rows 3 and 4 show how it is better to first enter the data into worksheet cells and then use the addresses, or references, of those cells in the formula. For example, =A3+B3.
One advantage of using cell references rather than the actual data in a formula is that if you want to change the data, you’ll replace the data in the cell rather than rewrite the entire formula. The results of the formula update automatically when the data changes.
Enter Cell References With Point and Click
Although it is possible to type the above formula into cell C3 and have the correct answer appear, it’s easier to use point and click to add the cell references to formulas. This approach reduces the possibility of errors created by typing the wrong cell reference.
Point and click involves selecting the cell containing the data to add the cell reference to the formula instead of manually typing it into the cell.
Use the Addition Formula in Excel
Creating the example shown below in cell C3 is simple when you use a formula to add the values of cells A3 and B3.
Here’s how to create an addition formula:
-
Select cell C3 and type an equal sign to begin the formula.
-
Select cell A3 to add that cell reference to the formula after the equal sign.
-
Type the plus sign into the formula after A3.
-
Select cell B3 to add that cell reference to the formula after the addition sign.
-
Press Enter to complete the formula.
-
The answer 20 appears in cell C3.
Select the cell to display the formula in the formula bar above the worksheet.
Change the Formula
To change or correct a formula, select one of two options:
- Double-click the formula in the worksheet to place Excel in Edit mode and then make changes to the formula.
- Select the cell containing the formula and recreate the entire formula.
Create More Complex Formulas
To write more complex formulas that include other mathematical operators, use the steps listed above to get started and then continue to add the correct mathematical operators followed by the cell references containing the new data.
Before mixing different mathematical operations together in a formula, make sure you understand the order of operations that Excel follows when evaluating a formula.
Create a Fibonacci Sequence
A Fibonacci sequence, created by the 12th-century Italian mathematician Leonardo Pisano, forms a continuous series of increasing numbers. These series are used to explain, mathematically, different patterns found in nature such as:
- The spiral shape of seashells.
- The arrangement of leaves on a tree branch.
- The reproduction pattern of bees.
After two starting numbers, each additional number in the series is the sum of the two preceding numbers. The simplest Fibonacci sequence, shown in the image above, begins with the numbers zero and one.
Since a Fibonacci series involves addition, it can be created with an addition formula in Excel, as shown in the image above.
The steps below detail how to create a simple Fibonacci sequence using a formula. The steps involve creating the first formula in cell A3 and then copying that formula to the remaining cells using the fill handle. Each iteration, or copy, of the formula adds together the previous two numbers in the sequence.
To create the Fibonacci series shown in the example:
-
In cell A1, type 0 (a zero) and press Enter.
-
In cell A2, type 1 and press Enter.
-
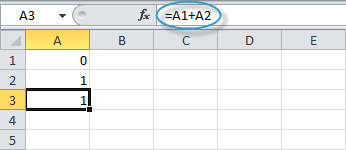
In cell A3, type the formula =A1+A2 and press Enter.
-
Select cell A3 to make it the active cell.
-
Place the mouse pointer over the fill handle (it’s the dot in the bottom right corner of cell A3). The pointer changes to a black plus sign when it is over the fill handle.
-
Drag the fill handle down to cell A19.
-
Cell A19 contains the number 2584.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe
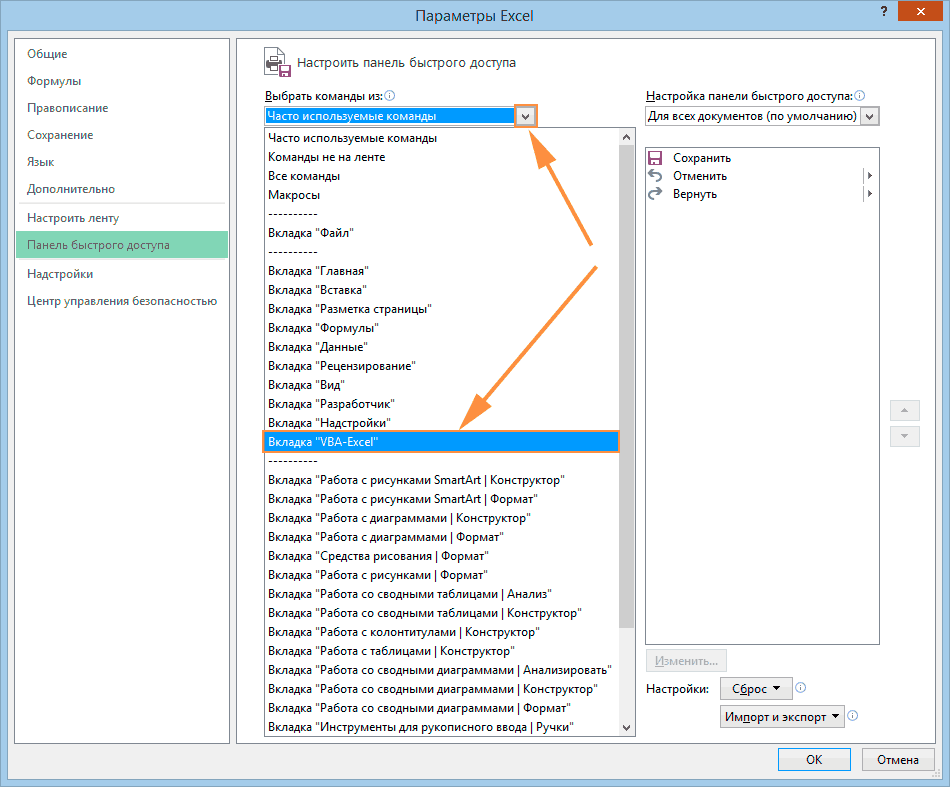
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |
|
1 / 1 / 0 Регистрация: 16.02.2010 Сообщений: 47 |
|
|
1 |
|
Число фибоначчи15.12.2010, 15:29. Показов 14624. Ответов 3
Всем доброго времени суток.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
15.12.2010, 15:29 |
|
3 |
|
671 / 177 / 10 Регистрация: 28.07.2010 Сообщений: 253 |
|
|
15.12.2010, 16:10 |
2 |
|
А в чем проблема?
0 |
|
1 / 1 / 0 Регистрация: 16.02.2010 Сообщений: 47 |
|
|
15.12.2010, 20:13 [ТС] |
3 |
|
а это точно правильно ?
0 |
|
956 / 596 / 11 Регистрация: 11.06.2010 Сообщений: 1,345 |
|
|
15.12.2010, 20:23 |
4 |
|
а это точно правильно ? Нет, Дмитрий просто пошутил. Вот из Википедии: Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,… (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
15.12.2010, 20:23 |
|
4 |
Увы, это доказательство не приносит полного удовлетворения, поскольку не отвечает на вопрос, откуда вообще берутся подобные удивительные формулы. Мы выясним это в разделе «Вывод формулы Бине».
Мы провели эксперимент, и выяснилось, что вычисление по формуле Бине даёт первую ошибку для числа F 71 : вместо правильного значения 308061521170129 получилось 308061521170130 .
Вывод формулы Бине
Для вывода формулы Бине мы без колебаний выбрали из миллиона различных методов самый, на наш взгляд, впечатляющий — метод производящих функций.
Пусть нас не волнует то, как именно будет вычисляться эта бесконечная сумма при тех или иных значениях z — мы отнесёмся к ней формально. Для наших целей важно лишь то, что определённые операции над последовательностями соответствуют определённым действиям над производящими функциями:
- Умножение всех элементов последовательности A на число q приводит к умножению на q её производящей функции: q A ⇄ q A z .
- Поэлементной сумме или разности двух последовательностей отвечает сумма или разность их производящих функций: A ± B ⇄ A z ± B z .
- Начальный элемент последовательности равен значению её производящей функции при нулевом z : A 0 = A 0 .
- Вставке нуля в начало последовательности соответствует умножение её производящей функции на z : ⊢ A = 0 A 0 A 1 A 2 A 3 … ⇄ z A z .
- Удаление первого элемента последовательности приводит к вычитанию этого элемента из производящей функции и последующему делению на z : ⊣ A = A 1 A 2 A 3 … ⇄ A z − A 0 z . Для удаления первых n элементов получаем ⊣ n A = A n A n + 1 A n + 2 … ⇄ A z − A 0 + A 1 z + A 2 z 2 + … + A n − 1 z n − 1 z n .
Сделаем небольшое замечание, которое читатели, не знакомые с производными, могут спокойно пропустить. Попытки вычислить A 1 как значение A z − A 0 z при нулевом z приводят к неопределённости типа 0 0 , которая раскрывается по правилу Лопиталя: A z − A 0 z 0 = A ′ 0 (штрих означает производную по z ). Впрочем, и так понятно, что A n = A n 0 n ! ( A n — n -я производная по z ).
Рекуррентное вычисление
Рекурсивная версия
Рекуррентная сводит задачу вычисления F n к задачам вычисления чисел F n − 1 и F n − 2 . Это соображение приводит нас к рекурсивному решению, в котором вычислению F n посвящена отдельная процедура F с параметром n . Она возвращает n , если n < 2 . В противном случае она дважды рекурсивно вызывает сама себя — с параметрами n − 1 и n − 2 , после чего возвращает сумму значений, возвращённых при этих вызовах. Проще некуда.
Но, несмотря на изящество и простоту алгоритма, мы получаем программу-катастрофу. Мы убедились в этом, попытавшись вычислить с её помощью всего-то F 40 — это заняло на нашем компьютере около 108 секунд. Чтобы дождаться F 50 , у нас уже не хватило терпения.
Постараемся разобраться, что же приводит к столь долгой работе программы. На рисунке 9.1. «Рекурсивные вызовы при вычислении чисел Фибоначчи» мы протянули стрелки от одного числа Фибоначчи к другому, если вычисление первого из них повлекло рекурсивный вызов для вычисления другого.
Теперь, глядя на рисунок, подсчитаем, сколько раз вызывалась рекурсивная процедура для вычисления F 5 :
| F 5 | 1 раз |
| F 4 | 1 раз (для вычисления F 5 ) |
| F 3 | 2 раза (1 раз для вычисления F 5 и 1 раз для F 4 ) |
| F 2 | 3 раза (1 раз для вычисления F 4 и 2 раза для F 3 ) |
| F 1 | 5 раз (2 раза для вычисления F 3 и 3 раза для F 2 ) |
| F 0 | 2 раза (для вычисления F 2 ) |
Всего для вычисления F 5 рекурсивная процедура вызывалась 14 раз, причём для каждого значения параметра в среднем больше двух раз. Это явный перебор, но пока это не производит столь жуткого впечатления. Что же будет при больших n ?
Рекурсивная версия с мемоизацией
Матричная версия
Матрицы
Матрица представляет собой прямоугольную таблицу, заполненную числами: a 1 , 1 a 1 , 2 ⋯ a 1 , n ⋮ ⋮ ⋮ ⋮ a k , 1 a k , 2 ⋯ a k , n . Каждое число (элемент матрицы) снабжается двумя индексами: первый — номер строки, а второй — столбца. Упомянутую матрицу можно кратко обозначить как a i , j , i = 1 ‥ k , j = 1 ‥ n .
Проиллюстрируем умножение матриц на примере: 2 3 1 − 5 4 6 − 1 7 3 0 2 4 1 5 8 − 2 0 4 = 2 ⋅ − 1 + 3 ⋅ 2 + 1 ⋅ 8 2 ⋅ 7 + 3 ⋅ 4 + 1 ⋅ − 2 2 ⋅ 3 + 3 ⋅ 1 + 1 ⋅ 0 2 ⋅ 0 + 3 ⋅ 5 + 1 ⋅ 4 − 5 ⋅ − 1 + 4 ⋅ 2 + 6 ⋅ 8 − 5 ⋅ 7 + 4 ⋅ 4 + 6 ⋅ − 2 − 5 ⋅ 3 + 4 ⋅ 1 + 6 ⋅ 0 − 5 ⋅ 0 + 4 ⋅ 5 + 6 ⋅ 4 = 12 24 9 19 61 − 31 − 11 44 .
Матричные соотношения для чисел Фибоначчи
Довольно интриговать читателей. Пора уже объяснить, какое отношение матрицы имеют к числам Фибоначчи.
Оказывается, рекуррентное соотношение для чисел Фибоначчи можно записать в матричной форме: F n + 1 F n + 2 = 0 1 1 1 F n F n + 1 = F n + 1 F n + F n + 1 . В качестве очевидного следствия этого равенства получим F n + k F n + k + 1 = 0 1 1 1 k F n F n + 1 . В частности, при n = 0 получим F k F k + 1 = 0 1 1 1 k 0 1 .
[expert_bq id=»1570″]При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах Liber abaci Книга абака , 1202; Practica geometriae Практика геометрии , 1220, Flos Цветок , 1225 год исследование на тему кубических уравнений и Liber quadratorum Книга квадратов , 1225 задачи о неопределенных квадратных уравнениях очень часто разбирал всевозможные математические задачи. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
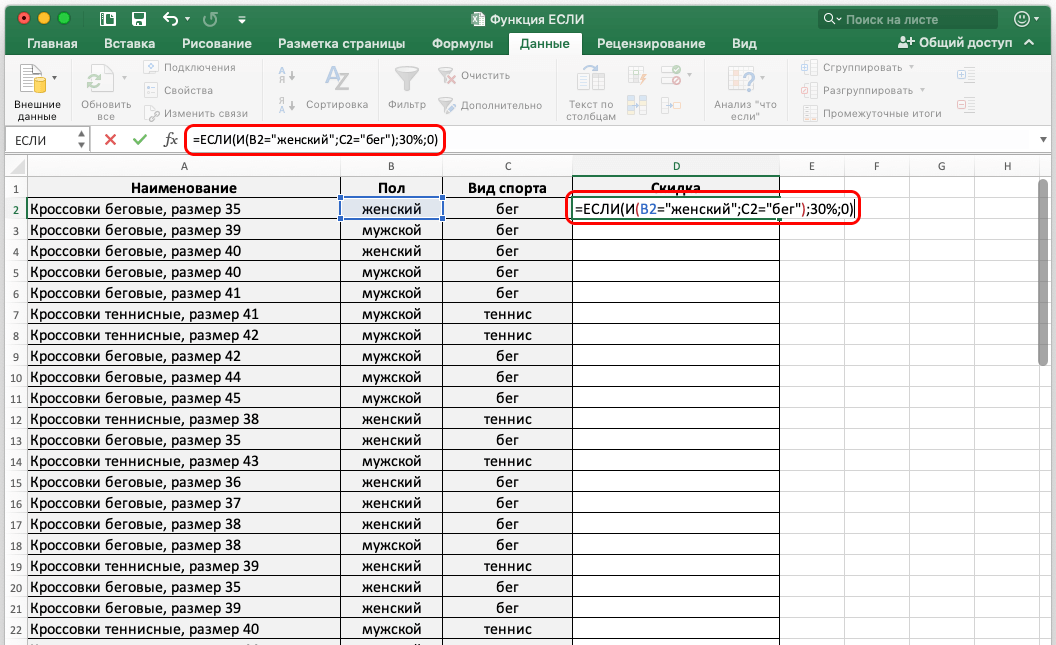
При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.
Как вычислить миллионное число Фибоначчи на Python
- Умножение всех элементов последовательности A на число q приводит к умножению на q её производящей функции: q A ⇄ q A z .
- Поэлементной сумме или разности двух последовательностей отвечает сумма или разность их производящих функций: A ± B ⇄ A z ± B z .
- Начальный элемент последовательности равен значению её производящей функции при нулевом z : A 0 = A 0 .
- Вставке нуля в начало последовательности соответствует умножение её производящей функции на z : ⊢ A = 0 A 0 A 1 A 2 A 3 … ⇄ z A z .
- Удаление первого элемента последовательности приводит к вычитанию этого элемента из производящей функции и последующему делению на z : ⊣ A = A 1 A 2 A 3 … ⇄ A z − A 0 z . Для удаления первых n элементов получаем ⊣ n A = A n A n + 1 A n + 2 … ⇄ A z − A 0 + A 1 z + A 2 z 2 + … + A n − 1 z n − 1 z n .
Метод 5 (Оптимизированный метод 4)
Способ 4 может быть оптимизирован для работы в O (Logn) временной сложности. Мы можем сделать рекурсивное умножение, чтобы получить мощность (M, n) в преобладающем методе (аналогично оптимизации, сделанной в этом посте)
| F 5 | 1 раз |
| F 4 | 1 раз (для вычисления F 5 ) |
| F 3 | 2 раза (1 раз для вычисления F 5 и 1 раз для F 4 ) |
| F 2 | 3 раза (1 раз для вычисления F 4 и 2 раза для F 3 ) |
| F 1 | 5 раз (2 раза для вычисления F 3 и 3 раза для F 2 ) |
| F 0 | 2 раза (для вычисления F 2 ) |
Использование
условных операторов и операторы цикла
при вычислении чисел Фибоначчи.
Любая
более или менее серьёзная программа
подразумевает использование управляющих
инструкций, среди которых особое место
занимают условные операторы и операторы
циклов. Рассмотрим особенности применения
таких операторов.
Общий
принцип действия условного оператора
заключается в следующем: проверяется
условие, и если оно истинно — выполняется
последовательность операций (цикл с
предусловием). Также можно определить
последовательность действий в случае
если условие ложно (цикл с постусловием,
выполняется до истинности условия).
Оператор
цикла позволяет выполнять последовательности
однотипных действий.
1)
Создадим с помощью оператора цикла FOR
макрос, который заполняет ячейки
документа числами Фибоначчи
(по
имени средневекового математика Леонардо
Пизанского, известного как Фибоначчи):
1,
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Числами
Фибоначчи называют последовательность
натуральных чисел, первые два из которых
равны 1, а каждое последующее равно сумме
двух предыдущих.
Примечание
3: Оказывается,
эта последовательность имеет множество
интересных с точки зрения математики
свойств. Вот пример: вы можете разделить
линию на два сегмента, так что соотношение
между большим и меньшим сегментом будет
пропорционально соотношению между всей
линией и большим сегментом. Этот
коэффицент пропорциональности,
приблизительно равный 1,618, известен как
золотое
сечение. В
эпоху Возрождения считалось, что именно
эта пропорция, соблюденная в архитектурных
сооружениях, больше всего радует глаз.
Если вы возьмете последовательные пары
из ряда Фибоначчи и будете делить большее
число из каждой пары на меньшее, ваш
результат будет постепенно приближаться
к золотому сечению. Другую интересную
информацию о числах Фибоначчи можно
найти в Интернете: http://elementy.ru/trefil/21136;
http://ru.wikipedia.org
и др..
Также,
в оператор For
добавим условный оператор, с помощью
которого обеспечим необходимость того,
чтобы числами ячейки заполнялись только
в том случае, если в активную ячейку
введено число большее 2. В VBA
существует условный оператор If….
Then….Else,
который реализует означенный алгоритм.
Программный код данного макроса приведен
в листинге 18:
Листинг 18: Программный код макроса Fibon ( )
Public Sub Fibon ( )
Dim N As Integer
Dim i As Integer
Dim a As Integer
Dim b As Integer
N = ActiveCell.Value
If N<2 Then
MsgBox Prompt: =
“Указано неверное значение!”, Title:
= “Ошибка!”
E
lse
a = 1
ActiveCell.Offset(1,-1).Value = 1
ActiveCell.Offset(1,0).Value = a
b = 1
For i = 2 To N
ActiveCell.Offset(i,-1).Value = i
ActiveCell.Offset(i,0).Value = b
b = b + a
a = b – a
Next i
End If
End Sub
Рис.
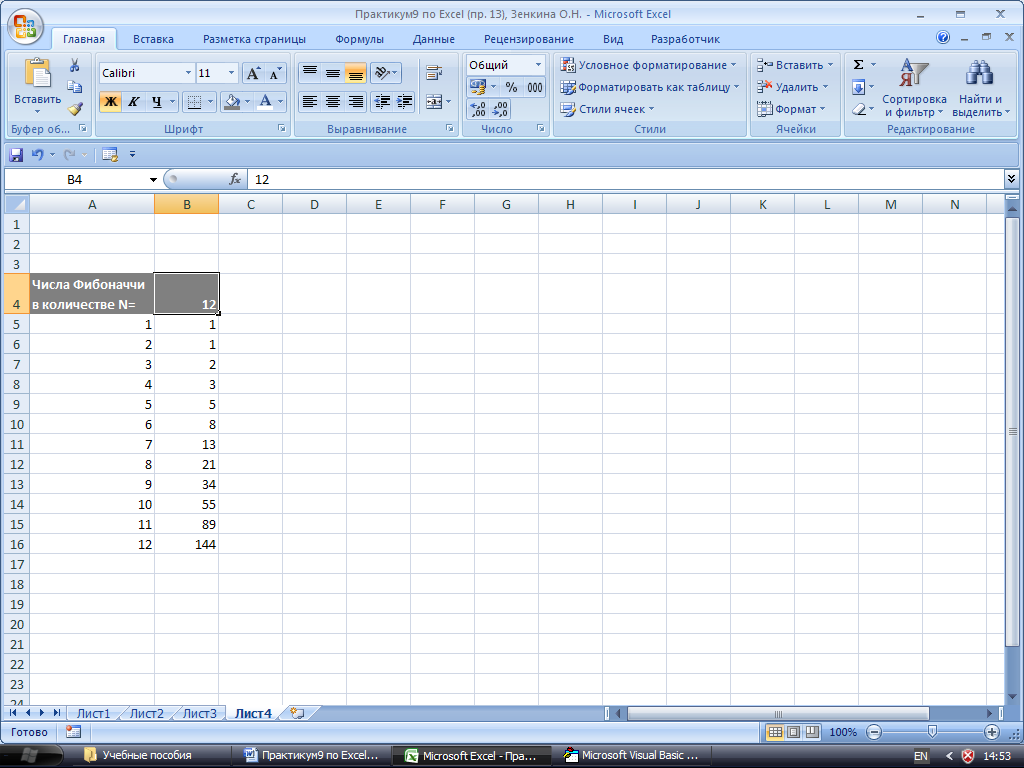
26.
Результат выполнения задания 6, п. 1.
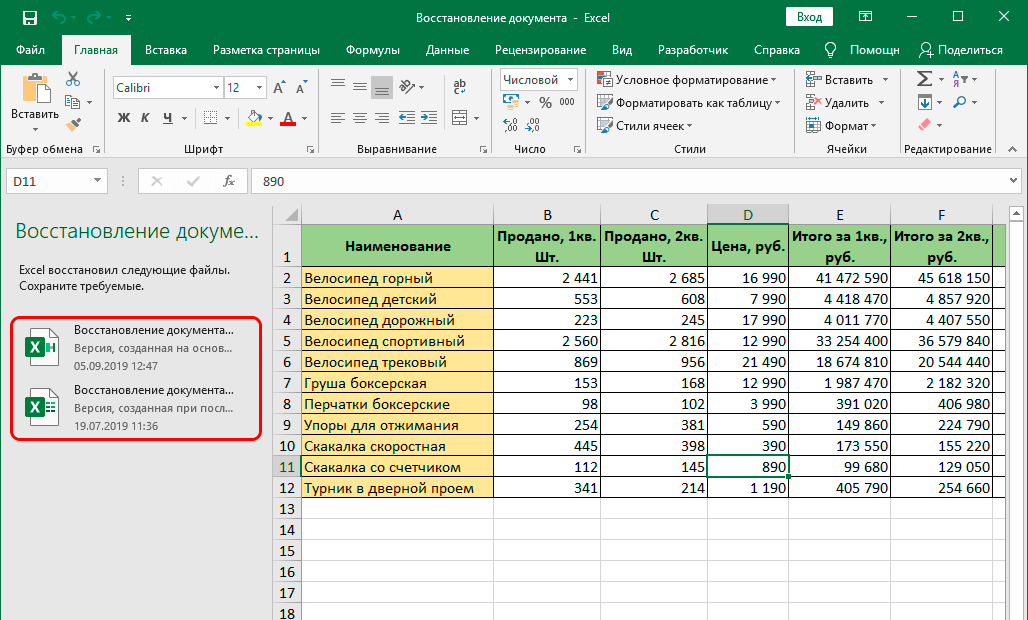
В
ячейку А4
введите слова: «Числа
Фибоначчи в количестве N
= »,
в ячейку В4
введите число 12 (сколько чисел Фибоначчи
будет выведено с помощью макроса), далее
выделите ячейку B4
со значением 12 (ячейка B4
станет активной) и далее запустите
макрос на выполнение. Результат выполнения
макроса будет выглядеть как на рис. 27.
Внизу, под ячейкой B4
(в ячейках B5:В16)
будут выведены 12 чисел Фибоначчи.
Поэкспериментируйте сами, с выполнением
данного макроса, задавая для вычисления
разное число чисел Фибоначчи в ячейке
B4.
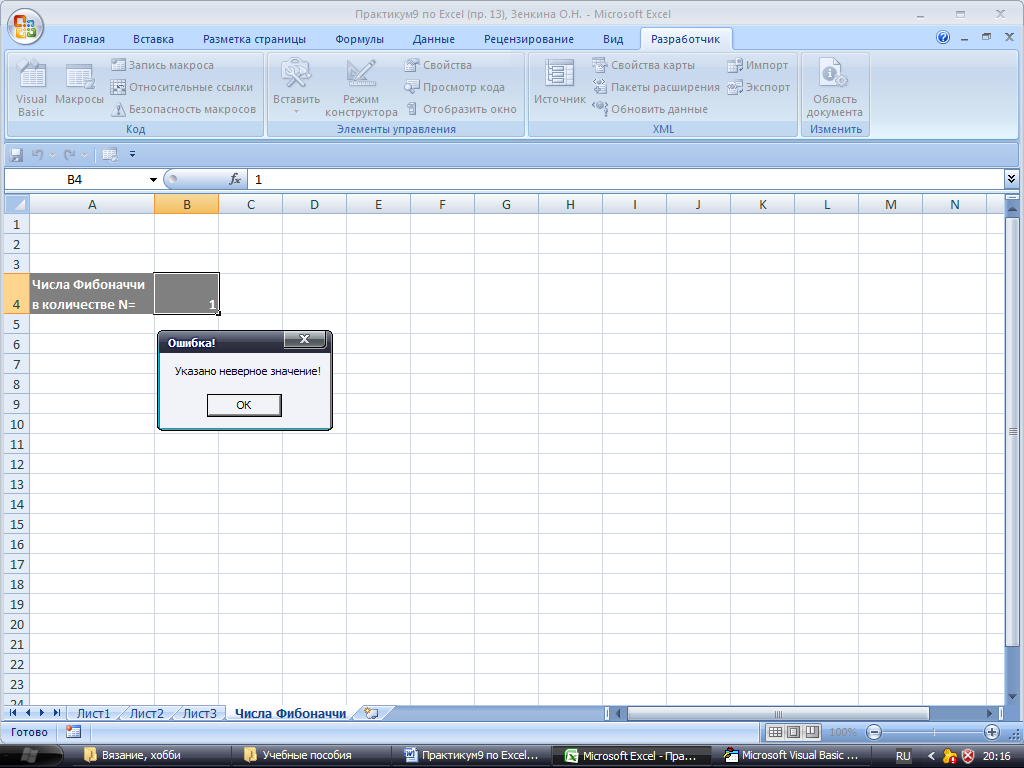
Если
в ячейку В4
будет введено число меньшее 2, то результат
будет иным, см. рис. 27:
Рис.
27. Результат
работы макроса при неверно указанном
значении ячейки.
Данный
макрос Fibon имеет
недостатки, в частности не может вывести
одно число Фибоначчи, когда значение
в
активной ячейке равно 1, а также не может
обработать случай, когда в ячейка В4
содержит нечисловое значение.
Приведённый
ниже макрос Fibon2
решает
эти проблемы (см. листинг 19):
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Циклические вычисления чисел Фибоначчи
Эта задача интересна тем, что она отчетливо демонстрирует ситуацию, когда начальный отрезок ряда чисел вычисляется по «своим» формулам и лишь, начиная с третьего числа, идут вычисления по рекуррентным соотношениям. Для того чтобы в каждый момент иметь не весь ряд вычисленных чисел, а только последние полученные значения, нам потребуются три ячейки таблицы Excel. Заметьте, двумя ячейками не обойтись. Формулы в двух первых ячейках используют конструкцию IF, позволяющую на первом шаге вычислений задать соответствующую константу, а затем перейти к рекуррентному соотношению. Третья ячейка необходима, как дополнительная память при пересылке значений. Для реализации задачи я выполнил следующие действия:
- В ячейку Fprev занес IF — формулу: » =ЕСЛИ(Fprev=0; 1; Fib) «
- В ячейку Fib занес IF — формулу: » =ЕСЛИ(Fib=0; 1; Fnext) «
- В ячейку Fnext ввел формулу: » =Fprev + Fib «
- Эти формулы порождают на первом шаге вычислений тройку чисел (1,1,2), на втором — (2,3,5) и т.д.
- Напомним, что важен порядок расположения этих формул на рабочем листе. Они должны идти сверху вниз, слева направо.
Взгляните, как выглядит на рабочем листе решение задач по нахождению корня уравнения и вычисления чисел Фибоначчи, использующее циклические вычисления.
Решение системы линейных уравнений методом простой итерации
Циклические вычисления можно проводить и над массивами. В качестве примера такой задачи рассмотрим итеративный способ решения системы линейных уравнений AX = B. Если применить метод простой итерации, то вектор решений X определяется следующим рекуррентным соотношением:
XK+1 = XK -(AXK -B) k= 1…N
Чтобы запустить процесс вычислений, нужно задать начальное приближение — вектор X1. Для сходимости процесса необходимо, но не достаточно, чтобы норма матрицы А была меньше 1. Иногда достаточно соответствующим образом масштабировать матрицу А и вектор В. Но нас конечно интересуют другие вопросы,- как реализовать на Excel это итеративное соотношение над векторами и матрицами, не прибегая к программированию на VBA и используя циклические вычисления. Покажем, что решение получить ненамного сложнее, в сравнении с применением схемы Ньютона для одного уравнения. Я сделал следующее:
-
Ввел матрицу А и вектор В, предварительно нормировав их. Заметим, что нужно правильно выбирать ориентацию векторов. В данном случае мне было удобнее представлять вектор В строкой. Вектор получил имя Veb.
-
Затем определил вектор с именем Vxinit, задающий начальное приближение.
-
Затем определил еще один вектор с именем Vxcur. Это вектор решений, его значения будут изменяться в цикле, пока не закончится итерационный процесс. Формула для вычислений будет определяться написанным выше рекуррентным соотношением, и представлять собой формулу над массивами. Учитывая то, что говорилось ранее о рекуррентных соотношениях, формула должна быть IF — функцией. Это позволит использовать на первом шаге начальное приближение, а потом уже вести вычисления по рекуррентной формуле. Приведем теперь саму формулу над массивами, вычисляющую рекуррентно вектор Vxcur:
{=ЕСЛИ(Vxcur=0; Vxinit; Vxcur - Axhor + Veb)}Здесь, как и ранее, используются нулевые значения, как признак начала процесса. Заметим, что, конечно, было бы лучше, если бы существовала возможность явной инициализации переменных при циклических вычислениях, а так наши действия немного напоминают фокус. Вектор Axhor, введенный в формулу — это вспомогательный вектор, равный произведению матрицы А на текущий вектор Vxcur. Если процесс вычислений сходится, и Vxcur сходится к решению системы уравнений, то вектор Axhor будет сходиться к вектору Veb.
-
Опишем подробнее формирование вспомогательного вектора Axhor. Содержательно, он представляет произведение матрицы на вектор. Но произведение матрицы на вектор дает вектор столбец, а в рекуррентном соотношении необходим вектор строка. По этой причине я формирую вначале вектор столбец Axver:
Конечно, для умножения матрицы на вектор можно воспользоваться стандартной функцией, но я хочу показать, как это делается с использованием более простых средств. Для этого достаточно написать формулу, вычисляющую его первый элемент:
и затем скопировать ее по столбцу. Обратите внимание, вектор, на который умножается матрица, должен быть строкой, а вектор — результат — столбцом. Строка матрицы задается в относительных адресах и при копировании меняется. Вектор, на который умножаются строки, задается своим именем, а значит абсолютным адресом, не изменяющимся при копировании. Каждая формула, задающая элемент вектора, является формулой над массивами.
-
Получив вектор столбец Axver, задающий нужное произведение, можно перейти к получению строки — Axhor, представляющей результат транспонирования вектора Axver. Для транспонирования я использовал стандартную функцию Transpose. Сама задача транспонирования и эта функция подробно будет рассмотрена чуть позже. Формула над массивами, определяющая вектор Axhor имеет вид:
-
Задав все вектора и все формулы, я получил решение системы линейных уравнений. Как ни странно, но даже столь плохой метод, как метод простой итерации сошелся к решению. Так, начав с начального приближения (1,1), я получил решение (1.6, 2.4) с заданной точностью.
-
Заметим, предложенная схема носит общий характер и позволяет решать любую систему линейных уравнений, не ограничиваясь системой из двух уравнений, рассмотренную в примере. Однако никому не рекомендую применять метод простой итерации для нахождения решения системы уравнений, — для этого есть другие точные методы. Просто мне было важно продемонстрировать возможность циклических вычислений при действиях с матрицами, и нужен был достаточно простой пример.
В заключение темы о циклических вычислениях покажем, как выглядят построенное решение на рабочем листе Excel: