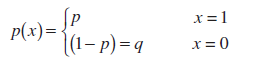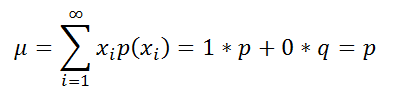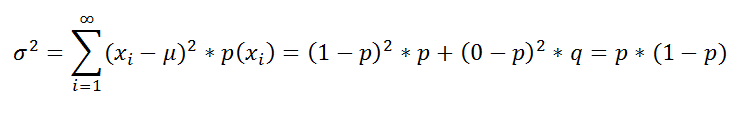Формула бернулли для excel

Формула Бернулли в Excel

В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}=C_n^k cdot p^k cdot q^{n-k}. qquad(1)
$$

Здесь $C_n^k$ — число сочетаний из $n$ по $k$.

Еще: онлайн калькуляторы для формулы Бернулли.

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

• Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
• Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
• События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Формула Бернулли в Эксель

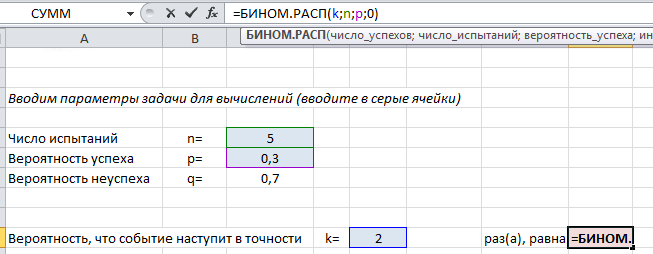
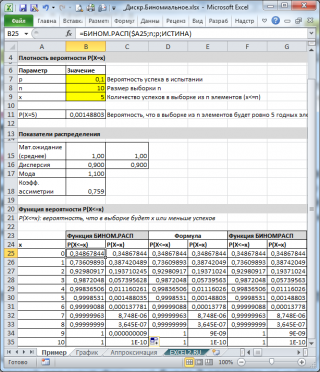
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

• Событие произойдет в точности $k$ раз из $n$:
  =БИНОМ.РАСП(k;n;p;0)
  $$P_n(k)=C_n^k cdot p^k cdot q^{n-k}$$
• Событие произойдет от $k_1$ до $k_2$ раз:
  =БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
  $$P_n(k_1le X le k_2)=sum_{i=k_1}^{k_2} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет не более $k_3$ раз:
  =БИНОМ.РАСП(k_3;n;p;1)
  $$P_n(0le X le k_3)=sum_{i=0}^{k_3} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет не менее $k_4$ раз:
  =1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
  $$P_n(k_4le X le n)=sum_{i=k_4}^{n} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет хотя бы один раз:
  =1-БИНОМ.РАСП(0;n;p;0)
  $$P_n( X ge 1)=1-P_n(0)=1-q^{n}$$
• Наивероятнейшее число наступлений события $m$:
  =ОКРУГЛВВЕРХ(n*p-q;0)
  $$np-q le m le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Полезное: расчетный файл по формуле Бернулли

Примеры решений задач

Рассмотрим решение типовых задач.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.

Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:

$$
P_7(5)=C_{7}^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146.
$$

Для вероятности 6 или 7 попаданий суммируем:

$$
P_7(6)+P_7(7)=C_{7}^6 cdot 0,75^6 cdot 0,25^1+C_{7}^7 cdot 0,75^7 cdot 0,25^0= \
= 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495.
$$

А вот это решение в файле эксель:

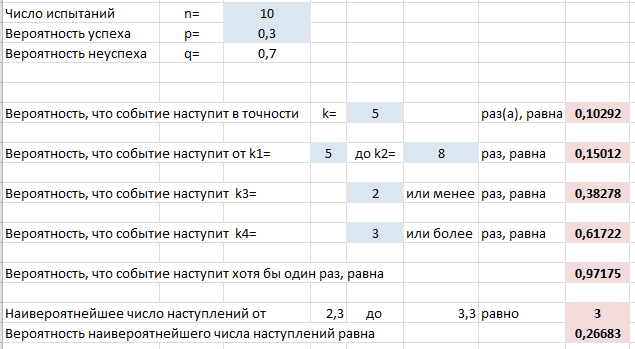
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?

Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k cdot 0,5^kcdot 0,5^{10-k}=C_{10}^k cdot 0,5^{10}$$
Приступим к вычислениям:

$$1. P_{10}(2)=C_{10}^2 cdot 0,5^{10} = frac{10!}{2!8!}cdot 0,5^{10} approx 0,044.$$

$$2. P_{10}(4)+P_{10}(5)=C_{10}^4 cdot 0,5^{10} + C_{10}^5 cdot 0,5^{10}=left( frac{10!}{4!6!} + frac{10!}{5!5!} right)cdot 0,5^{10} approx 0,451.$$

$$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 cdot 0,5^{10} + C_{10}^1 cdot 0,5^{10}+ C_{10}^2 cdot 0,5^{10}=left( 1+10+ frac{10!}{2!8!} right)cdot 0,5^{10} approx 0,055.$$

$$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\ = C_{10}^7 cdot 0,5^{10} + C_{10}^8 cdot 0,5^{10}+ C_{10}^9 cdot 0,5^{10}+ C_{10}^10 cdot 0,5^{10} =\=left(frac{10!}{3!7!}+ frac{10!}{2!8!} + 10 +1right)cdot 0,5^{10} approx 0,172.$$

$$5. P_{10}(ge 1)=1-P_{10}(0)=1-C_{10}^0 cdot 0,5^{10} = 1- 0,5^{10} approx 0,999.$$

Наивероятнейшее число мальчиков найдем из неравенства:

$$
10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \
4,5 le m le 5,5,\
m=5.
$$

Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).

Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.

Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?

Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!

Полезные ссылки

Расчетный файл эксель для расчетов по формуле Бернулли

Калькуляторы на формулу Бернулли Примеры решений задач

Как решать задачи по теории вероятностей? Решение заданий на заказ

Решебник задач по вероятности

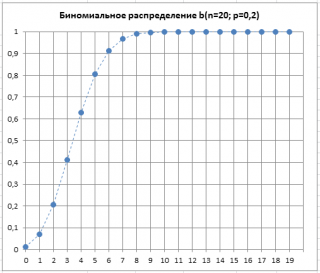
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL

БИНОМ.РАСП()

построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.

Определение

. Пусть проводятся

n

испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью

p

или событие «неудача» с вероятностью

q

=1-p (так называемая

Схема Бернулли,

Bernoulli

trials

).

Вероятность получения ровно

x

успехов в этих

n

испытаниях равна:

Примечание

:

Порядок получения успехов значения не имеет. Если важен порядок, то см. статью

Отрицательное Биномиальное распределение

.

Количество успехов в выборке

x

является случайной величиной, которая имеет

Биномиальное распределение

(англ.

Binomial

distribution

)

p

и

n

–

являются параметрами этого распределения.

Примечание

: Запись

означает количество

сочетаний

из

n

элементов по

x

. Для сочетаний также используется запись

. Подробнее о сочетаниях см. статью

Сочетания без повторений: Комбинаторика в MS EXCEL

.

Напомним, что для применения

схемы Бернулли

и соответственно

Биномиального распределения,

должны быть выполнены следующие условия:

• каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
• результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
• вероятность успеха
  
  p
  
  должна быть постоянной для всех испытаний.

Биномиальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Биномиального распределения

имеется функция

БИНОМ.РАСП()

, английское название — BINOM.DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно

х

«успехов» (т.е.

функцию плотности вероятности

p(x), см. формулу выше), и

интегральную функцию распределения

(вероятность того, что в выборке будет

x

или меньше «успехов», включая 0).

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

До MS EXCEL 2010 в EXCEL была функция

БИНОМРАСП()

, которая также позволяет вычислить

функцию распределения

и

плотность вероятности

p(x).

БИНОМРАСП()

оставлена в MS EXCEL 2010 для совместимости.

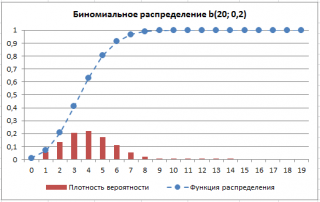
В

файле примера

приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Биномиальное распределения

имеет обозначение

B

(

n

;

p

)

.

Примечание

: Для построения

интегральной функции распределения

идеально подходит диаграмма типа

График

, для

плотности распределения

–

Гистограмма с группировкой

. Подробнее о построении диаграмм читайте статью Основные типы диаграмм.

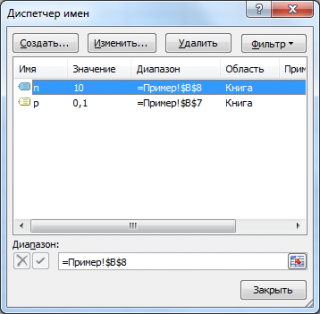
Примечание

: Для удобства написания формул в

файле примера

созданы Имена для параметров

Биномиального распределения

: n и p.

В

файле примера

приведены различные расчеты вероятности с помощью функций MS EXCEL:

Как видно на картинке выше, предполагается, что:

• В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр
  
  p
  
  , третий аргумент функции =
  
  БИНОМ.РАСП()
  
  )
• Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр
  
  n
  
  , второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу:
  
  =БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
  
• Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции
  
  плотности распределения
  
  .

Если значение четвертого аргумента =ИСТИНА, то функция

БИНОМ.РАСП()

возвращает значение

интегральной функции распределения

или просто

Функцию распределения

. В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).

Для этого нужно записать формулу: =

БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)

Примечание

: При нецелом значении х,

дробная часть отбрасывается

. Например, следующие формулы вернут одно и тоже значение:

=БИНОМ.РАСП(

2

; 10; 0,1; ИСТИНА)

=БИНОМ.РАСП(

2,9

; 10; 0,1; ИСТИНА)

Примечание

: В

файле примера

плотность вероятности

и

функция распределения

также вычислены с использованием определения и функции

ЧИСЛКОМБ()

.

Показатели распределения

В

файле примера на листе Пример

имеются формулы для расчета некоторых показателей распределения:

• математического ожидания

  =n*p;

• дисперсии

  (квадрата стандартного отклонения) = n*p*(1-p);

• моды

  = (n+1)*p;

• коэффициента асимметрии

  =(1-2*p)*КОРЕНЬ(n*p*(1-p)).

Выведем формулу

математического ожидания

Биномиального распределения

, используя

Схему Бернулли

.

По определению случайная величина Х в

схеме Бернулли

(Bernoulli random variable) имеет

функцию распределения

:

Это распределение называется

распределение Бернулли

.

Примечание

:

распределение Бернулли

– частный случай

Биномиального распределения

с параметром n=1.

Найдем

математическое ожидание

(

среднее,

mean

)

распределения Бернулли

(

x

принимает только 2 значения).

Предположим, что мы провели

n

последовательных

испытаний Бернулли

и у нас сформировалась

выборка

, состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь

Биномиальное распределение

с параметрами

n

и

p

.

Учитывая, что

математическое ожидание

для каждого

x

_i

равно

p

, то для соответствующего

Биномиального распределения μ=p*n.

Аналогичным образом, можно вычислить

дисперсию

Биномиального распределения.

Для этого сначала найдем

дисперсию

(

второй момент, variance

)

распределения Бернулли

:

Соответственно, дисперсия для

Биномиального распределения

равна

σ

²

=n*p*(1-p)= n*p*q.

Генерация случайных чисел. Распределение Бернулли

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

распределения Бернулли

.

СОВЕТ

: О надстройке

Пакет анализа

можно прочитать в статье

Надстройка Пакет анализа MS EXCEL

.

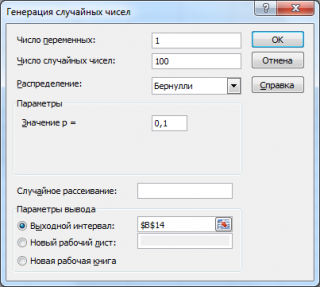
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

Примечание

: Если установить опцию

Случайное рассеивание

(

Random Seed

), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции

Случайное рассеивание

может запутать. Лучше было бы ее перевести как

Номер набора со случайными числами

.

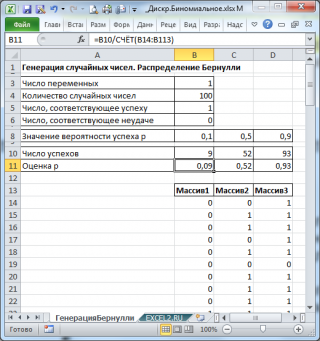
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Число успехов/100

(см.

файл примера лист ГенерацияБернулли

).

Примечание

: Для

распределения Бернулли

с p=0,5 можно использовать формулу

=СЛУЧМЕЖДУ(0;1)

, которая соответствует

дискретному равномерному распределению

.

Генерация случайных чисел. Биномиальное распределение

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

Биномиального

распределения

.

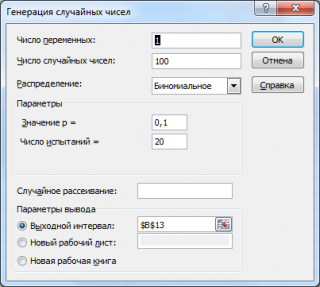
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

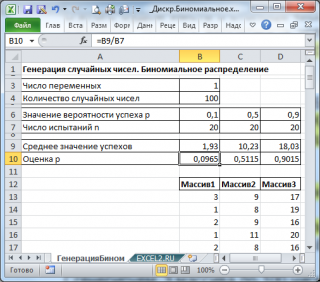
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Среднее значение успехов/

n

(см.

файл примера лист ГенерацияБином

).

Примечание

: Для генерирования массива чисел, распределенных по

Биномиальному закону

, можно использовать формулу

=БИНОМ.ОБР(20; p; СЛЧИС())

, где p – вероятность успеха. Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист ГенерацияБином

).

Оценка параметра p

В

схеме Бернулли

оценить параметр распределения

p

можно по формуле

=СУММ(B14:B113)/СЧЁТ(B14:B113)

. В формуле предполагается, что массив случайных чисел находится в диапазоне

B14:B113

.

Оценить параметр

Биномиального распределения

p

можно по формуле

= СРЗНАЧ(B13:B112)/n

(предполагается, что случайные числа сгенерированы формулой

=БИНОМ.ОБР(n; p; СЛЧИС()

). Также в формуле предполагается, что массив случайных чисел находится в диапазоне

B13:B112

.

Обратная функция БИНОМ.ОБР()

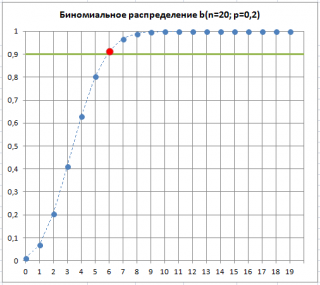
Вспомним график функции

Биномиального распределения

:

Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.

Задана величина выборки из партии (

n

=20) и

р=

0,2 — доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить

ошибку 1-го рода

(см.

статью про уровень доверия

) равная 90%. Пороговый приемочный критерий можно вычислить по формуле

=БИНОМ.ОБР(20; 0,2; 90%)

. Формула вернет значение 6 — наибольшее количество дефектных изделий, допустимое в

выборке

.

Примечание

: Третий аргумент функции

БИНОМ.ОБР()

называется

Альфа

(

α error, type I error, риск производителя, альфа-риск

) и представляет собой вероятность допустить

ошибку 1-го рода

при

проверке статистической гипотезы

(см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

).

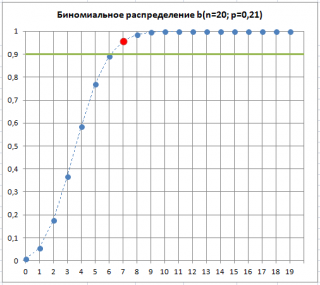
Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий

p

, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же

p

осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении

Альфа

. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке,

p

«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б

о

льший процент бракованных изделий.

Примечание

: До MS EXCEL 2010 в EXCEL была функция

КРИТБИНОМ()

, которая эквивалентна

БИНОМ.ОБР()

.

КРИТБИНОМ()

оставлена в MS EXCEL 2010 и выше для совместимости.

Связь Биномиального распределения с другими распределениями

Если параметр

n

Биномиального распределения

стремится к бесконечности, а

p

стремится к 0, то в этом случае

Биномиальное распределение

может быть аппроксимировано

Распределением Пуассона

. Можно сформулировать условия, когда приближение

распределением Пуассона

работает хорошо:

• 
  p
  <0,1
  
  (чем меньше
  
  p
  
  и больше
  
  n
  
  , тем приближение точнее);
• 
  p
  
  >0,9
  
  (учитывая, что
  
  q
  
  =1-
  
  p
  
  , вычисления в этом случае необходимо производить через
  
  q
  
  (а
  
  х
  
  нужно заменить на
  
  n
  
  —
  
  x
  
  ). Следовательно, чем меньше
  
  q
  
  и больше
  
  n
  
  , тем приближение точнее).

При 0,1<=p<=0,9 и n*p>10

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

.

В свою очередь,

Биномиальное распределение

может служить хорошим приближением

Гипергеометрического распределения

, когда размер совокупности N

Гипергеометрического распределения

гораздо больше размера выборки n (т.е., N>>n или n/N<<1).

Подробнее о связи вышеуказанных распределений, можно прочитать в статье

Взаимосвязь некоторых распределений друг с другом в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

В данной лабораторной
работе будут рассмотрены и построены
с помощью MS
Excel
наиболее распространенные распределения
вероятности: биномиальное и нормальное.

2.1. Расчет вероятности по формуле Бернулли

Биномиальное
распределение (распределение Бернулли)
представляет собой распределение
вероятностей числа наступлений некоторого
события («удачи») в n
повторных
независимых испытаниях, если при каждом
испытании вероятность наступления
этого события равна p.
Примером
практического
использования биномиального распределения
может являться контроль качества партии
фармакологического препарата, вероятность
рождения мальчиков или девочек,
количество успешно сданных тестов из
серии

В MS
Excel
функция БИНОМРАСП
применяется для вычисления вероятности
в задачах с фиксированным числом тестов
или испытаний, когда результатом любого
испытания может быть только успех или
неудача.

Функция использует
следующие параметры:

БИНОМРАСП
(число_успехов; число_испытаний;
вероятностъ_успеха; интегральная),

где число_успехов
— это
количество успешных испытаний;

число_испытаний
— это число
независимых испытаний (число успехов
и число испытаний должны быть целыми
числами);

вероятность_
успеха —
это вероятность успеха каждого испытания;

интегральная
— это логическое значение, определяющее
форму функции. Если данный параметр
имеет значение ИСТИНА
(=1),
то считается интегральная функция
распределения (вероятность того, что
число успешных испытаний не менее
значения число_
успехов);
если этот параметр имеет значение ЛОЖЬ
(=0),
то вычисляется значение функ­ции
плотности распределения (вероятность
того, что число успешных испытаний в
точности равно значению аргумента
число_
успехов).

Пример 1.
Какова вероятность того, что трое из
четырех новорож­денных будут мальчиками?

Решение:

1. Устанавливаем
табличный курсор в свободную ячейку,
например в А1.
Здесь должно оказаться значение искомой
вероятности.

2. Для получения
значения вероятности воспользуемся
специальной функцией: нажимаем на панели
инструментов кнопку Вставка
функции (fx).

3. В появившемся
диалоговом окне Мастер
функций —
шаг 1 из 2 слева в поле Катего­рия
указаны виды
функций. Выбираем Статистическая.
В поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно функции.

В поле Число_s
вводим с клавиатуры количество успешных
испытаний (3). В поле Испытания
вво­дим с клавиатуры общее количество
испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха
в отдельном испытании (0,5 – либо мальчик,
либо девочка). В поле Интегральный
вводим с клавиатуры вид функции
распределения — интегральная или
весовая (0). Нажимаем на кнопку ОК.

В ячейке А1 появляется
искомое значение вероятности р
= 0,25. Ровно
3 мальчика из 4 новорожденных могут
появиться с вероят­ностью 0,25.

Если изменить
формулировку условия задачи и выяснить
вероятность того, что появится не более
трех мальчиков, то в этом случае в рабочее
поле Интегральный
вводим 1 (вид функции распределения
интегральный). Вероятность этого события
будет равна 0,9375.

Соседние файлы в папке Занятие 3

• #
• #

Лабораторная работа 2

Повторные независимые испытания. Формула Бернулли

1. Цель работы − научиться находить наивероятнейшие события и

вероятность появления события в повторных независимых испытаниях.

2. Задачи работы:

– вычислять по формуле Бернулли средствами Excel вероятности

появления события заданное число раз;

– уметь пользоваться локальной теоремой Лапласа;

– уметь пользоваться интегральной теоремой Лапласа;

– уметь использовать аппарат функций Excel для вычислений

вероятностей по локальной и интегральной теоремам Лапласа;

– уметь вычислить наивероятнейшее число событий;

– находить вероятность появления наивероятнейшего числа событий.

3. Общее описание задания

Лабораторная работа посвящена повторным независимым испытаниям и

предполагает знание необходимых по теме определений понятий и теорем. В ходе

выполнения работы нарабатываются навыки использования в качестве справочных

таблиц для вычисления функций средств Excel, размещённых в разделе

«Статистические функции». Кроме того, рассматривается задача прогнозирования

наиболее вероятного числа появления событий в ходе многократного повторения

опытов при заданной вероятности его появления в одном опыте.

Расчёты, проведенные по локальной и интегральной теоремам

Лапласа, следует провести двумя способами: с использованием таблиц

локальной и интегральной функций Лапласа и средствами Excel.

Полученные результаты должны быть сопоставлены.

5. Требования к оформлению результатов

В ходе выполнения лабораторной работы на ПК студент формирует свой

файл, в котором в табличном процессоре Excel последовательно записывает

исходные данные задачи, ход решения и полученные результаты. При этом следует

указать номер лабораторной работы, номер решаемой задачи. Отдельно выделить

полученный ответ.

Повторные независимые испытания. Формула Бернулли

Пусть производится несколько испытаний, в каждом из которых может

появиться событие A. Если вероятность события A в каждом испытании не зависит

от того, появилось или не появилось это событие в других испытаниях, то такие

испытания называются независимыми относительно события A. Примером

независимых испытаний является последовательность появления герба или решки

Страница 1 из 1 1
Модератор форума: китин, _Boroda_

Мир MS Excel » Вопросы и решения » Вопросы по Excel » Как применить формулу Бернулли в Excel (Формулы/Formulas)

Мир MS Excel » Вопросы и решения » Вопросы по Excel » Как применить формулу Бернулли в Excel (Формулы/Formulas)
Страница 1 из 1 1
	Поиск: