Изучим как сделать арифметическую и геометрическую прогрессии в Excel, а также в общем случае рассмотрим способы создания числовых последовательностей.
Перед построением последовательностей и различных прогрессий, как обычно, вспомним их детальные определения.
Числовая последовательность — это упорядоченный набор произвольных чисел a1, a2, a3, …, an, … .
Арифметической прогрессией называется такая числовая последовательность, в которой каждый член, начиная со второго, получается из предыдущего добавлением постоянной величины d (также называют шагом или разностью):
Геометрическая прогрессия — это последовательность чисел, в котором каждый член, начиная со второго, получается умножением предыдущего члена на ненулевое число q (также называют знаменателем):
С определениями закончили, теперь самое время перейти от теории к практике.
Рассмотрим 2 способа задания прогрессии в Excel — с помощью стандартного инструмента Прогрессия и через формулы.
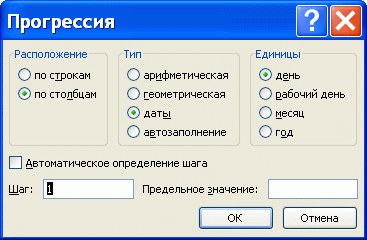
В первом случае на панели вкладок выбираем Главная -> Редактирование -> Заполнить -> Прогрессия:
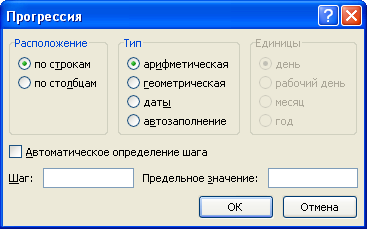
Далее мы увидим диалоговое окно с настройками параметров:
В данных настройках мы можем выбрать дополнительные параметры, которые позволят нам более детально настроить и заполнить прогрессию в Excel:
- Расположение — расположение заполнения (по столбцам или строкам);
- Тип — тип (арифметическая, геометрическая, даты и автозаполнение);
- Единицы — вид данных (при выборе даты в качестве типа);
- Шаг — шаг (для арифметической) или знаменатель (для геометрической);
- Автоматическое определение шага — автоматическое определение шага, если заданы несколько значений последовательности;
- Предельное значение — ограничение по значению последнего элемента последовательности.
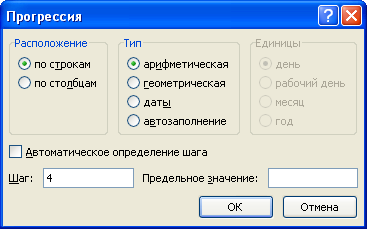
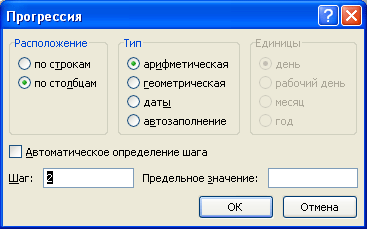
Разберем как сделать арифметическую прогрессию в Excel на конкретном примере.
Создадим набор чисел 3, 7, 11, … , то есть первый элемент равняется 3, а шаг равен 4.
Выделяем диапазон (к примеру, A1:J1) в котором мы хотим разместить набор чисел (диапазон можно и не выделять, однако в этом случае в настройках будет необходимо указать предельное значение), где в первой ячейке будет указан первый элемент (в нашем примере это 3 в ячейке A1), и указываем параметры (расположение, тип, шаг и т.д.):
В результате мы получим заполненный диапазон с заданным набором чисел:
Аналогичный результат можно получить и при задании элементов с помощью формул.
Для этого также задаем начальный элемент в первой ячейке, а в последующих ячейках указываем рекуррентную формулу члена арифметической прогрессии (то есть текущий член получается как сумма предыдущего и шага):
Геометрическая прогрессия в Excel
Принцип построения геометрической прогрессии в Excel аналогичен разобранному выше построению арифметической.
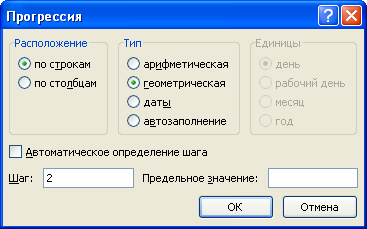
Единственное отличие — в настройках характеристик указываем в качестве типа геометрическую прогрессию.
Например, создадим набор чисел 4, 8, 16, … , то есть первое число равно 4, а каждое последующее в 2 раза больше предыдущего.
Также задаем начальный элемент (4 в ячейке A1), выделяем диапазон данных (например, A1:J1) и указываем параметры:
В итоге получаем:
Идентичного результата также можно добиться и через использование формул:
Числовая последовательность в Excel
Арифметическая и геометрическая прогрессии являются частными случаями числовой последовательности, в общем же случае ее можно создать, как минимум, тремя способами:
- Непосредственное (прямое) перечисление элементов;
- Через общую формулу n-го члена;
- С помощью рекуррентного соотношения, которое выражает произвольный член через предыдущие.
Первый способ подразумевает под собой ручной ввод значений в ячейки. Удобный вариант при вводе небольшого количества значений, в обратном же случае данный способ достаточно трудозатратный.
Второй и третий способы более универсальны, так как позволяют автоматически посчитать значения членов с помощью формул, что удобно при большом количестве элементов.
Поэтому поподробнее остановимся на построении последовательностей данными способами.
Рассмотрим создание числовой последовательности на примере построения обратных чисел к натуральным, то есть набора чисел 1, 1/2, 1/3, … , в котором общая формула n-го члена принимает вид Fn=1/n.
Создадим дополнительный ряд в отдельной строчке, куда для удобства расчета поместим порядковые номера (1, 2, 3 и т.д.), на которые будут ссылаться формулы:
В варианте с рекуррентной формулой рассмотрим пример с набором чисел Фибоначчи, в котором первые два числа равны 1 и 1, а каждый последующее число равно сумме двух предыдущих.
В итоге произвольный член можно представить в виде рекуррентного соотношения Fn = Fn-1 + Fn-2 при n > 2.
Определяем начальные элементы (две единицы) в двух ячейках, а остальные задаем с помощью формулы:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Инструмент Прогрессия дарит нам несколько замечательных возможностей. С помощью него можно заполнить диапазон ячеек данными по определенному закону: в арифметической или геометрической прогрессии. Для этого не нужно даже знать формулы. Для значений в формате дат предусмотрено создание специфических последовательностей.
Инструмент Прогрессия доступен через меню
Для начала работы введите начальное значение (первый член) прогрессии. Затем выделите диапазон ячеек, куда будут вводиться данные, и вызовите инструмент.
Числовые последовательности
Арифметическая прогрессия представляет собой
числовую последовательность
, где каждое число больше (или меньше) предыдущего на одно и тоже значение (шаг).
Примеры:
Арифметическая прогрессия с шагом 2 — это последовательность чисел 1, 3, 5, 7, 9, 11, … В окне инструмента
Прогрессия
нужно выбрать
Арифметическая
и установить
Шаг
равным 2.
Геометрическая прогрессия с шагом 2 — это последовательность чисел 2, 4, 8, 16, …. Этот пример позволяет быстро вспомнить степени 2. В окне инструмента
Прогрессия
нужно выбрать
Геометрическая
и установить
Шаг
равным 2.
Конечно, арифметическую прогрессию 1, 3, 5, 7, 9, 11, … можно организовать путем формулы
=А1+2
, а геометрическую 2, 4, 8, 16, … —
=А1*2
. Это уже как кому удобнее.
Последовательности дат и рабочих дней
В инструменте
Прогрессия
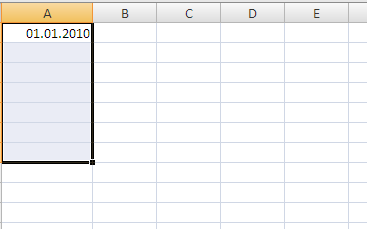
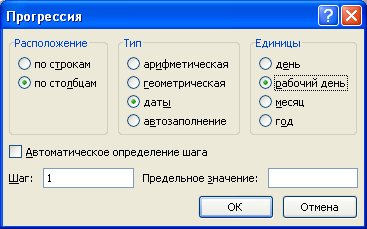
есть одна замечательная возможность по заполнению значений в формате дат. Вводим дату, выбираем диапазон,
вызываем инструмент
Прогрессия
, выбираем Тип
Даты
, выбираем Единицы
Рабочий день
.
В итоге получаем диапазон, заполненный только одними
рабочими днями
(не суббота и не воскресенье).
Если выберем в качестве единиц месяц, то месяц будет прибавляться к начальной дате и т.д. Эти возможности уже за несколько секунд не реализуешь, нужно вспоминать формулы. А если вспомнить, что еще можно и шаг прогрессии задавать, то можно гарантировать, что формула простой не получится.
Автозаполнение ячеек в Excel однотипными данными — одна из популярнейших «фишек» этого табличного редактора. Этот простейший процесс — когда вы вводите два числа, а затем просто протягиваете выделение насколько нужно, а программа автоматически заполняет столбец или строку следующими цифрами (датами, буквами и т.п.) идущими по порядку, сэкономил нам столько времени на ввод, что и подумать страшно!
Простейшая арифметическая прогрессия в excel — ввести два первых числа прогрессии (чтобы установить шаг), выделить их, и протащить мышью правый нижний угол выделения до нужной строки
Если записать в соседние ячейки числа, например 1 и 2, то в следующих ячейках появятся значения 4, 5, 6, если записать 500 и 1000, следующими числами будут 1500, 2000 и т.д.
Оба этих числовых ряда будут простейшими арифметическими прогрессиями с заданным шагом — в первом случае с шагом 1, во втором — с шагом 500.
Но, что если мы имеем дело не с простейшей арифметической, а с геометрической прогрессией?
Нет никаких проблем. Введите начальное число в одну из ячеек, а затем выделите диапазон ячеек, в котором и хотите увидеть свою прогрессию.
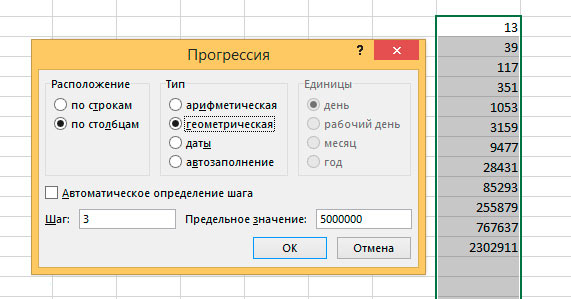
Инструмент для построения сложных прогрессий в MS Excel
На вкладке «Главная» в группе «Редактирование» найдите инструмент «Заполнить» и выберите пункт «Прогрессия».
В открывшемся окне установите нужные параметры (шаг прогрессии, тип прогрессии и предельное значение, если необходимо), а затем жмите «Ок».
Выбранная вами прогрессия будет мгновенно выведена в пределах выделенного вами диапазона на листе табличного редактора.
Пример построения геометрической прогрессии с шагом равным 3 и максимальным числом ограниченным 5000000
Также вас может заинтересовать:
Расчет арифметической прогрессии и построение диаграммы
Формула
для вычисления n-го члена арифметической
прогрессии имеет вид: an
= a1
+ d * (n-1).
Сумма
n первых членов — Sn
арифметической прогрессии равна
Sn
= (a1
+ an)
* n/2, где a1
— первый член прогрессии, an
— n-й член прогрессии, d — разность
арифметической прогрессии.
Следующие задания
нужно выполнять на разных рабочих листах
в одной рабочей книге.
Задание.
Составить таблицу, вычисляющую n-й член
и сумму арифметической прогрессии.
Первый член прогрессии n1
равен – 2, разность d равна 0,725. Построить
точечную диаграмму для 10 членов и 10 сумм
арифметической прогрессии как показано
на рис. 5.
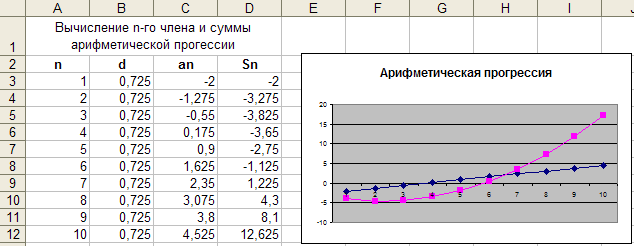
Рис.
5. Таблица с вычислениями n-го члена и
суммы арифметической прогрессии с
точечной диаграммой
Этапы
выполнения задания
Создание
таблицы
В
ячейку А1 ввести заголовок «Вычисление
n-го члена и суммы арифметической
прогрессии». Оформите строку заголовка.
При
оформлении строки заголовка в ячейках
C2 и D2 потребуется использовать нижний
индекс. В строке формул выделите нужный
символ и задайте ему способ отображения,
для этого выберите команду
Формат-Ячейки-Шрифт-Нижний
индекс.
Заголовки должны быть выровнены по
центру, шрифт полужирный (см. рис. 5).
Разместите
последовательность чисел от 1 до 10. Для
этого введите в А3 число 1 и затем в А4
ячейку число 2. Выделите обе
ячейки А3 и
А4. В правом нижнем углу прямоугольника
выделения находится небольшой квадратик
– маркер автозаполнения.
Поместите
указатель мыши на маркер заполнения
(при этом указатель примет вид тонкого
креста), нажмите левую кнопку мыши и
протащите указатель до ячейки А12 (рис.
6).
Рис. 6. Автозаполнение
При таком способе
выделения ячеек для последующего
автозаполнения (копирования) Excel
«запоминает» принцип, по которому нужно
заполнять ячейки, а справа появляется
подсказка со значением числа в
соответствующей ячейке.
Введите
в ячейку В4 значение разности арифметической
прогрессии d: 0,725. Зацепите маркер
автозаполнения и заполните нижние
ячейки.
В
ячейку С3 введите значение первого члена
арифметической прогрессии: –2.
В
ячейку С4 запишите формулу: =С3+В3,
т.е (сумма первого члена прогрессии и
разности прогрессии).
Выделите С4 и
скопируйте формулу на оставшиеся ячейки.
Обратите внимание, что имена ячеек
изменяются, т.к. формула содержит
относительную ссылку.
В
ячейку D3 введите формулу, вычисляющую
сумму n первых членов арифметической
прогрессии, которая для записи в Excel
имеет вид:
=(-2+C3)*A3/2
или =($C$3+C3)*A3/2,
что соответствует формуле нахождения
суммы арифметической прогрессии.
Скопируйте
эту формулу на оставшиеся ячейки.
Обратите внимание, что имя одной ячейки
не изменяется, так как была задана
абсолютная
ссылка.
Создание
диаграммы
Выделите
диапазон
ячеек С3:D12
со значениями
членов арифметической прогрессии и
суммы членов арифметической прогрессии.
Вызовите
Мастер
диаграмм
и выберите тип График,
затем График
с накоплением, на котором отдельные
значения помечены маркерами.
После
выполнения задания измените в ячейке
С3 значение первого члена прогрессии
на –3 и после этого придется в ячейках
D3:D12 изменить формулы расчета суммы
прогрессии, если была использована
формула
=(-2+C3)*A3/2, если же использовалась
формула =($C$3+C3)*A3/2 изменения вносить не
потребуется, т.к. она не содержит числового
значения первого члена прогрессии.
Обратите внимание
на изменения точечной диаграммы.
В
завершении переименуйте Лист2 на Арифм.
прогрессия.
Составленная
таблица не очень удобна для анализа
различных арифметических прогрессий,
т.к. при изменении одного параметра
прогрессии изменения приходится вносить
во все соответствующие ячейки.
Задание. На Листе3
составьте универсальную таблицу для
расчета арифметической прогрессии и
анализа ее с помощью диаграмм – рис. 7.
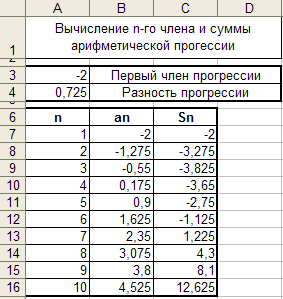
Рис. 7. Универсальная
таблица для анализа арифметической
прогрессии
Указания
Первый
член и разность арифметической прогрессии
находятся в ячейках А3 и А4, соответственно.
Формулы
для вычисления значений членов
арифметической прогрессии: ячейка В7:
=А3;
ячейка В8:
=
В7+$А$4
(используется
формула с абсолютной ссылкой на ячейку
А4). Эта формула копируется на оставшиеся
ячейки столбца В. Обратите внимание на
изменение относительных ссылок при
копировании формулы. Ячейка С7:
=($А$3+В7)*А7/2
(содержит абсолютную ссылку на ячейку
А3).
Переименуйте
Лист3 и дайте ему новое имя –
Универс.таб.арифм.прогрес.
Не забудьте
построить диаграмму!
После
выполнения задания убедитесь в том, что
полученная таблица «работает» при
различных значениях исходных данных
арифметической прогрессии.
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сумма сумм арифметических прогрессий
Время на прочтение
8 мин
Количество просмотров 13K
Пускай у нас есть некий ряд ячеек, часть которых можно пометить как «занятые»:
Нам нужно узнать, сколько всего существует вариантов расположения занятых ячеек.
К этой схеме сводится множество задач. Например, разбиение периода из N + 1 календарных дней на l + 1 следующих друг за другом меньших периодов. Допустим, мы хотим провести оптимизационный расчет методом «грубой силы», рассчитав целевую функцию для каждого возможного варианта разбиения периода, чтобы выбрать наилучший вариант. Чтобы заранее оценить время расчета, нужно определить количество вариантов. Это поможет принять решение, стоит ли вообще начинать расчет. Согласитесь — полезно будет заранее предупредить пользователя вашей программы, что с теми параметрами, которые он задал, расчет займет 10000 лет.
Существует простая формула, позволяющая для любых N и l получить количество всех возможных вариантов расположения занятых ячеек:
, где n = N – l + 1, n ≠ 0.
Это формула суммы сумм сумм … сумм арифметических прогрессий вида 1 + 2 + 3 + … + n; слово «сумма» в разных склонениях в этой фразе повторяется ровно l – 1 раз. Другими словами, эта формула позволяет быстро вычислять вот такие суммы:
У обычного настольного ПК уходит слишком много времени на вычисление этих сумм «в лоб» (особенно с использованием длинной арифметики — а без нее не обойтись).
Когда я только начинал решать эту задачу (и еще не знал этой формулы), я забивал в поисковик фразу «сумма сумм арифметических прогрессий» и ничего не находил. Именно так я и назвал свою статью — в расчете, что следующий искатель этой формулы сможет быстро найти ее здесь.
Ссылки на авторитетный источник касательно этой формулы у меня нет. Я ее вывел аналитически и проверил численно, проведя свыше 4000 тестов. Ее вывод, если кому интересно, приведен в конце статьи.
Скоро я расскажу, какое отношение имеют арифметические прогрессии к подсчету вариантов расположения ячеек, а пока приведу еще несколько готовых формул.
Введем дополнительное условие: допустим, в любом раскладе должна быть хотя бы 1 группа из r смежных незанятых ячеек. В этом случае, количество вариантов определяется так:
Вывод этой формулы следует в самом конце статьи.
Если ваша программа проводит какие-либо расчеты для каждого варианта расположения ячеек, то расчеты для разных вариантов наверняка однотипные. Это значит, что их легко распределить по нескольким потокам. В статье будет рассказано, как организовать итерацию по вариантам, чтобы каждому потоку досталось равное количество вариантов.
1. Причем тут прогрессии?
Это самый легкий вопрос. Сгруппируйте все занятые ячейки в левом конце вашего ряда ячеек — чтобы они следовали одна за другой, начиная с крайней левой ячейки в ряду:
Сколько существует вариантов расположения самой правой из занятых ячеек (будем называть ее последней занятой ячейкой), при условии, что остальные ячейки остаются на своих местах? Ровно n. Теперь сдвиньте ПРЕДпоследнюю занятую ячейку вправо на 1 позицию. Сколько останется позиций для последней ячейки? n – 1. Предпоследнюю ячейку можно сдвинуть вправо n раз. Значит, вариантов расположения двух последних занятых ячеек будет вот столько: S2(n) = 1 + 2 + 3 + … + n. Сдвиньте третью справа занятую ячейку на 1 позицию и снова подсчитайте количество вариантов расположения последней и предпоследней ячеек. Получится S2(n – 1). Третью ячейку тоже можно сдвинуть вправо только n раз, и всего вариантов расположения трех последних ячеек будет S3(n) = S2(1) + S2(2) + … + S2(n).
Рассуждая так, доберемся наконец и до количества вариантов расположения всех l занятых ячеек:
2. Дополнительное условие: хотя бы 1 группа из r незанятых смежных ячеек
Сначала рассмотрим частные случаи. Если n + l – 1 ≥ r(l + 1), то ни при каком раскладе мы не получим варианта, в котором нет хотя бы 1 группы из r незанятых ячеек. Даже в самом худшем случае — когда занятые ячейки в ряду расположены равномерно, так чтобы расстояние между ними и краями ряда было равно r – 1, количества занятых ячеек просто не хватит на то, чтобы ВСЕ эти расстояния были не больше r – 1. Хотя бы одно будет равно как минимум r. Следовательно:
r = 0 означает, что нас устраивает любое расположение ячеек. Условие «n + l – 1 ≥ r(l + 1)» в этом случае выполняется при любых n и l:
Если же r = 1, то условие «n + l – 1 ≥ r(l + 1)» выполняется только при n > 1:
n ≤ r означает, что число незанятых ячеек меньше r, и нет никакой возможности получить r незанятых ячеек, смежных или нет. Поэтому в предыдущей формуле и стоит 0 при n = 1.
Если занятых ячеек нет, то вариант их расположения всего один:
Теперь — обобщенная формула для всех остальных случаев.
Если зафиксировать самую левую занятую ячейку в крайнем левом положении, вариантов расположения всех остальных ячеек будет Sr(l – 1) (n). Если сдвинуть ее на 1 позицию вправо, вариантов будет Sr(l – 1) (n – 1). Начиная с позиции r + 1, у нас всегда будет промежуток длиной не менее r в левом конце ряда, так что остальные варианты можно будет посчитать без рекурсии: Sl (n – r). Получается вот что:
Формула верная, но я предпочитаю пользоваться вот этой:
По моим замерам, она в десятки раз быстрее предыдущей. Выводить ее несложно, но описывать вывод долго. В конце статьи расскажу.
Теперь мы можем перейти к распределению итераций по потокам. Чтобы разобраться в этом, вы должны ясно понимать, как выводилась первая формула Srl (n), т.к. в этом выводе заложен определенный порядок итерации по вариантам расположения занятых ячеек.
3. Как организовать итерацию в нескольких потоках
Порядок итерации будет общим для всех потоков. Вначале все l ячеек располагаются в левом конце ряда, занимая позиции с 1 по l. Это первая итерация. Крайняя правая ячейка на каждой итерации сдвигается вправо на 1 позицию, пока не окажется в конце ряда, затем ячейка слева от нее сдвигается на 1 позицию вправо, и крайняя ячейка снова проходит все возможные положения между ячейкой слева и правым концом ряда. Когда обе ячейки оказываются в крайнем правом положении, ячейка слева от них сдвигается на 1 позицию вправо. И так пока все ячейки не окажутся в правом конце ряда. При итерации мы пропускаем варианты, в которых нет ни одной группы из r смежных незанятых ячеек.
Выберем согласно этому порядку итерации первые k вариантов и назначим их первому потоку, затем следующие k вариантов назначим второму потоку, и так далее. Допустим, мы решили задействовать nt потоков, количество итераций в каждом из которых мы определили как ki, i = 1, …, nt.
Порядковый номер первой итерации для каждого потока назовем hi:
Имея начальное расположение ячеек для варианта под номером hi, не составит труда провести ki итераций, начиная с этого варианта (я даже описывать не буду, как это делается). Однако нам понадобится функция, вычисляющая положение занятых ячеек по порядковому номеру варианта:
using Anylong = boost::multiprecision::cpp_int;
using Opt_UVec = boost::optional<std::vector<unsigned> >;
Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0);
Функция arrangement принимает номер варианта index и параметры ряда: n = N – l + 1, l и r, — а возвращает вектор с позициями занятых ячеек в ряду. Позиция занятой ячейки — это целое число от 1 до N.
Число вариантов очень быстро растет с увеличением параметров l и n, поэтому для представления этого числа нам требуется длинная арифметика. Я использовал класс boost::multiprecision::cpp_int, способный представлять целые числа любой длины.
Если параметр index превышает число возможных вариантов расположения ячеек, функция возвращает пустой объект boost::optional. Если параметр index или параметр n равен 0, это рассматривается как ошибка программиста, и функция генерирует исключение.
Сначала переведем на C++ формулы для определения числа вариантов:
struct Exception
{
enum class Code { INVALID_INPUT = 1 } code;
Exception(Code c) : code(c) {}
static Exception InvalidInput() { return Exception(Code::INVALID_INPUT); }
};
Anylong S(unsigned n, unsigned l)
{
if (!n) throw Exception::InvalidInput();
if (l == 1) return n;
if (n == 1 || l == 0) return 1;
Anylong res = 1;
for (unsigned i = 1; i <= l; ++i) {
res = res * (n + i - 1) / i; // порядок действий важен!
}
return res;
}
Anylong S(unsigned n, unsigned l, unsigned r)
{
if (!n) throw Exception::InvalidInput();
if (r == 0) return S(n, l);
if (r == 1) if (n == 1) return 0; else return S(n, l);
if (n + l - 1 >= r * (l + 1)) return S(n, l);
if (n <= r) return 0; else if (l == 0) return 1;
Anylong res = (l + 1) * S(n - r, l);
for (unsigned j = 0; j <= l - 1; ++j)
for (unsigned i = r; i <= n - r - 1; ++i)
res -= S(i + 1, j, r) * S(n - r - i, l - j - 1);
return res;
}
Обратите внимание на эту строчку:
res = res * (n + i - 1) / i;Здесь важен порядок действий. Произведение множителей res и (n + i – 1) всегда делится нацело на i, а каждый из них в отдельности — нет. Нарушение порядка действий приведет к искажению результатов.
Теперь стоит вопрос, как определить вариант расположения по индексу.
Вспомним принятый нами порядок итерации. Чтобы сдвинуть крайнюю левую ячейку на 1 позицию вправо, потребуется X1=Srl – 1 (n) итераций. Сдвинуть ее еще на 1 ячейку правее можно за X2=Srl – 1 (n – 1) итераций. Если в какой-то момент X1 + X2 + … + Xi + Xi + 1 оказалось больше, чем index, значит, мы только что определили положение первой занятой ячейки. Она должна находиться на i-й позиции. Далее вычисляем, сколько итераций требуется, чтобы сдвинуть вправо вторую ячейку: X1=Srl – 2 (n – i + 1). Так продолжается, пока мы не доберемся до варианта под номером index. Если хоть раз i оказалось больше r, все последующие вызовы Srl (n) заменяются на Sl (n), ведь у нас уже есть как минимум один промежуток длиной не меньше r слева от текущей ячейки.
Короче будет написать код, чем объяснять словами.
Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0)
{
if (index == 0) throw Exception::InvalidInput();
if (index > S(n, l, r)) return {};
std::vector<unsigned> oci(l); /* occupied cells indices - позиции
занятых ячеек в ряду (индексы от 1 до N) */
if (l == 0) return oci;
if (l == 1) {
assert(index <= std::numeric_limits<unsigned>::max());
oci[0] = (unsigned)index;
return oci;
}
oci[0] = 1;
unsigned N = n + l - 1;
unsigned prev = 1;
Anylong i = 0; auto it = oci.begin();
while (true) {
auto s = S(n, --l, r);
while (i + s <= index) {
if ((i += s) == index) {
auto it1 = --oci.end();
if (it1 == it) return oci;
*it1 = N;
for (it1--; it1 != it; it1--) *it1 = *(it1 + 1) - 1;
return oci;
}
s = S(--n, l, r);
assert(n);
(*it)++;
if (r && (*it) > prev + r - 1) r = 0;
}
prev = *it++;
assert(it != oci.end());
*it = prev + 1;
}
assert(false);
}
4. Вывод формул
Порадую любителей школьной алгебры еще одним разделом.
Начнем с суммы сумм арифметических прогрессий:
Как видим, при l = 0 S0 (n) = 1 — это многочлен 0-й степени. При l = 1 S1 (n) = n — это многочлен 1-й степени. При l = 2 используется известная формула суммы арифметической прогрессии S2 (n) = n(n + 1)/2. И это многочлен 2-й степени. Можно предположить, что при l = 3 у нас будет многочлен 3-й степени. Вычислим вручную значения S3 (n) при n = 1, 2, 3 и 4, составим систему линейных уравнений и найдем коэффициенты этого многочлена. Результат разложим на множители и получим вот это:
У нас тут очевидная закономерность. Запишем вот такую формулу:
Она еще не доказана для l = 3, но уже доказана для l = 1 и l = 2. Воспользуемся методом математической индукции. Предположим, что формула Sl – 1 (n) верна для любых n и докажем, что в этом случае верна и формула Sl (n).
Применим метод мат. индкции еще раз, но уже в отношении параметра n, а не l. Ясно, что формула верна при n = 1. Предположим, что она верна для n — 1:
Вычтем это из предыдущей формулы:
Получилось верное тождество.
Теперь вернемся к формуле подсчета вариантов при r ≠ 0:
Выводится она следующим образом.
Подсчитаем количество вариантов, когда промежуток между последней занятой ячейкой и правым концом ряда больше или равен r. Это как если бы последняя занятая ячейка выросла в размерах до r + 1, а размеры ряда при этом остались бы прежними:
Такое количество вариантов равно Sl(n – r).
Теперь прибавим к нему количество вариантов, в которых промежуток между последней и предпоследней занятыми ячейками больше или равен r. Это количество вариантов снова будет равно Sl(n – r). Но некоторые из этих вариантов мы уже посчитали, когда вычисляли предыдущие Sl(n – r). А именно — те варианты, в которых промежуток между последней занятой ячейкой и правым концом ряда больше или равен r. Значит, к первым Sl(n – r) вариантов нужно прибавить не Sl(n – r), а Sl(n – r) – X, где X — количество вариантов, в которых промежуток между последней и предпоследней занятыми ячейками больше или равен r, равно как и промежуток между последней занятой ячейкой и правым концом ряда.
Ровно то же самое придется сделать для каждой j-й занятой ячейки — из Sl(n – r) вычесть Xj, равное количеству вариантов, в которых промежуток между j-й ячейкой и ячейкой слева от нее (в случае крайней левой ячейки — промежуток между нею и левым концом ряда), а также хотя бы один из промежутков справа от j-й ячейки — больше или равны r.
Всего у нас l – 1 промежутков между занятыми ячейками, плюс 2 промежутка между занятой ячейкой и концом ряда. Значит, слагаемое Sl(n – r) входит в нашу формулу l + 1 раз. А вот Xj не вычисляется для промежутка между крайней правой занятой ячейкой и правым коном ряда. Значит, этих слагаемых будет только l.
j находится в диапазоне от 0 до l – 1. Такой уж я принял порядок индексации. Тогда количество занятых ячеек справа от j-й ячейки равно j.
Посмотрите на этот рисунок:
j-я ячейка (та, что увеличивается до размера r + 1 при итерации по j) обозначается как M. Она может находиться в n – r возможных положениях, которые определяются параметром i (i ∈ [0, n – r – 1]). Первые r положений можно не рассматривать, поскольку при i < r все промежутки справа от M будут меньше r. Следовательно, i ∈ [r, n – r – 1].
Количество вариантов расположения ячеек справа от M, в которых хотя бы 1 промежуток больше или равен r, равно Srj (i + 1). Количество вариантов расположения ячеек слева от M равно Sl – j – 1 (n – i – r). Всего вариантов получается Srj (i + 1)∙Sl – j – 1 (n – i – r) для всех i ∈ [r, n – r – 1] и всех j ∈ [0, l – 1]:
Это и есть наша формула.