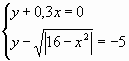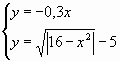Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Задание: решить графически систему
уравнений:
Цель работы: научиться использовать
табличный редактор (Microsoft Excel) при решении системы
уравнений графическим методом.
Теоретические сведения: для решения данной
задачи потребуется преобразование обоих
уравнений системы к виду y = f(x) (приведенный вид) и
построение графиков получившихся функций. Точки
пересечения графиков и являются ответом задачи.
Однако следует помнить, что графическое решение
системы уравнений является приближенным,
поэтому решение задачи разбивается на два
основных этапа:
Построение графиков функций и определение
координат точек пересечения.
Уточнение решения системы уравнений с
использованием Надстройки М. Excel «Поиск
решения»
Необходимое программное и методическое
обеспечение: ОС Windows XP, Office 2003, Microsoft Excel 2003.
Решение:
1. Запустить приложение Microsoft Excel, сохранить файл
к себе в папку, имя любое.
2. Преобразуем исходную систему уравнений в
приведенную:
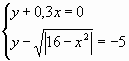
3. Производим построение графиков функций.
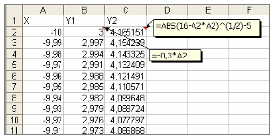
На Лист1 создаем таблицу координат графиков
функций:
Столбец Х заполняем значениями от -10 до 10 с
шагом 0,01 (Правка — Заполнить — Прогрессия)
Столбец Y1 заполняем по формуле [=-0,3*A2]
Столбец Y2 заполняем по формуле [=КОРЕНЬ(ABS(16-B4^2))-5]
Построение графиков (Вставка, Мастер диаграмм).
Шаг 1 из 4. Выбрать График, левый в первом
ряду.
Шаг 2 из 4. Вкладка Диапазон данных.
Установить по столбцам и диапазон — столбцы
значений Y1, Y2. Вкладка Ряд. Подписи оси
X — столбец значений Х. Имя Ряд1 — Y1, имя Ряд2
— Y2 Далее.
Шаг 3 из 4. Вкладка Заголовки. Заполнить Название
диаграммы: Графическое решение системы
уравнений, Ось Х (категорий): Х, Ось Y
(значений): Y. Далее
Шаг 4 из 4. Выбрать на отдельном листе. Готово.
Перенос оси Y(значений) в Х (категорию) = 0.
Определение категории содержащей 0. Перейти на
лист с таблицей, выделить любую ячейку в столбце
Х. Использовать меню Правка, Найти. Искать
0, ячейка целиком.
Определение категории, содержащей значение 0 в
системе координат графика: от номера найденной
строки вычесть количество строк над таблицей,
получается 1001.
Перейти на лист Диаграмма. Войти в Формат
оси категорий на вкладку Шкала, в окне
Пересечение с осью Y (значений) в категории номер:
ввести новое значение категории — 1001. Выровнять
число категорий между делениями и между
подписями по максимальному из двух чисел.
Уточнение решения системы уравнений
На листе Диаграмма определить значения Х в
точках пересечения графиков (Приложение
1).
На Лист1 создаем таблицу координат для точек
пересечения
Уточнение решения системы уравнений
производим с помощью Надстройки М. Excel «Поиск
решения» на основании малой таблицы.
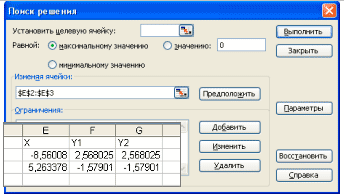
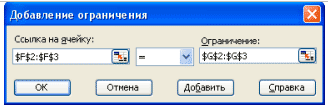
Окно Установить целевую ячейку очищаем, в
Окно Изменяя ячейки вносим, выделяя в малой
таблице (Рис.1), адреса ячеек со значениями Х, в
Окно Ограничения добавляем ограничения:
ячейки со значениями Y1 приравниваем ячейкам со
значениями Y2 (Рис.2).
Рис. 1
Рис. 2
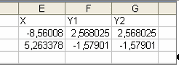
Нажимаем ОК, затем Выполнить и Сохранить
найденное решение. Значения Х, Y1 и Y2 в таблице
ясно показывают что решения найдены (Рис.3).
Рис. 3
5. Оформление решения системы.
Полученные значения X и Y имеют избыточную
точность, поэтому произведем округление
полученных координат точек пересечения.
Произведем копирование и Специальную вставку
(значения) координат точек пересечения графиков
функций.
Создадим форму для простановки координат на
лист Диаграмма.
Используем функцию СЦЕПИТЬ (категория —
текстовые) затем копирование и Специальную
вставку (значения) полученных форм и в заключении
копирование формы через Строку формул и
вставка ее на лист Диаграмма.
Оформить График в соответствии с Приложением
2.
В точках пересечения поставить маркеры.
Создать объект с записью системы (Вставка,
Объект, Microsoft Equation 3.0 — Редактор формул). Объект
создавать на Лист1 затем перенести на лист Диаграмма.
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
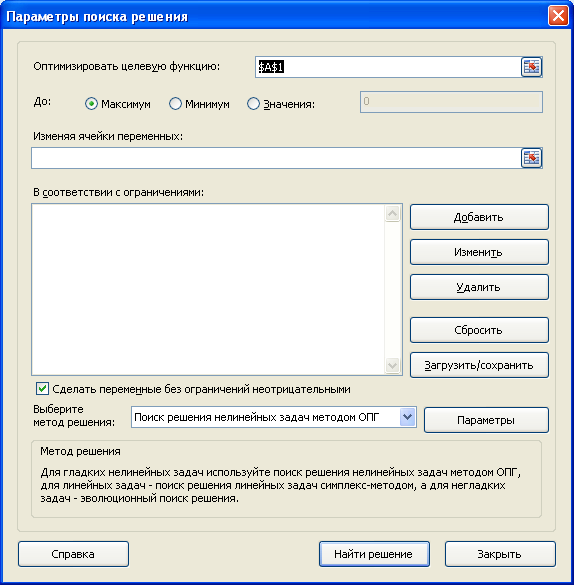
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
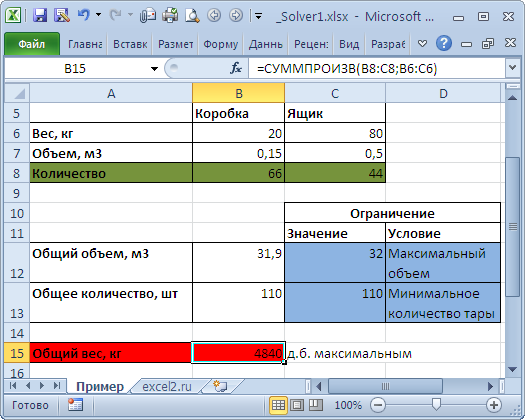
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
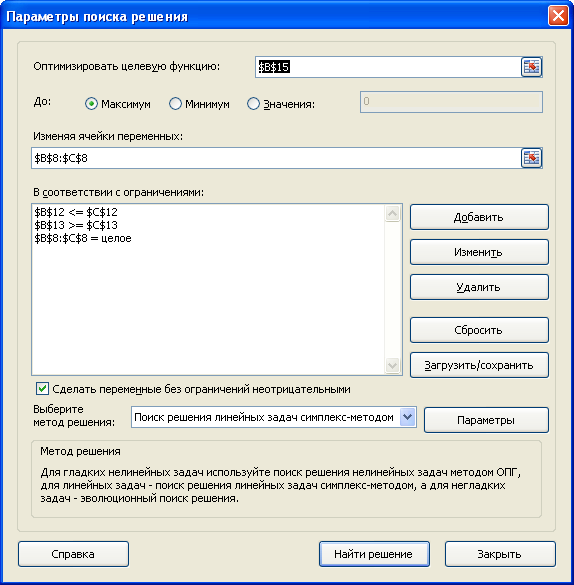
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
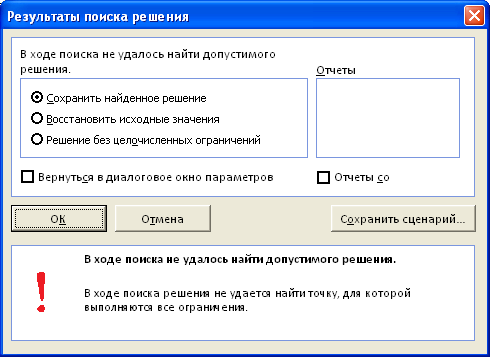
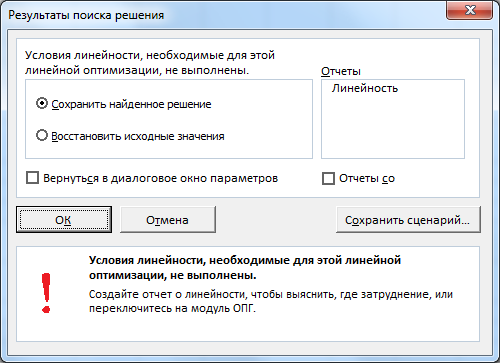
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
. РЕШЕНИЕ
ЭКОНОМИЧЕСКИХ ЗАДАЧ В MS Excel
5.1.
Моделирование как метод познания
Моделирование — исследование каких-либо явлений, процессов
или систем объектов путем построения и изучения их моделей; использование
моделей для определения или уточнения характеристик и рационализации способов
построения вновь конструируемых объектов. На идее моделирования базируется
любой метод научного исследования — как теоретический (при котором используются
различного рода знаковые, абстрактные модели), так и экспериментальный
(использующий предметные модели).
В исследуемой сложной системе выделяются наиболее существенные
признаки, свойства, связи, а несущественные, с точки зрения исследователя,
признаки, свойства, связи не учитываются. Такой подход позволяет построить
упрощенную модель сложной системы и приступить к ее изучению. Модель, в широком
смысле слова, любой аналог (изображение, описание, схема, чертеж, график, план,
карта и т. п.) какого-либо объекта, процесса или явления, используемый для
изучения или исследования.
На рисунке 3.1. в виде представлены этапы моделирования, которые, в
зависимости от возраста и рода деятельности может применять человек в процессе
познания мира и практической деятельности.
Рисунок 3.1. — Этапы познания мира
Прикладное моделирование. В процессе своей повседневной деятельности люди
используют различные модели. Появились целые отрасли, в которых моделирование
играет ведущую роль. Художники-модельеры конструируют одежду. Дизайнеры создают
проекты, предназначенные для формирования эстетических и функциональных качеств
окружающего пространства или предметов. Внедрение компьютерных технологий
многократно умножило созидательный потенциал творческих людей, позволяя
оперативно решать задачи, на которые в недавнем прошлом уходили значительные
временные ресурсы.
Научное моделирование призвано подтвердить или опровергнуть научную
гипотезу. Гипотеза часто выступает как теоретическое утверждение, которое на
данный момент времени еще не доказано экспериментально или имеющимися
средствами не может быть доказано в принципе. В научном моделировании можно
выделить два базовых направления: материальное моделирование и абстрактное
моделирование. Материальное (предметное или физическое) моделирование в
качестве моделей использует материальные предметы, абстрактное — математические
модели, мысленный эксперимент, образное мышление.
Физическое (экспериментальное) моделирование — замена изучения некоторого объекта или
явления экспериментальным исследованием его модели, имеющей ту же физическую
природу.
Математическое моделирование — замена изучения некоторого объекта или явления теоретическим
исследованием его модели, в основу которой положены подтвержденные практикой
теоретические законы.
Модели по области использования классифицируются на:
игровые модели (стратегические, ролевые, имитационные — симуляторы,
тренажеры, спортивные);
учебные модели (наглядные пособия, имитационные – тренажеры, обучающие
программы);
научно-технические модели (модели объектов, явлений, связей, модели
технологических процессов, имитационные — испытательные стенды).
По способу представления модели классифицируются на:
материальные модели (детские игрушки, наглядные пособия,
экспериментальные лабораторные установки и модели);
информационные (абстрактные) модели (вербальные[1], знаковые — книги, карты,
схемы, рисунки, компьютерное моделирование).
В процессе моделирования на языке программирования Microsoft
Excel можно выделить несколько этапов: постановка задачи;
формализация; составление алгоритма; программирование; тестирование; отладка;
оформление; прогнозирование.
В зависимости от сложности поставленной задачи некоторые этапы
моделирования могут менять очередность, объединяться или исключаться, в силу
отсутствия в них необходимости и/или очевидности решения.
Постановка задачи
1. Ознакомление с условием задачи.
2. Сбор необходимых дополнительных сведений.
3. Определение необходимости использования
универсальных констант.
4. Перевод величин в единую систему измерений,
например, СИ, СГС.
5. Определение математических или физических
законов, описывающих явления, изображаемые в условии задачи.
3.2. Пример моделирования в среде Microsoft Excel
Построить компьютерную модель электрических нагрузок двухкомнатной
квартиры. При превышении суммарных нагрузок более 5 000 Вт выдавать
сигнал опасности.
Как показывает статистика возникновения пожаров, более половины пожаров
возникает из-за неисправности в электрооборудовании и короткого замыкания в
проводке. Плавкие предохранители, которые применяются в большинстве
электрических приборов, не являются панацеей. Специалисты указывают на два
существенных недостатка плавких предохранителей:
1. Инертность (замедленное срабатывание). Пока
плавкий предохранитель перегорит, объект охраны уже сгорел.
2. Статистический разброс параметров. Плавкий
предохранитель, промаркированный на определенный номинал, может выдержать
превышение нагрузки в 15–20 раз. Если рабочая нагрузка в 3–5 раз превышает
номинальную, то плавкий предохранитель не сгорит, а сгорит объект охраны.
Снизить пожарную опасность объектов можно только внедрением в систему
охраны электронных предохранителей, которые отличаются повышенным
быстродействием и способны отключить объект охраны при превышении нагрузки на
0,1% и менее.
Дополнительные сведения задачи — список электроприборов обычной
двухкомнатной квартиры. В таблице 3.1. представлен список электрических
приборов. Нумерация приборов произведена в соответствии с номером строки
таблицы (2, 3, … 15).
Таблица 3.1. Список электрических
приборов
|
Электроприбор |
Мощность, Вт |
|
|
2. Лампы (зал) |
180 |
|
|
3. Лампа (кухня) |
100 |
|
|
4. Лампа (спальня) |
100 |
|
|
4. Лампа (ванная) |
60 |
|
|
6. Лампа (туалет) |
60 |
|
|
7. Лампа (прихожая) |
60 |
|
|
8. Телевизор |
300 |
|
|
9. Холодильник |
600 |
|
|
10.Стиральная |
1 000 |
|
|
11. Электрическая |
1 500 |
|
|
12. Пылесос |
600 |
|
|
13. Компьютер |
150 |
|
|
14. Утюг |
800 |
|
|
15. Тостер |
100 |
На рисунке 3.2. представлена схема контроля электрических нагрузок. На
схеме присутствуют:
A2:A15 — электрические приборы;
B2:B15 — селективные переключатели;
С2:С15 — цифровые индикаторы потребляемой мощности;
S — программный сумматор электрических нагрузок.
E4 — цифровой индикатор суммарной мощности;
D6 — излучатель сигнала тревоги.
Вот такую функциональную схему необходимо запрограммировать в среде Microsoft
Excel.
Рисунок 2. — Схема электрических нагрузок
Формализация, алгоритмизация и
программирование
1. Распределение, именование ячеек памяти (ячеек
таблицы).
2. Определение направления потоков данных:
входные (ввод) и выходные (вывод).
3. Определение и задание формата данных.
4. Составление математического закона (формулы),
описывающего алгоритм решения задачи.
5. Составление программы на языке
программирования.
В таблице 3.2. и на рисунке 3.3. представлено распределение ячеек
рабочего листа.
Таблица 3.2. — Распределение
ресурсов рабочего листа Microsoft Excel
|
Ячейка |
Направление потока |
Имя ячейки (Заголовок) |
Величина |
|
A2:A15 |
(Электроприбор) |
Названия |
|
|
В2:B15 |
Ввод |
(Состояние) |
Селективный 0 — 1 — включено. |
|
С2:C15 |
Вывод |
Мощность |
Цифровые 0 — Pi — если Состояниеi = 1. |
|
E4 |
Вывод |
Цифровой |
|
|
D6 |
Вывод |
Излучатель «Норма», «Пожар», |
Ячейки A1, B1, C1 содержат заголовки списка.
В ячейки A2:A15 внесены названия электрических приборов.
Ячейки B2:B15, будут работать в режиме селективного переключателя с
двумя возможными состояниями: 0 — выключено; 1— включено.
Ячейки C2:C15 отображают мощность включенного прибора Pi, где Pi — мощность отдельного прибора, i —
номер строки таблицы (i = 2, 3,
…, 15).
Ячейка E4 получена путем объединения четырех ячеек диапазона E4:F5.
Ячейка D6 получена путем объединения двадцати ячеек диапазона D6:G10.
Рисунок 3.3. — Распределение ячеек рабочего листа
Объединение
ячеек
Для объединения диапазона ячеек в одну ячейку необходимо выделить
требуемый диапазон ячеек и нажать кнопку Объединить и поместить в центре панели
инструментов Форматирование.
Селективные
переключатели
Ячейки B2:B15 должны
работать в режиме селективных переключателей с двумя состояниями: 0 —
выключено; 1 — включено.
Для того чтобы для ячеек B2:B15 запрограммировать два возможных состояния, необходимо
их выделить и командой Формат4Условное
форматирование открыть окно
диалога Условное форматирование (рисунок 3.4.).
Условие 1 имеет три поля кнопку Формат:
Раскрывающийся список типов условных форматов, применяется для выделенной ячейки или их
диапазона. Для форматирования ячейки на основе ее значения или содержимого
используется параметр значение. Для форматирования ячейки на основе указанной пользователем формулы
используется параметр формула. Значение формулы должно быть истинно или ложно.
Раскрывающийся список операторов, используется при задании условия для
выделенного диапазона ячеек. При выборе значений между или вне
необходимо указать верхнее и нижнее значения для условия форматирования.
Рисунок 3.4. — Окно диалога Условное форматирование
Поле ввода значения или формулы для применения условия форматирования к
выделенному диапазону ячеек. При выборе значений между или вне
необходимо указать верхнее и нижнее значения для условия форматирования.
Кнопка Формат предназначена для выбора
элементов отображения содержимого ячейки (диапазона ячеек) при условном
форматировании. В каждой операции форматирования к ячейке применяется только
один условный формат. В данной задаче для диапазона ячеек B2:B15 выбраны следующие параметры условного
форматирования:
если значение ячейки равно 1 , то ее
содержимое отображается черными буквами на зеленом фоне (условие 1);
если значение ячейки равно 0 , то ее
содержимое отображается белыми буквами на красном фоне (условие 2).
Цвета букв и фона в каждом условии форматирования задается в окне
диалога Формат ячеек, которое открывается нажатием на соответствующую
кнопку Формат.
После применения условного форматирования к диапазону ячеек B2:B15 любая выделенная ячейка принимает форму
раскрывающегося списка с двумя возможными значениями 0 и 1 (рисунок
3.5.).
Рисунок 3.5. — Ячейки B2:B15 после применения условного форматирования
Для того чтобы исключить ввод в ячейки B2:B15 любых чисел, кроме 0 и 1, необходимо выделить этот диапазон ячеек и
командой Данные 4Проверка4 Параметры открыть вкладку Параметры
окна диалога Проверка вводимых значений (рисунок 3.6). В
раскрывающемся списке Тип данных установить параметр Список. В поле Источник набрать список из
двух чисел: 0;
1.
Рисунок 3.6. — Вкладка Параметры окна диалога Проверка
вводимых значений
Цифровые
индикаторы
Ячейки C2:C15 играют роль цифровых индикаторов потребляемой
мощности каждой нагрузкой. Например, если переключатель B2 выключен (0), то индикатор C2 отображает 0. Если переключатель B2 включен (1), то индикатор C2 отображает номинальную мощность, в
соответствии с таблицей 3.1.
Для ячейки C2, расчетная формула примет вид: =ЕСЛИ(B2=1;180;0).
Для ячейки C3: =ЕСЛИ(B3=1;100;0).
Аналогично заполняются ячейки C4:C15. На рисунке 3.7 показан внешний вид рабочего листа
после заполнения ячеек A1:A15; B1:B15; C1:C15.
Рисунок 3.7. — Функционирование переключателей и
цифровых индикаторов
К диапазону ячеек C2:C15 можно применить условное форматирование, показанное
на рисунке 3.8, а именно: значение включенной нагрузки (значение нагрузки
больше 0) отображать красным цветом.
Для большего цветового контраста рекомендуется выделить ячейки C2:C15 и установить желтый цвет шрифта кнопкой Цвет шрифта
панели инструментов Стандартная. Тогда все нулевые значения нагрузок
будут отображаться желтым цветом, а ненулевые (включенные) — красным.
Рисунок 3.8. — Параметры условного
форматирования ячеек C2:C15
Цифровой
индикатор суммарной мощности
Ячейка E4 играет роль
цифрового индикатора суммарной мощности. В ней должна отображаться сумма ячеек C2:C15. Для повышения наглядности формулы присвоим
диапазону ячеек C2:C15 имя
Мощность. Напомним, что для этого необходимо выделить
диапазон ячеек C2:C15 и
командой Вставка4Имя4Создать
присвоить диапазону имя Мощность.
Для расчета суммарной мощности необходимо в ячейке E4 набрать формулу: =СЦЕПИТЬ(СУММ(Мощность);»
Вт»).
В этой формуле применена функция СЦЕПИТЬ категории Текстовые функции (см. таблицу 3.3),
имеющая формат:
Таблица 3.3.
|
СЦЕПИТЬ(текст_1;текст_2;…) |
|
|
текст_1, текст_2, … |
от 1 до 30 элементов текста, объединяемых |
Внимание! Вместо функции
СЦЕПИТЬ для объединения текстов можно использовать оператор конкатенации
«&».
Излучатель
сигнала тревоги
Ячейка D6 играет роль
излучателя сигнала тревоги, который работает по алгоритму:
Этот алгоритм можно запрограммировать, если в ячейке D6 набрать формулу: =ЕСЛИ(СУММ(Мощность)>=5000;»Пожар»;»Норма»).
Тестирование и отладка
1. Запуск программы в работу.
2. Проверка правильности записи операторов и
формул.
3. Проверка соответствия ссылок именам ячеек.
4. Оценка истинности результата.
На рисунке 3.9 показан момент подачи сигнала тревоги при превышении
заданного порога суммарных нагрузок.
Рисунок 3.9. — Тестирование модели электрических
нагрузок
Оформление
1. Сопровождение программы комментариями.
2. Создание дружелюбного интерфейса пользователя.
3. Ограничение доступа пользователя к содержимому
ячеек.
Применяя условное форматирование для ячеек E4, D6 в совокупности с изменением размера шрифта можно изменить внешний вид
и цифрового индикатора суммарной мощности, и излучателя сигнала тревоги
(рисунок 3.10).
Рисунок 3.10. — Оформление рабочего листа
Границы
и заливка ячеек
Команда Формат4Ячейки4Вид
позволяет изменять цвета заливки и границы ячеек или диапазонов ячеек по
усмотрению пользователя без ущерба для условного форматирования.
Сокрытие
сетки
Команда Сервис4Параметры4Вид
открывает вкладку Вид окна диалога Параметры. Для сокрытия сетки
необходимо выключить переключатель с флажком Сетка.
О
защите ячеек
Защита ячеек предназначена для ограничения доступа пользователя к
содержимому ячеек. По умолчанию все ячейки рабочего листа защищены. Но защита
ячеек включается после установки защиты рабочего листа или книги. Перед
установкой защиты рабочего листа необходимо разрешить доступ к ячейкам B2:B15, в которые будет осуществляться ввод
информации.
Для снятия защиты ячеек необходимо:
выделить диапазон ячеек B2:B15 и командой Формат 4Ячейки 4Защита открыть вкладку Защита окна диалога Формат
ячеек;
выключить переключатель с флажком Защищаемая ячейка.
Для установки защиты рабочего листа необходимо:
командой Сервис4Защита4Защитить лист.. открыть окно диалога Защита
листа;
в списке Разрешить всем пользователям этого листа
установить необходимые переключатели с флажками;
в поле Пароль для отключения защиты листа, если
есть необходимость, то можно набрать пароль. В этом случая снять защиту листа
сможет только пользователь, который знает пароль.
Прогнозирование
Варьирование в допустимых пределах значениями
переменных с целью изучения их влияния на результат вычислений.
Выдача прогноза о возможностях совершенствования
производственного процесса, условий эксперимента и т.п.
Задание.
По итогам моделирования сделайте выводы о необходимости:
ограничения суммарной нагрузки;
модернизации охранных устройств.
Дополните таблицу 3.1. Список электрических приборов следующими бытовыми электроприборами:
малогабаритный телевизор;
радиоприемник, магнитофон;
настольная лампа;
торшер;
люстра на пять ламп (5 ´ 60 Вт);
музыкальный центр;
микроволновая печь;
кофеварка;
соковыжималка;
электрическая мясорубка;
кухонный комбайн.
Слайд 1
Описание слайда:
Решение прикладных и неформализованных задач в Excel
Интегрированный урок математики и информатики
Слайд 2
Описание слайда:
«Примеры полезнее правил.»
«Примеры полезнее правил.»
И.Ньютон
Слайд 3
Описание слайда:
Что мы будем делать?
Решать прикладные задачи по математике при помощи табличного редактора Excel
Решать неформализованные задачи по информатике в табличном редакторе Excel
Учиться строить таблицы по заданному условию
Учиться формализовать задачи
Строить графики и диаграммы по заданным условиям
Пробовать себя в роли будущей профессии согласно избранному профилю обучения
Слайд 4
Описание слайда:
Прикладные задачи
Прикладная (практическая) задача – это задача, поставленная вне математики и решаемая математическими средствами.
Математические знания и навыки необходимы практически во всех профессиях, прежде всего в тех, которых связаны с естественными науками, техникой, экономикой
Слайд 5
Описание слайда:
Неформализованные задачи
Формализация информации о некотором объекте – это ее отражение в определенной форме.
То есть формализация – это сведение содержания к форме. Результатом формализации может быть таблица, формула, уравнение, неравенство и т.п.
Формализованная информационная модель – это определенные совокупности знаков (символов), которые существуют отдельно от объекта моделирования, могут подвергаться передаче и обработке.
Слайд 6
Описание слайда:
Кем мне быть?
Химико-биологический профиль – химик-теоретик, химик-аналитик.
Социально-гуманитарный профиль – журналист, аналитик, социолог.
Социально-экономический профиль – финансист, менеджер, маркетолог.
Слайд 7
Описание слайда:
Как работать в Excel
Решаем математические задачи
Анализируем условие
Заполняем данные в таблицу
Строим график
Слайд 8
Описание слайда:
Работаем по профилям
Решаем неформализованные задачи
Анализируем условие
Заполняем данные в таблицу
Строим график
Слайд 9
Описание слайда:
Пример
Рассмотрим способ решения задачи «Курс воздушных ванн»:
Курс воздушных ванн предполагает увеличение продолжительности процедуры с 15 минут до 1 часа 45 минут. Через сколько дней стоит прекратить процедуры, если каждый день курс будет увеличиваться на 10 минут?
Слайд 10
Описание слайда:
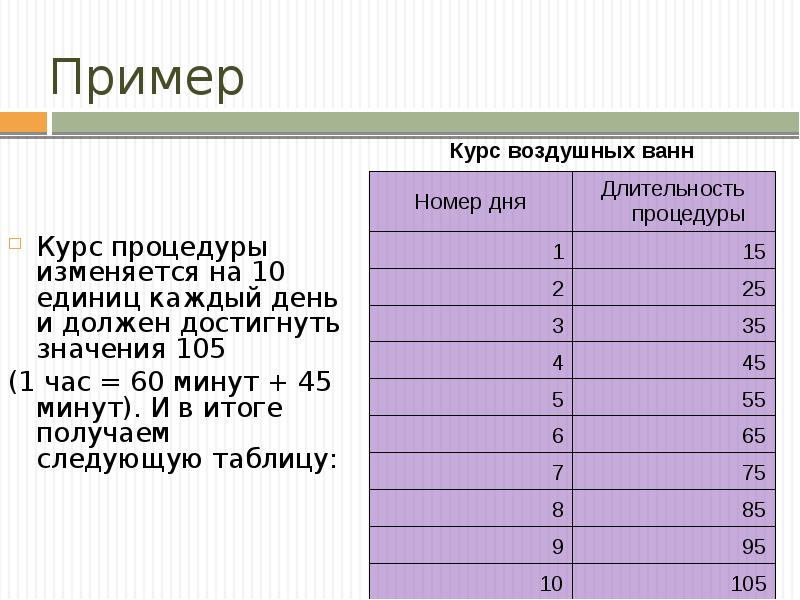
Пример
Курс процедуры изменяется на 10 единиц каждый день и должен достигнуть значения 105
(1 час = 60 минут + 45 минут). И в итоге получаем следующую таблицу:
Слайд 11
Описание слайда:
Техника безопасности
Если вы обнаружили какую-либо неисправность, немедленно сообщите об этом преподавателю. Не работайте на неисправном оборудовании!
Не включайте и не выключайте компьютеры самостоятельно.
Не дергайте и вообще не трогайте различные провода.
Не стучите по клавиатуре и мышке.
Не садитесь за клавиатуру с грязными руками.
Слайд 12
Описание слайда:
Работаем по группам
Слайд 13
Описание слайда:
Физкультминутка
Слайд 14
Описание слайда:
Демонстрируем результаты
Слайд 15
Описание слайда:
Подведение итогов урока:
Используя таблицу «Оценка урока учащимися», выставить свою оценку за урок.
Слайд 16
Описание слайда:
Домашнее задание:
Составить каждому свою неформализованную задачу, можно использовать как пример, задачи, рассмотренные на уроке.
Оцениваться будет оригинальность и практичность (жизненность) задачи.
Слайд 17
Описание слайда:
Спасибо за внимание!
1
Решение задач в электронных таблицах Excel
2
Цели работы Я показала в данной работе, как с помощью электронных таблиц эффективно решать задачи из разных сфер жизни: Решение задач по физике(аналогично можно решить задачи по химии, математике и т. д)физике( Решение статистической задачистатистической задачи Решение задачи по результатам исследованийисследований Составление интерактивного тестаинтерактивного теста Решение задачи моделирования жизненной ситуациижизненной ситуации
3
Введение Огромные возможности для моделирования несет в себе среда электронной таблицы. Это объясняется тем, что она: 1. одна из самых распространенных программных сред общего назначения и владение технологий работы в ней является одним из показателей информационной культуры человека. 2. позволяет обрабатывать большие массивы числовых данных, например статистические данные, результаты экспериментов и многое другое. 3. позволяет достаточно просто решить большое разнообразие задач (Самое главное-это связать параметры, описывающие объект, явление или процесс, некоторыми математическими соотношениями). 4. позволяет получить результаты моделирования практически мгновенно, с использованием простых технологий
4
Достоинства электронных таблиц Меня привлекло это задание тем, что в нем нужно показать решение множества задач из различных сфер в электронных таблицах. Поставленные задачи обычно решают с помощью языков программирования или другими средствами, хотя эти задачи можно легко и эффективно решать средствами Excel.
5
Этапы решения задач(эл. табл.) 1. Постановка задачи(выяснение условий, оформление решения разделов «дано» и «найти», заполнение таблицы данными, которые содержит в себе задача). 2. Составление математической модели.математической модели 3. Составление алгоритма решения. 4. Оформление решения формул в виде текста в разделе «математическая модель». 5. Создание сетки вычислений в разделе «решение». 6. Анализ полученных результатов.
6
Пример: Шарик плотностью 0.8 г/см 3, радиусом 5 см бросили вверх с начальной скоростью 25 м/с, какова максимальная высота подъема шарика, и какой энергией он будет при этом обладать? Постановка задачи Составление математической модели Составление алгоритма решения
7
Пример: Создание сетки вычислений в разделе «решение» Анализ полученных результатов
8
Ввод формул. Задачи
9
Пример: Благодаря Excel мы можем исследовать разного рода зависимости, в данном случае проанализировать и построить функцию Ep(V), Как видно это самый универсальный способ просчитывания и составления таблиц, простым перемещением курсора была составлена таблица в 50 строк. назад
10
Представление о математической модели Модель-это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Часто исследуемый объект или процесс может быть описан в виде формул, связывающих его количественные параметры(т.е. математическая модель-это описание объекта или процесса математическими формулами, связывающими их количественные параметры). Для описания математических моделей используется различные системы обозначений, принятые в той или иной науке. Составление математической модели заключается в выводе математических формул, связывающих ее параметры, по которым в дальнейшем будет производиться расчет. Компьютер позволяет на качественно новом уровне перевести мысленную модель в знаковую формулу. назад
11
Общие сведения Автор: Никитина Анна Программные средства: Excel,Word,PowerPoint. Руководитель проекта: Палецкая Алла Юрьевна Используемый материал: «Практикум по компьютерной технологии» О. Ефимова, М. Моисеева, Ю. Шафрин; «Информатика 9 класс» Н. Макарова; «Информатика и информационные технологии» Н. Угринович; «Медицинская энциклопедия». Затраченное время: 6 месяцев Примерная стоимость продукта: 200 рублей