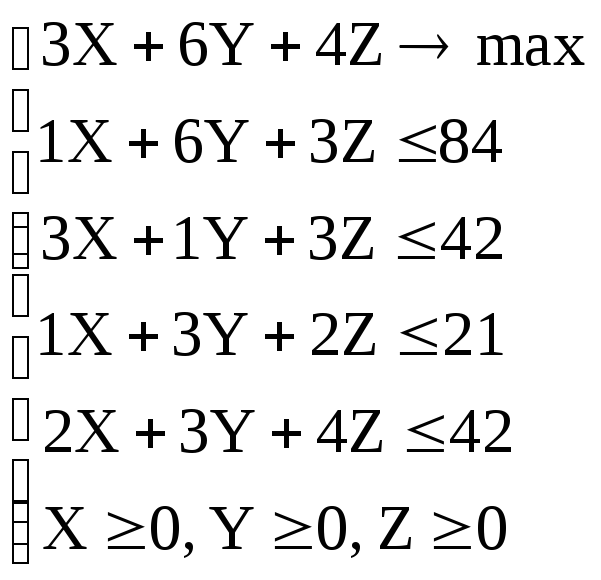Оптимизация в Excel
В старших классах школы при изучении
Excel рассматривается тема
«Оптимизация», для которой можно
использовать первые задачи главы 11
сборника примеров и задач С.М. Лавренова.
Доступное изложение материала в сборнике
и практическая направленность задач
всегда приводит к хорошему усвоению
материала.
Здесь представлено решение трех задач
сборника. Задачи решаются учениками
самостоятельно после объяснения первого
примера главы «Оптимизация» сборника
(Лавренов С.М. «Excel: Сборник
примеров и задач.- М.: Финансы и статистика,
2000.)
Перед объяснением примера нужно
рассказать о том, что в Excel
имеется надстройка «Поиск решения»,
которая позволяет решать задачи отыскания
наибольших и наименьших значений, а
также решать уравнения.
В начале надо убедиться, что Excel
использует надстройку «Поиск решения».
В меню «Сервис» найдем команду «Поиск
решения». Если ее нет, надстройку нужно
установить. Для этого в меню «Сервис»
выбираем команду «Надстройки». В
диалоговом окне находим в списке
надстроек «Поиск решения» и устанавливаем
слева от него флажок. В дальнейшем «Поиск
решения» будет устанавливаться
автоматически, пока мы не снимем флажок
в окне «Надстройки».
Задача1. Фирма производит три вида
продукции (A, B,
C), для выпуска каждого
требуется определенное время обработки
на всех четырех устройствах I,
II, III, IV
(Рис.1).
|
Вид продукции |
Время |
Прибыль, |
|||
|
I |
II |
III |
IV |
||
|
A |
1 |
3 |
1 |
2 |
3 |
|
B |
6 |
1 |
3 |
3 |
6 |
|
C |
3 |
3 |
2 |
4 |
4 |
Рис.1
Пусть время работы на устройствах
соответственно 84, 42, 21 и 42 часа. Определить,
какую продукцию и в каких количествах
стоит производить для максимизации
прибыли. (Рынок сбыта для каждого продукта
неограничен).
Решение. Составим математическую
модель. Обозначим: X –
количество изделий модели А, выпускаемых
в течение недели, Y –
количество изделий модели B,
Z – количество изделий
модели C. Прибыль от этих
изделий равна 3X+6Y+4Z.
Эту прибыль нужно максимизировать.
Функция, для которой ищется экстремум
(максимум или минимум), носит название
целевой функции. Беспредельному
увеличению количества изделий препятствуют
ограничения. В нашем случае ограничено
время обработки на четырех устройствах,
отсюда неравенства:
I устройство — 1X+6Y+3Z
II устройство — 3X+1Y+3Z
III устройство — 1X+3Y+2Z
IV устройство — 2X+3Y+4Z
Кроме того, количество изделий –
неотрицательное число, поэтому X
≥ 0, Y ≥ 0, Z
≥ 0.
Формально наша задача оптимизации
записывается так:
Теперь решим эту задачу в Excel.
Создадим новую рабочую книгу, сохраним
ее под именем Оптимизация.xls.
Введем в ячейки рабочего листа информацию
(рис. 2).
|
A |
B |
C |
D |
|
|
1 |
Переменные |
|||
|
2 |
Изделие А |
0 |
X |
|
|
3 |
Изделие В |
0 |
Y |
|
|
4 |
Изделие С |
0 |
Z |
|
|
5 |
||||
|
6 |
Целевая функция |
|||
|
7 |
Прибыль |
0 |
=3*X+6*Y+4*Z |
|
|
8 |
||||
|
9 |
Ограничения |
|||
|
10 |
Время обработки на |
0 |
=1*X+6*Y+3*Z |
<= 84 |
|
11 |
Время обработки на |
0 |
=3*X+1*Y+3*Z |
<=42 |
|
12 |
Время обработки на |
0 |
=1*X+3*Y+2*Z |
<=21 |
|
13 |
Время обработки на |
0 |
=2*X+3*Y+4*Z |
<=42 |
Рис.2
Ячейкам B2, B3
и B4 присвойте имена X,
Y, Z командой
Вставка-Имя-Присвоить. В ячейках С6, С10,
С11, С12 представлены формулы, занесенные
в соответствующие ячейки столбца В.
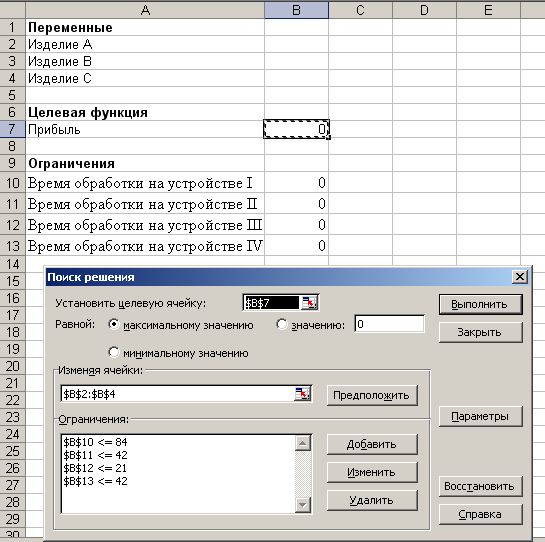
Выделим ячейку, в которой вычисляется
целевая функция и выполним Поиск решения.
В диалоговом окне в поле ввода «Установить
целевую ячейку:» уже содержится адрес
ячейки с целевой функцией $B$7.
Установим переключатель: «Равным
максимальному значению». Перейдем к
полю ввода «Изменяя ячейки:» и выделим
блок $B$2: $B$4.
Перейдем ко вводу ограничений. Щелкнем
кнопку «Добавить». Появится диалоговое
окно «Добавление ограничения». В поле
ввода «Ссылка на ячейку:» укажем $B$10.
Правее расположен выпадающий список с
условными операторами (раскройте его
и посмотрите). Выберем условие <= . В
поле «Ограничение:» введем число 84. У
нас есть еще три ограничения, поэтому,
не выходя из этого диалогового окна,
щелкаем последовательно кнопку «Добавить»
и вводим соответствующие ограничения
$B$11 <= 42, $B$12<=21,
$B$13<=42. После ввода всех
ограничений нажимаем «ОК». Мы вновь
оказываемся в диалоговом окне «Поиск
решения» (рис. 3):
Рис.3
Щелкнем кнопку «Параметры». Мы оказываемся
в диалоговом окне «Параметры поиска
решения». Чтобы узнать назначение полей
ввода этого окна, щелкнем кнопку
«Справка». Менять в этом окне ничего не
будем, только установим два флажка:
«Линейная модель» (так как наши ограничения
и целевая функция являются линейными
по переменным X и Y)
и «Неотрицательные значения» (для
переменных X и Y).
Мы подготовили задачу оптимизации.
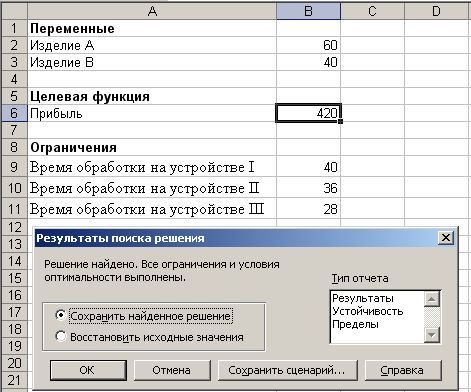
Нажимаем кнопку «Выполнить». Появляется
диалоговое окно «Результаты поиска
решения». В нем мы читаем сообщение
«Решение найдено. Все ограничения и
условия оптимальности выполнены». На
выбор предлагаются варианты: «Сохранить
найденное решение» или «Восстановить
исходные значения». Выбираем первое.
Можно вывести отчеты: по результатам,
по устойчивости, по пределам. Можно
выполнить их все, чтобы иметь представление,
какая информация в них размещена. Отчеты
не комментируются учителем, поскольку
их полное понимание требует существенного
углубления в методы оптимизации.
После нажатия «ОК» вид таблицы меняется:
в ячейках X и Y
появляются оптимальные значения. Ответ:
максимальная прибыль составляет 55, 125.
Задача 2. Фирма производит два продукта
А и В, рынок сбыта которых неограничен.
Каждый продукт должен быть обработан
каждой машиной I, II,
III. Время обработки в часах
для каждого из изделий приведено на
рис.4:
-
I
II
III
A
0,5
0,4
0,2
B
0,25
0,3
0,4
Рис. 4
Время работы машин I, II,
III соответственно 40, 36 и
36 часов в неделю. Прибыль от изделий А
и В составляет соответственно 5 и 3
доллара. Фирме надо определить недельные
нормы выпуска изделий А и В, максимизирующие
прибыль.
Окно решения:
Рис.5
Задача 3. Фирма занимается составлением
диеты, содержащей по крайней мере 20
единиц белков, 30 единиц углеводов, 10
единиц жиров и 40 единиц витаминов. Как
дешевле всего достичь этого при указанных
на рис.4 ценах (в рублях) на 1 кг (или 1 л)
пяти имеющихся продуктов?
|
Хлеб |
Соя |
Сушеная рыба |
Фрукты |
Молоко |
|
|
Белки |
2 |
12 |
10 |
1 |
2 |
|
Углеводы |
12 |
0 |
0 |
4 |
3 |
|
Жиры |
1 |
8 |
3 |
0 |
4 |
|
Витамины |
2 |
2 |
4 |
6 |
2 |
|
Цена |
12 |
36 |
32 |
18 |
10 |
Рис.6
Решение:
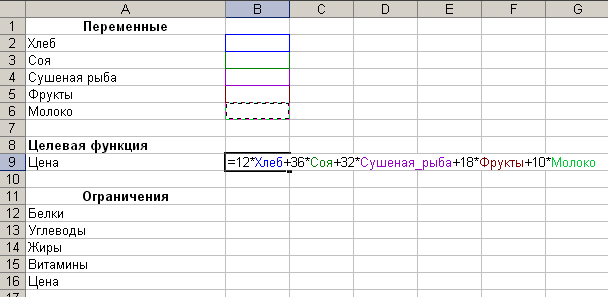
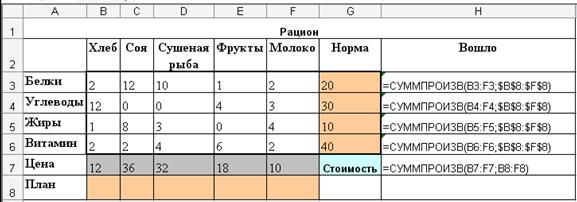
Выполняем ввод данных:
Рис.7
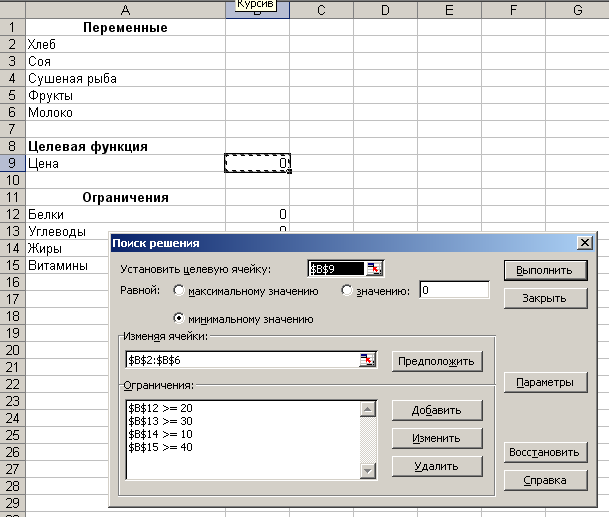
Заполняем поля диалогового окна Поиска
решения:
Рис.8
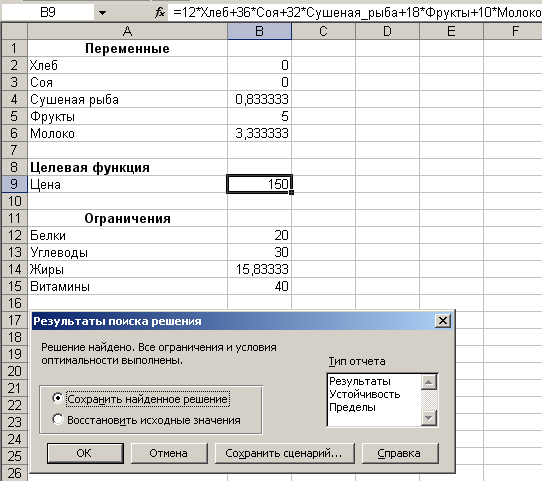
Получаем результат:
Рис. 9
Задачи оптимизации
Общие сведения
Различные аспекты оптимизации занимают очень важное место в бизнесе и деятельности современных организаций и предприятий. С подобными задачами в своей повседневной работе сталкиваются менеджеры, экономисты, финансисты, фермеры и др. Проблемы оптимизации присутствуют в самых различных процессах производства:
· поставка сырья;
· оптимальный выпуск продукции;
· оптимальное управление запасами;
· оптимальное распределение ресурсов;
· планирования инвестиций;
· оптимальный рацион (смесь, сплав);
· назначение на должность;
· оптимальная замена оборудования и т. д.
Модели всех задач на оптимизацию состоят из следующих элементов:
1. Переменные – неизвестные величины, которые нужно найти при решении задачи.
2. Целевая функция – величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
3. Ограничения – условия, которым должны удовлетворять переменные.
Пример
Фирма занимается составлением диеты, которая должна содержать по крайней мере 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах (ден. ед.) за 1 кг (или 1 л) пяти имеющихся продуктов?
| Хлеб | Соя | Сушеная рыба | Фрукты | Молоко | |
| Белки | |||||
| Углеводы | |||||
| Жиры | |||||
| Витамины | |||||
| Цена |
Рассмотрим экономико-математическую модель решения данной задачи.
1. Найти количество каждого продукта x, y, z, t, f,
где
x – количество хлеба,
y – количество сои,
z – количество сушеной рыбы,
t – количество фруктов,
f – количество молока,
2. При котором общая стоимость S=12*x+36*y+32*z+ 18*t+10*f – min
3. При ограничениях:
количество белков = 12*x+12*y+10*z+ 1*t+2*f >=20;
количество углеводов = 12*x+0*y+0*z+ 4*t+3*f >=30;
количество жиров = 1*x+8*y+3*z+ 0*t+4*f >=10;
количество витаминов = 2*x+2*y+4*z+ 6*t+2*f >=40;
и предельных условиях: x, y, z, t, f >=0.
Рассмотрим этапы реализации данной задачи в MS Excel.
В Excel необходимо создать таблицу с формулами, которые связывают план, ограничения и целевую функцию Стоимость (рис. 2.2):
Рис. 2.2. Таблица с исходными данными и формульными зависимостями
В столбец «Вошло» в каждую ячейку вводится формула вычисления количества компонентов, вошедших в диету:
=СУММПРОИЗВ(Норма; План).
В целевую ячейку «Стоимость» вводится формула:
=СУММПРОИЗВ(Цена; План).
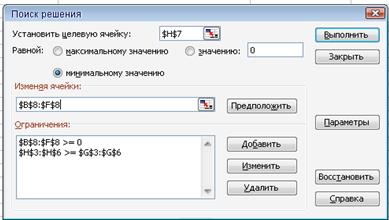
Программа Поиск решений запускается командой Сервис – Поиск решения. В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводятся соответствующие данные (рис. 2.3).
Рис. 2.3. Окно Поиск решения
Так как это линейная модель (целевая функция S является линейной), то необходимо установить в окне Параметры поиска решений переключатель в позицию Линейная модель. После нажатия на кнопку Выполнить в появившемся окне Результаты поиска решения укажите Отчет по устойчивости. Результаты поиска решения и полученный отчет представлены на рисунках 2.4 и 2.5.
Рис. 2.5. Отчет по устойчивости
Отчет по устойчивости отражает чувствительность структуры полученного плана до изменений начальных данных и дальнейшие действия менеджера с целью улучшения результатов. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел.
1. Результирующее значение – оптимальный план задачи.
В данной конкретной задаче оптимальный рацион минимальной стоимости 150 д. ед. состоит из 0,83 кг. сушеной рыбы, 5 кг. фруктов и 3,33 л. молока.
2. Нормированная стоимость неизвестных плана указывает, как изменится стоимость рациона при желании добавить в его состав «невыгодный» продукт, например, единица хлеба в рационе увеличит его стоимость на 0,2 д. ед., единица сои – на 4,6 д. ед.
3. Коэффициенты целевой функции.
4, 5. Границы изменений значений коэффициентов целевой функции при условии, что количество оптимальной продукции (план) не изменится. Например, если целевой коэффициент Фруктов (КФ) равен 18 (цена за 1 кг. товара), то изменяя его в рамках 18-0,22<КФ<18+2, 17,78<КФ<20 план не изменится, но значения стоимости может уменьшиться или увеличиться.
6. Количество использованных ресурсов;
7. Теневые цены показывают уровень влияния значения норм (в сравнении с другими ресурсами) на стоимость рациона относительно ее увеличения. В данном примере нормы на состав витаминов более «влиятельные» на стоимость, чем белки (2,5>2,2).
Например, увеличить норму витаминов на 1 единицу (до 41), то стоимость увеличиться на 2,5 д. ед. и будет составлять 152,5 д. ед.
8. Нормы белков, жиров, углеводов и витаминов в дневном рационе. Соответствуют условию задачи.
9, 10. Задают диапазон для 8, в котором действует теневая цена 7 (аналогично 4, 5).
Варианты заданий
1. Фирма производит три вида изделий – А, В и С. Для их выпуска требуется обработка на станках I, II, III, IV. Время обработки каждого изделия на станках приведено в таблице.
| Изделие | Время обработки, ч | Прибыль, $ | |||
| I | II | III | IV | ||
| А | |||||
| В | |||||
| С |
Составить план выпуска изделий дающий максимальную прибыль, если известно, что фонд рабочего времени станков соответственно равен 84, 42, 21 и 24 часа.
2. Фирме для производства требуется уголь с содержанием фосфора не более 0.03% и с примесью пепла не более 3.25%. Доступны три сорта угля – А, В и С, параметры которых приведены в таблице.
| Сорт угля | Содержание фосфора, % | Содержание пепла, % | Цена, $ |
| А | 0,06 | 2,0 | |
| В | 0,04 | 4,0 | |
| С | 0,02 | 3,0 |
Составить из указанных сортов такую смесь, чтобы она удовлетворяла требованиям производства по содержанию фосфора и пепла и имела минимальную цену.
3. Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой машиной I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице.
| I | II | III | |
| А | 0,5 | 0,4 | 0,2 |
| В | 0,25 | 0,3 | 0,4 |
Недельный фонд рабочего времени машин I, II, III равен соответственно 40, 36 и 36 часам. Прибыль от изделий А и В составляет соответственно 5 и 3 доллара. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль.
4. На кондитерскую фабрику г. Ступино перед Новым годом поступили заказы на подарочные наборы конфет из трех магазинов. Возможные варианты наборов, их стоимость и оставшиеся товарные запасы на фабрике представлены в таблице.
Определить оптимальное количество подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.
| Наименование конфет | Вес конфет в наборе, кг | Запасы конфет, кг | ||
| А | В | С | ||
| «Сникерс» | 0,3 | 0,2 | 0,4 | |
| «Марс» | 0,2 | 0,3 | 0,2 | |
| «Баунти» | 0,2 | 0,1 | ОД | |
| Цена, руб. |
5. В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес одного изделия составляют 400 руб.и 12 кг для первого типа, 500 руб.и 16 кг для второго типа, 600 руб.и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить максимальную и минимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
6. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель выпускается на отдельной технологической линии. Максимальная производительность линий составляет 60 и 75 радиоприемников в сутки. На приемники первой модели расходуется 10 типовых электронных схем, а на вторую – 8 схем. Суточный запас схем равен 800 единиц. Прибыль от реализации одного радиоприемника первой и второй модели равна соответственно 30 и 20$. Определить оптимальный суточный объем производства радиоприемников первой и второй моделей.
7. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Суточный фонд машинного времени каждого станка равен 10 часов. Время обработки и прибыль от продажи каждого изделия приведены в таблице.
| Изделие | Время обработки одного изделия, мин | Прибыль, $ | ||
| Станок 1 | Станок 2 | Станок 3 | ||
Найти оптимальный объем производства изделий каждого вида.
8. Фирма производит два вида продукции – А и В. Объем сбыта продукции А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции используется одно и то же сырье, суточный запас которого равен 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены на продукцию А и В равны соответственно 20 и 40$. Составить план распределения сырья для изготовления продукции А и В так, чтобы затраты были минимальные.
9. Кондитерская фабрика в Покрове освоила выпуск новых видов шоколада «Лунная начинка» и «Малиновый дождик», спрос на которые составляет соответственно не более 12 тонн и 7,7 тонны в месяц. По причине занятости трех цехов выпуском традиционных видов шоколада, каждый цех может выделить только ограниченный ресурс времени в месяц. В силу специфики технологического оборудования затраты времени на производство шоколада разные и представлены в таблице.
| Номер цеха | Время на производство шоколада, ч | Время, отведенное цехами под производство, ч/мес | |
| |
«Лунная начинка» | «Малиновый дождик» | |
| I | |||
| II | |||
| III | |||
| Оптовая цена, руб./т. |
Определить оптимальный объем выпуска шоколада, обеспечивающий максимальную выручку от продажи.
10. Фирма решила открыть на основе технологии производства чешского стекла, фарфора и хрусталя линию по изготовлению ваз и графинов и их декорирование. Затраты сырья на производство этой продукции представлены в таблице.
| Сырье | Расход сырья на производство, г | Поставки сырья в неделю, кг | |
| ваза | графин | ||
| Кобальт | |||
| Сусальное 24-каратное золото | |||
| Оптовая цена, руб. /шт. |
Определите оптимальный объем выпуска продукции, обеспечивающий максимальный доход от продаж, если спрос на вазы не превышает 200 шт. в неделю.
11. Изделия четырех типов проходят последовательную обработку на двух станках. Суточный фонд машинного времени каждого станка равен 10 часов. Время обработки и прибыль от продажи каждого изделия приведены в таблице.
| Изделие | Время обработки одного изделия, мин | |||
| Тип 1 | Тип 2 | Тип 3 | Тип 4 | |
| Прибыль, $ |
Найти объем производства изделий каждого типа, позволяющий получить максимальную прибыль.
12. Завод выпускает изделия трех моделей – I, II и III. Для их изготовления используются два вида ресурсов. – А и В, запасы которых составляют 4000 и 6000 единиц соответственно. Расход ресурсов и прибыль на каждое изделие приведены в таблице.
| Ресурс | Расход ресурса на изделие | ||
| I | II | III | |
| А | |||
| В | |||
| Прибыль,$ |
Найти объем производства изделий каждого типа, позволяющий получить максимальную прибыль.
13. Фирма выпускает два типа автомобильных деталей (А и В). Для этого закупается литье, подвергаемое затем токарной обработке, сверлению и шлифованию. В таблице приведены параметры станочного парка фирмы.
| Станок | Деталь А, шт./ч | Деталь В, шт./ч |
| Токарный | ||
| Сверлильный | ||
| Шлифовальный |
Каждая отливка, из которой изготавливают деталь А, стоит 2$, а для детали В стоимость отливки равна 3$. Продажные цены деталей равны 5 и 6$. Стоимость часа станочного времени по указанным типам станков составляет 20, 14 и 17,5$. Определить план выпуска изделий, дающий максимальную прибыль.
14. Бройлерное хозяйство насчитывает 20000 цыплят. Для того, чтобы цыплята к моменту продажи достигли определенного веса, их кормовой рацион должен удовлетворять следующим требованиям:
– содержание кальция не менее 0,8% и не более 1,2%;
– содержание белка не менее 22%;
– содержание клетчатки не более 5%.
Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Пусть в распоряжении хозяйства имеются только ингредиенты, указанные в таблице. Там же указаны их параметры.
| Ингредиент | Содержание питательных веществ | Стоимость, $/кг | ||
| кальций | белок | клетчатка | ||
| Известняк | 0,38 | – | – | 0,04 |
| Зерно | 0,001 | 0,09 | 0,02 | 0,16 |
| Соевые бобы | 0,002 | 0,5 | 0,08 | 0,4 |
Необходимо составить кормовую смесь минимальной стоимости, содержание питательных веществ в которой удовлетворяет указанным выше требованиям.
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
Большая просьба, помогите, пожалуйста, решить задачки в Excel.
№1. На предприятии освоены четыре технологии производства основной продукции. В таблице указаны запасы потребляемых ресурсов, затраты их в течение месяца и объемы выпуска готовой продукции при каждой технологии за тот же период. Установите такое время работы предприятия по каждой технологии, при котором выпуск продукции будет максимальным, а расход ресурсов не превысит их наличия.
Ресурсы Запас ресурса Расход ресурса при технологии
I II III IV
Р1 34 2 4 1 5
Р2 16 4 1 4 1
Р3 22 2 3 1 2
Объем выпуска продукции 7 3 4 2
№2 — Фирма занимается составлением диеты, содержащей по крайней мере 20 едениц белков, 30 едениц углеводов, 10 едениц жиров и 40 едениц витаминов. Как дешевле всего достичь этого при указанных ниже ценах (в рублях) на 1 кг или (1 л) пяти имеющихся продуктов?
хлеб соя сушеная рыба фрукты молоко
белки 2 12 10 1 2
углеводы 12 0 0 4 3
жиры 1 8 3 0 4
витамины 2 2 4 6 2
цена 12 36 32 18 10
№3 — используя поиск решения решить:
Z=6×1-x3+x4+2×5 стремится max
система: 2×1-x2+x4=2
4×1+x2+x3+2×4+x5=8
x1+x2+x5=2
xj>=0; j=1,5 с полочкой вверху
Lis04ka,
во вложении решение задачи №1
По аналогии решите и остальные.
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Решение экономических задач в Excel`e
Разработка проекта «Решение оптимизационных задач средствами Excel»
Место темы в учебном курсе: уроки в 10-м классе
План работы над проектом
|
Стадия работы |
Результат работы |
Домашнее задание |
|
Урок 1. Знакомство с программой «Поиск решения» в Excel на примере задачи из учебника [2] |
Учащиеся решают совместно в программе Excel предложенную задачу |
Найти информацию о Леониде Канторовиче |
|
Урок 2. Оформление презентации по этапам решения задачи |
Учащиеся готовят презентацию по решенной задаче из 7 слайдов
|
Выбор индивидуальной задачи, создание математической модели, проект электронной таблицы с данными |
|
Урок 3. Решение индивидуальной задачи |
Учащиеся решают свою задачу |
Подготовка текста главы проекта Введение |
|
Урок 4. Знакомство с требованиями оформления работы |
В программе WORD учащиеся оформляют свой проект |
Требования по оформлению рефератов |
|
Урок 5. Знакомство с требованиями оформления работы |
В программе WORD учащиеся оформляют свой проект |
Требования по оформлению рефератов |
|
Урок 6. Выполнение итогового теста |
Учащиеся выполняют итоговый тест и сдают папку с законченным проектом |
Урок 1. Знакомство с программой «Поиск решения» в Excel
Построить математическую модель задачи и решить её средствами Excel.
Задача. Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
|
Ресурсы |
Нормы расхода ресурсов на одно изделие |
Общее количество ресурсов |
|
|
стол |
шкаф |
||
|
Древесина 1 вида |
0,2 |
0,1 |
40 |
|
Древесина 2 вида |
0,1 |
0,3 |
60 |
|
Трудоемкость |
1,2 |
1,5 |
371,1 |
|
Прибыль от реализации одного изделия |
6 |
9 |
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
РЕШЕНИЕ.
Составим математическую модель задачи. Пусть фабрика изготавливает x1 столов и x2 шкафов. По смыслу задачи эти переменные неотрицательны, x x1, 2 ≥ 0 . Прибыль от реализации такого количества шкафов и столов составит F = 6x1 +9x2 рублей, ее нужно максимизировать:
F = 6x1 +9x2 → max .
Теперь составим ограничения задачи.
Для изготовления x1 столов и x2 шкафов потребуется 0,2x1 +0,1x2 древесины первого вида, запасы которой составляют 40 куб.м., поэтому 0,2x1 +0,1x2 ≤ 40 , или 2x1 + x2 ≤ 400. Для изготовления x1 столов и x2 шкафов потребуется 0,1x1 +0,3x2 древесины второго вида, запасы которой составляют 60 куб.м., поэтому 0,1x1 +0,3x2 ≤ 60 , x1 +3x2 ≤ 600.
Для изготовления x1 столов и x2 шкафов потребуется 1,2x1 +1,5x2 древесины третьего вида, запасы которой составляют 371,1 куб.м., поэтому 1,2x1 +1,5x2 ≤ 371,1, 12x1 +15x2 ≤ 3711,
4x1 +5x2 ≤ 1237
Получаем задачу линейного программирования:
F = 6x1 +9x2 → max,
2x1 + x2 ≤ 400,
x1 +3x2 ≤ 600,
4x1 +5x2 ≤1237,
x1, 2 ≥ 0.
Решим задачу средствами Excel. Заполним ячейки исходными данными (в виде таблицы) и формулами математической модели. Вычисляемые ячейки пометим цветом.
Таблице в режиме чисел:
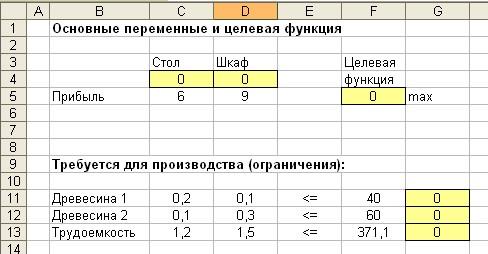
Таблица в режиме формул: (для отображения формул можно перед знаком равно поставить пробел)

Вызываем надстройку «Поиск решения» и заполняем параметры: (для активирования данной функции необходимо выполнить команду СЕРВИС, НАДСТРОЙКА и установить галочку против программы Поиск решения)
Вносим целевую функцию и ограничения.
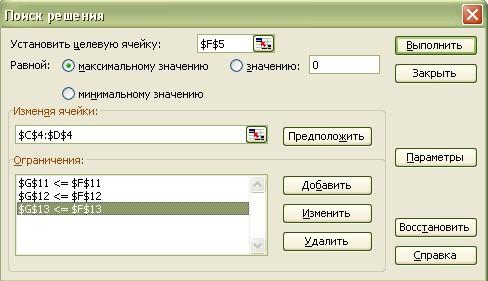
Запускаем решение:

Получаем решение:
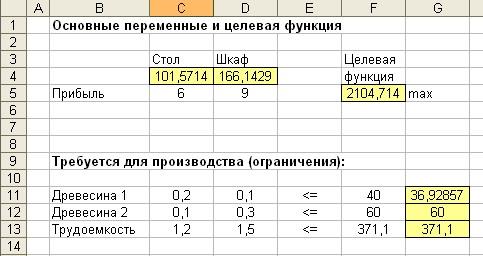
Получили нецелочисленное решение – 101,571 столов и 166,143 стульев. Чтобы получить более «реальное» в экономическом смысле решение, добавим ограничение целочисленности переменных, тогда получим:
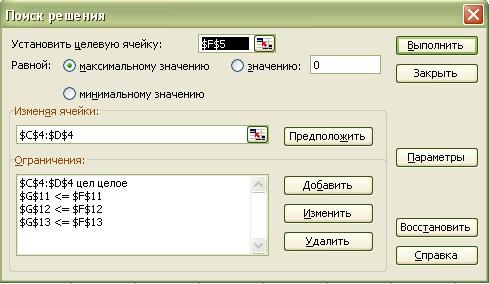
Искомое решение:
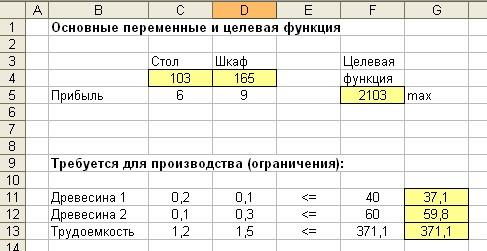
Таким образом, следует производить 103 стула и 165 шкафов, при этом прибыль от реализации будет максимальна и составит 2103 рубля. В процессе производства будут остатки древесины первого и второго типа: 2,9 и 0,2 кубометра соответственно. Трудоемкость будет «использована» в полном размере.
Урок 3. Индивидуальные задания для учащихся
Задача 1. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки? Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5?
Задача 2. Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 3. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить 11 кг сырья первого типа, 21 кг сырья второго типа, 31 кг сырья третьего типа. На изготовление единицы Изделия 2 требуется затратить 12 кг сырья первого типа, 22 кг сырья второго типа, 32 кг сырья третьего типа. Производство обеспечено сырьем каждого типа в количестве 100 кг, 150 кг, 180 кг соответственно. Рыночная цена единицы Изделия 1 составляет 3 тыс. руб., а единицы Изделия 2 — 4 тыс.руб. Требуется составить план производства изделий, обеспечивающий максимальную выручку от их реализации.
Задача 4. Для производства двух видов продукции А и В предприятие использует четыре группы оборудования 1, 2, 3, 4. На производство одной штуки продукции А требуется занять в течение одной единицы времени 1, 0, 5, 2 единиц соответственно 1, 2, 3, 4 оборудования. На производство одной штуки продукции В требуется 1, 1, 0, 2 единиц оборудования 1, 2, 3, 4. Имеется оборудования по группам 1-10, 2-12, 3-24, 4-20 единиц. Предприятие получает с одной штуки продукции А доход 4 тыс. рублей, а продукции – 6 тыс. руб.
Сколько штук продукции каждого вида должно производить предприятие, чтобы получить максимальную прибыль?
Задача 5. В мастерской промартели освоили производство столов и тумбочек для торговой сети. Для их изготовления имеется два вида древесины 1- 72м3 и 2-56 м3.
На каждое изделие требуется древесина м3 каждого вида
|
Изделия |
1 |
2 |
|
Стол |
0,18 |
0,08 |
|
Тумбочка |
0,09 |
0,28 |
От производства одного стола промартель получает чистого дохода 1,1 тыс. руб. и от производства тумбочки 700 руб. Определить, сколько столов и тумбочек должна производить промартель, чтобы получить максимальную прибыль?
Задача 6. Цех выпускает трансформаторы двух видов. На один трансформатор первого вида расходуется 3 кг. Проволоки и 5 кг. Железа, а на один трансформатор второго вида требуется 3 кг железа и 2 кг. Проволоки. От реализации одного трансформатора первого вида цех получает прибыль в 1,2 тыс. руб., а от реализации одного трансформатора второго вида 1 тыс. руб. Сколько трансформаторов каждого вида должен производить цех, чтобы получить максимальную прибыль, если цех располагает 480 кг. Железа и 300 кг. Проволоки?
Задача 7. Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33 единиц вещества А, 23 единицы питательного вещества В. Для откорма используется два вида кормов. Данные о содержании питательных веществ и стоимости весовой единицы представлены в таблице.
|
В одной весовой единице |
А |
В |
Стоимость одной весовой единицы |
|
Корм 1 Корм 2 |
4 3 |
3 2 |
20 руб 20 руб |
Составьте наиболее дешевый рацион, при котором каждое животное получило бы необходимое количество питательных веществ А и В?
Задача 8. Имеется три вида сырья А, В, С, которые используются для производства двух видов продуктов 1 и 2. В распоряжении находится 500 единиц сырья А, 750 единиц сырья В и 200 единиц сырья С. Продукт 1 состоит из 1 единицы сырья А и двух единиц сырья В. Продукт 2 состоит из двух единиц сырья А, одной единицы сырья В и одной единицы сырья С. Доход от производства одной единицы продукта 1 составляет 4 тыс. руб, а от одной единицы продукта 2 – 3 тыс. руб. Сколько единиц каждого вида продукции производить, чтобы получить максимальную прибыль?
Задача 9. Имеется два вида сырья для производства двух видов продуктов 1 и 2. Продукт 1 состоит из двух единиц сырья А и пяти единиц сырья В. Продукт 2 состоит из трех единиц сырья А и четырех единиц сырья В. Доход от производства одной единицы продукта 1 составляет 4 тыс. руб., а от одной единицы продукта 2 – 5 тыс. руб. Сколько единиц каждого вида продукта нужно производить, чтобы максимизировать прибыль, если в распоряжении имеется 500 единиц сырья А и 750 единиц сырья В?
Задача 10. Фирма производит два вида продукции А и В. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III:

Пусть время работы на устройствах соответственно 40, 36, 36 часов в неделю. Прибыль от изделий А и В соответственно составляет 5$ и 3$. Определите недельные нормы выпуска изделий для максимизации прибыли. (Рынок сбыта для каждого продукта неограничен.)
Задача 11. В рационе животных используется два вида кормов. Животные должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные сведены в таблицу.
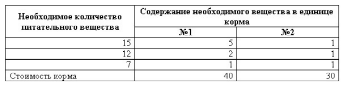
Задача 12. В рационе лошадей используется два вида кормов (сено и рожь). Лошади должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные сведены в таблицу.

Задача 13. Фирма производит три вида продукции: А, В и С. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III, IV:
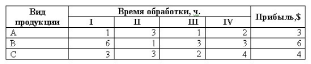
Пусть время работы на устройствах соответственно 84, 42, 21, 42 часа. Определите, какую продукцию и в каких количествах стоит производить для максимизации прибыли. Рынок сбыта для каждого продукта неограничен.
Задача 14. Фирма занимается составлением диеты, содержащей, по крайней мере, 20 ед. белков, 30 ед. углеводов, 10 ед. жиров и 40 ед. витаминов. Как дешевле всего достичь этого при указанных ценах в рублях на 1 кг (1 литр) пяти имеющихся продуктов?
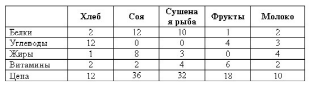
Задача 15. Фирма производит два набора удобрений для газонов: обычный и улучшенный. В обычный входят 3 фунта азотных, 4 фунта фосфорных и один фунт калийных удобрений, а в улучшенный — 2 фунта азотных, 6 фунтов фосфорных и 2 фунта калийных удобрений. Известно, что для некоторых газонов требуется, по меньшей мере, 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3$, а улучшенный — 4$. Сколько (целое число) и каких наборов удобрений надо купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Задача 16. Производятся изделия А и В, при изготовлении которых используется два типа технологического оборудования 1 и 2. На производство единицы изделия А оборудование 1 используется 2 часа, а оборудование 2 1 час. На производство единицы изделия В оборудование 1 используется 1 час, а оборудование 2 – 2 часа. Администрация на изготовление изделий может выделить оборудование 1 – на 10 часов, а оборудование 2 – на 8 часов. Спланировать производство изделий А и В так, чтобы общая прибыль была наибольшей, если от реализации единицы изделия А прибыль 5 тыс руб, В – 2 тыс. руб
Задача 17. Цех двойного суперфосфата выпускает два вида минеральных удобрений А и В. На производство 1 кг удобрений А используют 5 кг питательных веществ 1 и 4 кг. Питательного вещества 2. На производство 1 кг удобрений В используют 3 кг питательных веществ 1 и 2 кг. Питательного вещества 2. От реализации 1 кг А цех получает прибыль 40 руб., а от реализации 1 кг В – 35 руб.
Какое количество удобрений должен производить цех, чтобы получить максимальную прибыль, если цех имеет всего 450 кг питательного вещества 1 и 400 кг питательного вещества 2?
Урок 4. План работы над проектом
-
Создать папку «Проект учащегося ФИО», в которую перенести файл с решенной задачей и создать текстовый документ.
-
Содержание работы:
-
Титульный лист
-
Оглавление
-
Теоретическая часть содержит информацию о линейном программировании и людях, которые этим занимались.
-
Практическая часть состоит из технологии решения вашей задачи.
-
Используемые источники
-
Параметры оформления документа
-
Лист книжный
-
Отступы 1,5 см со всех сторон
-
Шрифт Times New Roman для основного текста, размер 12
-
Шрифт Arial для заголовков, размер 14, начертание Ж
-
Номер в правом нижнем углу и без номера на титульном листе
-
Каждый раздел документа располагается с нового листа.
-
Оформление проекта
1. Набрать текст
2. Разделить документ на страницы: титульный лист, оглавление, введение, теоретическая часть, практическая часть, список литературы. Установить курсор в начало новой страницы, выполнить ВСТАВКА/РАЗРЫВ/НОВАЯ СТРАНИЦА
Обратите внимание, что страница ОГЛАВЛЕНИЕ пока пустая.
3. Заполните титульный лист, предмет, свою фамилию. Выровняйте текст, кроме таблицы, по центру.
4. Выделите все заголовки и присвойте им стиль ЗАГОЛОВОК 1.
5. Вставить нумерацию в правом нижнем углу. ВСТАВКА/НОМЕРА СТРАНИЦ/ справа внизу и без номера на первой странице.
6. Перейти на страницу ОГЛАВЛЕНИЕ, вставить оглавление. ВСТАВКА/ССЫЛКА/ОГЛАВЛЕНИЕ И УКАЗАТЕЛИ/ Выбрать выкладку ОГЛАВЛЕНИЕ, задать УРОВНИ -1, убрать отметку о гиперссылках, но задать отметки
-
ПОКАЗАТЬ НОМЕРА СТРАНИЦ
-
НОМЕРА СТРАНИЦ ПО ПРАВОМУ КРАЮ.
Урок 5. Образец выполненного проекта
Урок 6. Вопросы итогового теста
-
Какую опцию главного меню необходимо открыть для выбора функции ПОИСК РЕШЕНИЯ?
-
Задача. Комплект мебели (парта и два стула) стоит 8500 рублей. Известно, что производитель М продает мебель упаковками по 6 комплектов в упаковке, а производитель N — по 4 комплекта в упаковке. Какое максимальное количество можно купить на 150 тыс. рублей? В ответе запишите два целых числа через пробел: количество комплектов и потраченную сумму в рублях. Решение
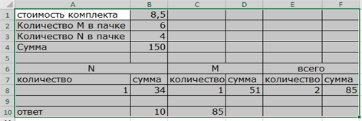
Какая ячейка оптимизируется?
-
Как оптимизируется ячейка? (варианты минимум, максимум, значение и т.д.)
-
Какие ячейки изменяются при оптимизации?
-
На какие ячейки накладываются ограничения при оптимизации?
-
Необходимое условие для автоматического собирания оглавления
-
Для нумерации страниц в работе необходимо выполнить
-
Расставьте по порядку основные разделы документа «Проект»
-
Выберите советского ученого, лауреата Нобелевской премии в области экономики (дан список имен)
-
Выберите верное утверждение (Предлагаются варианты размещения нумерации)
Источники информации
-
Практикум по вычислительной математике: Метод. Разработка/ Сост. Н.Л.Грохульская, С.Г.Ершова, А.Н.Новогрудская; Свердловский педагогический институт. Свердловск, 1990, 215 с, с.111-122
-
Культура информационной деятельности: Учебное пособие для основной школы (9 класс)./ В.В.Мочульский, А.Г.Гейн, В.И.Жильцова, В.И.Кадочникова, Т.В.Шпота, Е.А.Гвоздева, В.Г.Мещеряков, А.Г.Мачульская.- Екатеринбург: Центр «Учебная книга»; Смоленск; Издательство «Ассоциация XXIвек», 2006. – 432 с, с.176-180
-
https://www.matburo.ru/Examples/Files/LP_Excel1.pdf
-
https://inecon.org/docs/Kantorovich_1.pdf
Приложение. Образец выполненного проекта
Министерство образования и молодежной политики Свердловской области
Управление образования администрации Чкаловского района
Образовательная область: технология
Предмет: технология
Проект
Решение оптимизационных задач средствами Excel
|
Исполнитель: Руководитель: |
Ученик 10 класса Фамилия Имя Преподаватель технологии Иванова З.И. |
Екатеринбург
2020 г.
Оглавление
Введение 3
Линейное программирование, оптимизационные задачи 4
Практическая часть 5
Источники информации 8
Введение
Информатизация общества, развитие информационных технологий ставят перед каждым человеком вопрос о необходимости постоянного повышения квалификации, а в некоторых случаях и о неоднократной смене профессиональной деятельности в течение жизни.
Общеобразовательная школа должна формировать новую систему универсальных знаний, умений, навыков, опыт самостоятельной деятельности и личной ответственности обучающихся за сохранение окружающей среды, за разумное использование сырья, то есть современные ключевые компетенции.
Парадокс компетентности состоит в том, что она обнаруживает себя за пределами учебных ситуаций, в задачах, не похожих на те, где знания и умения приобретались.
Старые методики обучения требуют переосмысления и развития по мере появления новых информационных технологий.
Разрешение приведенных противоречий обуславливает актуальность настоящей работы и определяет ее проблему: какие средства могут быть использованы для формирования ИКТ-компетентности у учащихся средней школы?
Этот анализ определил следующий выбор темы проекта: «Методика решения оптимизационных задач средствами Excel».
Объект исследования: формирование ИКТ-компетентности.
Предмет исследования: использование разработки методики решения оптимизационной задачи средствами Excel для формирования ИКТ-компетентности.
Цель исследования: формирование ИКТ-компетентности средствами решения оптимизационной задачи в Excel.
При достижении поставленной цели мы руководствовались следующей гипотезой: разработка проекта будут способствовать формированию ИКТ—компетентности, если будет построена модель методики решения оптимизационных задач средствами Excel.
На основании цели исследования и рабочей гипотезы была сформулирована следующая задача исследования: разработать методику решения оптимизационной задачи средствами Excel для формирования ИКТ-компетентности.
Теоретическую основу исследования составили работы по линейному программированию:
-
https://www.matburo.ru/Examples/Files/LP_Excel1.pdf
-
https://inecon.org/docs/Kantorovich_1.pdf
Теоретическая значимость исследования заключается в следующем: описана последовательность решения оптимизационных задач средствами Excel.
Практическая значимость исследования состоит в том, что теоретические результаты доведены до уровня практического применения: решена конкретная задача.
Линейное программирование, оптимизационные задачи
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась ещё в XIX веке.
Развитие экономики потребовало количественных показателей, и в начале XX века были созданы и исследованы математические модели, которые повлияли на работы экономиста и статистика Василия Васильевича Леонтьева. Он разработал межотраслевую модель производства и распределения продукции.
В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная. В 1939 году Леонид Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования. Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов. В 1975 году он стал лауреатом Нобелевской премии по экономике совместно с Тьяллингом Купмансом за вклад в теорию оптимального распределения ресурсов»).
Общей (стандартной) задачей линейного программирования называется задача нахождения минимума (максимума) линейной целевой функции (линейной формы). Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП).
Примеры задач:
-
транспортная задача;
-
максимальный поток;
-
задача экономного использования сырья.
Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод.
Практическая часть
Задание. Фирма производит два вида продукции A и В. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III:
Пусть время работы на устройствах соответственно 40, 36, 36 часов в неделю. Прибыль от изделий А и В соответственно составляет 5$ и 3$. Определите недельные нормы выпуска изделий для максимизации прибыли. (Рынок сбыта для каждого продукта неограничен.)
Решение.
Составим математическую модель задачи. Пусть фабрика изготовит х изделий А и у изделий В. По смыслу задачи эти переменные неотрицательные, х,у=0.
Прибыль от реализации такого количества продукции составит F=5*x+3*y.
Эту функцию надо максимизировать
Теперь составим ограничения задачи.
Для изготовления х изделий А и у изделий В потребуется:
0,5*х+0,25*у времени работы I устройства;
0,4*х+0,3*у времени работы II устройства;
0,2*х+0,4*у времени работы III устройства;
Но время работы I устройства ограничено 40 часами, т.е.
0,5*х+0,25*у
время работы II устройства ограничено 36 часами, т.е.
0,4*х+0,3*у
время работы III устройства ограничено 36 часами, т.е.
0,2*х+0,4*у
Получаем задачу линейного программирования:
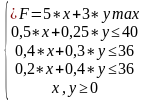
Решаем задачу средствами Excel. Заполняем ячейки исходными данными (в виде таблицы) и формулами математической модели.
Таблица в режиме чисел
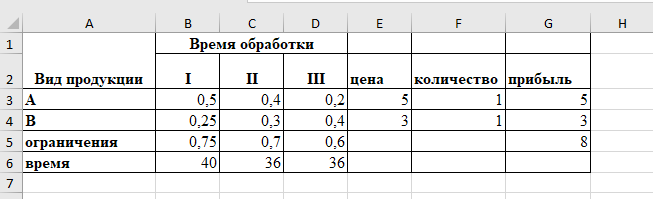
Таблица в режиме формул:
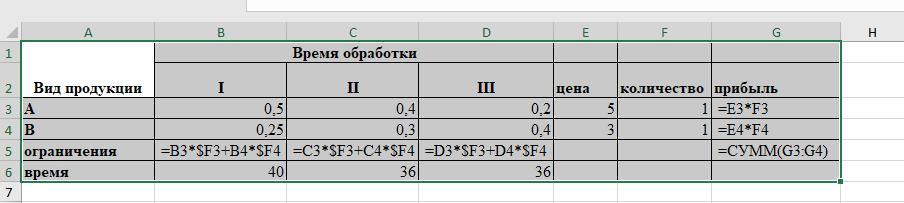
Вызываем надстройку «Данные / Поиск решения» и заполняем параметры:
Вносим целевую функцию и ограничения.
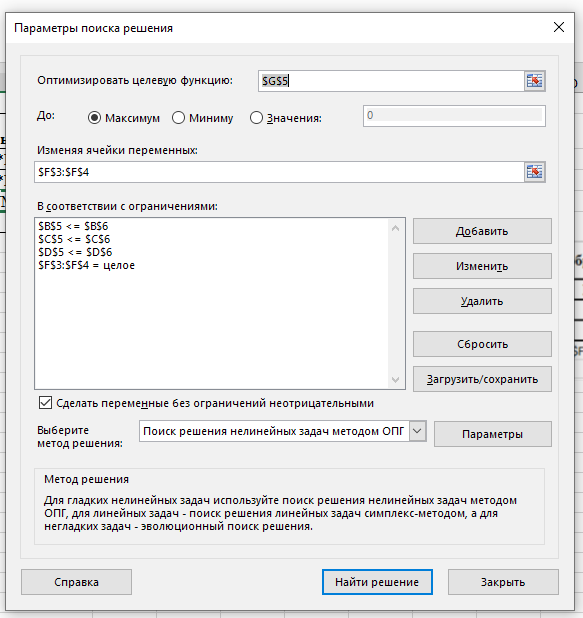
Получаем решение
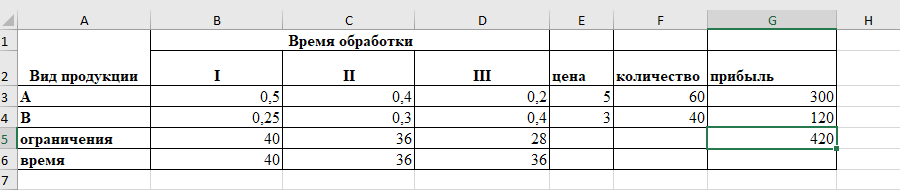
Получили следующий результат:
При заданных ограничениях предприятие может получить максимальную прибыль
420 единиц, изготовляя 60 единиц изделия А и 40 единиц изделия В.
Источники информации
-
Симоненко В.Д. Технология: базовый уровень: 10-11 классы: учебник для учащихся общеобразовательных учреждений / В.Д. Симоненко, О.П.Очинин, Н.В.Матяш: под ред. В.Д.Симоненко. – М.: Вентана-Граф., 2010. – 224 с, : ил.
-
http://www.apmath.spbu.ru/ru/staff/kuzyutin.d/files/vved_v_lp_lekciya.pdf
-
https://math.semestr.ru/simplex/simplex_lectures.php
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5

Задача линейного программирования с использованием MathCAD
Фирма занимается составлением диеты, содержащей по крайне мере 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах на 1кг (или 1л) пяти имеющихся продуктов?
Хлеб Соя Сушеная рыба Фрукты Молоко
Белки 2 12 10 1 2
Углеводы 12 0 0 4 3
Жиры 1 8 3 0 4
Витамины 2 2 4 6 2
Цена 12 36 32 18 10
ЗАРАНЕЕ ОГРОМНОЕ СПАСИБО!!!