Финансовые функции в excel практические задания

Практическая работа №9

ФИНАНСОВЫЕ ФУНКЦИИ MS EXCEL В
ЭКОНОМИЧЕСКИХ РАСЧЕТАХ

Цель:
научиться использовать финансовые функции для экономических расчётов.

Задания:

1.

Функции даты и времени для финансовых расчетов

Время – один из важнейших факторов в
финансовых операциях и сделках. Для проведения финансовых расчетов необходимо
находить срок между начальной и конечной датами операции, обычно заданный в
днях или годах.

Если рассчитывается точное число дней, то
надо просто вычесть из конечной даты (даты завершения операции) начальную
дату. 

Однако в финансовой практике есть правило,
согласно которому в месяце считается 30 дней, а в году 360. В этом случае
используется функция ДНЕЙ360. Ее назначение – расчет количества дней между
двумя датами на основе 360-дневного года (12 30-дневных месяцев), аргументы:
нач_дата – начальная дата сделки; кон_дата – конечная дата сделки; метод –
логическое значение, если отсутствует, есть «ЛОЖЬ».

Аргументы «нач_дата» и «кон_дата» могут
быть введены как текстовые строки в двойных кавычках или в числовом формате,
могут также использоваться ссылки на ячейки, в которых заданы даты в формате
дата. Если аргумент «метод» принимает значение «ЛОЖЬ» или опущен, то
используется американский метод определения приближенного числа дней между
двумя датами, а если «ИСТИНА» – то европейский (эти два метода различаются,
только если конечная дата – 31-е число месяца).

Для определения срока между датами в годах
надо использовать функцию ДОЛЯГОДА с аргументами (нач_дата, кон_дата,
базис). 

Первые два аргумента имеют то же значение,
что и у функции ДНЕЙ360. Аргумент «базис» может принимать пять различных
значений в зависимости от правила, установленного для расчета срока в годах:

0      
или опущен – правило 30/360 (приближенный срок между
датами в днях

(американский метод расчета), приближенное
число дней в году);

1      
– АСТ/АСТ (точный срок между датами в днях, точное
число дней в году);

2      
– АСТ/360 (точный срок между датами в днях,
приближенное число дней в году);

3      
– АСТ/365 (точный срок между датами в днях, но в любом
году 365 дней);

4      
– 30/360 европейский (приближенный срок между датами в
днях (европейский метод

расчета), приближенное число дней в году).

Пример.

Дата
получения кредита – 15 января 2008 г., дата погашения – 15 марта того же года.
Найти срок кредита в днях и годах.

Решение выполнить на Листе 1. 

Откройте Лист 1 и переименуйте его в
Задание 1.

Точное число дней = «15/03/2008» –
«15/01/2008» = 59.

Приближенное число дней =
ДНЕЙ360(«15/01/2008», «15/03/2008») = 60. Срок кредита в годах по правилу

АСТ/АСТ = ДОЛЯГОДА(«15/01/2008»,
«15/03/2008») = 0,161644.

Расчет
ипотечной ссуды осуществляются с использованием финансовой функции ПЛТ

Функция ПЛТ вычисляет величину постоянной
периодической выплаты ренты (например, регулярных платежей по займу) при
постоянной процентной ставке.

Синтаксис: ПЛТ(Ставка;Кпер;Пс;Бс;Тип).

Аргументы:

§  Ставка
– процентная ставка по ссуде,

§  Кпер
– общее число выплат по ссуде,

§  Пс
– приведенная к текущему моменту стоимость, или общая сумма, которая на текущий
момент равноценна ряду будущих платежей, называемая также основной суммой,

§  Бс
– требуемое значение будущей стоимости, или остатка средств после последней
выплаты.

Если
аргумент Бс опущен, то он полагается равным 0 (нулю), т.е. для займа, например,
значение Бс равно 0, Тип – число 0 (нуль) или 1, обозначающее, когда должна
производиться выплата.

Отметим, что очень важно быть
последовательным в выборе единиц измерения для задания аргументов Ставка и
Кпер.

Например,
если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12

%
годовых, то для задания аргумента Ставка используйте 12 %/12, а для задания
аргумента Кпер – 4*12. Если вы делаете ежегодные платежи по тому же займу, то
для задания аргумента Ставка используйте 12 %, а для задания аргумента Кпер –
4.

Для нахождения общей суммы, выплачиваемой
на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на
величину Кпер. Интервал выплат – это последовательность постоянных денежных
платежей, осуществляемых за непрерывный период.

Например, заем под автомобиль или заклад
являются интервалами выплат. В функциях, связанных с интервалами выплат,
выплачиваемые вами деньги, такие как депозит на накопление, представляются
отрицательным числом, а деньги, которые вы получаете, такие как чеки на
дивиденды, представляются положительным числом.

Например,
депозит в банк на сумму 1000 руб. представляется аргументом – 1000, если вы

вкладчик,
и аргументом -1000, если вы – пpeдставитель банка.

Пример
1. Вычислить 30-летнюю ипотечную ссуду покупки квартиры за 201900 руб. с
годовой ставкой 8% и начальным взносом 20%. Сделать расчет для ежемесячных и
ежегодных выплат (табл. 1).

Решение:

1.                 
Откройте Лист 2 и переименуйте его в
Задание 2.

2.                 
Введите в ячейки A1:B6 данные,
представленные на рис. 1.

 

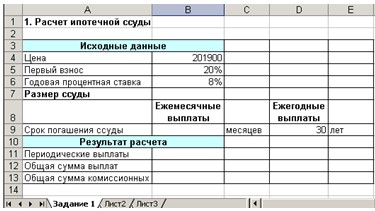
Рис.
1. Форма для расчета ипотечной ссуды

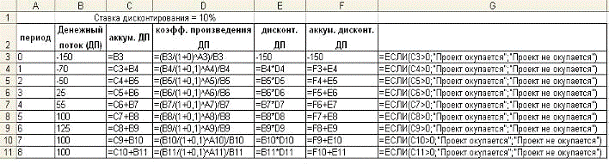
3.                 
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.

2.

 

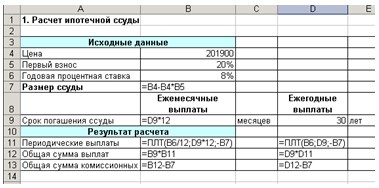
Рис.
2. Формулы для расчета ипотечной ссуды

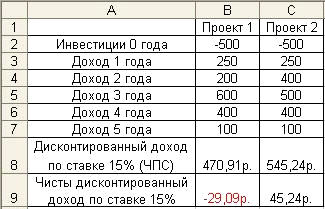
4.                 
Результаты расчеты должны быть следующими
(рис. 3):

 

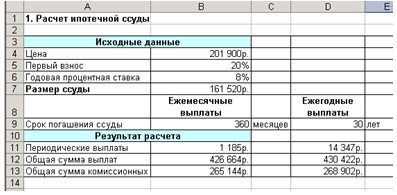
Рис.
3. Расчет ипотечной ссуды

3.
Функции для расчета годовой процентной ставки

Функция ЧПС возвращает чистый текущий
объем вклада, вычисляемый на основе ряда последовательных поступлений наличных
денег и нормы амортизации.

Чистый текущий объем вклада – это
сегодняшний объем будущих платежей (отрицательные значения) и поступлений
(положительные значения).

Например, вам предлагают следующую сделку.
У вас берут в долг некоторую сумму денег и предлагают через k1 лет вернуть
сумму, равную Рk1, через k2 лет – Рk2 и т. д. и, наконец, через kn лет – Рkn.
Кроме данной сделки, у вас есть альтернативный способ использования ваших
денег, например, положить их в банк под i процентов годовых. Тогда чистым
текущим объемом вклада является та сумма денег, которой вам нужно располагать
начальный год, чтобы, положив их в банк под i % годовых, получили предлагаемую
прибыль.

Синтаксис:
ЧПС(Ставка;Значение1;Значение2;…..) Аргументы:

§  ставка
– ставка дисконтирования за один период;

§  значение
1, значение 2, – от 1 до 29 аргументов, представляющих расходы и доходы:

• значение 1,
значение 2, … должны быть равномерно распределены во времени, выплаты должны
осуществляться в конце каждого периода.

ЧПС использует порядок аргументов значение
1, значение 2, … для определения порядка поступлений и платежей. Убедитесь в
том, что ваши платежи и поступления введены в правильном порядке.

Считается, что инвестиция, значение
которой вычисляет функция ЧПС, начинается за один период до даты денежного
взноса 1-го значения и заканчивается с последним денежным взносом в списке.

Вычисления функции ЧПС базируются на
будущих денежных взносах. Если первый денежный взнос приходится на начало
первого периода, то первое значение следует добавить к результату функции ЧПС,
но не включать в список аргументов.

Функция ЧПС
связана с функцией ВСД (внутренняя скорость оборота). ВСД – это скорость
оборота, для которой ЧПС равняется нулю:

ЧПС(ВСД(…);…)=0.

Функция ВСД возвращает внутреннюю скорость
оборота для ряда последовательных операций с наличными деньгами,
представленными числовыми значениями. Объемы операций не обязаны быть
регулярными, как в случае ренты.

Внутренняя скорость оборота – это
процентная ставка дохода, полученного от инвестиций, состоящих из выплат
(отрицательные значения) и поступлений (положительные значения), которые
происходят в регулярные периоды времени.

Синтаксис: ВСД (Значения;Предположение).

Аргументы:

§    
значения – массив или ссылка на ячейки, содержащие
числовые величины, для которых вычисляется внутренняя ставка доходности.
Значения должны включать, по крайней мере, одно положительное значение и одно
отрицательное значение, для того чтобы можно было вычислить внутреннюю скорость
оборота.

Функция ВСД
использует порядок значений для интерпретации порядка денежных выплат или
поступлений, поэтому нужно следить, чтобы значения выплат и поступлений
вводились в правильном порядке.

§    
предположение – величина, о которой предполагается,
что она близка к результату ВСД.

Для вычисления ВСД Excel использует метод
итераций. Начиная со значения прогноз, функция ВСД выполняет циклические
вычисления, пока не получит результат с точностью 0,00001. Если функция ВСД не
может получить результат после 20 попыток, то возвращается значение ошибки
#ЧИСЛО!

В большинстве случаев нет необходимости
задавать прогноз для вычислений с помощью функции ВСД. Если прогноз опущен, то
он полагается равным 0,1 (10 %).

Если
ВСД выдает значение ошибки #ЧИСЛО! Или результат далек от ожидаемого, можно

попытаться
выполнить вычисления еще раз, но уже с другим значением аргумента прогноз.

Пример
3. Вас просят в долг 10000 руб. и обещают вернуть через год 2000 руб., через
два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной
ставке эта сделка выгодна?

Решение.

1. Откройте Лист 3 и
переименуйте его в Задание 3. 2. Введите в ячейки A1:B7 данные, представленные
на рис. 4.

 

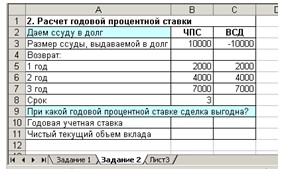
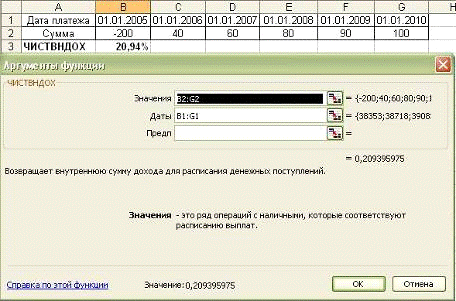
Рис. 4. Форма для расчета годовой
процентной ставки

3.                  
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.

5.

 

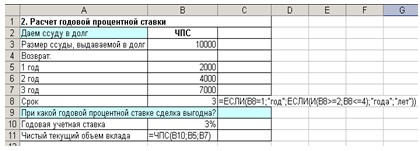
Рис. 5. Формулы для расчета годовой
процентной ставки

4.                  
Первоначально в ячейку В10 введите
произвольный процент, например 3 %.

В ячейку В11 введите формулу
=ЧПС(В10;В5:В7) (см. рис. 5).

5.                  
В ячейку С8 введите формулу:

=ЕСЛИ(В8=1;»год»;ЕСЛИ(И(В8>=2;B8<=4)
;»года»;»лет»)) В результате должно получиться (см. рис. 6):

 

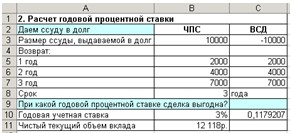
Рис. 6. Расчет чистого текущего объема
вклада

6.                  
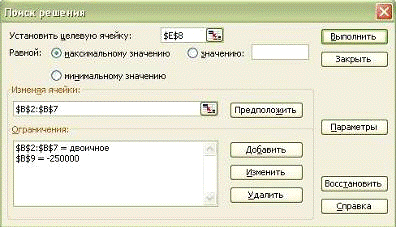
Затем выбираем команду Сервис / Подбор
параметра и заполняем открывшееся

диалоговое окно Подбор параметра, как
показано на рис. 7.

 

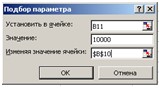
Рис. 7. Диалоговое окно Подбор параметра
при расчете годовой процентной ставки

7.                  
В поле Установить в ячейке: укажите ссылку
на ячейку В11, в которой вычисляется чистый текущий объем вклада по формуле:

=ЧПС(B10;B5:B7).

В поле Значение установить 10000 – размер
ссуды.

В
поле Изменения значения ячейки укажите ссылку на ячейку В10, в которой
вычисляется годовая процентная ставка.

После
нажатия кнопки ОК средство подбора параметров определит, при какой годовой
процентной ставке чистый текущий объем вклада равен 10000 руб. Результат
вычисления выводится в ячейку В10.

8.                  
В нашем случае годовая учетная ставка
равна 11,79 %.

Вывод:
если банки предлагают большую годовую процентную ставку, то предлагаемая сделка
не выгодна. 9. Результаты расчеты должны быть следующими:

 

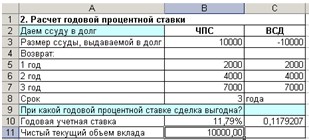
Рис. 8. Расчет годовой процентной ставки

4.   Функции для расчета
эффективности капиталовложений

Расчет
эффективности капиталовложений осуществляется с помощью функции ПС.

Функция ПС возвращает текущий объем вклада
на основе постоянных периодических платежей.

Функция ПС аналогична функции ЧПС.
Основное различие между ними заключается в том, что функция ПС допускает, чтобы
денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в
отличие от функции ЧПС, денежные взносы в функции ПС должны быть постоянными на
весь период инвестиции.

Синтаксис:
ПС(Ставка;Кпер;Плт;Бс;Тип) Аргументы:

§    
Ставка – процентная ставка за период,

§    
Кпер – общее число периодов платежей по аннуитету,

§    
Плт – выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов,

§    
Бс – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент опущен, он полагается равным 0
(будущая стоимость займа, например, равна 0),

§    
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.

Пример
4. У вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 7
лет. Будет ли выгодна эта сделка при годовой ставке 7 %?

Решение:

1. 
Откройте Лист 4 и переименуйте его в
Задание 4.

2. 
Введите в ячейки A1:B6 данные,
представленные на рис. 9.

 

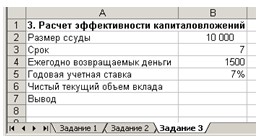
Рис. 9. Форма расчета эффективности
капиталовложений

3. 
В ячейку В6 введите формулу:
=ПС(В5;В3;-В4)

4. 
В ячейку С3 введите формулу:

=ЕСЛИ(В3=1;
«год»;ЕСЛИ(И(В3>=2;В3<=4); «года»;»лет»))
5. В ячейку В7:

=ЕСЛИ (В2<В6; «Выгодно дать деньги
в долг»; ЕСЛИ(В6=В2; «Варианты равносильны»;

«Выгоднее деньги положить под
проценты»))

 

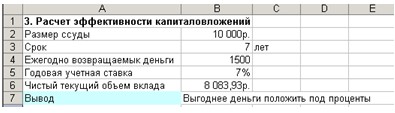
Рис. 10. Расчет эффективности
капиталовложений

5.   Функции для расчета основных
платежей и платы по процентам

Основные платежи и платы по процентам
вычисляются с помощью формул или финансовых функций ОСПЛТ и ПРПЛТ.

Функция ПРПЛТ возвращает платежи по
процентам за данный период на основе периодических постоянных выплат и
постоянной процентной ставки.

Синтаксис: ПРПЛТ (Ставка; Период; Кпер;
Пс; Бс; Тип).

Функция ОСПЛТ возвращает величину выплаты
за данный период на основе периодических постоянных платежей и постоянной
процентной ставки.

Синтаксис: ОСПЛТ(Ставка; Период; Кпер; Пс;
Бс; Тип).

Аргументы функций ПРПЛТ: и ОСПЛТ:

§    
Ставка – процентная ставка за период,

§    
Период – задает период, значение должно быть в
интервале от 1 до «Кпер»,

§    
Кпер – общее число периодов выплат годовой ренты,

§    
Пс – приведенная стоимость, то есть общая сумма,
которая равноценна ряду будущих платежей,

§    
Бс – требуемое значение будущей стоимости, или остатка
средств после последней выплаты.

Если аргумент Бс
опущен, то он полагается равным 0 (нулю), то есть для займа, например, значение
Бс равно 0.

§    
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.

Функции
ПРПЛТ и ОСПЛТ тесно связаны между собой, а именно ПЛПj= i Bj-1, ОСНПj = А —

ПЛПj,
Bj = Вj-1 — ОСНПj при j ∈[0,
n], где j – номер периода, п – КПЕР,

ПЛПj,
ОСНПj и Bj – это ПРПЛТ, ОСПЛТ и остаток долга, соответственно, за j-й период,

ПЛПо
= 0, ОСНПо = 0, Bо – Пс,

А – величина выплаты за один период
годовой ренты на основе постоянных выплат и постоянной процентной ставки,
вычисляемая с помощью функции ПЛТ.

Пример
5. Вычислить основные платежи, платы по процентам, общей ежегодной платы и
остатка долга на примере ссуды 100000 руб. на срок 5 лет при годовой ставке 2
%.

Решение:

1.                 
Откройте Лист 5 и переименуйте его в
Задание 5.

2.                 
Введите данные, представленные на рис. 13.

3.                 
Ежегодная плата вычисляется в ячейке В4 по
формуле: =ПЛТ(процент; срок; -размер_ссуды), где ячейки В2, В3 и В5 имеют
имена: процент, срок и размер_ссуды, соответственно. 

4.                 
За первый год плата по процентам в ячейке
В8 вычисляется по формуле:

=D7*процент.

 

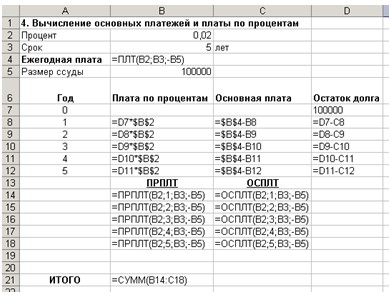
Рис. 13. Функции для вычисления основных
платежей и платы по процентам.

5.                 
Основная плата в ячейке С8 вычисляется по
формуле: =ежегодная_плата-В8, где ежегодная_плата – имя ячейки В4.

Остаток долга в ячейке D8
вычисляется по формуле: =D7-C8.

6.                 
В оставшиеся годы эти платы определяются с
помощью протаскивания маркера заполнения выделенного диапазона B8:D8 вниз по
столбцам.

7.                 
Данные результаты расчетов должны быть
следующими (рис. 14.):

 

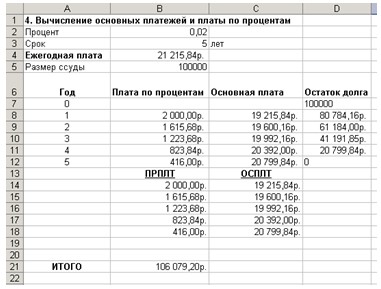
Рис. 14. Вычисление основных платежей и
платы по процентам

6. Функции для расчета
будущего значения вклада, процентной ставки и количества периодов выплаты долга

Функция БС вычисляет будущее значение
вклада на основе периодических постоянных платежей и постоянной процентной
ставки.

Функция
БС подходит для расчета итогов накоплений при ежемесячных банковских взносах. Синтаксис:
БС (Ставка; Кпер; Плт; Пс; Тип).

Аргументы:

§    
Ставка – процентная ставка за период,

§    
Кпер – общее число периодов выплат,

§    
Плт – величина постоянных периодических платежей,

§    
Пс – текущее значение, то есть общая сумма, которую
составят будущие платежи, § Тип – число 0 или 1,
обозначающее, когда должна производиться выплата.

Если
тип равен 0 или опущен, то оплата производится в конце периода, если 1 – в
начале

периода.
Если тип = 0 и БС = 0, то функция БС вычисляется по формуле (6):

                                                                       (6)

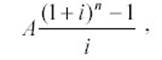
где
А – Плт; i – Ставка; n – Кпер.

Функция КПЕР вычисляет общее количество
периодов выплаты для данного вклада на основе периодических постоянных выплат и
постоянной процентной ставки.

Синтаксис: КПЕР(Ставка; Плт; Пс; БС; Тип).

Аргументы:

§    
Ставка – процентная ставка за период,

§    
Плт – величина постоянных периодических платежей,

§    
Пс – текущее значение, т.е. общая сумма, которую
составят будущие платежи,

§    
БС – будущая стоимость или баланс наличности, который
нужно достичь после последней выплаты.

Если аргумент БС опущен, он полагается
равным 0 (например, будущая стоимость займа равна 0), тип – число 0 или 1,
обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен,
то оплата производится в конце периода, если 1 – то в начале периода. Если тип
= 0 и БС = 0 функция КПЕР вычисляется по формуле (7):

                        (7)

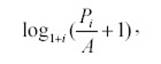
где
Р – ПС; i – Ставка; А – Плт.

Пример
6. Вы хотите зарезервировать деньги для специального проекта, который будет
осуществлен через год. Предположим, вы собираетесь вложить 1000 руб. при
годовой ставке 6 %. Вы собираетесь вкладывать по 100 руб. в начале каждого
месяца в течение года. Сколько денег будет на счете в конце 12 месяцев?

Решение:

1.                  
Откройте Лист 6 и переименуйте его в
Задание 6.

2.                  
Ведите данные в ячейки А1:С6 (см. рис.
15).

 

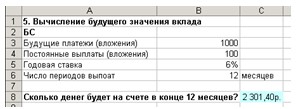
Рис. 15. Расчет будущего значения вклада

3.                  
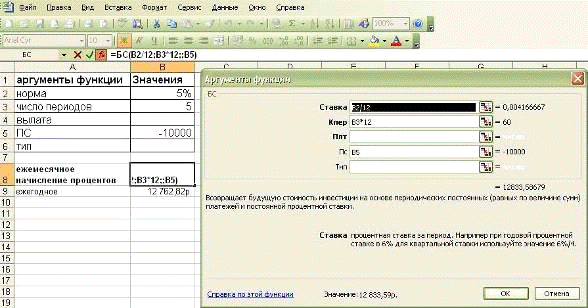
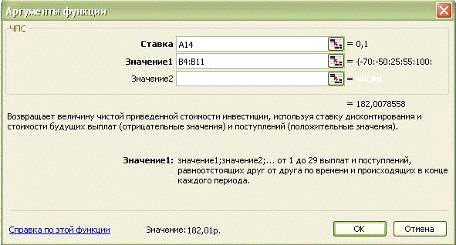
В ячейку С8 введите формулу:

=БС(6 %/12; 12; -100;
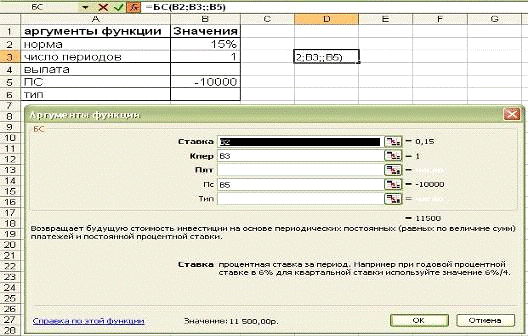
-1000; 1) получаем ответ: 2 301,40 руб (см. рис. 16).

 

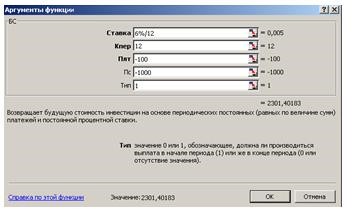
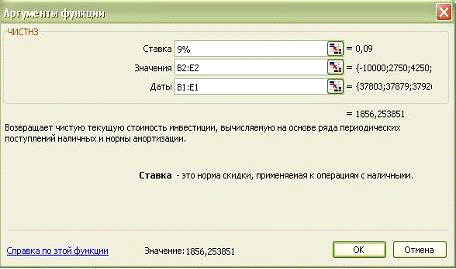
Рис. 16. Диалоговое окно Аргументы функции
БС

Пример
7. Вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать
по 100 руб. в год, Какое будет число выплат долга?

Решение:

1.                  
Откройте Лист 7 и переименуйте его в
Задание 7.

2.                  
Ведите данные в ячейки А1:В6 (см. рис.
17).

 

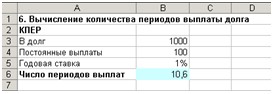
Рис. 17. Расчет количества периодов выплат

3.                  
В ячейку В6 введите формулу: =КПЕР(B5;
-B4; B3) В результате получаем ответ: ≈11. (см. рис. 18).

 

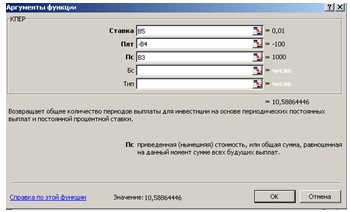
Рис. 18. Диалоговое окно Аргументы функции
КПЕР

Вычисление
процентной ставки

Функция СТАВКА вычисляет процентную
ставку, необходимую для получения определенной суммы в течение заданного срока
путем постоянных взносов, за один период.

Следует отметить, что функция СТАВКА
вычисляет процентную ставку методом итераций, поэтому решение может быть и не
найдено. Если после 20 итераций погрешность определения ставки превышает
0,0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО!

Синтаксис: СТАВКА(КПЕР; Плт; Пс; БС; Тип;
Предположение).

Аргументы:

§    
КПЕР – общее число периодов платежей по аннуитету;

§    
Плт – регулярный платеж (один раз в период), величина
которого остается постоянной в течение всего срока аннуитета. Обычно Плт состоит
из платежа основной суммы и платежа процентов, но не включает других сборов или
налогов. Если аргумент опущен, должно быть указано значение аргумента БС;

§    
Пс – приведенная к текущему моменту стоимость или
общая сумма, которая на текущий момент равноценна ряду будущих платежей;

§    
БС – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент БС опущен, то он полагается
равным 0 (например, БС для займа равно 0); тип – число 0 или 1, обозначающее,
когда должна производиться выплата; предположение – предполагаемая величина
ставки.

Если
БС = 0 и тип = 0, функция СТАВКА является корнем уравнения (8):

                                                                       (8)

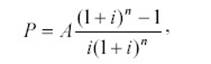
Пример
8. Определить процентную ставку для четырехлетнего займа размером в 8000 руб. с
ежемесячной выплатой 200 руб.

Решение:

1.                  
Откройте Лист 8 и переименуйте его в
Задание 8.

2.                  
Ведите данные в ячейки А1:В7 (см. рис.
19).

 

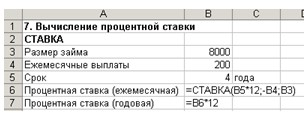
Рис. 19. Расчет процентной ставки

3.                  
В ячейку В6 введите формулу:
=СТАВКА(B5*12;-B4;B3).

4.                  
В ячейку В7 введите формулу: = В6*12.

В
результате получаем: месячная (так как период равен месяцу) процентная ставка
равна 0,77 %. Процентная ставка годовая равна 9 % см. рис 20).

 

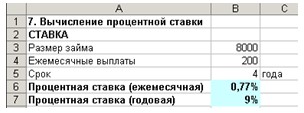
Рис.20. Результаты вычисления процентной
ставки

Контрольные вопросы:

1.   
Как
рассчитать дату и временя с использованием финансовых функций?

2.   
Каким
образом можно рассчитать ипотечную ссуду, годовую процентную ставку в Excel?

3.   
Назовите
функции расчета постоянных рент.

Самостоятельная
 практическая работа по теме:

«ФИНАНСОВЫЕ
ФУНКЦИИ В EXCEL»

КПЕР
– общее  число периодов выплат займа или инвестиций

ПЛТ
– выплата, производимая в каждый период и не
меняющаяся за все время выплаты займа или инвестиций

ПС
– приведенная (нынешняя) стоимость – общая сумма,
равноценная на настоящий момент серии будущих платежей

БС
– будущая стоимость, или баланс наличности, который
нужно достичь после последней выплаты (при отсутствии значения БС
принимается равной 0)

ТИП
– логическое значение (0 или 1), обозначающая, должна ли производиться выплата
в конце периода (0 или отсутствие значения) или в начале периода (1)

СТАВКА
– возвращает процентную ставку за один период.
Например, при годовой процентной ставке в 6 % для квартальной ставки используется
значение 6%/4.

ПС(ставка; кпер; плт; бс; тип);
ПРПЛТ(ставка; период; кпер; пс; бс);
АСЧ(нач_стоимость; ост_стоимость; время_эксплуатации; период);
ФУО(нач_стоимость; ост_стоимость; время_эксплуатации; период; месяцы);
ОСПЛТ(ставка; период; кпер; пс; бс; тип);
ДДОБ(нач_стоимость; ост_стоимость; время_эксплуатации; период;
коэффициент).

Задание 1

Ваше предприятие рекламирует свою
деятельность с использованием четырех источников массовой информации: телевидения,
радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом
показал, что вложенные в рекламу средства приводят к увеличению прибыли на 10
руб., 5 руб., 7 руб. и 4 руб. соответственно в расчете на 1 руб.,
затраченный на рекламу. На рекламу выделено 50 000 руб., причем
руководство намерено тратить на телевидение не более 50% выделенной суммы, на
радио — не более 20%, на газеты — не более 35%, на расклейку объявлений — не
более 30%. С помощью Поиска решения рассчитайте объем вложений в
каждый вид рекламы, чтобы получить максимальную прибыль от рекламной кампании.

Задание 2

Для решения задачи: «Кредит в 45 000 руб. дается под 12%
годовых со сроком погашения 5 лет. Какую сумму будут составлять ежемесячные
выплаты?» — заполнили таблицу.

Столбец А – комментарии
к данным, столбец В – необходимые для вычислений данные. Запишите
содержимое ячеек диапазона А1:В3, ячейка ответа В4,
содержит формулу: =ОКРУГЛ(ПЛТ(B3/12;B2*12;B1;0;0);2).

Задание 3

 «Пусть начальная
стоимость оборудования составляет 45 000 руб., срок полной амортизации,
когда стоимость оборудования станет нулевой — 5 лет. Определите сумму, ежегодно
подлежащую списанию»

Финансовые функции Microsoft Excel

Функция БС

1. Необходимо определить будущую стоимость единовременного вклада с текущей стоимостью 20000 рублей, на который в течение 10 лет ежегодно начисляются сложные проценты по ставке 7 процентов годовых. Начисление процентов производится 1 раз в год.

2. Организация взяла заем размером 100000 рублей на срок 3 года под 30 процентов годовых. Необходимо определить сумму, подлежащую возврату.

3. Предположим, фирма собирается зарезервировать деньги для специального проекта, который будет осуществлен через год. Фирма открывает счет, единовременно на него вносятся 10000 рублей под 6% годовых (это составит в месяц 6/12, или 0,5%). Далее предполагается вносить 1000 рублей в начале каждого месяца в течение следующих 12 месяцев. Необходимо определить сумму денег на счете через год.

4. Есть два варианта инвестирования средств на 4 года. Первый вариант предполагает начисление 26 процентов годовых в начале каждого года. Второй вариант — начисление 38 процентов годовых в конце каждого года. Фирма имеет возможность ежегодно вносить 300000 рублей. Необходимо определить, какой вариант предпочтительнее.

Функция ПС

1. Рассматриваются два варианта покупки оборудования. Первый вариант предполагает, что сразу будет выплачена вся сумма 99000 рублей. Второй вариант — рассрочка на 15 лет при ежемесячной выплате по 940 рублей в конце каждого месяца. Годовая процентная ставка – 8 процентов. Необходимо определить, какой вариант предпочтительнее.

2. Организации потребуется 5000000 рублей через 12 лет. В настоящее время фирма располагает средствами и готова разместить деньги на депозит единым вкладом с тем, чтобы через 12 лет иметь необходимые деньги. Годовая процентная ставка — 12 процентов. Необходимо определить, сколько средств размещать на депозите.

Функция КПЕР

1. Для обеспечения будущих расходов фирмы создается фонд, величина которого должна составить 1000000 рублей. Деньги на создание фонда поступают ежегодно в конце года в виде фиксированных отчислений в 160000 рублей. На поступившие платежи начисляется 11,18% процентов годовых. Необходимо определить, через сколько лет будет накоплена необходимая сумма.

2. Фирма получила ссуду в размере 66000 рублей под 36 процентов годовых и предполагает рассчитываться ежемесячно по 6630 рублей в конце каждого месяца. Необходимо определить срок полного расчета по полученной ссуде.

Задачи для самостоятельного решения

1. Сумма 5000 руб. размещена на счете под 20 процентов годовых с начислением процентов 4 раза в год на срок 3 года. Какова будет величина вклада в конце периода?

1. На накопительный счет в начале каждого месяца вносится сумма 1000 руб. Определите, какая сумма окажется на счете через 3 года при ставке 12 процентов годовых.

1. Фирме предлагается инвестировать средства на 5 лет по одной из двух схем:

   • Первоначально инвестируется 100000 руб. и далее в конце каждого года – по 10000 руб. на вклад под 24 процента годовых, начисляемых в конце каждого года.

   • Ежеквартально в начале квартала инвестируется 10000 руб. под 32 процента годовых, и проценты начисляются в начале квартала.

Какая схема выгоднее?

1. Определите текущую стоимость ежеквартальных платежей размером 350 руб., осуществляемых в конце каждого квартала в течение 7лет при ставке 11 процентов годовых.

1. Фирма получила ссуду в размере 65000 рублей под 16% годовых и предполагает рассчитываться ежемесячно по 3500 рублей в конце каждого месяца. Необходимо определить срок полного расчета по полученной ссуде.

1. Для обеспечения будущих расходов предприятия создается фонд, величина которого должна составить 1900000 рублей. Деньги на создание фонда поступают ежегодно в начале года в виде фиксированных отчислений в 80000 рублей. На поступившие платежи начисляются 17% годовых. Необходимо определить через сколько лет будет накоплена необходимая сумма.

Министерство науки и высшего образования Российской Федерации

Университетский колледж

федерального государственного бюджетного образовательного учреждения высшего образования

«Оренбургский государственный университет»

Н.А. Кривошеева

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ

В ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ

Финансовые функции Excel

Методические указания

Рекомендовано к изданию редакционно-издательским советом федерального государственного бюджетного образовательного учреждения высшего образования «Оренбургский государственный университет» для обучающихся по программе среднего профессионального образования по специальности 38.02.07 Банковское дело

Оренбург

2019

УДК 004(075.32)

ББК 32.97я723

К19

Рецензент – доцент кафедры программного обеспечения вычислительной техники и автоматизированных систем И.А. Щудро

Кривошеева, Н.А.

К82 Информационные технологии в профессиональной деятельности: финансовые функции Excel: методические указания / Н.А. Кривошеева; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2019. – 55 с.

Методические указания предназначены для выполнения лабораторных работ по дисциплине «Информационные технологии в профессиональной деятельности» в Университетском колледже ОГУ для обучающихся третьего курса специальности 38.02.07 Банковское дело.

Методические указания составлены с учетом Федерального государственного образовательного стандарта среднего профессионального образования.

УДК 004(075.32)

ББК 32.97я723

©Кривошеева Н.А.,2019

©ОГУ, 2019

Содержание

Введение

Изначально данные методические указания планировались для обучающихся Университетского колледжа ОГУ по специальности 38.02.07 Банковское дело, которым по роду своей деятельности предстоит работать с финансами и банковскими расчетами. При написании методических указаний были внесены корректировки по теоретической части и внесены дополнения по практической части, методические указания были дополнены индивидуальными заданиям для обучающихся, заданиями для самостоятельного решения и контрольным вопросам для самопроверки усвоенного материала.

Прежде, чем приступить к освоению финансовых функций, необходимо изучить материал, который облегчит работу с оформлением формул и поможет усвоить материал по применению функций в короткие сроки. Особенность данных методических указаний заключается в том, что за несколько практических занятий, сопровождающихся теоретическим материалом, изложенным в доступной форме, обучающийся сможет выполнить не только элементарные операции, но и научится пользоваться функциями Excel. Все примеры дополнены наглядными рисунками. Материал методических указаний рассчитан для самостоятельно изучения и дает возможность использовать его не только на аудиторных (практических) занятиях, но и в домашних условиях, а в дальнейшем и в профессиональной деятельности.

Методические указания изложены в краткой и понятной форме, учтен необходимый минимум теоретического материала по изучению отдельного раздела Microsoft Excel (финансовые функции). Пользователем данных методических указаний могут быть не только обучающиеся колледжей, но и учащиеся школ, а также любой человек, которому интересно данное направление. Первый раздел знакомит пользователя с интерфейсом Excel, после чего пользователь может спокойно переходить к изучению функций.

1 Знакомство с интерфейсом

При первом запуске Microsoft Excel открывается новый файл, который принято называть книгой (рисунок 1). Книга изначально содержит три чистых листа (в левом нижнем углу есть ярлычки Лист1, Лист2, Лист3). Листы помогают распределить информацию в одной книге по целевому назначению. Количество листов в книге не ограничено. Можно добавить новый лист с помощью кнопки добавления листа; удалить ненужный лист, переименовать лист и выделить его цветом (нажав правую кнопку мыши на листе). Если листов в книге больше, чем может поместиться в области отображения ярлычков, то передвигаться между листами можно с помощью кнопок прокрутки листов.

Рисунок 1 – Интерфейс Excel 2010

Рабочую зону условно можно разделить на несколько областей, каждая из которых имеет свое значение и выполняет определенную функцию. Пользователю очень важно познакомиться с ними на начальном этапе изучения Excel. Рассмотрим их поподробнее.

В версии Office 2010 есть отличия от более ранней версии 2007, на которые мы будем обращать внимание. Кнопка Office заменена на вкладку Файл (рисунок 2). Здесь находятся команды создания, сохранения, открытия документов, а также печать.

Рисунок 2 – Вкладка «Файл»

Панель быстрого доступа расположена в левом верхнем углу (рисунок 3) и позволяет разместить часто встречающиеся команды для пользователя, обозначенные соответствующими кнопками. Эти кнопки называются инструментами.

Рисунок 3 – Панель быстрого доступа

Изначально на панели расположены три кнопки, но в зависимости от потребностей конкретного пользователя она может быть дополнена или изменена, так как панель быстрого доступа является настраиваемой.

Для того, чтобы настроить панель быстрого доступа нужно нажать на стрелочку вниз справа на панели и выбрать часто встречающиеся команды (рисунок 4).

Рисунок 4 – Настройка панели быстрого доступа через стандартные команды

Если в предложенном списке не обнаружено нужной команды, необходимо выбрать «Другие команды…», найти необходимую команду и с помощью кнопки «Добавить» настроить Панель быстрого доступа. Выбранные кнопки появятся на Рабочем столе Панели (рисунки5, 6).

Рисунок 5 – Добавление других команд на Панель быстрого доступа

В поле «Выбрать команды из:» выбрать нужный раздел или воспользоваться предлагаемым вариантом — «Часто используемые команды». В предлагаемом списке выбрать нужную команду, нажав на нее левой кнопкой мыши и с помощью кнопки «Добавить», в центре окна, перенести нужную команду из левой части экрана в правую, которая отвечает за наличие данной кнопки на Панели быстрого доступа. Удалить ненужную команду можно аналогичным образом, но в другой последовательности выбора ненужной команды из окна Панель быстрого доступа и выбрать кнопку «Удалить» в центре экрана.

Рисунок 6 – Настройка панели быстрого доступа через настройку параметров

Далее рассмотрим уже известные нам по MicrosoftOffice 2007 кнопки, вспомним их предназначение.

В верхнем правом углу расположены кнопки управления основным окном программы (развернуть, свернуть и закрыть основное окно программы).

Лента инструментов располагается в верхней части экрана исостоит из вкладок, которые, в свою очередь, позволяют получить быстрый доступ к определенной категории команд и кнопок, собранных по функциональному признаку в отдельные группы (рисунок 7).

Рисунок 7 – Лента с расположенными на ней вкладками и группами

При наведении курсора мыши на любой из инструментов отображается подсказка, которая обозначаетназвание используемого инструмента.

Рабочая область экрана состоит из строк и столбцов. Строки нумеруются цифрами, столбцы обозначаются буквами латинского алфавита (рисунок 8).

Рисунок 8 – Рабочая область Excel

На пересечении строк и столбцов образуется ячейка, каждая из которых имеет свое имя – по умолчанию имя ячейки включает букву столбца и номер строки. По имени ячейки можно к ней «обращаться», чтобы сделать ссылку в формуле.Имя текущей ячейки отображается в поле«Имя ячейки», например А1, В2, С12 и т.д. (рисунок 9).

Рисунок 9 – Обозначение имени текущей ячейки

Справа от «Имени ячейки» расположена «Строка формул», которая дублирует информацию, зафиксированную в текущей ячейке. Если в ячейке использовался текст или число, то в строке формул информация дублируется. Если в ячейке применялась формула, то на экране будет отображаться результат выполнения формулы, а в строке формул сама формула (рисунок 10).

Рисунок 10 – Отображение формулы в Строке формул

Получив элементарные навыки работы в Excel, можно переходить к следующему разделу.

Познакомившись с интерфейсом Excel2010 и рассмотрев небольшую часть возможностей настроек табличного процессора можно сделать вывод, что каждый пользователь может легко настроить внешний вид программы «под себя», изменив ряд параметров, сделав его удобным и привлекательным для себя.

2 Полезные «мелочи»

В этом разделе мы рассмотрим несколько полезных кнопок и команд, которые помогут вам эргономично расположить элементы окна в зоне видимости и наиболее рационально использовать время для поиска нужной информации на экране.

2.1 Стиль ссылок

Привычным стилем оформления ссылок на ячейки служит ссылка на строку и столбец, которые определяются соответственно буквой и цифрой, например F5 или А8. Бывают случаи, когда вы открываете присланный вам файл, а ссылки на ячейки выглядят как на рисунке 11.

Рисунок 11 – Стиль цифровой нумерации столбцов

Стиль цифровой нумерации выставлен в Excel 2010 по умолчанию, но не для всех пользователей он удобен. Особенно это заметно, когда необходимо использовать ссылки, тогда не опытному пользователю прочитать ссылку становится трудно. Вернуть привычное буквенное обозначение столбцов не составит труда, выполнив несколько несложных операций.

Для этого на вкладке «Файл» необходимо выбрать команду «Параметры» (рисунок 12). В открывшемся диалоговом окне выбрать вкладку «Формулы» и отключить «галочку» со строки «Стиль ссылок R1C1» (рисунки 12, 13).

Рисунок 12 – Настройка параметров нумерации столбцов

Рисунок 13 – Вкладка формулы для изменения стиля ссылок

2.2 Инструменты вкладки Вид

С помощью вкладки Вид (рисунок 14) можно настроить расположение окон при одновременном открытии нескольких документов, разделить область рабочего листа или закрепить видимую область экрана.

Рисунок 14– Вкладка Вид – группа Окно

Команда «Разделить» выводит в рабочую область текущего листа разделительные линии (рисунок 15), которые можно перемещать влево, вправо, вверх, вниз, причем области разделения листа становятся независимыми друг от друга по навигации. Вы можете заметить, что появилось несколько линеек прокрутки (и вертикальных, и горизонтальных).

Рисунок 15 – Разделение рабочей области листа

На рисунке 15 приведен пример разделение окна при работе с одним листом. Можно заметить, что нумерация строк и обозначение столбцов прерываются во всех зонах, но мы все равно находимся на одном листе. Такое разделение листа позволяет работать с удаленными друг от друга данными одного текущего листа.

Другая команда «Закрепить области», в отличие от ранее рассмотренной команды «Разделить», не добавляет дополнительные полосы прокрутки и делает разделительные линии на листе практически не заметными. Такая команда незаменима в тех случаях, когда нужно, чтобы «шапка таблицы» (верхняя строка или первый столбец) была всегда видимой. На рисунке 16 можно заметить, что после первой строки сразу идет двадцатая. Данные остальных строк никуда не исчезли, они, как будто «прокручены» вверх. Если переместить линейку прокрутки вверх, то нижние строчки сместятся вниз, а верхние появятся на экране.Перемещение по листу можно производить с помощью колесика мыши, верхняя строка всегда будет оставаться видимой.

Рисунок 16 – Закрепление области верхней строки

2.3 Маркер автозаполнения

При необходимости ввода повторяющихся данных в несколько смежных ячеек можно скопировать данные одной ячейки и вставить в другую, но можно воспользоваться более простым способом – использовать Маркер автозаполнения.

Обратите внимание на нижний правый угол текущей ячейки и вы увидите небольшой черный квадратик, который называется Маркером автозаполения и несет в себе несколько важных функций. Если выделено несколько смежных ячеек, то маркер находится также в правом нижнем углу выделенного диапазона. Далее мы рассмотрим несколько примеров применения данного маркера.

При заполнении ячейки произвольными данными Маркер автозаполнения (далее Маркер)позволяет скопировать данные этой ячейки в соседние (рисунок 17). Маркер можно протягивать вниз, вверх, вправо, влево – данные будут копироваться.

Рисунок 17 – Использование Маркера автозаполнения

Если в текущую ячейку, например, А1 записать название месяца, дня недели или даты, то Маркер позволит заполнить соседние ячейки последовательными месяцами, днями недели или датами соответственно (рисунки 18, 19, 20). Причем, протягивая Маркер вправо или вниз происходит наращивание приведенных показателей на одну условную единицу, а при протягивании влево или вверх происходит уменьшение на одну условную единицу.

Рисунок 18 – Применение Маркера при вводе месяцев

Рисунок 19 – Применение Маркера при вводе дней недели

Рисунок 20 – Применение Маркера при заполнении дат

При создании в ячейке формулы, нет необходимости перенабирать эту формулу в остальные ячейки столбца или строки. Маркер автозаполнения позволяет копировать формулу относительно перемещения курсора (ссылка называется относительной). Ссылки на ячейки, используемые в копируемой формуле сместятся ровно на столько ячеек, насколько переместился курсор (рисунок 21).

Рисунок 21 – Применение Маркера при копировании формул

Теперь вы познакомились с некоторыми особенностями работы в Excel, которые помогут вам в дальнейшей работе. Применяя эти несложные правила, вы сможете быстро вводить данные и находить нужную информацию в созданном документе.

3Вычисления в Excel 2010

3.1 Общие сведения о создании формул

При наборе формулы важно помнить о том, что формула обязательно начинается со знака равенства (=). Основными операторами для создания формулы или функции являются:

— оператор сложения (+);

— оператор вычитания (-);

— оператор умножения (*);

— оператор деления (/);

— оператор возведения в степень (^);

— оператор процента (%).

На рисунке 22 приведены примеры использования основных операторов.

Рисунок 22 – Использование основных операторов

3.2 Относительные и абсолютные ссылки

При работе с формулами возникает необходимость ссылаться на ячейки с данными расположенными не только на текущем рабочем листе, но и на другом листе или даже в другой книге. Причем эти данные могут быть как числовые, так и текстовые. При создании формулы ссылка идет на ячейку, а вычисления производятся с данными, расположенными в указанной ячейке.

В подразделе 2.2 на рисунке 21 был приведен пример использования относительной ссылки. При копировании относительной ссылки вниз или вверх по столбцу ссылки на ячейки в формуле тоже будут меняться. Если ячейку, содержащую относительную ссылку переместить, например перетаскиванием, копированием или вырезанием, то ссылка станет абсолютной.

Абсолютная ссылка всегда указывает на одну и ту же фиксированную ячейку, которая не меняется ни при каких обстоятельствах ее перемещения (при перетаскивании, копировании, вырезании).Отличие в использовании формулы с относительной и абсолютной ссылкой приведено на рисунке 23.

Чтобы создать абсолютную ссылку самостоятельно, нужно добавить знак доллара ($) перед каждым элементом имени ячейки в формуле, например $A$1. Знак доллара можно использовать при создании смешанной ссылки:

— если нужно, чтобы строка менялась, а столбец не менялся, то знак доллара добавляется только перед обозначением столбца, например А$1;

— если нужно, чтобы столбец менялся, а строка не менялась, то знак доллара добавляется только перед обозначением строки, например $А1.

Переключение между относительными и абсолютными ссылками производится клавишей F4.

Рисунок 23 – Применение относительных и абсолютных ссылок

3.3 Как читать сообщение об ошибке

При работе с формулами и финансовыми вычислениями в Excel есть вероятность допустить неточность в оформлении ссылок или ошибку в написании функции. Опытному пользователю не составит труда выявить и устранить этот недочет, но как разобраться с формулировками об ошибке тому, кто только начинает осваивать Excel? Рассмотрим на примере часто встречающиеся записи об ошибках и дадим рекомендации как их устранить.

3.3.1 Ошибка #### самая распространенная и легко устранимая. Такая ошибка означает, что ширина столбца не достаточна велика для отображения значения в ячейке (рисунок 24).

Рисунок 24 – Ошибка#### недостаточная ширина столбца

Чтобы исправить ошибку, нужно увеличить ширину столбца с помощью мыши. Можно отрегулировать ширину столбца по самому длинному значению в столбце нажав, для этого два раза левой кнопкой мыши на разделительной полосе между названиями соседних столбцов.

Такая же ошибка может появиться в том случае, если после производимых вычислений с датами или временем появляется отрицательное число, так как дата и время должны быть положительными (рисунок 25).

Рисунок 25 – Ошибка#### дата или время

Чтобы исправить появившуюся ошибку нужно или исправить ссылки в используемой формуле, чтобы вычисляемое число часов (дней) было положительными или изменить формат выводимых данных.

3.3.2 Ошибка #ИМЯ? означает, что используемой в данной формуле ячейке изначально не было определено Имя или оно в процессе редактирования было удалено (рисунок 26).

Рисунок 26– Ошибка #ИМЯ? в Имени ячейки

Для того, чтобы устранить данную ошибку нужно сначала определить Имя ячейки, на которую будет ссылаться формула, только после этого применять ссылку на Имя. Внимательно работать с Диспетчером имен при удалении Имен.

Аналогичная ошибка может появиться в том случае, если в написании функции допущена ошибка (рисунок 27).

Рисунок 27 — Ошибка #ИМЯ? в функции

Для решения этой проблемы нужно проверить написание функции. В данном примере при написание функции должно быть ПОИСКПОЗ. Диапазон здесь указан правильно. Можно привести другой пример, когда ошибка возникает из-за неправильно указанного диапазона (рисунок 28).

Рисунок 28 – Ошибка #ИМЯ? в диапазоне ячеек

В данном примере между А1 и А3 пропущено двоеточие. Правильно будет указать диапазон следующим образом: А1:А3.

Если в формуле используется текстовое значение, то оно должно быть заключено в кавычки, иначе в ячейке появится такая же ошибка (рисунок 29).

Рисунок 29- Ошибка #ИМЯ? в текстовом значении

Ошибка будет устранена при заключении текста в двойные кавычки: =»Итого»&А4.

3.3.3 Ошибка #ЧИСЛО означает, что в формуле используется некорректное число (рисунок 30).

Рисунок 30 – Ошибка #ЧИСЛО при некорректном использовании чисел

При анализе данной функции можно сделать вывод, что корень извлекается из положительного числа, а в ячейке А1 введено отрицательное. Достаточно будет убрать минус в числе 64 и ошибка будет исправлена.

3.3.4 Ошибка #ЗНАЧ! Означает, что в формуле используется аргумент, значение которого не допустимо для данной формулы.

Например в формуле складываются ячейки, но в одной или нескольких из них вместо числа стоит пробел, символ или текст, которые, как очевидно, не могут складываться с числом (рисунок 31).

Рисунок 31 – Ошибка #ЗНАЧ! при текстовом значении

Исправить такую ошибку не составит труда, поставив в нужную ячейку число.

Такая же ошибка появится в том случае, если при использовании функции вы введете диапазон ячеек в том месте, где предполагается ввод одного значения (рисунок 32).

Рисунок 32 — Ошибка #ЗНАЧ! при задании аргументов функции

Устранить ошибку можно в строке формул, указав правильную ссылку или пересмотреть используемую функцию через Мастер функций.

3.3.5 Ошибка #ССЫЛКА появляется в том случае, когда формула содержит ссылку на несуществующую или удаленную ячейку (рисунок 33).

Рисунок 33 — Ошибка #ССЫЛКА при несуществующей ячейке

В данном случае рекомендуется изменить формулу и внести корректные ссылки на существующие ячейки.

3.3.6 Ошибка #ДЕЛ/0!

При появлении данной ошибки у пользователя появляется неправильное восприятие, читаемое как ДЕЛО, на самом деле, все довольно просто. Такая ошибка появляется при делении на ноль, так как делить на ноль нельзя! (рисунок 34).

Рисунок 34 — Ошибка #ДЕЛ/0! при делении на ноль

3.3.7 Ошибка #Н/Д означает, что в данной формуле использовалось недоступное значение (рисунок 35).

Рисунок 35 — Ошибка #Н/Д недопустимое значение

Такая ошибка может возникнуть в функциях ВПР (вертикальный просмотр), ГПР (горизонтальный просмотр), ПРОСМОТР, ПОИСКПОЗ (поиск позиции) и означает, что задан неверный аргумент для поиска (искомое_значение). По формуле видно, что ищется значение 255, в используемом списке такого значения нет. Такая же ошибка появится в том случае, если в функции будет пропущен один или несколько обязательных аргументов.

3.3.8 Ошибка #ПУСТО! означает, что в формуле были использованы непересекающиеся значения (рисунок 36).

Рисунок 36 – Ошибка #ПУСТО! непересекающиеся значения

Для исправления формулы рекомендуется проверить правильность написания формулы и выставить правильный диапазон.

4 Финансовые функции

Большой популярностью у экономистов пользуется Excel благодаря которому выполнение различных финансовых расчетов можно автоматизировать у упростить с помощью финансовых функций. Многие из них могут пригодиться не только специалистам экономического профиля, но и работникам банковской сферы и других смежных отраслей. Обычному пользователю подобные расчеты пригодятся в их бытовых нуждах. Рассмотрим особенности создания финансовых функций с помощью возможностей Excel, обратив внимание на самые популярные операторы группы финансовых функций.

Для того, чтобы создать финансовую функцию можно воспользоваться Мастером создания функций. Для этого нажать кнопку «Вставить функцию», которая расположена на вкладке «Формулы».

Поместить курсор в ячейку, в которой будет производиться расчет и выводится результат. На вкладке «Формулы» нажать кнопку «Вставить функцию». На первом шаге Мастера функций изначально будут выведены 10 недавно использовавшихся функций (рисунок 37).

Рисунок 37 – Первый шаг Мастера функций

В поле Категория выбираем финансовые функции (рисунок 38).

Рисунок 38 – Выбор категории Финансовые функции

Выбрав одну из предложенных функций, вы перейдете в окно заполнения аргументов данной функции (в нашем примере функция БС). Переменные можно вводить несколькими способами:

1) с клавиатуры ввести числовые данные (рисунок 39);

2) мышкой поочередно выделить ячейки в которой хранятся данные той или иной переменной (рисунок 40), на экране ячейка будет выделена рамкой;

3) ввести имя ячейки (например А1, В2 и т.д.) с клавиатуры в английской раскладке. В этом случае процесс заполнения визуально будет похож на второй способ. Если ссылки на ячейки ошибочно введены на русской раскладке клавиатуры, то вычислений не произойдет, будет отображена ошибка введение имен ячеек (рисунок 41).

Рисунок 39 – Заполнение аргументов функции БС с клавиатуры

Рисунок 40 – Заполнение аргументов функции БС с помощью ссылок на соответствующие ячейки

Рисунок 41 – Заполнение аргументов функции БС с записью имен ячеек с клавиатуры (ошибочный ввод)

Обратите внимание как выглядят формулы на рисунках 39-41. Результат вычислений получается во всех случаях одинаковый.

Во вкладке «Формулы» в группе «Библиотека функций» также можно воспользоваться вставкой функции, для этого нужно выбрать категорию функций «Финансовые» (рисунок 42).

Рисунок 42 – Выбор финансовых функций в группе «Библиотека функций» текущей вкладки «Формулы»

Из появившегося списка выбрать необходимую функцию (рисунок 43) и далее в появившемся диалоговом окне выбрать аргументы функции.

Рисунок 43 – Выбор финансовой функции через список функций

В зависимости от применяемой функции количество переменных и их очередность в формуле может меняться.

Рассмотрим основные переменные, используемые при создании финансовых функций:

1) кпер – число периодов платежей по кредиту (указывается количество лет, если выплаты производятся ежемесячно, тогда указанное количество лет умножается на 12, а процентная ставка в этом случае будет делиться на 12);

2) ставка – процентная ставка (годовая — указывается в процентах, если выплаты производятся ежемесячно, то необходимо ставку поделить на 12, то есть 17%/12);

3) плт – платеж, производимый в каждый период (состоит из основного платежа и платежа по процентам);

4) пс – сумма на текущий момент;

5) бс – будущая стоимость;

6) тип – по умолчанию принимаетсяноль — означает, что оплата производится в конце периода, если оплата производится в начале периода, то в формуле вместо нуля ставится единица.

При создании финансовых функций нужно запомнить, что переменные могут быть как отрицательными числами, так и положительными, в зависимости от того получаем мы деньги или отдаем (поступления задаются положительными числами, а выплаты – отрицательными).

Рассмотрим наиболее востребованные финансовые функции в деятельности банковского работника на конкретных примерах. Усвоив принцип работы по созданию основных финансовых функций, вы сможете перейти к решению более сложных задач, связанных с вашей профессиональной деятельностью.

4.1 Функция БС определяетбудущую стоимость инвестиций

Функция БС() — рассчитывает будущую стоимость периодических постоянных платежей и будущее значение вклада (или займа) на основе постоянной процентной ставки.

Синтаксис функции БС: =БС(ставка;кпер;плт;[пс];[тип]). Аргументы [пс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 1. Определить наращенную сумму для вклада в размере 10000 рублей, размещенного под 15% годовых на один год

Результат =БС(B2;B3;;B4) = 11500 рублей.

Рисунок 44 – Результат выполнения примера 1

Пример 2.На банковский счет под 11,5% годовых внесли 37000 рублей. Определить размер вклада по истечение 3 лет, если проценты начисляются каждые полгода.

Результат =БС(B10;B11;;B13) = 51746,86 рублей.

Рисунок 45 – Результат выполнения примера 2

Пример 3. Определить, сколько денег окажется на банковском счете, если ежегодно в течение 5 лет под 17% годовых вносятся 20000 рублей. Взносы осуществляются в начале каждого года.

Результат =БС(B20;B21;B22;;B24) = 164136,96 рублей.

Рисунок 46 – Результат выполнения примера 3

Пример 4. Если нам необходимо сделать вклад под 15 % годовых с ежемесячным начислением процентов на сумму 100000 рублей на три года. Какую сумму мы получим в конце периода?

В этом примере переменная ПС равна минус 100000 рублей, так как мы отдаем деньги, тогда результат у нас будет положительными числом, так как получаем доход.

Результат: =БС(B1;B2;;B4) = 156394,38 рублей.

Рисунок 47 – Результат выполнения примера 4

4.2 Функция ПС определяет сумму денег в настоящий момент

Функция ПС() — предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Текущий объем — это общая сумма, которую составят будущие платежи. Например, когда деньги берутся взаймы, заимствованная сумма и есть текущий объем для заимодавца. Этот расчет является обратным к определению будущей стоимости при помощи функции ПС.

Синтаксис: =ПС(ставка;кпер;плт;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

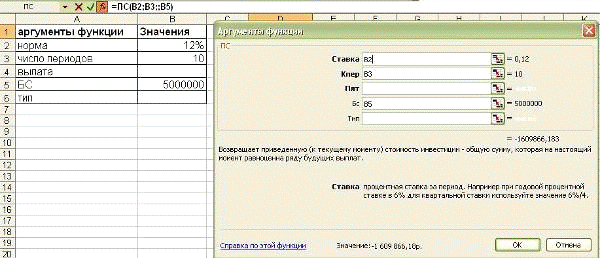
Пример 5. Фирме потребуется 5000000 рублей через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму. Определить необходимую сумму текущего вклада если ставка процента по нему составляет 12% в год.

Результат =ПС(B2;B3;;B5) = -1609866,18 рублей. Результат отрица-тельный, так как эти деньги фирме нужно отдать в настоящий момент.

Рисунок 48 – Результат выполнения примера 5

Пример 6. Клиент заключает с банком договор о выплате ему в течение 5 лет ежегодной ренты в размере 5000 рублей в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20%?

Результат =ПС(B10;B11;B12) = — 14953,06 рублей. Результат о трица-тельный, так как клиент должен ее отдать.

Рисунок 49 – Результат выполнения примера 6

Пример 7. Предположим, что мы хотим получать доход, равный 1000 рублей в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых, выплаты производятся вначале года.

Результат =ПС(B18;B19;B20;;1) = — 3486,85 рублей.

Рисунок 50– Результат выполнения примера 7

Пример 8. На какую сумму можно взять кредит, если ставка 17 % годовых и выплачивать мы можем по 10000 рублей в месяц на протяжении двух лет?

Результат: =ПС(B1;B2;B3) = 202256,11 рублей.

Рисунок 51 – Результат выполнения примера 8

Пример 9. Какую сумму кредита можно взять под 17 % годовых с ежемесячным начислением процентов, если выплачивать мы можем ежемесячно на протяжении двух лет и в итоге готовы выплатить 300000 рублей?

В этом примере нет переменной ПЛТ, но есть переменная БС, которую пишем с минусом, так как отдаем эту сумму.

Результат: =ПС(B1;B2;;B4) = 214041,15 рублей.

Рисунок 52 – Результат выполнения примера 9

4.3 Функция ПЛТ определяет сумму ежемесячных платежей

Функция ПЛТ() — позволяет рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа при известных сумме займа, ставки процентов и срока на который выдан заем.

Синтаксис: =ПЛТ(ставка;кпер;нз;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 10. Необходимо накопить 4000 рублей за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.

Результат =ПЛТ(B2;B3;;B5) = — 92,86 рублей.

Рисунок 53 – Результат выполнения примера 10

Пример 11. Клиент банка осуществляет заем в размере 5000 рублей под 6 % годовых на 6 месяцев. Определить ежемесячные платежи клиента, если платежи осуществляются в конце месяца.

Результат =ПЛТ(B10;B11;B12) = — 922,99 рублей.

Рисунок 54 – Результат выполнения примера 11

Пример 12. Допустим, банк выдал ссуду 200000 рублей, на 4 года под 18 % годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды

Результат =ПЛТ(B20;B21;B22) = -74347,73 рубля.

Рисунок 55 – Результат выполнения примера 12

4.4 Функция КПЕР определяет количество периодов платежей

Функция КПЕР() — вычисляет количество периодов начисления процентов.

Синтаксис: КПЕР(ставка;плт;пс;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

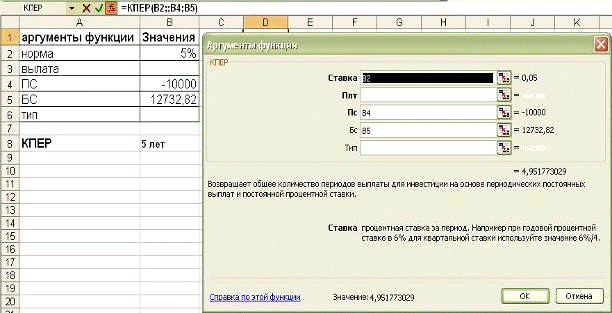
Пример 13. По вкладу в 10000 рублей, помещенному в банк под 5% годовых, начисляемых ежегодно была выплачена сумма 12762,82 рубля. Определить срок проведения операции (количество периодов начисления)

Результат=КПЕР(B2;;B4;B5) = 5 периодов (5 лет).

Рисунок 56 – Результат выполнения примера 13

Пример 14. Через сколько лет вклад размером 500 рублей достигнет величины 1000 рублей при ставке процентов 10% с ежемесячным начислением процентов.

Результат:

а)=КПЕР(B10;;B12;B13) = 7,27 лет;

б)=КПЕР(D10;;D12;D13) = 83,52 месяцев.

Рисунок 57 – Результат выполнения примера 14

Пример 15. Пусть ставка кредита 17 % годовых, сумма кредита 100000 рублей и мы можем выплачивать по 5000 рублей ежемесячно. Определить за сколько периодов мы погасим кредит?

Пишем минус 5000, так как мы отдаем деньги. Получаем приблизительно 23,68 периодов, то есть месяцев, что соответствует почти двум годам.

Результат: =КПЕР(B1;B2;B3) = 23,68 (месяцев), примерно 2 года.

Рисунок 58 – Результат выполнения примера 15

4.5 Функция СТАВКА определяет процентную ставку за период

Функция СТАВКА() — вычисляет процентную ставку, которая в зависимости от условий операции может выступать либо в качестве цены, либо в качестве нормы ее рентабельности.

Синтаксис: СТАВКА(кпер;плт;пс;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 16. Фирме через 2 года потребуется 100000 рублей. Для достижения этой цели фирма готова положить на депозит 25000 рублей (ежемесячно). Каким должен быть процент на инвестированные средства с тем, чтобы к концу второго года была получена необходимая сумма

Результат =СТАВКА(B2;;B4;B5) = 6 %.

Рисунок 59 – Результат выполнения примера 16

Пример 17. На полтора года в долг дана сумма 20000 рублей с условием возврата 30000 рублей. Вычислить годовую процентную ставку.

Результат =СТАВКА(B10;;B12;B13) = 31 %.

Рисунок 60 – Результат выполнения примера 17

Пример 18. Допустим мы хотим взять кредит в 100000 рублей на два года, выплачивать мы можем по 5000 рублей ежемесячно. Какая ставка нам подходит?

Результат: =СТАВКА(B1;B2;B3) = 1,51 % на месяц = 18,157 % годовых.

Рисунок 61 – Результат выполнения примера 18

При заполнении поля КПЕР было указано 24 месяца, следовательно в результате получили ставку за месяц, умножим ее на 12 месяцев, получим годовую ставку равную 18,157 %.

Мы рассмотрели часто встречающиеся функции и на конкретных примерах увидели процесс решения той или иной задачи. Если вы разобрались с принципом создания основных финансовых функций, то вам не составит труда рассмотреть и другие функции данного раздела. Для закрепления полученных знаний обучающимся предлагается выполнить практическую работу с аналогичными заданиями. Для закрепления пройденного материала обучающимся предлагаются задания для самостоятельного решения с применением и других функций данного раздела.

5 Практическая часть работы

Цель работы: обобщить полученные знания по теме «Финансовые функции», уметь находить верное решение, научиться пользоваться функциями.

Ход работы:

1) внимательно прочитайте заданиясвоего варианта (вариант определяется по номеру рабочего места);

2) определите с помощью какой финансовой функции нужно произвести расчет для данных задач;

3) откройте Ecxel, создайте новую книгу, создайте в ней пять листов;

4) каждое заданиевыполняйте на новом листе, переименовав листы под название функции для расчета;

5) на каждом листе задайте параметры для вычислений и решите задачу;

5) покажите работу преподавателю, обоснуйте свое решение.

Вариант 1

1) Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 4 года под 13,5% годовых. Проценты начисляются каждые полгода.

2) Компании X потребуется 100000 тыс. руб. через 2 года:

а) компания готова вложить 5000 тыс. руб. сразу и по 2500 тыс. руб. каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года.

б) компания отказалась от ежемесячных платежей и готова единовременно вложить 40000 тыс. руб. Определите, как изменится в этом случае процентная ставка.

3) Банк выдал ссуду 150 тыс. руб. на 3 года под 17% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды.

4). Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

Вариант 2

1) У Вас есть возможность ежегодно в течение 4 лет инвестировать 300 тыс. руб. в два проекта: под 26% в начале каждого года или 38% в конце года. Определите, какой из вариантов вложения средств предпочтительнее.

2) По вкладу в 10000 помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82. Определить срок проведения операции (количество периодов начисления).

3) Фирме через 2 года потребуется 100000 руб. Для достижения этой цели фирма готова положить на депозит 25000 руб. Каким должен быть процент на инвестированные средства с тем, чтобы к концу второго года была получена необходимая сумма?

4) Необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых

5) Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб.в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

Вариант 3

1) Вы решили приобрести автомобиль стоимостью 200000 руб. Какую сумму Вы должны вложить в банк под 12% годовых для того, чтобы иметь возможность его приобретения:

а) начисление процентов производится один раз в начале года;

б) начисления производятся 2 раза в год в начале периода.

2) Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты. Размер разового платежа составляет 16 млн. руб. На поступившие взносы начисляется 11,18% годовых. Определить, когда величина фонда будет равна 100 млн. руб.

3) Вычислить 10 годичную ипотечную ссуду покупки квартиры за 800000 руб. с годовой ставкой 13% и начальным взносом 25%. Сделать расчет для ежемесячных и ежегодных выплат.

4) Пусть в долг на полтора года дана сумма 20000 руб. с условием возврата 30000 руб. Вычислить годовую процентную ставку.

5) На счет в банке в течение пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит владельцу счета.

Вариант 4

1) Предположим, что выкупается страховка, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 % годовых. Необходимо определить, будет ли это хорошим способом инвестировать капитал.

2)Какую сумму необходимо ежемесячно вносить на счет, чтобы через три года получить 10 тыс. руб., если годовая процентная ставка 13,5%.

3) Рассчитайте процентную ставку для четырехлетнего займа в 7000 тыс. руб. с ежемесячным погашением по 250 тыс. руб. при условии, что заем полностью погашается.

4)Предположим, что каждый год ежемесячно в банк помещается сумма в 1000 руб. Ставка равна 12% годовых, начисляемых в конце каждого месяца. Какова будет величина вклада к концу 4-го года?

5) Рассчитайте, через сколько месяцев вклад размером 15000 руб. достигнет величины 24500 руб. при ежемесячном начислении процентов и ставке процента 22% годовых.

Вариант 5

1) Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6% годовых (что составит в месяц 6%/12 или 0,5%). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?

2) За какой срок в годах сумма, равная 75 000 руб., достигнет 200 000 руб. при начислении процентов по сложной ставке 15%раз в году и поквартально.

3) Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл.

4)Банк выдал ссуду 200 тыс. руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды

5). Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

Вариант 6

1) Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб.в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

2) Ожидается, что ежегодные доходы от реализации проекта составят 33 млн. руб. Рассчитайте срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн.руб., а норма дисконтирования – 12,11%.

3) Заем в 144 тыс. руб. погашается равномерными периодическими платежами по 14 тыс. руб. каждые полгода в течение восьми лет. Определите годовую ставку процента.

4) Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?

5) Необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых

Вариант 7

1) Фирма создает фонд для погашения долгосрочных обязательств, срок которых истекает через пять лет, путем ежегодного пополнения депозита, с начальной суммой 10000 тыс. руб. Размер ежегодного взноса 1000 тыс. руб. Ставка по депозиту – 5% годовых, начисляемых в конце каждого периода. Определите величину фонда к концу пятого года.

2) Рассчитайте, через сколько месяцев вклад размером 15000 руб. достигнет величины 24500 руб. при ежемесячном начислении процентов и ставке процента 22% годовых.

3) В долг на 2 года дана сумма 150 000 руб. с условием возврата 190 000 руб. Вычислить годовую процентную ставку.

4) Фирме потребуется 5000 тыс. руб. через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.

Определитьнеобходимую сумму текущего вклада если ставка процента по нему составляет 12% в год

5) Определите ежемесячные выплаты по займу в 220 тыс. руб., взятому на семь месяцев под 11% годовых.

Вариант 8

1) Ссуда в 20 000 руб. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.

2) Ссуда 87000 руб., выданная под 30% годовых, погашается ежеквартальными платежами по 9500 руб. Рассчитайте срок погашения ссуды.

3) Какой должна быть годовая процентная ставка по вкладу размером 10000 руб., если ее величина к концу года составила 11723 руб., а проценты начислялись ежемесячно.

4) Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

5) Банк выдал ссуду 150 тыс. руб. на 3 года под 17% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды.

Вариант 9

1) Вексель на 3 000 000 руб. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года. Найти исходную сумму, выданную под этот вексель. В данном случае задача осложняется тем, что задана ставка дисконта, а аргумент норма подразумевает процентную ставку. Поэтому предварительно нужно пересчитать дисконтную ставку в процентную (9%/2/(1-9%/2)).

2) Ссуда размером 61000 руб. погашается ежемесячными платежами по 2144 руб. Рассчитайте, через сколько лет произойдет погашение, если годовая славка процента 16%.

3) Рассчитайте годовую ставку процента по вкладу размером 230 тыс.руб., если за 11 лет эта сумма возросла до 3 млн. руб. при ежеквартальном начислении процентов.

4) Определить, какая сумма окажется на банковском счете, если 52000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.

5) Какую сумму необходимо ежемесячно вносить на счет, чтобы через три года получить 10 тыс. руб., если годовая процентная ставка 13,5%.

Вариант 10

1) Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?

2) Физическому лицу выдан кредит 97 000 руб. на три года. Проценты начисляются ежегодно. Определить величину процентной ставки за период, если известно, что возврат составит 140 000 руб.

3) Ссуда 63200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб. Рассчитайте срок погашения ссуды.

4) Определите ежемесячные выплаты по займу в 220 тыс. руб., взятому на семь месяцев под 11% годовых.

5) Фирме потребуется 5000 тыс. руб. через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.

Определитьнеобходимую сумму текущего вклада если ставка процента по нему составляет 12% в год

6 Задачи для самостоятельного решения

Ознакомьтесь с другими функциями раздела «Финансовые функции» самостоятельно. Перечень финансовых функций приведен в приложении А. Найдите решение для приведенных ниже задач, используя изученный материал.

1) На банковский счет под 11,5 % годовых внесли 37000 рублей. Определить размер вклада по истечение трех лет, если проценты начисляются каждые полгода.

2) Определить сколько денег окажется на банковском счете, если ежегодно в течение пяти лет под 17 % годовых вносится 20000 рублей. Взносы осуществляются в начале каждого года.

3) Достаточно ли положить на счет 85000 рублей для приобретения через пять лет легкового автомобиля стоимостью 160000 рублей? Банк начисляет проценты ежеквартально, годовая ставка 12 %. Определить необходимую сумму (с помощью «подбора параметра»).

4) По облигации номиналом 50000 рублей, выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов:

а) в первый год – 10 %;

б) в следующие два года – 20 %;

в) в оставшиеся три года – 25 %.

Определить будущую стоимость облигации с учетом переменной процентной ставки.

5) По облигации, выпущенной на шесть лет, предусмотрен порядок начисления процентов, приведенный в задаче 4. Рассчитать номинал облигации, если известно, что ее будущая стоимость составила 216562,50 рублей.

6) Фирме требуется 500000 рублей через три года. Определить, какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500000 рублей, если процентная ставка составляет 12 % годовых.

7) Клиент заключает с банком договор о выплате ему в течение пяти лет ежегодной ренты в размере 5000 рублей в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20 %?

Пусть инвестиции в проект к концу первого года его реализации составят 20000 рублей. В последующие четыре года ожидаются годовые доходы по проекту: 6000 рублей, 8200 рублей, 12600 рублей и 18800 рублей. Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10 % годовых.

9) Инвестор с целью инвестирования рассматривает два проекта, рассчитанные на пять лет. Проекты характеризуются следующими данными:

а) по первому проекту – начальные инвестиции составляют 550000 рублей, ожидаемые доходы за пять лет соответственно 100000, 190000, 270000, 300000 и 35000 рублей;

б) по второму проекту – начальные инвестиции составляют 650000 рублей, ожидаемые доходы за пять лет соответственно 150000, 230000, 470000, 180000 и 320000 рублей.

Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15 % годовых.

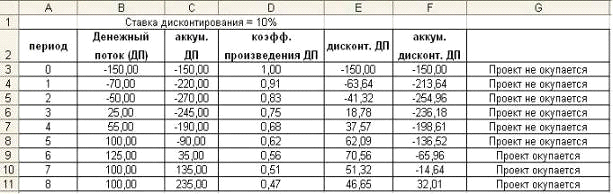
10)Определите чистую текущую стоимость по проекту на 05.04.2018 при ставке дисконтирования 8 %, если затраты по нему на 05.08.2018 составят 90 млн.рублей, а ожидаемые доходы в течение следующих месяцев будут:

а) 10 млн.руб. на 10.01.2019;

б) 20 млн.руб. на 01.03.2019;

в) 30 млн.руб. на 15.04.2019;

г) 40 млн.руб. на 25.07.2019.

11) Рассчитать через сколько лет вклад размером 100000 рублей достигнет 1000000 рублей, если годовая процентная ставка по вкладу 13,5 % и начисление процентов производится ежеквартально.

12) Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде годовой ренты в конце года. Сумма разового платежа 16000 рублей. На поступившие взносы начисляются 11,2 % годовых. Необходимо определить, когда величина фонда будет равна 100000 рублей.

13) Предположим, что для получения через два года суммы в 1000000 рублей предприятие готово вложить 250000 рублей сразу и затем каждый месяц по 25000 рублей. Определить годовую процентную ставку.

14) Выдан кредит 50000 рублей на 2,5 года. Проценты начисляются раз в полгода.Определить величину процентной ставки за период, если известно, что возврат составит 700000 рублей.

15) Клиент банка осуществляет заем в размере 5000 рублей под 6 % годовых на 6 месяцев. Определите ежемесячные платежи клиента. Платежи осуществляются в конце месяца.

16) Клиенту банка необходимо накопить 200000 рублей за два года. Клиент обязуется вносить в начале каждого месяца постоянную сумму под 9 % годовых. Какой должна быть сумма?

17) Определите платежи по процентам за первый месяц от трехгодичного займа в 100000 рублей из расчета 10 % годовых.

18) Клиент ежегодно в течение пяти лет вносил деньги на свой счет в банке и накопил 40000 рублей. Определите, какой доход получил клиент банка за последний год, если годовая ставка составила 13,5 %.

19) Определите значение основного платежа для первого месяца двухгодичного займа в 60000 рублей под 12 % годовых.

20) Организация взяла ссуду в банке в размере 500000 рублей на 10 лет под 10,5 % годовых, проценты начисляются ежемесячно. Определите сумму выплат по процентам за первый месяц и за третий год периода.

21) Ссуда размером 1000000 рублей выдана под 13 % годовых сроком на три года. Проценты начисляются ежеквартально.Определите величину общих выплат по займу за второй год.

22) Рассчитать сумму процентов, начисленных на вклад в 750000 рублей за два года, если банк начисляет проценты ежеквартально из расчета 28 % годовых. Какова должна быть годовая депозитная ставка, если за два года необходимо удвоить первоначальный вклад?

23) Потребитель получает заем на покупку автомобиля 20000$ под 8 % годовых сроком на три года при ежемесячных выплатах. Какова будет сумма по процентам и основной платеж за первый и последний месяцы выплат?

24) Потребитель занимает сумму 250000$, подлежащую выплате в течение 10 лет при 12 % годовых на ежемесячной основе. Какова сумма процента и основного капитала на первом году займа?

25) Кредит в сумме 5000000 рублей предоставлен под 20 % годовых сроком на 10 лет. Рассчитайте величину остатка основной суммы без учета выплаченных процентов на начало третьего года.

7 Контрольные вопросы

Интерфейс Excel 2010

Вкладка «Файл»

Настройка Панели быстрого доступа

Рабочая область Excel

Строка формул

Абсолютные и относительные ссылки

Стили ссылок

Инструменты вкладки Вид

Разделение рабочей области листа

Закрепление областей

Применение Маркера автозаполнения

Общие правила при создании формул

Сообщения об ошибках

Способы устранения ошибок

Мастер создания функций

Расчет будущей стоимости инвестиций

Расчет суммы денег в настоящий момент

Расчет суммы ежемесячных платежей

Расчет количества периодов платежей

Расчет процентной ставки на период

Список использованных источников

1 Зимин, В.П. Информатика. Лабораторный практикум. В 2ч. Ч.1 : учеб. пособие для спо / В.П. Зимин.- М.: Юрайт, 2018.- 110 с.- (Профессиональное образование).- ISBN 978-5-534-03446-0.

2 Каджаева, М.Р. Ведение расчетных операций : учебник для спо / М.Р. Каджаева.- 3-е изд., стер.- М.: Академия, 2017. – 272с. — (Профессиональное образование).- ISBN 978-5-4468-4267-2.

3 Коршунов, М.К. Экономика и управление: применение информационных технологий : учеб. пособие для спо / М.К. Коршунов; под ред. Э.П. Макарова.- М.: Юрайт; Екатеринбург : Изд-во Урал. ун-та, 2018. – 111 с.- (Профессиональное образование).- ISBN 978-5-534-007725-4.

4 Информационные технологии [Электронный ресурс]: лабораторный практикум / авт.-сост. С.В. Говорова, М.А. Лапина; Министерство образования и науки Российской Федерации, Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северо-Кавказский федеральный университет». — Ставрополь : СКФУ, 2016. — 168 с. –ЭБС Университетская библиотека Online. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=459048.

Финансовые задачи в Excel

Экономический
факультет

Кафедра
Информационных технологий

Информационные
системы в экономике

Финансовые
задачи в Excel

Содержание

Раздел 1 Технология работы с
финансовыми Функциями Еxcel. Основные понятия финансовых методов расчета         4

.1 Операции наращения.
Функция бс().   11

.2 Операции дисконтирования       16

.3 Определение срока
финансовой операции   17

.4 Определение процентной
ставки         18

.5 Расчет эффективной и
номинальной ставки процентов  19

.6 Начисление процентов по
плавающей ставке         20

Раздел 2. Потоки платежей и
финансовые ренты       22

.1 Определение будущей
(наращенной) стоимости потока платежей. Функция бс()         23

.2 Современная (текущая)
величина аннуитета. Функция пс()      25

.3 Расчет периодических
платежей 27

Раздел 3. Оценка
инвестиционных процессов  36

.1.Чистый приведенный доход.
Функция чпс   37

.2 Срок окупаемости    41

.3 Индекс рентабельности     43

.4 Внутренняя норма
доходности.Функция чиствндох       45

.5 Модифицированная
внутренняя норма доходности.Функция мсвд  46

.6 Денежный поток
инвестиционного проекта с произвольными периодами поступления платежей    49

Раздел 4. Функции excel для
расчета амортизации    51

Аргументы функций excel для
расчета амортизации 51

Контрольные работы   55

        
Раздел 1. Технология работы с финансовыми функциями Еxcel. Основные понятия финансовых методов расчета

финансовый программа функция

Рассмотрим процесс наращения (accumulation), т.е. определения денежной сумм
будущем, исходя из заданной суммы сейчас.

Экономический смысл операции наращения состоит в
определении величины той суммы, которой будет или желает располагать инвестор
по окончании этой операции. Здесь идет движение денежного потока от настоящего
к будущему.

Существуют различные способы начисления процентов и
соответствующие процентных ставок

Величина FV показывает будущую стоимость «сегодняшней» величины инвестиции PV при заданном уровне интенсивности
начисления процентов r

Простая процентная ставка — применяется к одной и той же первоначальной сумме
долга на протяжении всего срока ссуд исходная база (денежная сумма) всегда одна
же.

Сложная процентная ставка — применяется к наращенной сумме долга, т.е сумме,
увеличенной на величину начисленных предыдущий период процентов, — таким
образом исходная база постоянно увеличивается.

Фиксированная процентная ставка — ставка, зафиксированная в виде
определенного числа (сумы) в финансовых контрактах.

Плавающая процентная ставка — привязанная к определенной величине, изменяющейся
во времени, включая надбавку к ней (маржу), которая определяется целым рядом
условий (сроком операции и т.п.).

Постоянная процентная ставка — неизменная на протяжении всего
периода ссуды.

Переменная процентная ставка — дискретно изменяющаяся во времени,
но имеющая конкретную числовую характеристику.

В любой простейшей финансовой операции всегда
присутствуют четыре величины:

время (n)

современная величина (PV),

— наращенная или будущая величина (FV),

 — процентная ставка (r)

n — Срок погашения долга (англ. number of periods) — интервал времени, по истечении которого сумму
долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов —
обычно равных по длине подинтервалов времени, в конце (или начале) которых
начисляются проценты.

Если начисление процентов будет производиться m раз в год, а срок погашения

долга — n лет, то общее количество периодов начисления за весь
срок финансовой операции составит

PV—
текущая стоимость (англ. present value) — исходная сумма или
оценка современной величины денежной суммы, поступление которой ожидается в
будущем, в пересчете на более ранний момент времени;

FV—
будущая стоимость (англ. future value) — наращенная сумма или
будущая стоимость, т.е. первоначальная сумма долга с начисленными на нее
процентами к концу срока ссуды;

I— Процентные деньги (англ. interest
money), называемые часто коротко «проценты», представляют
собой абсолютный доход от предоставления долга.

I=FV—PV

Оценка
эффективности финансовых операций по величине процентных денег на практике
используется достаточно редко, так сама их величина, не учитывающая фактор
времени, мало что может сказать о реальной доходности операции. Необходимо
иметь возможность сопоставить ее с темпом обесценивания денег (инфляции) или
результатами другой финансовой операции. Поэтому в финансово-экономических
расчетах наиболее широко пользуются относительные показатели:

г
— процентная ставка (rate of interest), характеризующая
интенсивность начисления процентов за единицу времени,- отношение суммы
процентных денег, выплачивающихся за определенный период времени, к величине
ссуды. Этот показатель выражается либо в долях единицы, либо в процентах.

На
рабочем листе в отдельных ячейках осуществляется подготовка значений основных
аргументов функции.

Для
расчета результата финансовой функции Excel курсор устанавливается в
новую ячейку для ввода формулы, использующей встроенную финансовую функцию.

Осуществляется
вызов «Мастера функций»

На
основной панели инструментов имеются кнопки «Мастер функций», с
помощью которой открывается диалоговое окно Диспетчера функций.

Диалоговое
окно «Диспетчер функций» организовано по тематическому принципу.
После выбора в левом списке «Категории» тематической группы «Финансовые»,
на экран будет выведено диалоговое окно с полным перечнем списка имен
функций, содержащихся в данной группе.

Поиск
необходимой финансовой функции осуществляется путем последовательного просмотра
списка.

Рис.1-3.
Последовательность действий при выборе необходимой финансовой функции

В
результате выполненных действий на экране откроется диалоговое окно выбранной
функции.

В
поля диалогового окна функции:

можно
вводить как сами значения аргументов, так и ссылки на адреса ячеек, содержащие
необходимые значения;

все
расходы денежных средств (платежи) представляются отрицательными числами, а все
поступления денежных средств — положительными числами;

процентная
ставка вводится в виде десятичной дроби, либо с использованием знаке %;

Для
исчисления характеристик финансовых операций с наращением и дисконтированием
вложенных сумм удобно использовать функции БС, IIC, KIIEP,
СТАВКА, БЗРАСПИС, НОМИНАЛ, ЭФФЕКТ. ПРПЛТ, ОБЩПЛАТ, ОСППЛАТ, ОБЩДОХОД.

Таблица
1.

Функции
рабочего листа Excel для оценки разовых и периодических (потоков)

Наименование функции	Формат функции	Назначение функции
БС	БС(ставка ;кпер;плт;пс;тип)	рассчитывает будущую стоимость периодических постоянных платежей и будущее значение вклада (или займа) на основе постоянной процентной ставки
ПС	ПС(ставка ;кпер;плт;бс;тип)	предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Текущий объем — это общая сумма, которую составят будущие платежи. Например, когда деньги берутся взаймы, заимствованная сумма и есть текущий объем для заимодавца. Этот расчет является обратным к определению будущей стоимости при помощи функции ПС
КПЕР	КПЕР(ставка ;плт;пс;бс;тип)	вычисляет количество периодов начисления процентов, исходя из известных величин r,, FV и PV.
СТАВКА	СТАВКА(кпер;плт;пс;бс;тип)	вычисляет процентную ставку, которая в зависимости от условии операции может выступать либо в качестве цены, либо в качестве нормы ее рентабельности.
БЗРАСПИС	БЗРАСПИС (сумма; массив ставок)	удобно использовать для расчета будущей величины разовой инвестиции в случае, если начисление процентов осуществляется по плавающей ставке. (Например, доходы по облигациям государственного сберегательного займа, начисляются раз в квартал по плавающей купонной ставке).
НОМИНАЛ	НОМИНАЛ (эф_ставка;кол_пер)	Возвращает номинальную годовую процентную ставку, если известны фактическая ставка и число периодов, составляющих год.
ЭФФЕКТ	ЭФФЕКТ (ном_ставка; кол_пер)	Возвращает фактическую годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов, составляющих год.
ПРПЛТ	ПРПЛТ(ставка;период;кпер;пс бс;тип)	Возвращает сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
ОСПЛТ	ОСПЛТ(ставка ;период;кпер;пс;бс;тип)	Возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянства периодических платежей и постоянства процентной ставки
ОБЩДОХОД	ОБДОХОД (ставка;кпер;нз;нач_период; кон_период,тип)	Вычисляет сумму основных платежей по займу, который погашается равными платежами в конце или начале каждого расчетного периода, между двумя расчетными периодами
ПЛТ	ПЛТ(ставка;кпер;нз;бс; тип)	позволяет рассчитать сумму постоянных периодических платежей (CF). необходимых для равномерного погашения займа при известных сумме займа, ставки процентов и срока на который выдан заем.
ЧПС	ЧПС (ставка;значение 1; значение 2;…)	Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования и стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения)
ЧИСТВНДОХ	ЧИСТВНДОХ (значения;даты;предп)	Возвращает внутреннюю сумму дохода для расписания денежных поступлений
ЧИСТНЗ	ЧИСТНЗ (ставка;значения;даты)	Возвращает чистую текущую стоимость инвестиций, вычисляемую на основе ряда периодических поступлений наличных и нормы амортизации
МСВД	МСВД (значения;ставка;ставка_финанс;ставка_реинвест)	Возвращает модифицированную внутреннюю ставку доходности для ряда периодических денежных потоков
ВСД	ВСД(значения;предположение)	Возвращает внутреннюю ставку доходности для ряда потоков денежных средств, представленнх численными значениями
АПЛ	АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации)	Возвращает величину амортизации актива за один период, рассчитанную линейным методом.
АСЧ	АСЧ(нач_стоимость;ост_стоимость; время_эксплуатации; период)	Возвращает величину амортизации актива за данный период, рассчитанную методом «суммы (годовых) чисел».
ДДОБ	ДДОБ(нач_стоимость;ост_стоимость;время_эксплуатации;период; коэффициент)	Возвращает значение амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
ФУО	ФУО(нач_стоимость;ост_стоимость; время_эксплуатации; период;месяцы)	Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.

Как видно из приведенной таблицы, большинство
финансовых функций имеет одинаковый набор базовых аргументов:

ставка — процентная ставка за период (норма
доходности или цена заемных средств — r)

Например, если получена ссуда на автомобиль под 10
процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц
составит 10%/12 или 0,83%. В качестве значения аргумента ставка нужно ввести в
формулу 10%/12 или 0,83% или 0,0083

кпер — срок (число периодов N) проведения операции. Например, если получена ссуда на
4 года под приобретение автомобиля и делаются ежемесячные платежи, то ссуда
имеет 4* 12 (или 48) периодов. В качестве значения аргумента кпер в
формулу нужно ввести число 48.

Плт — выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов. Например,
ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов
годовых составит 263,33 руб. В качестве значения аргумента выплата нужно ввести
в формулу число -263,33.

Пс — это приведенная к текущему моменту стоимость
(величина PV) или общая сумма, которая на текущий момент равноценна
ряду будущих платежей. Если аргумент ПС опущен, то он полагается равным
0. В этом случае должно быть указано значение аргумента Плт.;

Бс — требуемое значение будущей стоимости (FV) или остатка средств после последней выплаты. Если
аргумент опущен, он полагается равным 0 (будущая стоимость займа, например,
равна 0). Например, если предполагается накопить 50000 руб. для оплаты
специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая
стоимость

[тип] — число 0 или 1, обозначающее, когда
должна производиться выплата, 1 — начало периода (обычная рента или
пренумерандо), 0 — конец периода (постнумерандо).

         1.1
Операции наращения. Функция БС().

Функции, обслуживающие расчеты по операциям наращения
позволяют рассчитать будущую стоимость разовой суммы по простым и сложным
процентам, а также будущее значение потока платежей, как на основе постоянной
процентной ставки, так и на основе переменной процентной ставки.

Функция БС() — будущее значение — рассчитывает
наращенную величину разовой денежной суммы или периодических постоянных
платежей на основе постоянной процентной ставки.

Простые проценты. Для решения задач наращения по схеме
простых процентов функция БС() в качестве аргументов использует только
аргументы: норма; число периодов; ПС.

Остальные аргументы не используются.

Пример 1-1

Определить наращенную сумму для
вклада в размере 10000 руб., размещенного под 15% годовых на один год.

Рис. 1-4 Решение примера 1-1.

Таким образом, через год наращенная
сумма составит 11500 руб.

В приведенном примере, в качестве аргумента функции Кпер
было указано целое число (1 год).

Если продолжительность финансовой операции
представлена в днях, то необходимо ввести корректировку в процентную ставку,
т.е. аргумент норма должен быть представлен как t/ T *r%.

Если время финансовой операции выражено в днях, то
расчет простых процентов может быть произведен одним из трех возможных
способов:

Обыкновенные проценты с приближенным числом дней
ссуды, или, как часто называют «германская практика расчета», когда
продолжительность года условно принимается за 360 дней, а целого месяца — 30
дней.

1.
Обыкновенные
проценты с точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года условно принимается за 360 дней, а продолжительность
суды рассчитывается точно по календарю.

2.
Точные проценты с
точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года и продолжительность ссуды берутся точно по календарю

Пример 1-2

Вклад размером в 2000 руб. положен с
06.06 по 17.09 невисокосного года под 30% годовых. Найти величину капитала на
17.09 по различной практике начисления процентов.

Решение

Германская практика расчета

В соответствии с германской практикой
расчета период накопления составляет 101 день.

БС(((В8-В7)-2)/360*В2;ВЗ;;В5) =2168,3
руб.

Рис. 1-5 Решение примера 1-2
(Германская практика расчета).

Французская система расчета

В соответствии с германской практикой
расчета период накопления составляет 103 дня.

БС(((В8-В7))/360*В2;ВЗ;;В5) = 2171,7
руб.

Рис. 1-6 Решение примера 1-2
(Французская система расчета).

Таким образом, начисление процентов
по германской практике приведет к получению суммы в размере 2168,33 руб., по
французской практике — 2171,7 руб.

Сложные проценты

При использовании сложных процентов используются те же
аргументы, что и в простых процентах, с использованием годовой процентной
ставки и целого числа лет.

Пример 1-3

Определить будущую величину вклада в
10000 руб. помещенного в банк на 5 лет под 5% годовых, если начисление
процентов осуществляется:

а)    раз в году;

б)    раз в месяц.

Решение

Рис. 1-7 Решение примера 1-3 при
ежемесячном начислении процентов

а) 12762,83 руб.

б) 12833,59 руб.

Обратите внимание, что если же период начисления
процентов будет меньше года, то необходимо модифицировать аргументы ставка
и число периодов:

ставка — берется ставка процентов за период
начисления, т.е. используется номинальная годовая ставка процентов,
скорректированная на число раз (т) начисления процентов в течение года r% / т;

число периодов — указывается общее число раз
начисления процентов за весь срок финансовой операции п • т.

        

         1.2
Операции дисконтирования

Для расчета приведенной к конкретному моменту времени
наращенной суммы Excel предлагает
использование встроенной финансовой функции ПС().

Расчет с использованием функции ПС() является
обратным к определению наращенной суммы при помощи функции БС, поэтому
сущность используемых аргументов в этих функциях аналогична. Вместе с тем,
аргумент ПС заменяется на аргумент БС — будущая стоимость или
будущее значение денежной суммы (FV).

Функция ПС() быть использована для расчета по простым
и сложным процентам.

Пример 1-4

Фирме потребуется 5000 тыс. руб.
через 10 лет. В настоящее время располагает деньгами и готова положить их на
депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.

Определить необходимую сумму текущего вклада
если ставка процента по нему составляет 12% в год.

Решение.

ПС(В2;ВЗ;;В5) = -1609866,18 руб.

Рис. 1-8 Решение примера 1-4

Обратите внимание, что результат получился
отрицательным, так как это сумма, которую фирма должна положить на депозит, с
тем, чтобы через 10 лет получить необходимую сумму.

         1.3
Определение срока финансовой операции

Для определения срока финансовой операции используется
функция КПЕР0, которая вычисляет общее число периодов начисления
процентов на основе постоянной процентной ставки. Данная функция используется
как для единого платежа, так и для платежей, распределенных во времени.

Синтаксис КПЕР (норма, выплата, нз, бс, тип).

Пример 1-5

По вкладу в 10000,00, помещенному в
банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82.
Определить срок проведения операции (количество периодов начисления).

Решение.

КПЕР(В2;;В5;В6) = 5 лет

Следует обратить особое внимание на то, что
результатом применения функции является число периодов (а не число лет),
необходимое для проведения операции.

Если платежи производятся несколько раз в год, то
значение функции означает общее число периодов начисления процентов.

Рис. 1-9 Решение примера 1-5

Пример 1-6

Через сколько лет вклад размером 500
руб. достигнет величины 1000 руб. при ставке процентов 10% с ежемесячным
начислением процентов?

Решение. КПЕР(10%/12;;-500;1000)
=83,5 мес. =83,5 мес./12мес. = 7 лет.

        

         1.4
Определение процентной ставки

Для определения величины процентной ставки при
известных величинах вложенных и наращенных сумм и количестве периодов
начисления процентов Excel
предлагает использование финансовой функции «Ставка».

Аргументы функции:

ПС — вложенная сумм

БС — наращенная сумма;

Кпер — количество периодов начисления
процентов.

Пример 1-7

Фирме через 2 года потребуется 100000
руб. Для достижения этой цели фирма готова положить на депозит 25000 руб. Каким
должен быть процент на инвестированные средства с тем, чтобы к концу второго
года была получена необходимая сумма?

Решение

СТАВКА(2*12;;-25000;100000)=6%

         1.5 Расчет
эффективной и номинальной ставки процентов

Для расчета эффективной и номинальной ставки процентов
Excel предлагает использование функций ЭФФЕКТ()
и НОМИНАЛ().

Функция ЭФФЕКТ()

Функция вычисляет действующие (эффективные) ежегодные
процентные ставки, если задана номинальная годовая процентная ставка и
количество периодов начисления в году.

Синтаксис ЭФФЕКТ (номинальная ставка, кол_пер).

Пример 1-8

Номинальная ставка составляет 11%. Рассчитайте
эффективную процентную ставку при следующих вариантах начисления процентов:
полугодовом; квартальном; ежемесячном.

Решение

ЭФФЕКТ =

11,3% — при полугодовом начислении
процентов

,46% — при квартальном начислении
процентов

,57% — при ежемесячном начислении
процентов

Функция НОМИНАЛ()

Функция вычисляет номинальную годовую процентную
ставку, если известны эффективная ставка и число периодов начисления в год.

Синтаксис НОМИНАЛ (эффект_ставка, кол_пер).

Пример 1-9

Эффективная ставка составляет 28%, а
начисление процентов производится ежемесячно. Необходимо рассчитать номинальную
ставку

Решение: Номинальная ежемесячная процентная
ставка будет равна:

НОМИНАЛ (28%,12) = 0,2494 или 29,14%

        

         1.6
Начисление процентов по плавающей ставке

Для расчета будущей величины разовой инвестиции в
случае, если начисление процентов осуществляется по плавающей ставке используется
функция БЗРАСПИС(). Подобные операции широко распространены в
отечественной финансовой и банковской практике. В частности, доходы по
облигациям государственного сберегательного займа (ОГСЗ), начисляются раз в
квартал по плавающей купонной ставке

Пример 1-10

Ставка банка по срочным валютным
депозитам на начало года составляет 20% годовых, начисляемых раз в квартал.
Первоначальная сумма вклада — $1000. В течении года ожидается снижение ставок
раз в квартал на 2, 3 и 5 процентов соответственно. Определить величину
депозита к концу года

Решение

Введем ожидаемые значения процентных
ставок в блок ячеек электронной таблицы, например: 20%/4 в ячейку В2, 18%/4 в
ячейку ВЗ, 17%/4 в ячейку В4 и 15%/4 в ячейку В5. Тогда функция будет иметь
следующий вид: =БЗРАСПИС(1000; С2:С5) = 1166,86$

Раздел
2. Потоки платежей и финансовые ренты

Проведение практически любой финансовой операции порождает движение
денежных средств. Такое движение может характеризоваться возникновением
отдельных платежей, или множеством выплат и поступлений, распределенных во
времени. В финансовой практике широко распространены контракты, предусматривающие
не разовое, а систематическое движение средств — выплаты/поступления по
заданному графику происходят регулярно.

В процессе количественного анализа финансовых операций, удобно
абстрагироваться от их конкретного экономического содержания и рассматривать
порождаемые ими движения денежных средств как численный ряд, состоящий из
последовательности распределенных во времени платежей CF₁, CF₂, …, CF_n. Для
обозначения подобного ряда в мировой практике широко используется термин
«поток платежей» или «денежный поток» {cashflow — CF).

Каждый отдельный элемент такого численного ряда CF представляет собой разность между
всеми поступлениями (притоками) денежных средств и их расходованием (оттоками)
на конкретном временном отрезке проведения финансовой операции. Таким образом,
величина CF_t может иметь как положительный, так и
отрицательный знак.

Количественный анализ денежных потоков, генерируемых
за определенный период времени в результате реализации финансовой операции, или
функционирования каких-либо активов, в общем случае сводится к исчислению
следующих характеристик:

— будущей стоимости потока за п периодов;

— современной стоимости потока за я периодов.

Часто возникает необходимость определения и ряда
других параметров финансовых операций, важнейшими из которых являются:

 — величина потока платежей в периоде t;

r
— процентная ставка;

п
— срок (количество периодов)
проведения операции.

Поток платежей, все члены которого имеют одинаковое
направление (знак), а временные интервалы между последовательными платежами
постоянны, называется финансовой рентой или аннуитетом (англ.
annuity).

При рассмотрении финансовой ренты используются
основные категории:

член ренты (CF_t) — величина каждого отдельного платежа;

период ренты (t) — временной интервал между членами ренты;

срок ренты (n) — время от начала финансовой ренты до конца последнего
ее периода;

процентная ставка (r) — ставка, используемая при наращении платежей, из которых
состоит рента.

В отличие от разовых платежей, рассмотренных
нами в предыдущем разделе, для количественного анализа аннуитетов нам
понадобятся все выделенные ранее характеристики денежных потоков: FV, PV, CF, r и n
( и соответственно, все аргументы рассмотренных ранее финансовых функций Excel, (функции: БС(); IIC(); КПЕР(); СТАВКА(); ПЛТ();
БЗРАСПИС(); НОМИНАЛ(); ЭФФЕКТ()) и др.)

         2.1 Определение будущей (наращенной стоимости
потока платежей. Функция БС()

Наращенная сумма — сумма всех платежей с начисленными
на них процентами к концу срока ренты. Это может быть обобщенная сумма
задолженности, итоговый объем инвестиций и т.п.

Пример 2-1

На счет в банке в течении пяти лет в
конце каждого года будут вноситься суммы в размере 500 руб., на которые будут
начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит
владельцу счета.

Решение:

БС(30%;5;-500;;0)=4521,55

сумма всех взносов с начисленными
процентами будет равна 4521,55 руб.

Пример 2-2

Предположим, что каждый год ежемесячно
в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце
каждого месяца. Какова будет величина вклада к концу 4-го года?

Общее количество платежей за 4 года
равно: 4* 12 = 48. Ежемесячная процентная ставка составит: 12% /12 = 1%.

Решение:

БС(12%/12;4*12;-1000)= 61222,61

         2.2 Современная (текущая) величина
аннуитета. Функция ПС()

Современная (текущая) величина потока
платежей (капитализированная
или приведенная величина) — это сумма платежей, дисконтированных на момент
начала ренты по ставке начисляемых сложных процентов.

Пример 2-3

Предположим, что мы хотим получать
доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит
получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

Решение.

PV = 1000*(1-(1+10%)-4)/10%= 3169,87.

При использовании финансовой функции Excel

=ПС(10%;4;-1000)=3169,87

Таким образом, для получения в течение четырех лет
ежегодного дохода в $1000 необходимо сегодня положить в банк $3169,87.

Пример 2-4

Рассматриваются два варианта
приобретения дома стоимостью 100 мл. руб.:

А) единовременный платеж.

Б) ежемесячно в течение 15 лет
вносить в банк по 1 млн., руб.

Определить какой из вариантов
приобретения дома предпочтительнее, если ставка процента — 8% годовых, а
проценты начисляются ежемесячно?

Решение.

Для ответа на поставленный вопрос нам
необходимо сравнить, что выгоднее: заплатить сегодня всю суммы полностью или
растянуть платежи на 15 лет.

Для сравнения необходимо привести эти
денежные потоки к одному периоду времени, т.е. рассчитать текущую стоимость
будущих фиксированных периодических выплат.

Таким образом, текущая стоимость
будущих периодических платежей больше запрашиваемой стоимости дома (104,64 млн.
руб. > 100 млн. руб.), следовательно, выгоднее покупать дом сразу.

         2.3 Расчет периодических платежей

Функции Excel
помимо расчета наращенной и приведенной стоимости позволяют выполнить основные
расчеты, связанные с оценкой периодических платежей:

) периодические постоянные по величине платежи,
осуществляемые на основе постоянной процентной ставки (функция ПЛТ);

2) платежи по процентам за конкретный период (функция ПРПЛТ);

3) сумму платежей по процентам за несколько периодов,
идущих подряд друг за другом (функция ОБЩПЛАТ);

4) основные платежи по займу (за вычетом процентов) за
конкретный период (функция ОСПЛТ);

) сумму основных платежей за несколько периодов,
идущих подряд (функция ОБЩДОХОД).

Наиболее часто все эти величины используются при
составлении плана (схемы) равномерного погашения займа. Если заем погашается
равными платежами в конце (начале) каждого периода, то будущая стоимость этих
платежей ( при его полном погашении) будет равна сумме займа с начисленными
процентами к концу последнего расчетного периода. В тоже время текущая
стоимость выплат по займу должна быть равна настоящей сумме займа.

Если известна величина займа, срок на который он был
выдан и процентная ставка, то можно легко, используя функцию ПЛТ, определить
величину периодических платежей, необходимых для равномерного погашения займа.

Вычисленные платежи включают в себя сумму процентов по
непогашенной части займа и основную выплату по нему. Эти величины зависят от
номера периода и могут быть рассчитаны с помощью функций ПРПЛТ, ОСПЛАТ. Накопленные
суммы могут быть определены с помощью функций ОБЩПЛАТ и ОБЩДОХОД.

2.3.1
Определение величины периодического платежа. Функция ПЛТ().

Функция вычисляет величину выплаты за один период на
основе фиксированных периодических выплат и постоянной процентной ставки.
Выплаты, рассчитанные функцией ПЛТ, включают основные платежи и платежи по
процентам.

Синтаксис ПЛТ (норма, кпер, нз, бс, тип).

Функция ПЛТ применяется в следующих расчетах.

1.
Допустим,
известна будущая стоимость фиксированных периодических выплат, производимых в
начале или в конце каждого расчетного периода. Требуется рассчитать размер этих
выплат.

Соответствующая запись в EXCEL имеет вид:

ПЛТ (норма, кпер,, бс, тип).

2.
Предположим,
рассчитываются равные периодические платежи по займу величиной нз, необходимые
для полного погашения этого займа через кпер число периодов. Текущая
стоимость этих выплат должна равняться текущей сумме займе.

Соответствующий расчет в EXCEL выполняется по формуле:

ПЛТ (норма, кпер, нз, ,тип).

Пример 2-6

Предположим, что необходимо накопить
4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой
должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.

Решение.

Определим общее число периодов
начисления процентов и ставку процента за период по таблице 2. Эти величины
составят соответственно 3*12 (аргумент кпер) и 12%/12 (аргумент норма).
Аргумент тип = 0, т.к. по условию это вклады постнумерандо. Рассчитаем величину
ежемесячных выплат: ПЛТ(12%/12,12-3„4000) = -92,86 руб.

Пример 2-7

Допустим, банк выдал ссуду 200 тыс.
руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение
начинается в конце года одинаковыми платежами. Определите размер ежегодного
погашения ссуды.

Решение

Ежегодные платежи составят

ПЛТ (18%,4,200000,,) = -74,3 тыс.
руб.

2.3.2
Расчет платежей по процентам. Функция ПРПЛТ

Функция
позволят определить сумму платежей процентов по инвестиции за данный период на
основе постоянства сумм периодических платежей и постоянства процентной ставки.

Синтаксис
ПРПЛТ (норма, период, кпер, пс,
бс, тип).

Функция
предназначена для следующих расчетов.

1.
При равномерном
погашении займа постоянная периодическая выплата включает в себя платежи по
процентам по непогашенной части займа и выплату задолженности. Так как
непогашенная часть займа уменьшается по мерс его погашения, то уменьшается и
доля платежей по процентам в общей сумме выплаты, и увеличивается доля выплаты
задолженности. Чтобы найти размер платежа по процентам на конкретный период,
следует использовать формулу:

ПРПЛТ (норма, период, кпер, пс), если погашение займа производится равными
платежами в конце каждого расчетного периода.

2.
Допустим,
необходимо вычислить доход, который приносят постоянные периодические выплаты
за конкретный период. Этот доход представляет собой сумму процентов,
начисленных на накопленную (с процентами) к данному моменту совокупную величину
вложений. Расчет ведется по формуле:

ПРПЛТ (норма, период, кпер,, бс, тип).

Пример 2-8

Необходимо определить величину
платежей по процентам за первый месяц трехгодичного займа в 800тыс.руб. Ставка
банка 10%.

Решение.

ПРПЛТ(10%/12;1;3*12;-800) = 6666,67
руб.

·  
В поле «Ставка»
диалогового окна заносится величина месячной процентной ставки;

·  
в поле «Период»
заносится номер периода для которого мы хотим определить величину платежей
по процентам;

·  
в поле
«Кпер»заносится количество периодов начисления процентов ( в нашем примере
3*12);

·  
в поле «Пс»
заносится величина займа.

После нажатия кнопки «ОК» мы получим, что платежи по
процентам за первый месяц составили -6666,67 руб.

За счет ежегодных отчислений в течении
6 лет был создан фонд в 5 млн. руб. Необходимо определить какой доход принесли
вложения за последний год, если ставка банка составляла 12%

Решение

Доход за последний год (6 период)
составил:

ПРПЛТ(12%;6;6;;5) =0,469 млн. руб.

.3.3 Расчет суммы платежей по
процентам по займу

Функция
ОБШПЛАТ

Функция
позволяет вычислить накопленный доход (сумму платежей по процентам) по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами выплат.

Синтаксис
функции: ОБЩПЛАТ

(ставка;
Кол_пер; Нз ; нач_период; кон_период;тип)

Пример
2-10

Для
приобретения недвижимости была взята ссуда 12000 тыс. руб. Условия ссуды:

Процентная
ставка — 9%;

Срок
— 25 лет

Проценты
начисляются ежемесячно

Необходимо
найти сумму выплат за 2-й год и за 1 -й месяц займа

Решение

В диалоговом окне функции ОБЩПЛАТ() :

·  
В строке «Ставка» заносится
величина процентной ставки, начислямой за период (9%/12);

·  
в строке «Кол_пер»
записывается количество периодов начисления платежей (25*12);

·  
в строке «Нз»
записывается величина займа;

·  
в строках «Нач_период»
и «Кон_период» записываются начальный и конечный периоды, для
которых вычисляется сумма выплат по процентам (13 и 24), соответственно;

После щелчка на кнопке «ОК» будет
рассчитана сумма платежей по процентам за второй год:

=ОБЩПЛАТ(9%/12;25*12;12000;13;24;0)
=-1062 тыс. руб.

Аналогичным образом может быть
вычислена сумма выплат по
процентам за первый месяц займа:

=ОБЩПЛАТ(9%/12;25*1;12000;1;1;0)= -90
тыс. руб.

2.3.4
Расчет величины основных платежей по займу. Функция ОСПЛT

Функция позволяет вычислить величину основного платежа
(выплаты) по займу, который погашается равными платежами в конце или начале
расчетного периода, на расчетный период.

Пример 2-11

Была взята ссуда в размере 70000тыс. руб. сроком на 3
года под 17% годовых. Необходимо рассчитать величины основных платежей для
каждого года займа.

Решение

Напомним, что сумма основного платежа по займу
получается как разность между фиксированной периодической выплатой и процентами
по непогашенной части долга.

Размер основных выплат по займу, определяемый с
помощью функции ОСПЛТ может быть определен как:

Период	Формула	Основной платеж
1-й год	=ОСПЛТ(17%;1;3;70000)	-19 780.16р.
2-й год	=ОСПЛТ(17%;2;3;70000)	-23 142.78р.
3-й год	ОСПЛТ(17%;3;3;70000)	-27 077.06р.
ИТОГО		-70 000.00р.

2.3.5 Расчет суммы основных платежей
по займу. Функция ОБЩДОХОД

Функция позволяет вычислить сумму основных платежей по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами.

Пример 2-12

Выдана ссуда в размере 1000 тыс. руб.
сроком на 6 лет под 15% годовых, начисляемых ежеквартально. Определить величину
основных выплат за 5-й год.

Решение

Периоды платежей за 5-й год будут
иметь номера 17 и 20, соответственно. Так как ссуда погашается равными
платежами в конце каждого периода (квартала), то размер выплаты за пятый год
составит:

=ОБЩДОХОД(15%/4;6*4;1000;17;20;0)=201,43
тыс. руб.

Раздел
3. Оценка инвестиционных процессов

Инвестиции — это долгосрочные финансовые
вложения экономических ресурсов с целью создания и получения выгоды в будущем,
которая должна быть выше начальной величины вложений.

Инвестиционный процесс — это последовательность связанных
инвестиций, растянутых во времени, отдача от которых также распределена во
времени. Этот процесс характеризуется двусторонним потоком платежей, где
отрицательные члены потока являются вложениями денежных средств в
инвестиционный проект, а положительные члены потока — доходы от инвестированных
средств.

Методы измерения доходности инвестиционных проектов
основаны на анализе равномерного денежного потока. Ожидаемые значения
элементов денежного потока, соответствующие будущим периодам, являются
результатом сальдирования всех статей доходов и расходов, связанных с
осуществлением проекта.

Для приведения значений элементов денежного потока к
сопоставимому во времени виду по выбранной норме дисконтирования оценивается
суммарная текущая стоимость на момент принятия решения о вложении капитала,
предшествующий началу движения средств. Уровень процентной ставки, применяемой
в качестве нормы дисконтирования, должен соответствовать длине периода,
разделяющего элементы денежного потока.

В качестве показателей эффективности инвестиционных
проектов обычно используются:

·  
чистый
приведенный доход —
текущая стоимость всех доходов и расходов по проекту;

·  
срок
окупаемости —
характеризует срок окупаемости средств, вложенных (инвестированных) в проект;

·  
внутренняя
норма доходности —
это ставка дисконтирования, приравнивающая сумму приведенных доходов от
инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не
приносят прибыль.

         3.1 Чистый приведенный доход. Функция
ЧПС

При оценке инвестиционных проектов используется метод
расчета чистого приведенного дохода, который предусматривает
дисконтирование денежных потоков: все доходы и затраты приводятся к одному
моменту времени.

Центральным показателем в рассматриваемом методе
является показатель NPV (net present value) — текущая стоимость денежных потоков за вычетом
текущей стоимости денежных оттоков. Это обобщенный конечный результат
инвестиционной деятельности в абсолютном измерении.

Показатель NPV характеризует абсолютный прирост, поскольку оценивает,
на сколько приведенный доход перекрывает приведенные затраты:

·  
при NPV > 0 проект может быть принят;

·  
при NPV < 0 проект не принимается,

·  
при NPV= 0 проект не имеет ни прибыли, ни убытков

Пример 3-1

Найти чистый дисконтированный доход
проекта, требующего стартовых инвестиций в объеме 150 тыс. руб., денежный поток
которого задан рис.6-1, по ставке дисконтирования 10% годовых.

Решение

На листе Excel создадим таблицу, подобную
приведенной на Рис. 3-1.

Рис. 3-2 Фрагмент рабочего листа MS Excel в режиме отображения формул с
вычислением величины чистого дисконтированного потока

В ячейках столбца:

·  
«А»
размещены периоды поступления (оттока) денежных средств;

·  
«В»
размещаются величины денежных потоков в соответствующие периоды;

·  
«С»
размещены аккумулированные значения денежных потоков в данном периоде.
Например, в ячейке «С4» может быть записано: =СЗ+В4;

·  
«D» размещаются формулы расчета величины
коэффициента дисконтирования денежных потоков. Например, в ячейке «D3» записывается: =(ВЗ/(1+0,1)^^А3)/ВЗ;
в ячейке «D4» записывается: =(В4/(1+0,1)^^А4)/В4 и т.д.;

 ^ — обозначение возведения в степень

·  
«Е»
значения дисконтированных денежных потоков. Например, в ячейке «Е4»
записывается: =B4*D4

·  
«F» записываются формулы расчеты
аккумулированных дисконтированных денежных потоков в соответствующий период
времени. Например, в ячейке «F3» записывается величина
денежного потока в начальный период (начальные инвестиции): =D3; в ячейке «F4» записывается: =F3+E4 и т.д.

·  
«G» записывается логическая функция
анализа окупаемости проекта. Например, в ячейке «G3» записывается формула: =ЕСЛИ(СЗ>0;
«Проект окупается»;»Проект не окупается»), которая
копируется в ячейки G4:G11 таблицы.

Таким образом, в результате
выполненных вычислений получаем:

Чистый дисконтированный доход = 32,01

Дисконтированный доход =
-(-150)+32,01 = 182,01

Готовый результат 182,01 в
одной клетке дает табличная формула =NPV(10%;B4:B11), вызывающая специальную финансовую
функцию со ссылкой на норму дисконтирования («Ставка») и табличные
координаты блока значений («Значения1».,..)элементов денежного
потока, расположенных в хронологическом порядке.

В русских версиях MS Excel функция NPV имеет название ЧПС.

Рис. 3-4. Диалоговое окно функции ЧПС

Пояснения.

Функция ЧПС() возвращает величину чистой приведенной
стоимости инвестиции, используя ставку дисконтирования, а также стоимости
будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис функции: ЧПС(ставка;значение1;значение2;…)

Ставка — ставка дисконтирования за один период.

Значение1, значение2,… — от 1 до 29 аргументов,
представляющих расходы и доходы.

Значение1, значение2,… должны быть равномерно
распределены во времени, выплаты должны осуществляться в конце каждого периода.

Значение1, значение2,… могут вводится либо в
отдельные окна либо списком (при этом, порядок ввода значений (либо значений в
списке) определяется порядком поступлений и платежей)

Для вычисления чистого дисконтированного дохода к
выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных
затрат нулевого периода, записанное в таблице в ячейке ВЗ=ЧПС(10%;В4:В11)+В3 =
32,01

Метод определения чистой текущей
стоимости часто используется при оценке эффективности инвестиций. Он позволяет
определить нижнюю границу прибыльности и использовать ее в качестве критерия
при выборе наиболее эффективного проекта.

Положительное значение NPV является показателем того, что
проект приносит чистую прибыль, после покрытия всех связанных с ним расходов

Пример 3-2

Сравним два проекта, денежные потоки
которых представлены на рис. 3-5 , при значениях ставки дисконтирования 15%

Рис. 3-5 Исходные данные и решение 
Примера 3-2

В ячейках «В9» и «С9» вычисляется
значения чистого дисконтированного дохода для Проектов 1 и 2.

Выполненные расчеты показывают целесообразность
принятия Проекта 2, не смотря на то, что величины денежных потоков обоих
проектов различаются несущественно

         3.2
Срок окупаемости

Для анализа эффективности инвестиций часто
используется такой показатель, как срок окупаемости — продолжительность
времени, в течение которого дисконтированные на момент завершения инвестиций
прогнозируемые денежные поступления равны сумме инвестиций. Иными словами — это
количество лет, необходимых для компенсации стартовых инвестиций.

Пример 3-3

Рассчитать срок окупаемости проекта,
для которого размер инвестиций составляет 1 млн. руб., а денежные поступления в
течение 5 лет будут составлять: 250; 400; 800; 900; 900 тыс. руб.
соответственно. Ставка дисконтирования 15%.

Решение.

Рис. 3-7. Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-3

Рис. 3-8. Фрагмент рабочего листа Excel в режиме отображения формул
исходными данными и решением примера 3-3

В ячейках:

·  
CI :G1 размещены номера периодов
поступления денежных средств;

·  
C2:G2 размещены величины поступления
денежных средств;

·  
C3:G3 размещены формулы дисконтирования
поступающих денежных средств. Например, в ячейке СЗ записана формула
=С2/((1+15%)^{^}С1),

 соответствующая левой части формулы 6-3;

·  
C4:G4 записаны формулы вычисления
накопленного в данный период дисконтированного денежного потока. Например, в
ячейке С4 записана формула =В4+С3 (сумма величины инвестиции и
поступивших в этот период (1) денежных средств), а в ячейке D4 записывается формула =C4+D3 (сумма величины накопленного
дисконтированного потока и поступивших в этот период (2) денежных средств) и
т.д.

Анализируя построенную таблицу легко
видеть, что инвестиции полностью окупаются в интервале между 2 и 3 периодами.
Следовательно, период окупаемости может быть найден как:

=Dl+(-D4/E3) =2+480,15/526,01 =2,91 года

Таким образом, период, реально
необходимый для возмещения инвестированной сумы, составит 2,91 года или 2 года
и 332 дня.

Период окупаемости может быть также
определен, если в ячейку С5 записать формулу: =ЕСЛИ(С4>0;С1-(В4+С3)/С3;0)
и скопировать ее в остальные ячейки строки.

        

         3.3
Индекс рентабельности

Индекс рентабельности (PI) показывает, сколько единиц современной величины
денежного потока приходится на единицу предполагаемых первоначальных затрат.

Если величина критерия РI> 1, то современная стоимость денежного
потока проекта превышает первоначальные инвестиции, обеспечивая тем самым
наличие положительной величины NPV. При
этом норма рентабельности превышает заданную и проект следует принять.

При РI=1 величина NPV= 0 и инвестиции не приносят дохода.

В случае, если PI < 1, проект не обеспечивает заданного
уровня рентабельности и его следует отклонить

Пример 3-4

Рис. 3-9 Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-4

Как следует из таблицы (столбец
«Е»), чистая приведенная стоимость всех проектов (NPV) больше нуля, а индекс
рентабельность (PI) больше 1. И, если бы инвестиционный бюджет фирмы не был ограничен
суммой в 250000 то все проекты следовало бы принять. Однако из-за
ограниченности бюджета может быть реализован только тот набор (портфель)
проектов, при котором суммарные инвестиции не превышают 250000.

Для выбора наиболее привлекательных
проектов воспользуемся операцией «Поиск решения».

В ячейке «Е8″запишем целевую
функцию: =СУММПРОИЗВ(В2:В7;Е2:Е7);

Примечание: в ячейках столбца «В»
размещаются результаты выбора проекта: «1» -проект выбран;
«0» — проект отклонен.

в ячейке «В9» запишем
формулу ограничений:

=СУММПРОИЗВ(В2:В7;С2:С7);

в диалоговом окне «Поиск
решения» выполним необходимые установки:

Рис. 3-10 Диалоговое окно «Поиск
решения»

В результате выполнения процедуры «Поиск
решения» оказывается оптимальным инвестирование четырех
проектов:»А», «И», «D» и «Е», при этом
суммарная величина NPV составит 121000 (см. рис. 3-11)

Рис. 3-11 Выбор проектов для инвестирования

        

         3.4
Внутренняя норма доходности. Функция ЧИСТВНДОХ

Под внутренней нормой доходности понимают процентную
ставку, при которой чистая современная стоимость инвестиционного проекта равна
нулю.

Функция ЧИСТВНДОХ возвращает внутреннюю сумму дохода
для расписания денежных поступлений

Пример 3-5

Фирма намерена 1 января 2005 г.
инвестировать 200 млн. руб. в проект, ожидаемые доходы по которому в
последующие 5 лет составят 40, 60, 80, 90 и 100 млн. руб.

Определите внутреннюю норму дохода по проекту,
если поступление доходов будет производится 1 января каждого года

Решение

Рис.3-12 Решение примера 3-5

Таким образом, при рыночной ставке дисконта менее 20,94%
инвестирование проекта — целесообразно.

         3.5 Модифицированная внутренняя норма доходности.
Функция МСВД

Функция возвращает модифицированную внутреннюю
скорость оборота средств для ряда периодических поступлений и выплат переменной
величины.

При этом учитывается как стоимость инвестиции, так и
доход, получаемый от реинвестирования.

Синтаксис МВСД (значения, финансовая норма,
реинвест_норма).

Значения — это массив или ссылка на ячейки,
содержащие числовые величины. Эти числа представляют ряд денежных выплат
(отрицательные значения) и поступлений (положительные значения), происходящие в
регулярные периоды времени.

Аргумент значения должен содержать по крайней мере
одно положительное и одно отрицательное значение для того, чтобы можно было
вычислить модифицированную внутреннюю скорость оборота. В противном случае
функция МВСД возвращает значение ошибки #ДЕЛУ0!.

Если аргумент, который является массивом или ссылкой,
содержит тексты, логические значения или пустые ячейки, то такие значения
игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.

Финансовая норма — это норма прибыли, выплачиваемой за
деньги, находящиеся в наличном обороте.

Реинвест_норма — это норма прибыли, получаемой за
деньги, находящиеся в наличном обороте при реинвестировании.

Замечания

МВСД использует порядок расположения чисел в аргументе
значения для определения порядка выплат и поступлений. Убедитесь, что значения
выплат и поступлений введены в нужной последовательности и с правильными
знаками (положительные зна чения для получаемых денег и отрицательные значения
для выплачиваемых).

Пример 3-6

Предположим, что Вы занимаетесь
рыболовным промыслом и только что завершили пятый год работы. Пять лет назад вы
взяли 120 000 руб. под 10 процентов годовых для покупки лодки.

Ваши годовые уловы принесли прибыль в
39 000 руб., 30 000 руб., 21 000 руб., 37 000 руб. и 46 000 руб.
соответственно. За эти годы Вы реинвестировали получаемую прибыль под 12%
процентов годовых. Пусть на рабочем листе Ваш заем введен как -120 000 в ячейку
В1 и в ячейки В2:В6 введены значения Вашей прибыли за каждый год.

Решение

Тогда модифицированная внутренняя
скорость оборота за пять лет вычисляется следующим образом:

МВСД(В1:В6; 10%; 12%) равняется 12,61
процентам

Модифицированная внутренняя скорость
оборота за три года вычисляется следующим образом:

МВСД(В1 :В4; 10%; 12%) равняется
-4,80 процентам

Модифицированная внутренняя скорость
оборота за пять лет, если значение аргумента реинвест_норма равно 14%,
вычисляется следующим образом:

МВСД(В1:В6; 10%; 14%) равняется 13,48
процентам

Примеры 3-7

         Предположим, пять лет назад была взята ссуда в размере 1 млн.
руб. под 10% годовых для финансирования проекта, прибыль по которому за эти
годы составила: 100, 270, 450, 340 и 300 тыс. руб. Эти деньги были
реинвестированы под 12% годовых. Найти модифицированную внутреннюю скорость
оборота инвестиции.

Решение

Пусть на рабочем листе заем введен
как -1000 в ячейку В1, и в ячейки В2.В6 введены значения прибыли за каждый год.
Тогда модифицированная внутренняя скорость оборота за пять лет вычисляется
следующим образом:

МВСД(В1:В6,10%,12%)= 12.25%.

Модифицированная внутренняя скорость
оборота за пять лет, если бы ставка реинвестирования составляла 14%,
вычисляется следующим образом:

МВСД(В1:В6,10%14%)= 12.99%.

        
3.6 Денежный поток инвестиционного проекта с произвольными периодами
поступления платежей

Функции ЧИСТНЗ

В том случае, если поступления (оттоки) денежных
средств происходят в произвольные периоды времени), то для расчета величины
чистого дисконтированного дохода может быть использована функция Excel ЧИСТНЗ

Ставка	это ставка дисконтирования, применяема денежным потокам
Значения	это ряд денежных потоков, соответствующих графику платежей приведенной в аргументе даты. Первый платеж является необязательным и соответствует выплате в начале инвестиции. Если первое значение является выплатой, оно должно быть отрицательным. Все последующие выплаты дисконтируются на основе 365-дневного года. Ряд значений должен содержать по крайней мере одно положительное и одно отрицательное значения.
Даты	это расписание дат платежей, которое соответствует ряду денежных потоков. Первая дата означает начальную величину в графике платежей. Все другие даты должны быть позже этой даты, но могут идти в произвольном порядке.

Пример 3-7

июля 2003 года была сделана инвестиция в проект
в размере 10000 тыс. рублей

В результате реализации проекта
ожидается получение прибыли: 15 сентября 200: — 2750 тыс. руб.; 1 ноября 2003г.
-4250 тыс. руб. и 1 января 2004г. — 5250 тыс. руб.

Норма дисконтирования 9%

Необходимо определить чистую текущую
стоимость инвестиции на 1 июля 2003 на 1 июля 2002г

Решение.

На листе Excel создайте таблицу, подобную
приведенной на рисунке.

Рис. 3-13 Исходные данные примера

Вызовите функцию ЧИСТНЗ, расположенную
в категории функций «Финансовые» и введите в диалоговое окно этой функции
необходимые аргументы:

Рис. 3-13 Диалоговое окно Функции ЧИСТНЗ

Чистая текущая стоимость инвестиции
на 1 июля 2003 составит = 1856,25 тыс. руб.

на 1 июля 2002 = 1702,98 тыс. руб.,
при этом формула будет иметь вид: =ЧИСТНЗ(9%;А2:Е2;А1:Е1).

Раздел 4. Функции Excel для расчета
амортизации

Группа функций для расчета амортизации основных фондов позволяет
рассчитать амортизационные отчисления следующими методами:

) равномерным, функция АПЛ;

) суммы чисел (лет), функция АСЧ;

) фиксированного уменьшения остатка с использ. функции ФУО;

) уменьшающегося остатка или двойного процента, функция ДДОБ.

         Аргументы функций Excel для расчета амортизации

Аргумент	Значение аргумента
без_переключения	Логическое значение, определяющее, следует ли переключаться на равномерный метод в случае, когда амортизируемая стоимость превышает накопленную сумму амортизации, по умолчанию равное 0 (переключаться на равномерный метод)
время_ амортизации	Срок эксплуатации имущества (число периодов амортизации)
время_полн_аморт
время_эксплуатации
кон_период	Конечный период для вычисления суммы накопленной амортизации
коэффициент	Коэффициент ускоренной амортизации, по умолчанию равный 2
месяц	Число месяцев в первом году эксплуатации имущества, по умолчанию равный 12
нач_период	Начальный период для вычисления суммы накопленной амортизации
остаточная_ стоимость	Остаточная стоимость имущества в конце срока экс-илуатации
ост_стоим
ликвидная_стоимость
период	Период, для которого требуется вычислить амортизацию
стоимость	Первоначальная стоимость имущества
ликв_стоимость

Пример 3-1.

Определить величину ежегодной амортизации оборудования
начальной стоимостью 400 тыс. руб., если срок эксплуатации оборудования 10 лет,
остаточная стоимость 250 тыс. руб., используя различные методы расчета и
функции Excel. Результаты представить в виде табл. 2.

Таблица 5. Расчет амортизации различными методами.

год	АПЛ	АСЧ	ФУО	ДДОБ
1	375,00	681,82	968,00	800,00
2	375,00	613,64	733,74	640,00
3	375,00	545,45	556,18	512,00
4	375,00	477,27	421,58	409,60
5	375,00	409,09	319,56	327,68
6	375,00	340,91	242,23	262,14
7	375,00	272,73	183,61	209,72
8	375,00	204,55	139,17	167,77
9	375,00	136,36	105,49	134,22
10	375,00	68,18	79,96	107,37
итого	3750,0	3750,0	3749,5	3570,5

Функция AПЛ

Функция АПЛ вычисляет амортизацию имущества за один
период равномерным методом. При использовании равномерного метода для каждого
периода величина амортизационных отчислений одинакова, а совокупная величина
отчислений к концу последнего периода равна стоимости амортизируемого
имущества.

Синтаксис AПЛ (нач_стоимость, остат_стоимость,
время_эксплуатации).

При равномерном методе расчета за
каждый год амортизация составит:

АПЛ(4000,250,10) = 375 тыс. руб.

Функция АСЧ

Функция АМГД позволяет рассчитать амортизационные
отчисления за заданный период методом суммы чисел. Этот метод характеризуется
постоянным понижением амортизационных отчислений и обеспечивает полное
возмещение амортизируемой стоимости имущества.

Синтаксис АСЧ (нач_стоимость, ост_стоимость,
время_эксплуатации, период).

Определим величину амортизации за
первый и третий годы эксплуатации методом суммы чисел. За первый год
амортизация составит:

АСЧ(8000,500,10,1) = 681,82 тыс.
руб.,

за третий год величина
амортизационных отчислений составит:

АСЧ (8000,500,10,3)= 545,45 тыс.руб.

Функция ФУО

Функция ФУО вычисляет величину амортизации имущества
для заданного периода с использованием метода постоянного учета амортизации.
Данный метод использует фиксированную норму амортизации.

Синтаксис ФУО (нач_стоимость, ост_стоимость,
время_эксплуатации, период, месяцы).

Рассчитаем величину амортизации за
первый, третий и последний годы эксплуатации этим методом. За первый год
амортизация

составит:

ФУО(4000,250,10,1) = 968 тыс. руб.,

за третий год амортизация составит:

ФУО (4000,250,10,3) = 566,18 тыс.
руб.,

а в последнем году амортизационные
отчисления составят: ФУО (4000,250,10,10)= 79,96 тыс. руб.

Функция ДДОБ

Функция ДДОБ позволяет рассчитать сумму амортизации
для заданного периода методом уменьшающегося остатка. При этом можно задать
коэффициент ускоренной амортизации, по умолчанию равный двум.

Синтаксис ДДОБ (нач_стоимость, ост_стоимость,
время эксплуатации, период, коэффициент).

Амортизационные отчисления при использовании метода
двукратного учета амортизации (аргумент коэффициент = 2) постоянно
уменьшаются на протяжении срока эксплуатации, но их суммарная величина в итоге
полностью не возмещает амортизируемую стоимость имущества.

Рассчитаем величину амортизации за
первый и третий годы эксплуатации методом двукратного учета амортизации. За
первый год амортизация составит:

ДДОБ(4000,250,10,1) = 800 тыс. руб.,

за третий год:

ДДОБ(4000,250,10,3) = 512 тыс. руб.

Вариант 1

1. Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 4 года под 13,5% годовых. Проценты начисляются каждые полгода	БС
2. Срок ссуды — 5 лет, договорная процентная ставка 12% годовых плюс маржа 0,5% в первые два года и 0,75% -в оставшиеся. Вычислить множитель наращения.	БЗРАСПИС
3. Компании X потребуется 100000 тыс. руб. через 2 года. а) Компания готова вложить 5000 тыс. руб. сразу и по 2500 тыс. руб. каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года. б) Компания отказалась от ежемесячных платежей и готова единовременно вложить 40000 тыс. руб. Определите, как изменится в этом случае процентная ставка.	СТАВКА
4. Определить эффективную ставку сложных процентов, с тем чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки 18% при ежеквартальном начислении процентов.	(ЭФФЕКТ)
5. Банк выдал ссуду 150 тыс. руб. на 3 года под 17% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды.	(ПЛТ)
6. Определите эффективность предполагаемой инвестиции размером 250 млн. руб., если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 25, 30, 35, 50, и 120 млн. руб. Издержки привлечения капитала составят 10,5%.	(ЧПС)
7. Определить величину ежегодной амортизации оборудования начальной стоимостью 145000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 10000 руб. Используйте равномерный метод.	(АПЛ)

Вариант 2

1. У Вас есть возможность ежегодно в течение 4 лет инвестировать 300 тыс. руб. в два проекта: под 26% в начале каждого года или 38% в конце года. Определите, какой из вариантов вложения средств предпочтительнее.	(БС)
2. По вкладу в 10000 помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82. Определить срок проведения операции (количество периодов начисления).	(КПЕР)
3. Определить величину ежегодной амортизации оборудования начальной стоимостью 44000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 2000 руб.  Используйте метод уменьшающегося остатка.	(ДДОБ)
4. Пять лет назад была взята ссуда в размере 1 млн. руб. под 10% годовых для финансирования проекта, прибыль по которому за эти годы составила 100, 270, 450, 340, и 300 тыс. руб. Эти деньги были реинвестированы под 12% годовых. Найти модифицированную внутреннюю скорость оборота инвестиций	(МСВД)
5. Определите сумму основных платежей по займу в 112 тыс. руб., выданному на четыре года под 13% годовых, за третий год, если проценты начисляются ежемесячно.	(ОБЩДОХОД)
6. Определите номинальную процентную ставку по облигации, выпущенной на пять лет, если эффективная ставка составила 11,96% при ежемесячном начислении процентов.	(НОМИНАЛ)
7. Рассмотрим инвестиции, которые начинаются в начале первого периода. Вы намерены приобрести обувной магазин. Стоимость предприятия — 40 000 руб. а) Вы ожидаете получить следующие доходы за первые пять лет: 8 000 руб., 9 200 руб., 10 000 руб., 12 000 руб. и 14 500 руб. Годовая учетная ставка равна 8%. Рассчитайте текущую стоимость проекта б) На шестой год работы магазина случилось непредвиденное и магазин потерпел убытки в размере 9000 руб. Рассчитайте текущую стоимость проекта	(ЧПС)

Вариант 3

1. Вы решили приобрести автомобиль стоимостью 200000 руб. Какую сумму Вы должны вложить в банк под 12% годовых для того, чтобы иметь возможность его приобретения. а) Начисление процентов производится один раз в начале года б) Начисления производятся 2 раза в год в начале периода.	(ПС)
2. Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты. Размер разового платежа составляет 16 млн. руб. На поступившие взносы начисляется 11,18% годовых. Определить, когда величина фонда будет равна 100 млн. руб.	(КПЕР)
3. Ставка банка по срочным валютным депозитам составляет 18% годовых. Какова реальная доходность вклада (т.е. эффективная ставка) если проценты выплачиваются:  а) ежемесячно; б) раз в год.	(ЭФФЕКТ)
4. Вычислить 10 годичную ипотечную ссуду покупки квартиры за 800000 руб. с годовой ставкой 13% и начальным взносом 25%. Сделать расчет для ежемесячных и ежегодных выплат.	(ПЛТ)
5. Определите чистую текущую стоимость проекта на 1.01.2005г., затраты по которому на 20.12.2005 составят 100 млн. руб. Ставка банка 12%. Ожидается, что за первые полгода 2006 года проект принесет следующие доходы: Дата Поступления (млн. руб.)  01.03.2006 18  15.04.2006 40  30.06.2006 51	(ЧИСТНЗ)
6. Определить величину ежегодной амортизации оборудования начальной стоимостью 648000 руб., если срок эксплуатации имущества 10 лет, а остаточная стоимость 23000 руб. Используйте метод суммы чисел.	(АСЧ)
7. Пусть в долг на полтора года дана сумма 20000 руб. с условием возврата 30000 руб. Вычислить годовую процентную ставку.	(СТАВКА)

Вариант 4

1. Предположим, что выкупается страховка, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 процентов годовых. Необходимо определить, будет ли это хорошим способом инвестировать капитал.	(ПС)
2. Рассчитайте внутреннюю скорость оборота инвестиции, если выплата 400 тыс. руб., произведенная 23 апреля 2003 принесет доходы: 28.11.2003 — 149 тыс. руб.;  20.05.2004 — 180 тыс. руб.;  01.01.2005 — 150 тыс. руб.	(ЧИСТВНДОХ)
3. Определить величину ежегодной амортизации оборудования начальной стоимостью 145000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 10000 руб. Используйте метод уменьшающегося остатка.	(ДДОБ)
4. Какую сумму необходимо ежемесячно вносить на счет, чтобы через три года получить 10 тыс. руб., если годовая процентная ставка 13,5%.	(ПЛТ)
5. Чему равна эффективная ставка при номинальной ставке 100%  А) при начислении 10 000 000 раз в год,  Б) при ежедневном начислении?	(ЭФФЕКТ)
6. Рассчитайте процентную ставку для четырехлетнего займа в 7000 тыс. руб. с ежемесячным погашением по 250 тыс. руб. при условии, что заем полностью погашается.	(СТАВКА)
7. Ссуда 63200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб.  Рассчитайте срок погашения ссуды.	(КПЕР)

Вариант 5

1. Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6% годовых (что составит в месяц 6%/12 или 0,5%). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?	(БС)
2. Ставка банка по срочным валютным депозитам на начало года составляет 20% годовых, начисляемых раз в квартал. Первоначальная сумма вклада — 2000 руб. В течении года ожидается снижение ставок раз в квартал на 2, 4 и 5 процентов соответственно. Определить величину депозита к концу года.	(БЗРАСПИС)
3. Определить величину ежегодной амортизации оборудования начальной стоимостью 145000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 10000 руб. Используйте метод постоянного учета амортизации.	(ФУО)
4. За какой срок в годах сумма, равная 75 000 руб., достигнет 200 000 руб. при начислении процентов по сложной ставке 15%раз в году и поквартально.	(КПЕР)
5. Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл.	(СТАВКА)
6. Эффективная ставка составляет 22%, проценты начисляются ежеквартально. Рассчитайте номинальную ставку.	(НОМИНАЛ)
7. Определите платежи по процентам по займу в 57 тыс. руб., выданному на три года под 13% годовых, за второй год, если проценты начисляются ежегодно.	(ПРПЛТ)

Вариант 6

1. Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб.в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?	(ПС)
2. Была выдана ссуда в размере 273 тыс. руб. сроком на 5 лет под 14,5% годовых, начисляемых ежемесячно. Определите величину основных выплат за 4-й год.	(ОБЩДОХОД)
3. Заем в 144 тыс. руб. погашается равномерными периодическими платежами по 14 тыс. руб. каждые полгода в течение восьми лет. Определите годовую ставку процента.	(СТАВКА)
4. Чему равна эффективная ставка при номинальной ставке 16%  А) при ежеквартальном начислении; Б) при ежемесячном начислении?	(ЭФФЕКТ)
5. Найдите сумму выплат за 3-й год и за 3 месяц кредита в размере 5000 тыс. руб. при процентной ставке 9%, если проценты начисляются ежемесячно. Срок кредита 15 лет.	(ОБЩПЛАТ)
6. Определите внутреннюю норму дохода по проекту, затраты по которому составили 200 тыс. руб., а ожидаемые доходы в последующие пять лет составят соответственно 40, 60, 80, 90 и 100 тыс. рублей. Оцените экономическую эффективность проекта, если рыночная норма дохода составляет 10%.	(ВСД)
7. Определить величину ежегодной амортизации оборудования начальной стоимостью 44000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 2000 руб. Используйте метод постоянного учета амортизации.	(ФУО)

Вариант 7

1. Фирма создает фонд для погашения долгосрочных обязательств, срок которых истекает через пять лет, путем ежегодного пополнения депозита, с начальной суммой 10000 тыс. руб. Размер ежегодного взноса 1000 тыс. руб. Ставка по депозиту — 5% годовых, начисляемых в конце каждого периода. Определите величину фонда к концу пятого года.	(БС)
2. Рассчитайте, через сколько месяцев вклад размером 15000 руб. достигнет величины 24500 руб. при ежемесячном начислении процентов и ставке процента 22% годовых.	(КПЕР)
3. В долг на 2 года дана сумма 150 000 руб. с условием возврата 190 000 руб. Вычислить годовую процентную ставку.	(СТАВКА)
4. Чему равна номинальная ставка при эффективной ставке 13,5 %  А) при ежеквартальном начислении Б) при ежемесячном начислении начислении?	(НОМНАЛ)
5. Определите основные платежи по займу в 75000 руб., выданному на три года под 20 % годовых, за три года.	(ОСПЛТ)
6. Для приобретения предприятия была взята ссуда в размере 300 млн. руб. под 12% годовых на три года. За эти три года предприятие принесло следующие доходы: 70, 100, 120 млн. руб. Эти деньги были реинвестированы под 17% годовых. Рассчитайте модифицированную внутреннюю норму дохода.	(МСВД)
7. Определить величину ежегодной амортизации оборудования начальной стоимостью 648000 руб., если срок эксплуатации имущества 10 лет, а остаточная стоимость 23000 руб. Используйте равномерный метод.	(АПЛ)

Вариант 8

1. Ссуда в 20 000 руб. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.	(БС)
2. Ссуда 87000 руб., выданная под 30% годовых, погашается ежеквартальными платежами по 9500 руб.  Рассчитайте срок погашения ссуды.	(КПЕР)
3. Какой должна быть годовая процентная ставка по вкладу размером 10000 руб., если ее величина к концу года составила 11723 руб., а проценты начислялись ежемесячно.	(СТАВКА)
4. Чему равна эффективная ставка при номинальной ставке 12%  А) при начислении 12 раз в год,  Б) при ежедневном начислении?	(ЭФФЕКТ)
5. Определите ежемесячные выплаты по займу в 220 тыс. руб., взятому на семь месяцев под 11% годовых.	(ПЛТ)
6. Затраты по проекту в начальный момент его реализации составляют 50000 руб., а ожидаемые доходы за первые пять лет : 3000; 5000; 8000; 12000; 13500. На шестой год реализации проекта ожидаются убытки в 5000 руб. Цена капитала- 10% годовых. Рассчитайте текущую стоимость проекта.	(ЧПС)
7. Определить величину ежегодной амортизации оборудования начальной стоимостью 648000 руб., если срок эксплуатации имущества 10 лет, а остаточная стоимость 23000 руб. Используйте метод уменьшающегося остатка.	(ДДОБ)

Вариант 9

1. Вексель на 3 000 000 руб. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года. Найти исходную сумму, выданную под этот вексель. В данном случае задача осложняется тем, что задана ставка дисконта, а аргумент норма подразумевает процентную ставку. Поэтому предварительно нужно пересчитать дисконтную ставку в процентную. (9%/2/(1 — 9%/2))	(ПС)
2. Ссуда размером 61000 руб. погашается ежемесячными платежами по 2144 руб. Рассчитайте, через сколько лет произойдет погашение, если годовая славка процента 16%.	(КПЕР)
3. Рассчитайте годовую ставку процента по вкладу размером 230 тыс. руб., если за 11 лет эта сумма возросла до 3 млн. руб. при ежеквартальном начислении процентов.	(СТАВКА)
4. Ставка банка по срочным валютным депозитам составляет 19% годовых. Какова реальная доходность вклада (т.е. эффективная ставка) если проценты выплачиваются:  а) ежемесячно б) ежеквартально	(ЭФФЕКТ)
5. Для приобретения недвижимости была взята ссуда 995000 руб. при процентной ставки 8,5% , если проценты начисляются ежемесячно. Срок ссуды 5 лет. Найдите сумму выплат за 2-й год и за 1 месяц.	(ОБЩПЛАТ)
6. Определите чистую текущую стоимость инвестиции, если 27 декабря 2003 г. предполагается выплата 5 млн. руб., ставка банка 10% и поступления составят:  Дата Поступления (млн. руб.)  20.06.2006 1  12.12.2006 3,8  17.07.2006 4,6	(ЧИСТНЗ)
7. Определить величину ежегодной амортизации оборудования начальной стоимостью 44000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 2000 руб. Используйте равномерный метод.	(АПЛ)

Вариант 10

1. Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?	(БС)
2. Физическому лицу выдан кредит 97 000 руб. на три года. Проценты начисляются ежегодно. Определить величину процентной ставки за период, если известно, что возврат составит 140 000 руб.	(СТАВКА)
3. Определите величину платежей по процентам за десятый месяц четырехгодичного займа 350 тыс. руб. Ставка банка 11,5%, если проценты начисляются ежемесячно.	(ПРПЛТ)
4. Сравните два проекта, денежные потоки которых представлены в таблице, тыс. руб.  Проект А Проект Б  Инвестиции 0 года -300 -300  Доход 1 года 190 190  Доход 2 года 210 320  Доход 3 года 350 170  Доход 4 года 180 290  Ставка дисконтирования 15%	(ЧПС)
5. Определите чистую текущую стоимость инвестиции, если 12 декабря 2004 г предполагается выплата 3,5 млн. руб., ставка банка 10% и поступления составят:  Дата Поступления (млн. руб.)  10.02.2006 1  15.06.2006 2,2  17.08.2006 4,4	(ЧИСТНЗ)
6. Определить величину ежегодной амортизации оборудования начальной стоимостью 145000 руб., если срок эксплуатации имущества 7 лет, а остаточная стоимость 10000 руб. Используйте метод суммы чисел.	(АСЧ)
7. Ожидается, что ежегодные доходы от реализации проекта составят ЗЗ млн. руб. Рассчитайте срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн.руб., а норма дисконтирования — 12.11%.	(КПЕР)