Содержание
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- БС
- ВСД
- МВСД
- ПРПЛТ
- ПЛТ
- ПС
- ЧПС
- СТАВКА
- ЭФФЕКТ
- Вопросы и ответы
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
- Запускается Мастер функций. Выполняем клик по полю «Категории».
- Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
- Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Урок: Мастер функций в Excel
ДОХОД
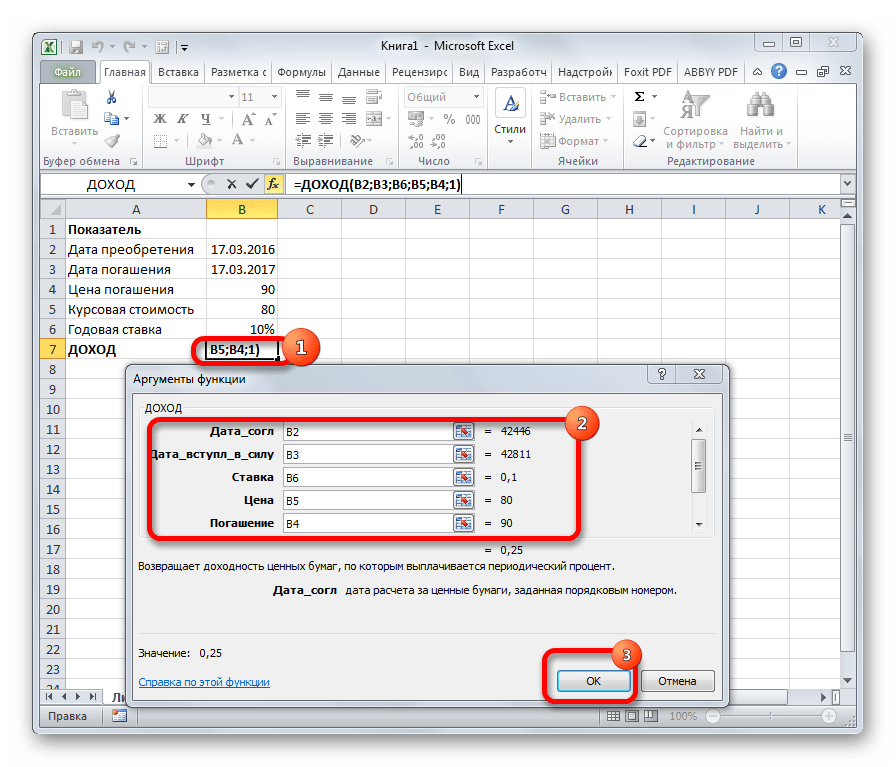
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])
БС
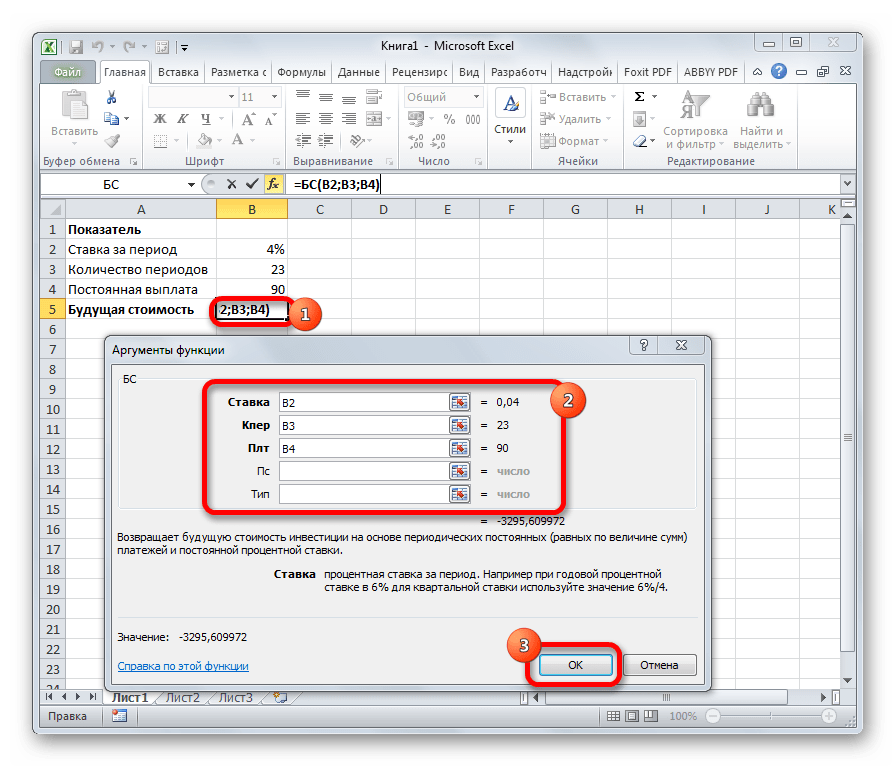
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])
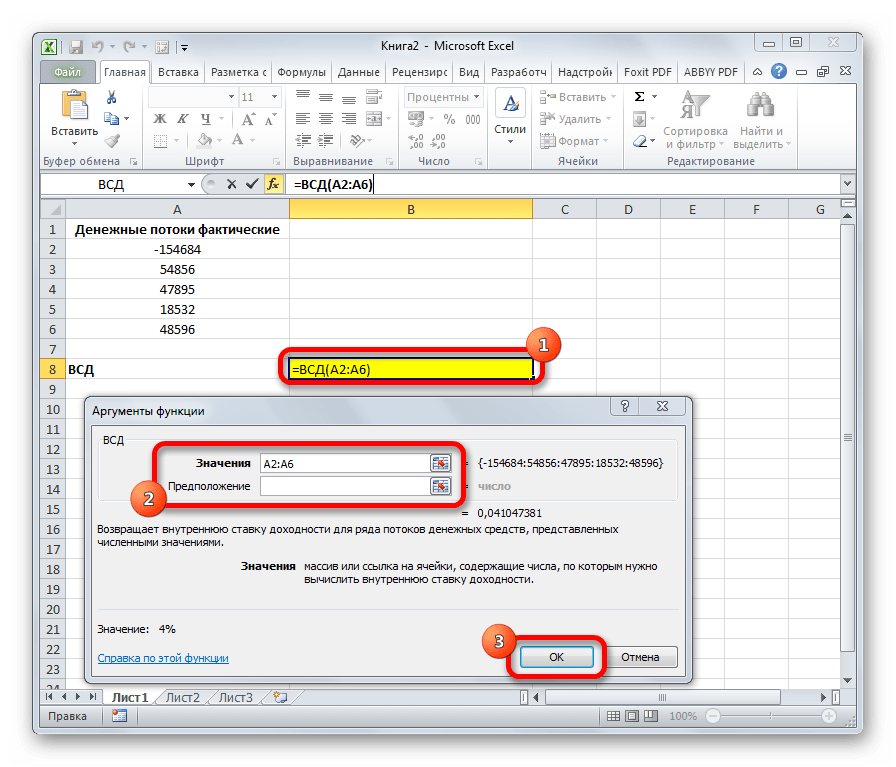
ВСД
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
=ВСД(Значения;[Предположения])
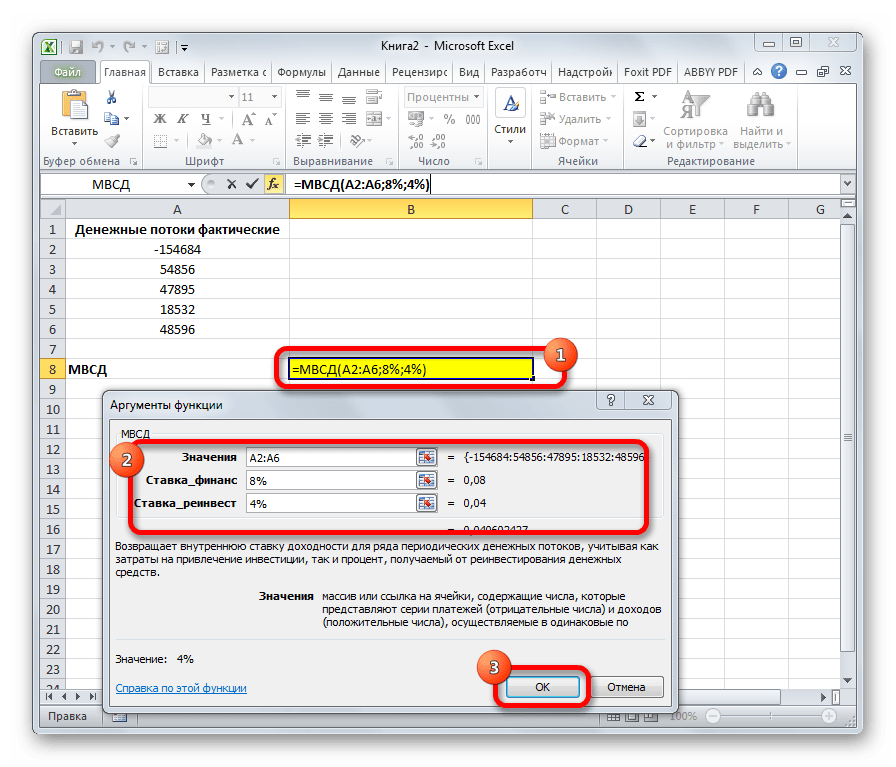
МВСД
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)
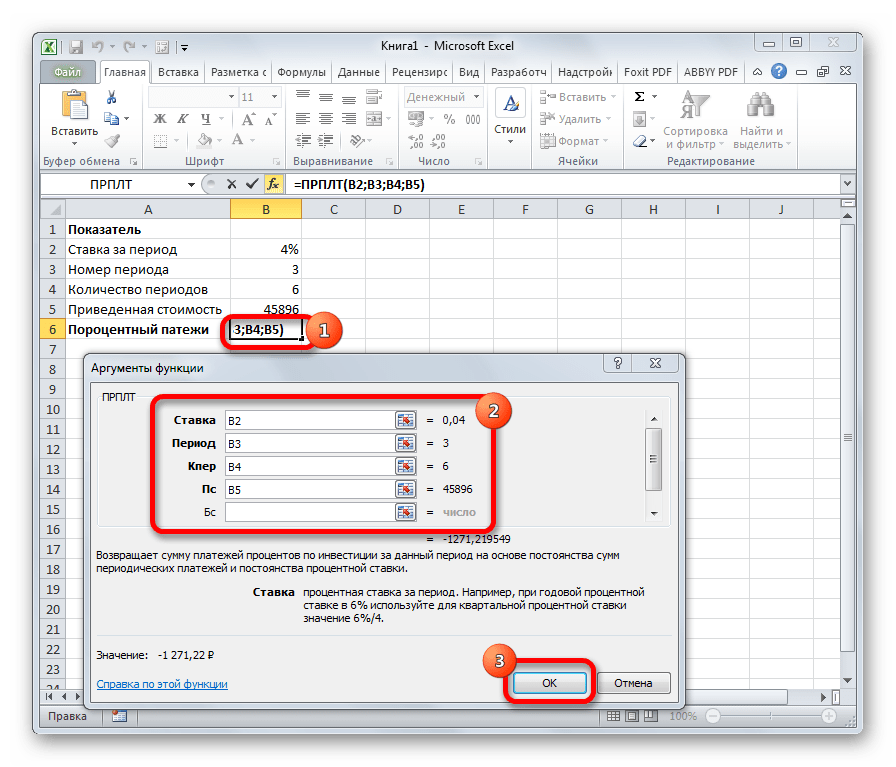
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])
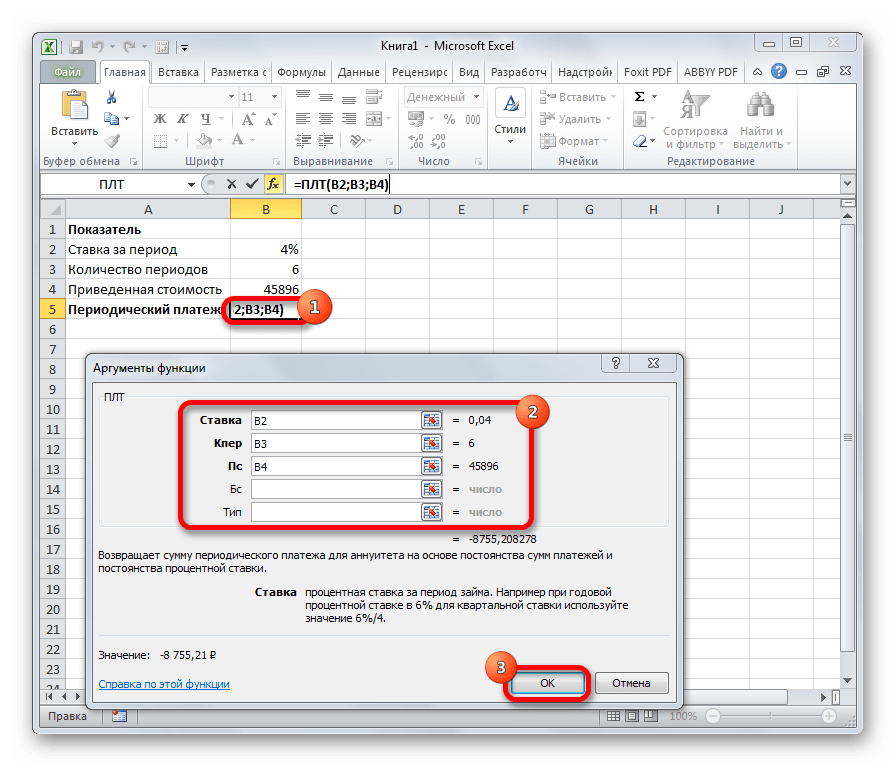
ПЛТ
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])
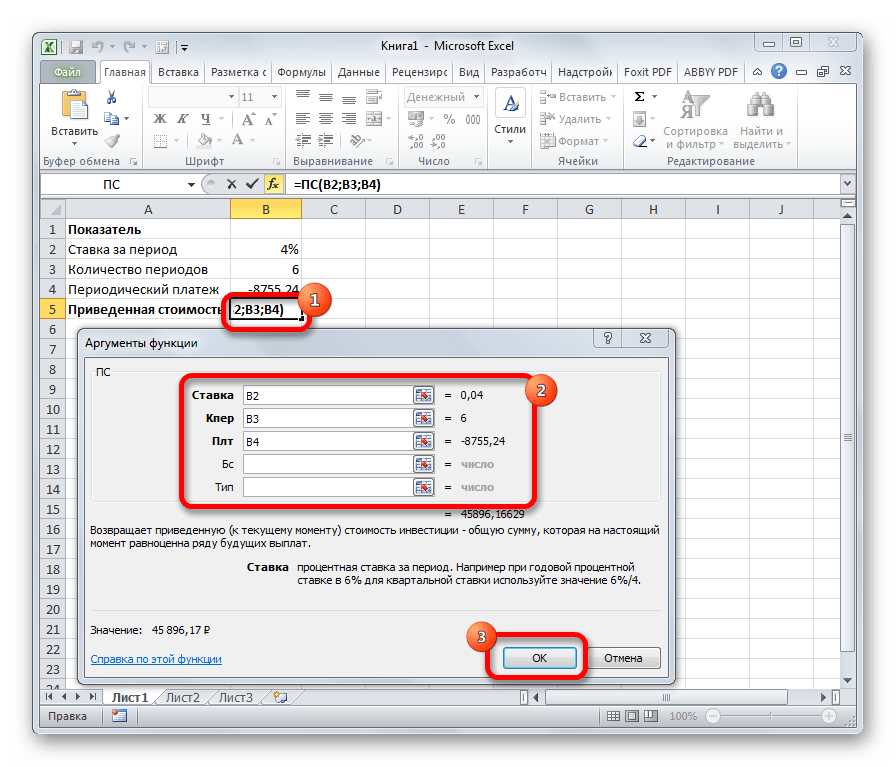
ПС
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])
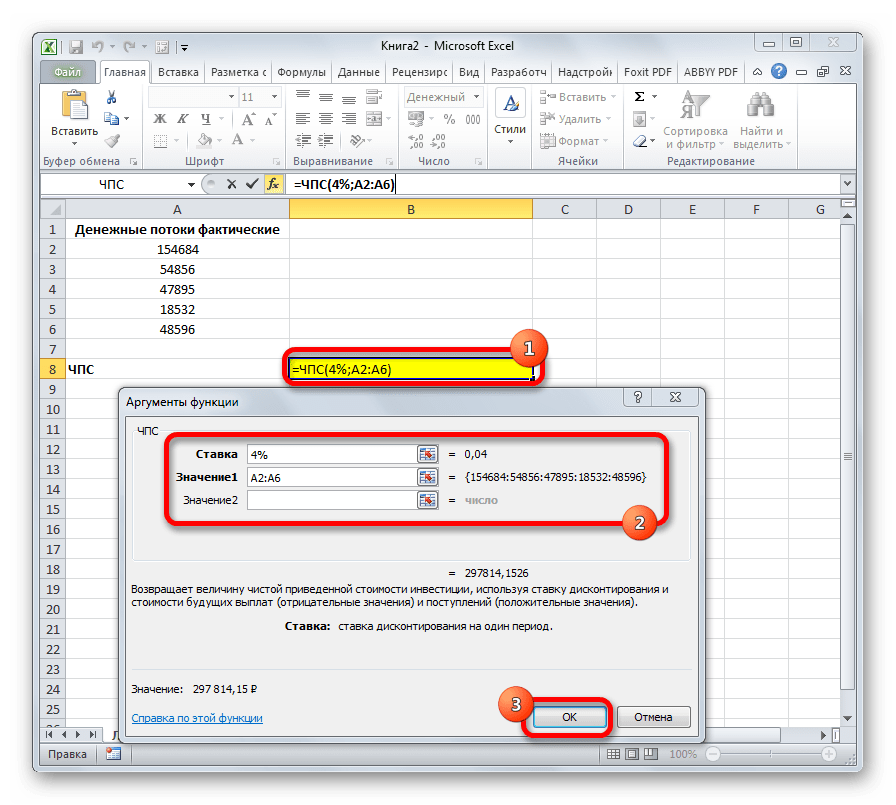
ЧПС
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
=ЧПС(Ставка;Значение1;Значение2;…)
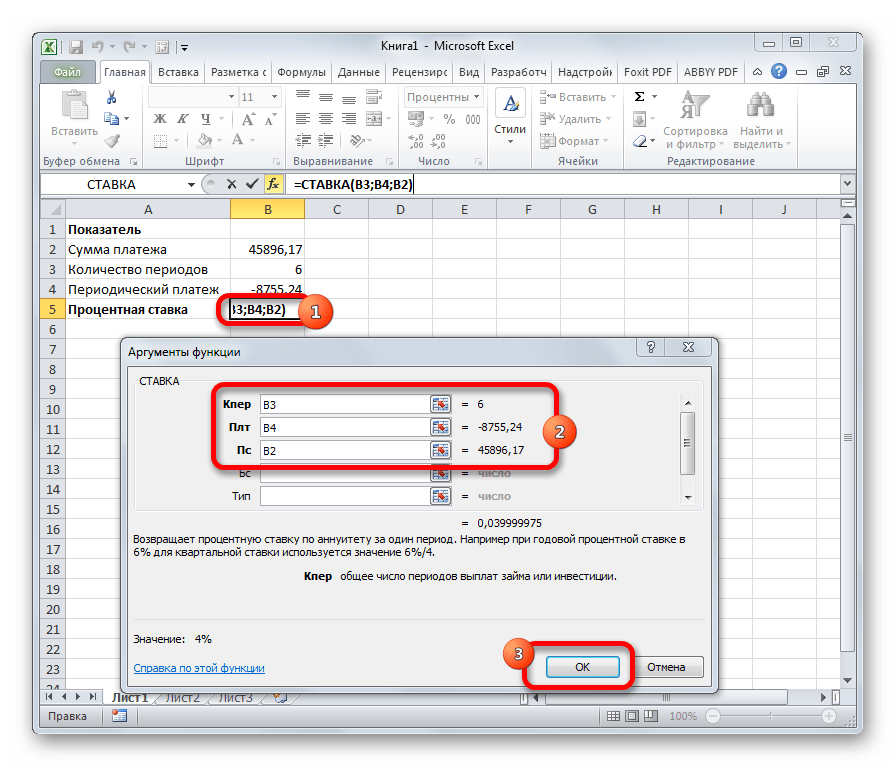
СТАВКА
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])
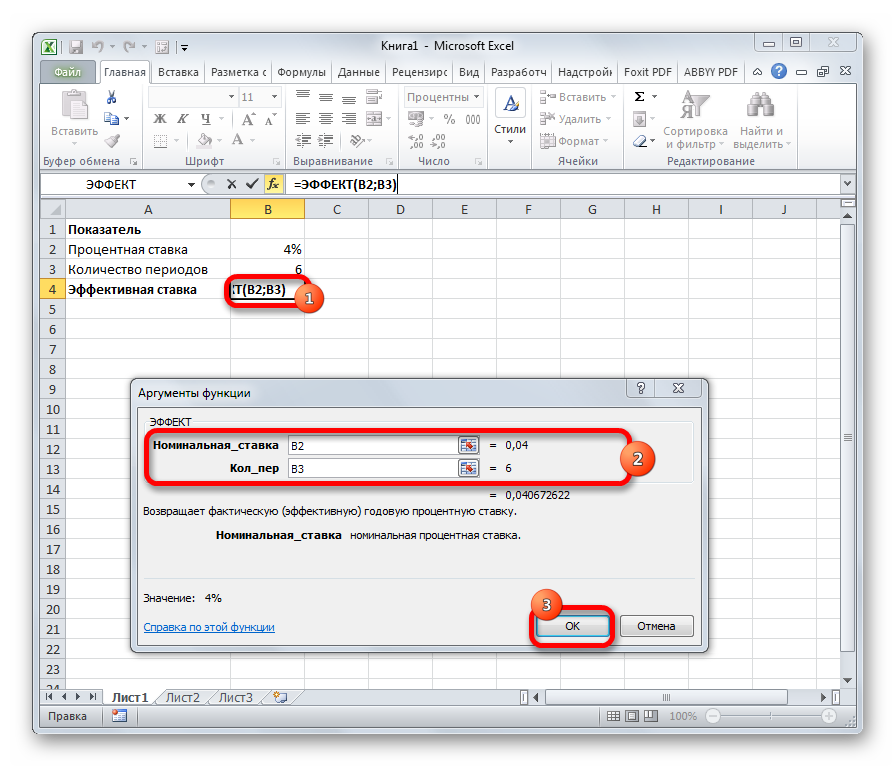
ЭФФЕКТ
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
=ЭФФЕКТ(Ном_ставка;Кол_пер)
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.
- Вставка функции
-
Популярные финансовые функции
-
БС
- ВСД
- ДОХОД
- МВСД
- ИНОРМА
- ПЛТ
- ПОЛУЧЕНО
- ПС
- СТАВКА
- ЦЕНА
-
ЧПС
-
БС
- Заключение
Вставка функции
Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:
- Выбрав нужную ячейку щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- Или переключаемся во вкладку “Формулы” и жмем аналогичную кнопку, расположенную в левом углу ленты программы.
Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.
На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.
Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).
Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).
Альтернативный способ
Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.
После этого сразу же откроется окно с аргументами функции для заполнения.
Популярные финансовые функции
Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).
БС
Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).
Обязательными аргументами (параметрами) для заполнения являются:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы:
- Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
- Тип – здесь указывается:
- 0 – выплата в конце периода;
- 1 – выплата в начале периода
- если поле оставить пустым, по умолчанию будет принято нулевое значение.
Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.
Синтаксис функции:
=БС(ставка;кпер;плт;[пс];[тип])
Результат в ячейке и выражение в строке формул:
ВСД
Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.
Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.
Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).
Синтаксис функции:
=ВСД(значения;[предположение])
Результат в ячейке и выражение в строке формул:
ДОХОД
С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
- Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Цена – цена ц.б. за 100 рублей номинальной стоимости;
- Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:
- 0 или не заполнен – армериканский (NASD) 30/360;
- 1 – фактический/фактический;
- 2 – фактический/360;
- 3 – фактический/365;
- 4 – европейский 30/360.
Синтаксис функции:
=ДОХОД(дата_согл;дата_вступл_в_силу;ставка;цена;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
МВСД
Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.
У функции только обязательные аргументы, к которым относятся:
- Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
- Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
- Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.
Синтаксис функции:
=МВСД(значения;ставка_финанс;ставка_реинвест)
Результат в ячейке и выражение в строке формул:
ИНОРМА
Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, вложенная в ц.б.;
- Погашение – сумма к получению при погашении ц.б.;
- аргумент “Базис” как и для функции ДОХОД является необязательным.
Синтаксис функции:
=ИНОРМА(дата_согл;дата_вступл_в_силу;инвестиция;погашение;[базис])
Результат в ячейке и выражение в строке формул:
ПЛТ
С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.
Обязательные аргументы:
- Ставка – процентная ставка за период займа;
- Кпер – общее количество периодов выплат;
- Пс – приведенная (нынешняя) стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
- Тип – здесь указывается, как будет производиться выплата:
- “0” или не указано – в конце периода;
- “1” – в начале периода.
Синтаксис функции:
=ПЛТ(ставка;кпер;пс;[бс];[тип])
Результат в ячейке и выражение в строке формул:
ПОЛУЧЕНО
Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, инвестированная в ц.б.;
- Дисконт – ставка дисконтирования ц.б.;
- “Базис” – необязательный аргумент (см. функцию ДОХОД).
Синтаксис функции:
=ПОЛУЧЕНО(дата_согл;дата_вступл_в_силу;инвестиция;дисконт;[базис])
Результат в ячейке и выражение в строке формул:
ПС
Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.
Обязательные аргументы:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы – такие же как и для функции “ПЛТ”:
- Бс – будущая стоимость;
- Тип.
Синтаксис функции:
=ПС(ставка;кпер;плт;[бс];[тип])
Результат в ячейке и выражение в строке формул:
СТАВКА
Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.
Обязательные аргументы:
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период;
- Пс – приведенная стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (см. функцию ПЛТ);
- Тип (см. функцию ПЛТ);
- Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).
Синтаксис функции:
=СТАВКА(кпер;;плт;пс;[бс];[тип];[предположение])
Результат в ячейке и выражение в строке формул:
ЦЕНА
Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Доход – годовой доход по ц.б.;
- Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” как и для оператора ДОХОД является необязательным.
Синтаксис функции:
=ЦЕНА(дата_согл;дата_вступл_в_силу;ставка;доход;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
ЧПС
С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.
Аргументы функции:
- Ставка – ставка дисконтирования за 1 период;
- Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
- Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.
Синтаксис функции:
=ЧПС(ставка;значение1;[значение2];...)
Результат в ячейке и выражение в строке формул:
Заключение
Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
НАКОПДОХОД |
Возвращает накопленный процент по ценным бумагам с периодической выплатой процентов. |
|
НАКОПДОХОДПОГАШ |
Возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения. |
|
АМОРУМ |
Возвращает величину амортизации для каждого учетного периода, используя коэффициент амортизации. |
|
АМОРУВ |
Возвращает величину амортизации для каждого учетного периода. |
|
ДНЕЙКУПОНДО |
Возвращает количество дней от начала действия купона до даты соглашения. |
|
ДНЕЙКУПОН |
Возвращает количество дней в периоде купона, который содержит дату расчета. |
|
ДНЕЙКУПОНПОСЛЕ |
Возвращает количество дней от даты расчета до срока следующего купона. |
|
ДАТАКУПОНПОСЛЕ |
Возвращает порядковый номер даты следующего купона после даты соглашения. |
|
ЧИСЛКУПОН |
Возвращает количество купонов между датой соглашения и сроком вступления в силу. |
|
ДАТАКУПОНДО |
Возвращает порядковый номер даты предыдущего купона до даты соглашения. |
|
ОБЩПЛАТ |
Возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат. |
|
ОБЩДОХОД |
Возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами. |
|
ФУО |
Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка. |
|
ДДОБ |
Возвращает величину амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод. |
|
СКИДКА |
Возвращает ставку дисконтирования для ценных бумаг. |
|
РУБЛЬ.ДЕС |
Преобразует цену в рублях, выраженную в виде дроби, в цену в рублях, выраженную десятичным числом. |
|
РУБЛЬ.ДРОБЬ |
Преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, выраженную в виде дроби. |
|
ДЛИТ |
Возвращает продолжительность Маколея для ценных бумаг, по которым выплачивается периодический процент. |
|
ЭФФЕКТ |
Возвращает фактическую (эффективную) годовую процентную ставку. |
|
БС |
Возвращает будущую стоимость инвестиции. |
|
БЗРАСПИС |
Возвращает будущее значение первоначальной основной суммы после применения ряда (плана) ставок сложных процентов. |
|
ИНОРМА |
Возвращает процентную ставку для полностью инвестированных ценных бумаг. |
|
ПРПЛТ |
Возвращает проценты по вкладу за данный период. |
|
ВСД |
Возвращает внутреннюю ставку доходности для ряда потоков денежных средств. |
|
ПРОЦПЛАТ |
Вычисляет выплаты за указанный период инвестиции. |
|
МДЛИТ |
Возвращает модифицированную продолжительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей. |
|
МВСД |
Возвращает внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разные значения ставки. |
|
НОМИНАЛ |
Возвращает номинальную годовую процентную ставку. |
|
КПЕР |
Возвращает общее количество периодов выплаты для инвестиции. |
|
ЧПС |
Возвращает чистую приведенную стоимость инвестиции, основанной на серии периодических денежных потоков и ставке дисконтирования. |
|
ЦЕНАПЕРВНЕРЕГ |
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) первым периодом купона. |
|
ДОХОДПЕРВНЕРЕГ |
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом купона. |
|
ЦЕНАПОСЛНЕРЕГ |
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) последним периодом купона. |
|
ДОХОДПОСЛНЕРЕГ |
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом купона. |
|
ПДЛИТ |
Возвращает количество периодов, необходимых инвестиции для достижения заданного значения. |
|
ПЛТ |
Возвращает регулярный платеж годичной ренты. |
|
ОСПЛТ |
Возвращает платеж с основного вложенного капитала за данный период. |
|
ЦЕНА |
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент. |
|
ЦЕНАСКИДКА |
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка. |
|
ЦЕНАПОГАШ |
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения. |
|
ПС |
Возвращает приведенную (к текущему моменту) стоимость инвестиции. |
|
СТАВКА |
Возвращает процентную ставку по аннуитету за один период. |
|
ПОЛУЧЕНО |
Возвращает сумму, полученную к сроку погашения полностью инвестированных ценных бумаг. |
|
ЭКВ.СТАВКА |
Возвращает эквивалентную процентную ставку для роста инвестиции. |
|
АПЛ |
Возвращает величину амортизации актива за один период, рассчитанную линейным методом. |
|
АСЧ |
Возвращает величину амортизации актива за данный период, рассчитанную методом суммы годовых чисел. |
|
РАВНОКЧЕК |
Возвращает эквивалентный облигации доход по казначейскому векселю. |
|
ЦЕНАКЧЕК |
Возвращает цену за 100 рублей номинальной стоимости для казначейского векселя. |
|
ДОХОДКЧЕК |
Возвращает доходность по казначейскому векселю. |
|
ПУО |
Возвращает величину амортизации актива для указанного или частичного периода при использовании метода сокращающегося баланса. |
|
ЧИСТВНДОХ |
Возвращает внутреннюю ставку доходности для графика денежных потоков, не обязательно носящих периодический характер. |
|
ЧИСТНЗ |
Возвращает чистую приведенную стоимость для денежных потоков, не обязательно носящих периодический характер. |
|
ДОХОД |
Возвращает доход по ценным бумагам, по которым производятся периодические выплаты процентов. |
|
ДОХОДСКИДКА |
Возвращает годовую доходность ценных бумаг, на которые сделана скидка (например, по казначейским векселям). |
|
ДОХОДПОГАШ |
Возвращает годовую доходность ценных бумаг, по которым процент выплачивается в срок погашения. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Вычислительные функции — это сердцевина Excel и то, что, по-сути, отличает программу от обычного калькулятора. Функций в программе довольно много — более 400. Часть из них дублируется, но тем не менее, возможности для экономических расчетов в программе огромные.
С помощью формул можно безошибочно рассчитать себестоимость товара, подготовить аналитические отчеты, свести планы. Решить как простые экономические задачи учета, так и составить полный баланс предприятия. Подборку инструментов Excel для бухгалтера мы уже делали. Настал черед рассмотреть основные функции Excel для экономиста, которые упростят работу с данными и большими таблицами.
Что такое функции Excel и где они находятся
Функции в Excel — это команды, которые помогают в считанные минуты откорректировать данные в ячейках, рассчитать значения по определенным критериям, изъять нужную информацию из огромного массива. Функции часто используют в формулах, чтобы их упростить и сделать более гибкими.
Как мы уже говорили, в программе функций много — около 10 категорий: есть математические, логические, текстовые. И специальные функции — финансовые, статистические и пр. Все функции лежат во вкладке «Формулы». Перейдя в нее, нужно нажать на кнопку «Вставить функцию» на панели инструментов, после чего запустится «Мастер функций».
Останется выбрать в «Категориях» нужную функцию для вычислений и заполнить данные по структуре в выпадающем окошке.
Если вы знаете, какая функция вам нужна, просто введите ее в строке формул, начиная со знака «=». Как только ввели, нажмите «Enter» для вычисления.
Запоминать, что делает каждая функция не нужно. В Excel есть удобные подсказки, зачем нужна та или иная формула, и как ее использовать.
Ниже рассмотрим основные и часто используемые формулы в Excel для экономистов: ЕСЛИ, СУММЕСЛИ, ВПР, СУММПРОИЗВ, СЧЁТ, СРЗНАЧ и МАКС/МИН.
Функция ЕСЛИ для сравнения данных
Самая популярная логическая функция, которая полезна экономистам, бухгалтерам. С ее помощью можно сравнить числовые и текстовые значения по определенным критериям. Например, рассчитать амортизацию, скидки, наценку или убрать ошибки из расчетов. Иногда используется встроенная функция ЕСЛИ в статистических, текстовых и математических формулах, что наделяет их способностью «принимать решения».
Функция ЕСЛИ помогает точно сравнить значения и получить результат, в зависимости от того, истинно сравнение или нет.
Так выглядит формула:
=ЕСЛИ(лог_выражение;[значение_если_истина];[значение_если_ложь])
- Лог_выражение — это то, что нужно проверить или сравнить (числовые или текстовые данные в ячейках)
- Значение_если_истина — это то, что появится в ячейке, если сравнение будет верным.
- Значение_если_ложь — то, что появится в ячейке при неверном сравнении.
Например, магазин торгует аксессуарами для мужчин и женщин. В текущем месяце на все женские товары скидка 20%. Отсортировать акционные позиции можно с помощью функции ЕСЛИ для текстовых значений.
Пропишем формулу в столбце «Скидка» так:
=ЕСЛИ(B2=»женский»;20%;0)
И применим ко всем строкам. В ячейках, где равенство выполняется, увидим товары по скидке.
Так применяется функция ЕСЛИ для текстовых значений с одним условием
Функции СУММЕСЛИ и СУММЕСЛИМН
Еще одна полезная функция СУММЕСЛИ, которая позволяет просуммировать несколько числовых данных по определенному критерию. Состоит формула из 2-х частей:
- СУММ — математическая функция сложения числовых значений. Записывается как =СУММ(ячейка/диапазон 1; ячейка/диапазон 2; …).
- и функция ЕСЛИ, которую рассмотрели выше.
Например, вам нужно просчитать общую сумму начисленной заработной платы менеджерам, а в отчете указаны данные по всем сотрудникам предприятия.
В формуле нужно прописать такие аргументы:
- Выделить диапазон всех должностей сотрудников — в нашем случае B2:B10.
- Прописываем критерий выбора через точку с запятой — “менеджер”.
- Диапазон суммирования — это заработные платы. Указываем C2:C10.
И получаем в один клик общую сумму заработной платы менеджеров:
С помощью СУММЕСЛИ можно просуммировать ячейки, которые соответствуют определенному критерию
Важно! Функция СУММЕСЛИ чувствительна к правильности и точности написания критериев. Малейшая опечатка может дать неправильный результат. Это также касается названий ячеек. Формула выдаст ошибку, если написать диапазон ячеек кириллицей, а не латиницей.
Более сложный вариант этой формулы — функция СУММЕСЛИМН. По-сути, это выборочное суммирование данных, отобранных по нескольким критериям. В отличие от СУММЕСЛИ, можно использовать до 127 критериев отбора данных. Например, с помощью этой формулы легко рассчитать суммарную прибыль от поставок разных товаров сразу в несколько стран.
В функции СУММЕСЛИМН можно работать с подстановочными символами, использовать операторы для вычислений типа «больше», «меньше» и «равно». Для удобства работы с функцией лучше применять абсолютные ссылки в Excel — они не меняются при копировании и позволяют автоматически пересчитать формулу, если данные в ячейке изменились.
Функции ВПР и ГПР — поиск данных в большом диапазоне
Экономистам часто приходится обрабатывать огромные таблицы, чтобы получить необходимые данные для анализа. Или сводить две таблицы в одну, что тоже не редкость. Функция ВПР или, как ее еще называют, вертикальный просмотр (англ. вариант VLOOKUP) позволяет быстро найти и извлечь нужные данные в столбцах. Либо перенести данные из одной таблицы в соответствующие ячейки другой.
Синтаксис самой простой функции ВПР выглядит так:
= ВПР(искомое_значение; таблица; номер_столбца; [интервальный просмотр]).
Например, вам нужно быстро извлечь наименование товара по номеру в списке. С помощью функции ВПР это сделать очень просто:
Функция ВПР позволяет быстро найти нужные данные и перенести их в выделенную ячейку.
В ячейке С1 мы указали номер товара. Потом выделили диапазон ячеек, где его искать (A1:B10) и написали номер столбца «2», в котором нужно взять данные. Нажали Enter и получили нужный товар в выделенной ячейке.
Есть менее популярная функция ГПР. Она работает также, как ВПР, но ищет данные в горизонтальных списках.
Важно! Чтобы увеличить область применения этой функции, можно задать данные с помощью подстановочных знаков.
Одна из задач этой функции — упростить подготовку исходных данных для аналитических и сводных таблиц. Как подготовить такую таблицу можете почитать бесплатно в книге Сводные таблицы в Excel.
Функция СУММПРОИЗВ в Excel
Четвертая функция нашего списка — СУММПРОИЗВ или суммирование произведений. Поможет быстро справиться с любой экономической задачей, где есть массивы. Включает в себя возможности предыдущих формул ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, а также позволяет провести расчеты в 255 массивах. Ее любят бухгалтеры и часто используют при расчетах заработной платы и других расходов.
Что в данном случае может быть произведениями? Как заданные диапазоны, так и целые массивы данных. Чтобы задать количество массивов, их нужно перечислить через точку с запятой, потом перемножить, а затем просуммировать. При этом, есть одно условие — массивы должны быть одинаковые по типу и длине.
Например, у вас есть месячный отчет по продажам в магазине, из которого нужно узнать, на какую сумму продали футболок размера «М».
Для этого используем функцию СУММПРОИЗВ и указываем 2 условия. Каждое из них берем в скобки, а между ними ставим «звездочку», которая в Excel читается как союз «и».
Запишем команду так: =СУММПРОИЗВ((A5:A11=A13)*(B5:B11=B13)*C5:C11), где
- первое условие A5:A11=A13— диапазон поиска и наименование нужного товара
- второе условие B5:B11=B13 — диапазон поиска и размер
- C5:C11 — массив, из которого берется итоговая сумма
С помощью функции СУММПРОИЗВ мы узнали за пару минут, что в магазине за месяц продали футболок М-размера на 100 у.е.
Чтобы узнать продажи по другому товару и размеру, нужно просто заменить данные в ячейках A13 и B13.
Данный пример слишком прост, по сравнению с тем, с какими объемами данных приходится работать экономистам. Но зная, что умеет данная формула, уже не так страшны таблицы в миллионы строк и сотни столбцов, а нужные данные находятся за считанные минуты.
Как применить МАКС, ВПР и ПОИСКПОЗ для решения задач
Функции МИН и МАКС помогают найти наименьшее или наибольшее значение данных. Функция ПОИСКПОЗ помогает найти номер указанного элемента в выделенном диапазоне. А формула ВПР, напомним, позволяет извлечь нужные данные из столбцов в указанные ячейки.
Рассмотрим комбинацию этих функций на примере решения задачи в Excel для экономистов. Составим комбинированную формулу, чтобы найти компанию с наибольшей суммой задолженности.
Для начала составим список должников, укажем сумму их задолженности и выставим дату окончания кредитного договора.
Для решения задачи, можно применить функции последовательно:
- Найти самый крупный долг поможет функция МАКС (=МАКС(B2:B10)), где B2:B10 — столбец с данными по задолженности.
- Чтобы найти номер компании-должника в списке, нужно в таблицу добавить столбец с нумерацией. Так как функция ПОИСКПОЗ ищет данные только в крайнем левом столбце выделенного диапазона.
Составляем функцию по формуле:
ПОИСКПОЗ(искомое_значение;просматриваемый_массив;[тип_сопоставления])
В нашем случае это будет =ПОИСКПОЗ(14569;C2:C10;0), где искомое — максимальная сумма долга. Тип сопоставления будет “0”, потому что к столбцу с долгами мы не применяли сортировку.
- Чтобы узнать название компании-должника, применим знакомую функцию ВПР.
Выглядеть она будет так =ВПР(D14;A2:B10;2), где D4 — искомое, A2:B10 — таблица или выделенный диапазон с названиями компаний и нумерацией, а “2” — номер столбца с должниками.
Этот же результат можно было получить, собрав одну формулу из 3-х:
=ВПР (ПОИСКПОЗ (МАКС (C2:C10); C2:C10;0); A2:B10;2).
В экономических расчетах функция ВПР помогает быстро извлечь нужное значение из огромного диапазона данных. Причем значение можно найти по разным критериям отбора. Например, цену товара можно извлечь по идентификатору, налоговую ставку — по уровню дохода и пр.
Кроме вышеупомянутых функций, экономисты часто используют формулу СРЗНАЧ, например, для расчета средней заработной платы. Функцию СЧЁТ, когда нужно рассчитать количество отгрузок в разрезе клиентов или стоимости товара за определенный период. Кстати, на примере отгрузок, формула МИН/МАКС поможет отследить диапазон, в котором изменялась стоимость товара.
Существует еще сотня математических и финансовых функций в Ехсеl, с помощью которых можно решить экономические задачи разной сложности. Например, обрабатывать заказы, планировать загрузку производства, рассчитывать налоги, вести кадровый учет и управлять сбытом. Но для решения подобных задач, подсказок в Excel будет уже недостаточно. Тут необходимо глубже погружаться в программу и учиться работать с разными ее инструментами: от функций и сводных таблиц, до диаграмм и макросов.
Цветные диаграммы лучше покажут вашу работу с данными, чем сетка Excel!
Освойте программу Power BI, создавайте визуальные отчеты в пару кликов после курса «ACPM: Бизнес-анализ данных в финансах»!
Насколько уверенно вы владеете Excel?
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Мы подумали, что блок статей о формулах Excel просто не сможет обойтись без обозревания таких удобных и востребованных функций, как финансовые. Поэтому представляем вашему вниманию небольшой экскурс в мир «денежных» функций.
По «старой» традиции начнем с того, как найти финансовые формулы в программе. Сделать это очень просто: на главной панели найти кнопку «Формулы», нажать на нее и выбрать в появившемся списке название раздела «Финансовые».
Дальше выпадет перечень формул, которые вы можете использовать:

В данном разделе больше 50 функций, которые могут помочь специалистам упростить расчеты и сэкономить время на составление формул.
Разумеется, рассказать о всех возможностях в рамках этой статьи мы не успеем, но рассмотрим некоторые их них. Если вы хотите узнать о функционале математических функций в Excel, то скачивайте бесплатный гайд «Математические функции Excel».
1. Функция ДОХОД()
Очень популярная формула у финансистов. Она позволяет высчитать доход от ценных бумаг, по которым происходят выплаты процентов за определенный период.
Аргументов у функции много, поэтому медленно и по порядку со всеми разберемся!
Дата_согл – дата покупки ценных бумаг.
Дата_вступл_в_силу – дата, показывающая истечение срока действия бумаг.
Ставка – купонная ставка ценных бумаг за год.
Цена – цена бумаг на 100 руб. номинальной стоимости.
Погашение – выкупная стоимость ценных бумаг на 100 руб. номинальной стоимости.
Частота – цифра, показывающая количество выплат в год. Ежегодные выплаты – 1, полугодовые – 2, ежеквартальные – 4.
Помимо перечисленных обязательных аргументов есть один необязательный:
Базис – число, характеризующее способ вычисления дня. По умолчанию ставится 0.
Примечание. Обязательные аргументы выделены жирным шрифтом, а необязательные – обычным.

Замечание. Не рекомендуется вводить дату как текстовую запись. Лучше использовать функцию ДАТА во избежание ошибок и проблем с работой функции.
Например, число 21 сентября 2013 г. лучше записать так: ДАТА(2013,09,21).
2. Функция ПЛТ()
Функция ПЛТ() помогает высчитать сумму, которую нужно платить периодически для погашения ссуды с учетом процентных переплат за один расчетный период. Предполагается, что объем платежей и ставка не меняются.
У функции 3 обязательных аргумента и 2 – необязательных. Разберемся со всеми по порядку.
Ставка – процент, на который возрастает сумма платежа за один период.
Кпер – количество выплат или периодов.
Пс – общая сумма, которую нужно выплатить.
БС – показывает, сколько останется выплатить после последней выплаты. По умолчанию подразумевается 0 (то есть после последней выплаты стоимость ссуды составит 0 руб.).
Тип – аргумент, который принимает значения: 0 – когда платежи совершаются в конце периода, 1 – если в начале.
Рассмотрим пример.
Нужно рассчитать ежемесячный платеж по кредиту в размере 500 000 руб., взятого на 4 года под 6% годовых:

Так как в условиях задачи была дана процентная ставка за год, то, чтобы рассчитать ставку за один месяц, мы разделили 6% на 12 месяцев.
Так как выплаты производятся каждый месяц, то количество периодов рассчитываем так: 4 * 12 = 48:

Обратим внимание на то, то результат получился отрицательным. Знак «-» показывает, что эту сумму нужно отдать (вычесть из задолженности).
3. Формула ПС()
Формулу ПС() необходима для нахождения приведенной стоимости (то есть общей суммы, которую нужно выплатить на текущий момент).
Её можно назвать обратной к предыдущему оператору ПЛТ(). У неё точно такие же аргументы, только вместо «Пс» – «Плт» – сумма периодической выплаты.
Функция записывается следующим образом:
ПС(Ставка; Кпер; Плт; Бс; Тип)
Рассмотрим пример:


Мы получили сумму, которую в итоге заплатил бы человек, взявший кредит под 6% годовых на 4 года с ежемесячными выплатами в размере 12 000 руб.
4. Формула ОСПЛТ()
Данная формула в качестве результата выводит основную часть выплат по кредиту за заданный период (то есть ту часть платежа, которая уходит на оплату именно ссуды, а не процентов).
При этом учитывается, что параметры Ставка и размер выплат не меняются.
У функции ОСПЛТ() такие же аргументы, как и предыдущая формула: Ставка, Кпер, Пс, БС, Тип.
Еще добавляется Период (обязательный аргумент) – число от 1 до Кпер.
Посмотрим результат функции на предыдущем примере. Нужно рассчитать, сколько денег от первого платежа идет на погашение ссуды, не учитывая оплату процентов:


Мы видим, что основная часть первого платежа равна 9 242,51 руб – это примерно 79% от ежемесячной выплаты.
Если посмотреть результат формулы за 48-ой период, то получим уже 11 684,1 – это 99,5%. Заметная разница говорит о том, что процентные начисления в большей степени выплачиваются в первые расчетные периоды.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
5. Формулы ПРПЛТ(), ОБЩПЛАТ()
Функция очень похожа на ОСПЛТ() с небольшой оговоркой: она помогает высчитать размер выплат по процентам за выбранный период, предполагая неизменяемыми размер платежей и ставку.
У функция ПРПЛТ() точно такие же аргументы, как и у ОСПЛТ(), и выглядит в строке ввода формул так:
ПРПЛТ(Ставка; Период; Кпер; Пс; БС; Тип)
Применим формулу к нашему примеру:


Получили, что за первый период сумма выплат по процентам составит 2 500 руб., а в 48 месяце – всего 58,4 руб.
То есть данная формула еще раз подтверждает факт, что большая часть выплат по процентам осуществляется в начальные периоды платежей.
Замечание. Чтобы рассчитать, какая сумма из ваших платежей ушла на оплату процентов между любыми периодами, нужно использовать формулу:
ОБЩПЛАТ(Ставка;Кпер; Пс; Нач_пер;Кон_пер)
Ниже представлен пример применения функции ОБЩПЛАТ(), где в качестве Нач_пер берем первый период и Кон_пер – второй.
Выплаты происходят в конце месяца:

С помощью этих формул даже рядовой пользователь сможет рассчитать самые выгодные условия кредитования!
6. Формула СТАВКА()
Мы уже узнали, как считать объем ежемесячных выплат, процентные переплаты, число будущих выплат и так далее. Помимо этих действий в Excel можно вычислить ставку по кредиту, используя одноименную функцию СТАВКА().
В качестве аргументов выступают хорошо известные нам критерии: Кпер, Плт, Пс, Бс, Тип.
Два последних аргумента – необязательные:


7. Формула БС()
Теперь поговорим о функции БС() – высчитывает стоимость инвестиций после определенного количества периодов при условии неизменной ставки.
Формула записывается следующим образом:
БС(Ставка; Кпер; Плт; Пс; Тип).
Здесь аргумент Пс является необязательным.
Рассмотрим пример:
Пусть 12% – годовая ставка, количество платежей – 12, каждая выплата – 1 000 руб. (знаком минус покажем, что эти деньги нужно отдавать).
Посчитаем стоимость инвестиций при таких условиях:


Отметим, что «сумму выплат» мы специально сделали отрицательной, чтобы показать, что эти деньги вычитаются, и что сумма инвестиций не может быть отрицательной.
Заключение
Мы с вами проделали большую работу и познакомились с базовыми финансовыми формулами, которые могут применять не только специалисты в узкой области, но и простые пользователи Excel.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
12 необходимых для работы с данными математических функций в Excel
Содержание статьи Microsoft Excel– одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп…
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль
На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.
В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.
Для удобства восприятия материала сгруппируем эти функции в три блока:
1. Функционал расчетных формул в Excel.
2. Функционал Excel для обработки табличных данных.
3. Инструменты Excel для моделирования и анализа экономических данных.
ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL
Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.
Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.
Решение экономической задачи с помощью формулы ЕСЛИ
Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.
С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.
Запись расчетной формулы в заданной ячейке в общем виде выглядит так:
=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),
где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);
значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;
значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.
Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.
Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.
Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).
Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).
В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.
Решение экономической задачи с помощью формулы СУММЕСЛИ
Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.
Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.
Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.
Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).
Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.
Результат решения задачи — в табл. 2.
Решение экономической задачи с помощью формул ВПР и ГПР
Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:
- ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
- ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.
Формулы прописывают в общем виде следующим образом:
=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);
=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).
Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.
Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:
- продажи в натуральном измерении;
- продажи в суммовом измерении;
- средняя цена реализации единицы продукции в рублях.
Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.
Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.
Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).
Пояснения к формуле:
В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;
Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;
3 — номер столбца, по которому нужно выбрать данные;
ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.
Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.
Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).
Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.
В результате выполненных действий появился искомый отчет о продажах (табл. 3).
На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.
Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.
Решение экономической задачи с помощью формулы СУММПРОИЗВ
Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).
Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.
Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).
Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).
Выполнив указанные действия, получим искомое решение задачи в табл. 4.
Решение экономической задачи с помощью формулы СЧЕТЕСЛИ
Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.
Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.
Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.
Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:
- выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
- в меню редактора выбираем путь: Данные → Проверка данных;
- в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
- в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
- в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».
Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).
ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ
Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.
Решение экономической задачи с применением функции сортировки данных
Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.
Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.
Сортировку данных выполнить просто:
- выделяем курсором столбцы таблицы;
- заходим в меню редактора: Данные → Сортировка;
- выбираем нужные параметры сортировки и получаем новый вид табличных данных.
Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.
Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).
Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.
Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.
Решение экономической задачи с использованием функционала Автофильтр
Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.
В табличном редакторе Excel есть два вида фильтров:
- автофильтр — используют для фильтрации данных по простым критериям;
- расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.
Автофильтр работает следующим образом:
- выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
- заходим в меню редактора: Данные → Фильтр → Автофильтр;
- выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.
Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.
Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.
Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».
Чтобы организовать «Диапазон условий», следует выполнить следующие действия:
- в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
- под каждым из заголовков задаем условие отбора данных.
Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».
Порядок работы с функционалом консолидации данных
Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.
Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:
- макеты всех консолидируемых таблиц одинаковые;
- названия столбцов во всех консолидируемых таблицах идентичные;
- в консолидируемых таблицах нет пустых столбцов и строк.
Работа с функционалом консолидации включает ряд последовательных действий:
1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;
2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;
3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;
4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);
5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);
6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;
7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.
Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета
Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.
Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.
В появившемся диалоговом окне формируем параметры будущей таблицы:
- указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
- указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
- в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.
Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.
ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ
Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.
Решение экономической задачи с помощью надстройки «Поиск решения»
Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.
Такими экономическими задачами могут быть:
- расчет оптимального объема выпуска продукции при ограниченности сырья;
- минимизация транспортных расходов на доставку продукции покупателям;
- решение по оптимизации фонда оплаты труда.
Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:
- в меню Excel выбрать путь: Файл → Параметры → Надстройки;
- в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
- вернуться в меню Excel и выбрать: Данные → Поиск решения.
Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:
1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).
2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).
3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).
Исходные данные, размещенные таким образом, показаны в табл. 8.1.
Далее приступаем к подготовке поиска решения.
1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.
2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).
3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):
- оптимизировать целевую функцию — ячейка J4;
- цель оптимизации — до минимума;
- изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
- ограничения поиска решения:
– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);
– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);
– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);
– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).
Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).
При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.
Пакет расширенного анализа данных
Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.
Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).
Специализированные надстройки для финансово-экономической работы
В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.
Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.
Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.
Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:
- финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
- работа с формулами;
- работа с текстом;
- работа с книгами и листами Excel;
- работа с ячейками Excel;
- поиск дубликатов и сравнение диапазонов данных;
- вставка дат и примечаний к диапазонам данных;
- загрузка курсов валют;
- создание выпадающих списков.
Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:
- кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
- депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
- вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
- набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.
Статья опубликована в журнале «Планово-экономический отдел» № 10, 2020.

В учебном пособии приведены материалы к заданиям для самостоятельного выполнения контрольных, лабораторных, практических работ, примеры и методика их решения. Предназначены для студентов, обучающихся по направлениям: 38.03.02 (080200.62) «Менеджмент» (профили: «Производственный менеджмент», «Финансовый менеджмент»), 38.03.01 (080100.62) «Экономика» (профили: «Финансы и кредит», «Экономика предприятия и организации») всех форм обучения, слушателей системы послевузовского образования, преподавателей. Рекомендовано УМО РАЕ по классическому университетскому и техническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям подготовки: 38.03.02 (080200.62) – «Менеджмент», 38.03.01 (080100.62) – «Экономика».
Оглавление
1. Модели и методы финансово — экономических расчетов
1.1. Общие положения
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Их используют вместо финансовых уравнений. Они работают быстрее, чем введенные формулы, и с меньшей вероятностью ошибок.
Количественный финансовый анализ предполагает применение унифицированных моделей и методов расчета финансовых показателей.
В этом контексте, Microsoft Excel предоставляет широкий спектр функций для финансово-экономических расчетов: от нахождения выплат по процентам, реализации задач дисконтирования, посторения моделей расчета амортизации оборудования, анализа показателей ценных бумаг, регулярных выплат по займу до оценки эффективности капитальных вложений и инвестиций, моделирования финансово-экономических аспектов деятельности предприятия, фирмы и т.п.
Рис. 1. Обобщенная классификация финансовых функций
Условно методы финансовой математики делятся на две категории: базовые и прикладные. К базовым методам и моделям относятся:
— простые и сложные проценты. Простые проценты используются, как правило, в краткосрочных финансово-экономических операциях (продолжительностью до года). Базой для исчисления процентов за каждый период в этом случае служит исходная сумма сделки. Сложные проценты применяются в среднесрочных и долгосрочных финансовых операциях (более одного года), но могут применяться и в краткосрочных, если это вызвано объективной необходимостью (риски, высокий уровень инфляции и т.п.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов;
— расчет последовательностей (потоков) платежей. При проведении большинства финансовых операций возникают чередующиеся в течение ограниченного или неограниченного промежутка времени поступления и выплаты денежных средств. Поток состоит из отдельных элементов потока — платежей. Поступление денежных средств считают положительными платежами, а выплаты — отрицательными. Денежные потоки делятся:
— по распределению во времени: регулярные (периодические) и нерегулярные;
— по величине элементов: на постоянные и переменные.
Наращенная сумма может представлять собой общую сумму накопленной задолженности к концу срока, итоговый объем инвестиций, накопленный денежный резерв и т.д.
Современная стоимость характеризует приведенные к началу осуществления проекта затраты, капитализированный доход или чистую приведенную прибыль от реализации проекта и т.д.
К прикладным методам финансовых расчетов относятся:
— планирование и оценка эффективности финансово-кредитных операций;
— расчет страховых аннуитетов;
— планирование погашения долгосрочной задолженности;
— планирование погашения ипотечных ссуд и потребительских кредитов;
— финансовые расчеты по ценным бумагам;
— лизинговые, факторинговые и форфейтинговые банковские операции;
— планирование и анализ инвестиционных проектов и др.
Особенностью всех финансовых расчетов является временная ценность денег, то есть принцип неравноценности денег, относящихся к разным моментам времени. Деньги — это мера стоимости товаров и услуг. Предполагается, что полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем, то есть будущие поступления менее ценны, чем современные. Неравноценность одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем.
Основными понятиями финансовых методов расчета являются:
— процент — абсолютная величина дохода от предоставления денег в долг в любой его форме;
— процентная ставка — относительная величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби, которая используется в качестве измерителя уровня (нормы) доходности задачу — нахождение величины на заданный момент времени по ее известному или предполагаемому значению в будущем.
Ввиду ограниченного объема данного учебного пособия, теоретические вопросы описания методов, расчетов, способов, определений, а также и другие характеристики рекомендуется изучать в специальной литературе [7].
1.2. Специфика использования финансовых функций Excel
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Методика изучения и использования финансовых функций Excel требует соблюдения определенной технологии.
1. На рабочем листе в отдельных ячейках осуществляется подготовказначений основных аргументов функции.
2. Для расчета результата финансовой функции Excel курсор устанавливается в новую ячейку для ввода формулы, использующей встроенную финансовую функцию; если финансовая функция вызывается в продолжение ввода другой формулы, данный пункт опускается.
3. Осуществляется добавление финансовой функции на рабочий листс помощью команды Формулы, из библиотеки функций активизацией опции Финансовые функции или одновременным нажатием клавиш Shift-F3, а также нажатием одноименной кнопки fx — Вставить функцию на панели инструментов Стандартная.
4. Выполняется выбор категории Финансовые (рис. 2). В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
Рис. 2. Экран вызова опции Вставка функции
В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
5. Выполняется выбор в списке требуемой финансовой функции, в результате выбора появляется диалоговое окно для ввода аргументов (рис. 2). Для каждой финансовой функции существует регламентированный по составу и формату значений перечень аргументов.
6. В поля ввода диалогового окна можно вводить как ссылки на адреса ячеек, содержащих собственно значения аргументов, так и сами значения аргументов.
7. Если аргумент является результатом расчета другой встроеннойфункции Excel, возможно организовать вычисление вложенной встроенной функции путем вызова опции Вставка функции одноименной кнопкой, расположенной перед полем ввода аргумента.
8. Возможна работа с экраном справки, поясняющей назначение иправила задания аргументов функции; вызов справки осуществляется путем нажатия кнопки Справка по этой функции.
9. Для отказа от работы со встроенной функцией нажимается кнопка Отмена.
10. Завершение ввода аргументов и запуск расчета значения встроенной функции выполняется нажатием кнопки ОК.
При необходимости корректировки значений аргументов функции (изменения ссылок, постоянных значений и т.п.) необходимо установить курсор в ячейку, содержащую формулу, и вызвать кнопку fx — Вставить функцию. При этом появляется окно для редактирования (рис. 3).
Рис.3. Диалоговое окно ввода аргументов функции
Возможен вариант непосредственного ввода формулы, содержащей имена и параметры встроенных финансовых функций.
Формула начинается со знака =. Далее следует имя функции, а в круглых скобках указываются её аргументы в последовательности, соответствующей синтаксису функции. В качестве разделителя аргументов используется выбранный при настройке Windows разделитель, обычно это точка с запятой или запятая.
Безусловно, функцию можно ввести, набрав ее прямо в ячейке. Однако Microsoft Excel предоставляет на стандартной панели инструментов кнопку fx — Вставить функцию (см. рис. 4).
Рис. 4. Стандартная панель инструментов (кнопка Вставитьфункцию)
Специфика задания значений аргументов финансовых функций заключается в следующем:
— все аргументы, означающие расходы денежных средств, представляются отрицательными числами (например, ежегодные платежи), а аргументы, означающие поступления, представляются положительными числами (например, дивиденды);
— все даты как аргументы функции имеют числовой формат представления, например, дата 1 января 1995 года представлена числом 34700. Если значение аргумента типа дата берется из ячейки, то дата в ячейке может быть записана в обычном виде;
— для аргументов типа логический возможен непосредственный ввод констант типа ИСТИНА или ЛОЖЬ, либо использование встроенных функций аналогичного названия категории Логические
Конец ознакомительного фрагмента.
Смотрите также
Лабораторнаяработа№5 Финансовыефункцииианализ
1. Функции для анализа инвестиций
1.1. Функция ПЗ(ПС)
Функция ПЗ рассчитывает текущую стоимость ряда равных по величине периодических платежей или единовременнойвыплаты. Этафункцияимеетследующийсинтаксис:
=ПЗ(ставка; число периодов; выплата; будущее значение; тип) гдеставка— процентнаяилиучетнаяставка; число периодов — срок вложения; выплата — постоянные периодические вы платы; будущее значение — будущий объем вложениявконцесрокаили0, еслиопущен; тип— число, котороеобозначает, когдадолженпроизводитьсяплатеж: 0 — в концепериода; 1 — вначалепериода.
Предположим, что нам предлагается некой организацией АО ЮЮЮ получать по 1000 рублей ежегодно в течение 5 лет, но при условии, что мы доверим этой замечательной организации 4000 рублей сейчас под 5% годовых. Функциюможнорасписатьтак:
=ПЗ(5%;5;1000)
Вэтой функции не заполнены два аргумента: будущее значение и тип. Будущее значение считается нулем, а тип по умолчанию равен 0, то есть выплаты производятся в конце периода. Возникает вопрос, а как программа узнает, что из пяти аргументов мы взяли только три первых? Да потому, что программа читает аргументы в том порядке, в каком они следуют. Следовательно, в данном случае считаны три первых аргумента, а два последних аргумента не указаны. Эту же формулуможно расписать и по-другому:
=ПЗ(5%;5;1000;;)
Здесьмыпослетретьегоаргументапоставилиточкусзапятой, какэтоипредусмотрено синтаксисом, а четвертый аргумент объявили пустым явнымобразом— поставилитакжеточкусзапятой. Послепятогоаргументаточкасзапятой не предусмотрена, и поэтому аргумент также объявлен пустым (в данном случае действует значение аргумента по умолчанию).
Врезультате расчета мы получим ответ -4 329,48 р. Это означает, что мы можем вложить сумму 4 329,48 р. сейчас, чтобыполучатьпо1000 р. втечение5 лет.
Если АО ЮЮЮ предложит нам другое предложение, например не брать по 1000 р. каждый год, а взять всю суммучерез5 лет. Составимформулурасчета:
=ПЗ(5%;5;;5000)
Вданном случае аргумент выплата не производится, но зато нужен аргумент будущее значение. Поэтому третий аргументзаданпустымявнымобразом, так как если не поставить точку с запятой, то программа будет считать опять с учетом выплаты, а не будущего значения. Ответ будет -3 917,63 р., то есть мы получим даже меньше, чем вкладывали. Поэтомуданноепредложение АО ЮЮЮ мыотклоним.
Рассмотрим еще один вопрос, который будет встречаться практически во всех функциях. При задании ставки мы всевремя задаем число впроцентахипоэтомууказываем символ процента(%). Нопри желанииможноуказывать ставку
ив числовом формате. Для этого нужно ставку в процентах разделить на 100, а символ процента опустить. Итоги, рассчитанные обоимиспособами, неотличаютсядруготдруга. Например, последнююформулуможнопереписатьтак:
=ПЗ(0,05;5;;5000)
1.2. Функция НПЗ (ЧПС)
Возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных и нормы амортизации. Чистый текущий объем вклада — это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения). Данная функция имеет следующий синтаксис:
=НПЗ(ставка; значение1; значение2; …) Ставка— этоучетнаяставказаодинпериод.
Значение1, значение2,… — этоот1 до29 аргументов, представляющихрасходыидоходы.
Значение1, значение2, … должны быть равномерно распределены по времени и осуществляться в конце каждого периода.
НПЗ использует порядок аргументов значение1, значение2, … для определенияпорядкапоступленийиплатежей. Поэтомунеобходимоубедиться в том, что платежи и поступления введены в правильном порядке.
Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми

представлениями чисел, учитываются. Аргументы, которые являются значениями различных ошибок или текстами или которые не могут быть преобразованы в числа, игнорируются.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, тексты или значения ошибок в массиве или ссылке игнорируются.
Считается, что инвестиция, значение которой вычисляет функция НПЗ, начинается за один период до даты денежного взноса значение 1 и заканчивается с последним денежным взносом в списке. Вычисления функции НПЗ базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции НПЗ, но не включать в список аргументов. Для получения более подробной информации смотрите примеры ниже.
Если n—это количество денежных взносов в списке значений, то формула для функции НПЗ имеет вид:
НПЗ аналогична функции ПЗ (текущее значение). Основное различие между функциями ПЗ и НПЗ заключается в том, что ПЗ допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции НПЗ денежные взносы в функции ПЗ должны быть постоянны на весь период инвестиции. Для получения информации о функциях платежей по ссуде и финансовых функциях смотрите ПЗ.
НПЗ также связана с функцией ВНДОХ (внутренняя скорость оборота). ВНДОХ — это скорость оборота, для которойНПЗравняетсянулю: =НПЗ(ВНДОХ(…); …)=0.
Предположим, что нам предоставляется возможность получать в течение четырех лет каждый год доход по 100 000 рублей, но при условии немедленного разового платежа в размере 300 000 рублей. Ставка равна 10%. Функция будетиметьвид:
=НПЗ( 10%; 100000; 100000; 100000; 100000;)-300000
В ответ получим 16 986,54 р. Это означает, что это предложение выгодно, так как даст нам небольшую прибыль. Этаприбыльбудетдотехпор, покаставканедостигнетвеличины12,59%.
1.3. Функция БЗ
Функция БЗ возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентнойставки. Синтаксис этойфункцииследующий:
=БЗ(ставка; число периодов; выплата; текущее значение; тип) гдеставка— процентнаяилиучетнаяставка; число периодов — срок вложения; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — вначалепериода.
Составим пример. Предположим, что человек, поступая на работу после окончания института, открыл счет в банке, предполагая вносить каждый год по 3000 рублей под 10% годовых. Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды), представляются положительными числами. Рассчитаем, сколько денег будет на счете через 38 лет:
=БЗ(10%;38;-3000;;1)
Нам приходится учитывать все пять аргументов, так как платеж необходимо производить в начале года. В ответе будет 1 201 343,33 р.
1.4. ФункцияППЛАТ(ПЛТ)
Эта функция возвращает величину выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки. Синтаксис этой функции следующий:
=ППЛАТ(ставка; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; число периодов — срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды),
представляются положительными числами.
Для примера рассмотрим следующую ситуацию: человек берет в банке ссуду на 15 лет в размере 1 000 000 рублей под 12 процентов годовых. Рассчитаем, какую сумму человек должен выплачивать ежемесячно:
=ППЛАТ(1%;180;1000000)
Рассмотрим записанное нами значение аргументов: в месяц человек должен выплачивать 1/12 часть ставки, то есть 12%/12 месяцев;. число платежных месяцев равно 15 лет* 12 месяцев в году. Ответ получится такой: человек должен ежемесячно платить -12 001,68 р.. Знак минус (-) означает, что человек должен платить, а не получать.
1.5.Функция ПЛПРОЦ (ПРПЛТ)
Данная функция возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставке. Синтаксис этой функции следующий:
=ПЛПРОЦ(ставка; период; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; период — номер периодической выплаты; число периодов
— срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды), представляются положительными числами.
Для примера рассмотрим следующую ситуацию: человек берет в банке ссуду на 15 лет в размере 1 000 000 рублей под 12 процентов годовых. В месяц человек должен выплачивать 1/12 часть ставки, то есть 12%/1 2 меся цев; число платежных месяцев равно 15 лет * 12 месяцев в году. Вопрос: какую сумму человек будет платить по процентам в первый и последний платежные месяцы?
=ПЛПРОЦ1 %; 1; 180; 1000000) =ПЛПРОЦ(1%;180;180; 1000000)
Ответ: в первый платежный месяц человек будет платить 10 000 рублей, а в последний — всего 118,83 рубля.
1.6. Функция ОСНПЛАТ (ОСПЛТ)
Функция ОСНПЛАТ возвращает величину выплаты на данный период на основе периодических постоянных платежей и постоянной процентной ставки. Синтаксис этой функции следующий:
=ОСНПЛАТ(ставка; период; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; период — номер периодической выплаты; число периодов
— срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Составим пример на основе данных, заданных в двух предыдущих разделах. Рассчитаем основные платежи в первый и последний месяцы:
=ОСНПЛАТ(1%;1;180; 1000000) =ОСНПЛАТ(1 %; 180; 180; 1000000)
Ответ: в первый месяц основой платеж будет 2 001,68 рубля, а в последний11 882,85 рубля.
1.7. Функция КПЕР
Функция КПЕР возвращает общее количество периодов выплаты для данного вклада на основе периодических постоянных выплат и постоянной процентной ставки. Синтаксис этой функции следующий:
=КПЕР(ставка; выплата; текущее значение; будущее значение; тип) где ставка — процентная или учетная ставка; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Воспользуемся условиями предыдущих разделов — определим число периодов, которое необходимо для погашения ссуды:
=КПЕР( 1 %;-12000; 1000000)
Ответ: -180,07 месяца. Эта неточность в 0,07 месяца произошла потому, что в предыдущих разделах мы определили, что в месяц нужно платить -12 001,68 рубля. Если нашу формулу немного подправить и сделать так:
=КПЕР(1%;-12001,68; 1000000)
то ответ будет 180 месяцев. Таким образом, мы определили, что путем многократной проверки мы выходим на одни и те же числа при использовании различных функций этой группы.
Если аргумент выплата мал для погашения ссуды при заданной процентной ставке, то функция возвращает сообщение об ошибке. Это означает, что данный кредит не будет выплачен никогда и необходимо или увеличить выплаты, или уменьшить процент ставки.
2. Функции для вычисления скорости оборота 2.1. Функция НОРМА (СТАВКА)
Функция НОРМА возвращает процентную ставку за один период при выплате ренты. Функция НОРМА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция НОРМА возвращает значение ошибки #ЧИСЛО! Синтаксис этой функции следующий:
=НОРМА( число периодов; выплата; текущее значение; будущее значение; тип; прогноз)
где число периодов — срок вложения; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода; прогноз — предполагаемая величина нормы. Если значение прогноза опущено, то оно полагается равным по умолчанию 10%. Если функция НОРМА не сходится, следует попытаться использовать различные значения прогноза. Обычнофункция НОРМА сходится, если прогноз имеет значение между 0
и 1.
Предположим, что мы должны получить пять ежегодных выплат по 15 000 рублейприсуммевложения50000 рублей. Формулабудетиметьследующийвид:
=НОРМА(5;15000;-50000)
Функциявозвращает скоростьоборота, котораяравна 15%.
2.2. Функция ВНДОХ (ВСД)
Функция ВНДОХ возвращает внутреннюю скорость оборота для ряда последовательных операций с наличными, представленными числовыми значениями. Объемы операций не обязаны быть регулярными, как в случае ренты. Внутренняя скорость оборота — это процентная ставка дохода, полученного от инвестиции, состоящая из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени. Синтаксисэтойфункцииследующий:
=ВНДОХ(значения; прогноз)
где значения должны включать по крайней мере одно положительное значение и одно отрицательное значение для того, чтобы можно было вычислить внутреннюю скорость оборота. ВНДОХ использует порядок значений для интерпретации порядка денежных выплат или поступлений. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются. Прогноз—это величина, о которой предполагается, что она близка к результату ВНДОХ. Microsoft Excel использует метод итераций для вычисления ВНДОХ. Начиная со значения прогноз, функция ВНДОХ выполняет циклические вычисления, пока не получит результат с точностью 0,00001 процента. Если функция ВНДОХ не может получить результат после 20 попыток, то возвращается значение ошибки #ЧИСЛО! В большинстве случаев нет необходимости задавать прогноз для вычислений с помощью функции ВНДОХ. Если прогноз опущен, то он полагается равным 0,1 (10 процентов). Если ВНДОХ выдает значение ошибки #ЧИСЛО! или если результат далек от ожидаемого, необходимо выполнить вычисленияещеразсдругимзначением аргумента прогноз.
Допустим, ваши вложения в проект составляют 50 000 рублей. Предполагается, что доходы в течение трех лет составят 22 000, 24 000, 26 000 рублей. Запишите эти значения в ячейки с Al no A4. Следующая формула вычисляет внутреннюю скоростьоборота инвестиции после трех:
=ВНДОХ(А1:А4)
Ответ— внутренняяскоростьоборотасоставляет20%.
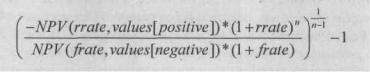
2.3. ФункцияМВСД
ФункцияМВСДвозвращаетмодифицированнуювнутреннююскоростьоборота средств для ряда последовательных периодических операций с наличными. Функция МВСД учитывает как стоимость инвестиции, так и доход, получаемый отреинвестирования. Синтаксисэтойфункцииследующий:
=МВСД(значения; финансовая_ставка; ставка_реинвестирования) Значения — это массив или ссылка на ячейки, содержащие числовые величины. Эти числа представляют ряд денежных выплат (отрицательные значения) и поступлений (положительные значения), происходящие в регулярные периоды времени. Аргумент значения должен содержать по крайней мере одно положительное и одно отрицательное значение для того, чтобы можно было вычислить модифицированную внутреннюю скорость оборота. В противном случае функция МВСД возвращает значение ошибки #ДЕЛ/0! Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются; финансовая_ставка — это норма прибыли, выплачиваемой за деньги, находящиеся в наличном обороте; ставка_реинвестирования — это норма прибыли, получаемой за деньги, находящиеся в наличном обороте при реинвестировании.
МВСД использует порядок расположения чисел в аргументе значения для определения порядка выплат и поступлений. Убедитесь, что значения выплат и поступлений введены в нужной последовательности и с правильными знаками (положительные значения ДЛЯ получаемых денег и отрицательные значения для выплачиваемых). Если n — это количество чисел в аргументе значения, f — это финансовая_ставка, а r — это ставка_реинвестирования, то формула длявычисления функции МВСД будет иметь вид:
Продолжим пример, условия которого заданы в предыдущем разделе. Модифицированная внутренняя скорость оборотазатригодавычисляетсяследующимобразом:
=МВСД(А1:А4;12%;10%)
Ответ: 16%.
3. Функции для вычисления амортизации
3.1. ФункцияAMP (АПЛ)
Функция AMP возвращает величину непосредственной амортизации имущества за один период. Синтаксис этой функции следующий:
=АМР(стоимость; остаток; время_эксплуатации)
где стоимость — первоначальная стоимость имущества; остаток — остаточная стоимость после полной амортизации имущества; время_эксплуатации — количество периодов, за которые имущество амортизируется.
Возьмем следующий пример: предположим, что необходимо рассчитать амортизацию станка с начальной стоимостью 25 000 рублей, время эксплуатации которого 10лет, с остаточной стоимостью 700 рублей. Тогда формула будетследующей:
=АМР(25000;700;10)
Врезультатерасчетабудетопределенаамортизациявразмере2430 рублей.
3.2. Функция ДОБ(ФУО) иДЦОБ (ПУО)
Функция ДОБ возвращает амортизацию имущества на заданный период, используя метод постоянного учета амортизации. Синтаксисэтойфункцииследующий:
=ДОБ(нач_стоимость; остстоимость; времяэксплуатации; период; месяц)
где нач_стоимость — это начальная стоимость имущества; ост_стоимость — это стоимость в конце периода амортизации (иногданазывается остаточнойстоимостью имущества); время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это период, для которого требуется вычислить амортизацию; период должен быть измерен в тех же единицах, что и время_эксплуатации; месяц — это количество месяцев в первом году. Если аргумент месяц опущен, то предполагается, чтоонравен12.
Методпостоянного учетаамортизации вычисляет амортизацию используяфиксированнуюпроцентнуюставку. Функция ДДОБ очень похожа на функцию ДОБ и возвращает величину амортизации имущества для указанного периода, используя метод двукратного учета амортизации или иной явно указанный метод. Синтаксис этой функции
следующий:
=ДДОБ(нач_стоимость; ост_стоимость; время_эксплуатации; период; коэффициент)
где нач_стоимость — это начальная стоимость имущества; ост_стоимость — это остаточная стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества); время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации; коэффициент —это норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, топредполагается, чтоонравен2 (методдвукратногоучетаамортизации).
Всепятьаргументовдолжныбытьположительными числами.
Метод двукратного учета амортизации предполагает ускоренную амортизацию имущества. При этом амортизациямаксимальна в первый период иснижаетсявпоследующиепериоды.
Предположим, что стоимость станка 25 000 рублей, время эксплуатации 10 лет, ликвидная стоимость 700 рублей. Составимформулу:
=ДЦОБ(25000;700;10;1)
Амортизация методом двукратного учета за первый год составит 5000 рублей.
3.3. Функция ПДОБ (ПУО)
Функция ПДОБ возвращает значение амортизации имущества за данный период, включая конкретные периоды, используя метод двойного процента со снижающегося остатка или иной явно указанный метод. ПДОБ представляет методснижающегосяостатка. Синтаксисэтойфункцииследующий:
= ПДОБ(стоимость; остаток; период; начальный_период; конечный_период; коэффициент; без_переключения)
где стоимость — это начальная стоимость имущества; остаток — это остаточная стоимость в конце амортизации (иногда называется ликвидной стоимостью имущества); период — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); начальный_период — это начальный период, для которого вычисляется амортизация, начальный_период должен быть задан в тех же единицах, что и период; конечный_период — это конечный период, для которого вычисляется амортизация, конечный_период должен быть заданвтехжеединицах, чтоипериод.
Коэффициент — это норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, то он полагается равным 2 (метод удвоенного процента со снижающегося остатка). Коэффициент необходимо изменить, если метод удвоенного процента со снижающегося остатка использовать не нужно. Описание метода удвоенного процента со снижающегося остатка смотрите в ДДОБ; без_переключения —это логическое значение, определяющее, следует ли использовать прямую амортизацию в том случае, когда амортизация превышает вычисленную величину амортизации.
Если аргумент без_переключения имеет значение ИСТИНА, то Microsoft Excel не переключается на метод равномерного начисления амортизации, даже если амортизация больше вычисленного снижающегося остатка. Если аргументбез_переключенияимеетзначениеЛОЖЬилиопущен, тоMicrosoft Excel переключаетсянаметодравномерного зачисления амортизации, если амортизация больше вычисленного снижающегося остатка. Все аргументы, за исключением аргументабез_переключения, должныбытьположительнымичислами.
Предположим, чтошвейнаямастерскаяприобрелатришвейныхмашины2 январянаобщуюсумму 25 000 рублей и ликвидной стоимостью через семь лет (7 лет * 4 квартала ежегодно = 28 кварталов) в 500 рублей. Таким образом в первый год эксплуатации все четыре квартала швейных машины работают. Чтобы определить амортизацию имущества заследующийгод(спятогоповосьмойкварталы), создадимформулу:
=ПДОБ(25000;500;28;4;8)
Ответ: амортизация за период с пятого по восьмой кварталы составит 4 768,10 рублей.
3.4. Функция АМГД (АСЧ)
Функция АМГД возвращает годовую амортизацию имущества для указанного периода. Синтаксис этой функции следующий:
АМГД(стоимость; остаточная_стоимость; время_эксплуатации; период)
где стоимость — это начальная стоимость имущества; остаточная_стоимость — это остаточная стоимость в конце периода амортизации; время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это интервал времени (должен быть измерен в
техжеединицах, чтоивремяполной амортизации).
Если взять условия примера из предыдущего раздела и рассчитать амортизацию за первый год эксплуатации, то можнонаписатьследующуюформулу:
=АМГД(25000;500;7;1)
Сумма амортизации за первый год эксплуатации будет составлять 6 125,00 рублей. Затретийгодсуммаамортизациидолжнабытьрассчитанапотакойформуле: =АМГД(25000;500;7;3)
Ответ: 4 375,00 рублей.
Заседьмойгодамортизация будетсчитатьсяпотакойформуле: =АМГД(25000;500;7;7) ибудетсоставлять875 рублей.
Суммаамортизацииплавно снижается, так какостаточная стоимость машинуменьшается.
.