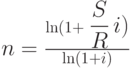Рассмотрим
схему с многократными взносами или
выплатами.
Поток
платежей, все члены которого имеют
одинаковую величину R
и разделены
равными промежутками времени, называют
постоянной
рентой.
Один
из возможных вариантов такого потока
{-Р, -R, -R, …, -R, S},
т.е. начальный
взнос Р и
последующие выплаты R
дают в итоге S.
Если платежи
производятся в конце периодов, то ренту
называют обыкновенной,
или постнумерандо.
Если же платежи
происходят в начале периодов, то ренту
называют пренумерандо.
Для
расчетов используется формулы:
Р
— современное
значение.
S
— будущее
значение.
R
— периодическая
выплата.
r
— процентная
ставка за период.
n
— количество
периодов.
type
— тип ренты, если type
= 0 или опущен,
то рента постнумерандо (выплата в конце
периода), если type
= 1, то рента
пренумерандо (выплата в начале периода).
|
Задача На |
Решение.
-
Перейдите
новый лист и переименуйте его в Задача
5. Для проведения
расчетов создайте таблицу согласно
рис. 9.
Рис.9.
-
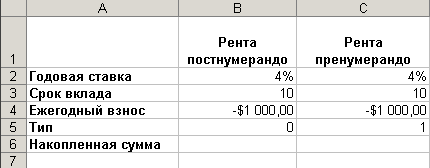
Если
платежи осуществляются в конце периодов
(рента постнумерандо), то тип = 0 (или его
можно опустить). В этом случае формула
для расчета накопленной суммы будет:
=БС(B2;B3;B4;;B5)
или = БС(
4%;10; -1000), где
ПЛТ (выплата за каждый период)=-1000 $. -
Если
же сумма вносится в начале года (рента
пренумерандо), то формула принимает
вид: =БС(C2;C3;C4;;C5)
или = БС( 4%;10;
-1000; ;1). -
Сравните
полученные результаты и сделайте вывод.
-
Сохраните
изменения в файле Финансовые
расчеты.xls.
|
Задача
Рассматриваются |
Примечание.
Для расчетов
создайте на новом листе Задача
6 таблицу согласно
рис. 10.
Рис.10.
Сравните
полученные результаты и сделайте вывод.
Сохраните изменения в файле Финансовые
расчеты.xls.
|
Задача За |
Решение.
-
Перейдите
новый лист и переименуйте его в Задача
7. Для проведения
расчетов создайте таблицу согласно
рис. 11.
Рис.
11.
-
Ставку
за квартал в ячейке С3рассчитайте
самостоятельно. -
Для
расчета срока вклада воспользуемся
новой финансовой функцией КПЕР,
которая возвращает общее количество
периодов выплаты для инвестиции на
основе периодических постоянных выплат
и постоянной процентной ставки.
Синтаксис функции кпер.
КПЕР(ставка;плт;пс;бс; тип)
СТАВКА—
процентная ставка за период.
ПЛТ —
выплата, производимая в каждый период;
это значение не может меняться в течение
всего периода выплат. Обычно платеж
состоит из основного платежа и платежа
по процентам и не включает налогов и
сборов.
ПС—
приведенная к текущему моменту стоимость
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.
БС—
требуемое значение будущей стоимости
или остатка средств после последней
выплаты. Если аргумент БС опущен, то он
полагается равным 0.
Тип—
число 0 или 1, обозначающее, когда должна
производиться выплата.
-
Рассчитаем
срок вклада, если начисление процентов
производится в конце каждого года. Для
этого в ячейку В5 введите формулу:
=КПЕР(B3;;B2;B4)или=КПЕР(15%;;-75000;200000).
В данном случае аргументПЛТопущен, т.к. не производится никаких
дополнительных вкладов. -
Аналогичным
образом в ячейке С5 рассчитайте срок
вклада, если начисление процентов
производится по кварталам. Обратите
внимание, что в данном случае результатом
расчета будет количество кварталов.
Поэтому полученный результат необходимо
разделить на 4. -
Сравните
полученные результаты и сделайте вывод.
-
Сохраните
изменения в файле Финансовые
расчеты.xls.
|
Задача
Ссуда |
Примечание.
Для расчетов
создайте на новом листе Задача
8 таблицу согласно
рис. 12.
Рис.12.
Сохраните
изменения в файле Финансовые
расчеты.xls.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6.7 Используем Excel
Как следует из материала, изложенного ранее в этой лекции, количественный анализ рент сводится к вычислению следующих их характеристик:
- приведенная ценность потока платежей,
- будущая величина потока платежей,
- величина отдельного платежа,
- норма доходности (процентная ставка),
- количество периодов проведения платежей./
Все эти характеристики, за исключением приведённой ценности, связывает зависимость, выражающаяся в простейшем случае, когда платежи и начисления процентов выполняются один раз в конце каждого периода, формулами (6.2) и (6.3):
Ранее в этой лекции на примерах было показано, как, зная значения величин R, n и i, вычислить наращенную сумму ренты S, или, зная значения величин S, n и i, вычислить величину платежа R. Не представляет труда записать приведенные решения примеров на рабочих листах Excel. Ещё раз отметим, что эти решения станут существенно компактней и наглядней, если создать на VBA две функции, которые мы назвали AnnCoeff и AnnPCoeff. Функция AnnCoeff реализует функцию 

Приведём тексты этих функций (листинг 6.1). Для читателей, хоть немного знакомых с программированием на VBA, не составит труда включить их в свой модуль и использовать при решении примеров и заданий из лекций. Всех остальных отсылаем к приложению Б в учебнике [5], в котором подробно объяснено, как это сделать.
Function AnnCoeff(n As Integer, i As Single) As Single AnnCoeff = ((1 + i) ^ n - 1) / i End Function Function AnnPCoeff(n As Integer, i As Single, p As Integer) _ As Single AnnPCoeff = ((1 + i) ^ n - 1) / p / ((1 + i) ^ (1 / p) - 1) End Function
Рис.
16.
Пример на вычисление наращенной суммы ренты
На рис. 16 приведен фрагмент рабочего листа с решением примера 4. В решении дважды используется функция AnnCoeff (ячейки C11 и C12).
Если известны значения величин R, S и n, а требуется вычислить, какая ставка процента i применялась, то прямую формулу для вычисления значения i написать невозможно, так как i является корнем уравнения степени n. Простейший выход в этом случае — использовать встроенную функция СТАВКА.
В том случае, если известны значения величин R, S и i, а требуется вычислить, сколько периодов n проводились платежи, можно вывести необходимую формулу. В простейшем случае, когда платежи и начисления процентов выполняются один раз в конце каждого периода, из формул (6.2) и (6.3) получим формулу:
Однако в этой ситуации имеется другая возможность для вычисления количества периодов n — воспользоваться имеющейся для этого в Excel встроенной финансовой функцией КПЕР. Но прежде чем привести пример с использованием этой функции, сообщим общую информацию о встроенных в Excel финансовых функциях, предназначенный для анализа потока платежей.
В Excel имеется девять встроенных функций для вычисления характеристик потока платежей. Эти функции, как и большинство финансовых функций в Excel, содержатся в Пакете анализа, поэтому перед выполнением примеров и упражнений из этой лекции проверьте, установлен ли этот пакет установлен на вашем компьютере.1Если Excel установлен в полном объеме, то Пакет анализа всегда доступен.
В пакете Excel в связи с реализацией набора финансовых функций выделено небольшое количество базовых понятий, которым присвоены имена, по возможности отражающие их содержание. В принципе в локализованной версии MS Office (а мы предполагаем, что читатель работает в русской версии) должны работать как английские, так и локальные наименования. Однако по нашему опыту это не всегда выполнено строго, поэтому рекомендуем использовать русские имена, а также учесть, что, в отличие от весьма стабильных наименований в английской версии, имена в русификации постоянно меняются от одного поколения продукта к другому (напомним, что мы в этих лекциях ориентируемся на MS Office 2010). Например, функция, вычисляющая процентную ставку ренты, в MS Office 2000 называлась НОРМА, тогда как, начиная с MS Office 2003, она превратилась в функцию СТАВКА, оставаясь, по-прежнему, RATE в базовом англоязычном пакете. Начнём с перечисления названий аргументов финансовых функций в той терминологии, которая использована в справочной системе MS Office 2010. Для удобства читателя соберем эти термины в следующей таблице:
| Аргумент | Назначение |
|---|---|
| ставка | процентная ставка |
| кол_пер | количество периодов проведения операции |
| период | порядковый номер периода (от 0 до кол_пер) |
| платеж | величина периодического платежа |
| нач_сум | начальная сумма |
| буд_ст | будущая стоимость |
| тип | тип начисления процентов (1 — начало, 0 — конец периода |
Приведем теперь таблицу, в которой содержатся имена функций (в русифицированной и англоязычной версиях) анализа регулярных потоков, их аргументы и вычисляемые величины:
| Функция | Аргумент | Вычисляемая величина |
|---|---|---|
| БС FV | (ставка;кол_пер;платеж[;нач_сум][;тип]) | будущая величина потока |
| КПЕР NPER | (ставка;платеж;нач_сум[;буд_ст][;тип]) | количество выплат |
| СТАВКА RATE | (кол_пер;платеж;нач_сум[;буд_ст][;тип]) | процентная ставка |
| ПЛТ PMT | (кол_пер;платеж;нач_сум[;буд_ст][;тип]) | величина периодического платежа |
| ПС PV | (ставка;кол_пер;платеж;[;буд_ст][;тип]) | современная ценность потока платежей |
| ПРОЦПЛАТ IPMT | (ставка;период;кол_пер;нач_сум;буд_ст[;тип]) | выплата по процентам в указанный период |
| ОСПЛТ PPMT | (ставка;период;кол_пер;нач_сум;буд_ст;[;тип]) | величина основного платежа в указанный период |
| ОБЩПЛАТ CUMIPT | (ставка;период;кол_пер;нач_сум;нач_пер;кон_пер;буд_ст;тип) | сумма накопленных процентов |
| ОБЩДОХОД CUMPRINC | (ставка;кол_пер;нач_сум;нач_пер;кон_пер;буд_ст;тип) | накопленная сумма погашенного долга |
Рис.
17.
Вычисления с использованием функции БС
На рис.17 приведен фрагмент рабочего листа с решением примера 54 с использованием встроенной функции БС и функции AnnCoeff. Как видно на рисунке, результаты вычислений совпадают с ранее вычисленными.
Как было отмечено выше, с помощью встроенных функций можно выполнить вычисления в ситуациях, когда отсутствуют формулы для прямого счета. Примером такой ситуации является необходимость определения срока погашения долга, взятого на определенных условиях. Рассмотрим конкретный пример.
Пример 61 Г-н Сидоров получил ссуду в размере 100 000 руб. под 8% годовых и согласен выплачивать ежемесячно по 2 000 руб. в счёт её погашения. Сколько месяцев потребуется для выплаты всей суммы ссуды?
Решение. В приведённой выше таблице находим функцию КПЕР, которая определяет необходимое для погашения ссуды количество выплат. Введем в любую ячейку формулу:
=КПЕР(8%/12;-2000;100000)
и определим, что для выплаты ссуды потребуется 61 месяц. Для того чтобы иметь возможность решать этот пример с другими данными (например, может измениться процент, под который предоставляется ссуда), следует использовать в формуле в качестве параметров не числа, а относительные адреса.
Рис.
18.
Пример на определение количества платежей
На рис.18 приведен фрагмент рабочего листа с решением примера 61.
Сделаем некоторые замечания, касающиеся применения функции КПЕР. Аргумент платеж может оказаться слишком мал, чтобы можно было вернуть ссуду. В этом случае в ячейке с формулой появится сообщение об ошибке: # ЧИСЛО!. Для возврата ссуды необходимо, чтобы ежемесячные выплаты были больше соответствующей процентной ставки, умноженной на полную величину ссуды. В рассмотренном примере величина ежемесячных выплат должна быть больше 666 руб.
Обратим внимание читателя на важное правило, которое касается аргументов функций, являющихся суммами денег. Оно касается всех функций из приведённой выше таблицы.
Если некоторый аргумент функции является платежом (расходом), то он должен иметь отрицательное значение. Например, в формуле в ячейке B14 (рис.17) знак минус поставлен перед аргументом из ячейки B6 (величина платежа). Знак минус можно указывать либо в ячейках с данными, либо в формуле перед соответствующими аргументами.
Если значением формулы является величина платежа, то это значение также выдаётся со знаком минус. На экране монитора в этом случае и число, и знак минус перед ним выделяются красным цветом.
Список ключевых терминов
Аннуитет — синоним финансовой ренты при страховании жизни.
Поток денежных платежей — несколько денежных платежей следующих друг за другом.
Период ренты — временной интервал между последовательными выплатами финансовой ренты.
Перпетуитет — бессрочная рента, выплаты которой не ограничены никаким сроком.
Сроком ренты — срок от начала первого до конца последнего периода ренты.
Финансовая рента — последовательность платежей, равных по величине и производящихся через равные промежутки времени.
Краткие итоги
В лекции рассмотрены финансовые ренты. Обсуждаются основные виды финансовых рент и их использование в повседневной практике денежных расчётов потребительский кредит, ипотека, купонные платежи по облигациям и т.п.). В рассмотренных в тексте примерах используется информация актуальная в июле-августе 2016 г. Продолжен обзор возможностей программы Excel для решения рассмотренных в курсе примеров.
Постоянные ренты
Мы рассматривали простейший финансовый поток: {-P, S} или {Р, -S}. Теперь рассмотрим схему с многократными взносами или выплатами.
Поток платежей, все члены которого имеют одинаковую величину R и разделены равными промежутками времени, называют постоянной рентой. Один из возможных вариантов такого потока {-Р, -R, -R, …, -R, S}, т.е. начальный взнос Р и последующие выплаты R дают в итоге S. Если платежи производятся в конце периодов, то ренту называют обыкновенной, или постнумерандо. Если же платежи происходят в начале периодов, то ренту называют пренумерандо.
Приведем формулу, которую используют функции Excel для расчетов:
Р — современное значение, S — будущее значение, R — периодическая выплата, r — процентная ставка за период, n — количество периодов, type — тип ренты, если type = 0 или опущен, то рента постнумерандо (выплата в конце периода), если type = 1, то рента пренумерандо (выплата в начале периода).
В Excel для расчета постоянных рент используются следующие основные финансовые функции:
| Функция | Синтаксис функции |
|
Приведенная (нынешняя) стоимость (ПС) |
ПС(ставка,кпер,плата,бс,тип) |
|
Будущая стоимость (БС) |
БС(ставка,кпер,плата,пс,тип) |
|
Плата (ПЛТ) |
ПЛТ(ставка,кпер,пс,бс,тип) = |
|
Количество периодов (КПЕР) |
КПЕР(ставка, плата, пс, бс, тип) |
|
СТАВКА |
СТАВКА(кпер,плата,пс,бс,тип,предположение) |
Функция ПС возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
Аргументы функции ПС:
Ставка — процентная ставка за период. Например, если получена ссуда на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 или 0,83%. В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
Кпер — общее число периодов платежей по аннуитету. Например, если получена ссуда на 4 года на покупку автомобиля и платежи производятся ежемесячно, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента «кпер» в формулу нужно ввести число 48.
Плт — выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ренты. Например, ежемесячная выплата по четырехгодичному займу в 10 000р. под 12 процентов годовых составит 263,33р. В качестве значения аргумента «выплата» нужно ввести в формулу число -263,33.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0). Предположим, что требуется накопить 50 000р. для оплаты специального проекта в течение 18 лет: в этом случае будущая стоимость равна 50 000р. Затем, предположив, что заданная процентная ставка останется без изменений, можно определить, какую сумму необходимо откладывать каждый месяц.
Тип — число 0 или 1, обозначающее срок выплаты.
| 0 или опущен | В конце периода |
| 1 | В начале периода |
Замечания
- Убедитесь, что единицы измерения, выбранные для аргументов «ставка» и «кпер», соответствуют друг другу. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, используйте значение12%/12 для задания аргумента «ставка» и 4*12 — для аргумента «кпер». Если платежи по тому же займу производятся ежегодно, используйте значение 12% для аргумента «ставка» и 4 — для аргумента «кпер».
Пример 1.
На счет в банке вносится сумма 10 000 долл. в течение 10 лет равными долями по 1000 долл. в конце каждого года. Годовая ставка 4%. Какая будет сумма на счете после 10 лет?
Решение. Применим функцию БС(ставка, число периодов, платеж, первоначальная стоимость, тип). Платежи осуществляются в конце периодов (рента постнумерандо), поэтому тип = 0 (или его можно опустить). Формула =БC(4%,10,-1000) (аргументы первоначальная стоимость и тип необязательны, и мы их опустили). Результат: $12 006.11. Если же сумма вносится в начале года (рента пренумерандо), то формула принимает вид: =БС(4%,10,-1000,,1). Результат, естественно, получается выше: $12 486.35. Разность между этими двумя значениями можно вычислить как =БС(4%,10,0,-1000)-1000. Подумайте почему.
Пример 2.
Теперь рассмотрим задачу: как по будущему значению определить современное значение.
Вексель на 3 000 000 руб. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года. Найти исходную сумму, выданную под этот вексель.
Решение. Воспользуемся функцией ПС — приведенная (современная) стоимость. Синтаксис функции ПС:
ПС(ставка, количество_периодов, выплата, будущая_стоимость, тип).
В нашем случае задача осложняется тем, что задана ставка дисконта, а аргумент «ставка» подразумевает процентную ставку. Поэтому предварительно нужно пересчитать дисконтную ставку в процентную. Ниже приведена таблица, решающая задачу.
| Параметр | Значение | Пояснение |
| d | 10% | Годовая учетная (дисконтная) ставка |
| n | 2 | Количество периодов в год |
| k | 2 | Количество лет |
| dp | 5% | Учетная (дисконтная)ставка за период =d/n |
| Ставка | 5,26% | Процентная ставка за период =dp/(1-dp) |
| Кпер | 4 | Количество периодов =n*k |
| плт | 0 | Платеж, производимый каждый период |
| Бс | -3 000 000,00р. | Будущая стоимость |
| Пс | 2 443 518,75р. | Приведенная стоимость =Пс(Ставка;Кпер;;Бс) |
Пример 3.
Теперь обратимся к задаче определения продолжительности ссуды при заданных начальном и будущем значениях, процентной ставке. За какой срок в годах сумма, равная 75 000 долл., достигнет 200 000 долл. при начислении процентов по сложной ставке 15% раз в году и поквартально.
Решение. Воспользуемся функцией КПЕР(ставка, выплата , начальное значение, будущее значение,тип). Решение дается формулами: раз в год =КПЕР(15%,0,-75,200) (=7.01786); по кварталам =КПЕР(15%/4,0,-75,200)/4 (=6.66071) Обратите внимание, что во втором случае КПЕР возвращает количество кварталов, поэтому, чтобы пересчитать их в годы, нужно поделить возвращаемый результат на 4. И еще: нет никакой необходимости набирать все нули в современной и будущей сумме — достаточно сохранить между ними пропорциональность. Перевести полученные результаты из дробного числа лет в число лет и дней.
Пример 4.
Представляет интерес и такая задача: как, зная современное и будущее значение суммы, а также периодические равные выплаты, вычислить процентную ставку. Эту задачу решает функция СТАВКА(количество_периодов, выплата, начальное_значение, будущее_значение, тип, предположение). Функция возвращает процентную ставку за один период. «Предположение» по умолчанию составляет 10%. Пусть в долг на полтора года дана сумма 2000 долл. с условием возврата 3000 долл. Вычислить годовую процентную ставку. Решение. =СТАВКА(1,5;;2000;-3000). Результат: 31%.
Пример 5.
Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл. Решение. =СТАВКА(2,5*2;;200000;-260000). Результат: 5.39%.
Но так как в договорах часто указывается именно годовая ставка, даже если период меньше года, то полученный результат следует обработать функцией НОМИНАЛ(ставка для периода, количество периодов в году). По заданной ставке для периода эта функция возвращает эквивалентную годовую ставку. Решение: =НОМИНАЛ(5.39%,2). Результат: 5.32%.
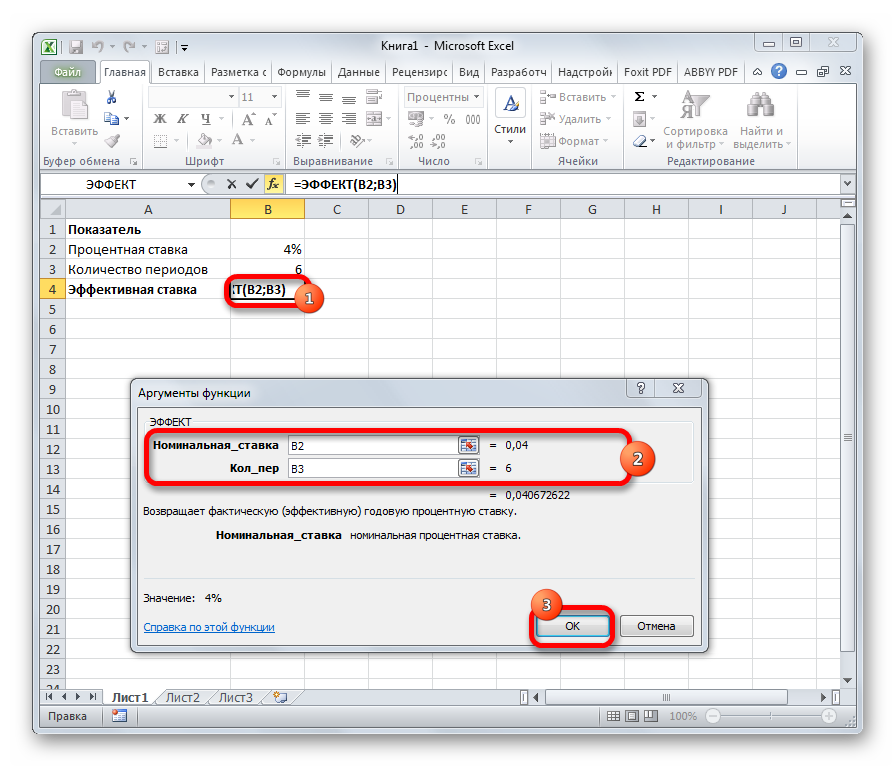
Пример 6.
С функцией НОМИНАЛ тесно связана функция ЭФФЕКТ(номинальная ставка, количество периодов в году). По заданной годовой ставке эта функция возвращает ставку для периода. Чтобы лучше уяснить понятия номинальной и эффективной ставок, рассмотрим следующий любопытный пример.
Чему равна эффективная ставка: 1) при номинальной ставке 100% и начислении 10 000 000 раз в год, 2) при ежедневном начислении?
Решение. =ЭФФЕКТ(1;10000000) (=1.718); =ЭФФЕКТ(1;365) (=1.714). Как видим, ответы получились очень близки. А чему равен коэффициент наращения? =БС(1/365;365;;-1) (=2.714). Нетрудно догадаться, что перед нами десятичное приближение числа е — основания натуральных логарифмов. Оно получается как «второй замечательный предел» при схеме непрерывного начисления процентов, часто применяемой в теоретических исследованиях.
Содержание
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- БС
- ВСД
- МВСД
- ПРПЛТ
- ПЛТ
- ПС
- ЧПС
- СТАВКА
- ЭФФЕКТ
- Вопросы и ответы
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
- Запускается Мастер функций. Выполняем клик по полю «Категории».
- Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
- Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Урок: Мастер функций в Excel
ДОХОД
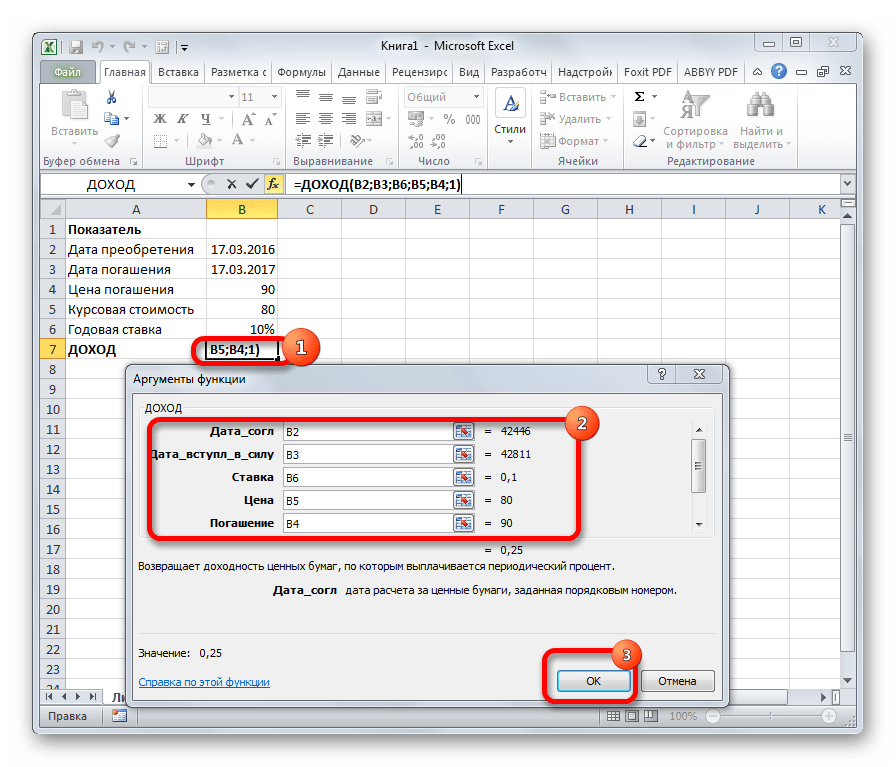
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])
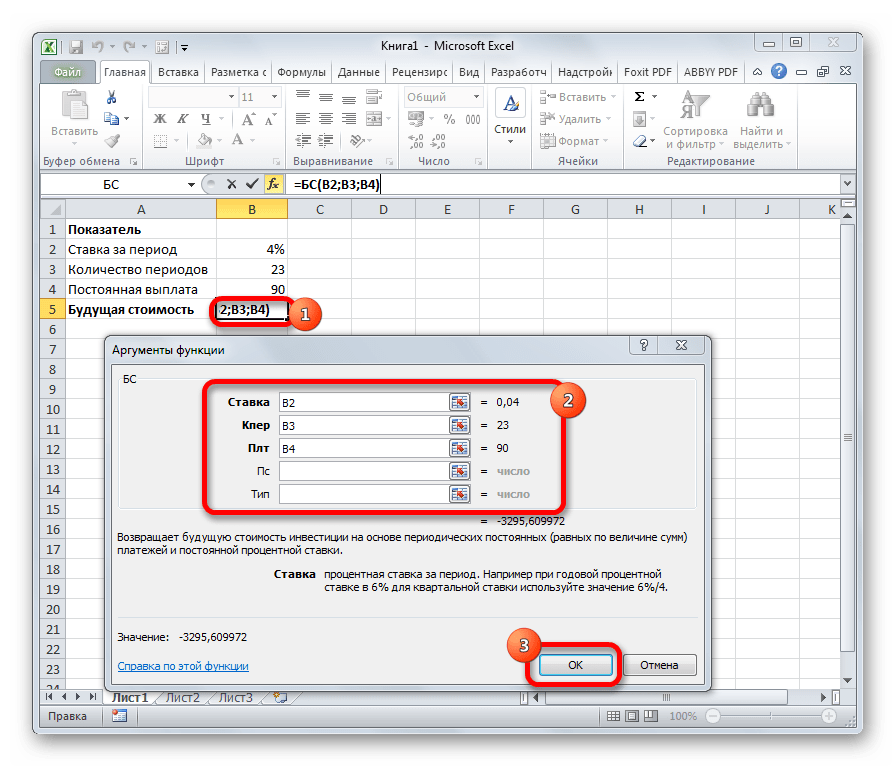
БС
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])
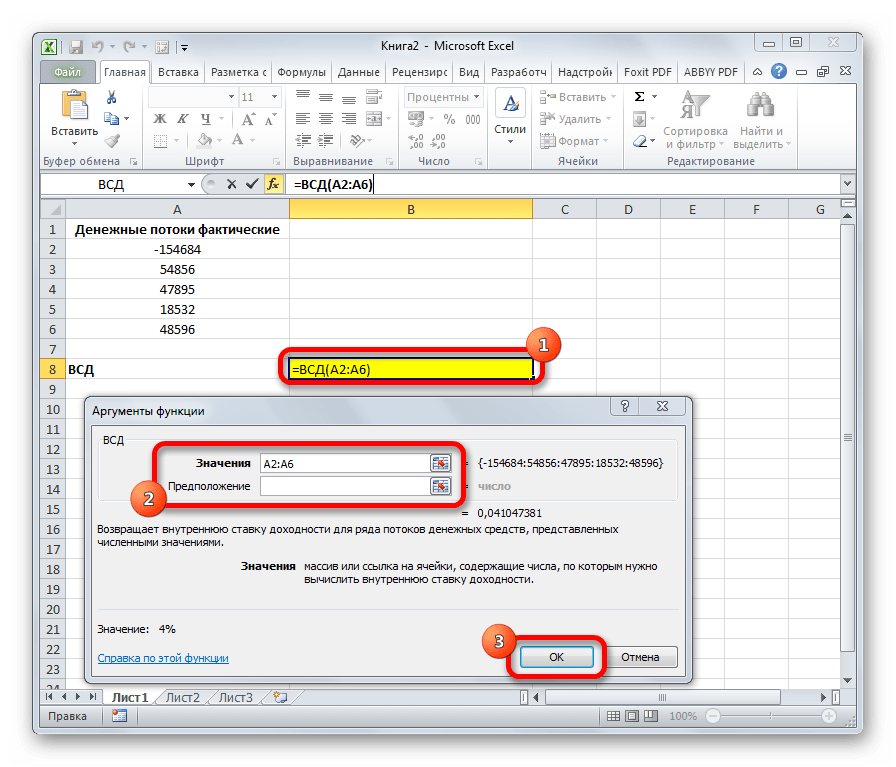
ВСД
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
=ВСД(Значения;[Предположения])
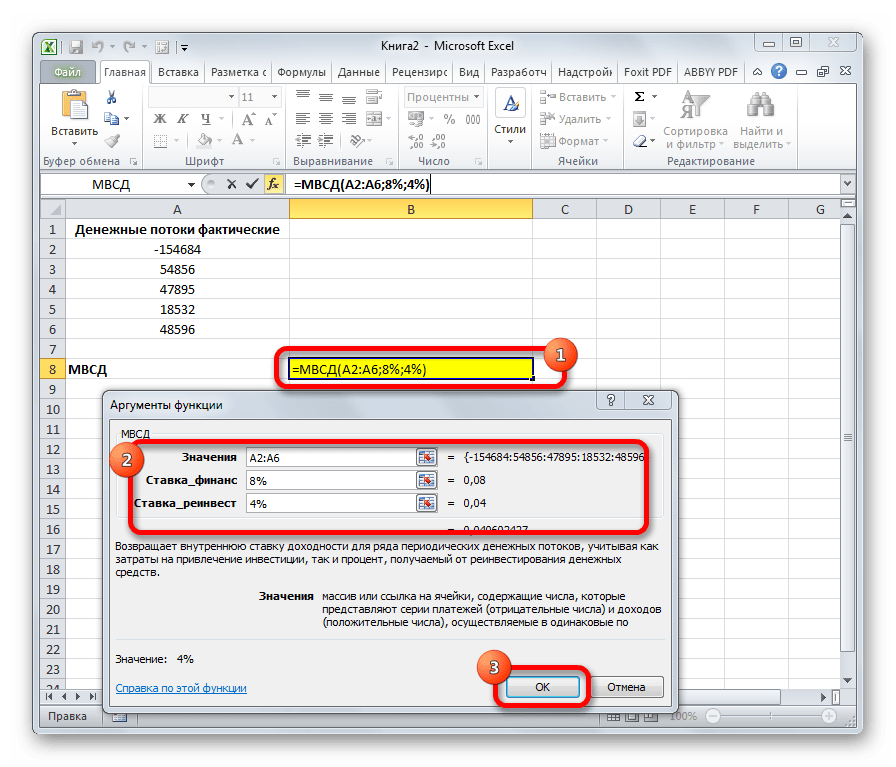
МВСД
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)
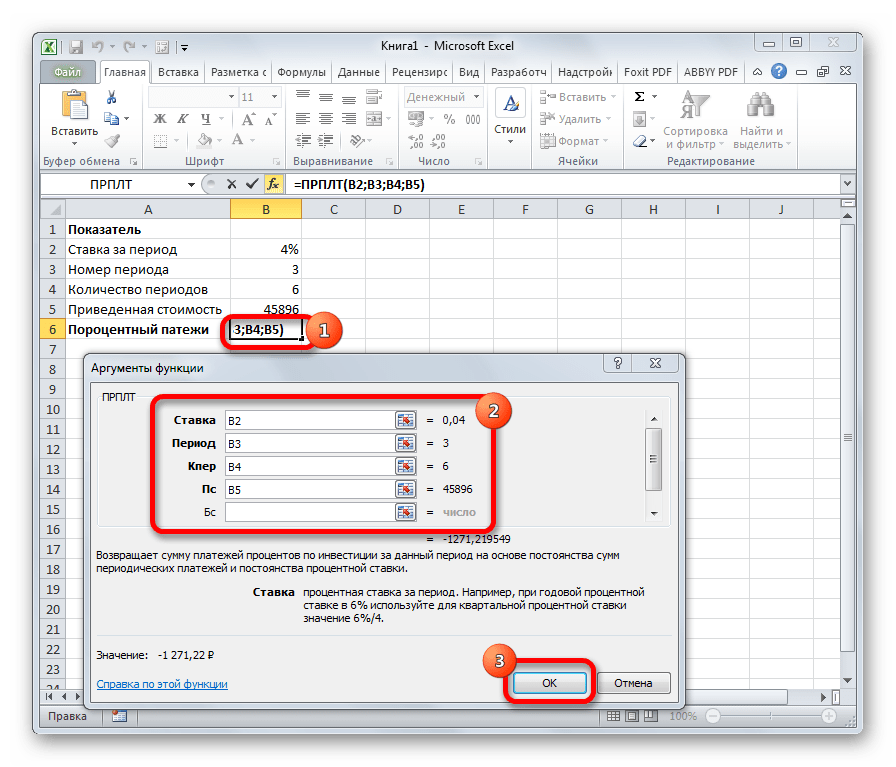
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])
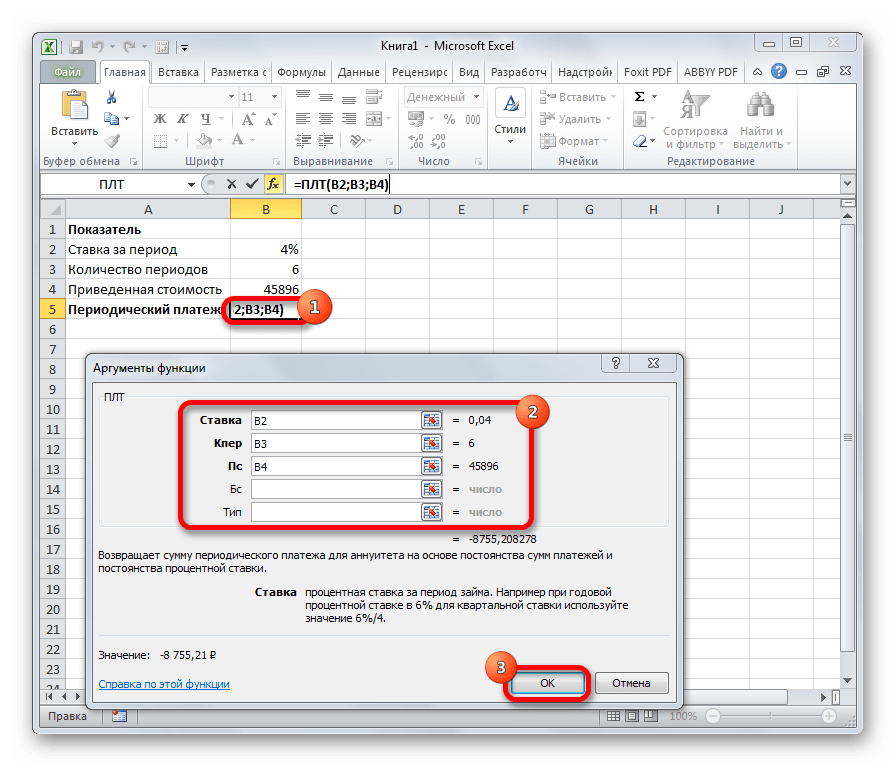
ПЛТ
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])
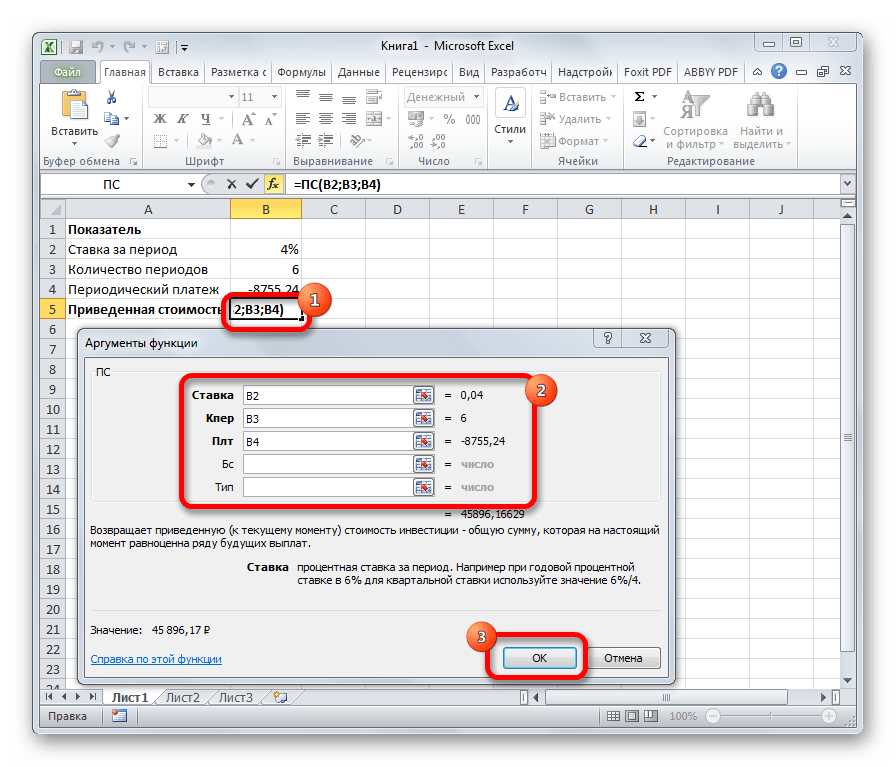
ПС
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])
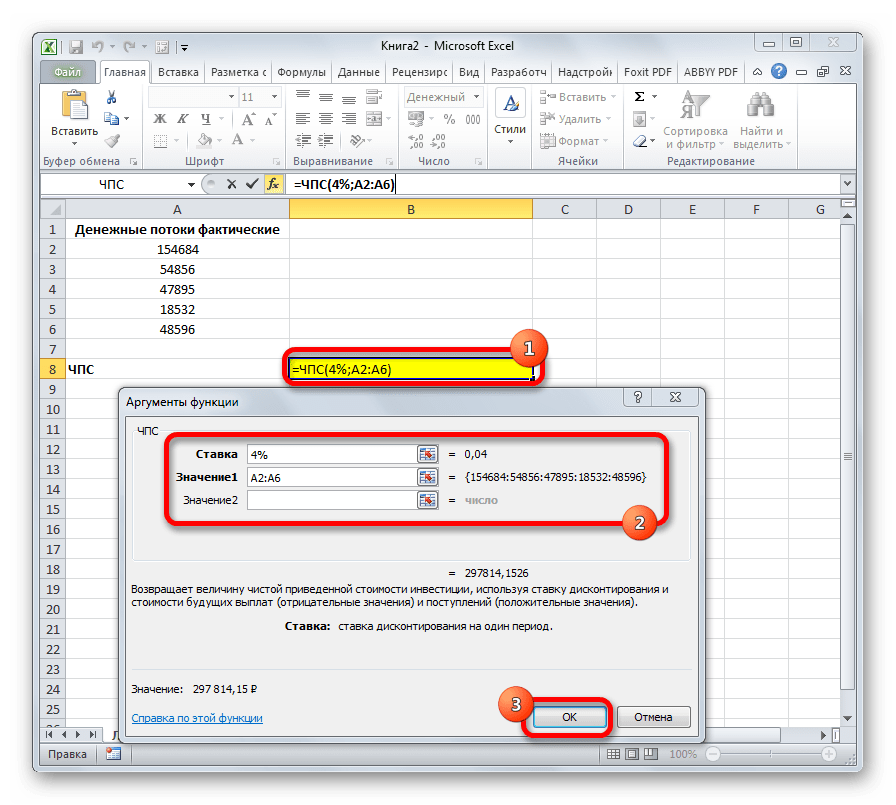
ЧПС
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
=ЧПС(Ставка;Значение1;Значение2;…)
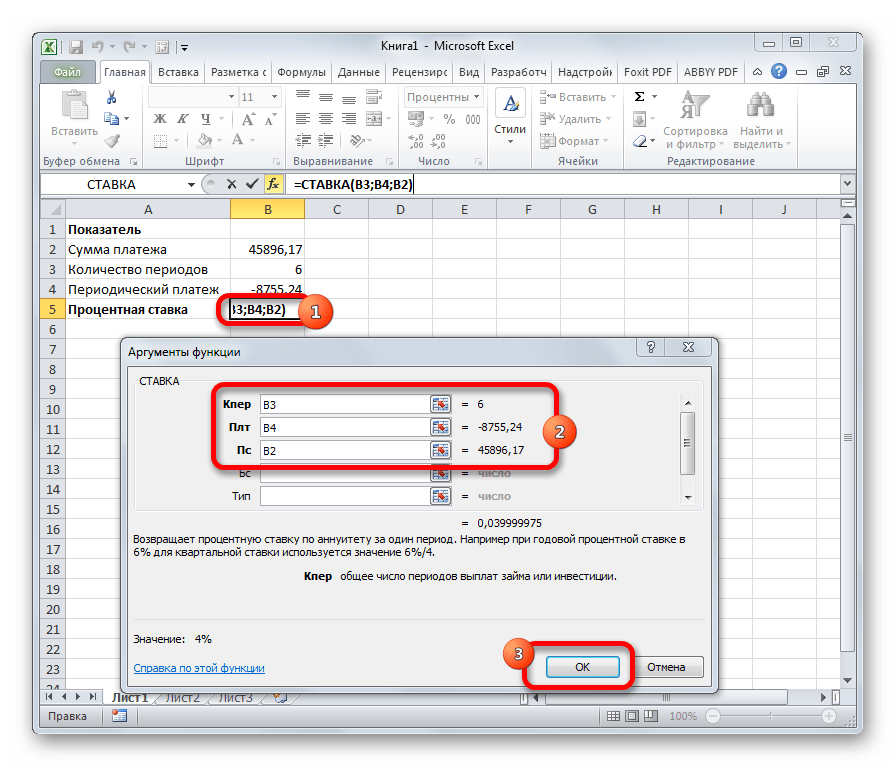
СТАВКА
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])
ЭФФЕКТ
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
=ЭФФЕКТ(Ном_ставка;Кол_пер)
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.
- Вставка функции
-
Популярные финансовые функции
-
БС
- ВСД
- ДОХОД
- МВСД
- ИНОРМА
- ПЛТ
- ПОЛУЧЕНО
- ПС
- СТАВКА
- ЦЕНА
-
ЧПС
-
БС
- Заключение
Вставка функции
Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:
- Выбрав нужную ячейку щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- Или переключаемся во вкладку “Формулы” и жмем аналогичную кнопку, расположенную в левом углу ленты программы.
Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.
На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.
Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).
Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).
Альтернативный способ
Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.
После этого сразу же откроется окно с аргументами функции для заполнения.
Популярные финансовые функции
Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).
БС
Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).
Обязательными аргументами (параметрами) для заполнения являются:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы:
- Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
- Тип – здесь указывается:
- 0 – выплата в конце периода;
- 1 – выплата в начале периода
- если поле оставить пустым, по умолчанию будет принято нулевое значение.
Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.
Синтаксис функции:
=БС(ставка;кпер;плт;[пс];[тип])
Результат в ячейке и выражение в строке формул:
ВСД
Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.
Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.
Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).
Синтаксис функции:
=ВСД(значения;[предположение])
Результат в ячейке и выражение в строке формул:
ДОХОД
С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
- Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Цена – цена ц.б. за 100 рублей номинальной стоимости;
- Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:
- 0 или не заполнен – армериканский (NASD) 30/360;
- 1 – фактический/фактический;
- 2 – фактический/360;
- 3 – фактический/365;
- 4 – европейский 30/360.
Синтаксис функции:
=ДОХОД(дата_согл;дата_вступл_в_силу;ставка;цена;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
МВСД
Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.
У функции только обязательные аргументы, к которым относятся:
- Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
- Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
- Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.
Синтаксис функции:
=МВСД(значения;ставка_финанс;ставка_реинвест)
Результат в ячейке и выражение в строке формул:
ИНОРМА
Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, вложенная в ц.б.;
- Погашение – сумма к получению при погашении ц.б.;
- аргумент “Базис” как и для функции ДОХОД является необязательным.
Синтаксис функции:
=ИНОРМА(дата_согл;дата_вступл_в_силу;инвестиция;погашение;[базис])
Результат в ячейке и выражение в строке формул:
ПЛТ
С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.
Обязательные аргументы:
- Ставка – процентная ставка за период займа;
- Кпер – общее количество периодов выплат;
- Пс – приведенная (нынешняя) стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
- Тип – здесь указывается, как будет производиться выплата:
- “0” или не указано – в конце периода;
- “1” – в начале периода.
Синтаксис функции:
=ПЛТ(ставка;кпер;пс;[бс];[тип])
Результат в ячейке и выражение в строке формул:
ПОЛУЧЕНО
Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, инвестированная в ц.б.;
- Дисконт – ставка дисконтирования ц.б.;
- “Базис” – необязательный аргумент (см. функцию ДОХОД).
Синтаксис функции:
=ПОЛУЧЕНО(дата_согл;дата_вступл_в_силу;инвестиция;дисконт;[базис])
Результат в ячейке и выражение в строке формул:
ПС
Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.
Обязательные аргументы:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы – такие же как и для функции “ПЛТ”:
- Бс – будущая стоимость;
- Тип.
Синтаксис функции:
=ПС(ставка;кпер;плт;[бс];[тип])
Результат в ячейке и выражение в строке формул:
СТАВКА
Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.
Обязательные аргументы:
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период;
- Пс – приведенная стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (см. функцию ПЛТ);
- Тип (см. функцию ПЛТ);
- Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).
Синтаксис функции:
=СТАВКА(кпер;;плт;пс;[бс];[тип];[предположение])
Результат в ячейке и выражение в строке формул:
ЦЕНА
Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Доход – годовой доход по ц.б.;
- Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” как и для оператора ДОХОД является необязательным.
Синтаксис функции:
=ЦЕНА(дата_согл;дата_вступл_в_силу;ставка;доход;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
ЧПС
С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.
Аргументы функции:
- Ставка – ставка дисконтирования за 1 период;
- Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
- Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.
Синтаксис функции:
=ЧПС(ставка;значение1;[значение2];...)
Результат в ячейке и выражение в строке формул:
Заключение
Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.






![s_{n;,i}=frac{(1+i)^{n}-1}{i},, %
s_{n;,i}^{(p)}=frac{(1+i)^{n}-1}{p[left(1+iright)^{{1over p}}-1]}](https://intuit.ru/sites/default/files/tex_cache/82a0c292f7128c49f13e90c04afe255e.png)