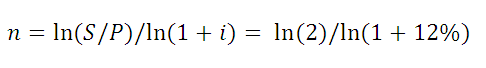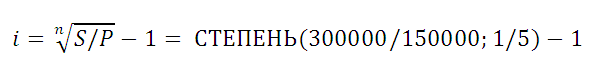В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.
За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f x , слева от строки ввода значений и адресов ячеек.
В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.
Составляющим формулы расчета будущей стоимости FV = PV(1+r)n в Excel соответствуют следующие функции:
| Общее название | Функция в Excel | Краткое описание |
|---|---|---|
| FV (Future Value) | БС (Будущая Стоимость) | Будущая сумма вклада |
| PV (Present Value) | ПС (Текущая Стоимость) | Текущая стоимость вклада |
| n | КПЕР (Количество Периодов) | Число периодов начисления процентов по вкладу |
| r | СТАВКА | Процентная ставка по вкладу |
Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.
Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.
Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:
- если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
- если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.
В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).
А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.
Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:
- капитализироваться;
- капитализироваться ежемесячно.
Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.
- Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!
А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.
Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.
- Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.
Обучение торговле на бирже
Перейти к основному контенту
Office
Office
Корзина
0 товары в корзине
Войти
Фиксируйте свои лучшие моменты с помощью наших премиум-шаблонов фотоальбомов.
СКАЧАТЬ ШАБЛОНЫ СЕЙЧАС.
Таблица расчета процентных выплат по вкладу
Таблица расчета процентных выплат по вкладу
Excel
Скачать
Поделиться
Другие похожие шаблоны
Ипотечный калькулятор
Excel
Счет за услуги по присмотру за домашними животными
Excel
Расчет платежа по кредиту за автомобиль
Excel
Колесо бюджета
Excel
Найдите вдохновение для вашего следующего проекта с тысячами идей на выбор
Адресные книги
Анимация и трехмерное оформление
Бизнес
Бизнес-планы
Бланки и общие шаблоны
Буклеты
Бюджеты
В дорогу
Весна
Визитные карточки
Временные шкалы
Все праздники
Выпускной
День рождения
Диаграммы
Для учебы
Документы и отчетность
Домашнее обучение
Еда и питание
Журналы
Запасы
Записки
Здоровье и фитнес
Зима
Игры и развлечения
Инфографика
Информационные бюллетени
Календари
Карты
Квитанции
Коммерческие предложения
Конверты
Лето
Листовки
Меню
Наклейки
Написание текстов
Образование
Обучение
Объявления
Опросы
Осень
Открытки
Письма
Плакаты
Планирование и учет
Платежные ведомости
Повестки
Подготовка
Поздравления
Презентации
Прибыль и убытки
Приглашения
Программы
Протоколы
Публикация
Расписания
Ребенок
Резюме и сопроводительные письма
Рождество
Свадьба
Семейные развлечения
Сертификаты
Снова в школу
Социальные сети
Списки
Схемы
Счета
Темы
Титульные страницы факсов
Украшения
Управление финансами
Фотоальбомы
Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.
Немного теории
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по
простым
и сложным процентам.
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
В
файле примера
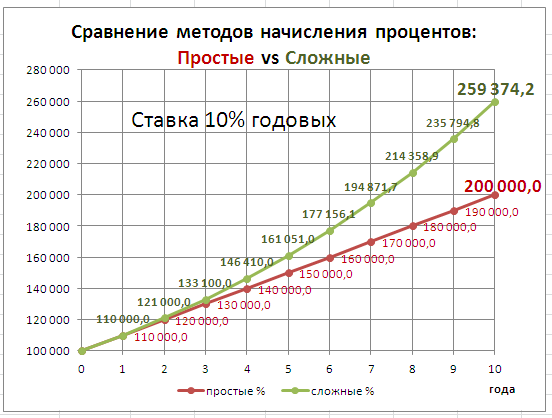
приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.
В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов
читайте здесь
.
Начисление процентов 1 раз в год
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.
Начисление процентов несколько раз в год
В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).
В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.
Рассмотрим задачу
: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.
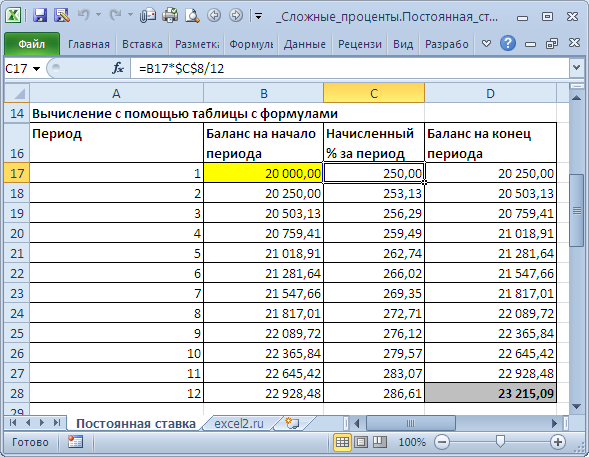
Способ 1. Вычисление с помощью таблицы с формулами
Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В
файле примера
это реализовано на листе
Постоянная ставка
.
За первый период будут начислены проценты в сумме
=20000*(15%/12)
, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.
Способ 2. Вычисление с помощью формулы Наращенных процентов
Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию
СТЕПЕНЬ()
=20000*СТЕПЕНЬ(1+15%/12; 12)
Способ 3. Вычисление с помощью функции БС().
Функция
БС()
позволяет определить
будущую стоимость
инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае
аннуитетных платежей
. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.
=-БС(15%/12;12;;20000)
Или так
=-БС(15%/12;12;0;20000;0)
Примечание .
В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов
используется функция
БЗРАСПИС()
.
Определяем сумму начисленных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.
Сумма начисленных процентов I равна разности между величиной наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.
файл примера
).
Определяем Срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.
В
файле примера
приведено решение, ответ 6,12 лет.
Вычисляем ставку сложных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?
В
файле примера
приведено решение, ответ 14,87%.
Примечание
. Об эффективной ставке процентов
читайте в этой статье
.
Учет (дисконтирование) по сложным процентам
Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.
Математический учет
. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.
Пример
. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .
Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв
сегодня
вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.
Тот же результат можно получить с помощью формулы
=ПС(15%;7;;-2000000;1)
Функция
ПС()
возвращает приведенную (к текущему моменту) стоимость инвестиции и
рассмотрена здесь
.
Банковский учет
. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи
Начисление процентов несколько раз в год
.
Расчет сложных процентов в случае регулярного пополнения вклада
В
файле примера
(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция
БС()
.
Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.
Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.
Примеры использования функции ЭФФЕКТ в Excel
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.
Исходная таблица данных:
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:
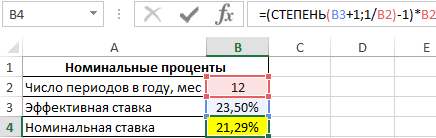
=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2
Полученный результат:
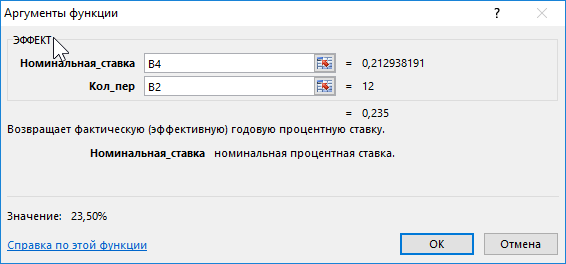
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:
Описание аргументов:
- B4 – полученное выше числовое значение номинальной ставки;
- B2 – число периодов погашения.
Результат:
Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.
Формула расчета процентов по вкладу в Excel
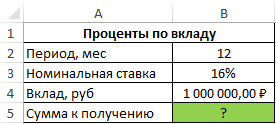
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.
Исходные данные:
Формула для расчета:
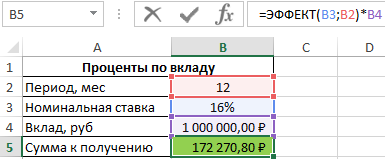
=ЭФФЕКТ(B3;B2)*B4
Описание аргументов:
- B2 – число периодов капитализации;
- B3 – номинальная ставка;
- B4 – сумма вклада.
Результат расчетов:
Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.
Как посчитать проценты на депозит в Excel для выбора вклада
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:
- Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
- Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.
Определить выгодный вариант, отобразить схему выплат.
Исходные данные:
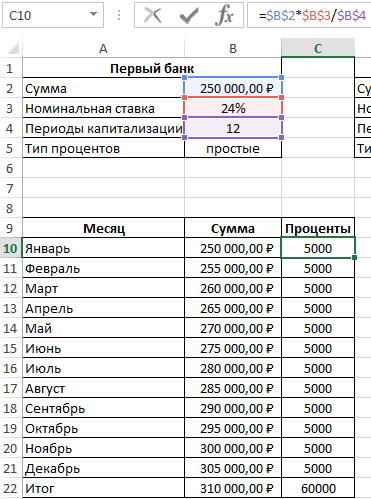
В первом случае таблица выплат выглядит так:
Проценты – постоянная величина, рассчитываемая по формуле:
=$B$2*$B$3/$B$4
Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):
- $B$2 – начальная сумма вклада;
- $B$3 – годовая ставка;
- $B$4 – число периодов капитализации вклада.
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.
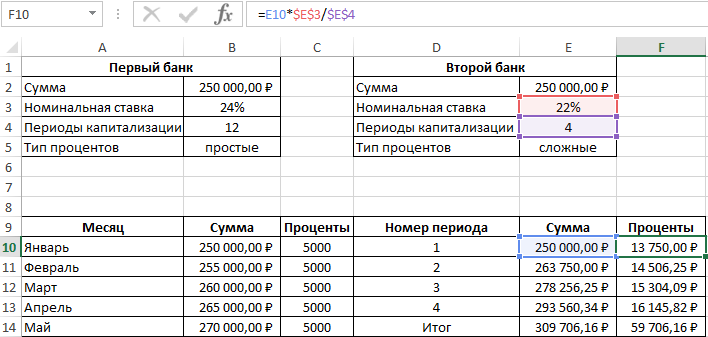
Таблица начисления процентов по условиям второго банка:
В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):
=L3*$E$3/$E$4
При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.
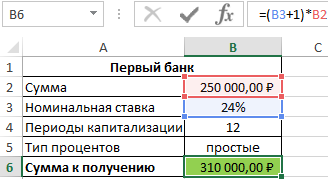
Для быстрого расчета итоговой суммы используем формулы:
- Первый банк:
- Второй банк:
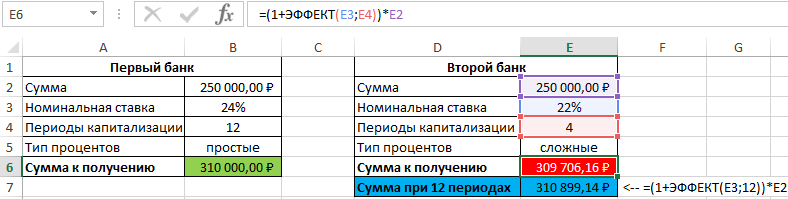
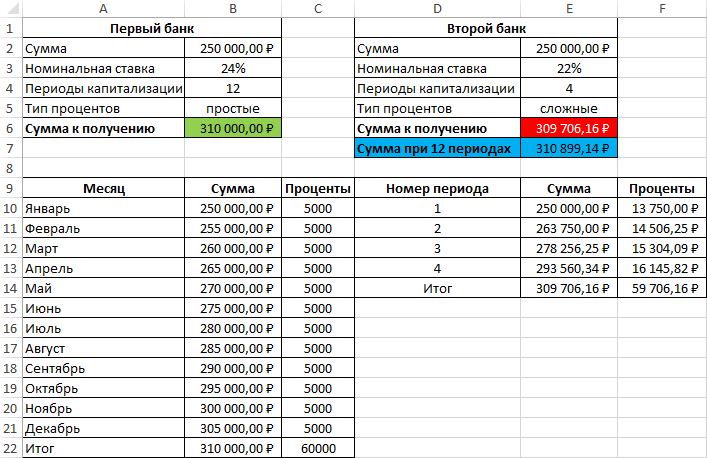
Результаты расчетов:
Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.
Особенности использования функции ЭФФЕКТ в Excel
Функция имеет следующий синтаксис:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
Описание аргументов:
- номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
- кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.
Примечания 1:
- Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
- Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
- Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
- Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:
- A1 – номинальная годовая ставка;
- A2 – число периодов, в которые происходит начисление сложных процентов.
Примечания 2:
- Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
- Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
- Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.
Содержание
- Сложные проценты в EXCEL. Постоянная ставка
- Начисление процентов 1 раз в год
- Начисление процентов несколько раз в год
- Определяем сумму начисленных процентов
- Определяем Срок долга
- Вычисляем ставку сложных процентов
- Учет (дисконтирование) по сложным процентам
- Расчет сложных процентов в случае регулярного пополнения вклада
- Расчет процентов по вкладу в Excel
- Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel
- Примеры использования функции ЭФФЕКТ в Excel
- Формула расчета процентов по вкладу в Excel
- Как посчитать проценты на депозит в Excel для выбора вклада
- Особенности использования функции ЭФФЕКТ в Excel
Сложные проценты в EXCEL. Постоянная ставка
history 3 февраля 2015 г.
Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.
Немного теории
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым и сложным процентам.
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
В файле примера приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.
В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов читайте здесь .
Начисление процентов 1 раз в год
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.
Начисление процентов несколько раз в год
В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).
В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.
Рассмотрим задачу : Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.
Способ 1. Вычисление с помощью таблицы с формулами Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В файле примера это реализовано на листе Постоянная ставка .
За первый период будут начислены проценты в сумме =20000*(15%/12) , т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.
Способ 2. Вычисление с помощью формулы Наращенных процентов Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию СТЕПЕНЬ() =20000*СТЕПЕНЬ(1+15%/12; 12)
Способ 3. Вычисление с помощью функции БС(). Функция БС() позволяет определить будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае аннуитетных платежей . Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов. =-БС(15%/12;12;;20000)
Или так =-БС(15%/12;12;0;20000;0)
Примечание . В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов используется функция БЗРАСПИС() .
Определяем сумму начисленных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.
Сумма начисленных процентов I равна разности между величиной наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см. файл примера ).
Определяем Срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.
В файле примера приведено решение, ответ 6,12 лет.
Вычисляем ставку сложных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?
В файле примера приведено решение, ответ 14,87%.
Примечание . Об эффективной ставке процентов читайте в этой статье .
Учет (дисконтирование) по сложным процентам
Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.
Математический учет . В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.
Пример . Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .
Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв сегодня вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.
Тот же результат можно получить с помощью формулы =ПС(15%;7;;-2000000;1) Функция ПС() возвращает приведенную (к текущему моменту) стоимость инвестиции и рассмотрена здесь .
Банковский учет . В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи Начисление процентов несколько раз в год .
Расчет сложных процентов в случае регулярного пополнения вклада
В файле примера (лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция БС() .
Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.
Источник
Расчет процентов по вкладу в Excel
В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.
За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f x , слева от строки ввода значений и адресов ячеек.
В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.
Составляющим формулы расчета будущей стоимости FV = PV(1+r) n в Excel соответствуют следующие функции:
| Общее название | Функция в Excel | Краткое описание |
|---|---|---|
| FV (Future Value) | БС (Будущая Стоимость) | Будущая сумма вклада |
| PV (Present Value) | ПС (Текущая Стоимость) | Текущая стоимость вклада |
| n | КПЕР (Количество Периодов) | Число периодов начисления процентов по вкладу |
| r | СТАВКА | Процентная ставка по вкладу |
Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.
Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.
Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:
- если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
- если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.
В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).
А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.
Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:
- капитализироваться;
- капитализироваться ежемесячно.
Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.
- Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!
А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.
Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.
- Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.
Источник
Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel
Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.
Примеры использования функции ЭФФЕКТ в Excel
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.
Исходная таблица данных:
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:
- B4 – полученное выше числовое значение номинальной ставки;
- B2 – число периодов погашения.
Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.
Формула расчета процентов по вкладу в Excel
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.
Формула для расчета:
- B2 – число периодов капитализации;
- B3 – номинальная ставка;
- B4 – сумма вклада.
Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.
Как посчитать проценты на депозит в Excel для выбора вклада
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:
- Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
- Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.
Определить выгодный вариант, отобразить схему выплат.
В первом случае таблица выплат выглядит так:
Проценты – постоянная величина, рассчитываемая по формуле:
Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):
- $B$2 – начальная сумма вклада;
- $B$3 – годовая ставка;
- $B$4 – число периодов капитализации вклада.
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.
Таблица начисления процентов по условиям второго банка:
В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):
При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.
Для быстрого расчета итоговой суммы используем формулы:
- Первый банк:
- Второй банк:
Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.
Особенности использования функции ЭФФЕКТ в Excel
Функция имеет следующий синтаксис:
- номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
- кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.
- Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
- Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
- Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
- Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:
- A1 – номинальная годовая ставка;
- A2 – число периодов, в которые происходит начисление сложных процентов.
- Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
- Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
- Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.
Источник
Почему важно иметь под рукой калькулятор вкладов
Если вы думаете сделать вклад, то важно понять, какой доход вы получите к концу срока. Кроме того, важно понимать какая сумма процентов будет выплачиваться каждый месяц. Эти проценты можно тратить и деньги будут работать на вас.
Loading …
Еще одной важной причиной держать калькулятор вкладов всегда под рукой является необходимость проверки вашего банка. Банк не всегда верно считает и выплачивает проценты по вкладу. Чтоб проверить банк, нужно иметь независимый инструмент для расчета дохода по депозиту.
? Скачать калькулятор вкладов в Excel
Ссылка на калькулятор представлена ниже.
Данный калькулятор подходит для расчета вкладов ВТБ, Сбербанка, банка Тинькофф, Райффайзенбанка и других банков РФ.
Скачать калькулятор в Excel можно по ссылке Калькулятор вкладов Excel.
Максим прошел «Тест: Грамотный вкладчик» и набрал 10 баллов.
Профессиональные калькуляторы вкладов
Мы рекомендуем скачать себе на телефон профессиональные мобильные калькуляторы вкладов.
Ниже представлены 2 калькулятора вкладов, которые можно установить на свой телефон. После их установки не нужен Excel. Да и расчёт получается точнее, т.к. есть учёт курсов валют и ключевой ставки ЦБ.
Бесплатный калькулятор вкладов для Windows 10
- Точный расчет вклада любого банка РФ
- Учет пополнений и снятий
- Возможность посчитать несколько вкладов
- Абсолютно бесплатен
- Понятная и подробная статистика
- Возможность учесть фиксированную и плавающую ставку, неснижаемый остаток, макс. дату пополнения
Банковский калькулятор вкладов для Андроид
- Подходит для расчета вкладов любого банка: Тинькофф, Сбербанка, ВТБ, МКБ
- Учитывает при расчете налоги и ставку рефинансирования
- Есть возможность задать пополнения и снятия
- Удобный график выплат и возможность посмотреть ваш доход на сегодня
- Возможность учитывать несколько вкладов и знать сколько денег всего
Основные возможности, которые предоставляет калькулятор вкладов в Excel
- Расчет вклада с помесячной и годовой капитализацией
- Расчет валютных и рублевых вкладов.
- Расчет суммы вклада в конце срока
- Расчет процентов по вкладу.
- Учет налогов, если ставка по вкладу превышает ставку, установленную ЦБ.
- Достоинства данного калькулятора — что его можно использовать офлайн, т.е. без выхода в интернет.
Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.
Калькулятор вкладов поможет вам правильно выбрать вклад. Просто нужно посчитать и сравнить несколько вкладов. Доходность какого будет лучше, тот и выбрать.
Если у вас один рублевый вклад, а один валютный, то придется провести конверсию по курсу ЦБ.
Также доступна онлайн версия депозитного калькулятора — калькулятор вкладов онлайн
Онлайн версия калькулятора является достаточно точной и позволяет посчитать различные вклады при различных условиях. К примеру вклады могут иметь плавающую ставку в зависимости от сроков — чем больше срок, тем выше ставка.
Калькулятор позволяте получить результаты расчета в Excel файле. Это полноценный Excel 2003. Можно распечатать ваши расчеты для похода в банк.
Все это можно рассчитать с помощью онлайн версии кредитного калькулятора, просто задаете номер дня и новую ставку.
Далее нажимаем рассчитать и получаем график платежей по вкладу и сумму к получению. Аналогично, если сумма вклада зависит от суммы — устанавливаем переключатель «Плавающая в зависимости от размера» для процентной ставки. Отдельный интерес составляет учет налогов — все вклады, ставка по которым превышает ставку рефинансирования ЦБ + 5 процентов. Для них происходит начисление налога по вкладу в размере 35 процентов от налогооблогаемой части.
Читайте также: Налоги на вклад: как они начисляются? Пример расчета
Следует отменить, что с налогов по ставке 35 процентов нельзя получить налоговый вычет на ипотеку, т.е. хотя это налоги на ваши доходы, которые являются официальными. Банк сам отчисляет налог и автоматически уменьшает доход по вкладу на сумму налогов.
Однако нужно внимательно проверять банк — рассчитывать вклад с помощю указанного выше депозитного калькулятора. Оставляйте свои пожелания к калькулятору вкладов. Все ваши пожелания будут учитываться в доработках .
Популярные вопросы по вкладам
Как рассчитать проценты по вкладу в банке?
Для расчета нужно сумму вклада умножить на число дней, в течение которого был открыт вклад, умножить на ставку по депозиту, деленную на 100%. Полученную сумму нужно разделить на число дней в году(365 или 366). Проще воспользоваться универсальным калькулятором вкладов на нашем сайте.
Что такое процентная ставка по вкладу
Процентная ставка по вкладу — это число, которое определяет доходность вклада. Чем она выше, тем больше доходность. Различают простую и эффективную ставку по вкладу. Ставка по вкладам зависит от ключевой ставки ЦБ.
Что такое капитализация процентов по вкладу?
Капитализация процентов по вкладу — это плюсование процентов, которые начислены за каждый период, к сумме вклада. К примеру, вы положили вклад на 1000 р и получили через месяц доход 10 р, эти 10 рублей плюсуются к сумме вклада — 1000 + 10 = 1010.
На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.
Что значит проценты не капитализируются?
Проценты не капитализируются — это значит проценты не прибавляются к сумме вклада каждый месяц. Обычно они выплачиваются на определенный счет в виде дохода. Их можно снимать и пользоваться этими деньгами. С одной строны это хорошо, сразу получаешь доход. С другой — плохо, т.к. доход по вкладу не растет

Дмитрий Тачков
Работник банка или другого фин. учреждения
Подробнее
Создатель проекта, финансовый эксперт
Привет, я автор этой статьи и создатель всех калькуляторов данного проекта. Имею более чем 3х летний опыт работы банках Ренессанс Кредит и Промсвязьбанк. Отлично разбираюсь в кредитах, займах и в досрочном погашении. Пожалуйста оцените эту статью, поставьте оценку ниже.
Полезное по теме
- Зачем банки привлекают вклады?
- Блог банкира — популярно о финансах с интересом.
- Вклады с досрочным снятием. Расчет суммы вклада при досрочном снятии.
- Расчет вклада без капитализации. Формулы и пример расчета.
На чтение 25 мин. Просмотров 1k. Опубликовано 29.11.2021
Содержание
- Выполнение расчетов с помощью финансовых функций
- Лабораторная работа № 4. некоторые финансовые функции excel
- Перечень финансовых функций:
- Расчет сложных процентов
- Таблица расчета процентов по вкладу
- Финансовые функции (справка)
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
Запускается Мастер функций. Выполняем клик по полю «Категории».
Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые».
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота).
Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки.
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»).
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»).
Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»).
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Лабораторная работа № 4. некоторые финансовые функции excel
Работа с финансовыми функциями в MS Excel предполагает использование следующей методики:
1. Подготовить на рабочем листе значения основных аргументов функции
2. Перейти к ячейке в которую вводиться формула, использующая встроенную финансовую функцию
3. Вызвать мастер функций и в списке финансовых функций выбрать необходимую финансовую функцию.
4. Если аргумент финансовой функции является результатом расчета другой вложенной функции, используйте повторный вызов мастера функций для данного аргумента
5. После ввода всех аргументов нажмите кнопку ОК и MS Excel произведет расчет по формуле.
При задании аргументов для финансовых функций необходимо помнить следующее:
− Все аргументы, означающие расходы денежных средств (например, ежегодные платежи), представляются отрицательными числами, а аргументы, означающие поступления, (например, дивиденды) – положительными;
− Все даты, как аргументы функции имеют числовой формат
− Для логических аргументов используются константы ИСТИНА или ЛОЖЬ, либо функции категории Логические
− Каждый аргумент должен находиться на своем месте. Если аргументы пропускаются, то следует поставить соответствующее число разделительных знаков.
Задание №1.
Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 000 000 000 сроком на 5 лет под 12% годовых.
Для основных платежей по займу, который погашается равными платежами в конце или в начале каждого расчетного периода используется функция ОСПЛТ, которая возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянства периодических платежей и постоянства процентной ставки.
ОСПЛТ(Ставка, Период, Кпер, Пс Бс)
Ставка — процентная ставка за период.
Период — задает период, значение должно быть в интервале от 1 до «кпер».
Кпер — общее число периодов платежей по аннуитету. Например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента кпер в формулу нужно ввести число 48.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0). Например, если предполагается накопить 50000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость. Можно сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.
Ввод данных и расчеты производятся в соответствии с рисунком
Задание №2.
Рассчитать 20-летнюю ипотечную ссуду со ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате.
Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ, которая возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
ПЛТ(Ставка; Кпер; Бс; Пс; Тип).
Ставка — процентная ставка по ссуде.
Кпер — общее число выплат по ссуде.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нолю), т. е. для займа, например, значение бс равно 0.
Тип — число 0 (ноль) или 1, обозначающее, когда должна производиться выплата.
В нашем случае функция ПЛТ имеет вид:
ПЛТ(10%/12;20*12;-(350000*(1-25%))) – ежемесячные выплаты;
ПЛТ(10%;20;-(350000*(1-25%))) – ежегодные выплаты.
Решение задачи приведено на рисунках.
Задание №3.
Определить, какая сумма окажется на счете, если 52000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.
Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС, которая возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постянной процентной ставки.
Ставка — процентная ставка за период.
Кпер — общее число периодов платежей по аннуитету.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
Тип — число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
Для нашей задачи функция БС примет вид:
Решение задачи приведено на рисунке, а формула для расчета ячейки В30:
Задание №4.
Ожидается, что ежегодные доходы от реализации проекта составят 54000000 руб. Рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 140000000 руб., а норма дисконтирования 7,67.
Для определения срока платежа используется функция КПЕР, которая возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
Ставка — процентная ставка за период.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам и не включает налогов и сборов.
Пс — приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, бс для займа равна 0).
Тип — число 0 или 1, обозначающее срок выплаты.
В нашей задаче функция выглядит следующим образом:
Задание №5.
Облигация номиналом 200000 руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год начисляется 11%,последующие три года – по 16%, в оставшиеся три года по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция БЗРАСПИС, которая возвращает будущую стоимость первоначальной основной суммы после применения ряда (плана) ставок сложных процентов. Функция БЗРАСПИС используется для вычисления будущей стоимости инвестиции с переменной процентной ставкой.
Первичное — стоимость инвестиции на текущий момент.
План — массив применяемых процентных ставок.
Решение приведено на рисунке
Формула для расчета примет следующий вид:
Задание №6.
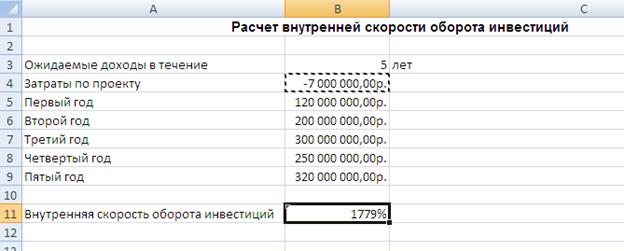
Затраты по проекту составят 600 млн. руб. Ожидаемые доходы в течение последующих 5 лет составят, соответственно, 50, 100,300,200, 300 млн. руб. Оценить экономическую целесообразность проекта по скорости оборота инвестиций, если рыночная норма дохода 15%.
Для вычисления внутренней скорости оборота инвестиции (внутренней нормы доходности) используется функция ВСД, Возвращает внутреннюю ставку доходности для ряда потоков денежных средств представленных их численными значениями. В отличие от аннуитета, денежные суммы в пределах этих потоков могут колебаться.
Однако обязательным условием является регулярность поступлений (например, ежемесячных или ежегодных). Внутренняя ставка доходности — это процентная ставка, принимаемая для инвестиции, состоящей из платежей (отрицательные величины) и доходов (положительные величины), которые имеют место в следующие друг за другом и одинаковые по продолжительности периоды.
Значения — массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности.
Значения должны содержать по крайней мере одно положительное и одно отрицательное значение.
В функции ВСД для интерпретации порядка денежных выплат или поступлений используется порядок значений. Убедитесь, что значения выплат и поступлений введены в нужном порядке.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, такие значения игнорируются.
Предположение — величина, предположительно близкая к результату ВСД.
В нашем случае функция для решения задачи использует только аргумент Значения, один из которых обязательно отрицателен. Если внутренняя скорость оборота инвестиций будет больше рыночной нормы доходности, то проект считается экономически целесообразным. В противном случае проект должен быть отвергнут.
Для принятия решения о экономической целесообразности проекта используйте логическую функцию ЕСЛИ:
Решение приведено на рисунке:
Задание №7.
Предполагается, что доходы по проекту в течение 5 лет составят 120000000 руб., 200000000., 300000000 руб., 250000000 руб., 320000000 руб. Определить первоначальные затраты на проект, чтобы обеспечить скорость оборота 12%.
Расчет внутренней скорости оборота инвестиций производится с помощью функции ВСД. Ввод исходных данных производиться в соответствии с рисунком:
Далее, на вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра. Находим величину первоначальных затрат на проект, обеспечивающих скорость обороты инвестиций в 12%:
Перечень финансовых функций:
АМОРУВ — возвращает величину амортизации для каждого периода.
НАКОПДОХОД — данная функция возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
НАКОПДОХОДПОГАШ — возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
АМОРУМ — возвращает величину амортизации для каждого периода.
ДНЕЙКУПОНДО — возвращает количество дней от начала действия купона до даты соглашения.
ДНЕЙКУПОН — вычисляет число дней в периоде купона, содержащем дату расчета.
ДНЕЙКУПОНПОСЛЕ — возвращает число дней от даты расчета до срока следующего купона.
ДАТАКУПОНДО — возвращает число, представляющее дату следующего купона от даты соглашения.
ЧИСЛКУПОН — возвращает количество купонов, которые могут быть оплачены между датой соглашения и датой вступления в силу, округленное до ближайшего целого купона.
ОБЩПЛАТ — вычисляет кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат. exсel финансовый электронный таблица
ОБЩДОХОД — вычисляет кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
ФУО — определяет величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
ДДОБ — определяет значение амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
СКИДКА — определяет ставку дисконтирования (норму скидки) для ценных бумаг.
РУБЛЬ.ДЕС — преобразует цену в рублях, представленную в виде дроби, в цену в рублях, выраженную десятичным числом. Функция РУБЛЬ.ДЕС используется для преобразования дробных значений денежных сумм, например стоимости ценных бумаг, в десятичное число.
РУБЛЬ.ДРОБЬ — преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, представленную в виде дроби. Функция РУБЛЬ.ДРОБЬ используется для преобразования десятичных чисел, например стоимости ценных бумаг, в дробные цены.
ДЛИТ — находит ежегодную продолжительность действия ценных бумаг с периодическими выплатами по процентам.
ЭФФЕКТ — определяет эффективную (фактическую) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году, за которые начисляются сложные проценты.
ЭФФЕКТ вычисляется следующим образом:
БС — вычисляет будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
БЗРАСПИС — вычисляет будущее значение начального вклада при изменяющихся сложных процентных ставках.
ИНОРМА — определяет ставку доходности полностью обеспеченной ценной бумаги.
ПРПЛТ — определяет сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
ВСД — вычисляет внутреннюю ставку доходности (отдачи) для серии потоков денежных средств.
ПРОЦПЛАТ — вычисляет проценты, выплачиваемые за определенный инвестиционный период.
МДЛИТ — определяет модифицированную длительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
МВСД — определяет внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разную ставку.
НОМИНАЛ — определяет номинальную годовую процентную ставку.
КПЕР — определяет общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
ЧПС — определяет величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции.
ЦЕНАПЕРВНЕРЕГ — находит цену за 100 рублей нарицательной стоимости ценных бумаг с нерегулярным первым периодом.
ДОХОДПЕРВНЕРЕГ — находит доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом.
ЦЕНАПОСЛНЕРЕГ — определяет цену за 100 рублей нарицательной стоимости ценных бумаг для нерегулярного (короткого или длинного) последнего периода купона.
ДОХОДПОСЛНЕРЕГ — определяет доход по ценным бумагам с нерегулярным последним периодом.
ПЛТ — Вычисляет величину выплаты по ссуде за один период.
ОСПЛТ — Вычисляет величину выплат на основной капитал для вклада в заданный период.
ЦЕНА — вычисляет цену за 100 рублей нарицательной стоимости ценных бумаг, по которым производится периодическая выплата процентов.
ЦЕНАПОГАШ — вычисляет цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
ЦЕНАСКИДКА — определяет цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
ПС — определяет приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
СТАВКА — определяет процентную ставку по аннуитету за один период
ПОЛУЧЕНО — вычисляет сумму, полученную в срок вступления в силу полностью обеспеченных ценных бумаг.
АПЛ — определяет величину амортизации актива за один период, рассчитанную линейным методом.
АСЧ — определяет величину амортизации актива за данный период, рассчитанную по сумме чисел лет срока полезного использования.
РАВНОКЧЕК — вычисляет эквивалентный облигации доход по казначейскому векселю.
ЦЕНАКЧЕК — вычисляет цену на 100 рублей номинальной стоимости для казначейского векселя.
ЦЕНАКЧЕК вычисляется следующим образом:
ДОХОДКЧЕК — вычисляет доходность по казначейскому векселю.
ПУО — определяет величину амортизации актива для любого выбранного периода, в том числе для частичных периодов, с использованием метода двойного уменьшения остатка или иного указанного метода.
ЧИСТВНДОХ — вычисляет внутреннюю ставку доходности запланированных непериодических денежных потоков.
ЧИСТНЗ — вычисляет чистую текущую стоимость инвестиции, вычисляемую на основе ряда поступлений наличных, которые не обязательно являются периодическими.
Функция ЧИСТНЗ вычисляется следующим образом:
ДОХОД — вычисляет доходность ценных бумаг, по которым производятся периодические выплаты процентов. Функция ДОХОД используется для вычисления доходности облигаций.
ДОХОДСКИДКА — вычисляет годовую доходность по ценным бумагам, на которые сделана скидка.
ДОХОДПОГАШ — определяет годовую доходность ценных бумаг, по которым проценты выплачиваются при наступлении срока погашения.
Расчет сложных процентов
Вот некоторые банковские опции по депозитам.
Вклады с капитализацией. Как мы уже рассмотрели, вклады с начислением процентов поэтапно внутри срока называются вкладами с капитализацией. Периодичность капитализации может быть разная, обычно — раз в месяц, но бывает ежедневная или раз в квартал.
Если банк капитализирует проценты по вкладу — начисляет и добавляет их к сумме депозита, при равных номинальных ставках такой вариант будет выгоднее, чем при начислении процентов в конце срока.
Рассмотрим варианты начисления процентов — от ежедневного до одного раза в квартал. Во всех случаях будем считать, что вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год.
Ежедневная капитализация. Каждый день банк начисляет проценты и добавляет их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Проценты за первый день: 100 000 × 4,8% / 365 = 13,15 Р — эту сумму банк добавит к сумме вклада по истечении первого дня.
За второй день: (100 000 13,15) × 4,8% / 365 = 13,15 Р.
За третий день: (100 000 13,15 13,15) × 4,8% / 365 = 13,16 Р.
С каждым днем сумма, на которую начисляются проценты, будет расти. Соответственно, и процентов каждый месяц будет начисляться больше.
Через год у вас на счете будет 104 916,73 Р. Эффективная ставка составит 4,92% годовых.
Ежемесячная капитализация. Каждый месяц банк будет начислять проценты и добавлять их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 907,02 Р. Эффективная ставка составит 4,91%.
Ежеквартальная капитализация. Проценты начисляются раз в три месяца. Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 887,09 Р. Эффективная ставка составит 4,89%.
Вклады с пополнением. Если по условиям договора вклад можно пополнять — вносить дополнительные средства, — с момента внесения процент начисляется на общую сумму.
Пример: вы открыли счет на 100 000 Р под 4,8% годовых на 1 год с возможностью пополнения, а через полгода внесли еще 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы депозита. Рассчитаем процентные начисления за каждые полгода отдельно.
Без учета капитализации сумма процентных начислений составит 6 000 Р. Вкладчик в этом случае получает фиксированный процент от вложенных денег, поэтому эффективная ставка здесь не меняется — 4,8% годовых.
Если вклад с капитализацией, для вычисления эффективной процентной ставки можно отдельно рассчитать периоды до и после пополнения — как будто это два разных депозита. Эффективная ставка у вкладов будет другой из-за изменения длительности.
где:
- СО — это средний остаток по счету в течение всего срока, как если бы вы клали деньги на беспроцентный депозит;
- Д — общая длительность вклада в годах.
Это и есть смысл эффективной ставки: она показывает, под какой процент нужно вложить средний остаток по счету, чтобы получить те же проценты за тот же срок.
Вклады с частичным снятием. Иногда по условиям договора банк разрешает снимать со счета часть средств, которые лежат на депозите. При этом проценты с момента открытия депозита до момента снятия не теряются.
Пример: вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год с возможностью частичного снятия, а через полгода сняли 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы вклада. Рассчитаем проценты за каждые полгода отдельно.
Без капитализации сумма процентов составит 3600 Р. Эффективная процентная ставка без ежемесячной капитализации — те же 4,8%.
Расчет эффективной ставки с капитализацией можно произвести аналогично вкладу с пополнением.
Таблица расчета процентов по вкладу
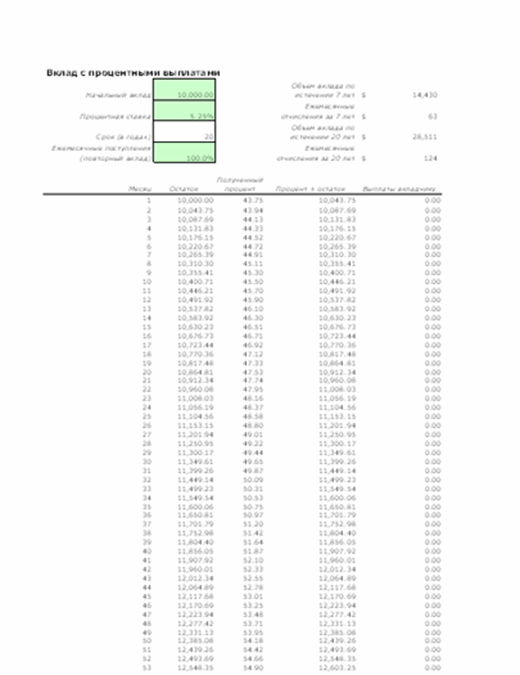
Предположим, вы решили положить на депозит в банк определенную сумму денег. Естественно, вы должны рассчитать, какую сумму с учетом процентов получите через определенное время. В расчетах необходимо учесть процентную ставку по депозиту и срок размещения вклада.
На основе имеющейся таблицы умножения создадим таблицу для автоматического расчета данной суммы. Область ввода таблицы должна содержать следующие управляющие параметры:
- первоначальную сумму вклада;
- начальное значение процентной ставки по депозиту и шаг ее изменения;
- начальное значение периода времени и шаг его изменения.
Процентные ставки будут располагаться в столбце Процент области вычислений, а периоды времени — в строке, озаглавленной как Годы. В области вычислений должны отображаться суммы, величина которых зависит от срока размещения вклада и процентной ставки (рис. 3.14 и 3.15).
Мы предполагаем, что процент по депозиту сложный и начисляется в конце года (то есть период капитализации равен одному году). В каждом следующем году расчет процентов производится для суммы, положенной на депозит, плюс проценты, начисленные за предыдущий год.
Сумма вклада на конец периода рассчитывается по такой формуле:
где Р0 — сумма, размещенная на депозите, r — ставка по депозиту, n — число периодов (лет).
Рис. 3.14. Фрагмент таблицы для расчета суммы на депозита (с формулами)
Рис 3.15. Таблица для расчета суммы на депозите (с числовыми значениями)
Нам кажется, что у вас не возникнет проблем с оформлением столбцов и строк, содержащих исходные данные для расчета. Вам требуется вставить две строки (после строк 2 и 
- Введите знак равенства, выделите ячейку D2 и нажатиями функциональной клавиши [F4] задайте абсолютную ссылку.
- Введите знак «*» (умножить), круглую открывающую скобку, цифру 1 и знак « ».
- Выделите ячейку А10 и три раза нажмите функциональную клавишу [F4] (будет создана абсолютная ссылка на имя столбца), затем введите круглую закрывающую скобку.
- Переключитесь на английский шрифт и введите знак возведения в степень «/» путем нажатия комбинации клавиш [Shift 6].
- Выделите ячейку В9 и дважды нажмите функциональную клавишу [F4] (будет создана абсолютная ссылка на номер строки). Затем введите круглую открывающую скобку.
- Завершите ввод формулы нажатием комбинации клавиш [Ctrl Enter].
На создание таблицы уходит около одной минуты. В отличие от статической таблицы она позволяет изменять сумму, ставки депозита и вычислять результат для разных временных периодов.
Финансовые функции (справка)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2022 означает, что данная функция доступна в выпуске Excel 2022 и всех последующих версиях.
Возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
Возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
Возвращает величину амортизации для каждого учетного периода, используя коэффициент амортизации.
Возвращает величину амортизации для каждого учетного периода.
Возвращает количество дней от начала действия купона до даты соглашения.
Возвращает количество дней в периоде купона, который содержит дату расчета.
Возвращает количество дней от даты расчета до срока следующего купона.
Возвращает порядковый номер даты следующего купона после даты соглашения.
Возвращает количество купонов между датой соглашения и сроком вступления в силу.
Возвращает порядковый номер даты предыдущего купона до даты соглашения.
Возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат.
Возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
Возвращает величину амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
Возвращает ставку дисконтирования для ценных бумаг.
Преобразует цену в рублях, выраженную в виде дроби, в цену в рублях, выраженную десятичным числом.
Преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, выраженную в виде дроби.
Возвращает продолжительность Маколея для ценных бумаг, по которым выплачивается периодический процент.
Возвращает фактическую (эффективную) годовую процентную ставку.
Возвращает будущую стоимость инвестиции.
Возвращает будущее значение первоначальной основной суммы после применения ряда (плана) ставок сложных процентов.
Возвращает процентную ставку для полностью инвестированных ценных бумаг.
Возвращает проценты по вкладу за данный период.
Возвращает внутреннюю ставку доходности для ряда потоков денежных средств.
Вычисляет выплаты за указанный период инвестиции.
Возвращает модифицированную продолжительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
Возвращает внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разные значения ставки.
Возвращает номинальную годовую процентную ставку.
Возвращает общее количество периодов выплаты для инвестиции.
Возвращает чистую приведенную стоимость инвестиции, основанной на серии периодических денежных потоков и ставке дисконтирования.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) последним периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом купона.
ПДЛИТ
Возвращает количество периодов, необходимых инвестиции для достижения заданного значения.
Возвращает регулярный платеж годичной ренты.
Возвращает платеж с основного вложенного капитала за данный период.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
Возвращает приведенную (к текущему моменту) стоимость инвестиции.
Возвращает процентную ставку по аннуитету за один период.
Возвращает сумму, полученную к сроку погашения полностью инвестированных ценных бумаг.
ЭКВ.СТАВКА
Возвращает эквивалентную процентную ставку для роста инвестиции.
Возвращает величину амортизации актива за один период, рассчитанную линейным методом.
Возвращает величину амортизации актива за данный период, рассчитанную методом суммы годовых чисел.
Возвращает эквивалентный облигации доход по казначейскому векселю.
Возвращает цену за 100 рублей номинальной стоимости для казначейского векселя.
Возвращает доходность по казначейскому векселю.
Возвращает величину амортизации актива для указанного или частичного периода при использовании метода сокращающегося баланса.
Возвращает внутреннюю ставку доходности для графика денежных потоков, не обязательно носящих периодический характер.
Возвращает чистую приведенную стоимость для денежных потоков, не обязательно носящих периодический характер.
Возвращает доход по ценным бумагам, по которым производятся периодические выплаты процентов.
Возвращает годовой доход по ценным бумагам, на которые сделана скидка (например, по казначейским векселям).
Возвращает годовую доходность ценных бумаг, по которым процент выплачивается в срок погашения.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль