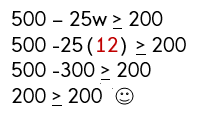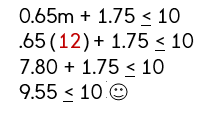This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivationEdit
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that are symbols representing real numbers — then a relevant solution to the word problem would, given the input , produce the output EQUAL, and similarly produce NOT_EQUAL from .
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that is the normal form of , , and , and devise a transformation system to rewrite those expressions to that form, in the process proving that all equivalent expressions will be rewritten to the same normal form.[2] But not all solutions to the word problem use a normal form theorem — there are algebraic properties which indirectly imply the existence of an algorithm.[1]
While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms containing variables have instances that are equal, or in other words whether the equation has any solutions. As a common example, is a word problem in the integer group ℤ,
while is a unification problem in the same group; since the former terms happen to be equal in ℤ, the latter problem has the substitution as a solution.
HistoryEdit
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systemsEdit
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system and two words (strings) , can be transformed into by applying rules from ? Note that the rewriting here is one-way. The word problem is the accessibility problem for symmetric rewrite relations, i.e. Thue systems.[27]
The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groupsEdit
Given a presentation for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable.[31]
The word problem in combinatorial calculus and lambda calculusEdit
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systemsEdit
Solving the word problem: deciding if usually requires heuristic search (red, green), while deciding is straightforward (grey).
The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under ?[29] The word problem for an ARS is undecidable in general. However, there is a computable solution for the word problem in the specific case where every object reduces to a unique normal form in a finite number of steps (i.e. the system is convergent): two objects are equivalent under if and only if they reduce to the same normal form.[33]
The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebraEdit
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free latticesEdit
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free groupEdit
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
- , and
share the same normal form, viz. ; therefore both terms are equal in every group.
As another example, the term and has the normal form and , respectively. Since the normal forms are literally different, the original terms cannot be equal in every group. In fact, they are usually different in non-abelian groups.
| A1 | ||
| A2 | ||
| A3 |
| R1 | ||
| R2 | ||
| R3 | ||
| R4 | ||
| R8 | ||
| R11 | ||
| R12 | ||
| R13 | ||
| R14 | ||
| R17 |
See alsoEdit
- Conjugacy problem
- Group isomorphism problem
ReferencesEdit
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
On this page you can find the explanations of the easy, medium and hard word problem tests
1.Leonardo arrives 12 minutes too late for the 14:12 train from Pisa to Milan. This train runs every hour at 12 minutes past the hour. How long must he wait for the next train?
Solution:
The train arrives every hour. Leonardo is 12 min late.
So 1 hour – 12 min = 60 min – 12 min = 48 min
2. Leonardo buys 6 abacuses for € 52 each. He sells all 6 for a total of € 372. How much does Leonardo make per abacus?
Solution:
6 abacuses * € 52,- = € 312,-
Sold for € 372,- dus € 372,- – € 312,- = € 60,- Profit
€ 60,- / 6 abacuses -= € 10,- per abacus
3. Leonardo wants to paint a wall that measures 5 by 3 m. A 2 litre can of white paint says that you need 1 litre of paint to paint 3 m2. How many cans must Leonardo at least buy to be able to paint the whole of the wall?
Solution:
Leonardo wants to paint 3 m * 5 m = 15 m2 white.
Usage 1 L paint per 3 m2
1 can consists of 2 L paint
So with 1 can of paint he can paint 2 * 3 m2 = 6 m2 schilderen
3 potten = 18 m2 This is a little bit too much however half cans of paint are not sold so 3 is the correct amount.
4. A globe has been designed based on a scale of 1:15,000,000. The distance between two places is 9 cm on this globe. How large is the actual distance between these places?
Solution:
9 cm * 15.000.000 = 135.000.000 cm
135.000.000 cm = 1.350.000 m = 1.350 km
5. Leonardo earns € 15 an hour. He works 8 hours a day from Monday to Friday. He works 4 hours on Saturdays. How much does he earn a week?
Solution:
Leonardo works (5 * 8 hours) + 4 hours = 40 + 4 hours= 44 hours per week
44 * € 15,- = € 660,-
6. Leonardo wants to visit his parents who live on the other side of the forest. He can use a car and go by road or use a bicycle to cycle through the forest. The path through the forest up to his parents’ house is 5 km. The road around the forest to his parents’ house is 12 km long. Leonardo cycles at an average speed of 20 km/h. He drives at an average speed of 50 km/h when he uses a car. Which method will get him the fastest to his parent’s house? If he uses a car or a bicycle?
Solution
Bike: 5 km / 20 km/h = 0,25 hours
Car: 12 km / 50 km/h = 0,24 hours
So the car is fastest.
7. A car costs € 12,000. The price of the car is reduced by 25% when accessories are at least bought for a value of € 2990 when buying the car. The discount only applies to the car and not the accessories. Leonardo buys this car and € 3000 worth of accessories. What does he need to pay?
Solution:
Leonardo gets a 25% discount due to the accessories.
For the car he pays 0,75 * € 12.000,- = € 9.000,-
For the accessories he pays € 3000,-
Total = € 9.000,- + € 3000,- = € 12.000,-
8. Aristotle solves an equation in 3 minutes and 42 seconds. Pythagoras does this twice as fast. Leonardo needs 42 seconds more than Pythagoras. How much time does Leonardo need?
Solution:
Time Pythagoras = 3 min 42 sec / 2 = 1 min 51 sec
Time Leonardo = 1 min 51 sec + 42 sec = 2 min 33 sec
Explanations Word Problems Medium
1. Leonardo sells an invention for € 1650. The customer can pay in 3 instalments. The first time he pays 2/5 of the total price. The second time he pays half of the remaining total. How much will Leonardo receive when the last payment is made?
Solution:
Payment 1: 2/5 * € 1650,00 = € 660,00
Residual debt after payment 1: € 1650,00 – € 660,00 = € 990,00
Payment 2 = Payment 3
Payment 3 = 1/2 * € 990,00 = € 495,00
2. Leonardo will be publishing his first book in 17 days. Today is Tuesday the 23rd of February. On which day will Leonardo be publishing his book?
Solution:
Starting day is Tuesday
Tuesday + 1 week is Tuesday
17 days is 2 weeks (2×7 days) + 3 days
Tuesday + 3 days is Friday
So on Friday.
3. Leonardo is looking for a catering company that can provide the food for this 50th birthday. He is given the following price estimates:
Ulti-Eat € 800 call-out charges + € 10 pp;
Munchers € 20 pp;
Uberchef € 650 call-out charges + € 12 pp;
La Cuisine € 1000 call-out charges + € 8 pp.
He is expecting 90 guests at his birthday party. Which catering company is the cheapest?
Solution:
Ulti-Eat: € 800,- + (90 * € 10,-) = € 1700,-
Munchers: 90 * € 20,- = € 1800,-
Uberchef: € 650,- + (90 * € 12,-) = € 1730,-
La Cuisine: € 1000,- + (90 * € 8,-) = € 1720,-
So Ulti-Eat is cheapest
4. How much is 6 m – 1 mm – 9 dm – 2 cm?
Solution:
Rewriting to mm gives:
6000 mm – 1 mm – 900 mm – 20 mm = 5079 mm = 5,079 m
5. Leonardo sees 23 boats in Venice. 2 boats have 14 people on-board each. 1/3 of the remaining boats have 4 people on-board. 3 people are on-board on each of half of the boats that have not yet been specified. 2 people are on each boat of the remaining ones. How many people are there on all boats when taken together?
Solution:
Total 23 boats
2 boats * 14 pers. = 28 persons
23 – 2 = 21 boats left
1/3 * 21 boats = 7 boats
7 boats * 4 pers. = 28 persons
21 – 7 = 14 boats left
½ * 14 = 7 boats
7 boats * 3 pers. = 21 personen
14 -7 = 7 boats over
7 * 2 = 14 persons
Total = 28 + 28 + 21 + 14 = 91 persons
6. Leonardo drives from Pisa to Milan at an average speed of 380 km/hour in his new Bugatti Veyron. It takes him 45 minutes. When he comes back, there is a traffic queue. The traffic queue is 15 km long and it takes him 1.5 hours to get through it. Next, an 80 km road section follows with slow traffic that drives at 40 km/hour. Because it is so busy, the average speed that he can attain when driving through the remaining section is only 190 km/hour. How long does it take Leonardo to drive back?
Solution:
Outward journey:
380 km/hour * ¾ = 285 km in 45 minutes
Homeward journey:
15 km in 1,5 hours
80 km with 40 km/hour so 80 km / 40 km/hour = 2 hours
Over: 285 km – 80 km – 15 km = 190 km with 190 km/hour = 1 hour
1,5 hours + 2 hours + 1 hour = 4,5 hours
7. Leonardo earns € 18 an hour. He works 8 hours a day from Monday to Friday. He works 6 hours on Saturdays and gets paid 150% of his normal wage. Leonardo works 4 hours in overtime every fortnight. He is paid 200% of his normal wage for overtime. How much does Leonardo earn a week?
Solution:
Mo – Fr he earns: € 18,- * 8 hours * 5 days = € 720,-
Saturday he earns: € 18,- * (150%)/(100%) * 6 hours = € 162,-
Per 2 weeks he works 4 hours in overtime.
On average per week he works 4 hours / 2 weeks = 2 hours overtime.
Overtime yields him per week : € 18,- * (200%)/(100%) * 2 = € 72,-
Total = € 720,- + € 162,- + € 72,- = € 954,-
8. Leonardo buys 3 notebooks that each cost € 3.40. He also buys 6 pencils and 3 rubbers. The pencils cost € 0.60 each. The rubbers cost € 0.50 each. Currently, the shopkeeper has an offer for a pencil and rubber bought together for € 1. How much does he have to pay in total?
Solution:
Notebooks: 3 * € 3,40 = € 10,20
Pencils together with rubbers: 3 * € 1,00 = € 3,00
Pencils separately: 3 * € 0,60 = € 1,80
Total: € 10,20 + € 3,00 + € 1,80 = € 15,00
9. Leonardo has bought a flock of sheep. He owns 60 + ¼ of his total quantity of sheep. How many sheep does Leonardo own?
Solution:
60 + ¼ for total amount of sheep
So 60 sheep = ¾ of his total amount of sheep
60 sheep / 3 = 20 sheep = ¼
Total = 4 * 20 sheep = 80 sheep
10. Leonardo has invented a new bicycle. He decides to test it on a 30 km track. He starts at a speed of 30 km/hour. He keeps it up for half an hour and, next, his speed drops by 5 km/hour. Every 12 minutes his speed drops by another 5 km/hour. How long will it take him to cover the track?
Solution:
First half hours: ½ hour * 30 km/hour = 15 km
So still 30 km – 15 km = 15 km to go
12 min = 1/5 hours so
15 km – (1/5 hours * 25 km/hour) = 15 km – 5 km = 10 km
15 km – (1/5 hours * 20 km/hour) = 10 km – 4 km = 6 km
15 km – (1/5 hours * 15 km/hour) = 6 km – 3 km = 3 km
15 km – (1/5 hours * 10 km/hour) = 3 km – 2 km = 1 km
15 km – (1/5 hours * 5 km/hour) = 1 km – 1 km = 0 km
so ½ hours + (5 * 1/5 hour) = 1 hour 30 min
11. Leonardo has a swimming pool that is 2 m high, 4 m wide and 6 m long. How many litres of water does he need to fill the swimming pool completely?
Solution:
Pool volume = 2 m * 4 m * 6 m = 48 m3
1 L = 1 dm3
48 m3 = 48.000 dm3
So 48.000 liters of water
12. A bag contains 26 red, 52 black and 39 yellow marbles. Leonardo takes out 1 marble. What is the probability that he will take out a yellow marble?
Solution:
Total amount of marbles = 26 + 52 + 39 = 117
of which 39 yellow so the chance is 39/117 = 1/3
13. Today it is Friday the 18th of June. It will be Leonardo’s weeding anniversary in 45 days. On which date did Leonardo get married?
Solution:
June has 30 days
July has 31 days
18 june + 12 days = 30 June
30 june + 31 days = 31 July
Days left = 45 days – 12 days – 31 days = 2 days
31 July + 2 days = 2 August
Explanations Word Problems Hard
1. Leonardo is heading out again in his Bugatti Veyron. Once more he drives from Pisa to Milan, at an average 380 km/hour. It takes him 45 minutes. On the return journey he gets stuck in traffic. The traffic jam is 10 km long, and it takes him 1.5 hours to get through. After this he drives another 60km in slow moving traffic at 40 km/hour, after which Leonardo can resume his route as normal. In total his average speed on both trips measures 114 km/hour. What was his average speed on the return journey when he wasn’t stuck in a traffic jam or slow moving traffic?
Solution:
Outward journey: ¾ * 380 km/hours = 285 km in 45 min (0,75 hours)
Return journey: 10 km in 1,5 hours
60 km / 40 km/hours = 1,5 hours so 60 km in 1,5 hours
Last part is 285 km – 10 km – 60 km = 215 km in x hours
Total time outward and return = 0,75 hours + 1,5 hours + 1,5 hours + x hours = 3,75 + x hours
Total time on full distance =570 km / 114 km/hours = 5 hours
3,75 hours + x hours = 5 hours
x = 1,25 hours
dus 215 km in 1,25 hours = 172 km/hours
2. Leonardo has 3 taps in his bath tub. If he only fully opens tap 1 it takes 10 minutes to fill the bath. If he only fully opens tap 2 it takes 15 minutes to fill the bath, and if he only fully opens tap 3 it takes 30 minutes to fill the bath. If Leonardo were to fully open all 3 taps how long would it take to fill the bath?
Solution:
To calculate this we need to use an arbitrary volume of the bath tub. This value doesn’t need to be realistic so lets take 10 liters.
Now we can calculate the amount of water running from the taps:
Tap 1: 10 L/ 10 min = 60 L/ hour
Tap 2: 10 L/ 15 min = 40 L/ hour
Tap 3: 10 L/ 30 min = 20 L/ hour
If all taps are opened this would mean 60 L/ hour + 40 L/ hour + 20 L/ hour = 120 L/hour will flow into the bath.
The volume of the bath tub is 10 L so (10 L / 120 L/hour) * 60 min = 5 min
3. Leonardo wants to make Invar. Invar is an alloy with an extremely low expansion coefficient, comprising 36% nickel and 64% iron. He has 20 kg of alloy comprising 20% nickel and 80% iron. And he has 180 kg of alloy comprising 50% nickel and 50% iron. How many maximum kilos of Invar can he make?
Solution:
Below is the calcolation based on the amount of Nickel
0,2 * 20 kg + 0,5 * x kg = 0,36(x + 20 kg)
4 + 0,5x = 0,36x + 7,2
0,14x = 3,2
x ˜ 23 kg (this is what he needs to ad)
In total he will end uop with 23 kg + 20 kg = 43 kg
4. Leonardo keeps ostriches and sheep: in total 80 animals. Together all the animals have 220 legs. How many ostriches does he have?
Solution:
80 animals
220 legs
x sheep
80-x ostriches
So the amount of legs gives 2*(80-x) + 4x = 220
– 2x + 4x = 220 – 160
2x = 60
x = 30
So 30 sheep and 80 – 30 = 50 ostriches
5. An aeroplane flies 800 km with the wind behind it. With the same capacity and in the same time it would fly into the wind at 720 km. The wind speed is 30 km/hour. What is the speed of the aeroplane without wind?
Set the speed of the plane without wind at v km/hours.
With the wind behind the plane v + 30 km/hours for 800 km
With the wind against the plane v – 30 km/hours for 720 km
Equation will be:
(v+30 km/hours)/800 km = (v-30 km/hours)/720 km cross-multiplication gives:
720v + 21600 = 800v – 24000
45600 = 80v
v = 570 km/hours
6. Leonardo wants to construct an ostrich run with 100 m fencing. Using this fencing he wants to make an ostrich run with as big a surface area as possible. The type of fencing that he uses cannot bend; but he does have 4 right-angled (90°) corner pieces. What will the surface area of this ostrich run be?
Solution:
Since he has 4 corner pieces of 90° and he can’t bend the fence he has to go for either a square or rectangular shape. It is a known fact that the biggest possible surface area with a known circumference is a square so 100 m / 4 = 25 m dus l = b = 25 m
If you don’t know this you can also use the following approach:
Circumference = 2(l + w) = 100 m
l + w = 50
l = 50 – w
Surface = l * w = (50 – w) * w = – w2 + 50w
This is a quadratic equation, when you put this in a graph, you will find a parabola of which you can pinpoint the top. The value at the y-axis at the top is maximum surface area, the value of the x-axis is the width at which the maximum surface area is reached.
There is also a possibility to do this without drawing a graph. We use the following formula for this: xparabooltop= (-b)/2a
a en b can be derived fromk the quadratic equation:
Every quadratic has the following form: y = ax2 + bx + c
In this case that gives: opp. = -w2 + 50w
So a = -1 and b = 50
so wparabolatop = (-50)/(2•-1)= (-50)/(-2) = 25 m
l + w = 50 m
l + 25 m = 50 m
50 m – 25 m = l = 25 m
Opp.max = 25 m * 25 m = 625 m2
7. Leonardo usually pays € 0.50 for 3 pencils. He sells a pair for € 0.50. In one day Leonardo makes € 2.50 profit. How many pencils did he sell that day?
Solution:
The smallest common divisor of 2 and 3 is 6 so the solution looks like this:
He pays € 0,50 for 3 pencils, for 6 pencils he pays 2 * € 0,50 = € 1,00 6 pencils he sells for (6 / 2) * € 0,50 = € 1,50
profit per 6 pencils is € 1,50 – € 1,00 = € 0,50
He has a profit of € 2,50 so € 2,50 / € 0,50 = 5
So he sold 5 * 6 = 30 pencils
8. Leonardo divides € 14,000 out over 2 bank accounts. Bank account A earns 5% interest; bank account B 7%. At the end of the year Leonardo receives € 798. How much has Leonardo paid into bank account B?
Solution:
bank account B = x
bank account A = 14.000 – x
0,07x + 0,05(14.000 – x) = 798
0,07x – 0,05x + 700 = 798
0,02x = 98
x = € 4.900,-
So Leonardo stalled € 4.900,- on bank account B
9. Leonardo takes part in a cycle race. He sets off at a good speed of 35 km/hour. Once Leonardo has ridden half the race (in distance) he realises he set off too quickly and reduces his speed to 25 km/hour. He finishes the race at this speed. In total it takes him 3 hours and 36 mins. What distance has Leonardo cycled?
Solution:
Set half of the total distance at x. This leads to the following set of equations:
3 hours en 36 min = 3,6 hours
(x/35) + (x/25) = 3,6 hours
25x/875 + 35x/875 =3,6
60x/875 = 3,6
60x = 3150
x = 52,5 km
x was only half the distance so the total distance is 2 * 52,5 km = 105 km
10. Every Monday Leonardo cleans his toilet and every fifth day he vacuums. If today he is cleaning his toilet as well as vacuuming how long will it be before he cleans his toilet and vacuums on the same day again?
Solution:
The lowest common divisor of 5 and 7 can be found by multiplying –> 5 * 7 = 35
So in 35 days
11. Leonardo has designed a solar panel. He uses some of the power he generates with this solar panel for personal use, and the rest he sells to his energy supplier. Within the space of a month Leonardo uses 390 m3 gas and sells 130 KWh electricity. His fuel bill for that month amounts to € 130. The following month he uses 360 m3 gas and sells 160 KWh electricity. His bill for that month amounts to € 110. How much does the energy supplier pay Leonardo for 1 KWh electricity?
Solution:
Price 1 m3 gas = x
Price 1 KWh electricity = y
2 equations:
130 = 390x + 130y
110 = 360x + 160y
Rewrite equation 1 to:
130 = 390x + 130y
1 = 3x + y
y = 1 – 3x
Rewrite equation 2 to:
110 = 360x + 160y
110 = 360x + 160(1-3x)
110 = 360x + 160 – 480x
-360x + 480x = 160 – 110
120x = 50
x = 5/12
y = 1 – 3x
y = 1 – 3(5/12)
y = 1 – 1,25
y = -0,25
So Leonardo earns € 0,25 per KWh electricity.
12. Plato is approximately just as many days old as Aristotle is weeks old and Plato is just as many months old as Leonardo is years old. Together Plato, Aristotle and Leonardo are 140 years old. How old is Leonardo? (assume 1 year = 12 months = 52 weeks = 365 days)
Solution:
age Leonardo
age Aristoteles
age Plato
P + A + L = 140
A = 7P
L = 12P
completing this gives:
P + 7P + 12P =140
20P = 140
Plato = 7 years old
Filling in gives:
P + 7P + L = 140
7 + 49 + L = 140
L = 84
Leonardo is 84 years old
13. For his mathematics exams Leonardo has to take 4 tests. He achieves a score of 9.4 and 9.8 in the first 2. What average score must he achieve for the next 2 is he wants to achieve an average score of 9.5? The 2 tests he still has to take together account for 25% of the final score.
Solution:
Average now:
(9,4 + 9,8) / 2 = 9,6
This one counts for 75% so:
0,75*9,6 + 0,25x= 9,5
7,2 + 0,25x =9,5
0,25x = 2,3
x = 9,2
14. Think of a 3 digit number that when you switch round the ten and hundred numbers the resulting number is 20% more than the original number.
Solution:
100a + 10b + c =1,2 * (10a + 100b + c)
100a + 10b + c = 12a + 120b +1,2c
set c at 0
100a + 10b = 12a +120b
88a = 110b
Also known:
b < a, a < 10, b < 10
So simply try some and you’ll find:
a = 5 b = 4
88(5) = 110(4)
440 = 440
So 540 is the resulting number. We are looking for the original number so the answer is 450.
15. Leonardo wants to place bird cages in his garden. For this he has set aside 52 m2 of garden and € 825. Bird cage A has a capacity of 14 m3 and a ground area of 4 m2 and costs € 50. Bird cage B has a ground area of 8 m2, a capacity of 30 m3 and costs € 125. How many of each bird cage does he need to place in order to attain as large a bird cage content as possible; within his budget and allocated space? The bird cages cannot be stacked due to their fragile construction.
First calculate the specific surface area(surface/volume) for both bird cages.
bird cage A: 4 m2 / 14 m3 = 2/7 = 30/105 m-1
bird cage B: 8 m2 / 30 m3 = 4/15 = 28/105 m-1
This shows that Leonardo wants to use as much bird cages of type B as possible since that one has the lowest specific surface area.
He has € 825 to spend:
€ 825 / € 125 = 6,6 so 6 bird cages of type B
He is left with € 825 – (6* € 125) = € 825 – € 750 = € 75 euro
Surface:
6 bird cages B * 8 m2 = 48 m2
52 m2 – 48 m2 = 4 m2
So he can also place 1 extra bird cage A of € 50 after which he ends up with € 50.
So:
bird cage A: 1 piece
bird cage B: 6 pieces
16. Leonardo is 9 years younger than 3x as old Archimedes. 4 years ago he was 10 years older than 2x as old Archimedes. How old is Leonardo?
Solution:
2 equations
L = 3A – 9
and
L-4 = 2(A – 4) + 10
This can be rewritten to:
3A – 9 – 4 = 2(A – 4) + 10
3A – 13 = 2A – 8 + 10
3A – 2A = -8 + 10 + 13
A = 15
Completing this gives:
L = 3 *15 – 9
L = 36 years
Solving Word Problems in Algebra
Inequality Word Problems
How are you with solving word problems in Algebra? Are you ready to
dive into the «real world» of inequalities? I know that solving word
problems in Algebra is probably not your favorite, but there’s no point
in learning the skill if you don’t apply it.
I promise to make this as easy as possible. Pay close attention to
the key words given below, as this will help you to write the
inequality. Once the inequality is written, you can solve the
inequality using the skills you learned in our past lessons.
I’ve tried to provide you with examples that could pertain to your
life and come in handy one day. Think about others ways you might use
inequalities in real world problems. I’d love to hear about them if you do!
Before we look at the examples let’s go over some of the rules and
key words for solving word problems in Algebra (or any math class).
Word Problem Solving Strategies
- Read through the entire problem.
- Highlight the important information and key words that you need to solve the problem.
- Identify your variables.
- Write the equation or inequality.
- Solve.
- Write your answer in a complete sentence.
- Check or justify your answer.
I know it always helps too, if you have key words that help you to write
the equation or inequality. Here are a few key words that we associate
with inequalities! Keep these handy as a reference.
Inequality Key Words
- at least — means greater than or equal to
- no more than — means less than or equal to
- more than — means greater than
- less than — means less than
Ok… let’s put it into action and look at our examples.
Example 1: Inequality Word Problems
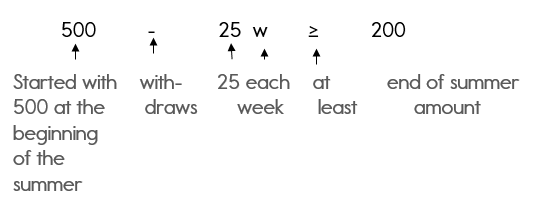
Keith has $500 in a savings account at the beginning of the summer. He wants to have at least $200 in the account by the end of the summer. He withdraws $25 each week for food, clothes, and movie tickets.
- Write an inequality that represents Keith’s situation.
- How many weeks can Keith withdraw money from his account? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: At least is a key word that notes that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know how many weeks.
Let w = the number of weeks
Step 3: Write your inequality.
500 — 25w > 200
I know you are saying, «How did you get that inequality?»
I know the «at least» part is tricky. You would probably think that at least means less than.
But… he wants the amount in his account to be at least $200 which means $200 or greater. So, we must use the greater than or equal to symbol.
Step 4: Solve the inequality.
The number of weeks that Keith can withdraw money from his account is 12 weeks or less.
Step 5: Justify (prove your answer mathematically).
I’m going to prove that the largest number of weeks is 12 by substituting 12 into the inequality for w. You could also substitute any number less than 12.
Since 200 is equal to 200, my answer is correct. Any more than 12 weeks and his account balance would be less than $200. Any number of weeks less than 12 and his account would stay above $200.
That wasn’t too bad, was it? Let’s take a look at another example.
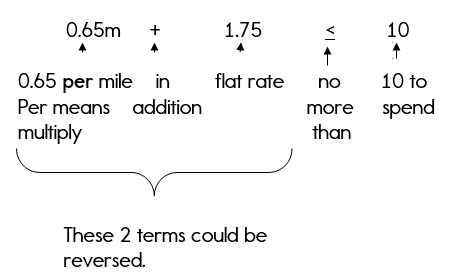
Example 2: More Inequality Word Problems
Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. Katie has no more than $10 to spend on a ride.
- Write an inequality that represents Katie’s situation.
- How many miles can Katie travel without exceeding her budget? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: No more than are key words that note that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know the number of miles Katie can travel.
Let m = the number of miles
Step 3: Write the inequality.
0.65m + 1.75 < 10
Are you thinking, «How did you write that inequality?»
The «no more than» can also be tricky. «No more than» means that you can’t have more than something, so that means you must have less than!
Step 4: Solve the inequality.
Since this is a real world problem and taxi’s usually charge by the mile, we can say that Katie can travel 12 miles or less before reaching her limit of $10.
Step 5: Justify (prove your answer mathematically).
Are you ready to try some on your own now? Yes… of course you are! Click here to move onto the word problem practice problems.
Take a look at the questions that other students have submitted:
- Home
- Inequalities
-
Inequality Word Problems
>
>
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!