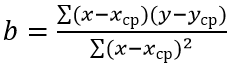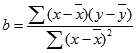17 авг. 2022 г.
читать 2 мин
Часто вам может понадобиться найти наклон линии тренда в Excel.
К счастью, это довольно легко сделать, и следующий пошаговый пример показывает, как это сделать.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных для работы:
Шаг 2: Создайте диаграмму рассеяния
Далее давайте создадим диаграмму рассеяния для визуализации данных.
Для этого выделите данные:
Затем щелкните вкладку « Вставка » на верхней ленте и выберите первый параметр в параметре « Вставить точечный» (X, Y) в группе « Диаграммы ». Это даст следующую диаграмму рассеяния:
Шаг 3: Добавьте линию тренда
Далее добавим линию тренда на диаграмму рассеяния.
Для этого щелкните в любом месте диаграммы рассеяния. Затем щелкните зеленый значок плюса (+) в правом верхнем углу графика и установите флажок рядом с линией тренда :
Шаг 4: Отображение наклона линии тренда
Чтобы найти наклон линии тренда, щелкните стрелку вправо рядом с линией тренда и выберите « Дополнительные параметры »:
В появившемся окне в правой части экрана поставьте галочку рядом с Display Equation on chart :
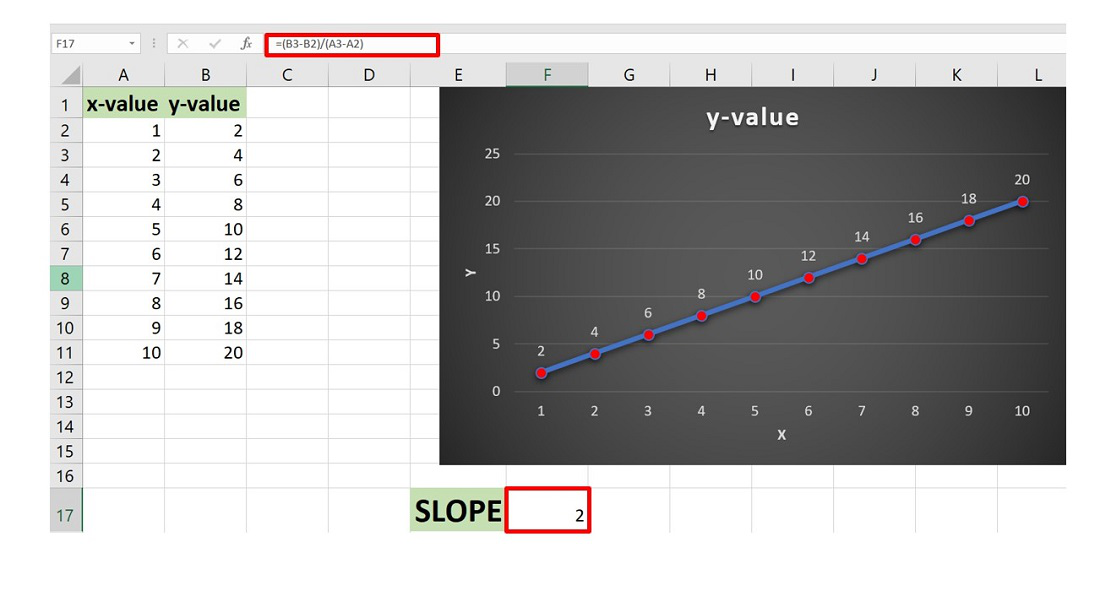
Уравнение линии тренда автоматически появится на диаграмме рассеяния:
Уравнение линии тренда оказывается y = 2,4585x – 1,3553 .
Это означает, что точка пересечения равна -1,3553 , а наклон равен 2,4585 .
Вы можете найти больше руководств по Excel на этой странице .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Функция НАКЛОН в Excel предназначена для определения угла наклона прямой, используемой для аппроксимации данных методом линейной регрессии, и возвращает значение коэффициента a из уравнения y=ax+b. Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).
Фактически, функция НАКЛОН вычисляет значение, которое характеризует скорость изменения данных вдоль линии регрессии. Зная наклон (коэффициент a) и значение коэффициента b можно рассчитать приближенные будущие значения какого-либо свойства y, которое меняется при изменении характеристики x.
Примеры использования функции НАКЛОН в Excel
Для расчета наклона линии регрессии используется уравнение:
где:
- x_ср – среднее значение для диапазона известных значений независимой переменной;
- y_ср – среднее значение для диапазона известных значений зависимой переменной.
Функция НАКЛОН не может быть использована для анализа коллинеарных данных и будет возвращать код ошибки #ДЕЛ/0! в отличие от функции ЛИНЕЙН, которая использует иной алгоритм расчета и возвращает как минимум одно полученное значение.
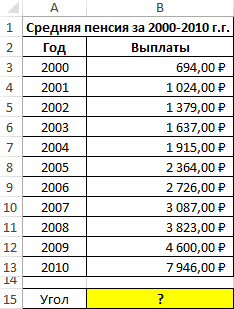
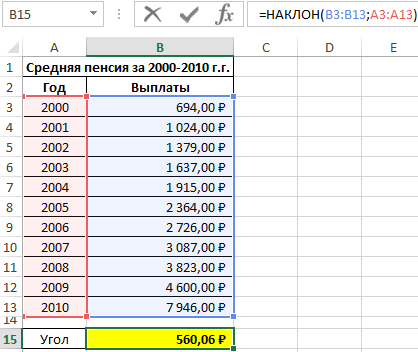
Пример 1. Определить наклон аппроксимирующей прямой для показателей средней пенсии на протяжении нескольких лет.
Вид исходной таблицы данных:
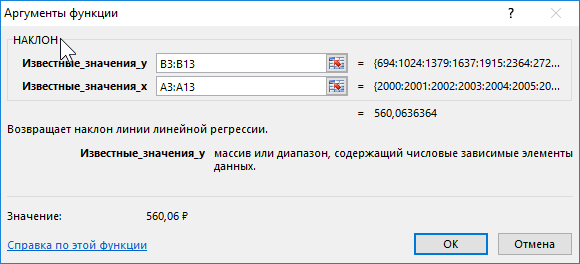
Для нахождения наклона используем следующую формулу:
Описание аргументов:
- B3:B13 – ссылка на диапазон ячеек, содержащих данные о средней пенсии, характеризующие зависимую переменную y;
- A3:A13 – диапазон ячеек с данными об отчетных периодах (годах), характеризующие независимую переменную x.
В результате вычислений получим:
Полученное значение свидетельствует о том, что на протяжении обозначенного периода размер пенсионных выплат в среднем увеличивался примерно на 560 рублей.
Прогноз объема продаж по линейно регрессии в Excel
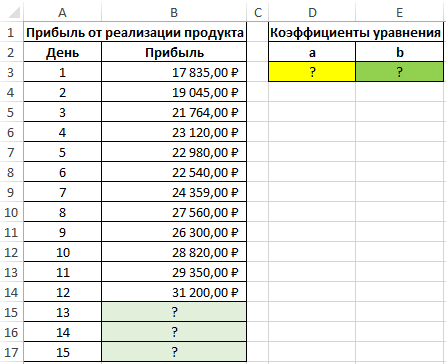
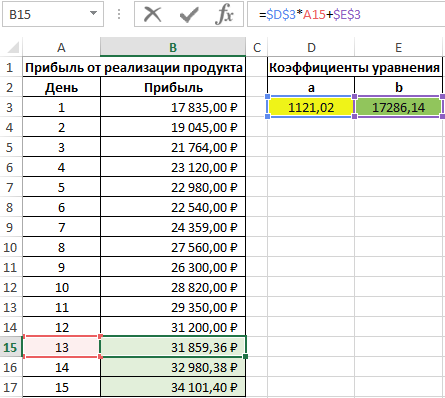
Пример 2. В таблице Excel содержатся данные о прибыли за продажи некоторого продукта компании на протяжении последних нескольких дней. Рассчитать коэффициенты a и b уравнения прямой y=ax+b, аппроксимирующей данные. На основе полученного уравнения спрогнозировать данные о продажах для трех последующих дней.
Вид таблицы с данными:
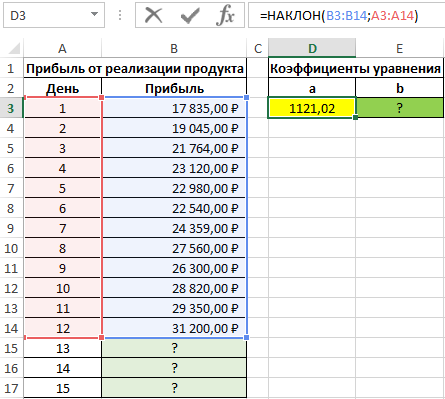
Для нахождения коэффициента a используем следующую формулу:
=НАКЛОН(B3:B14;A3:A14)
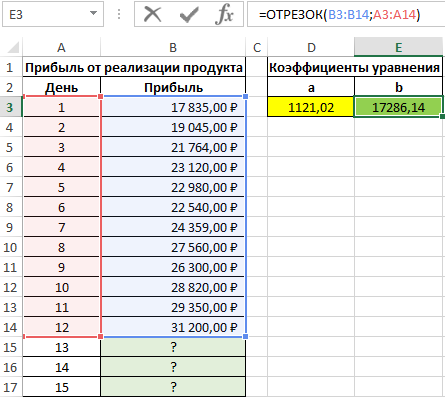
Коэффициент b рассчитывается с помощью следующей функции:
=ОТРЕЗОК(B3:B14;A3:A14)
Искомое уравнение имеет вид:
y=1121,02x+17286,14
Для определения последующих значений y достаточно лишь подставить требуемое значение x. Выполним расчет предполагаемой прибыли для 13-го дня:
=$D$3*A15+$E$3
Описание аргументов:
- D3 – полученное значение коэффициента a;
- A15 – новое значение x;
- E3 – значение коэффициента b.
Используем функцию автозаполнения чтобы получить значения для остальных дней:
Анализ корреляции спроса и объема производства в Excel
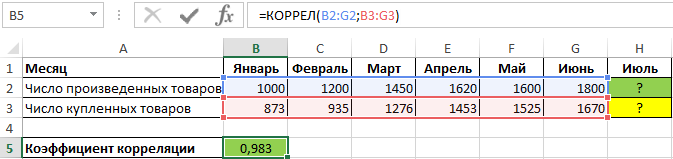
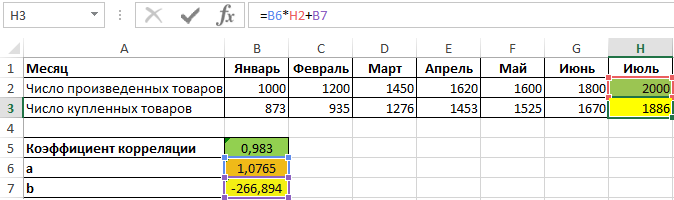
Пример 3. В таблице содержатся данные о количестве произведенной продукции за месяц, а также о числе приобретенных товаров данной марки покупателями. Отобразить взаимосвязь между данными графически, определить, целесообразно ли использовать уравнение линейно регрессии для описания корреляции между спросом и числом произведенных товаров.
Вид таблицы данных:
Для определения зависимости между двумя рядами числовых данных рассчитаем коэффициент корреляции по формуле:
=КОРРЕЛ(B2:G2;B3:G3)
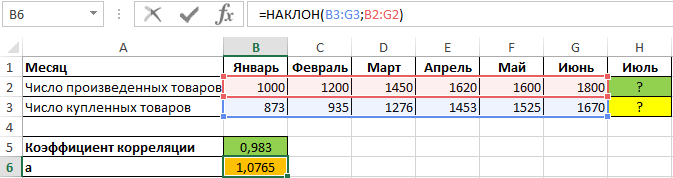
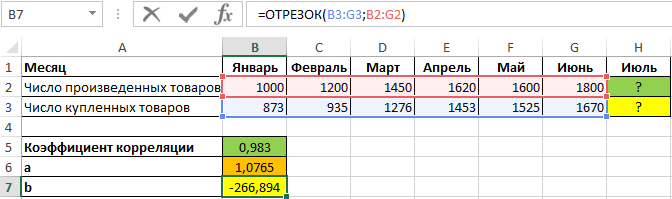
Полученное значение (0,983) свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Поэтому целесообразно использовать аппроксимирующую прямую, для нахождения коэффициентов уравнения которой используем формулы:
=НАКЛОН(B3:G3;B2:G2)
=ОТРЕЗОК(B3:G3;B2:G2)
Для нахождения спроса на товары за июль при условии, что будет произведено, например, 2000 единиц продукции, используем полученное уравнение:
=B6*H2+B7
Полученное значение:
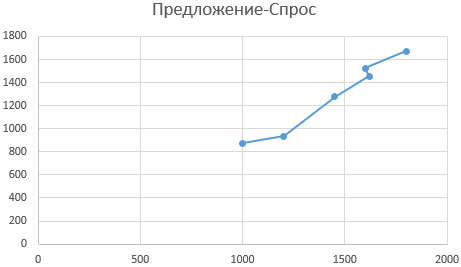
Альтернативным использованию функции НАКЛОН вариантом нахождения наклона в Excel является графический метод. Построим график на основе имеющихся данных, при этом для значений X выберем диапазон ячеек со значениями числа произведенных товаров, а для Y – с числом купленных товаров:
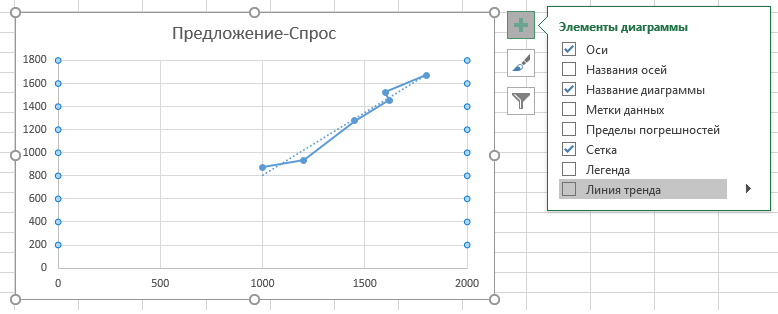
Отобразим на графике линию тренда:
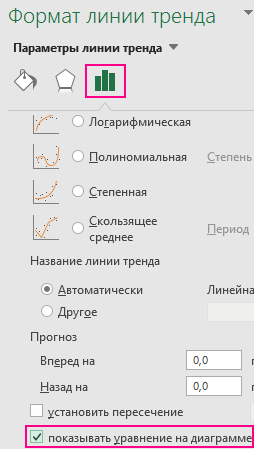
В меню «Формат линии тренда» установим флажок напротив пункта «показывать уравнение на диаграмме»:
График примет следующий вид:
Как видно, найденные коэффициенты a и b соответствуют отображаемым на графике.
Особенности использования функции НАКЛОН в Excel
Функция имеет следующий синтаксис:
=НАКЛОН(известные_значения_y;известные_значения_x)
Описание аргументов (все являются обязательными для заполнения):
- известные_значения_y – аргумент, принимающий массив числовых значений или ссылку на диапазон ячеек, которые содержат числа, характеризующие значения зависимой переменной y, которые определены для известных значений x;
- известные_значения_x – аргумент, который может быть указан в виде массива чисел или ссылки на диапазон ячеек, содержащих числовые значения, которые характеризуют известные значения независимой переменной x.
Примечания:
- В качестве аргументов должны быть переданы массивы чисел либо ссылки на диапазоны ячеек с числовыми значениями или текстовыми строками, которые могут быть преобразованы к числам. Строки, не являющиеся текстовыми представлениями числовых данных, а также логические ИСТИНА и ЛОЖЬ в расчете не учитываются.
- Если в качестве аргументов были переданы массивы, содержащие разное количество элементов, или ссылки на диапазоны с разным количеством ячеек, функция НАКЛОН вернет код ошибки #Н/Д. Аналогичный код ошибки будет возвращен в случае, если оба аргумента принимают пустые массивы или ссылки на диапазоны пустых ячеек.
- Если оба аргумента ссылаются на нечисловые данные, функция НАКЛОН вернет код ошибки #ДЕЛ/0!.
- Если в диапазоне, переданном в качестве любого из аргументов, содержатся пустые ячейки, они игнорируются в расчете. Однако ячейки, содержащие значение 0 (нуль) будут учтены.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции НАКЛОН в Microsoft Excel.
Описание
Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой; иными словами, наклон — это скорость изменения значений вдоль прямой.
Синтаксис
НАКЛОН(известные_значения_y;известные_значения_x)
Аргументы функции НАКЛОН описаны ниже.
-
Известные_значения_y Обязательный. Массив или диапазон ячеек, содержащих зависимые числовые точки данных.
-
Известные_значения_x Обязательный. Множество независимых точек данных.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
-
Если аргументы известные_значения_y и известные_значения_x пусты или количество содержащихся в них точек не совпадает, функция НАКЛОН возвращает значение ошибки #Н/Д.
-
Уравнение наклона линии регрессии имеет следующий вид:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
-
Основной алгоритм, используемый в функциях НАКЛОН и ОТРЕЗОК, отличается от основного алгоритма функции ЛИНЕЙН. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то справедливо указанное ниже.
-
Наклон и ОТОКП возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритм НАКЛОН и ОТОКП предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Известные значения y |
Известные значения x |
|
|
02.01.1900 |
6 |
|
|
03.01.1900 |
5 |
|
|
09.01.1900 |
11 |
|
|
01.01.1900 |
7 |
|
|
08.01.1900 |
5 |
|
|
07.01.1900 |
4 |
|
|
05.01.1900 |
4 |
|
|
Формула |
Описание |
Результат |
|
=НАКЛОН(A3:A9;B3:B9) |
Наклон линии линейной регрессии для точек данных в диапазонах A3:A9 и B3:B9. |
0,305556 |
Нужна дополнительная помощь?
In this article, we will look into how to calculate the slope of a line in an Excel graph.
Slope of a line basically determines two parameters :
- The direction of a line.
- The steepness of a line (rise or fall).
It is generally denoted by the letter “m”. The equation of a line is given by the expression :
Where,
- m: Slope
- c: Intercept
The mathematical formula for the slope of a line is given by the ratio of rise and run and in geometry, it is denoted using tan theta.
In this article we are going to discuss various methods on how to find the slope of a line in Excel using a few examples.
Example 1 : Consider the dataset having x and y coordinates of a particle moving in 2-D plane.
Line Graph
Finding Slope:
There are three methods :
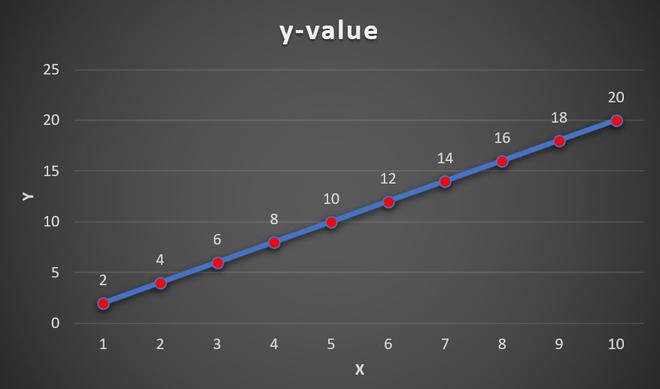
1. By using the Excel in-built function SLOPE. The syntax is :
=SLOPE(known_ys,knownx_s) known_ys : An array of numeric data points which are dependent. These are dependent on value of horizontal axis. known_xs : An array of numeric data points which are independent.
2. By using the slope formula as discussed.
The steps are :
- From the data set take any pair of points.
- The points are (x1, y1) and (x2, y2).
- Use the formula and “-“,”/” operators to find the slope, m.
3. By plotting a trendline on the line graph and find its equation. From the equation of the trendline we can easily get the slope.
Method 1: Using Slope function
Here, Y-axis array is stored in B column. The array ranges from B2 to B11.
The X-axis array is stored in A column of the Excel sheet. The array ranges from A2 to A11.
Method 2: Using Slope formula
Consider the points (1,2) and (2,4). Here, y1=2 and stored in the location B2 and y2=4 stored in location B3 and x1=1 stored in the location A2 and x2=2 stored in the location A3 of the worksheet.
Method 3:
The steps are :
- Plot the line graph by selecting the dataset and then go to the Insert Tab and then click on Insert Line or Area Chart.
- The line chart is plotted.
- Now select the chart and then click on the “+” button in the top right corner of the Chart.
- The Chart Elements dialog box appears. In this check the Trendline option. This will add the trendline to the existing line graph.
- Now select the Trendline in the chart and right-click on it and then click on Format Trendline.
- The Format Trendline dialog box opens. By default, the trendline will be linear.
- Now, check the box “Display Equation on the chart”.
- This will add the equation of the line on the chart.
The equation of the line is
y=2x
By comparing with the general equation y = mx + c, we get
m=2, c=0
The slope is 2 for the given line.
Example 2: Consider the dataset shown below :
Similarly, by using the trendline and its equation you can easily find the slope of the line is -0.5.
Содержание
- Как найти наклон линии тренда в Excel
- Шаг 1: Создайте данные
- Шаг 2: Создайте диаграмму рассеяния
- Шаг 3: Добавьте линию тренда
- Шаг 4: Отображение наклона линии тренда
- Как найти тангенс угла наклона в excel
- Функция TAN
- Описание
- Синтаксис
- Замечания
- Пример
- Построение линии тренда в Excel
- Генерация сезонных трендов в MS EXCEL
- Сезонные тренды на основе ломаных линий
- Построение ломаной линии тренда и границ разброса
- Равномерный разброс
- Нормальный разброс
- Сезонные тренды на основе периодических функций
Как найти наклон линии тренда в Excel
Часто вам может понадобиться найти наклон линии тренда в Excel.
К счастью, это довольно легко сделать, и следующий пошаговый пример показывает, как это сделать.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных для работы:
Шаг 2: Создайте диаграмму рассеяния
Далее давайте создадим диаграмму рассеяния для визуализации данных.
Для этого выделите данные:
Затем щелкните вкладку « Вставка » на верхней ленте и выберите первый параметр в параметре « Вставить точечный» (X, Y) в группе « Диаграммы ». Это даст следующую диаграмму рассеяния:
Шаг 3: Добавьте линию тренда
Далее добавим линию тренда на диаграмму рассеяния.
Для этого щелкните в любом месте диаграммы рассеяния. Затем щелкните зеленый значок плюса (+) в правом верхнем углу графика и установите флажок рядом с линией тренда :
Шаг 4: Отображение наклона линии тренда
Чтобы найти наклон линии тренда, щелкните стрелку вправо рядом с линией тренда и выберите « Дополнительные параметры »:
В появившемся окне в правой части экрана поставьте галочку рядом с Display Equation on chart :
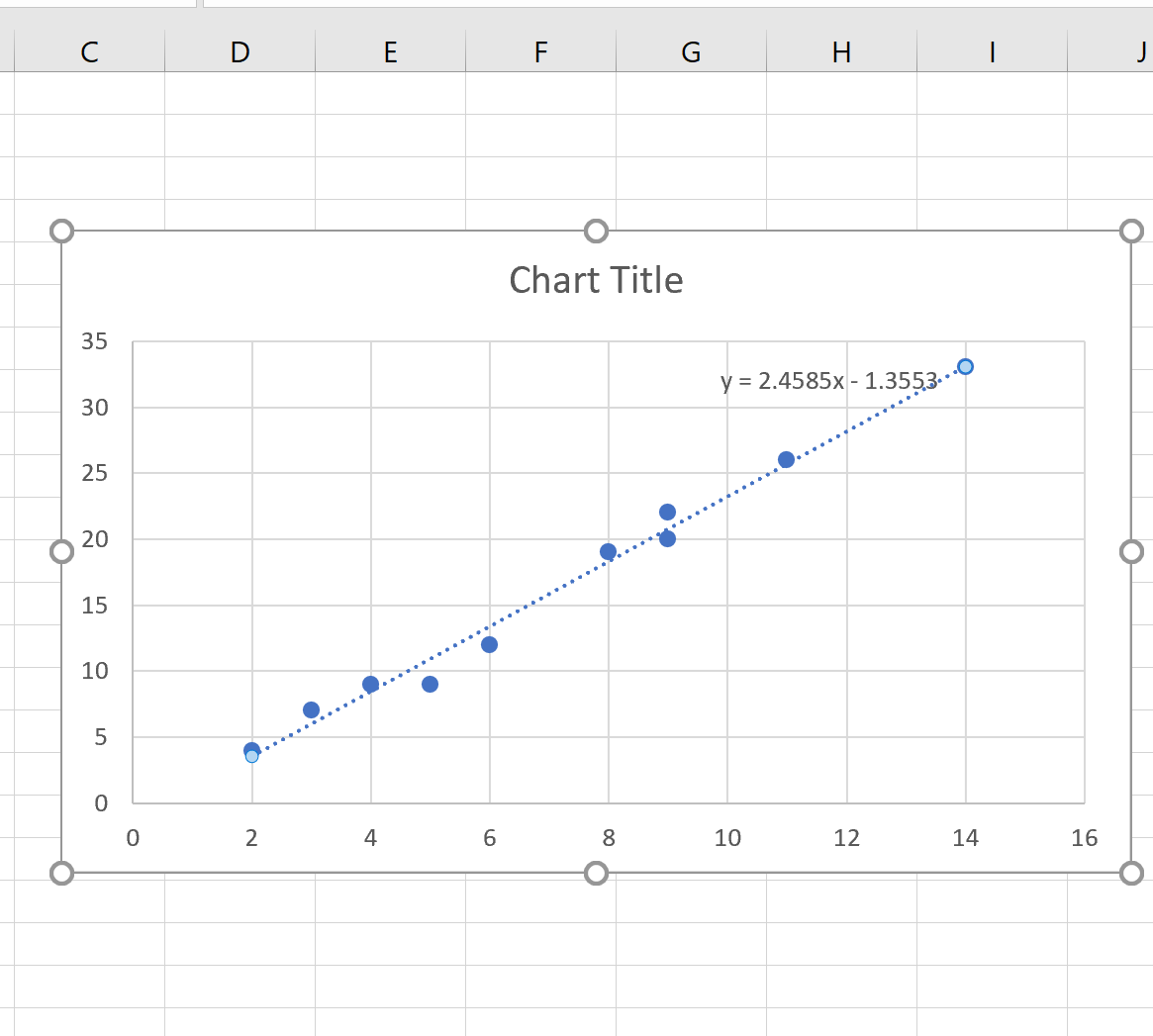
Уравнение линии тренда автоматически появится на диаграмме рассеяния:
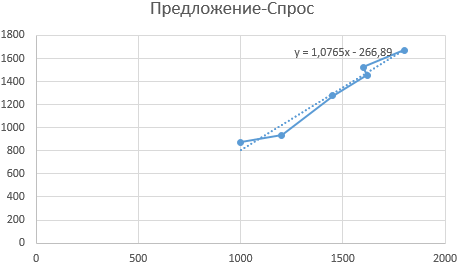
Уравнение линии тренда оказывается y = 2,4585x – 1,3553 .
Это означает, что точка пересечения равна -1,3553 , а наклон равен 2,4585 .
Вы можете найти больше руководств по Excel на этой странице .
Источник
Диаграммы и графики используются для анализа числовых данных, например, для оценки зависимости между двумя видами значений. С этой целью к данным диаграммы или графика можно добавить линию тренда и ее уравнение, прогнозные значения, рассчитанные на несколько периодов вперед или назад.
Линия тренда представляет собой прямую или кривую линию, аппроксимирующую (приближающую) исходные данные на основе уравнения регрессии или скользящего среднего. Аппроксимация определяется по методу наименьших квадратов. В зависимости от характера поведения исходных данных (убывают, возрастают и т.д.) выбирается метод интерполяции, который следует использовать для построения тренда.
Предусмотрено несколько вариантов формирования линии тренда.
Линейной функцией: y=mx+b
где m — тангенс угла наклона прямой, b — смещение.
Прямая линия тренда (линейный тренд) наилучшим образом подходит для величин, изменяющихся с постоянной скоростью. Применяется в случаях, когда точки данных расположены близко к прямой.
Логарифмической функцией: y=c*lnx+b
где с и b — константы.
Логарифмическая линия тренда соответствует ряду данных, значения которого вначале быстро растут или убывают, а затем постепенно стабилизируются. Может использоваться для положительных и отрицательных данных.
Полиномиальной функцией (до 6й степени включительно): y= b + c1*x + c2*x 2 + c3*x 3 + . + c6*x 6
Полиномиальная линия тренда используется для описания попеременно возрастающих и убывающих данных. Степень полинома подбирают таким образом, чтобы она была на единицу больше количества экстремумов (максимумов и минимумов) кривой.
Степенной функцией: y = cxb
где c и b — константы.
Степенная линия тренда дает хорошие результаты для положительных данных с постоянным ускорением. Для рядов с нулевыми или отрицательными значениями построение указанной линии тренда невозможно.
Экспоненциальной функцией: y = cebx
где c и b — константы, е — основание натурального логарифма.
Экспоненциальный тренд используется в случае непрерывного возрастания изменения данных. Построение указанного тренда не возможно, если в множестве значений членов ряда присутствуют нулевые или отрицательные данные.
С использованием линейной фильтрации по формуле: Ft= (At+A(t-1)+⋯+A(t-n+1))/n
где n — общее число членов ряда, t — заданное число точек (2 ≤ t
Информационные технологии. Другие материалы
Источник
Как найти тангенс угла наклона в excel
Функция TAN
В этой статье описаны синтаксис формулы и использование tan в Microsoft Excel.
Описание
Возвращает тангенс заданного угла.
Синтаксис
Аргументы функции TAN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется тангенс.
Замечания
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Построение линии тренда в Excel
Диаграммы и графики используются для анализа числовых данных, например, для оценки зависимости между двумя видами значений. С этой целью к данным диаграммы или графика можно добавить линию тренда и ее уравнение, прогнозные значения, рассчитанные на несколько периодов вперед или назад.
Линия тренда представляет собой прямую или кривую линию, аппроксимирующую (приближающую) исходные данные на основе уравнения регрессии или скользящего среднего. Аппроксимация определяется по методу наименьших квадратов. В зависимости от характера поведения исходных данных (убывают, возрастают и т.д.) выбирается метод интерполяции, который следует использовать для построения тренда.
Предусмотрено несколько вариантов формирования линии тренда.
Линейной функцией: y=mx+b
где m — тангенс угла наклона прямой, b — смещение.
Прямая линия тренда (линейный тренд) наилучшим образом подходит для величин, изменяющихся с постоянной скоростью. Применяется в случаях, когда точки данных расположены близко к прямой.
Логарифмической функцией: y=c*lnx+b
где с и b — константы.
Логарифмическая линия тренда соответствует ряду данных, значения которого вначале быстро растут или убывают, а затем постепенно стабилизируются. Может использоваться для положительных и отрицательных данных.
Полиномиальной функцией (до 6й степени включительно): y= b + c1*x + c2*x 2 + c3*x 3 + . + c6*x 6
Полиномиальная линия тренда используется для описания попеременно возрастающих и убывающих данных. Степень полинома подбирают таким образом, чтобы она была на единицу больше количества экстремумов (максимумов и минимумов) кривой.
Степенной функцией: y = cxb
где c и b — константы.
Степенная линия тренда дает хорошие результаты для положительных данных с постоянным ускорением. Для рядов с нулевыми или отрицательными значениями построение указанной линии тренда невозможно.
Экспоненциальной функцией: y = cebx
где c и b — константы, е — основание натурального логарифма.
Экспоненциальный тренд используется в случае непрерывного возрастания изменения данных. Построение указанного тренда не возможно, если в множестве значений членов ряда присутствуют нулевые или отрицательные данные.
С использованием линейной фильтрации по формуле: Ft= (At+A(t-1)+⋯+A(t-n+1))/n
где n — общее число членов ряда, t — заданное число точек (2 ≤ t
Информационные технологии. Другие материалы
Источник
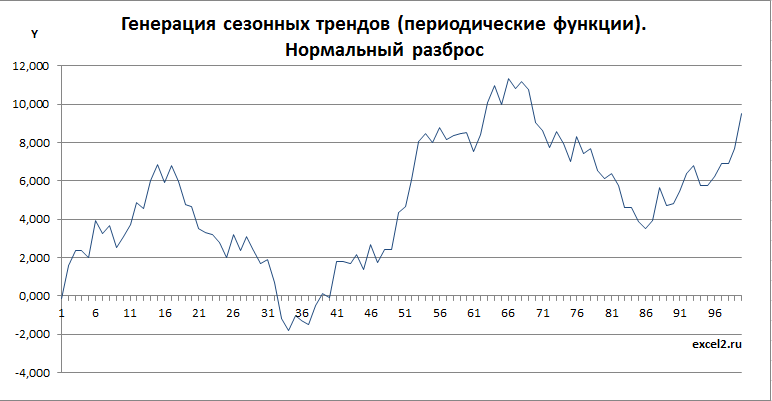
Генерация сезонных трендов в MS EXCEL
history 12 февраля 2021 г.
Для построения статистических моделей часто требуются наборы случайных данных, которые бы содержали нужный тип тренда. Их можно найти в открытом доступе (например, в этой статье ), но иногда их удобно быстро сгенерировать самостоятельно.
Сезонные тренды на основе ломаных линий
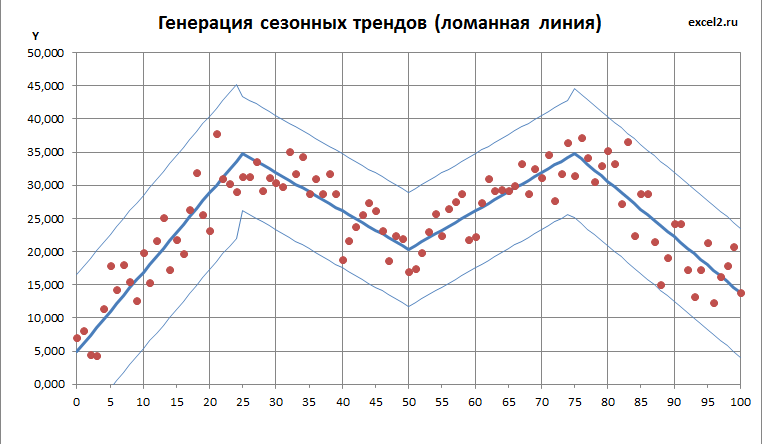
Зададим сезонный тренд с помощью нескольких прямых линий (см. файл примера ).
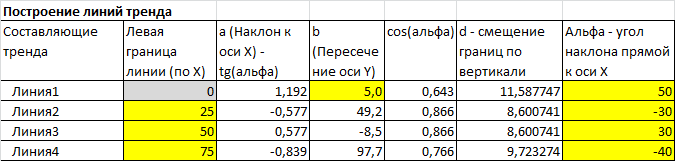
Как известно, уравнение прямой линии y=a*x+b. Чтобы задать прямую линию нужно 2 параметра: наклон прямой к оси Х (параметр а, он также является тангенсом угла наклона прямой к оси Х) и координата пересечения прямой с осью Y (параметр b).
В файле примера , вместо параметра b мы будем задавать координаты по оси Х, в которых происходит излом прямой линии – это удобнее. Для первой линии придется все же задать параметр b, для других отрезков ординату точки пересечения прямой линией оси Y (оси ординат), т.е. параметр b, будем вычислять. Наклон будем задавать, указывая угол в градусах (острый угол – восходящий тренд: 30, 45, 60 и т.п., отрицательные значения – для тупого угла (нисходящий тренд)).
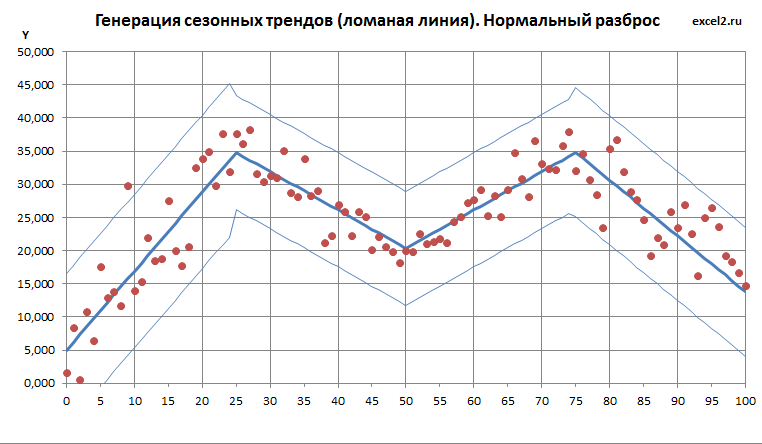
Построение ломаной линии тренда и границ разброса
Для этого чтобы вычислить tg угла наклона (параметр а ) нам понадобится формула = TAN(РАДИАНЫ(G8)) . Функция TAN() воспринимает радианы, поэтому для перевода градусов в радианы используем функцию РАДИАНЫ() . Градусы в радианы можно перевести просто умножив значение в градусах на дробь ПИ()/180 .
Для разброса случайных значений вокруг линии тренда нам потребуется задать границы разброса. В файле примера в качестве меры разброса предложено использовать диапазон изменения величины Y первой линии тренда (для этого достаточно умножить тангенс угла наклона первой линии на диапазон изменения по Х первого отрезка). Используя вместо абсолютного значения диапазон изменения величины Y первой линии тренда, нам не потребуется вычислять величину разброса каждый раз, когда мы меняем тренда.
Примечание : диапазон изменения величины Y первой линии тренда не может быть равен 0, т.к. диапазон разброса будет также равен 0. Иными словами, первая линия не должна быть горизонтальной.
Чтобы иметь возможность менять границы разброса независимо от параметров первой линии тренда, в ячейке В14 введем коэффициент разброса K – это просто доля от диапазона изменения величины Y первого отрезка. Итак, пусть h — расстояние от линии тренда до верхней (или нижней) границы (в перпендикулярном к линии направлении), формула для вычисления h=a*∆x*K
Остается еще одна проблема – для разных линий, имеющих разный наклон нужно чтобы границы разброса отстояли от линии тренда на одну и туже величину h (в перпендикулярном к линии направлении). Для этого для каждой линии будем вычислять проекцию h на ось Y, назовем ее величиной d. Для этого используем формулу =h*COS(РАДИАНЫ(G8)), в ячейке находится G8 находится величина h.
Примечание : Для того чтобы на диаграмме EXCEL границы разброса отстояли от разных линий тренда визуально на одну и туже величину требуется, чтобы диаграмма имела одинаковый масштаб по Х и по Y. Если по Х откладывается время, а по Y, например, стоимость акции, то физический смысл «равенства» масштабов не понятен. Можно вообще пренебречь изменением границ разброса по Y в зависимости от угла наклона прямой – в этом случае не требуется вычислять величину d, просто используйте величину h. В файле примера масштабы осей совпадают и введен поправочный коэффициент COS(РАДИАНЫ(G8)) , поэтому диапазон разброса у всех отрезков ломаной линии тренда одинаков (это видно на рисунке выше).
С границами определились, переходим к построению точек, имитирующих разброс около линии тренда. Разброс значений случайной величины будем осуществлять с помощью нормального и равномерного распределения . Про генерацию случайных чисел можно прочитать здесь .
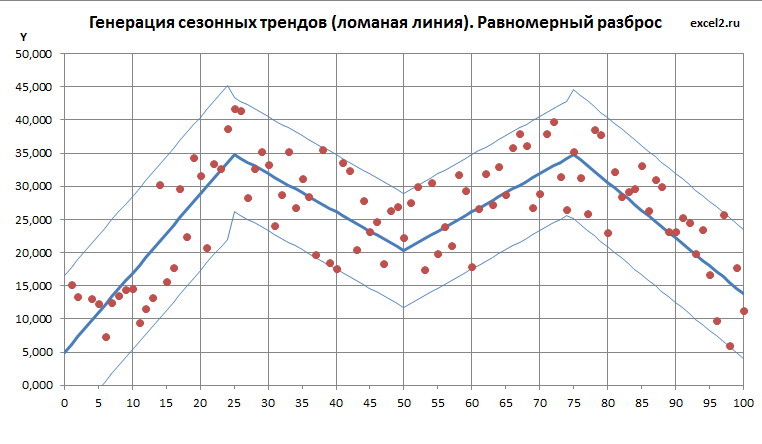
Равномерный разброс
Про равномерный разброс написана целая статья, здесь только укажем, что нам понадобится функция СЛУЧМЕЖДУ() , которая возвращает случайное целое число между заданных границ. Границы мы вычислили в предыдущем разделе, окончательная формула выглядит так: = СЛУЧМЕЖДУ(J19*10;K19*10)/10 , где J19 содержит координату Y нижней границы для заданного Х, а K19 – верхней. Умножение и деление на 10 нужно, чтобы результат возвращался не в целых числах, а с точностью до десятых. В этом случае точки будут размещаться более естественно, без стратификации (это зависит от диапазона изменения Y в каждой конкретной задаче).
Примечание : вместо функции СЛУЧМЕЖДУ() можно использовать СЛЧИС() , возвращающей случайное вещественное число от 0 до 1 .
Как видно на картинке выше точки случайных значений равномерно распределены между границами, ни одна точка не может выйти за границы (вероятность этого события равна 0). Это принципиальное отличие от разброса по нормальному закону.
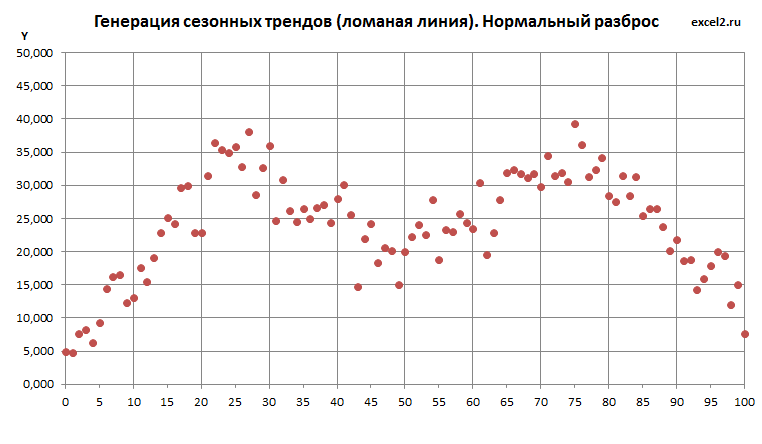
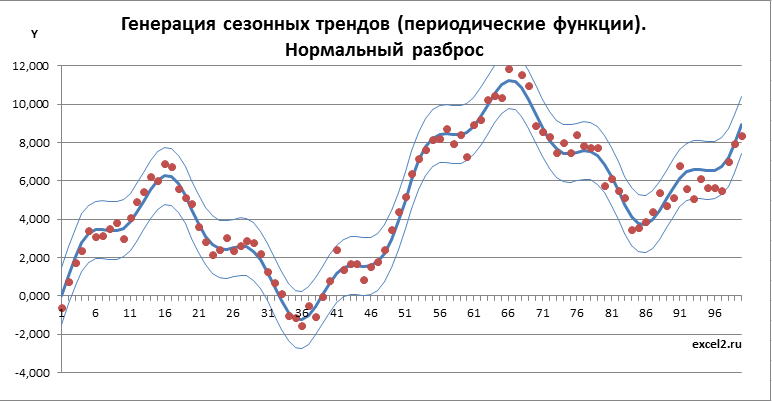
Нормальный разброс
Про нормальный разброс также написана целая статья . Нам понадобится функция НОРМ.ОБР() , которая возвращает значение случайной величины имеющей нормальное распределение (для указанного среднего и стандартного отклонения , а также заданной вероятности). В качестве среднего нужно взять линию тренда, точнее координату Y линии тренда для заданного Х. Т.к. известно, что 99,7% значений такой случайной величины находится на расстоянии не более 3 сигма от среднего (сигма — стандартное отклонение), то в качестве стандартного отклонения логично взять 1/3 расстояния от тренда до границы (d).
Формула для генерации значений, имеющих нормальный разброс, выглядит так:
= НОРМ.ОБР(СЛЧИС();I19;ВПР(A19;$B$8:$F$11;5)/3)
Функция СЛЧИС() задает вероятность (от 0 до 1) того, что случайная величина, распределенная по заданному нормальному закону, менее или равна величине возвращаемой формулой. Подробнее про обратные функции см. в статье про квантили распределения . Функция ВПР() просто возвращает расстояние от тренда до границы.
Как видно на картинке выше, точки случайных значений в основном находятся ближе к линии тренда, однако вероятность выхода точек за границы не равна 0 (точка с Х=9). Это принципиальное отличие от разброса по равномерному закону (см. предыдущий график).
Для отображения различных законов распределения в файле примера использован Элемент управления Переключатель .
Для скрытия тренда и/ или границ разброса использован Элемент управления Флажок .
После каждого изменения на листе (ввод значения, нажатие клавиши F9 или вставка значения в ячейку) функция СЛЧИС() заново генерирует новое значение, поэтому точки на диаграмме автоматически перестраиваются. Чтобы этого избежать отключите автоматический пересчет листа (в MS EXCEL 2010 это вкладка Формулы, группа Вычисления, кнопка Параметры вычислений).
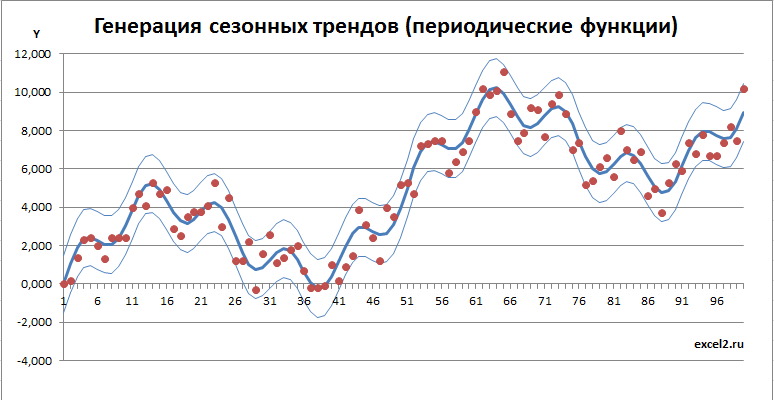
Сезонные тренды на основе периодических функций
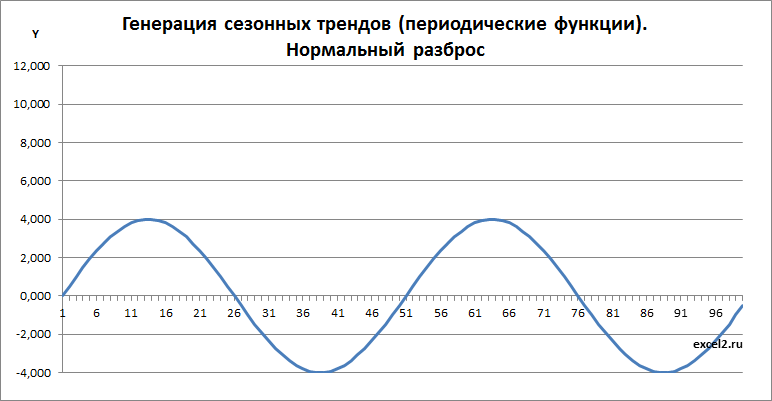
Построим сезонный тренд на основе 2-х периодических функций (синус) с добавлением линейного тренда.
Всего будет 3 составляющих тренда:
• Краткосрочный (на оси Х укладывается 8-10 циклов)
• Долгосрочный (2-4 цикла с увеличенной амплитудой по сравнению с краткосрочным)
• Линейный (восходящий или нисходящий)
Как и для тренда на основе ломаной линии разброс будет сделан по 2-м законам: равномерному и нормальному (см. файл примера ).
Краткосрочный тренд можно задать с помощью функции синус:
=SIN(2*ПИ()/100*A16*$B$7)
В ячейке B7 укажем число периодов функции синус, которое должно укладываться на всей оси Х диаграммы. 2*ПИ() – это значение периода функции синус. Деление на 100 (количество точек на диаграмме в файле примера, равномерно распределенных по оси Х) необходимо, чтобы на диаграмме разместилось целое количество периодов (для целых значений в ячейке В7, конечно). В целом, конечно, это больше для красоты.
Примечание : Чтобы на диаграмме в файле примера отображался только краткосрочный тренд установите 0 в ячейке С8 (масштаб долгосрочного тренда) и в ячейке В11 (наклон линейного тренда).
Долгосрочный тренд можно задать с помощью аналогичной формулы:
=$C$8*SIN(2*ПИ()/100*A16*$B$8)
В ячейке С8 указан масштаб долгосрочного тренда относительно амплитуды краткосрочного (равного 1).
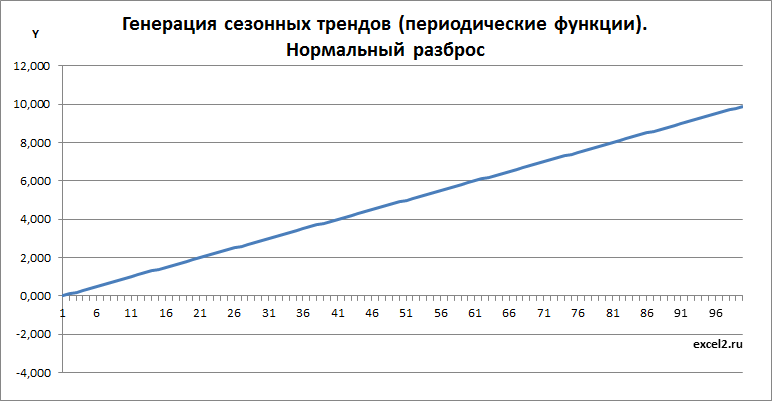
Линейный тренд можно получить путем умножения координаты Х на константу.
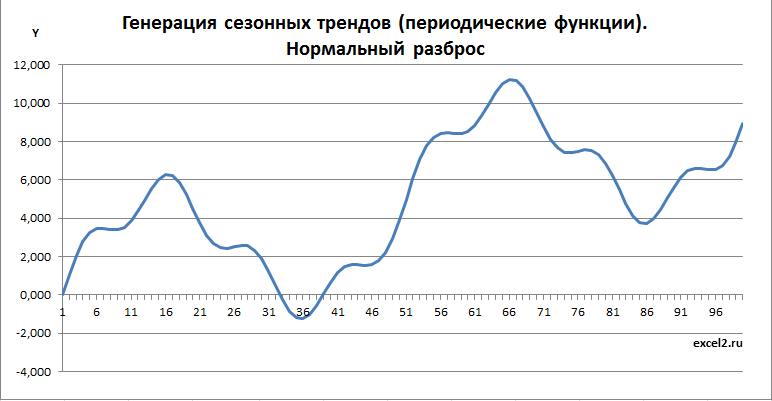
Арифметическая сумма трех составляющих тренда дает специфический тренд:
Добавив границы и точки, соответствующие случайным значениям, получим вот такую картинку.
Если убрать границы, линию тренда, а также маркеры точек и соединить их линиями, то получим вот такой сезонный тренд.
Добавив нужное количество точек и подобрав соотношение между краткосрочным и долгосрочным трендом, уверен, можно получить вполне реалистичную картинку, наподобие графика индекса S&P 500.
Источник
Содержание:
- Что такое наклон? Обзор
- Метод 1: Использование функции наклона Excel
- Синтаксис функции НАКЛОН в Excel
- Что следует помнить при использовании функции НАКЛОН в Excel
- Способ 2 — Использование точечной диаграммы для получения значения наклона
В склон линии регрессии является мерой крутизны линии.
Это числовое значение, которое говорит нам, как связаны две переменные. Он сообщает нам, насколько изменится зависимая переменная в случае изменения независимой переменной.
Есть три способа найти наклон линии регрессии для заданного набора переменных в Excel:
- Использование функции НАКЛОН
- Использование точечной диаграммы Excel
В этом уроке я покажу вам, как рассчитать уклон, используя каждый из трех вышеупомянутых методов.
Что такое наклон? Обзор
Наклон — это значение, которое сообщает нам, как два значения (обычно называемые значениями x и y) связаны друг с другом.
Чтобы дать вам простой пример, если у вас есть данные о росте и годовом доходе некоторых людей и вы рассчитываете наклон для этих данных, он скажет вам, существует ли положительная или отрицательная корреляция между этими точками данных.
Значение наклона может быть положительным или отрицательным.
В нашем примере, если значение наклона равно 138, это означает, что существует положительная корреляция между ростом и доходом людей. Так что, если рост увеличится на 1 сантиметр, доход, скорее всего, увеличится на 138 долларов.
Помимо наклона, еще одна вещь, о которой вам нужно знать, — это Intercept.
Позвольте мне объяснить это уравнением:
Y = наклон * X + точка пересечения
В этом уравнении мы уже вычислили наклон, но чтобы точно знать, каким будет значение Y для данного значения X, вам также необходимо знать точку пересечения.
К счастью, в Excel есть формула для этого, и я расскажу, как вычислить перехват во всех методах.
Метод 1: Использование функции наклона Excel
Самый простой способ рассчитать уклон в Excel — использовать встроенную НАКЛОН функция.
Он находит значение наклона заданного набора х-у координаты за один шаг.
Хотя вычисление уклона вручную может быть трудным, с функцией НАКЛОН вам просто нужно указать ей значения x и y, и она выполняет всю тяжелую работу в бэкэнде.
Синтаксис функции НАКЛОН в Excel
Синтаксис функции наклона:
= НАКЛОН (y_val, x_val)
Здесь, y_val и x_val каждый состоит из массива или диапазона ячеек, содержащих числовые зависимые значения данных.
Помните, что вам нужно дать Значения Y в качестве первого аргумента и значения X в качестве второго аргумента. Если вы сделаете наоборот, вы все равно получите результат, но он будет неверным.
Предположим, у вас есть приведенный ниже набор данных, как показано ниже, где у меня есть рост (в см) как значения X и средний годовой доход (в долларах США) как значения Y.
Ниже приведена формула для расчета уклона с использованием этого набора данных:
= НАКЛОН (B2: B11; A2: A11)
Приведенный выше результат говорит мне, что из этого набора данных я могу предположить, что в случае увеличения роста на 1 см доход увеличится на 138,58 долларов США.
Еще одна распространенная статистическая величина, которую люди часто вычисляют при работе с уклоном, — это вычисление Значение перехвата.
Чтобы обновить, уравнение наклона выглядит примерно так:
Y = наклон * X + точка пересечения
Хотя нам известен наклон, нам также необходимо знать значение точки пересечения, чтобы убедиться, что мы можем вычислить значения Y для любого значения X.
Это легко сделать с помощью следующей формулы:
= ПЕРЕСЕЧЕНИЕ (B2: B11; A2: A11)
При этом наше уравнение для этого набора данных становится:
Y = 138,56 * X + 65803,2
Итак, если я спрошу вас, каков будет доход любого человека, чей рост составляет 165 см, вы легко сможете рассчитать его стоимость.
Y = 138,56 * 165 + 65803,2
Значения наклона и точки пересечения могут быть положительными или отрицательными.
Что следует помнить при использовании функции НАКЛОН в Excel
Вот несколько моментов, которые следует помнить при нахождении наклона линии регрессии с помощью функции НАКЛОН:
- Аргументы функции НАКЛОН должны быть числовыми (значения DATE также принимаются). Если какая-либо из ячеек пуста или содержит текстовую строку, они будут проигнорированы.
- Если в какой-либо ячейке / ячейках стоит «0», он будет использоваться при вычислении.
- Должно быть равное количество Икс и у значения при использовании в качестве входных данных для функции НАКЛОН. Если вы укажете диапазоны неравных размеров, вы получите ошибку # N / A
- Должно быть несколько наборов точек, иначе функция НАКЛОН вернет #DIV! ошибка
Способ 2 — Использование точечной диаграммы для получения значения наклона
Если вы предпочитаете визуализировать данные и линию регрессии, вы можете нанести данные на диаграмму рассеяния и использовать ее, чтобы найти наклон и точку пересечения линии тренда (также называемой линией наилучшего соответствия).
Предположим, у вас есть набор данных, показанный ниже, и вы хотите узнать наклон и точку пересечения для этих данных:
Ниже приведены шаги для этого:
- Выберите точки данных X и Y (в нашем примере это будут столбцы высоты и дохода).
- Перейдите на вкладку «Вставка» на ленте.
- Щелкните раскрывающееся меню «Вставить разброс» (под группой «Диаграммы»).
- В появившемся раскрывающемся списке выберите вариант «Точечная диаграмма».
- Это вставит точечную диаграмму в ваш рабочий лист, отображая ваши значения x-y в виде точек разброса (как показано ниже).
- Щелкните правой кнопкой мыши одну из точек разброса и выберите «Добавить линию тренда» в появившемся контекстном меню. Линия тренда будет вставлена, а справа откроется панель «Форматировать линию тренда».
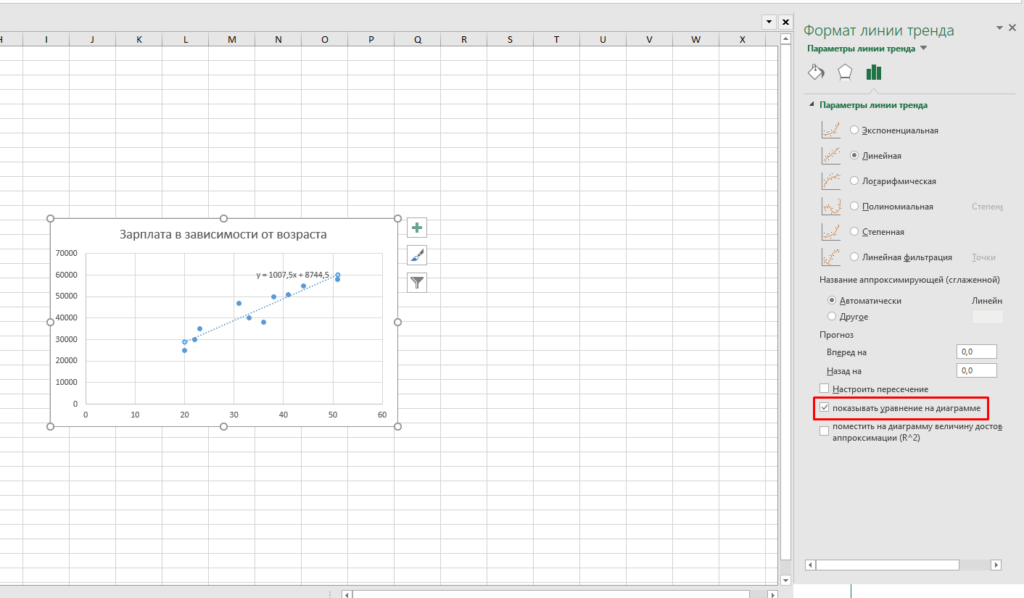
- На панели «Форматирование линии тренда» в разделе «Параметры линии тренда» установите флажок «Отображать уравнение на диаграмме».
- Закройте панель «Форматировать линию тренда»
Приведенные выше шаги позволят вставить диаграмму рассеяния с линией тренда, а линия тренда также имеет уравнение наклона и пересечения.
В нашем примере мы получаем следующее уравнение:
у = 138,56x + 65803
Здесь:
- 138,56 — наклон линии регрессии
- 65803 — точка пересечения линии регрессии
Вы можете сравнить это со значениями, которые мы получили от функций НАКЛОН и ПЕРЕСЕЧЕНИЕ (это то же значение).
Если значение наклона положительное, вы увидите, что линия тренда идет вверх, а если значение наклона отрицательное, вы увидите, что линия тренда идет вниз. Крутизна склона будет зависеть от его значения уклона.
Хотя метод формулы для вычисления наклона и пересечения несложен, преимущество использования метода точечной диаграммы состоит в том, что вы можете визуально увидеть распределение точек данных, а также наклон линии регрессии.
И в случае, если вы все равно создаете диаграмму рассеяния для своих данных, получение значения наклона путем добавления линии тренда на самом деле будет быстрее, чем использование формул.
Итак, это два действительно простых способа, которые вы можете использовать для вычисления наклона и значения пересечения набора данных в Excel.
Надеюсь, вы нашли этот урок полезным.
Наклон линии линейной регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X).
Это цифра, означающая уровень корреляции переменных X и Y. Грубо говоря, с помощью этого мы можем понять как изменится зависимая переменная, если мы поменяем независимую.
Всего в Excel есть два метода нахождения этой переменной.
- С помощью функции НАКЛОН;
- С помощью диаграммы.
В этой статье я продемонстрирую вам оба этих способа.
Содержание
- Что такое наклон линии линейной регрессии?
- С помощью функции НАКЛОН
- Составление формулы для функции НАКЛОН
- Инструкция по использованию функции НАКЛОН и ОТРЕЗОК
- С помощью диаграммы
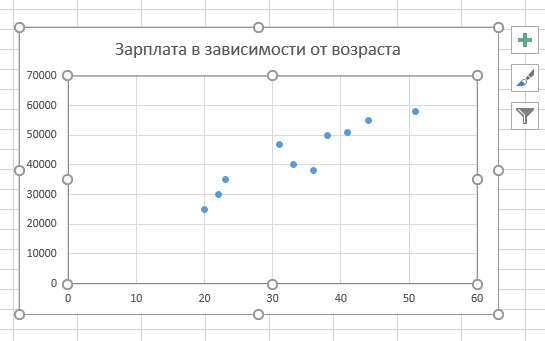
Что такое наклон линии линейной регрессии?
Наклон линии линейной регрессии — это численное значение, которое указывает на то, как два числовых значения(часто их называют переменными X и Y) зависят друг от друга, если точнее то одна из них зависимая переменная, а другая независимая.
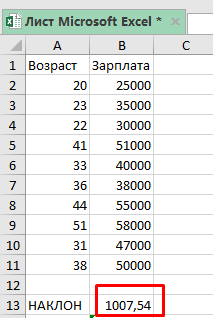
К примеру, мы имеем информацию о возрасте людей и их среднем месячном доходе. Если мы будем вычислять для них наклон линии регрессии, он покажет есть ли связь между этими двумя параметрами.
«Наклон» бывает положительный, либо отрицательный.
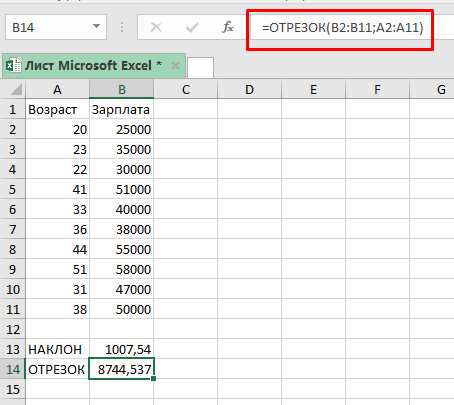
В данной ситуации мы имеем положительный наклон, это значит что есть положительная связь между возрастом людей и их зарплатой. Из этого значения наклона мы можем понять, что в среднем при увеличении возраста человека на 1 год, он зарабатывает на 1007,54 больше.
Кроме наклона линии, есть кое-что еще интересное, это функция ОТРЕЗОК.
Проще всего объяснить так:
Y = НАКЛОН*X + ОТРЕЗОКВ прошлом шаге мы рассчитали наклон линии, но чтобы вычислить значение Y, нам нужно знать еще и ОТРЕЗОК.
Я также продемонстрирую вам как вычислять и ОТРЕЗОК.
С помощью функции НАКЛОН
С помощью функции НАКЛОН можно рассчитать наклон линии, это стандартный способ.
Нам нужно просто указать значение независимой и зависимой переменных. Далее функция сделает все сама.
Составление формулы для функции НАКЛОН
Формула функции выглядит следующим образом:
=НАКЛОН(Y; X) Аргументы функции X и Y состоят из диапазона ячеек для которых нужно определить зависимость.
Не забывайте, что первым аргументом функции является Y, а вторым уже X. Если вы забудете об этом, то получите неправильный результат.
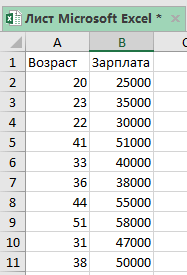
Допустим, у нас есть таблица, как на картинке. X в данном случае это возраст человека, а Y — его зарплата.
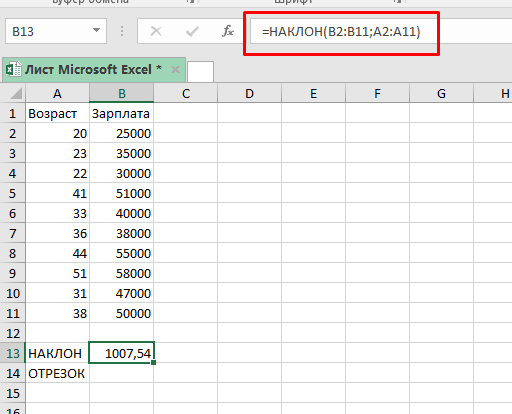
Конкретно для нашего примера, функция примет следующий вид:
=НАКЛОН(B2:B11;A2:A11) Вычисление закончено. С помощью цифры, которую вывела наша функция, мы можем сказать, что в среднем, по этим данным, зарплата человека увеличивается на 1007,54 с каждым годом.
Расчет наклона тесно связан с еще одной важной величиной — ОТРЕЗКОМ.
Есть уравнение:
Y = Наклон*X + ОтрезокВ нашем примере мы вычислили наклон линии, но чтобы знать значение Y для абсолютно любого X, мы должны знать еще и значение отрезка.
Вычислить его, мы можем с помощью специальной функции в Excel:
=ОТРЕЗОК(B2:B11;A2:A11) Итак, уравнение, которое мы показывали выше, теперь, принимает такую форму:
Y = 1007,54*X + 8744,537На данный момент, зная возраст человека, мы уже можем сказать, сколько будет его средняя зарплата. Подставим все значения, в наше уравнение:
Y =1007,54*37 + 8744,537 Оба параметра, которые мы с вами научились вычислять, могут быть как положительными, так и отрицательными.
Инструкция по использованию функции НАКЛОН и ОТРЕЗОК
Мы с вами уже научили вычислять значения обеих функций, но есть кое-что о чем нужно знать:
- Аргументы обеих функций могут быть только числовыми.
- В этом случае, Excel не будет игнорировать нули, они участвуют во всех операциях.
- Важный момент, что в первом и втором аргументе должен быть одинаковый по количеству ячеек диапазон, иначе Excel будет возвращать вам ошибку.
- Также, в диапазоне ячеек должно быть больше, чем одна ячейка.
С помощью диаграммы
В случае если вам нравится использовать диаграммы, можно использовать эту функцию построения диаграммы в Excel чтобы вычислить НАКЛОН и ОТРЕЗОК.
Допустим, у нас есть все та же табличка с данными, которую мы использовали в первом способе.
Чтобы построить диаграмму, следуйте пошаговому руководству:
- Выделите диапазон ячеек, которые будут являться зависимыми и независимыми переменными .
- Щелкните на раздел «Вставка» в меню Excel.
- Выберите функцию «Вставить диаграмму».
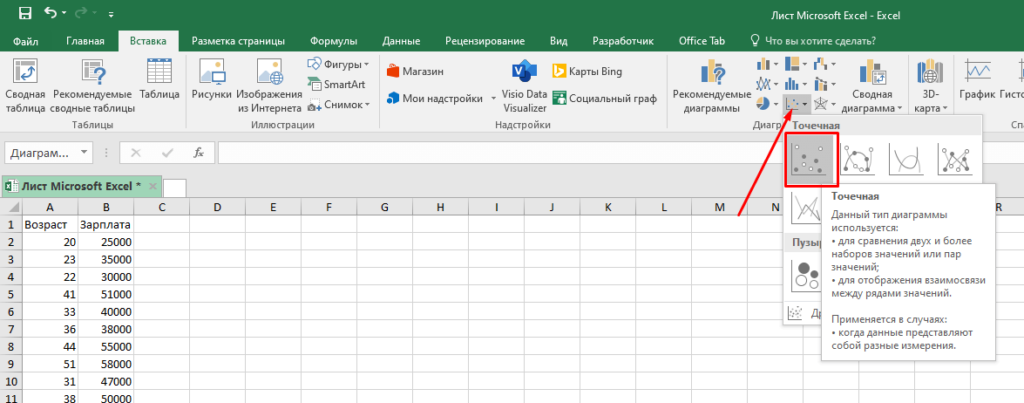
- И укажите, что вам нужна точечная диаграмма.
- Теперь Excel построит вам график, где будут соответствующие значения X и Y.
- Чтобы получить более детальную информацию, нажмите правой кнопкой мышки на любую из точек на графике. И щелкните на функцию «Добавить линию тренда». Откроется панель «Формат области построения».
- На этой панели, вам нужно поставить галочку на параметре «показывать уравнение на диаграмме».
Теперь на этой диаграмме нам показывает полную информацию по наклону линии и отрезку.
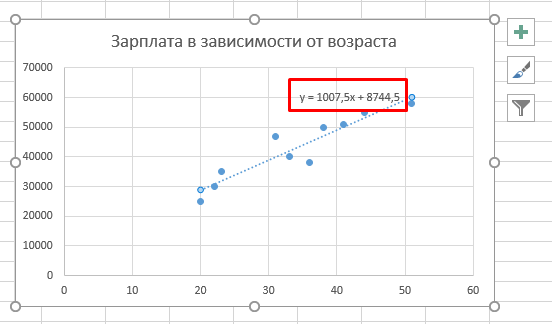
На графике, вы увидите точно такое же уравнение, которое мы составляли в прошлом способе.
y =1007,5x + 8744,5 Вот:
- 1007,5 — наклон линии линейной регрессии
- 8744,5 — отрезок линии линейной регрессии
Если, в вашем случае, получилось положительное значение наклона, то вы увидите что линия направлена вверх, если же отрицательное, то вниз.
Что ж, вот и все. Оба этих способа довольно простые, но я все же рекомендую вам использовать диаграмму. Потому что на графике вы можете увидеть как располагаются имеющиеся точки данных.
И к тому же, я думаю, этот способ будет гораздо быстрее, чем вариант с помощью формул.
Это были 2 простых метода, как можно рассчитать параметры наклона линии регрессии и отрезка в Excel.
Надеюсь, вам помогло данное руководство!
Диаграммы и графики используются для анализа числовых данных, например, для оценки зависимости между двумя видами значений. С этой целью к данным диаграммы или графика можно добавить линию тренда и ее уравнение, прогнозные значения, рассчитанные на несколько периодов вперед или назад.
Линия тренда представляет собой прямую или кривую линию, аппроксимирующую (приближающую) исходные данные на основе уравнения регрессии или скользящего среднего. Аппроксимация определяется по методу наименьших квадратов. В зависимости от характера поведения исходных данных (убывают, возрастают и т.д.) выбирается метод интерполяции, который следует использовать для построения тренда.
Предусмотрено несколько вариантов формирования линии тренда.
Линейной функцией: y=mx+b
где m — тангенс угла наклона прямой, b — смещение.
Прямая линия тренда (линейный тренд) наилучшим образом подходит для величин, изменяющихся с постоянной скоростью. Применяется в случаях, когда точки данных расположены близко к прямой.
Логарифмической функцией: y=c*lnx+b
где с и b — константы.
Логарифмическая линия тренда соответствует ряду данных, значения которого вначале быстро растут или убывают, а затем постепенно стабилизируются. Может использоваться для положительных и отрицательных данных.
Полиномиальной функцией (до 6й степени включительно): y= b + c1*x + c2*x 2 + c3*x 3 + . + c6*x 6
Полиномиальная линия тренда используется для описания попеременно возрастающих и убывающих данных. Степень полинома подбирают таким образом, чтобы она была на единицу больше количества экстремумов (максимумов и минимумов) кривой.
Степенной функцией: y = cxb
где c и b — константы.
Степенная линия тренда дает хорошие результаты для положительных данных с постоянным ускорением. Для рядов с нулевыми или отрицательными значениями построение указанной линии тренда невозможно.
Экспоненциальной функцией: y = cebx
где c и b — константы, е — основание натурального логарифма.
Экспоненциальный тренд используется в случае непрерывного возрастания изменения данных. Построение указанного тренда не возможно, если в множестве значений членов ряда присутствуют нулевые или отрицательные данные.
С использованием линейной фильтрации по формуле: Ft= (At+A(t-1)+⋯+A(t-n+1))/n
где n — общее число членов ряда, t — заданное число точек (2 ≤ t
Информационные технологии. Другие материалы
Линия тренда в Excel на разных графиках
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
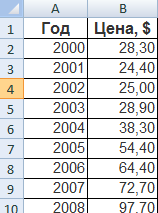
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
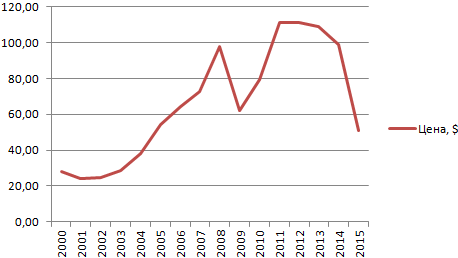
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
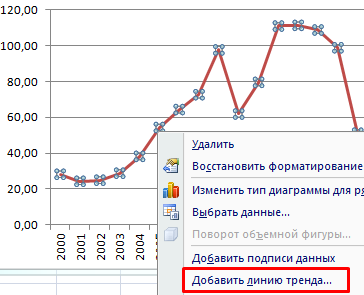
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
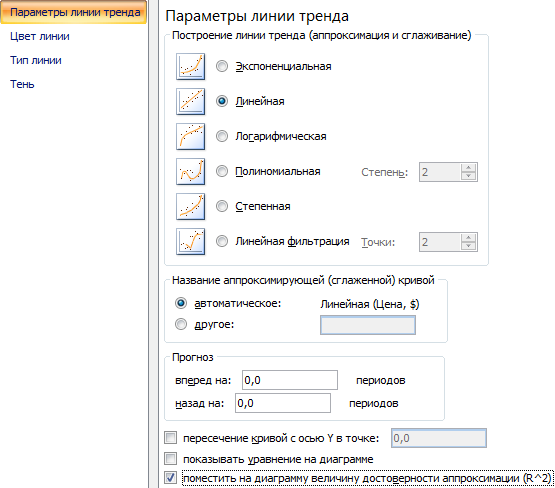
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
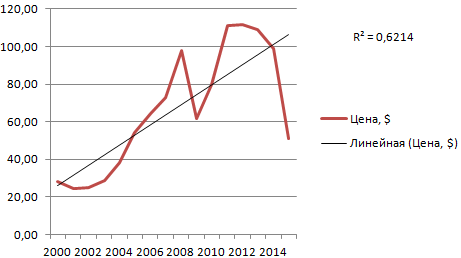
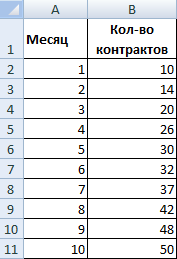
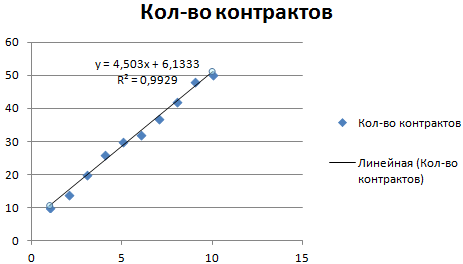
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
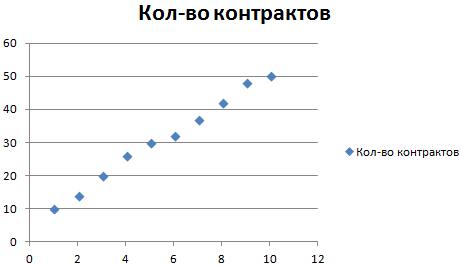
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
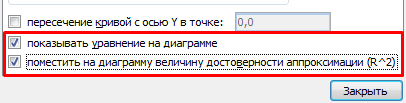
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
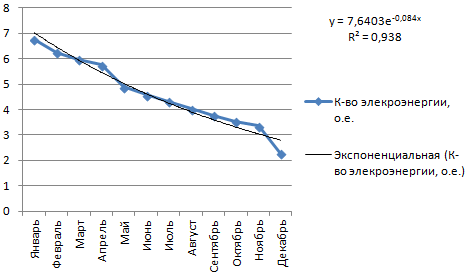
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
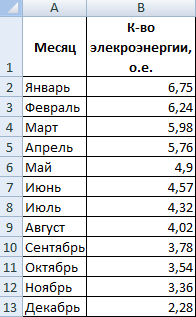
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
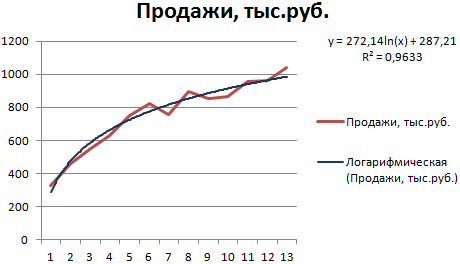
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
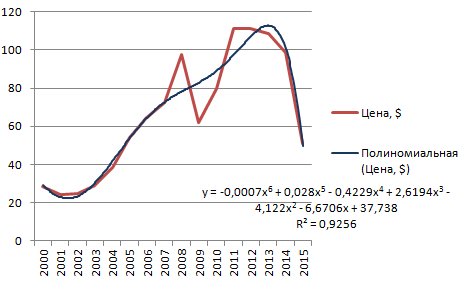
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Excel расчет линии тренда
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
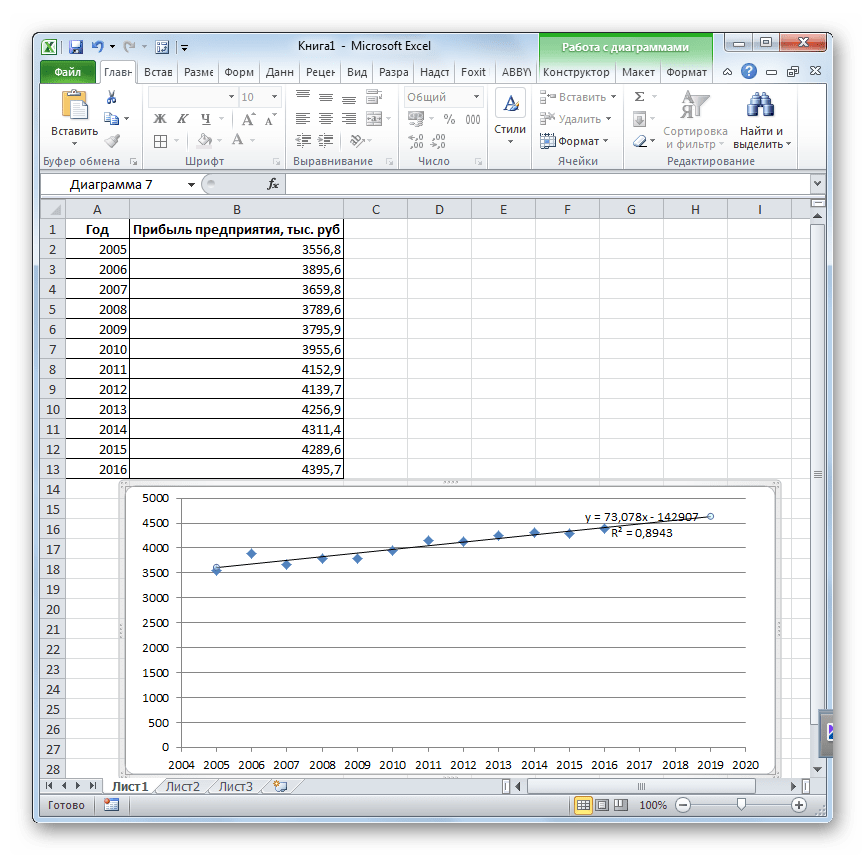
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
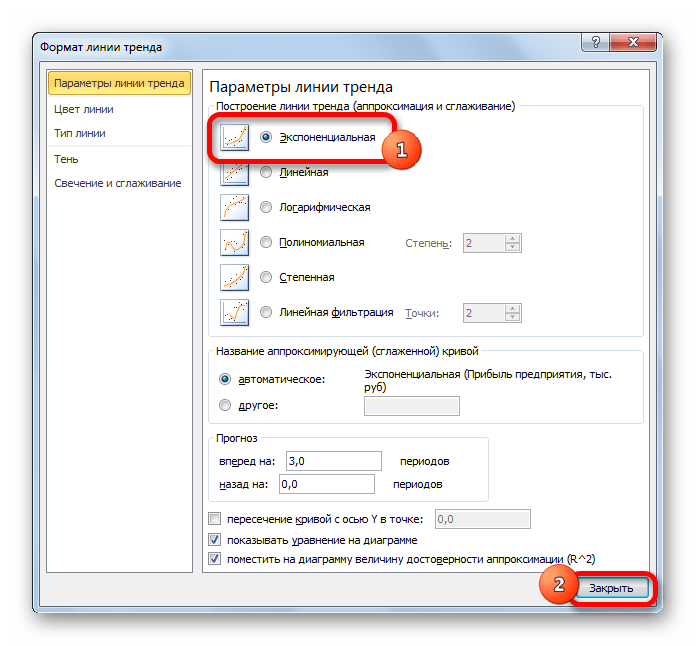
Давайте для начала выберем линейную аппроксимацию.
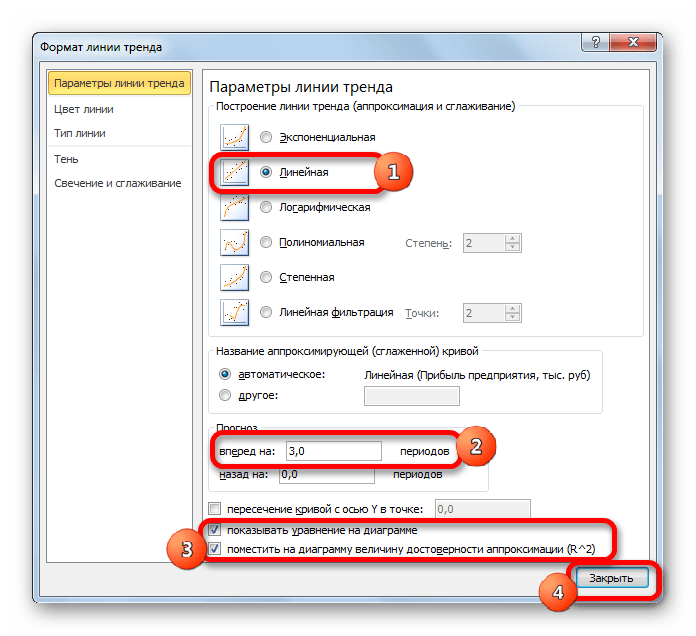
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
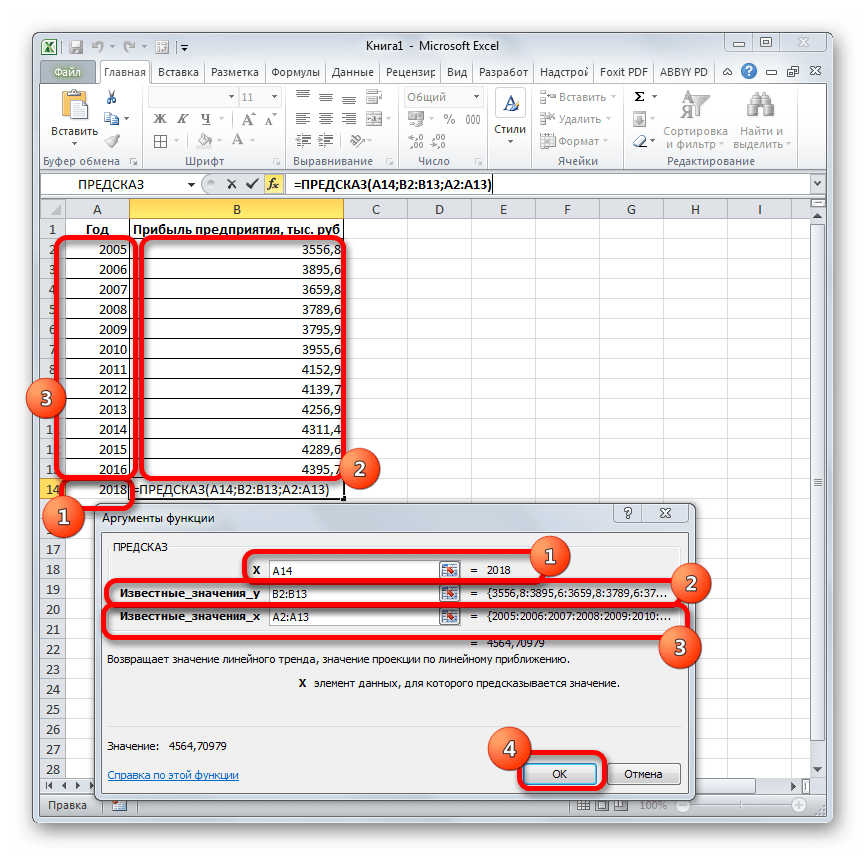
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
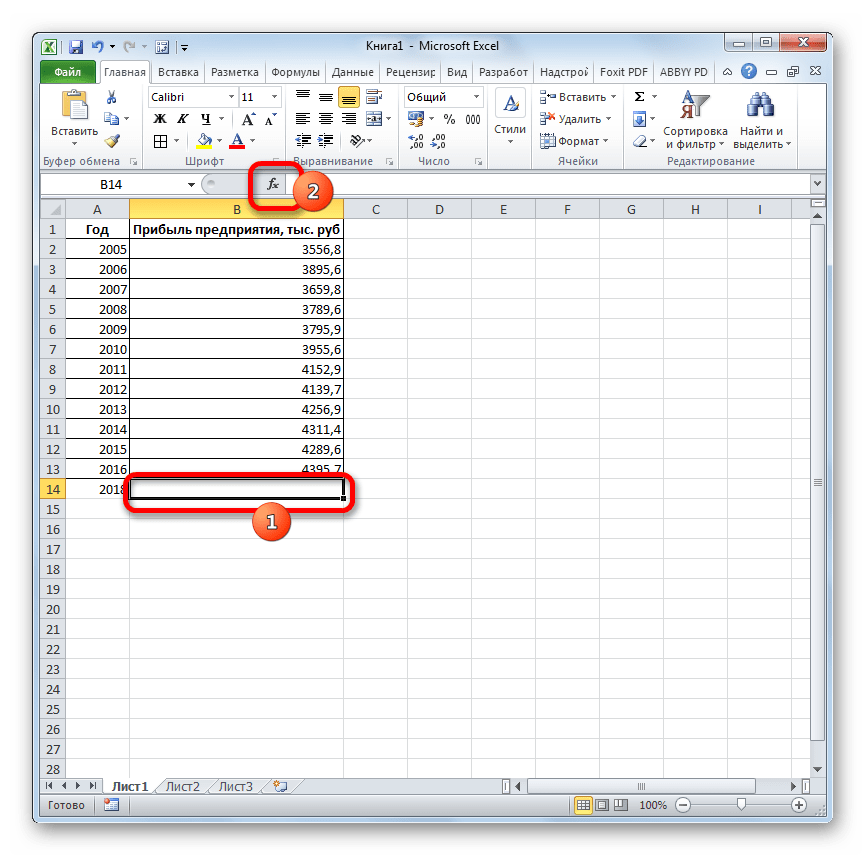
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
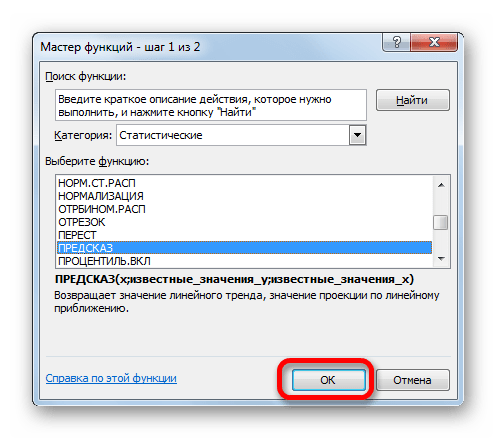
Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
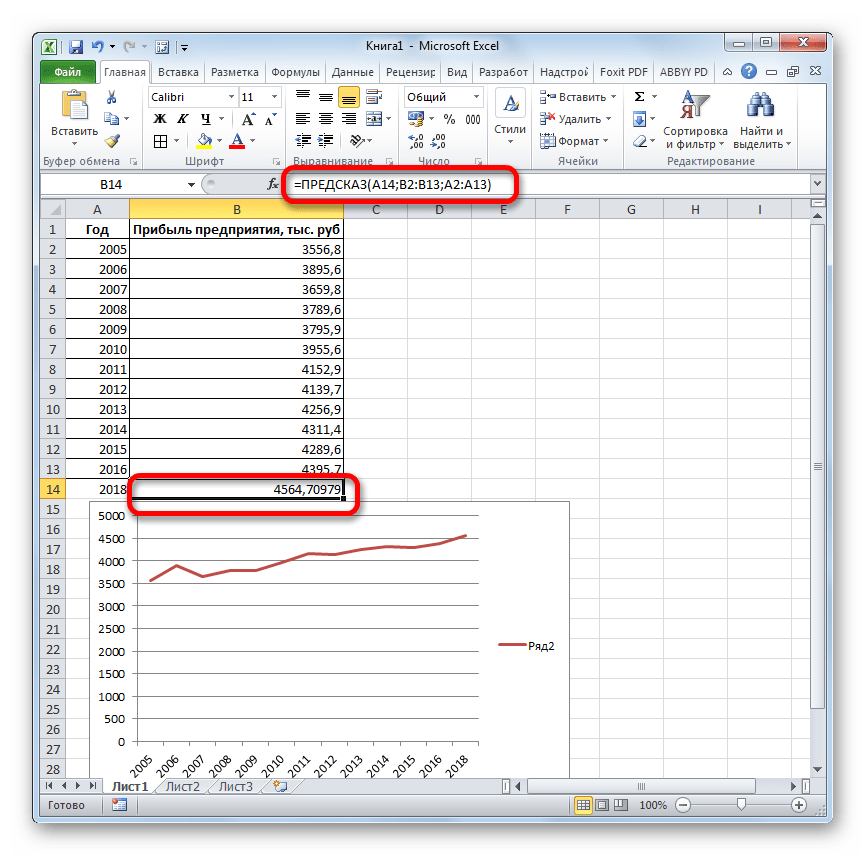
Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
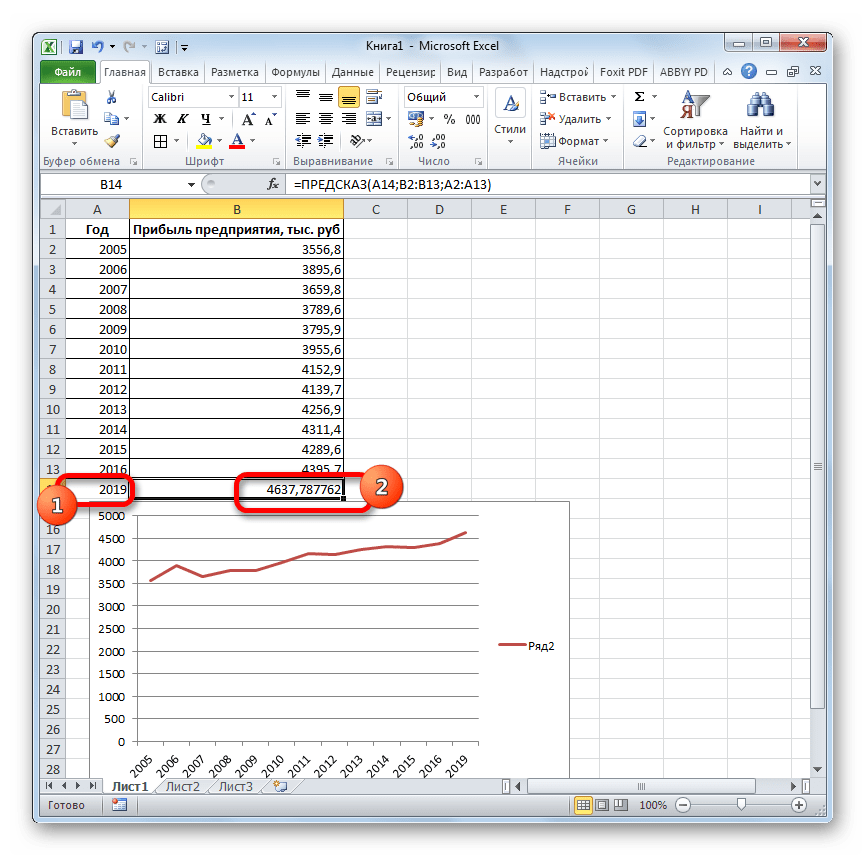
Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
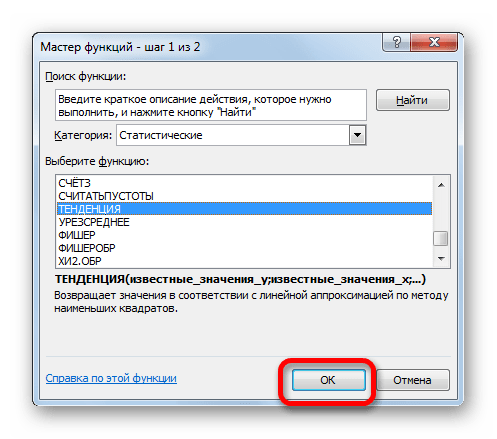
Способ 3: оператор ТЕНДЕНЦИЯ
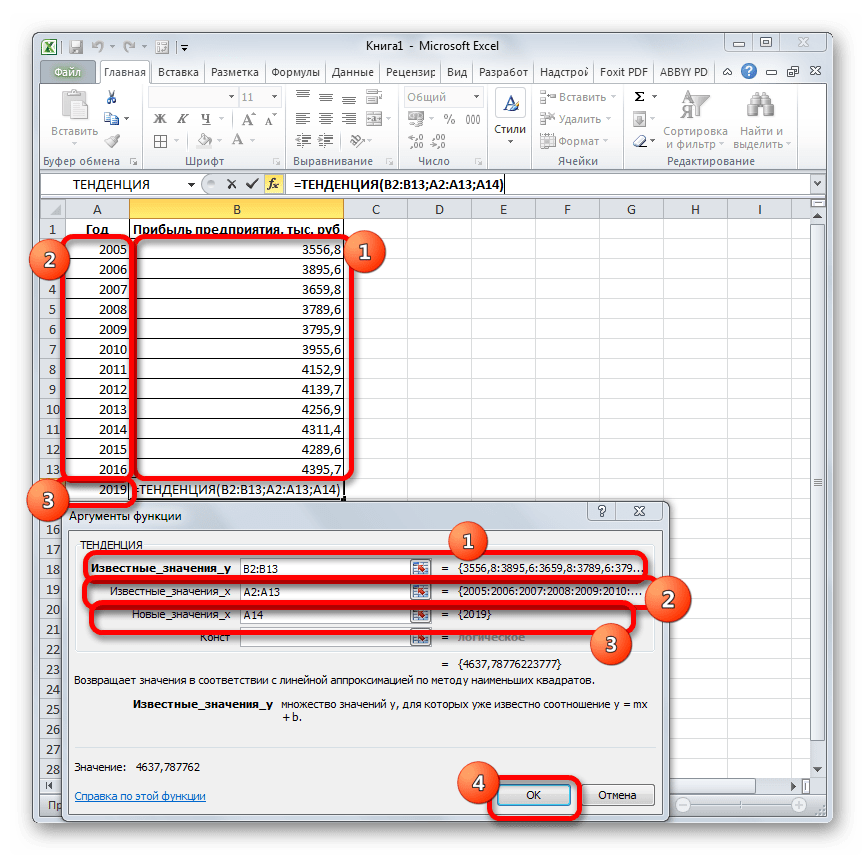
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
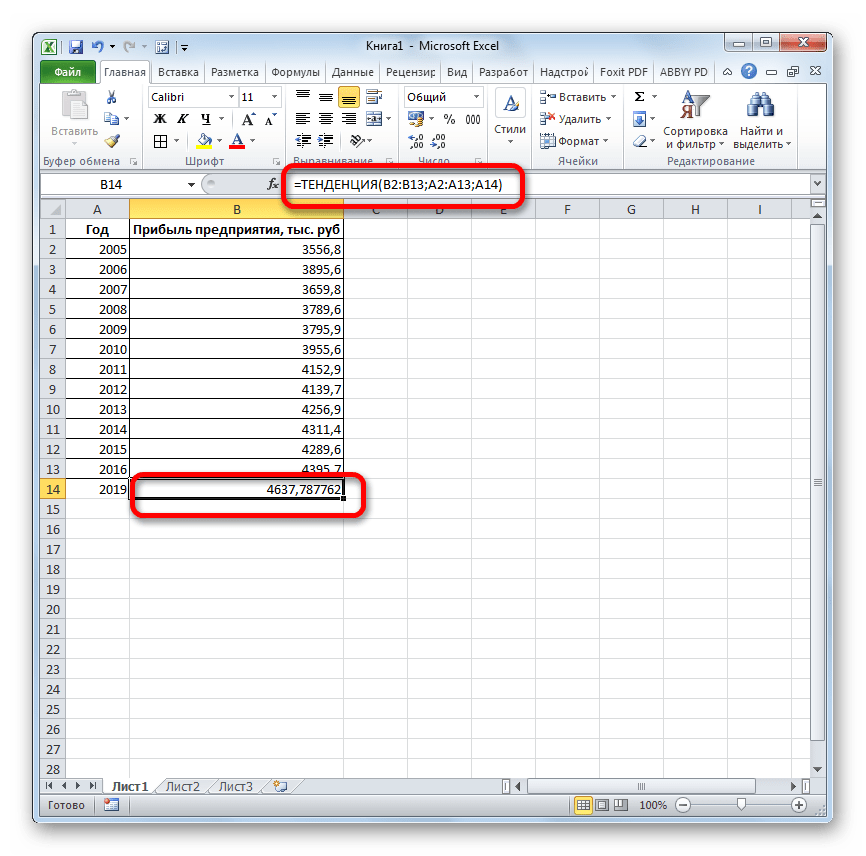
Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
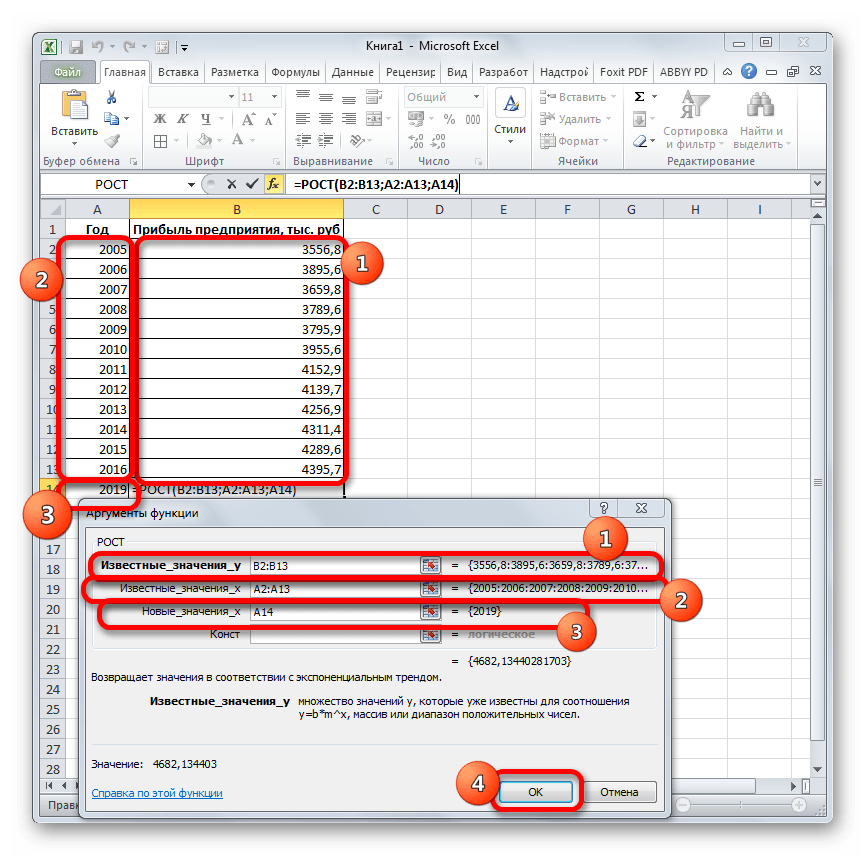
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
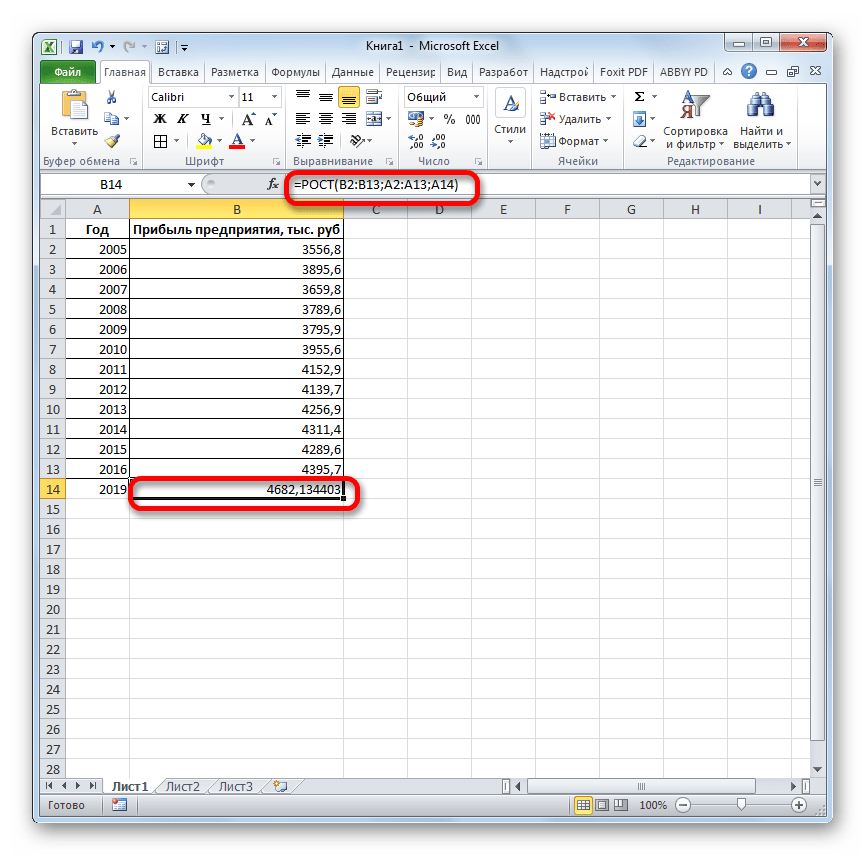
Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
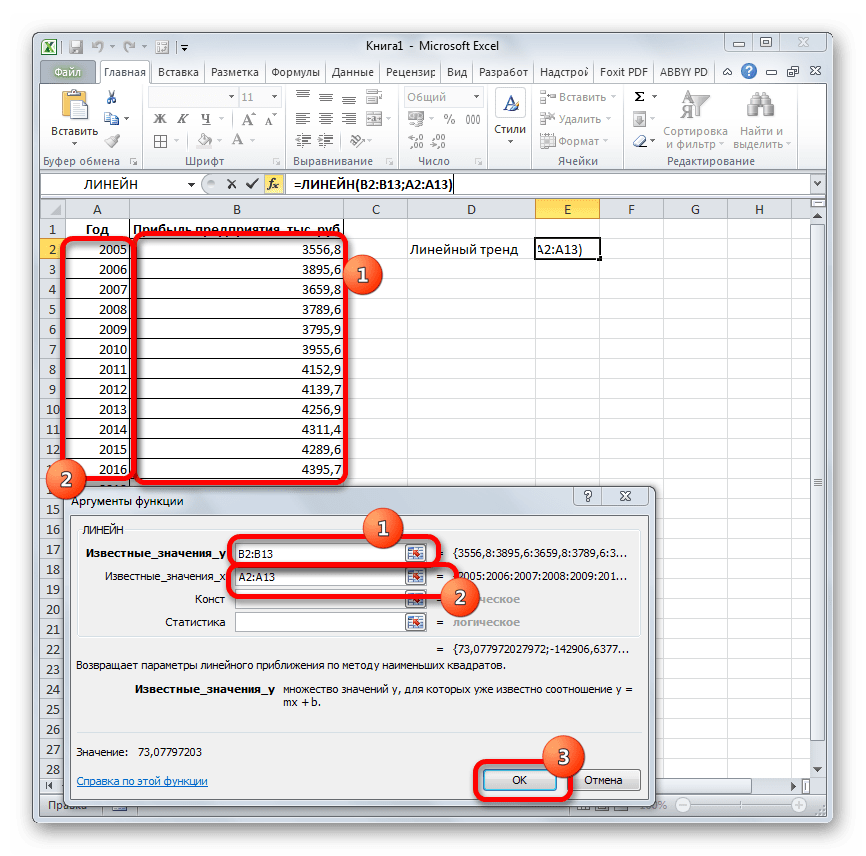
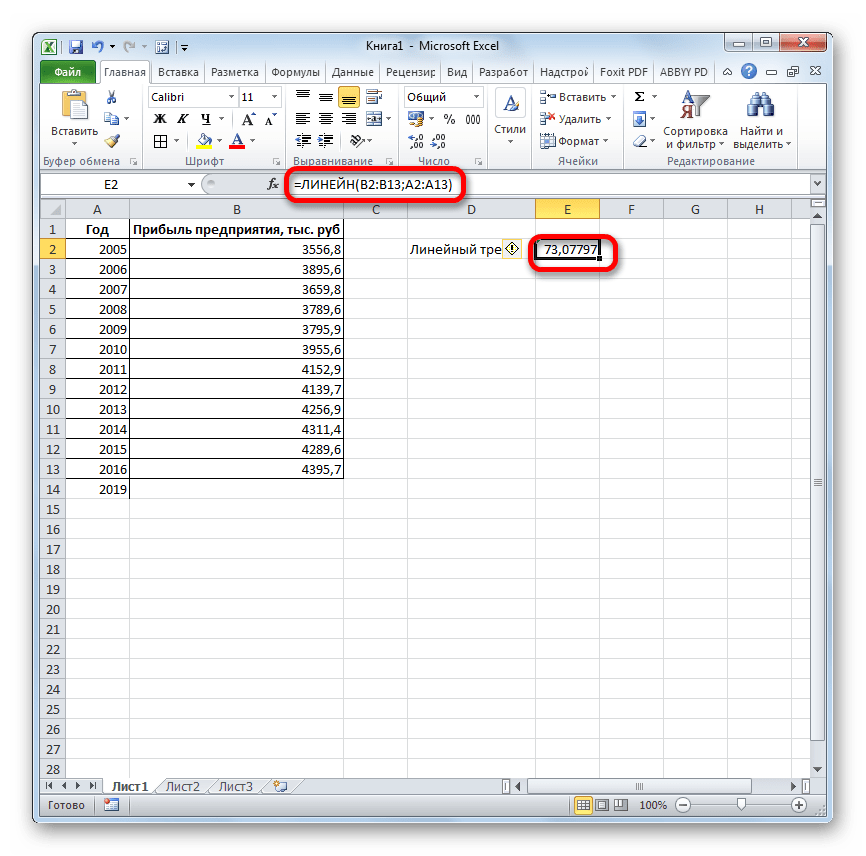
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
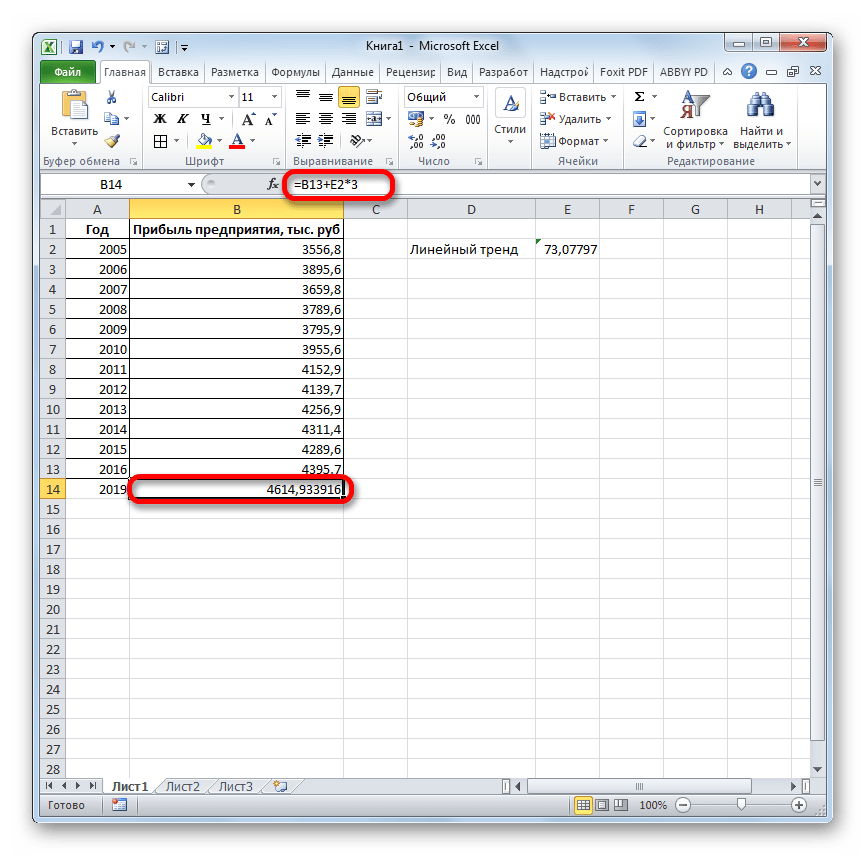
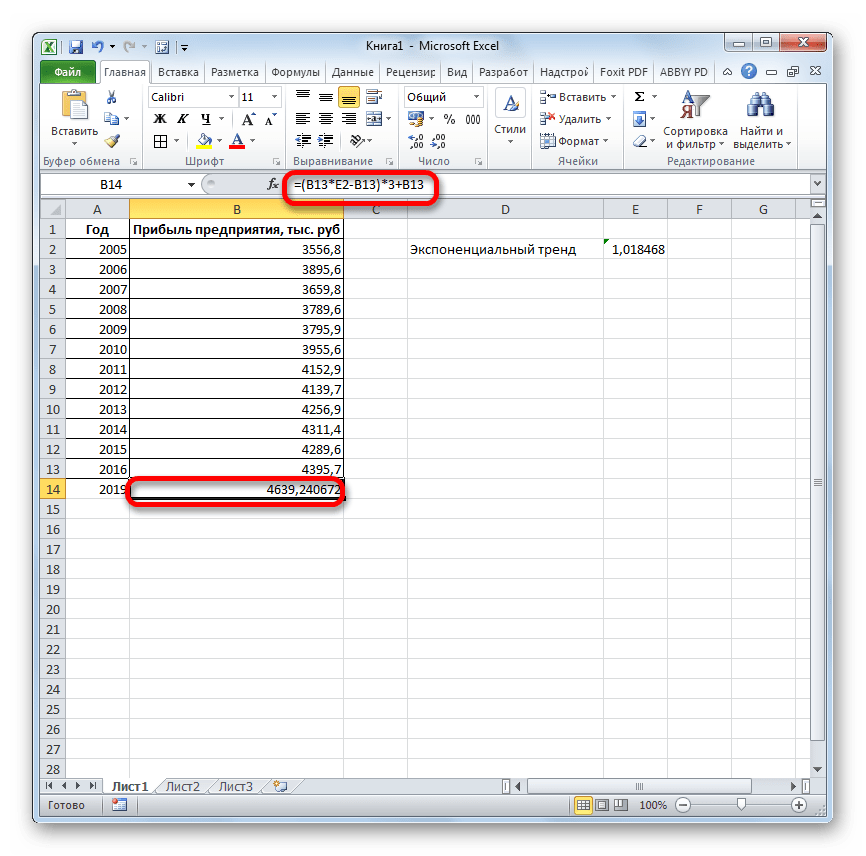
Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
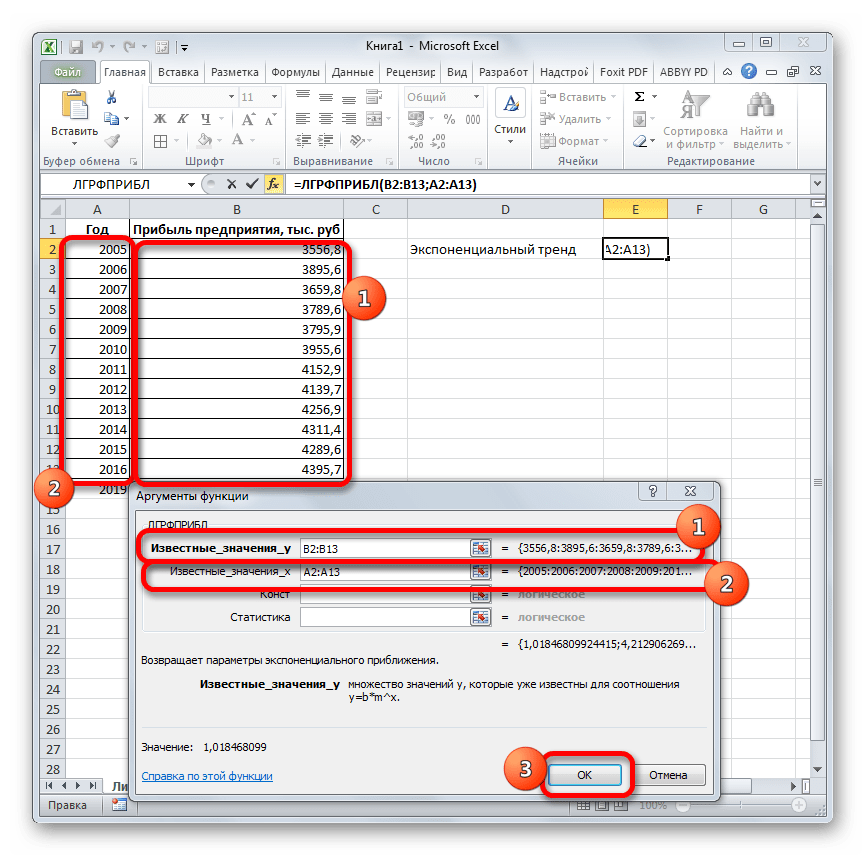
Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
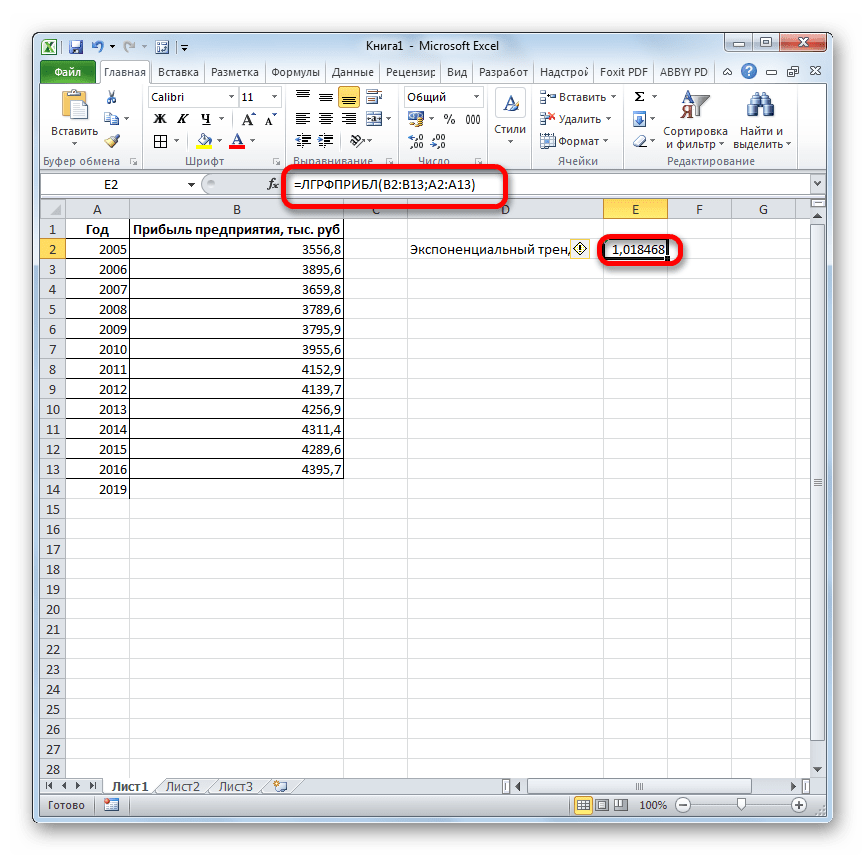
Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Это первая статья из серии «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности», из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.
Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:
- Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
- Расчет сезонности;
- Расчет прогноза;
После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.
Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.
Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд продажи по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (минимальный уровень);
b – это значение, на которое увеличивается следующее значение временного ряда;
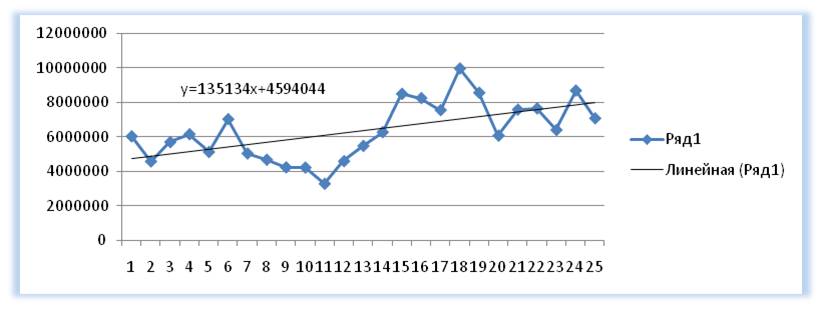
1-й способ расчета значений линейного тренда в Excel с помощью графика
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
вместо константы ставим 1,
вместо статистики 0,
Получаем 135135 — значение (b) линейного тренда y=a+bx;
Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо
- установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;
- нажимаем клавишу F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых хотим рассчитать значения линейного тренда.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.
3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y — это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x — это номера периодов x для известных значений объёмов продаж y;
- новые значения x — это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа — ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в «новые значения x» вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Вместо X поставляем номер периода, для которого рассчитываем значение тренда.
Вместо «известные значения y» — объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
«известные значения x» — это номера периодов для каждого выделенного объёма продаж.
3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье «О линейном тренде».
5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
2. Заходим в меню программы и нажимаем «Start_Forecast». Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В следующих статье «Как самостоятельно сделать прогноз продаж с учетом роста и сезонности» мы:
О том, что еще важно знать о линейном тренде, вы можете узнать в статье «Что важно знать о линейном тренде».
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
источники:
http://exceltable.com/grafiki/liniya-trenda-v-excel
http://web-shpargalka.ru/excel-raschet-linii-trenda.php