Вычислим скалярное произведение векторов и проверим вектора на ортогональность. Подберем координаты вектора, ортогонального заданному, а также отобразим вектора в прямоугольной системе координат.
Скалярным произведением двух векторов
называется действительное число (скаляр), равное произведению длин умножаемых векторов на косинус угла между ними.
СОВЕТ
: о нахождении длин векторов см. статью
Вычисление длины (модуля) вектора в MS EXCEL
.
В случае двухмерной задачи скалярное произведение векторов
a
= {
a
x
;
a
y
} и
b
= {
b
x
;
b
y
} можно найти воспользовавшись следующей формулой:
a
·
b
=
a
x
·
b
x
+
a
y
·
b
y
Для вычисления скалярного произведения векторов в MS EXCEL идеально подходит функция
СУММПРОИЗВ()
СОВЕТ
: о функции
СУММПРОИЗВ()
см. статью
Функция СУММПРОИЗВ() — Сложение и подсчет с множественными условиями в MS EXCEL
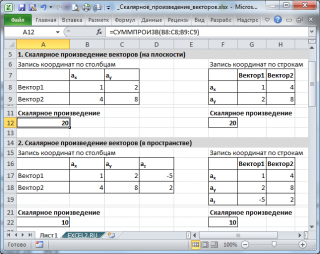
Если координаты 2-х векторов введены в диапазоны
B8:C8
и
B9:C9
соответственно, то формула
=СУММПРОИЗВ(B8:C8;B9:C9)
подсчитает скалярное произведение векторов (см.
файл примера
).
Естественно, для трехмерного случая можно записать аналогичную формулу.
Ортогональность векторов
Два вектора называются ортогональными если угол между ними равен 90 градусов. Т.к. косинус угла 90 градусов равен 0, то и их скалярное произведение равно 0.
Интерес представляет поиск вектора, ортогонального заданному.
Поиск одной координаты.
Сначала подберем одну из координат трехмерного вектора, так, чтобы он стал ортогональным заданному (2 другие координаты известны). Такая координата всегда существует и решение единственно.
Для нахождения третьей координаты будем использовать инструмент MS EXCEL Подбор параметра (подробнее см.
Подбор параметра в MS EXCEL
).
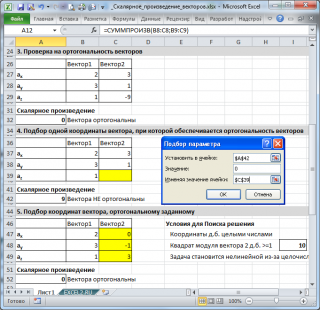
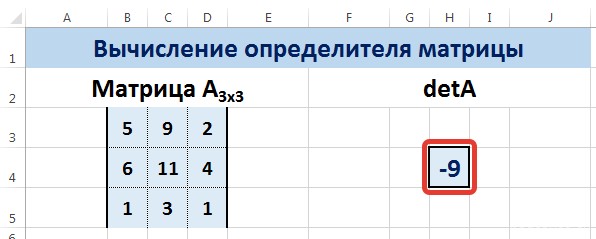
Пусть координаты заданного вектора равны {2; 3; 1} (и размещены в ячейках
В37:В39
), а известные координаты искомого ортогонального вектора равны {3; 1; ?} (размещены в ячейках
С37:С39
) См. рисунок выше и
файл примера
.
Вычислим в ячейке
А42
скалярное произведение векторов с помощью формулы
=СУММПРОИЗВ(B37:B39;C37:C39)
Вызовем окно
Подбора параметра
для ввода критериев поиска и установим их как показано на рисунке выше. После нажатия кнопки ОК в ячейке
С39
(искомая координата) будет введено значение -9, а скалярное произведение станет равно 0.
Поиск всех координат ортогонального вектора.
Если заданы координаты только исходного вектора и требуется определить все 3 координаты вектора, ортогональному к нему, то, понятно, что решение не единственно.
Например, для двухмерного случая (на плоскости), можно построить 2 разных вектора, которые будут ортогональны заданному (точнее не 2, а бесконечное множество коллинеарных векторов в двух противоположных направлениях).
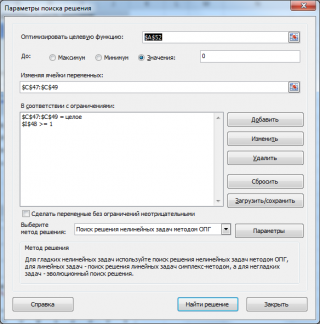
Так как нам придется одновременно подбирать сразу 3 координаты, то Подбор параметра нам не подходит, нужно использовать
Поиск решения
(См.
файл примера)
.
В качестве ограничений для Поиска решения можно установить: найденные координаты должны быть целыми числами, а квадрат модуля искомого вектора д.б. >1 (иначе 0 вектор будет предложен в качестве решения). Также можно наложить ограничение на максимальную длину вектора.
После запуска инструмента Поиск решения будут найдены координаты {0; -1; 3}
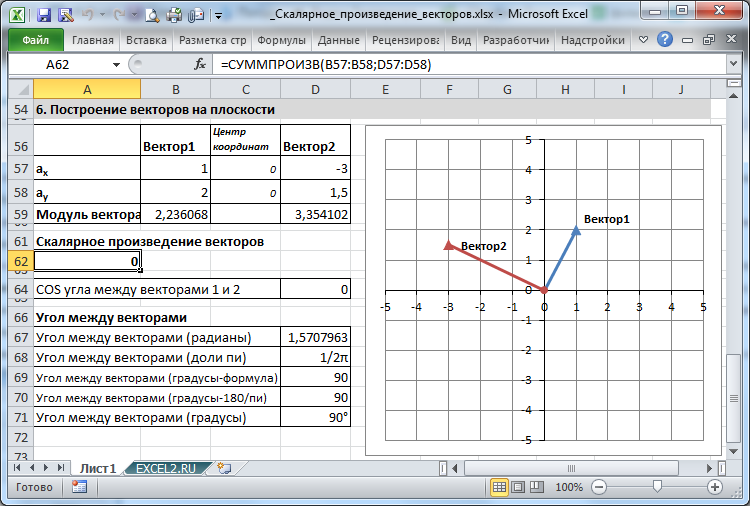
Отображение (ортогональных) векторов на плоскости
В двухмерном случае можно отобразить 2 ортогональных вектора.
Тип диаграммы установлен График (см.
Основные типы диаграмм в MS EXCEL
, раздел График).
Чтобы вектора выглядели ортогональными, необходимо зафиксировать минимальные и максимальные значения, отображаемые осями (см.
Основы построения диаграмм в MS EXCEL
, раздел 7.Оси), иначе при построении различных пар векторов MS EXCEL будет применять автомасштабирование графика и масштабы осей могут стать не равными (это приведет к тому, что угол 90 градусов не будет выглядеть прямым).
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
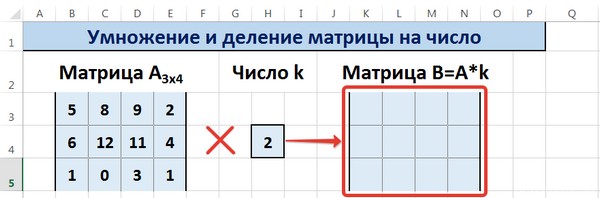
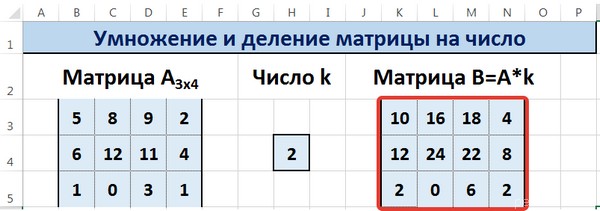
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
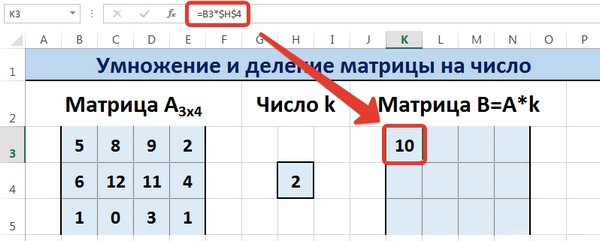
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
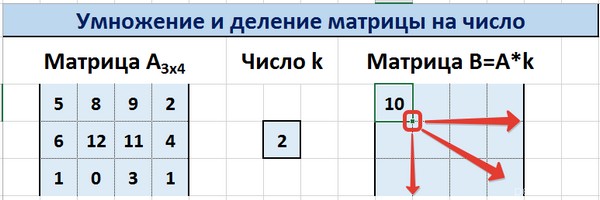
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
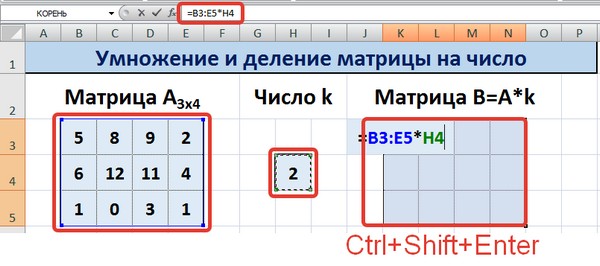
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
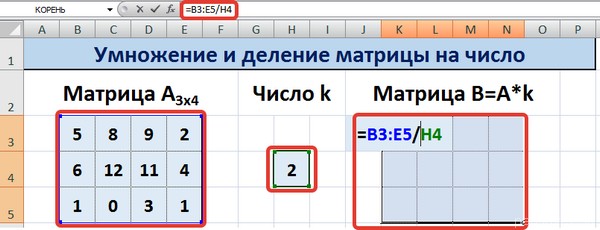
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
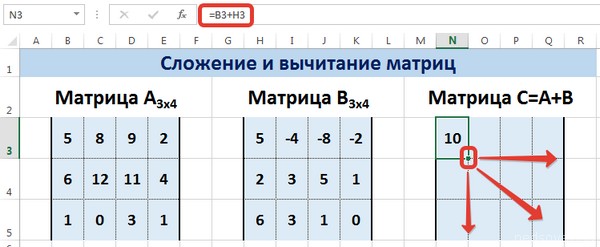
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
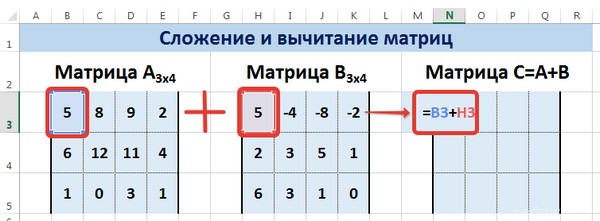
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
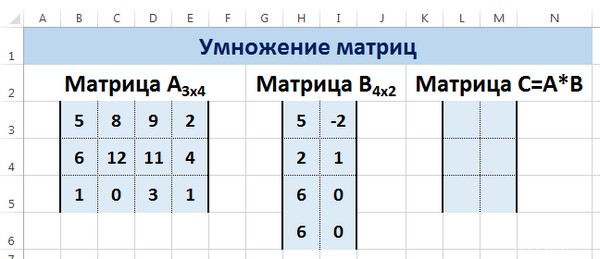
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
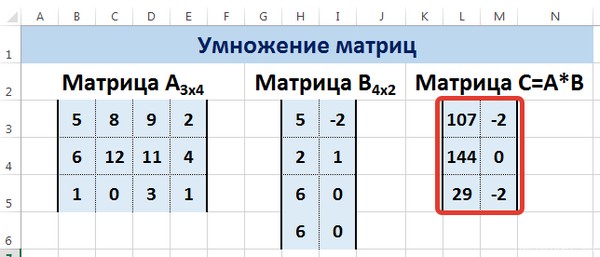
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
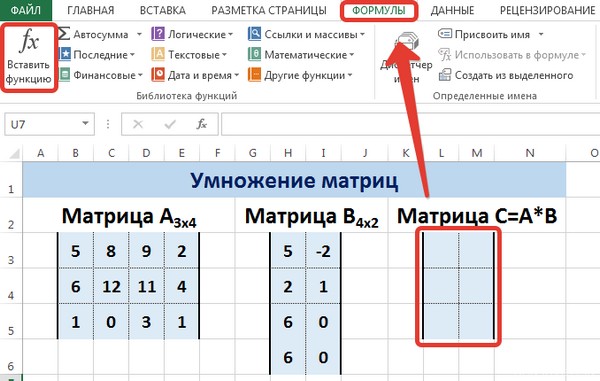
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
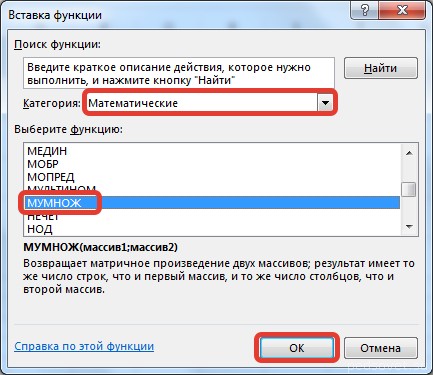
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
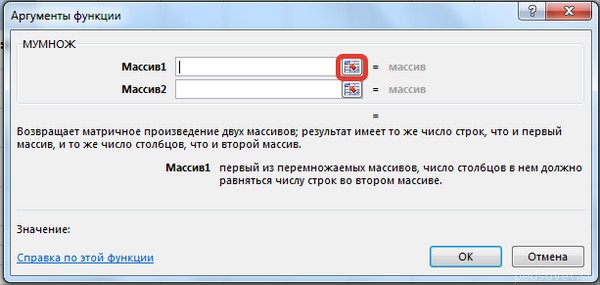
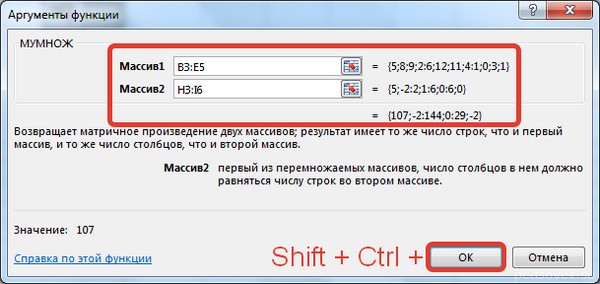
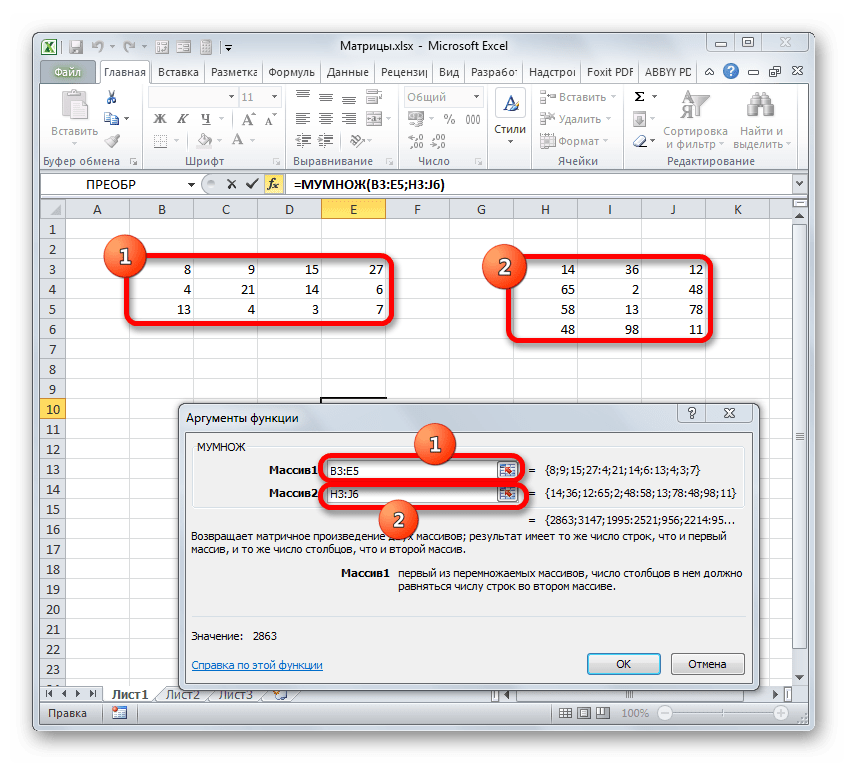
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
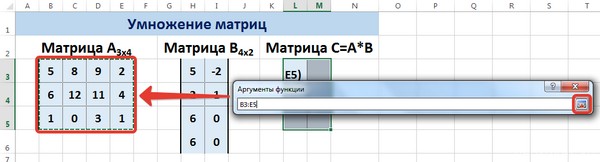
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
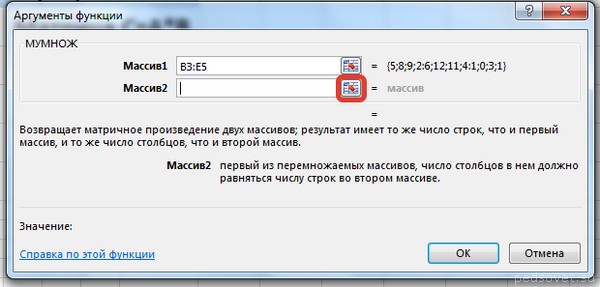
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
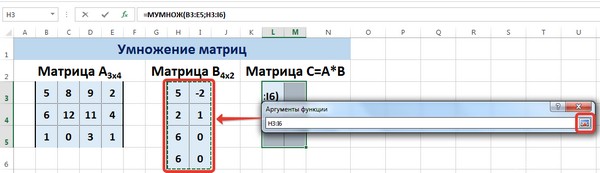
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
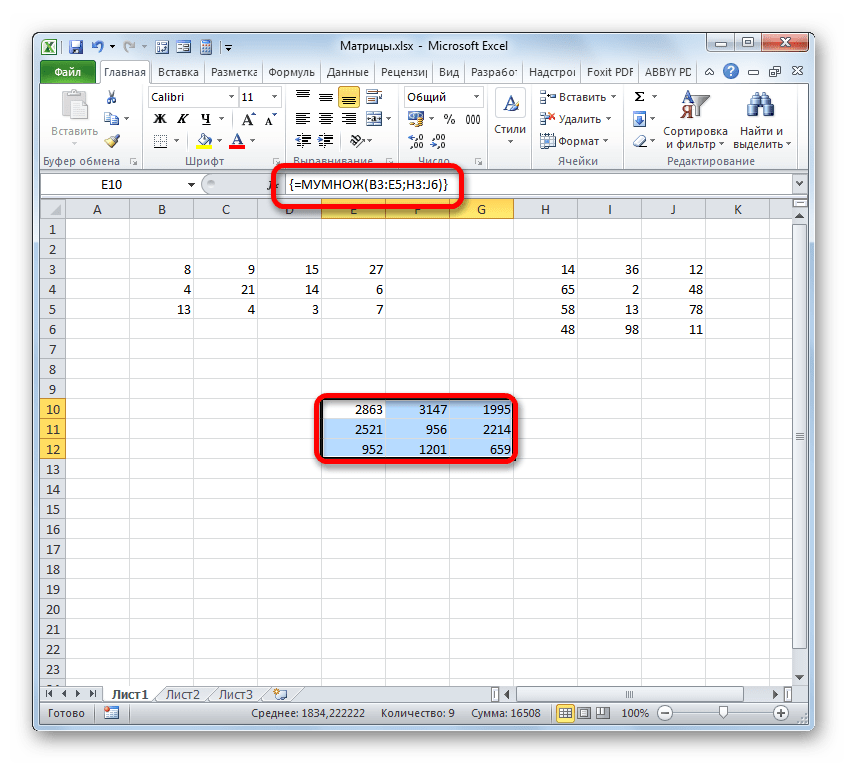
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
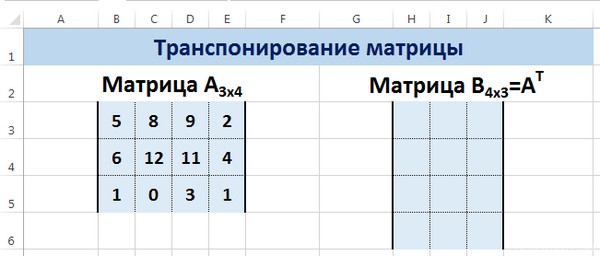
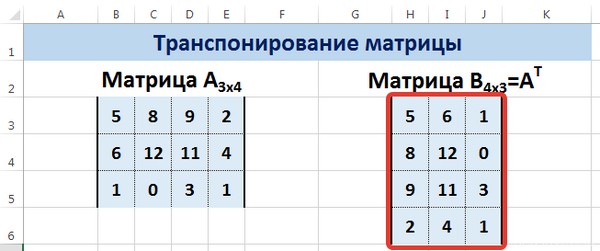
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
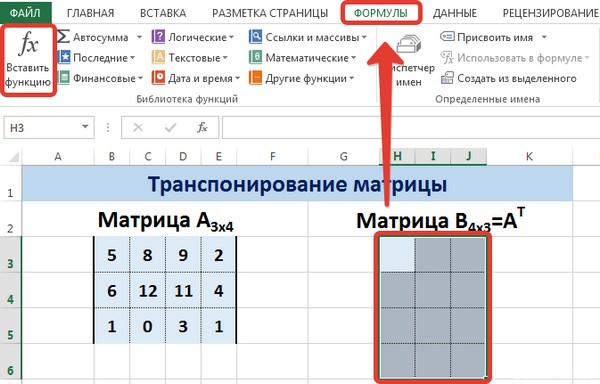
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
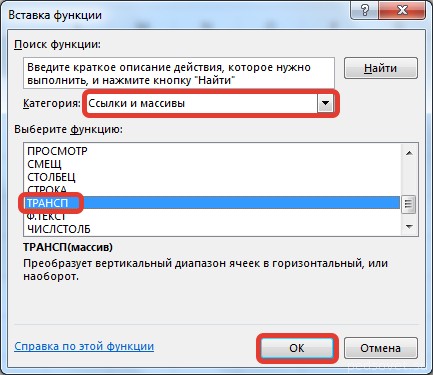
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
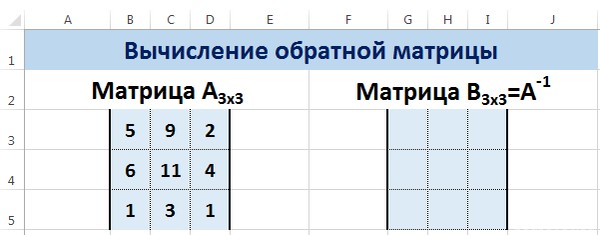
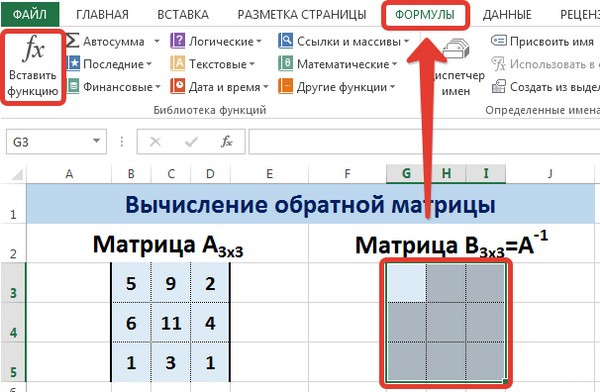
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
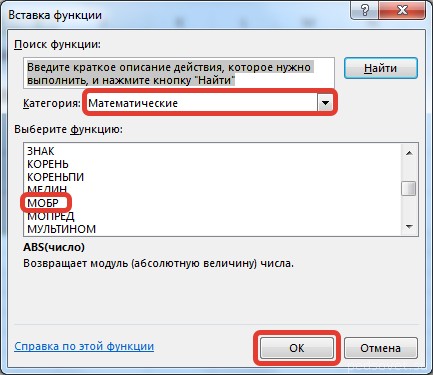
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
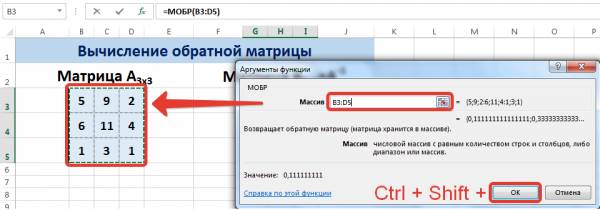
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
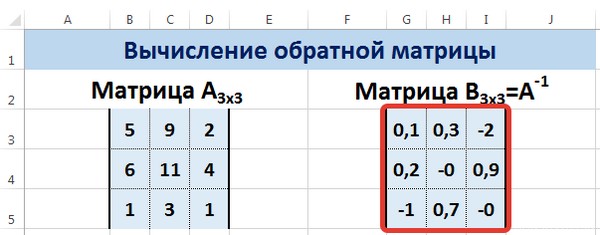
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
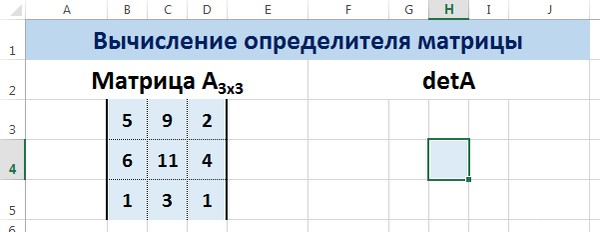
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
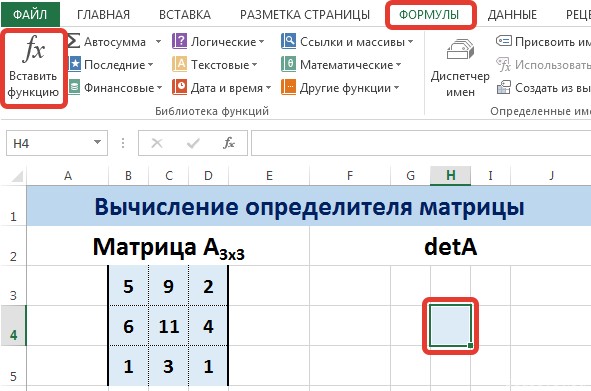
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
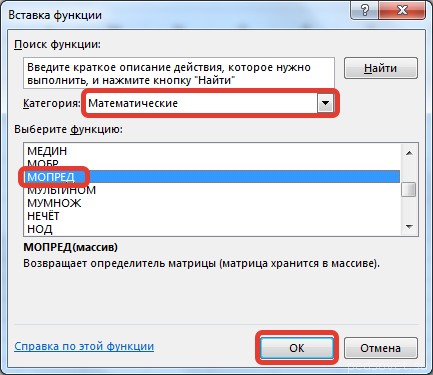
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
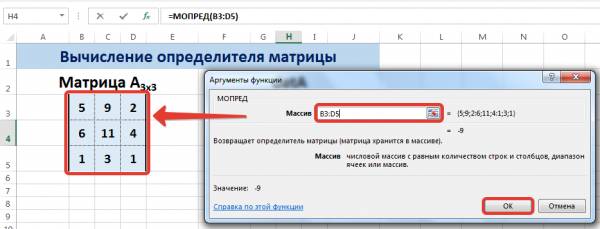
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
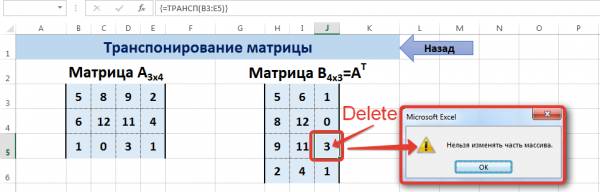
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Векторы и матрицы в Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Векторы и матрицы в Excel
C овокупность n чисел 
Два n -мерных вектора 


Суммой двух n -мерных векторов 

Операция сложения векторов обладает свойствами коммутативности 

Вектор 
Вектор 

Операция вычитания векторов определяется как сложение с противоположным вектором 
Под произведением вектора 

Умножение вектора на число обладает свойством ассоциативности 

Модуль (норма, длина) вектора 
Пример вычисления модуля вектора 
Р
исунок 1 – Вычисление длины вектора
Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.
В общем случае скалярное произведение двух векторов 




Операция скалярного умножения векторов обладает следующими свойствами:

В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).
Векторным произведением вектора 







Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.
Р
исунок 2 – Определение скалярного произведения двух векторов
Значение векторного произведения определяется следующим образом:
На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов 
Р
исунок 4 – Вычисление векторного произведения векторов
Перейдем к рассмотрению основных операций матричного исчисления.
Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :
Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:
Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.
Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается
При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы 
Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:
Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:
Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица
называемая транспонированной по отношению к матрице А.
Если А=А Т , то такая матрица называется симметричной.
В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.
Р
исунок 5 – Вызов функции ТРАНСП
Пример. Имеем исходную матрицу

Из определения ясно, что транспонированной будет матрица А Т :

Решение задачи в Excel представлено на рисунке 6
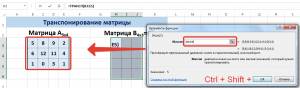
Рисунок 6 – Транспонирование матрицы
Порядок решения следующий:
— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);
— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);
— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;
— нажать Shit + Ctrl + Enter .
Суммой матриц А


Произведение матрицы на число — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:
Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы 





В Excel для вычисления произведения матриц используется функция
= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).
Р
исунок 7 – Умножение матриц
Формула для расчета произведения матриц должна быть введена как формула массива!
Пусть даны матрицы
Вычислим их произведение в Excel (рисунок 8).
— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);
— 
—
шаг 3 – выделить результирующий массив и нажать F2;
—
шаг 3 – нажать Shift+Ctrl+Enter.
Рисунок 8 – Вычисление произведения матриц
Действие умножения матрицы на матрицу обладает свойствами:
Отметим, что в общем случае
Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.
При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).
Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.
Для матрицы 2х2 определитель вычисляется как
Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:



Возможно разложение как по строкам, так и по столбцам.
В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).
Рисунок 9 – Расчет определителя матрицы
Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .
Детерминант треугольной матрицы равен произведению ее диагональных элементов
Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E
Обратную матрицу можно найти по следующей формуле:



Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).
Рисунок 10 – Расчет обратной матрицы
Заметим, что функция применяется к массиву как в ранее приведенных примерах.
Проверим выполнение условия А А -1 = E (рисунок 11)
Р
исунок 11- Произведение матрицы на обратную матрицу
Собственным числом квадратной матрицы
называется такое число 

Или, по-другому, собственными числами матрицы А являются корни уравнения 
Матрица 


Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:
Необходимо найти такие значения , при котором
Оформим лист Excel следующим образом (рисунок 12):
Рисунок 12 – Вычисление собственного числа матрицы
В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.
Из рисунка 12 видно, что при =0 определитель также равен 0, т.е. =0 есть первое собственное число матрицы.
Д
ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения , отображаемом в ячейке $F$2.
Рисунок 13 – Вычисление собственного числа матрицы
О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).
Рисунок 14 – Результат поиска решения
Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат =0.
П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):
Рисунок 15 – Ввод ограничения
В результате поиска получаем второе значение собственного числа: =3.
Повторим поиск при ограничении.
Если установить в ограничениях >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях
П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)
Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении
Рисунок 17 — Результат поиска третьего собственного числа
Собственным вектором соответствующим собственному числу λ называют такой вектор 
Найдем собственный вектор матрицы
Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.
1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).
2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.
3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.
4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор 
5. В ячейки (H2:H4) заносим умножение столбца 
6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).
7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.
Нажать кнопку « Выполнить ».
В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).
Рисунок 18 – Определение собственного вектора матрицы
Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.
Задания для самостоятельной работы
Повторить решение всех примеров, приведенных в Лекции №5.
Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15
Определить длину векторов.
Вычислить сумму и разность векторов.
Определить скалярное произведение этих векторов.
Определить угол между векторами.
Определить векторное произведение двух векторов.
Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.
Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.
Получить транспонированные матрицы исходных матриц.
Проверить правильность решения путем умножения исходной матрицы на транспонированную.
Определить произведение исходных матриц.
Найти матрицу 3-го порядка для исходной квадратной матрицы.
Определить детерминант исходной квадратной матрицы.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
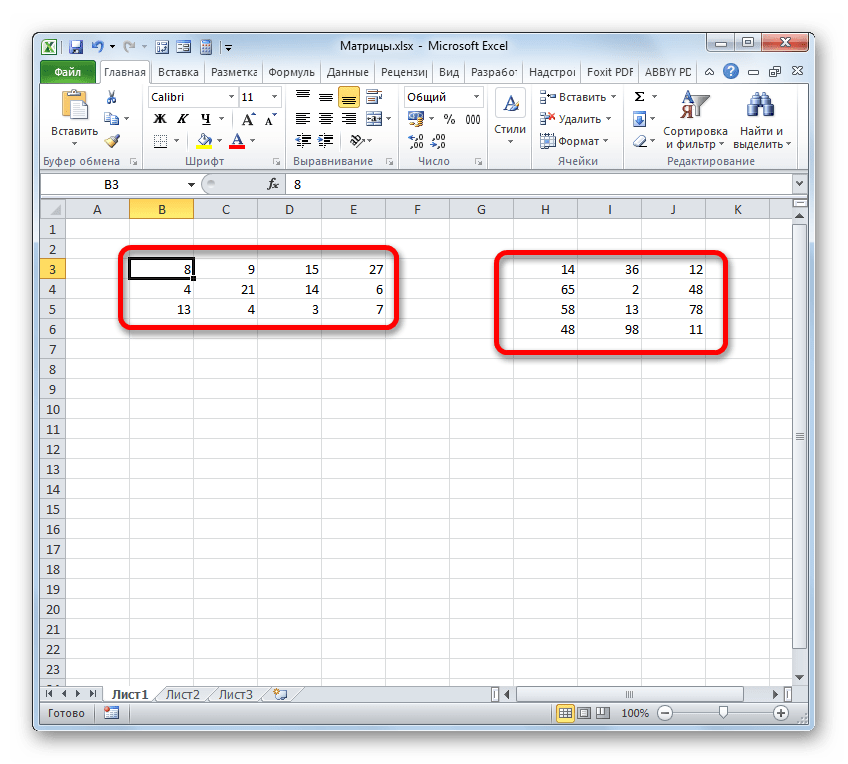
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
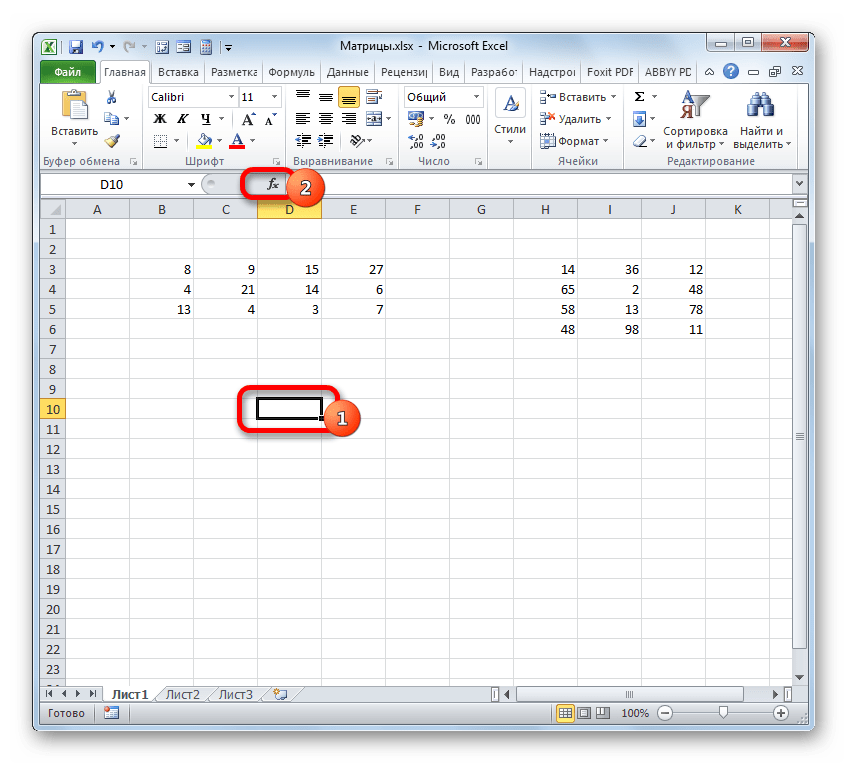
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
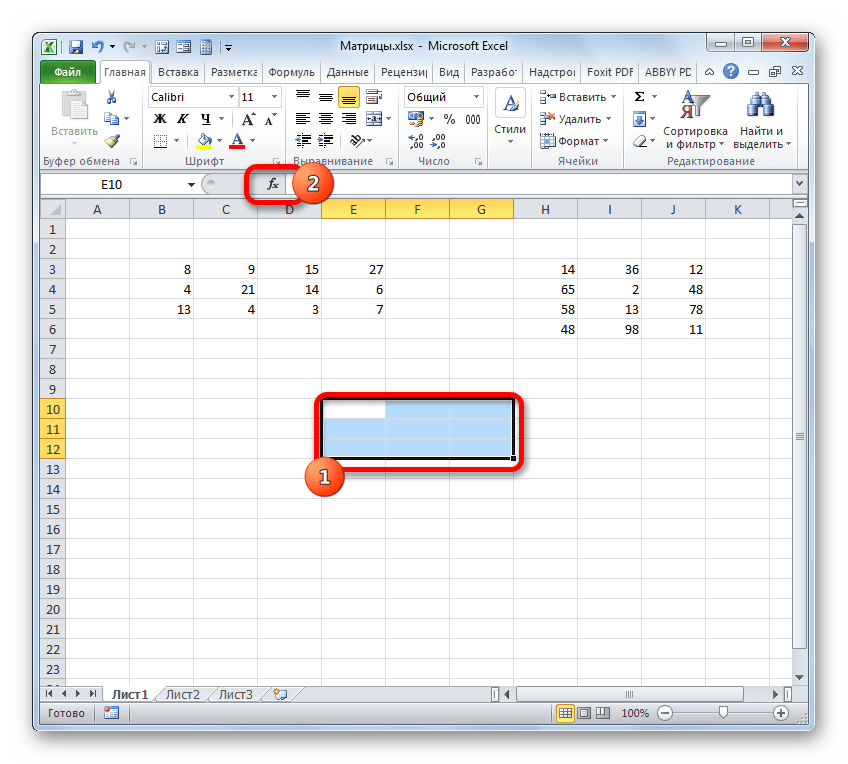
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
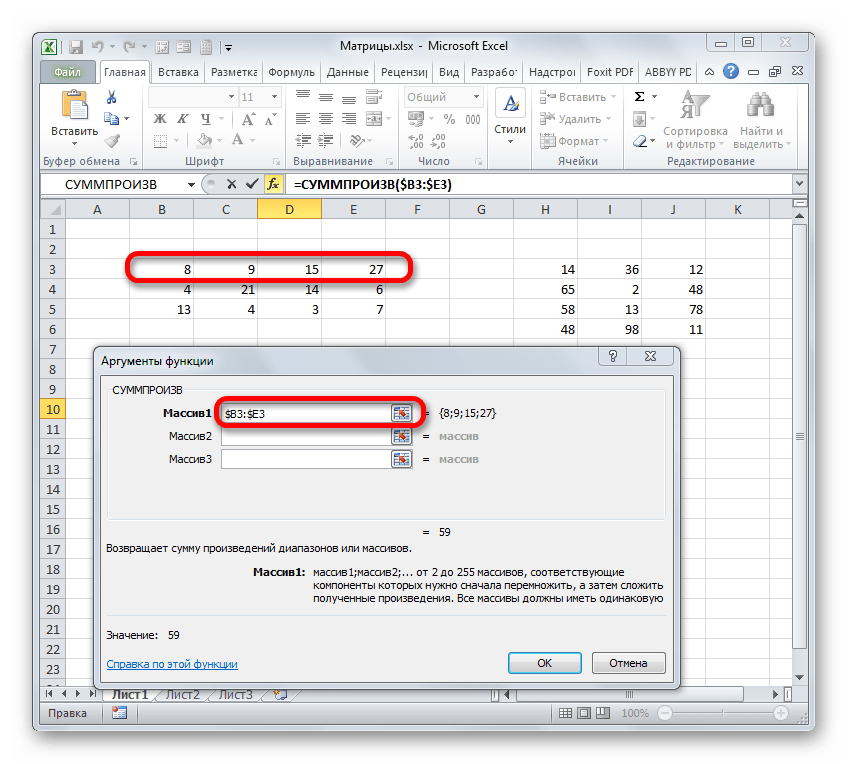
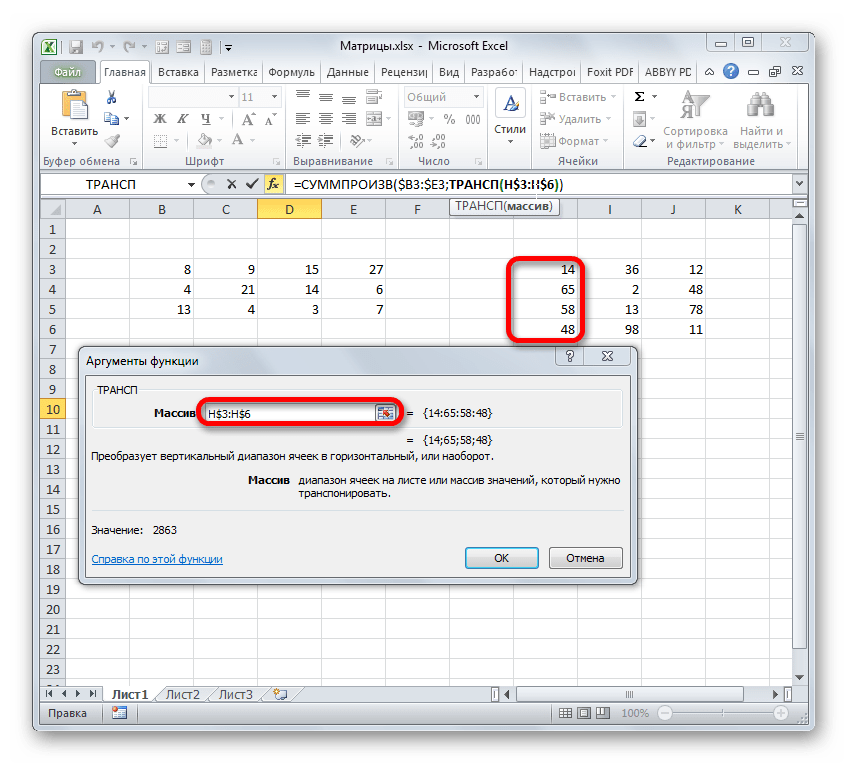
Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
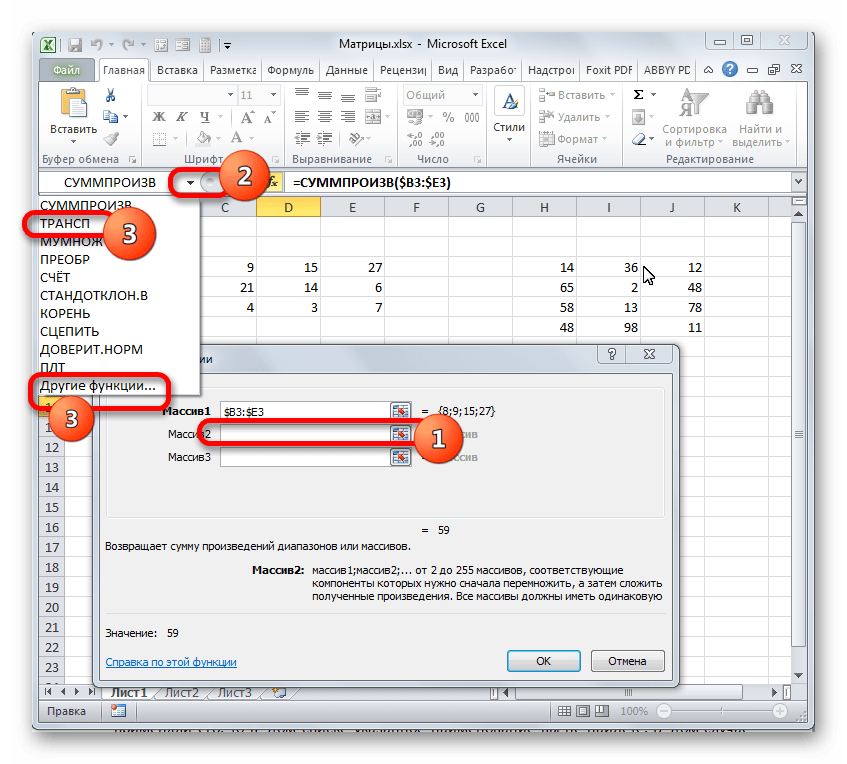
После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
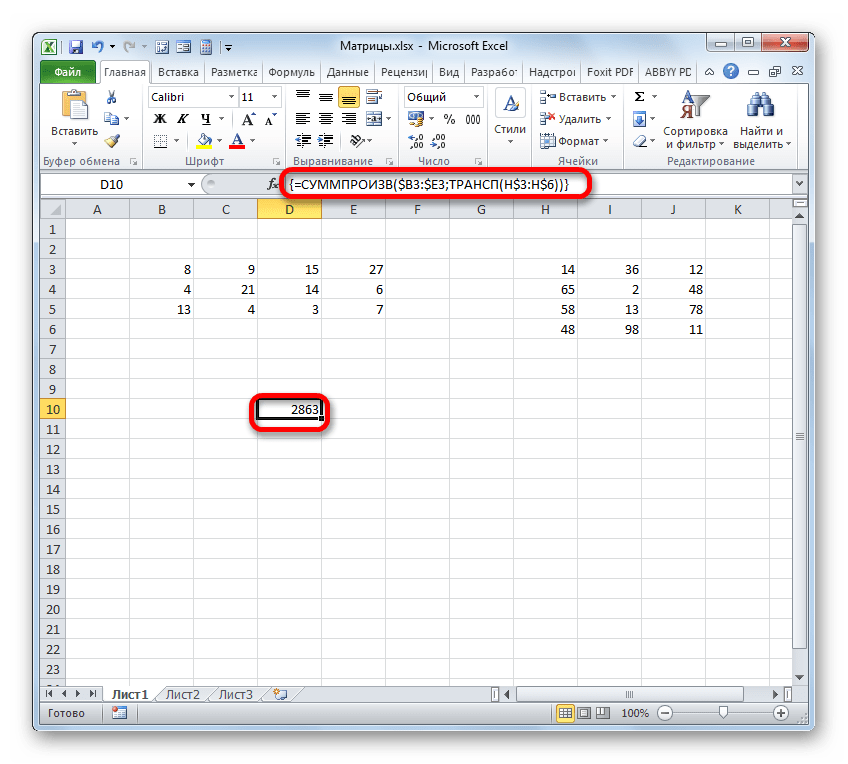
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
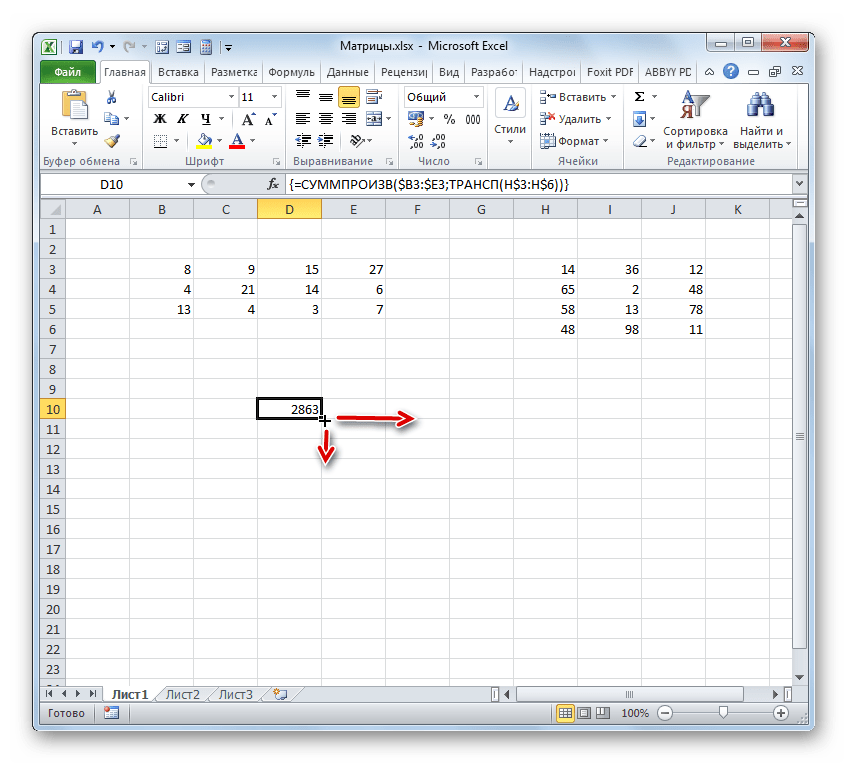
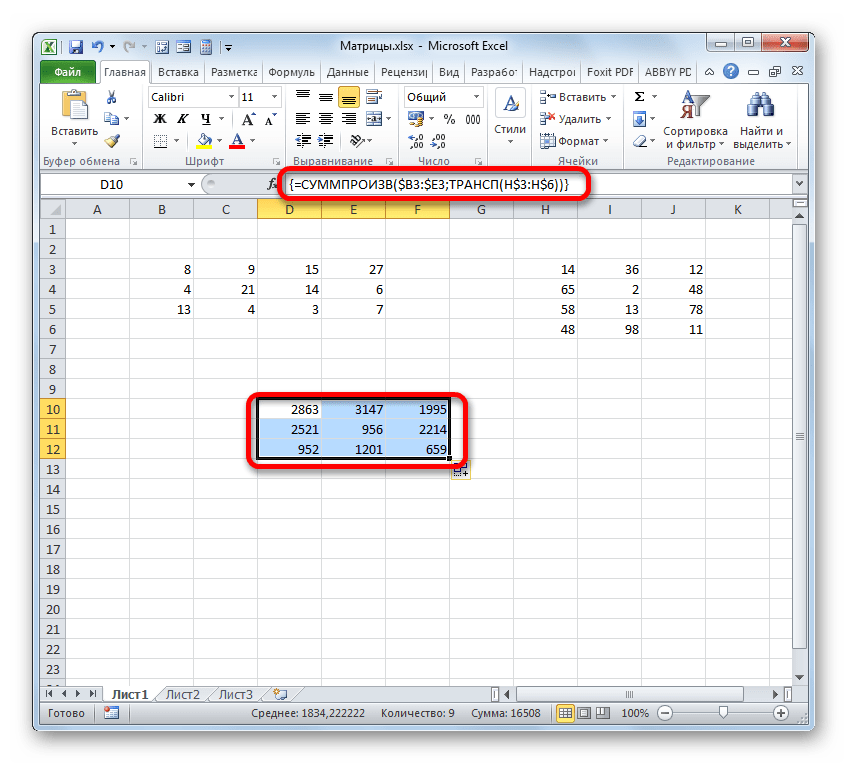
Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Помимо этой статьи, на сайте еще 12604 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
источники:
http://infourok.ru/vektori-i-matrici-v-ecel-1119397.html
http://lumpics.ru/how-to-multiply-matrices-in-excel/
|
messiah Пользователь Сообщений: 5 |
Добрый вечер, уважаемые. Прикрепленные файлы
|
|
Пытливый Пользователь Сообщений: 4586 |
У вас, по сути, даны два катета прямоугольного треугольника. Прилежащий (Х) и противолежащий (У). Вспоминая школьную тригонометрию, рискну предположить, что отношение противолежащего к прилежащему — не что иное, как тангенс угла. Кому решение нужно — тот пример и рисует. |
|
Михаил С. Пользователь Сообщений: 10514 |
#3 20.08.2015 23:59:57 messiah, у вас не обозначено ни одной прямой, в лучшем случае — координаты отдельных точек. Между точками понятия угла не существует.
Где вы там катеты увидели? Изменено: Михаил С. — 21.08.2015 10:52:42 |
||
|
messiah, может, Вы имеете в виду углы между отрезками, которые соединяют эти точки? |
|
|
Doober Пользователь Сообщений: 2201 |
#5 21.08.2015 02:05:19 Вспоминаем физический смысл первой производной и получаем формулу
<#0> |
||
|
messiah Пользователь Сообщений: 5 |
Доброе утро всем, Прикрепленные файлы
|
|
MCH Пользователь Сообщений: 3875 |
А так не подойдет? Или нужно от каждой точки к каждой определять угол? Тогда см. вложение Изменено: MCH — 21.08.2015 08:43:20 |
|
messiah Пользователь Сообщений: 5 |
MCH, к сожалению, нет. Эта фукнция считает угол между осью Х и прямой от (0;0) до указанной координаты. В моем варианте по другому. Изменено: messiah — 21.08.2015 09:30:08 |
|
xSilverSx Пользователь Сообщений: 6 |
Наверное как то так? Тут без макроса |
|
MCH Пользователь Сообщений: 3875 |
#10 22.08.2015 07:58:22
messiah, Вы мое вложение смотрели? там, как мне кажется, считается именно так, как Вам нужно |
||
|
JeyCi Пользователь Сообщений: 3357 |
#11 07.09.2015 15:04:55
Doober , MCH — спасибо и от меня, тоже буду считать на досуге… Изменено: JeyCi — 07.09.2015 15:05:11 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||
В данной публикации мы рассмотрим, что такое угол меду двумя векторами, и приведем формулу, с помощью которой можно найти его косинус. Также разберем пример решения задачи по этой теме.
- Нахождение угла между векторами
- Пример задачи
Нахождение угла между векторами
Угол между двумя векторами, берущими начало в одной и той же точке – это наименьший угол, на который можно повернуть один из данных векторов вокруг своей начальной точки до положения, при котором он будет сонаправлен со вторым вектором.
Косинус угла между двумя векторами равняется скалярному произведению векторов, разделенному на произведение длин (модулей) этих векторов.
Для расчета косинуса угла используется формула ниже:
Пример задачи
Найдем угол между векторами a = {4; 3} и b = {12; 5}.
Решение
1. Для начала рассчитаем их скалярное произведение:
a · b = 4 · 12 + 3 · 5 = 48 + 15 = 63.
2. Теперь найдем длины (модули) заданных векторов:
3. Применим формулу для нахождения косинуса угла:
4. Следовательно, угол приблизительно равняется 14,26° (arccos 0,9692).
17 авг. 2022 г.
читать 2 мин
В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.
Что такое скалярный продукт?
Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:
а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3
Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:
а · б = 2*4 + 5*3 + 6*2
а · б = 8 + 15 + 12
а · б = 35
По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.
Как найти точечный продукт в Excel
Чтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:
1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:
2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:
СУММПРОИЗВ(массив1, [массив2], …)
- array — первый массив или диапазон, который необходимо умножить, а затем добавить.
- array2 — второй массив или диапазон для умножения, а затем добавления.
В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :
=СУММПРОИЗВ(A1:A3, B1:B3)
Это дает значение 35 , которое соответствует ответу, который мы получили вручную.
Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:
=СУММПРОИЗВ(A1:A20, B1:B20)
Возможные ошибки при вычислении скалярного произведения
Функция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.
Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.
Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:
Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84
|
0 / 0 / 0 Регистрация: 14.02.2011 Сообщений: 6 |
|
|
1 |
|
Найти угол между векторами и, используя формулу14.02.2011, 13:51. Показов 3332. Ответов 4
Visual Basic: Найти угол между векторами A(n) и B(n), используя формулу: Честно сказать даже не представляю как это реализовать. Сделать нужно в MS Exel. Надеюсь на помощь. Так же можно реализовать на delphi Изображения
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
14.02.2011, 13:51 |
|
Ответы с готовыми решениями: Известны ориентированные углы между векторами: угол(АВ,АС)=120 и угол (АВ,АД)=-60. Определите угол (АС,АД) Найти угол между векторами А и В Трехмерные векторы заданы своими координатами, например, А =… найти угол между векторами мне…
4 |
|
0 / 0 / 0 Регистрация: 05.02.2011 Сообщений: 9 |
|
|
14.02.2011, 15:08 |
2 |
|
мало исходных данных.
0 |
|
6644 / 1511 / 169 Регистрация: 09.01.2010 Сообщений: 4,298 |
|
|
14.02.2011, 17:21 |
3 |
|
скорее координаты вектора , ну и его размерность как то определить бы
0 |
|
730 / 406 / 95 Регистрация: 19.12.2010 Сообщений: 756 |
|
|
14.02.2011, 18:15 |
4 |
|
Как вариант.
1 |
|
0 / 0 / 0 Регистрация: 14.02.2011 Сообщений: 6 |
|
|
15.02.2011, 02:41 [ТС] |
5 |
|
Как вариант. + в репу. Спасибо большое
0 |
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ATAN2 в Microsoft Excel.
Описание
Возвращает арктангенс для заданных координат x и y. Арктангенс — это угол между осью x и линией, проведенной из начала координат (0, 0) в точку с координатами (x, y). Угол определяется в радианах в диапазоне от -пи до пи, исключая -пи.
Синтаксис
ATAN2(x;y)
Аргументы функции ATAN2 описаны ниже.
-
x — обязательный аргумент. X-координата точки.
-
y — обязательный аргумент. Y-координата точки.
Замечания
-
Положительный результат соответствует отсчету угла против часовой стрелки от оси x; отрицательный результат соответствует отсчету угла по часовой стрелке.
-
ATAN2(x;y) равняется ATAN(y/x), за исключением того, что в ATAN2 аргумент x может принимать значение 0.
-
Если x_num и y_num 0, ATAN2 возвращает #DIV/0! значение ошибки #ЗНАЧ!.
-
Чтобы выразить арктангенс в градусах, умножьте результат на 180/ПИ( ) или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ATAN2(1;1) |
Арктангенс точки с координатами (1;1) в радианах, пи/4 |
0,785398163 |
|
=ATAN2(-1;-1) |
Арктангенс точки с координатами (-1;-1) в радианах, -3*пи/4 |
-2,35619449 |
|
=ATAN2(-1;-1)*180/ПИ() |
Арктангенс точки с координатами (1;1) в градусах |
-135 |
|
=ГРАДУСЫ(ATAN2(-1; -1)) |
Арктангенс точки с координатами (1;1) в градусах |
-135 |
Нужна дополнительная помощь?
If you’re working with any triangle with a right angle in it somewhere, it’s simple to find the tangent angle, so long as you know the length of two sides of the triangle.
Doing so is even easier in Microsoft Excel because there are built-in functions you can use.
Information in this article applies to Excel for Microsoft 365, Excel 2019, 2016, 2013, 2010, and Excel for Mac.
What Is the Tangent Angle?
A tangent angle is an angle in the triangle where you know the length of the side opposite the angle and the side adjacent to it.
Imagine, for example, that your boss tells you to adjust a ladder at precisely 70 degrees from the ground. Unless you have some special tools, it would be complicated to measure whether the angle between the ladder and the ground is exactly 70 degrees.
However, if you have a measuring tape, you could measure the distance from the bottom of the ladder to the wall. Since the ladder against the wall forms a triangle, this would be the side that’s adjacent to the tangent angle you’re trying to calculate.
Next, you’d measure the distance from the bottom of the wall to where the top of the ladder touches it. This is the distance of the side that’s opposite from the tangent angle.
With the measurement of the opposite and adjacent sides, you can calculate the angle at the ladder base using the arctangent function.
If the wall (opposite) side is 10 feet, and the ground (adjacent) side is 5 feet, the formula for the tangent angle is the opposite side divided by the adjacent side. This is 10 divided by 5, or 0.5.
To find the value for the angle, you need to take the arctangent of 0.5.
Find the Tangent Angle With Excel
You could find a calculator that calculates the arctangent of a value, but Excel has a built-in function called ATAN that you can use.
The formula returns the angle in radians, which your boss probably won’t understand.
You’ll want to convert radians to degrees by multiplying it by 180/pi. Excel also has a PI function you can use for this purpose.
The answer, in this case, is 63.43 degrees. This means you’ll need to adjust one of the lengths until the angle is precisely 70 degrees.
Doing this is easy in Excel because you can change the opposite side’s value until the arctangent result is 70.
Using ASIN and ACOS in Excel
In this same scenario, let’s say you don’t have a tape measure long enough to measure the wall. You only know that the ladder is 15 feet and that it’s placed five feet from the wall.
Excel has two other functions that you can use to calculate the angle.
The ladder’s length is the hypotenuse of the triangle, and the ground distance is the adjacent side to the angle. So long as the triangle has one right (90 degree) angle, the information you have determines the formula you need to use.
- Cosine: Calculate the cosine angle if you know the length of the hypotenuse and the adjacent side.
- Sine: Calculate the sine angle if you know the length of the hypotenuse and the opposite side.
In this case, the angle is the arccosine of the adjacent side divided by the hypotenuse.
Since you know the adjacent side (the ground distance) is 5 feet, and the ladder length (hypotenuse) is 15 feet, the cosine of the angle is 5 divided by 15, or 0.333.
To calculate the angle, use the arccosine formula in Excel.
The result of the arccosine function is Excel is in radians, so you need to multiply it by 180/PI to convert it to degrees.
For a 15 foot ladder with its base 5 feet from the wall, the angle is 70.53 degrees.
If you knew that the height of the wall (the opposite side) is 10 feet, instead of the ground distance from the wall (the adjacent side), you’d use the arcsine formula in Excel.
In this case, the sine of the angle is the opposite side divided by the hypotenuse.
After converting to degrees, the angle, in this case, would be 48.12 degrees.
Why Use ATAN, ACOS, or ASIN?
Here are a few examples of situations where you may need to use one of these functions in Excel:
- In carpentry and construction, angles and lengths are used in all aspects of building houses and buildings.
- Photographers use angles to align lighting and their creative shots carefully.
- In sports, understanding angles can enhance skills and improve strategy.
- Ships and airplanes are located on radar using angles and distances.
- If you want to be sure furniture will fit right in your room, you’ll need to know how to calculate lengths and angles.
You may be able to accomplish these calculations on a scientific calculator. But if you don’t have one handy, Excel can help you make those calculations.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a→ и b→ , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы OA→=b→ и OB→=b→
Углом между векторами a→ и b→ называется угол между лучами ОА и ОВ.
Полученный угол будем обозначать следующим образом: a→,b→^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a→,b→^=0, когда векторы являются сонаправленными и a→,b→^=π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π2 радиан.
Если хотя бы один из векторов является нулевым, то угол a→,b→^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a→, b→=a→·b→·cosa→,b→^.
Если заданные векторы a→ и b→ ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cosa→,b→^=a→,b→a→·b→
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a→ и b→ . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно -9. Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cosa→,b→^=-93·6=-12 ,
Теперь определим угол между векторами: a→,b→^=arccos (-12)=3π4
Ответ: cosa→,b→^=-12, a→,b→^=3π4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a→=(ax, ay), b→=(bx, by) выглядит так:
cosa→,b→^=ax·bx+ay·byax2+ay2·bx2+by2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a→=(ax, ay, az), b→=(bx, by, bz) будет иметь вид: cosa→,b→^=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
Исходные данные: векторы a→=(2, 0, -1), b→=(1, 2, 3) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cosa→,b→^=2·1+0·2+(-1)·322+02+(-1)2·12+22+32=-170⇒a→,b→^=arccos(-170)=-arccos170
- Также можно определить угол по формуле:
cosa→,b→^=(a→, b→)a→·b→,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a→=22+02+(-1)2=5b→=12+22+32=14a→,b→^=2·1+0·2+(-1)·3=-1cosa→,b→^=a→,b→^a→·b→=-15·14=-170⇒a→,b→^=-arccos170
Ответ: a→,b→^=-arccos170
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A(2, -1), B(3, 2), C(7, -2). Необходимо определить косинус угла между векторами AC→ и BC→.
Решение
Найдем координаты векторов по координатам заданных точек AC→=(7-2, -2-(-1))=(5, -1)BC→=(7-3, -2-2)=(4, -4)
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cosAC→, BC→^=(AC→, BC→)AC→·BC→=5·4+(-1)·(-4)52+(-1)2·42+(-4)2=2426·32=313
Ответ: cosAC→, BC→^=313
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы OA→=a→ и OB→=b→ , тогда, согласно теореме косинусов в треугольнике ОАВ, будет верным равенство:
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) ,
что равносильно:
b→-a→2=a→+b→-2·a→·b→·cos(a→, b→)^
и отсюда выведем формулу косинуса угла:
cos(a→, b→)^=12·a→2+b→2-b→-a→2a→·b→
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
cos(a→, b→)^=a→, b→a→·b→
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

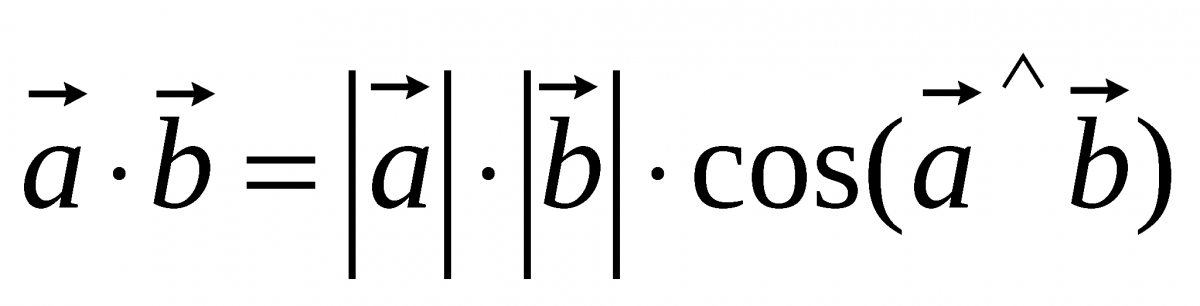

















































 Найти угол между векторами
Найти угол между векторами
