Содержание
- 1 Строим графики с точками пересечений
- 2 Находим точку пересечения графиков в Excel
- 3 Точки пересечения для трех показателей
- 4 Хороший вопрос…
- 5 Скачать пример
-
- 5.0.1 ChartsIntersection.xlsx
-
- 6 Решение
- 6.1 Шаг 1
- 6.2 Шаг 2
- 6.3 Шаг 3
- 7 Пересечение двух графиков
- 8 Как найти точку пересечения графиков функций в excel
- 9 Как найти точку пересечения графиков функций в excel
- 10 Точка пересечения графиков в Excel
- 11 Пересечение двух графиков
- 12 Пересечение графика с осями координат
-
-
- 12.0.0.1 Поделиться с друзьями:
- 12.0.0.2 Поиск по сайту:
-
- 12.1 Похожие статьи:
-
- 13 Комментарии (6)
- 13.1 Добавить комментарий Отменить ответ
- 13.2 Свежие записи
- 13.3 Содержание
-
- 13.3.0.1 Обратная матрица в Excel
-
- 14 Как найти точку пересечения графиков функций в excel
- 15 Точки пересечения графиков — MS Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Хороший вопрос…
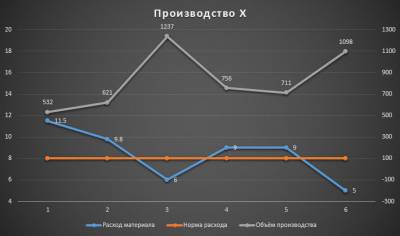
Задали мне тут недавно вопрос. Есть график, на котором имеем 3 показателя работы производства: удельный расход материала, норматив расхода и объём производства, а по горизонтальной оси временной период (недели, например).
Исходные данные выглядят так:
Удельный расход материала зависит от объёма производства. Он то выше, то ниже норматива по итогам периода и возникает естественный вопрос показать на диаграмме те моменты времени и те объёмы производства, когда линия расхода пересекает линию норматива. Может быть эта проблема и лишена какого-то великого смысла, но тем не менее вопрос был задан, значит потребность такая у людей есть.
А это наша конечная цель:
Скачать пример
ChartsIntersection.xlsx
Решение
Шаг 1
Для начала обратим внимание, что исходный тип диаграммы — График с маркерами.
Ряды этого типа описываются так:
Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X — общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.
Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то «между периодами». Поэтому тип диаграммы мы меняем для всех рядов с «графика с маркерами» на «точечную с прямыми отрезками и маркерами».
Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.
Шаг 2
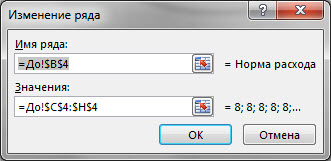
Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:
-
Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.
-
Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная.
-
Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18.
Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите «Выбрать данные…», далее воспользуйтесь кнопкой «Добавить».
Пример одного из рядов:
Шаг 3
Отформатируйте линии и маркеры новых рядов данных, так как вам необходимо. Готово! 🙂
Изучим способы поиска точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel.
Поиск точек пересечения графиков может применяться, к примеру, при графическом способе решения различных уравнений в математике или при поиске точки безубыточности предприятия в бизнесе.
Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу.
В данной статье мы разберем как найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная).
Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну.
Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения:
Общий принцип поиска координат следующий: для каждых двух соседних пар точек на оси абсцисс (на рисунке x1 и x2 расположены по горизонтали) проверяется условие пересекаются ли линии, то есть выполняется ли условие y1 ≥ z1 и y2 ≤ z2, или наоборот y1 ≤ z1 и y2 ≥ z2 (на рисунке y1, y2, z1 и z2 расположены по вертикали).
Пересечение двух графиков
Предположим, что у нас имеется таблица с координатами двух линий:
Построим на основе этих данных точечную диаграмму. Выделяем диапазон данных A1:K3 и на панели вкладок выбираем Вставка -> Диаграмма -> Точечная -> Точечная с прямыми отрезками.
В итоге получаем точечную диаграмму с двумя линиями:
Как видим на диаграмме линии пересеклись в 5 местах. В общем случае подобных точек может быть сколь угодно много, поэтому вручную находить каждую из них представляется достаточно трудоемким процессом.
Чтобы упростить работу и автоматизировать расчет воспользуемся средствами Visual Basic.
Переходим в редактор VBA (в панели вкладок выбираем Разработчик -> Visual Basic или воспользуемся сочетанием клавиш Alt + F11), создаем модуль и записываем в него макрос (напротив каждой строчки даются пояснения к коду):
|
Sub IntersectionGraph() X = ActiveChart.SeriesCollection(1).XValues ‘Значение по оси X Y = ActiveChart.SeriesCollection(1).Values ‘Значения 1-ой линии по оси Y Z = ActiveChart.SeriesCollection(2).Values ‘2-ой TotalCount = ActiveChart.SeriesCollection(1).Points.Count ‘Подсчет количества точек по X Dim ArrayT1() As Double ‘Определение массива для хранения координат по X Dim ArrayT2() As Double ‘по Y ReDim ArrayT1(TotalCount) ‘Определение размера массива ReDim ArrayT2(TotalCount) k = 0 ActiveChart.SeriesCollection(1).Select For i = 1 To TotalCount — 1 ‘Цикл по всем точкам X1 = X(i) X2 = X(i + 1) Y1 = Y(i) Y2 = Y(i + 1) Z1 = Z(i) Z2 = Z(i + 1) If (Y1 >= Z1 And Y2 РЕШЕНИЕ: ||| Вариант решения 1. ||| 1) Высота, проведенная из вершины прямого угла, делит треугольник на два подобных треугольника между собой и подобных данному. Из подобия треугольников АВС и НСВ следует: В=НСА. 2) Медиана, проведенная из вершины прямого угла, равна половине. Как найти точку пересечения графиков функций в excelЭтот файлик может пригодиться для оформления задач поиска точки пересечения линейных графиков, построенных по экспериментальным данным. Графики выстраиваются по точкам эксперимента. Рассчитываются коэффициенты А и В функций, рассчитывается точка пересечения и отображается на графике. Теперь при изменении значений точка корректно отображается на графике. Нашел у Павлова пример с поиском многоточечных пересечений. Совсем немножко добавил от себя. Может тоже пригодиться для оформления лабораторных. Как найти точку пересечения графиков функций в excelТочка пересечения графиков в ExcelИзучим способы поиска Точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel. Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу. В данной статье мы разберем как Найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная). Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну. Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения: Пересечение двух графиковПредположим, что у нас имеется таблица с координатами двух линий: Построим на основе этих данных точечную диаграмму. Выделяем диапазон данных A1:K3 и на панели вкладок выбираем Вставка -> Диаграмма -> Точечная -> Точечная с прямыми отрезками. В итоге получаем точечную диаграмму с двумя линиями: Как видим на диаграмме линии пересеклись в 5 местах. В общем случае подобных точек может быть сколь угодно много, поэтому вручную находить каждую из них представляется достаточно трудоемким процессом. Чтобы упростить работу и автоматизировать расчет воспользуемся средствами Visual Basic. Переходим в редактор VBA (в панели вкладок выбираем Разработчик -> Visual Basic или воспользуемся сочетанием клавиш Alt + F11), создаем модуль и записываем в него макрос (напротив каждой строчки даются пояснения к коду): Переходим обратно в Excel, нажимаем на диаграмму (для активации) и запускаем макрос: Осталось только добавить на свое усмотрение некоторые детали для улучшения визуализации и получаем итоговый вариант: Для удобства и экономии времени, определение вида и цвета отображаемой точки, формата подписи данных и прочих настроек, можно также добавить в код макроса. Пересечение графика с осями координатАналогичное решение можно применить и в случае поиска мест пересечения графика с осью абсцисс. Для этого в качестве координат одной из линий установим нулевые значения: Применяем к графику макрос и получаем: Удачи вам и до скорых встреч на страницах блога Tutorexcel. ru! Поделиться с друзьями:Поиск по сайту:Похожие статьи:Комментарии (6)Очень здорово, вопрос один. А если график 3 или более функций и можно ли как то значения автоматом в таблицу занести В случае если на графике 3 линии, то в макросе нужно будет дополнительно прописать проверки на пересечение каждой пары линий (т. е. первой и второй, первой и третьей, второй и третьей). Координаты точек пересечений хранятся в массивах ArrayT1 (ось X) и ArrayT2 (ось Y), соответственно чтобы занести эти координаты в таблицу, мы должны приравнять значения ячеек таблицы к элементам массивов. Спасибо за ответ, только если честно я конструктор, и незнаком с программированием, скажите возможно ли связаться с Вами для решения моей проблемы? Здравствуйте, помогите пожалуйста, мне нужно найти пересечение двух графиков, точки взяты произвольно, формул никаких нет. Я пробовала вставить вашу программу, но выдает ошибку Анастасия, в данной статье разбирается случай, когда графики имеют одинаковые координаты по горизонтальной оси, и разные координаты по вертикальной. В приведенном примере, в случае с красной линией, это условие не выполняется, вероятно по этой причине возникает ошибка. Добавить комментарий Отменить ответСвежие записиСодержаниеЧитайте ранее: Обратная матрица в ExcelПодробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР. Как найти точку пересечения графиков функций в excelТочки пересечения графиков — MS ExcelНадо найти точки пересечения их. я сделал, но они почему то не пересекаются, может кто подсказать что я делал не так? сейчас скину формулу из ячеек Как в графике отобразить точки пересечения? А также также рядом указать сумму точки x+y как в примере. То есть пример точки 31=30+1 или. Доброго времени суток! Являюсь полным нубом относительно Excel. Задача такая: Построить графики двух уравнений и найти их точки. Здравствуйте! Помогите, пожалуйста, правильно построить графики в Excel. Вот на этом рисунке данные и графики, которые у меня получаются. Доброго времени суток. Нужна ваша помощь. Есть некие графики сделанные мною в другой программе, но потребовалась все это построить в. Помогите построить 5 графиков в одной сетке(поле) зависимость объема от обратного давления. Первый столбец — объем, он постоянен для всех. Здравствуйте, у меня есть задания которые необходимо выполнить в excele. У меня не получается выполнить задание под буквой В в первом. Да, дейстаительно они не пересекаются. Т.е. система уравнений не имеет корней. А откуда третье уравнение? Решение из маткад, у системы комплексные корни Bantline везет же вам с задачами. Krasme, я знаю, что не окружность. то я вчера где-то накосячил. Сам сегодня удивился Здравствуйте, уважаемые Специалисты! Помогите пожалуйста с совмещением двух графиков различного типа(если это конечно возможно). У меня. Помогите разобраться! Что к чему? Выделенные слова вообще могут использоваться в тексте программы? Private Sub CommandButton1_Click() . Всем привет. Как можно отобразить все значения на одном графике, а не на двух? |
The intersection of the two curves is the point where the two curves meet, and their coordinates are the same. In this article, we will learn about how to find the intersection point of the two curves in excel. Finding the intersection point of two curves can be very useful in data analysis. Let’s learn the steps for the same,
Intersection Point of two curves in Excel
Consider two sales curves of different regions Vs the year, and if they intersect at some point, then we would have insight at what time interval the sales of two different regions are matching or how close or how apart they are. For example, “Arushi” is a data analyst, and she notices that sales pattern 1 follows the curvey = x2 and sales pattern 2 follows the curvey = 2.7x. Her task is to find the intersection point of the two sales curves. Given a data set with x, y1, and y2 values, the formula used to calculate y1 values is by sales pattern 1, and the formula used to calculate y2 values is by sales pattern 2. A chart is also created.
Following are the steps,
Step 1: Create a new table range with headings x, y1, y2, and differences. Write any random value of x in cell D14. For example, 4.
Step 2: Write the same formula used in y1, as above, i.e.,y = x2. For example, =D14*D14. Press Enter.
Step 3: The value appears in cell E14. For example, 16.
Step 4: Write the same formula used in y2, as above, i.e.,Y = 2.7x. For example, =2.7^D14. Press Enter.
Step 5: The value appears in cell F14. For example, 53.1441.
Step 6: In the difference column, we are storing the difference between y1 and y2. This is done because we know that, at the intersection, the value y of both curves will be equal. This will be helpful in the later stages. Write =E14 – F14 is the cell G14. Press Enter.
Step 7: The value appears in cell G14. For example, -37.1441.
Step 8: Your active cell should be G14. Go to the Data tab, under the Forecast section, and click on the What-if Analysis. Click on the ribbon, and a drop-down appears. Select Goal Seek.
Step 9: Goal Seek dialogue box appears. In the set cell, select the cell G14, i.e., the difference column cell.
Step 10: We know that at the point of intersection, the difference between the y coordinates of the 2 curves is the same. So, it states that we need to put our difference value to zero(0).
Step 11: As all the formulas are dependent on the x value, we need to calculate the difference of 0 by changing the x value. So, select D14 in by changing Cell. Click Ok.
Step 12: The intersection point appears. The value of x is -0.70468, y1 is 0.49658, and y2 is 0.49662. The difference is 10-5, which tends to be 0.
Step 13: By graph also, we can observe that our values are correct.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
ОТРЕЗОК(известные_значения_y; известные_значения_x)
Аргументы функции ОТРЕЗОК описаны ниже.
-
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
-
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
-
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
-
Если аргументы «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
-
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
где наклон b вычисляется следующим образом:
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
-
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то справедливо указанное ниже.
-
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
-
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
Формула |
Описание |
Результат |
|
=ОТРЕЗОК(A2:A6; B2:B6) |
Определяет точку пересечения линии с осью y, используя приведенные выше известные значения x и известные значения y |
0,0483871 |
Нужна дополнительная помощь?
Программы-редакторы электронных таблиц упрощают не только сбор и классификацию данных, но и обработку математических выражений; в частности, позволяют без лишних сложностей найти итоговую сумму или рассчитать значение по формуле. Пользователь, уже представляющий, как закрепить строку в Excel при прокрутке, сможет построить любой график. Как это сделать — попробуем разобраться.
Эксель позволяет начертить график или сделать диаграмму в несколько шагов, без предварительной обработки данных и в рамках основного пакета. Не нужно подключать дополнительные модули и устанавливать сторонние плагины — всё, что требуется, чтобы нарисовать зависимость, содержится в «ленте»; главное — правильно пользоваться предлагаемыми функциями.
Важно: работа в MS Excel мало отличается от пользования бесплатными редакторами. Посчитать проценты или создать график в любом из них можно, следуя приведённой далее инструкции — нужно лишь слегка адаптировать её под конкретный программный продукт.
Все приготовления, которые требуется сделать пользователю, заключаются в выяснении задачи и поиске исходных данных; как только всё будет готово, можно запускать Excel и приступать к делу.
Простейший
Самый простой график в Экселе — это зависимость одного ряда значений от другого. Рисовать её предельно просто: достаточно задать параметры и сделать несколько кликов мышью. Вполне естественно, на графике будет отображаться только одна линия; если их больше, необходимо вернуться к началу инструкции и проверить правильность совершённых действий.
Чтобы построить простой график в Excel, нужно:
- Составить таблицу исходных данных. Взаимозависимые значения для большего удобства следует располагать в столбцах с заголовками; чтобы получить на графика не только линию, но и автоматически подписанные оси, нужно выделить мышью не таблицу целиком.
- Перейти на вкладку «Вставка» и, отыскав в разделе «Диаграммы» подраздел «Вставить график», вызвать щелчком мыши выпадающее меню. Представленная рядом с «Диаграммами» функция «Спарклайн-график» для построения простой зависимости не подходит!
- Построенная системой зависимость полностью соответствует введённым данным, однако не слишком хорошо оформлена; как исправить положение и сделать визуальное представление по-настоящему красивым, будет рассказано в соответствующем разделе нашего материала. Рисунок можно перемещать, копировать, вставить в текстовый документ и удалить, щёлкнув по нему и нажав на клавишу Delete.
Важно: щёлкая по линии графика или оси, юзер увидит, к какому из рядов данных они относятся — будет подсвечен соответствующий столбец исходной таблицы.
С несколькими рядами данных
Чтобы нарисовать график с несколькими рядами значений, нужно:
- Перейти на вкладку «Вид» и выбрать в выпадающем меню соответственно функцию «График» или «График с маркерами» — в результате возле таблицы появится зависимость, содержащая уже две линии, для каждого ряда чисел.
Важно: применять эту опцию можно только в указанном случае — иначе построенный график будет некорректно отображать взаимозависимость данных.
Как построить график в Excel — простая инструкция
Важно: работа в MS Excel мало отличается от пользования бесплатными редакторами. Посчитать проценты или создать график в любом из них можно, следуя приведённой далее инструкции — нужно лишь слегка адаптировать её под конкретный программный продукт.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
В электронной таблице Excel можно производить вычисления, используя формулы, а на основе их результатов строить различные диаграммы, в частности, графики. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Как объединить графики в Excel — Построение графиков функций в Excel — Как в офисе.
- Составить в Excel таблицу с заголовками, отображающими суть каждой зависимости. Пусть для примера это будут просто X, Y, Z и R. В этой таблице сразу можно задать значения оси абсцисс (X) и параметра R, не выражаемого известной функцией.
Построить график в Excel можно, создав таблицу значений, перейдя на вкладке «Вставка» в раздел «Диаграммы» и выбрав требуемый тип линии. Чтобы визуально представить функцию, необходимо задать её в исходной таблице, используя стандартные операции. Настройка графика осуществляется с помощью меню «Элементы диаграммы», а также на вкладках «Конструктор» и «Формат».
Пошаговый процесс создания диаграммы
Создание графика происходит после подготовки исходной таблицы.
На простейшем примере рассмотрим, как отображаются конкретные события в разные промежутки времени:
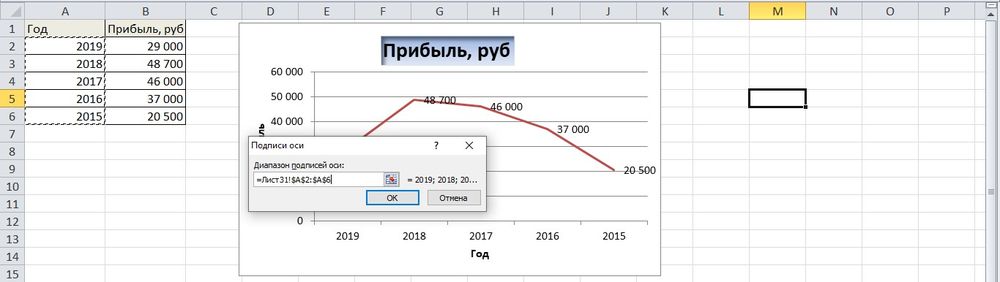
Важно! При наведении курсора на любую диаграмму всплывает подсказка, для каких данных ее лучше использовать.
- Поскольку есть только одна кривая, справа стоит удалить легенду «прибыль, руб.». Выделить ее кликом мышки и нажать «Del».
- Перейти в раздел «Макет», где с помощью опции «Подписи данных» определить расположение цифр.
- Использование дополнительных параметров опции «Название диаграммы» поможет переместить или вовсе удалить заголовок, изменить его стиль, добавить заливку, градиент или тень и т.д.
- Чтобы на горизонтальной оси вместо порядковых чисел были года 2015-2019, выделить числа кликом, вызвать контекстное меню правой кнопкой мышки и «Выбрать данные». Изменить подписи, указав диапазон годов.
Если нужно перенести созданный рисунок на другой лист книги, следует перейти на вкладку «Конструктор», где на верхней панели справа есть опция «Переместить…». В новом окне клацнуть по пункту «На отдельном листе» и подтвердить действие нажатием на «Ок».
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Чтобы добавить на любую линию графика подписи размещаются прямо на сетке или выноски данных в отдельных окошечках , нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню Добавить подписи данных. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
Как построить график зависимости в Excel
- Выделить ось, для которой будет добавлена еще одна. Клацнуть по ней правой кнопкой мышки, из контекстного меню выбрать «Формат ряда данных». В новом открывшемся окне во вкладке «Параметры ряда» отметить пункт «По вспомогательной оси».
В электронной таблице Excel можно производить вычисления, используя формулы, а на основе их результатов строить различные диаграммы, в частности, графики. С их помощью в книге отображаются колебания и изменения данных во времени, показывается зависимость одних значений от других. Такой метод визуализации очень облегчает восприятие числовой информации.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
Графическое решение уравнений средствами Microsoft Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Применение табличного процессора Microsoft Excel для графического решения уравнений n-ой степени
Из курса математики известно, что корнями уравнения являются значения точек пересечения графика функции с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями будут координаты точек пересечения графиков функций. Этот метод нахождения корней уравнения называется графическим. Мы уже знаем, что с помощью EXCEL можно строить практически любые графики. Воспользуемся этими знаниями для нахождения корней системы уравнений:
Преобразуем данную систему в приведенную:
Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций. Сначала построим таблицу:
Первая строка – строка заголовков.
При заполнении столбца А: в ячейку А2 заносится начальное значение аргумента Х = – 10, для автоматического заполнения всего столбца в ячейку А3 занести формулу “= А2 + 1” и скопировать ее до ячейки А22.
При заполнении столбца В: в ячейку В2 заносится формула “= А2 * А2”, которая затем копируется до ячейки В22.
При заполнении столбца С: в ячейку С2 заносится формула “ = 2 * А2 + 9”, и также копируется до С22
С помощью Мастера диаграмм построим в одной координатной плоскости графики заданных функций для первоначальной оценки решений/
На диаграмме видно, что оба графика имеют точки пересечения – координаты этих точек и есть решения системы. Так как шаг изменения аргумента достаточно велик, то мы получим приближенные значения решений.
Уточним их, построив два графика в интервалах от – 3 до 0, где находится первое решение, и от 3 до 5, где находится второе решение. Составим новые таблицы. Для первого решения – рисунок 4, для второго – рисунок 5.
Для более точного построения мы уменьшили шаг изменения аргумента. Решением нашей системы будут координаты точек пересечения графиков: Х 1 = – 2,2; Y 1 = 4,6; Х 2 = 4,2; Y 2 = 17,4. Как вы уже поняли, графическое решение системы дает приблизительные результаты.
Это можно сделать, построив график и определив координаты точек его пересечения с осью OX, либо построив два графика: Y = X3;
Y = 2X2 + 4X – 12 и определив точки их пересечения.
источники:
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
http://infourok.ru/graficheskoe-reshenie-uravneniy-sredstvami-microsoft-ecel-2404628.html


















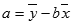
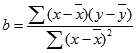




































 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):










