Функция LOG в Microsoft Excel
Одним из востребованных математических действий при решении учебных и практических задач является нахождение логарифма из заданного числа по основанию. В Экселе для выполнения данной задачи существует специальная функция, которая называется LOG. Давайте поподробнее узнаем, как её можно применять на практике.
Использование оператора LOG
Оператор LOG относится к категории математических функций. Его задачей является вычисление логарифма указанного числа по заданному основанию. Синтаксис у указанного оператора предельно простой:
Как видим, функция располагает всего двумя аргументами.
Аргумент «Число» представляет собой число, из которого нужно вычислить логарифм. Он может принимать вид числового значения и являться ссылкой на ячейку, его содержащую.
Аргумент «Основание» представляет собой основание, по которому будет вычисляться логарифм. Он тоже может иметь, как числовой вид, так и выступать в виде ссылки на ячейку. Данный аргумент не является обязательным. Если он опущен, то считается, что основание равно нулю.
Кроме того, в Экселе существует ещё одна функция, позволяющая вычислять логарифмы – LOG10. Её главное отличие от предыдущей в том, что она может вычислять логарифмы исключительно по основанию 10, то есть, только десятичные логарифмы. Её синтаксис ещё проще, чем у ранее представленного оператора:
Как видим, единственным аргументом данной функции является «Число», то есть, числовое значение или ссылка на ячейку, в которой оно расположено. В отличие от оператора LOG у этой функции аргумент «Основание» вообще отсутствует, так как принимается, что основание обрабатываемых ею значений равно 10.
Способ 1: применение функции LOG
Теперь давайте рассмотрим применение оператора LOG на конкретном примере. Имеем столбец числовых значений. Нам нужно вычислить из них логарифм по основанию 5.
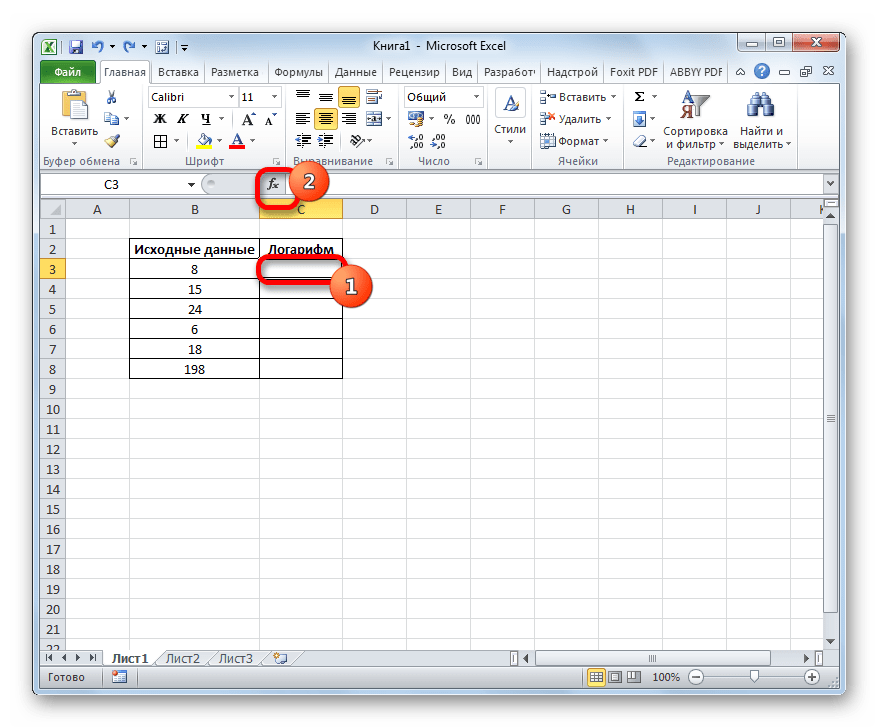
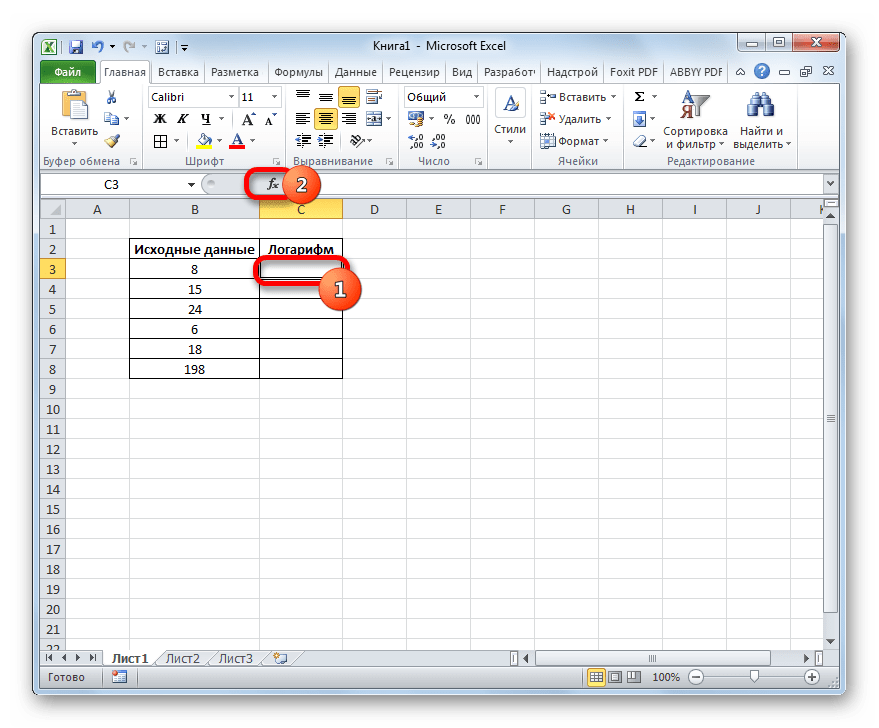
- Выполняем выделение первой пустой ячейки на листе в колонке, в которую планируем выводить итоговый результат. Далее щелкаем по пиктограмме «Вставить функцию», которая располагается возле строки формул.
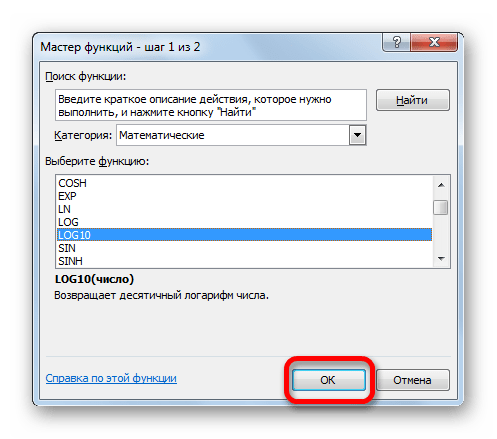
Происходит запуск окошка Мастера функций. Перемещаемся в категорию «Математические». Производим выделение наименования «LOG» в списке операторов, после чего производим щелчок по кнопке «OK».
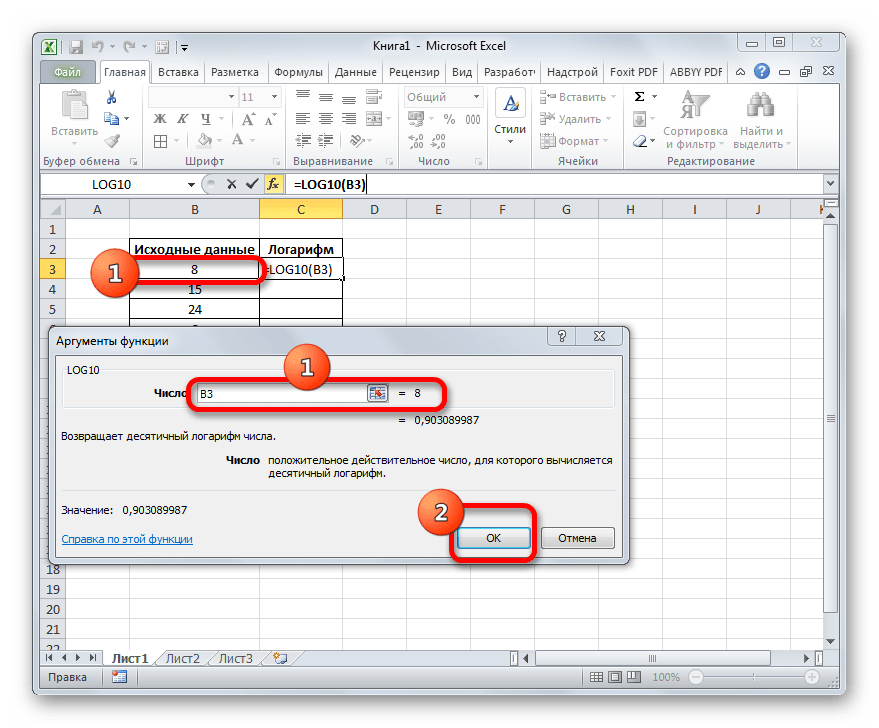
Происходит запуск окошка аргументов функции LOG. Как видим, оно имеет два поля, которые соответствуют аргументам данного оператора.
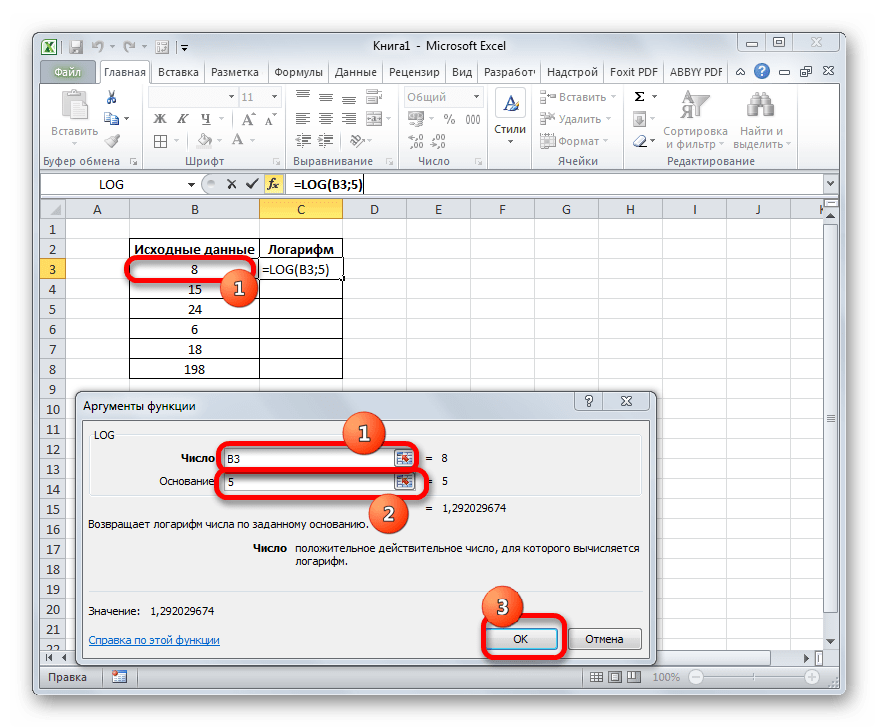
В поле «Число» в нашем случае следует ввести адрес первой ячейки того столбца, в котором находятся исходные данные. Это можно сделать, вписав его в поле вручную. Но существует и более удобный способ. Устанавливаем курсор в указанном поле, а затем щелкаем левой кнопкой мыши по ячейке таблицы, содержащей нужное нам числовое значение. Координаты данной ячейки тут же отобразятся в поле «Число».
В поле «Основание» просто вписываем значение «5», так как оно будет одинаково для всего обрабатываемого числового ряда.
После произведения указанных манипуляций щелкаем по кнопке «OK».
Но мы заполнили только первую ячейку столбца. Для того, чтобы заполнить и остальные, нужно скопировать формулу. Устанавливаем курсор в нижний правый угол ячейки её содержащей. Появляется маркер заполнения, представ в виде крестика. Выполняем зажим левой кнопки мыши и перетягиваем крестик до конца столбца.
Способ 2: применение функции LOG10
Теперь давайте рассмотрим пример использования оператора LOG10. Для примера возьмем таблицу с теми же исходными данными. Но теперь, понятное дело, предстоит задача вычислить логарифм чисел, расположенных в столбце «Исходные данные» по основанию 10 (десятичный логарифм).
- Производим выделение первой пустой ячейки столбца «Логарифм» и щелкаем по пиктограмме «Вставить функцию».
В открывшемся окне Мастера функций опять выполняем переход в категорию «Математические», но на этот раз останавливаемся на наименовании «LOG10». Щелкаем внизу окошка по кнопке «OK».
Происходит активация окна аргументов функции LOG10. Как видим, оно располагает только одним полем – «Число». Вносим в него адрес первой ячейки столбца «Исходные данные», тем же способом, который мы использовали в предыдущем примере. Затем щелкаем по кнопке «OK» внизу окна.
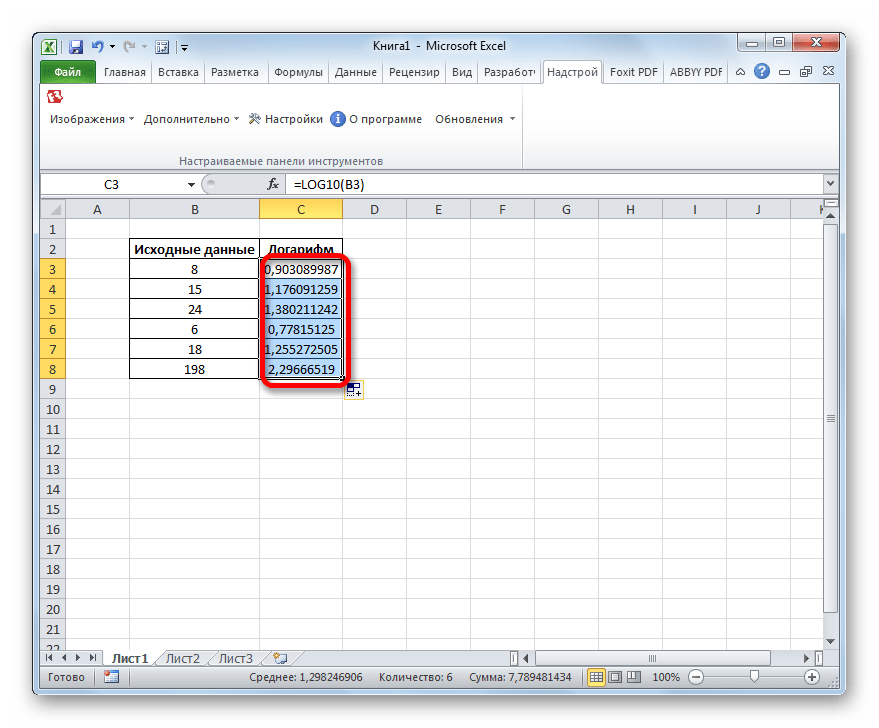
Результат обработки данных, а именно десятичный логарифм заданного числа, выводится в предварительно указанную ячейку.
Применение функции LOG позволяет в Экселе просто и быстро посчитать логарифм от указанного числа по заданному основанию. Этот же оператор может посчитать и десятичный логарифм, но для указанных целей более рационально использовать функцию LOG10.
Помимо этой статьи, на сайте еще 12688 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Как рассчитать логарифм в Excel с помощью функции LOG
Вычисление логарифмов – это одна из самых востребованных математических задач, в том числе, в программе Эксель, в которой специально для этого разработана функция под названием LOG. В этой статье мы рассмотрим, каким образом работает данная функция.
Вычисление логарифма в Эксель
Функция в Excel, позволяющая считать логарифмы из определенного числа по указанному основанию, называется LOG.
Формула функции LOG выглядит следующим образом:
=LOG(число;[основание])
Как мы видим, формула имеет два аргумента:
- “Число” – конкретное число (или адрес ячейки, которая содержит число), из которого требуется вычислить логарифм.
Помимо вышеописанной функции, в Эксель есть еще один оператор – LOG10, который вычисляет логарифмы с основанием, равным цифре 10. Другими словами, он умеет работать исключительно с десятичными логарифмами.
Формула функции LOG10 выглядит следующим образом:
=LOG10(число).
В данном случае оператор имеет только один аргумент – “Число”, который, как и в случае с функцией LOG, прописывается в виде числового выражения (либо ссылкой на ячейку с требуемым числом). Это и есть то значение, логарифм которого нужно рассчитать. Второго аргумента под названием “Основание” в этой формуле нет, так как ему присваивается безусловное значение, равное 10.
Использование оператора LOG
Для лучшего понимания работы функции LOG давайте разберем ее, применив на практике. Для этого возьмем таблицу имеющую колонку с числами. Наша задача – в отдельном столбце вычислить логарифмы из этих числовых значений по основанию, равному 3.
Давайте начнем выполнение нашей задачи:
- Выбираем первую ячейку столбца, в которой хотим произвести вычисления. Затем кликаем по кнопке “Вставить функцию” (с левой стороны от строки формул).
- В результате откроется окно Мастера функций. Здесь мы щелкаем по текущей категории и в открывшемся перечне выбираем строку “Математические”.
- Из предложенного списка операторов кликаем по функции “LOG” и подтверждаем действие нажатием OK.
- В открывшемся окне задаем настройки функции, после чего нажимаем OK. Согласно количеству аргументов оператора, в открывшемся окне имеется два поля:
- в поле “Число” указываем координаты ячейки с числом, из которого требуется рассчитать логарифм. Можно прописать информацию вручную, но есть более простой и удобный метод. Кликаем сначала по области поля “Число”, после чего – по требуемой ячейке.
Применение оператора LOG10
А сейчас предлагаем познакомимся с оператором LOG10. Теперь наша задача – это получении десятичных логарифмов исходных чисел.
- Проделываем те же действия, что и при первом способе, т.е. выбираем верхнюю ячейку столбца, куда будем выводить результаты и жмем кнопку “Вставить функцию”.
- В перечне математических операторов кликаем по строке “LOG10”, после чего подтверждаем выбор нажатием OK.
- Затем выполняем настройку функции. В данном случае она имеет всего лишь один аргумент – “Число”. Указываем адрес нужной ячейки с числом, логарифм из которого нужно рассчитать, и жмем кликаем по кнопке OK, чтобы получить результат.
- В итоге, в выбранной ячейке с формулой будет выведен результат вычислений десятичного логарифма от заданного числового значения. Методом, который был описан в первом способе, растягиваем формулу на все оставшиеся строки результирующего столбца.
Заключение
Итак, в Microsoft Excel вычисление логарифма от заданного числового значения по указанному основанию реализовано через функцию “LOG”, которая также позволяет рассчитать логарифм по основанию, равному 10. Однако, для десятичных логарифмов целесообразнее и проще использовать специально разработанный для этого отдельный оператор под названием “LOG10”.
Функции LN и LOG для расчета натурального логарифма В EXCEL
Функция LN в Excel предназначена для расчета натурального логарифма числа и возвращает соответствующее числовое значение. Натуральным логарифмом является логарифм с основанием e (число Эйлера, равное примерно 2,718).
Функция LOG в Excel используется для расчета логарифма числа, при этом основание логарифма может быть указано явно в качестве второго аргумента данной функции.
Функция LOG10 в Excel предназначена для расчета логарифма числа с основанием 10 (десятичный логарифм).
Примеры использования функций LN, LOG и LOG10 в Excel
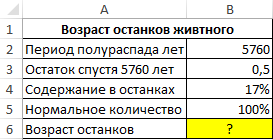
Пример 1. Археологи нашли останки древнего животного. Для определения их возраста было решено воспользоваться методом радиоуглеродного анализа. В результате замеров оказалось, что содержание радиоактивного изотопа C 14 составило 17% от количества, которое обычно содержится в живых организмах. Рассчитать возраст останков, если период полураспада изотопа углерода 14 составляет 5760 лет.
Вид исходной таблицы:
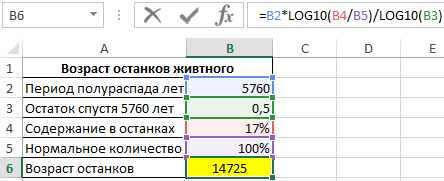
Для решения используем следующую формулу:
Данная формула была получена на основе формулы x=t*(lgB-lgq)/lgp, где:
- q – количество изотопа углерода в начальный момент (в момент смерти животного), выраженное единицей (или 100%);
- B – количество изотопа в момент проведения анализа останков;
- t – период полураспада изотопа;
- p – числовое значение, указывающее, во сколько раз изменяется количество вещества (изотопа углерода) за период времени t.
В результате вычислений получим:
Найденным останкам почти 15 тыс. лет.
Депозитный калькулятор со сложным процентом в Excel
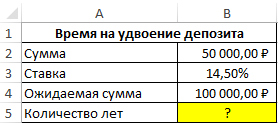
Пример 2. Клиент банка внес депозит на сумму 50000 рублей с процентной ставкой 14,5% (сложные проценты). Определить, сколько времени потребуется на удвоение вложенной суммы?
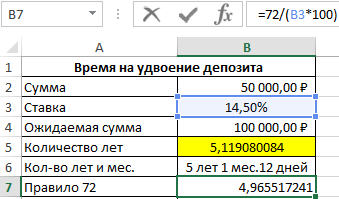
Интересный факт! Для быстрого решения данной задачи можно воспользоваться эмпирическим способом приблизительной оценки сроков (в годах) на удвоение инвестиций, вложенных под сложный процент. Так называемое правило 72 (или 70 или правило 69). Для этого нужно воспользоваться простой формулой – число 72 разделить на процентную ставку: 72/14,5 = 4,9655 лет. Главный недостаток правила «магического» числа 72 заключается в погрешности. Чем выше процентная ставка, тем выше погрешность в правиле 72. Например, при процентной ставки 100% годовых погрешность в годах достигает до 0,72 (а в процентах это аж 28%!).
Для точного расчета сроков удвоения инвестиций будем использовать функцию LOG. За одно и проверим величину погрешности правила 72 при процентной ставке 14,5% годовых.
Вид исходной таблицы:
Для расчета будущей стоимости инвестиции при известной процентной ставке можно использовать следующую формулу: S=A(100%+n%) t , где:
- S – ожидаемая сумма по истечению срока;
- A – размер депозита;
- n – процентная ставка;
- t – срок хранения депозитных средств в банке.
Для данного примера эту формулу можно записать как 100000=50000*(100%+14,5%) t или 2=(100%+14,5%) t . Тогда для нахождения t можно переписать уравнение как t=log(114,5%)2 или t=log1,1452.
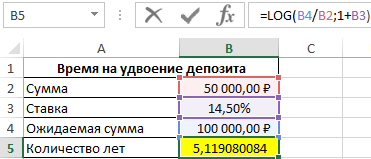
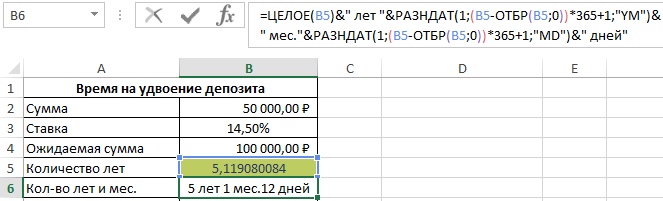
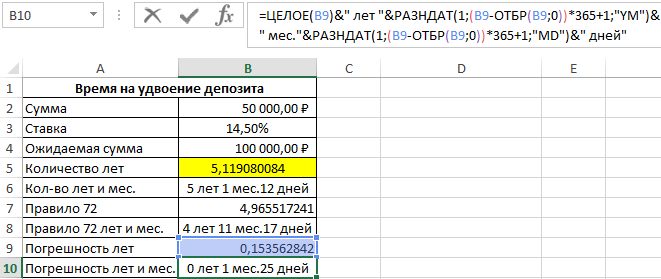
Для нахождения значения t запишем следующую формулу сложного процента по депозиту в Excel:
- B4/B2 – соотношение ожидаемой и начальной сумм, которое является показателем логарифма;
- 1+B3 – прирост процентов (основание логарифма).
В результате расчетов получим:
Депозит удвоится спустя немного более чем 5 лет. Для точного определения лет и месяцев воспользуемся формулой:
Функция ОТБР отбрасывает в дробном числе все что после запятой подобно функции ЦЕЛОЕ. Разница между функциями ОТБР и ЦЕЛОЕ заключается лишь в расчетах с отрицательными дробными числами. Кроме того, ОТБР имеет второй аргумент где можно указать количество оставляемых знаков после запятой. Поэтом в данном случаи можно воспользоваться любой из этих двух функций на выбор пользователя.
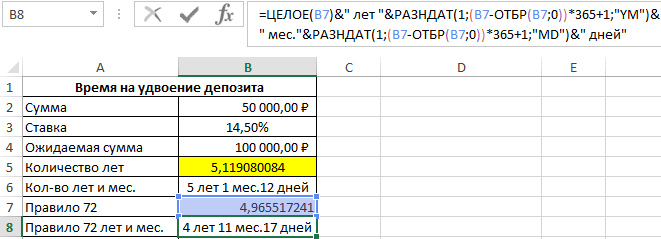
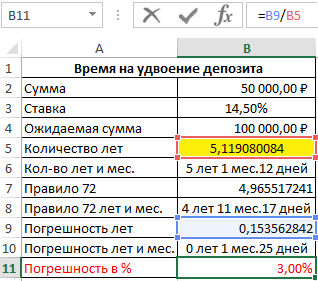
Получилось 5 лет и 1 месяц и 12 дней. Теперь сравним точные результаты с правилом 72 и определим величину погрешности. Для данного примера формула, следующая:
Мы должны умножить значение ячейки B3 на 100 так как ее текущее значение 0,145, которое отображается в процентном формате. В результате:
После скопируем формулу из ячейки B6 в ячейку B8, а в ячейке B9:
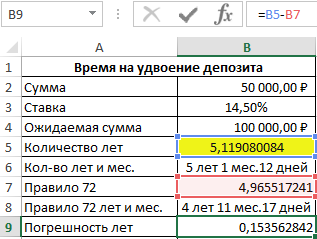
Посчитаем сроки погрешности:
Затем в ячейку B10 снова скопируем формулу из ячейки B6. В результате получим разницу:
И наконец посчитаем разницу в процентах, чтобы проверить как изменяется размер отклонения и насколько существенно влияет рост процентной ставки на уровень расхождения правила 72 и факта:
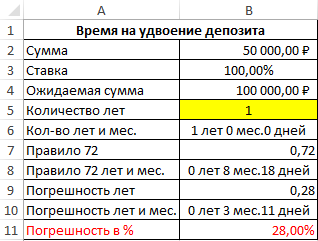
Теперь для наглядности пропорциональной зависимости роста погрешности и роста уровня процентной ставки повысим процентную ставку до 100% годовых:
На первый взгляд разница погрешности не существенная по сравнению с 14,5% годовых — всего около 2-ух месяцев и 100% годовых — в пределах 3-х месяцев. Но доля погрешности в сроках окупаемости более чем ¼, а точнее 28%.
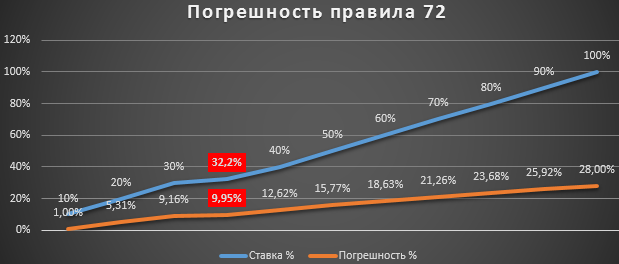
Составим простой график для визуального анализа как коррелируется зависимость изменения процентной ставки и процента погрешности правила 72 от факта:
Чем выше процентная ставка, тем хуже работает правило 72. В итоге можно сделать следующий вывод: до 32,2% процентов годовых можно смело пользоваться правилом 72. Тогда погрешность составляет менее 10-ти процентов. Вполне сойдет если не требуются точные, но сложные расчеты по срокам окупаемости инвестиций в 2 раза.
Инвестиционный калькулятор сложных процентов с капитализацией в Excel
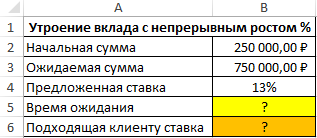
Пример 3. Клиенту банка предложили сделать вклад с непрерывным ростом итоговой суммы (капитализация со сложными процентами). Процентная ставка составляет 13% годовых. Определить, сколько потребуется времени, чтобы утроить начальную сумму (250000 рублей). Насколько необходимо увеличить процентную ставку, чтобы уменьшить время ожидания вдвое?
Примечание: так как мы в данном примере утраиваем сумму вложений, то здесь уже правило 72 не работает.
Вид исходной таблицы данных:
Непрерывный рост может быть описан формулой ln(N)=p*t, где:
- N – отношение конечной суммы вклада к начальной;
- p – процентная ставка;
- t – количество лет, прошедших с момента внесения депозита.
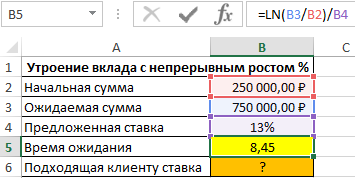
Тогда t=ln(N)/p. Исходя из этого равенства запишем формулу в Excel:
- B3/B2 – соотношение конечной и начальной сумм депозита;
- B4 – процентная ставка.
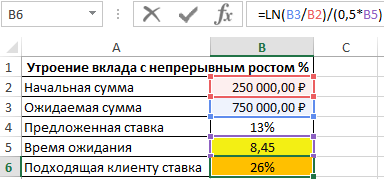
На утроение начальной суммы вклада потребуется почти 8,5 лет. Для расчета ставки, которая позволит сократить время ожидания вдвое, используем формулу:
То есть, необходимо удвоить начальную процентную ставку.
Особенности использования функций LN, LOG и LOG10 в Excel
Функция LN имеет следующий синтаксис:
- число – единственный аргумент, являющийся обязательным для заполнения, который принимает действительные числа из диапазона положительных значений.
- Функция LN является обратной функцией EXP. Последняя возвращает значение, полученное в результате возведения числа e в указанную степень. Функция LN указывает, в какую степень необходимо возвести число e (основание), чтобы получить показатель логарифма (аргумент число).
- Если аргумент число задан числом из диапазона отрицательных значений или нулем, результатом выполнения функции LN будет код ошибки #ЧИСЛО!.
Синтаксис функции LOG имеет следующий вид:
=LOG( число ;[основание])
- число – обязательный для заполнения аргумент, характеризующий числовое значение показателя логарифма, то есть число, полученное в результате возведения основания логарифма в некоторую степень, которая и будет вычислена функцией LOG;
- [основание] – необязательный для заполнения аргумент, характеризующий числовое значение основания логарифма. Если аргумент явно не указан, логарифм считается десятичным (то есть основание равно 10).
- Несмотря на то, что результат вычисления функции LOG может являться отрицательным числом (например, функция =LOG(2;0,25) вернет значение -0,5), аргументы данной функции должны быть взяты из диапазона положительных значений. Если хотя бы один из аргументов является отрицательным числом, функция LOG вернет код ошибки #ЧИСЛО!.
- Если в качестве аргумента [основание] было передано значение 1, функция LOG вернет код ошибки #ДЕЛ/0!, поскольку результат возведения 1 в любую степень будет всегда одинаковым и равным 1.
Функция LOG10 имеет следующую синтаксическую запись:
- число – единственный и обязательный для заполнения аргумент, смысл которого тождественен одноименному аргументу функций LN и LOG.
Примечание: если в качестве аргумента число было передано отрицательное число или 0, функция LOG10 вернет код ошибки #ЧИСЛО!.
источники:
http://microexcel.ru/kak-rasschitat-logarifm/
http://exceltable.com/funkcii-excel/primery-funkciy-ln-log
17 авг. 2022 г.
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
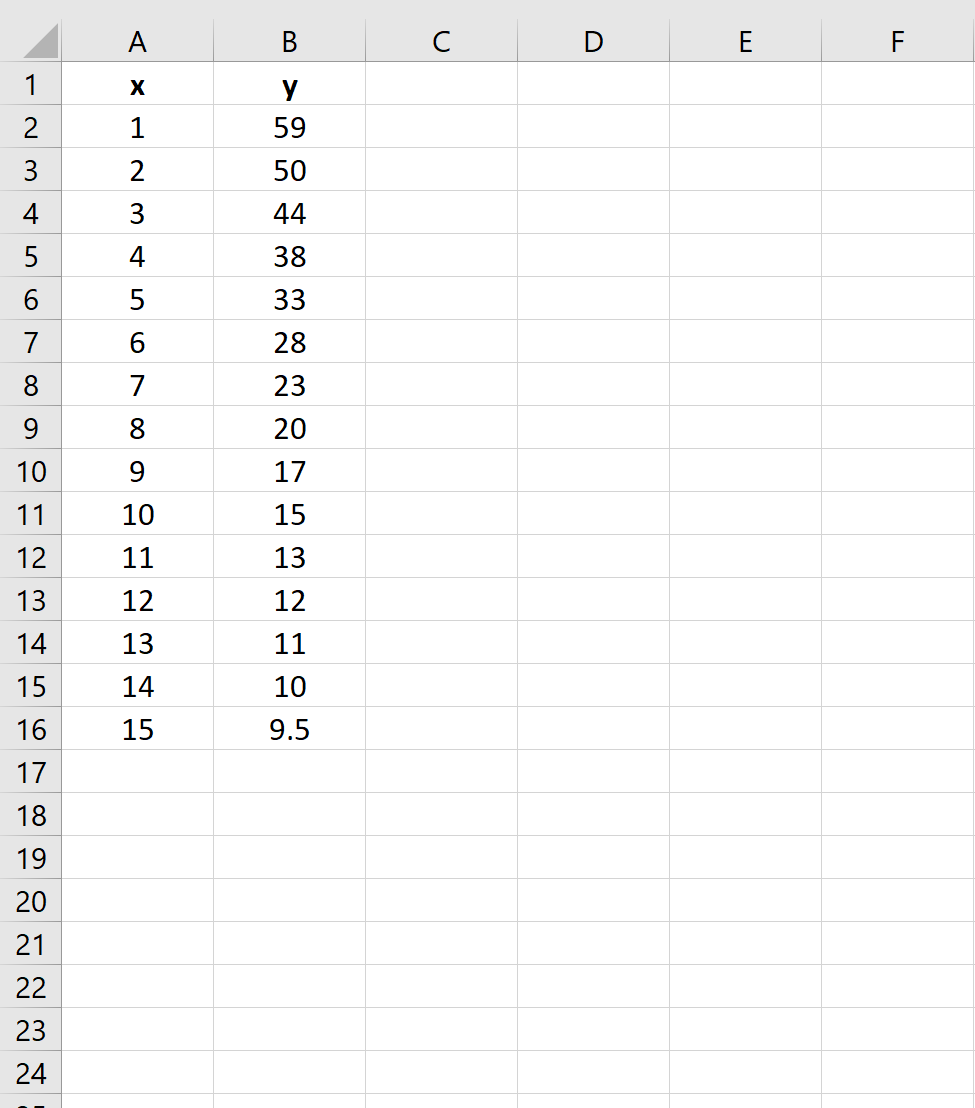
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
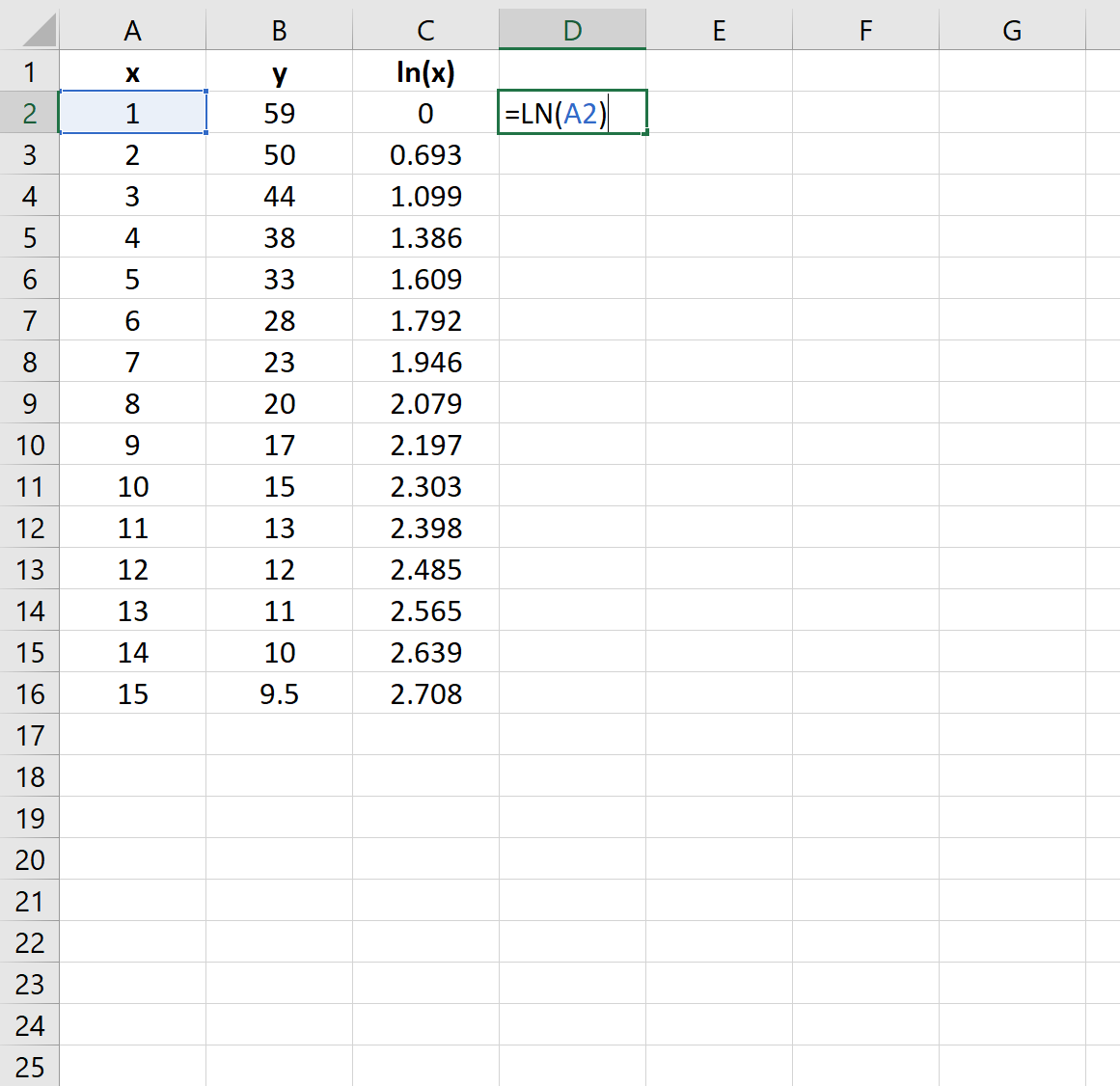
Шаг 2: возьмите натуральный логарифм переменной-предиктора
Далее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессии
Далее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
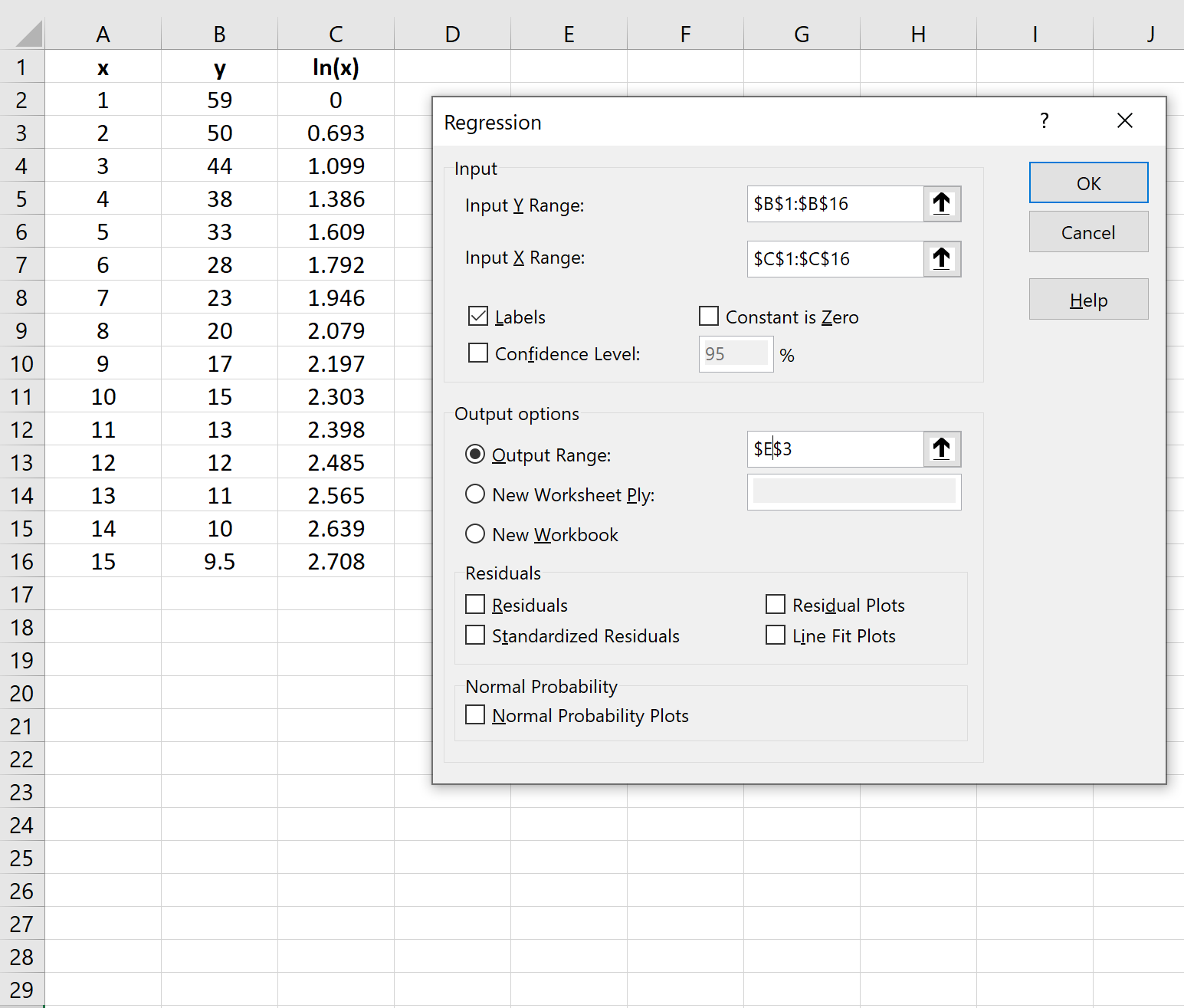
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
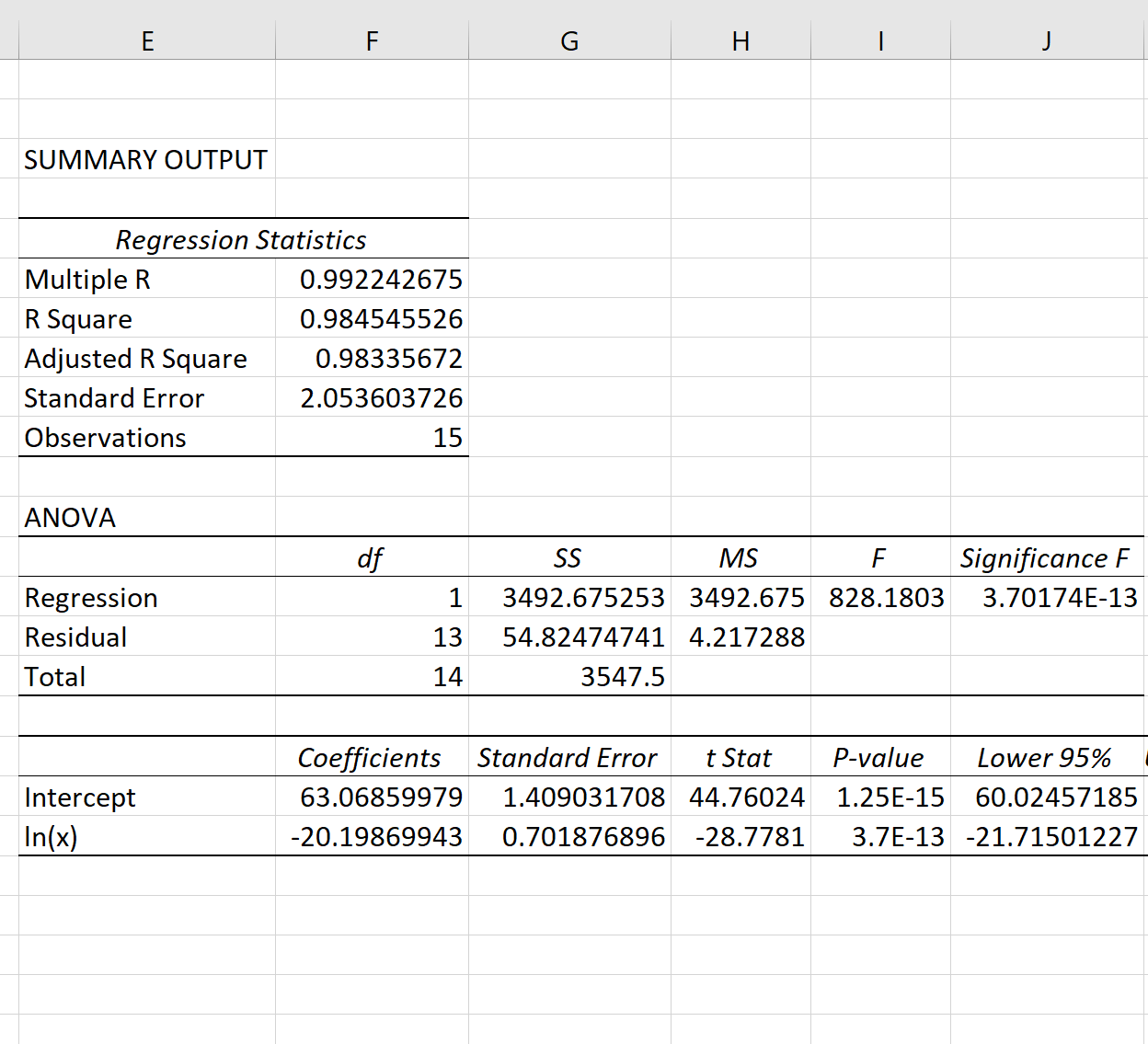
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Тема:
Решение логарифмических уравнений.
Правила записи чисел в MS Exsel
Учебник
«Алгебра и начала математического анализа. 10-11 класс» под ред. Колмогорова
А.Н.,Угринович Н.Д. «Информатика и ИКТ 11 класс».
Тип
урока: Обобщения и систематизации
полученных знаний.
Форма
проведения урока: урок творчества.
Применяемые
технологии: технология уровневой дифференциации,
технология
сотрудничества, игровая технология, групповая деятельность учащихся.
Цель
урока: Научиться решать логарифмические и
показательные уравнения с применением электронных таблиц.
Обучающая:
·
обобщение и систематизация знаний учащихся
об общих методах решения показательных и логарифмических уравнений;
Развивающая
·
развитие умений обобщать, правильно отбирать
методы решения уравнений, переносить знания в новую ситуацию;
·
формирование умений осуществлять
самоконтроль, взаимоконтроль.
Воспитательная
·
воспитание ответственного отношения к
коллективной деятельности, высокой познавательной активности и самостоятельности.
План
урока
1. Цель
и задачи урока.
2. Повторение
математических основ.
3. Разбор
формата логической функции ЕСЛИ.
4. Объяснение
задания.
5. Практическая
работа
Ход
урока:
1. Цель
и задачи урока.
Сегодняшний
урок посвящен решению логарифмических уравнений и проверка решения с помощью
табличного процессора. Также на уроке мы повторим логическую операцию ЕСЛИ.
2. Повторение
математических основ.
3. Актуализация
знаний об условном операторе ЕСЛИ.
В
табличном процессоре EXCEL
кроме математических функций можно использовать и логические функции.
Рис.36.
Логические
функции
—
Назовите логические функции, которые вам известны. ( И, ИЛИ, ЕСЛИ).
—
Повторим формат этого условного оператора.
4.
Разбор примера
—
На данном этапе урока мы с вами разберем
алгоритм выполнения одного из примеров практической работы.
—
Перед нами логарифмическое уравнение по основанию 3, в котором нужно найти
значение переменной Х.
(
один ученик у доски решает аналитически данное уравнение)
Ответ:
5
Разбор
примера ввода данной функции в табличном процессоре.
1. В
ячейку В3 ввести значение логарифма (правую часть) в данном случае число 2.
2. В
ячейку В4 вводим ответ, который мы нашли с вами при решении данного уравнения ,
то есть вводим число 5.
3. В
ячейку В5 вводим саму формулу и вместо Х уже подставляем адрес ячейку, в
которую мы ввели полученный корень
Рис.37
Проверка решения
логарифмического уравнения
4. При
вводе в ячейку В5 формулы следует повторить :
Приоритет
выполнения операций:
•
операторы ссылок (адресные) «:», «,», « »;
•
знаковый минус «-»;
•
вычисление процента %;
•
арифметические ^, *, /, +, -;
•
текстовый оператор &;
•
операторы сравнений =, <, >, <=,
>=, <>.
Правила
ввода чисел:
•
Числовые значения, заключенные в круглые
скобки, интерпретируются как отрицательные. Например, (5) интерпретируется, как
-5.
•
Символ Е или е используется при вводе
чисел в потенциальном представлении. Например, 1Е6 интерпретируется как 1 000
000 (единица, умноженная на десять в шестой степени).
•
При вводе больших чисел позволяется
вставлять пробел для отделения сотен от тысяч, тысяч от миллионов и т. д. При
таком вводе числа в ячейках появляются пробелами, а в строке формул без
пробелов.
•
Если ввод числа начать со знака денежной
единицы, к ячейке будет применен денежный формат.
•
Если ввод числа закончить знаком %, к
ячейке будет применен процентный формат.
•
Перед вводом рациональной дроби, чтобы
Excel не итерпретировал ее как дату, следует ввести 0 и пробел, например 3/4
ввести 0 3/4. Числа можно вводить в различных форматах. В Excel имеется набор
стандартных числовых форматов, которые при желании могут быть изменены. Также
можно создать собственные пользовательские форматы. (Ученики записывают
данные правила в тетрадь)
5. В
ячейке В6 нам нужно, чтобы появлялась фраза «правильно» при безошибочном
выполнении, и фраза «неправильно», если допущена ошибка. Для этого
воспользуемся логической функцией ЕСЛИ.
6. Если
полученный в табличном процессоре результат, записанный в ячейку В3 совпадает
с правой частью уравнения, записанной в ячейку В5, то в выполняется действие
при истинности данного высказывания, то есть в ячейке В6 должна появится фраза
« правильно». Если же полученный результат не совпадает с правой частью
уравнения выполняется действие, для ложного высказывания, то есть в ячейке В6
появляется фраза « неправильно».
7. =ЕСЛИ(B3=B5;»
правильно»; « неправильно»).
4. Объяснение
задания
Вы
получили на листочках примеры, которые нужно решить для начала в тетради.
После этого ввести результат в электронную таблицу, придерживаясь, правил,
которые мы записали при разборе. И сравнить полученный корень в тетради и с
помощью электронной таблицы.
5. Практическая
работа
Задание
Решите
уравнения:
Итог
урока. Обсуждение методов решения уравнения
Тема: Решение логарифмических уравнений. Проверка решения логарифмических уравнений с помощью программы MS Exsel.
10 класс
Тип урока: урок рефлексии
Форма проведения урока: комбинированный урок
Применяемые технологии: технология уровневой дифференциации,
ИКТ-технологии.
Цель урока:
повторить изученные способы решения логарифмических уравнений, научиться проверять решение логарифмических уравнений с помощью программы MS Exsel.
Задачи:
Обучающая:
- систематизация знаний учащихся об общих методах решения логарифмических уравнений;
Развивающая
- развитие умений правильно отбирать методы решения уравнений;
- формирование умений осуществлять самоконтроль.
Воспитательная
- воспитание высокой познавательной активности и самостоятельности.
План урока
- Постановка цели и задач урока.
- Повторение понятия «функция», логарифмических функций и способов решения логарифмических уравнений.
- Самостоятельное решение логарифмических уравнений с последующей проверкой.
- Решение и проверка логарифмических уравнений с помощью программы MS Exsel.
- Практическая работа и проверка с помощью программы MS Exsel.
- Объяснение домашнего задания.
- Рефлексия.
Ход урока:
- Цель и задачи урока.
Сегодняшний урок посвящен решению логарифмических уравнений и проверки решения с помощью табличного процессора.
- Исключить лишнюю картинку на доске.
- Решение логарифмических уравнений
4. Разбор примера
— На данном этапе урока мы с вами разберем алгоритм выполнения одного из примеров практической работы.
— Перед нами логарифмическое уравнение по основанию 3, в котором нужно найти значение переменной Х.
( один ученик у доски решает аналитически данное уравнение)
Ответ: 5
Разбор примера ввода данной функции в табличном процессоре.
- В ячейку В3 ввести значение логарифма (правую часть) в данном случае число 2.
- В ячейку В4 вводим ответ, который мы нашли с вами при решении данного уравнения , то есть вводим число 5.
- В ячейку В5 вводим саму формулу и вместо Х уже подставляем адрес ячейку, в которую мы ввели полученный корень
Рис.37 Проверка решения логарифмического уравнения
- При вводе в ячейку В5 формулы следует повторить :
Приоритет выполнения операций:
- операторы ссылок (адресные) «:», «,», « »;
- знаковый минус «-»;
- вычисление процента %;
- арифметические ^, *, /, +, -;
- текстовый оператор &;
- операторы сравнений =, <, >, <=, >=, <>.
Правила ввода чисел:
- Числовые значения, заключенные в круглые скобки, интерпретируются как отрицательные. Например, (5) интерпретируется, как -5.
- Символ Е или е используется при вводе чисел в потенциальном представлении. Например, 1Е6 интерпретируется как 1 000 000 (единица, умноженная на десять в шестой степени).
- При вводе больших чисел позволяется вставлять пробел для отделения сотен от тысяч, тысяч от миллионов и т. д. При таком вводе числа в ячейках появляются пробелами, а в строке формул без пробелов.
- Если ввод числа начать со знака денежной единицы, к ячейке будет применен денежный формат.
- Если ввод числа закончить знаком %, к ячейке будет применен процентный формат.
- Перед вводом рациональной дроби, чтобы Excel не итерпретировал ее как дату, следует ввести 0 и пробел, например 3/4 ввести 0 3/4. Числа можно вводить в различных форматах. В Excel имеется набор стандартных числовых форматов, которые при желании могут быть изменены. Также можно создать собственные пользовательские форматы. (Ученики записывают данные правила в тетрадь)
- В ячейке В6 нам нужно, чтобы появлялась фраза «правильно» при безошибочном выполнении, и фраза «неправильно», если допущена ошибка. Для этого воспользуемся логической функцией ЕСЛИ.
- Если полученный в табличном процессоре результат, записанный в ячейку В3 совпадает с правой частью уравнения, записанной в ячейку В5, то в выполняется действие при истинности данного высказывания, то есть в ячейке В6 должна появится фраза « правильно». Если же полученный результат не совпадает с правой частью уравнения выполняется действие, для ложного высказывания, то есть в ячейке В6 появляется фраза « неправильно».
- =ЕСЛИ(B3=B5;» правильно»; « неправильно»).
- Объяснение задания
Вы получили на листочках примеры, которые нужно решить для начала в тетради. После этого ввести результат в электронную таблицу, придерживаясь, правил, которые мы записали при разборе. И сравнить полученный корень в тетради с помощью электронной таблицы.
- Практическая работа
Задания:
1 уровень
2 уровень
3 уровень
- Объяснение домашнего задания.
Задание на карточках. Вам необходимо решить логарифмические уравнения и проверить результат с помощью табличного редактора.
- Рефлексия. Обсуждение методов решения уравнения.
2вариант
1)Найдите корень уравнения 
2) Найдите корень уравнения 
3) Найдите корень уравнения 
4) Найдите корень уравнения 
5) Найдите корень уравнения 
Содержание
- Использование оператора LOG
- Способ 1: применение функции LOG
- Способ 2: применение функции LOG10
- Вопросы и ответы
Одним из востребованных математических действий при решении учебных и практических задач является нахождение логарифма из заданного числа по основанию. В Экселе для выполнения данной задачи существует специальная функция, которая называется LOG. Давайте поподробнее узнаем, как её можно применять на практике.
Использование оператора LOG
Оператор LOG относится к категории математических функций. Его задачей является вычисление логарифма указанного числа по заданному основанию. Синтаксис у указанного оператора предельно простой:
=LOG(число;[основание])
Как видим, функция располагает всего двумя аргументами.
Аргумент «Число» представляет собой число, из которого нужно вычислить логарифм. Он может принимать вид числового значения и являться ссылкой на ячейку, его содержащую.
Аргумент «Основание» представляет собой основание, по которому будет вычисляться логарифм. Он тоже может иметь, как числовой вид, так и выступать в виде ссылки на ячейку. Данный аргумент не является обязательным. Если он опущен, то считается, что основание равно нулю.
Кроме того, в Экселе существует ещё одна функция, позволяющая вычислять логарифмы – LOG10. Её главное отличие от предыдущей в том, что она может вычислять логарифмы исключительно по основанию 10, то есть, только десятичные логарифмы. Её синтаксис ещё проще, чем у ранее представленного оператора:
=LOG10(число)
Как видим, единственным аргументом данной функции является «Число», то есть, числовое значение или ссылка на ячейку, в которой оно расположено. В отличие от оператора LOG у этой функции аргумент «Основание» вообще отсутствует, так как принимается, что основание обрабатываемых ею значений равно 10.
Способ 1: применение функции LOG
Теперь давайте рассмотрим применение оператора LOG на конкретном примере. Имеем столбец числовых значений. Нам нужно вычислить из них логарифм по основанию 5.
- Выполняем выделение первой пустой ячейки на листе в колонке, в которую планируем выводить итоговый результат. Далее щелкаем по пиктограмме «Вставить функцию», которая располагается возле строки формул.
- Происходит запуск окошка Мастера функций. Перемещаемся в категорию «Математические». Производим выделение наименования «LOG» в списке операторов, после чего производим щелчок по кнопке «OK».
- Происходит запуск окошка аргументов функции LOG. Как видим, оно имеет два поля, которые соответствуют аргументам данного оператора.
В поле «Число» в нашем случае следует ввести адрес первой ячейки того столбца, в котором находятся исходные данные. Это можно сделать, вписав его в поле вручную. Но существует и более удобный способ. Устанавливаем курсор в указанном поле, а затем щелкаем левой кнопкой мыши по ячейке таблицы, содержащей нужное нам числовое значение. Координаты данной ячейки тут же отобразятся в поле «Число».
В поле «Основание» просто вписываем значение «5», так как оно будет одинаково для всего обрабатываемого числового ряда.
После произведения указанных манипуляций щелкаем по кнопке «OK».
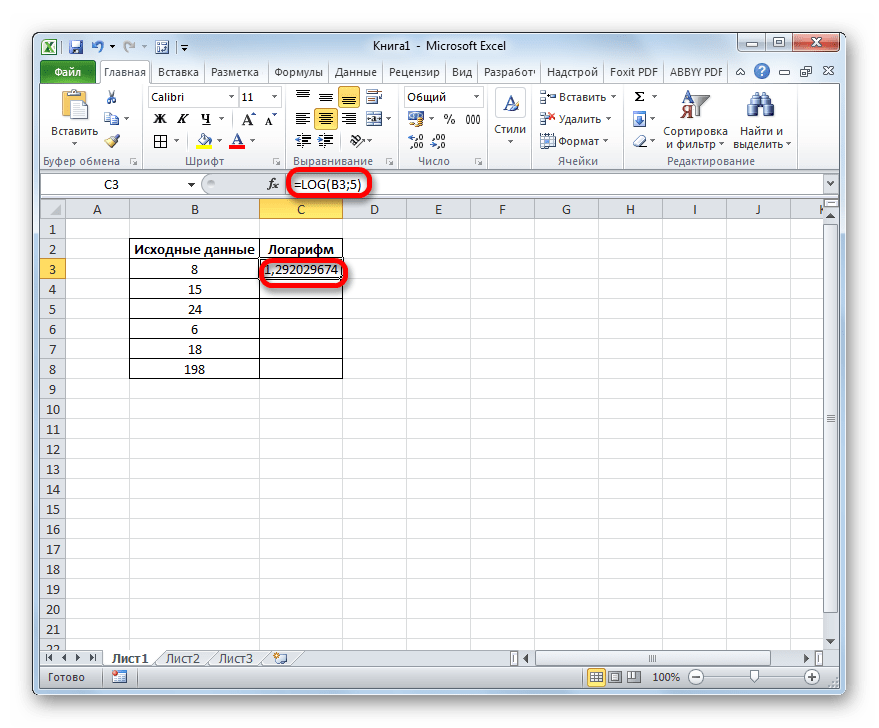
- Результат обработки функцией LOG тут же выводится в ячейку, указанную нами на первом шаге этой инструкции.
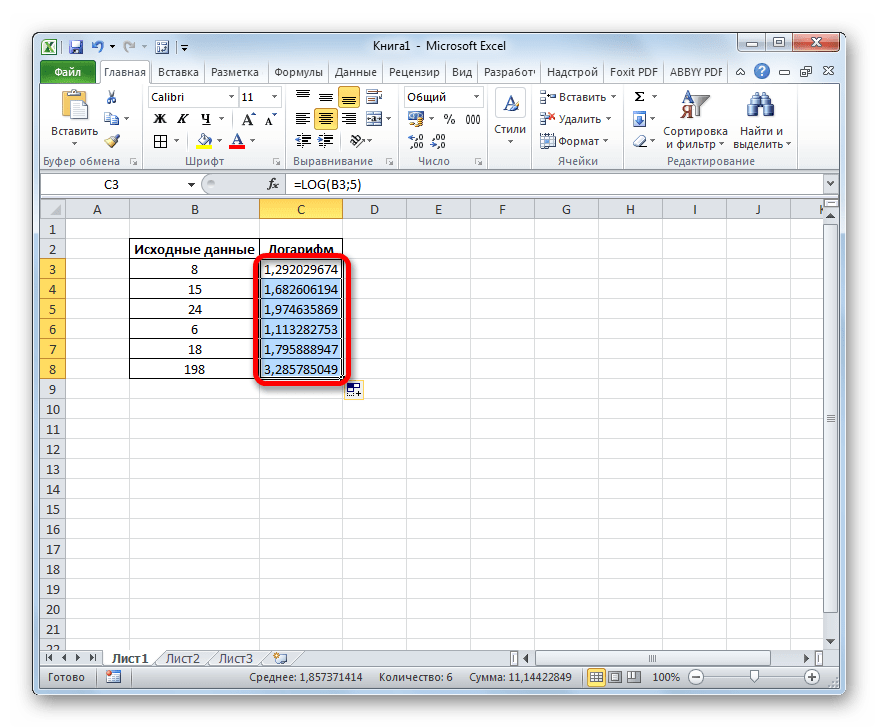
- Но мы заполнили только первую ячейку столбца. Для того, чтобы заполнить и остальные, нужно скопировать формулу. Устанавливаем курсор в нижний правый угол ячейки её содержащей. Появляется маркер заполнения, представ в виде крестика. Выполняем зажим левой кнопки мыши и перетягиваем крестик до конца столбца.
- Вышеуказанная процедура привела к тому, что все ячейки столбца «Логарифм» заполнены результатом вычисления. Дело в том, что ссылка, указанная в поле «Число», является относительной. При перемещении по ячейкам изменяется и она.
Урок: Мастер функций в Экселе
Способ 2: применение функции LOG10
Теперь давайте рассмотрим пример использования оператора LOG10. Для примера возьмем таблицу с теми же исходными данными. Но теперь, понятное дело, предстоит задача вычислить логарифм чисел, расположенных в столбце «Исходные данные» по основанию 10 (десятичный логарифм).
- Производим выделение первой пустой ячейки столбца «Логарифм» и щелкаем по пиктограмме «Вставить функцию».
- В открывшемся окне Мастера функций опять выполняем переход в категорию «Математические», но на этот раз останавливаемся на наименовании «LOG10». Щелкаем внизу окошка по кнопке «OK».
- Происходит активация окна аргументов функции LOG10. Как видим, оно располагает только одним полем – «Число». Вносим в него адрес первой ячейки столбца «Исходные данные», тем же способом, который мы использовали в предыдущем примере. Затем щелкаем по кнопке «OK» внизу окна.
- Результат обработки данных, а именно десятичный логарифм заданного числа, выводится в предварительно указанную ячейку.
- Для того, чтобы произвести вычисления и для всех остальных чисел представленных в таблице, производим копирование формулы посредством маркера заполнения, таким же способом, что и в предыдущий раз. Как видим, результаты расчетов логарифмов чисел выведены в ячейки, а значит, поставленная задача выполнена.
Урок: Другие математические функции в Экселе
Применение функции LOG позволяет в Экселе просто и быстро посчитать логарифм от указанного числа по заданному основанию. Этот же оператор может посчитать и десятичный логарифм, но для указанных целей более рационально использовать функцию LOG10.
Еще статьи по данной теме: