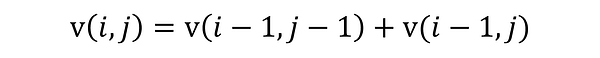Рекурсивным называется уравнение, в котором переменная появляется по обе стороны от знака равенства. Следующие уравнения можно назвать рекурсивными:
x = 1/(х+1)
x = COS(x)
x = К0РЕНЬ(x+5)
x = 2^(1/х)
x = 5 + (1/x)
Вы можете решать рекурсивные уравнения, используя преднамеренную циклическую ссылку.
Этот метод использует итеративные вычисления. По умолчанию Excel их не выполняет, так что вам нужно изменить настройки, установив флажок Включить итеративные вычисления в разделе Формулы диалогового окна Параметры Excel (рис. 129.1).
Рис. 129.1. Для решения рекурсивных уравнений необходимо включить возможность итеративных вычислений
Первый шаг заключается в преобразовании рекурсивного уравнения в ссылающуюся на саму себя формулу. Для решения первого уравнения введите следующую формулу в ячейку А1:
=1/(A+1). Формула сходится к 0,618033989, что является значением х, удовлетворяющим уравнению.
Excel использует итеративный процесс для вычисления решения. Максимальное количество итераций, выполняющееся для каждого вычисления, указано в разделе Формулы диалогового окна Параметры Excel. Вам, возможно, потребуется нажать F9 несколько раз, прежде чем решение перестанет изменяться.
Однако иногда этот метод не работает. Например, формула допускает возможность деления на нуль. Решение заключается в проверке на ошибки. Если формула выводит ошибку, то измените незначительно повторное значение. Так, предыдущая формула может быть переписана с использованием функции ЕСЛИОШИБКА:
=ЕСЛИОШИБКА(1/(A1+1);A1+0.01).
Функция ЕСЛИОШИБКА работает только с Excel 2007 и более поздними версиями. Следующий вариант формулы совместим с предыдущими версиями Excel:
=ЕСЛИ(ЕОШ(1/(A1+1));A1+0,01;1/(A1+1)).
На рис. 129.2 показан рабочий лист, где вычисляется несколько рекурсивных уравнений в столбце В. Формулы в столбце D обеспечивают проверку результатов. Например, формула в столбце D2 будет следующей:
=1/(B2+1).
Формулы в столбце Е отображают разницу между значениями в столбцах В и D. Если решение верное, то столбец Е выводит 0 (или значение, очень близкое к 0).
Рис. 129.2. Для вычисления нескольких рекурсивных уравнений применяются циклические ссылки
1.
Задание №16: рекурсия
Решение через Excel
Время выполнения: 9 минут
Эта неполная презентация. На экзамене может
потребоваться решить задачу с помощью собственной
программы на Python/Pascal/C++.
2.
ЕГЭ-16: решение через Excel
В этой презентации рассмотрено решение некоторых
задач из 16 задания ЕГЭ через Excel.
Презентация не подготовит Вас полностью к решению
16-го задания!
Нужно будет также научиться решать задачи
программированием: некоторые типы задач невозможно
или слишком тяжело решить с помощью Excel.
3.
Задача 1
4.
Задача 1
Алгоритм вычисления функции F(n) задан следующими
соотношениями:
F(n) = 1 при n = 1
F(n) = n + F(n–1), если n чётно,
F(n) = 2· F(n–2), если n > 1 и n нечётно.
Чему равно значение функции F(26)?
5.
Решение задачи 1 — Excel
Решение с помощью Excel является усовершенствованным способом решения через
таблицу. Будьте очень аккуратны при решении задач таким методом: очень легко
допустить ошибку, скопировав не в ту ячейку.
Требуется создать таблицу из двух строк и 27 колонок:
Заполним ячейку B2 (значение F(1)). По условию задачи F(1) = 1.
6.
Решение задачи 1 — Excel
Следующая ячейка, которую нужно заполнить, B3 (значение F(2)). 2 – чётное число,
поэтому:
F(n) = n + F(n–1)
Если n = 2, F(2) = 2 + F(1)
Чтобы формулу в дальнейшем можно было растиражировать, везде, там, где в
формуле стоит n и F(n -1), мы поставим ссылки на конкретные ячейки в таблице.
Конкретные значения (2 и 1) подставлять ни в коем случае не нужно!
n = 2 — это ячейка C1
F(n — 1) = F(1) – это ячейка B2
Формула в ячейка выглядит так:
= C1 + B2
Формулу требуется переписать прямо вместе с равно.
7.
Решение задачи 1 — Excel
Для F(3):
F(n) = 2· F(n–2)
Т.е. в ячейке D2 нужно написать =2*B2
8.
Решение задачи 1 — Excel
Получаем:
Для F(4), F(6), F(8), F(10) … F(26) будет работать та же формула, что и для F(2), а для
F(5), F(7), F(9), F(11) … F(25) – та же формула, что и для F(3).
Растиражируем формулу:
<- нужно зажать квадратик в правом нижнем углу выделения и протянуть
до числа 26
9.
Решение задачи 1 — Excel
Получаем:
Ответ: 4122
10.
Самостоятельно
11.
Самостоятельно
1.1) Чему равно значение функции F(10)?
F(n) = 1 при n = 1
F(n) = 2·F(n–1) + n + 3, если n > 1
1.2) Чему равно значение функции F(1)?
F(n) = 2n – 5 при n > 12
F(n) = 2·F(n+2) + n – 4, если n <= 12
1.3) Чему равно значение F(64)?
F(n) = 1 при n = 1
F(n) = 2·F(n–1), если n чётно,
F(n) = 5n + F(n–2), если n нечётно.
12.
Ответы
1.1) 3569
1.2) 1671
1.3) 10232
13.
Задача 2
14.
Задача 2
Алгоритм вычисления функции F(n) задан следующими
соотношениями:
F(n) = 5–n при n < 5
F(n) = 4· (n – 5)·F(n–5), если n делится на 3,
F(n) = 3n + 2·F(n–1) + F(n–2), если n не делится на 3.
Чему равно значение функции F(20)?
15.
Решение задачи 2 — Excel
Решение подстановкой выходит очень сложным – слишком много возможностей
допустить арифметическую ошибку. Гораздо удобнее решать эту задачу в Excel.
Требуется создать таблицу из двух строк и 21 колонки:
По условию задачи F(n) = 5–n при n < 5. На самом деле это – выход из рекурсии
(потому что значение F(n) можно вычислить сразу же).
Определим, какую формулу нужно записать в ячейку B2:
5 – это константа, поэтому так и перепишем в формулу;
n находится в ячейке B1. Нельзя подставлять сюда значение 1: так формулу не
получится растиражировать.
16.
Решение задачи 2 — Excel
Итоговая формула для ячейки B2:
=5 – B1
Формула F(n) = 5 – n справедлива при n < 5, т.е. для ячеек B2 – E2. Растиражируем:
<- нужно зажать квадратик в правом нижнем углу выделения и протянуть
до числа 4 (ячейка E2)
17.
Решение задачи 2 — Excel
Получаем:
Для остальных ячеек эта формула уже не подойдёт.
Для n=5:
F(n) = 3n + 2·F(n–1) + F(n–2)
3 и 2 – константы, их просто переписываем в формулу. Значение n для n=5 находится
в ячейке F1, значение F(n-1) находится в ячейке E2, значение F(n – 2) находится в
ячейке D2, значение F(n) (т.е. F(5)) находится в ячейке F2. Итоговая формула в
ячейке F2:
=3*F1 + 2*E2 + D2
18.
Решение задачи 2 — Excel
19.
Решение задачи 2 — Excel
Для F(6) (ячейка G2):
F(n) = 4· (n – 5)·F(n–5), т.к. 6 делится на 3
4 – константа, так и переписываем, n — это ячейка G1, F(n – 5) – это F(1), т.е. ячейка
B2. Получаем:
= 4 * (G1 — 5) * B2
20.
Решение задачи 2 — Excel
Для F(7) (ячейка H2) формула строится по такому же принципу, как и для F(5).
Получаем, что в ячейку H2 надо записать формулу:
=3*H1+2*G2+F2
Для F(9), F(12), F(15), F(18) формула строится таким же образом, как и для F(6).
Для F(8), F(11), F(14), F(17), F(20) формула строится так же, как и для F(5).
Для F(10), F(13), F(16), F(19) формула строится так же, как и для F(7).
Все значения n «покрыты». Можно тиражировать формулу.
21.
Решение задачи 2 — Excel
<- нужно зажать квадратик в правом
нижнем углу выделения и протянуть до
числа 4 (ячейка E2)
Обратите внимание: тиражируются ячейки F2-H2, первые ячейки таблицы мы не
трогаем.
После тиражирования:
полностью значение в ячейки S2-U2 не
влезает, чтобы увидеть ответ, растяните
ячейку U2
22.
Решение задачи 2 — Excel
Ответ: 1343116
23.
Самостоятельно
24.
Самостоятельно
2.1) Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = 2 · n · n · n + n · n при n > 25
F(n) = F(n+2) + 2 · F(n+3), если n <= 25
Чему равна сумма цифр значения функции F(2)?
2.2) Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = 1+2n при n < 5
F(n) = 2·(n + 1)·F(n–2), если n делится на 3,
F(n) = 2·n + 1 + F(n–1) + 2·F(n–2), если n не делится на 3.
Чему равно значение функции F(15)?
2.3) Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n + 3 при n < 3
F(n) = (n + 2)·F(n–4), если n делится на 3,
F(n) = n + F(n–1) + 2·F(n–2), если n не делится на 3.
Чему равно значение функции F(20)?
25.
Ответы
2.1) 33
2.2) 5158048
2.3) 1112057
26.
Задача 3
27.
Задача 3
Алгоритм вычисления функций F(n) и G(n) задан
следующими соотношениями:
F(1) = G(1) = 1
F(n) = 2·F(n–1) + G(n–1) – 2, если n > 1
G(n) = F(n–1) +2·G(n–1), если n > 1
Чему равно значение F(14) + G(14)?
28.
Решение задачи 3 – Excel
Создадим таблицу из 3 строк и 15 колонок.
По условию задачи F(1) = 1, G(1) = 1.
29.
Решение задачи 3 – Excel
Разберём формулу F(n) = 2·F(n–1) + G(n–1) – 2, если n > 1
Для F(2) получаем: F(2) = 2*F(1) + G(1) – 2
F(1) – это ячейка B2
G(1) – это ячейка B3
F(2) – это ячейка C2
Т.е. в ячейку C2 нужно записать формулу:
= 2*B2 + B3 – 2
30.
Решение задачи 3 – Excel
Получаем:
Сразу же тиражируем на всю 2-ю строчку. Значения получатся
неправильные, но мы потом их исправим.
31.
Решение задачи 3 – Excel
Разберём формулу G(n) = F(n–1) +2·G(n–1), если n > 1
Для G(2) получаем: G(2) = F(1) + 2*G(1)
F(1) – это ячейка B2
G(1) – это ячейка B3
G(2) – это ячейка C3
Т.е. в ячейку C3 нужно записать формулу:
= B2 + 2*B3
32.
Решение задачи 3 – Excel
Получаем:
Сразу же тиражируем на всю 3-ю строчку. Теперь значения во всей
таблице будут правильными.
33.
Решение задачи 3 – Excel
Растянем последний столбец, чтобы увидеть, чему равны
значения F(14) и G(14).
Т.к. в ответе требуется сумма F(14)+G(14), в какой-нибудь
произвольной пустой ячейке запишем:
= O2 + O3
34.
Решение задачи 3 – Excel
Получаем:
Ответ: 1595324
35.
Самостоятельно
36.
Самостоятельно
3.1) Алгоритм вычисления функций F(n) и G(n) задан следующими соотношениями:
F(n) = G(n) = 1 при n = 1
F(n) = F(n–1) – n· G(n–1), при n > 1
G(n) = F(n–1) + 2· G(n–1), при n > 1
Чему равно значение функции G(18)?
3.2) Алгоритм вычисления функций F(n) и G(n) задан следующими соотношениями:
F(n) = G(n) = 1 при n = 1
F(n) = F(n–1) – 2 · G(n–1), при n > 1
G(n) = F(n–1) + G(n–1) + n, при n > 1
Чему равна сумма цифр значения функции G(36)?
3.3) Алгоритм вычисления функций F(n) и G(n) задан следующими соотношениями:
F(n) = G(n) = 4*n – 2 при n > 7
F(n) = F(n+1) — G(n+2) + n, при n <= 7
G(n) = 2*F(n+2) — G(n+1), при n <= 7
Чему равно значение F(-9) + G(-9)?
37.
Ответы
3.1) 87810480
3.2) 40
3.3) -219
На данный момент в Microsoft Excel имеется почти пять сотен функций рабочего листа, доступных через окно Мастера функций — кнопка fx в строке формул. Это весьма приличный набор, но, тем не менее, почти каждый пользователь рано или поздно сталкивается с ситуацией, когда в этом списке не оказывается нужной ему функции — просто потому, что её нет в Excel.
До сих пор единственным способом решить эту проблему были макросы, т.е. написание своей пользовательской функции (UDF = User Defined Function) на Visual Basic, что требует соответствующей программистской квалификации и бывает, порой, совсем непросто. Однако, с последними обновлениями Office 365 ситуация изменилась в лучшую сторону — в Excel была добавлена специальная «обёрточная» функция LAMBDA. С её помощью задача по созданию собственных функций теперь решается легко и красиво.
Давайте рассмотрим принцип её использования на следующем примере.
Как вы, скорее всего, знаете в Excel есть несколько функции для разборки даты позволяющие определить номер дня, месяца, недели и года для указанной даты. Но почему-то нет функции, определяющий номер квартала, который тоже часто нужен, правда? Давайте исправим этот недостаток и создадим с помощью LAMBDA собственную новую функцию для решения этой задачи.
Шаг 1. Пишем формулу
Начём с того, что вручную привычным образом напишем формулу в ячейке листа, которая вычисляет то, что нам нужно. В случае с номером квартала это можно сделать, например, так:
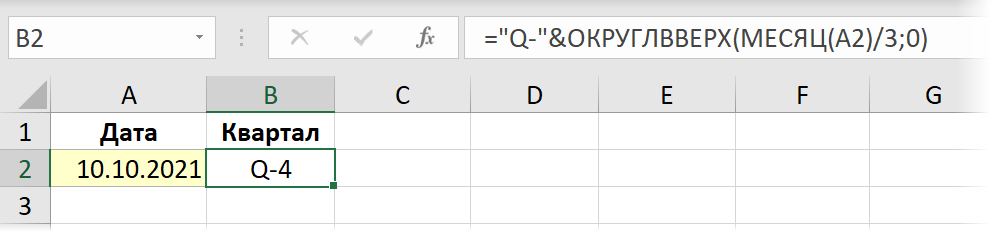
Шаг 2. Заворачиваем в LAMBDA и тестируем
Теперь пришло время применить новую функцию LAMBDA и завернуть в неё нашу формулу. Синтаксис у функции следующий:
=LAMBDA(Переменная1; Переменная2; … ПеременнаяN ; Выражение)
где сначала перечисляются имена одной или нескольких переменных, а последним аргументом всегда идёт формула или вычисляемое выражение, которое их использует. Имена переменных не должны быть похожи на адреса ячеек и не должны содержать точки.
В нашем случае переменная будет только одна — дата, для которой мы считаем номер квартала. Переменную для неё давайте назовем, допустим, d. Тогда завернув нашу формулу в функцию LAMBDA и подменив адрес исходной ячейки A2 на придуманное имя переменной, мы получим:
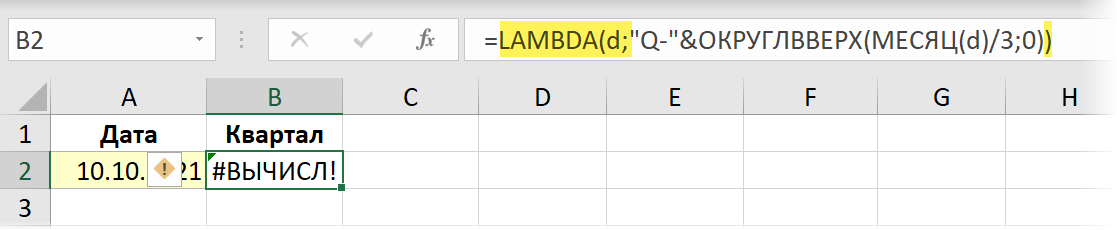
Обратите внимание, что после такого преобразования наша формула (по сути — правильная!) стала выдавать ошибку, т.к. теперь в неё не передается исходная дата из ячейки А2. Для тестирования и уверенности, можно передать ей аргументы, дописав их после функции LAMBDA в круглых скобках:

Шаг 3. Создаем имя
Теперь самая легкая и приятная часть. Открываем Диспетчер имен на вкладке Формулы (Formulas — Name Manager) и создаём новое имя кнопкой Создать (Create). Придумываем и вводим имя для нашей будущей функции (например, НОМКВАРТАЛА), а в поле Ссылка (Reference) аккуратно копируем из строки формул и вставляем нашу функцию LAMBDA, только без последнего аргумента (А2):
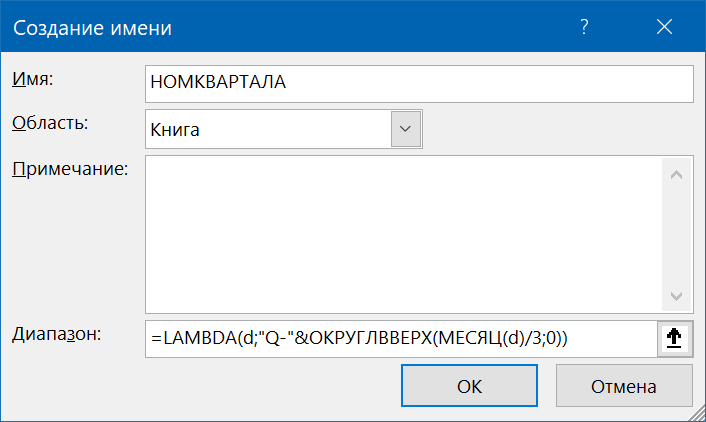
Всё. После нажатия на ОК созданную функцию можно использовать в любой ячейке на любом листе этой книги:
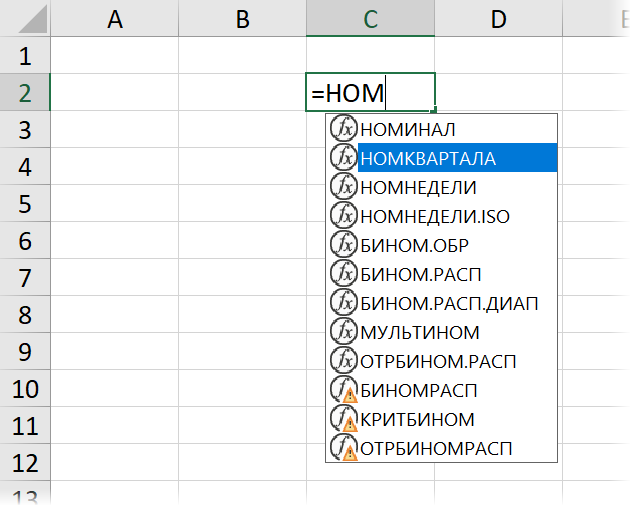
Использование в других книгах
Поскольку созданные с помощью LAMBDA пользовательские функции представляет из себя, по сути, именованные диапазоны, то можно легко сделать их доступными не только в текущей книге. Достаточно будет скопировать ячейку с функцией и вставить в любое место листа другого файла.
LAMBDA и динамические массивы
Пользовательские функции, создаваемые с помощью функции LAMBDA успешно поддерживают работу с новыми динамическими массивами и их функциями (ФИЛЬТР, УНИК, СОРТ), добавленными в Microsoft Excel в 2020 году.
Допустим, мы хотим создать новую пользовательскую функцию, которая сравнивала бы два списка и выдавала разницу между ними — те элементы из первого списка, которые отсутствуют во втором. Жизненная задача, не правда ли? Раньше для такого использовали либо функции а-ля ВПР (VLOOKUP), либо сводные таблицы, либо запросы Power Query. Теперь же можно обойтись одной формулой:
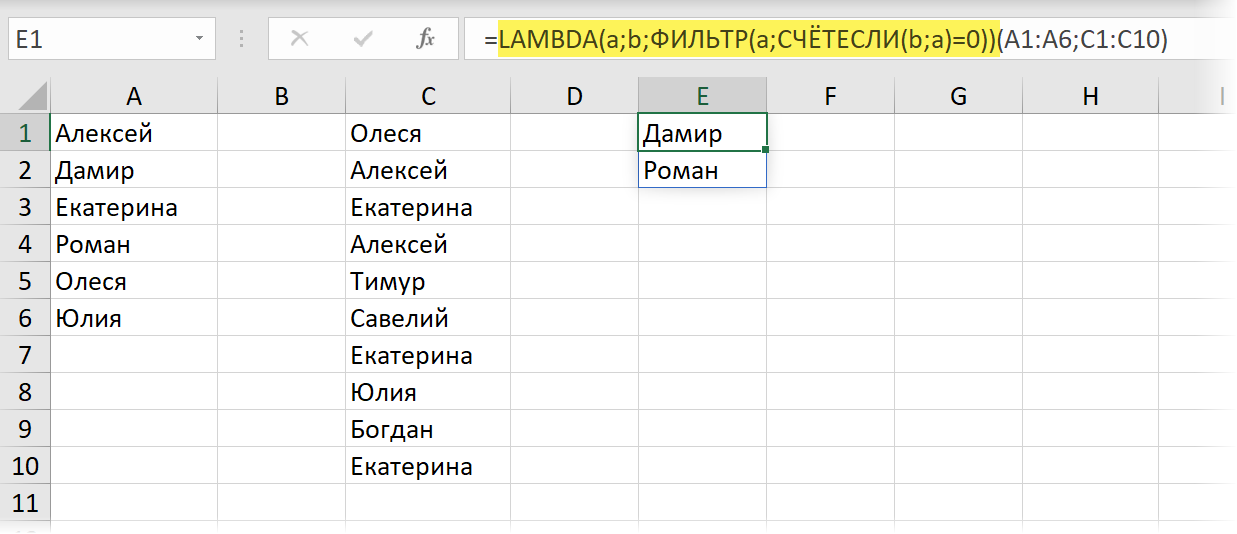
В английской версии это будет:
=LAMBDA(a;b;ФИЛЬТР(a;СЧЁТЕСЛИ(b;a)=0))(A1:A6;C1:C10)
Здесь функция СЧЁТЕСЛИ подсчитывает количество вхождений каждого элемента первого списка во второй, а затем функция ФИЛЬТР отбирает только те из них, у кого этих вхождений не оказалось. Завернув эту конструкцию в LAMBDA и создав на её основе именованный диапазон с названием, например, ПОИСКОТЛИЧ — мы получим удобную функцию, выдающую результат сравнения двух списков в виде динамического массива:
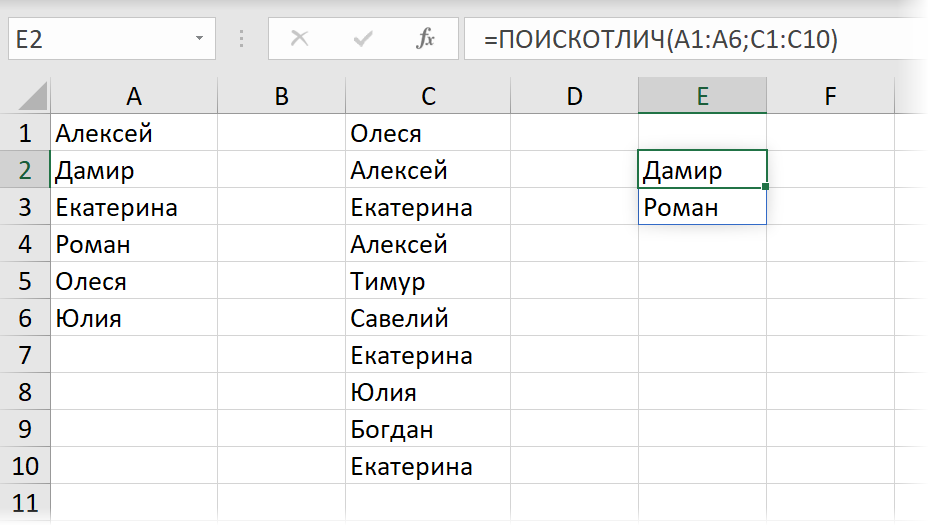
Если в качестве исходных данных будут не обычные, а «умные» таблицы — наша функция тоже справится без проблем:
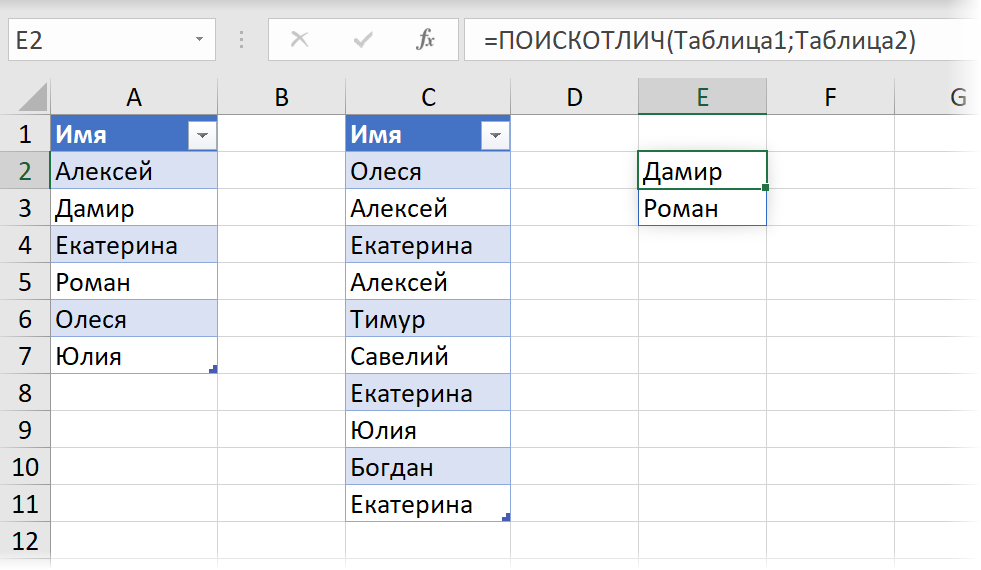
Другой пример — динамическое разделение текста путём превращения его в XML и последующего разбора по ячейкам с помощью функции ФИЛЬТР.XML, которое мы недавно разбирали. Чтобы не воспроизводить эту сложную формулу каждый раз вручную, проще будет завернуть её в LAMBDA и создать на её основе динамический диапазон, т.е. новую компактную и удобную функцию, назвав её, например, РАЗДТЕКСТ:

Первым аргументом этой функции будет ячейка с исходным текстом, а вторым — символ-разделитель, в возвращать результат она будет в виде горизонтального динамического массива. Код функции при этом будет следующим:
=LAMBDA(t;d; ТРАНСП(ФИЛЬТР.XML(«<x><y>»&ПОДСТАВИТЬ(t;d;»</y><y>»)&»</y></x>»;»//y»)))
Список примеров можно продолжать бесконечно — в любой ситуации, где вам часто приходится вводить одну и ту же длинную и громоздкую формулу функция LAMBDA сделает жизнь ощутимо проще.
Рекурсивный перебор символов
Все предыдущие примеры демонстрировали только одну, наиболее очевидную, сторону функции LAMBDA — её применение в качестве «обёртки» для заворачивания в неё длинных формул и упрощения их ввода. На самом деле, у LAMBDA есть ещё одна, гораздо более глубокая, сторона, превращающая её почти что в полноценный язык программирования.
Дело в том, что принципиально важной особенностью LAMBDA-функций является возможность реализации в них рекурсии — логики вычислений, когда в процессе расчета функция вызывает сама себя. С непривычки, возможно, звучит жутковато, но в программировании рекурсия — обычное дело. Даже в макросах на Visual Basic можно её реализовать, а теперь, вот, как видите, дошло и до Excel. Давайте попробуем разобраться в этой технике на практическом примере.
Предположим, нам требуется создать пользовательскую функцию, которая удаляла бы из исходного текста все заданные символы. Полезность такой функции, думаю, доказывать вам не нужно — с её помощью было бы очень удобно очищать замусоренные входные данные, правда?
Однако, по сравнению с предыдущими, нерекурсивными примерами, нас ожидают две сложности.
- Нам придётся придумать название для нашей функции до того, как мы начнём писать её код, т.к. в нём это название уже будет использоваться для вызова функцией самой себя.
- Ввести такую рекурсивную функцию в ячейку и отлаживать её, указав после LAMBDA аргументы в скобках (как мы делали ранее) не получится. Придётся создавать функцию сразу «с нуля» в Диспетчере Имен (Name Manager).
Назовём нашу функцию, допустим, ОЧИСТКА и хотелось бы, чтобы у неё было два аргумента — текст, который нужно почистить и список исключаемых символов в виде текстовой строки:

Создадим, как делали ранее, на вкладке Формулы в Диспетчере имён именованный диапазон, назовём его ОЧИСТКА и введём в поле Диапазон следующую конструкцию:
=LAMBDA(t;d;ЕСЛИ(d=»»;t;ОЧИСТКА(ПОДСТАВИТЬ(t;ЛЕВСИМВ(d);»»);ПСТР(d;2;255))))
Здесь переменная t — это исходный очищаемый текст, а d — список символов на удаление.
Работает всё это следующим образом:
Итерация 1
Фрагмент ПОДСТАВИТЬ(t;ЛЕВСИМВ(d);»»), как легко догадаться, заменяет в исходном тексте t первый слева символ из удаляемого набора d на пустую текстовую строку, т.е. удаляет букву «А». В качестве промежуточного результата получаем:
Вш зкз н 125 руб.
Итерация 2
Затем функция вызывает сама себя и в качестве входных данных (первый аргумент) получает уже то, что осталось после очистки на предыдущем шаге, а вторым аргументом задавая строку исключаемых символов начиная не с первого, а со второго символа, т.е. «БВГДЕЁЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,» без начальной «А» — это делает функция ПСТР. Как и до этого, функция берет первый слева символ из оставшихся (Б) и заменяет его в данном ей тексте (Зкз н 125 руб.) на пустую строку — получаем в качестве промежуточного результата:
Вш зкз н 125 ру.
Итерация 3
Функция опять вызывает сама себя, получая в качестве первого аргумента то, что осталось от зачищаемого текста на предыдущей итерации (Вш зкз н 125 ру.), а в качестве второго — урезанный слева ещё на один символ набор исключаемых знаков, т.е. «ВГДЕЁЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,» без начальной «Б». Затем опять берёт из этого набора первый символ слева (В) и удаляет его из текста — получаем:
ш зкз н 125 ру.
И так далее — надеюсь, вы ухватили идею. С каждой итерацией список удаляемых символов будет обрезаться слева и мы будем искать и заменять на пустоту очередной символ из набора.
Когда все символы закончатся нам необходимо будет выйти из цикла — эту роль как раз и выполняет функция ЕСЛИ (IF), в которую завернута наша конструкция. Если символов для удаления не осталось (d=»»), то функция не должна больше вызывать саму себя, а просто должна вернуть зачищаемый текст (переменная t) в его финальном виде.
Рекурсивный перебор ячеек
Похожим образом можно реализовать и рекурсивный перебор ячеек в заданном диапазоне. Предположим, что мы хотим создать лямбда-функцию с именем ЗАМЕНАПОСПИСКУ для оптовой замены фрагментов в исходном тексте по заданному списку-справочнику. Выглядеть всё это в результате должно так:
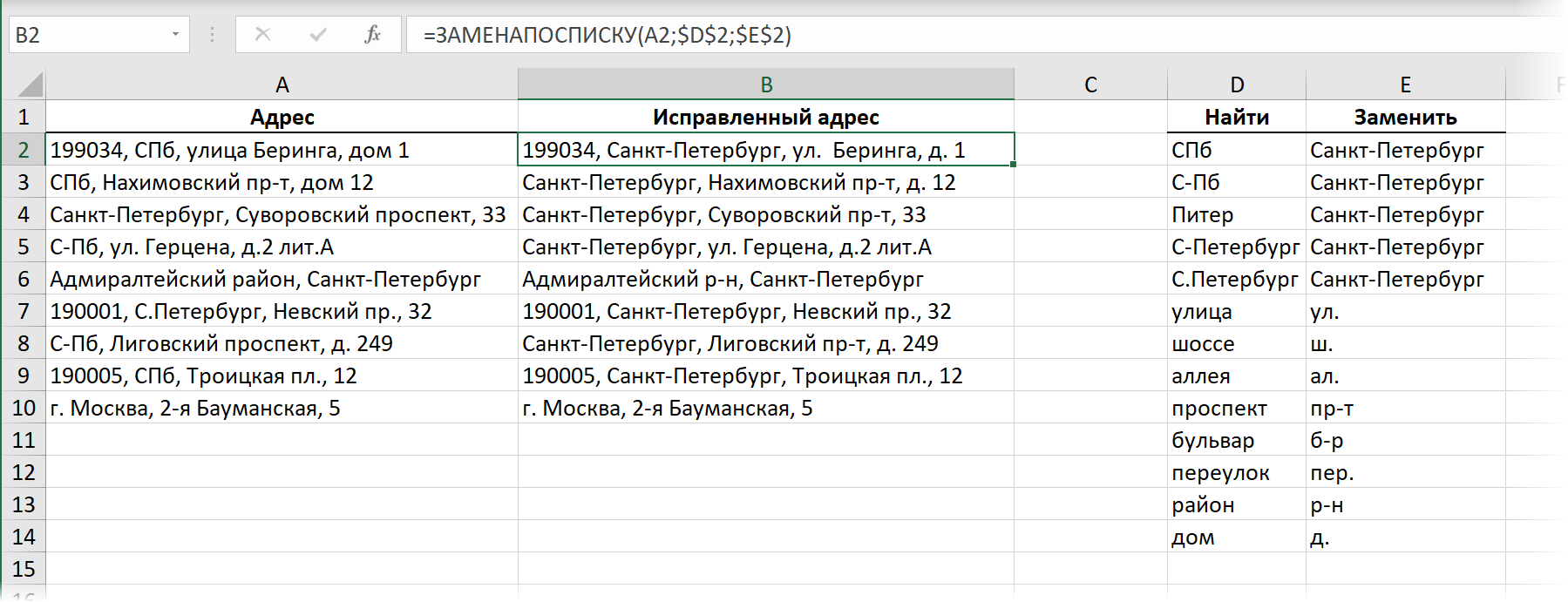
Т.е. у нашей функции ЗАМЕНАПОСПИСКУ будет три аргумента:
- ячейка с текстом для обработки (исходный адрес)
- первая ячейка столбца со значениями для поиска из справочника
- первая ячейка столбца со значениями на замену из справочника
Функция должна проходить сверху-вниз по справочнику и заменять последовательно все варианты из левого столбца Найти на соответствующие варианты из правого столбца Заменить. Реализовать такое можно следующей рекурсивной лямбда-функцией:

Здесь в переменной t хранится исходный текст из очередной ячейки столбца Адрес, а переменные n и z указывают на первые ячейки в столбцах Найти и Заменить, соответственно.
Как и в предыдущем примере, сначала эта функция заменяет в исходном тексте с помощью функции ПОДСТАВИТЬ (SUBSTITUTE) данные по первой строке справочника (т.е. СПб на Санкт-Петербург), а затем вызывает сама-себя, но со сдвигом по справочнику вниз на следующую строку (т.е. заменяет С-Пб на Санкт-Петербург). Затем вызывает себя ещё раз со сдвигом вниз — и заменяет уже Питер на Санкт-Петербург и т.д.
Сдвиг вниз на каждой итериации реализован стандартной экселевской функцией СМЕЩ (OFFSET), у которой в данном случае три аргумента — исходный диапазон, сдвиг по строкам (1) и сдвиг по столбцам (0).
Ну, и как только мы достигаем конца справочника (n=»»), то должны закончить рекурсию — прекращаем вызывать сами себя и выводим то, что накопилось после всех выполненных замен в переменной исходного текста t.
Вот и всё. Никаких хитрых макросов или запросов Power Query — вся задача решается одной функцией.
Ссылки по теме
- Как использовать новые функции динамических массивов Excel: ФИЛЬТР, СОРТ, УНИК
- Замена и зачистка текста функцией ПОДСТАВИТЬ
- Создание макросов и пользовательских функций (UDF) на VBA
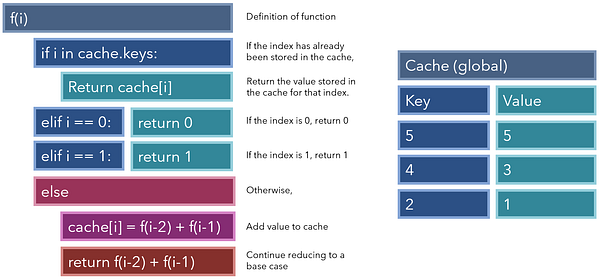
Recursive function is a term for describing behavior of a function that calls itself from within its own code. This is necessary for solving a problem where the solution relies on the results from multiple instances of the same problem. In this guide, we’re going to show you how to create recursive functions in Excel.
Download Workbook
LAMBDA Function
Before the LAMBDA function, the only option for creating recursive calculations in Excel was using VBA. VBA allows you to create your own user defined functions. However, VBA requires some coding knowledge.
With the new LAMBDA function, you can create your own functions using only Excel formulas. Briefly, the LAMBDA function is a special function that you can use in a named range, and it allows you to use that named range as a function. It also supports recursive calculations.
To create a user defined function with LAMBDA, follow the steps below:
- Open the New Name dialog by following Formulas > Define Name path in the Ribbon.
- Type in a friendly name for your formula. To call the formula recursively, you should use this name inside your formula. For example, “MyFormula”.
- Enter the LAMBDA formula e.g., =LAMDBA(x,y,x+y)
- Click the OK button to create your user defined function.
- Once the named range is saved, you can use it just like any other formula.
Let us briefly explain how the LAMBDA function works. The LAMBDA function’s last argument should always be the formula itself. The arguments before the formula are the arguments which will be used in the formula.
For example, the x+y function needs 2 arguments: x and y. Thus, the first arguments in the LAMBDA function are x and y. The last argument is the formula that uses these arguments.
As of writing this article, the LAMBDA function is only available to Office 365 users.
Creating recursive functions with LAMBDA
Fibonacci sequence
Let’s see the LAMBDA function on an example. Our first example is about the Fibonacci sequence, which is a sequence of numbers where each number is the sum of the two preceding values, starting from 0 and 1.
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
The function below returns the nth number in a Fibonacci sequence.
The function of n depends on same function’s instances for n-1 and n-2. Thus, the function needs to be recalculated until n is equal to 2, and F(0) and F(1) return 0 and 1 respectively.
With the help of the LAMBDA function we can create this function like this:
=LAMBDA(n,IF(n<=1,n,Fib(n-1)+Fib(n-2)))
Note that we have named our function “Fib”. As a result, the function can be recalled as Fib(n-1) and Fib(n-2) in the same function. Remember to change this if your formula has a different name.
Ackermann Function and recursion
The Ackermann function, named after Wilhelm Ackermann, is a multi-variable function from natural numbers to natural numbers with a very fast rate of growth. It is accepted one of the simplest examples of a function that is computable but not primitive recursive.
Here is the equation:
If m and n values are not equal to 0 (third line), the function calls itself to calculate its second argument. The called function will call another, until the conditions in the first two rows are met.
The following is the Excel version of the Ackermann Function. We named it “Ack”.
=LAMBDA(m,n,IF(m=0,n+1,IF(n=0,Ack(m-1,1),Ack(m-1,Ack(m,n-1)))))
Remove unwanted characters with a recursive function
The LAMBDA function can also be used to remove a set characters from strings. You can use functions like SUBSTITUTE and REPLACE to do this, but both functions can work with an entire string value, and not specific characters.
=LAMBDA(string,characters,IF(characters=»»,string,RemoveCharacters(SUBSTITUTE(string,LEFT(characters,1),»»),RIGHT(characters,LEN(characters)-1))))
The RemoveCharacters function replaces each character with a an empty string (“”) starting from the left. It sends the lastly calculated character set without the first character each time it runs, until there are no characters left in the set.
Использование табличного процессора MS Excel при решении задач на рекурсию Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Наталья Шамшина
Табличный процессор Excel целесообразно использовать для решения задач на рекурсию , чтобы освоить рекурсивный подход к решению математических и практических задач.
Похожие темы научных работ по математике , автор научной работы — Наталья Шамшина
Using MS Excel spreadsheet to solve problems on recursion
Excel spreadsheet useful for solving problems on recursion to learn a recursive approach to solving mathematical and practical problems.
Текст научной работы на тему «Использование табличного процессора MS Excel при решении задач на рекурсию»
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
PHYSICAL AND MATHEMATICAL EDUCATION
Has been issued since 2013.
Видається з 2013.
Шамшина Н. Использование табличного процессора MS Excel при решении задач на рекурсию // Фізико-математична освіта. Науковий журнал. — Суми: СумДПУ ім.А.С.Макаренка, 2013. — № 1 (1). — С. 57-64.
Сумский государственный педагогический университет имени А.С. Макаренко,
ИСПОЛЬЗОВАНИЕ ТАБЛИЧНОГО ПРОЦЕССОРА MS EXCEL ПРИ РЕШЕНИИ ЗАДАЧ НА РЕКУРСИЮ
Рекурсия — это тонкий и изящный инструмент, который при умелом использовании способен сослужить добрую службу программисту. Одно из важных достоинств рекурсивных алгоритмов заключается в том, что они просты и наглядны. Изящество рекурсии в программировании можно сравнить только с изяществом метода индукции в математике. «Когда изучаются циклы — основа вычислительных процессов, без рекурсивных определений не обойтись. Циклы и рекурсия — близнецы-братья» [2]. С их помощью строятся лаконичные и легко понимаемые алгоритмы, а затем и соответствующие информационные модели в виде рекурсивных программ на том или ином языке программирования [4].
Обычно начинающий программист, впервые услышавший про рекурсию, впадает в легкое замешательство. Первоначальное знакомство с ней может вызвать непонимание и легкий шок. В общеобразовательной школе изучению рекурсии уделяют мало внимания. Тема трудна и для учеников, и для учителей. Умение описывать вычислительный процесс как циклический или рекурсивный дело далеко не простое.
Между тем, немало практических задач и большинство нетривиальных (олимпиадных) задач имеют рекурсивную природу. Следовательно, необходимо не только знакомить студентов различных специальностей и старших школьников с рекурсивными алгоритмами, но и уделять внимание поиску новых методик и технологий обучения, ориентированных на прочное усвоение соответствующих знаний.
Анализ современных методологических исследований 4 показывает, что преподаватели информатики педагогических вузов и популяризаторы информационных технологий в Интернете заинтересованно относятся к данному вопросу, хотя исследований теоретического и практического характера по теме очень мало.
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
Дидактические преимущества рекурсивного подхода, по сравнению с простым описанием функций и решением с его помощью соответствующих прикладных задач, положительно оценили коллеги Тульского государственного педагогического университета имени Л.Н. Толстого. Экспериментальная группа студентов показала лучшие результаты, по сравнению с контрольной группой, при решении задач через год после освоения курса «Финансовые функции». Сделан вывод о том, что рекурсивный подход «дает возможность не только всесторонне понять содержание излагаемого материала, но сделать это быстро и эффективно. И что особенно важно, полученные знания становятся достоянием долговременной памяти» [3]. Исследования проводились с использованием экономических задач, решения которых оформлялись в виде рекурсивных программ-функций на языке программирования вычислительной среды Mathcad.
Специализированные математические програмы, языки високого уровня, а вместе с ними и основи программирования студенты изучают на старших курсах сталкиваясь при этом с некоторыми трудностями, поскольку им приходится осваивать незнакомый язык программирования и одновременно логику программы. Можно ли студентов первых курсов и старших школьников учить понятиям «рекурсия» и «циклы» как можно раньше, просто и наглядно, например, используя табличный процессор Excel? Ответ — ДА! Excel является прекрасной средой для начального обучения программированию в школе и ВУЗе.
Видимо это утверждение не слишком охотно воспринимается опытными программистами, так как автор лекций «Основы офисного программирования и документы Excel» В.А. Биллиг на страницах Интернет-Университета Информационных Технологий пишет следующее: «Я высказываю и пытаюсь обосновать здесь
«крамольную» мысль о том, что Excel является прекрасной средой начального обучения программированию в школе и в вузах» [2].
Цель данной статьи — показать дидактические возможности Excel и целесообразность его использования при решении математических и практических задач по теме «Рекурсивные вычисления».
Итак, покажем, что применяя Excel можно освоить рекурсивный подход к решению математических и практических задач. Рассмотрим конкретные задачи на рекурсию и их реализацию в программе Excel.
Рекурсией в программировании называется ситуация, в которой какая-либо подпрограмма прямо или через другие подпрограммы вызывает себя в качестве подпрограммы. Реализуемый при этом алгоритм называется рекурсивным [4].
В математике очень часто встречаются последовательности чисел, в которых каждый следующий член выражается через предыдущие. Формулы, выражающие очередной член последовательности через один или несколько предыдущих членов, называют рекуррентными соотношениями.
В арифметической прогрессии, например, каждый следующий член равен предыдущему, увеличенному на разность прогрессии: a(i) = a(i-1) + d.
При вычислении факториала n!, который определяют как произведение первых n чисел натурального ряда n!=1*2*3*. *n, также можно использовать рекуррентное соотношение, в котором n! выражается через предыдущий (n-1)!, т.е. используется рекуррентная формула:
0!=1, для любого n>0 n!=n*(n-1)!
Аналогично при вычислении суммы ряда чисел S=1+2+3+. +n можно использовать рекуррентное соотношение:
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
S(1)=1, для любого n>0 S(n)=n+S(n-1)
Важное место в математике занимает последовательность чисел известная как ряд Фибоначчи, так как проявляется в самых неожиданных ее приложениях. Строгое определение этого ряда следующее: каждое число ряда, начиная со второго, равно сумме двух предыдущих. Вот эта задача в том виде, как формулирует ее сам Фибоначчи: «Пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца — три пары, а через четыре месяца — пять, так как к паре, рожденной первой парой, добавятся первые дети от второй пары. ». Продолжая процесс, получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56. эти числа и представляют ряд, названный по имени автора задачи [2].
Рекуррентные соотношения, определяющие вычисление чисел Фибоначчи: F(1) = 1; F(2) = 2; при k = 3. N F(k) = F(k-2) + F(k-1)
Наличие рекуррентного соотношения позволяет использовать рекурсию. Эти и другие задачи используются при обучении программированию в темах: циклы, рекурсия. Иногда их решение вызывает у студентов некоторые трудности, поскольку им приходится осваивать незнакомый язык программирования и одновременно логику программы. В табличном процессоре Excel эти задачи решаются наглядно просто и без программирования, путем создания и копирования формул на рабочем листе.
Это возможно благодаря тому, что одним из преимуществ Excel, его важной особенностью, является применяемый способ задания ссылок на ячейки в формулах. Excel позволяет задавать разные типы ссылок на ячейки: абсолютные, относительные и полуабсолютные. Относительные ссылки — это ссылки относительно положения самого объекта-формулы. Если изменяется положение формулы, то соответственно меняется и ячейка, на которую она ссылается. Ссылки на ячейки можно задавать в двух форматах: A1 и R1C1. По умолчанию ссылки в первом формате являются относительными. Так, например, ссылка F20 является относительной и при копировании формулы (смене положения формулы) будет определять другую ячейку, в зависимости от изменения первоначального положения формулы. Чтобы сделать ссылку абсолютной, нужно добавить символы $ перед именем столбца и индексом строки: $F$20, в этом случае при смене положения формулы на листе ссылка будет указывать на ту же самую ячейку. Пример полуабсолютной ссылки: F$20, $F20.
В формулах часто используются относительные ссылки в формате R1C1, в котором явно можно указывать смещение относительно объекта-формулы, например следующим образом: =RC[-2]*RC[-1], что означает перемножить ячейки, одна из которых находится в той же строке, но на два столбца левее от формулы, а другая в той же строке, но на один столбец левее от формулы. Правило записи таких ссылок легко понять из нижеследующей таблицы:
R Абсолютная ссылка на текущую строку
С Абсолютная ссылка на текущий столбец
R2C2 Абсолютная ссылка на ячейку, расположенную во второй строке и во втором столбце
R[-1] Относительная ссылка на строку, расположенную выше текущей ячейки
С[-1] Относительная ссылка на столбец, расположенный левее текущего столбца
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО) № 1(1), 2013
R[-2]C Относительная ссылка на ячейку, расположенную на две строки выше и в том же столбце
RC [-2] Относительная ссылка на ячейку, расположенную на два столбца левее и в той же строке
R[2]C[2] Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее
Стиль ссылок R1C1 полезен при вычислении положения столбцов и строк в макросах.
Рассмотрим программную реализацию задачи Фибоначчи в Excel с использованием модуля VBA. При указании ссылок в формуле (Formula) задано смещение по строкам, а столбец не указан, что по умолчанию предполагает использование столбца A объекта (Range). Относительные ссылки позволяют реализовать рекурсивные вычисления.
Range(«A1») = 1: Range(«A2») = 2 Range(«A3:A20»).Formula = «=R[-2]+R[-1]»
Однако та же задача совершенно естественно решается в Excel без всякого программирования. Достаточно записать значение 1 в ячейку A1, значение 2 — в ячейку A2, формулу «=A1+A2» — в ячейку A3, после чего скопировать формулу в нужный диапазон ячеек от A4 до A20. При копировании формулы будет учтена относительность ссылок, так что в ячейке A20 соответствующая формула будет иметь вид — «=A18+A19».
Аналогично можно решить задачи для факториала, суммы ряда чисел, вычислить члены арифметической или геометрической прогрессии. Пример рабочего листа Excel з формулами и результатами расчетов приведен на рис.1 и рис.2.
А В с D E F G Н I J
1 1 1 =С1 =ФАКТР(С1) 1 =G1 =СУММ(ЇЄЇ1 :G1)
2 2 2 =D1*C2 =ФАКТР(С2) 2 =G2+H1 -Cyiv1M($G$1 :G2)
3 =А1 +А2 3 =D2*C3 =ФАКТР(СЗ) 3 =G3+H2 -CyMM($G$1 :G3) =
4 =А2+А3 Ч 4 =D3*C4 =ФАКТР(С4) 4 =G4+H3 -CyMM($G$1 :G4)
5 =АЗ+А4 И 5 =D4*C5 =ФАКТР(С5) 5 =G5+H4 -CyMM($G$1 :G5) c —
6 =А4+А5 с 6 =D5*C6 =ФАКТР(С6) Ф 6 =G6+H5 -CyMM($G$1 :G6)
7 =А5+А6 л 7 =D6*C7 =ФАКТР(С7) А 7 =G7+H6 -CyMM($G$1 :G7) J
8 =А6+А7 а 8 =D7*C8 =ФАКТР(С8) К 8 =G8+H7 =CVMM($G$1:G3)
9 =А7+А8 9 =D8*C9 =ФАКТР(С9) Т 9 =G9+H8 =CVMM($G$1:G9)
10 =А8+А9 ф 10 =D9*C10 =ФАКТР(С10) 0 10 =G10+H9 =CVMM($G$1:G10)
11 =А9+А10 и 11 =D10*C11 =ФАКТР(С11) р 11 =G11+H10 -Cyiv1M($G$1 :G11)
12 =А10+А11 б 12 =D11*012 =ФАКТР(С12) и 12 =G12+H11 -СУММ(ЇСЇ1 :G12)
13 = А11+А12 0 13 =D12*C13 =ФАКТР(С13) А 13 =G13+H12 -Cyiv1M($G$1 :G13)
14 =А12+А13 н 14 =D13*C14 =ФАКТР(С14) Л 14 =G14+H13 -CyMM($G$1 :G14)
15 =А13+А14 а 15 =D14*C15 =ФАКТР(С15) 15 =G15+H14 -CyMM($G$1 :G15)
16 =А14+А15 ч 16 =D15*C16 =ФАКТР(С16) 16 =G16+H15 -CyMM($G$1 :G16)
17 =А15+А16 и 17 =D16*C17 =ФАКТР(С17) 17 =G17+H16 -CyMM($G$1 :G17)
18 =А16+А17 18 =D17*C18 =ФАКТР(С18) 18 =G18+H17 -CyMM($G$1 :G18)
19 = А17 +А18 19 =D18*C19 =ФАКТР(С19) 19 =G19+H18 -CVMM($G$1 :G19)
20 =А18+А19 20 =D19*020 =ФАКТР(С20) 20 =G20+H19 =CVMM($G$1:G20) r ■
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
А В С D Е F G Н I J А
1 1 1 1 1 1 1 1
2 2 2 2 2 2 Зг 3
3 3 3 6 6 3 6Г 6 =
4 5 Ч 4 24 24 4 10г 10
5 8 н 5 120 120 5 15 г 15 г —
6 13 с 6 720 720 Ф 6 21 г 21
7 21 л 7 5040 5040 А 7 28 г 28 У м м
8 34 а 8 40320 40320 К 8 36 г 36
9 55 9 362880 362880 Т 9 45 г 45
10 89 Ф 10 3628800 3628800 0 10 55 г 55
11 144 н 11 39916800 39916800 Р 11 66 г 66
12 233 б 12 479001600 479001600 И 12 78 г 78 Р
13 I 377 0 13 6227020800 6227020800 А 13 91 г 91 д
14 610 н 14 87178291200 87178291200 Л 14 105 г 105
15 987 а 15 1.30767 Е+12 1.30767Е+12 15 120 г 120
16 1597 ч 16 2.09228 Е+13 2.09228 Е+13 16 136 г 136
17 2584 н 17 3.55687 Е+14 3.55687 Е+14 17 153 г 153
18 4181 18 6.40237 Е+15 6.40237 Е+15 18 171 г 171
19 6765 19 1.21Є45Е+17 1.21Є45Е+17 19 190 г 190
20 10946 20 2.4329Е+18 2.4329Е+18 20 210 210 IV
Рис. 2. Результаты расчетов
5 =А4+1 =В4*$В$1/А5 =С4+В5
6 =А5+1 =В5*$В$1/А6 =С5+В6
7 =А6+1 =В6*$В$1/А7 =С6+В7
8 =А7+1 =В7*$В$1/А8 =С7+В8
9 =А8+1 =В8*$В$1/А9 =С8+В9
10 =А9+1 =В9*$В$1/А10 =С9+В10 =
11 =А10+1 =B10*SBS1/A11 =С10+В11
12 =А11 +1 =В1ГЇВЇ1/А12 =011 +В12
13 =А12+1 =В12*$В$1/А13 =С12+В13
14 =А13+1 =В13*$В$1/А14 =С13+В14
15 =А14+1 =B14*SBS1/A15 =С14+В15
16 =А15+1 =B15*SBS1/A16 =С15+В16
17 =А16+1 =В16*$В$1/А17 =С16+В17
18 =А17+1 =B17*SBS1/A18 =017 +В18
19 =А18+1 =B18*SBS1/A19 =018+В19
Рис. 3. Вычисление ex
Значение х заносим в ячейку В1, в дальнейшем используем абсолютную ссылку на эту ячейку $B$1 при подсчете A(k). Для значений k, A(k) и Sum(Ak) заносим в строку 4 базу рекурсии, в строку 5 — формулы рекуррентного соотношения, копируем эти формулы с помощью автозаполнения вниз. Для проверки в ячейку В2 занесем формулу расчета с использованием встроенной функции EXP(x).
Изменяя в ячейке В1 значение х можно увидеть как стремится к нулю текущий член суммы ряда, насколько точность вычислений зависит от количества членов ряда, как взаимосвязаны значения х и скорость сходимости ряда. Например, если учитывать 4 десятичных разряда, при х=2,5 ряд сходится с 12 члена (k=12), при х=3 с k=13, при х=5
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
с k=21 и т.д. Одним словом, можно исследовать поведение ряда и воочию увидеть закономерности изменения. Такой подход помогает легче понять и запомнить математические понятия и зависимости.
В каких же ситуациях требуется прибегать к циклическим вычислениям? Это следует делать, если речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. Иногда приходится вводить формулы, в которых одна ячейка явно или неявно ссылается на саму себя, возникают циклические ссылки. Если не предпринять специальных мер, то циклические ссылки породят бесконечные вычисления. Excel следит за тем, возникают ли циклические ссылки, и в нормальном режиме не допускает таких вычислений, требуя скорректировать формулы так, чтобы циклов не было.
Однако можно включить специальный режим вычислений, допускающий циклические ссылки. В последнем случае требуется, чтобы число повторений цикла было конечным, только тогда Excel допускает переход к новому режиму, обеспечивающему проведение циклических вычислений. Для этого достаточно на вкладке Вычисления (меню Сервис, пункт Параметры) включить флажок Итерации и при необходимости изменить число повторений цикла в окошке «Предельное число итераций». Можно также задать погрешность вычислений в окошке «Относительная погрешность», что также приводит к ограничению числа повторений цикла. По умолчанию максимальное число итераций и погрешность вычислений соответственно имеют значения 100 и 0,001.
Необходимо также учитывать при решении таких задач особенности циклических вычислений, а именно:
1. Формулы, связанные циклическими ссылками, вычисляются многократно.
2. Размещение формул на листе определяет последовательность их вычисления. Формулы вычисляются сверху вниз, слева направо.
3. Число повторений цикла определяется параметрами, заданными на вкладке Вычисления.
4. Цикл заканчивается, когда изменения значений во всех ячейках не превосходят заданной погрешности или при достижении максимального числа итераций.
Рассмотрим пример практической задачи с использованием цикла для расчета сметы работ [1, с.316]:
Допустим необходимо рассчитать цену работ, если фонд заработной платы составляет 2 000 грн., запланированные средства на служебные командировки -200 грн., затраты на материалы — 150 грн. При этом отчисления (налог) в фонд социального страхования составляет 37% заработной платы. В расчет цены закладывается прибыль предприятия — 10% от цены работ, а также накладные затраты — 10% и другие прямые затраты 2,2% от цены работ. Решения задачи в Excel показано на рис.4.
В данном примере встречается неявная циклическая ссылка: значение ячейки С9 рассчитывается как сумма ячеек С2:С8, часть из которых в свою очередь зависят от С9. Формулы в ячейках С4, С7-С9 содержат рекурсию. В обычном режиме работы Excel по данным формулам невозможно провести вычисления, программа выдает сообщение об ошибке — циклической ссылке. После перехода к новому режиму, допускающему циклические ссылки, получаем представленный на рис.5 результат.
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
1 Статті витрат % Сума _
2 Заробітна плата 2000
3 Відрахування на соц. Страхування 0,37 =С2*ВЗ
4 Накладні витрати 0,15 =С9*В4
5 Матеріали 150
6 Витрати на службові відрядження 200
7 Інші прямі витрати 0,022 =С9*В7
8 Прибуток 0,1 =С9*В8
9 Л П Ціна =СУММ(С2:С8) і 1 —
Рис. 4. Расчет сметы работ. Формулы Рабочего Листа
1 Статті витрат % Сума І
2 Заробітна плата 2 000,00 грн.
3 Відрахування на соц. Страхування 37% 740,00 грн.
4 Накладні витрати 15% 636,68 грн.
5 Матеріали 150,00 грн.
6 Витрати на службові відрядження 200,00 грн.
7 Інші прямі витрати 2,20% 93,38 грн.
8 Прибуток 10% 424,45 грн.
9 Ціна 4 244,51 грн.
Рис. 5. Результаты расчета сметы работ
Эта и подобные ей задачи часто встречаются в реальной жизни предпринимателей, бизнесменов, бухгалтеров, экономистов, и на помощь им приходит такой простой, доступный инструмент для подобных вычислений каким является Excel. Как видим, не только математические задачи приходится решать с помощью рекурсии и циклов, не только математикам и программистам необходимо понимание рекурсивных алгоритмов.
Из всего выше изложенного можно сделать выводы.
Преимущества табличного процессора Excel для обучения понятию «рекурсия» состоят в следующем:
o Excel идеально приспособлен к тому, чтобы простые рекурсивные вычисления, заданные рекуррентными соотношениями, определялись почти автоматически. В Excel при копировании формул ссылки на переменные меняются автоматически, благодаря этому реализуются рекуррентные соотношения. Достаточно скопировать формулу, чтобы реализовать рекурсивное вычисление.
о Достаточно сложные на начальном этапе обучения задачи решаются без программирования, путем задания и копирования формул на рабочем листе. Это важно для поэтапного обучения.
o Простые рекурсивные вычисления приобретают необходимую наглядность так, что ничего не остается скрытым. Можно видеть, как меняется формула, тут же в ячейке видеть значение, рассчитанное по этой формуле.
о При решении многих задач появляется совершенно новое качество, крайне важное для обучения — показан процесс решения, а не только конечный результат. Решение позволяет наглядно видеть, как сходится процесс вычислений, изучать влияние аргумента на скорость сходимости. Такое подход способствует тому, чтобы стать исследователем, вместо того, чтобы оставаться простым наблюдателем.
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
Рекурсивные алгоритмы и их вычисления в Excel могут служить весьма подходящим фоновым материалом для начального освоения рекурсии как достаточно общего и эффективного метода решения задач. Примеры решения задач, рассмотренные в данной статье, заставляют по-новому оценить дидактические возможности табличного процессора Excel и осознать его роль и место в построении современного курса информатики в педагогических вузах.
Задачи, которые приведены в данной статье, используются в лабораторной работе по курсу «Решение математических задач средствами Excel».
Список использованных источников
1. Баженов В.А., Венгерський П.С. Інформатика. Комп’ютерна техніка. Комп’ютерні технології. — К.: Каравелла, 2008. — 640 с.
2. Биллиг В.А Основы офисного программирования и документы Excel http://www.intuit.rU/department/office/vbaexcel/1/.
3. Добровольский Н.М., Есаян А.Р., Пихтильков С. A., Стеценко В.Я. Об одном вычислительном эксперименте. Межвузовский сборник статей. Ч.1-Тула: Изд-во Тул. гос. пед. ун-та, 1999.10 с.
4. Есаян А.Р. Фракталы и рекурсия. Учеб. пособие для студентов педвузов. — Тула, 1999. -52с.
Аннотация. Шамшина Н. Использование табличного процессора MS Excel при решении задач на рекурсию.
Табличный процессор Excel целесообразно использовать для решения задач на рекурсию, чтобы освоить рекурсивный подход к решению математических и практических задач.
Ключевые слова: табличный процессор MS Excel, рекурсия, решение задач.
Анотація. Шамшина Н. Використання табличного процесора MS Excel при розв’язуванні задач на рекурсію.
Табличний процесор Excel доцільно використовувати для розв’язування задач на рекурсію, щоб засвоїти рекурсивний підхід до розв’язування математичних і практичних задач.
Ключові слова: табличний процесор MS Excel, рекурсія, розв’язування задач.
Abstract. Shamshyna N. Using MS Excel spreadsheet to solve problems on recursion.
Excel spreadsheet useful for solving problems on recursion to learn a recursive approach to solving mathematical and practical problems.
Keywords: spreadsheet MS Excel, recursion, solving problems.
Excel. Использование циклических ссылок для решения уравнений итерационным способом
Ранее я описал, как найти и исправить циклическую ссылку. Напомню, что циклическая ссылка появляется, если в ячейку Excel введена формула, содержащая ссылку на саму эту ячейку (напрямую или через цепочку других ссылок). Например (рис. 1), в ячейке С2 находится формула, ссылающаяся на саму ячейку С2.
Рис. 1. Пример циклической ссылки
Но. Не всегда циклическая ссылка является бедствием. Циклическую ссылку можно использовать для решения уравнений итерационным способом. Для начала нужно позволить Excel вести вычисления, даже при наличии циклической ссылки. В обычном режиме Excel, обнаружив циклическую ссылку, выдаст сообщение об ошибке, и потребует ее устранения. В обычном режиме Excel не может провести вычисления, так как циклическая ссылка порождает бесконечный цикл вычислений. Можно, либо устранить циклическую ссылку, либо допустить вычисления по формуле с циклической ссылкой, но ограничив число повторений цикла. Для реализации второй возможности щелкните на кнопке «Office» (в левом верхнем углу), а затем на «Параметры Excel» (рис. 2).
Скачать заметку в формате Word, примеры в формате Excel
Рис. 2. Параметры Excel
В открывшемся окне «Параметры Excel» перейдите на вкладку Формулы и отметьте «Включить итеративные вычисления» (рис. 3). Помните, что эта опция включается для приложения Excel в целом (а не для одного файла), и будет действовать, пока вы ее не отключите.
Рис. 3. Включить итеративные вычисления
На этой же вкладе, можно выбрать, как будут вестись вычисления: автоматически или вручную. При автоматическом вычислении Excel сразу рассчитает конечный результат, при вычислениях, вручную, можно будет наблюдать результат каждой итерации (простым нажатием F9 запуская каждый новый цикл вычисления).
Решим уравнение третьей степени: х 3 – 4х 2 – 4х + 5 = 0 (рис. 4). Для решения этого уравнения (и любого другого уравнения совершенно произвольного вида) понадобится всего одна ячейка Excel.
Рис. 4. График функции f(x)
Для решения уравнения нам понадобится рекуррентная формула (то есть, формула, выражающая каждый член последовательности через один или несколько предыдущих членов):
(1) x = x – f(x)/f’(x), где
f(x) – функция, задающая уравнение, корни которого мы ищем; f(x) = х 3 – 4х 2 – 4х + 5
f’(x) – производная нашей функции f(x); f’(x) = 3х 2 – 8х – 4; производные основных элементарных функций можно посмотреть здесь.
Если вы заинтересовались, откуда взялась формула (1), можете почитать, например, здесь.
Итоговая рекуррентная формула имеет вид:
(2) х = x – (х 3 – 4х 2 – 4х + 5)/(3х 2 – 8х – 4)
Выберем любую ячейку на листе Excel (рис. 5; в нашем примере это ячейка G19), присвоим ей имя х, и введем в нее формулу:
Можно вместо х использовать адрес ячейки… но согласитесь, что имя х, смотрится привлекательнее; следующую формулу я ввел в ячейку G20:
Рис. 5. Рекуррентная формула: (а) для поименованной ячейки; (б) для обычного адреса ячейки
Как только мы введем формулу и нажмем Enter, в ячейке сразу же появится ответ – значение 0,77. Это значение соответствует одному из корней уравнения, а именно второму (см. график функции f(x) на рис. 4). Поскольку начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке х и равного нулю. Как же получить остальные корни уравнения?
Для изменения стартового значения, с которого рекуррентная формула начинает свои итерации, предлагается использовать функцию ЕСЛИ: [1]
Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения:
| Начальное значение | Корень уравнения |
| 1 | 0,77 |
| -5 | -1,40 |
| 8 | 4,63 |
[1] Идея подсмотрена здесь
7 комментариев для “Excel. Использование циклических ссылок для решения уравнений итерационным способом”
Офигенный сайт!
И как всегда когда не нужно все находишь!
Блин у меня по экономическому моделированию в Excell курсовик был в институте, вот время помню кучу потерял а тут все в одном флаконе:)
Все равно инфа пригодится, даже очень!
И нам зараза в этом гребанном институте мать их так этих учителей даже близко ничего подобного не рассказывали. Я не про этот пример говорю а про остальные..
«Вычисление стандартного отклонения для данных с тенденцией», «Нормальное распределение» и т.п.. даже объяснить не могли или не хотели как это все применять, а тут все наглядно и понятно! Огромное спасибо! Не зря я на этот сайт наткнулся, чую он мне еще окажет неплохую помощь))))
В упор не понимаю откуда берется предел для определения корней уравнения, если «Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения»
У меня график получается, который с осью Х не имеет вообще пересечений, мож где накосячила?
Пожалуйста подскажите, а то у меня взрыв мозга будет скоро…((((
Тамара, если Вы строите график на основе моих данных, откройте файл Excel; если Вы используете собственные данные, пришлите мне на mail Ваш файл, попробую помочь))
Спасибо заранее за беспокойство, вот такое уравнение у^3-20у^2-158у-420=0, если не трудно объясните пожалуйста как вы определяте предел в каких знчениях надо считать корни.
Продвинутый взгляд на рекурсию
Рекурсия является одним из наиболее мощных подходов в программировании. С ее помощью можно решать чрезвычайно сложные задачи, печатая при этом невероятно малый объем кода. Тем не менее понимание данного принципа нередко вызывает сложности, поскольку для этого требуется нестандартный взгляд на процесс выполнения команд.
Сложность примеров, описанных в данной статье, будет возрастать постепенно, начиная от самых простых и заканчивая достаточно трудными. При этом каждый из них будет сопровождаться подробной диаграммой:
- Рекурсивный способ мышления.
- Рекуррентные соотношения.
- Мемоизация.
- Стратегия “разделяй и властвуй”.
Рекурсия используется для решения задач, в которых функция вызывает сама себя в рамках собственного определения. В каждой реализации рекурсии должно присутствовать два элемента:
- Заключительный базовый кейс или кейсы, в которых рекурсивный поиск ответа более не производится.
- Набор правил (рекуррентных соотношений), который инициирует очередные циклы рекурсии, сводя таким образом общие кейсы к базовому.
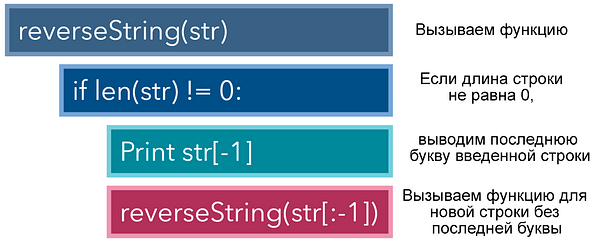
В качестве примера давайте рассмотрим задачу по выводу развернутого варианта строки. В этом случае на выходе из вводного слова ‘hello’ должно получиться ‘olleh’. Итеративный метод решения этой задачи — применение цикла for и вывод каждого знака, начиная с последнего и заканчивая первым.
В рекурсивном же подходе мы сначала создаем функцию reverseString , получающую интересующую нас строку в качестве параметра. Если длина ввода не равна 0, то такой кейс является базовым или заключительным, и мы выводим последнюю букву, а затем инициируем еще один экземпляр reverseString для той же строки, исключив последнюю букву, поскольку ее мы уже вывели.
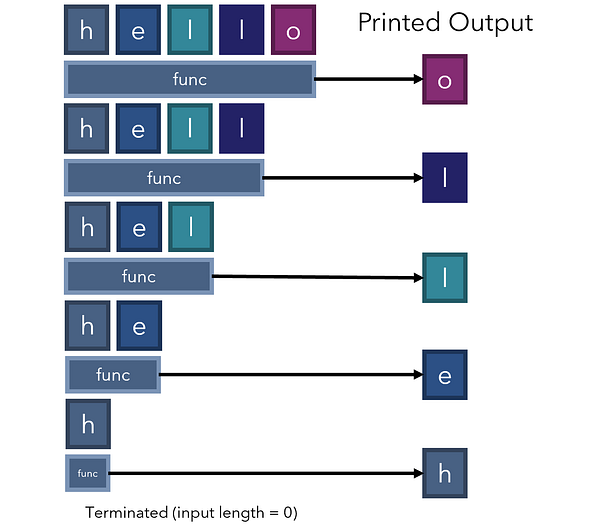
Обратите внимание: поскольку функция вызывается изнутри себя, она сама создает цикл for . Кроме того, наличие инструкции if перед вызовом другого экземпляра функции обязательно, в противном случае будет выброшена ошибка RecursionError или RuntimeError , поскольку скрипт не увидит конца бесконечного цикла. Данная ситуация аналогична бесконечному циклу While True .
Давайте посмотрим, как эта рекурсивная функция работает с ‘hello’:
Рекуррентность в более сложных задачах может вызвать трудности при определении двух ее компонентов — рекуррентного соотношения, т.е. соотношения между результатом задачи и результатом ее подзадач и базовым кейсом, представляющим кейс, который можно вычислить напрямую без дополнительных рекурсивных вызовов. Иногда базовые кейсы называются “нижними кейсами”, потому что они являются кейсами, в которых задача уменьшена до наименьшего масштаба.
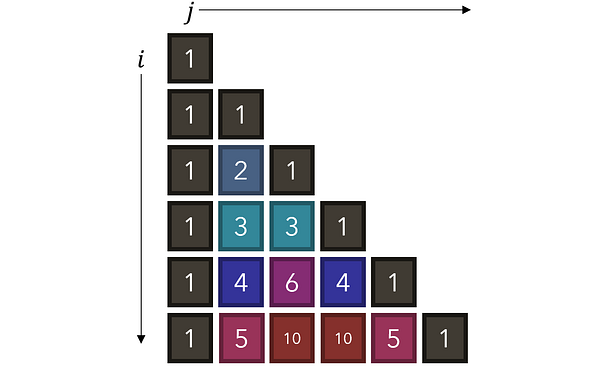
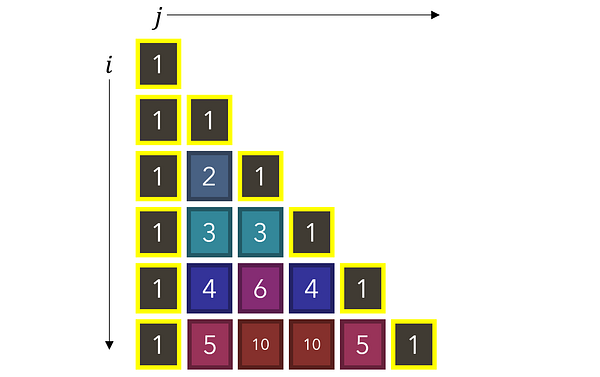
Рассмотрите в качестве примера треугольник Паскаля, в котором каждое число является суммой двух, находящихся над ним, и который имеет по сторонам единицы. Как можно использовать рекурсию для нахождения значения любого значения в точке (i, j)? Каково будет рекуррентное соотношение и базовый/заключительный кейс?
Рекуррентное соотношение можно выразить следующим уравнением:
Это очевидно, когда смотришь на график треугольника. Еще более примечательно в этой формуле то, что если мы продолжим с ее помощью разбивать любую точку (i, j) на сумму двух других точек, то в итоге неизбежно получим базовый кейс — 1. Треугольник Паскаля начинается с единиц, и из их сумм строится весь сложный паттерн.
Как же нам это реализовать?
Для начала давайте найдем набор правил, чтобы определять, когда выполняется базовый кейс, при котором значение ячейки равняется 1. Обратите внимание, что 1-цы появляются при выполнении одного из двух условий: когда располагаются либо в первом столбце (j=0), либо по диагонали (i=j).
Теперь выполнить реализацию просто. Если условия для базового кейса выполнены, мы возвращаем базовое значение (1). В противном случае мы продолжаем уменьшать задачу до тех пор, пока не достигнем базового кейса, до которого, как мы определили, будет неизбежно разбит любой ввод.
Теперь рекурсия раскрылась для вас во всей красе. Здесь, с помощью всего пяти строк кода, мы, по сути, создаем саморазвивающееся дерево. При желании число строк кода можно даже уменьшить до трех. Вызывая функцию pascal дважды, мы инициируем две ветви поиска, каждая из которых также инициирует еще две, предполагая, что базовый кейс достигнут не был.
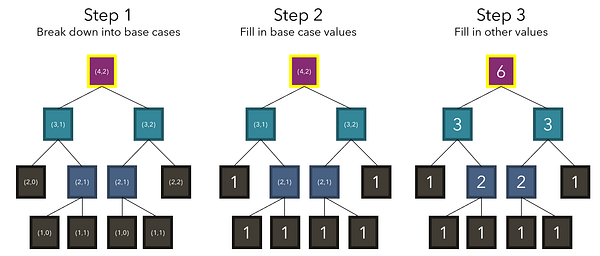
Такая эффективность рекурсии может показаться магической и даже может запутать. Давайте рассмотрим работу ее алгоритма на примере.
В соответствии с нашим рекуррентным соотношением (4, 2) разбивается на (3, 1) и (3, 2), которые являются двумя числами, стоящими над ней. Обратите внимание, что алгоритм на деле не знает, что значения этих ячеек представлены 3. Он просто учитывает их местоположение. Мы не знаем или даже не интересуемся никакими значениями, пока выполняются базовые условия. На основе базовых кейсов (1) мы можем вычислить другие не базовые точки, но для начала должны быть найдены все базовые.
Согласно нашему рекуррентному соотношению, кейсы итеративно разбиваются до тех пор, пока не достигается базовый (j = 0 или i = j). Поскольку нам известны значения этих базовых кейсов (1), мы можем заполнить и другие значения, зависимые от базового кейса.
Это, конечно же, очень, а возможно и чересчур подробное представление принципа работы рекурсивного алгоритма. В действительности ни один из этих трех шагов не нужно программировать, так как они выполняются скриптом автоматически. Все, что вам нужно, — это вызвать функцию внутри ее самой и обеспечить ее завершение в некоторых точках при достижении базового случая.
При вызове return pascal(i-1, j) + pascal(i-1, j-1) мы рассматриваем возврат не как процесс, а как число. Поскольку pascal(i-1, j) инициирует собственные процессы ветвления, а в итоге возвращает другое число (например, 3), будет правильным воспринимать его именно как число, а не как процесс, что может вызвать ненужную сложность и затруднение в понимании.
С некоторой точки зрения этот рекурсивный алгоритм можно назвать неэффективным. В конце концов ‘6′ разбивается на ‘3′, которое, с позиции значения, имеет идентичные разбивки, но при этом зачем-то вычисляется второй раз. Это стандартный случай в рекурсии, когда базовые кейсы одного кейса, будучи вычисленными ранее, вычисляются повторно. Для устранения этой проблемы мы используем мемоизацию.
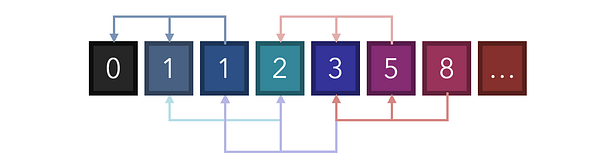
Возьмите в качестве примера последовательность Фибоначчи, в которой первые два числа представлены 0 и 1, а последующие числа являются суммой двух, им предшествующих. На основе уже сформированного знания мы понимаем, что базовыми кейсами здесь будут 0 и 1, а рекуррентное соотношение будет выглядеть как v(i) = v(i-2) + v(i-1). В таком случае мы можем построить простую рекурсивную функцию для нахождения значения последовательности Фибоначчи в любом индексе, начиная с 0.
Обратите внимание, что хоть это и грамотное применение рекурсии, оно весьма неэффективно. 8 разбивается на 3 и 5, а 5, в свою очередь, разбивается на 3 и 2. Мы вычисляем все с самого начала и строим завершенное дерево поиска со множеством повторений.
С помощью мемоизации мы можем решить эту проблему, создав кэш. Это можно реализовать, используя словарь и сохраняя значения, заданные ранее. Например, когда индекс 6 (значение 
Чтобы включить в нашу функцию мемоизацию, мы добавим две функциональности: во-первых, если текущий индекс был сохранен в кэше, мы будем просто возвращать его сохраненное значение; во-вторых, прежде чем продолжать уменьшать значение, мы будем добавлять это значение к кэшу,чтобы ускорить дальнейшие операции. Обратите внимание, что кэш должен быть либо глобальной переменной, либо такой, которую можно извлечь и изменить независимо от области вызова команды.
После добавления мемоизации наша рекурсивная функция стала намного быстрее и мощнее.
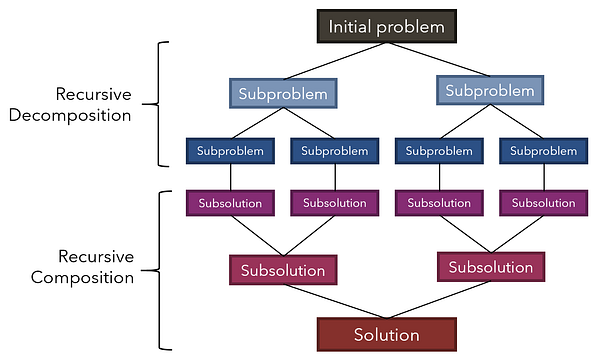
Рекурсия занимает центральное место среди многих наибыстрейших алгоритмов сортировки. Цель этих алгоритмов — получить список чисел и вернуть их в порядке от меньшего к большему. Поскольку очень много приложений опираются на быструю сортировку, весьма важно найти такой, который сможет сортировать списки максимально быстро. При этом некоторые из самых быстрых алгоритмов используют рекурсивный подход, называемый “разделяй и властвуй”.
В стратегии “разделяй и властвуй” изначальная задача рекурсивно разбивается на несколько подзадач. После того, как каждая подзадача достигает размера единицы (аналог базового кейса), выявляются их подрешения, которые вновь рекурсивно совмещаются для формирования окончательного решения.
Рассмотрите, к примеру, QuickSort — один из наиболее быстрых алгоритмов сортировки, который при грамотной реализации может выполняться в 2–3 раза быстрее своих соперников и предшественников.
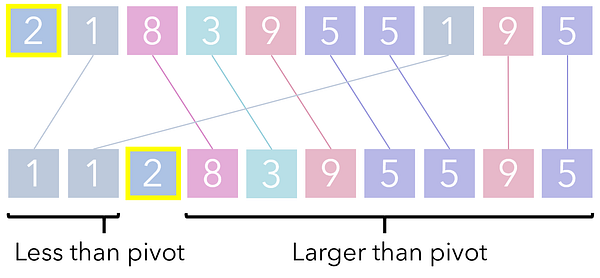
QuickSort начинает выполнение с выбора “опоры”. В простейших реализациях и для наших целей такую опору можно выбрать произвольно. Однако в более специализированных реализациях к ее выбору уже стоит подходить осторожно.
Все элементы со значениями меньше опоры переносятся левее нее, а все, чьи значения больше — правее. Выполнить это можно, пройдя по каждому элементу и переместив те, что меньше опоры, в один список, а те, что больше нее — в другой. Заметьте, что эта операция справляется с задачей только частично.
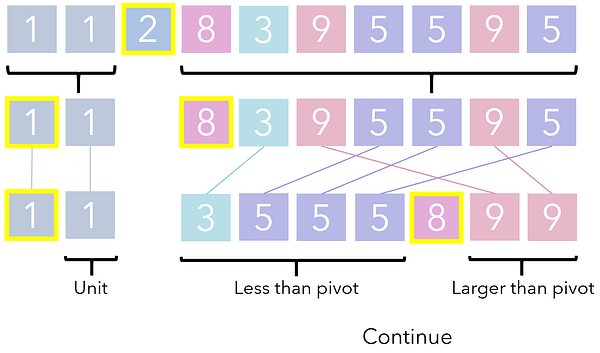
Процесс сортировки списка на основе его опорной точки называется разделением, так как опора разделяет этот список на два раздела, иначе говоря, на две стороны. Каждый их этих разделов вызывает очередную итерацию разделения сам на себя и так продолжается до тех пор, пока раздел не достигнет базового кейса (1 единицы, просто одного числа)
После достаточного числа рекурсивных вызовов исходный список будет разделен до точки, когда эти вызовы продолжить уже невозможно. В этой точке композиция подрешений выполняется простым составлением их в горизонтальном порядке. Результат такой композиции — отсортированный список.
Обратите внимание, что QuickSort следует многим из перечисленных основ рекурсии, рассмотренных нами ранее, только на более высоком уровне. Рекуррентное соотношение является разделением компонента, а базовый кейс — это разделение размера 1. Начиная с оригинального списка, те же процессы (выбор опоры и разделение) вызываются рекурсивно до тех пор, пока результат не будет состоять только из базовых кейсов.
источники:
http://baguzin.ru/wp/excel-ispolzovanie-tsiklicheskih-ssylok-d/
http://nuancesprog.ru/p/9668/
Как посчитать в Excel x=x+15% и так заданное количество раз.
задан 26 дек 2013 в 22:40
С учетом последнего комментария @mikelsv, задачу следует сформулировать так:
у=x+15%=x*1.15
А если «заданное количество раз», то
y=x*k^n
где k — коэффициент, n — «заданное количество раз».
В Excel есть функция СТЕПЕНЬ. Если A1, B1 и C1 — это x, k и n, то в D1 запишем
=A1*СТЕПЕНЬ(B1;C1)
ответ дан 27 дек 2013 в 3:33
paulgripaulgri
9994 серебряных знака7 бронзовых знаков
3
Циклом?
Sub cycle_()
Dim iVal As Double, n As Long
Dim i As Long
iVal = 5 ' значение х
n = 20 ' количество
For i = 1 To n
iVal = iVal * 1.15
Next i
MsgBox iVal
End Sub
ответ дан 26 дек 2013 в 23:08
1
|
Рекурсия для вычисления последовательности |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |