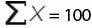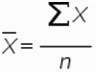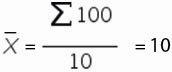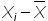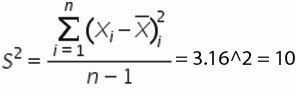Содержание
- Определение среднего квадратичного отклонения
- Расчет в Excel
- Способ 1: мастер функций
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Вопросы и ответы
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
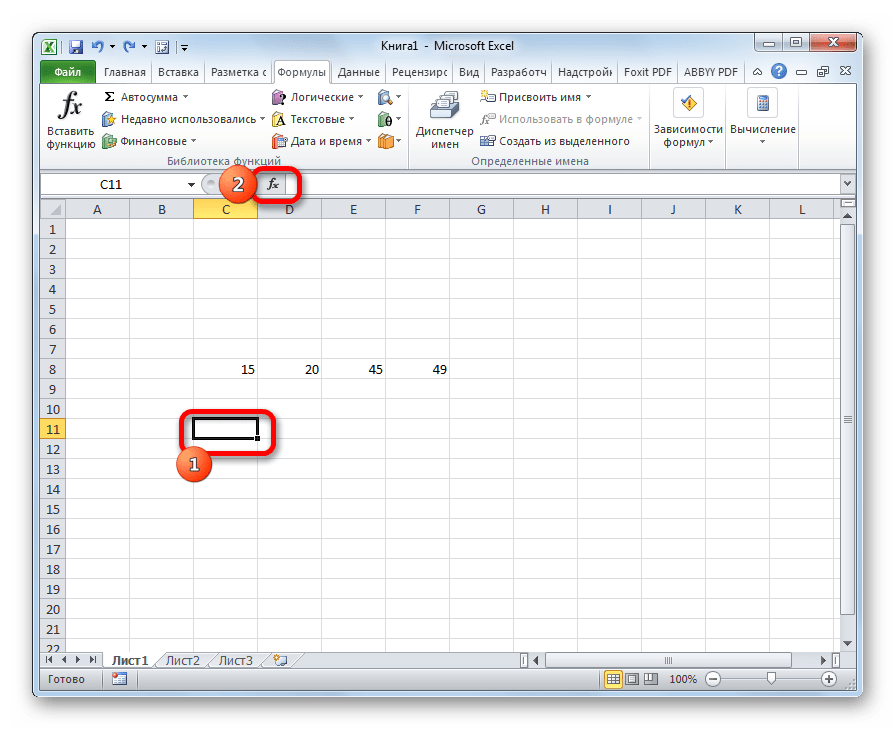
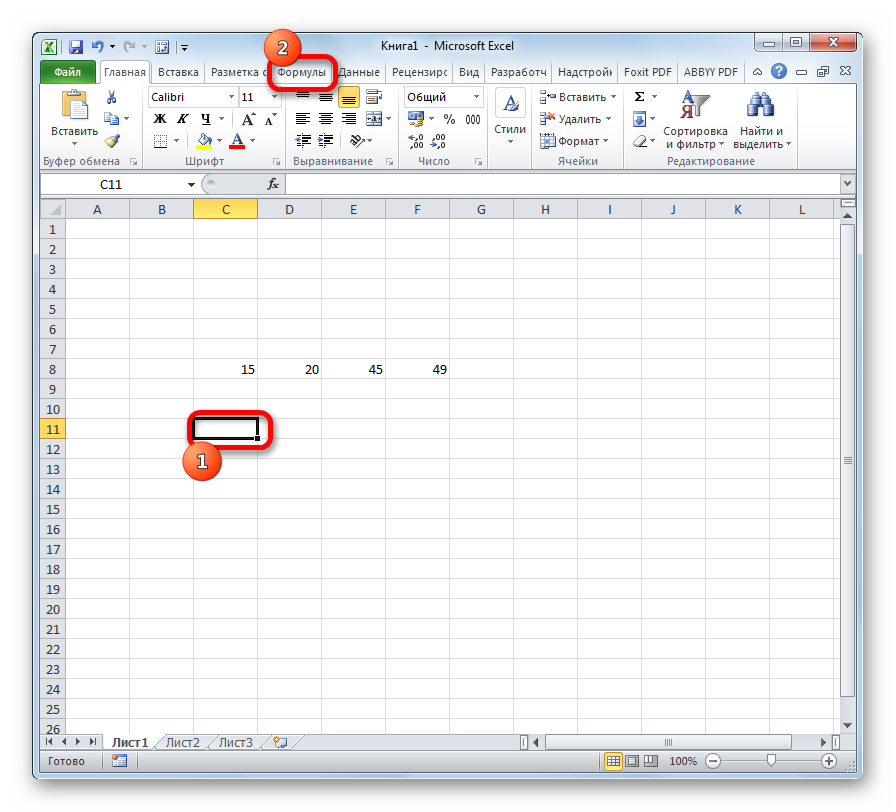
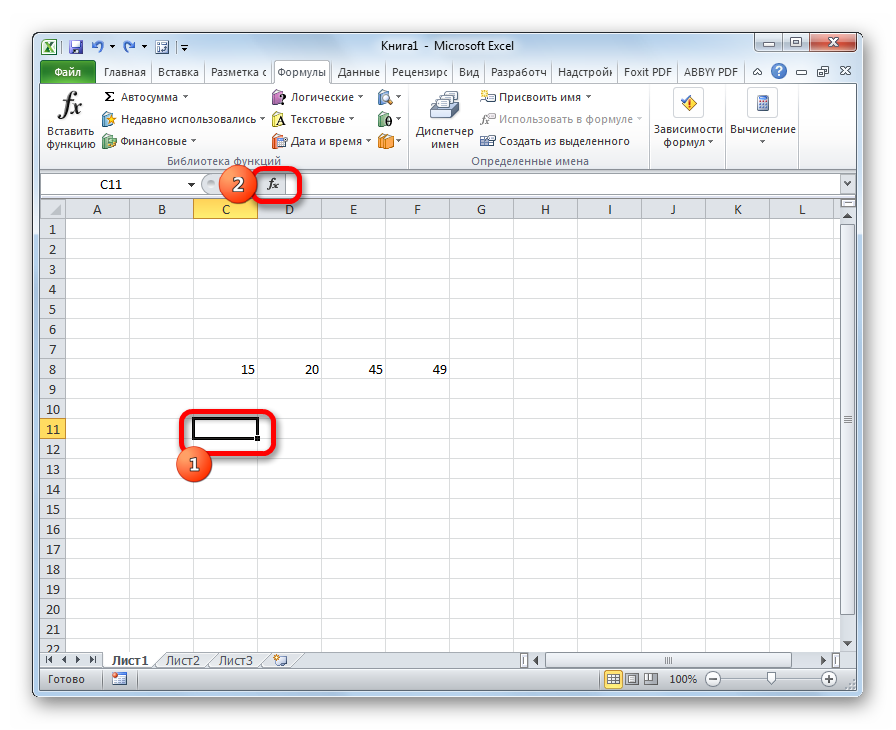
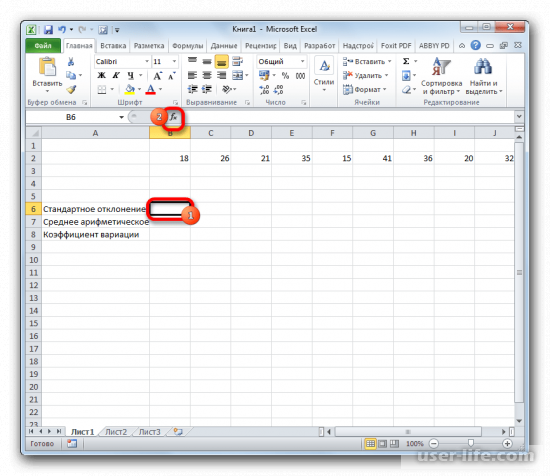
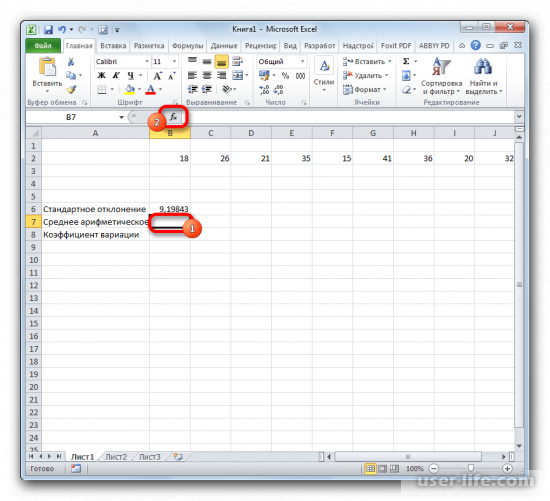
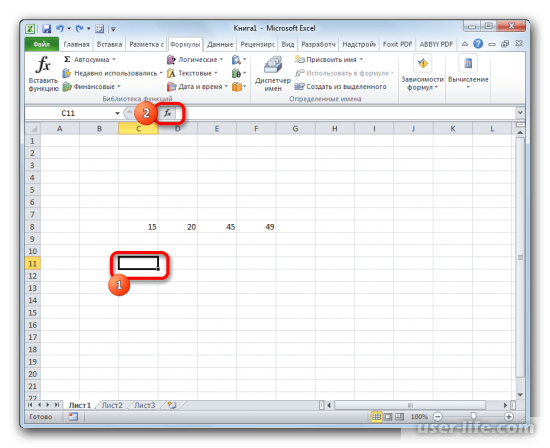
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
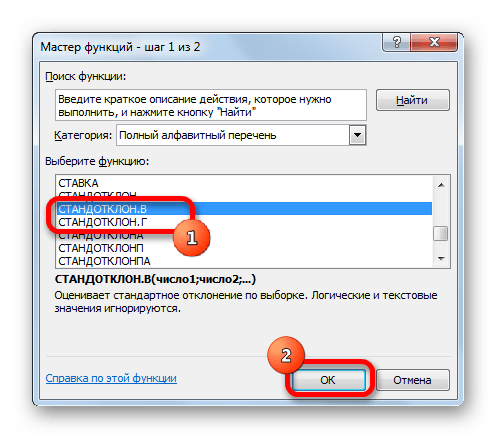
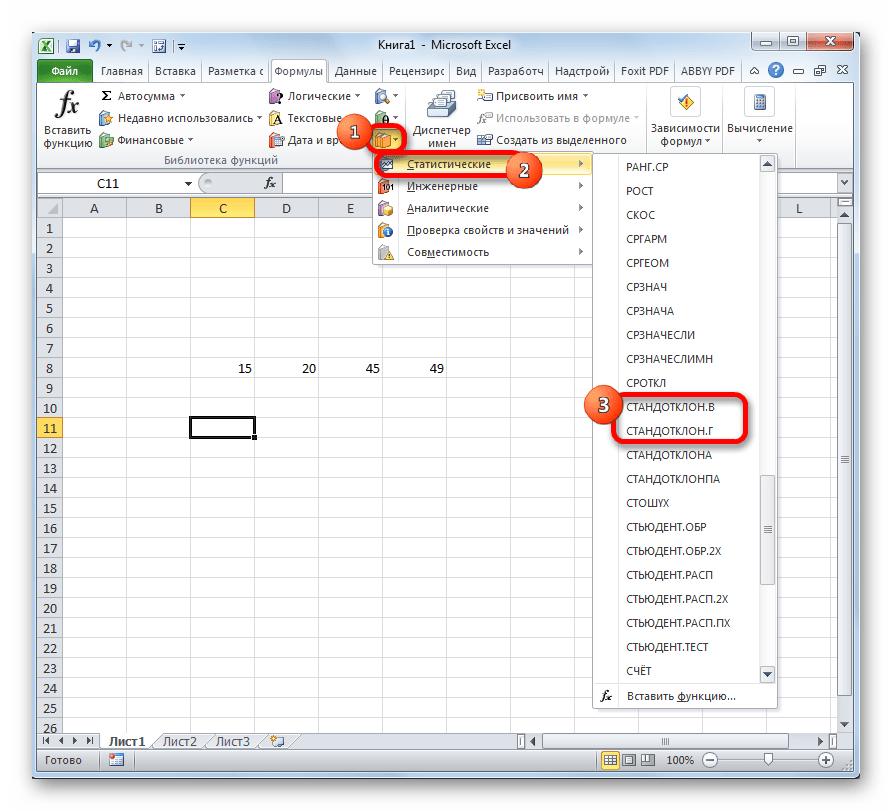
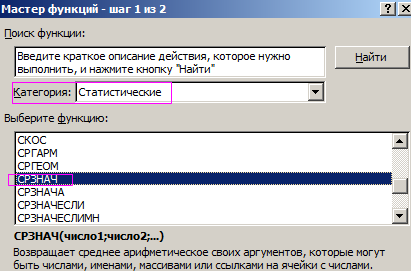
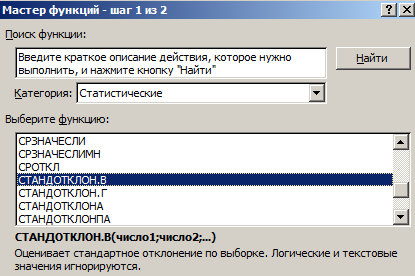
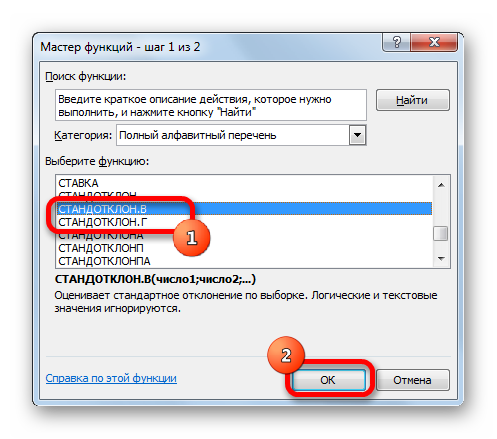
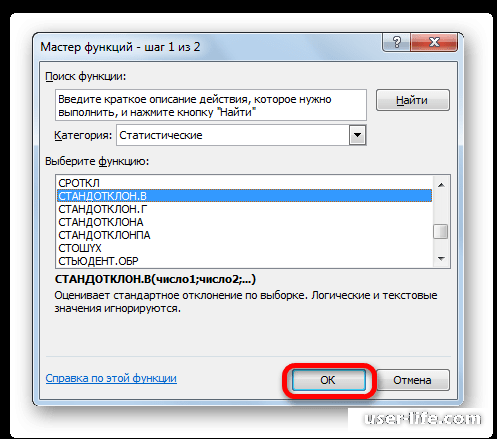
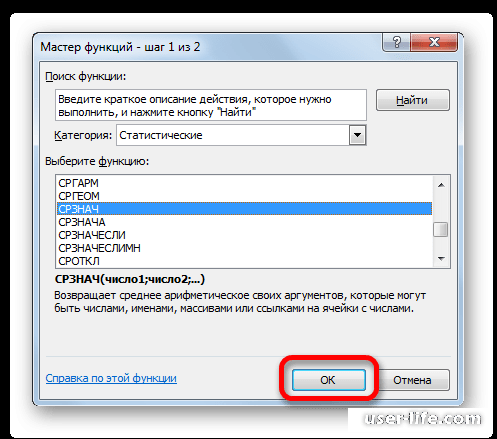
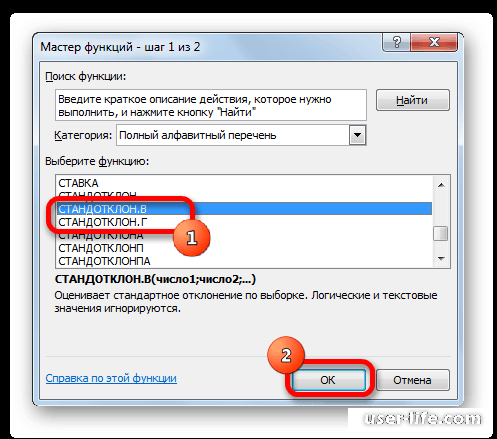
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
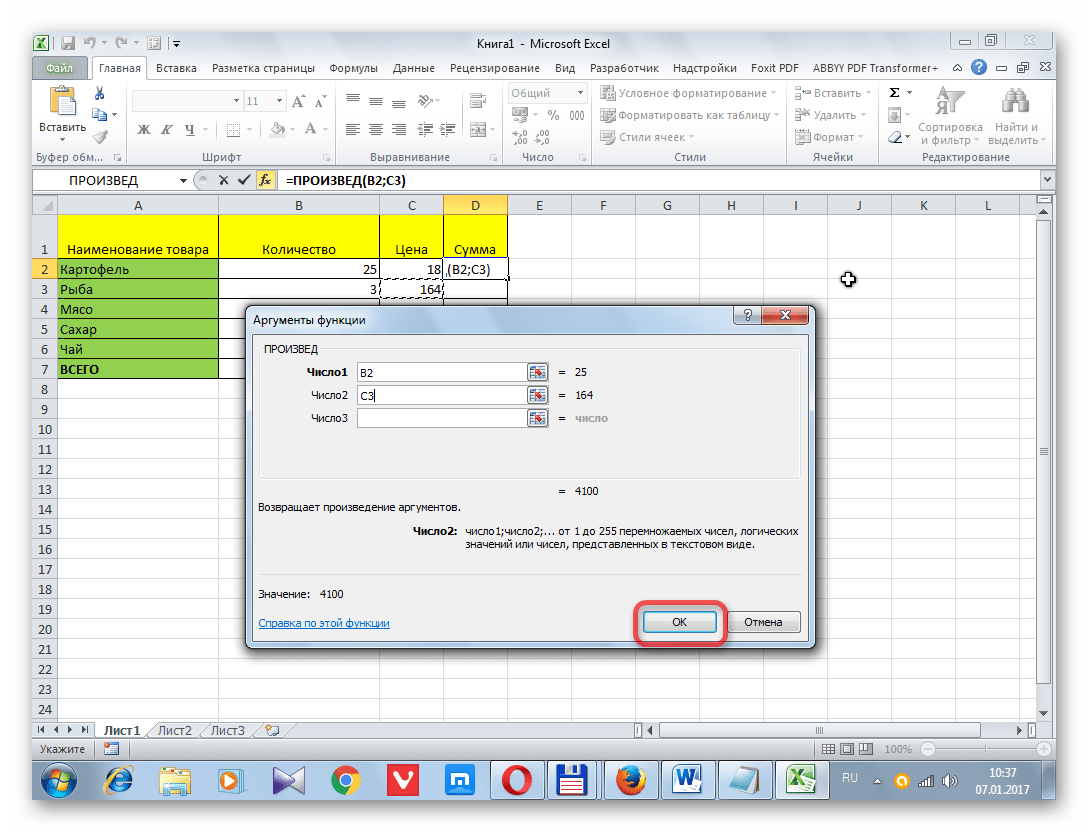
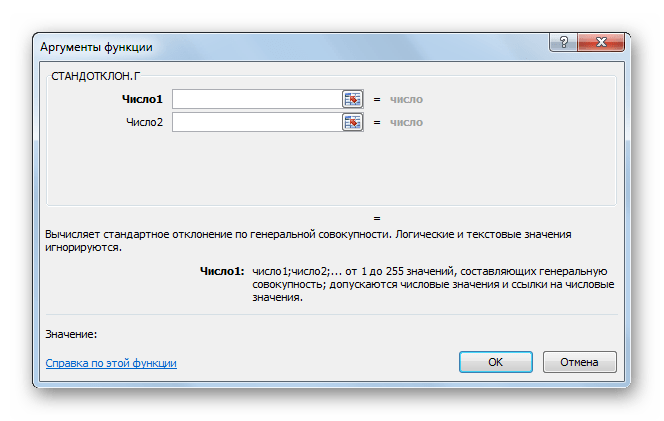
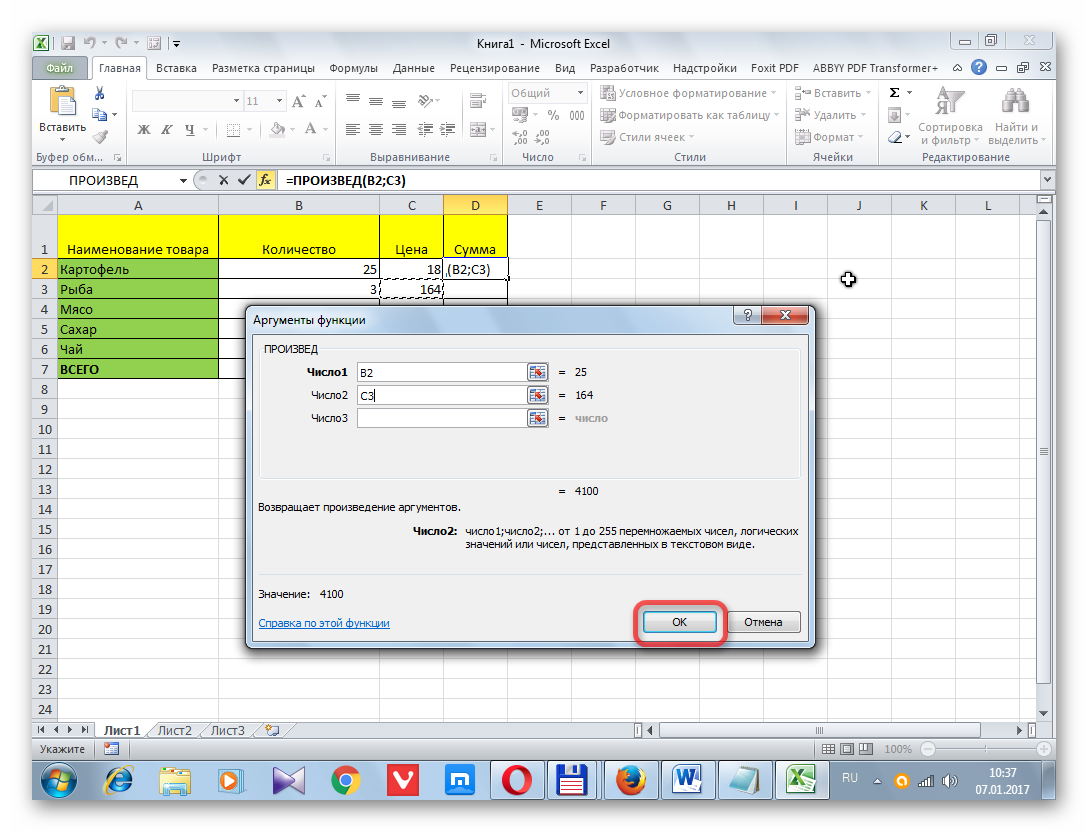
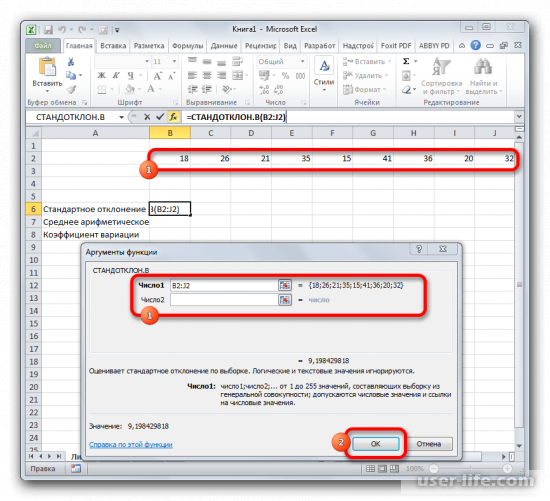
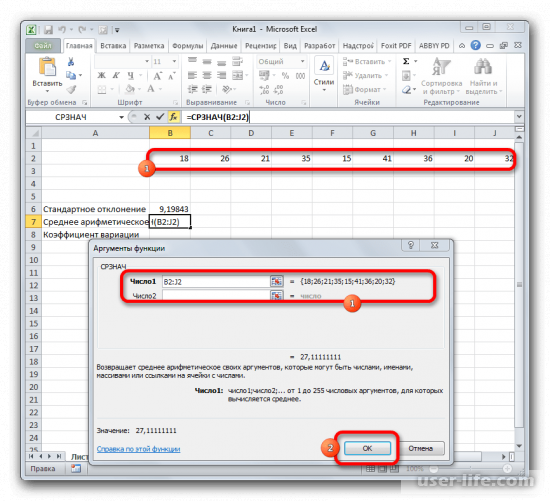
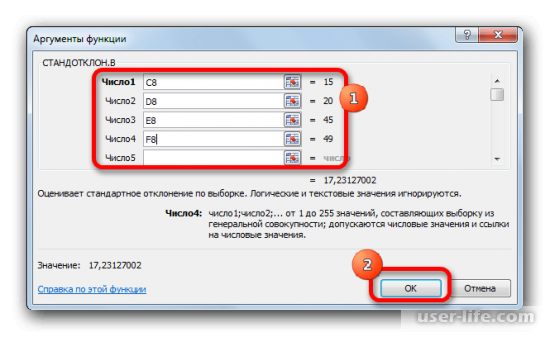
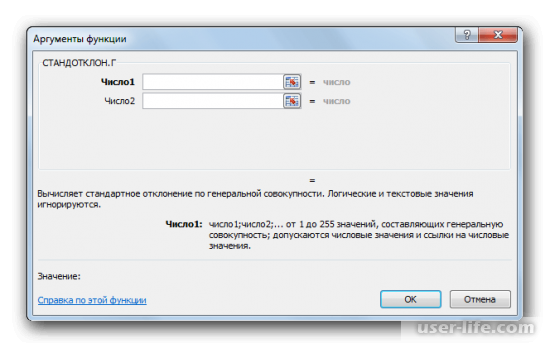
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
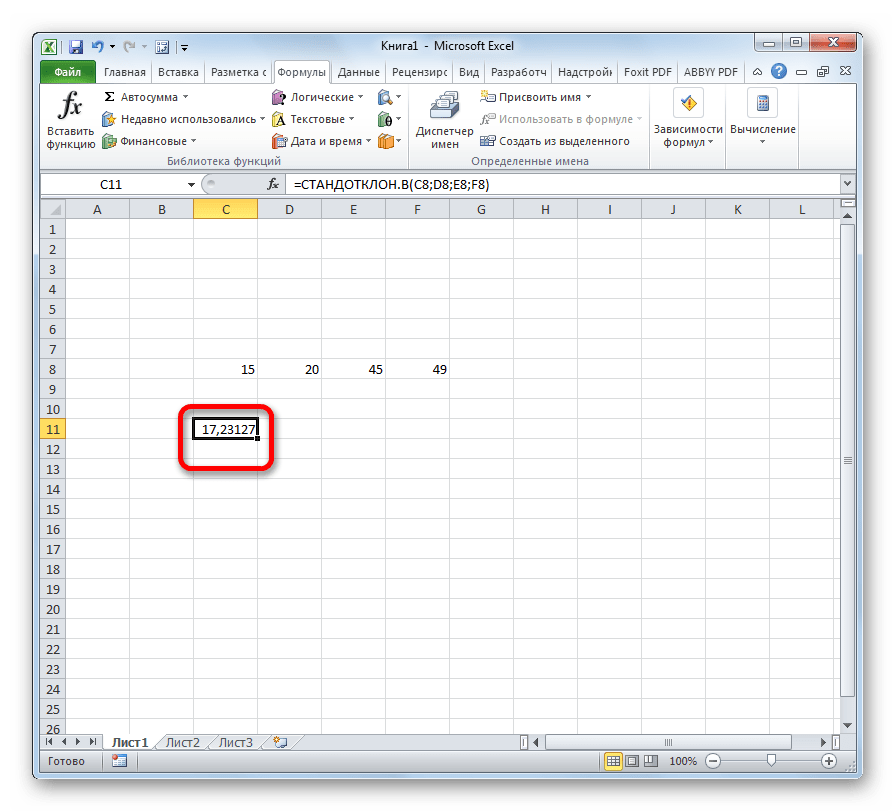
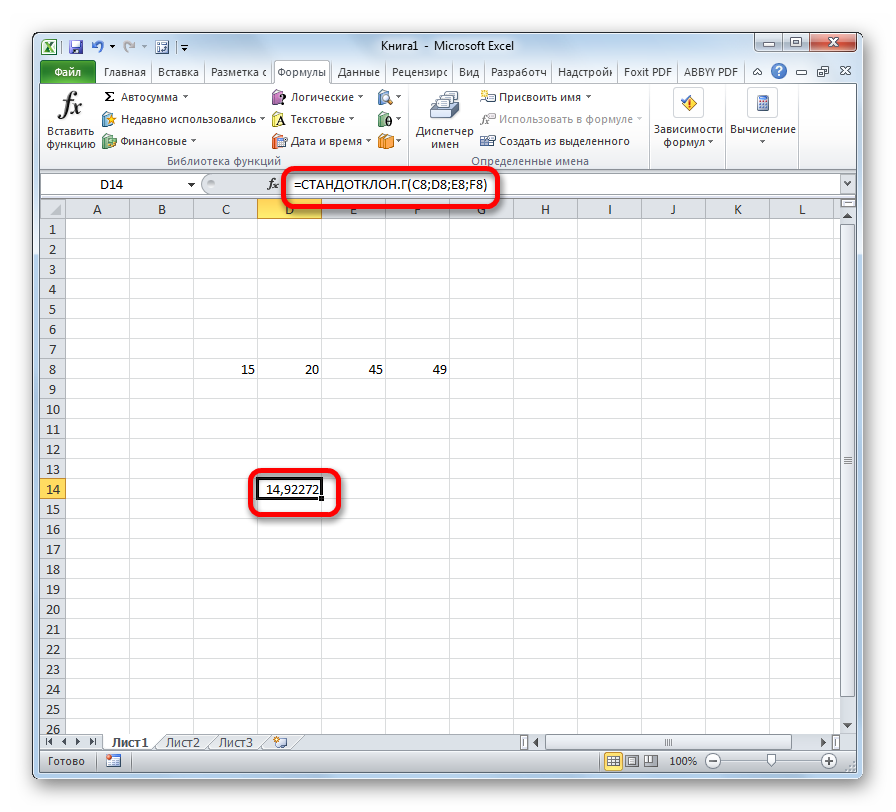
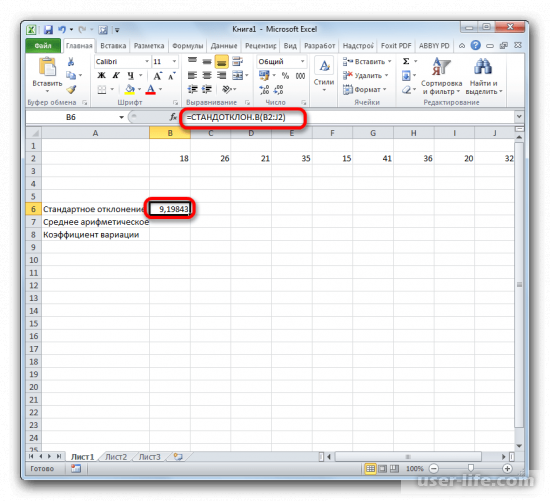
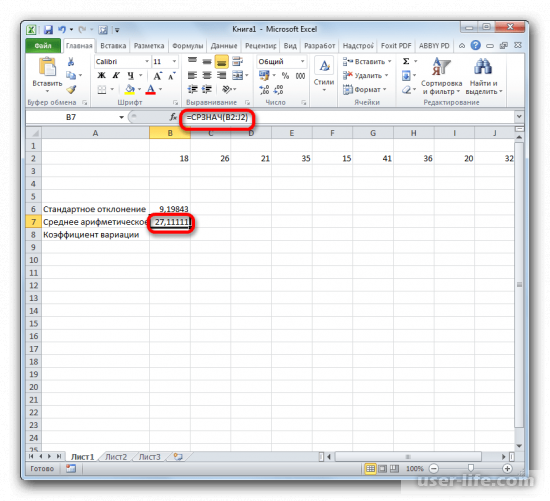
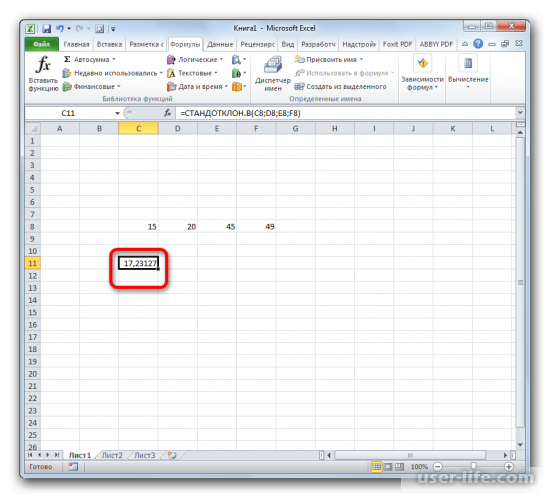
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
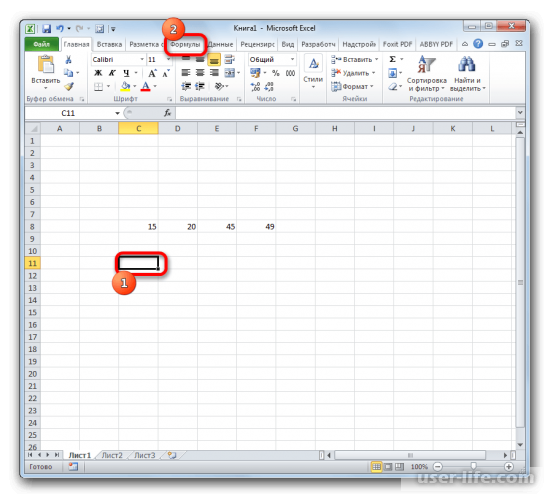
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
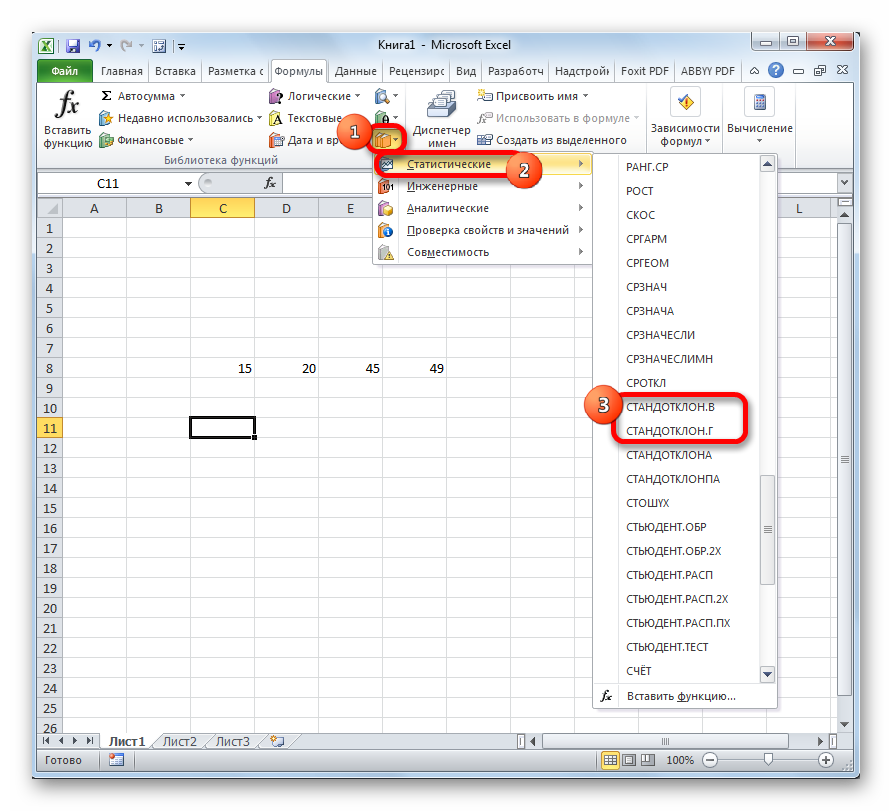
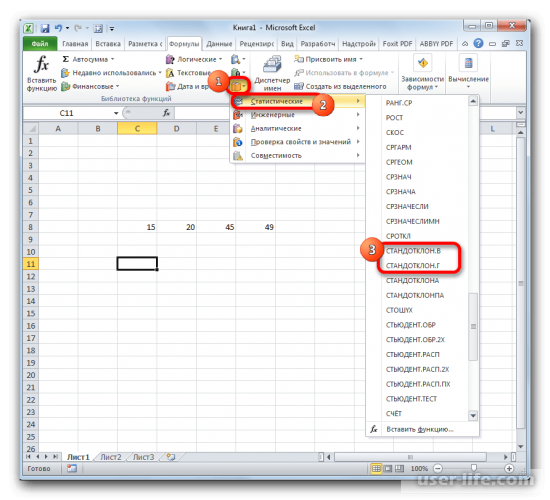
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
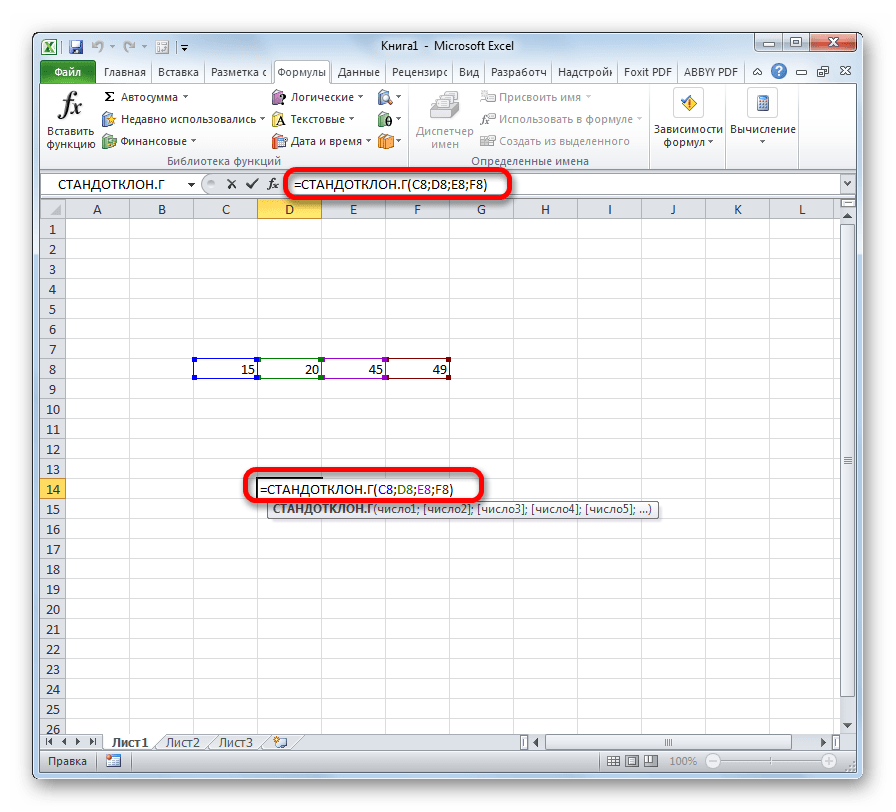
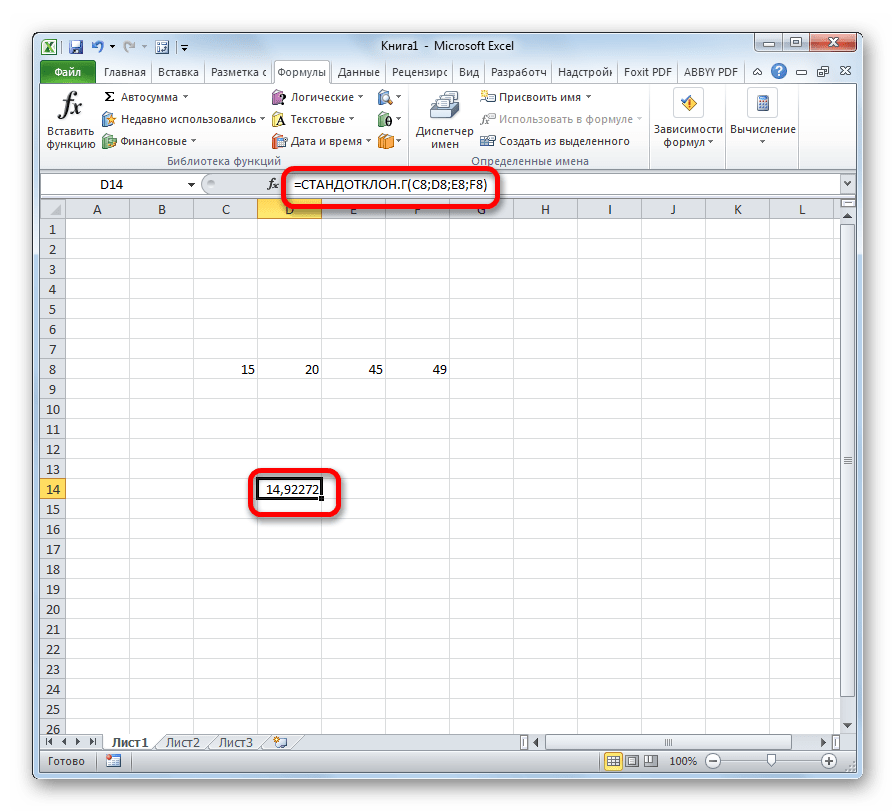
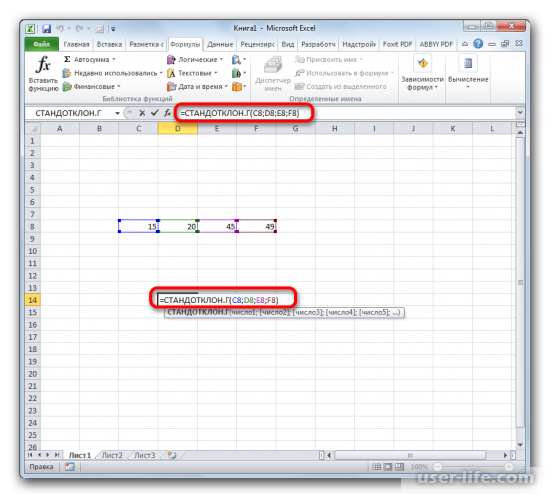
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Еще статьи по данной теме:
Помогла ли Вам статья?
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
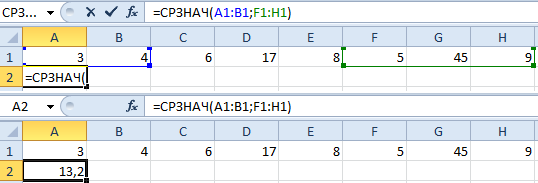
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
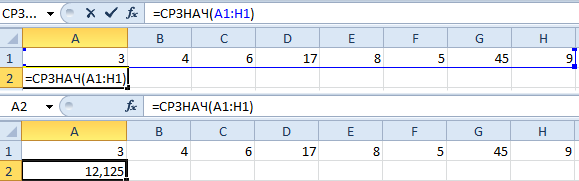
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:
Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
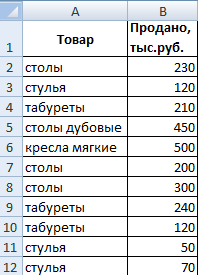
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
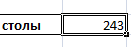
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
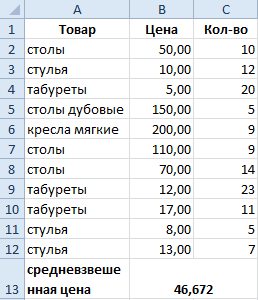
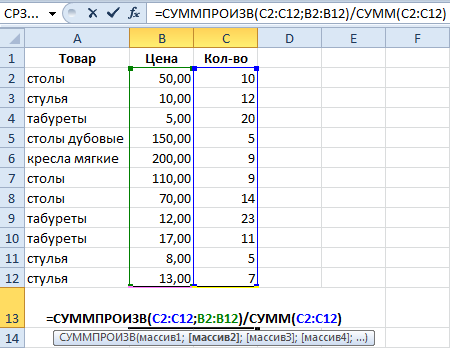
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
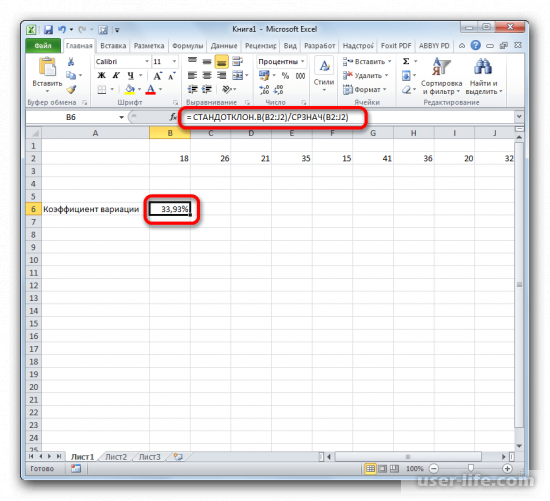
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
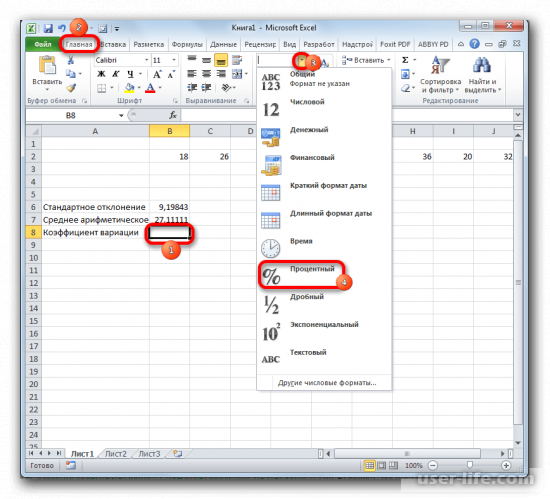
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Среднее арифметическое – один из самых популярных статистических методов, который рассчитывается повсеместно. Но сам по себе он абсолютно ненадежный. Многие знают поговорку, что один человек ест капусту, другой – мясо, а в среднем они оба едят голубцы. На примере средней зарплаты очень легко это изобразить. Несколько процентов людей, которые зарабатываются миллионы, не сильно повлияют на статистику, но способны значительно испортить ее объективность, завышая показатель на несколько десятков процентов.
Чем ниже разброс между значениями, тем больше можно доверять этому статистическому показателю. Поэтому настоятельно рекомендуется всегда вместе со средним арифметическим рассчитывать и стандартное отклонение. Сегодня мы разберемся, как правильно это делать средствами Microsoft Excel.
Содержание
- Среднеквадратичное отклонение — что это
- Расчет среднеквадратичного отклонения в Excel
- Метод 1. Ручной ввод формулы
- Метод 2. Вкладка «Формулы»
- Метод 3. Мастер функций
- Заключение
Среднеквадратичное отклонение — что это
Стандартное (или среднеквадратичное) отклонение – это квадратный корень из дисперсии. В свою очередь, под последним термином подразумевается степень разброса значений. Для получения дисперсии, и, как следствие, ее производного в виде стандартного отклонения, существует специальная формула, которая, впрочем, нам не так важна. Она довольно сложная по своей структуре, но при этом ее можно полностью автоматизировать средствами Excel. Главное – знать, какие параметры нужно передавать функции. В целом как для вычисления дисперсии, так и стандартного отклонения, аргументы используются одинаковые.
- Сначала мы получаем среднее арифметическое.
- После этого каждое исходное значение сопоставляется со средним и определяется разница между ними.
- После этого каждая разница возводится во вторую степень, после чего получившиеся результаты складываются между собой.
- Наконец, финальный шаг – деление получившегося значения на общее количество элементов в данной выборке.
Получив разницу между одним значением и средним арифметическим всей выборки, мы можем узнать расстояние к нему от определенной точки на координатной прямой. Начинающему человеку вся логика понятна равно до третьего шага. Зачем возводить значение в квадрат? Дело в том, что иногда разница может быть отрицательной, а нам нужно получить положительное число. И, как известно, минус на минус дает плюс. А далее нам нужно определить среднее арифметическое из получившихся значений. Дисперсия имеет несколько свойств:
- Если выводить дисперсию из одного числа, то она всегда будет равняться нулю.
- Если случайное число умножить на константу А, то дисперсия увеличится в количество раз, равное А в квадрате. Проще говоря, константу можно вынести за знак дисперсии и возвести его во вторую степень.
- Если к произвольному числу добавить константу А или же отнять ее, то дисперсия от этого не поменяется.
- Если два случайных числа, обозначаемых, к примеру переменными X и Y не зависят друг от друга, то в таком случае для них справедлива формула. D(X+Y) = D(X) + D(Y)
- Если же в предыдущую формулу внести изменения и пытаться определить дисперсию разницы этих значений, то она также будет составлять сумму этих дисперсий.
Среднеквадратическое отклонение – это математический термин, являющийся производным от дисперси. Получить его очень просто: достаточно извлечь квадратный корень из дисперсии.
Разница между дисперсией и стандартным отклонением находится сугубо в плоскости единиц измерения, если можно так выразиться. Стандартное отклонение является значительно более простым для считывания показателем, поскольку оно показывается не в квадратах числа, а непосредственно в значениях. Простыми словами, если в числовой последовательности 1,2,3,4,5 средним арифметическим является 3, то соответственно, стандартным отклонением будет число 1,58. Это говорит о том, что в среднем одно число отклоняется от среднего числа (которым является тройка в нашем примере), на 1,58.
Дисперсия же будет тем же самым числом, только возведенным в квадрат. В нашем примере – чуть меньше, чем 2,5. В принципе, можно использовать как дисперсию, так и стандартное отклонение для статистических расчетов, только надо четко знать, с каким именно показателем пользователь работает.
Расчет среднеквадратичного отклонения в Excel
У нас есть два главных варианта формулы. Первый рассчитывается по выборочной совокупности. Второй – по генеральной. Чтобы рассчитать стандартное отклонения по выборочной совокупности, необходимо использовать функцию СТАНДОТКЛОН.В. Если же необходимо осуществить расчет по генеральной совокупности, то надо пользоваться функцией СТАНДОТКЛОН.Г.
Отличие выборочной совокупности от генеральной заключается в том, что в первом случае идет обработка непосредственно тех данных, на основе которых рассчитывается среднее арифметическое и среднеквадратическое отклонение. Если же мы говорим про генеральную совокупность, то это весь набор количественных данных, связанных с исследуемым явлением. В идеале выборка должна быть полностью репрезентативной. То есть, в исследовании должны участвовать люди, которых можно соотнести с генеральной совокупностью в равных пропорциях. Например, если в условной стране 50% мужчин и 50% женщин, то такие же пропорции должны быть у выборки.
Следовательно, стандартное отклонение для генеральной совокупности может несколько отличаться от выборочной, поскольку во втором случае исходные цифры меньше. Но в целом, обе функции работают одинаково. Сейчас мы распишем, что нужно сделать для того, чтобы их вызвать. А сделать это можно сразу тремя способами.
Метод 1. Ручной ввод формулы
Ручной ввод – довольно сложный метод, на первый взгляд. Тем не менее, каждый должен им владеть, если хочет быть профессиональным пользователем Excel. Его преимущество в том, что не нужно вообще вызывать окно ввода аргументов. Если хорошо потренироваться, это будет значительно быстрее, чем пользоваться двумя остальными способами. Главное – чтобы пальцы были тренированные. В идеале каждый пользователь Excel должен владеть слепым методом, чтобы быстро вводить формулы и функции.
- Делаем левый клик мышью по той ячейке, в которой будет записываться формула для получения стандартного отклонения. Также можно ее вводить в качестве аргумента любой другой из функций. В таком случае нужно кликнуть по строке ввода формул, а потом начать ввод в том аргументе, куда результат должен выводиться.
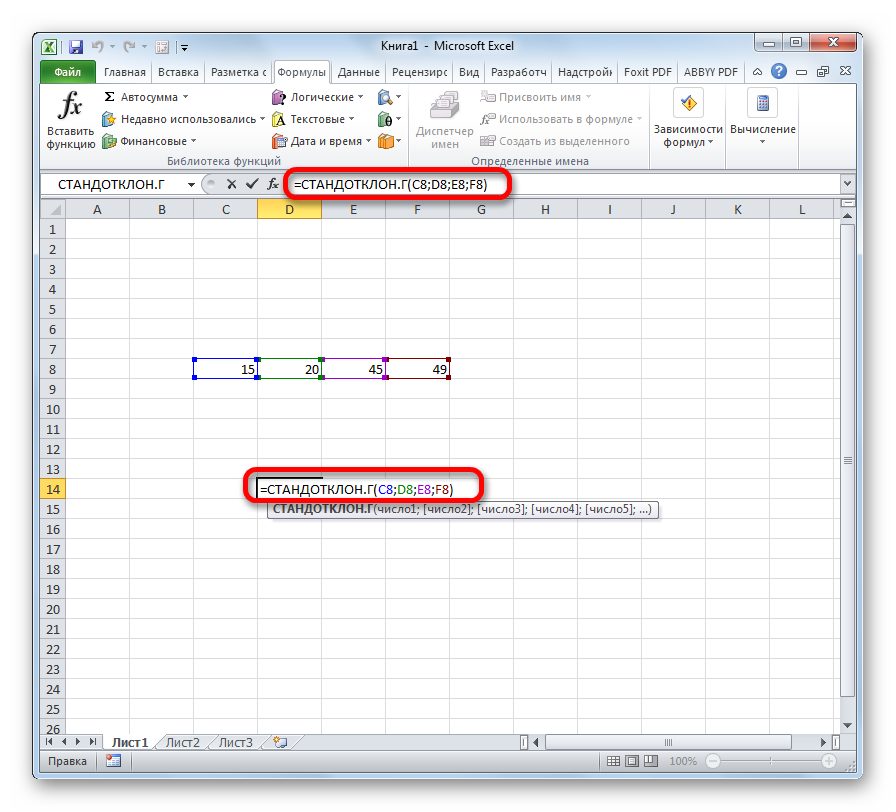
- Общая формула следующая: =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Если мы используем второй вариант, то все осуществляется в точности так же, только буква Г в названии функции меняется на В. Максимальное количество поддерживаемых аргументов – 255.
- После того, как ввод формулы будет закончен, подтверждаем свои действия. Для этого нужно нажать клавишу ввода.
Таким образом, для вычисления стандартного отклонения нам нужно использовать те же аргументы, что и для получения среднего арифметического. Все остальное программа сможет сделать самостоятельно. Также в качестве аргумента можно использовать целый диапазон значений, на основе которых будет осуществляться расчет среднеквадратического отклонения. Теперь давайте рассмотрим другие методы, которые будут более понятными для начинающего пользователя Excel. Но в долгосрочной перспективе от них нужно будет отказаться, поскольку:
- Ручной ввод формулы способен значительно сэкономить время. Пользователь Excel, который помнит формулу и ее синтаксис, имеет существенное преимущество перед тем человеком, который только начинает и долго ищет нужную функцию в перечне в мастере функций или на ленте. Кроме этого, сам по себе ввод с клавиатуры является гораздо более быстрым, чем использование мыши.
- Меньше устают глаза. Не нужно постоянно переключать фокус внимания с таблицы на окно, потом на еще одно окно, потом на клавиатуру, а потом снова на таблицу. Это же помогает существенно сэкономить время и силы, которые потом можно тратить на обработку реальной информации, а не техническое обслуживание формул.
- Ручной ввод формул гораздо более гибкий по сравнению с использованием двух следующих методов. Пользователь может сразу указать нужные ячейки диапазона, не выделяя его непосредственно или сразу посмотреть на всю таблицу, избегая риска, что ее перекроет диалоговое окно.
- Использование формул вручную является своеобразным мостиком к написанию макросов. Конечно, это не поможет выучить язык VBA, но зато формирует правильные привычки. Если человек привык давать команды компьютеру с помощью клавиатуры, ему будет значительно проще освоить любой другой язык программирования, в том числе, и для разработки макросов для электронных таблиц.
Но конечно, да. Использование других методов значительно лучше, если вы новичок, и только начинаете. Поэтому переходим к рассмотрению иных способов, как можно рассчитать стандартное отклонение.
Метод 2. Вкладка «Формулы»
Еще один метод, доступный пользователю, желающему получить стандартное отклонение из диапазона – воспользоваться вкладкой «Формулы» в главном меню. Давайте более подробно распишем, что нужно сделать для этого:
- Выделить ту ячейку, в которую мы хотим записывать результат.
- После этого находим на ленте вкладку «Формулы» и переходим в нее.
- Воспользуемся блоком «Библиотека функций». Там есть кнопка «Другие функции». В перечне, который будет, мы найдем пункт «Статистические». После этого выбираем, какую разновидность формулы мы собираемся использовать.
- После этого появляется окно ввода аргументов. В нем указываем все числа, ссылки на ячейки или диапазоны, которые будут принимать участие в расчетах. После того, как закончим, нажимаем кнопку «ОК».
Преимущества этого метода:
- Скорость. Данный способ довольно быстрый и позволяет ввести нужную формулу буквально в несколько кликов.
- Точность. Нет риска случайно написать не ту ячейку или написать не ту букву, а потом тратить время на переделку.
Можно сказать, что это способ номер два по хорошести после ручного ввода. НО третий метод также полезен в некоторых ситуациях.
Метод 3. Мастер функций
Мастер функций – еще один удобный метод ввода формул для новичков, которые еще не запомнили названия и синтаксис функций. Кнопка для запуска мастера функций находится возле строки ввода формул. Его главное преимущество для новичка на фоне предыдущих способов заключается в детальных подсказках программы, какая функция за что отвечает и какие аргументы вводить в какой последовательности. Она являет собой две буквы – fx. Нажимаем на нее.
После этого появится перечень функций. Можно как попытаться найти в полном алфавитном перечне, так и открыть категорию «Статистические», где также можно найти этот оператор.
Мы можем увидеть в списке, что функция СТАНДОТКЛОН все еще присутствует. Это сделано для того, чтобы сделать старые файлы совместимыми с новой версией Excel. При этом настоятельно рекомендуется пользоваться новыми функциями, приведенными выше, потому что в один момент эта устаревшая функция может перестать поддерживаться.
После того, как мы нажмем «ОК», у нас будет возможность открыть окно аргументов. Каждый аргумент являет собой отдельное число, адрес на ячейку (если в ней содержится числовое значение) или диапазоны значений, которые будут использоваться для среднего арифметического и получения стандартного отклонения. После того, как мы введем все аргументы, нажимаем на кнопку «ОК». Данные будут занесены в ту ячейку, в которой мы вводили формулу.
Заключение
Таким образом, вычислить стандартное отклонение средствами Excel несложно. Да и сама функция является основой статистических расчетов, которая является интуитивно понятной. Ведь очевидно, что важно не только среднее значение, но и разброс значений, из которых выводится среднее арифметическое. Ведь если половина народа богатая, а половина – бедная, то среднего класса по факту и не будет. Но при этом если вывести среднее арифметическое, то окажется, что среднестатистический гражданин как раз и является представителем среднего класса. Но это звучит, как минимум, странно. В общем, успехов в использовании этой функции.
Оцените качество статьи. Нам важно ваше мнение:
Расчет среднего квадратичного отклонения в Microsoft Excel
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
-
Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
-
Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).
Всего можно записать при необходимости до 255 аргументов.
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Разбираем формулы среднеквадратического отклонения и дисперсии в Excel
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
Для этого временного ряда i=1, n=10 , 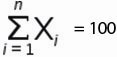
Рассмотрим формулу среднего значения:
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
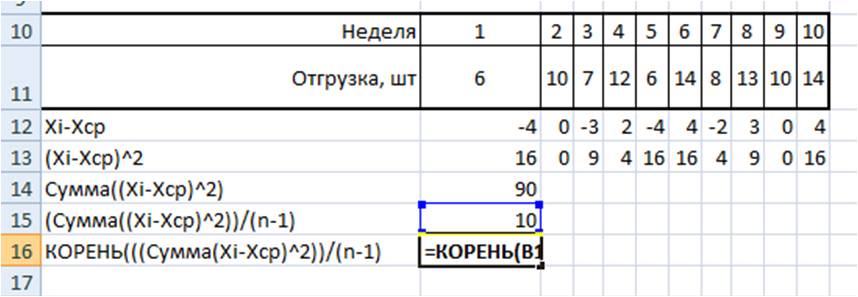
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
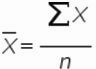
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего 
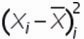

5. 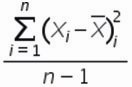
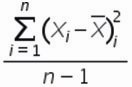
6. Среднеквадратическое отклонение равно 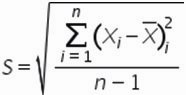
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Как найти среднее арифметическое число в Excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
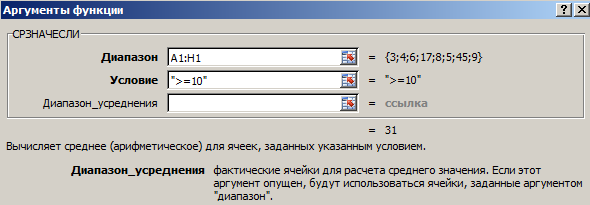
Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Как рассчитать коэффициент вариации в Эксель
Microsoft Excel позволяет максимально упростить пользователю ряд задач. С помощью данной утилиты можно в одно мгновение производить сложнейшие расчеты, применяя исходные данные. Сегодня мы поговорим о том, как использовать коэффициент вариации в Excel.
Коэффициент вариации показывает отношение стандартного отклонения к среднему арифметическому, а результат отображается в процентах.
Шаг 1. Расчет стандартного отклонения
Данный инструмент также называют среднеквадратичным отклонением, которое представляет собой квадратный корень из дисперсии. Чтобы рассчитать стандартное отклонение, применяется функция СТАНДОТКЛОН. В последних версиях Excel она разделена на две части, в зависимости от того, как происходит вычисление: СТАНДОТКЛОН.Г(по генеральной совокупности), СТАНДОТКЛОН.В(по выборке). Записываются функции следующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) — Для старой версии
= СТАНДОТКЛОН.В(Число1;Число2;…) — Для новой версии соответственно.
1. Чтобы начать расчет стандартного отклонения, выделите подходящую ячейку и нажмите кнопку «Вставить функцию», расположенную в верхней панели инструментов.
2. Откроется окно мастера функций. Перейдите в категорию «Статистические», затем выберите строку с названием «СТАНДОТКЛОН»(СТАНДОТКЛОН .В или .Г соответственно). Нажмите «ОК».
3. В открывшемся окне аргументов необходимо указать диапазон ячеек, с которыми будет производиться расчет. Также можно ввести конкретные числа. После указания параметров нажмите кнопку «ОК».
4. В ранее выделенной ячейке отобразится итоговый расчет стандартного отклонения.
Шаг 2. Расчет среднего арифметического
Среднее арифметическое отражает общую сумму значений числового ряда, поделенных на их количество. Для этого используем функцию СРЗНАЧ.
1. Выделите нужную ячейку для отображения конечного результата, затем воспользуйтесь кнопкой «Вставить функцию».
2. Перейдите в категорию «Статистические» и выберите поле с наименованием «СРЗНАЧ», после этого нажмите «ОК».
4. В раннее выбранной ячейке выведется результат вычислений среднего арифметического.
Шаг 3. Нахождение коэффициента вариации
Мы получили все предварительные данных для конечных вычислений, поэтому приступаем к последнему шагу, а именно к расчету коэффициента вариации.
1. Выделите ячейку для конечного результата, затем поменяйте формат ячейки на процентный. Сделать это можно во вкладке «Главная», кликнув по полю формата и выбрав соответствующий.
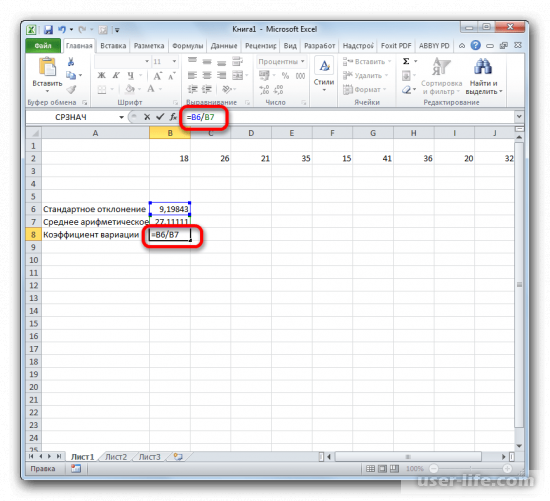
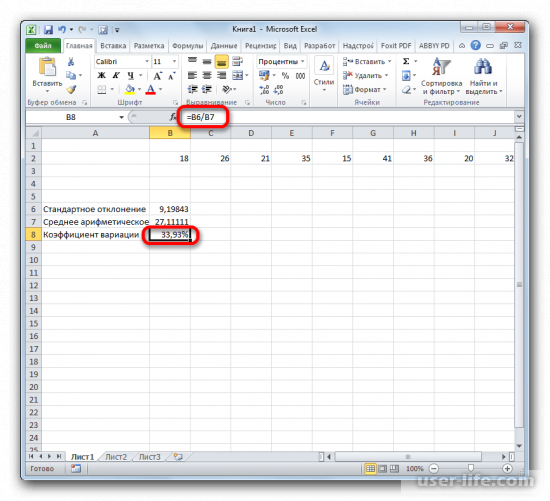
2. Снова вернитесь к ранее выбранной ячейке и выделите ее двойным щелчком левой кнопки мыши. Поставьте в ней знак «=», затем выделите ячейку с результатом вычислений стандартного отклонения. Теперь нажмите кнопку «/»(разделить) на клавиатуре и выберите ячейку со средним арифметическим. После ввода данных нажмите клавишу Enter.
3. Результат будет автоматически выведен на экран.
Также существует способ рассчитать коэффициент вариации без предварительных шагов, который мы рассмотрим ниже:
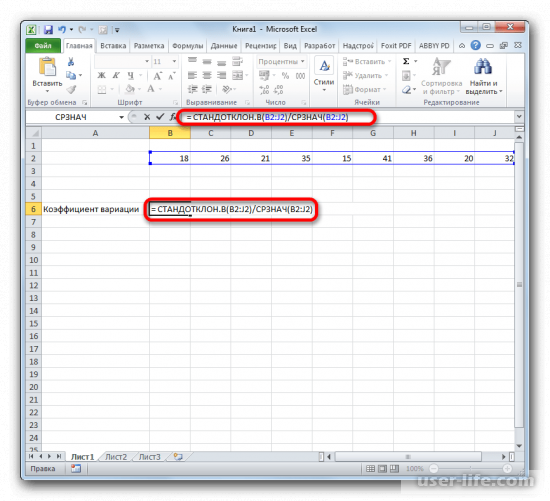
1. Аналогично выделите ячейку, затем придайте ей процентный формат. Впишите в нее следующую формулу:
«Диапазон значений» указывает с исходными данными. Можете указать его вручную, либо просто выделив нужный диапазон ячеек. Вместо оператора СТАНДОТКЛОН также можно ввести СТАНДОТКЛОН .В или СТАНДОТКЛОН .Г соответственно(для новых версий Excel).
2. После занесения всех параметров нажмите клавишу Enter, чтобы получить конечный результат.
С помощью Excel мы смогли максимально упростить выполнение сложных расчетов. Для этого нам понадобилось лишь грамотное использование встроенных инструментов приложения. Как видите, пока не существует способа рассчитать коэффициент вариации в одно действие, поэтому мы воспользовались обходными путями. Надеемся, вам помогла наша статья.
Как посчитать среднее квадратичное отклонение в Excel (расчет)
На листе Excel нужно выделить ячейку, в которой появится готовый результат. Нажимаете на «Вставить функцию», которая находится слева от строки функций.
Появится список, в котором нужно найти и выбрать СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г, и нажать ОК.
Перед вами появится окно аргументов функций. В каждой строке следует ввести число совокупности. Если числа расположены в ячейках листа, тогда можно указать их координаты или просто нажать на них. Адреса должны сразу показаться в соответствующих полях. Кликаете на ОК.
Расчет занесется в ячейку, которую выделили в самом начале процедуры поиска среднего квадратичного отклонения.
Следует выделить ячейку для занесения результата расчета. Захотите во вкладку «Формулы.
В блоке инструментов «Библиотека функций» нажимаете на «Другие функции», а в списке, который появится, выбираете «Статистические». Дальше необходимо определиться со значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г (будет зависеть от того, выборочная или генеральная совокупность будет принимать участие в расчетах).
Затем запускается окно аргументов. Все дальнейшие действия будут производиться также как написано в первом методе выше.
Ручной ввод формулы
Выделяете ячейку, в которую будет выводиться результат. Далее прописываете в ней или в строке формул выражение по такому шаблону — =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Если нужно, то можно записать максимально 255 аргументов.
Когда запись будет совершена, следует кликнуть Enter на клавиатуре.
17 авг. 2022 г.
читать 3 мин
В статистике регрессионный анализ — это метод, который мы используем для понимания взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим регрессионный анализ, мы получаем модель, которая сообщает нам прогнозируемое значение для переменной ответа на основе значения переменной-предиктора.
Один из способов оценить, насколько «хорошо» наша модель соответствует заданному набору данных, — это вычислить среднеквадратичную ошибку , которая представляет собой показатель, который говорит нам, насколько в среднем наши прогнозируемые значения отличаются от наших наблюдаемых значений.
Формула для нахождения среднеквадратичной ошибки, чаще называемая RMSE , выглядит следующим образом:
СКО = √[ Σ(P i – O i ) 2 / n ]
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
Технические примечания:
- Среднеквадратичную ошибку можно рассчитать для любого типа модели, которая дает прогнозные значения, которые затем можно сравнить с наблюдаемыми значениями набора данных.
- Среднеквадратичную ошибку также иногда называют среднеквадратичным отклонением, которое часто обозначается аббревиатурой RMSD.
Далее рассмотрим пример расчета среднеквадратичной ошибки в Excel.
Как рассчитать среднеквадратичную ошибку в Excel
В Excel нет встроенной функции для расчета RMSE, но мы можем довольно легко вычислить его с помощью одной формулы. Мы покажем, как рассчитать RMSE для двух разных сценариев.
Сценарий 1
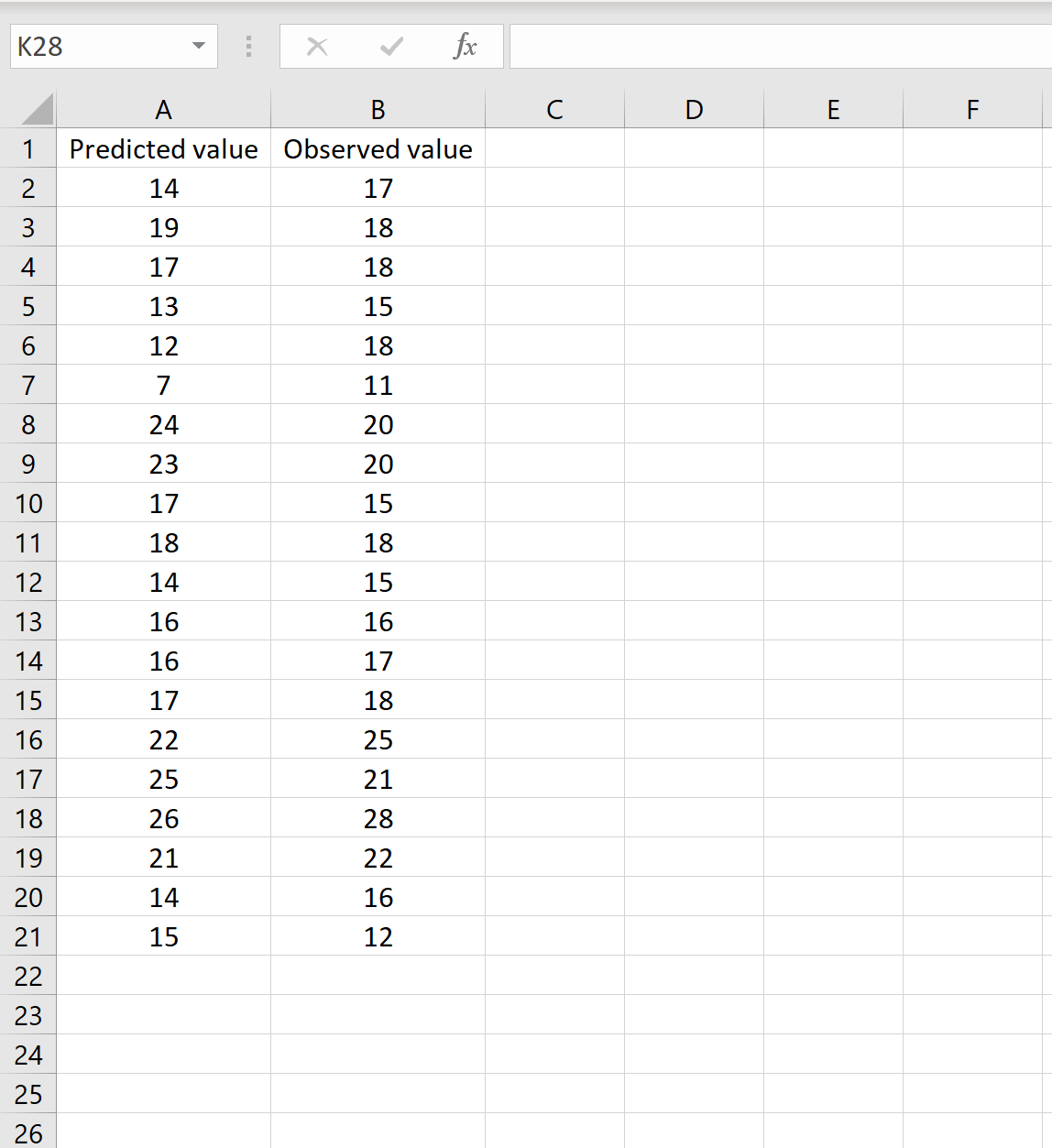
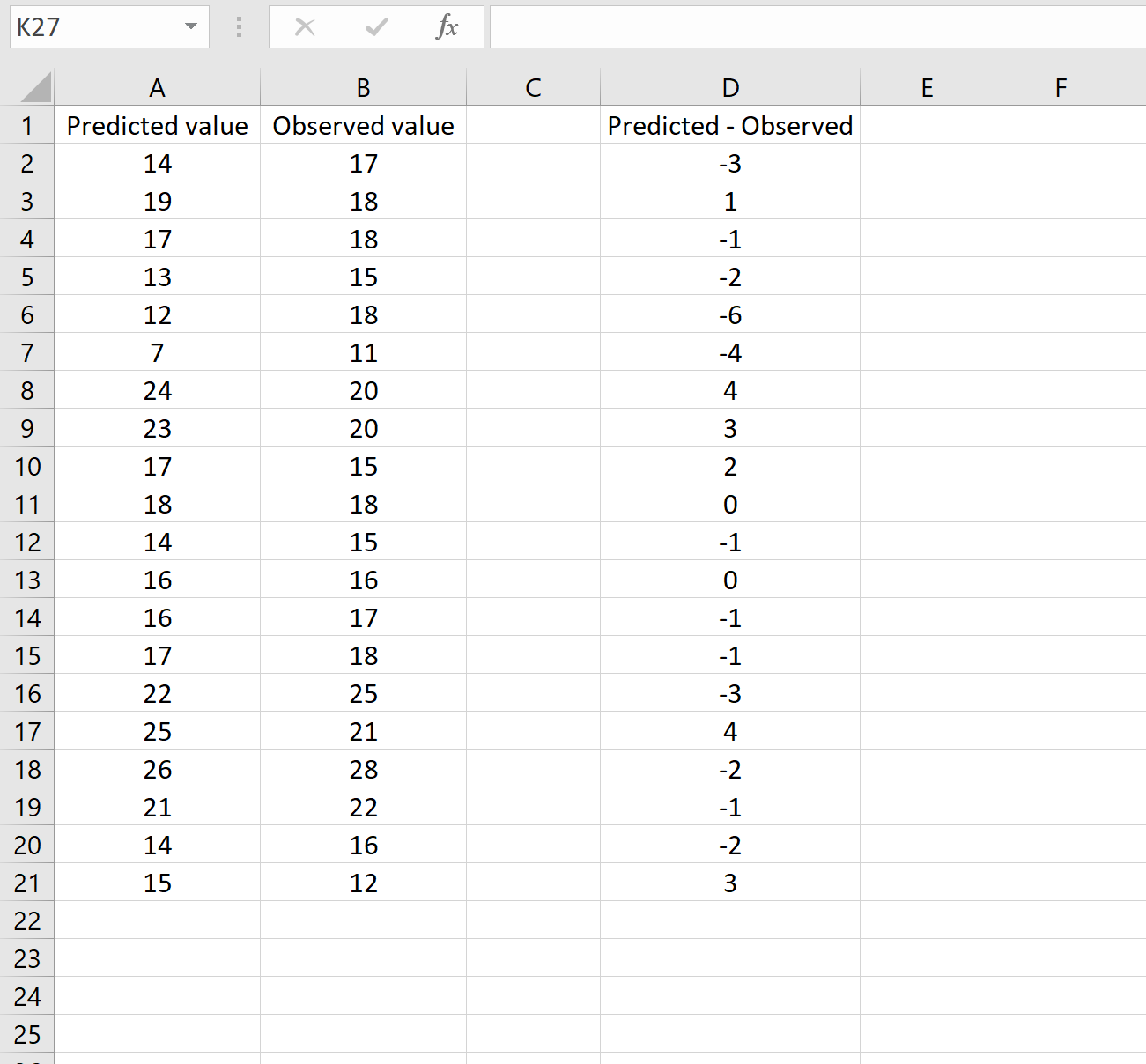
В одном сценарии у вас может быть один столбец, содержащий предсказанные значения вашей модели, и другой столбец, содержащий наблюдаемые значения. На изображении ниже показан пример такого сценария:
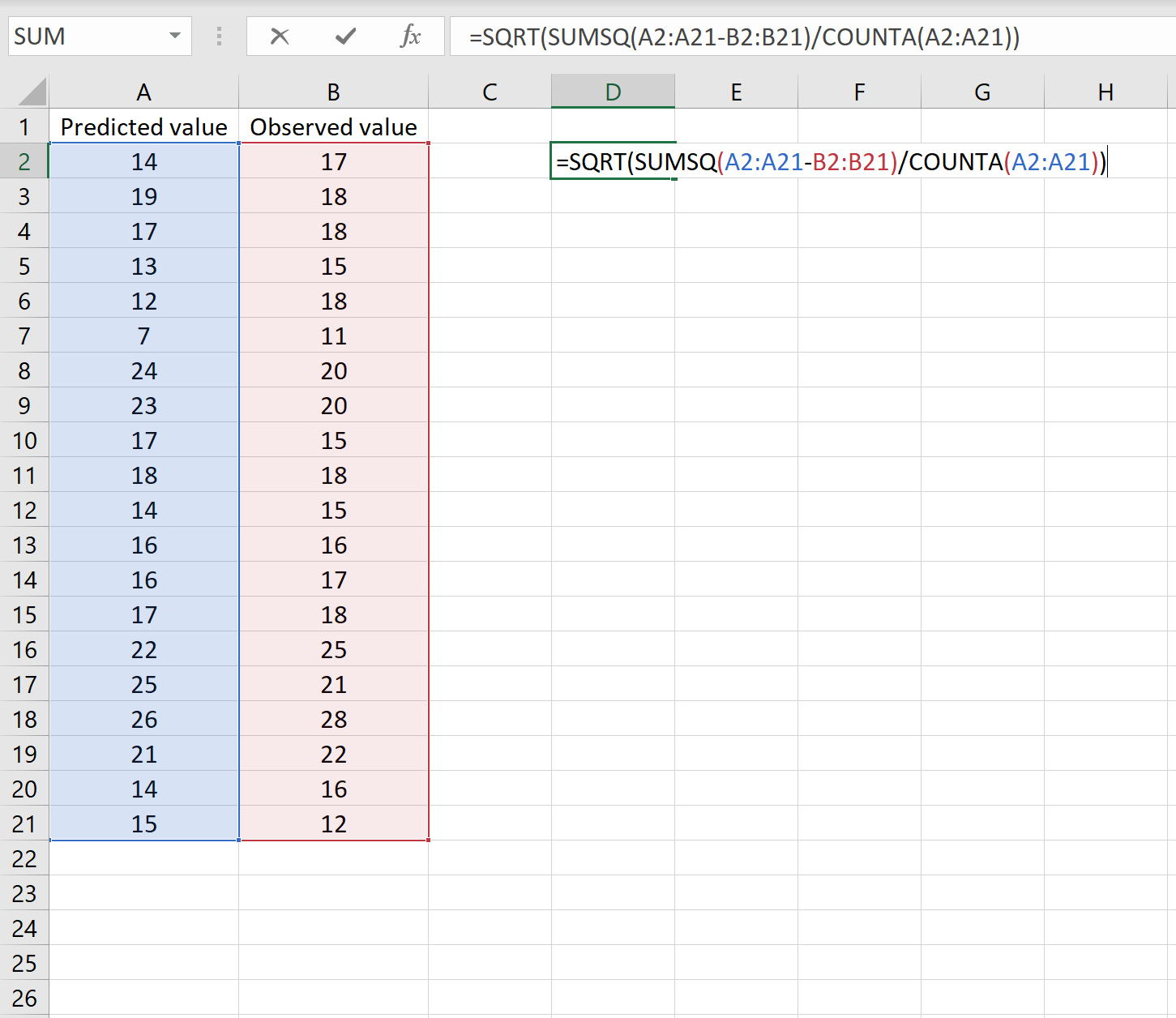
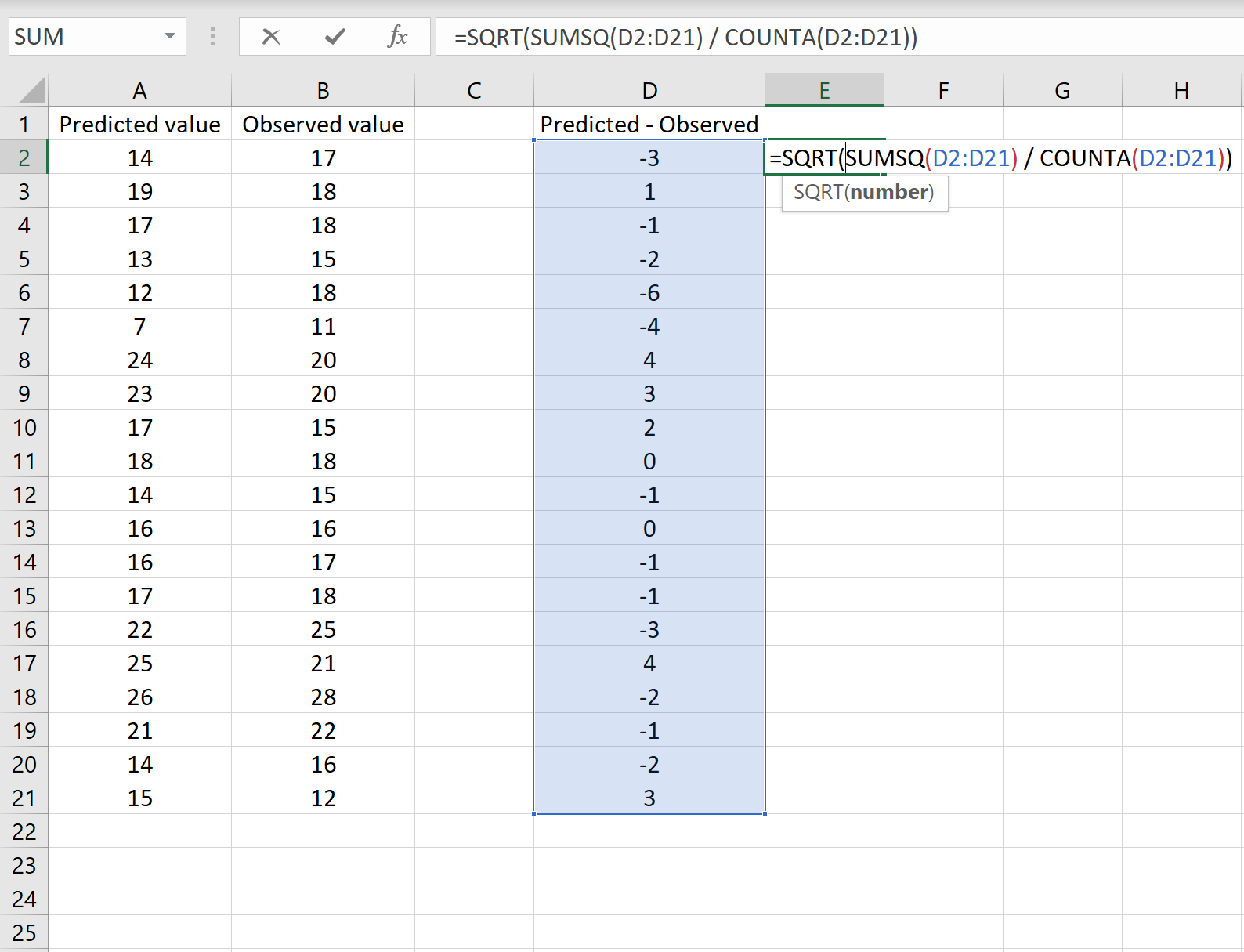
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21))
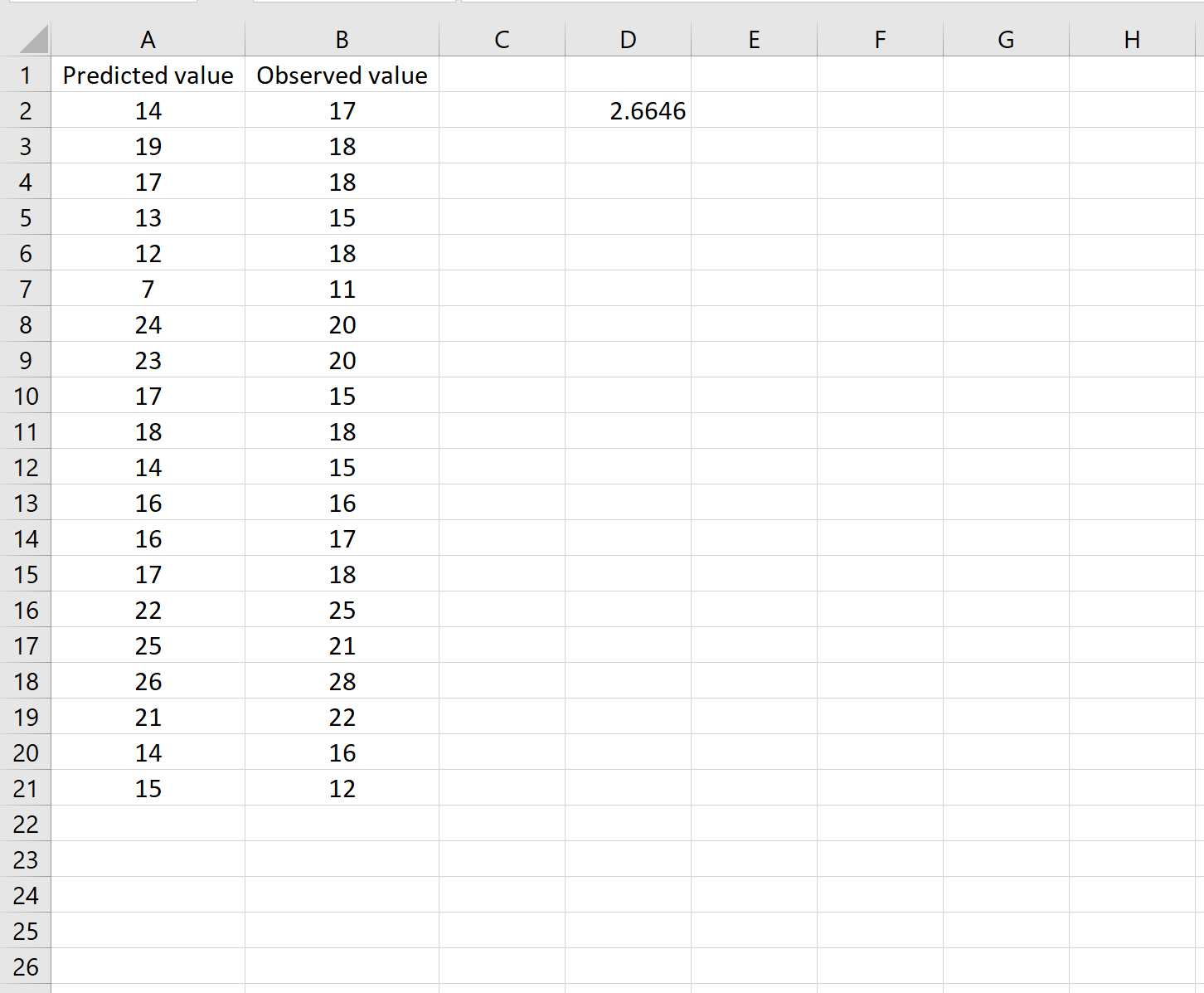
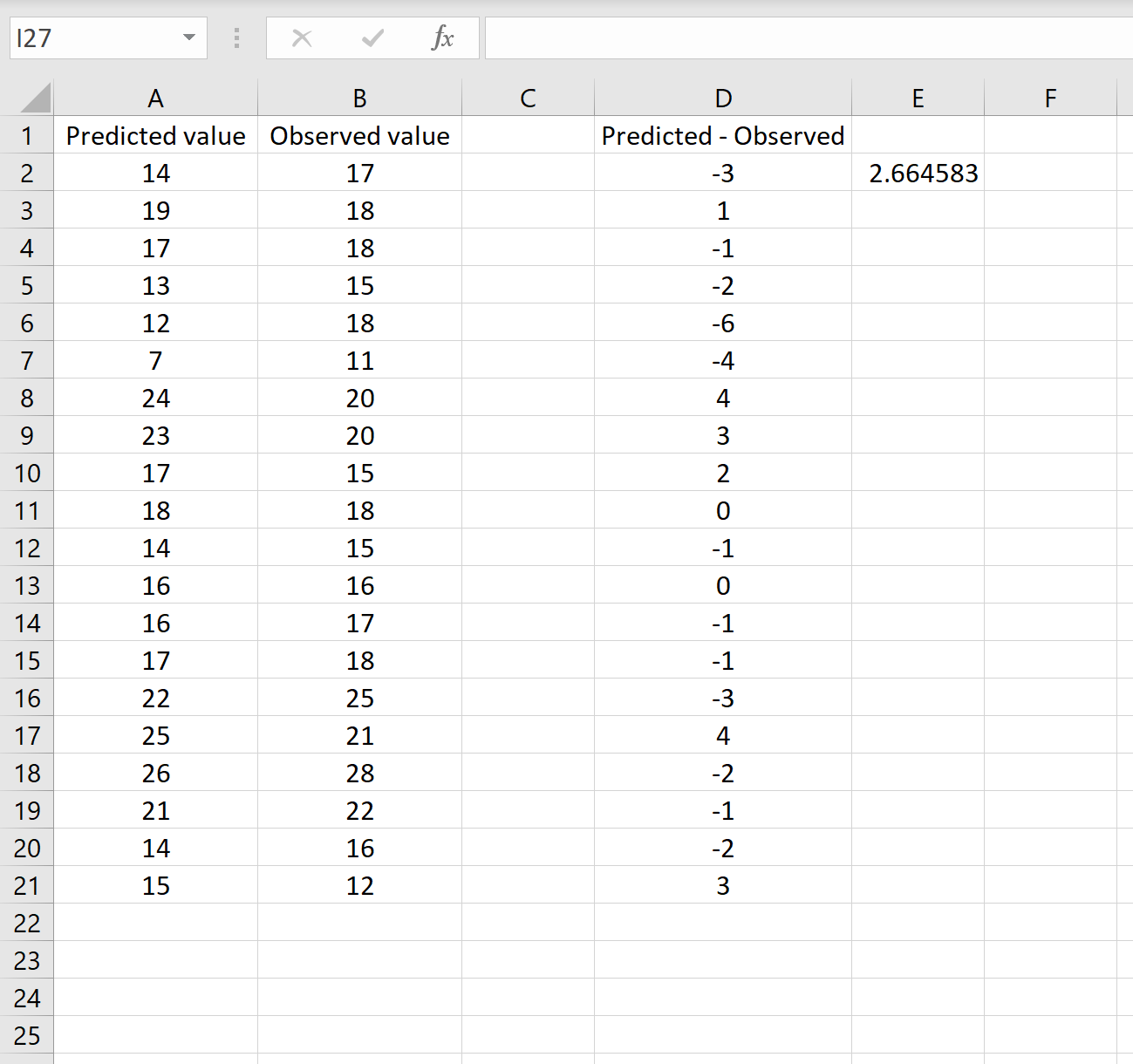
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 .
Формула может показаться немного сложной, но она имеет смысл, если ее разобрать:
= КОРЕНЬ( СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21) )
- Во-первых, мы вычисляем сумму квадратов разностей между прогнозируемыми и наблюдаемыми значениями, используя функцию СУММСК() .
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Сценарий 2
В другом сценарии вы, возможно, уже вычислили разницу между прогнозируемыми и наблюдаемыми значениями. В этом случае у вас будет только один столбец, отображающий различия.
На изображении ниже показан пример этого сценария. Прогнозируемые значения отображаются в столбце A, наблюдаемые значения — в столбце B, а разница между прогнозируемыми и наблюдаемыми значениями — в столбце D:
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(D2:D21) / СЧЕТЧ(D2:D21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 , что соответствует результату, полученному в первом сценарии. Это подтверждает, что эти два подхода к расчету RMSE эквивалентны.
Формула, которую мы использовали в этом сценарии, лишь немного отличается от той, что мы использовали в предыдущем сценарии:
= КОРЕНЬ (СУММСК(D2 :D21) / СЧЕТЧ(D2:D21) )
- Поскольку мы уже рассчитали разницу между предсказанными и наблюдаемыми значениями в столбце D, мы можем вычислить сумму квадратов разностей с помощью функции СУММСК().только со значениями в столбце D.
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Как интерпретировать среднеквадратичную ошибку
Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо регрессионная модель (или любая модель, которая выдает прогнозируемые значения) способна «соответствовать» набору данных.
Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель регрессии хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.
Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашей страницей руководств по Excel , на которой перечислены все учебные пособия Excel по статистике.
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Сморите пример расчета здесь: среднеквадратическое отклонние и дисперсия
Для этого временного ряда i=1, n=10, 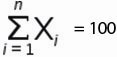
Рассмотрим формулу среднего значения:
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
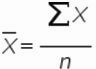
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего 
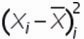

5. 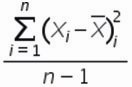
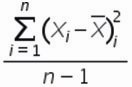
6. Среднеквадратическое отклонение равно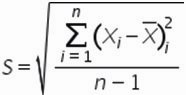
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Скачать файл с примером
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Скачать файл с примером
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.