Excel построить график тригонометрической функции в excel - Word и Excel

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x).

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).

Чтобы создать эту диаграмму, выполните следующие действия.

Выделите диапазон А1:В22.
Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22.
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Источник

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

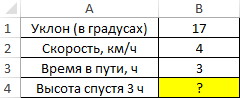
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

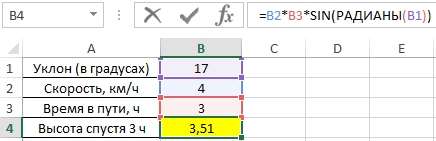
Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Таблица синусов и косинусов в Excel

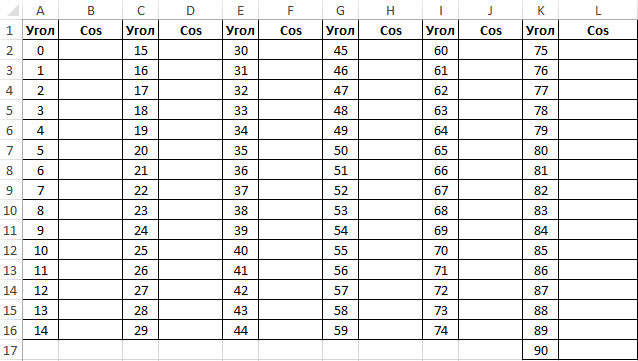
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

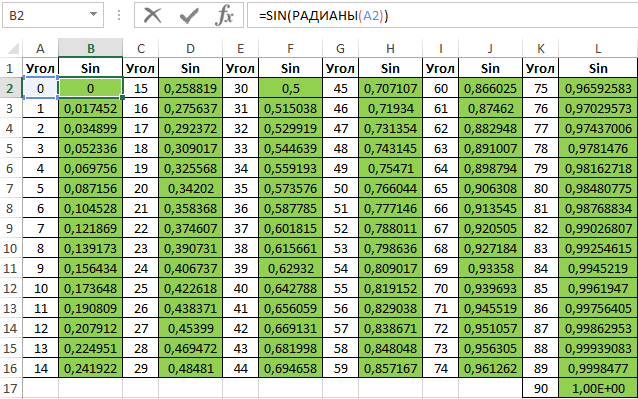
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

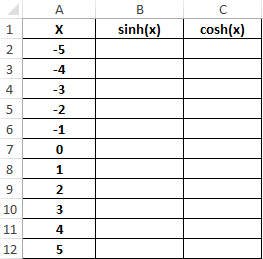
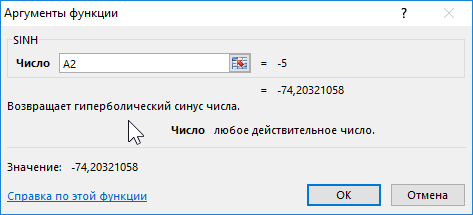
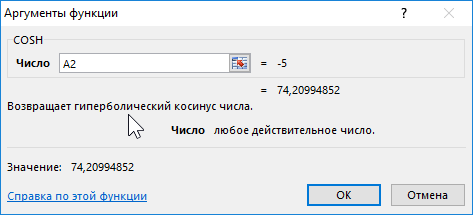
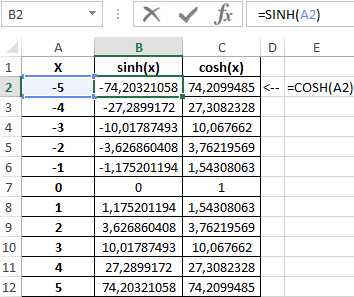
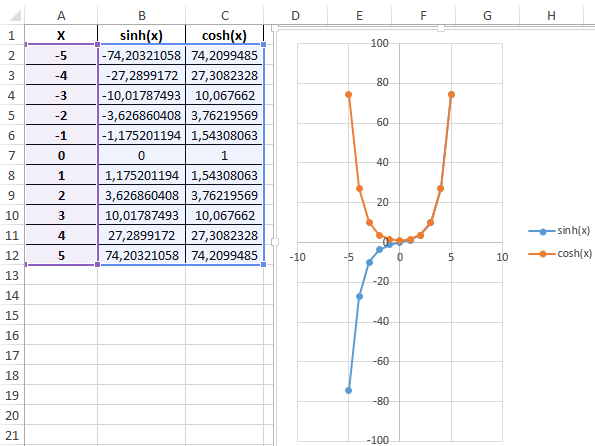
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

Таблица полученных значений:

COSH.

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Скачать примеры тригонометрических функций SIN и COS

Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
Выражение ПИ()*угол_в_градусах/180.

Источник

Содержание

Microsoft Excel
Построение в Excel графиков математических и тригонометрических функций
Построение графиков математических функций с одной переменной
Построение графиков математических функций с двумя переменными
Как построить график функции в Excel
Как в экселе построить график косинуса?
Видео
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
Вариант 2: График функции y=sin(x)

Microsoft Excel

трюки • приёмы • решения

Построение в Excel графиков математических и тригонометрических функций

Построение графиков математических функций с одной переменной

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

Выделите диапазон А1:В22 .
Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22 .
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)

Источник

Как построить график функции в Excel

Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.

Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.

Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.

У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.

Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.

График функции выглядит следующим образом.

Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .

Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .

Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .

Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.

Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .

Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .

В поле «Элементы легенды» кликаем на кнопочку «Добавить» .

Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .

Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .

Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .

Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.

В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .

Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.

Источник

Как в экселе построить график косинуса?

Построить график косинуса в программе эксель несложна задача, которую нужно сделать в несколько этапов, рассмотрим каждый по отдельности:

Первый этап. Построим график косинуса от нуля до ста восьмидесяти градусов, шаг точки возьмем пятнадцать градусов.

Второй этап. Переведем градусы в радианы, для этого воспользуемся функцией «РАДИАНЫ(Х)», где «Х» — это значение в градусах, которое необходимо перевести в радианы. Сначала в ячейке «В2» пишем формулу: =РАДИАНЫ(A2), потом копируем эту формулу на другие ячейки.

Третий этап. Посчитаем значение косинуса для каждого значения, для этого сначала пропишем в ячейке «С2» формулу: =COS(B2). После снова нужно скопировать эту формулу на остальные ячейки. В итоге все готово, чтобы начать строить график косинуса.

Четвертый этап. Выделим область ячеек с «В2» по «С14». На верхней панели настроек, активируем панель «Вставка», в ней отыскиваете блок «Диаграммы» и выбираете «Точечная», после нажатия на данную иконку, отразиться выбор графиков, нужно выбрать в первой строке вторую картинку.

В итоге получаем небольшой участок графика косинуса, дальше можно его строить в обоих направления, используя вышеописанный алгоритм.

Видео

Источник

Варианты построения графика функции в Microsoft Excel

Вариант 1: График функции X^2

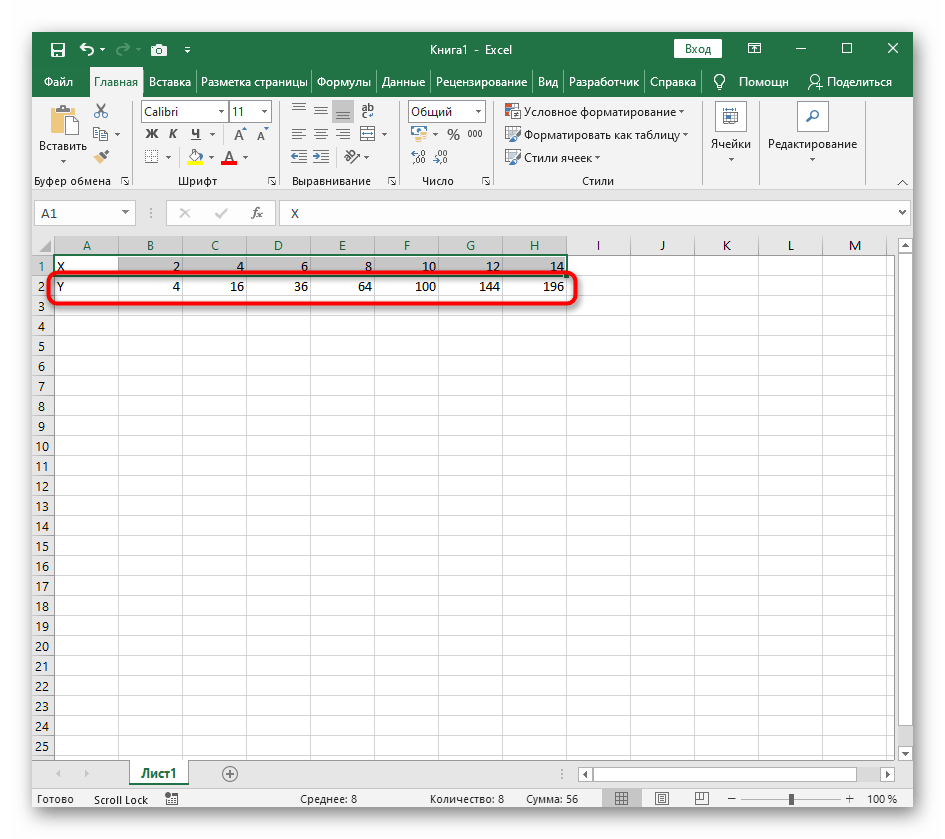
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
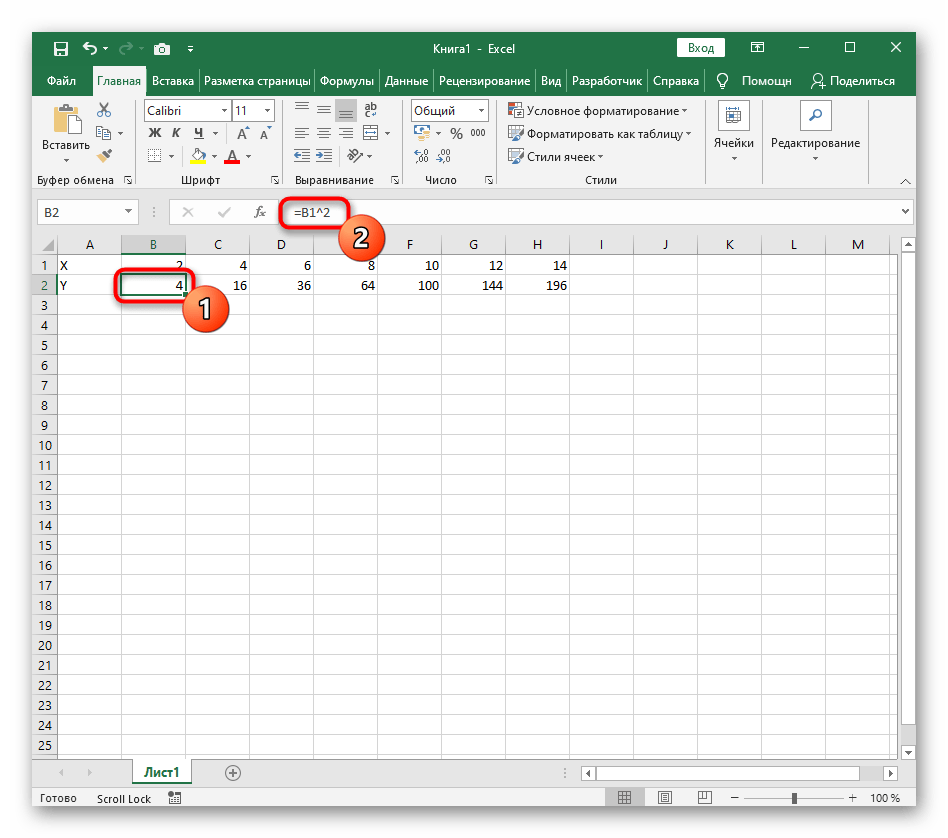
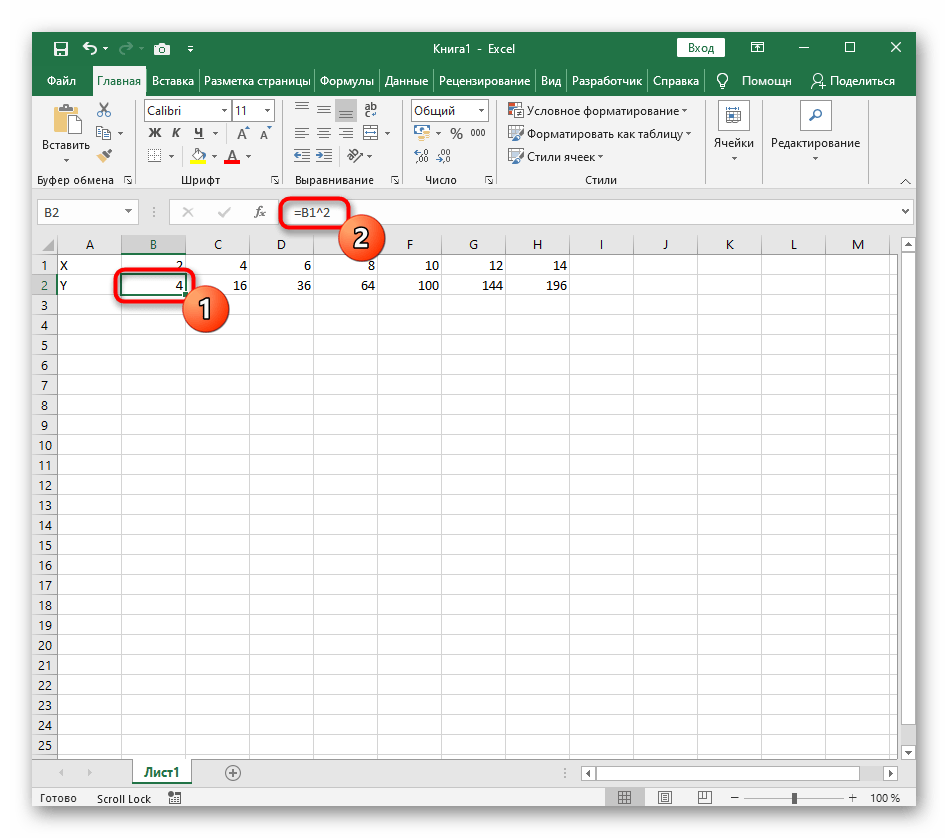
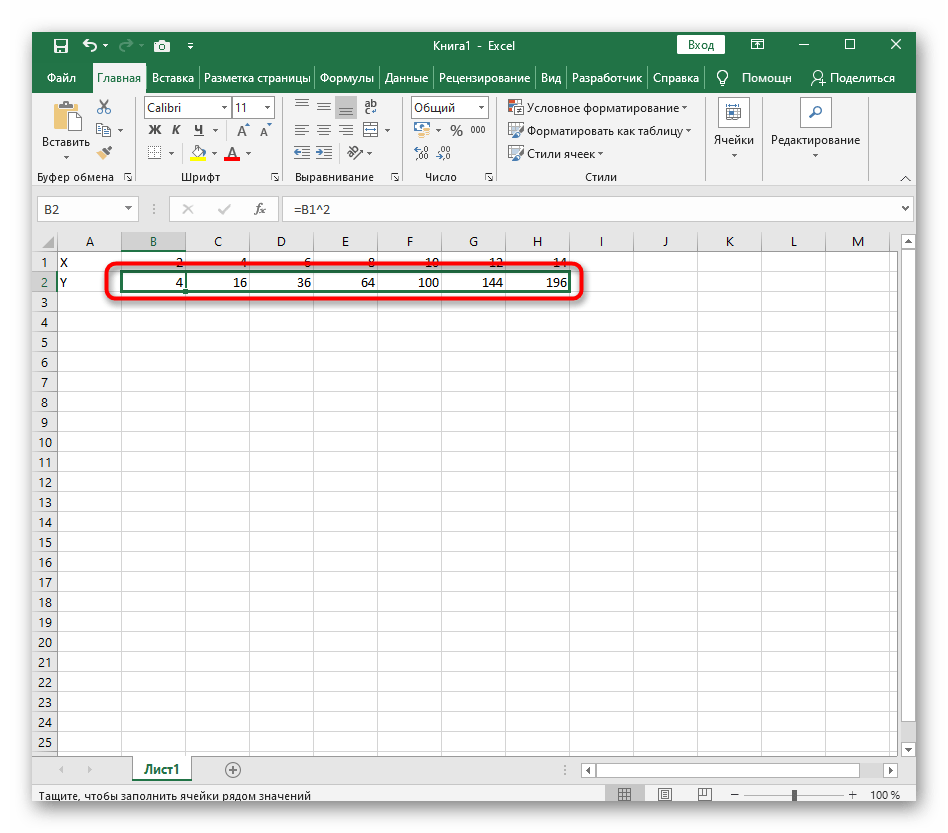
Нажмите по первой ячейке и впишите =B1^2 , что значит автоматическое возведение указанной ячейки в квадрат.

Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

Создайте сразу два столбца — X и Y, куда будете записывать данные.

Запишите самостоятельно первые два или три значения с указанным шагом.

Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.

Сама функция автоматически высчитает синус заданного числа.

Растяните столбец точно так же, как это было показано ранее.

Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

Выделите столбец с Y и перейдите на вкладку «Вставка».

Создайте стандартный график, развернув выпадающее меню.

График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Источник

Тип урока: урок обобщения и
систематизации знаний

Цели:

научить строить графики тригонометрических
функций средствами MS Excel
закрепить навыки работы в электронных таблицах,
углубить представления учащихся о взаимосвязи
предметов и прикладной ориентации курса
информатики.

ХОД УРОКА

Если вычислений много, а времени мало,
то доверьтесь электронным таблицам

1. Сообщение целей и задач урока

– Ребята, сегодня мы продолжим знакомиться с
возможностями электронных таблиц Excel. Давайте
вспомним, для чего предназначены электронные
таблицы? (Автоматизация расчетов).
– Что вы уже умеете делать в электронных
таблицах? (Создавать и форматировать таблицу,
работать с типами данных, решать задачи
используя относительную и абсолютную ссылки,
строить диаграммы).
– На уроках математики вы изучили
тригонометрические функции и их графики. При
построении графиков тригонометрических функций
необходимо учесть множество нюансов. Начертить
синусоиду или косинусоиду красиво – это уже
искусство, а если необходимо график растянуть,
сжать или симметрично отобразить относительно
какой-либо оси – это может вызвать затруднения. И
здесь нам на помощь нам придут электронные
таблицы MS Excel. Вы узнаете как с их помощью быстро и
красиво построить график.
Сегодня на уроке мы познакомимся с алгоритмом
построения графика тригонометрической функции.
Эпиграфом к уроку я взяла слова «Если
вычислений много, а времени мало, то доверьтесь
электронным таблицам»

2. Актуализация знаний

Фронтальный опрос (за правильный ответ даем
красную карточку)

С чего начинается ввод формулы в ячейку? (Со
знака равенства)
На каком языке набирается формула в MS Excel? (Английском)
Как скопировать формулу в другие ячейки?(С
помощью маркера автозаполнения)
Как изменить число десятичных знаков после
запятой в отображаемом числе? (Выделить,
Формат, Ячейки, вкладка Число, Числовой формат,
…..)
Что означает запись ###### в ячейке? (Длина
водимых данных превышает ширину ячейки)
Каким образом набирается формула, содержащая
какую-либо функцию? (Выделить ячейку, в которую
нужно вставить первое значение функции;Вставка,
Функция, выбрать Категорию и саму функцию)
Каким образом набирается формула, содержащая
сложную функцию, например, y = |x²|? (Вставляется
внешняя функция с пустым аргументом, затем левее
строки редактирования формул из раскрывающегося
списка выбирается внутренняя функция)
Как вставить какой-либо символ, например,
математический в ячейку? (Вставка, Символ, в
появившемся диалоговом окне выбрать шрифт Symbol и
нужный символ)

На прошлом уроке вы строили графики
элементарных функций. Давайте повторим алгоритм
построения графика (Учащиеся называют шаги
построения графика функции, а учитель показывает
соответствующий пункт алгоритма на доске
(используется проектор) и если необходимо
дополняет ответ учеников) (см. Приложение
1).

3. Изучение нового

С использованием презентации (см. Приложение
2) учитель рассказывает, как строится
график тригонометрической функций, а затем
выполняет его построение в электронных таблицах.

Задание. Построить в MS Excel графики
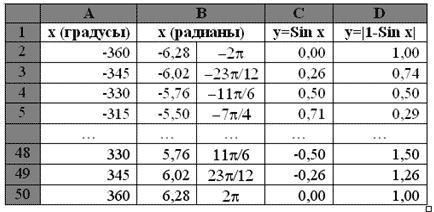
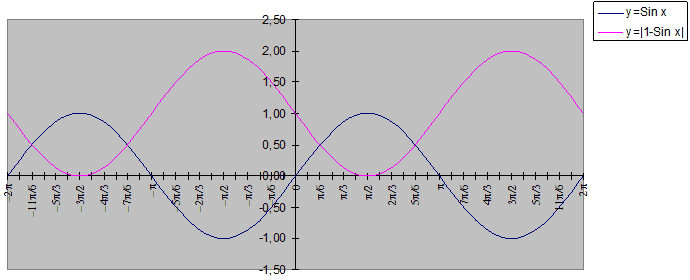
функций y = Sin x и y = |1 – sin x| на
промежутке [–360^о; 360^о] с шагом 15^о.

Построенные графики смотри в Приложении
3

4. Закрепление полученных знаний

Каждому ученику даётся карточка с заданием и
оценочный лист, который после выполнения задания
отдается учителю (Каждый пункт в оценочном
листе является шагом построения графика
тригонометрической функции с использованием
MSExcel). Презентация находится в
сетевой папке, и любой ученик может ею
воспользоваться при выполнении своего задания.

Задание. Построить в MS Excel графики
функций на промежутке [–36^о;36^о] с
шагом 15^о.

5. Проверка построенных графиков и разбор
нюансов

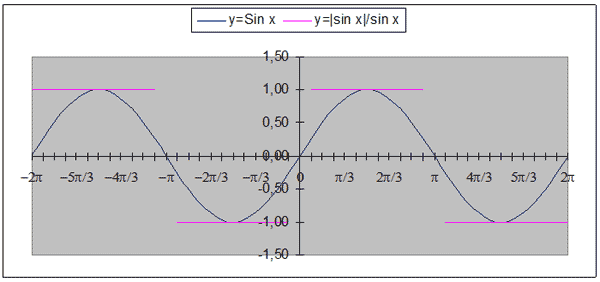
Один из учеников строил график y = |Sin x|
/ Sin x на промежутке [–360^о;360^о] с
шагом 15^о. На доске демонстрируется этот
график и график, построенный традиционным
алгебраическим способом.

С помощью этого примера обращается внимание
учащихся, что существуют функции, графики
которых в электронных таблицах строятся неточно.
Учащихся можно попросить найти неточности в
графике, построенном с помощью MS Excel и попросить
объяснить их.

График, построенный традиционным
алгебраическим

График, построенный с использованием МS
Exel

6. Подведение итогов

Учеников просят ответить на вопросы:

В чем достоинства и недостатки алгебраического
метода построения графиков функций и построения
графиков с использованием электронных таблиц?
Каким образом можно использовать полученные на
уроке знания в учебе?

Вывод. MS Excel облегчает построение
графиков функций, но без глубоких математических
знаний построить точные графики сложных функций
(тригонометрических функций, функций с модулем,
функций имеющих точки разрыва) невозможно.

Математика – это царица всех наук!

7. Постановка Д/З.

Построить график функции y= 1 + 0,5*ctg(X–П/4) на
промежутке [–360^о;360^о] с шагом 15^о.

8. Рефлексия

Оцени свое настроение на уроке

Оценочный лист

Фамилия, имя	Количество баллов
Создание заголовка таблицы	0,2
Заполнение ряда значений аргумента х в градусах	0,1
Заполнение ряда значений аргумента х в радианах (перевод градусов в радианы)	0,5
Запись формулы для вычисления значений сложной функции	1
Запись формулы для вычисления значений элементарной функции	0,5
Заполнение рядов значений функций (для обеих функций)	0,1
Установка числового формата данных	0,2
Построение графиков функций	1
Перенос оси	0,2
Подпись значений х на оси абсцисс (в градусах)	*0,2*
Создание ряда значений аргумента х (в радианах, например П/3)	0,7
Подпись значений х на оси абсцисс (в радианах, например П/3)	0,5
ИТОГО	5
Если вы обращаетесь к учителю, то ставится 0 баллов

Источник

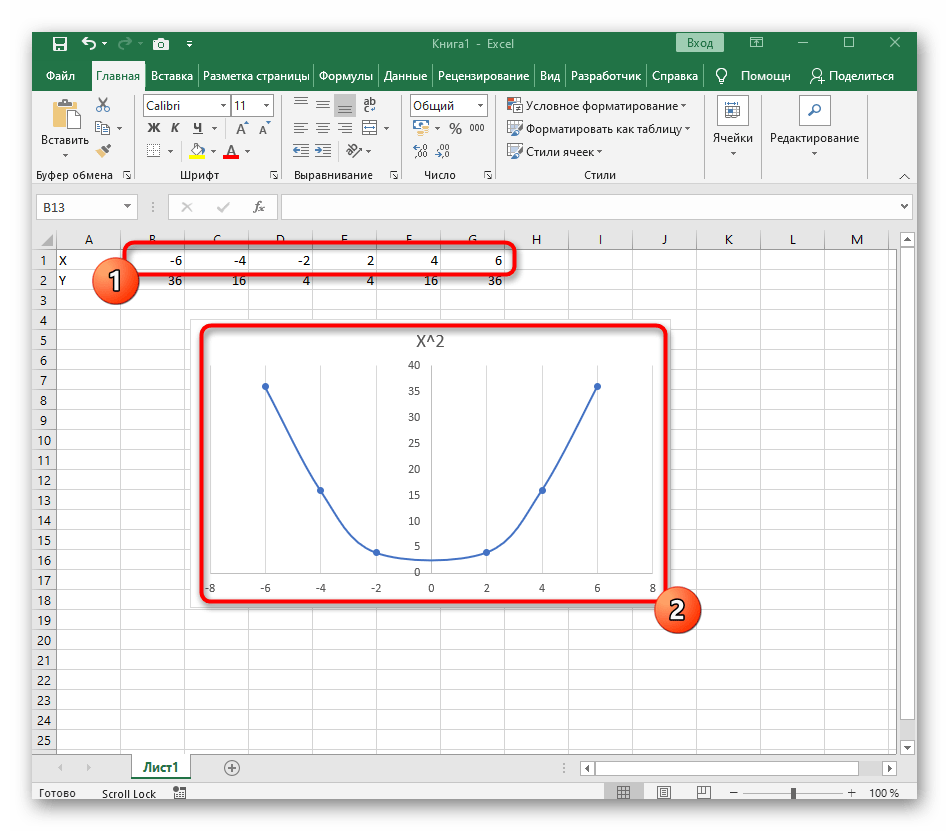
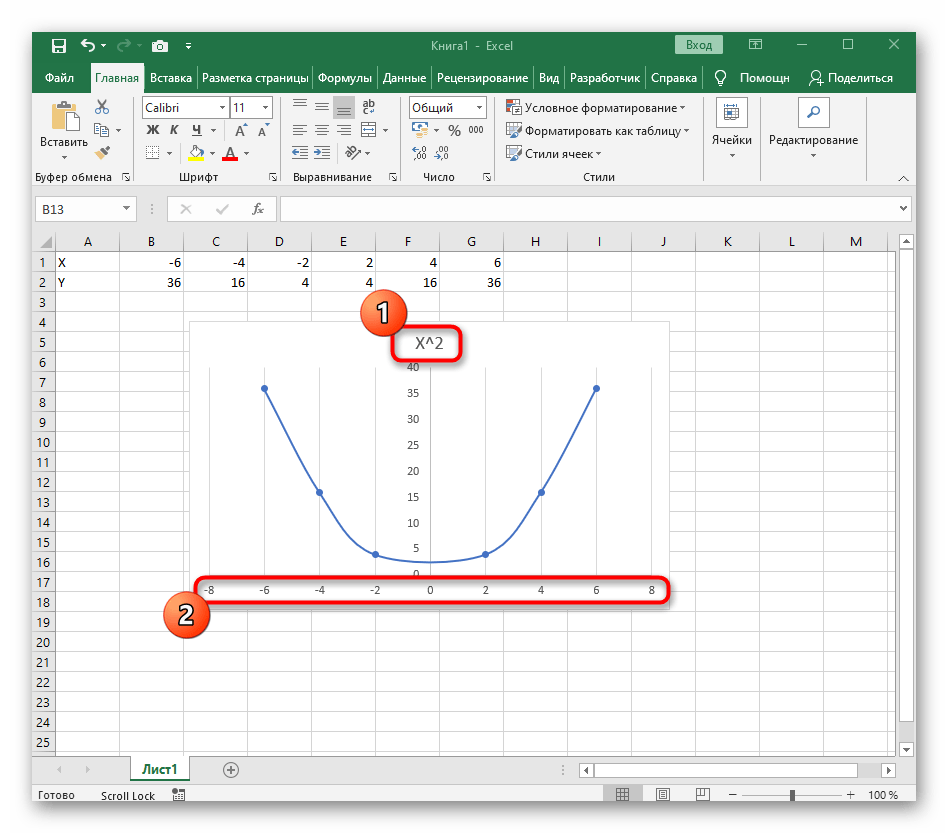
Вариант 1: График функции X^2

Создайте строку X, где укажите необходимый диапазон чисел для графика функции.

Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.

Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.

Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.

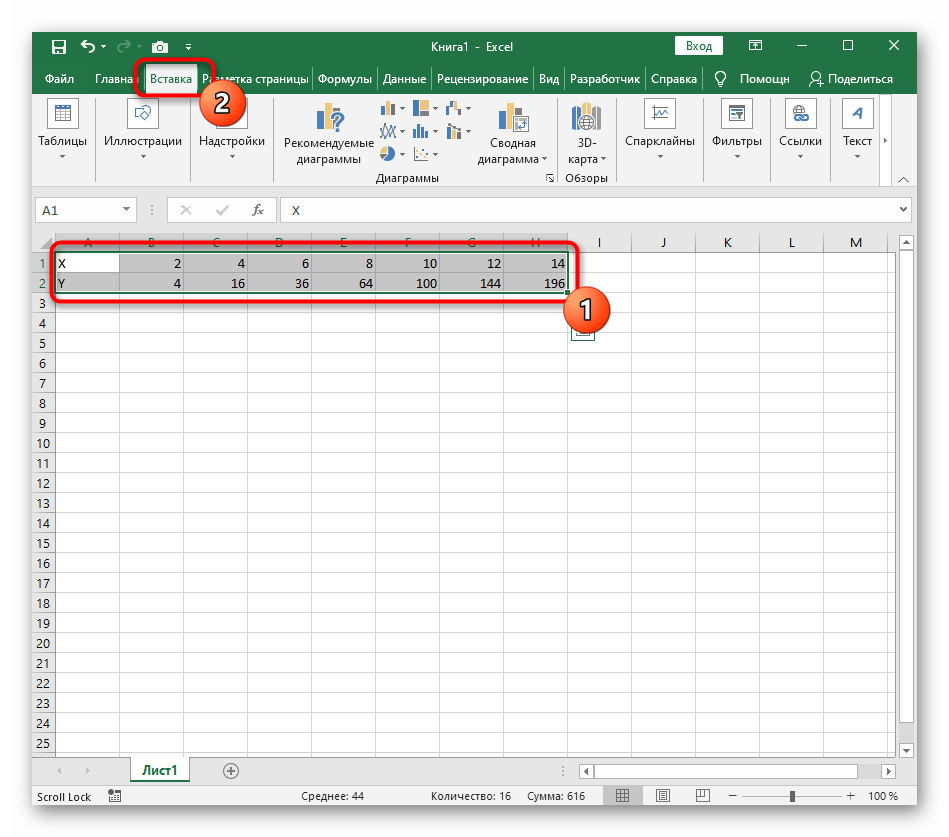
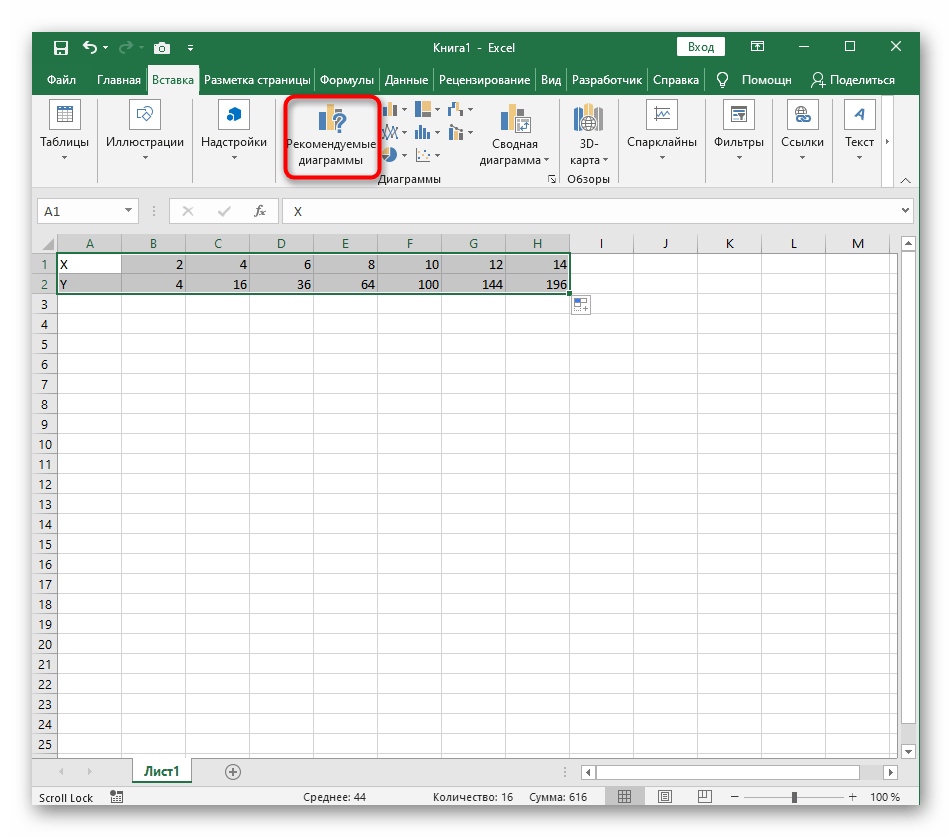
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».

На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».

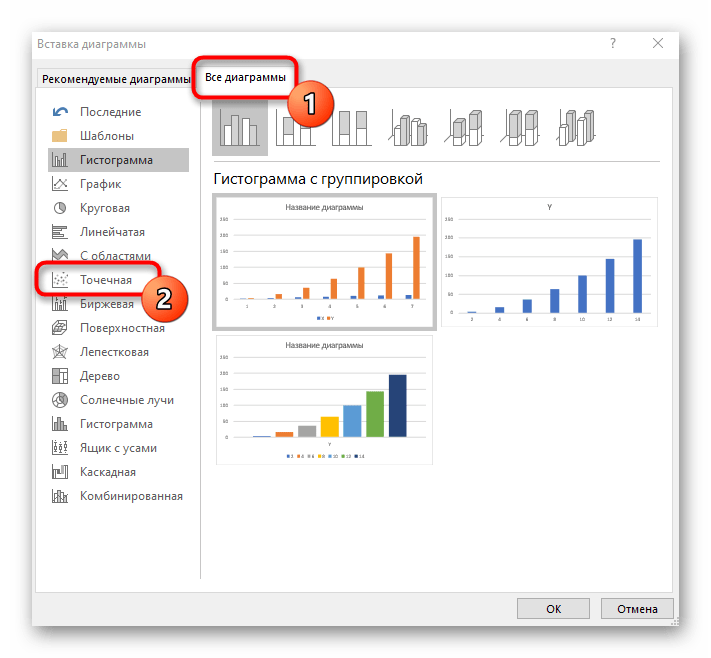
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».

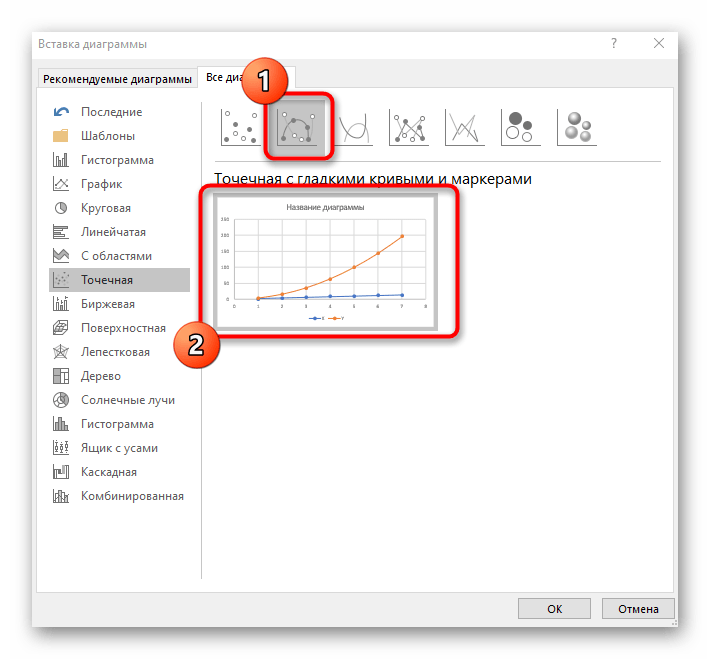
Подойдет вариант «Точечная с гладкими кривыми и маркерами».

После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.

Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.

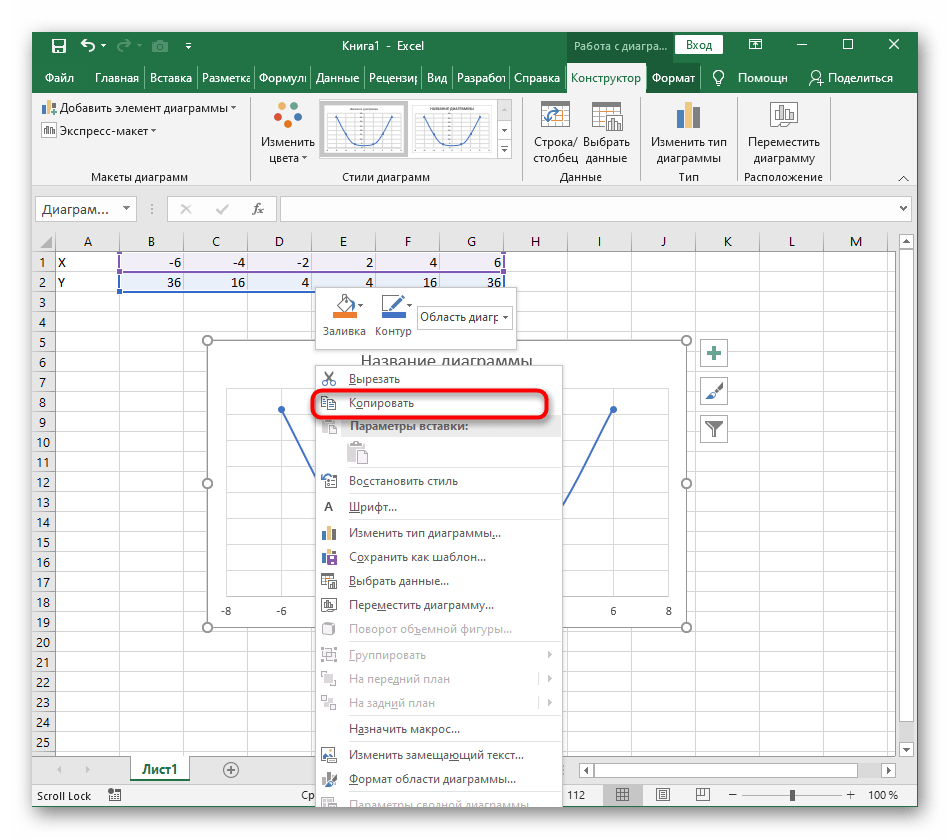
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».

Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

Вариант 2: График функции y=sin(x)

Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

Создайте сразу два столбца — X и Y, куда будете записывать данные.

Запишите самостоятельно первые два или три значения с указанным шагом.

Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.

Сама функция автоматически высчитает синус заданного числа.

Растяните столбец точно так же, как это было показано ранее.

Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

Выделите столбец с Y и перейдите на вкладку «Вставка».

Создайте стандартный график, развернув выпадающее меню.

График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Содержание статьи (кликните для открытия/закрытия)

Построение графика линейной функции в Excel
Подготовка расчетной таблицы
Построение графика функции
Построение графиков других функций
Квадратичная функция y=ax2+bx+c
Кубическая парабола y=ax3
Гипербола y=k/x
Построение тригонометрических функций sin(x) и cos(x)

Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле

Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].

Подготовка расчетной таблицы

В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.

Установка шага значений аргумента функции

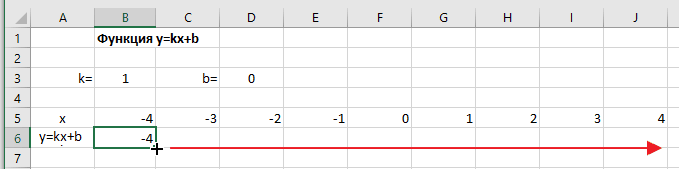
Далее строим таблицу значений линейной функции:

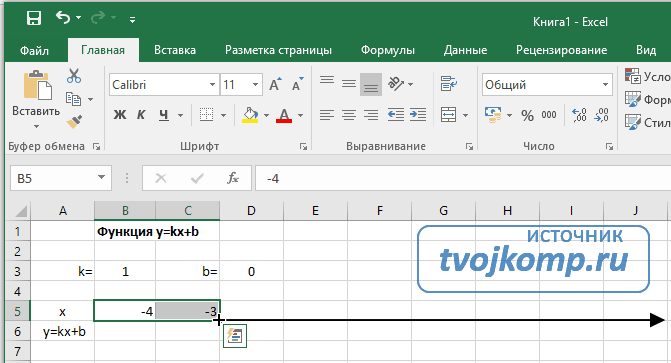
В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
Выделяем эти ячейки.
Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.

Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Автозаполнение значений аргумента функции

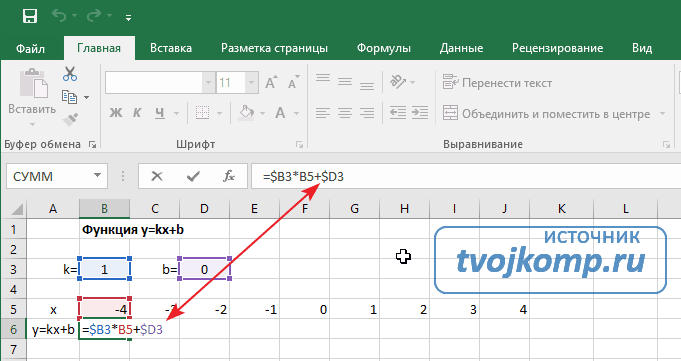
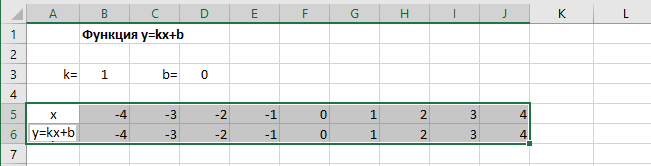
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3

Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.

Запись расчётной формулы для значений функции

Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.

Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.

Копирование формулы

Построение графика функции

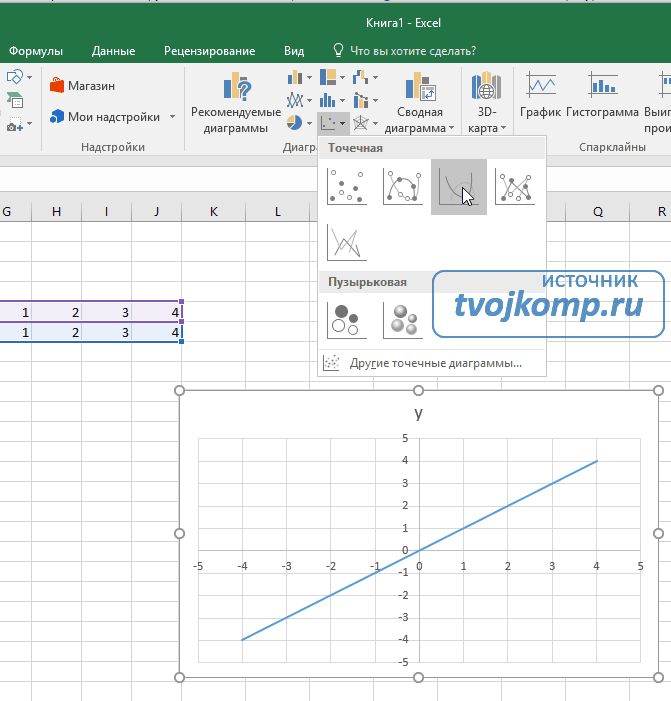
Выделяем прямоугольный диапазон ячеек A5:J6.

Выделение таблицы функции

Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.

Построение диаграммы типа «График»

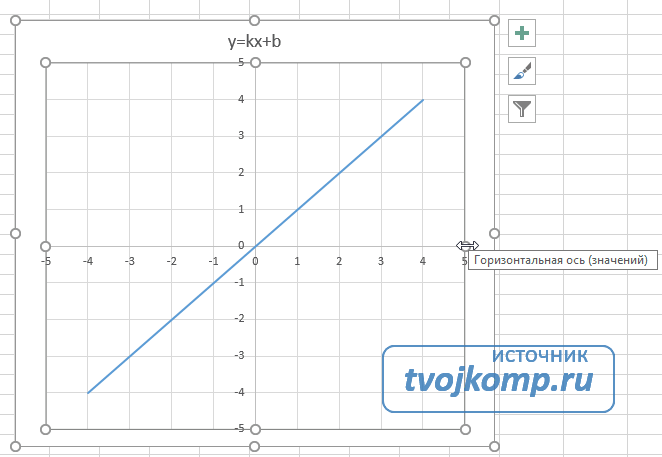
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.

График линейной функции

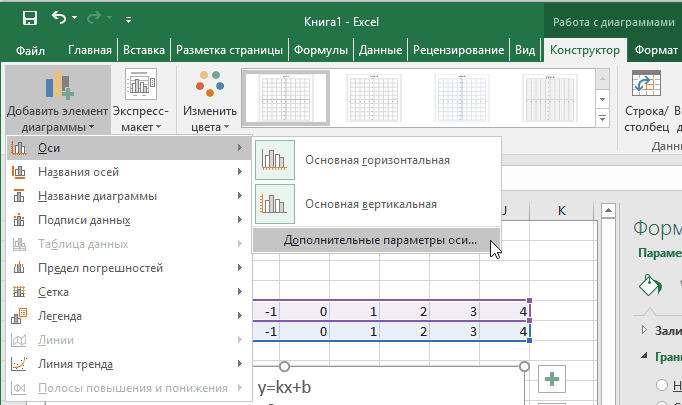
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..

Вход в режим изменения параметров координатных осей

В правой части окна появиться боковая панель настроек Формат оси.

Редактирование параметров координатной оси

Кликните на раскрывающийся список Параметры оси.
Выберите Вертикальная ось (значений).
Кликните зеленый значок диаграммы.
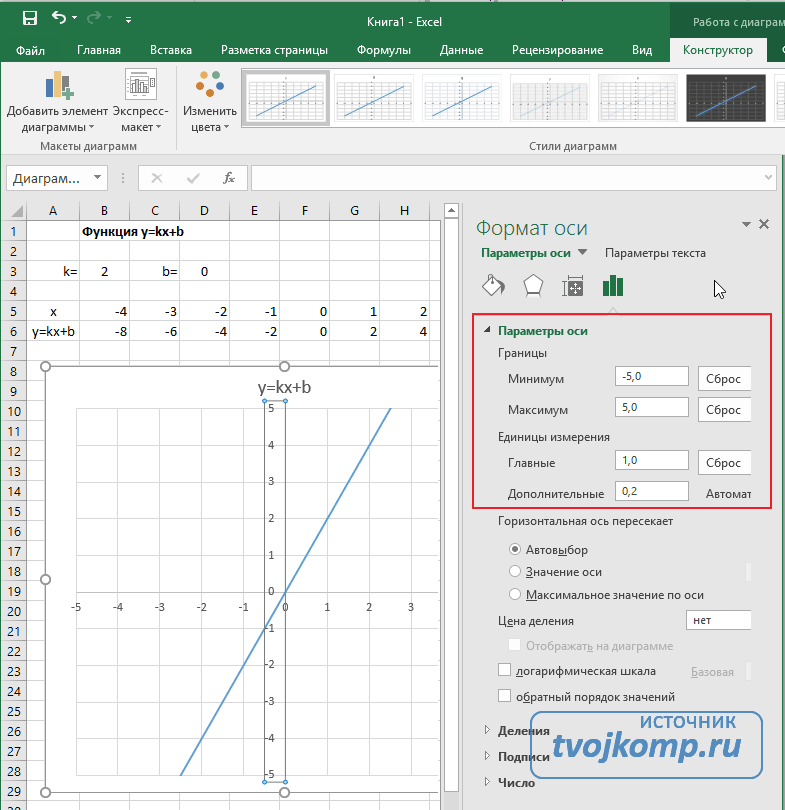
Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
Повторите тоже для горизонтальной оси.

Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.

Построение графиков других функций

Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.

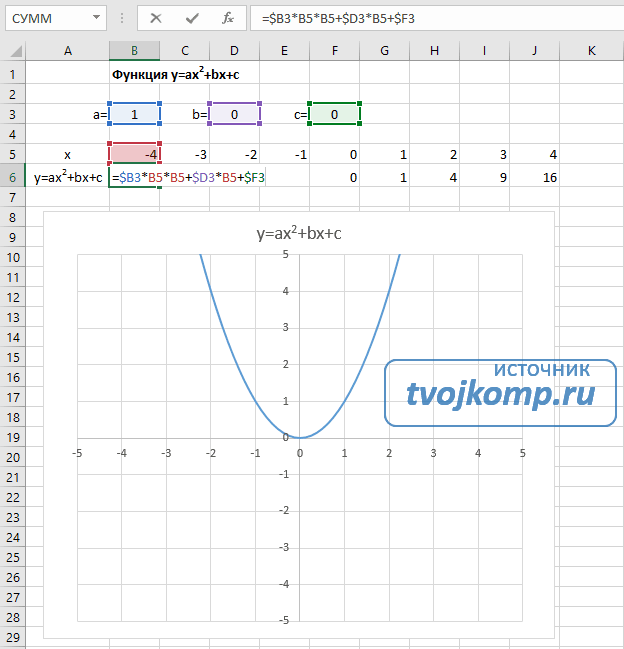
Квадратичная функция y=ax²+bx+c

Выполните следующие действия:

В первой строке меняем заголовок
В третьей строке указываем коэффициенты и их значения
В ячейку A6 записываем обозначение функции
В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График квадратичной функции

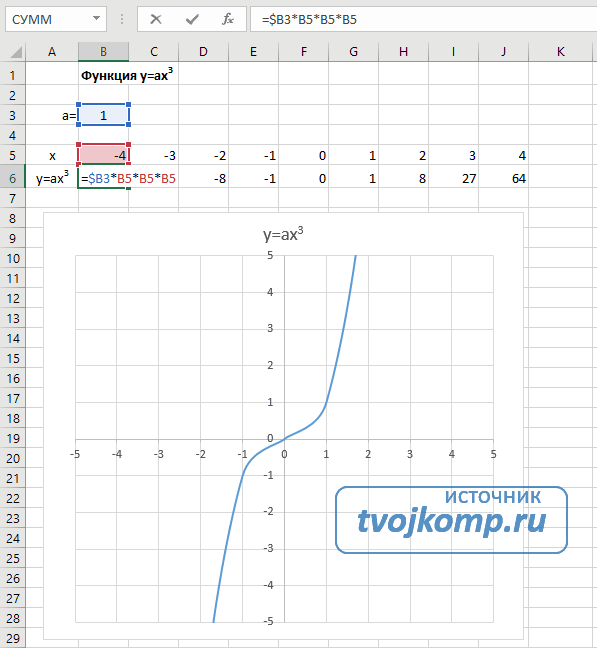
Кубическая парабола y=ax³

Для построения выполните следующие действия:

В первой строке меняем заголовок
В третьей строке указываем коэффициенты и их значения
В ячейку A6 записываем обозначение функции
В ячейку B6 вписываем формулу =$B3*B5*B5*B5
Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График кубической параболы

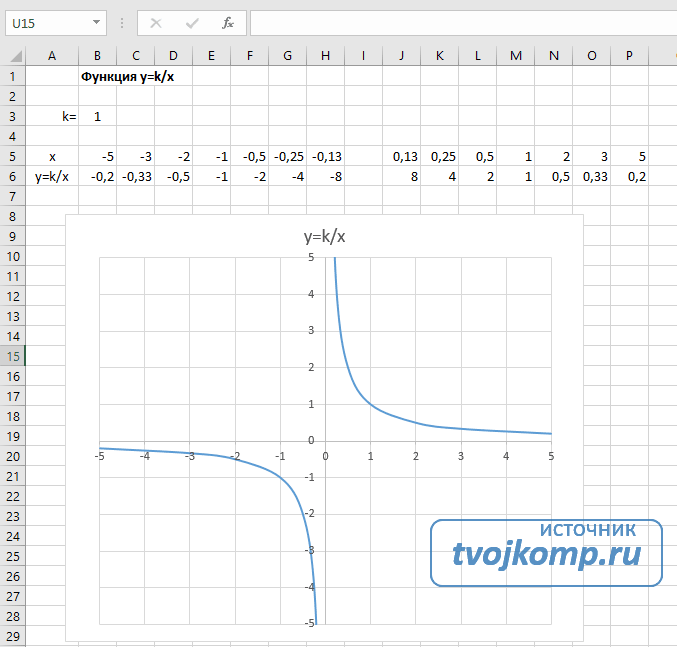
Гипербола y=k/x

Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.

Далее выполните действия:

В первой строке меняем заголовок.
В третьей строке указываем коэффициенты и их значения.
В ячейку A6 записываем обозначение функции.
В ячейку B6 вписываем формулу =$B3/B5
Копируем её на весь диапазон значений аргумента вправо.
Удаляем формулу из ячейки I6.

Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.

Кликните диаграмму
На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
Откроется окно мастера ввода данных
Выделите мышкой прямоугольный диапазон ячеек A5:P6
Нажмите ОК в окне мастера.

Получаем результат

График гиперболы

Построение тригонометрических функций sin(x) и cos(x)

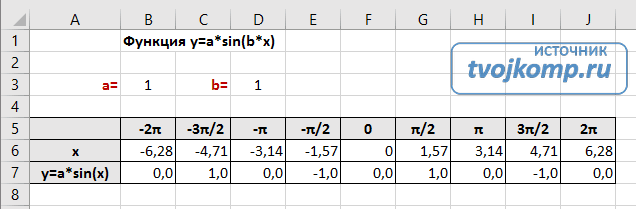
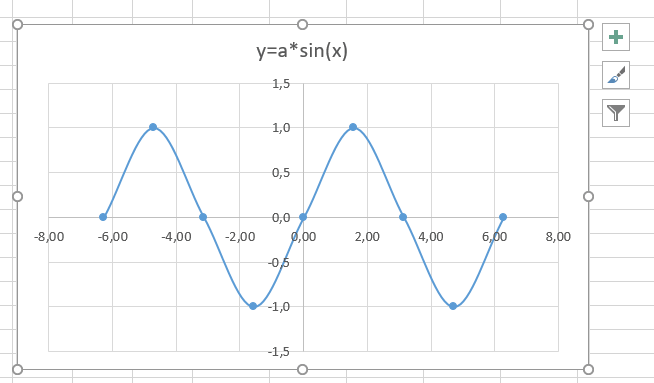
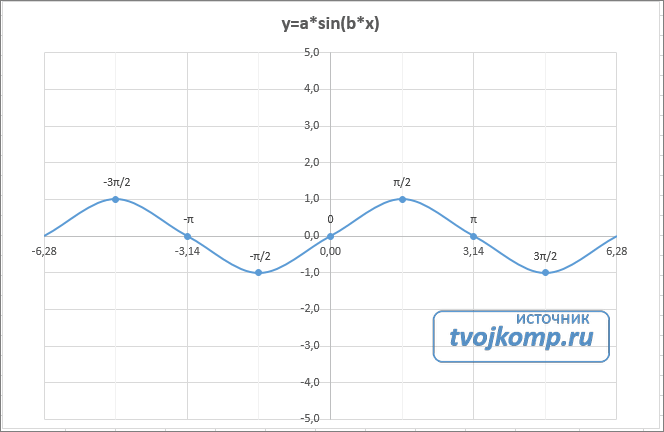
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже

Таблица значений функции sin(x)

В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
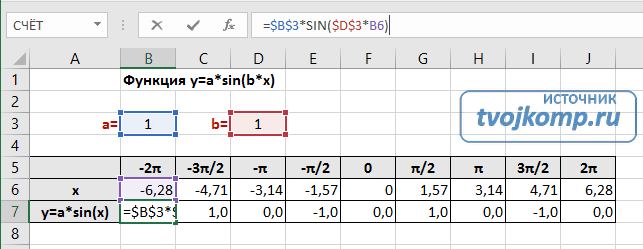
В седьмой строке записываются расчетные формулы тригонометрической функции.

Запись расчетной формулы функции sin(x) в Excel

В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.

Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.

Построение диаграммы Точечная с гладкими кривыми

В итоге получим диаграмму.

График sin(x) после вставки диаграммы

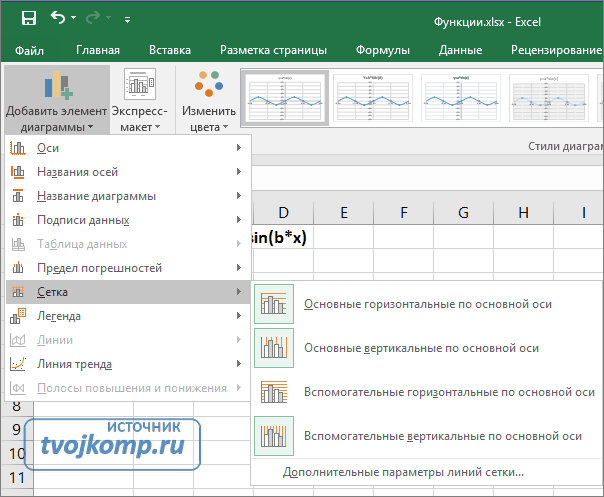
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.

Настройка сетки при построении графика

Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.

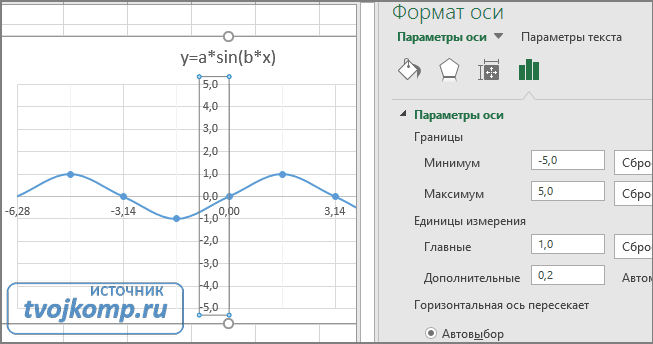
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.

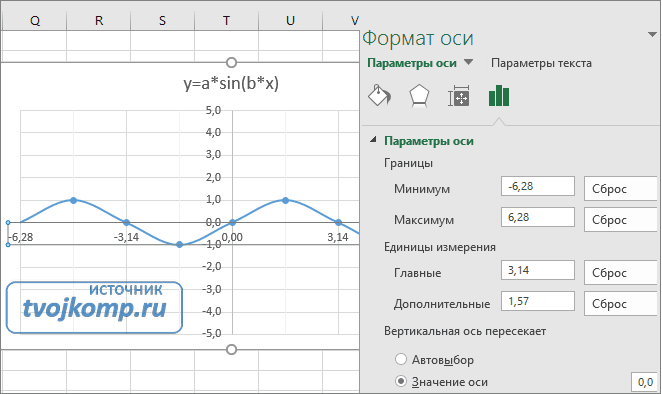
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.

Настройка формата горизонтальной оси Х графика функции

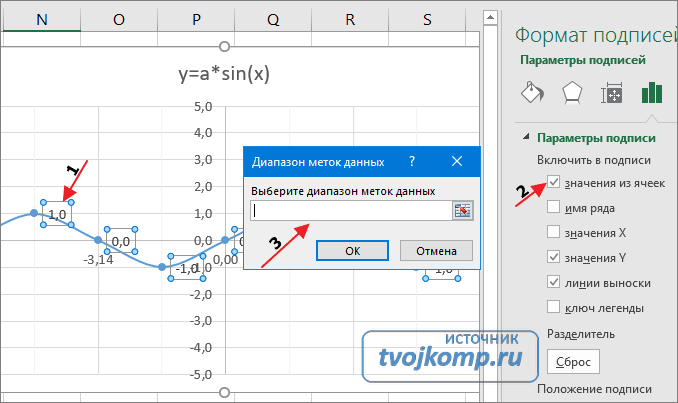
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.

Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.

Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).

Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.

Дополнительные статьи по теме:

Знакомство с таблицами в Excel
Изменение строк и столбцов в Excel
Работа с ячейками: объединение, изменение, защита…
Ошибки в формулах: почему excel не считает
Использования условий в формулах Excel
Функция CЧЕТЕСЛИМН
Работа с текстовыми функциями Excel
Все уроки по Microsoft Excel

Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.

ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

Источник

1

Построение графиков тригонометрических функций в программе Excel Катенина Валентина Геннадьевна МОУ Дмитровская СОШ 10 Учитель информатики

2

Цели урока: 3. Развивать познавательный интерес на уроках информатики при изучении тригонометрических функций. 2. Закрепить навыки работы в электронных таблицах. 1. Научить строить графики тригонометрических функций средствами Excel.

3

Задания Задания 1. Построить график функции y=Sin x для всех значений х в интервале [-360; 360] с шагом 10°. 2. Построить график функции y=Sin|x| для всех значений х в интервале [-360; 360] с шагом 10°.

4

Порядок выполнения работы 1. Создание таблицы значений функций y=Sin x и y=Sin|x|. 2. Построение графика y=Sin x. 3. Построение графика y=Sin|x|.

5

Вводим в ячейки столбца «А» (А2 : А74) значения аргумента x в интервале [-360; 360] через 10°. Используем маркер автозаполнения Создаем заголовок таблицы 1. Создание таблицы значений функций y=Sin x и y=Sin|x|

6

В ячейку В2 вводим формулу перевода градусов в радианы, используя функцию РАДИАНЫ. Для этого: В ячейку В2 вводим формулу перевода градусов в радианы, используя функцию РАДИАНЫ. Для этого: Устанавливаем курсор в ячейку В2 Вставить функцию Мастер функций Категория Математические РАДИАНЫ Вставить функцию

7

В ячейке B2 появляется значение x в радианах. Значение угла берем из ячейки A2.

8

Вычисление значений |x| Устанавливаем курсор в то место, где должна быть написана функция ABS. Для этого: Устанавливаем курсор в ячейку C2 Вставить функцию Мастер функций Категория Математические ABS Значение x берем из ячейки B2

9

В ячейке C2 вычисляется значение | x | в радианах. Используя маркер автозаполнения, заполняем ряды значений x (радианы) (B2 : B74) и |x| (C2 : C74). Используя маркер автозаполнения, заполняем ряды значений x (радианы) (B2 : B74) и |x| (C2 : C74).

10

Вычисление значений функции y=Sin x В ячейку D2 вводим формулу для нахождения значений функции y=Sin x. Для этого: Устанавливаем курсор в ячейку D2 Вставить функцию Мастер функций Категория Математические SIN

11

В ячейке D2 появляется значение функции y=SIN(B2). Значение угла берем из ячейки B2.

12

Вычисление значений функции у=Sin|x| В ячейку E2 введите формулу для нахождения значений функции y=Sin |x|. Для этого: Устанавливаем курсор в ячейку E2 Вставить функцию Мастер функций Категория Математические SIN Значение |x| берем из ячейки С2

13

Используя маркер автозаполнения, заполняем ряды значений функций y=Sin x (D2 : D74) и y= Sin|x|(E2 : E74). В ячейке E2 появляется значение функции y=SIN(C2).

14

Для ячеек столбцов B (B2 : B74), C (C2 : C74), D (D2 : D74), E (E2 : E74) устанавливаем числовой формат с двумя десятичными знаками после запятой. Для ячеек столбцов B (B2 : B74), C (C2 : C74), D (D2 : D74), E (E2 : E74) устанавливаем числовой формат с двумя десятичными знаками после запятой.

15

Выделяем ячейки столбца D (D2 : D74), в которых записаны значения функции y=Sin x Вставка График 2. Построение графика функции y=Sin x Появляется график функции y=Sin x

16

График функции y=Sin x Заполняем Элементы легенды (ряды), имя ряда — название функции. Для этого: Щелкните диаграмму. Появится окно Работа с диаграммами Конструктор Выбрать данные Изменить y Sin x

17

Изменить Работа с диаграммами Конструктор Выбрать данные

18

Вносим имя ряда y Sin x

19

Параметры оси Y Щелчок правой кнопкой мыши на цифрах по оси Y Формат оси

20

Перенос оси Y в начало координат Щелчок правой кнопкой мыши на цифрах по оси X Формат оси Параметры оси устанавливаем в категории с номером: 37

21

Появляется требуемый график y=Sin x

22

3. Построение графика функции y=Sin|x| Выделяем ячейки столбца E (E1 : E74) Вставка График Появляется график функции y=Sin|x|

23

Переносим ось Y в начало координат: Щелчок правой кнопкой мыши на цифрах по оси X Формат оси Параметры оси в категории с номером: 37 Появляется требуемый график y=Sin|x|

24

Источники 1. Алгебра и начало математического анализа классы: учеб. для общеобразоват. учреждений; базовый уровень/[П.А. Алимов, Ю.М. Калягин, М. В.Ткачева и др.]-М.Просвещение, Microsoft Excel 2010 / Никита Культин, Лариса Цой. Санкт-Петербург: БХВ-Петербург, Microsoft Excel 2010.

Источник

Интегрированный урок (информатика – математика).

Тема: Графические возможности MS Excel при изучении темы «Построение графиков тригонометрических функций».

Тема урока: Построение графиков тригонометрических функций в электронных таблицах Excel.

Цели урока: освоение технологии построения и редактирования различных видов графиков.

Задачи урока:

Обучающая: обобщение и систематизация знаний, умений и навыков, полученных учащимися при изучении графических возможностей MS Excel.

Развивающие: развитие у учащихся способности анализировать и выделять главное, самостоятельности в приобретении знаний, формирование умения видеть в конкретных практических действиях обобщенные знания и умения.

Воспитательная: воспитание информационной культуры, уверенности в себе.

Используемые на уроке методы, педагогические приёмы: моделирование, проблемный метод, фронтальная работа.

Тип урока: комбинированный – объяснение нового материала и закрепление полученных знаний, умений и навыков.

Вид урока: сдвоенный, продолжительность 1 час 20 минут.

Оборудование урока: Компьютеры с ОС MS Windows; Приложение MS Windows – MS Excel; Карточки-задания для самостоятельной работы.

Ход урока.

Рассматривается необходимость графического представления числовых данных. Вводятся понятие диаграммы и ее объектов: области диаграммы, области построения диаграммы, рядов данных, осей, категорий, легенды, заголовка.

Некоторые типы диаграмм и технология построения диаграмм поясняются в ходе демонстрации интерактивного урока через видеопроектор.

Кратко объясняются возможности редактирования диаграммы и ее объектов.

При выполнении заданий компьютерного практикума учащиеся осваивают технологию построения и редактирования различных видов диаграмм.

Диаграмма – это визуальное представление числовых данных. Представление числовых данных в форме наглядных диаграмм делает эти данные более понятными и доступными.

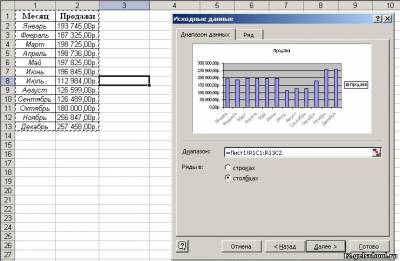
Построим простую гистограмму (один из видов диаграммы), на которой изображены продажи компании по месяцам.

Заполним таблицу исходных данных (по столбцам).

Выделим данные столбцы, как диапазон ячеек для диаграммы.

Вызовем Мастера диаграмм. Это можно сделать, нажав соответствующую кнопку на Панели инструментов Стандартная, или выбрав в меню Вставка пункт Диаграмма…

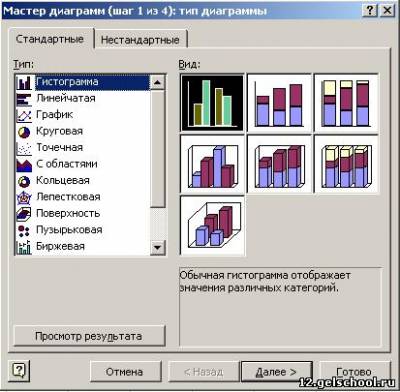
На экране появится диалоговое окно Мастера диаграмм: тип диаграммы.

Мы выбираем – Гистограмма.

Нажимаем кнопку Далее. Мы увидим внешний вид гистограммы, а также в разделе Диапазон указанные адреса выделенных нами ячеек исходных данных. Нажимаем кнопку Готово.

Для того, чтобы получить другое представление диаграммы, в диалоговом окне Мастер диаграмм можно выбрать другой тип диаграммы из широкого набора предлагаемых типов.

Представьте преподавателю результаты работы.

Преподаватель: В чем необходимость графического представления числовых данных?

Уч.: В любой сфере деятельности существует множество задач, в которых исходные данные и результаты должны быть представлены в графической форме. Умение наглядно представлять информацию в виде графиков и диаграмм – неотъемлемая часть современного образования. При решении различных задач, подготовке отчетов по различным предметам, выполнении заданий нередко возникает необходимость графического представления числовых данных. Основное достоинство такого представления – наглядность. Электронные таблицы предоставляют большой набор возможностей по графическому представлению данных в виде диаграмм и графиков.

Пр.: Что представляет собой диаграмма?

Дать определение объектов диаграммы: области диаграммы, 2) области построения диаграммы, 3) легенды, 4) заголовка, 5) маркера данных, 6) рядов данных, 7) оси.

Уч.: Дает основные определения и понятия объектов диаграммы, используя мультимедийный проектор.

Пр: Следующее задание: построить графики тригонометрических функций.

Постановка задачи: построить графики функций у = cos (x) и y=sin(x)

Диапазон изменения аргумента: от -180⁰ до + 180⁰ с шагом 10.

Технология работы.

Подготовительный этап: подготовка таблицы.

1. Переименовать Лист1 в «Таблица»:

Щелкните правой клавишей мыши на ярлыке Лист1 – вызов контекстного меню;
Выберите команду Переименовать.

2. Подготовьте на листе «Таблица» таблицу данных согласно рисунку:

Введите в ячейки А2:E2 названия столбцов; в дальнейшем названия функций составят текст легенды;
Задайте шаг;

Заполните столбцы — «Градусы», «Радианы», у=соs(х), y=sin(x) любым известным вам способом автозаполнения диапазона;

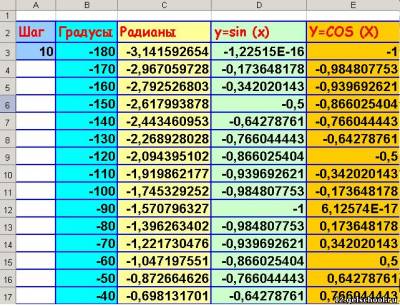
Представьте преподавателю результаты работы.

Построение графиков функций у=соs(х) и y=sin(x).

1. Выделите диапазон данных для построения графика С3:E39.

2. Постройте график, используя Мастер диаграмм: тип диаграммы – точечная, вид — точечная диаграмма со значениями, соединенными сглаживающими линиями.

3. Отредактируйте график по образцу.

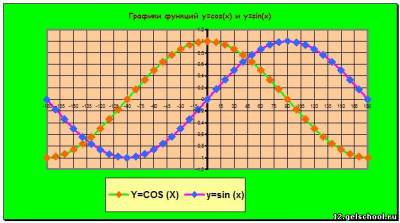
1. Представьте преподавателю результаты работы.

Пр: обратите внимание, что на каждом рабочем месте находятся карточки для самостоятельной индивидуальной работы. Внимательно изучите задания и приступайте к их реализации.

Учащиеся получают задания на карточках:

Карточка №1

Задание:

1. Построить в одной координатной плоскости графики функций:

y=sin(x), y=2*sin(x), y=1/2*sin(x).

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции
Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=sin(x).

Карточка №2

Задание:

2. Построить в одной координатной плоскости графики функций: y=cos(x), y=2*cos(x), y=1/2*cos(x).

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции

Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=cos(x).

Карточка №3

Задание:

1. Построить в одной координатной плоскости графики функций:

y=-sin(x), y=-sin(2x), y=-sin(2x+1).

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции
Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=sin(x).

Карточка №4

Задание:

1. Построить в одной координатной плоскости графики функций:

y=cos(x), y=cos(2x), y=cos(2x+1).

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции
Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=cos(x).

Карточка №5

Задание:

1. Построить в одной координатной плоскости графики функций:

y=cos(x), y=|cos(x)|-1, y=cos|x|.

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции

Карточка №6

Задание:

1.Построить в одной координатной плоскости графики функций:

y=sin(x), y=|sin(x)|+1, y=sin|x|.

2. Представьте преподавателю результаты работы.

3. Продумать ответы на вопросы:

Основные свойства, построенных вами тригонометрических функций:
Область определения
Область значений
Периодичность
Промежутки возрастания и убывания функции.

Источник

Построение графиков математических функций с одной переменной

Построение графиков математических функций с двумя переменными

Примеры использования функций SIN, SINH, COS и COSH в Excel

Таблица синусов и косинусов в Excel

Построение графика функций SINH и COSH в Excel

Особенности использования тригонометрических функций в Excel

Microsoft Excel

Построение в Excel графиков математических и тригонометрических функций

Построение графиков математических функций с одной переменной

Построение графиков математических функций с двумя переменными

Как построить график функции в Excel

Как в экселе построить график косинуса?

Видео

Варианты построения графика функции в Microsoft Excel

Вариант 1: График функции X^2

Вариант 2: График функции y=sin(x)

Вариант 1: График функции X^2

Вариант 2: График функции y=sin(x)

Еще статьи по данной теме:

Помогла ли Вам статья?

Подготовка расчетной таблицы

Построение графика функции

Построение графиков других функций

Квадратичная функция y=ax2+bx+c

Кубическая парабола y=ax3

Гипербола y=k/x

Построение тригонометрических функций sin(x) и cos(x)

Квадратичная функция y=ax²+bx+c

Кубическая парабола y=ax³