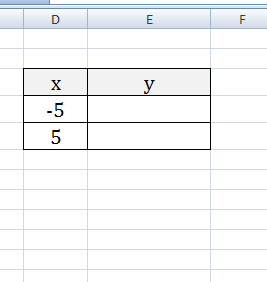Содержание
- Создание параболы
- Создание таблицы
- Построение графика
- Редактирование диаграммы
- Вопросы и ответы
Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
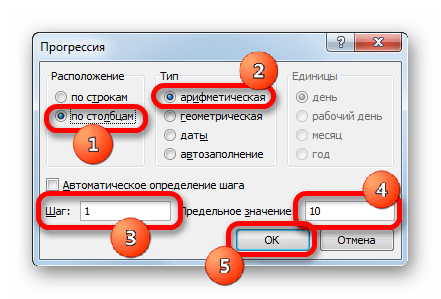
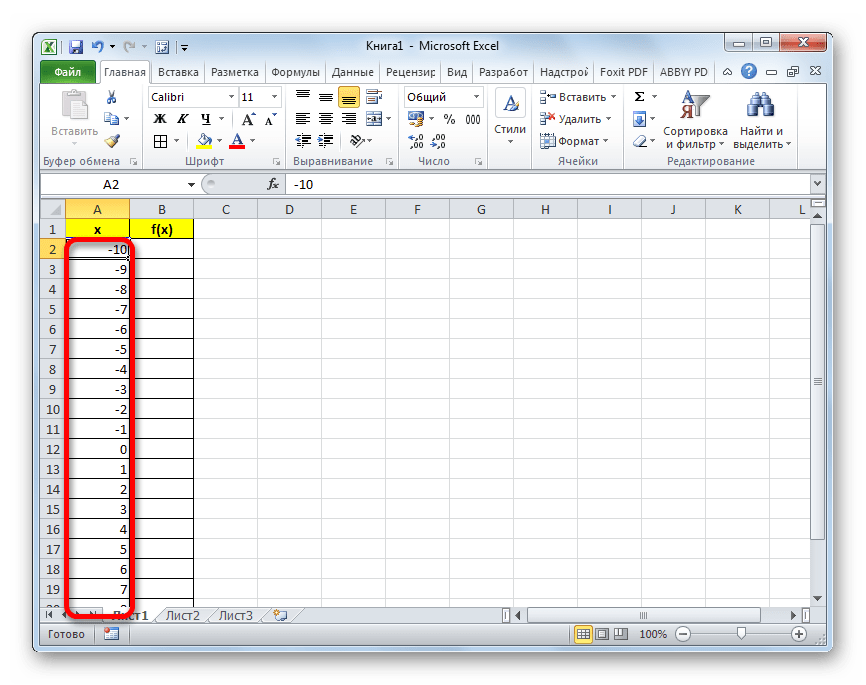
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
- Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
- После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
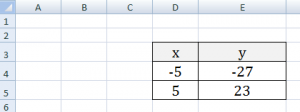
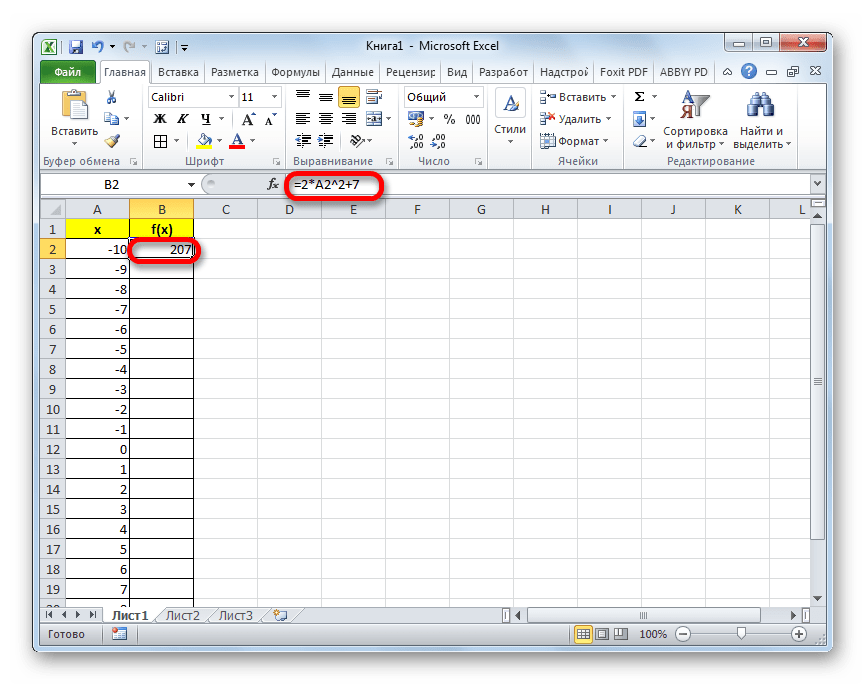
- Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:
=2*x^2+7Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
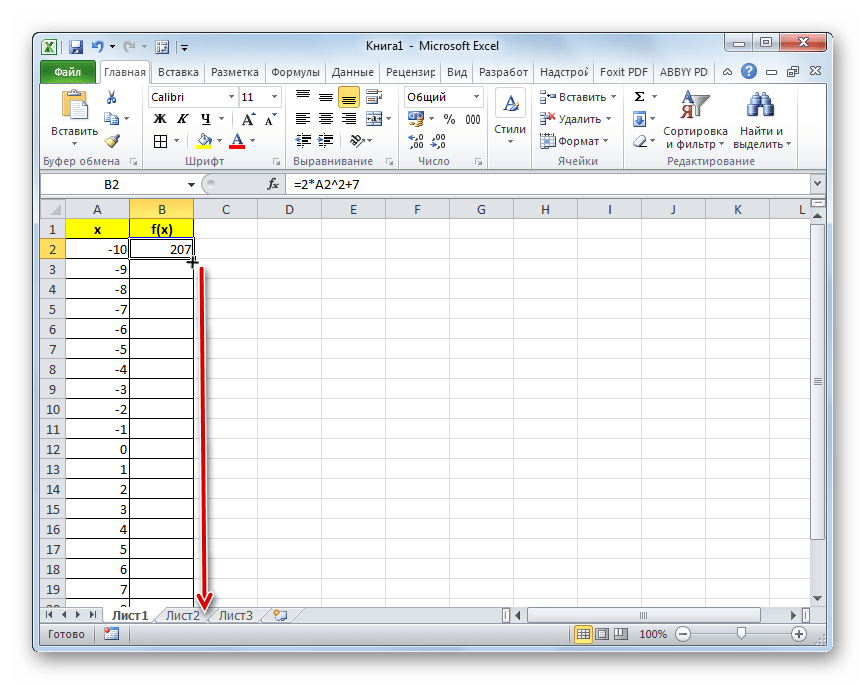
=2*A2^2+7 - Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.
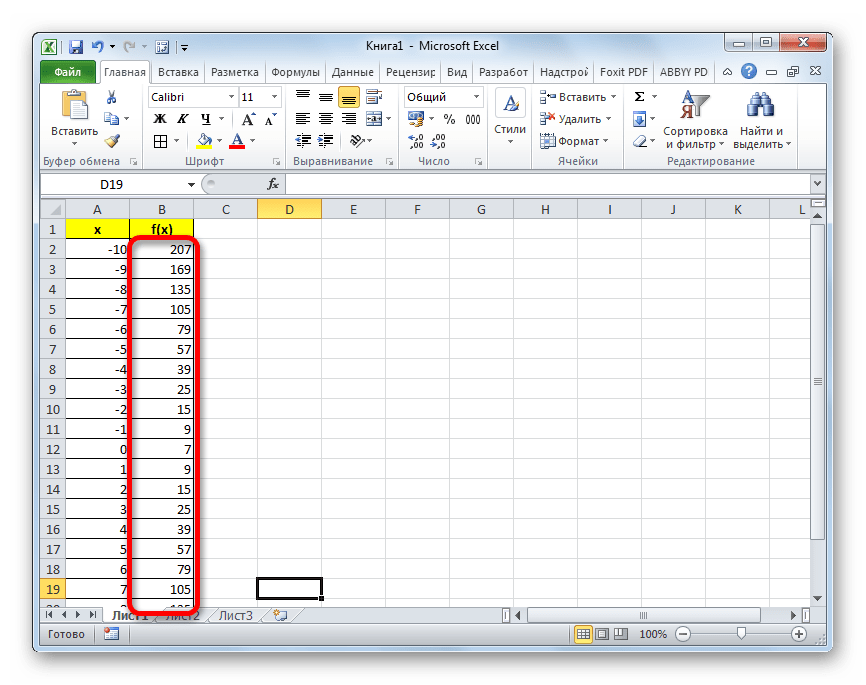
- Как видим, после этого действия столбец «f(x)» тоже будет заполнен.
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Урок: Как сделать автозаполнение в Экселе
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
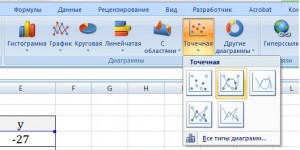
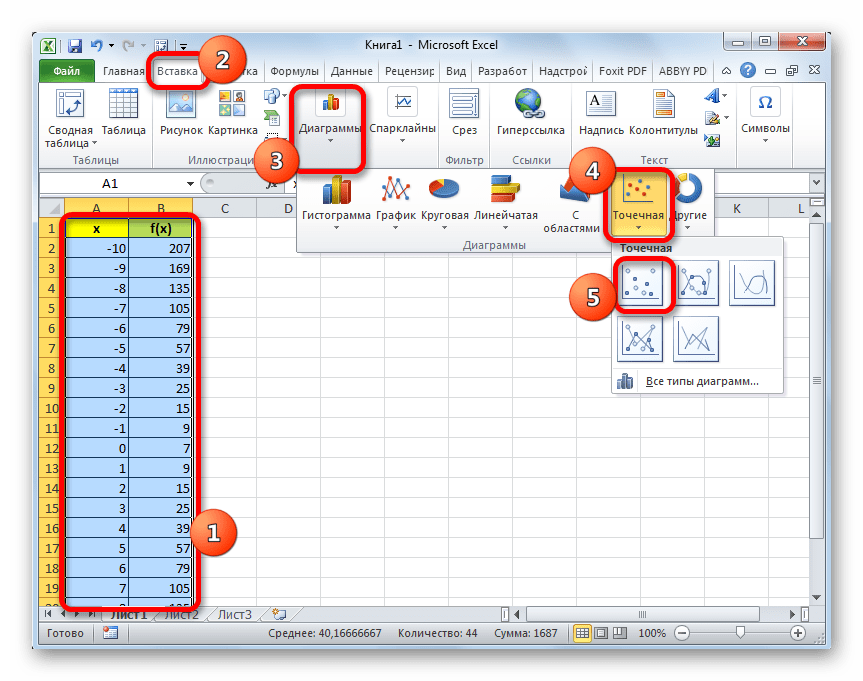
- Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
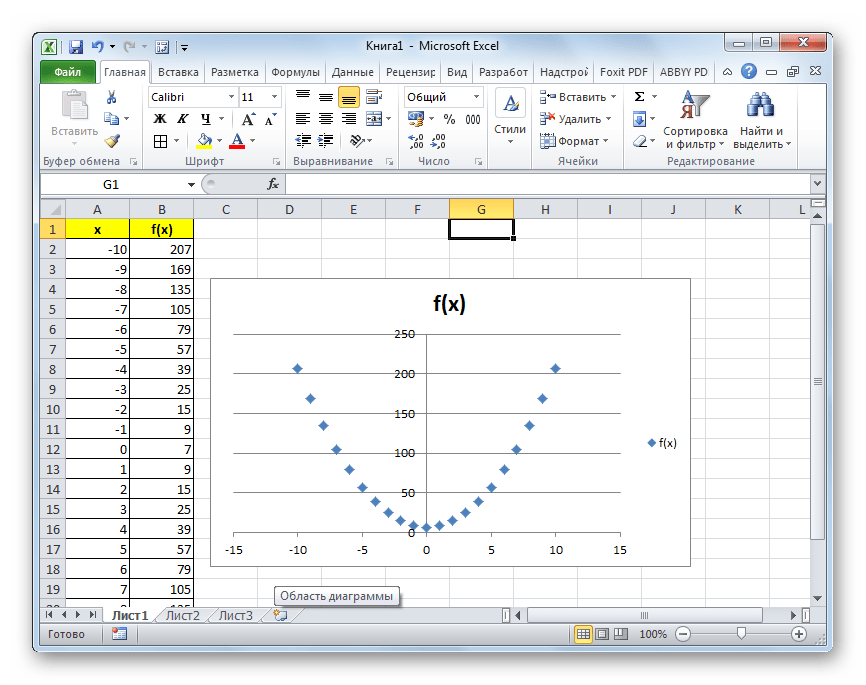
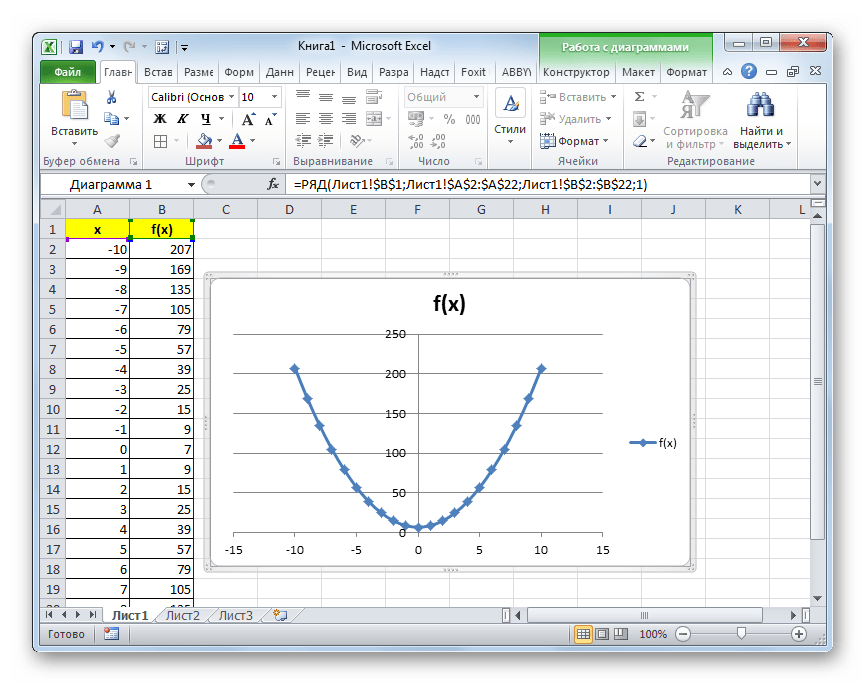
- Как видим, после этих действий, парабола построена.
Урок: Как сделать диаграмму в Экселе
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
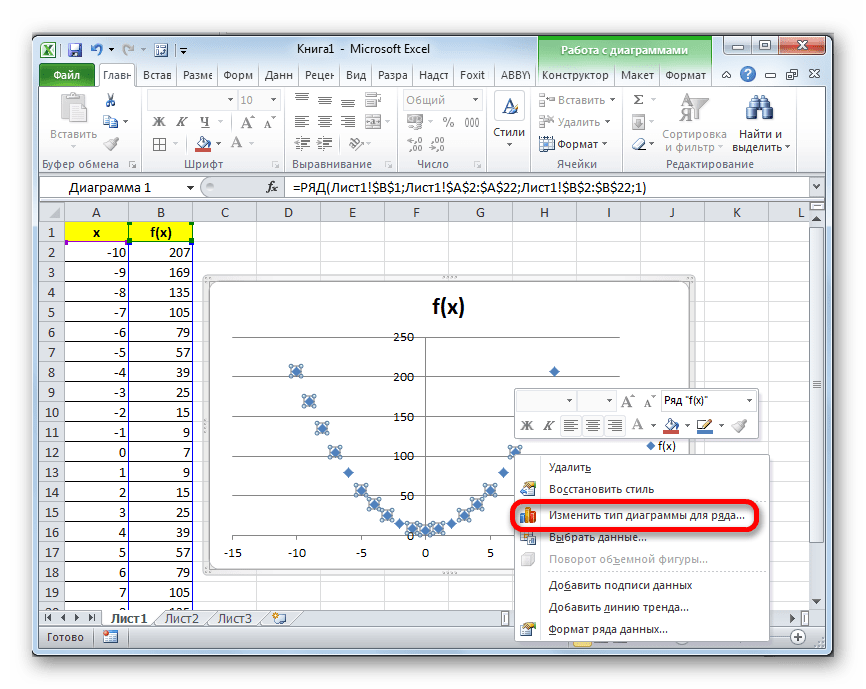
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
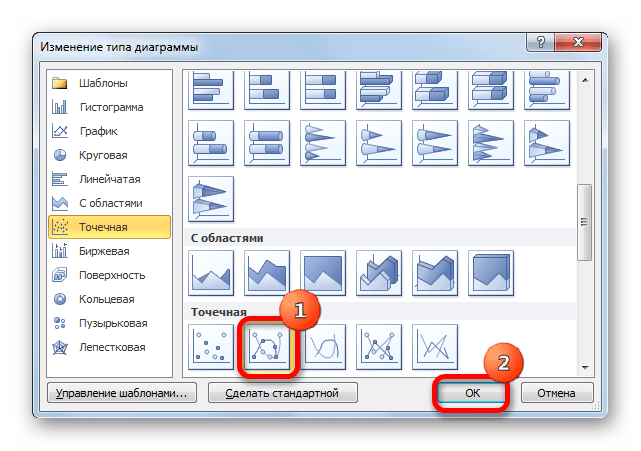
- Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
- Теперь график параболы имеет более привычный вид.
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Урок: Как подписать оси диаграммы в Excel
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Еще статьи по данной теме:
Помогла ли Вам статья?
Содержание
- Как построить в экселе параболу?
- Видео
- Excel построение графика квадратичной функции
- Построение параболы в Microsoft Excel
- Создание параболы
- Создание таблицы
- Построение графика
- Редактирование диаграммы
- Как построить график функции в Microsoft Excel
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax 2 +bx+c
- Кубическая парабола y=ax 3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Как построить в экселе параболу?
В программе эксель можно строить разнообразные графики: гистограммы, круговые диаграммы, параболы, гиперболы и т.п. Давайте разберемся, как можно построить в экселе параболу.
Первый этап. Построим простую параболу по функции: y=x 2 . Для этого в программе эксель сделаем таблицу из двух столбцов: «Значение X» и «Значение Y». В столбце «А» напишем значения от -5 до 5 с шагом 1. Чтобы посчитать значение Y, в ячейке «В2» пропишем формулу =СТЕПЕНЬ(A2;2), где «A2» значение первой точке, 2 – степень, в которую мы будем возводить. В итоге мы получим первое значение.
Второй этап. Нужно рассчитать оставшиеся значения, для этого мы выделяем ячейку «В2», нажимаем на правую кнопку мыши, чтобы появилось меню, в котором выбираем строчку «Копировать».
Третий этап. Выделяем диапазон ячеек с «В3» по «В12» и нажимаем на клавиатуре клавишу «Enter», в итоге у нас должны посчитаться все значения функции параболы.
Четвертый этап. Выделим теперь полностью область со значениями. После нужно перевести взгляд на верхнюю панель настроек, где отыщите вкладку «Вставка» и активируйте её. В ней есть блок «Диаграммы», в которой ищем иконку с надписью «Точечная», нажмите на неё. На экране отобразиться дополнительное меню, среди представленного выбора, выберем в первой строке вторую иконку.
Пятый этап. На экране появиться график параболы. Осталось его немного оформить, сначала подпишем оси. Для этого в верхней панели настроек снова заходим во вкладку «Вставка», где слева есть блок «Текст», следует нажать на иконку с надписью «Надпись». После на экране появится крести, нажмите им рядом с одной из оси, напишите «Y» и поставьте рядом с осью, тоже самое нужно сделать с ось «Х».
Шестой этап. Подпишем линию, для этого выделяем квадрат с надписью «Ряд1» и жмем на правую кнопку мыши, в появившемся меню выбираем «Выбрать» данные.
Седьмой этап. Появиться новое меню «Выбор источника данных», выделяем в нем запись «Ряд1» и нажимаем на кнопку «Изменить». В небольшой таблице, в строке «Имя радя» даем новое название, после закрываем все меню.
В итоге наш график параболы имеет следующий вид:
Видео
Источник
Excel построение графика квадратичной функции
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
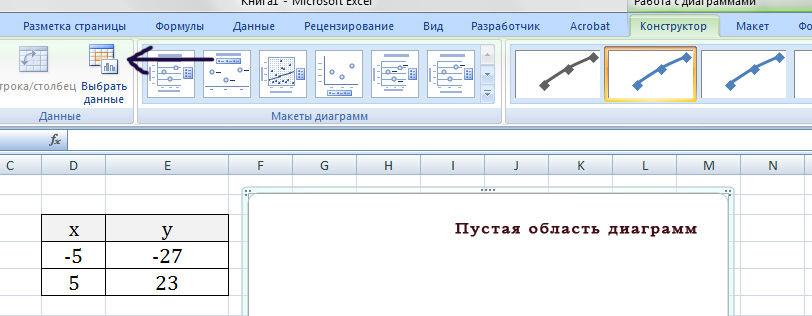
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
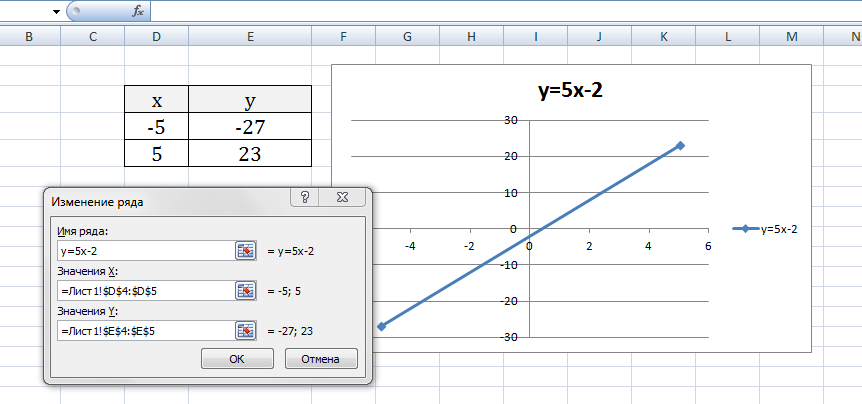
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
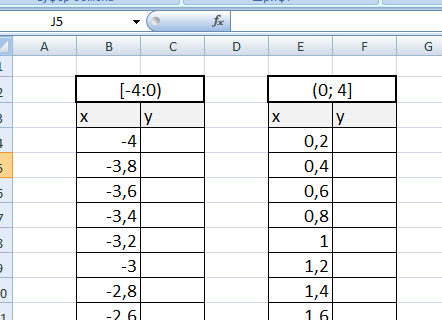
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
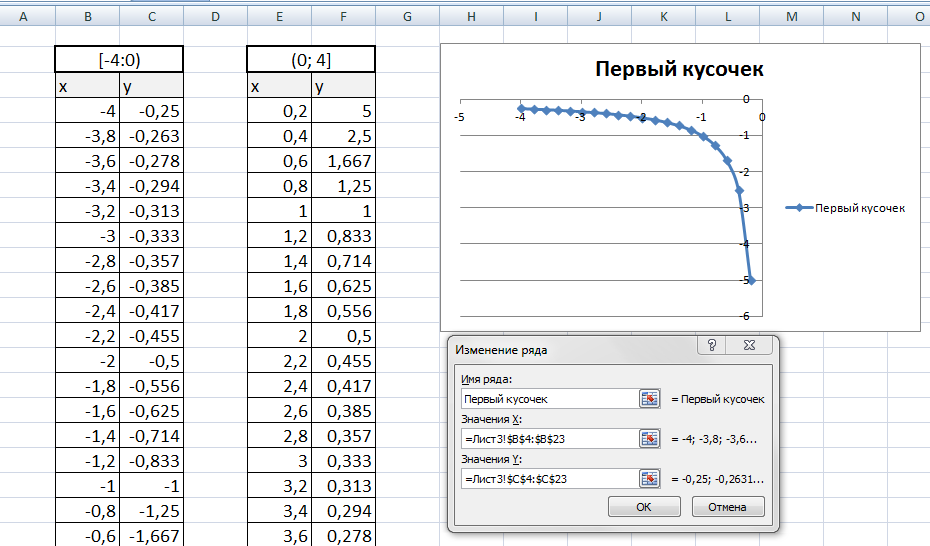
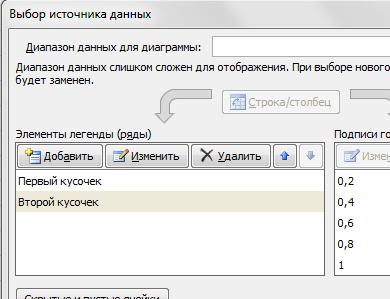
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Источник
Построение параболы в Microsoft Excel
Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
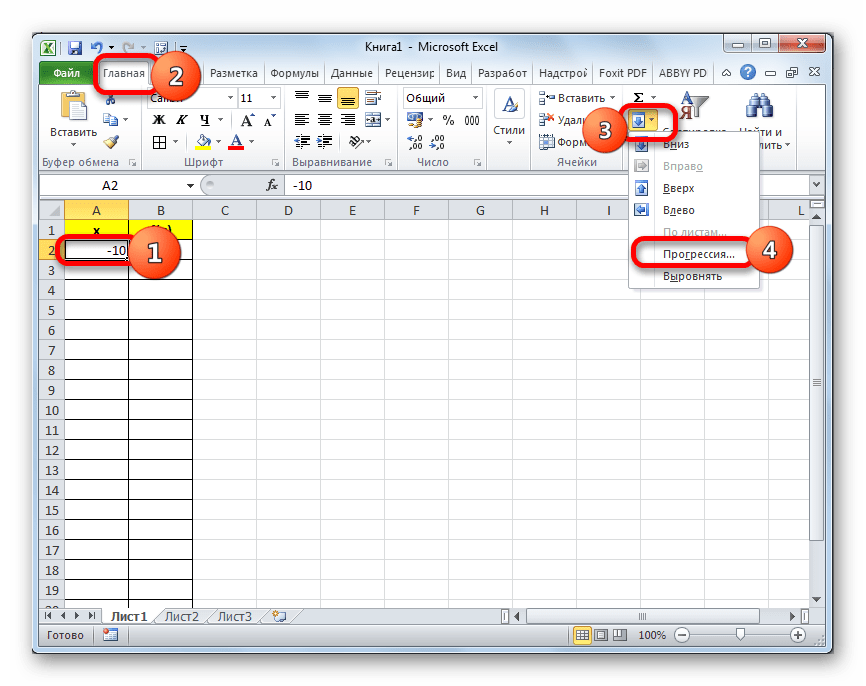
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
=2*A2^2+7
Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
- Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
- Как видим, после этих действий, парабола построена.
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
- Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
- Теперь график параболы имеет более привычный вид.
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Источник
Как построить график функции в Microsoft Excel
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графика линейной функции в Excel
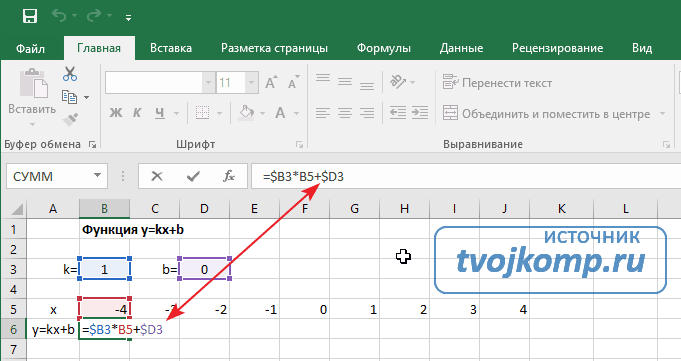
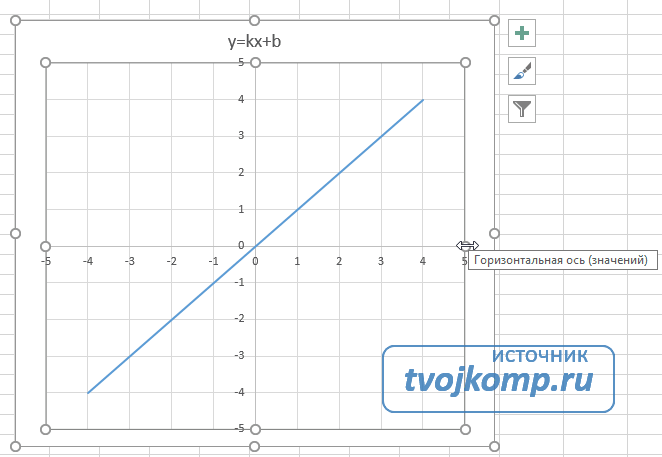
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
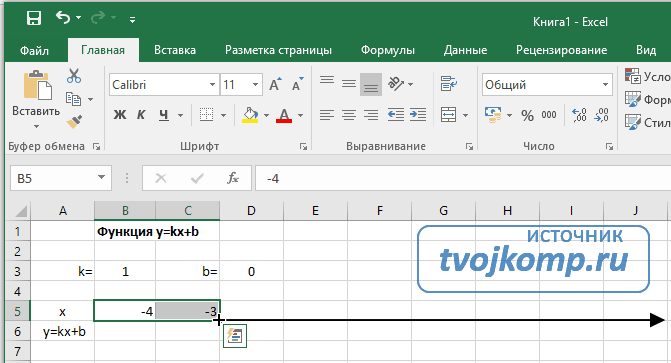
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
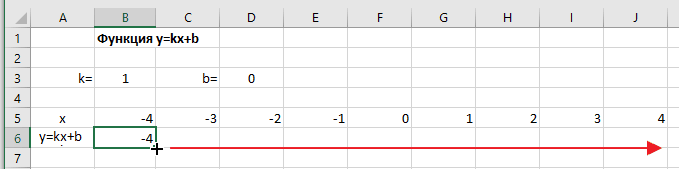
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
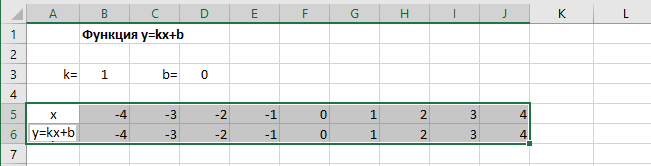
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
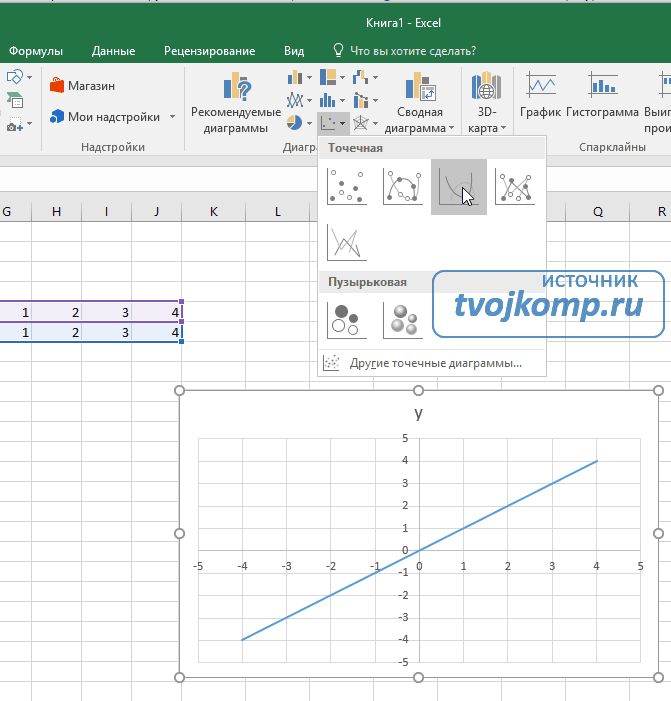
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
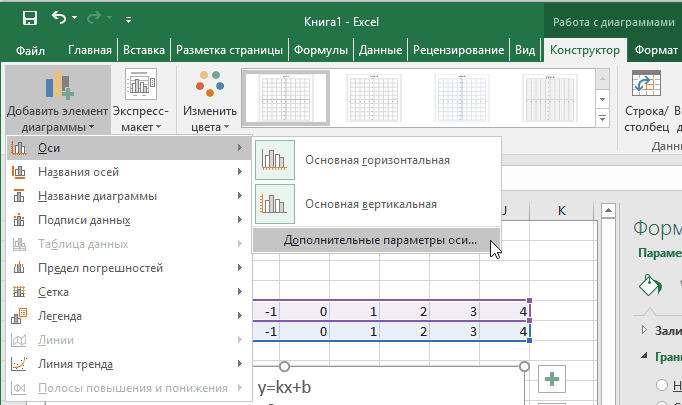
В правой части окна появиться боковая панель настроек Формат оси.
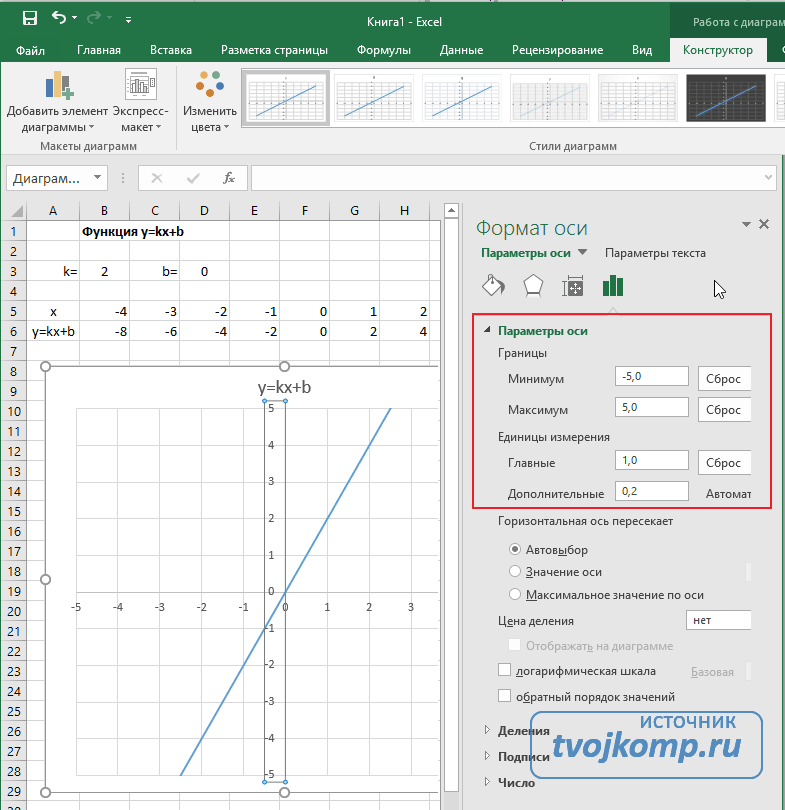
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
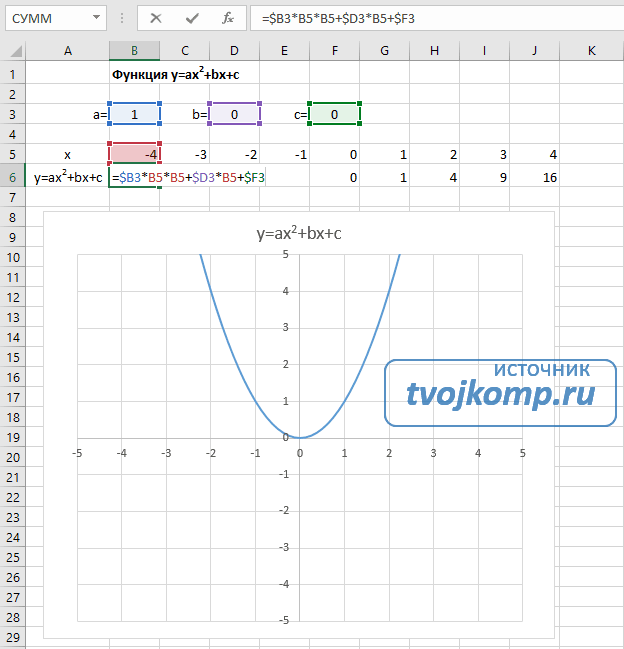
Квадратичная функция y=ax 2 +bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
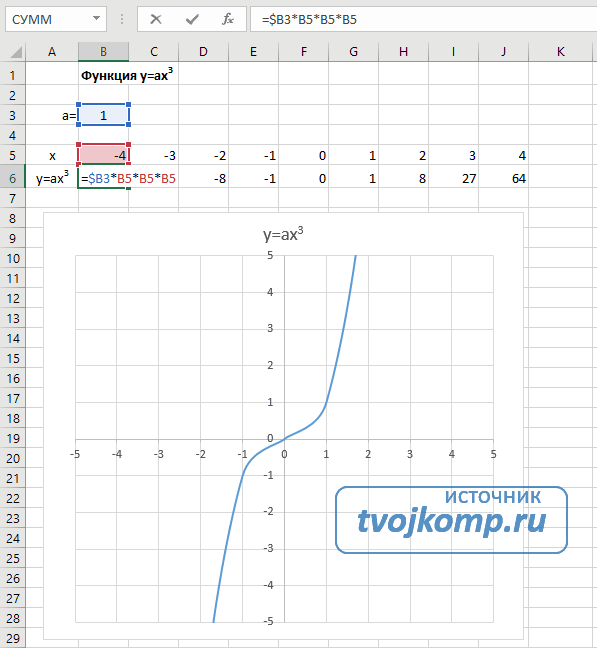
Кубическая парабола y=ax 3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
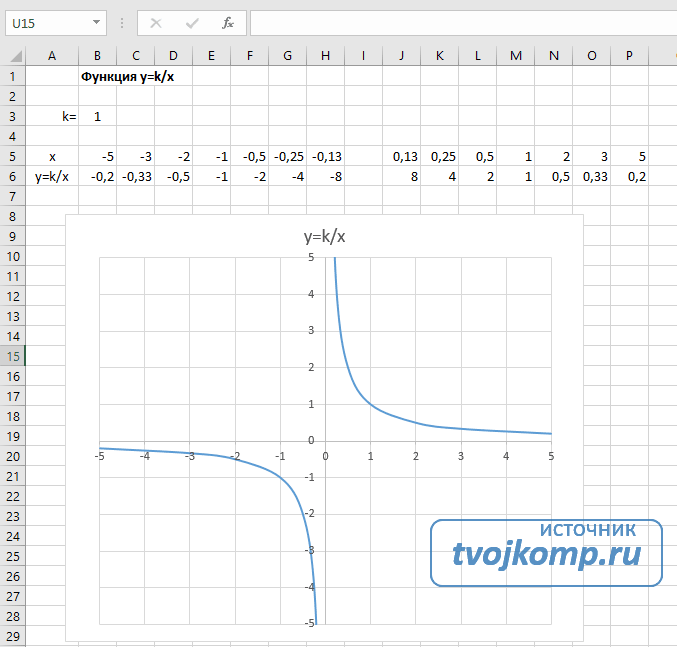
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Построение тригонометрических функций sin(x) и cos(x)
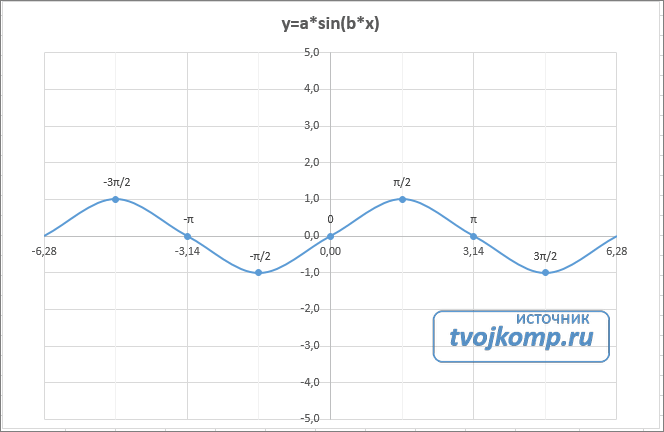
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
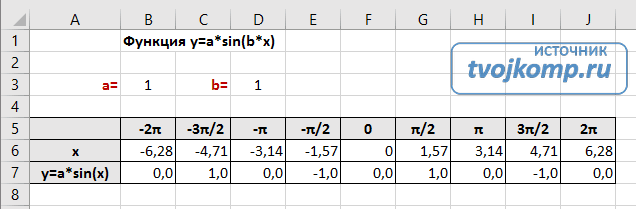
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
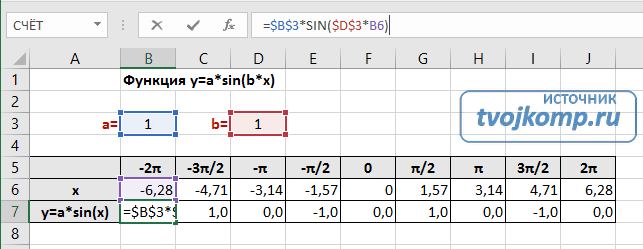
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
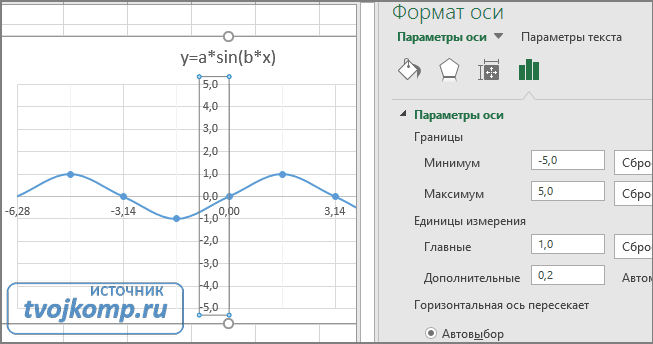
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
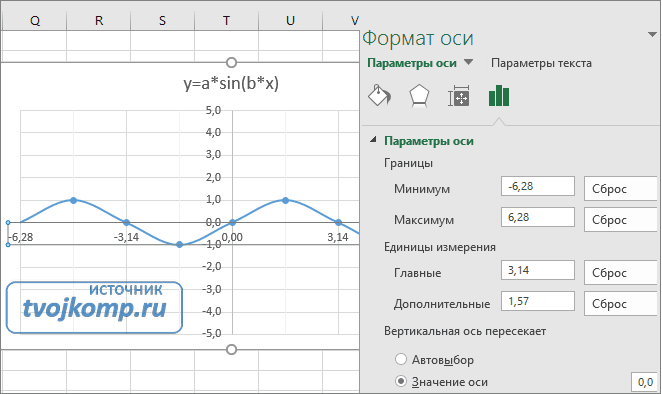
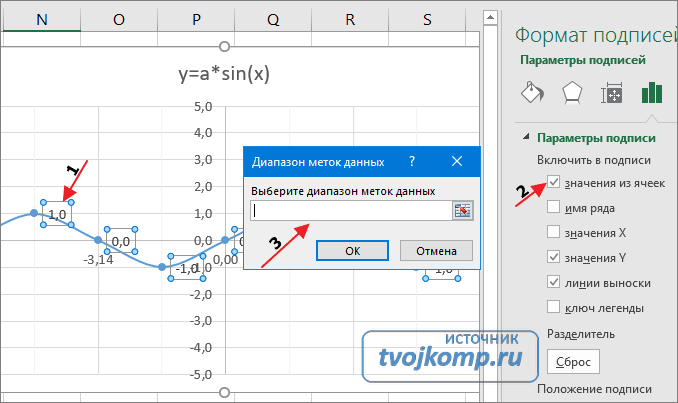
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
Дорогой читатель! Вы посмотрели статью до конца. Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью! 

Подскажите, пожалуйста, на какой версии Excel у вас основаны скриншоты? Спасибо за статью, и у вас и тут похоже одинаковая версия, но на мою не похоже.
Илья, скриншоты сделаны для версии Excel2016, в начале статьи это упоминается. Предыдущие версии имеют отличия в интерфейсе, но следуя описанной последовательности действий, можно уловить логику и других интерфейсов.
Источник
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!



Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
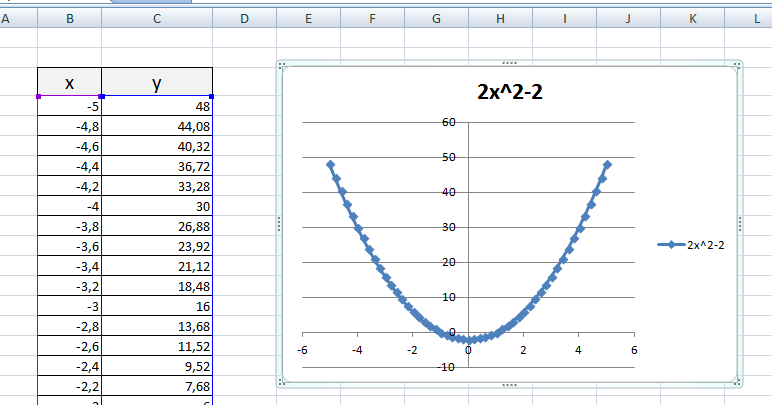
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
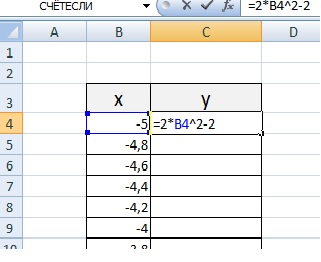
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
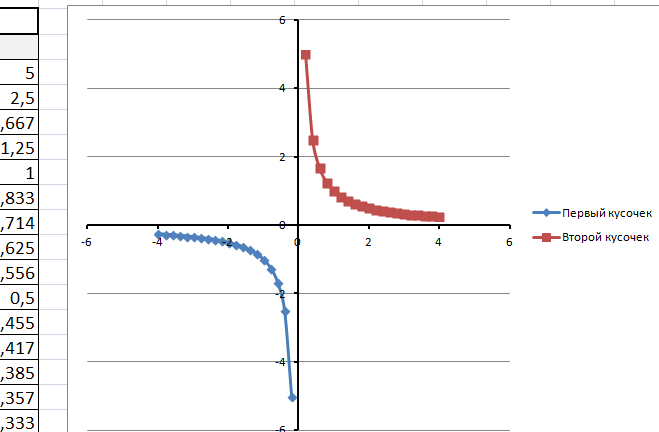
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички

В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Душевые термостаты, лучшие модели на http://tools-ricambi.ru/ изготавливаются из материалов высшего качества
Оставить комментарий
history 8 января 2023 г.
- Группы статей
- Диаграммы и графики
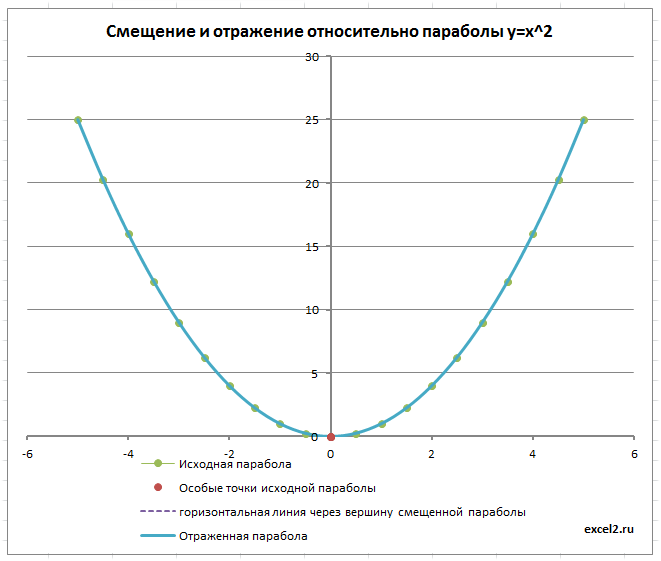
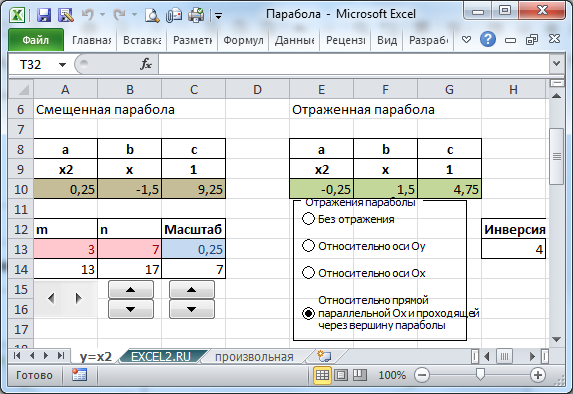
Построим параболу, используя стандартную диаграмму MS EXCEL. C помощью элементов управления построим удобную форму для смещения вершины параболы вверх/низ, отражения ее относительно осей координат.
Задача
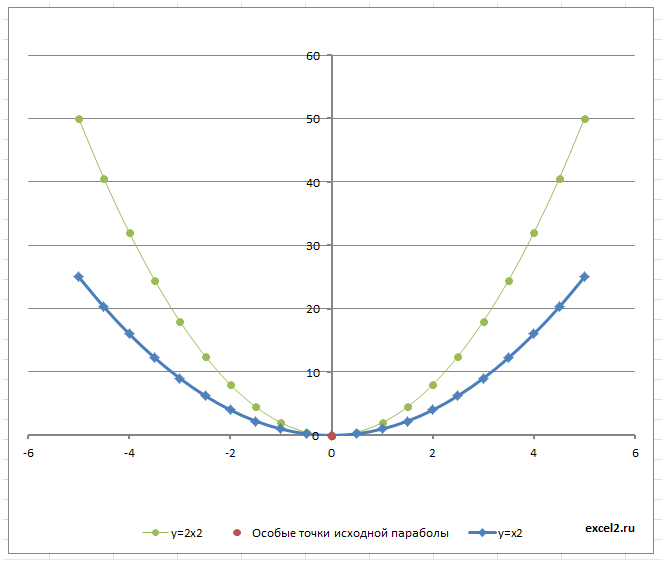
- Построим Параболу имеющую уравнение y=x2.
- Отметим на диаграмме ее особые точки: пересечения с осями (осью) и вершину.
- Создадим на листе кнопки для смещения вершины параболы в произвольном направлении
- Выберем такой шаг по оси Х и диапазон изменения переменной Х, чтобы после смещения параболы на диаграмме обе ее ветви отображались одинаковой длины и присутствовали все особые точки
- Вычислим новые значения параметров параболы y=ax2 + bx + с
Построение исходной параболы
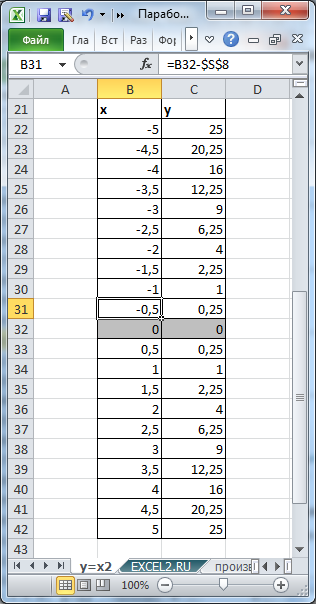
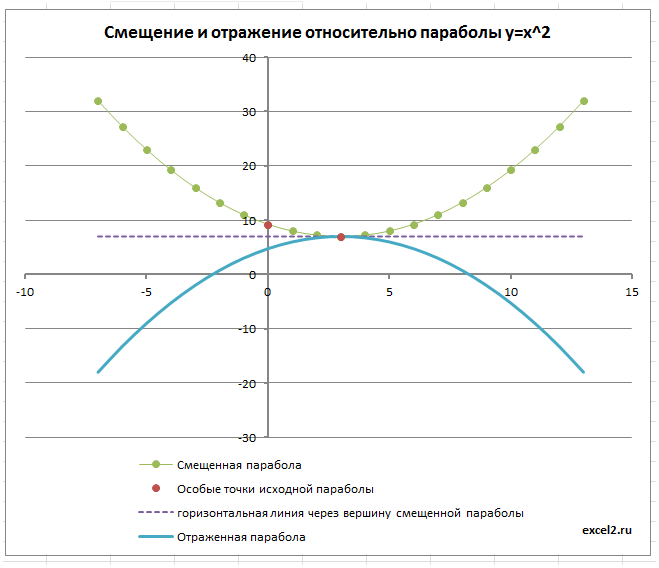
С помощью точечной диаграммы построим Параболу имеющую уравнение y=x2, назовем ее исходной параболой.
Для этого на листе в файле примера подготовлена таблица исходных значений по Х и Y.
Особенностью этого набора данных является то, что значения Х отсчитываются от координат вершины параболы с определенным шагом.
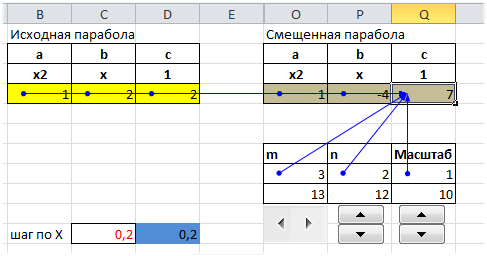
Для определения вершины параболы можно использовать различные формулы, например через производную или по формуле х0=-b/2a. Для этого в файле примера делаются соответствующие вычисления (при изменении местоположения параболы эти вычисления производятся автоматически).
Для определения масштаба изменения переменной Х, вычисляются точки пересечения, а затем вычисляется такой шаг по Х, чтобы все эти точки пересечения гарантированно были отражены на диаграмме.
Чтобы шаг по Х не был равен значениям с длинной десятичной частью, используется округление до первой значащей цифры.
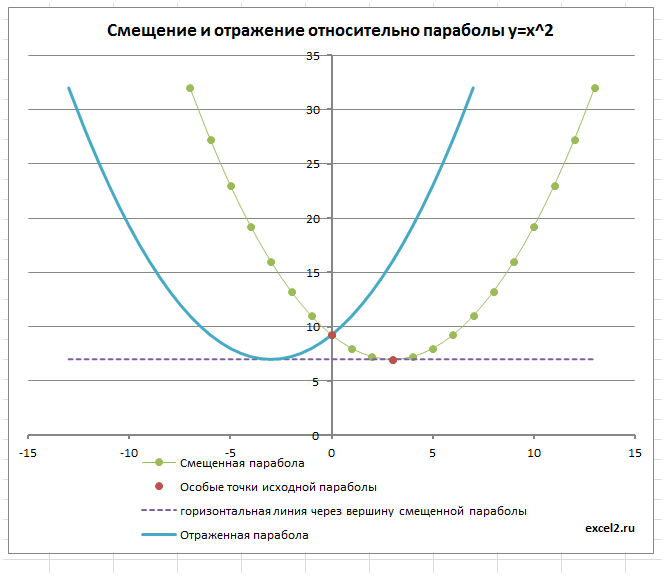
Смещение исходной параболы
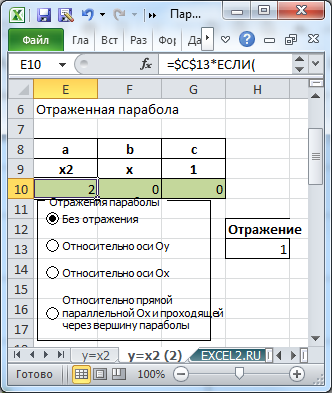
Смещение вершины параболы будем производить с помощью Полосы прокрутки и Элемента управления Счетчик.
Смещение по оси Х будем обозначать m, а по Y обозначим n. Значения m и n являются новыми координатами вершины смещенной параболы.
Изменив, например, с помощью Счетчика значение n на 2, автоматически пересчитаются значения параметров параболы в строке 10: y=ax2 + bx + с, а следовательно и координаты вершины вместе со всеми значениями исходной таблицы — парабола сместится на величину 2 по Y.
Примечание: альтернативная запись параболы через координаты вершины: y=a(x-m)2+n
Изменение масштаба параболы (параметр а)
Параметр а отвечает за масштаб параболы. Например, парабола с уравнением y=2x2 будет вытянута по оси Х в 2 раза по отношению к y=x2.
В файле примера изменение масштаба параболы реализовано с помощью элемента Счетчик, аналогичным образом, как и смещение.
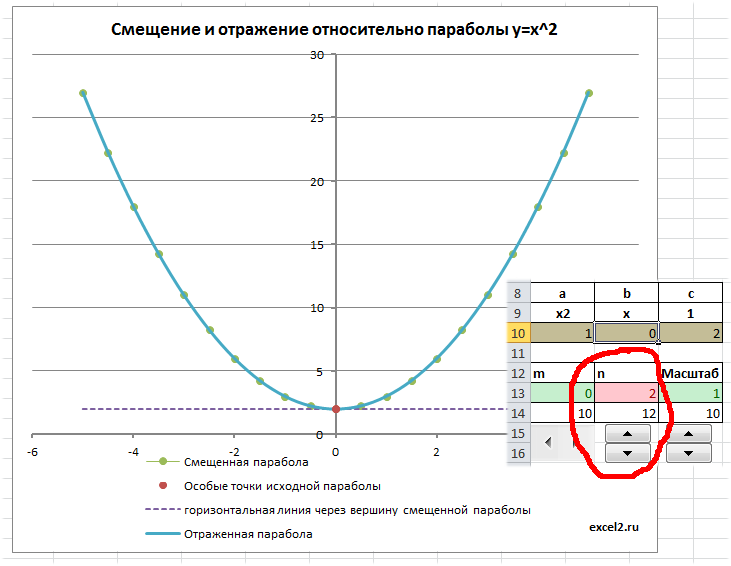
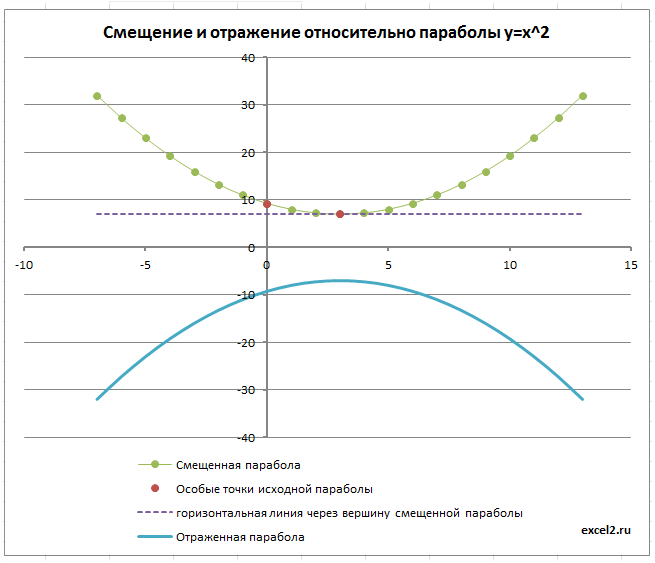
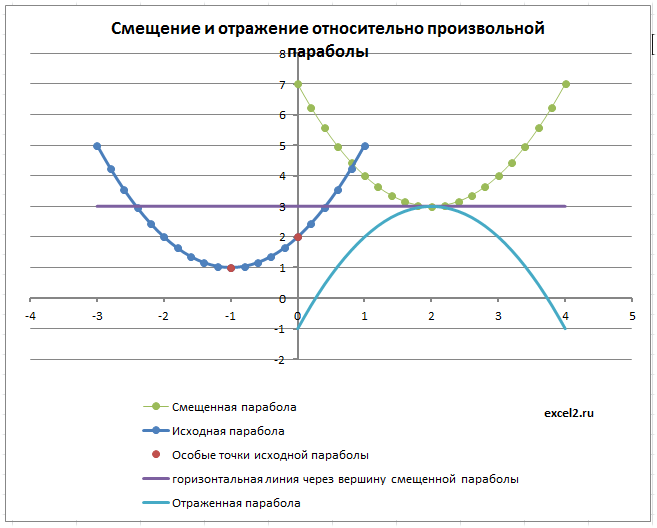
Отражение параболы
Смещенную параболу можно отразить относительно оси Х, относительно оси Y и относительно прямой параллельной Ох и проходящей через вершину параболы. Все эти манипуляции реализованы с помощью формул и элементов управления Переключатель.
Выбирая нужный тип отражения параболы, диаграмма отобразит нужный график.
Вычисления параметров параболы
Построить параболу не сложно, сложнее вычислить значения параболы (a, b, с), которая была смещена, у которой также был изменен масштаб и, наконец, она была отражена.
Все эти вычисления приведены в формулах строки 10 в файле примера. На листе «произвольная» расчеты параметров сделаны относительно исходной параболы с произвольными значениями параметров. Формулы получаются в этом случае достаточно громоздкими, т.к. параметры смещенной параболы зависят как от параметров исходной параболы, так и от значений m, n и масштаба.
Автор: Пенский Владимир Константинович
Предмет: алгебра, информатика.
Тема урока: Квадратичная функция в MS EXCEL.
Класс: 9.
Продолжительность: 45 минут.
Цель урока: применение
электронных таблиц для построения графика и изучения основных свойств квадратичной
функции.
Задачи урока:
Образовательные:
·
систематизация знаний о свойствах квадратичной
функции;
·
закрепить умение строить графики квадратичной
функции и по графику определять ее основные свойства;
·
закрепление умения работать с электронными
таблицами.
Развивающие:
·
формирование умения сравнивать, обобщать изучаемые
факты;
·
повышение уровня учебной мотивации с использованием
компьютерных технологий, развитие логического мышления;
·
развитие умения грамотно
излагать свои мысли, обосновывать свои действия.
Воспитательные:
·
развитие коммуникативных умений, формирование адекватной
оценки собственной деятельности;
·
развитие чувства
товарищества, взаимопомощи, деликатности,
дисциплинированности.
Оборудование: компьютерный класс, мультимедийный проектор, экран.
Ход урока
1. Организационный момент.
2. Постановка
цели урока.
Сегодня на уроке мы повторим свойства квадратичной функции и научимся
строить соответствующие графики функций с помощью прикладного программного
обеспечения компьютера и, используя полученный график, определим свойства этой
функции.
3. Актуализация
знаний. Фронтальный опрос.
Вспомним определение и
основные свойства квадратичной функции. Для этого ответьте на вопросы.
1.
Как называется функция вида у = aх2 +
bx + c (а ≠ 0), где а, b, c – действительные
числа?
- Что является графиком
квадратичной функции? - При каких
значениях х квадратичная функция у = х2 возрастает?
убывает? - Как называются
значения переменной х, при которых значение функции равно нулю. - При а >
0 ветви параболы у = ах2 направлены … . - Если а
< 0 и х < 0, то квадратичная функция у = ах2
принимает …(положительные, отрицательные) значения.
3. Повторение
изученного материала.
1. Обоснуйте, что областью определения функции у
= aх2 + bx + c является множество всех
действительных чисел.
2. Выясните, какие из следующих квадратичных функций являются: чётными;
нечётными; не являются ни чётными, ни нечётными.
а) y = x2; б)
y = 3 − 2x
+ x2.
3. Найдите нули квадратичной функции:
а) y = 2x2 + x − 3; б)
y = x2 − 8x + 15.
4. Найдите координаты вершины параболы у = х2
– 4х + 4.
5. Укажите наибольшее (наименьшее) значение
функции:
а) y = x2; б) y = 3x2 + 1.
4. Изложение нового
материала.
Можно ли, не проводя
аналитических рассуждений определить свойства квадратичной функции?
Действительно, по графику квадратичной функции можно определить все ее основные
свойства.
Как построить график
квадратичной функции? На помощь приходят современные компьютерные технологии.
Сегодня существует множество программ, которые позволяют строить графики различных
функций. Одним из простейших способов построения графика (в нашем случае
графика квадратичной функции) является использование электронных таблиц Microsoft
Excel.
Вспомним, каким образом
можно построить график функции в данной программе.
Построим, например,
график квадратичной функции у =
х2 + 2х – 3 и исследуем ее свойства.
1) Составим таблицу
значений зависимости переменной у от х:
–
в ячейку А1 введите заголовок столбца «х»;
–
в ячейку А2 введите значение –5, а в ячейку А3 – –4,5;
–
выделите содержимое ячеек А2 и А3, далее с помощью функции автозаполнения скопируйте
до ячейки А18 (получим соответствующие значения х от –5 до 3);
–
в ячейку В1 введите заголовок столбца у = х2 + 2х
– 3;
–
в ячейку В2 введите формулу = В1^2 + 2*B1 – 3;
–
скопируйте формулу из ячейки В2 (используя функцию автозаполнения) до ячейки В19.
2) Построение
графика с помощью мастера диаграмм:
– выделите
подготовленные данные, начиная с заголовка В1:В18.
– вызовите
мастер диаграмм (Вставка – график – график);
– при
задании параметров название диаграммы оставить;
– нажмите
«ОК» и график автоматически вставится.
3) Работа с
графиком:
–
вставьте названия осей (Макет – названия осей – название основной горизонтальной
оси – название под осью; Макет – названия осей – название основной вертикальной
оси – горизонтальное название) и перенесите (х справа от оси, у
выше оси);
– щелчком
мыши в готовой диаграмме по каждой из осей, вызовите контекстное меню и установите:
«горизонтальная ось пересекает значение оси 0», «вертикальная ось пересекает в
категории с номером 11»;
–
добавьте сетку (Макет – сетка – вертикальные линии сетки по основной оси –
основные линии сетки).
Задание. С помощью построенного графика квадратичной
функции у = х2 +
2х – 3 определите:
а) четность-нечетность
функции;
б) нули функции;
в) промежутки
монотонности;
г) наибольшее и
наименьшее значение функции.
5. Проверка усвоения нового материала.
Класс делится на две
группы. Каждой группе предлагается решить определенное задание. После того как
все обучающиеся в группе решили это задание, происходит взаимопроверка
полученных решений.
1 группа.
1. Найдите координаты
точек пересечения параболы у = х2 + х – 12 с
осями координат.
2. Постройте график квадратичной функции y =
−3x2 в программе Microsoft Excel и определите по графику значения этой функции в точках x1 = 5, x2 = −3.
2 группа.
1. Найдите значения квадратичной функции y =
−3x2 в точках x1 = 5, x2 = −3.
2. Постройте график квадратичной функции у = х2 +
х – 12 в программе Microsoft Excel и по графику
определите координаты точек пересечения параболы с осями координат.
6. Подведение итогов.
Итак, мы повторили
материал, касающийся свойств квадратичной функции, решали задачи.
Что нового вы
узнали сегодня?
Довольны
ли вы своей работой?
7. Домашнее задание.
Задайте аналитически квадратичную функцию, которая:
а) имеет два нуля −3 и 0;
б) имеет только один нуль −3;
в) не имеет нулей.
Однозначно ли можно выполнить задание во всех случаях?
Список использованной литературы:
1. Алгебра: учебник для 9 класса / Гельфман Э.Г., Демидова Л.Н., Терре
А.И. и др. – М: БИНОМ. Лаборатория знаний, 2013. – 272 с.
2. Семакин И.Г. Информатика и ИКТ: учебник для 9 класса / И.Г. Семакин,
Л.А. Залогова, и др. – М: БИНОМ. Лаборатория знаний, 2012. – 341 с.
3. Социальная сеть работников образования «Наша сеть». – Режим доступа: http://nsportal.ru/shkola/informatika-i-ikt/library/2013/11/02/integrirovannyy-urok-po-algebre-i-informatike







_m.jpg)