Excel поиск решения в целых числах - Word и Excel - помощь в работе с программами

history 23 марта 2015 г.

Надстройка «Поиск решения»

Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.

Поиск решения будем рассматривать в MS EXCEL 2010 (эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в MS EXCEL 2007) . В этой статье рассмотрим:

создание оптимизационной модели на листе MS EXCEL
настройку Поиска решения;
простой пример (линейная модель).

Установка Поиска решения

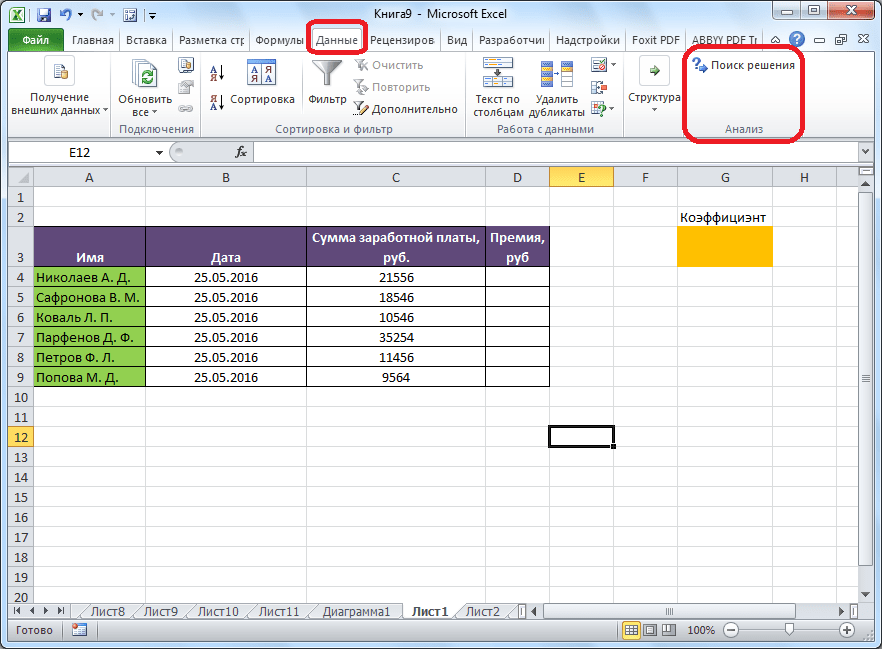
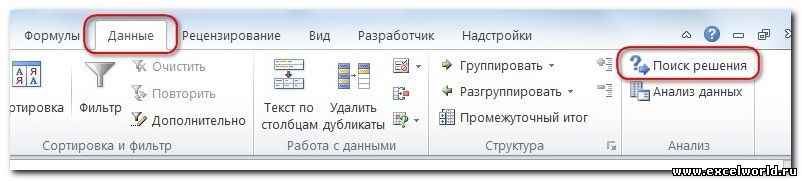
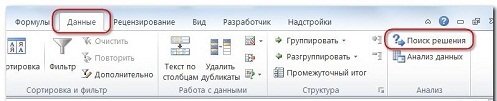
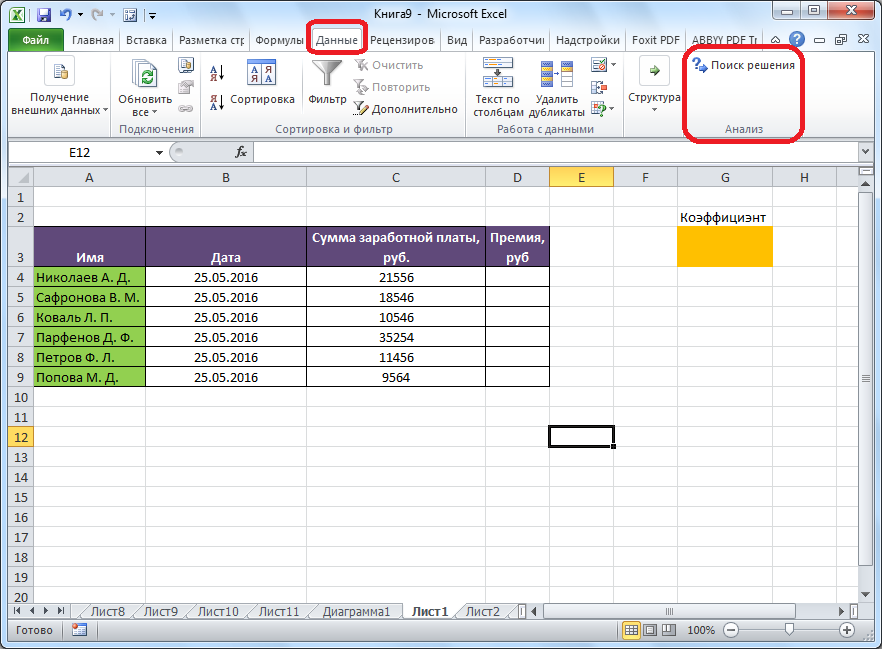
Команда Поиск решения находится в группе Анализ на вкладке Данные .

Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:

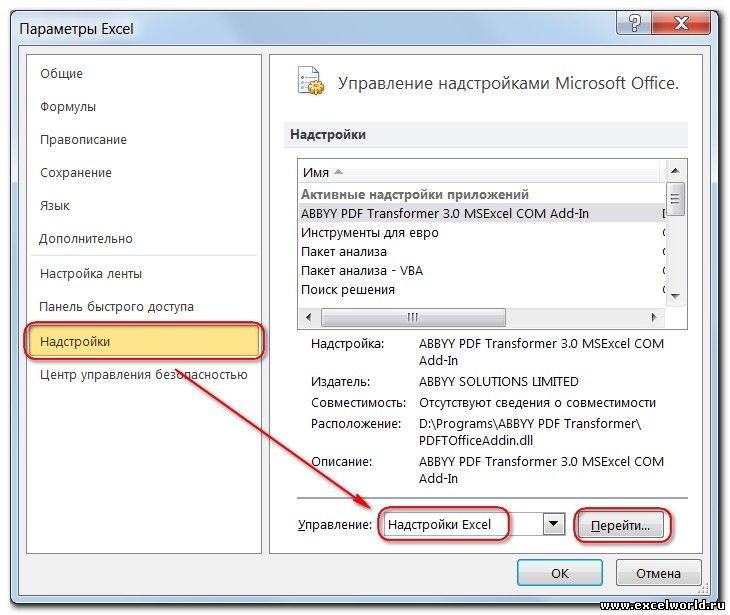
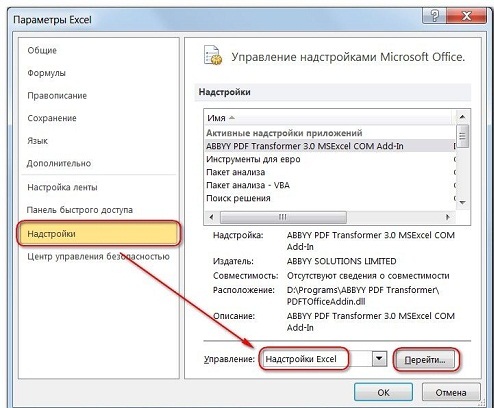
На вкладке Файл выберите команду Параметры , а затем — категорию Надстройки ;
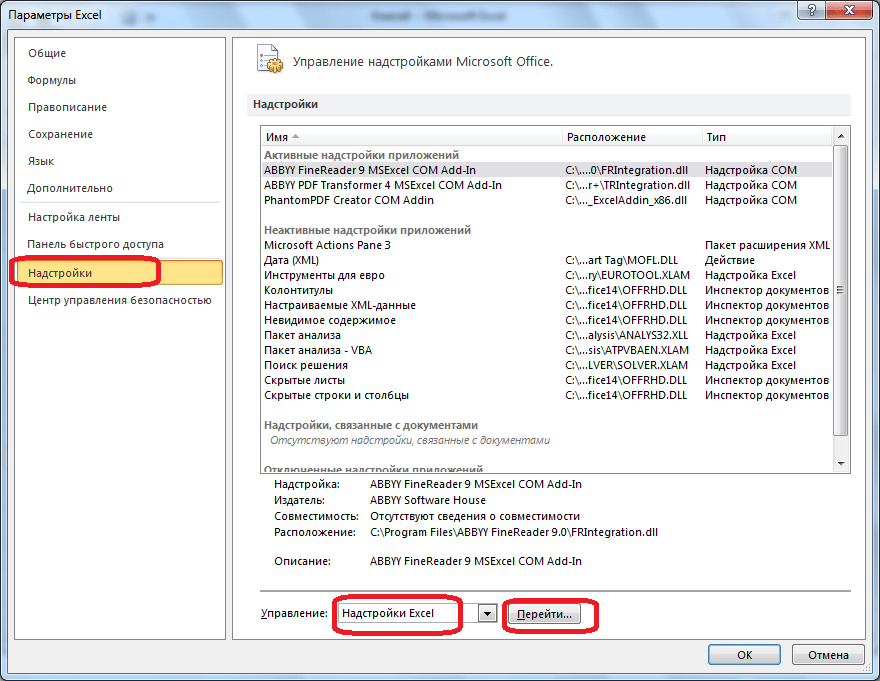
В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
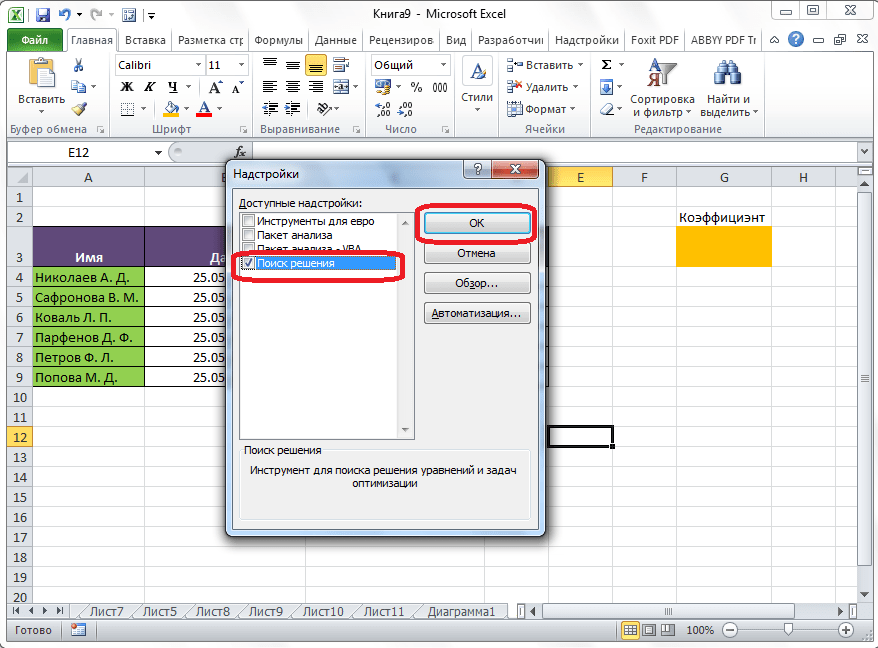
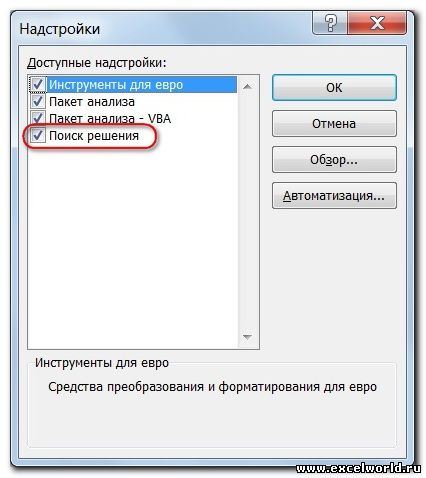
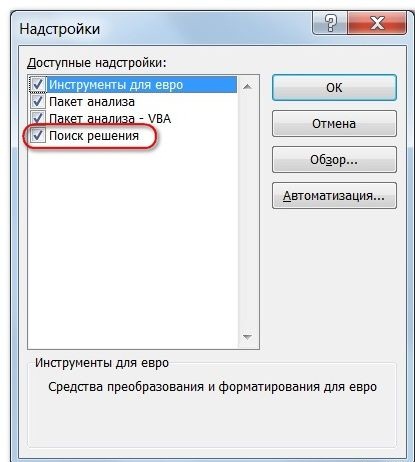
В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

Примечание . Окно Надстройки также доступно на вкладке Разработчик . Как включить эту вкладку читайте здесь .

После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно .

При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа .

О моделях

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет . Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка Поиск решения помогает определить лучший способ сделать что-то :

«Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
«Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

Определить план производства , при котором доход от реализации произведенной продукции максимальный;
Определить схему перевозок , при которой общие затраты на перевозку были бы минимальными;
Найти распределение нескольких станков по разным видам работ , чтобы общие затраты на производство продукции были бы минимальными;
Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией ). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание . В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра . Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра . Основные отличия Подбора параметра от Поиска решения :

Подбор параметра работает только с моделями с одной переменной;
в нем невозможно задать ограничения для переменных;
определяется не максимум или минимум целевой функции, а ее равенство некому значению;
эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Подготовка оптимизационной модели в MS EXCEL

Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет . Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).

Приведем алгоритм работы с Поиском решения , который советуют сами разработчики ( ]]> www.solver.com ]]> ):

Определите ячейки с переменными модели (decision variables);
Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
Запустите Поиск решения для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Простой пример использования Поиска решения

Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см. файл примера ).

Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) . Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.

После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.

Совет : в статье » Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями » показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.

Резюме

На самом деле, основной проблемой при решении оптимизационных задач с помощью Поиска решения является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью Поиска решения . Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью Поиска решения рассмотрено в этом разделе .

Поиску решения не удалось найти решения (Solver could not find a feasible solution)

Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете Симплекс метод решения линейных задач , то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).

Примечание . О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства .

В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.

При ограничении 17 м3 Поиск решения найдет решение.

Некоторые настройки Поиска решения

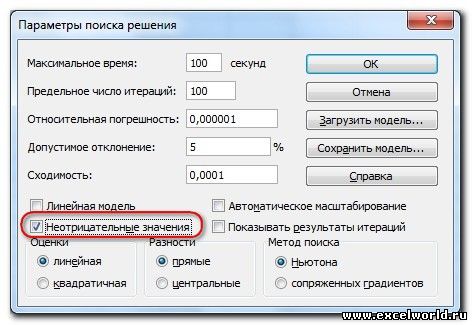
Метод решения Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2

Использование поиска решений в Excel 2010 для решения сложных задач

«Поиск решения» и является одним из таких инструментов, максимально удобных для «задач оптимизации». И если ранее вам еще не приходилось его использовать, то сейчас самое время исправить это.

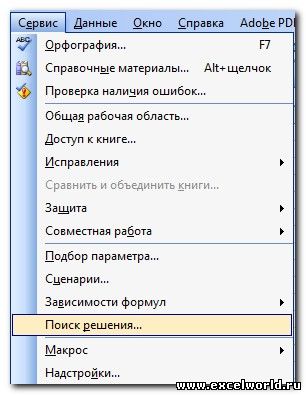
Итак – начинаем с установки данной надстройки (поскольку самостоятельно она не появится). К счастью сейчас сделать это можно достаточно просто и быстро – открываем меню «Сервис», а уже в нем «Надстройки»

Останется только в графе «Управление» указать «Надстройки Excel», а после нажать кнопочку «Перейти».

После этого несложного действия кнопка активации «Поиска решения» будет отображаться в «Данных». Как и показано на картинке

Давайте рассмотрим, как правильно используется поиск решений в Excel 2010, на нескольких простых примерах.

Пример первый.

Допустим, что вы занимаете пост начальника крупного отдела производства и необходимо правильно распределить премии сотрудникам. Допустим, общая сумма премий составляет 100 000 рублей, и необходимо, чтобы премии были пропорциональны окладам.

То есть, сейчас нам необходимо подобрать правильный коэффициент пропорциональности, чтобы определить размер премии относительно оклада.

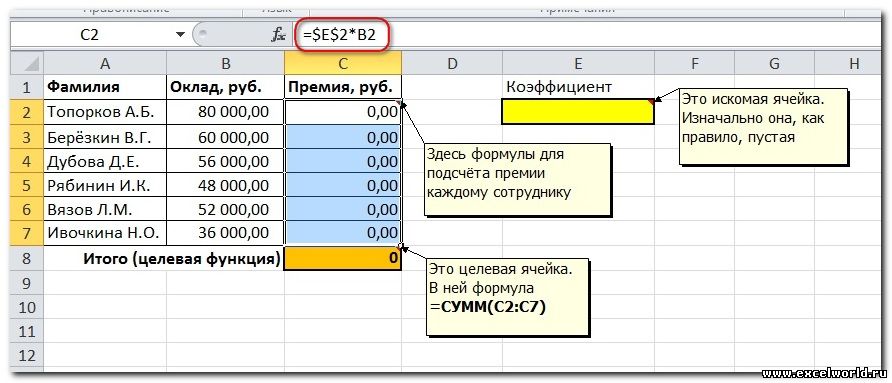
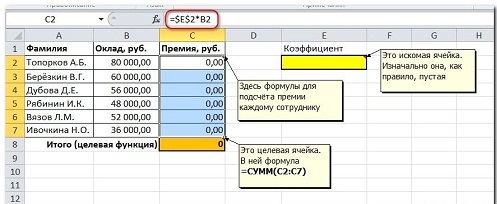
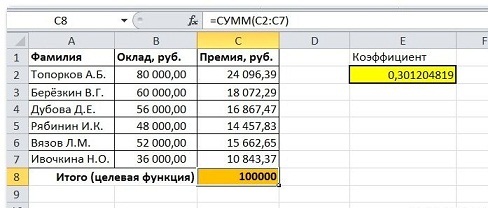
В первую очередь необходимо быстро составить (если ее еще нет) таблицу, где будут хранится исходные формулы и данные, согласно которым и можно будет получить желаемый результат. Для нас этот результат – суммарная величина премии. А сейчас внимание – целевая ячейка С8 должна быть с помощью формул связана с искомой изменяемой ячейкой под адресом Е2. Это критично. В примере мы связываем их используя промежуточные формулы, которые и отвечают за высчитывание премии каждому сотруднику (С2:С7).

Теперь можно активировать «Поиск решений». Откроется новое окошко, в котором нам необходимо указать необходимые параметры.

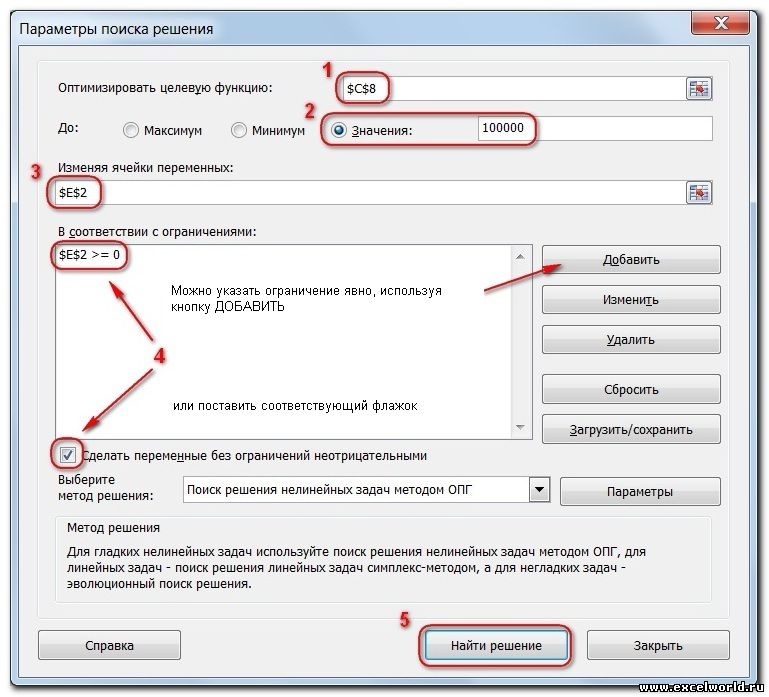
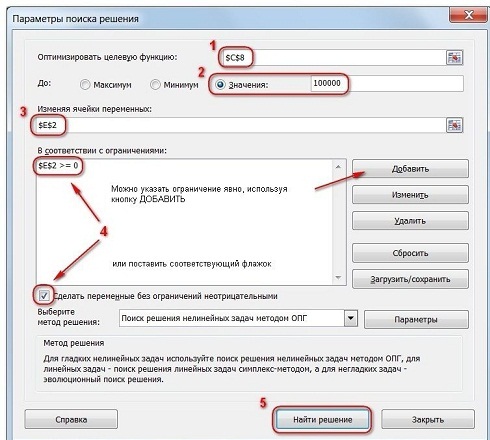
Под «1» обозначена наша целевая ячейка. Она может быть только одна.

«2» — это возможные варианты оптимизации. Всего можно выбрать «Максимальное», «Минимальное» или «Конкретное» возможные значения. И если вам необходимо именно конкретное значение, то его нужно указать в соответствующей графе.

«3» — изменяемых ячеек может быть несколько (целый диапазон или же отдельно указанные адреса). Ведь именно с ними и будет работать Excel, перебирая варианты так, чтобы получилось значение, заданное в целевой ячейке.

«4» — Если понадобиться задать ограничения, то стоит воспользоваться кнопкой «Добавить», но мы это рассмотрим чуть позже.

«5» — кнопка перехода к интерактивным вычислениям на основе заданной нами программы.

Но теперь вернемся к возможности изменять наше задание, воспользовавшись кнопкой «Добавить». Данный этап является довольно ответственным (не менее чем построение формул), поскольку именно ограничение позволяют получить правильный результат на выходе. Здесь все сделано максимально удобно, так что задать их вы сможете не только для всего диапазона сразу, но и для определенных ячеек.

Для этого можно использовать ряд определенных (и знакомых всем пользователям Excel 2010) знаков «=», «>=», « 3 досок, а модель «В» — на 1 м 3 больше (то есть – 4). От своих поставщиков вы за неделю получаете максимум 1700 м 3 досок. При этом модель «А» создается за 12 минут работы станка, а «В» — за 30 минут. Всего в неделю станок может работать не более 160 часов.

Вопрос – сколько всего изделий (и какой модели), должна выпускать фирма за неделю, чтобы получить максимально возможную прибыль, если полочка «А» дает 60 рублей прибыли, а «В» — 120?

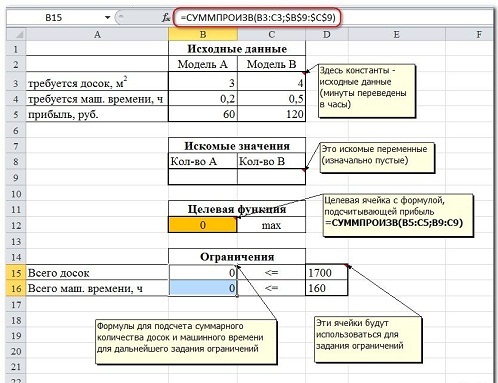
Поскольку порядок действия известен, то начинаем создавать необходимую нам таблицу с данными и формулами. Расположение ячеек, как и ранее, вы можете установить на свое усмотрение. Или же воспользоваться нашим

Любым удобным способом запускаем наш «Поиск решений», вводим данные, производим настройку.

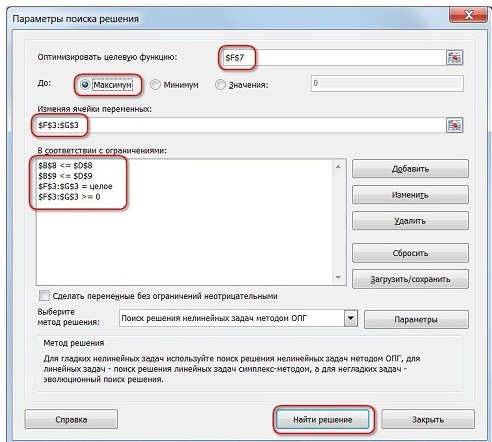
Итак, рассмотрим то, что мы имеем. В целевой ячейке F7 содержится формула, которая и рассчитает прибыль. Параметр оптимизации устанавливаем на максимум. Среди изменяемых ячеек у нас значится «F3:G3». Ограничения – все обнаруженные значения должны быть целыми числами, неотрицательными, общее количество потраченного машинного времени не превышает отметку 160 (наша ячейка D9), количество сырья не превышает 1700 (ячейка D8).

Конечно, в этом случае можно было не указывать адреса ячеек, а напрямую прописать необходимые цифровые значения, однако если использовать адреса, то изменения ограничений можно будет проводить и в таблице, что поможет рассчитывать прибыль этого предприятия в будущем, при смене исходных данных.

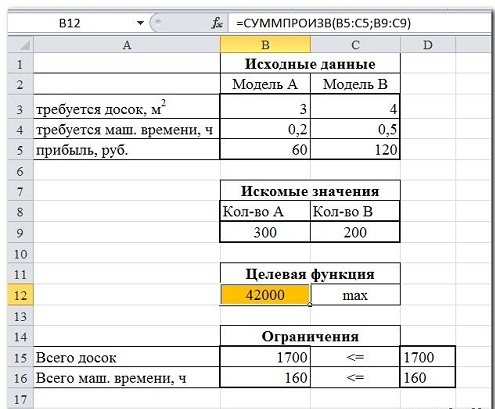
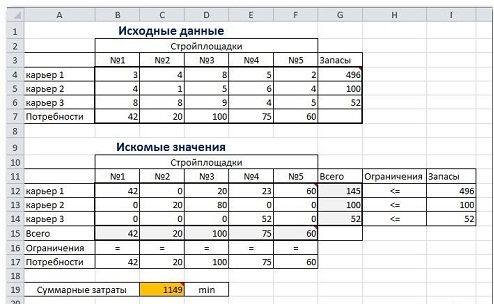
Активируем программу, и она подготавливает решение.

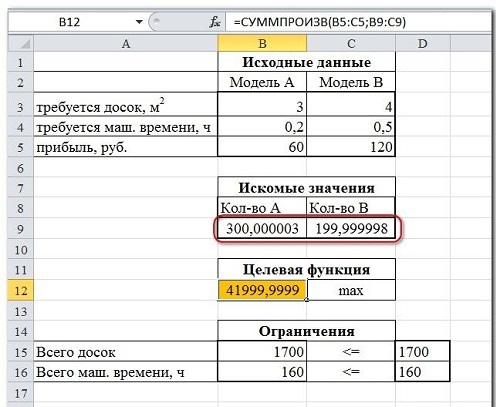
Впрочем, это не единственное решение и у вас вполне может выскочить другой результат. Это может произойти даже в том случае, если все данные были указаны верно и ошибок в формулах тоже не было

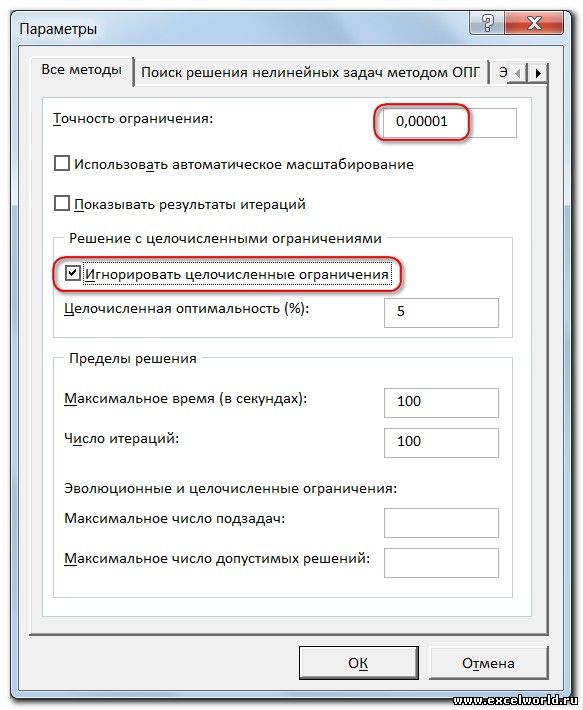
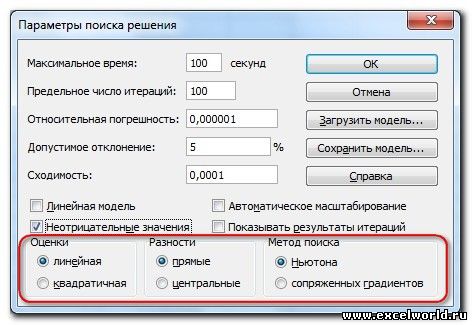
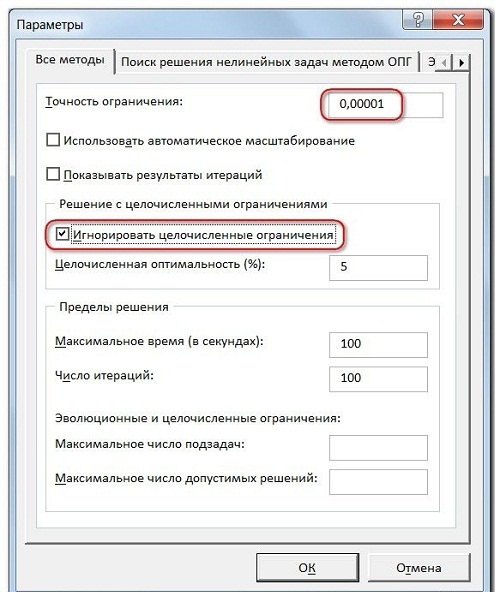
Да. Это может произойти даже в том случае, если мы сказали программе искать целое число. И если это вдруг произошло, то необходимо просто провести дополнительную настройку «Поиска решений». Открываем окно «Поиска решений» и входим в «Параметры».

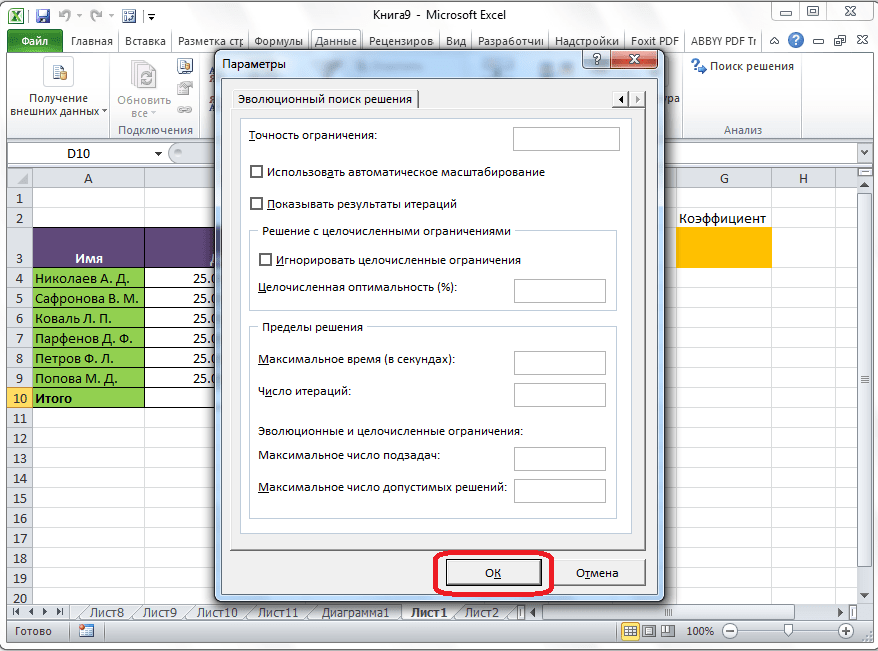
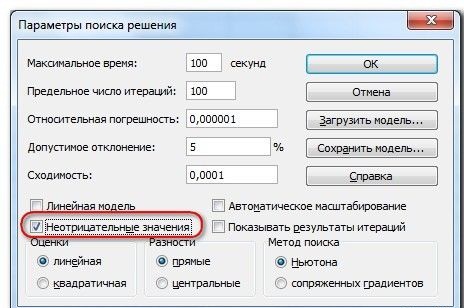
Наш верхний параметр отвечает за точность. Чем он меньше, тем выше точность и в нашем случае это значительно повышает шансы получить целое число. Второй параметр («Игнорировать целочисленные ограничения») и дает ответ на вопрос, как мы смогли получить такой ответ с тем, что в запросе явно указали целое число. «Поиск решений» просто проигнорировал это ограничение в связи с тем, что так ему сказали расширенные настройки.

Так что будьте предельно внимательны в будущем.

Третий и, пожалуй, последний пример. Попробуем минимизировать затраты транспортной компании используя поиск решений в Excel 2010.

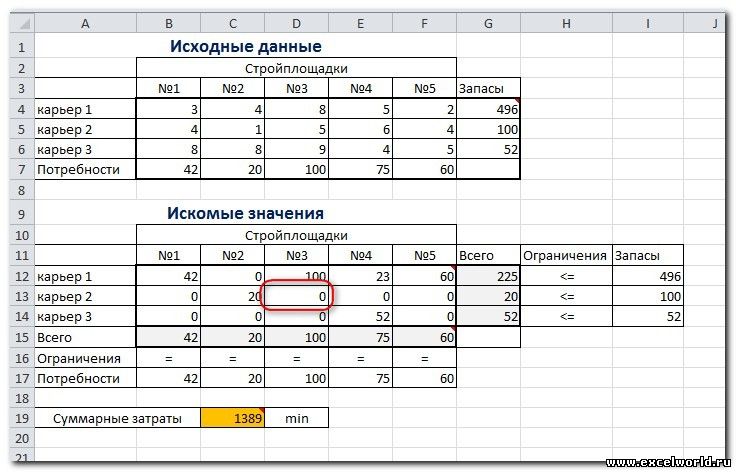
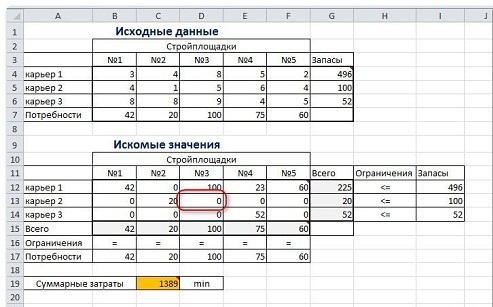
Итак, строительная компания дает заказ на перевозку песка, который берется от 3 поставщиков (карьеров). Его необходимо доставить 5 разным потребителям (которыми выступают строительные площадки). Стоимость доставки груза включена в себестоимость объекта, так что наша задача обеспечить доставку груза на стройплощадки с минимальными затратами.

Мы имеем – запас песка в карьере, потребность стройплощадок в песке, затрату на транспортировку «поставщик-потребитель».

Необходимо найти схему оптимальной перевозки груза (куда и откуда), при которой общая затрата на перевозку была бы минимальной.

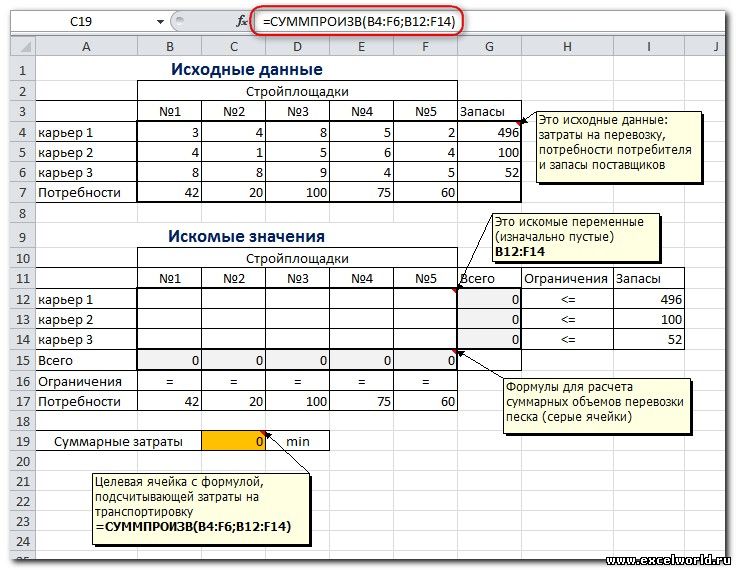
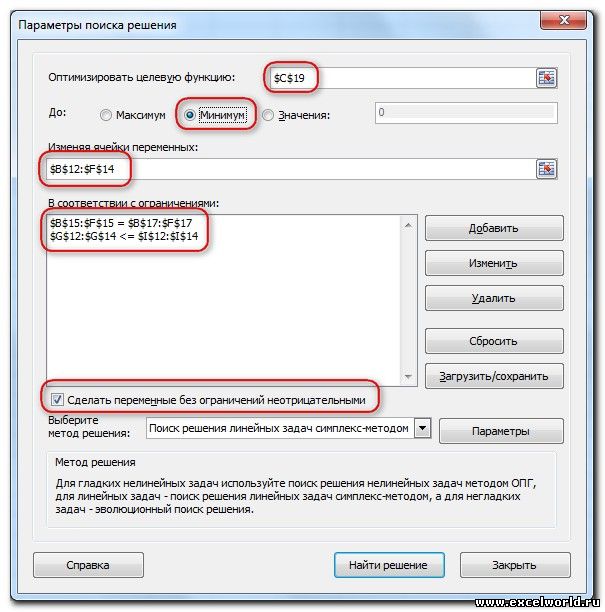
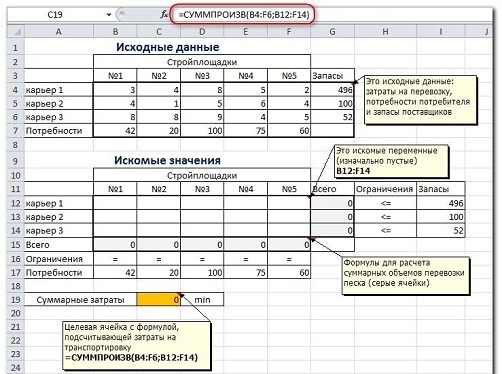
Серые ячейки нашей таблицы содержат формулы суммы по столбцам и строкам, а целевая ячейка – формула для общего подсчета затраты на доставку груза. Запускаем наш «Поиск решения» и вносим необходимые настройки

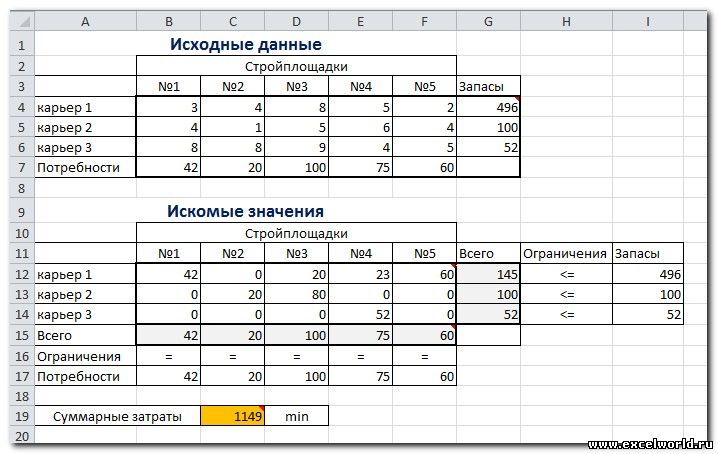
После этого приступаем к поиску решения этой задачки

Впрочем, не будем забывать, что достаточно часто транспортные задачи могут быть усложнены некоторыми дополнительными ограничителями. Допустим, возникло осложнение на дороге и теперь из карьера 2 просто технически невозможно доставить груз на стройплощадку 3. Чтобы учесть это, необходимо просто дописать дополнительное ограничение «$D$13=0». И если теперь запустить программу, то результат будет иным

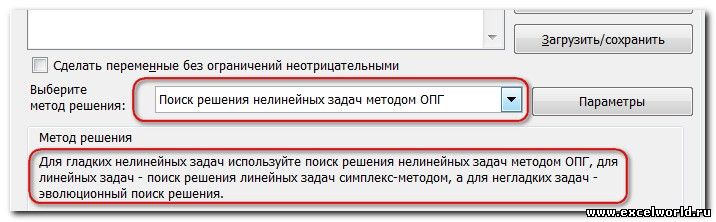
Напоследок осталось сказать только о выборе метода решения. И если задачка действительно очень сложная, то чтобы получить необходимый результат, скорее всего, понадобиться подобрать необходимый метод решения.

Вот и все по данному вопросу.

Мы выполнили поиск решений в Excel 2010 — для решения сложных задач

Источник

Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.

Включение функции

Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.

Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».

В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».

Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».

После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».

Подготовка таблицы

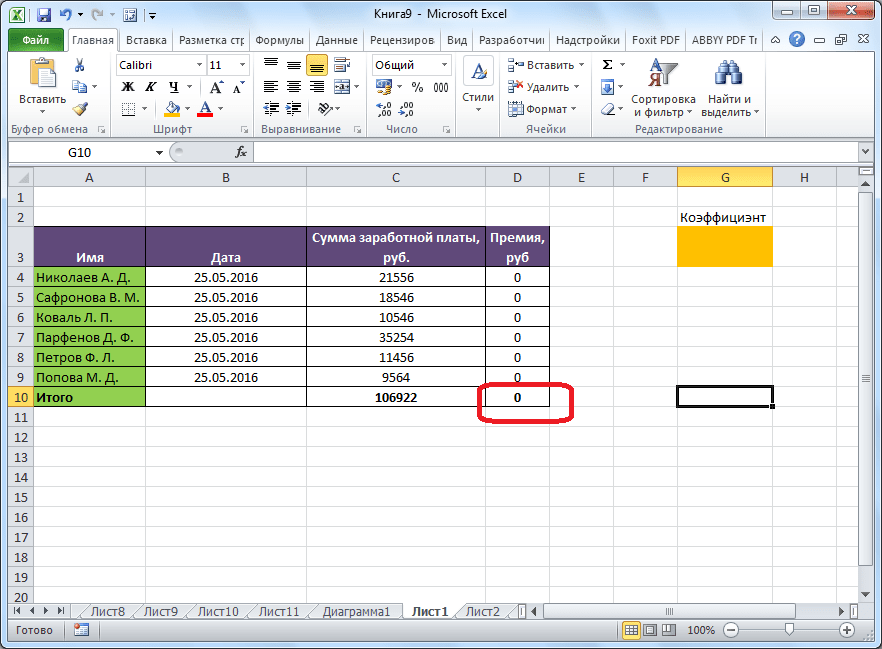
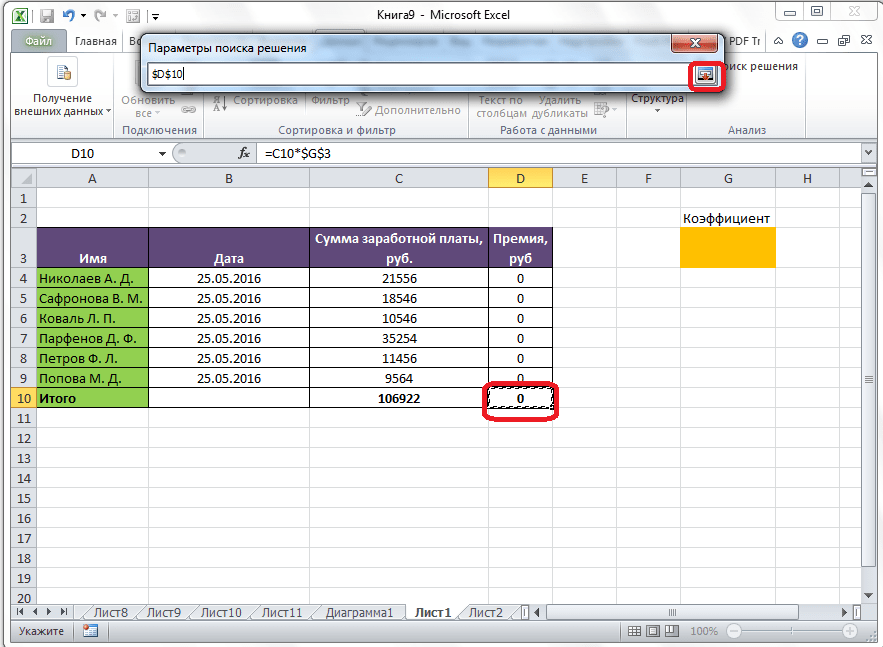
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

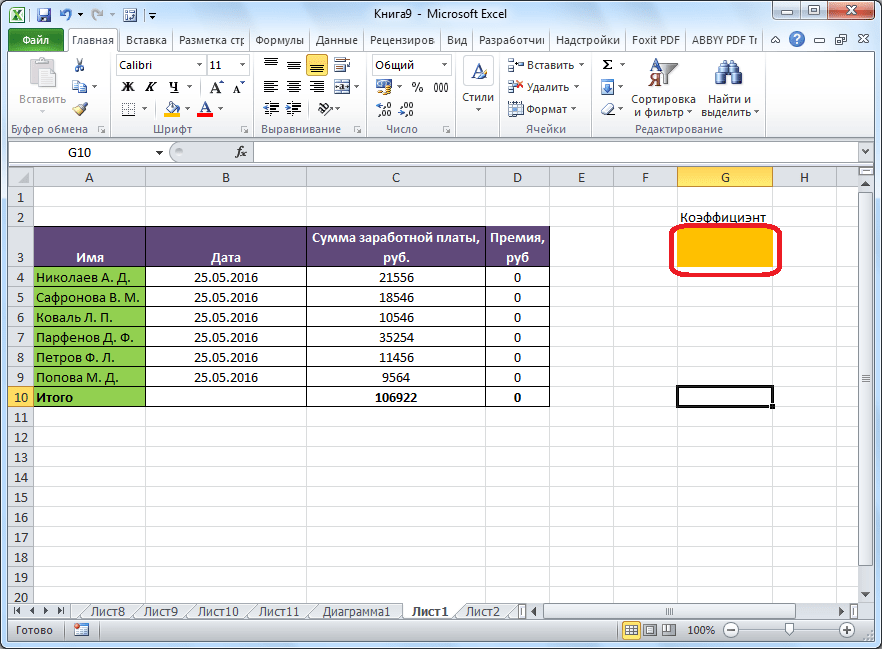
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

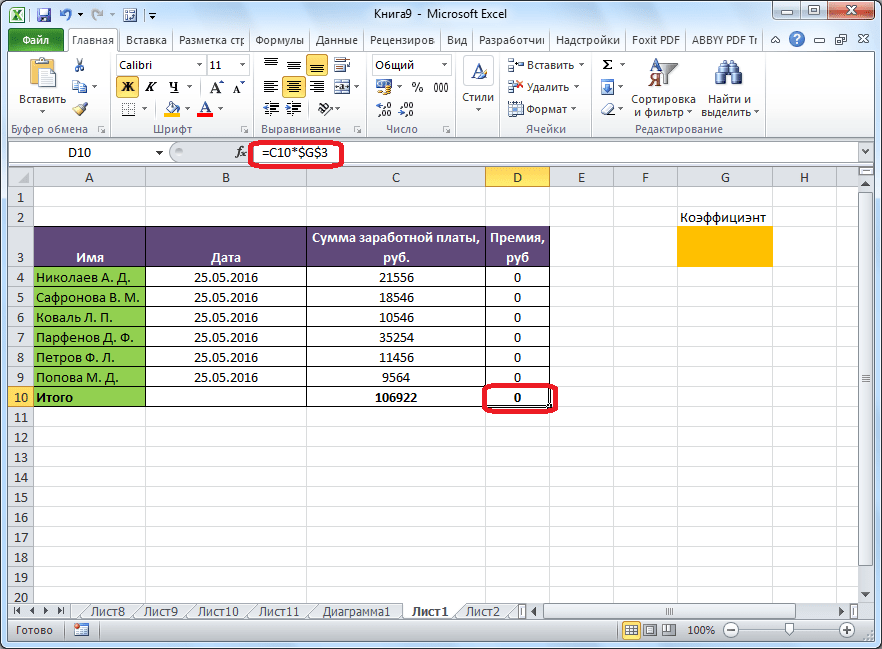
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

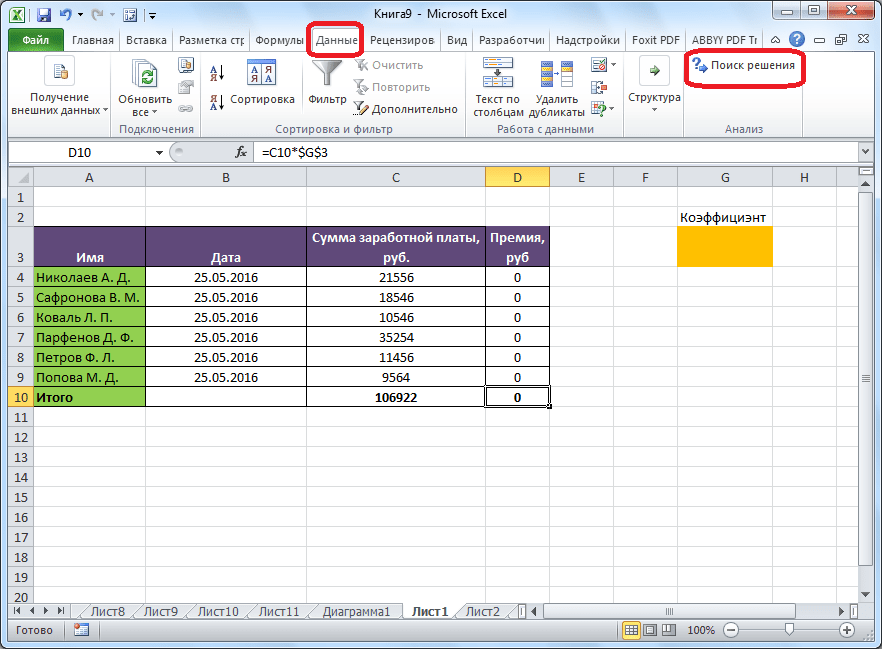
Запуск инструмента Поиск решения

После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».

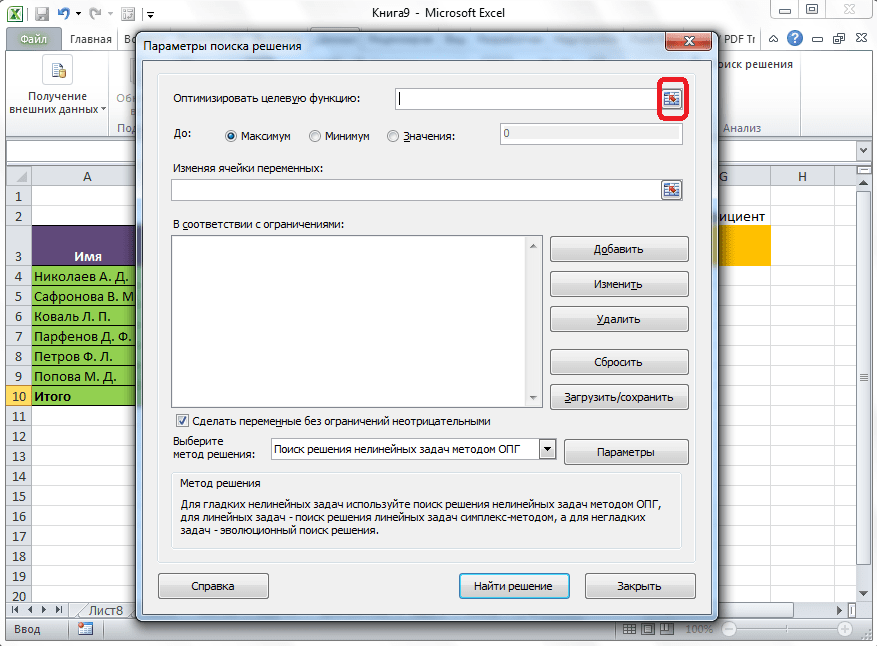
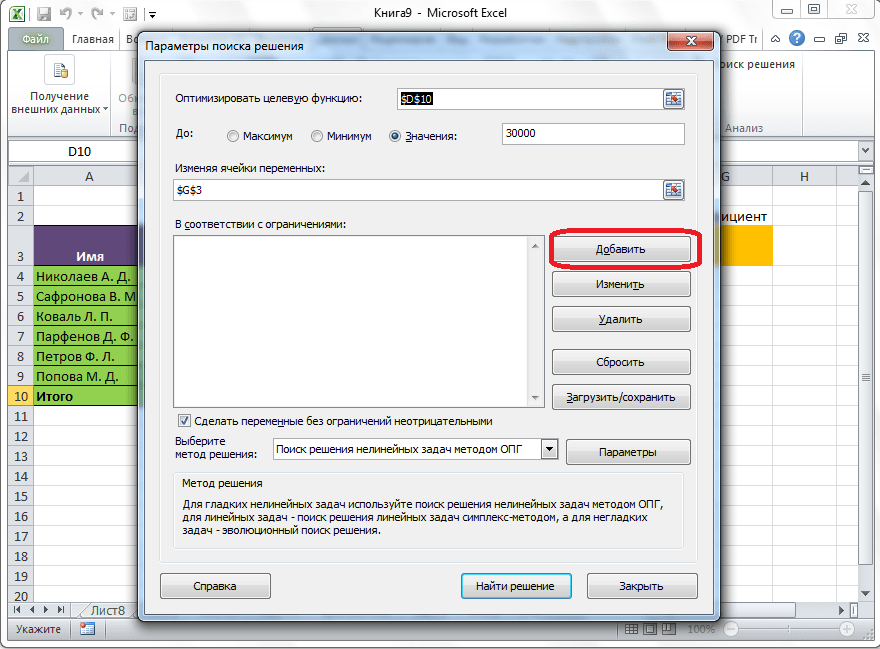
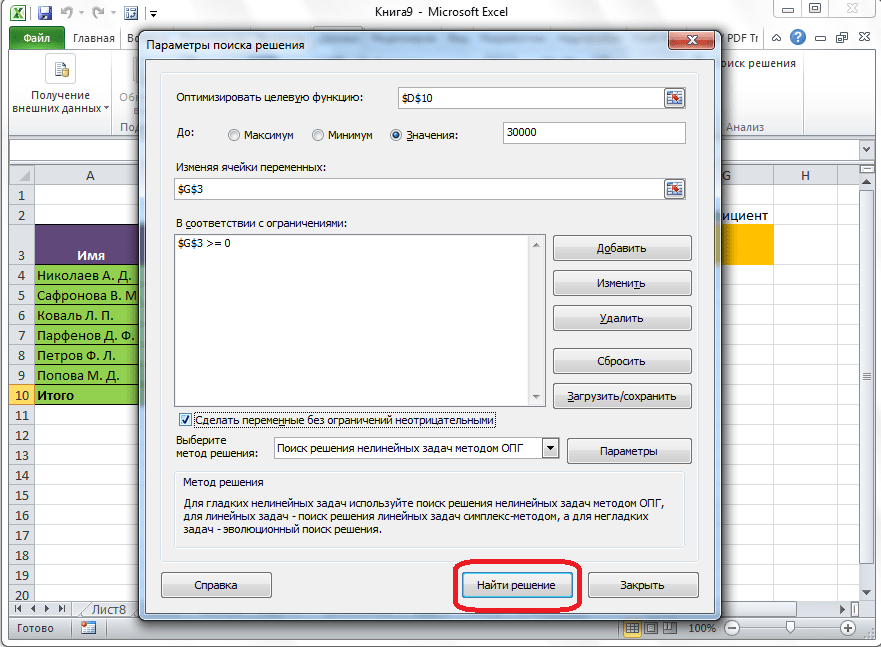
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.

После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.

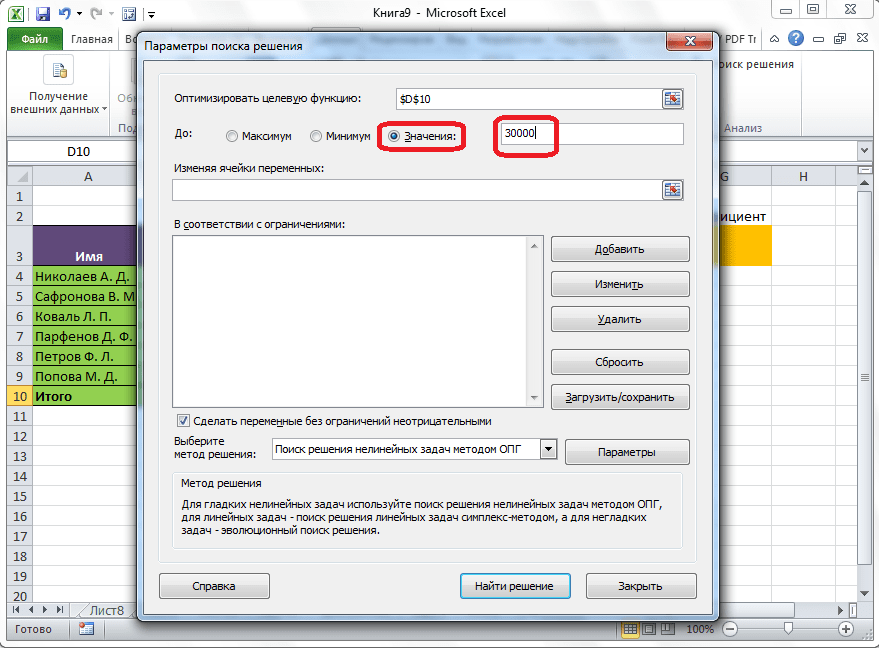
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.

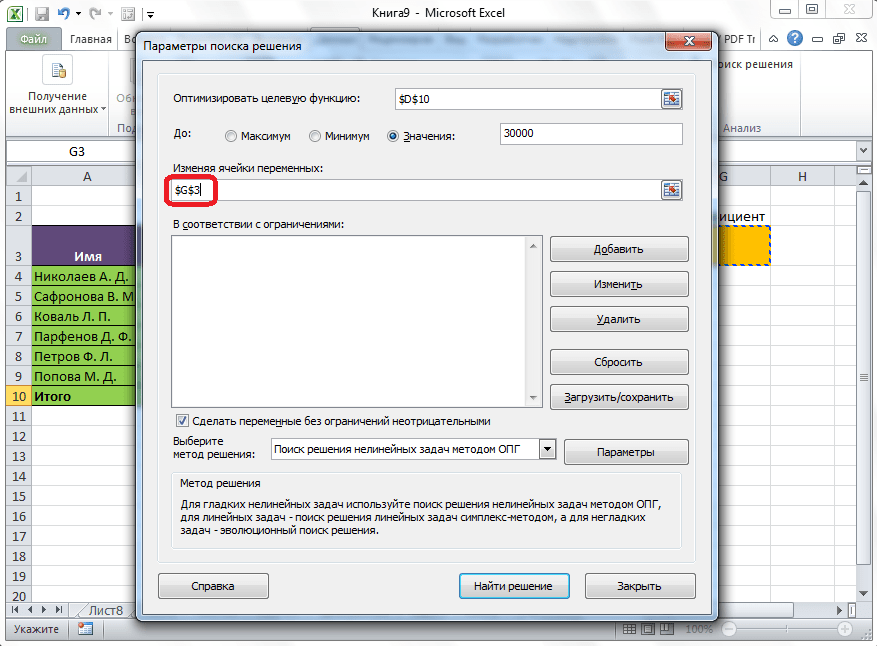
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.

В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».

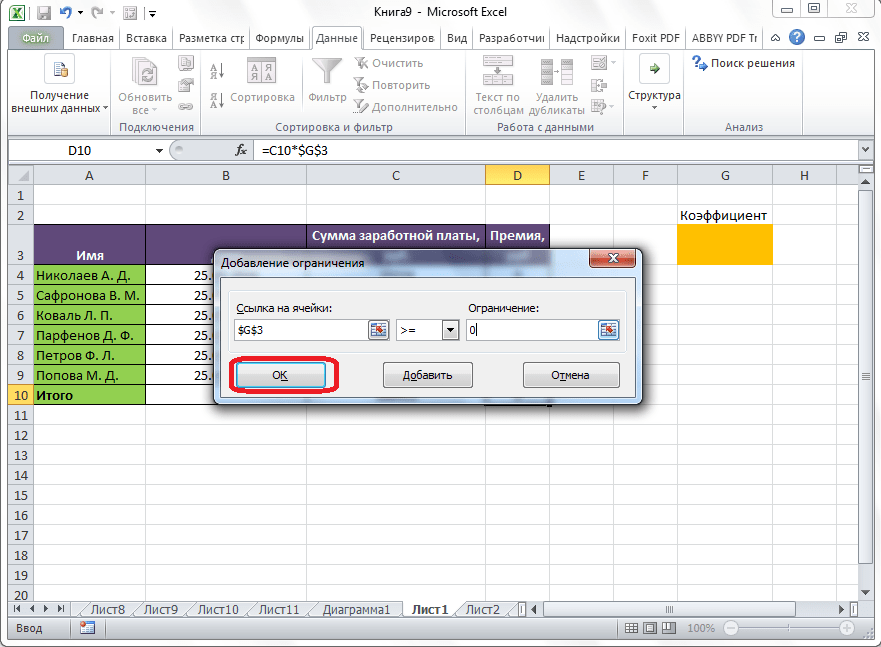
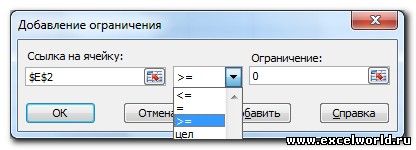
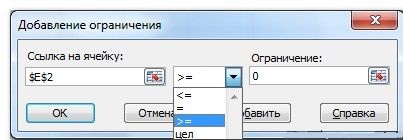
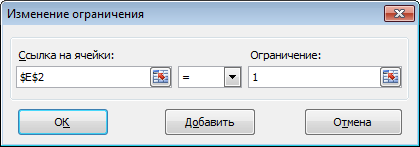
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.

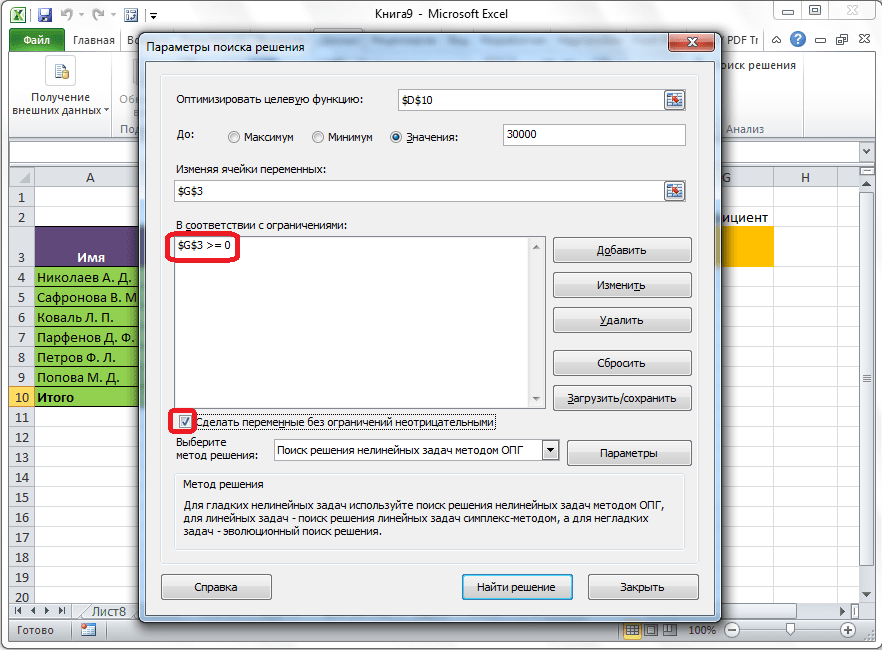
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.

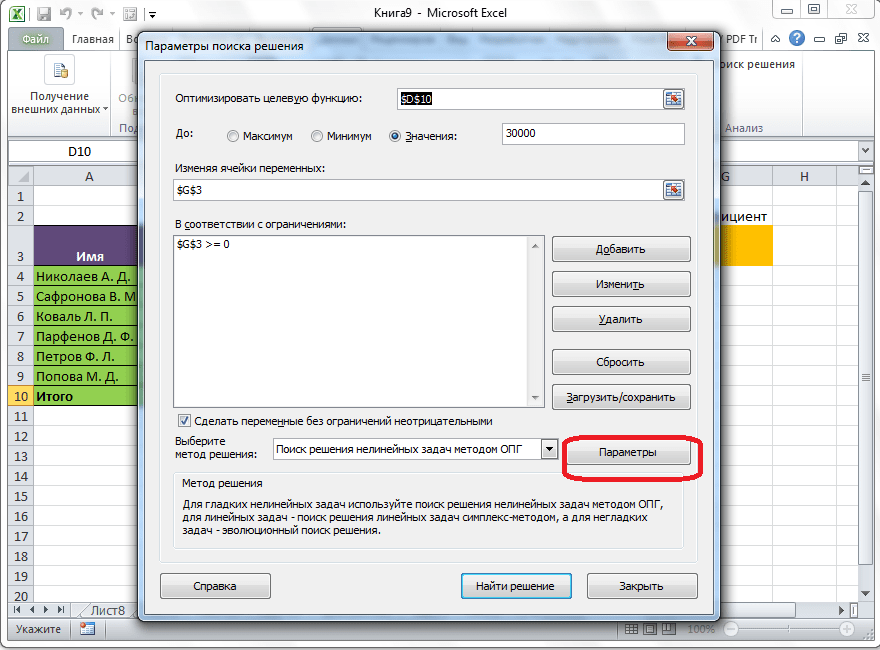
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».

Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.

После того, как все настройки установлены, жмем на кнопку «Найти решение».

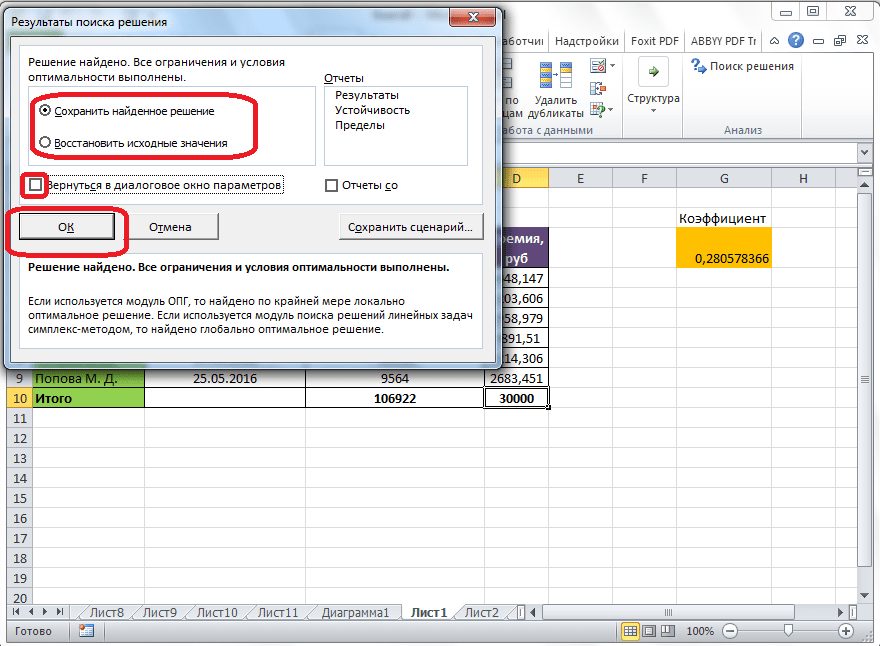
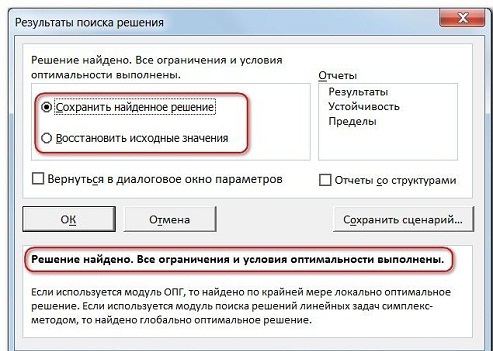
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».

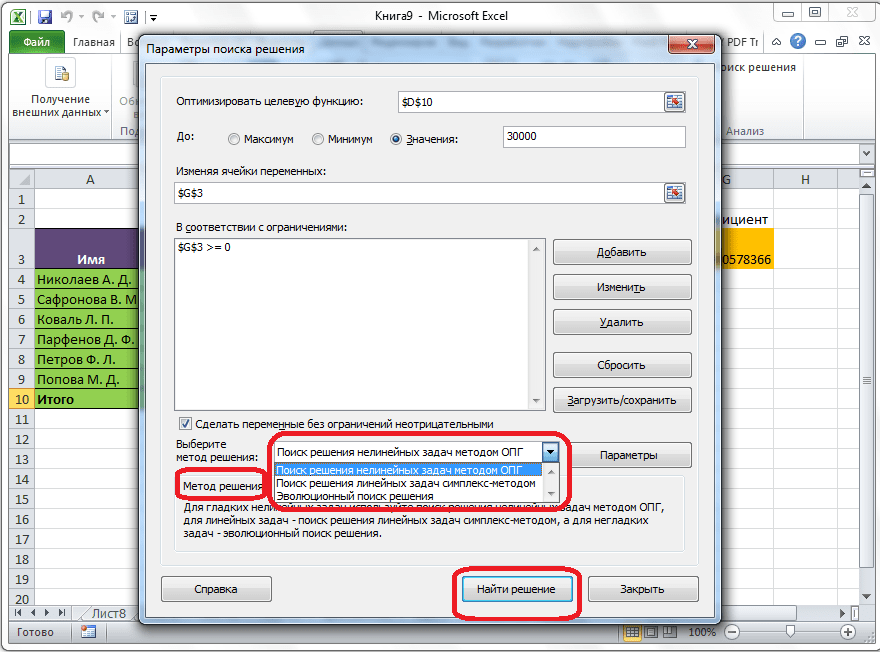
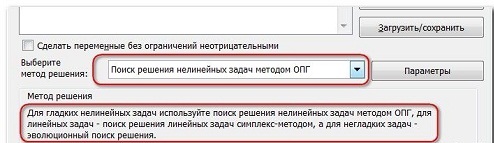
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.

Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.

Источник

Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».

Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.

Сделать это можно так:

для версий старше Excel 2007 через команду меню Сервис —> Надстройки;

начиная с Excel 2007 через диалоговое окно Параметры Excel

Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.

В версиях до Excel 2007 аналогичная команда появится в меню Сервис

Разберём порядок работы Поиска решения на простом примере.

Пример 1. Распределение премии

Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.

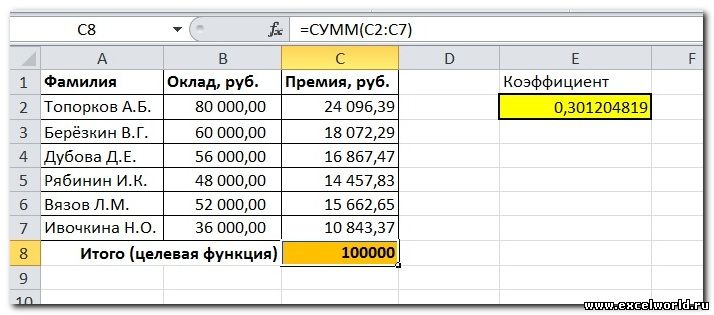
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).

Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:

Начиная с Excel 2010

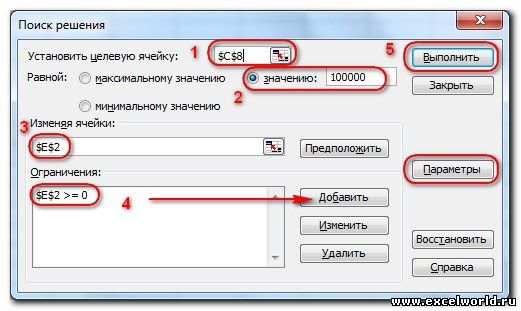
До Excel 2010

Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
Кнопка, включающая итеративные вычисления с заданными параметрами.

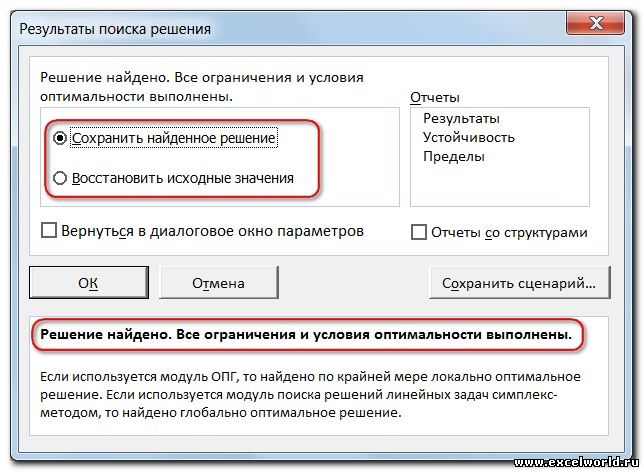
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.

Начиная с Excel 2010

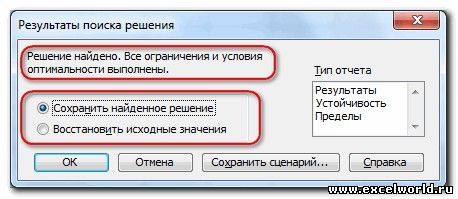
До Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных книжных полок.

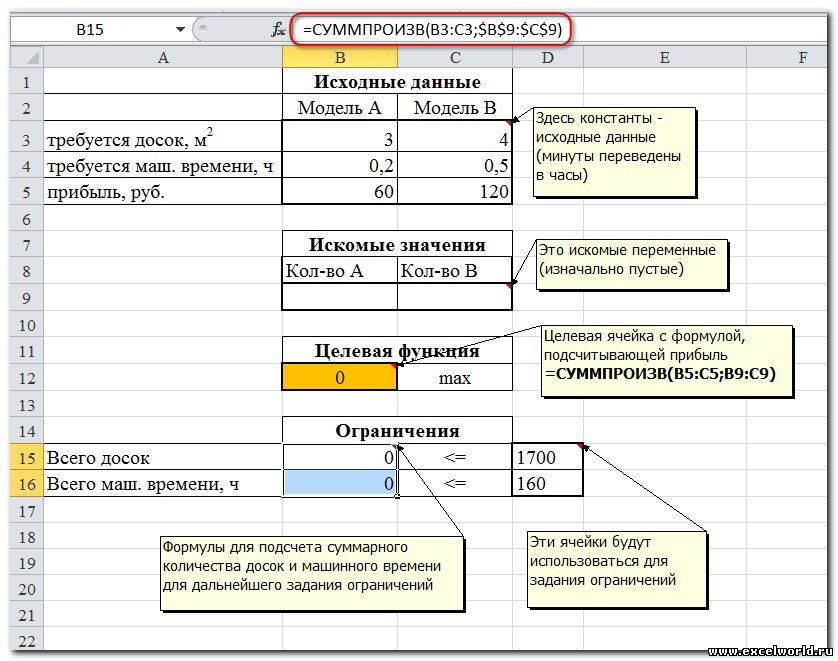
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?

Порядок действий нам уже известен.

Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке

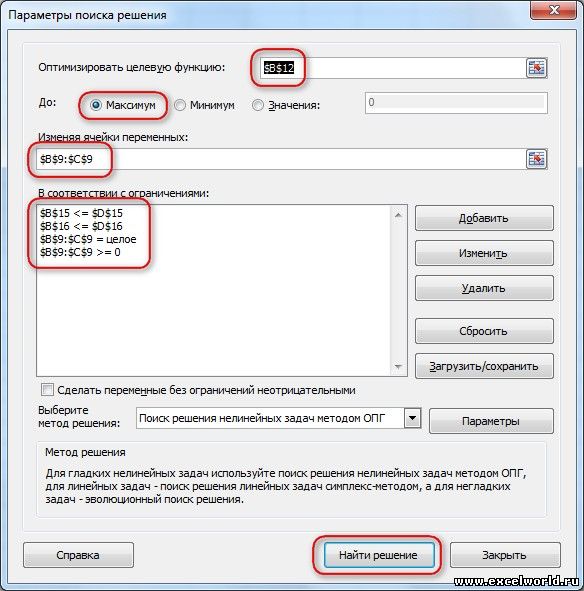
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры

Целевая ячейка B12 содержит формулу для расчёта прибыли
Параметр оптимизации — максимум
Изменяемые ячейки B9:C9
Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
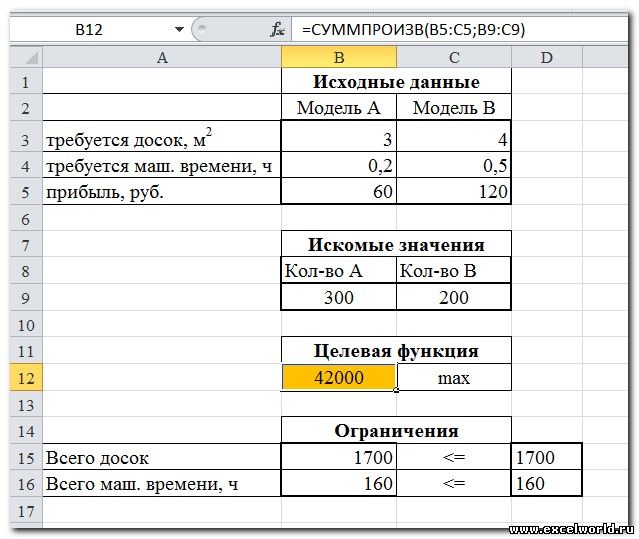
Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

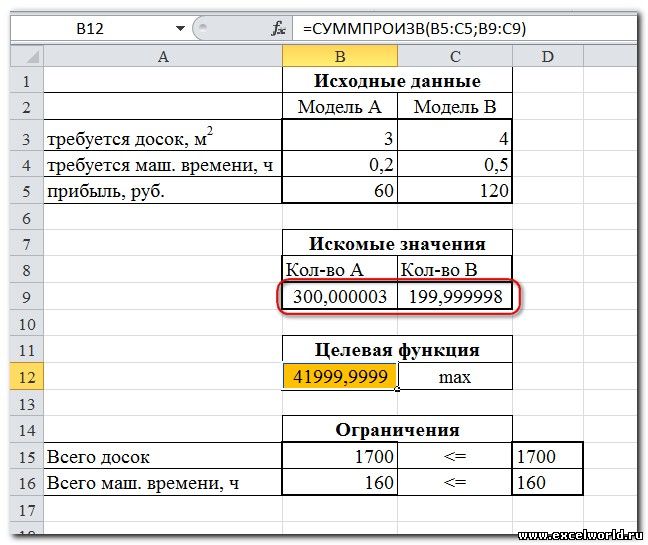
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:

И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно

Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.

Пример 3. Транспортная задача (минимизация затрат)

На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.

Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.

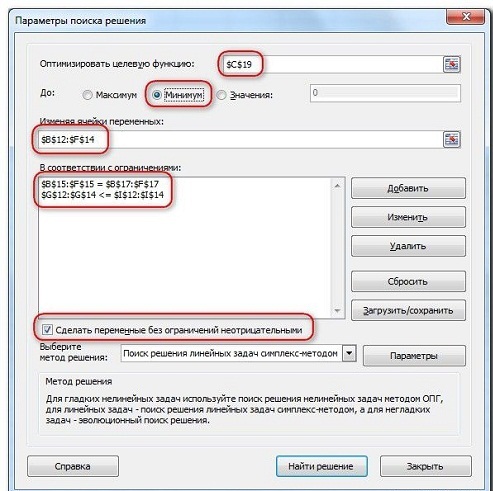
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат

И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения

Начиная с Excel 2010

До Excel 2010

В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:

Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?

Источник

Значительная часть задач, которые решаются с помощью электронных таблиц, предполагают, что для обнаружения нужного результата у пользователя уже есть хоть какие-то исходные данные. Однако Exсel 2010 располагает необходимыми инструментами, с помощью которых можно решить эту задачу наоборот – подобрать нужные данные, чтобы получить необходимый результат.

Останется только в графе «Управление» указать «Надстройки Excel», а после нажать кнопочку «Перейти».

Давайте рассмотрим, как правильно используется поиск решений в Excel 2010, на нескольких простых примерах.

Пример первый.

Под «1» обозначена наша целевая ячейка. Она может быть только одна.

«5» — кнопка перехода к интерактивным вычислениям на основе заданной нами программы.

Для этого можно использовать ряд определенных (и знакомых всем пользователям Excel 2010) знаков «=», «>=», «<=», а также варианты «цел» (от «целое»), «бин» («бинарное» или же «двоичное»), «раз» («все разные»).

Но в нашем примере ограничение может быть лишь одно – положительный коэффициент. Задать его, конечно, можно несколькими способами – либо используя «Добавить» (что называют «явно указать ограничение»), либо просто отметить действующей функцию «Сделать переменные без ограничений неотрицательными». Это можно сделать в надстройке «Поиск решения», нажав на кнопочку «Параметры».

Кстати, после подтверждения параметров и запуска программы (кнопочка «Выполнить»), вы сможете в таблице просмотреть полученный результат. Тогда программа продемонстрирует окошко «результатов поиска».

Если продемонстрированный результат полностью вам подходит, тогда останется только вновь подтвердить его (кнопочка «ОК»), что зафиксирует результат в вашей таблице. Если же что-то в расчетах вас не устраивает, то необходимо отменить результат (кнопочка «Отмена»), вернуться к предыдущему состоянию нашей таблицы и исправить допущенные ошибки.

Правильное решение задачи примера должно получиться вот таким

Очень важно — чтобы получить правильный результат даже при малейшем изменении исходных данных необходимо перезапустить «Поиск решений».

Чтобы более подробно взглянуть на то, как действует данная программа, давайте разберем еще один пример.

Допустим, вы являетесь владельцем крупного мебельного предприятия и необходимо наладить производство таким образом, чтобы получить максимально возможную прибыль. Вы производите только книжные полки, при этом всего двух моделей – «А» и «В», производство которых ограничивается исключительно наличием (или отсутствием) высококачественных досок, а также машинным временем (обработка на станке).

Модель «А» требует 3 м³ досок, а модель «В» — на 1 м³ больше (то есть – 4). От своих поставщиков вы за неделю получаете максимум 1700 м³ досок. При этом модель «А» создается за 12 минут работы станка, а «В» — за 30 минут. Всего в неделю станок может работать не более 160 часов.

Любым удобным способом запускаем наш «Поиск решений», вводим данные, производим настройку.

Активируем программу, и она подготавливает решение.

Так что будьте предельно внимательны в будущем.

После этого приступаем к поиску решения этой задачки

Вот и все по данному вопросу.

Мы выполнили поиск решений в Excel 2010 — для решения сложных задач

Источник

Оптимизация значений таблицы Excel, удовлетворяющих определенным критериям, может быть сложным процессом. К счастью, Microsoft предлагает надстройку Решение проблем для численной оптимизации. Хотя данный сервис не может решить всех проблем, он может быть полезным в качестве инструмента что-если. Данный пост посвящен надстройке Решение проблем в Excel.

Надстройка Решение проблем доступна во всех версиях Excel. Обратите внимание, что скриншоты могут не соответствовать вашей версии. Несмотря на то, что некоторые функции могут менять свое местоположение в зависимости от версии надстройки, функционал остается практически неизменным.

Что такое Поиск решений

Поиск решений – надстройка Excel, которая помогает найти решение с помощью изменения значений целевых ячеек. Целью может быть минимизация, максимизация или достижение некоторого целевого значения. Проблема решается путем регулировки входных критериев или ограничений, определенных пользователем.

Где в Excel поиск решений

Надстройка Поиск решений поставляется вместе с Excel, но по умолчанию отключена. Чтобы включить его, перейдите по вкладке Файл в группу Параметры. В появившемся диалоговом окне Параметры, выберите Надстройки -> Управление: Надстройки Excel -> Перейти. В окне Надстройки устанавливаем галочку напротив поля Поиск решения, жмем ОК.

Теперь во вкладке Данные появилась новая группа Анализ с кнопкой Поиск решения.

Пример использования Поиска решения

Данный пост основан на примере использования Надстройки Поиск решения. Файл совместим со всеми версиями Excel.

Определение проблемы

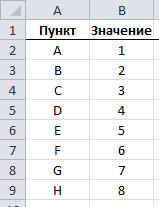
Предположим, что у нас есть набор данных, состоящий из 8 пунктов, каждому из которых соответствует свое значение.

… и нам необходимо скомбинировать значения в две группы так, чтобы суммы значений этих групп примерно совпадали.

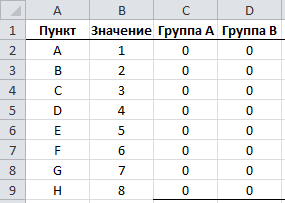
Для начала требуется определить каждый пункт к какой-нибудь группе.

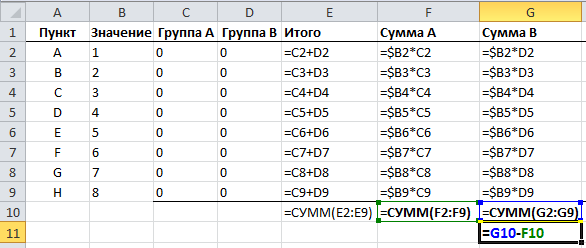
Чтобы указать привязанность пункта к группе, будем помечать их единицей (1), в противном случае нулем (0).

В следующем столбце мы будем суммировать значения каждого пункта в группе, и затем подведем итог в конце столбца.

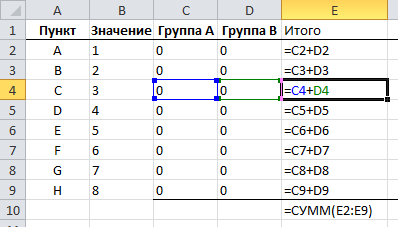
Нам также необходимо обработать значение каждого пункта в каждой группе, для этого умножаем значение пункта на значение группы, соответствующее этому пункту.

Наконец, нам необходимо свести сумму групп и работать с разницей между ними.

Наша задача минимизировать разницу между суммами групп.

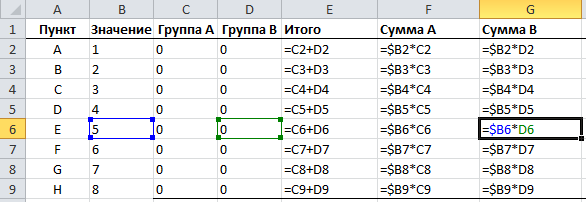
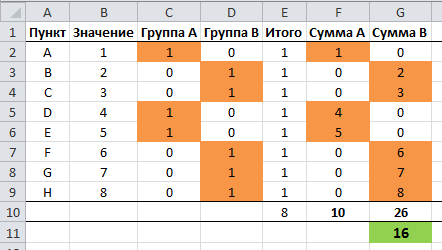
Теперь мы можем присвоить каждой группе пункты, для этого вручную проставляем единицы в столбцах С и D. Excel отобразит разницу сумм групп в ячейке G11.

Для большей наглядности я добавил условное форматирование для ячеек, имеющих значение >0.

Проблема в том, что количество возможных комбинаций 2⁸, т.е. 256 вероятных ответов на вопрос. Если на каждый из них тратить по 5 секунд, это займет у нас 21,3 минуты, предполагая, что мы сможем выдержать темп и запомнить лучшую комбинацию.

Вот где Поиск решения находит применение.

Поиск оптимального решения в Excel

Чтобы применить сервис Поиск решения, нам необходимо определить ряд требований, правил и ограничений, которые позволят надстройке найти правильный ответ.

Наши правила

Наше основное требование – это минимизировать разницу между двумя группами. В нашем примере она находится в ячейке G11 – Группа B минус Группа A. Нам нужно, чтобы значение в ячейке G11 было настолько малым насколько это возможно, но больше или равно 0.

Мы также знаем, что пункт может находиться либо в Группе A, либо в Группе B, к тому он не может быть дробным. Таким образом у нас два ограничения для каждого элемента:

Во-первых: Значение элемента в колонке Итог должна равняться единице.

Во-вторых: Значения элементов в группах должны быть целыми.

Мы также знаем, что общее количество элементов 8, это еще одно ограничение. Как использовать эти ограничения мы обсудим в следующем разделе.

Диалоговое окно Поиска решения

В этом разделе описано окно надстройки Поиск решения и его использования для определения проблемы.

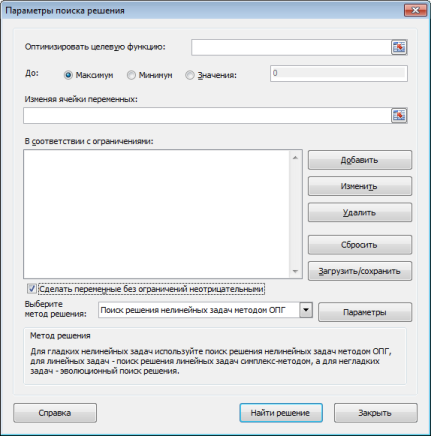
Пустое окно Поиска решения

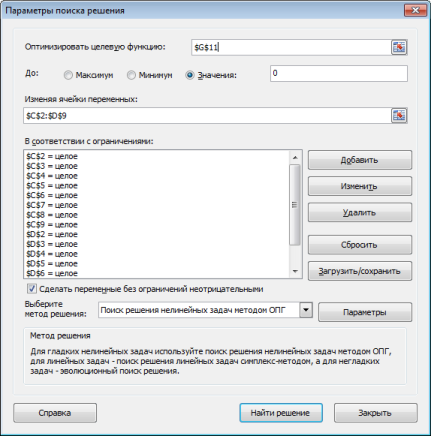
Заполненное окно Поиска решения

Оптимизировать целевую функцию

Это целевая ячейка, в которой мы пытаемся решить проблему. Наша целевая ячейка G11 – разница в группах.

До

Здесь мы указываем, каких результатов хотим добиться от целевой функции.

Мы хотим, чтобы суммы обоих групп совпадали, т.е. чтобы разница сумм была равна 0. Это может показаться странным, но нам не требуется минимизировать разницу, потому что при этом все элементы будут помещены в Группу A, что приведет к значению ячейки G11 меньше нуля.

Другой способ наложения ограничения – изменить G11 на =ABS(G10-F10). При этом мы сможем установить маркер на Минимум, как результат достижения целевой функции.

Но пока мы остановимся на формуле =G10-F10 и установим маркер в значение равным 0.

Изменяя ячейки переменных

Изменяемые ячейки – ячейки, которые надстройка попытается изменить, чтобы решить задачу. В нашем случае это привязка элемента к конкретной группе: $C$2:$D$9.

В соответствии с ограничениями

Ограничения – это правила, которые лимитируют возможные решения проблемы.

Нам необходимо добавить несколько ограничений в наш список:

В колонке Итого каждый элемент должен равняться 1
Элементы групп должны быть целым числом
Сумма значений столбца Итого должна равняться 8

Чтобы наложить ограничения, жмем кнопку Добавить

Для каждой ячейки диапазона E2:E9 устанавливаем ограничение значения равным 1
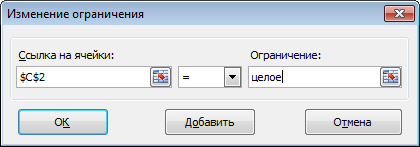
Для каждой ячейки диапазона C2:D9 устанавливаем ограничение значение целое число.
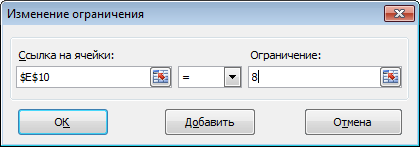
Необходимо добавить ограничение на сумму обоих групп, ячейка E10 = 8.

Вы можете Изменить или Удалить ограничение, если допустили ошибку, выбрав конкретное ограничение и нажав соответствующие кнопки в диалоговом окне.

Загрузить/сохранить параметры поиска решений

Сервис поиска решений позволяет сохранять и загружать параметры надстройки. Для этого в окне существует кнопка Загрузить/сохранить. Параметры модели сохраняются в диапазон, который вы указали ранее. Данный подход позволяет быстро настраивать и изменять параметры Поиска решения.

Запуск поиска оптимального решения в Excel

Предупреждение!!! Надстройка поиск решения является сложной вычислительной надстройкой, поэтому перед запуском сохраните рабочую книгу.

Прежде чем запустить модель, необходимо задать еще несколько параметров, чтобы убедиться, что сервис отработает корректно. В основном диалоговом окне убедитесь, что стоит маркер напротив поля Сделать переменные без ограничений неотрицательными. В этом же окне нажмите кнопку Параметры.

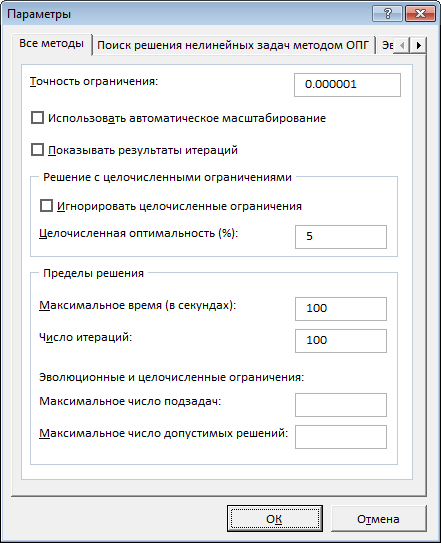
Два параметра, которые необходимо будет менять время от времени:

Точность ограничения: значение от 0 до 1, где, чем больше цифра, тем больше ограничение

Целочисленная оптимальность: показывает насколько далеко от целого числа ограничение имеет право быть.

Запуск модели

Чтобы запустить надстройку нажмите кнопку Найти решение в основном окне.

В строке состояния вы увидите ряд статических данных, которые будут отображать внутреннюю работу надстройки. Как правило, они быстро меняются, и читать их сложно. Если модель сложная, то работа может остановится на некоторое время, надстройка обычно восстанавливается от этих проблем сама.

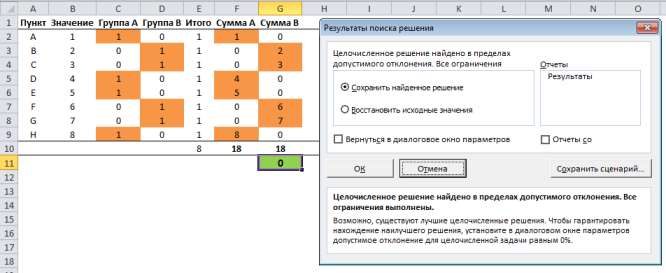
После того, как Поиск решения закончит свою работу, Excel отобразит диалоговое окно Результаты поиска решения с некоторой информацией. Первое, на что стоит обратить внимание – это надпись Решение найдено в пределах допустимого отклонения. Если решение найдено, ячейки рабочей книги изменятся с предложенным решением.

Теперь у вас есть 4 варианта на выбор:

— Запустить отчет

— Сохранить сценарий

— Восстановить исходные значения

— Сохранить найденное решение

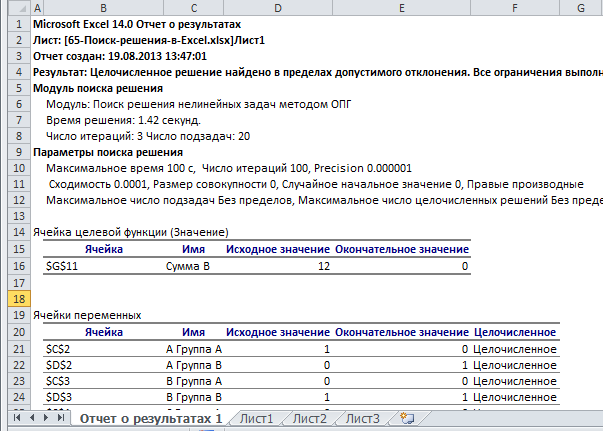
Запустить отчет

Вы можете создать отчет, выбрав доступные из списка отчетов. Будет создан новый лист Отчет о результатах1.

Обратите внимание, что в зависимости от установленных вами ограничений, будут доступны различные отчеты.

Сохранить сценарий

Если вы нажмете кнопку Сохранить сценарий, Excel откроет следующее диалоговое окно:

Где необходимо ввести название вашего сценария модели и нажать кнопку ОК.

Все сценарии доступны в Диспетчере сценариев, который находится во вкладке Данные в группе Работа с данными –> Анализ что-если -> Диспетчер сценариев.

Вернуться к модели

К тому же, вы можете вернуться к модели и:

— Восстановить исходные значения

— Сохранить найденное решение

Проверка результатов

Сервис Поиск решения, вероятно, самая непредсказуемая система в Excel. Таким образом, все найденные решения, которые он выдает необходимо перепроверять вручную, для дальнейшего использования.

Данная проверка на реалистичность должна начинаться с подтверждения, что все результаты удовлетворяют заданным критериям:

— Являются ли результаты примерно похожими на ваши ожидания?

— Не нарушены ли максимумы и минимумы?

Источник

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.

Основные параметры поиска решений

Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.

Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:

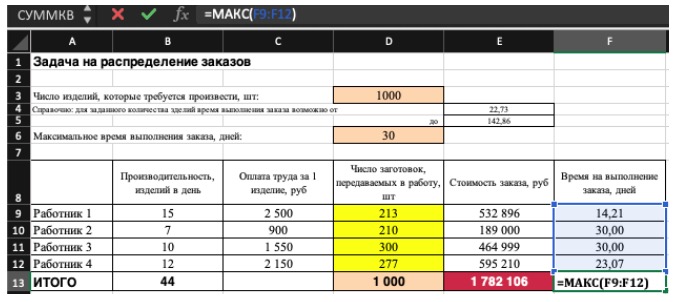
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.

Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Пример использования поиска решений

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

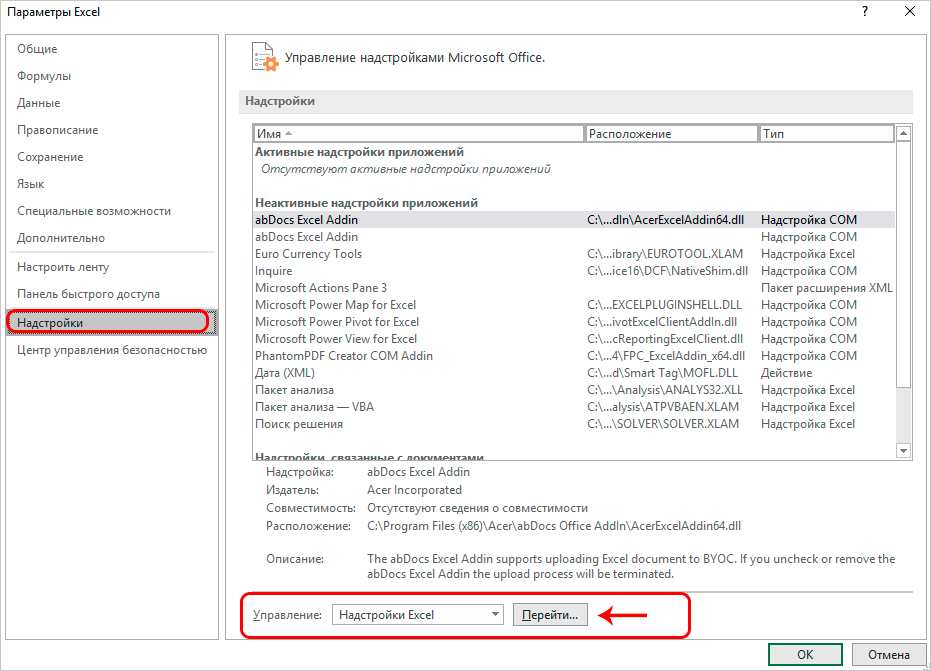
нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
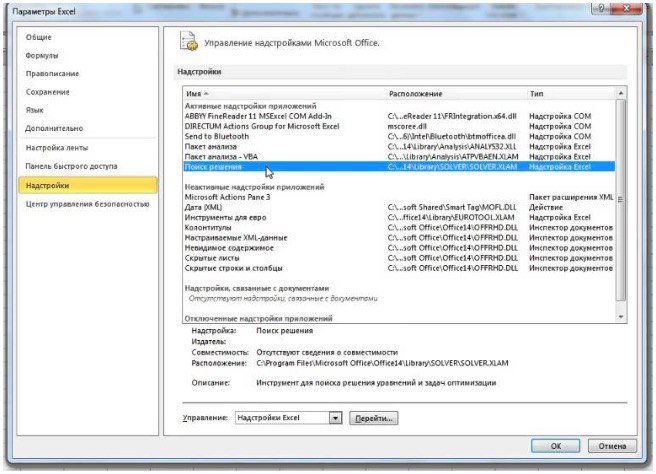
в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

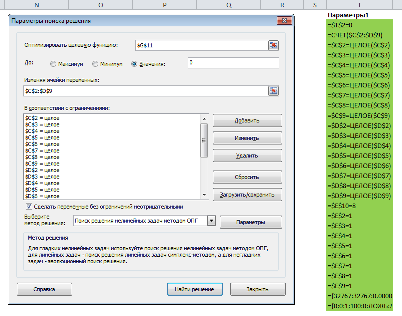
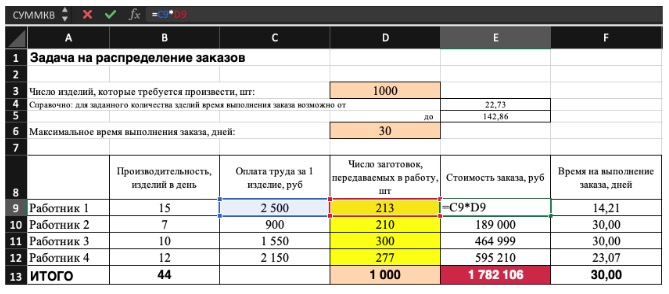
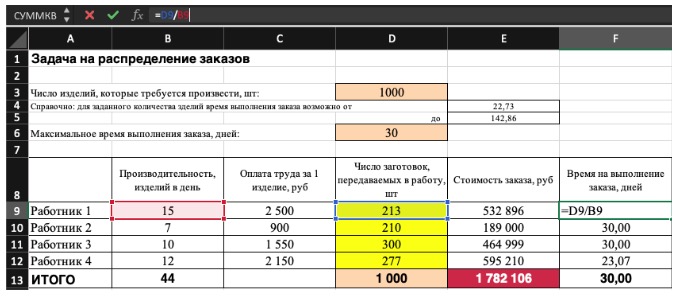
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

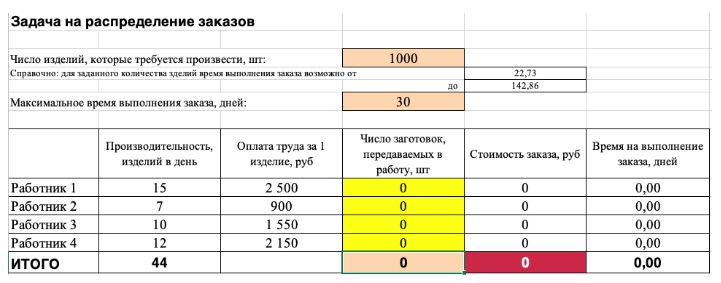
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

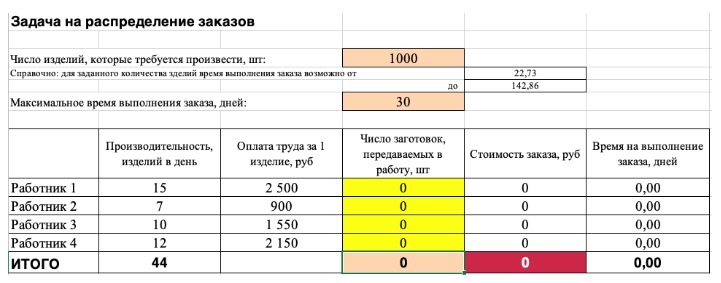
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

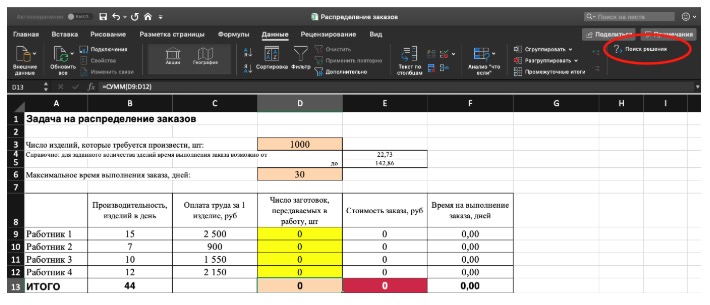
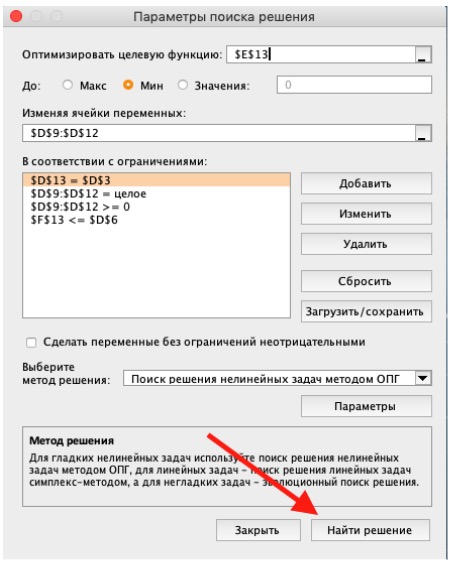
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

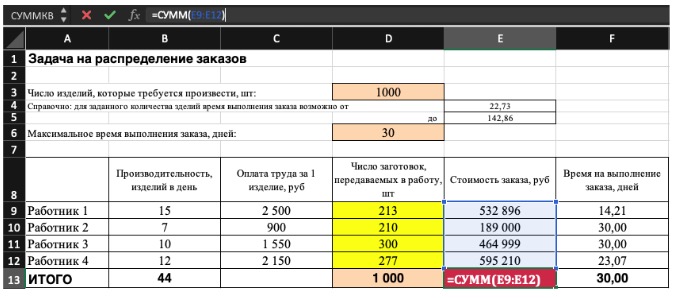
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

общее количество изделий 1000 штук ($D$13 = $D$3);
число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).

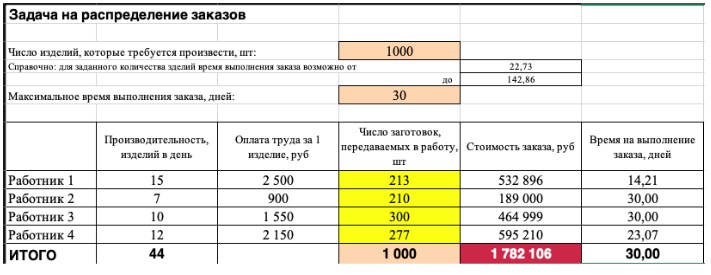
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.

Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!

Источник

«Поиск решения» является надстройкой Эксель, посредством которой возможно подобрать лучшее решение задач на основе указанных ограничений. Функция дает возможность составлять график работников, распределять расходы либо инвестиционные вложения. Знание принципа работы такой функции поможет сэкономить время и силы.

Содержание

Что такое Поиск решений
Как включить функцию «Поиск решения»
О моделях
Подготовительный этап
Применение функции и ее настройка
Загрузить/сохранить параметры Поиска решений
Простой пример использования Поиска решения
Поиску решения не удалось найти решения
Заключение

Что такое Поиск решений

В комплексе с различными другими опциями в Excel существует одна менее популярная, однако крайне нужная функция «Поиск решения». Невзирая на то, что отыскать ее бывает нелегко, ознакомление с ней и использование помогает в разрешении множества задач. Опция обрабатывает данные и выдает оптимальное решение из допустимых. В статье описывается, как непосредственно функционирует «Поиск решения».

Как включить функцию «Поиск решения»

Невзирая на эффективность, рассматриваемая опция не находится на видном месте панели инструментов либо контекстного меню. Большинство юзеров, которые работают в Эксель, не знают о ее наличии. По умолчанию такая функция выключена, для ее отображения следует произвести такие действия:

Открываем «Файл», нажимая на соответствующее название.
Кликаем на раздел «Параметры».
Затем выбираем подраздел «Надстройки». Тут будут отображены все надстройки программы, внизу появится надпись «Управление». С правой стороны от нее будет всплывающее меню, где следует выбрать «Надстройки Excel». Потом нажимаем «Перейти».

1
На мониторе высветится дополнительное окно «Надстройки». Устанавливаем флажок возле искомой функции и кликаем «ОК».
Нужная функция появится на ленте справа от раздела «Данные».

О моделях

Данная информация будет крайне полезна тем, кто лишь ознакамливается с понятием «оптимизационная модель». До того, как воспользоваться «Поиском решения», рекомендуется исследовать материалы о методах построения моделей:

рассматриваемая опция даст возможность выявить оптимальный метод, чтобы осуществить выделение средств на вложения, загрузку помещения, поставку товаров либо иные действия, где необходимо отыскать оптимальный вариант решения.
«Оптимальный метод» в такой ситуации будет означать: увеличение доходов, снижение трат, улучшение качества и др.

Типовые задачи по оптимизации:

Определение плана производства, во время чего прибыль от продажи выпущенных товаров будет максимальной.
Определение карт перевозок, во время чего траты на транспортировку минимализируются.
Поиск распределения нескольких станков по различным видам работ, чтобы траты на производство были снижены.
Определение наименьшего срока выполнения работ.

Важно! Чтобы формализовать поставленную задачу, необходимо создать модель, отражавшую основные параметры предметной области. В Эксель модель является комплексом формул, использующих переменные. Рассматриваемая опция подыскивает такие показатели, чтобы целевая функция была больше (меньше) либо равнялась указанному значению.

Подготовительный этап

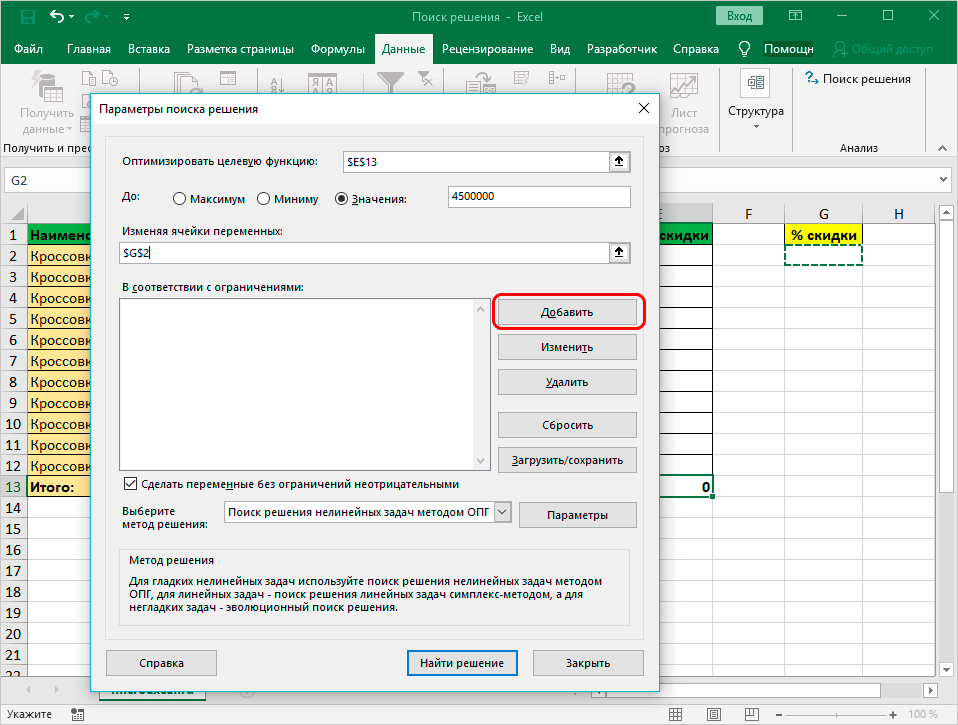
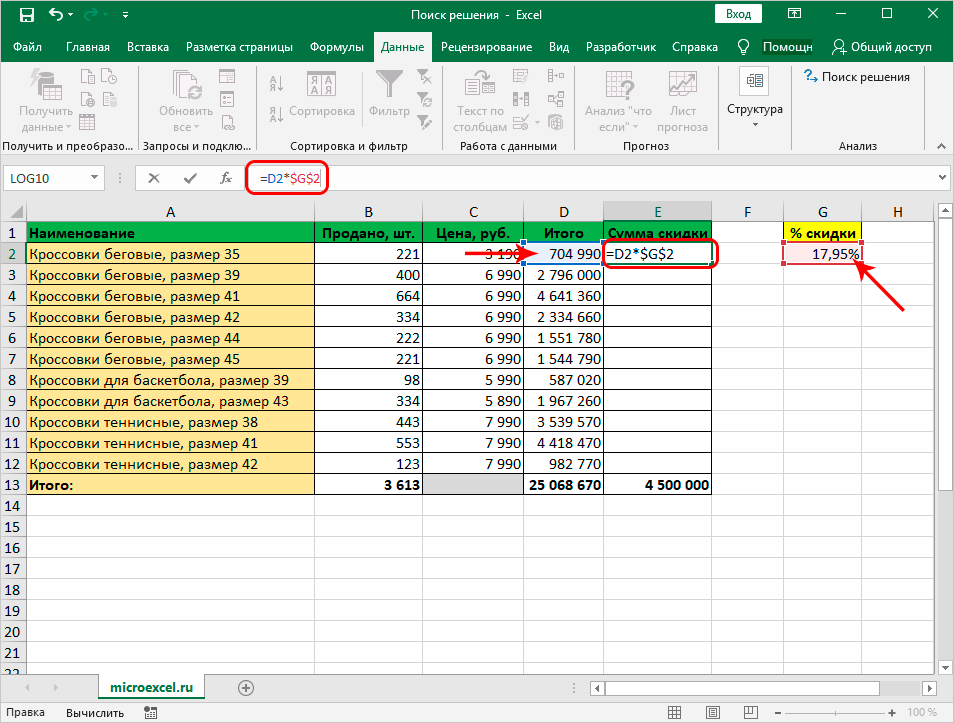
Перед тем как разместить функцию на ленте, необходимо изучить принцип функционирования опции. К примеру, есть сведения по реализации товаров, указанные в таблице. Задачей является назначение для каждого наименования скидки, которая составляла бы 4.5 млн. рублей. Параметр отображается внутри ячейки, именуемой целевой. Отталкиваясь от нее, рассчитываются прочие параметры.

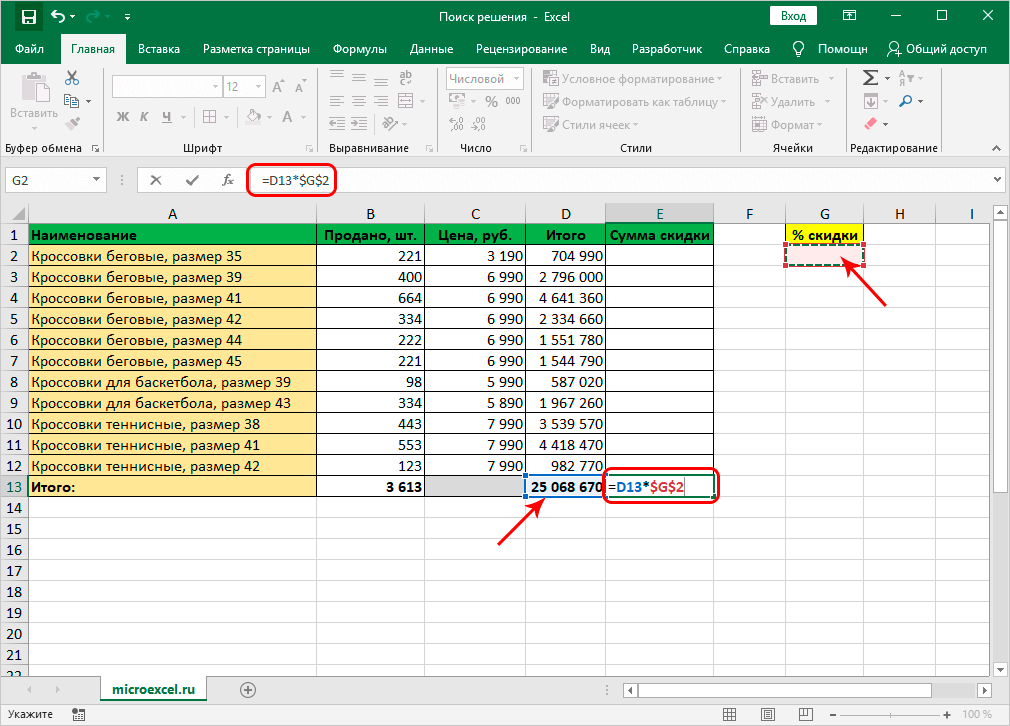
Нашей задачей станет вычисление скидки, на которую умножаются суммы по реализации различной продукции. Эти 2 элемента связываются формулой, прописываемой так: =D13*$G$2. Где в D13 прописывается суммарное количество по реализации, а $G$2 – адрес искомого элемента.

Применение функции и ее настройка

Когда формула будет готова, необходимо использовать непосредственно саму функцию:

Нужно переключиться в раздел «Данные» и нажать «Поиск решения».

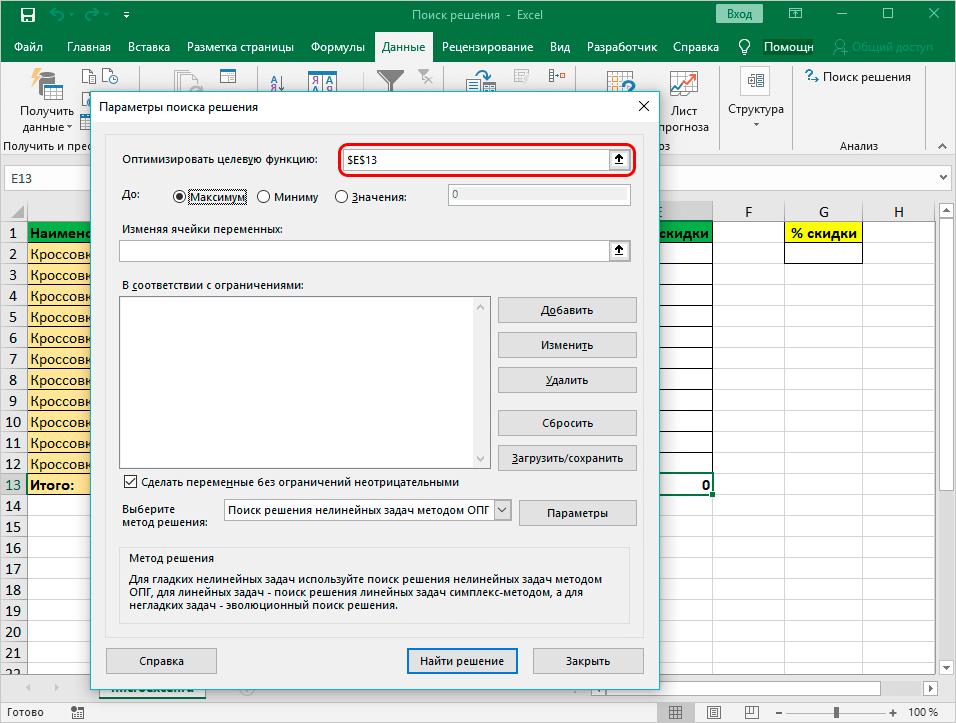
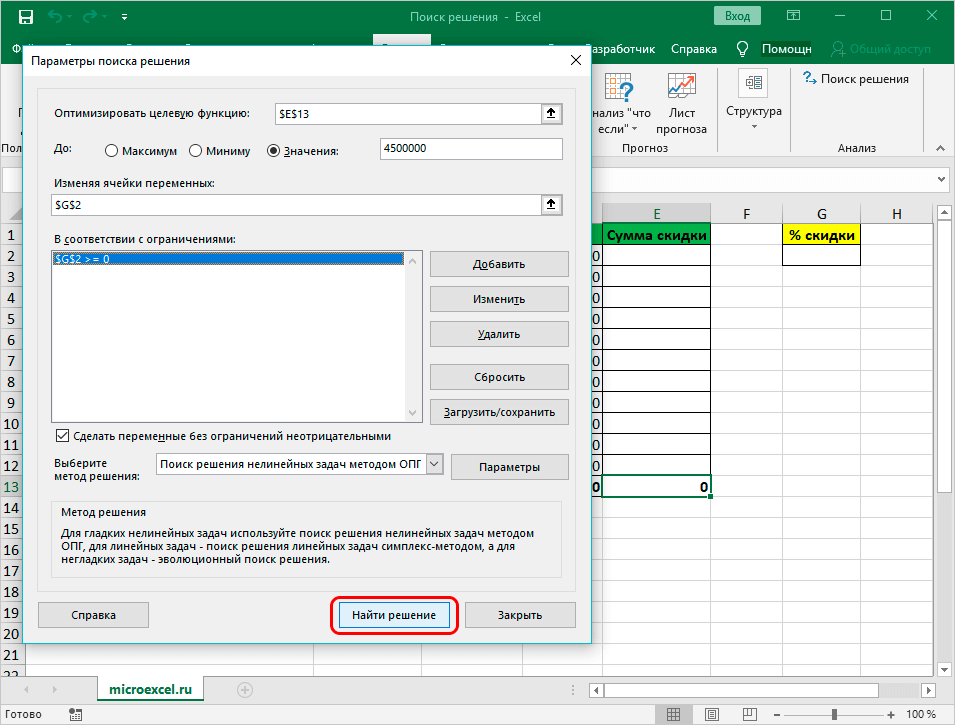
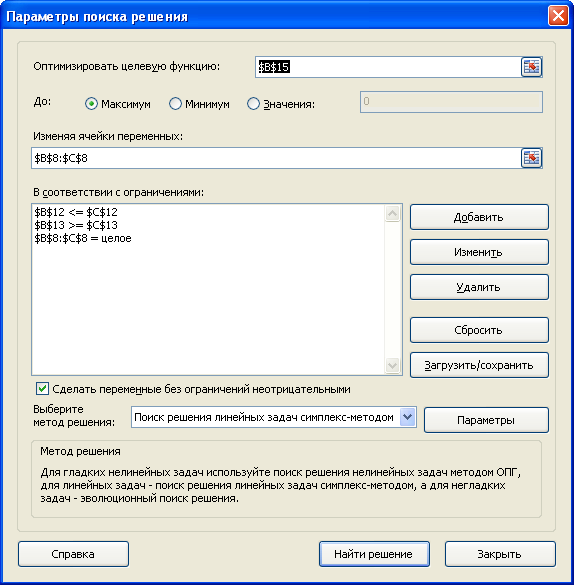
Откроются «Параметры», где задаются требуемые настройки. В строке «Оптимизировать целевую функцию:» следует указать ячейку, где выводится сумма по скидкам. Есть возможность прописать координаты самостоятельно или выбрать из документа.

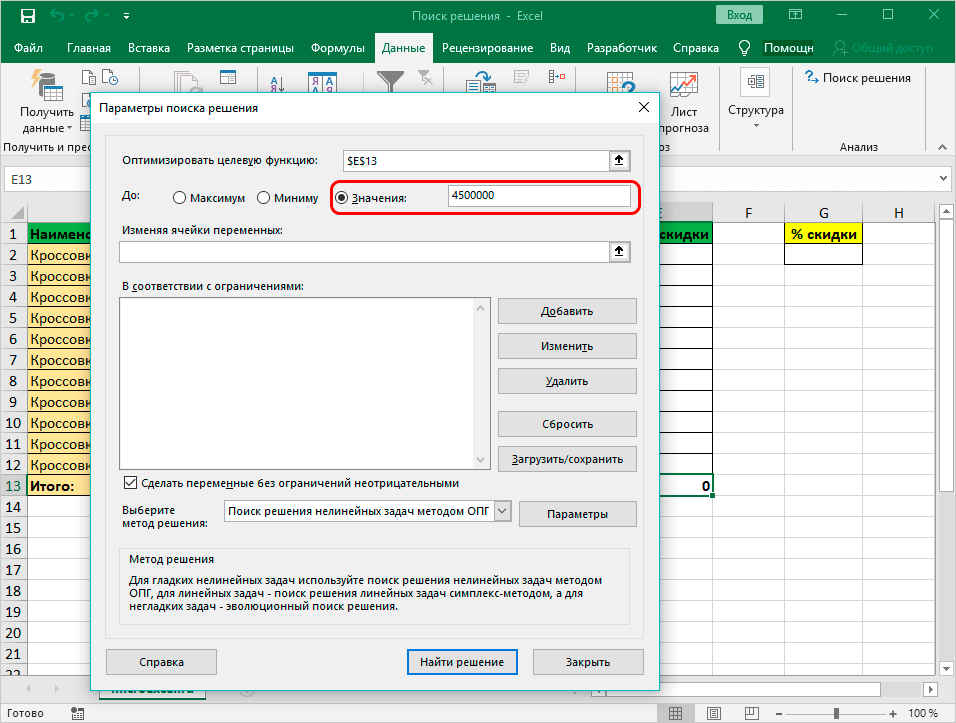
Далее нужно перейти к настройкам прочих параметров. В разделе «До:» есть возможность задать максимальную и минимальную границу либо точное число.

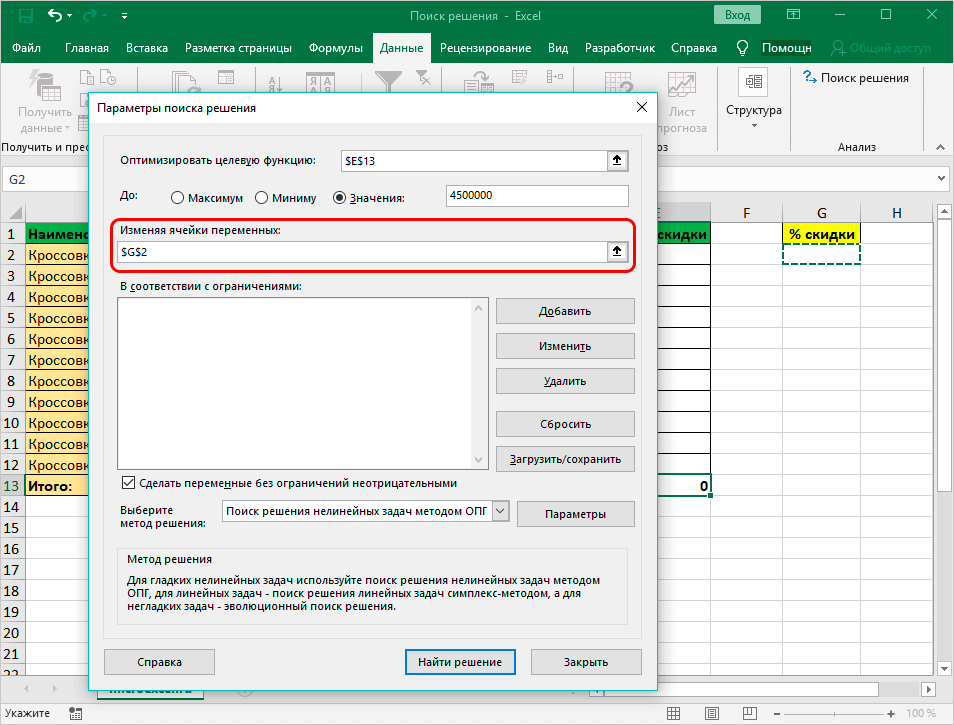
Потом заполняется поле «Изменяя значения переменных:». Здесь вносятся данные искомой ячейки, которая содержит конкретное значение. Координаты прописываются самостоятельно или кликается соответствующая ячейка в документе.

Затем редактируется вкладка «В соответствии с ограничениями:», где задаются ограничения применяемых данных. К примеру, исключаются десятичные дроби либо отрицательные числа.

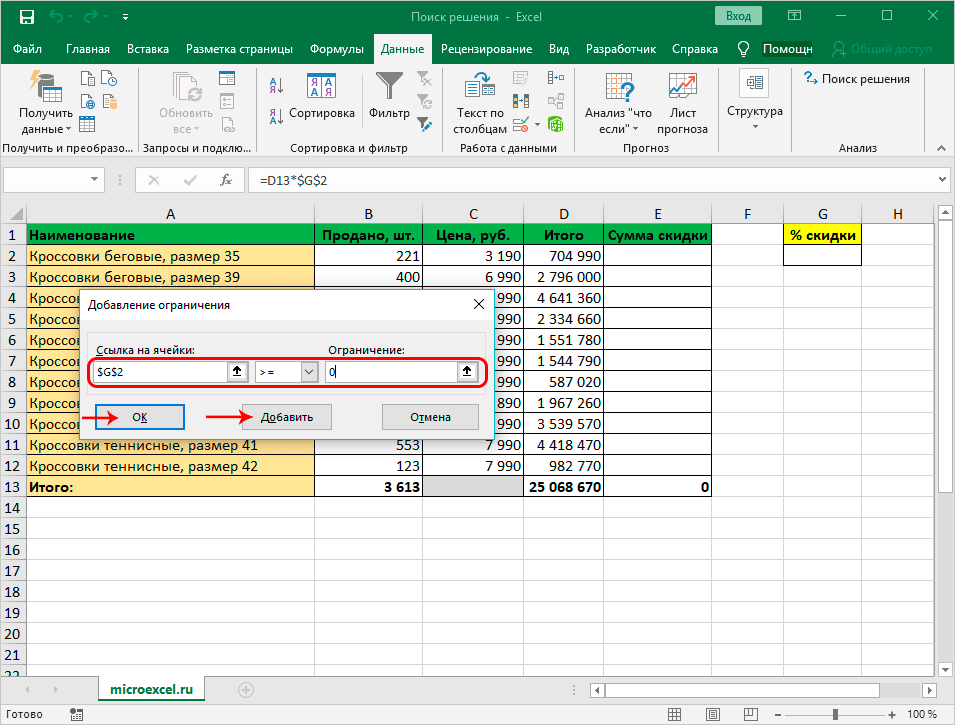
После открывается окно, которое позволяет добавлять ограничения при расчетах. В начальной строке указываются координаты ячейки либо целого диапазона. Следуя условиям задачи, указываются данные искомой ячейки, где выводится показатель скидки. Затем определяется знак сравнения. Устанавливается «больше либо равно», чтобы конечное значение не было со знаком «минус». «Ограничение», устанавливаемое в 3 строке, в такой ситуации равняется 0. Возможно выставить также ограничение посредством «Добавить». Последующие действия аналогичны.

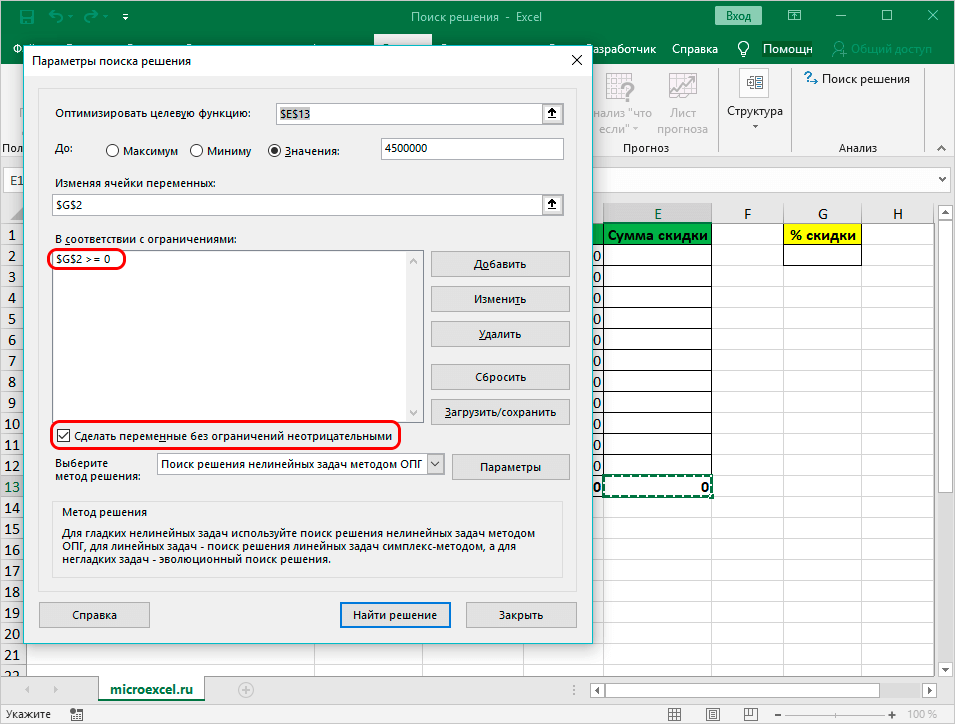
Когда выполнены вышеописанные действия, в самой большой строке появляется установленное ограничение. Перечень бывает большим и будет зависеть от сложности расчетов, однако в конкретной ситуации достаточно 1 условия.

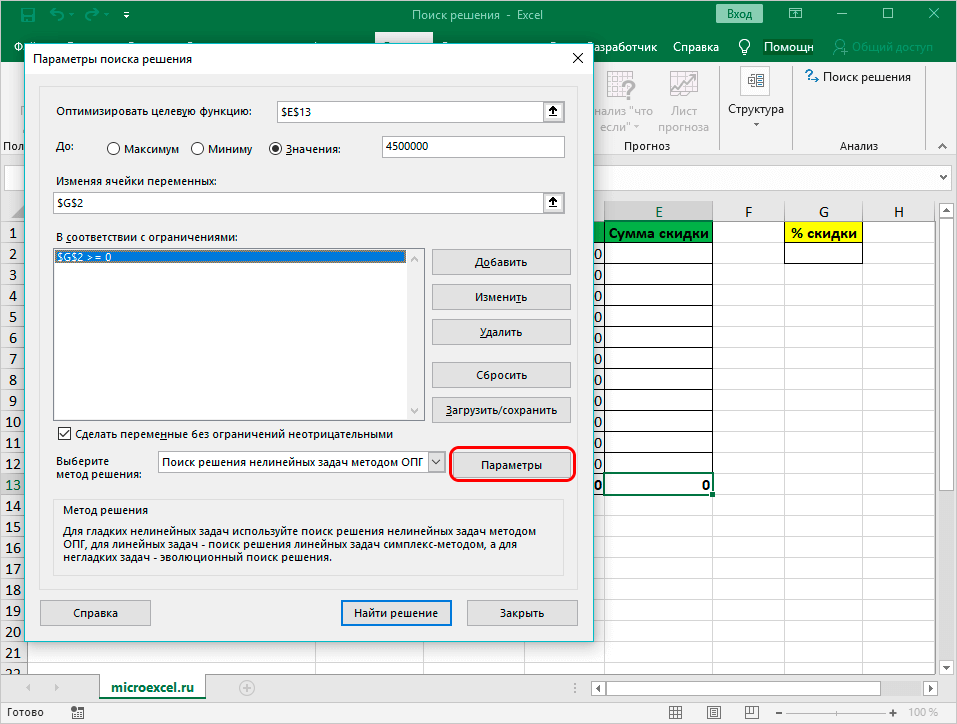
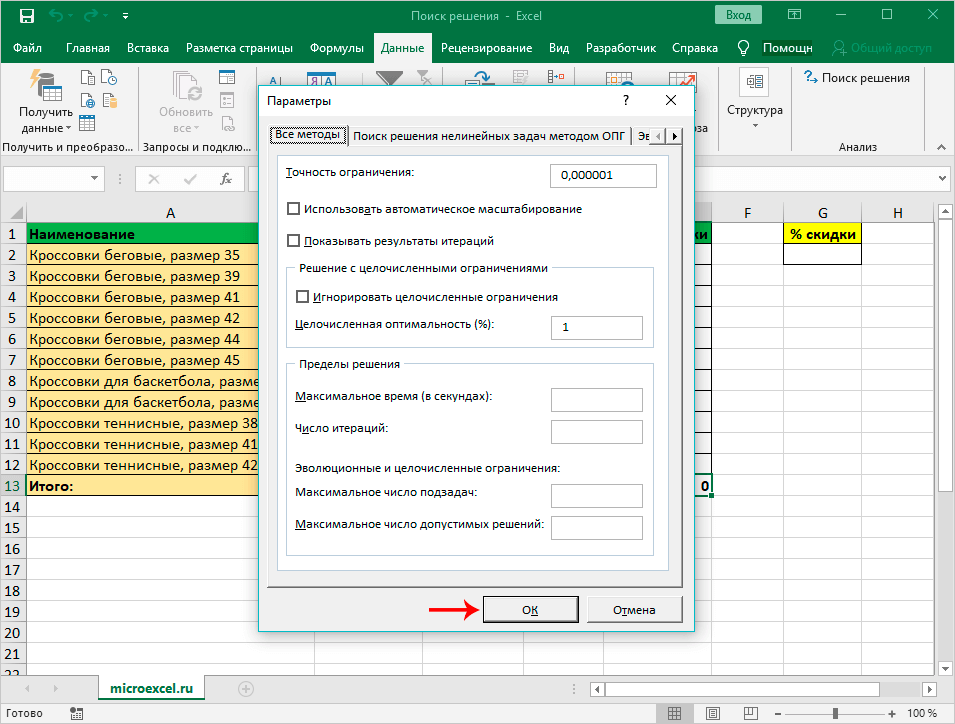
Кроме того, возможно выбирать другие дополнительные настройки. Внизу с правой стороны присутствует опция «Параметры», которая позволяет это сделать.

В настройках можно выставить «Точность ограничения» и «Пределы решения». В нашей ситуации использовать эти опции нет нужды.

Когда настройки завершены, запускается сама функция – нажимается «Найти решение».

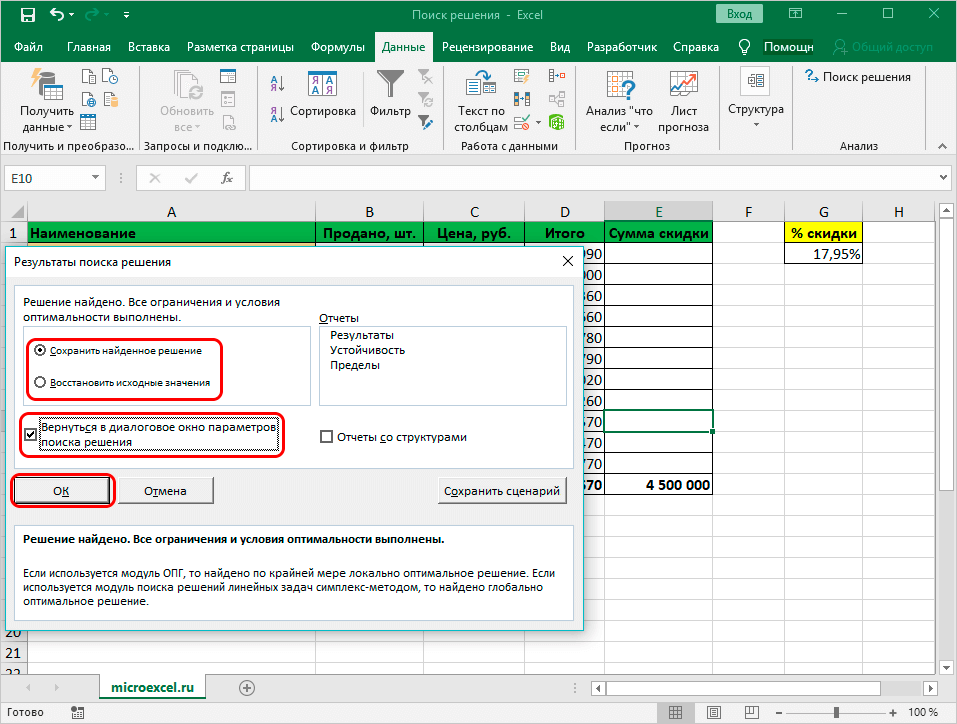
После программа проводит требуемые расчеты и выдает конечные расчеты в необходимых ячейках. Потом открывается окно с результатами, где сохраняются/отменяются итоги либо настраиваются параметры поиска по новой. Когда данные соответствуют требованиям, то найденное решение сохраняется. Если заранее установить отметку «Вернуться в диалоговое окно параметров поиска решения», будет открыто окно с настройками функции.

Есть вероятность, что расчеты оказались ошибочными или есть необходимость в изменении исходных данных в целях получения других показателей. В такой ситуации требуется вновь открыть окно с настройками и перепроверить сведения.
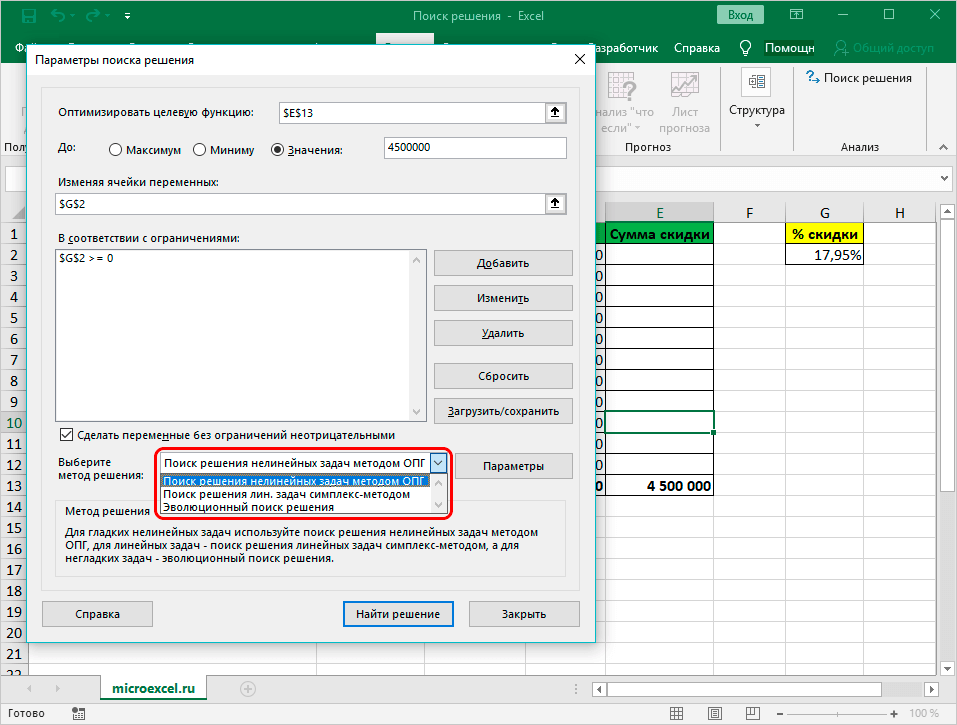
Когда данные точны, можно воспользоваться альтернативным методом. В этих целях нужно нажать на текущий вариант и из появившегося списка выбрать самый подходящий способ:

Поиск решения посредством обобщенного градиента для нелинейных задач. По умолчанию применяется такой вариант, однако возможно воспользоваться и другими.
Поиск решения для линейных задач на основе симплекс-метода.
Использование эволюционного поиска в целях выполнения задачи.

Внимание! Когда вышеназванные варианты не смогли справиться с задачей, следует осуществить проверку данных в настройках снова, так как это зачастую бывает основной ошибкой в таких задачах.

Когда получена искомая скидка, остается ее применить для подсчета суммы скидок по каждому наименованию. В этих целях выделяется начальный элемент столбика «Сумма скидки», прописывается формула «=D2*$G$2» и жмется «Enter». Значки доллара проставляются, чтобы во время растягивания формулы на смежные строчки G2 не изменялась.

Теперь будет получена сумма скидки для начального наименования. Затем следует навести курсор на угол ячейки, когда он станет «плюсом», зажимается ЛКМ и формула растягивается на необходимые строки.
После этого таблица будет окончательно готова.

Загрузить/сохранить параметры Поиска решений

Данная опция полезна при применении различных вариантов ограничений.

В меню «Параметры поиска решения» следует нажать «Загрузить/сохранить».
Вводится диапазон для области модели и нажимается «Сохранить или Загрузить».

Во время сохранения модели вводится ссылка на 1 ячейку пустого столбца, где будет размещена модель оптимизации. В процессе загрузки модели вводится ссылка на весь диапазон, где содержится модель оптимизации.

Важно! Для сохранения последних настроек в меню «Параметры поиска решения» сохраняется книга. Каждый лист в ней имеет собственные параметры надстройки «Поиск решения». Помимо того, для листа возможно выставить больше 1 задачи при нажатии кнопки «Загрузить или сохранить» в целях сохранения отдельных задач.

Простой пример использования Поиска решения

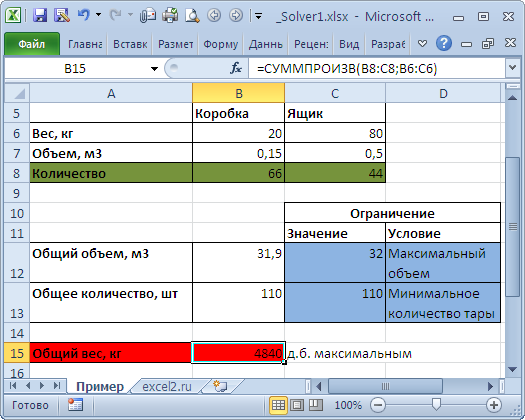
Нужно провести загрузку контейнера тарой, чтобы его масса была максимальной. Емкость обладает объемом в 32 куб. м. Наполненная коробка имеет вес в 20 кг, ее объем равен 0,15 куб. м. Ящик – 80 кг и 0,5 куб. м. Требуется, чтобы общее число тары составляло не менее 110 шт. Данные организовываются так:

Переменные модели отметим зеленым. Целевая функция выделяется красным. Ограничения: по наименьшему количеству тары (больше либо равно 110) и по массе (=СУММПРОИЗВ(B8:C8;B6:C6) – суммарный вес тары, находящейся в контейнере.

По аналогии считаем общий объем: =СУММПРОИЗВ(B7:C7;B8:C8). Такая формула необходима, чтобы выставить ограничение на суммарный объем тары. Потом посредством «Поиск решения» вводятся ссылки на элементы с переменными, формулами и самими показателями (либо ссылки на конкретные ячейки). Разумеется, что количество тары – целое число (также является ограничением). Нажимаем «Найти решение», в результате чего находится такое число тары, когда общая масса максимальна и учтены все ограничения.

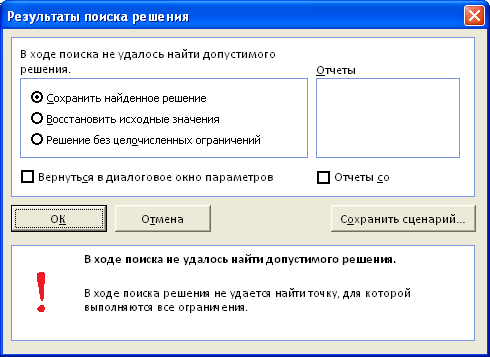
Поиску решения не удалось найти решения

Такое уведомление выскакивает, когда рассматриваемая функция не нашла сочетаний показателей переменных, удовлетворяющих каждому ограничению. При использовании Симплекс-метода вполне возможно, что решения нет.

Когда используется способ решения нелинейных задач, во всех случаях начинающийся с начальных показателей переменных, это свидетельствует о том, что возможное решение далеко от таких параметров. Если запустить функцию с прочими начальными показателями переменных, то, вероятно, решение найдется.

К примеру, во время использования нелинейного способа, элементы таблицы с переменными не заполнялись, и функция не нашла решений. Это не значит, что решения нет. Теперь, с учетом результатов определенной оценки, в элементы с переменными вводятся другие данные, близкие к получаемым.

В любой ситуации изначально следует изучить модель на отсутствие противоречия ограничений. Зачастую подобное взаимосвязано с ненадлежащим подбором соотношения либо предельного показателя.

В вышеуказанном примере показатель максимального объема указан 16 куб. м вместо 32, потому такое ограничение противоречит показателям по минимальным количествам мест, поскольку ему будет соответствовать число 16,5 куб. м.

Заключение

Исходя из этого, опция «Поиск решения» в Excel поможет в разрешении конкретных задач, которые довольно трудно либо невозможно решить обычными способами. Сложность в применении такого метода состоит в том, что изначально эта опция скрыта, ввиду чего большинство пользователей не знают о ее наличии. Кроме того, функция достаточно сложна в изучении и использовании, однако при надлежащем исследовании, она принесет большую пользу и облегчит расчеты.

Оцените качество статьи. Нам важно ваше мнение:

Источник