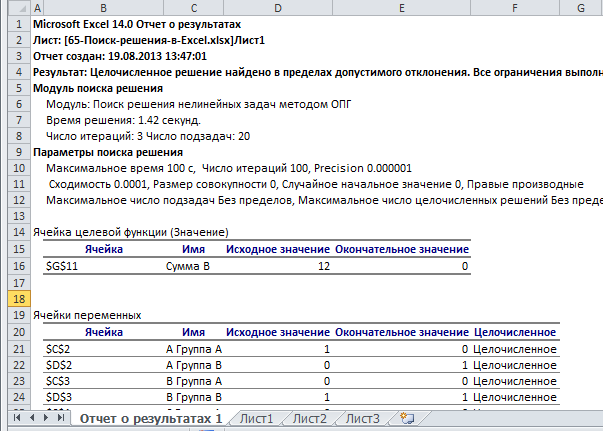
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
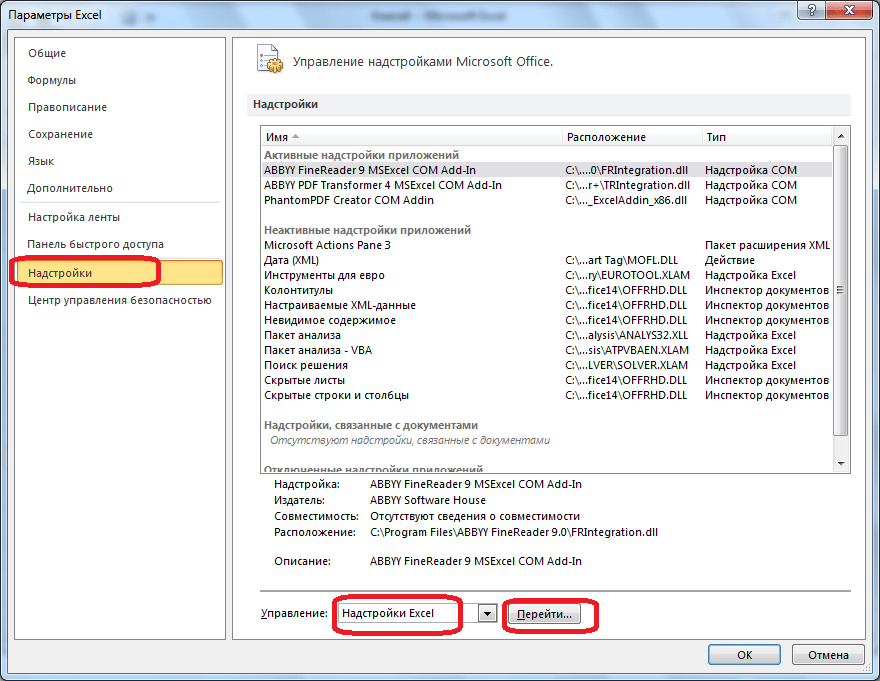
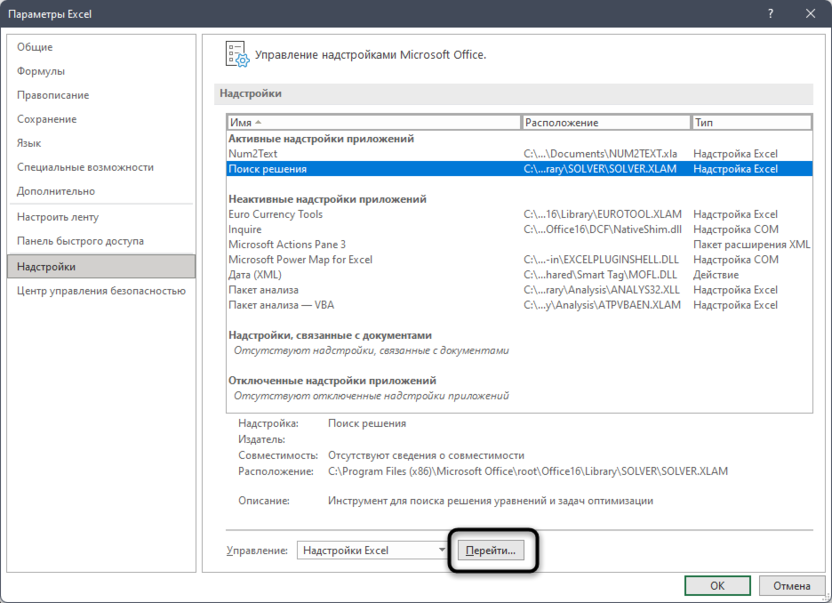
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
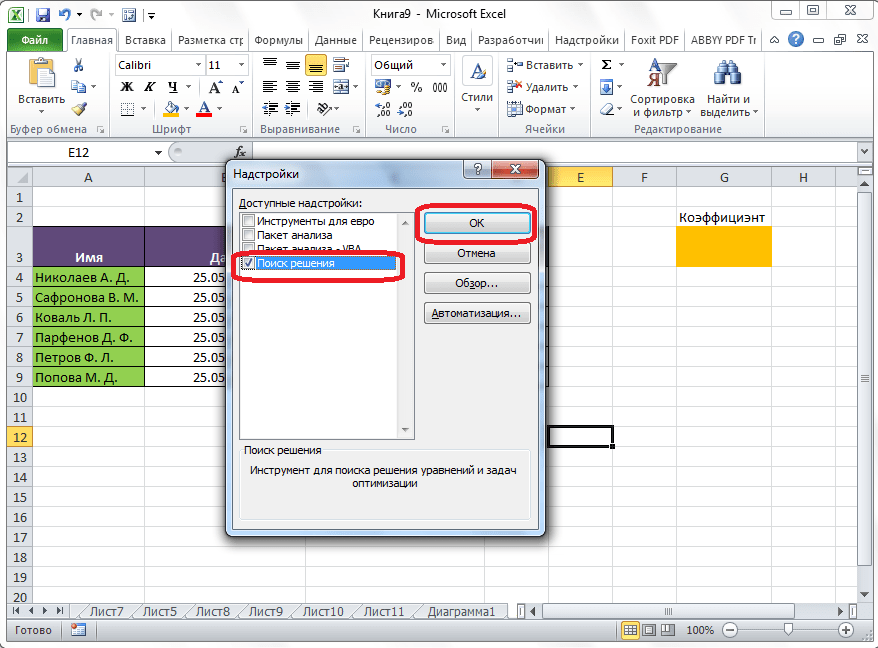
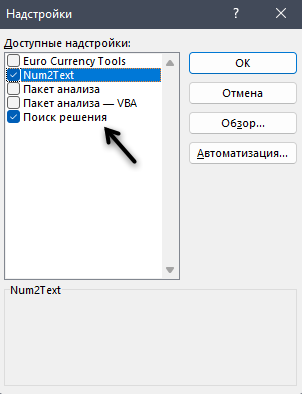
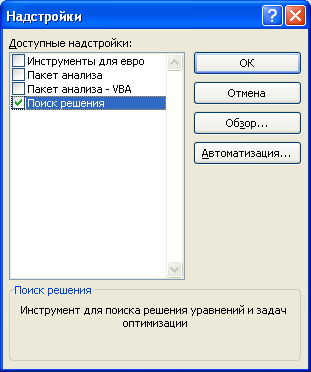
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
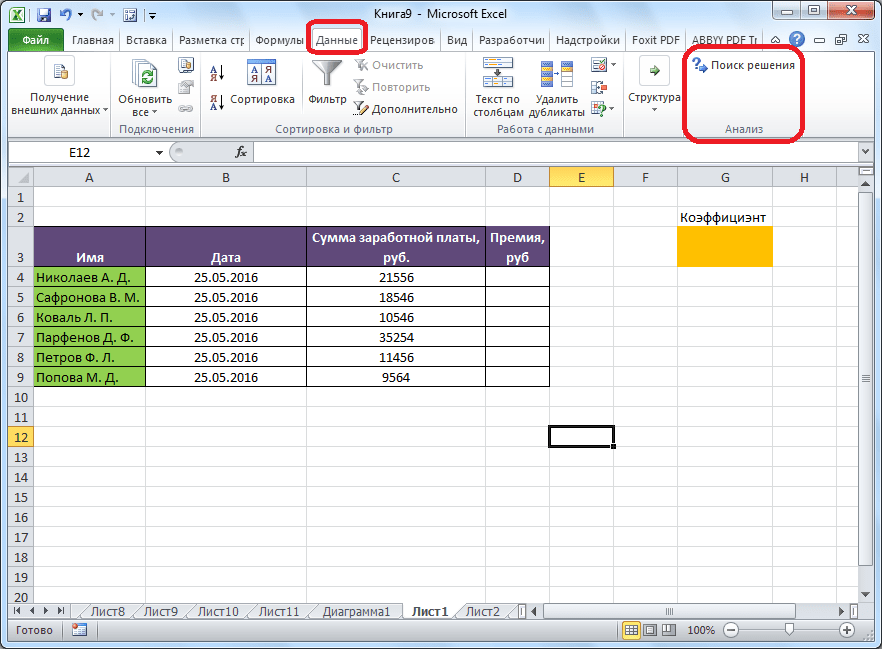
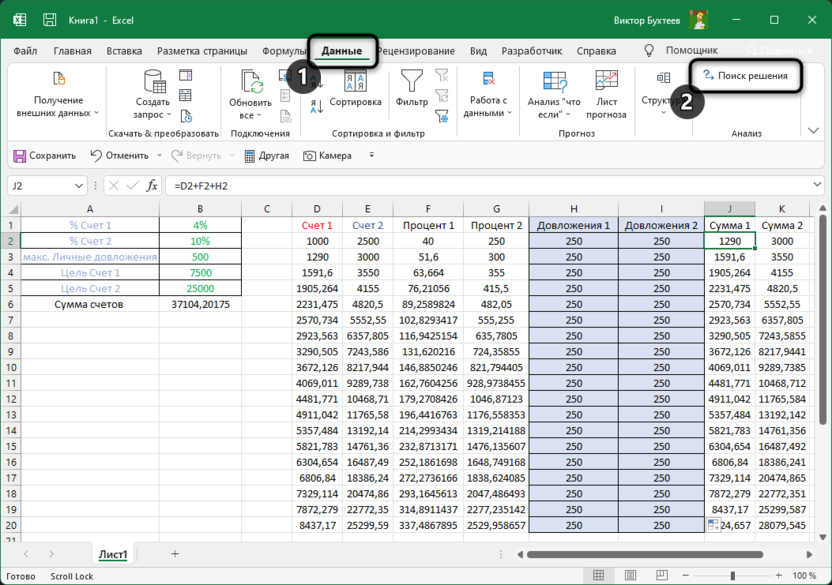
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
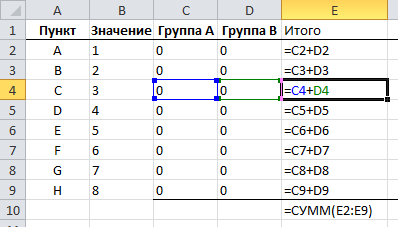
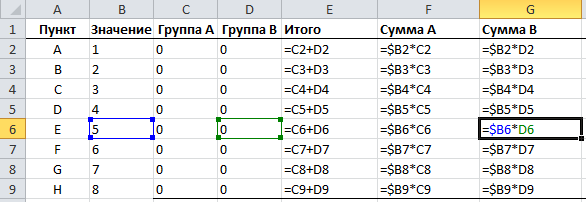
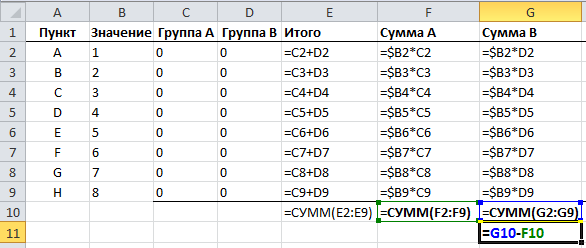
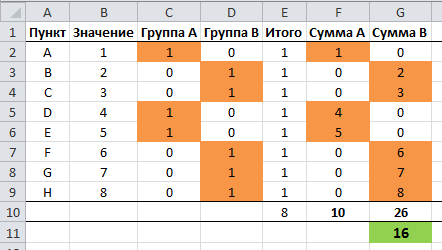
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
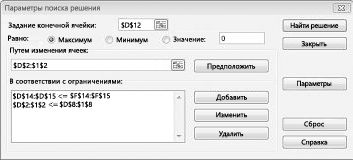
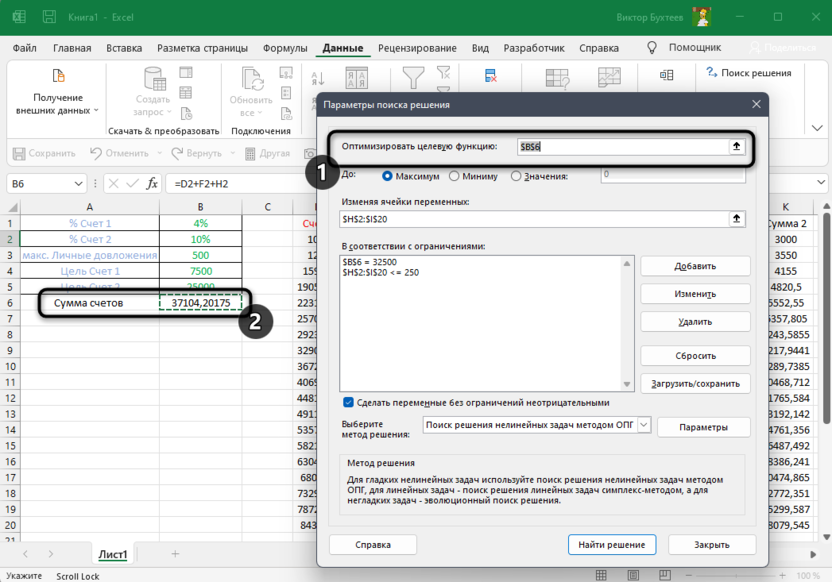
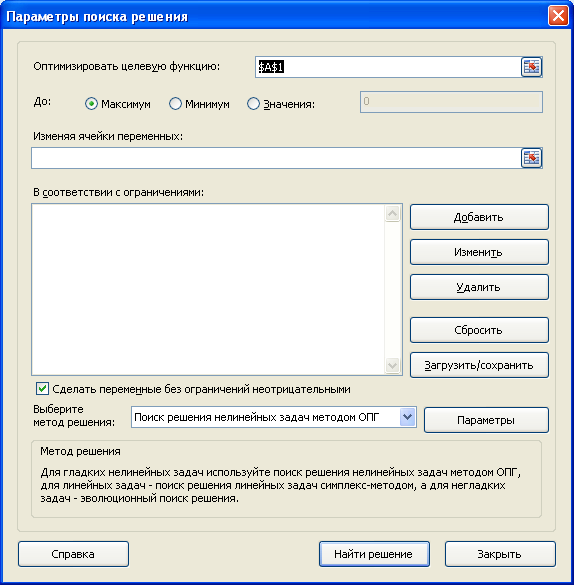
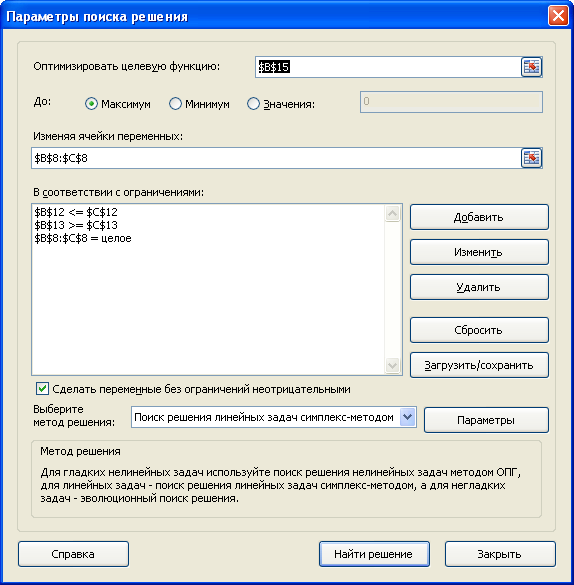
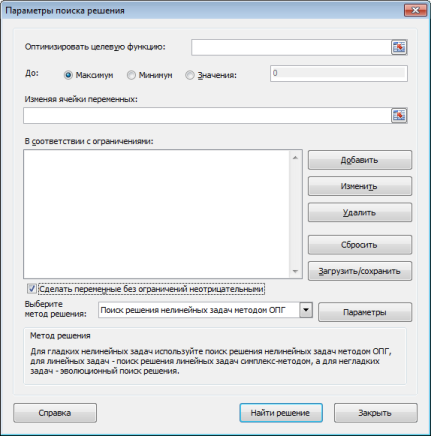
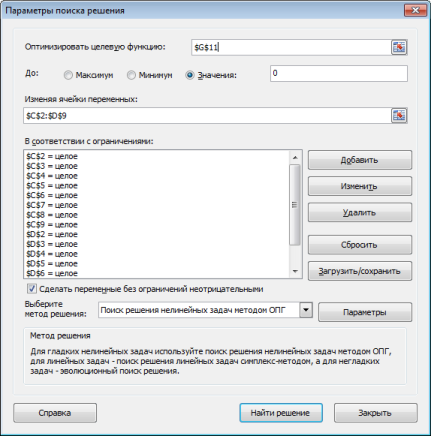
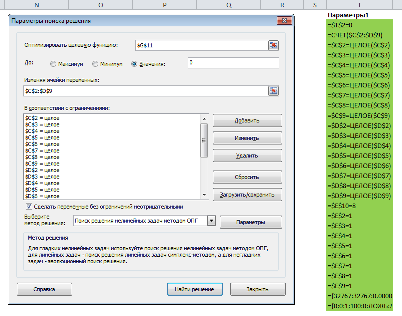
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
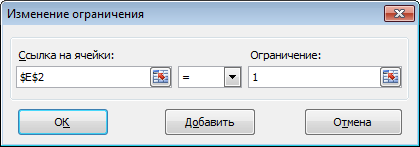
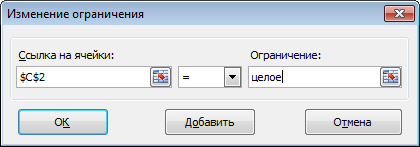
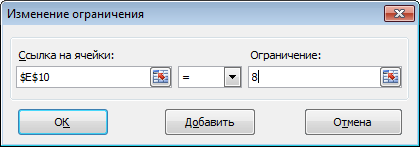
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
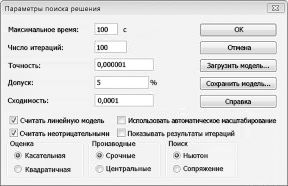
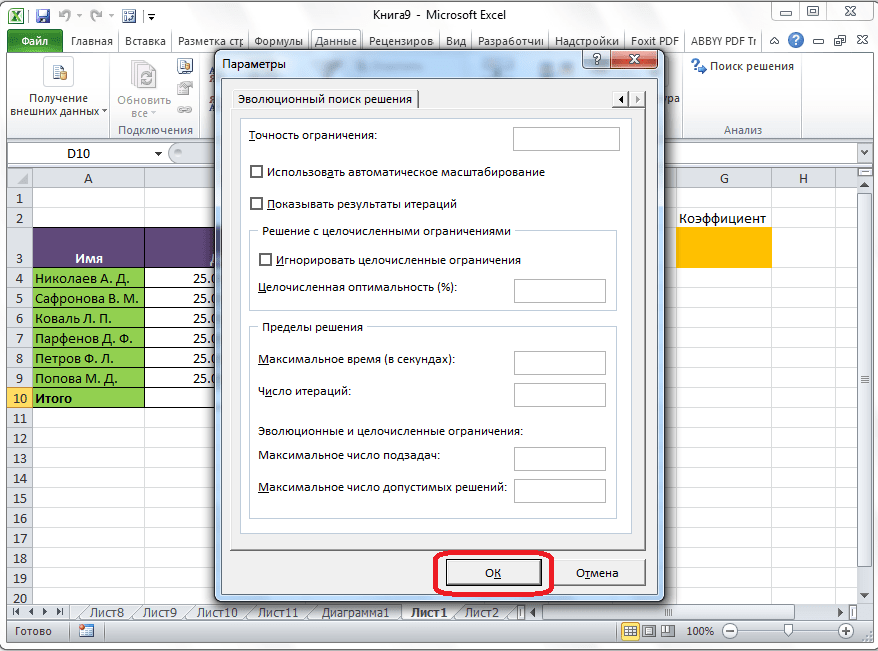
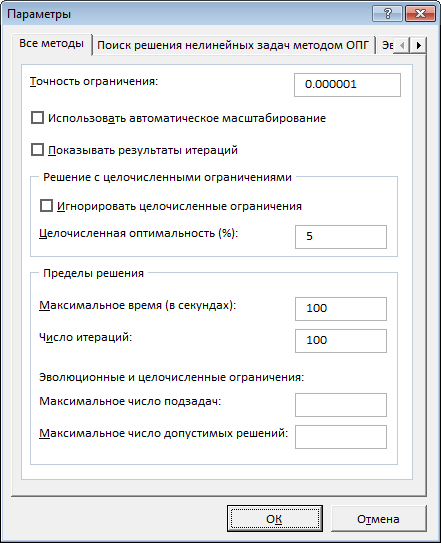
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
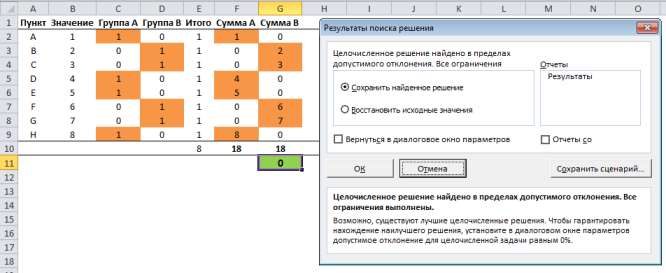
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
Использование надстройки «Поиск решения» для определения оптимального набора продуктов
В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
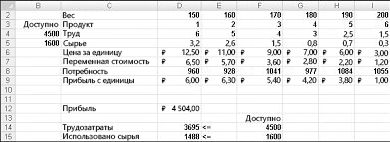
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + .
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2* E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + .
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
Ограничения. В этом примере есть следующие ограничения:
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
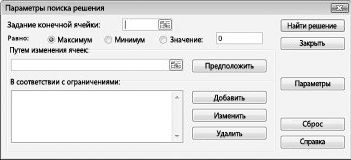
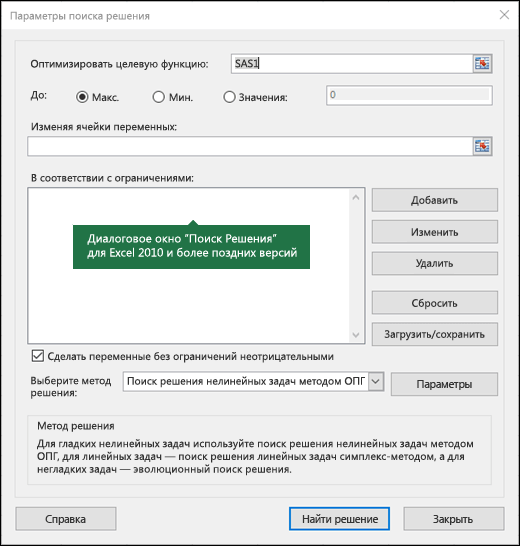
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
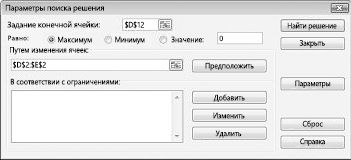
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
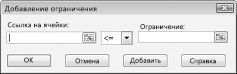
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите D14 D15 D2
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + .
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мы ed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1) (От 2 досье 2) (от 6 досье 6) ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
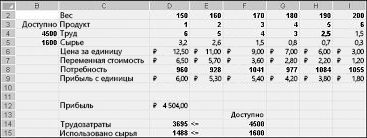
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
Мы выпускаем больше 5, чем за него требуются.
Мы используем больше трудоемких ресурсов, чем доступно.
Мы используем больше необработанных материалов, чем доступно.
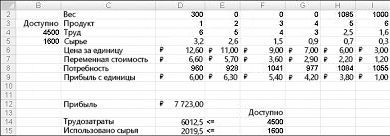
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
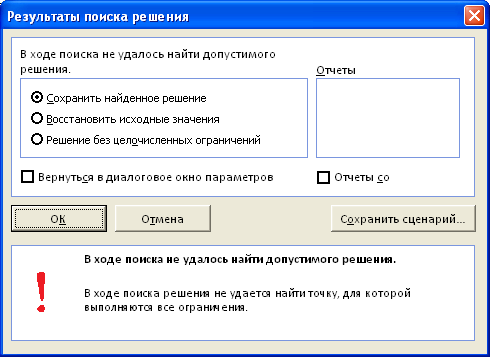
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2 D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2 =, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Источник
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
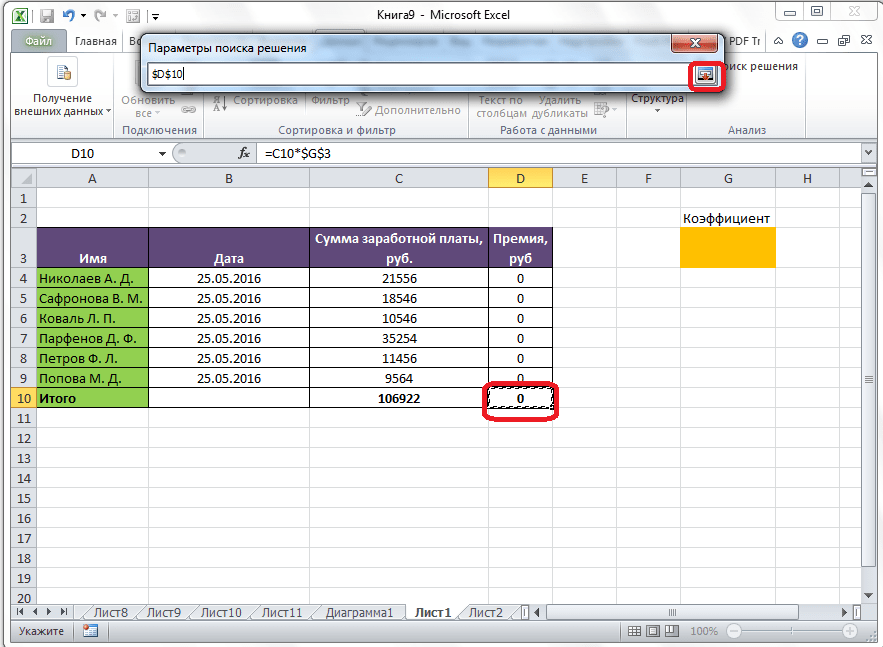
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
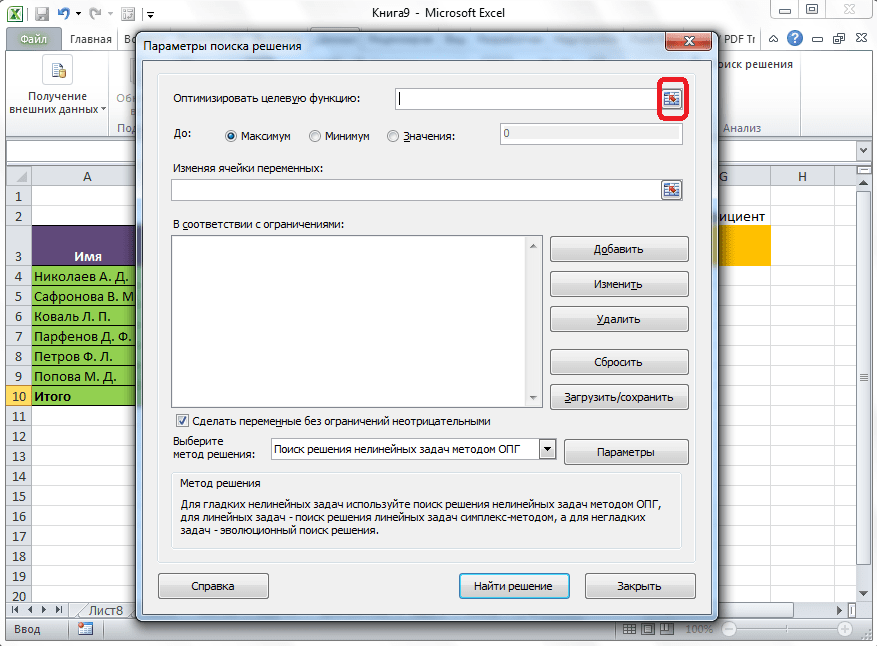
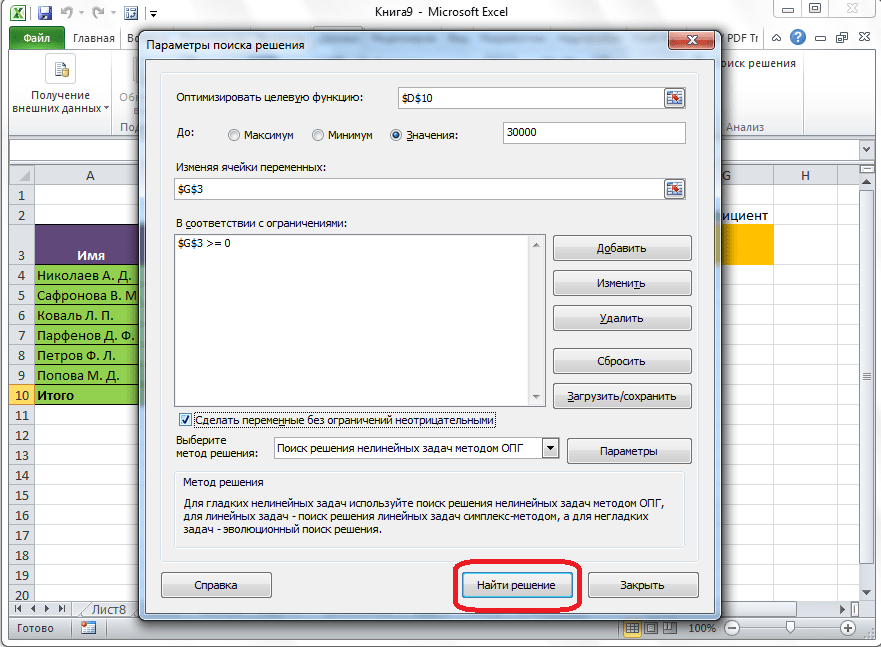
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
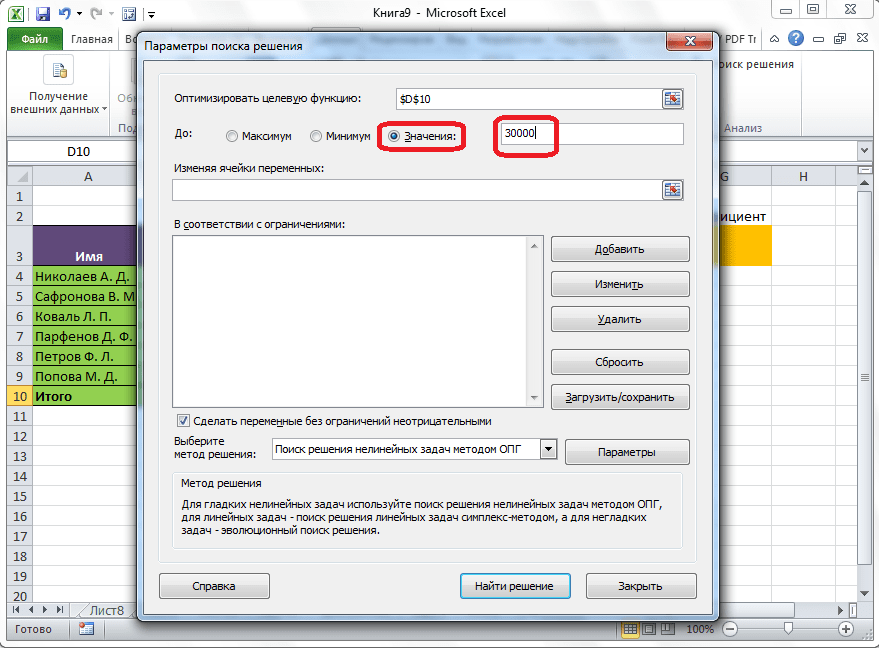
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
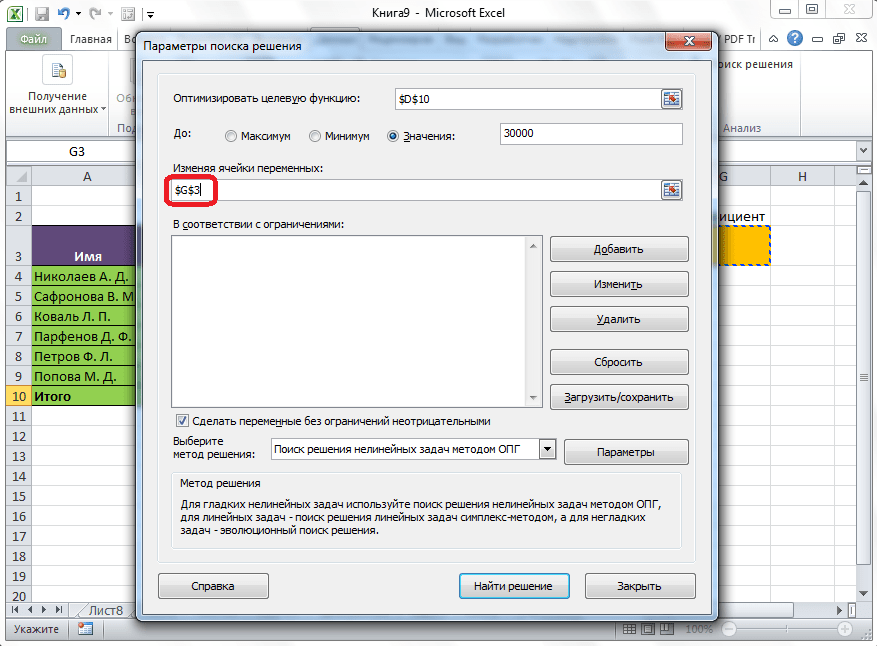
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
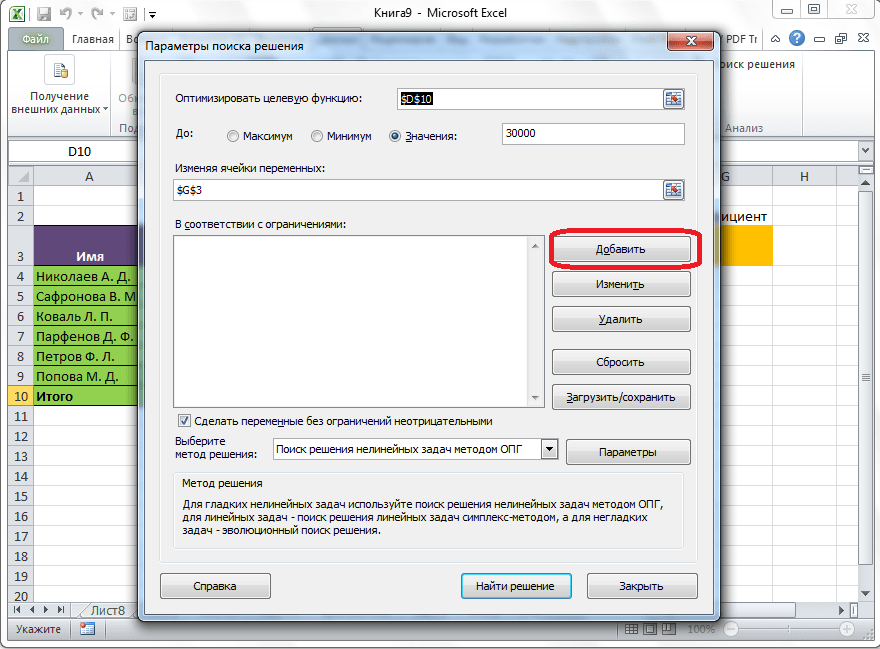
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
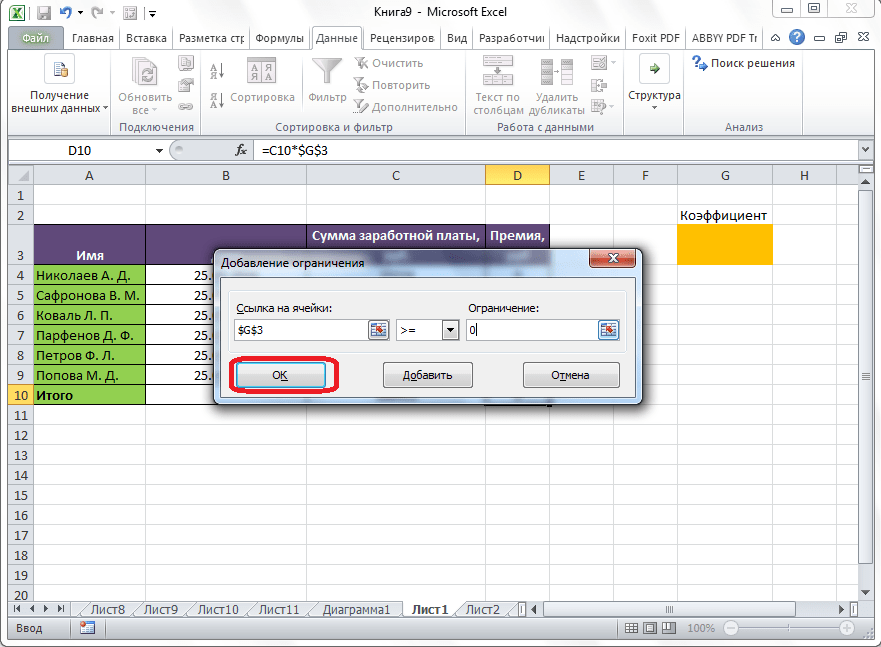
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
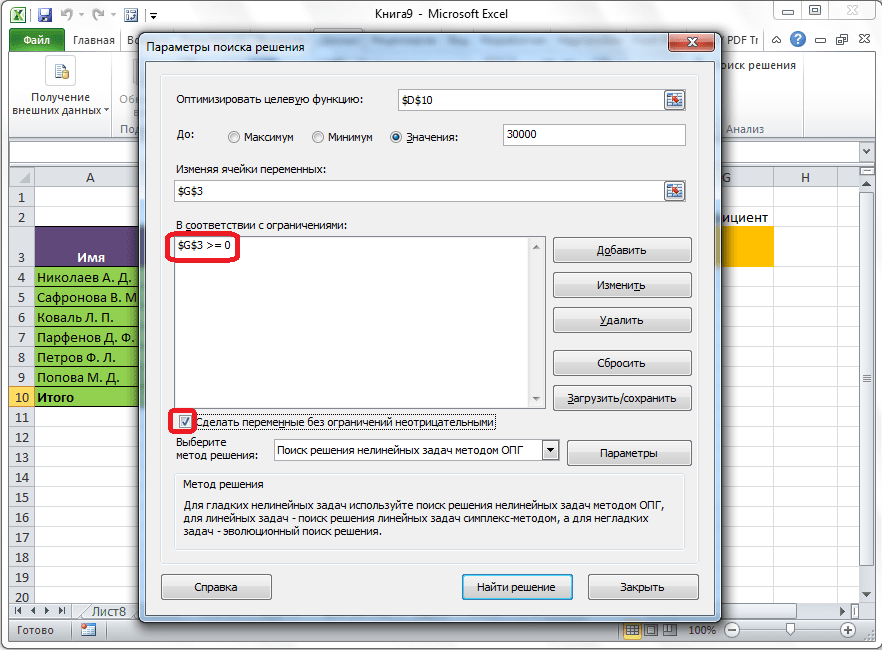
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
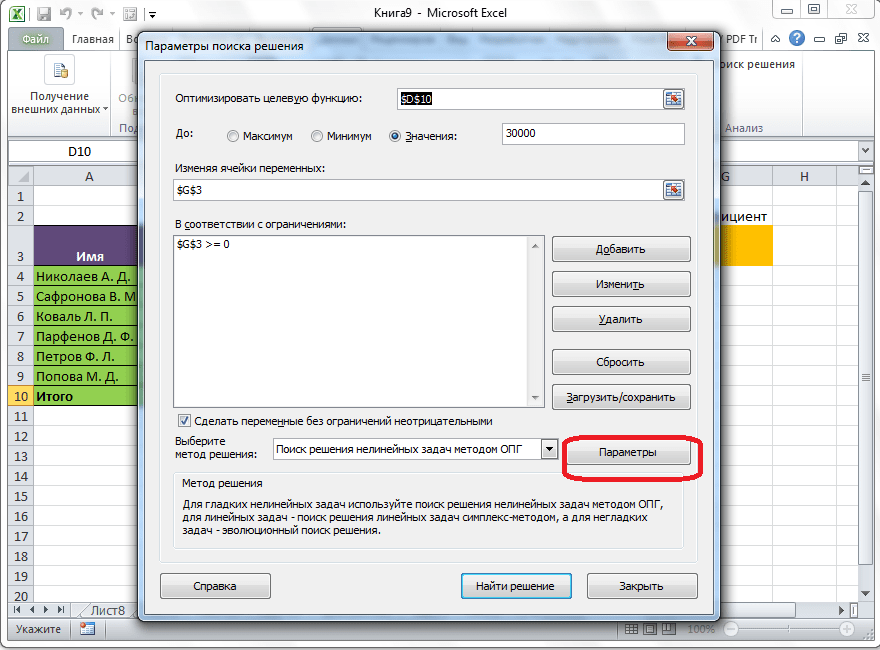
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
После того, как все настройки установлены, жмем на кнопку «Найти решение».
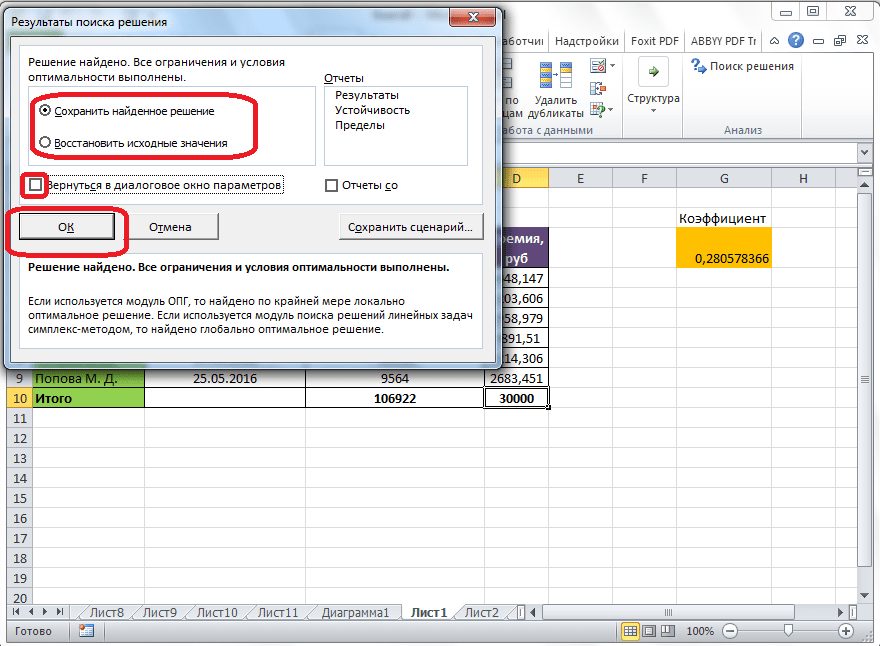
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
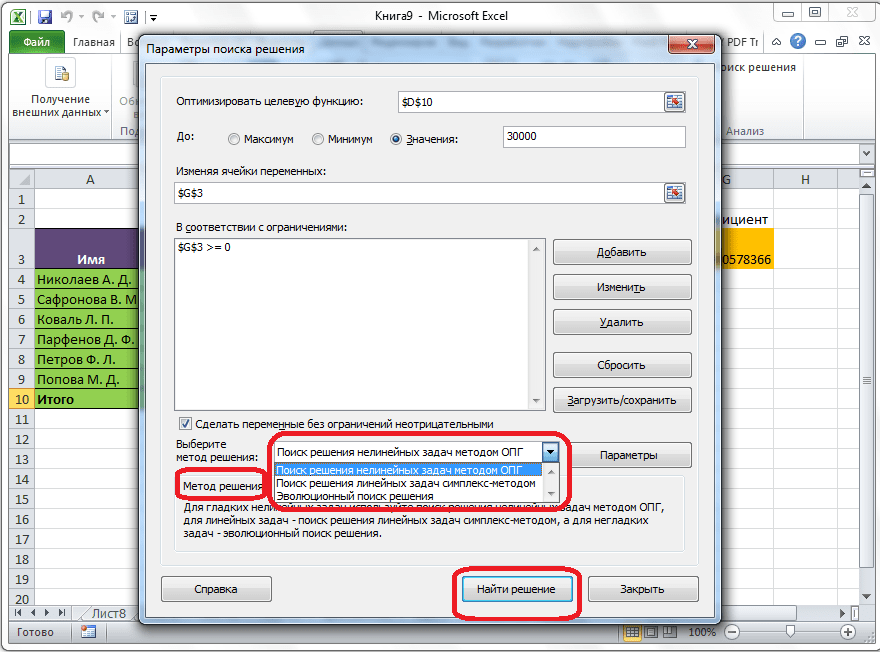
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
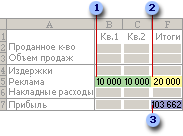
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
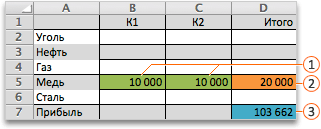
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование «Решения» для бюджетов с использованием средств на счете вех
Использование «Решение» для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Создатель сложной таблицы в Microsoft Excel, в которой требуется найти оптимальное значение для определенного диапазона данных, может вручную перебирать все возможные варианты или использовать вспомогательные формулы для расчетов. Однако это все сложно и часто не нужно, ведь можно обратиться к надстройке «Поиск решения», задать для нее цель, ограничения и указать область с переменными значениями, чтобы программа сама высчитала идеальное решение для вас.
Как раз об этой опции и пойдет речь далее.
Используемый пример для поиска решения
Сначала я хочу остановиться на исходной таблице и разобраться, в каких целях может применяться рассматриваемая надстройка. К тому же описываемый далее шаблон сделает понятным принцип устанавливаемых целей и ограничений, чтобы вы могли использовать его как исходную точку, оптимизировав под себя. Поиск решения поможет вам рассчитать кредитную ставку, узнать, как лучше вкладывать средства для достижения желаемого результата, определить лучшие маршруты для логистики, сбалансировать цены и потребление и многое другое, что требуется для обработки довольно большого массива данных.
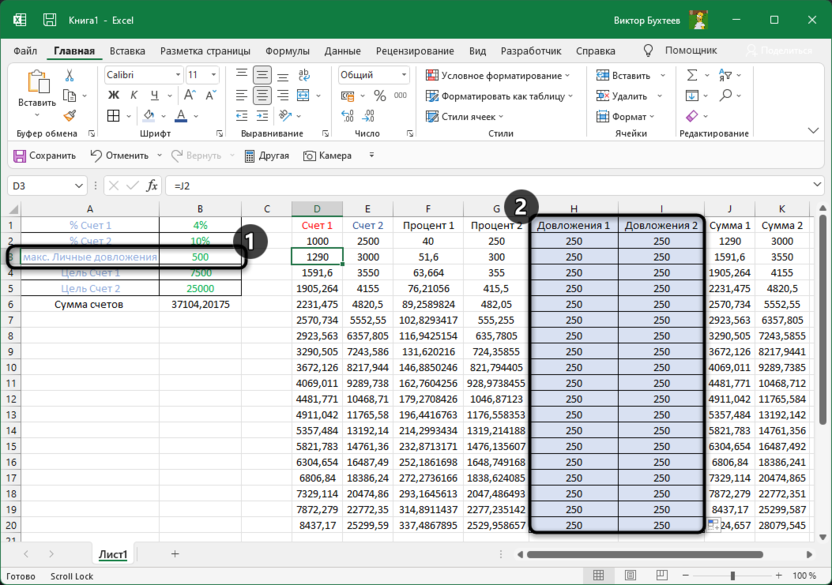
В моем примере мы возьмем два депозитных счета, на каждый из которых каждый цикл начисляется фиксированный процент. Это вы видите в обводке на следующем изображении, где двойкой отмечены начальные суммы на каждом счете. Именно от них и отталкиваются следующие расчеты.
Процент каждый раз начисляется одинаковый, поэтому является константой. Его я растягиваю на все допустимые циклы начислений. Не обращайте внимание на то, что какие-то значения уже есть, поскольку сначала нужно заполнить таблицу полностью, подставив любые значения для начислений.
Помимо начисления процентов каждый цикл я буду докладывать на каждый счет до 500 условных единиц. Для удобства разделю их пополам на каждый счет, чтобы каждый цикл поступало не больше 250 на отдельный баланс. В итоге количество этих довложений и будет считаться надстройкой, чтобы сэкономить максимальное количество средств до конца всех циклов.
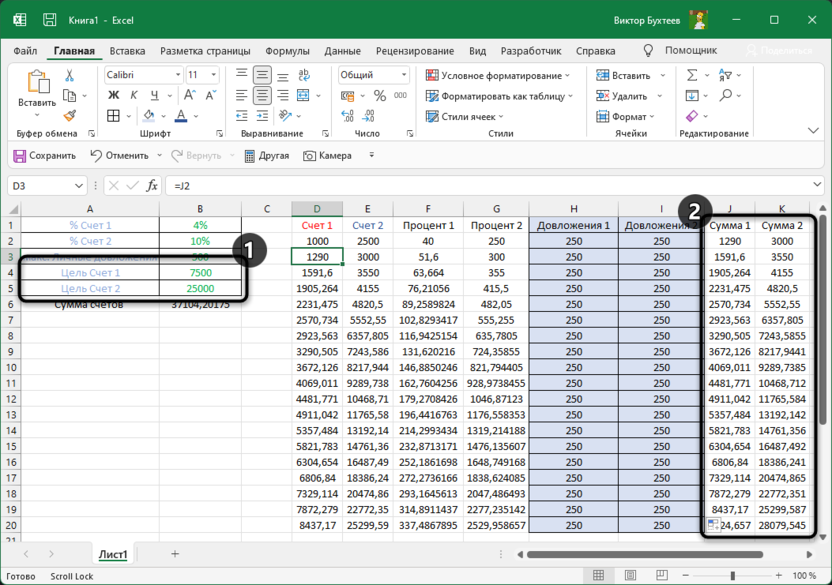
Теперь нужно решить, к чему мы хотим прийти. Я выставил две отдельные цели для каждого счета, но они будут только примерными, поскольку в итоге я хочу прийти к общему балансу, чтобы он соответствовал моим требованиям.
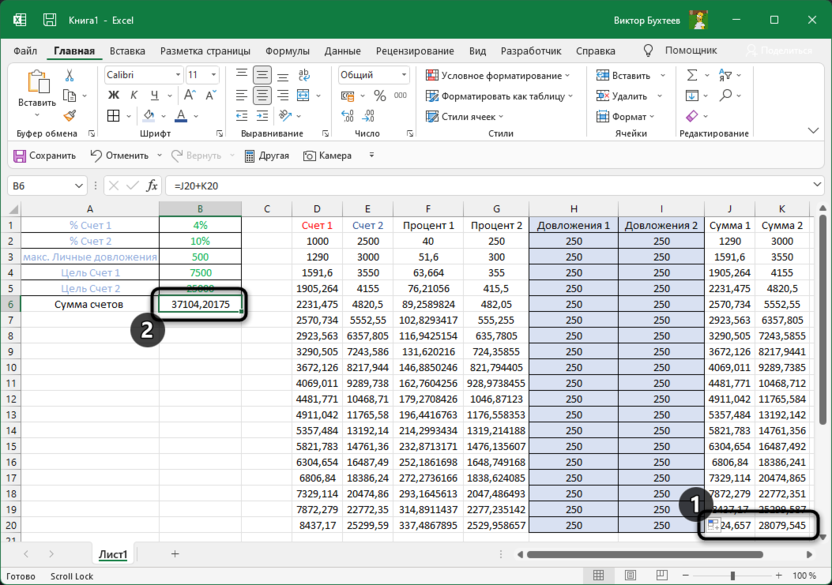
Для этого я сначала добавляю функцию СУММ для суммы счетов и считаю сумму каждого в последнем цикле.
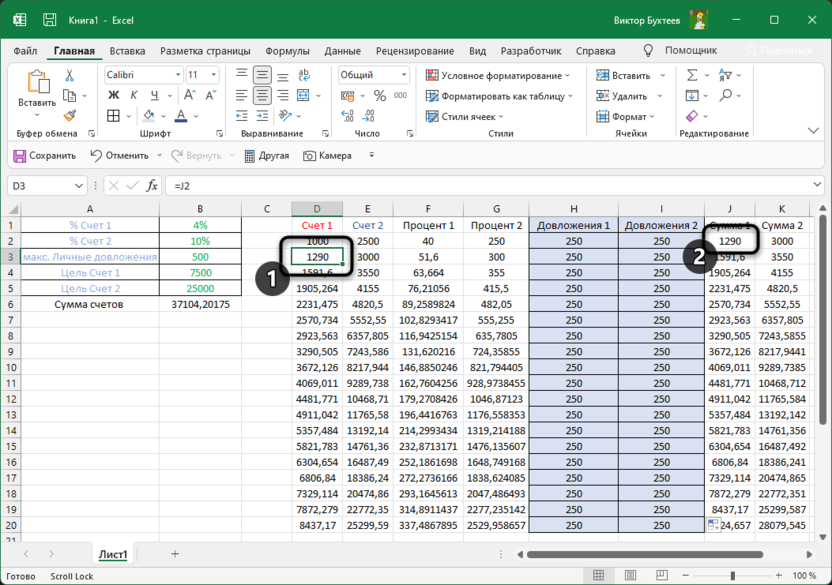
Если вы собираетесь строить примерно такую же таблицу, как у меня, обращу ваше внимание на то, что в начале каждого следующего цикла сумма на счете будет переноситься автоматически, поэтому нужно самостоятельно ссылаться во втором цикле на конечную сумму счета из первого, чтобы при растяжении таблицы всегда получать корректные результаты.
Сама сумма же формируется из исходного баланса, постоянного процента и суммы довложений, которая будет меняться в зависимости от того, как решит надстройка «Поиск решения».
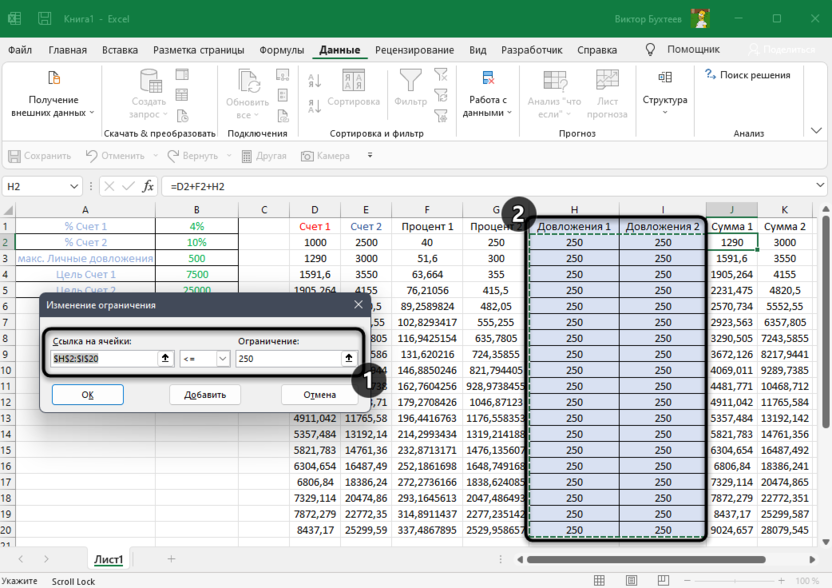
Возможно, текстом описать принцип работы этой таблицы сложно, но я постарался сделать это максимально доходчиво. В итоге получил таблицу с двумя счетами с разными процентами начислений и разными целями. Общая сумма довложений не должна быть более 500, а цель является общей, поскольку предполагается, что весь баланс с депозитных счетов все равно будет выведен на один. Поэтому далее я сделаю так, чтобы баланс к концу всех циклов получился 32500 (7500 + 25000, это предполагаемые цели первого и второго счета). При этом количество довложений должно быть минимальным, чтобы не тратить личные средства, и, соответственно, не превышать установленное ограничение в 500 условных единиц. Теперь давайте разберемся с тем, как реализовать это при помощи рассматриваемой надстройки.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Включение надстройки «Поиск решения»
Прежде чем обращаться к самой надстройке, ее необходимо включить, поскольку по умолчанию в Экселе она не отображается на необходимой вкладке с инструментами. Выполните следующий алгоритм действий, чтобы активировать эту функцию.
-
В таблице перейдите на вкладку «Файл».
-
Откройте раздел «Другие».
-
Из появившегося меню выберите пункт «Параметры».
-
Откройте категорию настроек «Надстройки» и отыщите пункт с названием «Поиск решения», после чего выделите его нажатием левой кнопки мыши.
-
Кликните по кнопке «Перейти», находящейся внизу окна.
-
Активируйте галочку возле пункта «Поиск решения» и нажмите «ОК», чтобы выйти из данного окна.
-
Теперь давайте убедимся в том, что надстройка появилась в таблице. Для этого откройте вкладку «Данные» и найдите блок «Анализ», где и должен находиться соответствующий инструмент.
Надстройка включена, поэтому смело переходите к следующему разделу статьи, чтобы справиться с поставленной задачей. Как я уже и сказал, буду использовать таблицу из своего примера, а вы можете менять параметры в зависимости от личных целей.
Настройка «Поиска решений» для таблицы
Давайте каждое действие буду описывать максимально детально, разбирая то, какие значения я выбираю и что это даст в итоге. По сути, принцип действий с параметрами поиска решения заключается в том, что мы должны оптимизировать целевую функцию, изменяя ячейки переменных. Функцией у нас является сумма счетов по окончании цикла, а переменные – довложения в каждый цикл. Соответственно, программа будет искать вариант достижения цели с минимальными количествами довложений.
-
Выбрав пункт «Поиск решения» на панели, о которой говорилось выше, вы будете перенаправлены в окно с параметрами. Сначала выберите «Оптимизировать целевую функцию» и выберите ту ячейку, в которой отображается конечный результат всех циклов.
-
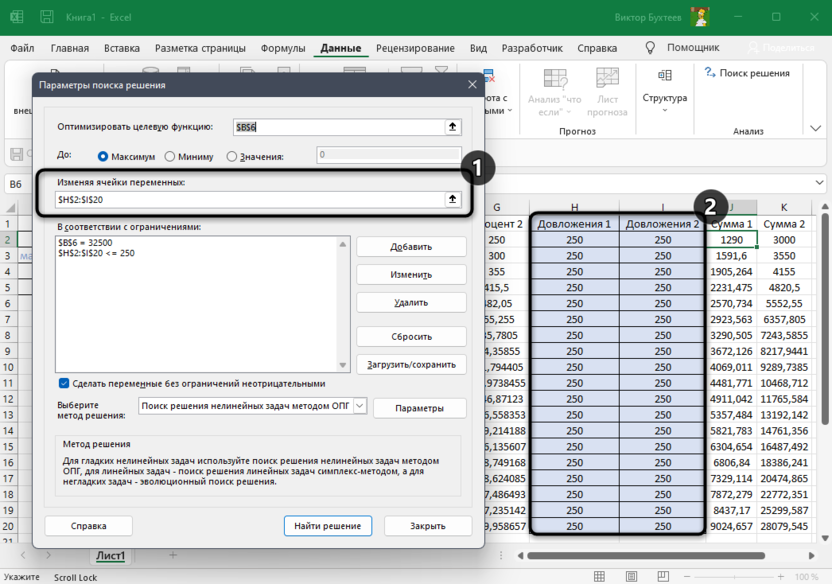
Для «Изменяя ячейки переменных» укажите область данных, куда могут вноситься изменения. В моем случае это будут довложения для каждого счета.
-
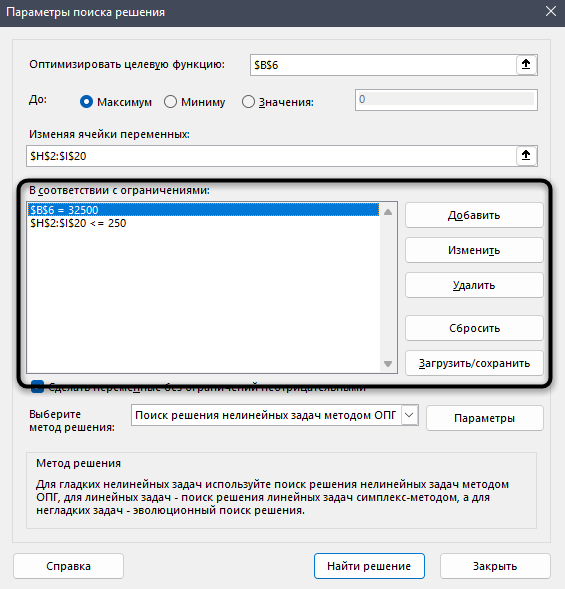
Теперь обратите внимание на «В соответствии с ограничениями». У нас есть ограничения, поэтому нужно указать их, чтобы программа понимала, какие значения может использовать и к какому результату ей стремиться. Нажмите «Добавить», чтобы создать первое ограничение.
-
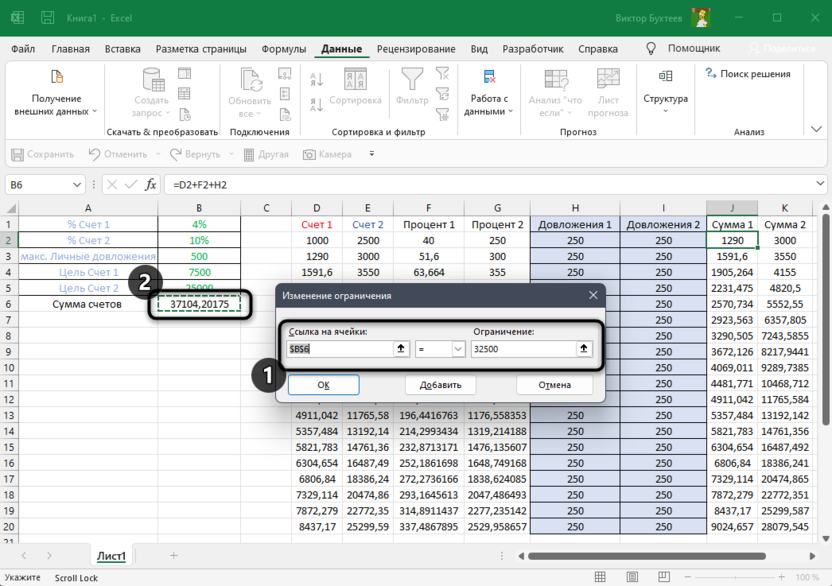
В моем случае первое ограничение – итоговая сумма в функции, которой нужно добавиться. Вы можете указать разные знаки неравенства, если, например, можно выбрать одно значение или меньше. В моем случае я хочу получить точный результат, поэтому указываю знак = и ввожу само ограничение в виде суммы.
-
Вторым ограничением является максимальное количество довложений для каждой ячейки. Оно может равняться или быть меньше 250. Соответственно, в вашем случае это будут совершенно другие значения в зависимости от того, с какими исходными данными вы работаете.
-
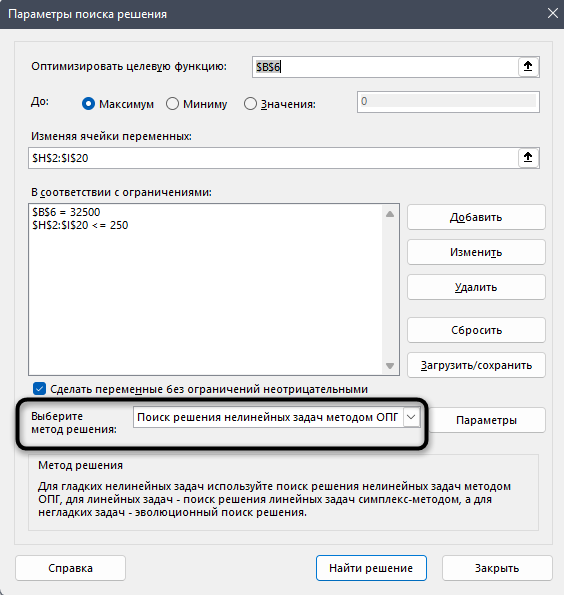
Сейчас это были все ограничения, но, если у вас их больше, продолжайте добавление в таком же ключе. По завершении убедитесь в том, что метод решения выбран как ОПГ, после чего запустите «Найти решение».
-
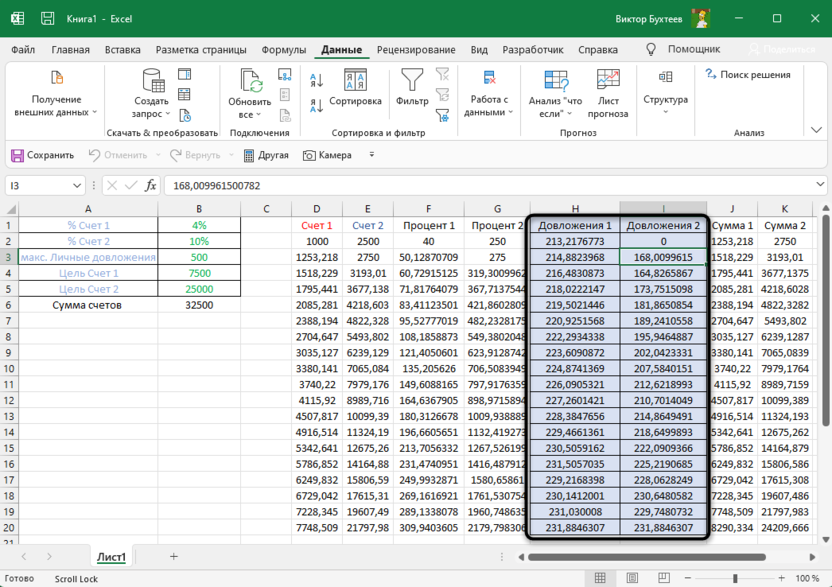
Расчет происходит буквально за несколько секунд, после чего мы видим оптимальное решение. В моем случае каждый цикл на балансы начислялось меньше 250, в один месяц даже 0, а в конце всех циклов получилось достичь нужной суммы с точностью до сотых. «Найти решение» показало, как мне действовать каждый цикл, чтобы вкладывать минимальную сумму, но дойти до нужного результата в конце. У вас решение может быть совершенно другим.
-
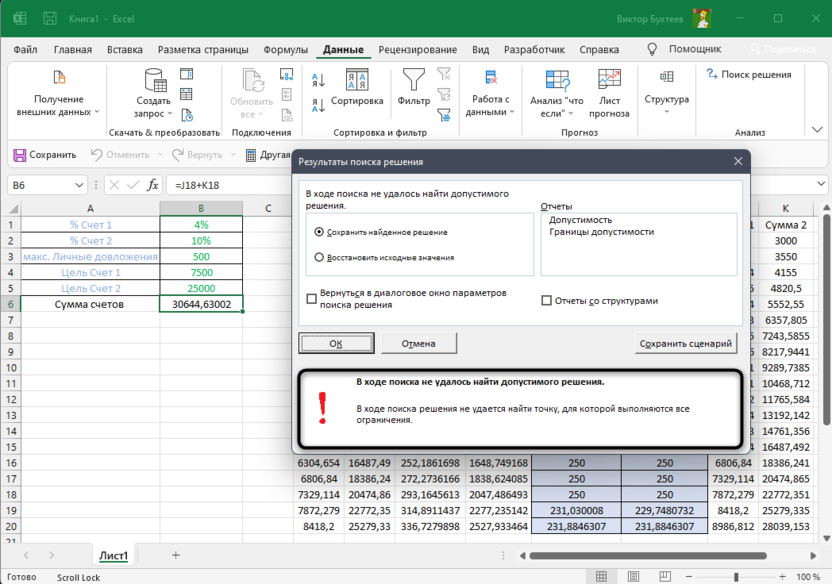
Если же программа посчитала все возможные исходы и в итоге не нашла решения, на экране появится информация об ошибке. Сравните полученные значения в таблице, чтобы понять, на каком этапе произошло завершение вычислений, то есть программа уперлась в установленные ограничения. В итоге вам нужно будет увеличить количество циклов или изменить эти самые ограничения.
В этой инструкции я пошел по самому простому пути, поскольку объединил два счета в одну итоговую сумму и проигнорировал минимальные начисления на каждом из них. В итоге на одном счете получилось немного больше средств, на другом меньше, но сумма все равно соответствовала требуемым условиям. Вы можете добавлять больше ограничений и разных значений, чтобы получить более эффективную оптимизацию в соответствии с вашими задачами.
Я ставил цель показать вам, как работает программа «Поиск решения» в Microsoft Excel, чтобы вы узнали, как можно автоматически найти оптимальные значения для большой таблицы, избегая ручной переборки значений. Надеюсь, все объяснения и примеры были вам понятны, и теперь вы освоили еще одну очень удобную функцию, упрощающую взаимодействие с электронными таблицами, созданными в Экселе.
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
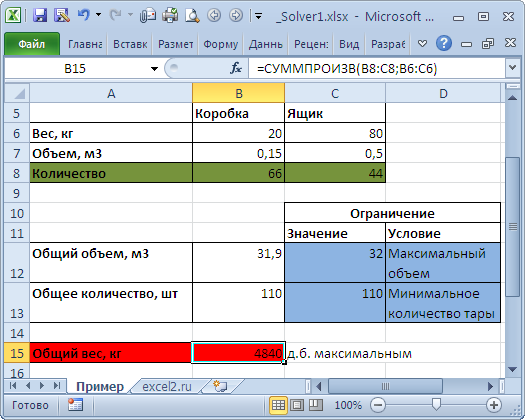
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
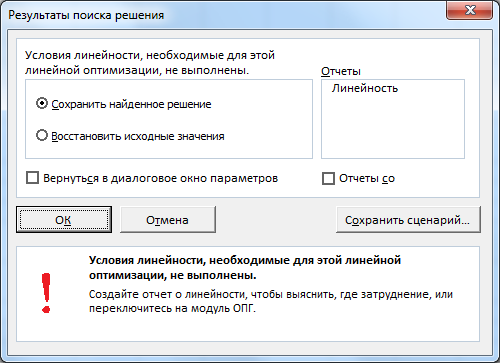
Поиска решения
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
Практическая работа №11
Тема: Задачи оптимизации (поиск решения) в MS Excel.
Цель: — изучение технологии поиска решения для задач
оптимизации (минимизации, максимизации).
Вид
работы: фронтальный
Время
выполнения: 2 часа
Задания к практической работе
Задание
1. Минимизация фонда заработной платы
фирмы.
Пусть известно, что для нормальной работы фирмы
требуется 5…7 курьеров, 8…10 младших менеджеров, 10 менеджеров, 3 заведующих
отделами, главный бухгалтер, программист, системный аналитик, генеральный
директор фирмы.
Общий месячный фонд зарплаты должен быть минимален.
Необходимо определить, какими должны быть оклады сотрудников фирмы, при
условии, что оклад курьера не должен быть меньше 1400 р.
В качестве модели решения этой задачи возьмем линейную
модель. Тогда условие задачи имеет вид N1*A1*x+N2*(A2*x+B2)+…+N8*(A8*x+B8)
= Минимум, где Ni – количество работников данной специальности; x
– зарплата курьера; Ai и Bi – коэффициенты заработной
платы сотрудников фирмы.
Ход работы
1.
Запустите редактор электронных
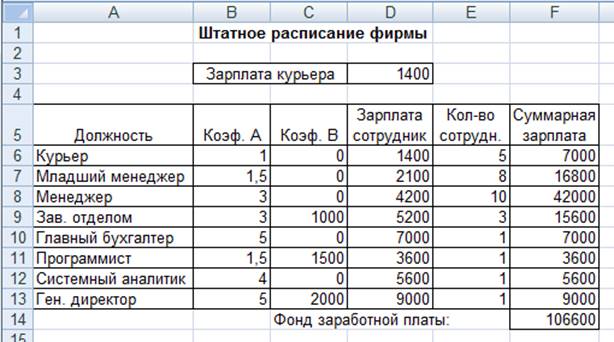
таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл
«Штатное расписание».
Скопируйте содержимое листа «Штатное расписание 1» на
новый лист и присвойте копии листа имя «Штатное расписание 2».
2.
В меню Данные – Анализ «что –
если» активизируйте команду Поиск решения (рис. 1).
3.
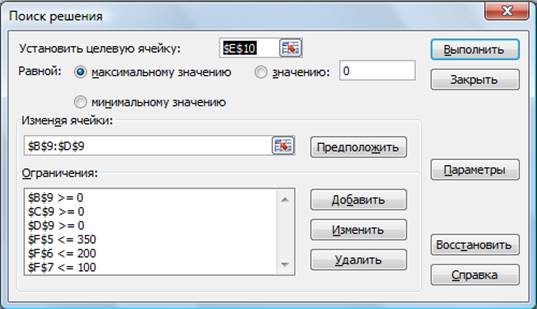
В окне Установить целевую
ячейку укажите ячейку F14, содержащую модель – суммарный фонд заработной
платы.
Рисунок 1 — Задание условий для минимизации фонда заработной
платы
Поскольку необходимо минимизировать общий месячный
фонд зарплаты, активизируйте кнопку равный – Минимальному значению.
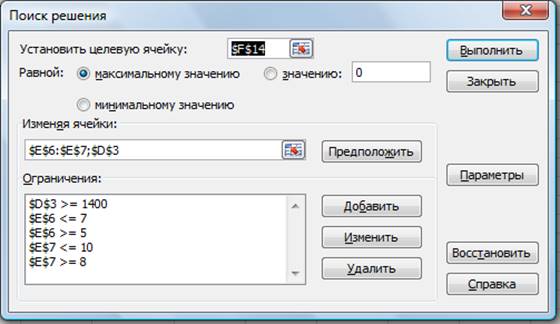
В окне Изменяя ячейки укажите адреса ячеек, в
которых будет отражено количество курьеров и младших менеджеров, а также
зарплата курьера — $E$6:$E$7:$D$3 (при задании ячеек E6, E7 и D3 держите
нажатой клавишу [Ctrl]).
Используя кнопку Добавить в окнах Поиск
решения и Добавление ограничений, опишите все ограничения задачи:
количество курьеров изменяется от 5 до 7, младших менеджеров од 8 до 10, а
зарплата курьера >1400 (рис.2).
Рисунок
2 — Добавление ограничений для минимизации фонда заработной платы
Ограничения наберите в виде
$D$3>=1400
$E$6>5
$E$6<7
$E$7>=8
$E$7 <=10.
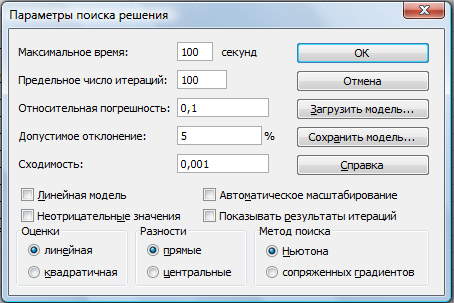
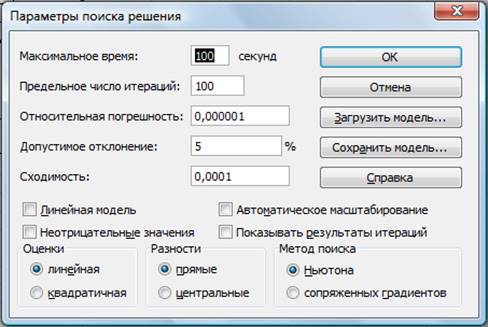
Активизируйте кнопку Параметры, введите
параметры поиска, как показано на рис. 3.
Рисунок
3 — Задание параметров поиска решения по минимизации фонда заработной платы.
Окончательный вид окна Поиск решения приведен
на рис. 1.
Запустите процесс поиска решения нажатием кнопки Выполнить.
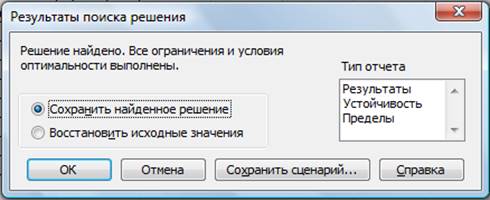
В открывшемся диалоговом окне Результаты поиска решения задайте
опцию Сохранить найденное решение (рис. 4).
Рисунок
4 — Сохранение найденного при поиске решения
Решение задачи приведено на рис. 5. Оно тривиально:
чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд
заработной платы.
Рисунок
5 — Минимизация фонда заработной платы
Задание
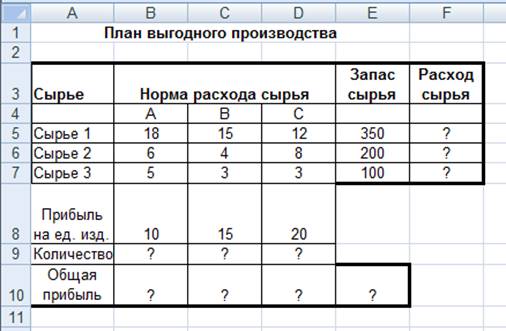
2. Составление плана выгодного
производства.
Фирма производит несколько видов продукции из одного и
того же сырья – А, В и С. Реализация продукции А дает прибыль 10 р., В – 15 р.
и С – 20 р. на единицу изделия.
Продукцию можно производить в любых количествах,
поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо
определить, какой продукции и сколько надо произвести, чтобы общая прибыль от
реализации была максимальной.
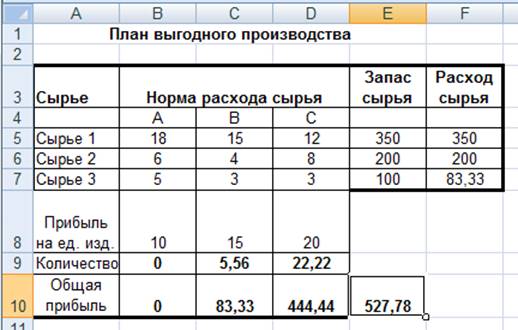
Нормы расхода сырья на производство продукции каждого
вида приведены в табл. 1.
Таблица 1
|
Сырье |
Нормы расхода сырья |
Запас сырья |
||
|
А |
В |
С |
||
|
Сырье |
18 |
15 |
12 |
350 |
|
Сырье |
6 |
4 |
8 |
200 |
|
Сырье |
5 |
3 |
3 |
100 |
|
Прибыль |
10 |
15 |
20 |
Ход работы
1.
Запустите редактор электронных таблиц
Microsoft Excel и создайте новую электронную книгу.
2.
Создайте расчетную таблицу как на
рис. 6. Введите исходные данные и формулы в электронную таблицу. Расчетные
формулы имеют такой вид:
Расход сырья 1=(количество сырья 1) * (норма расхода
сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья
1) * (норма расхода сырья С).
Значит, в ячейку F5 нужно ввести формулу =
B5*$B$9+C5*$C$9+D5*$D$9.
Обратите внимание, что значения количества сырья
каждого вида пока не известны и будут подобраны в процессе решения задания
(ячейки В9:D9 пока пустые).
(Общая прибыль по А) = (прибыль на ед.
изделий А) * (количество А),
Следовательно в ячейку В10 следует
ввести формулу = В8 * В9.
Итоговая общая прибыль = (Общая прибыль
по А) + (Общая прибыль по В) + (Общая прибыль по С),
значит в ячейку Е10 следует ввести
формулу = СУММ(В10:D10).
Рисунок 6 — Исходные
данные для Задания 2
3.
В меню Данные активизируйте
команду Поиск решения и введите параметры поиска, как указано на рис 7.
Рисунок 7 — Задание
условий и ограничений для поиска решений
В качестве целевой ячейки укажите ячейку «Итоговая
общая прибыль» (Е10), в качестве изменяемых ячеек – ячейки количества сырья –
(В9:D9).
Не забудьте задать максимальное значение суммарной
прибыли и указать ограничения на запас сырья:
расход сырья 1<=350; расход сырья 2<=200; расход
сырья 3<=100, а также положительные значения количества сырья А, В, С
>=0.
Установите параметры поиска решения (рис. 8). Для
этого кнопкой Параметры откройте диалоговое окно Параметры поиска
решения, установите параметры по образцу, задайте линейную модель расчета (Линейность
модели).
Рисунок 8 — Задание
параметров поиска решения
4.
Кнопкой Выполнить запустите
Поиск решения. Если вы сделали все верно, то решение будет как на рис.
9.
Рисунок 9 — Найденное
решение максимизации прибыли при заданных ограничениях
5.
Сохраните созданный документ под
именем «План производства».
Вывод. Из решения видно, что оптимальный план выпуска предусматривает
изготовление 5,56 кг продукции В и 22,22
кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом
состоит 527,78 р.
Задание
3. Используя файл «План производства»
(см.задание 2), определить план выгодного производства, т. е. какой продукции и
сколько необходимо произвести, чтобы общая прибыль от реализации была
максимальной.
Выберите нормы расхода сырья на производство продукции
каждого вида и ограничения по запасам сырья из таблицы соответствующего
варианта (5 вариантов):
Вариант 1
|
Сырье |
Норма расхода сырья |
Запас |
||
|
А |
В |
С |
||
|
Сырье 1 |
25 |
17 |
11 |
500 |
|
Сырье 2 |
9 |
7 |
10 |
400 |
|
Сырье 3 |
15 |
8 |
5 |
300 |
|
Прибыль на ед. изделия |
5 |
10 |
12 |
|
|
Количество продукции |
? |
? |
? |
|
|
Общая прибыль |
? |
? |
? |
? |
Вариант 2
|
Сырье |
Норма расхода сырья |
Запас |
||
|
А |
В |
С |
||
|
Сырье 1 |
12 |
11 |
8 |
3500 |
|
Сырье 2 |
14 |
15 |
2 |
280 |
|
Сырье 3 |
8 |
9 |
10 |
711 |
|
Прибыль на ед. изделия |
10 |
9 |
8 |
|
|
Количество продукции |
? |
? |
? |
|
|
Общая прибыль |
? |
? |
? |
? |
Вариант 3
|
Сырье |
Норма расхода сырья |
Запас |
||
|
А |
В |
С |
||
|
Сырье 1 |
10 |
20 |
15 |
2700 |
|
Сырье 2 |
16 |
25 |
13 |
3800 |
|
Сырье 3 |
8 |
9 |
10 |
1200 |
|
Прибыль на ед. изделия |
7 |
8 |
6 |
|
|
Количество продукции |
? |
? |
? |
|
|
Общая прибыль |
? |
? |
? |
? |
Вариант 4
|
Сырье |
Норма расхода сырья |
Запас |
||
|
А |
В |
С |
||
|
Сырье 1 |
14 |
15 |
19 |
460 |
|
Сырье 2 |
7 |
8 |
12 |
820 |
|
Сырье 3 |
17 |
24 |
6 |
214 |
|
Прибыль на ед. изделия |
15 |
10 |
25 |
|
|
Количество продукции |
? |
? |
? |
|
|
Общая прибыль |
? |
? |
? |
? |
Вариант 5
|
Сырье |
Норма расхода сырья |
Запас |
||
|
А |
В |
С |
||
|
Сырье 1 |
12 |
18 |
3 |
625 |
|
Сырье 2 |
16 |
25 |
13 |
227 |
|
Сырье 3 |
8 |
9 |
10 |
176 |
|
Прибыль на ед. изделия |
18 |
15 |
9 |
|
|
Количество продукции |
? |
? |
? |
|
|
Общая прибыль |
? |
? |
? |
? |
Рекомендуемая
литература: 1, 2, 3, 4
Оптимизация значений таблицы Excel, удовлетворяющих определенным критериям, может быть сложным процессом. К счастью, Microsoft предлагает надстройку Решение проблем для численной оптимизации. Хотя данный сервис не может решить всех проблем, он может быть полезным в качестве инструмента что-если. Данный пост посвящен надстройке Решение проблем в Excel.
Надстройка Решение проблем доступна во всех версиях Excel. Обратите внимание, что скриншоты могут не соответствовать вашей версии. Несмотря на то, что некоторые функции могут менять свое местоположение в зависимости от версии надстройки, функционал остается практически неизменным.
Что такое Поиск решений
Поиск решений – надстройка Excel, которая помогает найти решение с помощью изменения значений целевых ячеек. Целью может быть минимизация, максимизация или достижение некоторого целевого значения. Проблема решается путем регулировки входных критериев или ограничений, определенных пользователем.
Где в Excel поиск решений
Надстройка Поиск решений поставляется вместе с Excel, но по умолчанию отключена. Чтобы включить его, перейдите по вкладке Файл в группу Параметры. В появившемся диалоговом окне Параметры, выберите Надстройки -> Управление: Надстройки Excel -> Перейти. В окне Надстройки устанавливаем галочку напротив поля Поиск решения, жмем ОК.
Теперь во вкладке Данные появилась новая группа Анализ с кнопкой Поиск решения.
Пример использования Поиска решения
Данный пост основан на примере использования Надстройки Поиск решения. Файл совместим со всеми версиями Excel.
Определение проблемы
Предположим, что у нас есть набор данных, состоящий из 8 пунктов, каждому из которых соответствует свое значение.
… и нам необходимо скомбинировать значения в две группы так, чтобы суммы значений этих групп примерно совпадали.
Для начала требуется определить каждый пункт к какой-нибудь группе.
Чтобы указать привязанность пункта к группе, будем помечать их единицей (1), в противном случае нулем (0).
В следующем столбце мы будем суммировать значения каждого пункта в группе, и затем подведем итог в конце столбца.
Нам также необходимо обработать значение каждого пункта в каждой группе, для этого умножаем значение пункта на значение группы, соответствующее этому пункту.
Наконец, нам необходимо свести сумму групп и работать с разницей между ними.
Наша задача минимизировать разницу между суммами групп.
Теперь мы можем присвоить каждой группе пункты, для этого вручную проставляем единицы в столбцах С и D. Excel отобразит разницу сумм групп в ячейке G11.
Для большей наглядности я добавил условное форматирование для ячеек, имеющих значение >0.
Проблема в том, что количество возможных комбинаций 28, т.е. 256 вероятных ответов на вопрос. Если на каждый из них тратить по 5 секунд, это займет у нас 21,3 минуты, предполагая, что мы сможем выдержать темп и запомнить лучшую комбинацию.
Вот где Поиск решения находит применение.
Поиск оптимального решения в Excel
Чтобы применить сервис Поиск решения, нам необходимо определить ряд требований, правил и ограничений, которые позволят надстройке найти правильный ответ.
Наши правила
Наше основное требование – это минимизировать разницу между двумя группами. В нашем примере она находится в ячейке G11 – Группа B минус Группа A. Нам нужно, чтобы значение в ячейке G11 было настолько малым насколько это возможно, но больше или равно 0.
Мы также знаем, что пункт может находиться либо в Группе A, либо в Группе B, к тому он не может быть дробным. Таким образом у нас два ограничения для каждого элемента:
Во-первых: Значение элемента в колонке Итог должна равняться единице.
Во-вторых: Значения элементов в группах должны быть целыми.
Мы также знаем, что общее количество элементов 8, это еще одно ограничение. Как использовать эти ограничения мы обсудим в следующем разделе.
Диалоговое окно Поиска решения
В этом разделе описано окно надстройки Поиск решения и его использования для определения проблемы.
Пустое окно Поиска решения
Заполненное окно Поиска решения
Оптимизировать целевую функцию
Это целевая ячейка, в которой мы пытаемся решить проблему. Наша целевая ячейка G11 – разница в группах.
До
Здесь мы указываем, каких результатов хотим добиться от целевой функции.
Мы хотим, чтобы суммы обоих групп совпадали, т.е. чтобы разница сумм была равна 0. Это может показаться странным, но нам не требуется минимизировать разницу, потому что при этом все элементы будут помещены в Группу A, что приведет к значению ячейки G11 меньше нуля.
Другой способ наложения ограничения – изменить G11 на =ABS(G10-F10). При этом мы сможем установить маркер на Минимум, как результат достижения целевой функции.
Но пока мы остановимся на формуле =G10-F10 и установим маркер в значение равным 0.
Изменяя ячейки переменных
Изменяемые ячейки – ячейки, которые надстройка попытается изменить, чтобы решить задачу. В нашем случае это привязка элемента к конкретной группе: $C$2:$D$9.
В соответствии с ограничениями
Ограничения – это правила, которые лимитируют возможные решения проблемы.
Нам необходимо добавить несколько ограничений в наш список:
- В колонке Итого каждый элемент должен равняться 1
- Элементы групп должны быть целым числом
- Сумма значений столбца Итого должна равняться 8
Чтобы наложить ограничения, жмем кнопку Добавить
- Для каждой ячейки диапазона E2:E9 устанавливаем ограничение значения равным 1
- Для каждой ячейки диапазона C2:D9 устанавливаем ограничение значение целое число.
- Необходимо добавить ограничение на сумму обоих групп, ячейка E10 = 8.
Вы можете Изменить или Удалить ограничение, если допустили ошибку, выбрав конкретное ограничение и нажав соответствующие кнопки в диалоговом окне.
Загрузить/сохранить параметры поиска решений
Сервис поиска решений позволяет сохранять и загружать параметры надстройки. Для этого в окне существует кнопка Загрузить/сохранить. Параметры модели сохраняются в диапазон, который вы указали ранее. Данный подход позволяет быстро настраивать и изменять параметры Поиска решения.
Запуск поиска оптимального решения в Excel
Предупреждение!!! Надстройка поиск решения является сложной вычислительной надстройкой, поэтому перед запуском сохраните рабочую книгу.
Прежде чем запустить модель, необходимо задать еще несколько параметров, чтобы убедиться, что сервис отработает корректно. В основном диалоговом окне убедитесь, что стоит маркер напротив поля Сделать переменные без ограничений неотрицательными. В этом же окне нажмите кнопку Параметры.
Два параметра, которые необходимо будет менять время от времени:
Точность ограничения: значение от 0 до 1, где, чем больше цифра, тем больше ограничение
Целочисленная оптимальность: показывает насколько далеко от целого числа ограничение имеет право быть.
Запуск модели
Чтобы запустить надстройку нажмите кнопку Найти решение в основном окне.
В строке состояния вы увидите ряд статических данных, которые будут отображать внутреннюю работу надстройки. Как правило, они быстро меняются, и читать их сложно. Если модель сложная, то работа может остановится на некоторое время, надстройка обычно восстанавливается от этих проблем сама.
После того, как Поиск решения закончит свою работу, Excel отобразит диалоговое окно Результаты поиска решения с некоторой информацией. Первое, на что стоит обратить внимание – это надпись Решение найдено в пределах допустимого отклонения. Если решение найдено, ячейки рабочей книги изменятся с предложенным решением.
Теперь у вас есть 4 варианта на выбор:
— Запустить отчет
— Сохранить сценарий
— Восстановить исходные значения
— Сохранить найденное решение
Запустить отчет
Вы можете создать отчет, выбрав доступные из списка отчетов. Будет создан новый лист Отчет о результатах1.
Обратите внимание, что в зависимости от установленных вами ограничений, будут доступны различные отчеты.
Сохранить сценарий
Если вы нажмете кнопку Сохранить сценарий, Excel откроет следующее диалоговое окно:
Где необходимо ввести название вашего сценария модели и нажать кнопку ОК.
Все сценарии доступны в Диспетчере сценариев, который находится во вкладке Данные в группе Работа с данными –> Анализ что-если -> Диспетчер сценариев.
Вернуться к модели
К тому же, вы можете вернуться к модели и:
— Восстановить исходные значения
— Сохранить найденное решение
Проверка результатов
Сервис Поиск решения, вероятно, самая непредсказуемая система в Excel. Таким образом, все найденные решения, которые он выдает необходимо перепроверять вручную, для дальнейшего использования.
Данная проверка на реалистичность должна начинаться с подтверждения, что все результаты удовлетворяют заданным критериям:
— Являются ли результаты примерно похожими на ваши ожидания?
— Не нарушены ли максимумы и минимумы?














 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.