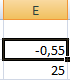Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра
.
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке
Данные,
группа
Работа с данным
.
Простейший пример
Найдем значение параметра
b
в уравнении
2*а+3*b=x
, при котором
x=21
, параметр
а=
3
.
Подготовим исходные данные.
Значения параметров
а
и
b
введены в ячейках
B8
и
B9
. В ячейке
B10
введена формула
=2*B8+3*B9
(т.е. уравнение
2*а+3*b=x
).
Целевое значение x
в ячейке
B11
введено
для информации.
Выделите ячейку с формулой
B10
и вызовите
Подбор параметра (на вкладке
Данные
в группе
Работа с данными
выберите команду
Анализ «что-если?»
, а затем выберите в списке пункт
Подбор параметра
…)
.
В качестве целевого значения для ячейки
B10
укажите 21, изменять будем ячейку
B9
(параметр
b
).
Нажмите ОК.
Инструмент
Подбор параметра
подобрал значение параметра
b
равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку
B9
последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без
Подбора параметра
параметр будет подобрать сложно
.
Примечание
: Уравнение
2*а+3*b=x
является линейным, т.е. при заданных
a
и
х
существует только одно значение
b
, которое ему удовлетворяет. Поэтому инструмент
Подбор параметра
работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то
Подбор параметра
найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в
файле примера
на листе
Простейший
.
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка
С13
). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (
С8
), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (
С14
) равно 0.
В структуре цены в ячейке
С9
(Цена продукции) введена формула Собственные расходы + Прибыль (
=С7+С8
). Стоимость договора (ячейка
С11
) вычисляется как Цена продукции + НДС (=
СУММ(С9:C10)
).
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент
Подбор параметра
.
Выделите ячейку
С14
, вызовите
Подбор параметра
(на вкладке
Данные
в группе
Работа с данными
выберите команду
Анализ «что-если?»
, а затем выберите в списке пункт
Подбор параметра
…). В качестве целевого значения для ячейки
С14
укажите 0, изменять будем ячейку
С8
(Прибыль).
Нажмите ОК.
Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание
: В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
Предположим, что нам необходимо
определить максимальную сумму кредита
, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция
ПЛТ()
для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см.
статьи про аннуитет
). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции
ПЛТ()
) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента
Подбор параметра
сумму займа пришлось бы подбирать в ручную с помощью функции
ПЛТ()
или использовать соответствующую формулу.
Введем в ячейку
B
6
ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку
B
7
, % ставку по кредиту введем в ячейку
B8,
а формулу
=ПЛТ(B8/12;B7;B6)
для расчета суммы ежемесячного платежа в ячейку
B9
(см.
файл примера
).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
-
на вкладке
Данные
в группе
Работа с данными
выберите команду
Анализ «что-если?»
, а затем выберите в списке пункт
Подбор параметра
…; -
в поле
Установить
введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка
B9
; -
введите искомый результат в поле
Значение
. В данном примере он равен
-1800
; -
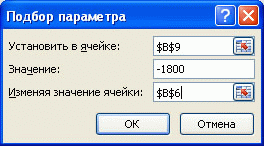
В поле
Изменяя значение ячейки
введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка
B6
; - Нажмите ОК
Что же сделал
Подбор параметра
? Инструмент
Подбор параметра
изменял по своему внутреннему алгоритму сумму в ячейке
B6
до тех пор, пока размер платежа в ячейке
B9
не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра
подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте
инструмент
Поиск решения
. Точность подбора параметра можно задать через меню
.
Вопросом об единственности найденного решения
Подбор параметра
не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент
Подбор параметра
позволяет сэкономить несколько минут по сравнению с ручным перебором.
-
Подбор параметра
Подбор
параметра также является частью блока
задача
анализа «чтоесли».
Когда желаемый результат одиночной
формулы известен, но неизвестны значения,
которые требуется ввести для получения
этого результата, можно воспользоваться
средством «Подбор
параметра»
на вкладке Данные
в группе Работа
с данными
.При
подборе параметра Microsoft Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока формула, зависимая от этой
ячейки, не возвращает нужный результат.
Например,
средство «Подбор
параметра»
можно использовать для изменения
процентной ставки в ячейке B3 до тех пор,
пока выплаты по кредиту не станутравными
1500,00р (рис. 52).
Рисунок
52. Подбор параметра
Целевая
ячейка
должна содержать формулу. Изменяемая
ячейка-параметр
должна прямо или косвенно зависеть от
исходной формулы и должна содержать
обязательно значение, а не формулу.
Влияние не обязательно должно быть
непосредственным, т.е. ячейка-параметр
может не присутствовать в формуле в
качестве аргумента.
Порядок
действий по подбору параметра.
-
Выделить
целевую ячейку В4 (рис. 53). -
На
вкладке Данные
в группе Работа
с данными
выберите команду Подбор
параметра. -
В
полеУстановить
в ячейке
указать целевую ячейку В4. -
В
полеЗначение
установить значение, которое необходимо
получить в целевой ячейке 1500 -
В
полеИзменяязначениеячейки
указать ссылку на ячейку-параметр В3,
ОК. -
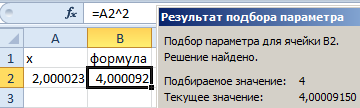
Диалоговое
окно Результат
подбора параметра -
Если
выполняется сложная задача подбора
параметра, можно нажать кнопку Пауза
и прервать вычисление, затем нажать
кнопку Шаг
и после просмотра результата вычисления
нажать кнопкуПродолжить -
ОК
– для замены значений рабочего листа
в соответствии с новым значением целевой
ячейки -
Отмена
– для сохранения прежних величин.
В
результате вычисления получим решение
– 15%(рис. 53)
Рисунок
53. Результат подбора параметра
Часто
известен желаемый результат формулы,
но не известны входные значения для его
достижения. Подбором параметра можно
варьировать значения в указанной входной
ячейке, пока формула, зависящая от этой
ячейки, не возвратит ожидаемый результат.
Точность
и множественность решений
По
умолчанию команда Подбор параметра
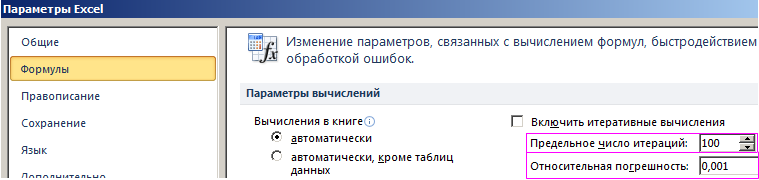
прекращает вычисления при выполнении
100 итераций или при получении результата
в пределах 0,001 от заданного целевого
значения. Для достижения большей точности
в окне Параметры
Excel(рис.
54)на вкладке Формулы-
установить флажокВключить
итеративные вычисления
и установить число итераций и погрешность.

Рисунок
54. Установка точности вычислений
-
Графический подбор параметра
Excel
предоставляет способ подбора параметра
с помощью манипулирования графиками.
Пример
графического подбора параметра.
Таблица
отображает прогнозируемый объем продаж
фирмы. Известно, что объем продаж за
первый, 2012 год составил 250000 у.е. Его хотят
довести до 10000000. Предположительным
коэффициентом роста был 1,40. Как видно
из таблицы и графика при таком коэффициенте
объем продаж составит лишь немногим
более 7000000 у.е.
Для
нахождения желаемого коэффициента
необходимо выделить последний столбик
диаграммы и изменить его значение до
10000000 (или насколько возможно).
В
появившемся диалоговом
окне Подбор параметра
ввести в поле
Изменяя значение ячейки
адрес ячейки B1. Программа вычислит
значение нового коэффициента, а диаграмма
изменится автоматически (рис. 55)
Рисунок
55. Графический подбор параметра
Задание33
Купец
купил 138 аршин черного и синего сукна
за 540 руб. Спрашивается, сколько аршин
купил он того и другого, если синее
стоило 5 руб. за аршин, а черное 3 руб.?
(табл. 28)
Таблица28
|
Количество |
Плата |
|||
|
цена |
3 |
|||
|
цена |
5 |
|||
|
Всего |
138 |
540 |
Задание34
Подобрать
цену товара, чтобы прибыль составила
2000 р. (табл. 29)
Таблица
29
|
количество |
1 |
|
|
доход |
количество*цену |
|
|
себестоимость |
Количество |
|
|
валовая |
доход-себестоимость |
|
|
з/плата |
2 |
|
|
реклама |
5 |
|
|
накладные |
12 |
|
|
валовые |
з/плата |
|
|
прибыль |
валовая |
|
|
цена |
35,00р. |
|
|
себестоимость |
15,00р. |
Задание35
Подобрать
цену продукции, чтобы прибыль составила
50000000р (табл.30).
Таблица
30
|
Квартал |
1 |
|
Количество |
20000 |
|
Доход |
|
|
Себестоимостьреализованной |
|
|
Валовая |
|
|
Накладных |
30% |
|
Затраты |
5 |
|
Затраты |
1 |
|
Накладные |
41 |
|
Валовые |
|
|
Прибыль |
|
|
Цена |
4000 |
|
Себестоимость |
2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».
В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.
Где находится «Подбор параметра» в Excel
Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.
Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.
Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.
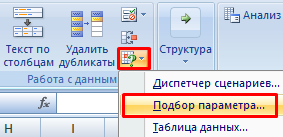
Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».
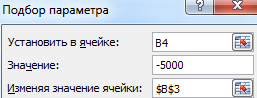
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).
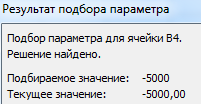
После нажатия ОК на экране появится окно результата.
Чтобы сохранить, нажимаем ОК или ВВОД.
Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.
Решение уравнений методом «Подбора параметров» в Excel
Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.
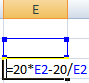
В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.
А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.
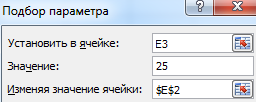
Запускам инструмент и заполняем поля:
«Установить в ячейке» — Е3 (ячейка с формулой);
«Значение» — 25 (результат уравнения);
«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).
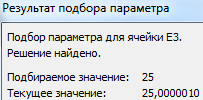
Результат функции:
Найденный аргумент отобразится в зарезервированной для него ячейке.
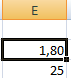
Решение уравнения: х = 1,80.
Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.
Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.
Примеры подбора параметра в Excel
Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.
Пример 1. Метод подбора начальной суммы инвестиций (вклада).
Известные параметры:
- срок – 10 лет;
- доходность – 10%;
- коэффициент наращения – расчетная величина;
- сумма выплат в конце срока – желаемая цифра (500 000 рублей).
Внесем входные данные в таблицу:
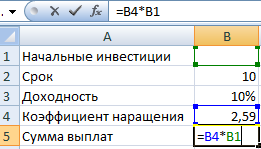
Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.
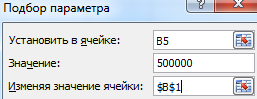
Вызываем окно команды «Подбор параметра». Заполняем поля:
После выполнения команды Excel выдает результат:
Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.
Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.
Входные данные:
- ежемесячные отчисления – 1000 руб.;
- период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
- пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
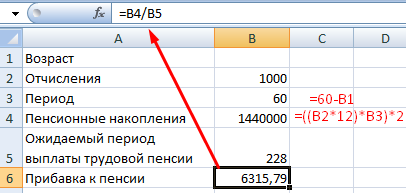
- ожидаемый период выплаты трудовой пенсии – 228 мес.;
- желаемая прибавка к пенсии – 2000 руб.
С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:
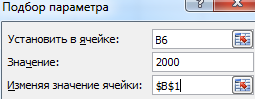
- Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.
- Нажимаем ОК – получаем результат подбора.
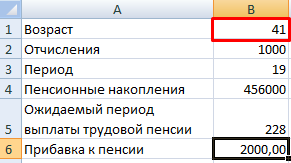
Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.
Функция «Подбор параметра» работает правильно, если:
- значение желаемого результата выражено формулой;
- все формулы написаны полностью и без ошибок.
Функция Excel: подбор параметра
Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.
Зачем нужна функция
Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.
Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.
Использование функции
Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.
Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).
Итак, алгоритм действий следующий:
- Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
- На экране появится окно для подбора параметра, которе нужно заполнить:
- в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.
Решение уравнений с помощью подбора параметра
Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.
Например, нам нужно решить уравнение: 7x+17x-9x=75 .
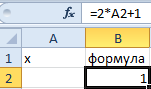
- Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так: =7*D2+17*D2-9*D2 .
- Щелкаем Enter и получаем результат в виде числа 0, что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.
Заключение
Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.
Задачи на подбор параметра в excel
Главная > Решение
| Информация о документе |
| Дата добавления: |
| Размер: |
| Доступные форматы для скачивания: |
Решение задач – Подбор параметра
Задачи оптимизации с одним неизвестным
Задача оптимизации затрат
Подбор параметра и таблицы подстановки
РЕШЕНИЕ ЗАДАЧ – Подбор параметра
Решение задач – одно из важных применений Excel. Самый простой инструмент предназначен для подбора значений и называется «что-если» анализ: задается некоторая целевая функция и ее числовое значение, Excel автоматически подбирает параметры целевой функции до получения целевого значения. Формула в целевой функции должна логически зависеть от подбираемого параметра.

Эти инструменты Excel (будут рассмотрены в следующих разделах) полезны экономистам, администраторам, менеджерам, которым для решения деловых проблем и принятия решений в сферах финансов, бухгалтерского учета, маркетинга, управления операциями, экономики, менеджмента необходимо применять количественные методы анализа и прогнозирования.
В качестве примера разберем расчет прибыли от продаж, показанный на рис. 1.20. В ячейках А3, А4 и А7 записаны формулы – формулы для наглядности продублированы в скобках. Поскольку Другие затраты и Количество здесь постоянны, то нужную прибыль можно получить подбором Цены единицы или Себестоимости единицы товара. Попробуем получить прибыль 20000, изменяя Цену единицы . Проделайте следующие действия:
Встаньте на целевую ячейку А7. Выберите пункт меню С е рвис П одбор параметра… . Введите значение ожидаемой прибыли. Для ввода адреса изменяемой ячейки, перейдите в нижнее поле и встаньте на ячейку А9 в таблице – адрес будет записан автоматически в поле. Нажмите ОК.
В следующем окне можно либо принять, либо отменить результат подбора параметра. Результат:
Самостоятельно попробуйте подобрать Себестоимость единицы , чтобы получить прибыль 20000 при Цене единицы =200.
Далее приводятся другие применения инструмента Подбор параметра .
Задачи оптимизации с одним неизвестным
Часто уравнения не имеют точного аналитического решения. Тогда их решают методом последовательных приближений (итераций) неизвестных параметров так, чтобы они давали минимум ошибки целевой функции.
Для численного решения уравнений с одним неизвестным в Excel имеется эффективный инструмент Подбор параметра . Целевая функция может быть линейной, квадратичной, третьей и выше степени.
Инструмент Подбор параметра был рассмотрен в предыдущем разделе для расчета прибыли от продаж. Здесь рассмотрим его применение для решения некоторого уравнения, например 2х 3 -3х 2 +х-5=0.
Решение задачи состоит из двух этапов. На первом этапе следует ввести уравнение в ячейку (В2), а в другую ячейку (А2) ввести некоторое ориентировочное значение, здесь 1:
На втором этапе следует воспользоваться инструментом Подбор параметра :
Встаньте на ячейку В2 и вызовите его – С е рвис П одбор параметра… .
В открывшемся окне введите искомое значение функции и адрес изменяемой ячейки:
После нажатия кнопки ОК Вы получите следующее решение:
Найденное решение приближенное, поэтому можно считать, что при х=1,918578609 значение уравнения 2х 3 -3х 2 +х-5 стремится к нулю, т.е. к 0,000107348. Смело установите для ячеек А2 и В2 числовой формат отображения данных и получите следующее:

Задача оптимизации затрат
С помощью подбора параметров можно решать задачи оптимального распределения ресурсов следующего плана. Требуется закупить составляющие (конфета карамельная, конфета шоколадная, упаковка печенья и мармелада) для комплектования подарочных наборов так, чтобы цена набора не превышала 100 руб. При этом известны соотношения цен относительно одной из компонент (здесь карамели): цена шоколадной конфеты в 2.5 раза выше цены карамели, цена печенья на 10 руб. больше карамели и цена мармелада в 8.5 раза выше цены карамели. В наборе должно быть 5-10 конфет карамель, 4-6 шоколадных конфет, 1-2 упаковки печенья и 1 упаковка мармелада. Рассчитать закупочные цены для разных комплектов.
Ниже показаны расчеты закупочных цен для максимального и минимального комплектов:
В ячейки В4:В6 запишите формулы: =B3*2.5, =B3+10 и =B3*8.5. В колонки D3:D6 поставьте формулы вычисления сумм по строкам, а в D7 вычислите общую сумму: =СУММ(D3:D6). В итоге целевая функция – стоимость набора D7 есть C3* x +C4*2.5* x +C5*( x +10)+C6*8.5* x , где x =B3 цена одной компоненты – конфеты карамель. Параметры инструмента Подбор параметра заполните так:
Подбор параметра и таблицы подстановки
В паре с инструментом Подбор параметра обычно применяют инструмент Таблица подстановки , который позволяет расширить количество одновременно рассчитываемых вариантов решений. Таблицы подстановки создаются на основе одной или двух изменяемых параметров.
Рассмотрим пример. Фирма производит изделия и продает их по цене 90руб. Ежемесячные постоянные затраты составляют 5000руб., переменные затраты на единицу изделия – 30руб. Необходимо определить точку безубыточности, т.е. вычислить количество изделий, при котором прибыль равна 0. Кроме того, требуется определить изменение прибыли для 10 следующих значений количества с шагом 5, а также прибыль при этих значениях количества для цен 80, 85, 95 и 100руб.
Решение. Введите в Excel исходные данные, приведенные ниже:
В точке безубыточности валовая прибыль равна валовым затратам, т.е. (В3*В4)-(В1+В2*В4)=0. Вызовите Подбор параметра , заполните параметры и нажмите ОК – в ячейке В4 будет вычислено значение 83.33 (рис. 17).
На следующем шаге рассчитаем 10 значений прибыли для следующих значений количества с шагом 5. Используем для этого таблицу подстановки с одним изменяемым параметром. Подготовьте исходные данные (рис. 2.35) : в ячейки C4:C13 запишите значения количества с шагом 5, а в колонке справа в строке выше (ячейка D3) — формулу из ячейки В7.
Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон C3:D13 (рис. 2.36), вызовите пункт Д анные Т аблица подстановки… , укажите изменяемую ячейку ($B$4) и порядок расположения исходных данных (в строках) в окне запроса – рис. 2.36. После нажатия ОК в ячейках D4:D13 будут рассчитаны значения прибыли.
На последнем шаге рассчитаем значения прибыли для тех же значений количества при ценах 80, 85, 95 и 100руб. Используем для этого таблицу подстановки с двумя изменяемыми параметрами. Результат показан на рис. 2.37.
Для его получения подготовьте исходные данные : в ячейки F4:F13 запишите значения количества, в строке G3:J3 запишите значения цен, на пересечении строки и столбца с данными в ячейке F3 запишите формулу из ячейки В7. Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон F3:F13 (рис. 2.37), вызовите пункт Д анные Т аблица подстановки… , укажите изменяемую ячейку по строкам ($B$4) и по столбцам ($B$3) в окне запроса – рис. 2.38. После нажатия ОК в ячейках G4:J13 будут рассчитаны значения прибыли.
Задания для самостоятельного выполнения:
Найдите решение уравнения х 3 +5х 2 -х+1=0
Найдите два решения уравнения х 2 -3х+2=0.
Найдите решение уравнения е х =20000.
Примените инструмент Таблица подстановки при решении предыдущей задачи комплектования подарочных наборов.
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y =7 является функцией x ;
- нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
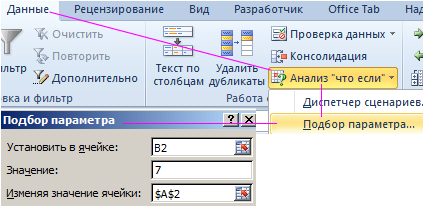
- Заполните ячейки листа, так как показано на рисунке:
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
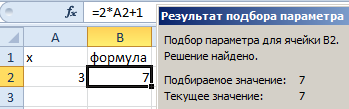
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
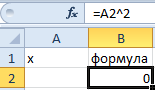
Немного усложним задачу. На этот раз формула выглядит следующим образом:
- Заполните ячейку B2 формулой как показано на рисунке:
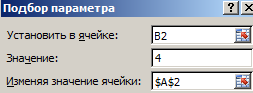
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.
Простейший пример
Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.
Подготовим исходные данные.
Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.
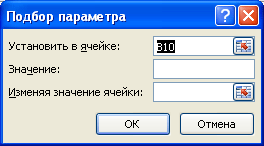
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).
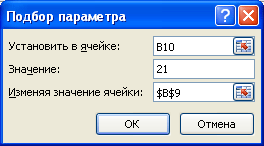
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).
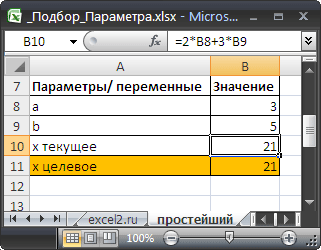
Инструмент Подбор параметра подобрал значение параметра b равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.
Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
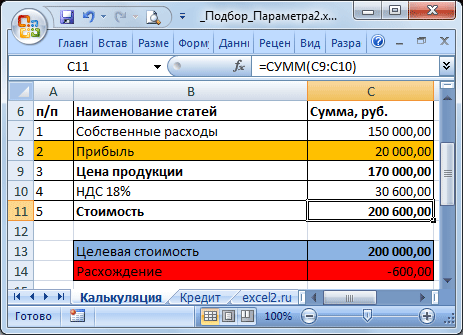
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).
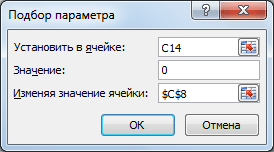
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.
Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).
Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.
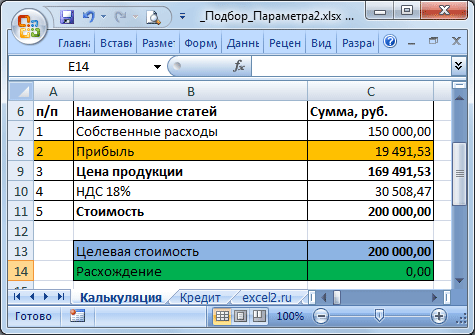
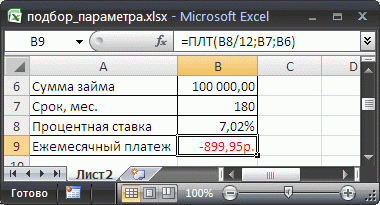
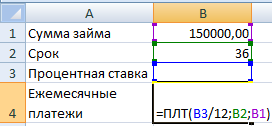
Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
- на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
- в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
- введите искомый результат в поле Значение. В данном примере он равен -1800;
- В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
- Нажмите ОК
Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.
Уравнения и задачи на подбор параметра в Excel
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y =7 является функцией x ;
- нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
- Заполните ячейки листа, так как показано на рисунке:
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
источники:
http://planshet-info.ru/kompjutery/zadachi-na-podbor-parametra-v-excel
http://exceltable.com/vozmojnosti-excel/uravnenie-i-podbor-parametra
Функции программы Microsoft Excel: подбор параметра
Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.
Суть функции
Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом. Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново. Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.
Применение функции на практике
Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.
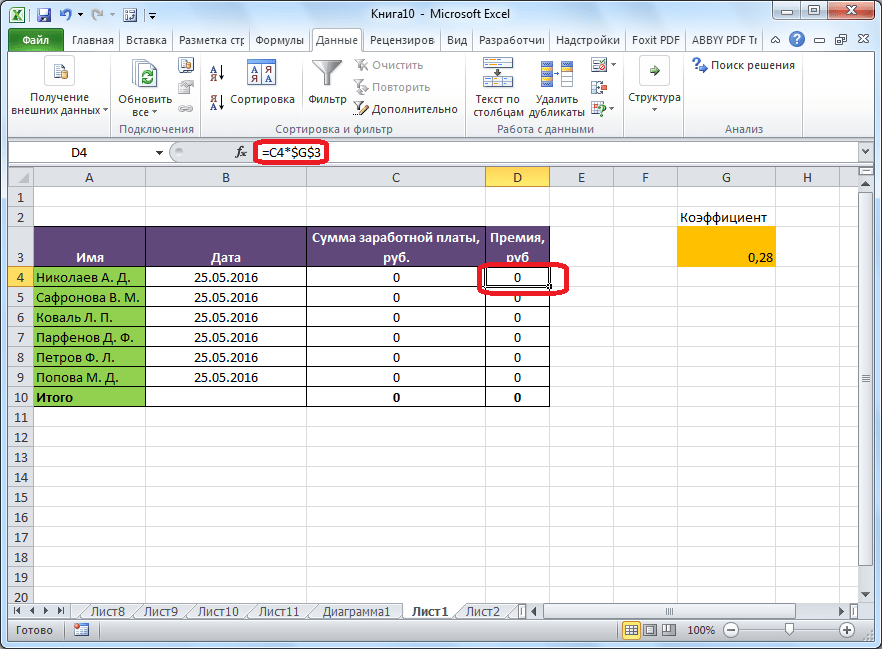
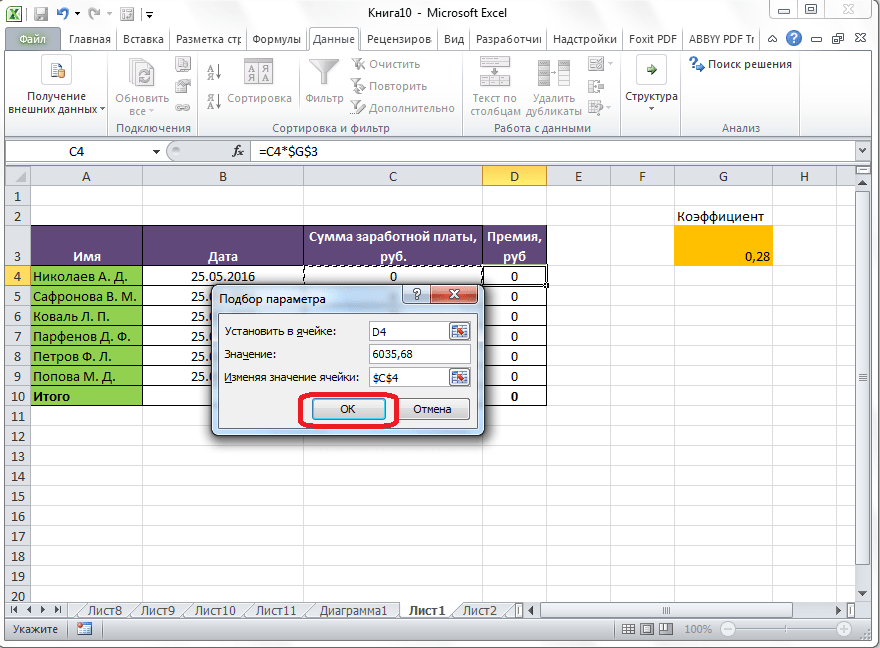
Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.
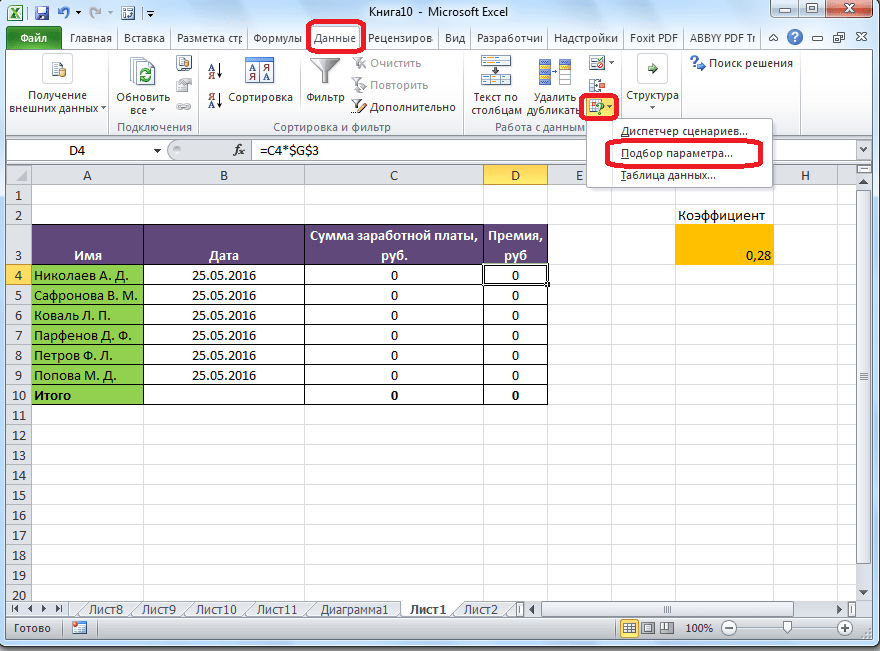
Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».
После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет. В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле. Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.
В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.
Когда все данные окна параметров заполнены, жмем на кнопку «OK».
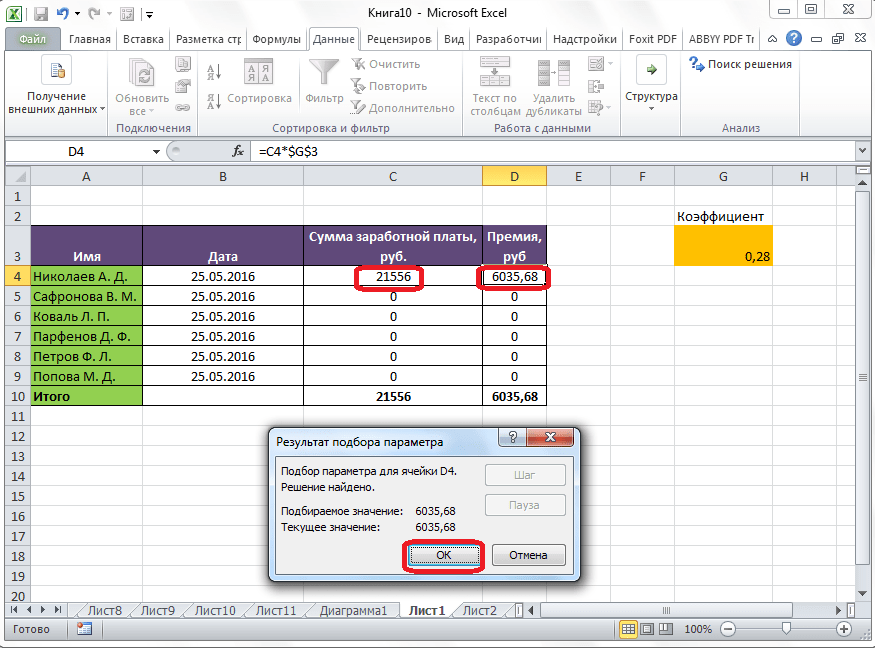
После этого, совершается расчет, и в ячейки вписываются подобранные значения, о чем сообщает специальное информационное окно.
Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.
Решение уравнений
Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.
Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.
В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».
Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».
В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2). В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46. В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».
Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.
Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным. Вместе с тем, по функционалу она уступает более мощному инструменту Поиск решения.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Подбор параметра в MS EXCEL
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.
Простейший пример
Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.
Подготовим исходные данные.
Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).
Инструмент Подбор параметра подобрал значение параметра b равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.
Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.
Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).
Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.
Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
- на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
- в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
- введите искомый результат в поле Значение. В данном примере он равен -1800;
- В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
- Нажмите ОК
Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.
Подбор параметра в Excel и примеры его использования
«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».
В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.
Где находится «Подбор параметра» в Excel
Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.
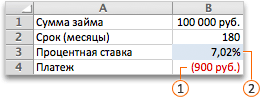
Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.
Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.
Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).
После нажатия ОК на экране появится окно результата.
Чтобы сохранить, нажимаем ОК или ВВОД.
Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.
Решение уравнений методом «Подбора параметров» в Excel
Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.
В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.
А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.
Запускам инструмент и заполняем поля:
«Установить в ячейке» — Е3 (ячейка с формулой);
«Значение» — 25 (результат уравнения);
«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).
Найденный аргумент отобразится в зарезервированной для него ячейке.
Решение уравнения: х = 1,80.
Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.
Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.
Примеры подбора параметра в Excel
Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.
Пример 1. Метод подбора начальной суммы инвестиций (вклада).
- срок – 10 лет;
- доходность – 10%;
- коэффициент наращения – расчетная величина;
- сумма выплат в конце срока – желаемая цифра (500 000 рублей).
Внесем входные данные в таблицу:
Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.
Вызываем окно команды «Подбор параметра». Заполняем поля:
После выполнения команды Excel выдает результат:
Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.
Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.
- ежемесячные отчисления – 1000 руб.;
- период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
- пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
- ожидаемый период выплаты трудовой пенсии – 228 мес.;
- желаемая прибавка к пенсии – 2000 руб.
С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:
- Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.
- Нажимаем ОК – получаем результат подбора.
Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.
Функция «Подбор параметра» работает правильно, если:
- значение желаемого результата выражено формулой;
- все формулы написаны полностью и без ошибок.
Использование средства подбора параметров для получения требуемого результата путем изменения входного значения
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.
Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.
Примечание: Подбор параметров поддерживает только одно входное значение переменной. Если вы хотите оставить более одного входного значения; Например, сумма ссуды и сумма ежемесячного платежа для ссуды можно использовать в надстройке «Поиск решения». Дополнительные сведения можно найти в статье определение и устранение проблем с помощью надстройки «Поиск решения».
Пошаговый анализ примера
Рассмотрим предыдущий пример шаг за шагом.
Так как вы хотите вычислить ставку процентных ценностей, необходимую для достижения цели, вы можете использовать функцию ПЛТ. Функция ПЛТ вычисляет сумму ежемесячного платежа. В данном примере эту сумму и требуется определить.
Подготовка листа
Откройте новый пустой лист.
Прежде всего добавьте в первый столбец эти подписи, чтобы сделать данные на листе понятнее.
В ячейку A1 введите текст Сумма займа.
В ячейку A2 введите текст Срок в месяцах.
В ячейку A3 введите текст Процентная ставка.
В ячейку A4 введите текст Платеж.
Затем добавьте известные вам значения.
В ячейку B1 введите значение 100 000. Это сумма займа.
В ячейку B2 введите значение 180. Это число месяцев, за которое требуется выплатить ссуду.
Примечание: Хотя вам известна необходимая сумма платежа, не вводите ее как значение, поскольку она получается в результате вычисления формулы. Вместо этого добавьте формулу на лист и укажите значение платежа на более позднем этапе при использовании средства подбора параметров.
Теперь добавьте формулу, результат которой вас интересует. Например, используйте функцию ПЛТ.
В ячейке B4 введите =ПЛТ(B3/12;B2;B1). Эта формула вычисляет сумму платежа. В данном примере вы хотите ежемесячно выплачивать 900 ₽. Это значение здесь не вводится, поскольку вам нужно определить процентную ставку с помощью средства подбора параметров, а для этого требуется формула.
Формула ссылается на ячейки B1 и B2, значения которых вы указали на предыдущих этапах. Она также ссылается на ячейку B3, в которую средство подбора параметров поместит процентную ставку. Формула делит значение из ячейки B3 на 12, поскольку был указан ежемесячный платеж, а функция ПЛТ предусматривает использование годовой процентной ставки.
Поскольку в ячейке B3 нет значения, Excel полагает процентную ставку равной 0 % и в соответствии со значениями из данного примера возвращает сумму платежа 555,56 ₽. Пока вы можете игнорировать это значение.
Использование средства подбора параметров для определения процентной ставки
На вкладке Данные в группе Работа с данными нажмите кнопку Анализ «что если» и выберите команду Подбор параметра.
В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула. В данном примере это ячейка B4.
В поле Значение введите нужный результат формулы. В данном примере это -900. Обратите внимание, что число отрицательное, так как представляет собой платеж.
В поле Изменяя значение ячейки введите ссылку на ячейку, в которой находится корректируемое значение. В данном примере это ячейка B3.
Примечание: Формула в ячейке, указанной в поле Установить в ячейке, должна ссылаться на ячейку, которую изменяет средство подбора параметров.
Нажмите кнопку ОК.
Выполняется подбор параметров, результат которого показан на рисунке ниже.
Напоследок отформатируйте целевую ячейку (B3) так, чтобы результат в ней отображался в процентах.
На вкладке Главная в группе Число нажмите кнопку Процент.
Чтобы задать количество десятичных разрядов, нажмите кнопку Увеличить разрядность или Уменьшить разрядность.
Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.
Примечание: Подбор параметров поддерживает только одно входное значение переменной. Если вы хотите присвоить несколько входных значений, например сумма займа и сумма ежемесячного платежа для займа, используйте надстройку «Поиск решения». Дополнительные сведения можно найти в статье определение и устранение проблем с помощью надстройки «Поиск решения».
Пошаговый анализ примера
Рассмотрим предыдущий пример шаг за шагом.
Так как вы хотите вычислить ставку процентных ценностей, необходимую для достижения цели, вы можете использовать функцию ПЛТ. Функция ПЛТ вычисляет сумму ежемесячного платежа. В данном примере эту сумму и требуется определить.
Подготовка листа
Откройте новый пустой лист.
Прежде всего добавьте в первый столбец эти подписи, чтобы сделать данные на листе понятнее.
В ячейку A1 введите текст Сумма займа.
В ячейку A2 введите текст Срок в месяцах.
В ячейку A3 введите текст Процентная ставка.
В ячейку A4 введите текст Платеж.
Затем добавьте известные вам значения.
В ячейку B1 введите значение 100 000. Это сумма займа.
В ячейку B2 введите значение 180. Это число месяцев, за которое требуется выплатить ссуду.
Примечание: Хотя вам известна необходимая сумма платежа, не вводите ее как значение, поскольку она получается в результате вычисления формулы. Вместо этого добавьте формулу на лист и укажите значение платежа на более позднем этапе при использовании средства подбора параметров.
Теперь добавьте формулу, результат которой вас интересует. Например, используйте функцию ПЛТ.
В ячейке B4 введите =ПЛТ(B3/12;B2;B1). Эта формула вычисляет сумму платежа. В данном примере вы хотите ежемесячно выплачивать 900 ₽. Это значение здесь не вводится, поскольку вам нужно определить процентную ставку с помощью средства подбора параметров, а для этого требуется формула.
Формула ссылается на ячейки B1 и B2, значения которых вы указали на предыдущих этапах. Она также ссылается на ячейку B3, в которую средство подбора параметров поместит процентную ставку. Формула делит значение из ячейки B3 на 12, поскольку был указан ежемесячный платеж, а функция ПЛТ предусматривает использование годовой процентной ставки.
Поскольку в ячейке B3 нет значения, Excel полагает процентную ставку равной 0 % и в соответствии со значениями из данного примера возвращает сумму платежа 555,56 ₽. Пока вы можете игнорировать это значение.
Использование средства подбора параметров для определения процентной ставки
Выполните одно из следующих действий:
В Excel 2016 для Mac: на вкладке данные щелкните анализ » что если«, а затем — Подборпараметров.
В Excel для Mac 2011: на вкладке данные в группе Работа с данными нажмите кнопку анализ » что если«, а затем выберите вариант Подборпараметров.
В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула. В данном примере это ячейка B4.
В поле Значение введите нужный результат формулы. В данном примере это -900. Обратите внимание, что число отрицательное, так как представляет собой платеж.
В поле Изменяя значение ячейки введите ссылку на ячейку, в которой находится корректируемое значение. В данном примере это ячейка B3.
Примечание: Формула в ячейке, указанной в поле Установить в ячейке, должна ссылаться на ячейку, которую изменяет средство подбора параметров.
Нажмите кнопку ОК.
Выполняется подбор параметров, результат которого показан на рисунке ниже.
Напоследок отформатируйте целевую ячейку (B3) так, чтобы результат в ней отображался в процентах. Выполните одно из указанных ниже действий.
В Excel 2016 для Mac: на вкладке Главная нажмите кнопку Увеличить разрядность 

В Excel для Mac 2011: на вкладке Главная в группе число нажмите кнопку Увеличить разрядность 

Функция Excel: подбор параметра
Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.
Зачем нужна функция
Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.
Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.
Использование функции
Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.
Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).
Итак, алгоритм действий следующий:
- Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
- На экране появится окно для подбора параметра, которе нужно заполнить:
- в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.
- В качестве значения указываем сумму скидки, которая нам известна – 560 руб.
- В поле “Изменяя значение ячейки” вручную или посредством клика мышью указываем координаты ячейки (должна участвовать в формуле расчета суммы скидки), в которой планируем вывести начальное значение.
- по готовности нажимаем OK.
- Программа выполнит расчеты и выдаст результат в небольшом окошке, которое можно закрыть, нажав кнопку OK. Также найденные значения автоматически появятся в заданных ячейках таблицы.
- Аналогичным образом можно посчитать цену без скидки для других товаров, если нам известна точная сумма скидки по каждому из них.
Решение уравнений с помощью подбора параметра
Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.
Например, нам нужно решить уравнение: 7x+17x-9x=75 .
- Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так: =7*D2+17*D2-9*D2 .
- Щелкаем Enter и получаем результат в виде числа , что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.
- Как было описано в первом разделе статьи, во вкладке “Данные” нажимаем кнопку “Анализ “что если” и выбираем “Подбор параметра”.
- В появившемся окошке заполняем параметры:
- В значении поля “Установить в ячейке” указываем координаты ячейки, в которой мы написали уравнение (т.е. B4).
- В значении, согласно уравнению, пишем число 75.
- В поле “Изменяя значения ячейки” указываем координаты ячейки, значение которой нужно найти. В нашем случае – это D2.
- Когда все готово, нажимаем OK.
- Как и в примере, рассмотренном выше, будут произведены вычисления и получен результат, о чем будет свидетельствовать небольшой окошко.
- Таким образом, нам удалось решить уравнение и найти значение x, которое оказалось равным числу 5.
Заключение
Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.
Главная > Решение
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Решение задач – Подбор параметра
Задачи оптимизации с одним неизвестным
Задача оптимизации затрат
Подбор параметра и таблицы подстановки
РЕШЕНИЕ ЗАДАЧ – Подбор параметра
Решение задач – одно из важных применений Excel. Самый простой инструмент предназначен для подбора значений и называется «что-если» анализ: задается некоторая целевая функция и ее числовое значение, Excel автоматически подбирает параметры целевой функции до получения целевого значения. Формула в целевой функции должна логически зависеть от подбираемого параметра.

Эти инструменты Excel (будут рассмотрены в следующих разделах) полезны экономистам, администраторам, менеджерам, которым для решения деловых проблем и принятия решений в сферах финансов, бухгалтерского учета, маркетинга, управления операциями, экономики, менеджмента необходимо применять количественные методы анализа и прогнозирования.
В качестве примера разберем расчет прибыли от продаж, показанный на рис. 1.20. В ячейках А3, А4 и А7 записаны формулы – формулы для наглядности продублированы в скобках. Поскольку Другие затраты и Количество здесь постоянны, то нужную прибыль можно получить подбором Цены единицы или Себестоимости единицы товара. Попробуем получить прибыль 20000, изменяя Цену единицы . Проделайте следующие действия:
Встаньте на целевую ячейку А7. Выберите пункт меню С е рвис П одбор параметра… . Введите значение ожидаемой прибыли. Для ввода адреса изменяемой ячейки, перейдите в нижнее поле и встаньте на ячейку А9 в таблице – адрес будет записан автоматически в поле. Нажмите ОК.
В следующем окне можно либо принять, либо отменить результат подбора параметра. Результат:
Самостоятельно попробуйте подобрать Себестоимость единицы , чтобы получить прибыль 20000 при Цене единицы =200.
Далее приводятся другие применения инструмента Подбор параметра .
Задачи оптимизации с одним неизвестным
Часто уравнения не имеют точного аналитического решения. Тогда их решают методом последовательных приближений (итераций) неизвестных параметров так, чтобы они давали минимум ошибки целевой функции.
Для численного решения уравнений с одним неизвестным в Excel имеется эффективный инструмент Подбор параметра . Целевая функция может быть линейной, квадратичной, третьей и выше степени.
Инструмент Подбор параметра был рассмотрен в предыдущем разделе для расчета прибыли от продаж. Здесь рассмотрим его применение для решения некоторого уравнения, например 2х 3 -3х 2 +х-5=0.
Решение задачи состоит из двух этапов. На первом этапе следует ввести уравнение в ячейку (В2), а в другую ячейку (А2) ввести некоторое ориентировочное значение, здесь 1:
На втором этапе следует воспользоваться инструментом Подбор параметра :
Встаньте на ячейку В2 и вызовите его – С е рвис П одбор параметра… .
В открывшемся окне введите искомое значение функции и адрес изменяемой ячейки:
После нажатия кнопки ОК Вы получите следующее решение:
Найденное решение приближенное, поэтому можно считать, что при х=1,918578609 значение уравнения 2х 3 -3х 2 +х-5 стремится к нулю, т.е. к 0,000107348. Смело установите для ячеек А2 и В2 числовой формат отображения данных и получите следующее:

Задача оптимизации затрат
С помощью подбора параметров можно решать задачи оптимального распределения ресурсов следующего плана. Требуется закупить составляющие (конфета карамельная, конфета шоколадная, упаковка печенья и мармелада) для комплектования подарочных наборов так, чтобы цена набора не превышала 100 руб. При этом известны соотношения цен относительно одной из компонент (здесь карамели): цена шоколадной конфеты в 2.5 раза выше цены карамели, цена печенья на 10 руб. больше карамели и цена мармелада в 8.5 раза выше цены карамели. В наборе должно быть 5-10 конфет карамель, 4-6 шоколадных конфет, 1-2 упаковки печенья и 1 упаковка мармелада. Рассчитать закупочные цены для разных комплектов.
Ниже показаны расчеты закупочных цен для максимального и минимального комплектов:
В ячейки В4:В6 запишите формулы: =B3*2.5, =B3+10 и =B3*8.5. В колонки D3:D6 поставьте формулы вычисления сумм по строкам, а в D7 вычислите общую сумму: =СУММ(D3:D6). В итоге целевая функция – стоимость набора D7 есть C3* x +C4*2.5* x +C5*( x +10)+C6*8.5* x , где x =B3 цена одной компоненты – конфеты карамель. Параметры инструмента Подбор параметра заполните так:
Подбор параметра и таблицы подстановки
В паре с инструментом Подбор параметра обычно применяют инструмент Таблица подстановки , который позволяет расширить количество одновременно рассчитываемых вариантов решений. Таблицы подстановки создаются на основе одной или двух изменяемых параметров.
Рассмотрим пример. Фирма производит изделия и продает их по цене 90руб. Ежемесячные постоянные затраты составляют 5000руб., переменные затраты на единицу изделия – 30руб. Необходимо определить точку безубыточности, т.е. вычислить количество изделий, при котором прибыль равна 0. Кроме того, требуется определить изменение прибыли для 10 следующих значений количества с шагом 5, а также прибыль при этих значениях количества для цен 80, 85, 95 и 100руб.
Решение. Введите в Excel исходные данные, приведенные ниже:
В точке безубыточности валовая прибыль равна валовым затратам, т.е. (В3*В4)-(В1+В2*В4)=0. Вызовите Подбор параметра , заполните параметры и нажмите ОК – в ячейке В4 будет вычислено значение 83.33 (рис. 17).
На следующем шаге рассчитаем 10 значений прибыли для следующих значений количества с шагом 5. Используем для этого таблицу подстановки с одним изменяемым параметром. Подготовьте исходные данные (рис. 2.35) : в ячейки C4:C13 запишите значения количества с шагом 5, а в колонке справа в строке выше (ячейка D3) — формулу из ячейки В7.
Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон C3:D13 (рис. 2.36), вызовите пункт Д анные Т аблица подстановки… , укажите изменяемую ячейку ($B$4) и порядок расположения исходных данных (в строках) в окне запроса – рис. 2.36. После нажатия ОК в ячейках D4:D13 будут рассчитаны значения прибыли.
На последнем шаге рассчитаем значения прибыли для тех же значений количества при ценах 80, 85, 95 и 100руб. Используем для этого таблицу подстановки с двумя изменяемыми параметрами. Результат показан на рис. 2.37.
Для его получения подготовьте исходные данные : в ячейки F4:F13 запишите значения количества, в строке G3:J3 запишите значения цен, на пересечении строки и столбца с данными в ячейке F3 запишите формулу из ячейки В7. Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон F3:F13 (рис. 2.37), вызовите пункт Д анные Т аблица подстановки… , укажите изменяемую ячейку по строкам ($B$4) и по столбцам ($B$3) в окне запроса – рис. 2.38. После нажатия ОК в ячейках G4:J13 будут рассчитаны значения прибыли.
Задания для самостоятельного выполнения:
Найдите решение уравнения х 3 +5х 2 -х+1=0
Найдите два решения уравнения х 2 -3х+2=0.
Найдите решение уравнения е х =20000.
Примените инструмент Таблица подстановки при решении предыдущей задачи комплектования подарочных наборов.
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y =7 является функцией x ;
- нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
- Заполните ячейки листа, так как показано на рисунке:
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.
Простейший пример
Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.
Подготовим исходные данные.
Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).
Инструмент Подбор параметра подобрал значение параметра b равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.
Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.
Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).
Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.
Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
- на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
- в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
- введите искомый результат в поле Значение. В данном примере он равен -1800;
- В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
- Нажмите ОК
Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.
Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.
Зачем нужна функция
Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.
Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.
Использование функции
Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.
Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).
Итак, алгоритм действий следующий:
- Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
- На экране появится окно для подбора параметра, которе нужно заполнить:
- в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.
- В качестве значения указываем сумму скидки, которая нам известна – 560 руб.
- В поле “Изменяя значение ячейки” вручную или посредством клика мышью указываем координаты ячейки (должна участвовать в формуле расчета суммы скидки), в которой планируем вывести начальное значение.
- по готовности нажимаем OK.
- Программа выполнит расчеты и выдаст результат в небольшом окошке, которое можно закрыть, нажав кнопку OK. Также найденные значения автоматически появятся в заданных ячейках таблицы.
- Аналогичным образом можно посчитать цену без скидки для других товаров, если нам известна точная сумма скидки по каждому из них.
Решение уравнений с помощью подбора параметра
Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.
Например, нам нужно решить уравнение: 7x+17x-9x=75.
- Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так:
=7*D2+17*D2-9*D2. - Щелкаем Enter и получаем результат в виде числа 0, что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.
- Как было описано в первом разделе статьи, во вкладке “Данные” нажимаем кнопку “Анализ “что если” и выбираем “Подбор параметра”.
- В появившемся окошке заполняем параметры:
- В значении поля “Установить в ячейке” указываем координаты ячейки, в которой мы написали уравнение (т.е. B4).
- В значении, согласно уравнению, пишем число 75.
- В поле “Изменяя значения ячейки” указываем координаты ячейки, значение которой нужно найти. В нашем случае – это D2.
- Когда все готово, нажимаем OK.
- Как и в примере, рассмотренном выше, будут произведены вычисления и получен результат, о чем будет свидетельствовать небольшой окошко.
- Таким образом, нам удалось решить уравнение и найти значение x, которое оказалось равным числу 5.
Заключение
Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.