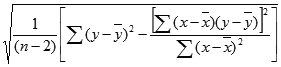ПОРЯДОК ПЕРЕВОДА «СЫРЫХ» ПОКАЗАТЕЛЕЙ ПСИХОДИАГНОСТИЧЕСКИХ МЕТОДИК В СТАНДАРТНЫЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ (СТЕНЫ)
Исследование психических явлений требует многоаспектного анализа и применения разнообразного набора его конкретных методов в соответствии с поставленными задачами и общей стратегией проведения комплексной психодиагностики. При проведении мероприятий по профессиональному психологическому отбору и профессионально-психологическому сопровождению обучающийся обследуется с помощью целого комплекса методик, которые могут иметь совершенно различный интервал тестовых показателей. Полученные при сборе данных «сырые» (первичные) оценки далеко не всегда удобно использовать в дальнейшей работе. Особенно, когда возникает необходимость сравнить показатели испытуемого по разным методикам, получить интегральный показатель развития изучаемых качеств или отнести их к какой либо группе («успешных», «не успешных», «норме»). Для этого «сырые» оценки тем или иным способом преобразуют в значения стандартных тестовых шкал. Данные преобразования позволяют оценивать индивидуальный результат тестирования путем сопоставления его с тестовыми нормами (стандартной тестовой шкалой), полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки стандартной шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест, методику. Для получения нормального распределения величины измеряемого тестом свойства требуемое число испытуемых в ней обычно составляет не менее 200 человек. Впоследствии при тестировании предполагается, что и испытуемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности. При стандартизации результатов тестовых испытаний чаще всего используется показатель среднеквадратичного отклонения – s. Стандартизация осуществляется при условии нормального распределения тестовых оценок в репрезентативной выборке испытуемых или близком к нему (рис. 1). Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нормой» всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.
График нормального распределения может быть получен из полигона эмпирического распределения при бесконечном увеличении числа наблюдений и сужении интервалов до размеров точки. Он представляет собой куполообразную кривую, симметричную относительно центра группирования, имеющую строго определенные пропорции.
Рисунок 1 – Нормальное распределение тестовых оценок в репрезентативной выборке испытуемых
Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака.
В реальных психофизиологических исследованиях оперируют не параметрами, а их приближенными значениями, так называемыми оценками параметров.
Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Наибольшее практическое значение имеют:
— характеристики положения исследуемой совокупности (среднее арифметическое значение признака, медиана, мода);
— характеристики рассеяния (дисперсия);
— характеристики асимметрии (показатели асимметрии и эксцесса).
Среднее арифметическое (оценка математического ожидания) вычисляется по формуле:
Символ S обозначает сумму всех значений xi, когда i принимает значения от 1 до n;
xi – общий член последовательности, подлежащий суммированию;
i – индекс суммирования, порядковый номер члена последовательности;
n – количество наблюдений.
Медианой (Ме) называется такое значение признака, когда одна половина значений экспериментальных данных меньше ее, а вторая больше.
Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.
При нормальном распределении признака значения среднего арифметического, медианы и моды близки или совпадают друг с другом
Среднее квадратическое отклонение (s) — мера рассеяния вариант или оценка дисперсии — определяется по формуле:
где: xi – каждое наблюдаемое значение признака;
`x — среднее арифметическое значение признака;
n – количество наблюдений.
При нормальном распределении наибольшее отклонение крайней варианты от среднего арифметического составляет примерно 3s (правило «трех сигм»). Имеется определенное статистическое соответствие между отклонением признака от среднего арифметического и положением его в упорядоченном вариационном ряду. Кривая нормального распределения с процентным выражением распределений относительных частот в зависимости от величины отклонения от среднего арифметического представлена на рисунке
Одним из способов преобразования «сырых» результатов тестирования является нормирование. Суть нормирования состоит в переходе к другому масштабу — стандартным единицам измерения. Значимость стандартных шкал заключается, прежде всего, в том, что они позволяют отражать в одинаковых единицах измерения разнородные параметры, которые в обычных для этих параметров единицах измерения несопоставимы.
Простейшей из стандартных шкал является Z-шкала. Первичные значения показателя могут быть преобразованы в Z-оценки по формуле:
где: `x – среднее арифметическое показателя в выборке стандартизации;
xi – величина показателя теста в выборке стандартизации;
s – среднее квадратическое отклонение величин признака в выборке стандартизации.
Положительные значения Z-оценки соответствуют величинам выше среднего уровня, отрицательные значения — величинам ниже среднего. Единицей этой шкалы измерения является величина среднего квадратического отклонения. Среднее значение шкалы Z-оценок равно нулю.
Использование Z-оценок не всегда удобно, т.к. они могут принимать отрицательные и дробные значения. Поэтому часто Z-оценки преобразуют в другие шкалы, имеющие заданные среднее квадратическое отклонение и среднее значение. При этом используется формула:
где: `xз – заданное среднее значение шкалы;
sз – заданное среднее квадратическое отклонение.
Например, Р.Б. Кеттелл для стандартизации показателей методики 16-ФЛО предложил шкалу стенов – «стандартной десятки», где: 5,5 – заданное среднее значение показателя; 2 – заданное среднее квадратическое отклонение. Стенирование является одним из способов приведения нормированных оценок к виду, удобному для практического использования. Оно представляет собой перевод исходных тестовых оценок в выборке стандартизации в 10-балльную равноинтервальную шкалу (шкалу стенов). Практически это достигается путем разбиения оси значений тестовых оценок в выборке стандартизации на 10 интервалов, соответствующих долям среднеквадратичного отклонения s. При этом M (средняя арифметическая величина признака в выборке стандартизации) принимается за среднюю точку шкалы стенов. При этом всякое значение тестовых оценок, входящее в интервал от M до M + 0,5s, приравнивается к 6 баллам по шкале стенов, а, входящее в интервал от M до M – 0,5s, – к 5 баллам этой шкалы. Такая же процедура с шагом увеличения равным 0,5s проводится для вычисления 7, 8, 9 и 10 баллов стеновой шкалы и с шагом уменьшения на 0,5 s – для вычисления 4, 3, 2, и 1 балла шкалы стенов (рис.1).
| 1 стен = М – 2,5 σ 2 стена = М – 2 σ 3 стена = М – 1,5 σ 4 стена = М – 1 σ 5 стенов = М – 0,5 σ | 6 стенов = М +0,5 σ 7 стенов = М + σ 8 стенов = М +1,5 σ 9 стенов = М +2 σ 10 стенов = М +2,5 σ |
Получение 10 балльного ряда и есть шкала перевода «сырых» оценок в стены. При такой системе стандартизации диапазон, который принято называть средним или нормой (диапазон в 1s), характеризуется стандартными единицами от 4 до 7 стенов. Стандартные оценки от 3 или 8 стенов свидетельствуют об индивидуальных различиях, выходящих за границы средней нормы. Оценки в 2 и 9 стенов получаются при значительном отклонении индивидуальных оценок, на 2s выше и ниже среднего группового значения. Максимальная оценка в 10 стенов достигается при отклонении индивидуального тестового результата на 2,5s и более, вверх от средней нормы. Аналогичным образом, оценка в 1 стен ставится за все отклонения индивидуального тестового результата от среднего значения на 2,5s и ниже.
Для перевода «сырых» оценок в стены можно также использовать формулу линейного преобразования шкалы Z – оценок ( ) нормального распределения в десятибальную шкалу стенов:
где Xi – значение признака (в «сырых» баллах); M – среднее арифметическое значение признака; σ – среднеквадратичное отклонение значений признака.
При отклонении распределения значений признака (оценок в «сырых» баллах) от их нормального распределения используют процентильную шкалу перевода оценок в стены. Процентиль (X%) – это такое значение «сырой» оценки, которое соответствует частоте оценок меньших и равных по значению данной «сырой» оценке в %.
Перевод значения «сырой» оценки, выраженной в процентилях, в стены осуществляется по стандартной шкале (рисунок 1, таблица 2), где значения оценок в стенах связаны с величинами частот.
Для каждого теста по результатам тестирования стандартизованной выборки с использованием шкалы перевода процентилей в стены определяют границы стеновых оценок в значениях «сырых» оценок и строят шкалу перевода «сырых» оценок теста в стены (рисунок 1, таблица 2),.
Границы стеновых оценок в значениях «сырых» оценок определяют по граничным значениям частотных интервалов, указанных в таблице 1 для каждой стеновой оценки.
Например, по результатам обследования результат испытуемого входит в диапазон «сырых» оценок (X5) стандартизованной выборки, что соответствует частоте оценок в % (процентиль) [30,86; 50,0] и, соответственно, 5 стенам.
Таблица 1. Перевод процентильной шкалы в стены
| Стены | ||||||||||
| Частота оценок (%) | ||||||||||
| Диапазон «сырых» оценок в стандартной выборке | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
При создании стеновой шкалы следует учитывать конструктивные особенности теста. Возможно создание стеновой шкалы на основе обратно пропорциональной зависимости, когда более высокий «сырой» балл свидетельствует о меньшей степени выраженности изучаемой характеристики, например, такая шкала применяется в тесте «Адаптивность».
Для расчетов уровней в Excel нам понадобятся следующие функции.
1. СРЗНАЧ (диапазон) – среднее арифметическое диапазона чисел
2. СТАНДОТКЛОН (диапазон) – находит стандартное отклонение.
3. СЧЁТЕСЛИ (диапазон; условие) – подсчитывает количество чисел в диапазоне, отвечающих условию.
Образец расчетов представлен на следующем скриншоте. Разберем его подробнее.
Для начала мы подсчитываем среднее арифметическое и стандартное отклонение (строка 120-121). Далее определяем границы баллов (122-123). В строке 124 вводим количество человек. В строке 125 определяем количество человек в низких баллах. В строке 127 в высоких. Строку 126 – со средними баллами находим как разницу общего количества и низких+высоких.
Пояснение к функции СЧЕТЕСЛИ. Условие, которое задаётся в этой функции, передаётся как текст, поэтому оно заключается в кавычки (в отличие от чисел, которые в кавычки не заключаются). В условии знак & обозначает всего лишь объединение двух текстовых значений: к примеру, мы объединяем текст “
Для расчетов
уровней в Excel
нам понадобятся следующие функции.
1. СРЗНАЧ (диапазон)
– среднее арифметическое диапазона
чисел
2. СТАНДОТКЛОН
(диапазон) – находит стандартное
отклонение.
3. СЧЁТЕСЛИ (диапазон;
условие) – подсчитывает количество
чисел в диапазоне, отвечающих условию.
Образец расчетов
представлен на следующем скриншоте.
Разберем его подробнее.

Для начала мы
подсчитываем среднее арифметическое
и стандартное отклонение (строка
120-121). Далее определяем границы баллов
(122-123). В строке 124 вводим количество
человек. В строке 125 определяем количество
человек в низких баллах. В строке 127 в
высоких. Строку 126 – со средними баллами
находим как разницу общего количества
и низких+высоких.
Пояснение к функции
СЧЕТЕСЛИ. Условие, которое задаётся в
этой функции, передаётся как текст,
поэтому оно заключается в кавычки (в
отличие от чисел, которые в кавычки не
заключаются). В условии знак & обозначает
всего лишь объединение двух текстовых
значений: к примеру, мы объединяем текст
“<=” и адрес конкретной ячейки “B122”.
2. Стэны.
Перевод сырых
балов в стэны можно производить двумя
путями.
Известно, что стэн
– это стандартизированное значение со
средним 5,5 и стандартным отклонением
2.
Исходя из этого,
для перевода
в стэны можно использовать формулу:
Стэн = 2
∙ (x-m)/σ
+ 5,5, где:
х – конкретное
значение,
m
– среднее арифметическое исследуемой
выборки,
σ – стандартное
отклонение исследуемой выборки.
Второй способ
перевода баллов в стэны:
1. Найти среднее
арифметическое и стандартное отклонение.
2. От среднего
отсчитать по пять интервалов в 1/2σ
в обе стороны.
3. Пронумеровать
10 полученных интервалов слева направо.
Номер интервала и будет стэном.
В случае нормального
распределения оба способа дадут один
и тот же результат. Если распределение
отличается от нормального, результаты
будут различаться.
В итоге, мы можем
составить таблицу перевода в стэны:
|
Сырой бал |
Стэн |
|
1-3 |
1 |
|
4 |
2 |
|
5 |
3 |
|
6-7 |
4 |
|
8 |
5 |
|
9 |
6 |
|
10-11 |
7 |
|
12 |
8 |
|
13-14 |
9 |
|
15 |
10 |
Или, сократив
формулу стандартизации (как в школе
учили), вывести
краткую формулу:
Для нашего примера,
Стэн = 0,73 ∙ сырой балл – 0,73
Расчет стэнов в Excel
Для расчета стэновых
баллов нам понадобится три функции, две
из которых нам уже известны – это СРЗНАЧ
и
СТАНДОТКЛОН.
И одна новая функция:
НОРМАЛИЗАЦИЯ. Этой
функции нужно сообщить среднее
арифметическое (m),
стандартное отклонение (σ)
и конкретное число (x)
из массива. Функция производит следующий
расчет:
= (x-m)/σ
Таким образом,
функция НОРМАЛИЗАЦИЯ стандартизирует
сырые баллы в z-шкалу,
которая является основой для стэнов,
станайнов, Т-баллов и IQ
баллов.
Чтобы на основе
z-шкалы
создать любую перечисленную, нужно
знать новое среднее арифметическое и
новое стандартное отклонение.
Стэн = 2
∙ (x-m)/σ
+ 5,5, где:
(x-m)/σ
– вычисляет функция НОРМАЛИЗАЦИЯ
В Excel
формула будет выглядеть так:
= 2
∙
НОРМАЛИЗАЦИЯ(сырой балл; среднее;
станд.откл) + 5,5
Проиллюстрируем
это:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 3 мин
В статистике z-показатель говорит нам, на сколько стандартных отклонений значение отличается от среднего.Мы используем следующую формулу для расчета z-показателя:
z = (X — μ) / σ
куда:
- X — это одно необработанное значение данных.
- μ — среднее значение набора данных
- σ — стандартное отклонение набора данных
В этом руководстве объясняется, как можно рассчитать z-значения для необработанных значений данных в Excel.
Как рассчитать Z-баллы в Excel
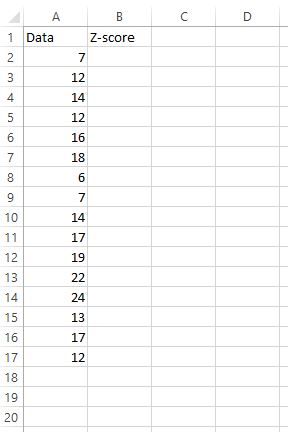
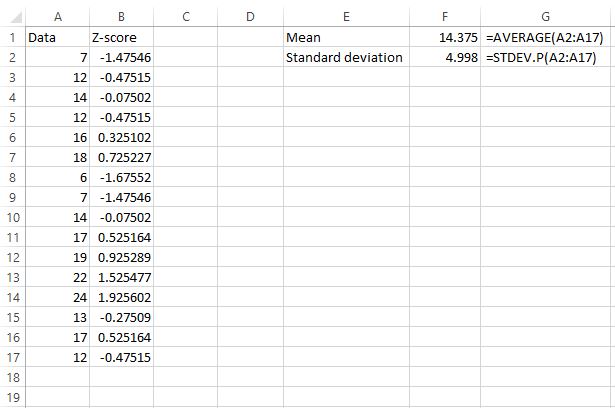
Предположим, у нас есть следующий набор данных, и мы хотели бы найти z-оценку для каждого значения необработанных данных:
Для этого мы можем выполнить следующие шаги.
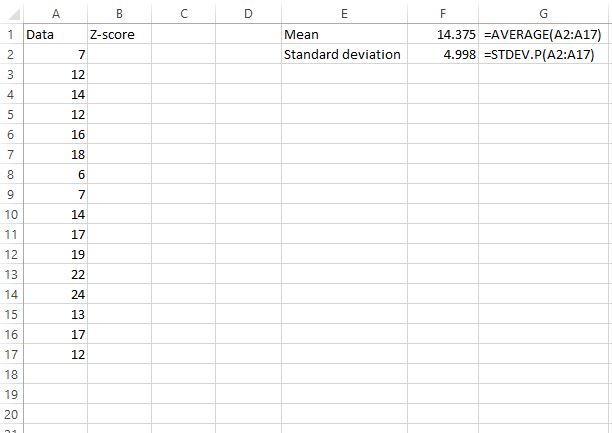
Шаг 1: Найдите среднее значение и стандартное отклонение набора данных.
Во-первых, нам нужно найти среднее значение и стандартное отклонение набора данных. Следующие формулы показывают, как это сделать:
Среднее значение оказывается равным 14,375 , а стандартное отклонение — 4,998 .
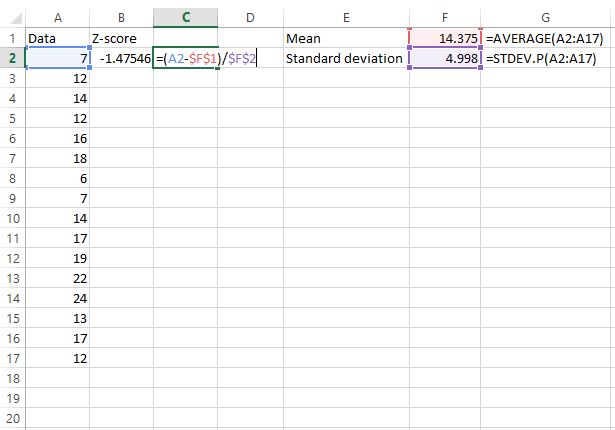
Шаг 2: Найдите z-оценку для первого значения необработанных данных.
Далее мы найдем z-показатель для первого значения необработанных данных, используя формулу z = (X – μ) / σ.
В ячейке C2 показана формула, которую мы использовали для вычисления значения z в ячейке B2.
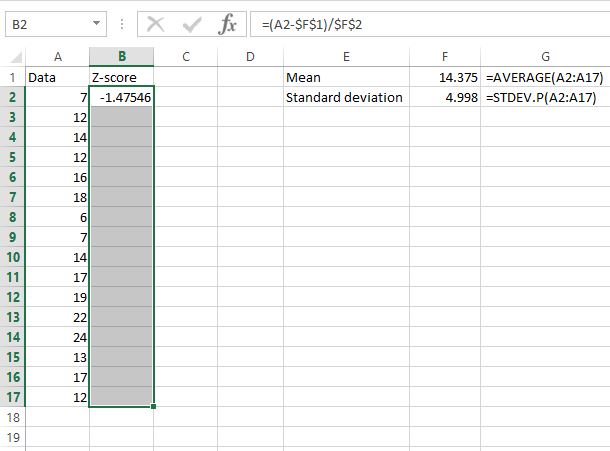
Шаг 3: Найдите z-показатели для всех оставшихся значений.
Теперь, когда мы нашли z-оценку для первого значения в наборе данных, мы можем просто скопировать формулу, которую мы использовали в ячейке B2, для остальных значений данных. Мы можем сделать это, выделив весь столбец z-оценки, начиная с первой z-оценки, которую мы уже вычислили:
Далее нажмите Ctrl+D.Это копирует формулу из первой ячейки во все ячейки под ней.
Теперь мы нашли z-оценку для каждого значения необработанных данных.
Как интерпретировать Z-значения в Excel
Напомним, что z-оценка просто говорит нам, на сколько стандартных отклонений значение отличается от среднего.
Z-оценка может быть положительной, отрицательной или равной нулю.
Положительный z-показатель указывает, что конкретное значение больше среднего, отрицательный z-показатель указывает, что конкретное значение меньше среднего, а нулевой z-показатель указывает, что конкретное значение равно среднему.
В нашем примере мы обнаружили, что среднее значение равно 14,375 , а стандартное отклонение — 4,998 .
Итак, первым значением в нашем наборе данных было 7, которое имело z-показатель (7-14,375) / 4,998 = -1,47546.Это означает, что значение «7» на -1,47545 стандартных отклонений ниже среднего.
Следующее значение в наших данных, 12, имело z-значение (12-14,375) / 4,998 = -0,47515.Это означает, что значение «12» на -0,47515 стандартных отклонений ниже среднего.
Чем дальше значение от среднего, тем выше будет абсолютное значение z-показателя для этого значения.
Например, значение 7 дальше от среднего (14,375) по сравнению с 12, что объясняет, почему 7 имеет z-значение с большим абсолютным значением.
Дополнительные ресурсы
В следующих статьях представлена дополнительная информация о том, как работать с z-значениями в Excel:
Как найти P-значение из Z-оценки в Excel
Как преобразовать Z-баллы в процентили в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТОШYX в Microsoft Excel.
Описание
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. Стандартная ошибка — это мера ошибки предсказанного значения y для отдельного значения x.
Синтаксис
СТОШYX(известные_значения_y;известные_значения_x)
Аргументы функции СТОШYX описаны ниже.
-
Известные_значения_y Обязательный. Массив или диапазон зависимых точек данных.
-
Известные_значения_x Обязательный. Массив или диапазон независимых точек данных.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Если аргументы «известные_значения_y» и «известные_значения_x» содержат различное количество точек данных, то функция СТОШYX возвращает значение ошибки #Н/Д.
-
Если known_y и known_x пустые или имеют менее трех точек данных, steYX возвращает #DIV/0! значение ошибки #ЗНАЧ!.
-
Уравнение для стандартной ошибки предсказанного y имеет следующий вид:
где x и y — выборочные средние значения СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Известные значения y |
Известные значения x |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
7 |
4 |
|
|
5 |
4 |
|
|
Формула |
Описание (результат) |
Результат |
|
=СТОШYX(A3:A9;B3:B9) |
Стандартная ошибка предсказанных значений y для каждого значения x в регрессии (3,305719) |
3,305719 |
Нужна дополнительная помощь?
Теплотехнический расчет стены
Опубликовано 24 Июл 2016
Рубрика: Теплотехника | 13 комментариев

Теплотехнический расчет стены определяет необходимые толщины слоев примененных материалов, обеспечивающие тепловую изоляцию помещений с точки зрения обеспечения комфортных санитарно-гигиенических условий для нахождения человека в здании и требований законодательства по энергосбережению.
Чем сильнее утеплены стены, тем меньше будущие эксплуатационные затраты на отопление здания, но при этом больше затраты на приобретение материалов при строительстве. До какой степени разумно утеплять ограждающие конструкции зависит от предполагаемого срока эксплуатации здания, целей, преследуемых инвестором строительства, и считается на практике в каждом случае индивидуально.
Санитарно-гигиенические требования определяют минимально допустимые сопротивления теплопередаче сечения стен, способные обеспечить комфорт в помещении. Эти требования следует обязательно выполнить при проектировании и строительстве! Обеспечение требований по энергосбережению позволит вашему проекту не только пройти экспертизу и потребует дополнительных разовых затрат при строительстве, но и обеспечит сокращение дальнейших затрат на отопление при эксплуатации.
Включаем MS Excel и начинаем рассмотрение примера теплотехнического расчета стены здания, строящегося в регионе — г. Москва.
Перед началом работы скачайте: СП 23-101-2004, СП 131. 13330.2012 и СП 50.13330.2012. Все перечисленные Своды Правил находятся в свободном доступе в Интернете.
В расчетном файле Excel в примечаниях к ячейкам со значениями параметров представлена информация, откуда следует брать эти значения, причем не только указаны номера документов, но и, зачастую, номера таблиц и даже столбцов.
Задавшись размерами и материалами слоев стены, мы проверим её на соответствие санитарно-гигиеническим нормам и нормам энергосбережения, а также вычислим расчетные температуры на границах слоев.
Исходные данные:
1…7. Ориентируясь на ссылки в примечаниях к ячейкам D4-D10, заполняем первую часть таблицы исходными данными для вашего региона строительства.
8…15. Во вторую часть исходных данных в ячейки D12-D19 вносим параметры слоев наружной стены – толщины и коэффициенты теплопроводности.
Значения коэффициентов теплопроводности материалов вы можете запросить у продавцов, найти по ссылкам в примечаниях к ячейкам D13, D15, D17, D19 или просто поиском в Сети.
В рассматриваемом примере:
первый слой — листы гипсовые обшивочные (сухая штукатурка) с плотностью 1050 кг/м3;
второй слой — кирпичная кладка из сплошного глиняного обыкновенного кирпича (1800 кг/м3) на цементно-шлаковом растворе;
третий слой — плиты минераловатные из каменного волокна (25-50 кг/м3);
четвертый слой — полимерцементная штукатурка с сеткой из стекловолокна.
Результаты:
Теплотехнический расчет стены будем выполнять, основываясь на предположении, что примененные в конструкции материалы сохраняют теплотехническую однородность в направлении распространения теплового потока.
Расчет ведется по ниже представленным формулам:
16. ГСОП=(tвр—tн ср)*Z
17. R0этр=0,00035*ГСОП+1,4
Формула применима для теплотехнического расчета стен жилых зданий, детских и лечебно-профилактических учреждений. Для зданий иного назначения коэффициенты «0,00035» и «1,4» в формуле следует выбрать иными согласно Таблице 3 СП 50.13330.2012.
18. R0стр=(tвр—tнр)/(Δtв*αв)
19. R0=1/αв+δ1/λ1+δ2/λ2+δ3/λ3+δ4/λ4+1/αн
Должны выполняться условия: R0>R0стр и R0>R0этр.
Если не выполняется первое условие, то ячейка D24 автоматически будет залита красным цветом, сигнализируя пользователю о недопустимости применения выбранной конструкции стены. Если не выполняется только второе условие, то ячейка D24 окрасится розовым цветом. Когда расчетное сопротивление теплопередачи больше нормативных значений, ячейка D24 окрашена в светло-желтый цвет.
20. t1=tвр— (tвр— tнр)/R0*1/αв
21. t2=tвр— (tвр— tнр)/R0*(1/αв+δ1/λ1)
22. t3=tвр— (tвр— tнр)/R0*(1/αв+δ1/λ1+δ2/λ2)
23. t4=tвр— (tвр— tнр)/R0*(1/αв+δ1/λ1+δ2/λ2+δ3/λ3)
24. t5=tвр— (tвр— tнр)/R0*(1/αв+δ1/λ1+δ2/λ2+δ3/λ3+δ4/λ4)
Теплотехнический расчет стены в Excel завершен.
Важное замечание.
Окружающий нас воздух содержит внутри себя воду. Чем выше температура воздуха, тем большее количество влаги он способен удерживать.
При 0˚С и 100% относительной влажности промозглый воздух ноября в наших широтах содержит в одном кубическом метре менее 5 граммов воды. В то же время раскаленный воздух в пустыне Сахара при +40˚С и всего 30% относительной влажности, удивительно, но удерживает внутри себя в 3 раза больше воды — более 15 г/м3.
Остывая и становясь холоднее, воздух не может удерживать внутри себя то количество влаги, что мог в более нагретом состоянии. В результате воздух выбрасывает из себя на прохладные внутренние поверхности стен капли влаги. Чтобы этого не происходило внутри помещений, следует при проектировании сечения стены обеспечить невозможность выпадения росы на внутренних поверхностях стен.
Так как средняя относительная влажность воздуха жилых помещений составляет 50…60%, то точка росы при температуре воздуха +22˚С составляет +11…14˚С. В нашем примере температура внутренней поверхности стены +20,4˚С обеспечивает невозможность образования росы.
Но роса может при достаточной гигроскопичности материалов образовываться внутри слоев стены и, особенно, на границах слоев! Замерзая, вода расширяется и разрушает материалы стен.
В рассмотренном выше примере точка с температурой 0˚С находится внутри слоя утеплителя и достаточно близко к наружной поверхности стены. В этой точке на схеме в начале статьи, отмеченной желтым цветом, температура меняет свое значение с положительного на отрицательное. Получается, что кирпичная кладка никогда в своей жизни не будет находиться под воздействием отрицательных температур. Это будет способствовать обеспечению долговечности стен здания.
Если мы поменяем в примере местами второй и третий слои – утеплим стену изнутри, то получим не одну, а две границы слоев в области отрицательных температур и наполовину промороженную кирпичную кладку. Убедитесь в этом самостоятельно, выполнив теплотехнический расчет стены. Напрашивающиеся выводы очевидны.
Ссылка на скачивание файла: teplotekhnicheskij-raschet-steny (xls 106,0KB).
Другие статьи автора блога
На главную