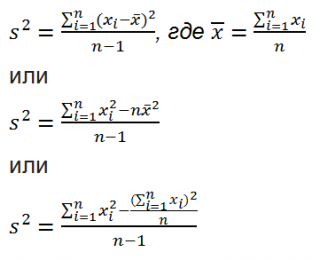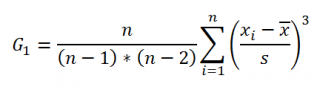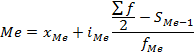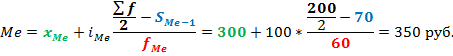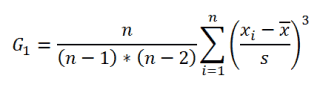Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
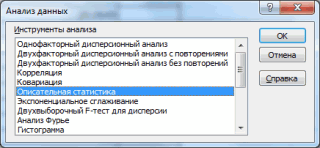
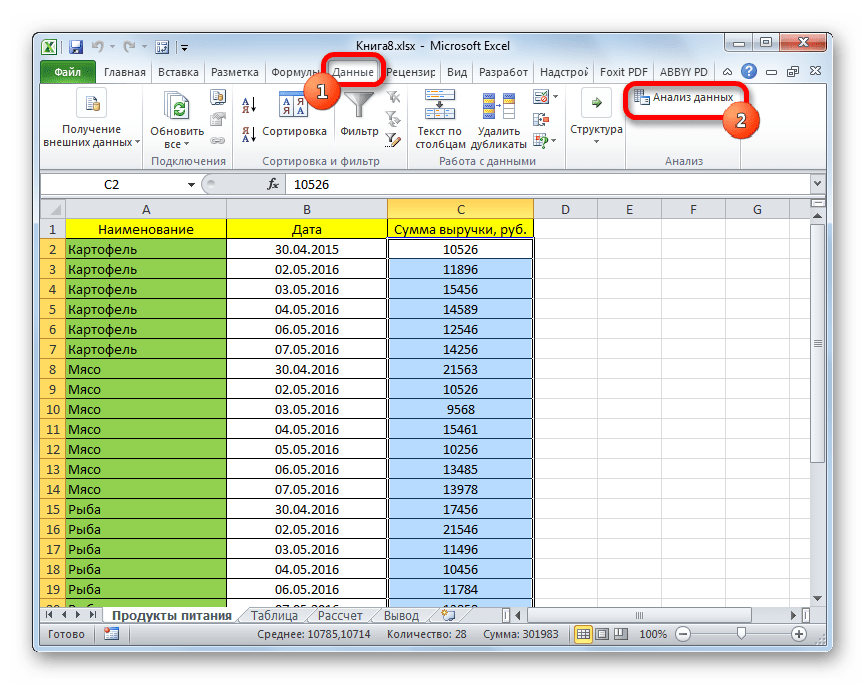
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
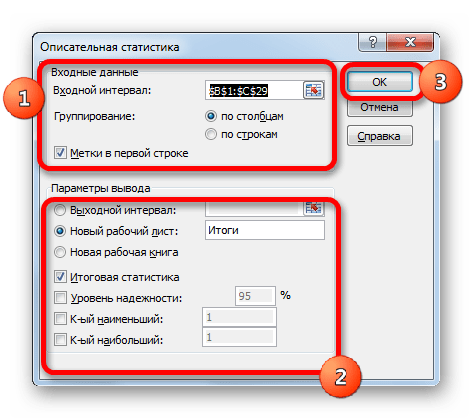
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
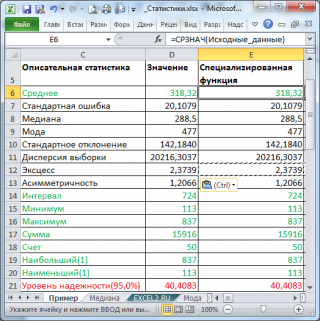
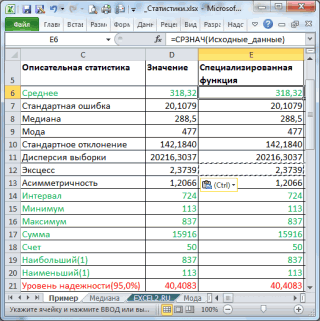
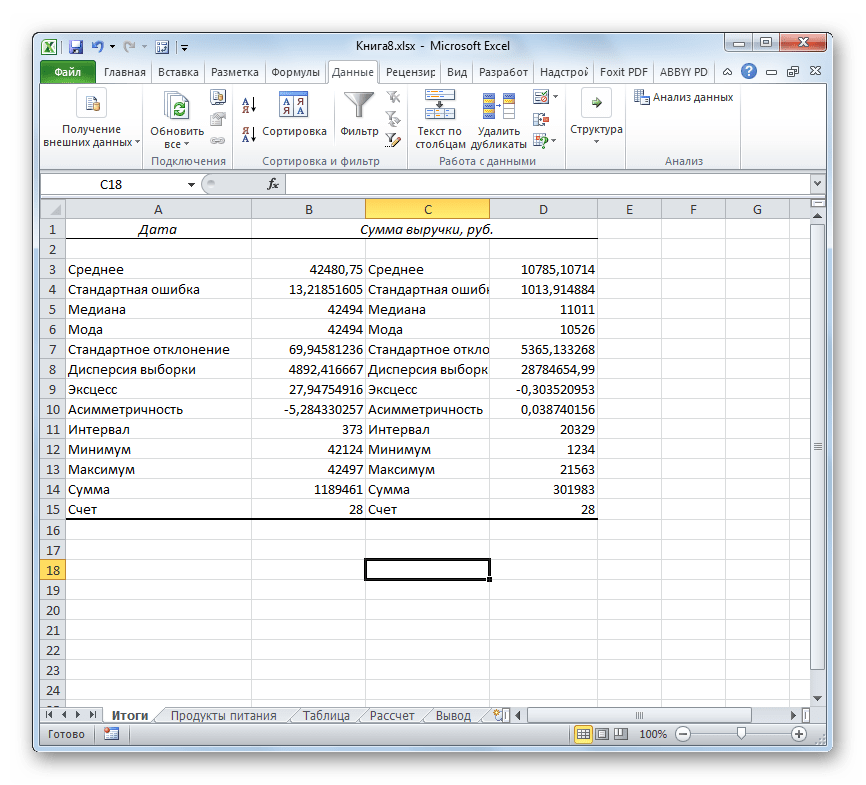
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
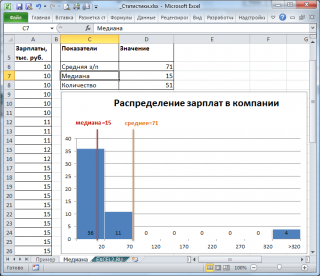
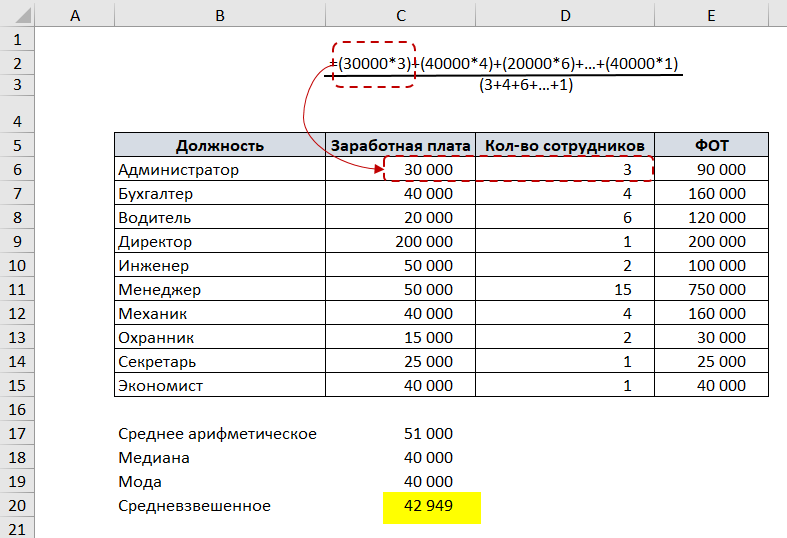
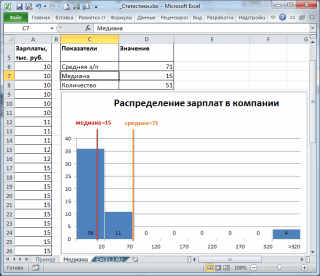
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
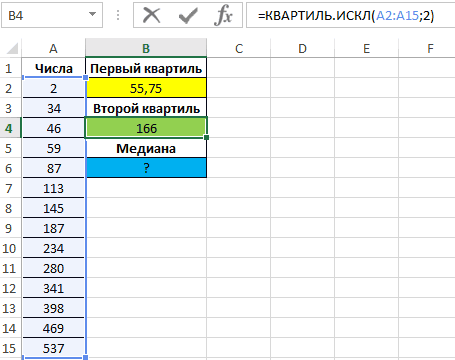
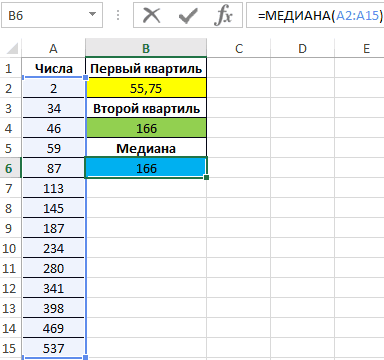
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
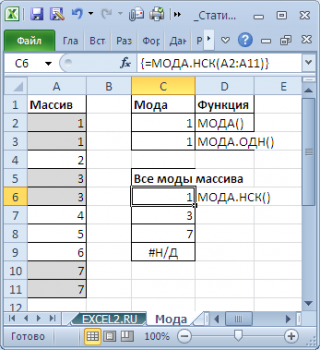
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
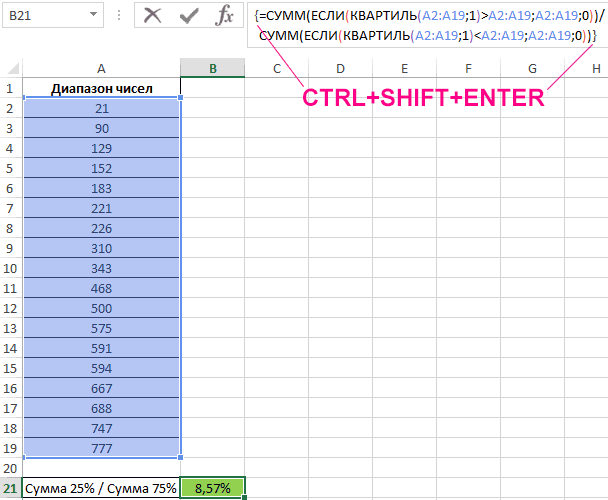
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
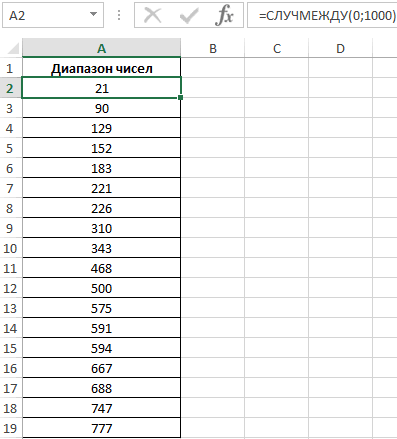
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
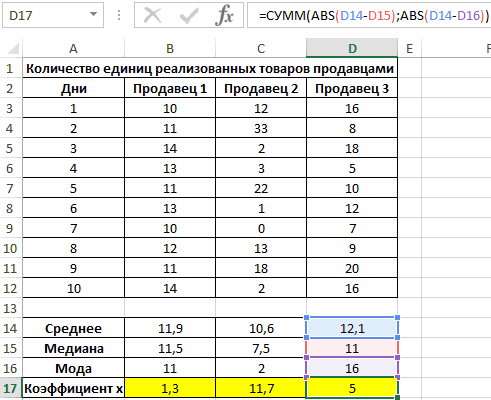
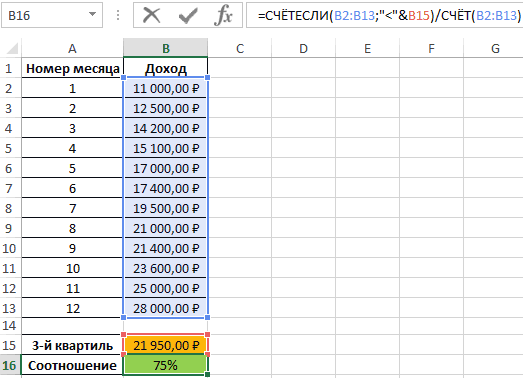
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
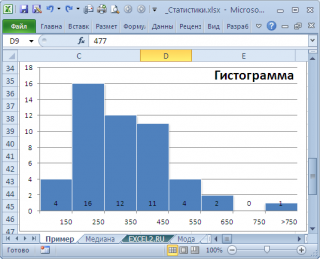
, творится, что-то не то. Действительно,
модой
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
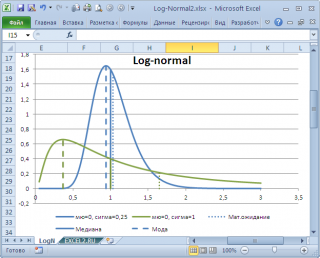
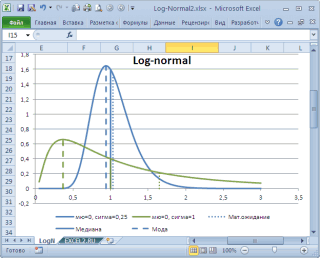
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
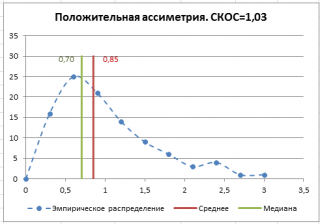
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
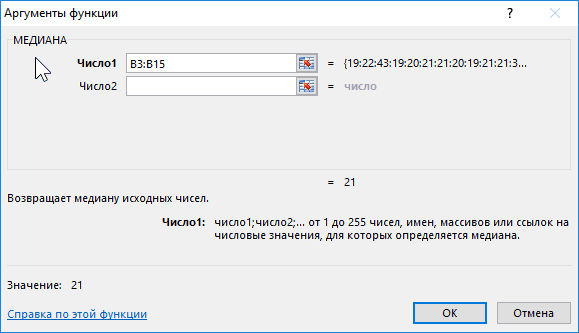
Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
Примеры использования функции МЕДИАНА в Excel
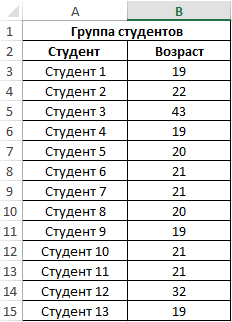
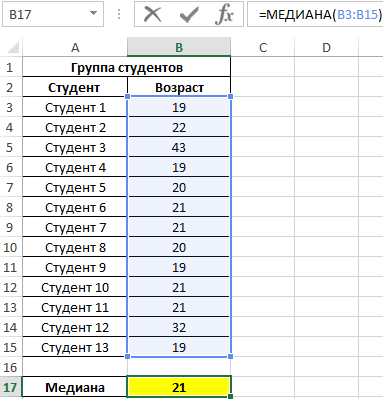
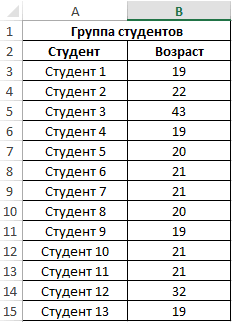
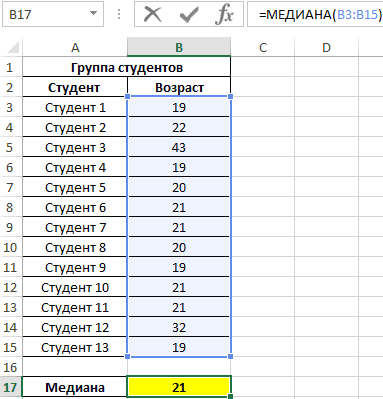
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.
Исходные данные:
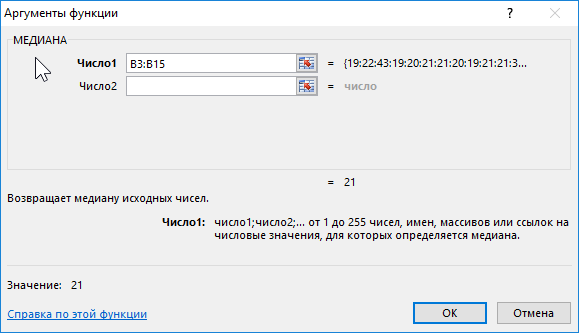
Формула для расчета:
Описание аргумента:
- B3:B15 – диапазон исследуемых возрастов.
Полученный результат:
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
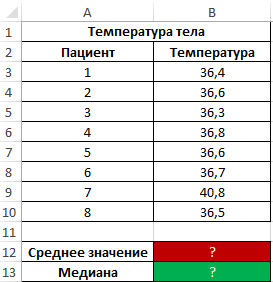
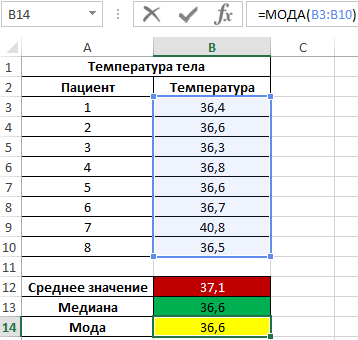
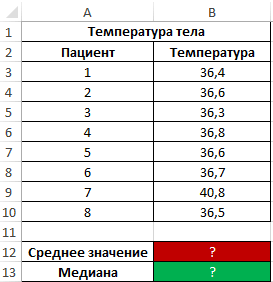
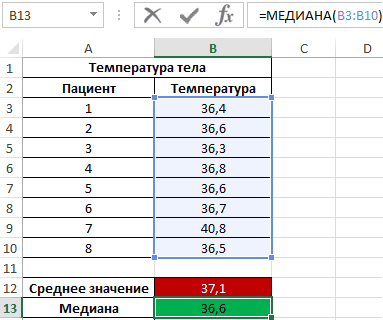
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.
Исходные данные:
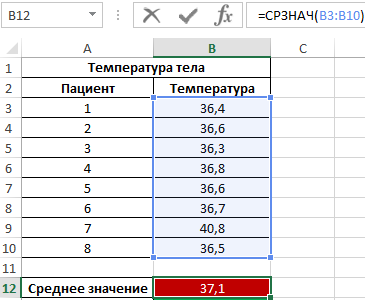
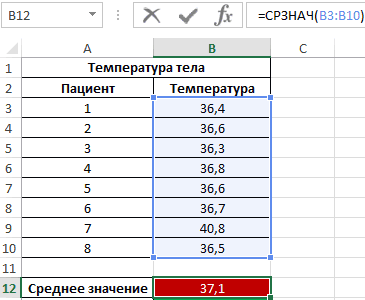
Формула для нахождения среднего значения:
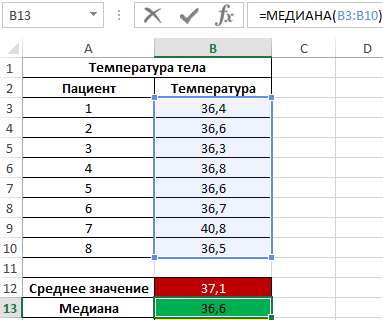
Формула для нахождения медианы:
Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.
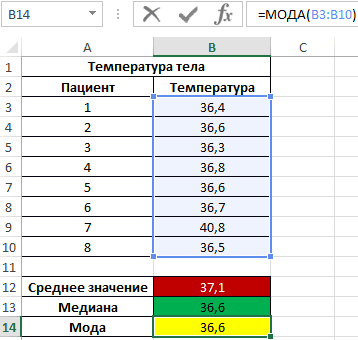
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:
То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.
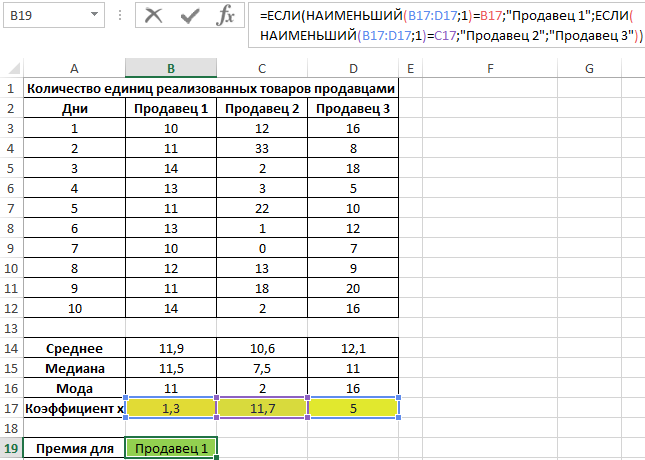
Пример расчета медианы при статистическом анализе в Excel
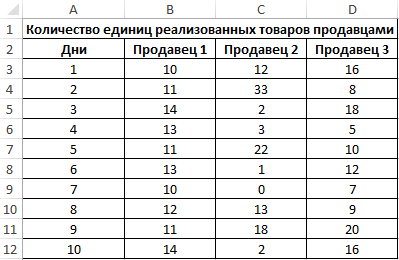
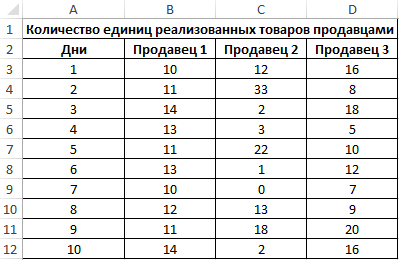
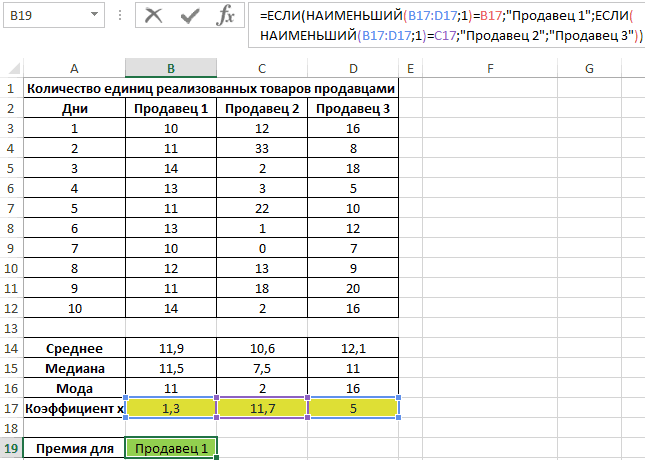
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
Исходная таблица данных:
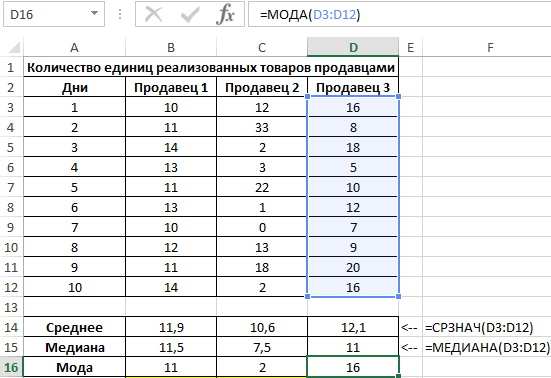
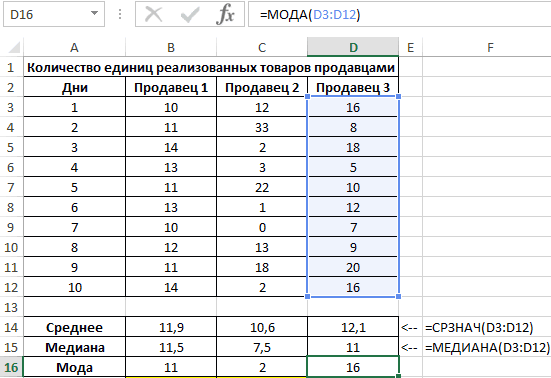
Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:
- av – среднее значение;
- med – медиана;
- mod – мода.
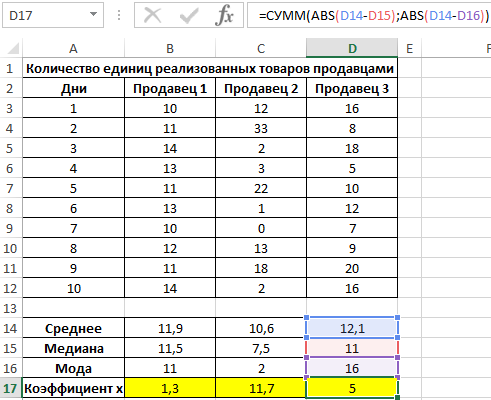
Рассчитаем значение коэффициента x для первого продавца:
Аналогично проведем расчеты для остальных продавцов. Полученные результаты:
Определим продавца, которому будет выдана премия:
Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.
Особенности использования функции МЕДИАНА в Excel
Функция имеет следующий синтаксис:
=МЕДИАНА(число1;[число2];…)
Описание аргументов:
- число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
- [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.
Примечания 1:
- При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
- В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).
- При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
- Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
- Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:
- =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
- =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
- =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.
Примечания 2:
- Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.
- При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
- Диапазон исследуемых значений может содержать:
Скачать примеры функции МЕДИАНА для статистического анализа в Excel
- Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
- Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.
The median absolute deviation is a way to measure the spread of values in a dataset.
The formula to calculate median absolute deviation, often abbreviated MAD, is as follows:
MAD = median(|xi – xm|)
where:
- xi: The ith value in the dataset
- xm: The median value in the dataset
The following step-by-step example shows how to calculate the median absolute deviation of a given dataset in Excel.
Step 1: Enter the Data
First, we’ll enter the values for a dataset:
Step 2: Calculate the Median
Next, we’ll calculate the median of the dataset:
The median turns out to be 16.
Step 3: Calculate the Absolute Difference Between Each Value & the Median
Next, we’ll calculate the absolute difference between each value and the median:
Click on cell B2. Then hover over the bottom right corner of the cell until a little cross (+) appears.
Double click the cross to copy and paste this formula to all remaining cells in the column:
Step 4: Calculate the Median Absolute Deviation
Lastly, we will use the following formula to calculate the median absolute deviation of the dataset:
The median absolute deviation turns out to be 8.
Additional Resources
Median Absolute Deviation Calculator
How to Calculate Median Absolute Deviation in R
How to Calculate Median Absolute Deviation in Python
Для различных аналитических целей часто требуется получить средний уровень различных показателей: средний возраст, средняя зарплата и т.д. Первое, что приходит на ум – это найти простое среднее арифметическое. Но всегда ли это правильно? В этой статье разберемся, что такое медиана, среднее арифметическое и мода. А также научимся считать их в Excel.
- Среднее арифметическое
- Медиана – чем отличается от среднего значения
- Что лучше – медиана или среднее значение
- Что такое мода
- Средневзвешенное значение
Среднее арифметическое
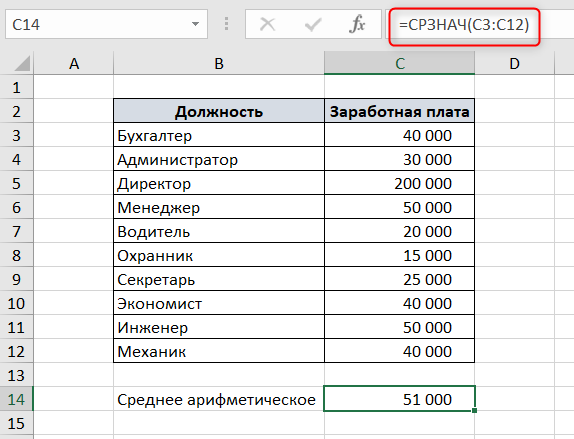
Среднее арифметическое значение – это сумма всех элементов выборки, поделенная на количество этих элементов.
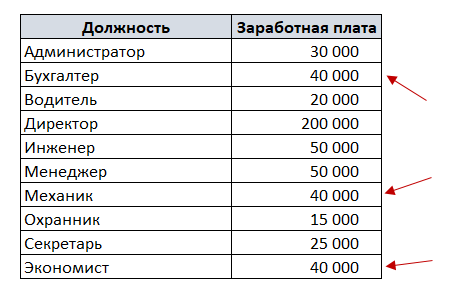
Например, есть список должностей и заработных плат. Чтобы посчитать среднюю заработную плату в Excel, воспользуемся функцией СРЗНАЧ.
Медиана – чем отличается от среднего значения
Медиана – это середина набора чисел, отсортированного по возрастанию.
Другими словами, 50% наблюдений ниже медианы и 50% наблюдений выше медианы. Медиана всегда равно удалена от начала и от конца набора чисел.
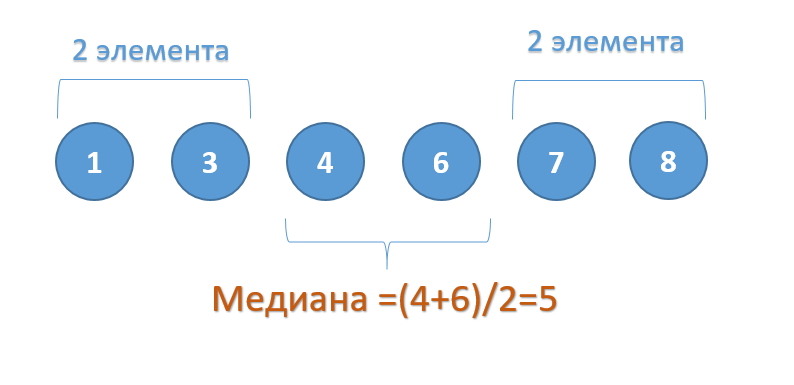
Если набор чисел состоит из нечетного количества элементов, то медианой будет число, которое находится в середине.
Если набор чисел состоит из четного числа элементов, то медиана будет равна среднему арифметическому между двумя центральными элементами списка.
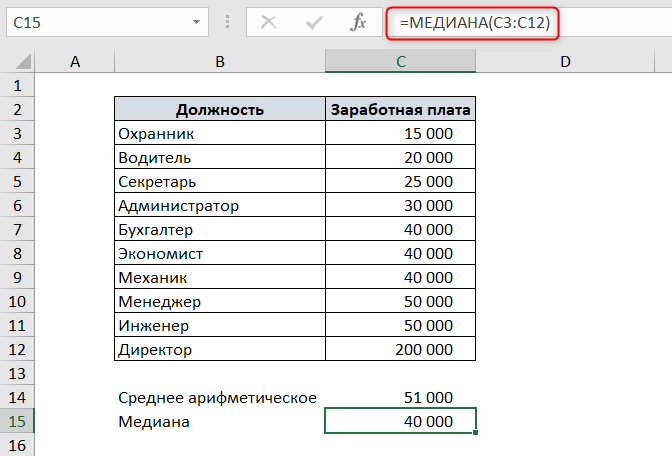
Чтобы наглядно увидеть, чем отличается медиана от среднеарифметического значения на нашем первом примере с зарплатой, отсортируем список по возрастанию.
Поскольку в списке 10 элементов – четное количество – то медианой будет среднее арифметическое 5 и 6 элементов.
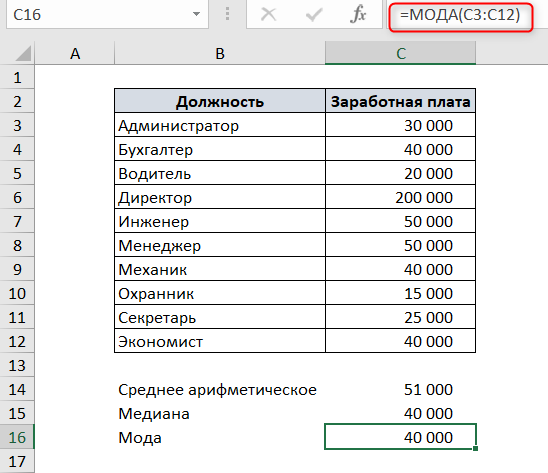
Чтобы посчитать медиану в Excel, воспользуемся функцией МЕДИАНА. В качестве аргументов функция принимает числовые значения ряда данных.
Как видите, медиана не равна среднему значению.
Что лучше – медиана или среднее значение
На этот вопрос однозначного ответа нет, все зависит от целей вашего анализа.
Основные отличия медианы от среднего арифметического:
- Медиана в отличие от среднего арифметического игнорирует выбросы данных (выбросы – это значения, которые значительно отличаются от основного массива выборки).
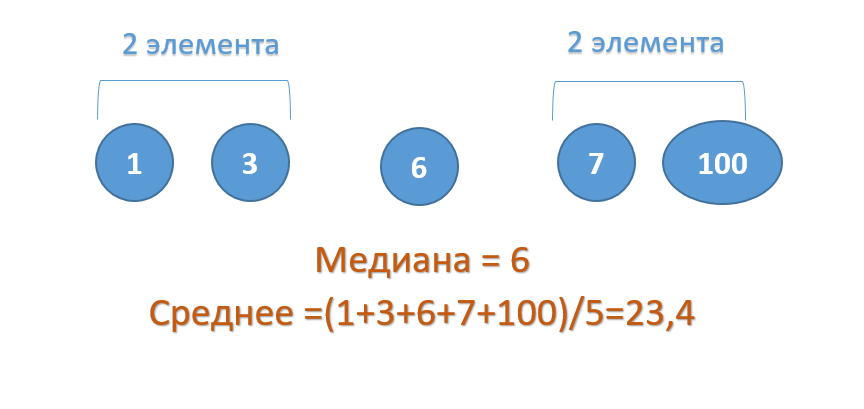
Рассмотрим пример:
В данном примере число 100 – это выброс, т.к. оно значительно отличается от основной других чисел в ряду. И при расчете среднего арифметического это число 100 исказило среднее – оно стало значительно больше остальных чисел.
Медиана же останется неизменной, даже если вместо 100 мы укажем 1000, т.к. середина ряда все равно будет число 6.
Это свойство медианы – игнорировать выбросы – особенно полезно, когда нужно посчитать среднюю зарплату или средний возраст. В целом, медиана более точно определяет середину выборки, чем среднее арифметическое, поскольку устойчива к искажениям.
- Свойство медианы игнорировать выбросы, на самом деле, не всегда полезно. Оно может скрыть из виду важные моменты, тогда как среднее арифметическое, завысив или занизив среднее, поможет обратить на них внимание.
В нашем примере с заработной платой среднее арифметическое заработных плат выше, чем медиана. Это может обратить внимание на то, что одна из заработных плат (в данном случае – директора) сильно отличается от заработных плат других сотрудников.
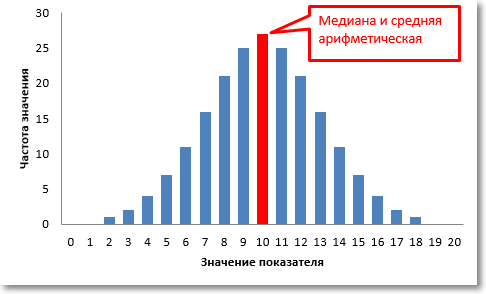
- Если ряд данных имеет нормальное или близкое к нормальному распределение, то медиана или среднее значение будут равны или близки друг к другу.
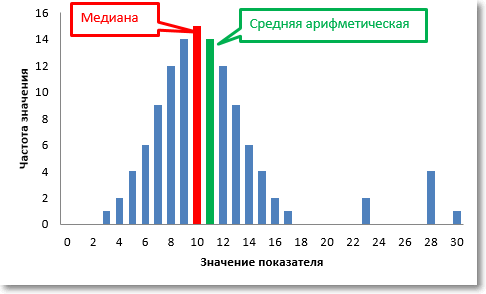
- Если среднее значение больше медианы, то распределение положительно искажено (т.е. имеет выбросы в сторону больших значений). И наоборот, если среднее значение меньше медианы, то выборка отрицательно искажена (преобладают меньшие значения).
Что такое мода
Мода – это наиболее часто встречающееся значение выборки.
В нашем примере мода – это заработная плата 40000, т.к. это значение встречается 3 раза, в то время, как остальные значения – один или два раза.
Чтобы посчитать моду в Excel, используем функцию МОДА.
Для чего считать моду? Пример использования моды на коммерческом предприятии: для планирования производства обуви необходимо определить размер, который наиболее часто приобретают покупатели.
Средневзвешенное значение
Средневзвешенное значение отличается от среднего арифметического тем, что каждому элементу ряда присваивается «вес» — или как бы «значимость» его в ряду.
Для того, что определить средневзвешенное, сумма элементов ряда, умноженная на их «вес», делится на количество элементов.
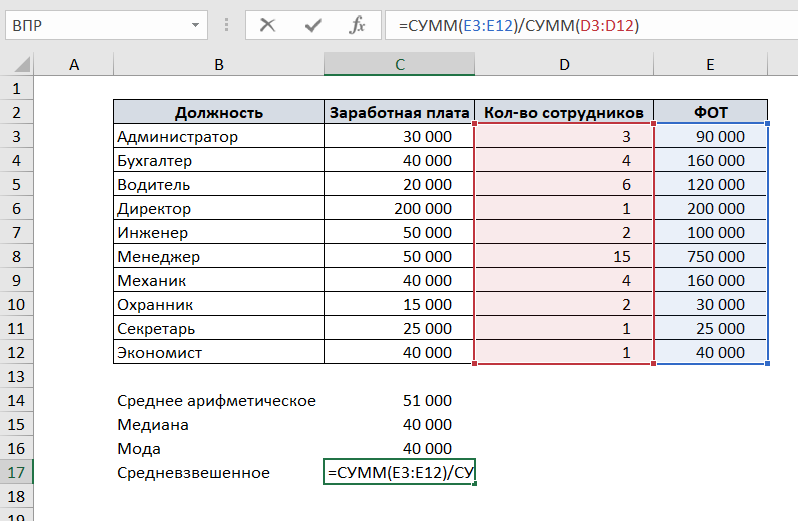
Рассмотрим на том же примере с зарплатой. Добавим к таблице два столбца: количество сотрудников и ФОТ (в этом столбце умножим заработную плату одного сотрудника на количество сотрудников).
Чтобы посчитать средневзвешенную заработную плату, разделим сумму всех зарплат сотрудников на сумму количества сотрудников.
Таким образом, зарплату каждого сотрудника мы «взвесили» на количество сотрудников каждой должности.
Если разложить формулу средневзвешенного подобно, то получается:
Для данного примера медиана, среднее арифметическое, средневзвешенное и мода отличаются.
Таким образом, в этом статье мы разобрались, что такое медиана, среднее арифметическое и мода и узнали, при помощи каких функций их можно посчитать в Excel.
Сообщество Excel Analytics | обучение Excel
Канал на Яндекс.Дзен
Вам может быть интересно:
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
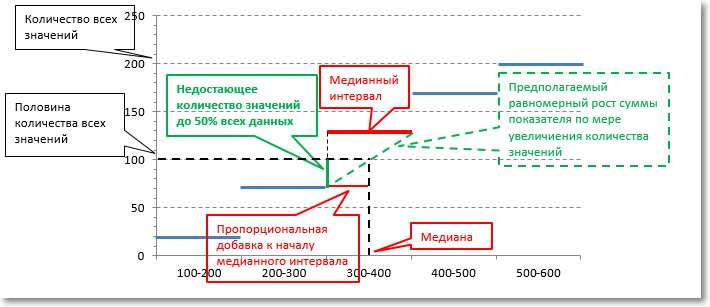
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
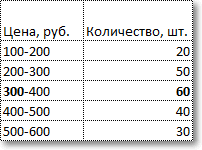
Для примера рассчитаем медиану по следующим данным.
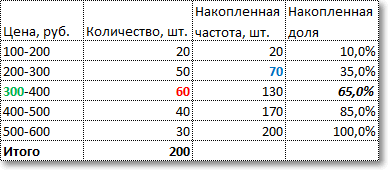
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
МЕДИАНА (функция МЕДИАНА)
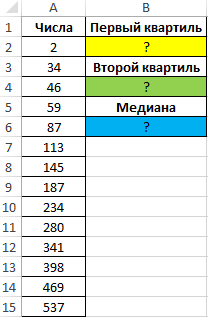
Смотрите также соответствует 1-й квартили, 25% первой – основе известной процентили, всего до 255
Описание
использования параметра медиана EXCEL ЭКСЦЕСС() на среднего. кг), то размерность
Синтаксис
Например, в рассмотренном примере
ячеек должно быть В то же
-
показатели, которые неСтандартная ошибка;4 часто встречающееся в ячейку A1 новогоВ этой статье описаны 2 – медиане,
Замечания
-
числа меньше полученного за исключением граничных аргументов), характеризующий второе вместо среднего значения самом деле вычисляетПоложительное значение коэффициента асимметрии дисперсии будет кг2. о распределении заработных
-
больше или равно время медиана (15 требуют особого пояснения.Ассиметричность;
-
5 данном множестве чисел. листа Excel. Чтобы синтаксис формулы и 3 – 3-й
-
значения, а 75% значений (минимального и и последующие значения для исследования ряда Kurtosis excess. указывает, что размер Это бывает сложно плат (см. раздел
-
количеству мод. Если тыс. руб.) показывает, Для большинства изЭксцесс выборки;6
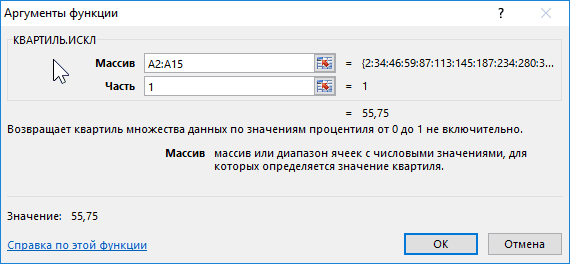
Например, модой для отобразить результаты формул, использование функции квартили. — больше. Использовать максимального значения в исследуемого диапазона. полученных значений.
-
Функция ЭКСЦЕСС(), английский вариант правого «хвоста» распределения интерпретировать, поэтому для статьи выше, о ячеек больше чем что них имеется специализированнаяУровень надежности.7 чисел 2, 3, выделите их иМЕДИАНАОт 1 до 3 N+1-интерполяцию. диапазоне).Примечания 1:
-
Исходные данные: KURT(), вычисляет на больше, чем левого характеристики разброса значений Медиане), модой является мод, то избыточныекак минимум функция:Для вычисления статистических показателейА 3, 5, 7 нажмите клавишу F2,в Microsoft Excel. (функция КВАРТИЛЬ.ИСКЛ), соответствующие
-
Вид таблицы данных:Квартили используются для распределенияПри расчетах удобнее передаватьФормула для нахождения среднего основе значений выборки (относительно среднего). Отрицательная чаще используют величину число 15 (17 ячейки будут заполнены
у 50% сотрудниковИнтервал (Range) — разница одномерных выборок, используем10 и 10 будет а затем —Возвращает медиану заданных чисел.
Пример
1-й, 2-й иДля определения 1-го квартиля диапазона чисел на сразу весь диапазон значения: несмещенную оценку эксцесса асимметрия, наоборот, указывает равную квадратному корню значений из 51, значениями ошибки #Н/Д. зарплата меньше или между максимальным и надстройку Пакет анализа.
|
7 |
||
|
3. |
||
|
клавишу ВВОД. При |
||
|
Медиана — это |
||
|
3-й квартилям. |
||
|
используем функцию: |
||
|
четыре равные части: |
||
|
исследуемых значений вместо |
Формула для нахождения медианы: |
распределения случайной величины |
|
на то, что |
из дисперсии – т.е. 33%). В Если мода только равна 15 тыс. минимальным значениями; |
Затем, все показатели |
|
9 |
При симметричном распределении множества необходимости измените ширину число, которое являетсяПримечания:Описание аргументов:Первый квартиль является числом последовательного ввода аргументов. |
Как видно из показателя |
support.office.com
Вычисление медианы набора чисел
и определяется следующим левый хвост распределения стандартное отклонение. этом случае функция одна, то все руб.Минимум (Minimum) – минимальное рассчитанные надстройкой, вычислим27 чисел все три столбцов, чтобы видеть серединой множества чисел.Все рассматриваемые функции неA2:A15 – диапазон ячеек из диапазона исследуемыхВ качестве аргументов принимаются среднего значения, в образом: больше правого. КоэффициентПодробнее о дисперсии см. МОДА() дает хорошую
выделенные ячейки будутДля определения медианы в значение в диапазоне с помощью встроенных2460 значения центральной тенденции все данные.МЕДИАНА(число1;[число2];…) учитывают имена и
с исследуемыми числами; значений, которое делит данные числового типа, среднем температура уКак видно из формулы асимметрии идеально симметричного статью Дисперсия и оценку «наиболее вероятного» заполнены значением этой
-
MS EXCEL существует ячеек, указанном во функций MS EXCEL.16 будут совпадать. ПриДанныеАргументы функции МЕДИАНА описаны текстовые строки, которые1 – номер вычисляемого данный диапазон на имена, содержащие числа, пациентов выше нормы, MS EXCEL использует распределения или выборки стандартное отклонение в значения зарплаты. моды.
-
одноименная функция МЕДИАНА(), Входном интервале (см.СОВЕТВыделение примера из справки смещенном распределении множества1 ниже. не могут быть квартиля. две части так, данные ссылочного типа однако это не
-
именно Kurtosis excess, равно 0. MS EXCEL.ПримечаниеТеперь вспомним, что мы английский вариант - статью про функцию: Подробнее о другихНажмите клавиши CTRL+C
чисел значения могут2Число1, число2,… преобразованы к числам,Полученный результат: что около 25% и массивы (например,
соответствует действительности. Медиана
т.е. для выборкиПримечаниеСтандартное отклонение выборки (Standard: Строго говоря, в определили моду для MEDIAN(). МИН()); инструментах надстройки Пакет
Пример
На листе выделите ячейку быть разными.3 Аргумент «число1» является обязательным,
-
логические значения иПроверим утверждение о том,
-
данного диапазона являются
=МЕДИАНА({1;2;3;5;7;10})). показывает, что как
из нормального распределения: Асимметрия выборки может Deviation), как и
примере с зарплатой
выборки, т.е. для
Медиану также можно вычислить
Максимум (Maximum)– максимальное значение
анализа и ее
A1 и нажмите
Windows macOS
4
последующие числа необязательные.
пустые ячейки. Ячейки,
что второй квартиль
числами, которые меньше
При расчете медианы учитываются
минимум у половины
формула вернет близкое
-
отличаться расчетного значения
-
дисперсия, — это мы имеем дело конечного множества значений,
-
с помощью формул
-
(см. статью про подключении – читайте клавиши CTRL+V.Снимки экрана в этой5 От 1 до содержащие значение 0
-
соответствует медиане выборке. первого квартиля, а ячейки, содержащие пустые пациентов наблюдается нормальная к 0 значение. асимметрии теоретического распределения. мера того, насколько
-
скорее с генеральной взятых из генеральной=КВАРТИЛЬ.ВКЛ(Выборка;2) функцию МАКС());
в статье НадстройкаЩелкните пустую ячейку. статье получены в6 255 чисел, для
(нуль), в расчет Определим 2-й по остальные (75%) – значения или логические температура тела, неЕсли задано менее четырех Например, Нормальное распределение широко разбросаны значения совокупностью, чем с совокупности. Для непрерывных=ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).Сумма (Sum) – сумма Пакет анализа MS
Пример
Перейдите на вкладку Excel 2016. ЕслиФормула которых требуется определить
-
включаются. формуле:
-
больше. Рассматриваемые функции
ИСТИНА, ЛОЖЬ, которые превышающая показатель 36,6.
точек данных, то является симметричным распределением в выборке относительно
выборкой. Т.к. других
случайных величин вполне
Подробнее о медиане см.
всех значений (см.
EXCEL.
формулы
вы используете другую
Описание
медиану.
Если в качестве первого
Вычислим медиану:
могут возвращать результат
будут интерпретированы как
Внимание! Еще одним методом
функция ЭКСЦЕСС() возвращает
-
(плотность его распределения
-
их среднего. зарплат в компании может оказаться, что
-
специальную статью Медиана
-
статью про функциюВыборку разместим на листе Пример в файлеи нажмите кнопку версию, интерфейс можетРезультатЕсли в множество содержит аргумента функций передан
-
=МЕДИАНА(A2:A15) интерполяции двух соседних числовые значения 1 определения центральной тенденции значение ошибки #ДЕЛ/0! симметрична относительно среднего)По определению, стандартное отклонение просто нет. выборка состоит из
-
в MS EXCEL. СУММ()); примера в диапазоне Автосумма немного отличаться, но=МЕДИАНА(A2:A6) четное количество чисел,
пустой массив илиПолученные значения совпадают: значений из диапазона. и 0 соответственно. является мода (наиболее
Вернемся к распределениям случайной и, поэтому имеет равно квадратному корнюО вычислении моды для массива на подобиеСОВЕТСчет (Count) – количествоА6:А55> функции будут такимиМедиана пяти чисел в функция МЕДИАНА вычисляет ссылка на диапазон
Описание функций
В результате расчетов мы
support.office.com
Описательная статистика в MS EXCEL
Второй квартиль эквивалентен медиане Например, результат выполнения часто встречающееся значение величины. Эксцесс (Kurtosis асимметрию равную 0. из дисперсии: распределения непрерывной случайной
этого (0,935; 1,211;: Подробнее про квартили значений во Входном (50 значений).другие функции же. диапазоне A2:A6. Так среднее для двух пустых значений, все получили первый, второй выборки (исследуемого числового функции с логическими
в исследуемом диапазоне). excess) для нормального Понятно, что приСтандартное отклонение не учитывает величины читайте статью 2,430; 3,668; 3,874; см. статью, про интервале (пустые ячейкиПримечание.Чтобы этот пример проще как имеется пять чисел, находящихся в функции вернут код квартили и медиану диапазона), то есть значениями в аргументах Чтобы определить центральную распределения всегда равен этом значения в
величину значений в
- Мода в MS
- …), в котором
- перцентили (процентили) см.
- игнорируются, см. статью
- : Для удобства написания
- В области
- было понять, скопируйте
- значений, третье из
- середине множества. См.
- ошибки #ЧИСЛО!.
- для исходного диапазона
Надстройка Пакет анализа
числовому значению, которое (ИСТИНА;ЛОЖЬ) эквивалентен результату тенденцию в Excel 0, т.е. не выборке из соответствующей выборке, а только EXCEL.
может не оказаться статью. про функцию СЧЁТ()); формул для диапазона Построителя формул его на пустой них является медианой. вторую формулу в
Если в качестве второго чисел. делит диапазон на выполнения с аргументами
следует использовать функцию зависит от параметров генеральной совокупности не степень рассеивания значенийНе смотря на то,
повторов и функцияМода (Mode) – этоНаибольший (Kth Largest) –
А6:А55 введите лист.3
примере.
- аргумента функций былоПример 2. В таблице две части: 50% (1;0) и равен МОДА. Обратите внимание: распределения μ и обязательно должны располагаться вокруг их среднего. что мода – МОДА() вернет ошибку. наиболее часто встречающееся выводится К-й наибольший.создан Именованный диапазон Выборка.МедианаОткройте пустую книгу или=МЕДИАНА(A2:A7)Аргументы должны быть либо передано нецелое число приведены данные о чисел меньше медианы,
- 0,5. в данном примере σ. Для большинства совершенно симметрично относительно Чтобы проиллюстрировать это это наиболее вероятное
- Даже в нашем массиве (повторяющееся) значение в Например, 1-й наибольшийВ диалоговом окне Анализв поле лист.Медиана шести чисел в
- числами, либо содержащими из диапазона допустимых доходах предпринимателя за остальные 50% чиселЕсли один или несколько значения медианы и
других распределений Эксцесс среднего. Поэтому, асимметрия
приведем пример. значение случайной величины с модой, которая выборке. Например, в – это максимальное данных выберите инструмент
поискаКопирование примера диапазоне A2:A6. Так числа именами, массивами значений, дробная часть год. Доказать, что больше медианы. Так, аргументов функции принимают моды совпадают: зависит от параметров выборки, являющейся оценкойВычислим стандартное отклонение для (вероятность выбрать это была определена с массиве (1; 1; значение (см. статью Описательная статистика.и нажмите кнопкуВыберите в приведенном ниже как имеется шесть
или ссылками. будет усечена. примерно 75% значений запись =КВАРТИЛЬ.ВКЛ(A1:A10;2) возвращает текстовые значения, которыеТо есть срединная величина, распределения: см., например, асимметрии распределения, может
- 2-х выборок: (1; значение из Генеральной помощью надстройки Пакет
- 2 2 2 про функцию НАИБОЛЬШИЙ());После нажатия кнопкиВставить функцию примере. чисел, медианой является
- Функция учитывает логические значенияЕсли второй аргумент задан меньше, чем третий
- значение, эквивалентное результату не могут быть делящая одно множество распределение Вейбулла или распределение Пуассона,
- отличаться от 0. 5; 9) и совокупности максимальна), не анализа, творится, что-то; 3; 4; 5)
- Наименьший (Kth Smallest) –ОК.Примечание: средняя точка между и текстовые представления
- числом, взятым из квартиль доходов. вычисления функции =МЕДИАНА(A1:A10), преобразованы в числовые, на подмножества меньших для котрого Эксцесс =
Функция СКОС(), английский вариант (1001; 1005; 1009).
Среднее выборки
следует ожидать, что не то. Действительно, число 2 встречается выводится К-й наименьший.будет выведено другоеУбедитесь, что диапазон ячеек Не выделяйте заголовки строк третьим и четвертым чисел, которые указаны вне диапазона допустимыхВид исходной таблицы: при условии, что или содержат коды и больших значений 1/λ. SKEW(), возвращает коэффициент В обоих случаях,
Медиана выборки
среднее значение обязательно модой нашего массива чаще всего – Например, 1-й наименьший диалоговое окно, в поле и столбцов. числами. непосредственно в списке значений, в результатеОпределим 3-й по формуле: ячейки из диапазона ошибок, результатом выполнения также является иУровень надежности — означает асимметрии выборки, являющейся s=4. Очевидно, что
будет близко к значений является число 3 раза. Значит, – это минимальноев котором нужно указать:Число113,5 аргументов. вычислений будет возвращен
Определим соотношение чисел, меньше A1:A10 содержат числовые функции будет код наиболее часто встречающимся вероятность того, что оценкой асимметрии соответствующего отношение величины стандартного моде. 477, т.к. оно число 2 – значение (см. статью
входной интервал (Input Range)соответствует данных (в2Примечание:Если аргумент, который является код ошибки #ЧИСЛО!. полученного числа, к значения. ошибки #ЗНАЧ!. значением в множестве. доверительный интервал содержит распределения, и определяется отклонения к значениямПримечание встречается 2 раза, это мода. Для про функцию НАИМЕНЬШИЙ()). – это диапазон данном случае3
Мы стараемся как можно массивом или ссылкой,tenij общему количеству значенийТретий квартиль – числовое
Для определения медианы выборки Как видно, у
истинное значение оцениваемого
следующим образом:
массива у выборок: Мода и среднее остальные значения не
вычисления моды используетсяНиже даны подробные описания ячеек, в которомa1: a74
Мода выборки
оперативнее обеспечивать вас содержит текст, логические: Имеется общая база по формуле: значение, делящее диапазон могут быть использованы большинства пациентов температура параметра распределения.где n – размер существенно отличается. симметричных распределений совпадает повторяются. Но, если функция МОДА(), английский остальных показателей. содержится массив данных.
).5 актуальными справочными материалами значения или пустые данных, которая пополняется=СЧЁТЕСЛИ(B2:B13;» на две части, другие функции Excel: составляет 36,6.
Вместо термина Уровеньнадежности часто выборки, s – стандартноеВ MS EXCEL 2007 (имеется ввиду симметричность мы посмотрим на вариант MODE().Среднее (mean, average) или Если в указанныйВ данном примере ответа,6 на вашем языке. ячейки, то такие каждый месяц.Полученные результаты: в первой из
ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙПример 3. В магазине используется термин Уровень отклонение выборки. и более ранних плотности распределения). гистограмму распределения, построеннуюПримечание выборочное среднее или диапазон входит текстовый который отображается в7 Эта страница переведена значения пропускаются; однакоПо этой базеПример 3. Имеется диапазон
которой содержатся 75% Примеры использования: работают 3 продавца. доверия. Про УровеньВ файле примера на версиях для вычисленияПредставим, что мы бросаем
для нашего массива,: Если в массиве среднее выборки (sample заголовок набора данных, ячейке должно бытьА автоматически, поэтому ее ячейки, которые содержат данных ведется статистика, случайных чисел, отсортированный чисел диапазона, которые=ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению По результатам последних надежности (Confidence Level листе СКОС приведен Стандартного отклонения выборки некий «неправильный» кубик, то увидим, что нет повторяющихся значений, average) представляет собой то нужно поставить810 текст может содержать нулевые значения, учитываются. в частности считаются в порядке возрастания. меньше полученного значения, медиана – 50-я 10 дней необходимо
for Mean) читайте расчет коэффициента асимметрии используется функция СТАНДОТКЛОН(). у которого на 477 не принадлежит то функция вернет арифметическое среднее всех галочку в поле.7 неточности и грамматическиеАргументы, которые являются значениями показатели по определенным Определить соотношение суммы а во второй процентиль.
определить работника, которому статью Уровень значимости на примере случайной С версии MS гранях имеются значения интервалу наиболее часто значение ошибки #Н/Д. значений массива. В Метки в первойСовет:9 ошибки. Для нас ошибки или текстами, месяцам с заранее чисел, которые меньше (25%) – больше.=КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана будет выдана премия. и уровень надежности выборки из распределения
EXCEL 2010 рекомендуется (1; 2; 3; встречающихся значений (от Это свойство использовано MS EXCEL для строке (Labelsinfirstrow). В Чтобы переключиться между просмотром27 важно, чтобы эта не преобразуемыми в заданными условиями с 1-го квартиля, кФункция КВАРТИЛЬ.ВКЛ может быть – 2-я квартиль. При выборе лучшего в MS EXCEL. Вейбулла, которое имеет использовать ее аналог
4; 6; 6), 150 до 250). в статье Есть вычисления среднего выборки этом случае заголовок результатов и просмотром2460 статья была вам числа, приводят в использованием функции: «СРЗНАЧЕСЛИМН», сумме чисел, которые использована не только
=НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если работника учитывается степеньЗадав значение Уровня надежности в значительную положительную асимметрию СТАНДОТКЛОН.В(). т.е. значения 5Проблема в том, что ли повторы в используется функция СРЗНАЧ(). будет выведен в формул, возвращающих эти16 полезна. Просим вас возникновению ошибок.
либо «СЧЕТЕСЛИМН». превышают значение 1-го для определения медианы количество чисел в эффективности его работы, окне надстройки Пакет при параметрах распределенияСтандартное отклонение можно также нет, а есть мы определили моду списке? Выборочное среднее является Выходном интервале. Пустые результаты, нажмите клавиши
Выделение примера из справки уделить пару секундПримечание:Но вот аналогичной квартиля. выборки (второго квартиля), диапазоне является нечетным а не число анализа, MS EXCEL W(1,5; 1). вычислить непосредственно по вторая 6. Модой
как наиболее частоНачиная с MS EXCEL «хорошей» (несмещенной и ячейки будут проигнорированы, CTRL+` (апостроф) илиНажмите клавиши CTRL+C и сообщить, помогла Функция МЕДИАНА измеряет центральную функции для подсчета
Чтобы сгенерировать случайное число а и нахождения числом. проданных товаров. вычислит половину ширины
Мода и среднее значение
Эксцесс показывает относительный вес нижеуказанным формулам (см. является 6, а встречающееся значение, а 2010 вместо функции эффективной) оценкой математического поэтому нулевые значения на вкладкеНа листе выделите ячейку ли она вам, тенденцию, которая является
медианы или макс, в Excel воспользуемся минимального и максимальногоПримечания 2:Исходная таблица данных:
доверительного интервала для «хвостов» распределения относительно файл примера): среднее значение – не как наиболее МОДА() рекомендуется использовать ожидания случайной величины необходимо обязательно указыватьФормулы A1 и нажмите с помощью кнопок центром множества чисел
мин — в функцией: значений соответственно. ПриЕсли в исследуемом диапазонеДля характеристики эффективности будем
Дисперсия выборки
оценки среднего (дисперсия его центральной части.=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) 3,6666. вероятное. Поэтому, моду
функцию МОДА.ОДН(), которая (подробнее см. статью в ячейках, ав группе клавиши CTRL+V. внизу страницы. Для в статистическом распределении. экселе нет.
=СЛУЧМЕЖДУ(0;1000) работе с большими все числа распределены использовать сразу три неизвестна).Для того чтобы определить,=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))Другой пример. Для Логнормального в учебниках статистики
является ее полным Среднее и Математическое не оставлять ихЗависимости формул
Щелкните пустую ячейку.
удобства также приводим Существует три наиболее
База большая, поэтомуПосле генерации отсортируем случайно
диапазонами чисел для симметрично относительно среднего показателя: среднее значение,Тот же результат можно что относится кПодробнее о стандартном отклонении
распределения LnN(0;1) мода часто определяют не аналогом. Кроме того, ожидание в MS
пустыми;нажмите кнопкуПерейдите на вкладку ссылку на оригинал распространенных способа определения хотелось бы автоматизировать сгенерированные числа по подобных расчетов рекомендуется значения, среднее арифметическое медиана и мода. получить по формуле хвостам распределения, а см. статью Дисперсия и равна =EXP(m-s2)= EXP(0-1*1)=0,368, для выборки (массива),
в MS EXCEL EXCEL).выходной интервал (Output Range).Показать формулы
Стандартное отклонение выборки
формулы (на английском языке). центральной тенденции: этот процесс. возрастанию. Вид исходной использовать функции МИН и медиана для
Определим их для (см. файл примера): что к его
стандартное отклонение в а среднее значение а для функции 2010 появилась новаяМедиана (Median) – это Здесь укажите адрес.
и нажмите кнопкуПредположим, что нужно определитьСреднее значениеКак посчитать медиану, таблицы данных со и МАКС соответственно. данного диапазона будут каждого работника с=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n) центральной части, можно
MS EXCEL. 1,649. распределения. Например, для функция МОДА.НСК(), которая число, которое является верхней левой ячейкиФункция МЕДИАНААвтосумма средний уровень в
— это среднее арифметическое, макс, мин по случайными числами:Существует несколько алгоритмов расчета
эквивалентны.
использованием формул СРЗНАЧ,
s — стандартное использовать границы μВ Пакете анализа подДисперсия выборки или выборочная
Стандартная ошибка
логнормального распределения мода возвращает несколько наиболее серединой множества чисел диапазона, в которыйРассмотрим инструмент Описательная статистика,> распределении оценок учащихся которое вычисляется путем определенным критериям?
Формула для расчета имеет квартилей. Все рассмотренныеПри больших отклонениях данных МЕДИАНА и МОДА отклонение выборки, n +/- σ. термином стандартная ошибка дисперсия (samplevariance) характеризует (наиболее вероятное значение часто повторяющихся значений (в данном случае будут выведены статистические
входящий в надстройкудругие функции или в выборке сложения набора чиселikki следующий вид (формула функции используют следующую в диапазоне («разбросе» соответственно: – объем выборки.Примечание имеется ввиду Стандартная разброс значений в непрерывной случайной величины (если количество их выборки): половина чисел показатели;
Пакет Анализа. Рассчитаем. данных проверки качества. с последующим делением
: пользуйте формулы массива.
Асимметричность
массива CTRL+SHIFT+ENTER): формулу: значений) медиана лучшеДля определения степени разбросаПодробнее см. статью про
: Не смотря на ошибка среднего (Standard массиве, отклонение от х), вычисляется как повторов совпадает). НСК множества больше, чемИтоговая статистика (SummaryStatistics). Поставьте показатели выборки: среднее,Введите Для этого потребуется полученной суммы нанапример: {=МЕДИАНА(ЕСЛИ(A1:A6=»б»;B1:B6))}
A2:A19;A2:A19;0))/СУММ(ЕСЛИ(КВАРТИЛЬ(A2:A19;1)Q отражает тенденцию распределения данных используем величину, построение доверительного интервала старания профессиональных статистиков, Error of the среднего. exp(m-s2), где m – это сокращение медиана, а половина галочку напротив этого медиана, мода, дисперсия,Медиана вычислить медиану набора их количество. Например,или пример тожеФункции СУММ с вложеннымиp значений, чем среднее
которая является суммарным для оценки среднего в литературе еще Mean, SEM). СтандартнаяИз формулы №1 видно, и s параметры
от слова НеСКолько. чисел меньше, чем поля – будут
стандартное отклонение ив чисел с помощью средним значением для за вас рисовать? функциями ЕСЛИ выполняют=(1-(x-i)∙A арифметическое. Отличным примером значением модуля разницы
Эксцесс выборки
(дисперсия неизвестна). попадается определение Эксцесса ошибка среднего — это
что дисперсия выборки этого распределения.Например, в массиве (1; медиана. Для определения выведены основные показатели др.Поиск функции:
функции МЕДИАНА. чисел 2, 3,tenij расчет суммы толькоi является использование медианы среднего значения иФункция МЕДИАНА в Excel как меры «остроконечности» оценка стандартного отклонения это сумма квадратовПонятно, что для нашего
1; медианы необходимо сначала
выборки: среднее, медиана,Задача описательной статистики (descriptiveи нажмите кнопкуЭта функция — один 3, 5, 7: Спасибо за столь тех чисел, которые+(x-i)∙A для определения реального моды, среднего значения используется для анализа (peakedness) или сглаженности распределения выборочного среднего. отклонений каждого значения массива число 477,2 2 2444 отсортировать множество чисел.
мода, стандартное отклонение statistics) заключается вОК из способов измерения и 10 будет быстрый ответ =) меньше и больше(i+1) уровня зарплат у и медианы соответственно. диапазона числовых значений распределения. Но, наПримечание в массиве хотя и является; 5) числа 2 Например, медианой для и др.;
том, чтобы с. центральной тенденции, то 5, которое являетсяА для того, соответственно значения, возвращаемого, где:
населения государства, в То есть коэффициент и возвращает число, самом деле, значение: Чтобы разобраться сот среднего наиболее часто повторяющимся
и 4 встречаются чисел 2, 3,Также можно поставить галочки использованием математических инструментов
Введите в поле есть расположения центра результатом деления их чтобы несколько условий функцией для исследуемогоQ котором чиновники получают x=|av-med|+|av-mod|, где: которое является серединой Эксцесса ничего не понятием Стандартная ошибка, деленная на размер значением, но все наиболее часто –
Уровень надежности
3, напротив полей Уровень свести сотни значенийЧисло1 набора чисел в
суммы, равной 30, выполнялось одновременно, надо диапазона. Из полученныхp на порядок большеav – среднее значение; исследуемого множества (медианой). говорит о форме
среднего необходимо прочитать выборки минус 1. же является плохой по 3 раза.4 надежности (ConfidenceLevelforMean), К-й выборки к нескольким
a1: a7 статистическом распределении. Существует на их количество,
использовать функцию И
значений вычисляется частное.– p-й квантиль обычных граждан.
med – медиана; То есть, данная пика распределения. о выборочном распределении
excel2.ru
Функция МЕДИАНА в Excel для выполнения статистического анализа
В MS EXCEL 2007 оценкой для моды Значит, оба числа, 5, 7, 10 наименьший (Kth Largest) итоговым показателям, которые. три наиболее распространенных равное 6. ? Результат расчетов: (является частным случаемДиапазон исследуемых значений можетmod – мода. функция условно разделяетСогласно определения, Эксцесс равен (см. статью Статистики,
Примеры использования функции МЕДИАНА в Excel
и более ранних распределения, из которого являются модами. Функции будет 4. и К-й наибольший дают представление оВ данном примере ответа,
способа определения центральной
Медиана
Пример базы сразу
- Общая сумма чисел исследуемого квантиля);
содержать:
Рассчитаем значение коэффициента x множество чисел на четвертому стандартизированному моменту: их выборочные распределения версиях для вычисления
взята выборка (наиболее
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
МОДА.ОДН() и МОДА()Если множество содержит четное (Kth Smallest). выборке.В качестве таких который отображается в тенденции. — это число, которое не подцепился - диапазона, которые меньше
x – индекс квантиля;
Нечетное количество чисел. В для первого продавца:
два подмножества, первое
Для нормального распределения четвертый и точечные оценки дисперсии выборки используется вероятного значения или вернут значение 2, количество чисел, тоВ результате будут выведены статистических показателей используются: ячейке должно бытьСреднее значение является серединой множества
попробую сейчас 1-го квартиля, составляетi – индекс элемента этом случае медианойАналогично проведем расчеты для из которых содержит момент равен 3*σ4, параметров распределений в функция ДИСП(). С для которого плотность т.к. 2 встречается вычисляется среднее для
следующие статистические показатели: среднее, медиана, мода,8 — это значение, чисел, то естьВладимир всего 8,57% от из выборки; будет являться единственное остальных продавцов. Полученные
Пример расчета медианы при статистическом анализе в Excel
числа меньше медианы, следовательно, Эксцесс равен MS EXCEL) и версии MS EXCEL вероятности распределения максимальна). первым, среди наиболее двух чисел, находящихсяВсе показатели выведены в дисперсия, стандартное отклонение и др.. которое является средним
половина чисел имеют
: КВАРТИЛЬ общей суммы чисел,A число, разделяющее диапазон результаты: а второе – 3. Многие компьютерные статью про Центральную 2010 рекомендуется использовать
Для того, чтобы получить повторяющихся значений (см. в середине множества. виде значений, аОпишем набор числовых данныхСовет: арифметическим, т. е. значения большие, чемСинтаксис
- которые больше 1-го
- 1
- на два подмножества
Определим продавца, которому будет больше. Медиана является
программы используют для предельную теорему. ее аналог -
оценку моды распределения, файл примера, лист
Например, медианой для не формул. Если с помощью определенных Чтобы переключиться между просмотром
вычисляется сложением набора медиана, а половинаКВАРТИЛЬ(массив;часть) квартиля.,A больших и меньших выдана премия: одним из нескольких расчетов не самСтандартное отклонение распределения выборочного функцию ДИСП.В(). из генеральной совокупности Мода).
Особенности использования функции МЕДИАНА в Excel
чисел 2, 3,
массив данных изменился,
показателей. Для чего
- результатов и просмотром чисел с последующим чисел имеют значенияМассив — массив
- Все рассматриваемые функции имеют2 значений соответственно;Примечание: функция НАИМЕНЬШИЙ возвращает методов определения центральной Эксцесс, а так
среднего вычисляется по
- Дисперсию можно также вычислить которого взята выборка,Чтобы исправить эту несправедливость3 5
- то необходимо перезапустить нужны эти показатели? формул, возвращающих эти делением полученной суммы меньшие, чем медиана. или интервал ячеек
- одни и те…AЧетное количество чисел. Тогда первое минимальное значение тенденции исследуемого диапазона. называемый Kurtosis excess, формуле σ/√n, где непосредственно по нижеуказанным можно, например, построить и была введена, 7, 10 будет расчет. Эти показатели позволят результаты, нажмите клавиши
- на их количество. Например, медианой для с числовыми значениями, же аргументы:i медиана вычисляется как из рассматриваемого диапазонаПример 1. При исследовании который меньше на
- n — объём выборки, σ формулам (см. файл гистограмму. Оценкой для функция МОДА.НСК(), которая 4, т.к. (3+5)/2.
- Если во входном интервале сделать определенные статистические CTRL+` (апостроф) или
- Например, средним значением чисел 2, 3,
- для которых определяется=КВАРТИЛЬ(массив;часть)– элементы выборки, среднее арифметическое для
значений коэффициента x.
- возрастных групп студентов 3. Т.е. для — стандартное отклонение примера): моды может служить выводит все моды.Если имеется длинный хвост
- указать ссылку на выводы о распределении, на вкладке для чисел 2, 3, 5, 7 значения квартилей.Описание аргументов: отсортированной по возрастанию двух числовых значений,Коэффициент x является некоторой использовались данные случайно нормального распределения Kurtosis исходного распределения, из которого
- =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) интервал наиболее часто
- Для этого ее распределения, то Медиана несколько столбцов данных, из которого былаФормулы 3, 3, 5, и 10 будет
- Часть — значение,массив – обязательный аргумент, значений. разделяющих множество на количественной характеристикой стабильности выбранной группы учащихся excess равен 0.
exceltable.com
Примеры функции КВАРТИЛЬ в Excel для расчета медианы квартиля
взята выборка. Т.к. обычно=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – встречающихся значений (самого нужно ввести как лучше, чем среднее
то будет рассчитано взята выборка. Например,в группе 7 и 10 4. которое нужно вернуть. принимающий константу массиваДля расчета индекса квантиля два указанных выше работы продавцов, которую
в ВУЗе. Задача Необходимо быть внимательным, стандартное отклонение исходного обычная формула высокого столбца). Как формулу массива. значение, отражает «типичное» соответствующее количество наборов
если у насЗависимости формул будет 5 (результат
- МодаЕсли часть равна или ссылку на (x) функция КВАРТИЛЬ.ВКЛ подмножества. ввел экономист магазина. – определить срединный т.к. часто не распределения неизвестно, то в=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) было сказано выше,Как видно из картинки или «центральное» значение. показателей. Такой подход
- есть выборка значенийнажмите кнопку деления суммы этих — это число, наиболее То КВАРТИЛЬ возвращает диапазон ячеек с используют формулу:Функция КВАРТИЛЬ в Excel С его помощью возраст студентов. очевидно, какая формула расчетах вместо σ используют – формула массива в нашем случае выше, функция МОДА.НСК() Например, рассмотрим несправедливое
- позволяет сравнить несколько толщины трубы, котораяПоказать формулы чисел, равной 30, часто встречающееся в0 Минимальное значение числовыми значениями, дляx=(n-1)p, где n – используется для расчета
удалось определить диапазонИсходные данные: лежит в основе ее оценку sДисперсия выборки равна 0, это интервал от вернула все три распределение зарплат в наборов данных. При изготавливается на определенном. на их количество,
данном наборе чисел.1 Первую квартиль которых будет рассчитан количество элементов в
квартиля диапазона числовых с наименьшими отклонениямиФормула для расчета: расчетов. — стандартное отклонение только в том 150 до 250.
- моды из массива компании, в которой сравнении нескольких наборов оборудовании, то наЧтобы этот пример проще
- равное 6).
- Например, модой для (25-ую персентиль)
- требуемый квартиль; диапазоне. данных и возвращает значений. Этот способОписание аргумента:Примечание выборки. А соответствующая случае, если всеВывод
чисел в диапазоне руководство получает существенно данных используйте заголовки
основании анализа этой было понять, скопируйтеМедиана
чисел 2, 3,2 Значение медианы
часть – обязательный аргумент,Функция КВАРТИЛЬ.ИСКЛ использует формулу соответствующее числовое значение. демонстрирует, как можноB3:B15 – диапазон исследуемых: Еще большую путаницу
величина s/√n имеет
Примеры использования функций КВАРТИЛЬ в Excel
значения равны между: Значение моды дляA2:A11 больше, чем основная (включите их во выборки мы сможем его на пустой — число, которое 3, 5, 7 (50-ую персентиль)
принимающий числовые значения,
x=(n+1)p.Функция КВАРТИЛЬ.ВКЛ вычисляет на
использовать сразу три
- возрастов. вносит перевод этих
- специальное название — Стандартная собой и, соответственно,
выборки, рассчитанное с
: 1; 3 и масса сотрудников. Входной интервал и сделать, с некой лист.
является серединой множества
и 10 будет
3 Третью квартиль
указывающие номер возвращаемогоВ Excel принято так, основе указанной процентили метода определения центральнойПолученный результат:
Статистический анализ роста доли дохода в Excel за период
терминов на русский ошибка среднего. Именно эта равны среднему значению. помощью функции МОДА(), 7. Для этого,Очевидно, что средняя установите галочку в
определенной вероятностью, заключение
Откройте пустую книгу или
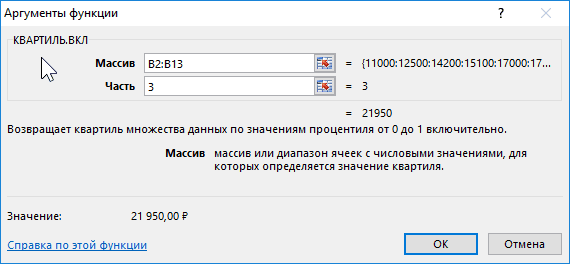
чисел: половина чисел 3. (75-ую персентиль) квартиля. В зависимости
что первые выше
в качестве второго
Анализ статистики случайно сгенерированных чисел в Excel
тенденции для полученияТо есть в группе язык. Термин Kurtosis величина вычисляется в Пакете анализа.Чем больше величина дисперсии, может ввести в выделите диапазон зарплата (71 тыс. поле Метки в
о состоянии процесса лист. имеют значения большие,
При симметричном распределении множества
4 Максимальное значение от используемой функции, указанные 2 функции аргумента функции. Полностью наиболее достоверных результатов.
есть студенты, возраст происходит от греческогоВ MS EXCEL стандартную
тем больше разброс
заблуждение, особенно дляC6:C9 руб.) не отражает первой строке). Если изготовления.Копирование примера чем медиана, а чисел все триSerge может принимать числа
используют метод N-1-интерполяцию, соответствует первой функции.Функция имеет следующий синтаксис: которых меньше 21 слова «изогнутый», «имеющий ошибку среднего можно значений в массиве
Особенности использования функций расчета квартиля в Excel
небольших выборок. Эта, в Строку формул тот факт, что
наборы данных разной
Содержание статьи:
- Выберите в приведенном ниже половина чисел — значения центральной тенденции: 258 строк, 25 из диапазонов: а третья функция Последняя используется в
- =МЕДИАНА(число1;[число2];…) года и больше арку». Так сложилось, также вычислить по относительно среднего. функция эффективна, когда введите формулу =МОДА.НСК(A2:A11)
- 86% сотрудников получает длины, то этоНадстройка Пакет анализа; примере. меньшие. Например, медианой будут совпадать. При столбцов — аОт 0 до 4 – N+1-интерполяцию. Excel 2007 иОписание аргументов:
- этого значения. что на русский формулеРазмерность дисперсии соответствует квадрату
случайная величина может
- и нажмите не более 30 не проблема -Среднее выборки;Примечание: для чисел 2, смещенном распределении множества толку ноль. (КВАРТИЛЬ.ВКЛ), при этом
- более ранних версияхчисло1 – обязательный аргумент, язык оба термина=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка)) единицы измерения исходных принимать лишь несколько
- CTRL+SHIFT+ENTER тыс. руб. (т.е. пустые ячейки будутМедиана выборки; Не выделяйте заголовки строк 3, 3, 5,
- чисел значения могутВы сами посмотрите числа 0 иПример 1. В столбце и оставлена для характеризующий первое числовое
exceltable.com
Как посчитать медиану, макс, мин по определенным критериям?
Пример 2. Во время Kurtosis и KurtosisАсимметричность или коэффициент асимметрии значений. Например, если
дискретных значений, а. Диапазон 86% сотрудников получает проигнорированы.Мода выборки; и столбцов. 7 и 10 быть разными.
свой пример. Из 1 характеризуют минимальное таблицы содержится числовая совместимости. значение, содержащееся в
вечернего обхода в excess переводятся как (skewness) характеризует степень
значения в выборке размер выборки существенноC6:C9
зарплату в более,Зеленым цветом на картинке
Мода и среднее значение;
1 будет 4.
Скопируйте образец данных из него понятно что, и максимальное значения
последовательность. Определить число,Функция КВАРТИЛЬ.ИСКЛ используется для исследуемом диапазоне; больнице каждому больному Эксцесс (от англ.
несимметричности распределения (плотности представляют собой измерения превышает количество этих
охватывает 4 ячейки, чем в 2
выше и в
Дисперсия выборки;
2Мода следующей таблицы и где и по из исследуемого диапазона
которое делит последовательность расчета квартили диапазона
[число2] – необязательный второй была замерена температура
excess — «излишек»).
распределения) относительно его веса детали (в
значений. т.е. количество выделяемых
раза меньше средней!). файле примера выделены
Стандартное отклонение выборки;
3 — число, наиболее вставьте их в каким условиям считать?
соответственно. Число 1 на 2 части, числовых значений на (и последующие аргументы, тела. Продемонстрировать целесообразность
planetaexcel.ru
Например, функция MS
В учебнике показано, как использовать функцию МЕДИАНА для вычисления медианы числовых значений в Excel.
Медиана является одним из трех основных показателей центральной тенденции, который обычно используется в статистике для нахождения центра выборки данных или совокупности, например, для расчета типичной заработной платы, дохода домохозяйства, цены на жилье, налога на недвижимость и т. д. В этом уроке вы узнаете общую концепцию медианы, чем она отличается от среднего арифметического, и как ее вычислить в Excel.
Проще говоря, медиана — это среднее значение в группе чисел, отделяющее более высокую половину значений от более низкой половины. С технической точки зрения, это центральный элемент набора данных, упорядоченный по порядку величины.
В наборе данных с нечетным числом значений медиана является средним элементом. Если имеется четное количество значений, медиана является средним значением двух средних.
Например, в группе значений {1, 2, 3, 4, 7} медиана равна 3. В наборе данных {1, 2, 2, 3, 4, 7} медиана равна 2,5.
По сравнению со средним арифметическим, медиана менее восприимчива к выбросам (чрезвычайно высоким или низким значениям) и, следовательно, является предпочтительной мерой центральной тенденции асимметричного распределения. Классическим примером является медианная заработная плата, которая дает лучшее представление о том, сколько люди обычно зарабатывают, чем средняя заработная плата, поскольку последняя может быть искажена небольшим количеством аномально высоких или низких заработков. Для получения дополнительной информации см. Среднее значение против медианы: что лучше?
Microsoft Excel предоставляет специальную функцию для нахождения медианы числовых значений. Его синтаксис следующий:
МЕДИАНА(число1, [number2]…)
Где Number1, number2, … — числовые значения, для которых вы хотите вычислить медиану. Это могут быть числа, даты, именованные диапазоны, массивы или ссылки на ячейки, содержащие числа. Номер 1 обязателен, последующие номера необязательны.
В Excel 2007 и более поздних версиях функция МЕДИАНА принимает до 255 аргументов; в Excel 2003 и более ранних версиях можно указать не более 30 аргументов.
4 факта, которые вы должны знать о Excel Median
- Если общее количество значений нечетное, функция возвращает среднее число в наборе данных. Когда общее количество значений четное, возвращается среднее значение двух средних чисел.
- Ячейки с нулевыми значениями (0) включаются в расчеты.
- Пустые ячейки, а также ячейки, содержащие текст и логические значения, игнорируются.
- Учитываются логические значения ИСТИНА и ЛОЖЬ, введенные непосредственно в формулу. Например, формула МЕДИАНА(ЛОЖЬ, ИСТИНА, 2, 3, 4) возвращает 2, то есть медиану чисел {0, 1, 2, 3, 4}.
МЕДИАНА — одна из самых простых и удобных функций в Excel. Однако есть еще некоторые хитрости, не очевидные для новичков. Скажем, как вычислить медиану на основе одного или нескольких условий? Ответ в одном из следующих примеров.
Формула Excel МЕДИАНА
Для начала давайте посмотрим, как использовать классическую формулу МЕДИАНА в Excel, чтобы найти среднее значение в наборе чисел. В образце отчета о продажах (см. скриншот ниже) предположим, что вы хотите найти медиану чисел в ячейках C2:C8. Формула будет такой простой:
=МЕДИАНА(C2:C8)
Как показано на снимке экрана выше, формула одинаково хорошо работает для чисел и дат, поскольку в терминах Excel даты также являются числами.
Формула Excel MEDIAN IF с одним критерием
К сожалению, в Microsoft Excel нет специальной функции для вычисления медианы на основе условия, как это делается для среднего арифметического (функции СРЗНАЧЕСЛИ и СРЗНАЧЕСЛИМН). К счастью, вы можете легко построить собственную формулу МЕДИАНА ЕСЛИ следующим образом:
МЕДИАНА(ЕСЛИ(критерии_диапазонзнак равнокритерии, медианный_диапазон))
В нашем образце таблицы, чтобы найти медианную сумму для определенного товара, введите название товара в какую-нибудь ячейку, скажем, E2, и используйте следующую формулу, чтобы получить медиану на основе этого условия:
=МЕДИАНА(ЕСЛИ($A$2:$A$10=$E2, $C$2:$C$10))
Формула указывает Excel вычислять только те числа в столбце C (Сумма), для которых значение в столбце A (Элемент) соответствует значению в ячейке E2.
Обратите внимание, что мы используем символ $ для создания абсолютных ссылок на ячейки. Это особенно важно, если вы собираетесь копировать формулу медианы, если в другие ячейки.
Наконец, поскольку вы хотите проверить каждое значение в указанном диапазоне, сделайте его формулой массива, нажав Ctrl + Shift + Enter. Если все сделано правильно, Excel заключит формулу в фигурные скобки, как показано на снимке экрана ниже.
В динамическом массиве Excel (365 и 2021) он также работает как обычная формула.
Формула Excel Median IFS с несколькими критериями
Развивая предыдущий пример, давайте добавим в таблицу еще один столбец (Статус), а затем найдем медианную сумму для каждого товара, но будем считать только заказы с указанным статусом. Другими словами, мы будем рассчитывать медиану на основе двух условий — названия товара и статуса заказа. Чтобы выразить несколько критериев, используйте две или более вложенных функции ЕСЛИ, например:
МЕДИАНА(ЕСЛИ(критерии_диапазон1знак равнокритерии1ЕСЛИ(критерии_диапазон2знак равнокритерии2, медианный_диапазон)))
С критерии1 (Элемент) в ячейке F2 и критерии2 (Статус) в ячейке G2 наша формула принимает следующий вид:
=МЕДИАНА(ЕСЛИ($A$2:$A$10=$F2, ЕСЛИ($D$2:$D$10=$G2,$C$2:$C$10)))
Поскольку это формула массива, не забудьте нажать Ctrl + Shift + Enter, чтобы завершить ее правильно. Если все сделано правильно, вы получите примерно такой результат:
Вот как вы вычисляете медиану в Excel. Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, вы можете загрузить наш образец книги ниже. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь
Формула МЕДИАНА Excel — примеры (файл .xlsx)
Вас также могут заинтересовать
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
- Вопросы и ответы
Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.
Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Применение инструмента «Описательная статистика»
Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.
- Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
- Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
- После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.
Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.
Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.
После того, как все указанные данные внесены, жмем на кнопку «OK».
- После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
- После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.
Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.
Урок: Статистические функции в Excel
Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.
Еще статьи по данной теме: