При выполнении самых разных иногда анализов возникает потребность в поиске и определении с выполнением вычислительных операций для непарных чисел в Excel. Чтобы не искать непарные числа вручную рационально автоматизировать этот процесс с помощью формулы где главную роль играет функция ЕСЛИ.
Пример работы функции ОСТАТ в Excel
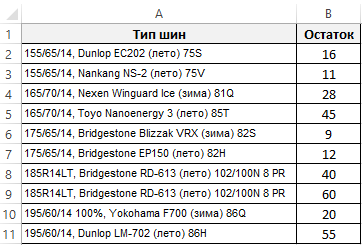
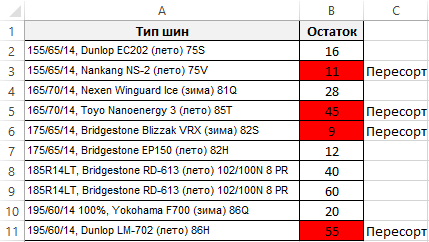
Для примера возьмем магазин с летними и зимними автомобильными шинами. Клиент покупает 4 или 2 шины для своего автомобиля. Если на остатках в складе магазина встречаются непарные числа, то скорее всего на складе пересорт товара.
Следует сбалансировать все остатки до переучета. Для этого нужно определить все позиции с непарным количеством товара на остатках. Если склад большой, то список наименований шин с различными маркировками и параметрами (размеры, диаметр, производитель и т.д.) может содержать тысячи позиций. Поэтому вручную искать все «грехи» складовщиков – это трудозатратный процесс, требующий много времени. Рекомендуем быстрое решение:
Чтобы найти все непарные числа:
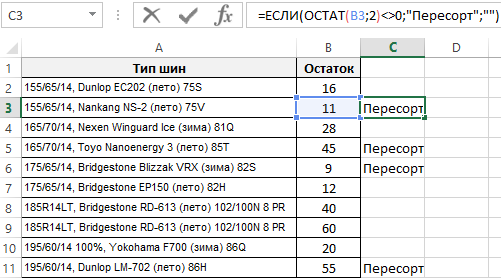
- В ячейку C2 введите следующую формулу:
- Скопируйте эту формулу на против всех ячеек столбца «Остаток».
На против всех позиций товара, которые имеют сомнительные остатки на складе, отображается слово «Пересорт».
Принцип работы формулы для поиска непарных чисел:
В первом аргументе главной функции ЕСЛИ применяется функция ОСТАТ. В данном примере она возвращает нам остаток от деления на число 2. Если остаток от деления не равно нулю (так происходит в случае деления непарных чисел на 2), формулой сразу же возвращается текстовое значение «Пересорт». В противные случаи ячейка остается пустой.
Не сложно догадаться как будет выглядеть формула для поиска парных чисел:
Если остаток от деления = 0, то число парное.
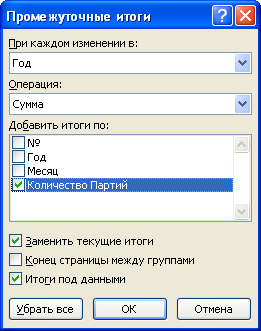
Использование функции ОСТАТ в условном форматировании
Поэтому же принципу можем легко выделить цветом все непарные числа, чтобы визуальный анализ остатков был максимально читабельным и комфортным. Для этого будем использовать функцию МОД с такими же аргументами в условном форматировании:
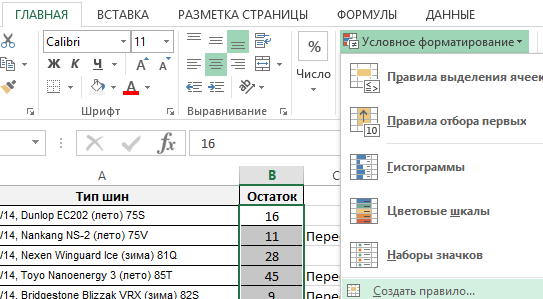
- Выделите диапазон B2:B11 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило».
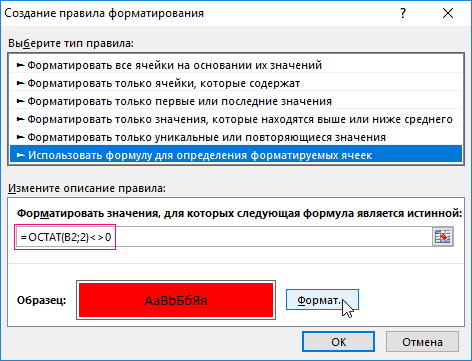
- В появившемся диалоговом окне «Создание правила форматирования» выберите опцию «Использовать формулу для определения форматируемых ячеек» и в поле ввода введите формулу:
- Нажмите на кнопку «Формат», чтобы задать оформление для ячеек с неправильными остатками.
- На всех открытых диалоговых окнах нажмите на кнопку ОК.
Теперь наш отчет по остаткам легко читается и сам находит неправильные остатки.
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Предположим, вам может потребоваться найти баланс покупок, чтобы не превысить ограничения на расходы. Вы можете использовать остаток на остаток, чтобы просмотреть сумму значений элементов в ячейках при вводе новых элементов и значений с течением времени. Чтобы вычислить остаток на счете, используйте следующую процедуру:
Примечание: Остаток на счете отличается от набегаемого итога (также называемого числом накладных), в котором при вводе новых элементов вы будете наблюдать за количеством элементов на скайпе. Дополнительные сведения см. в этойExcel.
-
Настройка таблицы, как в примере ниже.
Пример данных:
A
B
C
1
Вклады
Выплаты
Остаток на счете
2
1000
625
=СУММ(A2-B2)
3
1245
740
=СУММ(C2;A3-B3)
-
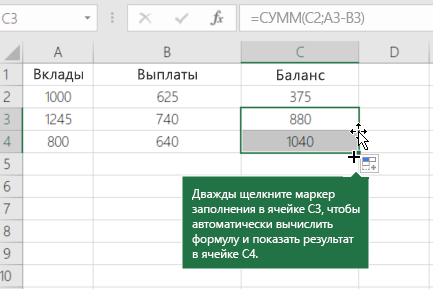
Щелкните в любом месте за пределами ячейки C3, чтобы увидеть вычисляемую сумму.
-
Чтобы сохранить остаток на счете, добавьте строку для каждой новой записи, выстроив следующее:
-
Введите сумму депозитов и средств на счет в пустые строки непосредственно под существующими данными.
Например, если вы использовали пример выше, введите вклады в A4, A5 и так далее, а затем средства будут сдвегались в B4, B5 и так далее.
-
Разместив формулу с накладным балансом в новые строки, выберем последнюю ячейку в столбце «Баланс» и дважды щелкните маркер заполнения.
Например, если вы использовали пример выше, нужно выбрать ячейку C3, а затем дважды щелкнуть ее ручку заполнения, чтобы распространить формулу на все новые строки, содержащие значения депозита и вывода средств.
-
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Содержание
- 1 Подключение пакета анализа
- 2 Виды регрессионного анализа
- 3 Линейная регрессия в программе Excel
- 4 Разбор результатов анализа
- 4.1 Помогла ли вам эта статья?
- 5 Регрессионный анализ в Excel
- 6 Корреляционный анализ в Excel
- 7 Корреляционно-регрессионный анализ
- 8 Пример работы функции ОСТАТ в Excel
- 9 Использование функции ОСТАТ в условном форматировании
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х1, Х2, …, Xk).
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Виды регрессионных моделей
В заметке Представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 1.
Рис. 1. Положительная линейная зависимость
Простая линейная регрессия:
(1) Yi = β0 + β1Xi + εi
где β0 — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β1 — наклон прямой Y, εi— случайная ошибка переменной Y в i-м наблюдении.
В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β0 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2.
Рис. 2. Диаграммы разброса, иллюстрирующие разные виды зависимостей
На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.
Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.
Вывод уравнения простой линейной регрессии
Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (рис. 3).
Рис. 3. Площади и годовые объемы продаж 14 магазинов сети Sunflowers: (а) исходные данные; (б) диаграмма разброса
Анализ рис. 3 показывает, что между площадью магазина X и годовым объемом продаж Y существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследования является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.
Метод наименьших квадратов
Данные, представленные на рис. 1а, получены для случайной выборки магазинов. Если верны некоторые предположения (об этом чуть позже), в качестве оценки параметров генеральной совокупности (β0 и β1) можно использовать сдвиг b0 и наклон b1 прямой Y. Таким образом, уравнение простой линейной регрессии принимает следующий вид:
где — предсказанное значение переменной Y для i-гo наблюдения, Xi — значение переменной X в i-м наблюдении.
Для того чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии — сдвиг b0 и наклон b1 прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения. Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями Yi, и предсказанными значениями . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
Поскольку = b0 + b1Xi, сумма квадратов принимает следующий вид:
Параметры b0 и b1 неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b0 и наклона b1 выборки Y. Для того чтобы найти значения параметров b0 и b1, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. При любых других значениях сдвига b0 и наклона b1 сумма квадратов разностей между фактическими значениями переменной Y и ее наблюдаемыми значениями лишь увеличится.
До того, как Excel взял на себя всю рутинную работу, вычисления по методу наименьших квадратов были очень трудоемкими. Excel позволяет решать подобные задачи двумя способами. Во-первых, можно воспользоваться Пакетом анализа (строка Регрессия). Результаты представлены на рис. 4. Во-вторых, можно, выделив точки на графике (как на рис. 3б), кликнуть правой кнопкой мыши и выбрать Добавить линию тренда. Далее можно выбрать вид линии тренда (в нашем случае – Линейная), отформатировать линию, показать на графике уравнение и величину достоверности аппроксимации (R2) (рис. 5).
Рис. 4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью Пакета анализа Excel)
Рис. 5. Диаграмма разброса и линия регрессии (тренда) в задаче о выборе магазина
Как следует из рис. 4 и 5, b0 = 0,9645, а b1 = 1,6699. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид: = 0,9645 + 1,6699Xi. Вычисленный наклон b1 = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b0 = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b0 необходимо относиться внимательно.
Пример 1. Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: Ŷi = –5,0 + 7Хi. Какой смысл имеют параметры сдвига b0 и наклона b1.
Решение. Сдвиг регрессии b0 равен –5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон b1 равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.
Пример 2. Вернемся к сценарию, изложенному в начале заметки. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров. Предположим, что площадь магазина равна 4000 квадратных футов. Какой среднегодовой объем продаж можно прогнозировать?
Решение. Подставим значение X = 4 (тыс. кв. футов) в уравнение линейной регрессии: = 0,9645 + 1,6699Xi = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала не всегда релевантна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (рис. 3а), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Оценки изменчивости
Вычисление сумм квадратов. Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений Yi вокруг среднего значения . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).
Рис. 6. Оценки изменчивости в модели регрессии
Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷi (предсказанным значением переменной Y) и (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:
(3) SST = SSR + SSE
Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением:
Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:
Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:
Суммы квадратов, вычисленные с помощью программы Пакета анализа Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 4.
Полная сумма квадратов разностей равна SST = 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR) равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.
Коэффициент смешанной корреляции. Величины SSR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции r2:
Коэффициент смешанной корреляции оценивает долю вариации переменной Y, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476 и SST = 116,9543. Следовательно, r2 = 105,7476 / 116,9543 = 0,904. Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина r2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.
Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен в таблице Регрессионная статистика на рис. 4.
Среднеквадратичная ошибка оценки. Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное ранее, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 5.
Среднеквадратичная ошибка оценки
где Yi — фактическое значение переменной Y при заданном значении Xi, Ŷi — предсказанное значение переменной Y при заданном значении Xi, SSE — сумма квадратов ошибок.
Поскольку SSE = 11,2067, по формуле (8) получаем:
Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл. (т.е. 966 400 долл.). Этот параметр также рассчитывается Пакетом анализа (см. рис. 4). Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная Y. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Cреднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной Y.
Предположения
Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы:
- Ошибка должна иметь нормальное распределение.
- Вариация данных вокруг линии регрессии должна быть постоянной.
- Ошибки должны быть независимыми.
Первое предположение, о нормальном распределении ошибок, требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 7). Как и t— и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.
Рис. 7. Предположение о нормальном распределении ошибок
Второе условие заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (см. рис. 7). Это свойство очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами.
Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.
Анализ остатков
Чуть выше при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.
Оценка пригодности эмпирической модели. Остаток, или оценка ошибки еi, представляет собой разность между наблюдаемым (Yi) и предсказанным (Ŷi) значениями зависимой переменной при заданном значении Xi.
(9) ei = Yi – Ŷi
Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения Xi — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями Xi и остатками еi.
Рассмотрим примеры (рис. 8). Панель А иллюстрирует возрастание переменной Y при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной Y падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными лучше подойдет квадратичная модель. Особенно ярко квадратичная зависимость между величинами Xi и ei проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и Y и выявить недостаточную точность модели простой линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью.
Рис. 8. Исследование эмпирической модели простой линейной регрессии
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные и расчеты приведены на рис. 9а (формулы можно посмотреть в Excel-файле). Построим диаграмму разброса, откладывая по вертикальной оси остатки ei, а по горизонтальной — независимую переменную Xi (рис. 9б). Несмотря на большой разброс остатков, между ei и Хi нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.
Рис. 9. Остатки ei, вычисленные при решении задачи о сети магазинов Sunflowers
Значения остатков (таблица на рис. 9а) и график остатков (аналог рис. 9б) можно получить непосредственно в процедуре Регрессия Пакета анализа. Просто поставьте соответствующие галки (рис. 10).
Рис. 10. Остатки ei и график остатков полученные с помощью Пакета анализа
Проверка условий. График остатков позволяет оценить вариации ошибок. На рис. 10 нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы. Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 11). На этом рисунке изображен эффект веера: при возрастании значений Хi ошибки увеличиваются. Таким образом, изменчивость значений Yi при разных значениях Хi является непостоянной.
Рис. 11. Пример нарушения условия независимости вариаций ошибок от Xi
Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим график нормального распределения на основе точечного графика, на вертикальной оси которого отложены значения остатков, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). Для построения такого графика значения остатков должны быть упорядочены по возрастанию (рис. 12). График нормального распределения может быть построен одним кликом с помощью Пакета анализа Excel – просто поставьте соответствующую галочку в окне Регрессия (см. рис. 10, самый низ окна Регрессия – опция График нормальной вероятности).
Рис. 12. График нормального распределения для остатков
Без визуализации данных (с помощью гистограммы, диаграммы «ствол и листья», блочной диаграммы или графика как на рис. 12) проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.
Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независимости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (см. ниже). Если данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени, гипотезу об их независимости проверять не имеет смысла.
Измерение автокорреляции: статистика Дурбина–Уотсона
Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией. Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.
Распознавание автокорреляции с помощью графика остатков. Для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером. Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель (рис. 13).
Рис. 13. Количество клиентов и объемы продаж за 15 недель
Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Построим регрессию с использованием Пакета анализа; включим вывод Остатков, но не будем включать График остатков (рис. 14).
Рис. 14. Параметры линейной регрессии, полученные с использованием Пакета анализа
Анализ рис. 14 показывает, что r2 = 0,657. Это значит, что 65,7% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг b0 переменной Y равен –16,032, а наклон b1 = 0,0308. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 15).
Рис. 15. Зависимость остатков от времени
Анализ рис. 15 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу о независимости остатков следует отклонить.
Статистика Дурбина-Уотсона. Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона. Эта статистика оценивает корреляцию между соседними остатками:
где еi — остаток, соответствующий i-му периоду времени.
Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части. Числитель представляет собой сумму квадратов разностей между соседними остатками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является суммой квадратов остатков. Вот, что по этому поводу написано в Википедии:
где ρ1 – коэффициент автокорреляции; если ρ1 = 0 (нет автокорреляции), D ≈ 2; если ρ1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ1 = -1 (отрицательная автокорреляции), D ≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями dL и dU для заданного числа наблюдений n, числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < dL, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > dU, гипотеза не отвергается (то есть автокорреляция отсутствует); если dL < D < dU, нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с dL и dU сравнивается не сам коэффициент D, а выражение (4 – D).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D = 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (dLи dU), зависящими от числа наблюдений n и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, dL= 1,08 и dU = 1,36. Поскольку D = 0,883 < dL= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t-критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y. Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = 0 (нет линейной зависимости), Н1: β1 = 0 (есть линейная зависимость). По определению t-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11) t = (b1 – β1) / Sb1
где b1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t-критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t-критерия, полученные с помощью Пакета анализа Excel
Поскольку число магазинов n = 14 (см. рис.3), критическое значение t-статистики при уровне значимости α = 0,05 можно найти по формуле: tL =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; tU =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t-статистика = 10,64 > tU = 2,1788 (рис. 19), нулевая гипотеза Н0 отклоняется. С другой стороны, р-значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н0 снова отклоняется. Тот факт, что р-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение F-критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. Однофакторный дисперсионный анализ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных k), к дисперсии ошибок (MSE = SYX2).
По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR/MSE, где MSR = SSR / k, MSE = SSE/(n– k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F-распределение с k и n – k – 1 степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > FU, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t-критерию F-критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F-статистике – на рис. 21.
Рис. 21. Результаты применения F-критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р-значение близко к нулю (ячейка Значимость F). Если уровень значимости α равен 0,05, определить критическое значение F-распределения с одной и 12 степенями свободы можно по формуле FU =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > FU = 4,7472, причем р-значение близко к 0 < 0,05, нулевая гипотеза Н0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β1. Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β1 и убедиться, что гипотетическое значение β1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β1, является выборочный наклон b1, а его границами — величины b1 ± tn–2Sb1
Как показано на рис. 18, b1 = +1,670, n = 14, Sb1 = 0,157. t12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b1 ± tn–2Sb1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование t-критерия для коэффициента корреляции. Ранее был введен коэффициент корреляции r, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: ρ = 0 (нет корреляции), Н1: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r = +, если b1 > 0, r = –, если b1 < 0. Тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
В задаче о сети магазинов Sunflowers r2 = 0,904, а b1— +1,670 (см. рис. 4). Поскольку b1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.
Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов) регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. Ранее для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X:
где , = b0 + b1Xi – предсказанное значение переменное Y при X = Xi, SYX – среднеквадратичная ошибка, n – объем выборки, Xi — заданное значение переменной X, µY|X=Xi – математическое ожидание переменной Y при Х = Хi, SSX =
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений Xi. Если значение переменной Y предсказывается для величин X, близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика YX=Xi при конкретном значении переменной Xi определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х8 = 19, Y8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
- Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Предыдущая заметка Критерий согласия «хи-квадрат»
Следующая заметка Введение в множественную регрессию
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
При выполнении самых разных иногда анализов возникает потребность в поиске и определении с выполнением вычислительных операций для непарных чисел в Excel. Чтобы не искать непарные числа вручную рационально автоматизировать этот процесс с помощью формулы где главную роль играет функция ЕСЛИ.
Пример работы функции ОСТАТ в Excel
Для примера возьмем магазин с летними и зимними автомобильными шинами. Клиент покупает 4 или 2 шины для своего автомобиля. Если на остатках в складе магазина встречаются непарные числа, то скорее всего на складе пересорт товара.
Следует сбалансировать все остатки до переучета. Для этого нужно определить все позиции с непарным количеством товара на остатках. Если склад большой, то список наименований шин с различными маркировками и параметрами (размеры, диаметр, производитель и т.д.) может содержать тысячи позиций. Поэтому вручную искать все «грехи» складовщиков – это трудозатратный процесс, требующий много времени. Рекомендуем быстрое решение:
Чтобы найти все непарные числа:
- В ячейку C2 введите следующую формулу:
- Скопируйте эту формулу на против всех ячеек столбца «Остаток».
На против всех позиций товара, которые имеют сомнительные остатки на складе, отображается слово «Пересорт».
Принцип работы формулы для поиска непарных чисел:
В первом аргументе главной функции ЕСЛИ применяется функция ОСТАТ. В данном примере она возвращает нам остаток от деления на число 2. Если остаток от деления не равно нулю (так происходит в случае деления непарных чисел на 2), формулой сразу же возвращается текстовое значение «Пересорт». В противные случаи ячейка остается пустой.
Не сложно догадаться как будет выглядеть формула для поиска парных чисел:
Если остаток от деления = 0, то число парное.
Использование функции ОСТАТ в условном форматировании
Поэтому же принципу можем легко выделить цветом все непарные числа, чтобы визуальный анализ остатков был максимально читабельным и комфортным. Для этого будем использовать функцию МОД с такими же аргументами в условном форматировании:
- Выделите диапазон B2:B11 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило».
- В появившемся диалоговом окне «Создание правила форматирования» выберите опцию «Использовать формулу для определения форматируемых ячеек» и в поле ввода введите формулу:
- Нажмите на кнопку «Формат», чтобы задать оформление для ячеек с неправильными остатками.
- На всех открытых диалоговых окнах нажмите на кнопку ОК.
Теперь наш отчет по остаткам легко читается и сам находит неправильные остатки.
Это материал служит продолжением серии моих предыдущих статей по эффективному управлению товарными запасами. Сегодня мы разберем тему, как в excel вести учет товара. Как в одну таблицу excel свести товарные остатки, заказы, ранее заказанные товары, АВС анализ и так далее.
Несомненно, эту статью можно рассматривать, как отдельный материал для учета и планирования товара и его запасов в excel. Я постараюсь все наглядно и просто показать, избегая макросов.
Содержание:
- Excel, как отличный инструмент учета товара
- Как в excel вести учет товара, самый простой шаблон
- Как в excel вести учет товара с учетом прогноза будущих продаж
- Расстановка в excel страхового запаса по АВС анализу
- Учет в excel расширенного АВС анализа
Аналитика в Excel
Итак, все начинается даже не с аналитики, а просто с упорядочивания данных по товарам. Excel, это отличный инструмент, для подобных задач. Лучшего пока не придумали. По крайней мере для малого и среднего бизнеса, это самый эффективный и доступный метод ведения товарных остатков, не говоря об аналитике запасов, АВС анализа, прогноза будущих закупок и так далее.
Мы начнем с самого простого. Затем будет углубляться и расширять возможности ведения товарного учета в excel. Каждый выберет, на каком уровне будет достаточно для своей работы.
Как в Excel вести учет товара, простой шаблон
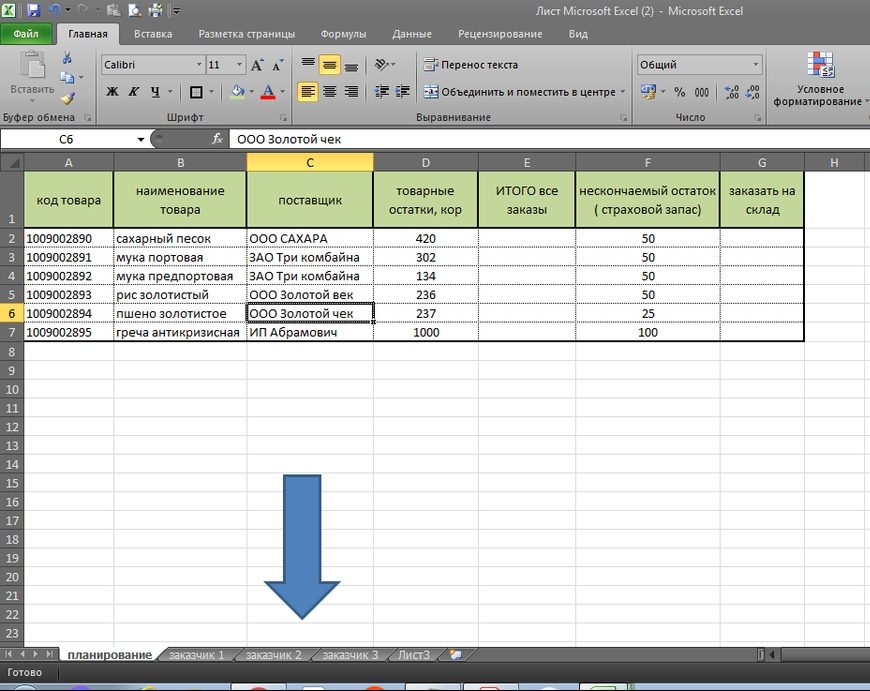
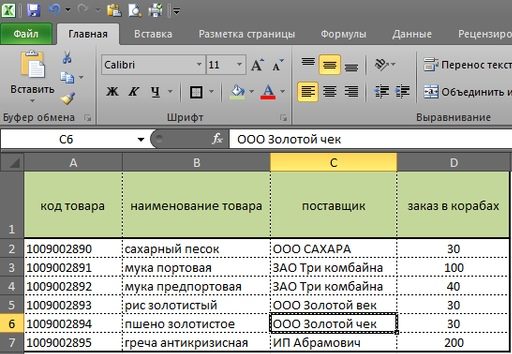
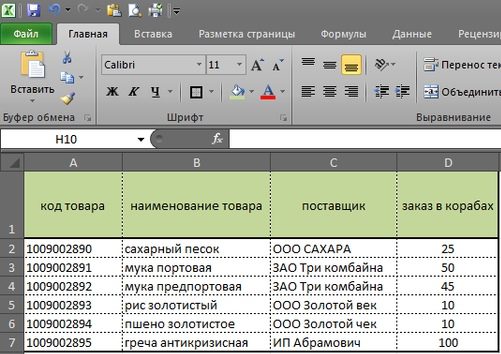
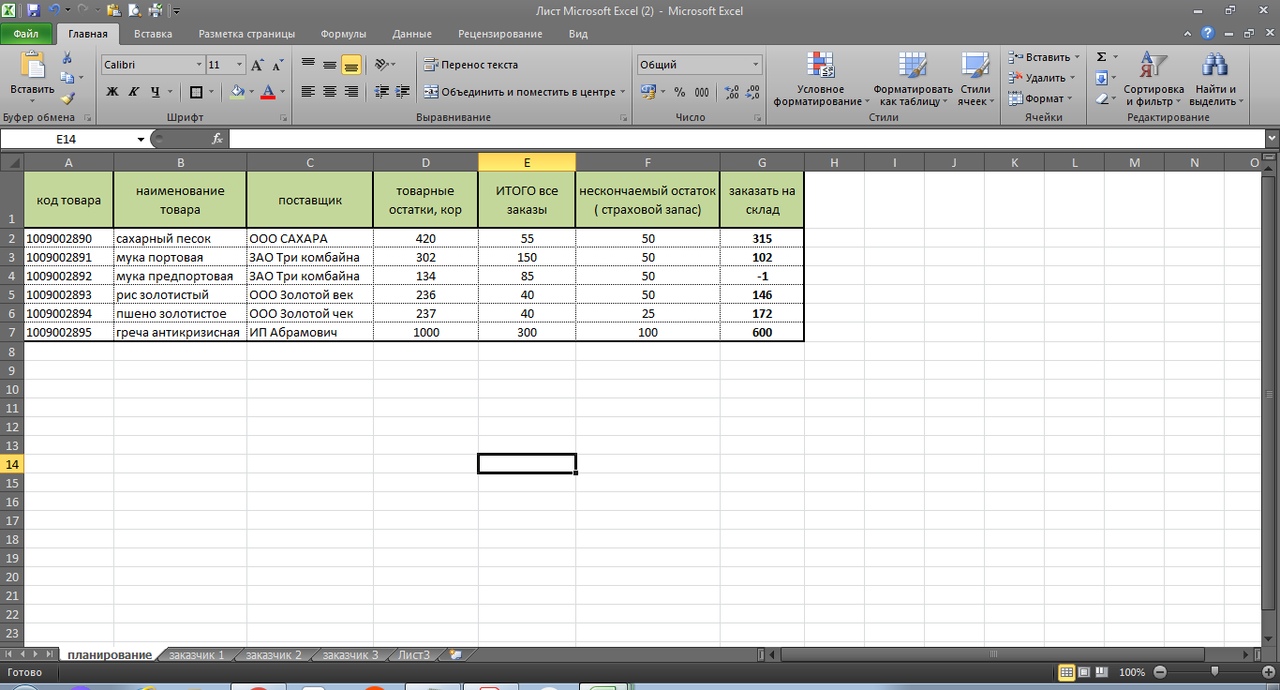
Начинаем с самого простого, а именно с того, когда организация собирает заявки с магазинов и нужно свести заказы воедино, сделать заказ поставщику. (см. рис 1)
В столбце Е, с помощью простой формулы мы сведем заявки с наших разных клиентов. Столбец F, это наш нескончаемый остаток или страховой запас. В столбец G мы получим данные, сколько нам потребуется заказать поставщику исходя из наших остатков, заявок магазинов и страхового запаса.
Синяя стрелка указывает на закладки, где «Заказчик 1», «Заказчик 2» и так далее. Это заявки с наших магазинов или клиентов, см рис 2 и рас. 3. У каждого заказчика свое количество, в нашем случае, единица измерения — в коробах.
Теперь мы можем рассмотреть, как в excel вести учет товара, когда требуется свести заявки в одну таблицу. С помощью простой формулы, в первую очередь, мы сводим все заявки с магазинов в столбец Е., см рис 4.
=(‘заказчик 1′!D2+’заказчик 2’!D2)
Протягиваем формулу вниз по столбцу Е и получаем данные по всем товарам. см. рис 5. Мы получили сводную информацию со всех магазинов. (здесь учтено только, 2 магазина, но думаю, суть понятна)
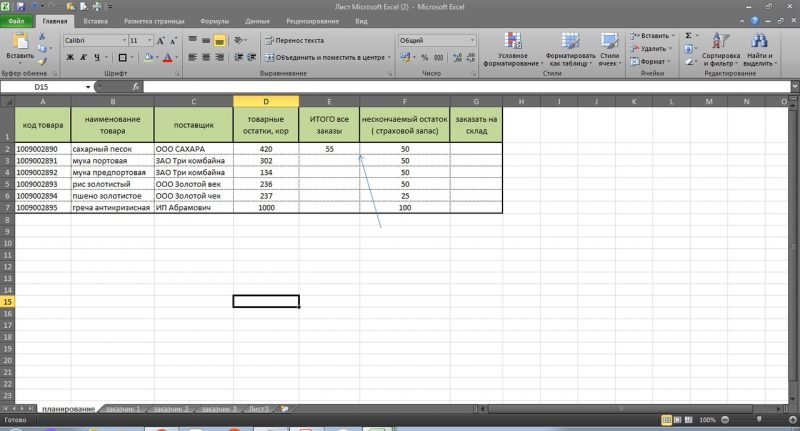
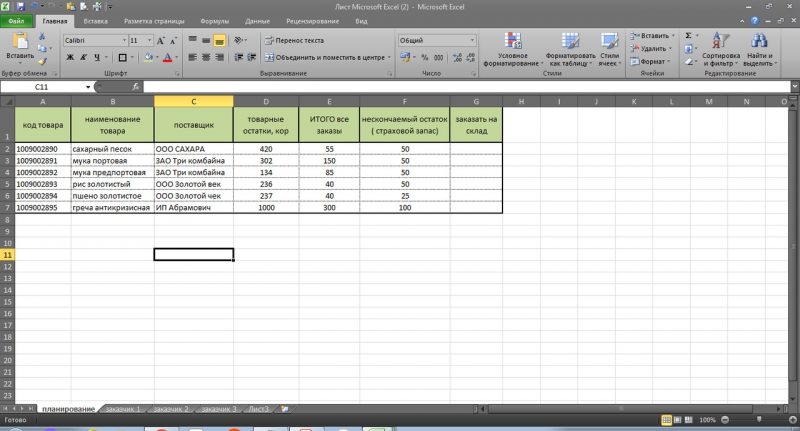
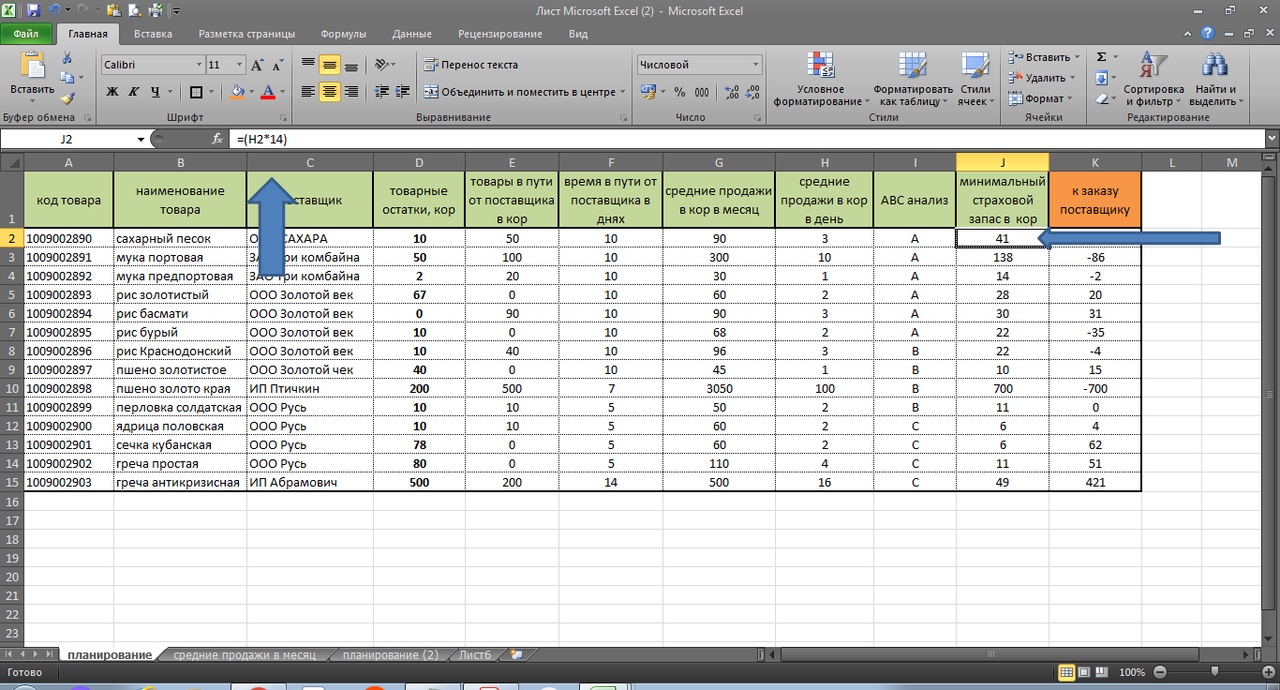
Теперь у нам остается учесть товарные остатки, и заданный минимальный страховой запас для того, что бы сделать заказ поставщику на нужное нам количество. Также прописываем простую формулу:
=(D2-E2)-F2
протягиваем формулу вниз по столбцу и получаем к заказу поставщику 1 короб по муке предпортовой. По остальным товарам есть достаточный товарный запас.
Обратите внимание, что F (страховой запас) мы также вычли из остатка, что бы он не учитывался в полученных цифрах к заказу.
Повторюсь, здесь лишь суть расчета.
Мы понимаем, что заказывать 1 короб, наверное нет смысла. Наш страховой запас, в данном случае не пострадает из-за одной штуки.
Теперь, мы переходим к более сложным расчетам, когда мы будем основываться на анализе продаж прошлых периодов, с учетом расширенного АВС анализа, страхового запаса, товаров в пути и так далее.
Как в Excel вести учет товара на основе продаж прошлых периодов
Как управлять складскими запасами и строить прогноз закупок в Excel основываясь на продажах прошлых периодов, применяя АВС анализ и другие инструменты, это уже более сложная задача, но и гораздо более интересная.
Я здесь также приведу суть, формулы, логику построения управления товарными запасами в Excel.
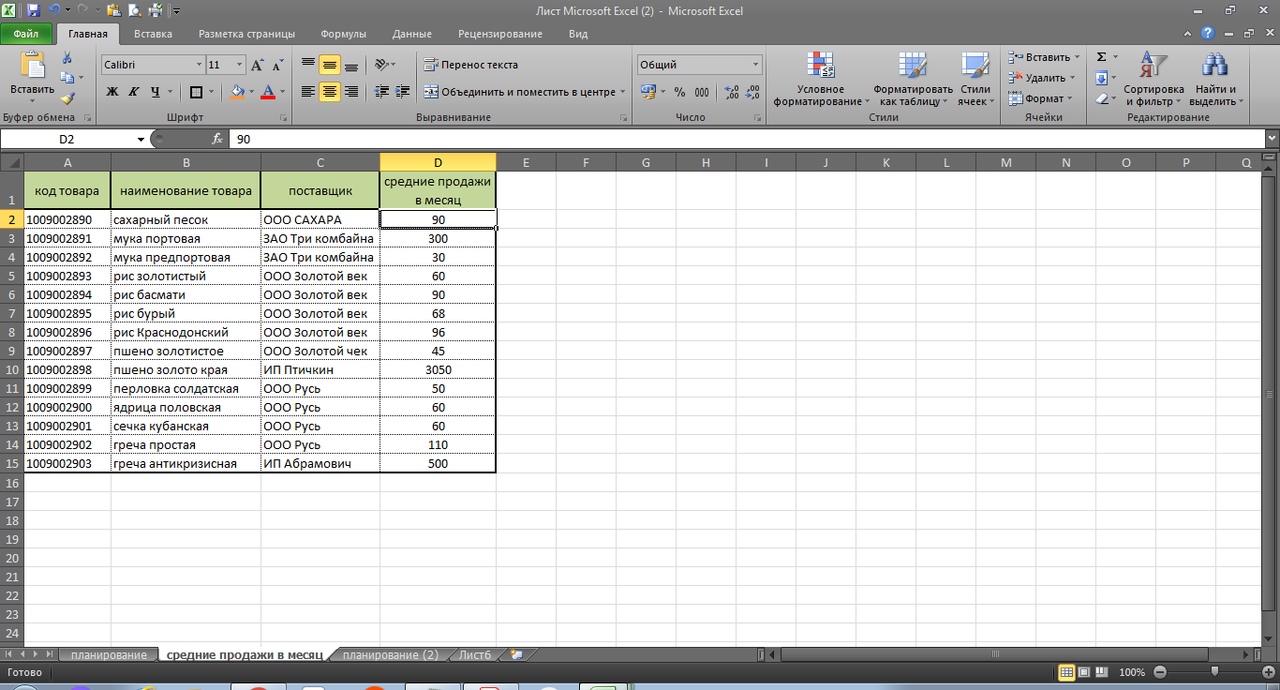
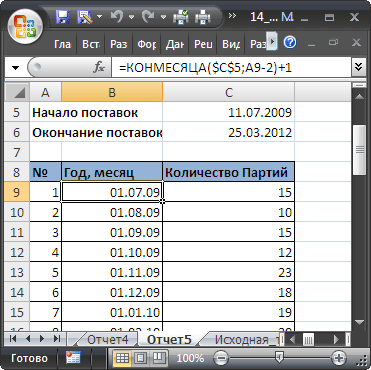
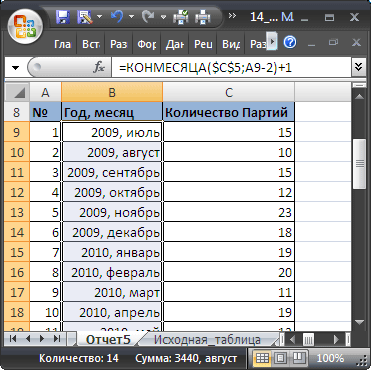
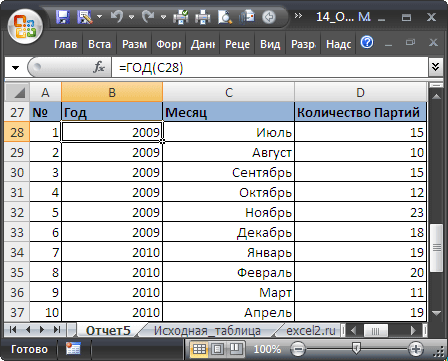
Итак, у мы выгружаем с базы средние продажи в месяц. Пока в данном варианте будем считать, что они стабильны.
Далее их подтягиваем средние продажи в столбец G нашего планировщика, то есть в сводный файл.
Делаем это с помощью формулы ВПР.
=ВПР(A:A;’средние продажи в месяц’!A:D;4;0)
Суть этой формулы заключается в том, что требуемые данные подтягиваются по уникальному коду или другому значению, не зависимо от того, в каком порядке они находятся в источнике денных.
Также мы можем подтянуть и другие требуемые данные, например нужную нам информацию, что уже везется нам поставщиком, как товары в пути. Мы их также обязательно должны учесть.
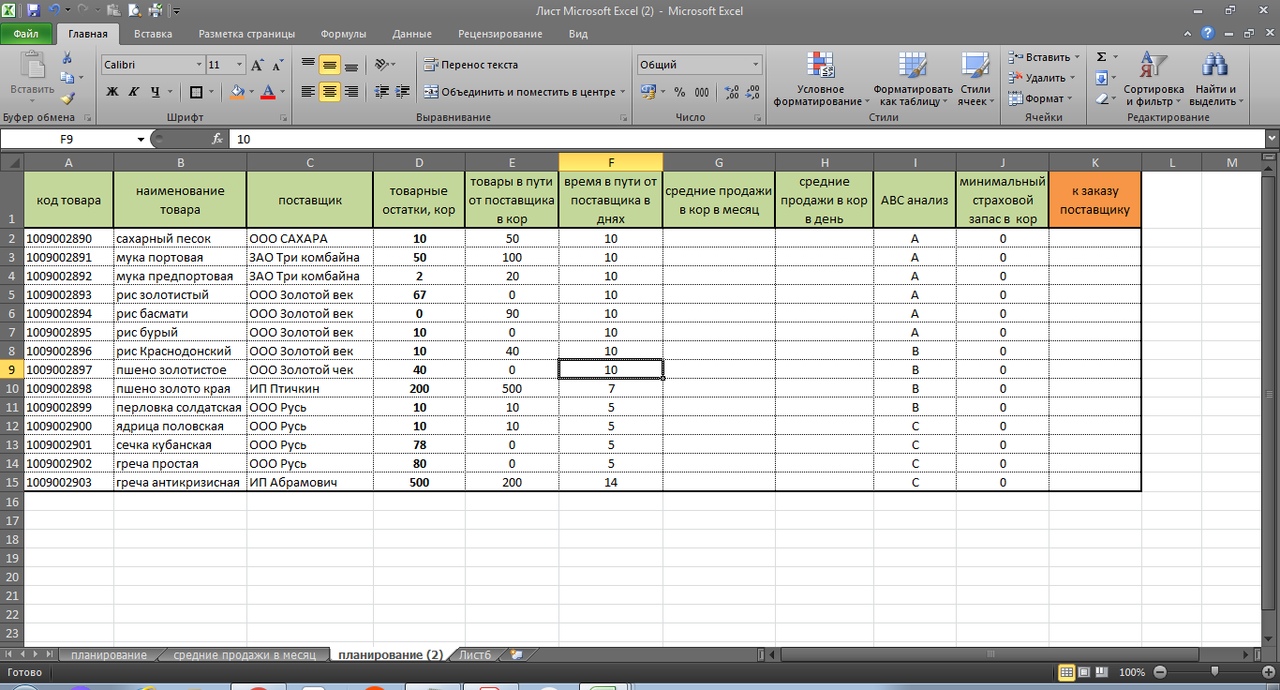
В итоге, у нас получается вот такая картина:
Первое. Средние продажи в месяц, мы превратили, в том числе для удобства в средние продажи в день, простой формулой = G/30,5 (см. рис 9). Средние продажи в день — столбец H
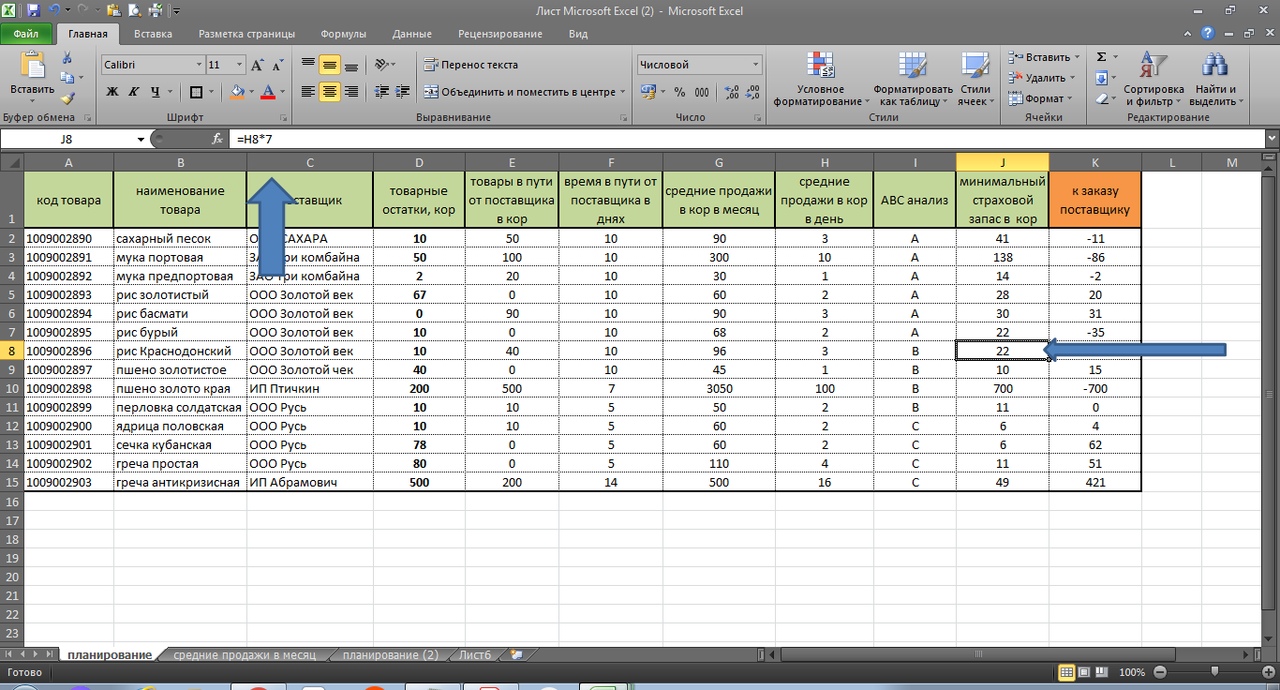
Второе. Мы учли АВС анализ по товарам. И ранжировали страховой запас относительно важности товара по рейтингу АВС анализа. (Эту важную и интересную тему по оптимизации товарных запасов мы разбирали в предыдущей статье)
По товарам рейтинга А, (где А — наиболее прибыльный товар) мы заложили страховой запас в днях относительно средних дневных продаж в 14 дней. Смотрим первую строку и у нас получилось:
3 коробки продажи в день *14 дней продаж = 42 дня. (41 день у нас потому, что Excel округлил при расчете 90 коробов в месяц/30,5 дней в месяце). См. формулу
=(H2*14)
Третье. По рейтингу товара В, мы заложили 7 дней страхового запаса. См рис 11. ( По товарам категории С мы заложили страховой запас всего 3 дня)
Вывод
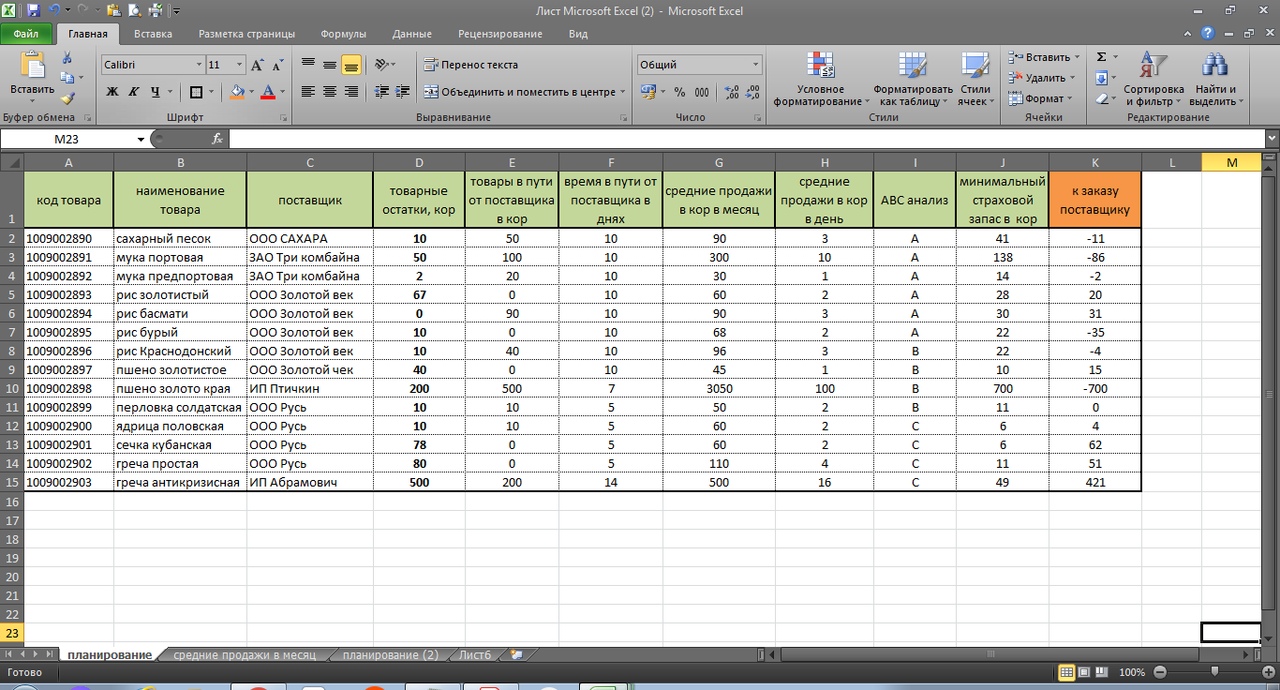
Таким образом, сахарного песка (см. первую строчку таблицы) мы должны заказать 11 коробов. Здесь учтены 50 коробов в пути, 10 дней поставки при средних продажах 3 короба в день).
Товарный остаток 10 коробов + 50 коробов в пути = 60 коробов запаса. За 10 дней продажи составят 30 коробов (10*3). Страховой запас у нас составил 41 короб. В итоге, 60 — 30 — 42 = минус 11 коробов, которые мы должны заказать у поставщика.
Для удобства можно (-11) умножить в Ecxel на минус 1. Тогда у нас получиться положительное значение.
Конечно, здесь показал только образец и суть как вести учет товара и запасов в Excel. Но уже большой шаг вперед относительно субъективных ощущений и возможностей небольших предприятий. И все можно детализировать и уточнять. В следующей главе мы рассмотрим это.
Складской учет товаров в Excel с расширенным АВС анализом.
Складской учет товаров в Excel можно делать аналитически все более углубленным по мере навыков и необходимости.
В предыдущей главе мы использовали для удовлетворения спроса покупателя и оптимизации страхового запаса, АВС анализ, когда по категории А мы сделали бОльший страховой запас, а по категории С, — минимальный страховой запас. Если в первой главе, ( в самом простом варианте) страховой запас мы создали вручную, во второй главе — отталкивались от среднедневных продаж. Страховой запас формировали в днях. Об этом более подробно мы говорили в моей предыдущей статье.
Здесь АВС анализ сделаем более углубленным, что поможет нам быть еще более точным.
Если ранжирование товара по АВС анализу, у нас велось с точки зрения прибыльности каждого товара, где А, это наиболее прибыльный товар, В — товар со средней прибыльностью и С — с наименьшей прибыльностью, то теперь АВС дополнительно ранжируем по следующим критериям:
«А» — товар с каждодневным спросом
«В» — товар со средним спросом ( например 7-15 дней в месяц)
«С» — товар с редким спросом ( менее 7 дней в месяц)
Этот же принцип можно использовать не по количеству дней в месяце, а по количеству месяцев в году.
И еще зададим один критерий. Это количество обращений к нам, к поставщику.
Здесь количество обращений, это сколько отдельных заказов, покупок было сделано по каждому товару не зависимо от количества, стоимости и прибыльности товара. Здесь мы видим картину, насколько наши покупатели часто обращаются к нам по каждому товару. Об этом подробно говорили в моей статье «Прогноз спроса в управлении товарными запасами. Анализ XYZ и другие инструменты эффективного анализа»
“А” – количество обращений от 500 и выше
“В” – 150 – 499 обращений.
“С” – менее 150 обращений в месяц.
В итоге, товары имеющие рейтинг ААА, это самый ТОП товаров, по которым требуется особое внимание.
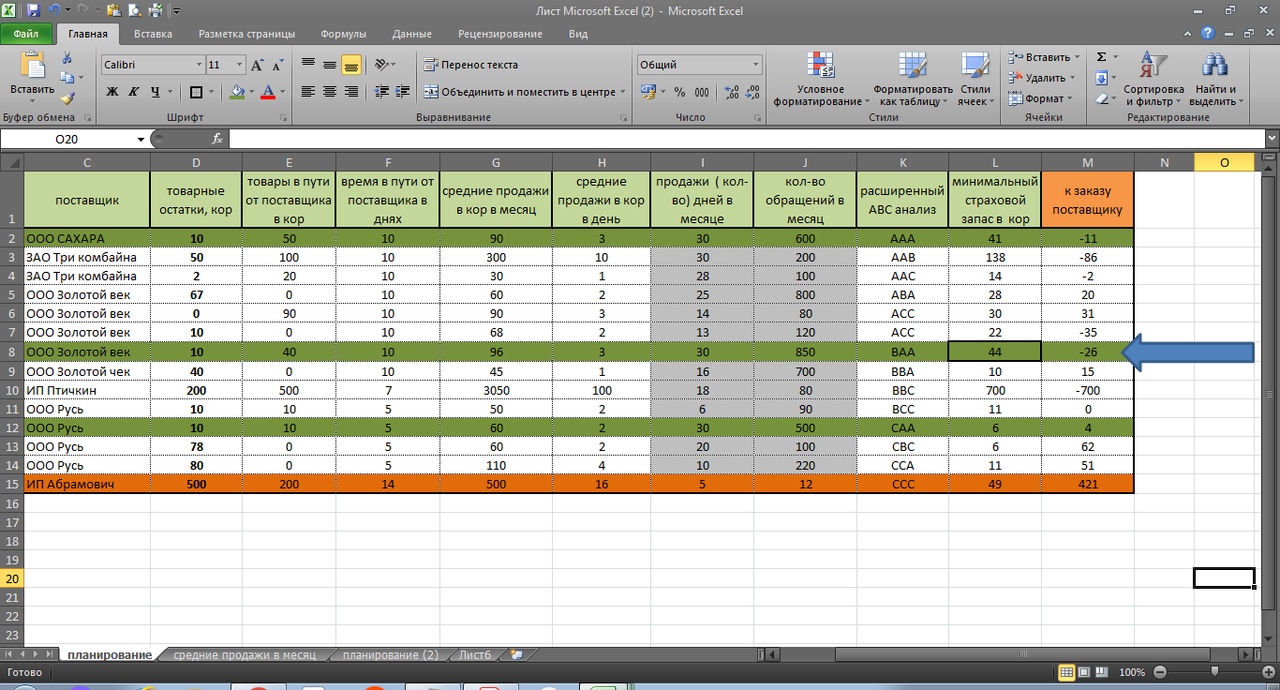
Расширенный АВС анализ в таблице Excel
См. рис. 12. Мы выделили серым цветом столбцы, где учли товар по АВС в части постоянного спроса в днях и по количеству обращений. Также эти данные можем перенести из выгруженных данных нашей базы с помощью формулы ВПР.
Теперь у нас рейтинг АВС анализа видоизменился и это может привести нас к пересмотру страхового запаса.
Обратите внимание на выделенную зеленым первую строку. Товар имеет рейтинг ААА. Также смотрим на восьмую строку. Здесь рейтинг товара ВАА. Может имеет смысл страховой запас этого товару сделать больше, чем заданных 7 дней?
Для наглядности, так и сделаем, присвоив этому товару страховой запас на 14 дней. Теперь по нему страховой запас выше, чем это было ранее. 44 коробки против 22 коробок. См. рис. 11.
А что на счет рейтинга «ССС»? Нужен ли по этому товару страховой запас? И вообще, при нехватке оборотных средств и площадей склада, нужен ли этот товар в нашей номенклатуре?
Также интересно по товару с рейтингом САА.
Прибыль не высокая, но именно к нам идут за этим товаром. Я бы уделил также особое внимание этому товару. За счет его высокой оборачиваемости, достигаемой, в том числе, за счет его постоянного наличия, мы и повышаем прибыль.
Управление товарными запасами в Excel. Заключение
В аналитику Excel можно и включить товар с признаком сезонности. Можно включить сравнение отклонений заказов с наших филиалов или магазинов, когда мы сразу же увидим несоизмеримо маленький или большой заказ. Это защитит нас от дефицита или излишнего товарного запаса.
Не важно сколько машин или партий товаров у нас в пути, и когда по каждому поставщику свой цикл поставки. Можно учесть многое, что конечном счете, оптимизирует наши запасы и увеличивает чистую прибыль.
Это лишь степень владения Excel. Сегодня мы разбирали достаточно простые таблицы.
Одна из следующих моих публикаций, будет посвящена, как, с помощью нескольких простых формул Excel можно быстро обрабатывать большой массив данных.
Буду рад, если по вопросу, как в Excel вести учет товара, был Вам полезен.
Пишите в комментариях, задавайте вопросы. Могу рассмотреть вариант взаимовыгодного сотрудничества по формированию и налаживанию учета товара и запасов в Excel. Эта работа для меня любима и интересна.
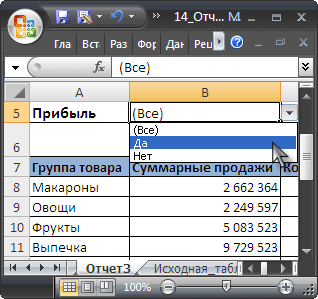
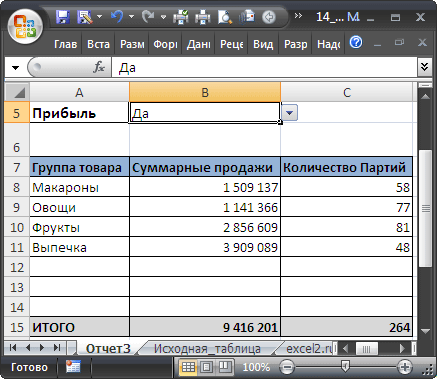
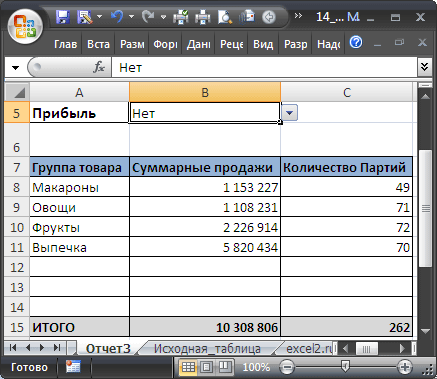
Для анализа больших и сложных таблиц обычно используют
Сводные таблицы
. С помощью формул также можно осуществить группировку и анализ имеющихся данных. Создадим несложные отчеты с помощью формул.
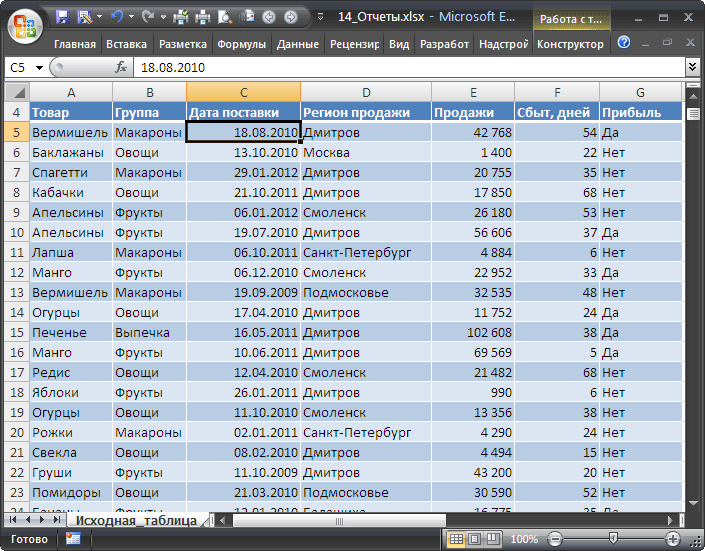
В качестве исходной будем использовать
таблицу в формате EXCEL 2007
(
), содержащую информацию о продажах партий продуктов. В строках таблицы приведены данные о поставке партии продукта и его сбыте. Аналогичная таблица использовалась в статье
Сводные таблицы
.
В таблице имеются столбцы:
Товар
– наименование партии товара, например, «
Апельсины
»;
Группа
– группа товара, например, «
Апельсины
» входят в группу «
Фрукты
»;
Дата поставки
– Дата поставки Товара Поставщиком;
Регион продажи
– Регион, в котором была реализована партия Товара;
Продажи
– Стоимость, по которой удалось реализовать партию Товара;
Сбыт
– срок фактической реализации Товара в Регионе (в днях);
Прибыль
– отметка о том, была ли получена прибыль от реализованной партии Товара.
Через
Диспетчер имен
откорректируем
имя
таблицы на «
Исходная_таблица
» (см.
файл примера
).
С помощью формул создадим 5 несложных отчетов, которые разместим на отдельных листах.
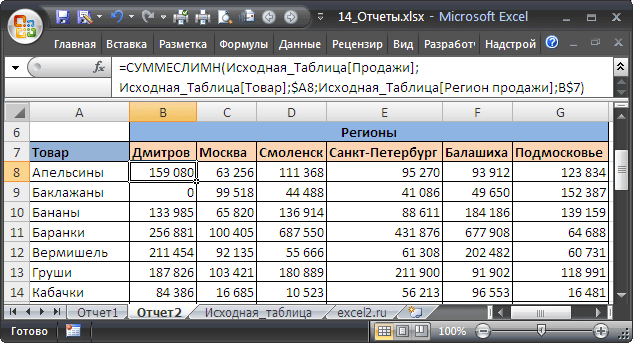
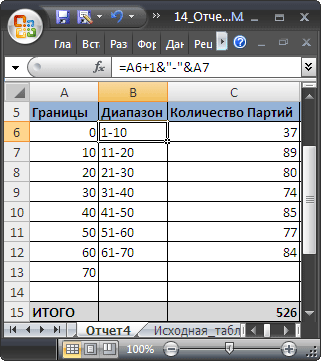
Отчет №1 Суммарные продажи Товаров
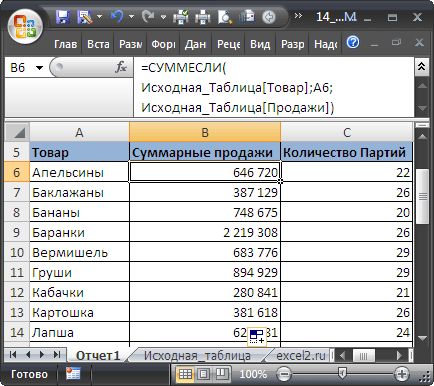
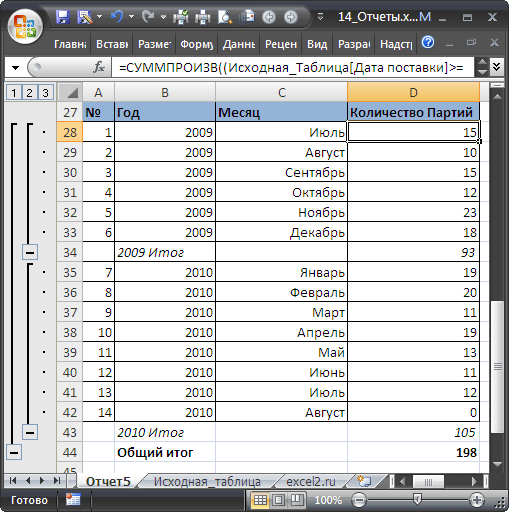
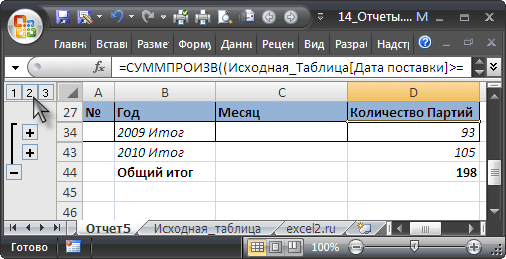
Найдем суммарные продажи каждого Товара. Задача решается достаточно просто с помощью функции
СУММЕСЛИ()
, однако само построение отчета требует определенных навыков работы с некоторыми средствами EXCEL.
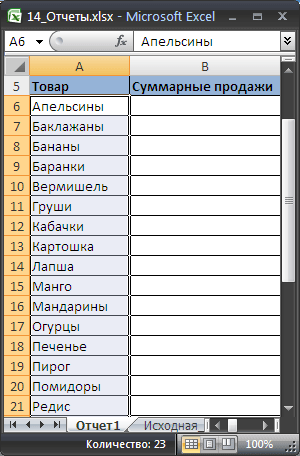
Итак, приступим. Для начала нам необходимо сформировать перечень названий Товаров. Т.к. в столбце Товар исходной таблицы названия повторяются, то нам нужно из него выбрать только
уникальные
значения. Это можно сделать несколькими способами: формулами (см. статью
Отбор уникальных значений
), через меню
или с помощью
Расширенного фильтра
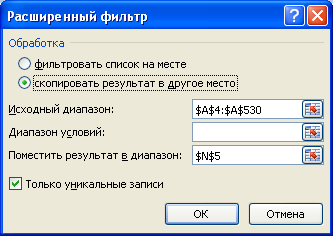
. Если воспользоваться первым способом, то при добавлении новых Товаров в исходную таблицу, новые названия будут включаться в список автоматически. Но, здесь для простоты воспользуемся вторым способом. Для этого:
- Перейдите на лист с исходной таблицей;
-
Вызовите
Расширенный фильтр
(
);
-
Заполните поля как показано на рисунке ниже: переключатель установите в позицию
Скопировать результат в другое место
; в поле Исходный диапазон введите $A$4:$A$530; Поставьте флажок
Только уникальные записи
.
- Скопируйте полученный список на лист, в котором будет размещен отчет;
-
Отсортируйте перечень товаров (
).
Должен получиться следующий список.
В ячейке
B6
введем нижеследующую формулу, затем скопируем ее
Маркером заполнения
вниз до конца списка:
=СУММЕСЛИ(Исходная_Таблица[Товар];A6;Исходная_Таблица[Продажи])
Для того, чтобы понять сруктурированные ссылки на поля в
таблицах в формате EXCEL 2007
можно почитать Справку EXCEL (клавиша
F1
) в разделе
Основные сведения о листах и таблицах Excel > Использование таблиц Excel
.
Также можно легко подсчитать количество партий каждого Товара:
=СЧЁТЕСЛИ(Исходная_Таблица[Товар];A6)
Отчет №2 Продажи Товаров по Регионам
Найдем суммарные продажи каждого Товара в Регионах. Воспользуемся перечнем Товаров, созданного для Отчета №1. Аналогичным образом получим перечень названий Регионов (в поле Исходный диапазон
Расширенного фильтра
введите $D$4:$D$530). Скопируйте полученный вертикальный диапазон в
Буфер обмена
и
транспонируйте
его в горизонтальный. Полученный диапазон, содержащий названия Регионов, разместите в заголовке отчета.
В ячейке
B
8
введем нижеследующую формулу:
=СУММЕСЛИМН(Исходная_Таблица[Продажи]; Исходная_Таблица[Товар];$A8; Исходная_Таблица[Регион продажи];B$7)
Формула вернет суммарные продажи Товара, название которого размещено в ячейке
А8
, в Регионе из ячейки
В7
. Обратите внимание на использование
смешанной адресации
(ссылки $A8 и B$7), она понадобится при копировании формулы для остальных незаполненных ячеек таблицы.
Скопировать вышеуказанную формулу в ячейки справа с помощью
Маркера заполнения
не получится (это было сделано для Отчета №1), т.к. в этом случае в ячейке
С8
формула будет выглядеть так:
=СУММЕСЛИМН(Исходная_Таблица[Сбыт, дней]; Исходная_Таблица[Группа];$A8; Исходная_Таблица[Продажи];C$7)
Ссылки, согласно правил
относительной адресации
, теперь стали указывать на другие столбцы исходной таблицы (на те, что правее), что, естественно, не правильно. Обойти это можно, скопировав формулу из ячейки
B8
, в
Буфер обмена
, затем вставить ее в диапазон
С8:
G
8
, нажав
CTRL
+
V
. В ячейки ниже формулу можно скопировать
Маркером заполнения
.
Отчет №3 Фильтрация Товаров по прибыльности
Вернемся к исходной таблице. Каждая партия Товара либо принесла прибыль, либо не принесла (см. столбец Прибыль в исходной таблице). Подсчитаем продажи по Группам Товаров в зависимости от прибыльности. Для этого будем фильтровать с помощью формул записи исходной таблицы по полю Прибыль.
Создадим
Выпадающий (раскрывающийся) список
на основе
Проверки данных
со следующими значениями:
(Все); Да; Нет
. Если будет выбрано значение фильтра
(Все)
, то при расчете продаж будут учтены все записи исходной таблицы. Если будет выбрано значение фильтра «
Да»
, то будут учтены только прибыльные партии Товаров, если будет выбрано «
Нет»
, то только убыточные.
Суммарные продажи подсчитаем следующей
формулой массива
:
=СУММПРОИЗВ((Исходная_Таблица[Группа]=A8)* ЕСЛИ($B$5=»(Все)»;1;(Исходная_Таблица[Прибыль]=$B$5))* Исходная_Таблица[Продажи])
После ввода формулы не забудьте вместо простого нажатия клавиши
ENTER
нажать
CTRL
+
SHIFT
+
ENTER
.
Количество партий по каждой группе Товара, в зависимости от прибыльности, можно подсчитать аналогичной формулой.
=СУММПРОИЗВ((Исходная_Таблица[Группа]=A8)* ЕСЛИ($B$5=»(Все)»;1;(Исходная_Таблица[Прибыль]=$B$5)))
Так будет выглядеть отчет о продажах по Группам Товаров, принесших прибыль.
Выбрав в фильтре значение
Нет
(в ячейке
B
5
), сразу же получим отчет о продажах по Группам Товаров, принесших убытки.
Отчет №4 Статистика сроков сбыта Товаров
Вернемся к исходной таблице. Каждая партия Товара сбывалась определенное количество дней (см. столбец Сбыт в исходной таблице). Необходимо подготовить отчет о количестве партий, которые удалось сбыть за за период от 1 до 10 дней, 11-20 дней; 21-30 и т.д.
Вышеуказанные диапазоны сформируем нехитрыми формулами в столбце
B
.
Количество партий, сбытые за определенный период времени, будем подсчитывать с помощью формулы
ЧАСТОТА()
, которую нужно ввести как
формулу массива
:
=ЧАСТОТА(Исходная_Таблица[Сбыт, дней];A7:A12)
Для ввода формулы выделите диапазон
С6:С12
, затем в
Строке формул
введите вышеуказанную формулу и нажмите
CTRL
+
SHIFT
+
ENTER
.
Этот же результат можно получить с помощью обычной функции
СУММПРОИЗВ()
:
=СУММПРОИЗВ((Исходная_Таблица[Сбыт, дней]>A6)* (Исходная_Таблица[Сбыт, дней]<=A7))
Отчет №5 Статистика поставок Товаров
Теперь подготовим отчет о поставках Товаров за месяц. Сначала создадим перечень месяцев по годам. В исходной таблице самая ранняя дата поставки 11.07.2009. Вычислить ее можно с помощью формулы:
=МИН(Исходная_Таблица[Дата поставки])
Создадим перечень дат —
первых дней месяцев
, начиная с самой ранней даты поставки. Для этого воспользуемся формулой:
=КОНМЕСЯЦА($C$5;-1)+1
В результате получим перечень дат — первых дней месяцев:
Применив соответствующий формат ячеек, изменим отображение дат:
Формула для подсчета количества поставленных партий Товаров за месяц:
=СУММПРОИЗВ((Исходная_Таблица[Дата поставки]>=B9)* (Исходная_Таблица[Дата поставки]
Теперь добавим строки для подсчета суммарного количества партий по каждому году. Для этого немного изменим таблицу, выделив в отдельный столбец год, в который осуществлялась поставка, с помощью функции
ГОД()
.
Теперь для вывода
промежуточных итогов
по годам создадим структуру через пункт меню
:
- Выделите любую ячейку модифицированной таблицы;
-
Вызовите окно
Промежуточные итоги
через пункт меню
;
- Заполните поля как показано на рисунке:
После нажатия ОК, таблица будет изменена следующим образом:
Будут созданы промежуточные итоги по годам. Нажатием маленьких кнопочек в левом верхнем углу листа можно управлять отображением данных в таблице.
Резюме
:
Отчеты, аналогичные созданным, можно сделать, естественно, с помощью
Сводных таблиц
или с применением
Фильтра
к исходной таблице или с помощью других функций
БДСУММ()
,
БИЗВЛЕЧЬ()
,
БСЧЁТ()
и др. Выбор подхода зависит конкретной ситуации.