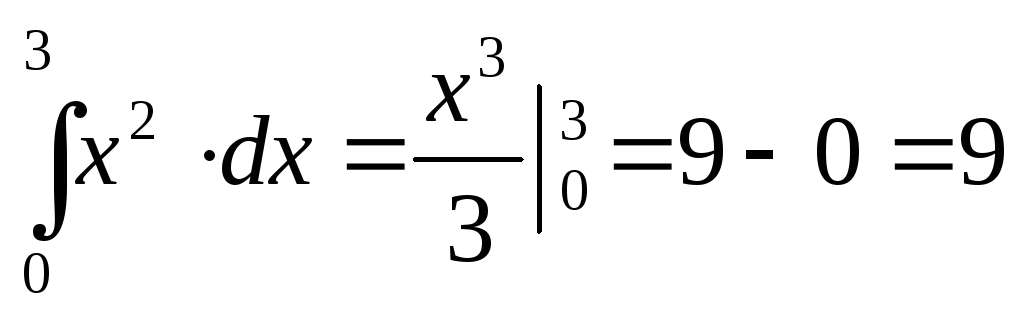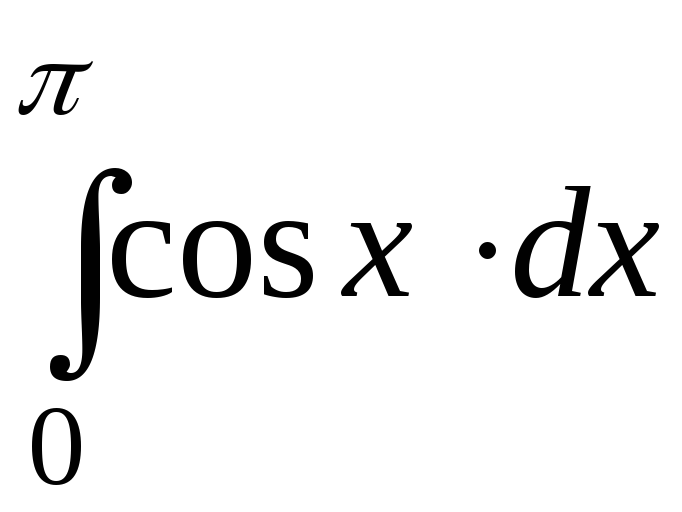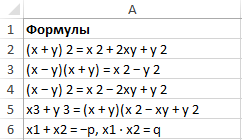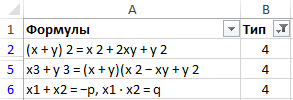Содержание
- Использование функций и вложенных функций в формулах Excel
- 6. Понятие функции в Excel.
- Как по графику определить функцию в excel
- Часть 10. Подбор формул по графику. Линия тренда
- Найти функцию по ее графику (аппроксимация)
- Решение
Использование функций и вложенных функций в формулах Excel
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления. Все функции Excel можно найти на вкладке «формулы» на ленте.
Синтаксис функции Excel
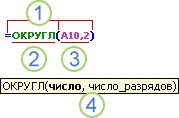
В приведенном ниже примере функции ОКРУГЛ , округленной на число в ячейке A10, показан синтаксис функции.
1. Structure. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающую круглую скобку, аргументы функции, разделенные запятыми, и закрывающая круглая скобка.
2. имя функции. Чтобы просмотреть список доступных функций, щелкните ячейку и нажмите клавиши SHIFT + F3, чтобы открыть диалоговое окно Вставка функции .
3. аргументы. Аргументы могут быть числами, текстом, логическими значениями, такими как Истина или ложь, массивами, значениями ошибок, например #N/a или ссылками на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Примечание: Вам не нужно вводить функции во все прописные буквы, например = «ОКРУГЛИТЬ», так как Excel автоматически заполнит ввод имени функции после нажатия кнопки «Добавить». Если вы неправильно наводите имя функции, например = СУМА (a1: A10), а не = сумм (a1: A10), Excel вернет #NAME? Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Ввод функций Excel
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. После выбора функции в диалоговом окне Вставка функции Excel запустит мастер функций, который выведет на экран имя функции, каждый из ее аргументов, описание функции и каждый аргумент, текущий результат функции и текущий результат всей формулы.
Для упрощения создания и редактирования формул, а также для минимизации ошибок ввода и синтаксиса используйте Автозаполнение формул. После ввода знака = (знак равенства) и начальных букв функции Excel отобразит динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих этим буквам. Затем вы можете выбрать один из раскрывающегося списка, и приложение Excel введет его автоматически.
Вложение функций Excel
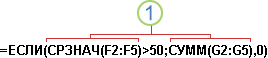
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в следующей формуле используется вложенная функция СРЗНАЧ , а результат сравнивается со значением 50.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. иметь значение ИСТИНА либо ЛОЖЬ, вложенная функция также должна возвращать логическое значение (ИСТИНА или ЛОЖЬ). В противном случае Excel выдаст ошибку «#ЗНАЧ!».
Предельное количество уровней вложенности функций . В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, функция СРЗНАЧ и функция сумм являются функциями второго уровня, если они используются в качестве аргументов функции если. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Источник
6. Понятие функции в Excel.
В математике понятие функции определяется следующим образом: функцией Y=f(X) называется зависимость переменной Y от переменной Х, если каждому значению Х соответствует некоторое значение Y. Многолетнее развитие математики привело к созданию большого количества функций: тригонометрические, логарифмические, линейные и т.д.
Функции в Excel используются для стандартных вычислений на рабочих листах. Значения, которые используются для вычисления, называются аргументами, а значения, возвращаемые функциям в качестве ответа, называются результатами. В Excel насчитывается около 400 различных функций. Каждая функция имеет своё имя и аргументы, которые записываются в круглые скобки. В качестве аргументов могут выступать: число, ячейка, диапазон, арифметическое выражение, функция.
.Работу многих функций можно продублировать формулами, например для хождения суммы чисел диапазона А1:А5 можно использовать формулу =А1+А2+А3+А4+А5, а можно и функцию =сумм(А1:А5). Самая простая и часто используемая функция- это автосуммирования, для нахождения значения которой используется кнопка в Панели инструментов
а) сложить числа диапазона A1:D1, результат записать в ячейку А1:
б) найти sinB2, результат записать в ячейку А2;
в) найти 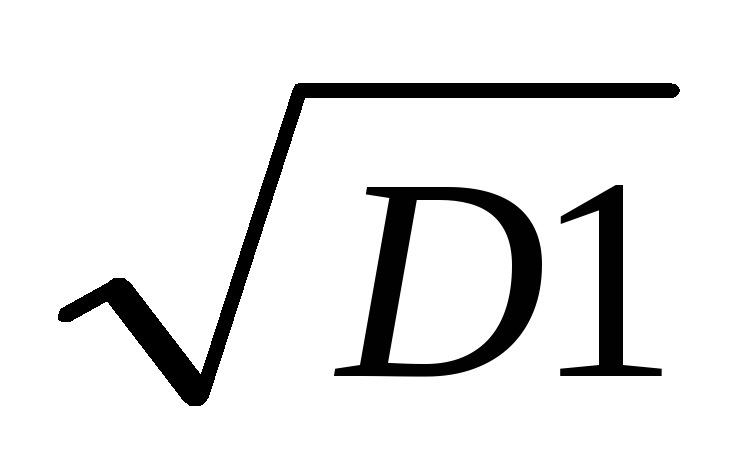
Указание: а) Курсор поставить в ячейку А1 и ввести =сумм(В1:D1);
в) в ячейку D2 ввести: =корень(D1).
Использование Мастера Функций
Не все функции в MS Excel определяются так же просто, как функция СУММ. Для некоторых из них нужно много аргументов, к тому же аргументы должны быть правильных типов и введены синтаксически правильно. Чем сложнее функция, тем сложнее правильно ёе использовать. Мастер функций существенно облегчит запись функций.
Мастера функций вызывается двумя способами:
Щелчок по кнопке fx в Панели инструментов
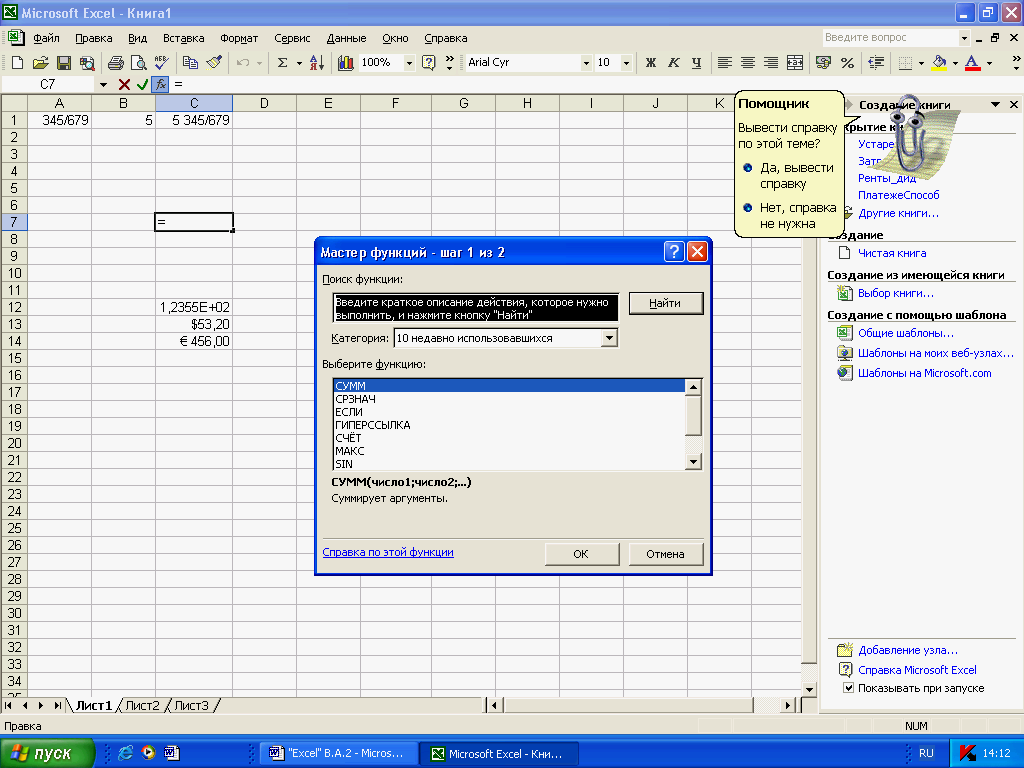
После вызова Мастера функций на экране появится окно.
отобразит список функций с их описанием;
на каждом шагу Мастер подскажет, какое количество и каких типов аргументы следует использовать;
предложит компактное описание каждой функции и ее аргументов;
поможет отредактировать уже имеющиеся на рабочем листе функции;
сформирует функцию с необходимыми аргументами, а затем поместит в выделенную ячейку.
Пример 10. Дан фрагмент таблицы
1) Найти максимальный, минимальный элемент столбца А, результат записать в ячейку А11 и А12 соответственно;
2) Найти среднее арифметическое диапазона А1:А9, результат записать в А13;
3) Найти значения синуса, косинуса и тангенса от содержимого ячейки В1, результат записать в ячейки В2, В3, В4 соответственно.;
4) В ячейку С1 записать 27% ( ячейка С1 имеет процентный формат);
5) Увеличить каждую ячейку диапазона А1:А9 на 27%, результат записать в столбец D;
6) Найти сумму положительных и отрицательных элементов диапазона Е1:Е9. Результатзаписать в ячейки Е11, Е12 соответственно;
7) Отрицательные элементы диапазона Е1:Е9 возвести в квадрат, положительные элементы оставить без изменения. Результат поместить в диапазон F1:F9.
Указания: 5) Для ячейки D1 задать формулу = А1+ А1*$C$1, раскопировать ячейку D1 в диапазон D1:D9.;
6) Для нахождения положительных элементов курсор поставить в ячейку Е11, вызвать Мастер функций (щелкнуть по кнопкеfx вПанели инструментов).В поле «Категория» выбрать Математические, в поле Функция выбрать СУММЕСЛИ. Щелкнуть по кнопке ОК. В появившемся диалоговом окне в поле Диапазон записать $E$1:$E$9 (или перейти на рабочий лист и выделить диапазон Е1:Е9), в поле Условия записать >0. Щелкнуть по кнопке ОК (Готово);
Для нахождения суммы отрицательных элементов в поле Условия записать ^ 2 Нажимаем клавишу Enter. В ячейке В2 появляется 0. Теперь необходимо раскопировать формулу из ячейки В2 в диапазон В2:В32;
В результате должна быть получена таблица данных для нахождения интеграла;
В ячейке В34 сформируем значение вычисляемого интеграла, т.е .в ячейке В34 найдем приближенное значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу = 0,1*((В2 + В32)/2 +сумм(В3:В31)). В ячейке В34 появляется приближенное значение искомого интеграла (9,005).
Найдем аналитически значения интеграла:
Сравнивая приближенное значение с аналитическим можно видеть, что абсолютная ошибка приближения метода трапеций в данном случае вполне приемлемая — 0,005.
Вычислите интеграл
Пример14.Вычислить промежуток времени между двумя датами (в числовом формате).
Источник
Как по графику определить функцию в excel
Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
расчет.xlsx (15.9 Кб, 22 просмотров)
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
расчет (1).xlsx (16.1 Кб, 55 просмотров)
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
Источник
Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Вложения
| расчет.xlsx (15.9 Кб, 22 просмотров) |
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
Вложения
| расчет (1).xlsx (16.1 Кб, 55 просмотров) |
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
Электронные таблицы EXCEL можно использовать при
изучении многих разделов физики, математики и
других предметов. Одной из данных тем является
математическая тема: “Анализ элементарных
функций”. Данная работа посвящена использованию
электронных таблиц EXCEL в анализе элементарных
функций.
Рис. 1 (см. Приложение 2)
На рис.1 представлена некоторая функция,
заданная с помощью таблицы, построение которой
приведено в Приложении 1.
Особенность анализа функций с помощью
электронных таблиц заключается в том, что анализ
проводится на дискретной информации.
Действительно, количество значений исследуемой
функции конечно и дано (как правило) с некоторым
постоянным шагом по аргументу.
При анализе исходной функции необходимо решить
следующие задачи:
- определение максимума (минимума) данной функции
на заданном интервале, - определение возрастания и/или убывания функции
на заданном интервале, - определение четности заданной функции,
- определение периодичности заданной функции,
- определение значения первой производной данной
функции и наличия экстремумов.
Для решения этих задач потребуется построить
таблицы ВводаИсходнойИнформации, таблицы
ВыводаРезультатов, Расчетной таблицы для
обработки информации и дополнительно построим
Вспомогательную таблицу. Таблицу
ВводаИсходнойИнформации и основу Расчетной
таблицу построены при введении значений
исследуемой функции в Приложении 1 и показанной
на рис.1. Построим решения задач анализа.
Приложение 1
Задача 1.
Для заданной функции на заданном интервале
аргумента определить ее минимальное и
максимальное значения.
Решение.
Для решения этой задачи построим таблицу
ВыводаРезультатов в виде
D E 1 комментарии Значения 2 Макс f(X) <формула> 3 Мин f(X) <формула>
В мастере функций Excel имеются функции МАКС(…) и
МИН(…), позволяющие решить нашу задачу. Для этого
необходимо в ячейки Е2 и Е3 ввести соответственно
формулы:
E2 => [=МАКС(с10:с50)]
и
E3 => [=МИН(с10:с50)]
Примечание. Если “протяжка” велась до
другой строки, то в интервале ссылок указать
соответствующий номер строки.
ЗАДАЧА РЕШЕНА.
Задача 2.
Определение возрастания и/или убывания функции
на заданном интервале.
Решение.
Для решения данной задачи в расчетной таблице
необходимо построить столбец D, в котором знак
будет указывать на возрастание или убывание
функции в данной точке. Для этого в ячейку D11
введем формулу
D11 => [=ЕСЛИ(a11<>””;ЗНАК(D11-D10);””)]
и “протянем” ее до строки №50.
И там, где знак положительный, функция
возрастает, а там, где знак отрицательный,
функция – убывает.
Далее построим вспомогательную таблицу, в
которой определим количество признаков
возрастания и убывания функции
F G 1 КОММЕНТАРИИ ЗНАЧЕНИЯ 2 Признак возрастания <формула> 3 Признак убывания <формула>
Для этого в ячейки g2 и g3 соответственно вводим
формулы:
G2 => [=СуммЕсли(d11:d50;”>0”)]
G3 => [=СуммЕсли(d11:d50;”<0”)]
Таблицу ВыводаРезультатов дополним строкой
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 Возрастание/Убывание <формула>
И для определения характера изменения заданной
функции остается ввести в ячейку Е4 формулу:
E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)
ЗАДАЧА РЕШЕНА.
Задача 3.
Определение четности данной.
Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком четности функции является
равенство f(X) = f(-X).
Для решения данной задачи в расчетной таблице
построим дополнительный столбец. В ячейку Е10
введем формулу
E10 => [=f(b10) – f(-b10)]
и “протянуть” ее до строки №50.
Таблицу ВыводаРезультатов дополним строкой
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 Возрастание/Убывание [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 четность <формула>
В ячейку Е4 таблицы ВыводаРезультатов вводим
формулу.
E4 => [ЕСЛИ(ABS(СУММ(E10:E50))<0,000001; “ЧЕТНАЯ”;
“НЕЧЕТНАЯ”)
ЗАДАЧА РЕШЕНА.
Задача 4.
Определить является ли введенный период
периодом заданной функции.
Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком периодичности функции
является равенство f(Х) = f(X+<период>).
Для данной задачи добавим в таблице
ВводаИсходнойИнформации строку №6, в которой
введем численное значение предполагаемого
периода.
А В 1 КОММЕНТАРИИ ЗНАЧЕНИЯ 2 Xn <значение> 3 Xk <значение> 4 Shag <значение> 5 N <формула> 6 период <значение>
В ячейку В6 вводится число – предполагаемый
период заданной функции.
Далее для решения данной задачи построим
дополнительный столбец в расчетной таблице, для
этого в ячейку F11 введем формулу
F10 => [=ЕСЛИ(a10<>””;f(b10)-f(b10+$b$6);””)]
и “потягиваем” эту формулу до строки №50.
В таблице ВыводаРезультатов добавим строчку.
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 период <формула>
В ячейке Е5 необходимо ввести формулу
Е5 => [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;”не
период”)]
Если данное значение предполагаемого периода
не подходит, то его можно изменить.
ЗАДАЧА РЕШЕНА.
Задача 5.
Для заданной функции определить:
- значения первой производной данной функции,
- наличия и количество экстремумов.
Решение.
Для решения первой части задачи, то есть
определения первой производной воспользуемся ее
разностным определение.
Построим столбец. Для этого в ячейку G11 вводим
формулу:
G11 => [= ЕСЛИ(a11<>””; ABS((c11-c10)/(b11-b10));””)]
и “протягиваем ее до строки с №50.
В результате получаем разностные приближенные
значения первой производной заданной функции в
заданных точках.
Для решения второй части задачи, то есть
определения наличия и количества экстремумов на
заданной функции в таблицу ВыводаРезультатов
дополнить строкой.
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 период [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;
”не период”)]6 Количество Экстремумов. <формула>
В ячейке Е6 необходимо ввести формулу
E6 => [=СчетЕсли(g11:g50;”<0,05”)]
ЗАДАЧА РЕШЕНА.
Рис 2, см. Приложение 3
На рис.2 приведена построенная таблица
решения задач.
Предложенные в данной работе задачи можно
использовать на интегрированных уроках
информатика-математика, на уроках информатики
при изучении электронных таблиц, в частности, в
теме: “Мастер функций”.
Когда вы пишете новую формулу в Microsoft Excel, половина дела — найти правильную функцию для использования. К счастью, Excel дает вам возможность быстро найти функцию, которая вам нужна в вашей ситуации.
Доступ к инструменту «Вставить функцию»
Откройте электронную таблицу в Excel и выберите ячейку. Если вы планируете вставить функцию, как только найдете ее, выбор ячейки даст вам фору. Затем вы можете открыть функцию вставки одним из двух способов.
- Щелкните значок «Вставить функцию» (fx) в левой части строки формул.
- Перейдите на вкладку «Формулы» и нажмите «Вставить функцию» в левой части ленты.
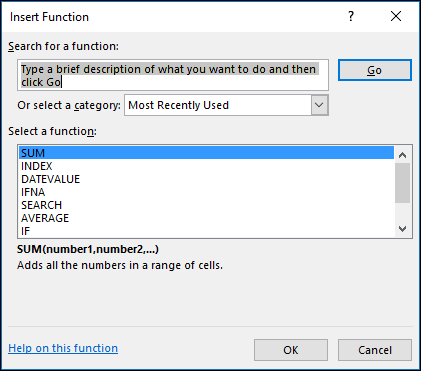
Когда откроется окно «Вставить функцию», вы увидите параметр поиска вместе с раскрывающимся списком. Это дает вам два простых метода поиска нужной функции.
Чтобы воспользоваться поиском, введите ключевое слово или фразу в поле «Поиск функции» в верхней части окна и нажмите «Перейти». Например, если вы ищете функцию, которая поможет вам в вычислениях, связанных со временем и датой, попробуйте выполнить поиск по запросу «время».
Выпадающий список также поможет вам быстро найти полезную функцию. Щелкните его рядом со словами «Или выберите категорию» и выберите категорию. Вы увидите общие параметры, такие как Финансовые, Логические, Текстовые и другие. Выбрав категорию, вы увидите все доступные в ней функции.
Еще одна категория, на которую следует обратить внимание, — это «Последние использованные». Как следует из названия, здесь вы найдете те функции, которые использовали в последнее время. Это может быть полезно, если вы использовали функцию, скажем, на прошлой неделе, но не можете вспомнить, что это было. Отметьте эту категорию, и функция может появиться у вас.
В большинстве случаев, независимо от того, выполняете ли вы поиск или выбираете категорию, это просто сужает для вас выбор. Итак, следующий шаг в поиске нужной функции — проверка ее описаний. Щелкните функцию в списке, и вы увидите ее описание и синтаксис в нижней части окна.
Например, вам может понадобиться функция квартиля. Вы можете видеть, что Excel предлагает несколько разных вариантов. Выбрав каждый из них и просмотрев их описания, вы сможете найти то, что вам нужно.
Если после того, как вы сузите выбор функций и просмотрите описания, вы все еще не уверены, подходит ли эта функция для вас, вы можете получить дополнительную помощь. Выберите функцию в списке и нажмите «Справка по этой функции» в нижнем левом углу окна.
Это приведет вас на веб-сайт поддержки Microsoft, где вы найдете функцию, которая предоставляет дополнительную информацию и примеры использования.
Используйте найденную функцию
Когда вы найдете функцию, которую хотите использовать, убедитесь, что у вас выделена ячейка, в которую вы хотите ее вставить. Затем либо дважды щелкните функцию в списке, либо выберите ее и нажмите «ОК».
Затем вы увидите инструмент «Аргументы функции», открытый для настройки формулы с помощью функции.
Вверху введите набор данных, число, массив или то, что вызывает функция.
Внизу вы еще раз увидите это краткое описание функции, но вы также увидите дополнительные детали и результат окончательной формулы.
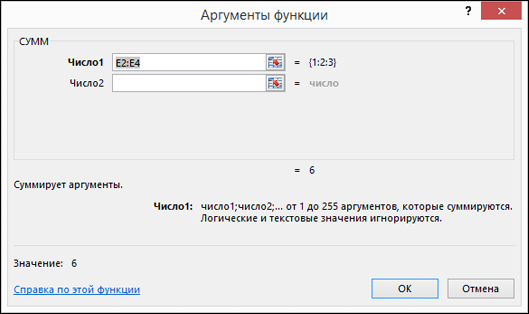
Давайте посмотрим на простой пример. Здесь мы выбрали функцию СУММ. В окне «Аргументы функции» мы ввели диапазон ячеек в поле «Число1». Вы можете видеть справа от поля значения в этих ячейках, и вы можете просмотреть результат формулы в двух местах в окне.
Когда вы закончите добавлять все детали для формулы, нажмите «ОК», и формула появится в вашей ячейке со своими результатами.
Попробуйте автозаполнение формул
Еще один способ найти функцию в Excel — использовать автозаполнение формул. Это полезно, если вы знаете, какая функция вам нужна, но не уверены в том, какой вариант вам нужен.
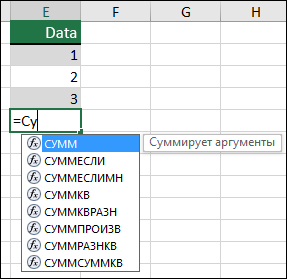
Когда вы вводите знак равенства (=) в ячейку и начинаете вводить первые буквы функции, вы увидите раскрывающийся список совпадений. Вы можете щелкнуть каждый параметр в списке, чтобы рядом с ним отобразилось его описание. Затем, чтобы использовать функцию, дважды щелкните ее, и вы увидите необходимые аргументы.
Например, мы знаем, что нам нужна функция COUNT, но не уверены, какая именно. Вводим = COUNT и видим выпадающий список опций. Описание COUNTIF дает нам понять, что это именно то, что нам нужно.
Мы дважды щелкаем «СЧЁТЕСЛИ» в списке и видим аргументы, необходимые для формулы. Это позволяет нам просто ввести то, что просят, и заполнить формулу.
Работа с функциями и формулами в Excel может быть немного пугающей, если вы не делаете это часто. Но с такими полезными функциями поиск и использование нужной функции может быть намного проще.
Используя таблицы Excel как базу данных, не обойтись без такой функции, как «Найти». Она понадобится для быстрого определения места ключевого слова в каждой строке таблицы.
Как использовать функцию НАЙТИ в Excel
Каждая функция с заполненными аргументами в Excel – это формула, с помощью которой выполняются сложные операции и вычисления в Excel. Перед ее введением ставится знак равенства. Именно так вы дадите знать программе, что вводится именно формула, а не текст и не значение. Функция состоит из двух частей: имени и аргумента.
Каждое название функции в Excel описывает ее операцию и назначение. В данном случае это слово «НАЙТИ».
Аргументов может быть несколько. Они могут быть числовыми, символьными или текстовыми и всегда заключаются в круглые скобки. Если аргументов больше одного, между ними ставится знак «;». Для поиска необходимо использовать следующие аргументы.
- Искомый текст. Сочетание знаков, которые мы разыскиваем в таблице. Это может быть цифро-буквенное сочетание, только цифры или только буквы, пробелы или знаки. Нужно помнить, что функция учитывает введенный регистр. Результаты поиска слов «Мир» и «мир» будут разными.
- Просматриваемый текст. Область поиска может быть указана с помощью мыши. Также ее значения могут быть введены с клавиатуры.
- Начальная позиция (опциональный аргумент). По умолчанию началом поиска признается первая ячейка первой строки таблицы. Вы можете вручную задать номер ячейки, которая будет начальной в процессе поиска.
Синтаксис функции выглядит таким образом:
НАЙТИ(«искомый текст»; просматриваемый текст; [начальная позиция])
Результатом применения функции будет номер места в строке, на котором располагается искомое ключевое слово. Если его нет, выдается символ ошибки #ЗНАЧ!
Примеры использования функции НАЙТИ
Эта формула редко используется самостоятельно. Тем не менее, чтобы наглядно продемонстрировать действие, стоит рассмотреть несколько примеров ее использования.
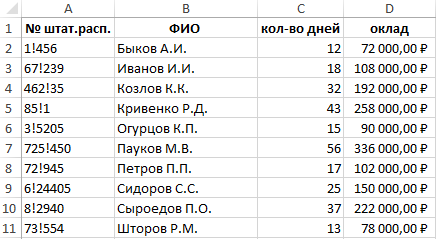
Пример 1. В таблице 4 столбца по 10 строк. В нее внесены:
- номера по штатному расписанию;
- ФИО работников;
- количество отработанных дней:
- оклад (размер оплаты).
Для отчета нужно выбрать информацию о том, сколько дней отработали и какую оплату получили специалисты, которые работают во вредных условиях, связанных с задымленностью.
Штатное расписание составлено особым образом. Номера рабочих единиц имеют пометку «!». В зависимости от расположения этой пометки можно понять, с какими вредными факторами сталкивается рабочий. Нам нужно отсортировать строки, штатные номера которых имеют пометку «!» на втором месте. Например, 3!7884, 8!6453 или 5!54.
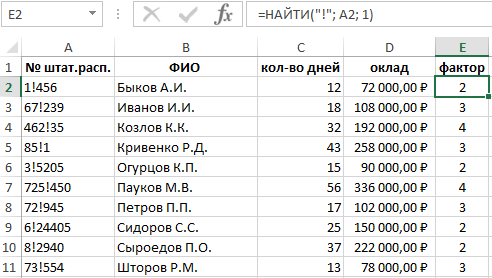
Для этого в ячейку, следующую за последней в первой строчке, нужно ввести функцию НАЙТИ. Она будет выглядеть так.
=НАЙТИ(«!»; A2; 1)
При этом, для указания области поиска можно выделить столбец с номерами. По окончанию набора функции, нажмите Enter. В ячейке появится номер места, на котором располагается пометка «!».
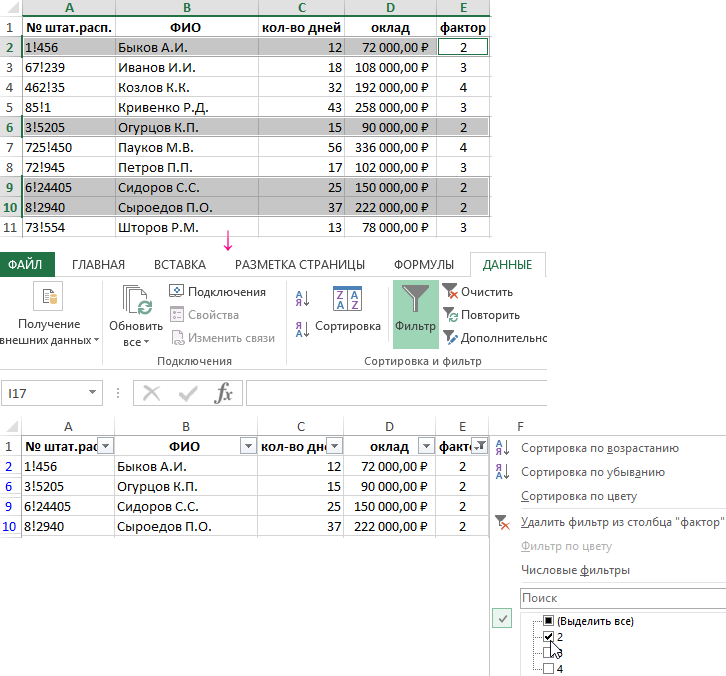
Теперь вы сможете выделить и скопировать строки, напротив которых стоит цифра 2 или воспользоваться автофильтром: «ДАННЫЕ»-«Фильтр».
Отчет готов за пару секунд.
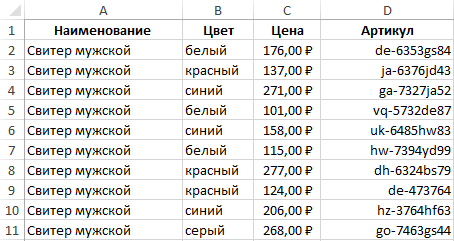
Пример 2. В таблице 4 столбца по 10 строк.
В нее сведены артикулы товаров, которые находятся на складе и указаны такие параметры;
- наименование товара;
- цвет;
- цена;
- артикул.
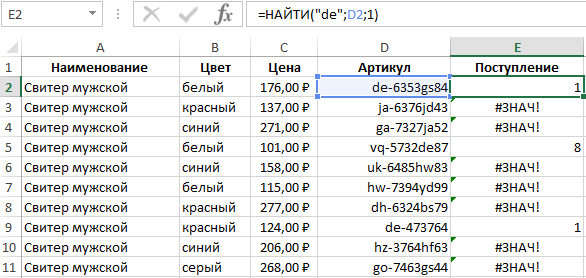
В зависимости от времени поступления на склад они по-разному маркируются. Нужно выбрать информацию по товарам артикулы которых начинаются на буквы «de». Эти буквосочетания встречаются и в других местах артикулов. Важно отсортировать только товары, в артикулах которых оно встречается на первом месте.
Алгоритм действий аналогичный. В ячейке, следующей за последней в первой строке прописываем функцию.
=НАЙТИ(«de»;D2;1)
После нажатия клавиши Enter появляется номер места заданных букв в артикуле товаров. Протянув за нижний угол выделенную ячейку вниз, вы получите аналогичные показатели по всем строкам.
В артикулах товаров, по которым выдана ошибка #ЗНАЧ!, нет заданных букв. Остается выполнить автофильтр, поиск по которым дал результат 1.
Выборка товаров готова.
Пример 3. В таблице 5 строк. В нее введены математические формулы.
Студент готовит шпаргалку на экзамен. Ему нужно выбрать формулы для расчета суммы. Он знает, что в таких формулах на четвертом месте всегда стоит знак «+».
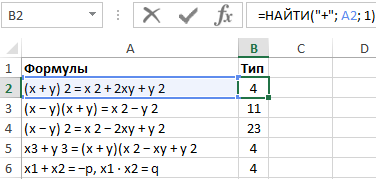
Как всегда, функция прописывается в ячейке, следующей за последней в первой строчке. Формула выглядит так.
=НАЙТИ(«+»; A1; 1)
Нажав Enter, вы получите результат функции.
Теперь можно выбрать формулы, в которых знак суммы находится на 4 месте.
Читайте также: Примеры использования функции НАЙТИ в Excel формулах.
Выбраны все необходимые формулы из списка по критерию – «4» указанном в условии для отбора строк автофильтром Excel.
Все выше описанные примеры применяют функцию НАЙТИ без формул. Но на практике чаще всего она используется как вспомогательная функция для формул с обработкой таблиц в режиме базы данных.