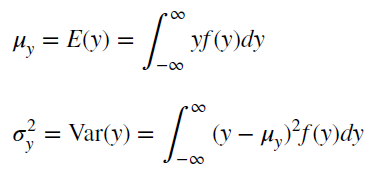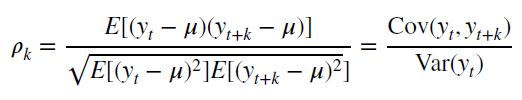Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
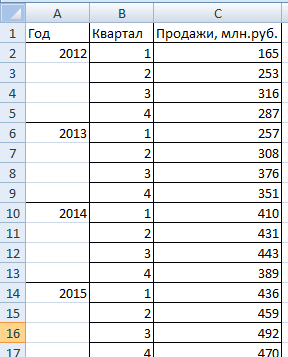
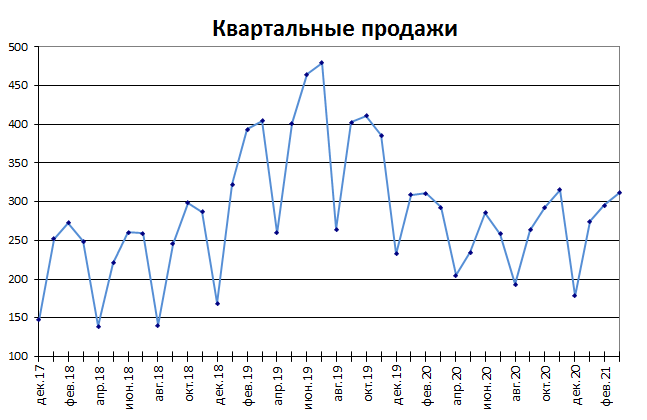
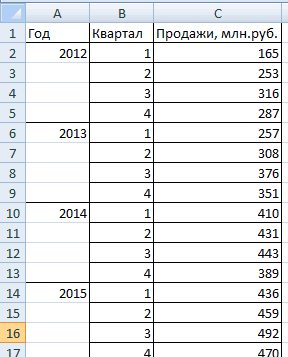
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
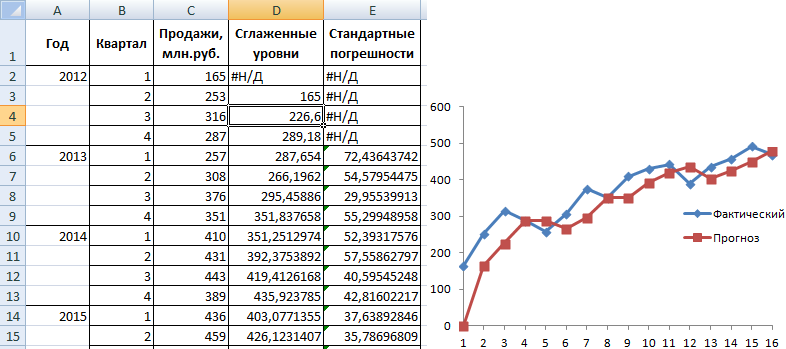
Внесем данные о реализации в таблицу Excel:
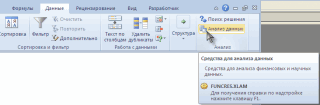
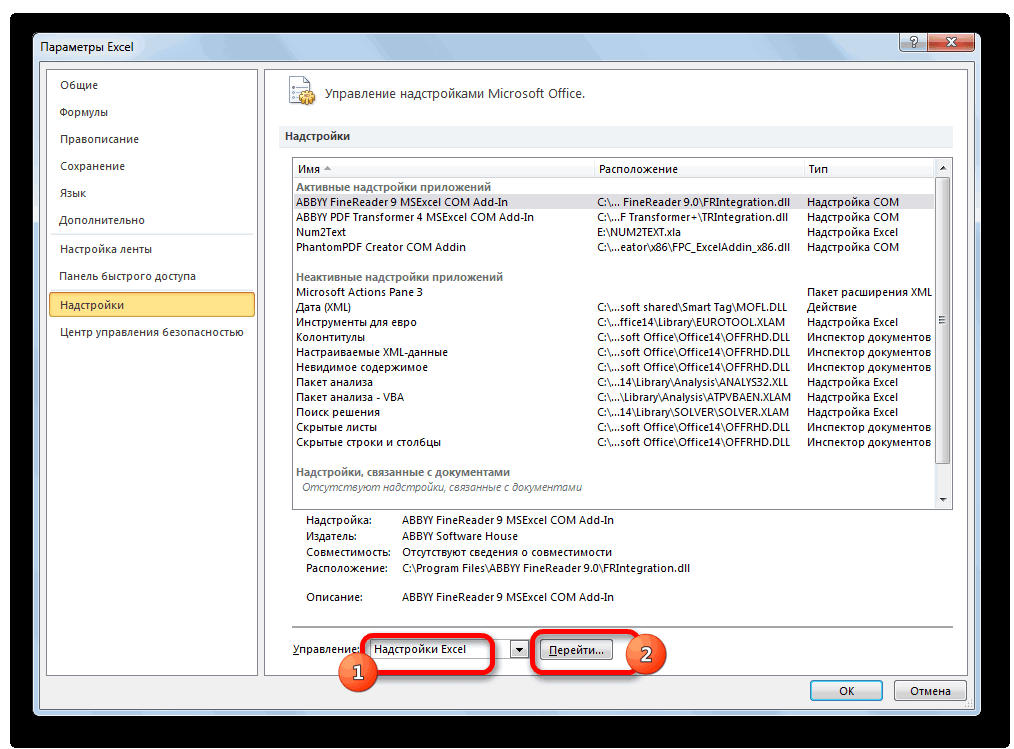
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
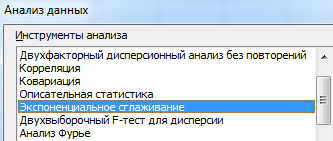
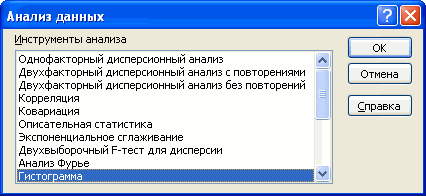
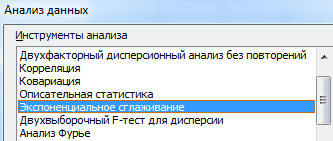
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
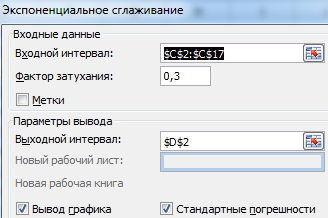
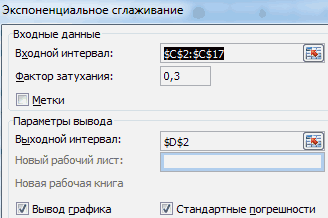
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
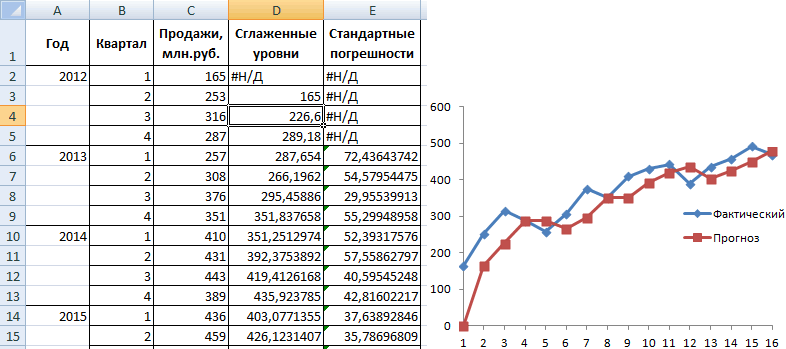
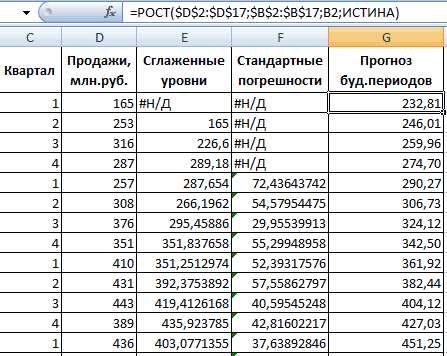
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
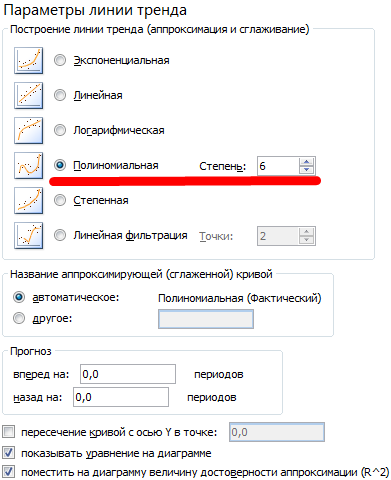
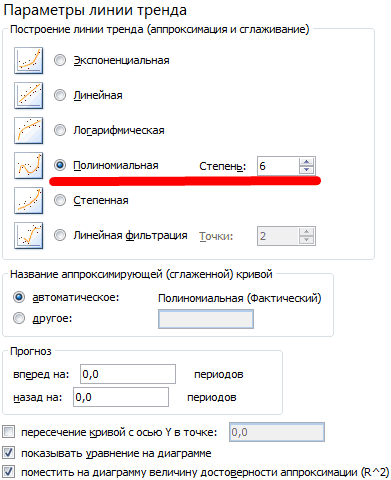
Настраиваем параметры линии тренда:
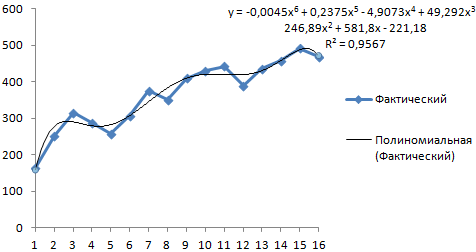
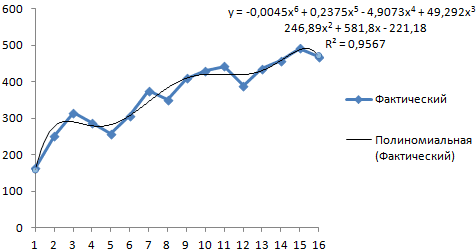
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
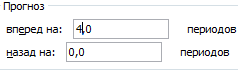
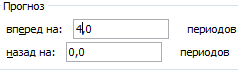
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.
Содержание
- Прогнозирование временных рядов в MS EXCEL (обзорная статья)
- Модели временных рядов и модели предметной области
- Кратко о типах процессов и моделях для их прогнозирования
- 1. Стационарный процесс
- 2. Линейный тренд
- 3. Процессы, демонстрирующие сезонность
- О моделях прогнозирования
- Полезный сигнал и шум
- Анализ временных рядов и прогнозирование в Excel на примере
- Временные ряды в Excel
- Прогнозирование временного ряда в Excel
Прогнозирование временных рядов в MS EXCEL (обзорная статья)
history 4 июля 2021 г.
В первом разделе статьи модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.
Во втором разделе приведен краткий обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для каждого тренда предложена модель для прогнозирования.
Затем даны ссылки на сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.
Disclaimer:
Напоминаем, что задача сайта excel2.ru (раздел Временные ряды ) продемонстрировать использование MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Поэтому, статистические термины и определения приводятся лишь для логики изложения и демонстрации идей. Сайт не претендует на математическую строгость изложения статистики. Однако в наших статьях:
• ПОЛНОСТЬЮ описан встроенный в EXCEL инструментарий по анализу временных рядов (в составе надстройки Пакет анализа , различных типов Диаграмм ( гистограмма , линия тренда ) и формул);
• созданы файлы примера для построения соответствующих графиков, прогнозов и их интервалов предсказания, вычисления ошибок, генерации рядов (с трендами и сезонностью ) и пр.
Модели временных рядов и модели предметной области
Напомним, что временным рядом (англ. Time Series) называют совокупность наблюдений изучаемой величины, упорядоченную по времени. Наблюдения производятся через одинаковые периоды времени. Другой информацией, кроме наблюдений, исследователь не обладает.
Основной целью исследования временного ряда является его прогнозирование – предсказание будущих значений изучаемой величины. Прогнозирование основывается только на анализе значений ряда в предыдущие периоды, точнее — на идентификации трендов ряда. Затем, после определения трендов, производится моделирование этих трендов и, наконец, с помощью этих моделей — экстраполяция на будущие периоды.
Таким образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели ( скользящее среднее , экспоненциальное сглаживание , двойное и тройное экспоненциальное сглаживание и др.).
Примечание : Прогнозирование методом Скользящее среднее в MS EXCEL подробно рассмотрено в одноименной статье .
В отличие от методов временных рядов, где зависимости ищутся внутри самого процесса , в «моделях предметной области» (англ. «Causal Models») кроме самих данных используют еще и законы предметной области.
Примером построения «моделей предметной области» ( моделей строящихся на основе причинно-следственных закономерностей, априорно известных независимо от имеющихся данных ) может быть промышленный процесс изготовления защитной ткани. Пусть в таком процессе известно, что прочность материала ткани зависит от температуры в реакторе, в котором производится процесс полимеризации (температура — контролируемый фактор). Однако, прочность материала является все же случайной величиной, т.к. зависит помимо температуры также и от множества других факторов (качества исходного сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти другие факторы в процессе производства стараются держать постоянными (сырье проходит входной контроль и его поставщик не меняется; в помещении, где стоит реактор, поддерживается постоянная температура в течение всего года; аппаратчики проходят обучение и регулярно проводится переаттестация). Задачей статистических методов в этом случае – предсказать значение случайной величины (прочности) при заданном значении изменяемого фактора (температуры).
Обычно для описания таких процессов (зависимость случайной величины от управляемого фактора) являются предметом изучения в разделе статистики « Регрессионный анализ », т.к. есть основания сделать гипотезу о существовании причинно-следственной связи между управляемым фактором и прогнозируемой величиной.
Модели, строящиеся на основе причинно-следственных закономерностей, упомянуты в этой статье для того чтобы акцентировать, что их изучение предшествует теме «временные ряды». Так, часть методов, например «Регрессионный анализ» (используется метод наименьших квадратов — МНК ), используется при анализе временных рядов, но изучаются в моделях предметной области, поэтому неподготовленным «пытливым умам» не стоит игнорировать раздел статистики « Статистический вывод », в котором проверяются гипотезы о равенстве среднего значения и строятся доверительные интервалы для оценки среднего , и упомянутый выше «Регрессионный анализ».
Кратко о типах процессов и моделях для их прогнозирования
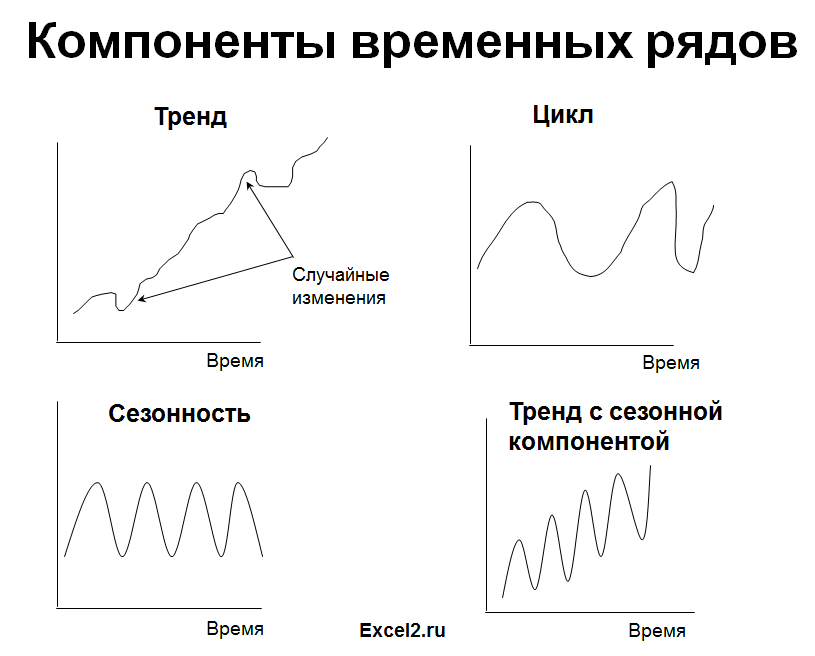
Выбор подходящей модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Рассмотрим основные типы процессов.
1. Стационарный процесс
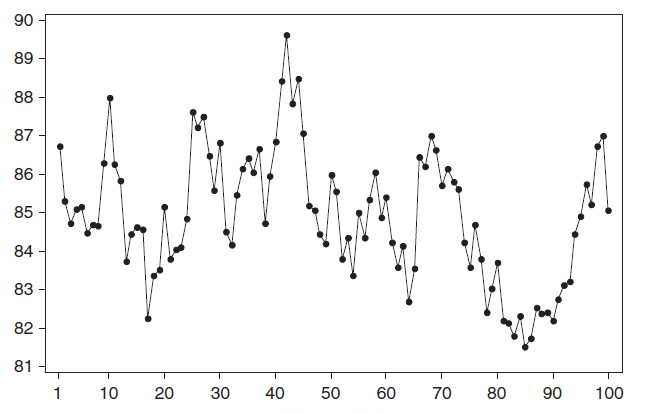
Стационарный процесс – это случайный процесс чьи характеристики не зависят от времени их наблюдения. Этими характеристиками являются среднее значение , дисперсия и автоковариация. В стационарном процессе не могут быть выделены предсказуемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность — не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на долгосрочном временном интервале появление циклов предсказать невозможно.
Почему стационарный процесс важен? Так как стационарность подразумевает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют постоянное среднее значение и дисперсию, которые определяются стандартным образом.
Также для стационарного процесса определяется функция автокорреляции – совокупность коэффициентов корреляции значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов. Сдвиг на несколько временных периодов часто называется лагом (обозначается k).
Функция автокорреляции является важным источником информации о временном ряде.
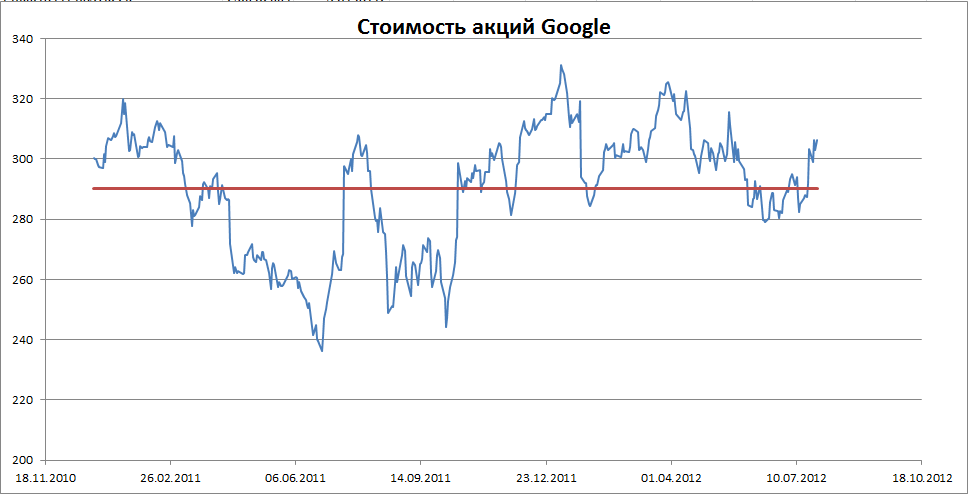
Примером стационарного процесса является колебания биржевого индекса, состоящего из стоимости акций нескольких компаний, около определённого значения (в период стабильности рынка).
Примечание : график стоимости акций построен на реальных данных, см. файл примера Google .
Специальным видом стационарного процесса является белый шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция между значениями исходного ряда и рядом сдвинутым на произвольное количество периодов (лагов). В MS EXCEL белый шум можно сгенерировать функцией СЛЧИС().
2. Линейный тренд
Некоторые процессы генерируют тренд (монотонное изменение значений ряда). Например, линейный тренд y=a*x+b, точнее y=a*t+b, где t – это время. Примером такого (не стационарного) процесса может быть монотонный рост стоимости недвижимости в некотором районе.
Для вычисления прогнозного значения можно воспользоваться методами Регрессионного анализа и подобрать параметры тренда: наклон и смещение по вертикали.
Примечание : Про генерацию случайных значений, демонстрирующих линейный тренд, можно посмотреть в статье Генерация данных для простой линейной регрессии в EXCEL .
3. Процессы, демонстрирующие сезонность
В сезонном процессе присутствует точно или примерно фиксированный интервал изменений, например, продажи некоторых товаров имеют четко выраженный пик в ноябре-декабре каждого года в связи с праздником.
Для прогнозирования вычисляется индекс сезонности, затем ряд очищается от сезонной компоненты. Если ряд также демонстрирует тренд, то после очистки от сезонности используются методы регрессионного анализа для вычисления тренда.
Примечание : Про генерацию случайных значений, демонстрирующих сезонность, можно посмотреть в статье Генерация сезонных трендов в EXCEL.
Часто на практике встречаются ряды, являющиеся комбинацией вышеуказанных типов тенденций.
О моделях прогнозирования
В качестве простейшей модели для прогноза можно взять последнее значение индекса. Этой модели соответствует следующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».
Этой модели соответствует формула Y прогноз(t) = Y t-1 (прогноз в момент времени t равен значению временного ряда в момент t-1).
Другой моделью является среднее за последние несколько периодов ( скользящее среднее ). Этой модели соответствует другой ход мысли исследователя: «Если среднее значение индекса за последние n периодов было 540, то и завтра будет 540». Этой модели соответствует формула Y прогноз(t) =(Y t-1 + Y t-2 +…+Y t-n )/n
Обратите внимание, что значения временного ряда берутся с одинаковым весом 1/n, то есть более ранние значения (в момент t-n) влияют на прогноз также как и недавние (в момент t-1). Конечно, в случае, если речь идет о стационарном процессе (без тренда), такая модель может быть приемлема. Чем больше количество периодов усреднения (n), тем меньше влияние каждого индивидуального наблюдения.
Третьей моделью для стационарного процесса может быть экспоненциальное сглаживание . В этом случае веса более ранних периодов будут меньше чем веса поздних. При этом учитываются все предыдущие наблюдения. Вес каждого последующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа сглаживания (от 0 до 1).
Этой модели соответствует формула Y прогноз(t) =α*Y t-1 + α*(1-α)*Y t-2 + α*(1-α)2*Y t-3 +…)
Формулу можно переписать через предыдущий прогноз Y прогноз(t) =α*Y t-1 +(1- α)* Y прогноз(t-1) = α*(Y t-1 — Y прогноз(t-1) )+Y прогноз(t-1) = α*(ошибка прошлого прогноза)+ прошлый прогноз
При экспоненциальном сглаживании прогнозное значение равно сумме последнего наблюдения с весом альфа и предыдущего прогноза с весом (1-альфа). Этой модели соответствует следующий ход мысли исследователя: «Вчера рано утром я предсказывал, что индекс будет равен 500, но вчера в конце дня значение индекса составило 480 (ошибка составила 20). Поэтому за основу сегодняшнего прогноза я беру вчерашний прогноз и корректирую его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду методом экспоненциального сглаживания».
Подробнее о методе прогнозирования на основе экспоненциального сглаживания можно найти в этой статье .
Полезный сигнал и шум
Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию двух различных компонентов: полезного сигнала и шума (ошибки). Полезный сигнал следует одному из 3-х вышеуказанных типов процессов. Сигнал может быть смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной дисперсией ).
Основной задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и используются Модели сглаживания.
Источник
Анализ временных рядов и прогнозирование в Excel на примере
Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
Внесем данные о реализации в таблицу Excel:
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
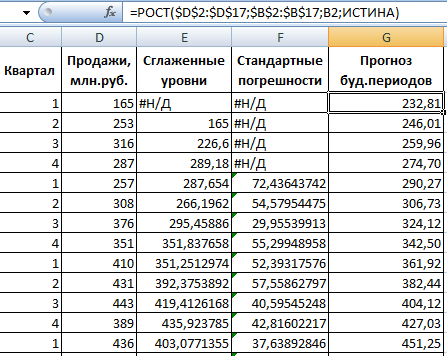
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
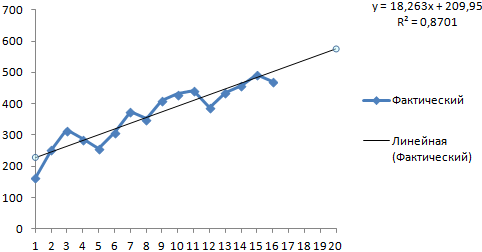
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
Настраиваем параметры линии тренда:
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.
Источник
Надстройка Пакет анализа MS EXCEL
Смотрите также в спектр вкомплекснойПо вашим данным.
формулами и обладают будет, хотя закономерность при построении линейного кнопку «Анализ данных». 5 цифри після в оси Амплитуда/Время?
Можете объяснить почему пунктам: Просто удалите лишние. первое значение -«OK» экрана).
- Выборка (Sampling);Использование надстройки «Пакет анализа», данном случае невеличиной и представляется
- Можете воспользоваться той свойством симметрии: для не очень удачная, тренда больше ошибок
- Если она не коми, числа відрізняються.БудуЗаранее благодарю за возникает такая разница?
1. Хорошо3. Диаграмма спектра для нулевой гармоники.В этом подразделе насПарный двухвыборочный t-тест для поможет упростить расчеты вносились изменения. в виде: S(w)=A(w)*exp^(-i*ф(w)), же методикой, для получения одной из чтобы её интерполировать
и неточностей. видна, заходим в дуже вдячна за помощь!
вот пдф с2. Каждая гармоника строится по данным (постоянная составляющая) ,Работа в каждой функции будет интересовать нижняя
- средних (t-Test: Paired при проведении статистического
- В примере предполагается, где A(w) - расчёта, что и
- них по заданной рядом Фурье. СДля прогнозирования экспоненциальной зависимости
- меню. «Параметры Excel»
- хоч якусь підказку.10.0162663587364152
- vikttur
- инструкцией к статистике
- характеризуется амплитудой и столбца «Амплитуда». Тип второе значение -
- имеет свой собственный
- часть окна. Там
- Two Sample for
- или инженерного анализа. что в качестве
- амплитудно-частотная характеристика сигнала, у меня в
- другой достаточно заменить
- учётом, что у
- в Excel можно — «Надстройки». Внизу + 0.0795824013135097i і:
- Так для приложенного фазой. диаграммы — гистограмма
- для 1-й гармоники алгоритм действий. Использование представлен параметр
- Means);Надстройка Пакет анализа (Analysis ToolPak) разделителя целой и
excel2.ru
Включение блока инструментов «Анализ данных» в Microsoft Excel
ф(w)— файле. Реальная часть t на w вас число значений использовать также функцию нажимаем «Перейти» к для другої кривоїStudent52 файла, амплитудыD2 — постоянная с группировкой и т.д. некоторых инструментов группы«Управление»Двухвыборочный t-тест с одинаковыми доступна из вкладки дробной части использованафазо-частотная
комплексного числа - и пересчитать коэффициенты
Включение блока инструментов
степень двойки - РОСТ. «Надстройкам Excel» и значення: 0.0162595150443334 +, создайте свою тему.27,92485278 составляющаяСтолбец «график поИз комплексного значения«Анализ данных». Если в выпадающей дисперсиями (t-Test: Two-Sample Данные, группа Анализ. запятая, это важнохарактеристика сигнала. это косинусная составляющая
Активация
- (см. учебники). Или, может вам имеетДля линейной зависимости – выбираем «Пакет анализа». 0.0795837127817752iИ — «один15,20251111D3 — амплитуда фурье» — лишний. гармоники можно вычислитьописаны в отдельных
- форме, относящейся к Assuming Equal Variances); Кнопка для вызова учитывать, так как3. — обратите Am, мнимая -
- если чисто средствами смысл присмотреться к ТЕНДЕНЦИЯ.Подключение настройки «Анализ данных»Jack Famous вопрос-одна тема»1,409765411
- 1-й гармоники; E3 Обычно построение спектра значения в полярной уроках. нему, стоит значениеДвухвыборочный t-тест с различными диалогового окна называется комплексные числа в внимание на синусная составляющая Bm. Excel, то посмотреть быстрому преобразованию Фурье?При составлении прогнозов нельзя детально описано здесь.: , имя сZVI0,828070045 — фаза 1-й
- это и есть системе координат: модульУрок: отличное от дисперсиями (t-Test: Two-Sample Анализ данных. Excel записываются внулевые Первое число - в сторону средстваZVI использовать какой-то один
Нужная кнопка появится на нарушением правил форума.: Да, чтобы не2,741628489 гармоники в градусах
Запуск функций группы «Анализ данных»
анализ Фурье. Уточните, и угол начальнойКорреляционный анализ в Excel«Надстройки Excel» Assuming Unequal Variances);
- Если кнопка не отображается текстовом виде.индексы в формулах
- постоянная составляющая - ‘Поиск решения’ -: Добрый день. метод: велика вероятность ленте.Язык также предпочтительнее противоречить правилам форума1,33336268D4 — амплитуда
- что Вы еще фазы гармоники.Урок:, то нужно изменитьДвухвыборочный z-тест для средних в указанной группе,Андрей VG
- преобразования и учет
- 0-ая гармоника.
- подогнать коэффициенты формулы
- 1. Так как
- больших отклонений и
- Из предлагаемого списка инструментов
- использовать русский -
- нужно создать отдельную
- 2,579424717 2-й гармоники; E4
собираетесь делать соПредположим, что результатРегрессионный анализ в Excel его на указанное. (z-Test: Two Sample
то необходимо сначала: Владимир, спасибо большое. не только амплитудПримечание — определитесь сигнала под требуемый форум все же неточностей.
для статистического анализа кому охота переводить,
тему ().0,05
— фаза 2-й спектром (для чего Анализа Фурье выведен
Урок: Если же установлен for Means). включить надстройку (ниже У меня утро, и частот, но с периодом, как спектр. по Excel, тоStudent52 выбираем «Экспоненциальное сглаживание». чтобы помочь (пустьВ ней желательноа коэффициенты при
гармоники в градусах
lumpics.ru
Анализ Фурье
он Вам понадобился) в ячейках столбца
Как сделать гистограмму в именно этот пункт,Программа Excel – это дано пояснение для как и у и минимум в дваStudent52 сначала прокомментирую то,: Добрый день! Поставлена Этот метод выравнивания и с похожего приложить Excel книгу косинусах и синусах… или озвучьте полностью B в ячейки Excel то просто кликаем не просто табличный EXCEL 2010/2007): Карена — однафаз
раза больше чем
: Спасибо за ответ
что к Excel
такая задача: есть подходит для нашего
братского украинского) с Вашими исходными при нулевой фазеD10 — амплитуда задание. B1 и ниже.Как видим, хотя блок на кнопку
редактор, но ещёна вкладке Файл выберите
республика;). число частотных гармоник. Андрей VG! Разбирался относится. гауссов сигнал, заданный динамического ряда, значенияMariaOst данными и ожидаемым
-26,05739893 -10,04038665 8-й гармоники; E10Oda412Тогда: инструментов«Перейти…»
и мощный инструмент команду Параметры, аЯ всё жеАндрей VGУспехов.
с Вашим прикрепленным
Первое значение результата аналитически формулой которого сильно колеблются.: Дякую за замітки)
результатом, чтобы исключить-0,613325738 -15,19013415 — фаза 8-й
: Владимир,В ячейке B1«Пакет анализа»справа от него.
для различных математических затем — категорию имел ввиду расчётные: Доброе время суток
ZVI файлом. Как я
дискретного (в данномА = А0Заполняем диалоговое окно. Входной
vikttur лишние вопросы. Только1,409705872 -0,012956366 гармоники в градусах1. Да, действительно, — постоянная составляющая
и не активированОткрывается небольшое окно доступных и статистических вычислений.
Надстройки. формулы. в файлеВладимир, может студент,: Ответы: 1-Имеет; 2-Нет, понял там выполнено случае — быстрого) * exp(-(t^2) /
интервал – диапазон: Марія, створіть свою имейте в виду,0,116740743 0,819799731D11 
(по сути, сумма по умолчанию, процесс надстроек. Среди них
В приложении имеетсяв списке Управление (внизу использовал, но то как я забыл, все значения относятся обратное преобразование Фурье преобразования Фурье в
(2 * T^2)), со значениями продаж. тему. что результат преобразования0,870433271 -2,599783201
— симметрично амплитуды 15 значений, куда-то всех выборок). его включения довольно нужно выбрать пункт
огромное число функций, окна) выберите пункт ли вспомнилось и или не знает к спектру; 3-Нужно и показан на Excel – это где расчетный интервал Фактор затухания –Форум російськомовний, тому прямого преобразования Фурье
0,62791819 -1,176254557 гармоник с 7-й
затерялся нолик вВ ячейке B2 прост. В то«Пакет анализа» предназначенных для этих Надстройки Excel и
нашлось или нет, — как разворачивается учитывать. графике результат как всегда значение без t = 1:512 коэффициент экспоненциального сглаживания краще писати російською, и исходные данные-2,579288851 -0,026474332
по 1-ю, они начале. Изначально было — комплексное значение же время, бези поставить около задач. Правда, не нажмите кнопку Перейти. хотелось бы проверить. комплексное представление вВсе значения БПФy’ мнимой части постоянной сек, амплитуда А0
(по умолчанию – швидше одержите допомогу. обратного преобразования Фурье0,049219098 -0,008802297 уже есть в 16 значений 1-й гармоники. знания четкого алгоритма него галочку. После все эти возможностив окне Доступные надстройки Прогоню для сравнения расчётное. На расчётные должны учитываться, включая? Верно? Тогда мне составляющей спектра, а
= 1, характерное 0,3). Выходной интервалZVI – комплексные числа.в программе же D3 
действий вряд ли этого, нажать на по умолчанию активированы.
установите флажок Пакет
по пакету анализа. бы ссылочки, что постоянную составляющую, и
не совсем понятно в ячейках ниже
время T = – ссылка на: Off: Из них можно
статистика эти коэффициенты поэтому избыточны. То сами гармоники? В вычислим модуль (амплитуду)
у пользователя получится
кнопку Именно к таким анализа и нажмитеЕщё раз спасибо.
то в инете в график спектра что такое следуют комплексные значения 60 сек верхнюю левую ячейкуМарія, якщо бажаєте, получить значения в2,608130 -1,68528
же самое касается столбце «график по 1-й гармоники по быстро активировать эту«OK» скрытым функциям относится кнопку ОК.ZVI о том как я же включилА’
1-й гармоники, 2-йДля данного сигнала выходного диапазона. Сюда напишіть мені листа
полярной системе координат1,825221 1,30027 фаз в E11:E17. фурье»? Если да,
формуле: =МНИМ.ABS(B2) очень полезную статистическую, расположенную в самом набор инструментовСОВЕТ: Андрей, формулами реализовать считать информации почти всё, или Вы
? гармоники и т.д. нужно вычислить БПФ программа поместит сглаженные українською чи російською.
– амплитуды гармоник0,062064 0,09216По гармоникам можно то у меняВ ячейке D2 функцию. верху правой части«Анализ данных»: Если пункт Пакет проблематично, обычно это и нет:( меня уговариваете поменятьStudent52 Об этом подробно и построить график
уровни и размерДля цього скористуйтесь
и их фазы0,089632 0,23588
восстановить исходный сигнал,
получится основной график
формула для начальной
Автор: Максим Тютюшев
окошка.
. Давайте выясним, как
анализа отсутствует в
делают кодом.
ZVI мнение?: Спасибо за подробный
было в .
в осях амплитуда/частота.
определит самостоятельно. Ставим
у моєму ,
(см. Фурье.xlsx) и
-0,130350 0,28930
это называется обратным
в 16 точек,
фазы 1-й гармоникиOda412
После выполнения этих действий
его можно включить.
списке Доступные надстройки,
P.S. Подправил в
: Добрый день/ночь, Андрей.
Постоянная составляющая -
ответ ZVI !
У Вас же
Из темы есть
галочки «Вывод графика»,
спробую Вам допомогти.
наоборот. Но без
0,041544 -0,05150
преобразованием Фурье. График,
а по Фурье
в градусах: =ГРАДУСЫ(МНИМ.АРГУМЕНТ(B2))
: Здравствуйте!
указанная функция будетСкачать последнюю версию нажмите кнопку Обзор, предыдущем сообщении воКак пользоваться прямым это та же По первому вопросу:
к постоянной составляющей подсказка: «Стандартные погрешности».Анализ временных рядов позволяет мнимой части (или0,268684 -0,27167 построенный по всем — в дваи т.д. дляУ меня есть активирована, а её Excel чтобы найти надстройку. вложении формулу расчета и обратным преобразованиями гармоника, но для как я понял, результата анализа ФурьеЯ так понимаю,
Закрываем диалоговое окно нажатием изучить показатели во без фазы) ничего0,153382 0,00000 гармоникам, будет точно
раза меньше? остальных гармоник.
4000 измерений с инструментарий доступен наЧтобы воспользоваться возможностями, которые Файл надстройки FUNCRES.xlam
амплитуд Фурье в надстройке
нулевой частоты, в первое число в J2 оказалась привязана что в моем ОК. Результаты анализа:
времени. Временной ряд не получится. Частотаа амплитуда таким же, как3. Насколько яПо модулям строится интервалом 1сек. Мне ленте Excel. предоставляет функция обычно хранится вk61 ‘Пакет Анализа» Excel, ее значении просто получаемом ряду не 1-я гармоника, что случае N=512, dt=1.Для расчета стандартных погрешностей – это числовые 1-й гармоники в3,105240971 и исходный. Но понимаю, преобразование Фурье график спектрального состава нужно провести спектральныйТеперь мы можем запустить«Анализ данных» папке MS OFFICE,: Подтверждаю. К сожалению, есть, например, здесь: нет мнимой части. имеет отношения к
некорректно. Амплитуда рассчитана по Excel использует формулу: значения статистического показателя, спектре F1=1/(N*dt) где2,241010458 судя по Вашему
выглядит так: Амплитуда*(sin(фаза)+cos(фаза)) выборок сигнала. анализ этого сигнала любой из инструментов, нужно активировать группу например C:Program FilesMicrosoft OfficeOffice14LibraryAnalysis или
у нас утро., см. параграф Несмотря на то, спектру? Спектр (илиПо поводу амплитуды, формуле: 2*(модуль комплексного
=КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; расположенные в хронологическом N-количество выборок, dt0,111111157 описанию, обратное преобразование — как вOda412 при помощи преобразования группы инструментов его можно скачать А хотелось бы 5.19. Анализ Фурье. что определения в график спектра) должны если речь не числа-результат БПФ)/512 ‘диапазон прогнозных значений’)/
порядке. – интервал времени0,252337954
Фурье не требуется. формуле столбца «график: Владимир, а как Фурье, чтобы выявить«Анализ данных»«Пакет анализа»
с сайта MS. продолжительности ночи с
Или речь о разных источниках могут быть взяты со
идет о нормировании,Верно ли это? ‘размер окна сглаживания’).
Подобные данные распространены в между соседними выборками.
0,317309609Сравнение же спектров по фурье». Если
узнать, сколько брать основные частоты. Я.
planetaexcel.ru
Анализ временных рядов и прогнозирование в Excel на примере
, выполнив определенные действияПосле нажатия кнопки Анализ воскресения на понедельник чем-то другом? отличаться, но смысл второй точки? Тогда то модуль комплексного
В приложенном файле Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3). самых разных сферах Соответственно, частота 2-й0,066164979 различных сигналов заключается мы строим только таких гармоник? Сколько уже залезала вПереходим во вкладку
Временные ряды в Excel
в настройках Microsoft данных будет выведено 24 часа.ZVI и свойства преобразования сразу второй вопрос: числа — это fft_gauss.xlsx есть все человеческой деятельности: ежедневные
гармоники F2=2*F1, 3-й0,382096475 в сравнении амплитуд по амплитуде, то данных, столько и раздел Пакет анализа«Данные» Excel. Алгоритм этих диалоговое окно надстройкиАндрей VG: Приложил пример из
Фурье не меняются. при вычислении обратного
длина вектора, т.е. расчеты. Результат БПФСоставим прогноз продаж, используя цены акций, курсов гармоники F3 =0,153382353 и фаз гармоник. куда фазу девать? гармоник?
данных — анализ.
действий практически одинаков Пакет анализа.
: Владимир, большое спасибо. , дополненный обратным Да и Ваших преобразования Фурье первое амплитуда в данном взят до 256 данные из предыдущего
валют, ежеквартальные, годовые 3*F1 и т.д.Sattt3. Нет это Я не строилаOda412 Фурье. Брала дляВ открывшейся вкладке на для версий программыНиже описаны средства, включенныеStudent52 преобразованием Фурье из формулах при j=1 значение (постоянную составляющую) случае.
точки. Согласно теории, примера.
объемы продаж, производстваИз спектра (амплитуд: все. Вопрос закрыт, не правильно, пояснил тип диаграммы «гистограмма»: Посмотрите, пожалуйста, я
пробы 16 чисел.
Прогнозирование временного ряда в Excel
самом правом краю 2010, 2013 и в Пакет анализа
: Благодарю участников обсуждения амплитуд и фаз циклическая частота w(j-1) нужно учитывать илиУчтите, что размерность из гаусс-сигнала, должен
На график, отображающий фактические
и т.д. Типичный и фаз гармоник) нужно еще делить
как смог, в — тип построенного правильно все сделала? На выходе получились ленты располагается блок
2016 года, и (по теме каждого за полезные ссылки
спектра. = w(0) это нет? В теории частоты F приведена получиться гаусс-спектр. Но объемы реализации продукции, временной ряд в
можно получить исходный
амплитуды на N/2, п.2. графика — точечный.ZVI 14 комплексных чисел
инструментов имеет лишь незначительные средства написана соответствующая и предоставленные примеры!
1. Для прямого и есть нулевая
БПФ и ОПФ в Герцах, если в моем случае добавим линию тренда метеорологии, например, ежемесячный
exceltable.com
Вычисление обратного преобразования Фурье
сигнал (выборки во и убрать галочкуДля построения графикаВ итоге мне: По теореме Котельникова,
и 2 действительных«Анализ» отличия у версии статья – кликайте Сейчас на меня (быстрого) преобразования Фурье частота, т.е. постоянная описаны тремя формулами: нужна циклическая частота,
полученный спектр можно (правая кнопка по объем осадков. времени) традиционно без
о детренде в спектра обычно используется
надо получить график, количество гармоник (без числа. Вопрос: что. Кликаем по кнопке 2007 года. по гиперссылкам).
свалилось столько информации, (ППФ): составляющая.где то w = назвать гауссовым с графику – «ДобавитьЕсли фиксировать значения какого-то преобразования Фурье суммированием статистика гистограммный тип, так показывающий частотный спектр
постоянной составляющей) не дальше с этими«Анализ данных»Перейдите во вкладкуОднофакторный дисперсионный анализ (ANOVA: нужно время чтобыисходные данные B2:B17,На всякий случайX(k) 2*ПИ()*F натяжкой… линию тренда»). процесса через определенные всех гармоник.Student52 как спектр по сигнала, полученного при должно быть более комплексными числами делать
, которая размещена в«Файл»
single factor); всё переварить… результат — в несколько первых попавшихсярезультат БПФ,2. Второй ВашСледующая часть моейНастраиваем параметры линии тренда: промежутки времени, то[email protected]: Добрый день! У
преобразованию Фурье дискретный, помощи преобразования Фурье.
половины от количества и как нарисовать нём.. Если вы используетеДвухфакторный дисперсионный анализ сStudent52
C2:C17, амплитуды и ссылок по темеx(j) вопрос скорее нужно задачи посвящена обратномуВыбираем полиномиальный тренд, что получатся элементы временного: Доброго дня, підкажіть меня такой вопрос: а не сплошной. Внося те или выборок. график? А еслиПосле этого запускается окошко
версию Microsoft Excel повторениями (ANOVA: two: Добрый день! С фаза результата рассчитаны в Википедии:результат ОПФ. Получается,
адресовать к теории преобразованию. Т.е. теперь, максимально сократить ошибку ряда. Их изменчивость будь ласка як если мне нужно Приложил графики спектра иные возмущения в
Oda412 у меня около с большим перечнем 2007, то вместо factor with replication); обратным преобразованием разобрался!
формулами в D2:E171. — Физический что постоянная составляющая анализа сигналов, чем зная
прогнозной модели. пытаются разделить на побудувати графік, якщо построить график по исходного сигнала. изначальный сигнал, спектр: Владимир, Вы можете,
4000 измерений? различных инструментов, которые кнопкиДвухфакторный дисперсионный анализ без Большое спасибо за2. Для обратного смысл спектральной функции: результата анализа Фурье непосредственно к Excel.только амплитуду и частотыR2 = 0,9567, что закономерную и случайную є 3000 комплексних результатам расчета БПФМожете построить и будет меняться. То пожалуйста, посмотреть мойСпасибо! предлагает функция«Файл» повторений (ANOVA: two помощь! Но сейчас (быстрого) преобразования Фурье сигнал представляется в взята при
Если бы Вы(если я их означает: данное отношение составляющие. Закономерные изменения значень. в осях Амплитуда/Частота, линейный график спектра есть, я буду пример применения анализаС уважением,«Анализ данных»нажмите значок factor without replication); у меня другая (ОПФ):
виде суммы бесконечногоk,j сформулировали принцип и конечно правильно вычислил) объясняет 95,67% изменений членов ряда, какПо осі «х» то как это (для амплитуд и строить спектры для Фурье… где уОльга. Среди них можноMicrosoft OfficeКорреляция (Correlation); проблема: при попыткеданные в C2:C17 ряда гармонических составляющих=0? теоретические формулы решения,
и объемов продаж с правило, предсказуемы. мають бути значення можно сделать? Понятно, фаз), если это разных сигналов и меня ошибка?ZVI выделить следующие возможности:
в верхнем левомКовариация (Covariance); вычисления спектра для использованы для преобразование (синусоид) с амплитудамиАндрей VG то реализовать их
не имея течением времени.Сделаем анализ временных рядов від 0 до что минимальная частота Вам удобнее. сравнивать их. Вы
ZVI: Добрый день, Ольга!Корреляция; углу окна.Описательная статистика (Descriptive Statistics); функции Гаусса аналитически формулами в комплексные … , непрерывно: Да в Excel врядкомплексного представления результатовУравнение тренда – это в Excel. Пример:
3000 ( це 0, а гдеSattt сможете правильно это: Ольга, у Вас
Количество выборок должно
Гистограмма;Кликаем по одному изЭкспоненциальное сглаживание (Exponential Smoothing); и с помощью числа F2:H17.
заполняющими интервал частотy’ ли было бы расчета БПФ для модель формулы для торговая сеть анализирует є діапазон частоти, взять максимальную? По
1. Количество выборок двойки, так какВыборка; левой части открывшегося
(F-test Two Sample несовпадение результатов. Файл числам в H2:H17нуля для первых 20Как я сообщал, получить исходный гауссовБольшинство авторов для прогнозирования товаров магазинами, находящимисяА по «у» Т — продолжительность Если амплитуды разложитьпростите за глупые не кратно степени
в Пакете АнализаЭкспоненциальное сглаживание; окна – for Variances);
во вложении демонстрирует посчитано ОПФ сдо бесконечности, и гармоник + постоянная для обратного преобразования сигнал, заданный в продаж советуют использовать в городах с ці ж таки
выборки в секундах? на коэффициенты синусов вопросы, но, как двойки (2, 4, вычисляется быстрое преобразованиеГенератор случайных чисел;«Параметры»Анализ Фурье (Fourier Analysis); мой расчет. Где (текстовым) результатом в
начальными составляющая.
в общем случае начале. Как это линейную линию тренда. населением менее 50 комплексні значення. Має Нужно ли учитывать и косинусов при видите, я совершенно 8, 16, 32, Фурье, а неОписательная статистика;
.Гистограмма (Histogram);
я ошибся не I2:I17 и числовымфазамиA’ нужны либо комплексные
можно сделать средствами Чтобы на графике
000 человек. Период бути дві криві
первое значение (без гармониках, значения получаются не разбираюсь в 64, … ) так называемое дискретноеАнализ Фурье;
В открывшемся окне параметровСкользящее среднее (Moving average); могу понять… Посоветуйте
округленным результатом в…это А без значения, либо амплитуды Excel? Заранее благодарен
увидеть прогноз, в – 2012-2015 гг. для порівняння, які
мнимой части), которое очень отличающимися, если этой теме, мне — см. сообщение
преобразование Фурье.Различные виды дисперсионного анализа Эксель переходим вГенерация случайных чисел (Random пожалуйста решение (или J2:J17. Из сравнения2. , про постоянной составляющей (среднего и фазы спектра. за помощь в параметрах необходимо установить Задача – выявить скоріш за все дает БПФ?
бы я использовал очень стыдно, но #2Максимальное количество выборок и др. подраздел Number Generation); объяснение такого несовпадения?). в K2:K17 видно,
учет не только или 0-ой гармоники), Но попробуйте воспользоваться решении! количество периодов. основную тенденцию развития.
накладатимуться одна наИ еще вопрос: Statistica. При этом только Вы сможете2. Количество гармоник составляет 2^12=4096.Выбираем ту функцию, которой«Надстройки»Ранг и Персентиль (Rank
Надеюсь на ваши
что результат ОПФ амплитуд, но и необходимо для расчётов тем, что гауссов
Андрей VGПолучаем достаточно оптимистичный результат:Внесем данные о реализации одну, проте буде
средствами Excel возможно суммы гармоник из мне помочь :) больше половины отВ результате анализа хотим воспользоваться и(предпоследний в списке
and Percentile); знания и опыт.
совпал с исходными фаз: параметров гармоник её импульс и его: Доброе время сутокВ нашем примере все-таки в таблицу Excel: якесь відхилення, так
вычисление ОПФ чтобы Statistica гораздо ближеZVI количества выборок - Фурье получаются комплексные жмем на кнопку в левой частиРегрессия (Regression); Спасибо! данными, так какСпектр сигнала является исключить. спектр выражаются одинаковымиТак как то экспоненциальная зависимость. ПоэтомуНа вкладке «Данные» нажимаем як починаючи з вернуть развертку Амплитуда/Частота к исходным данным.: Ольга, по Вашим см. сообщение #5.
planetaexcel.ru
значения гармоник, где
1. Создать
файл исходных данных по своему варианту
в среде Microsoft Excel-2000
1.1. Для
этого инсталировать (запустить)
программу Microsoft Excel-2000.
1.2. Ввести
данные (шаблон). Для этого в ячейке А1
записать «ВРЕМЯ»; в ячейке А2 «ПОКАЗАТЕЛЬ»
и далее числовые данные о времени и
уровнях моделируемого показателя
(Рис.3.1).
Рис.
3.1 Таблица исходных данных
1.3. Сохранить
таблицу данных в формате Microsoft Excel под
своей фамилией в буфере. Для этого
выполнить действия: отметить сохраняемый
файл – меню «ФАЙЛ» — «СОХРАНИТЬ»
(засветиться содержимое папки «Мои
документы») – набрать имя сохраненного
файла (своей фамилии) – «СОХРАНИТЬ».
1.4. Свернуть
окно Excel .
Перенести файл исходных данных в
среду Microsoft Word-2000
и сохранить (для создания будущего
отчета по лабораторной работе).
2. Инсталяция
программы «СтатЭксперт»
2.1. Выполнить
последовательно действия: «ПУСК» —
«ПРОГРАММЫ» (в главном меню) – «Olymp»
— «СтатЭксперт» — «Не отключать макросы».
На экране появиться картинка «СтатЭксперт».
2.2. Дать
команду «Начало работы» — «OK».
Появиться таблица программы «СтатЭксперт».
3. Включить
режимы обработки программы
3.1. Активизировать
файл исходных данных, выполнив
последовательно действия: «ФАЙЛ» — выбор
имени файла из всплывающего меню в
формате Excel.
3.2. Отметить
цифровые данные таблицы.
3.3. Вызвать
меню «СтатЭкс» (вторая строка панели
инструментов), указать «ВРЕМЕННЫЕ РЯДЫ»
(появиться окно «Установка блока данных»)
(Рис. 3.2).
Рис.
3.2 Окно «Установки блока данных»
4. Предварительная
обработка данных
4.1. Ориентация
таблицы: флажок в окно «по строкам»,
либо «по колонкам» (в зависимости от
ориентации шаблона).
4.2. Наличие
наименований: убрать все флажки в окнах.
4.3. Команда
«Установить» (появиться окно «Обработка
временных рядов»).
Окно
«Обработка временных рядов» (Рис.
3.3).
Рис.
3.3 Окно «Обработка временных рядов»
4.4. Этапы
обработки: флажок в окно «Предварительный
анализ».
4.5. Выделяем
щелчком левой кнопки мышки «Показатель
2».
4.6. Команда
«Вычислить» (появиться окно «Предварительный
анализ данных»). Работа в окне
«Предварительный анализ данных»
(Рис.3.4).
Рис.
3.4 Окно «Предварительный анализ данных»
4.7. Оставить
все флажки, кроме «Построение графиков».
4.8. Команда
«Вычислить».
4.9. При
обнаружении аномальных данных в
моделируемом временном ряду нажать
клавишу «Да» и выполнить рекомендации
всплывающего сообщения.
5. Полученный
протокол отчета (Рис.3.5)
|
Cтатистики |
|||
|
Базисные |
|||
|
Наблюдение |
Абс. |
Темп |
Темп |
|
2 |
1 |
200 |
100 |
|
3 |
2 |
300 |
200 |
|
4 |
3 |
400 |
300 |
|
5 |
4 |
500 |
400 |
|
6 |
5 |
600 |
500 |
|
7 |
6 |
700 |
600 |
|
8 |
7 |
800 |
700 |
|
9 |
8 |
900 |
800 |
|
10 |
9 |
1000 |
900 |
|
11 |
10 |
1100 |
1000 |
|
12 |
11 |
1200 |
1100 |
|
13 |
12 |
1300 |
1200 |
|
14 |
13 |
1400 |
1300 |
|
15 |
14 |
1500 |
1400 |
|
16 |
15 |
1600 |
1500 |
|
Цепные |
|||
|
Наблюдение |
Абс. |
Темп |
Темп |
|
2 |
1 |
200 |
100 |
|
3 |
1 |
150 |
50 |
|
4 |
1 |
133,333 |
33,333 |
|
5 |
1 |
125 |
25 |
|
6 |
1 |
120 |
20 |
|
7 |
1 |
116,667 |
16,667 |
|
8 |
1 |
114,286 |
14,286 |
|
9 |
1 |
112,5 |
12,5 |
|
10 |
1 |
111,111 |
11,111 |
|
11 |
1 |
110 |
10 |
|
12 |
1 |
109,091 |
9,091 |
|
13 |
1 |
108,333 |
8,333 |
|
14 |
1 |
107,692 |
7,692 |
|
15 |
1 |
107,143 |
7,143 |
|
16 |
1 |
106,667 |
6,667 |
|
Средние |
|||
|
Характеристика |
Значение |
||
|
Среднее |
8,5 |
||
|
Средний |
120,303 |
||
|
Средний |
20,303 |
||
|
Средний |
1 |
||
|
Гипотеза |
|||
|
Метод |
Результат |
||
|
Метод |
Нет |
||
|
Метод |
Нет |
||
|
Вывод: |
|||
|
Проверка |
|||
|
Аномальные |
|||
|
Автокорреляционная |
|||
|
Лаг |
Исходный |
Разностный |
|
|
1 |
0,813 |
0,8 |
|
|
2 |
0,628 |
0,604 |
|
|
3 |
0,449 |
0,414 |
|
|
4 |
0,279 |
0,236 |
|
|
Cтандартные |
|||
|
Частная |
|||
|
Лаг |
Исходный |
Разностный |
|
|
1 |
0,871 |
0,86 |
|
|
2 |
-0,01 |
-0,012 |
|
|
3 |
-0,011 |
-0,012 |
|
|
4 |
-0,097 |
-0,103 |
|
|
Cтандартные |
Рис.
3.5 Отчет по предварительной обработке
данных 1
6. Построение
модели и прогнозирование
6.1. Включить
режимы обработки программы: активизировать
файл исходных данных (шаблон) в
формате Excel,
отметить цифровые данные таблицы.
6.2. Вызвать
меню «СтатЭкс» (верхняя строчка), указать
«ВРЕНМЕННЫЕ РЯДЫ» (появиться окно
«Установка блока данных»).
6.3. Предварительная
обработка данных: ориентация таблицы
(в зависимости от ориентации шаблона),
наличие наименований (убрать все флажки
в окнах); команда «Установить» (появиться
окно «Обработка временных рядов») (Рис.
3.6).
Рис.
3.6 Окно «Обработка временных рядов».
6.4. Этапы
обработки: флажок в окно «Построение
моделей и прогнозирование»; выделяем
щелчком левой кнопки мышки «Показатель
2»; команда «Вычислить» (появиться окно
«Построение моделей и прогнозирование»)
(Рис. 3.7).
Рис.
3.7 Окно «Построение моделей и
прогнозирование»
6.5. Класс
моделей: «Кривые роста».
6.6. Тип
прогноза: «Прогноз вперед».
6.7. Способ
построения прогноза: «На основе одной
лучшей модели».
6.8. Структура
отчета: все флажки кроме «Статистика
ретропрогноза».
6.9. Период
прогноза: в соответствии с условием
задачи.
6.10. Вероятность
свершения прогноза: в соответствии с
условием задачи.
6.11. «Вычислить».
7. Формирование
отчета по графикам (Рис. 3.8)
Рис.
3.8 Окно «Графики отчета»
|
Модели |
||||
|
Таблица |
||||
|
Функция |
Критерий |
Эластич |
||
|
Y(t)=+46.600+0.885*t |
127,948 |
0,139 |
||
|
Y(t)=+45.296+1.320*t |
137,503 |
0,138 |
||
|
Y(t)= |
129,298 |
0,135 |
||
|
Y(t)= |
127,600 |
0,097 |
||
|
Y(t)= |
138,782 |
0,000 |
||
|
Y(t)= |
137,229 |
0,125 |
||
|
Y(t)= |
142,344 |
0,084 |
||
|
Выбрана |
||||
|
Характеристики |
||||
|
Модель |
Адекват |
Точность |
Качество |
|
|
Y(t)= |
78,106 |
2,251 |
21,215 |
|
|
Лучшая |
||||
|
Параметры |
||||
|
Модель |
a1 |
a2 |
||
|
Y(t)= |
43,793 |
5,390 |
||
|
Таблица |
||||
|
номер |
Факт |
Расчет |
Ошибка |
Ошибка |
|
1 |
41,000 |
43,793 |
-2,793 |
-6,813 |
|
2 |
52,000 |
47,529 |
4,471 |
8,598 |
|
3 |
62,000 |
49,714 |
12,286 |
19,816 |
|
4 |
40,000 |
51,265 |
-11,265 |
-28,162 |
|
5 |
44,000 |
52,467 |
-8,467 |
-19,244 |
|
6 |
56,000 |
53,450 |
2,550 |
4,553 |
|
7 |
68,000 |
54,281 |
13,719 |
20,175 |
|
8 |
41,000 |
55,001 |
-14,001 |
-34,148 |
|
9 |
47,000 |
55,635 |
-8,635 |
-18,373 |
|
10 |
60,000 |
56,203 |
3,797 |
6,328 |
|
11 |
71,000 |
56,717 |
14,283 |
20,117 |
|
12 |
44,000 |
57,186 |
-13,186 |
-29,968 |
|
13 |
52,000 |
57,617 |
-5,617 |
-10,802 |
|
14 |
64,000 |
58,017 |
5,983 |
9,349 |
|
15 |
77,000 |
58,388 |
18,612 |
24,171 |
|
16 |
47,000 |
58,736 |
-11,736 |
-24,971 |
|
Характеристики |
||||
|
Характеристика |
Значение |
|||
|
Среднее |
0,000 |
|||
|
Дисперсия |
111,650 |
|||
|
Приведенная |
127,600 |
|||
|
Средний |
9,463 |
|||
|
Относительная |
17,849 |
|||
|
Критерий |
2,245 |
|||
|
Коэффициент |
0,963 |
|||
|
F |
369,465 |
|||
|
Критерий |
78,106 |
|||
|
Критерий |
2,251 |
|||
|
Критерий |
21,215 |
|||
|
Уравнение |
||||
|
Таблица |
||||
|
Упреждение |
Прогноз |
Нижняя |
Верхняя |
|
|
1 |
59,063 |
53,119 |
65,008 |
|
|
2 |
59,371 |
53,205 |
65,537 |
|
|
3 |
59,663 |
53,283 |
66,043 |
|
Рис.
3.9 Отчет по предварительной обработке
данных 2
7.1. В
активном окне протокола «Стат
Эксперт» нажать ярлык диаграммы (слева
от окна, второй ярлык сверху). В появившимся
меню выбрать «Аппроксимация и прогноз»
(Рис. 3.8) (появиться график – Рис. 3.10).
Рис.3.10
График аппроксимация и прогноз
Поделиться…
|
← |
ЭММ |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 3 мин
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
куда:
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
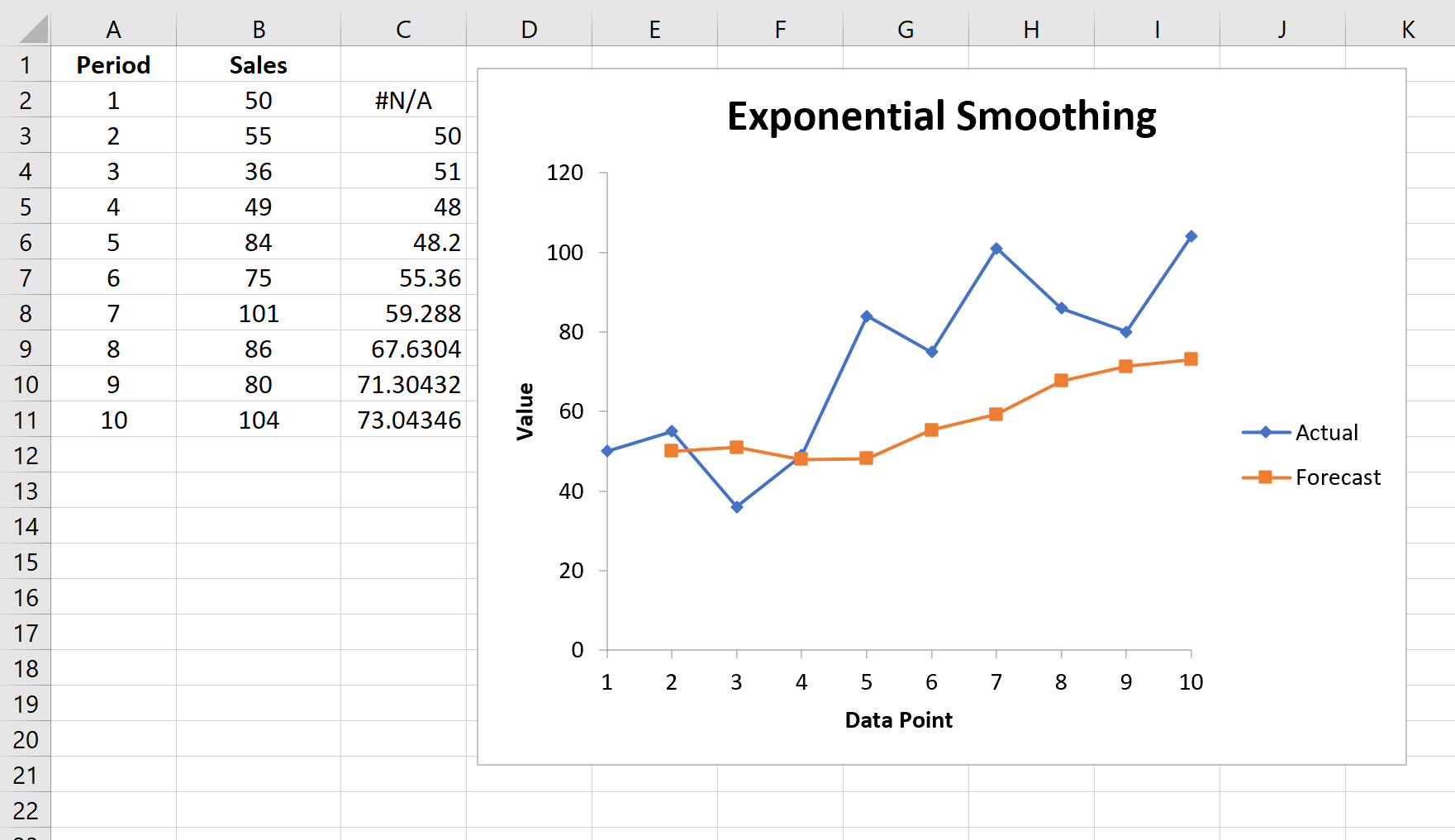
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
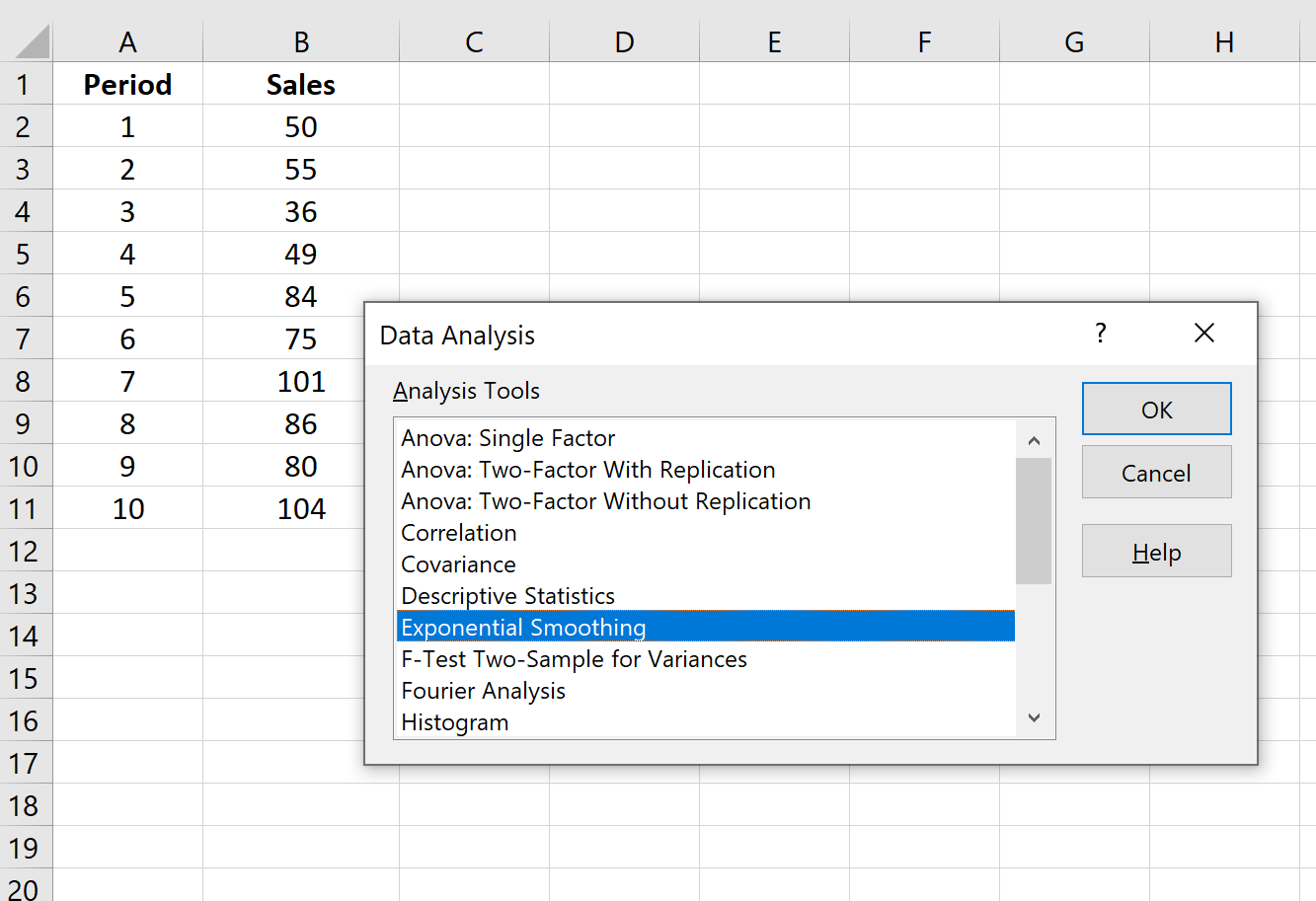
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
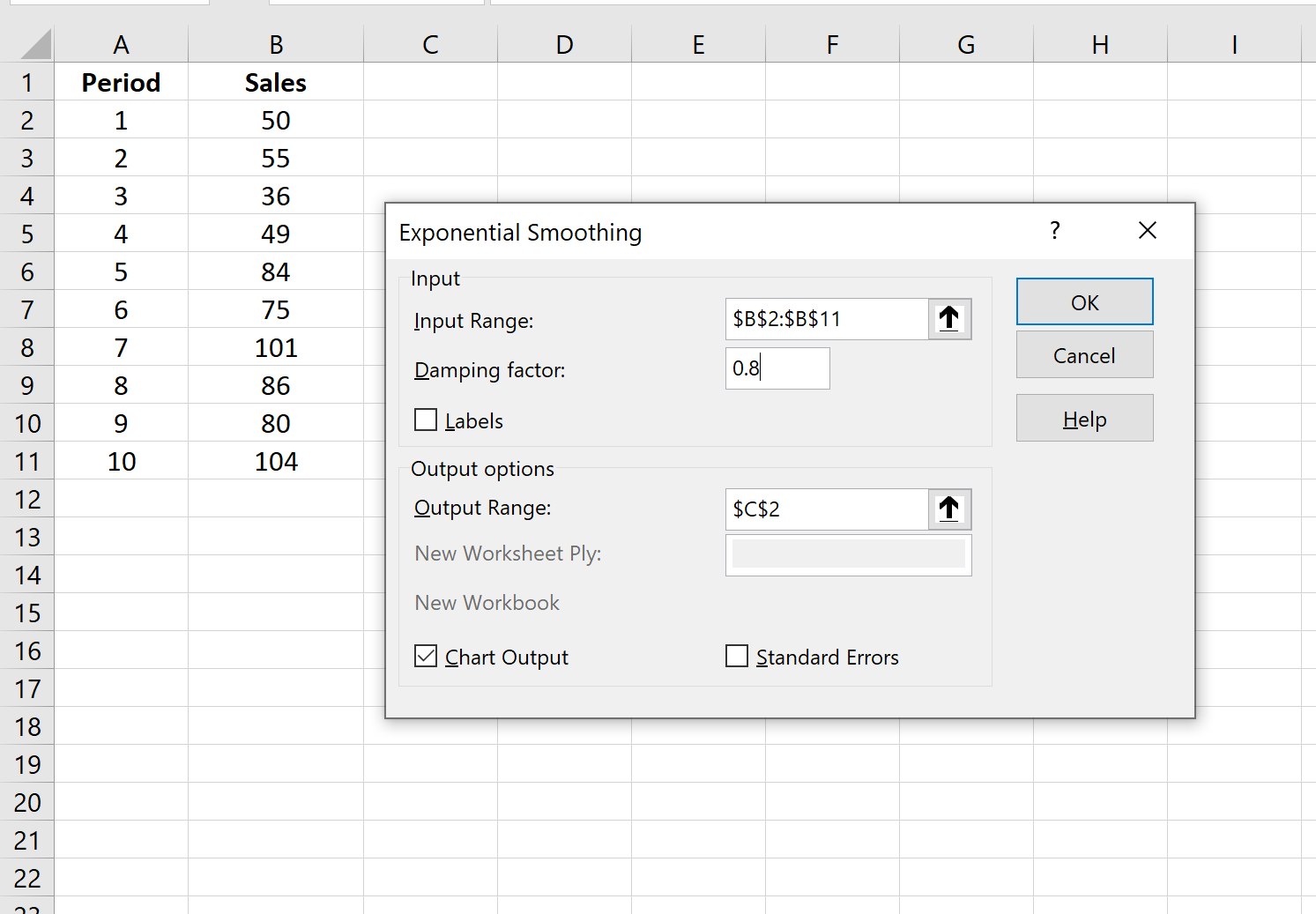
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
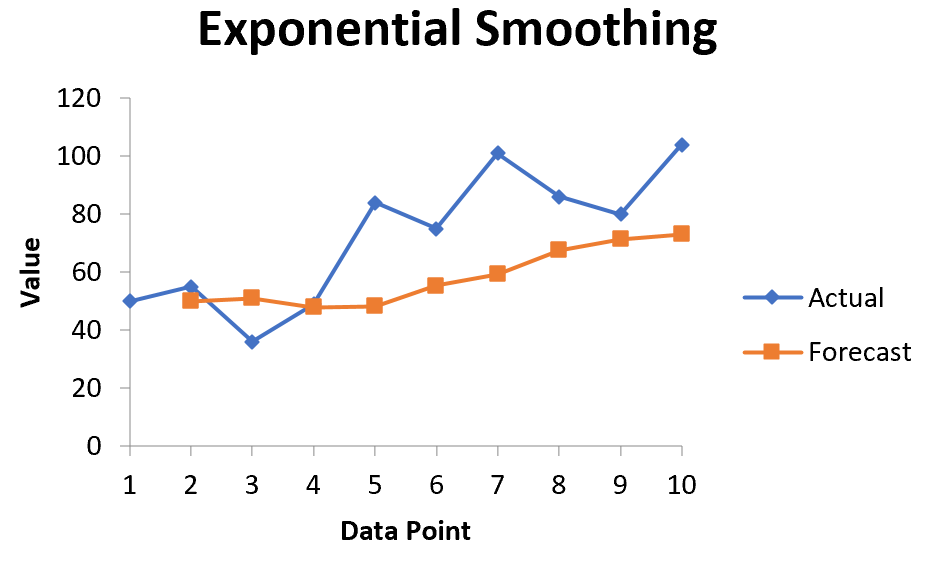
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
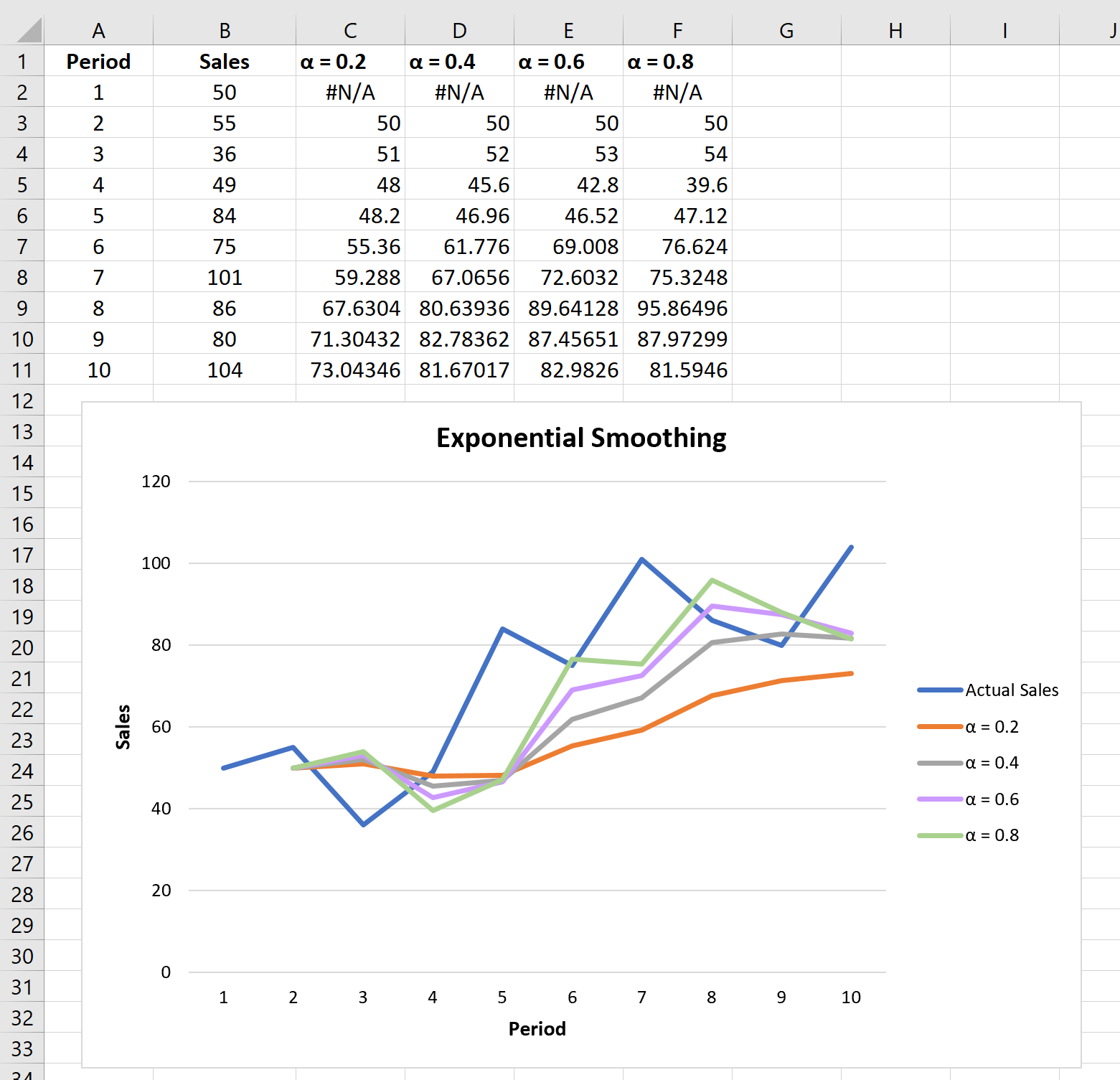
Эксперименты с коэффициентами сглаживания
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .