Продолжая тему решения транспортных задач средствами MS Excel, рассмотрим вариант, когда количество запасов меньше потребностей и у поставщиков есть обязательства перед потребителями. Другими словами, решаем несбалансированную транспортную задачу с обязательными поставками.
Смотрите также видеоверсию статьи «Решение транспортной задачи в Excel (задача с обязательными поставками)».
Решение простой сбалансированной транспортной задачи можно найти здесь, а решение простой несбалансированной задачи – здесь.
В основном, задача с обязательными поставками повторяет условие задачи с дисбалансом между спросом и предложением.
|
Поставщик |
Потребитель |
Запас |
||
| В1 | В2 | В2 | ||
| А1 | 6 | 5 | 2 | 250 |
| А2 | 3 | 7 | 4 | 100 |
| А3 | 7 | 8 | 1 | 80 |
| А4 | 2 | 2 | 3 | 80 |
|
Потребность |
150 | 150 | 250 |
Запасов меньше потребностей на 40 единиц, соответственно необходимо ввести фиктивного поставщика, сбалансировать задачу и решить ее в Excel. Вся процедура была описана ранее, здесь повторяться не будем, а остановимся на тех отличиях, которые появляются в связи с обязательными поставками.
Допустим, у первого поставщика есть обязательство перед потребителем B3 в обязательной поставке 200 единиц товара, а у второго – перед потребителем B2, в обязательной поставке 80 единиц товара.
Записанное условие в таблицах MS Excel выглядит следующим образом:
Здесь объемы обязательных поставок записаны просто для ориентира, самого ограничение на поставки накладывается в механизме «Поиск решения».
И решение транспортной задачи с обязательными поставками:
Как видим, минимальная стоимость перевозки несколько больше предыдущей задачи (1690 против 1280), поскольку контракты на обязательную поставку снизили общую эффективность перевозки.
Также можно скачать файл MS Excel с проведенными расчетами (на листах находятся различные типы задач):
-
Решение несбалансированной транспортной задачи
Пусть
необходимо организовать оптимальные
по транспортным расходам перевозки
муки с двух складов в три хлебопекарни.
Ежемесячные запасы муки на складах (т),
ежемесячные потребности хлебопекарен
(т) и транспортные расходы (руб./т) по
доставке муки представлены в таблице
(Таблица 21). В связи с ремонтными работами
временно невозможна перевозка из второго
склада в третью хлебопекарню.
Таблица 21
Транспортные
расходы по доставке муки (руб./т)
-
Хлебопекарни
Запас, мешки
Склады
Х1
Х2
Х3
С1
16
9
19
1667
С2
18
5
ремонт
2265
Потребность, мешки
1512
556
2609
-
Построение
модели
Построим
математическую модель для данной
транспортной задачи.
1 шаг. Определение переменных
Обозначим
через
[меш.] количество мешков с мукой, которые
будут перевезены сi-го
склада вj-ю хлебопекарню.
2 шаг. Проверка сбалансированности
задачи
Для
данной ТЗ имеет место соотношение (0)
|
|
(0) |
Ежемесячный
суммарный запас муки на складах меньше
суммарной потребности хлебопекарен на
4677-3932=745 мешков муки, откуда следует
вывод: ТЗ не сбалансирована.
3 шаг. Построение сбалансированной
транспортной матрицы
Сбалансированная транспортная матрица
представлена ниже (Таблица 22).
Для
установления баланса необходим
дополнительный фиктивный
склад, то есть дополнительная строка в
транспортной таблице задачи.
Фиктивные
тарифы перевозки зададим таким образом,
чтобы они были дороже реальных тарифов,
например,
50,00
руб./меш.
Невозможность
доставки грузов со второго склада в
третью хлебопекарню задается в модели
с помощью запрещающего
тарифа, который должен превышать величину
фиктивного
тарифа.
В нашей
задаче, например,
руб./меш.
Таблица 22
Транспортная матрица задачи
-
Хлебопекарни
Запас, мешки
Склады
Х1
Х2
Х3
С1
16
9
19
1667
С2
18
5
100,00
2265
Сф
50,00
50,00
50,00
745
Потребность, мешки
1512
556
2609
4677
4 Шаг. Задание целевой функции
Формальная
ЦФ, то есть суммарные затраты на все
возможные перевозки муки, учитываемые
в модели, задается следующим выражением:
|
|
(0) |
При
этом следует учитывать, что вследствие
использования фиктивных тарифов,
реальнаяЦФ (то есть средства, которые
в действительности придется заплатить
за транспортировку муки) будет меньшеформальнойЦФ (0) на стоимость
найденных в процессе решения фиктивных
перевозок.
5 Шаг. Задание ограничений
|
|
(0) |
-
Нахождение решения транспортной задачи в Microsoft Excel
Задание 13
Найдите оптимальный план перевозок,
используя MicrosoftExcel,
для этого выполните следующие действия:
-
Запустите приложение MicrosoftExcel.
-
Откройте из папки МАТ_МОД файл lab_3(b),
содержащий экранную форму для ввода
условия задачи. -
Введите исходные данные в экранную
форму. -
Проверьте выполнение условия баланса,
для этого:
-
в ячейку G9введите
формулуСУММ(C9:F9), а в ячейкуH8введите формулуСУММ(H3:H5); -
если суммы равны, то в ячейке H9
напишитеБАЛАНС (Рис. 24).
-
Введите зависимости из математической
модели (0), (0) в экранную форму,
воспользовавшись подсказкой, приведенной
ниже (Таблица 23).
Таблица 23
Соседние файлы в папке Исслед_опер
- #
24.04.201517.92 Кб148lab_3(b).xls
- #
24.04.201517.92 Кб88lab_3(а).xls
- #
24.04.201527.14 Кб114lab_4(a).xls
- #
24.04.201523.04 Кб91lab_4(b).xls
- #
24.04.201519.97 Кб143lab_5.xls
- #
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Задача о назначениях является частным случаем классической транспортной задачи и, как следствие, является задачей транспортного типа.
Транспортная задача – задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пункта производства (станций отправления), в пункты потребления (станции назначения) – является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта.
Во время решения некоторых математических задач приходится назначать исполнителей (людей, механизмы и т.п.) для выполнения некоторых однотипных работ. При этом дополнительно известны значения сij — эффективность (неэффективность) выполнения i-м исполнителем j-ой работы. Требуется распределить исполнителей по работам таким образом, чтобы максимизировать (минимизировать) суммарный критерий эффективности (неэффективности) выполнения всех работ.
Данная задача носит название «задача о назначениях» и является частным случаем более общей транспортной задачи. Если число исполнителей равно числу выполняемых работ, то такая задача является сбалансированной, в противном случае — не сбалансированной. В случае сбалансированной задачи о назначениях выполняются два условия: каждый исполнитель выполняет только одну работу и каждая работа выполняется только одним исполнителем.
1. Сбалансированная и несбалансированная задача о назначениях и ее решение в среде ЭТ MSExcel и математического пакета MathCad
1.1. Сбалансированная задача о назначениях
Задача о назначениях может быть сформулирована различными способами. Решить задачу о назначении − распределить исполнителей (людей или механизмы) по имеющимся работам так, чтобы обеспечить выполнение всех работ с минимальными суммарными затратами. При этом, если количество исполнителей равно количеству выполняемых работ, то задача о назначениях является сбалансированной. Задача о назначениях является частным случаем транспортной задачи.
Пусть управление механизации имеет n подъемных кранов, с помощью которых требуется возвести n объектов. Известна себестоимость cij строительства каждым краном отдельного объекта. Требуется так распределить подъемные краны по объектам, чтобы обеспечить возведение всех объектов с минимальными суммарными затратами.
Для решения поставленной задачи сформулируем её математическую модель, первоначально сведя исходные данные в следующую таблицу:
Таблица 2. Исходные данные к сбалансированной задаче о назначениях
|
Обьект Оj Кран Кi |
О1 |
О2 |
… |
Оn |
|
K1 |
C11 |
C12 |
… |
C1n |
|
K2 |
C21 |
C22 |
… |
C2n |
|
… |
… |
… |
… |
… |
|
Kn |
Cn1 |
Cn2 |
… |
Cnm |
Для решения сформулированной задачи составим ее математическую модель.
1.2 Математическая модель задачи
Математическая модель сбалансированной задачи. Для построения математической модели задачи:
1. Определим неизвестные и их количество.
Введем переменные xij, которые равны 1, если i-й кран работает нa j-м объекте, и 0, если он не работает там. Так как областью допустимых изменений каждой переменной xij является не множество неотрицательных чисел, а конечное множество (0,1), то мы имеем дискретную задачу оптимизации. Таким образом, бинарные (двоичные) элементы xij образуют матрицу назначений Xnхn.
2. Запишем целевую функцию – суммарные затраты на возведение всех объектов
3. Сформулируем ограничения рассматриваемой задачи:
3.1. Каждый кран может работать только на одном объекте. Т. е. каждая строка матрицы назначений Х содержит только один элемент, равный 1, а все остальные равны 0. Таким образом, сумма элементов каждой строки матрицы Х равна единице. Это ограничение можно записать в виде:
3.2. Каждый объект может возводиться только одним краном. Т. е. каждый столбец матрицы назначений Х содержит только один элемент, равный 1, а все остальные равны 0. Это ограничение можно записать:
3.3. Бинарность переменных xij. Поскольку переменные xij принимают значения или 1 или 0, то ограничение запишем в виде:
xij − бинарные (двоичные). (4)
Совокупность целевой функции (1) и ограничений (2− 4) образует математическую модель типичной экстремальной комбинаторной задачи о назначении. Решение такой задачи представляет собой некоторую перестановку чисел, а количество перестановок с ростом n резко возрастает и равно N = n!. Для задачи, приведенной ниже, N = 3! =1 · 2 · 3 = 6, а для n = 7 число перестановок составляет 5040. Задача относится к классу задач линейного программирования, так как ограничения и целевая функция имеют линейный вид, т. е. искомые переменные xij находятся в первой степени.
Более подробно разберем сбалансированную задачу о назначениях на следующем примере:
Требуется:
1. Выполнить математическую постановку задачи линейного программирования (ЗЛП);
2. Решить ЗЛП в среде электронных таблиц MS Excel и пакета Mathcad.
Пусть управление механизации имеет 3 подъемных крана и управлению требуется возвести 3 объекта. Известна себестоимость (тыс. руб.) возведения каждым краном отдельного объекта. Исходная информация представлена в таблице.
Таблица 3 – Данные для сбалансированной задачи о назначениях
|
Объект Оj Кран Кi |
О1 |
О2 |
О3 |
|
K1 |
C11 |
C12 |
C13 |
|
K2 |
C21 |
C22 |
C23 |
|
K3 |
C31 |
C32 |
C33 |
Требуется распределить подъемные краны по объектам так, чтобы обеспечить возведение всех объектов с минимальными суммарными затратами. Для решения сформулированной задачи составим ее математическую модель.
1.3Решение в среде ЭТ MSExcel
Для решения задачи с помощью надстройки «Поиск решения» в среде ЭТ MS Excel необходимо:
1. создать таблицу для ввода условий задачи и ввести исходные данные.
2. Запишем матрицу затрат на выполнение работ С3х3.
3. Составим матрицу назначений Х3х3 с пока нулевыми значениями элементов xij.
4. Дополните матрицу перевозок столбцом справа и строкой снизу, в которые запишите суммы элементов соответствующих строк и столбцов.
5. Дополним матрицу перевозок столбцом справа и строкой снизу, в которые запишем суммы элементов соответствующих строк и столбцов.
Рисунок 8 – MS Excel-документ решения сбалансированной задачи о назначениях
6. Записать целевую функцию F(X), используя встроенную функцию MS Excel – СУММПРОИЗВ().
7. Вызвать диалоговое окно надстройки «Поиск решения» и выполнить необходимые установки.
Рисунок 9 – MS Excel-документ настройки поиск решения для сбалансированной задачи о назначениях
8. Сохраним полученное решение.
1.4 Решение с помощью пакета MathCad
Для решения задачи в среде пакета MathСad:
1. Зададим исходные данные.
2. Определим вектор-столбцы переменных Х и затрат С.
3. Определим целевую функцию – минимальные затраты.
4. Вызовем блок решения, занесем в него ограничения.
5. Найдем оптимальное решение с помощью функции Minimize.
Рисунок 10 – MathCad-документ решения сбалансированной задачи о назначениях
2.1 Несбалансированная задача о назначениях
Рассмотрим теперь решение несбалансированной задачи о назначениях, когда число исполнителей n не равно числу выполняемых работ m.
Таблица 4 – Исходные данные для несбалансированной задачи о назначениях
|
Работы Pj Исполнители Иi |
P1 |
P2 |
… |
Pm |
|
И1 |
С11 |
С12 |
… |
С1n |
|
И2 |
C21 |
C22 |
… |
C2n |
|
… |
… |
… |
… |
… |
|
Иn |
Cn1 |
Cn2 |
… |
Cnm |
При этом возможны два случая:
а) число исполнителей n больше числа выполняемых работ m (n > m),
б) число исполнителей n меньше числа выполняемых работ m (n < m).
В обоих случаях для решения несбалансированной задачи ее сводят к сбалансированной, путем введения фиктивных работ или фиктивных исполнителей с нулевыми значениями сij – эффективности (неэффективности) выполнения i-м исполнителем j-й работы.
В первом случае, когда n > m, вводится k = n – m фиктивных работ Pm+1, Pm+2, …, Pm+k. Во втором случае (n < m) – рассматриваются k = m – n фиктивных исполнителя Иn+1,Иn+2, …, Иn+k.
Решим задачу о назначениях, когда 6 исполнителей претендуют на выполнение 4 работ. Таблица себестоимостей (тыс. руб.) выполнения претендентами каждой из четырех работ представлена ниже.
Таблица 5 – Исходные данные для несбалансированной задачи о назначениях
|
Работы Pj Исполнители Иi |
P1 |
P2 |
P3 |
P4 |
|
И1 |
75 |
30 |
10 |
25 |
|
И2 |
20 |
35 |
40 |
50 |
|
И3 |
15 |
55 |
70 |
65 |
|
И4 |
25 |
30 |
20 |
100 |
|
И5 |
30 |
40 |
55 |
60 |
|
И6 |
70 |
80 |
25 |
30 |
Требуется распределить претендентов по четырем работам так, чтобы обеспечить выполнение всех работ с минимальными суммарными затратами.
Для решения сформулированной задачи составим ее математическую модель. Математическая модель несбалансированной задачи о назначениях. Для построения математической модели задачи сведем ее к сбалансированной введением фиктивных работ Р5 и Р6, себестоимость выполнения которых для всех претендентов равна 0. После этого составляем математическую модель по алгоритму, приведенному в решении сбалансированной задачи о назначениях.
2.2 Решение задачи в среде ЭТ MSExcel
Для решения задачи с помощью
надстройки «Поиск решения» в среде ЭТ MS Excel необходимо:
1. Создадим таблицу для ввода условий задачи и введите исходные данные − матрицу себестоимостей С6х4.
3. Сформируем матрицу себестоимостей С6х6 сбалансированной задачи о назначениях.
4. Составим матрицу перевозок Х6х6 с нулевыми значениями xij.
5. Дополним матрицу перевозок столбцом справа и строкой снизу, в которые запишем суммы элементов соответствующих строк и столбцов.
6. Запишите целевую функцию F(X), используя встроенную функцию MS Excel СУММПРОИЗВ()
Рисунок 11 – MS Excel-документ исходных данных несбалансированной задачи о назначениях
7. Вызовем диалоговое окно надстройки «Поиск решения», и выполним необходимые установки.
Рисунок 12 – MS Excel-документ, надстройка поиск решения для несбалансированной задачи о назначениях
8. Сохраним полученное решение.
Рисунок 13 – MS Excel-документ решения несбалансированной задачи о назначениях
2.3 Решение с помощью пакета MathCad
Для решения задачи в среде пакета MathСad:
1. Зададим исходные данные, сведем несбалансированную задачу к сбалансированной
2. Определим вектор-столбцы переменных Х и затрат С.
3. Определим целевую функцию – минимальные затраты.
4. Вызовем блок решения, занесем в него ограничения.
5. Найдем оптимальное решение с помощью функции Minimize.
Рисунок 14 – MathCad-документ решения несбалансированной задачи о назначениях
Рисунок 15 – MathCad-документ решения несбалансированной задачи о назначениях
Решив эту задачу в среде ЭТ MS Excel и в математическом пакете Mathcad, мы получили одинаковые решения: минимальное значение целевой функция равна 85 т.руб.
ЗАКЛЮЧЕНИЕ
Данная работа показывает широкие возможности работы с пакетами ЭТ MS Excel и MathCad. Результатом данного исследования является решение сбалансированной и несбалансированной задачи о назначениях.
Как видно, результаты таблицы Excel и программы MathCad совпадаю, что говорит о правильном решении поставленной задачи. Так же, следует заметить, что решение задачи в среде MathCad требует больших затрат времени, а также, следует учесть, что в среде MathCad, нельзя задать ограничение целочисленности.
СПИСОК ЛИТЕРАТУРЫ
1. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986. – 321 с.
2. Математические методы и модели исследования операций: Учебник для студентов вузов/ под ред. В.А. Колемаева.–М.:ЮНИТИ-ДАНА, 209. – 592 с.
3. Супрун А.Н., Найденко В.В. Вычислительная математика для инженеров – экологов. – М.: АСВ, 1996. – 391с.
4. Леоненков А.В. Решение задач оптимизации в среде MS Excel СПб.: БХВ – Петербург, 2005. – 704 с.
5. И. Спира. Microsoft Excel и Word 2013. Учится некогда не поздно. Издательство: Питер, 2014. – 250 с.
6. Аверьянова С.Ю., Растеряев Н.В. Содержательные задачи линейного программирования и их решение с помощью ЭТ MS EXCEL и пакета MATHCAD: учебное пособие/Южный федеральный университет. –Ростов-на-Дону: Издательство ЮФУ, 2014. – 132 с.
7. Бородакий Ю.В. Линейное программирование в современных задачах оптимизации / Ю.В. Бородакий. – М.: МИФИ, 2008. – 564с.
8. Киселева Э.В. Математическое программирование (линейное программирование) / Э.В. Киселева, С.И. Соловьева. – Новосибирск: НГАСУ, 2002. – 256с.
9. Кремер Н.Ш. Исследование операций в экономике/ Н.Ш. Кремер. — М.:Юнити,2000. — 400 с.
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
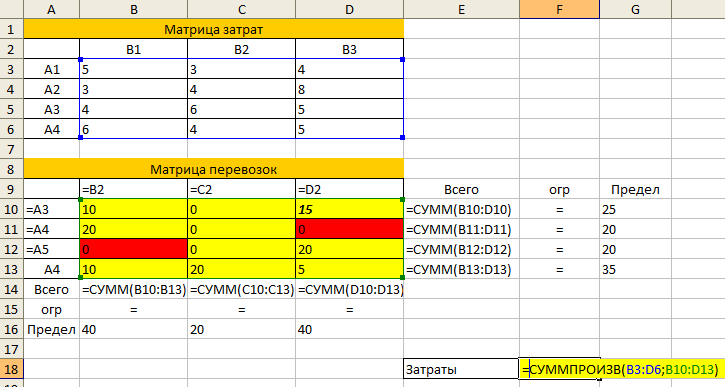
В режиме формул таблица будет выглядеть так:
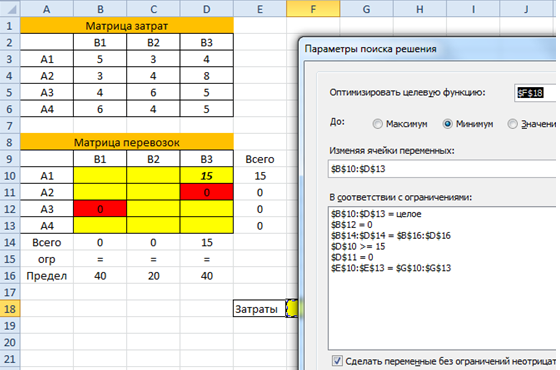
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
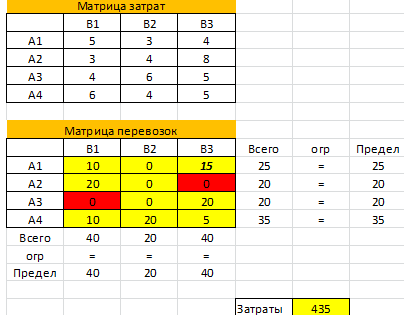
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Полезная страница? Сохрани или расскажи друзьям
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|
Цель работы: изучение технологии решения транспортных задач линейного программирования с использованием инструмента поиска оптимальных решений табличного процессора MS Excel.
Постановка задачи. Рассматривается логистическая задача минимизации затрат на доставку товаров от нескольких производителей, источников (заводов, складов) к нескольким потребителям (складам, магазинам). Поставка товара от конкретного производителя конкретному потребителю обычно может быть выполнена несколькими маршрутами с разной стоимостью перевозки по ним. Поэтому возможно определение оптимального маршрута и, соответственно, минимальной стоимости доставки единицы товара от конкретного производителя до потребителя. Особенностью задачи является однородность груза: потребителю не важно, с какого склада и каким маршрутом привёзен заказанный товар. Стоимость доставки любой партии условно принимается пропорциональной стоимости доставки единицы товара (вид транспорта, снижение/повышение стоимости доставок малых/крупных партий не учитывается). Подобные задачи решаются на уровне территориально распределённых транспортных, логистических и торговых компаний, подобным образом может осуществляться маршрутизация информации в сетях связи.
Исходные данные
1. Число поставщиков N и общее количество потребителей M. Для определённости принимается N = 5 и M = 3, что отражается в размерности последующих таблиц
2. Стоимости доставки единицы товара от каждого поставщика до каждого потребителя сведены в матрицу стоимостей перевозок С с элементами , где i = 1. M — номер потребителя; j = 1. N — номер поставщика.
Таблица 2.5.1
Таблица стоимостей перевозок
|
Стоимость перевозки единицы товара от поставщика к потребителю |
Поставщики |
|||
|
1 |
2 |
3 |
4 |
5 |
|
Потребители |
А |
|||
|
Б |
||||
|
В |
3. Каждый поставщик характеризуется наличием ресурса, где i = 1. N — номер поставщика.
4. Каждый потребитель характеризуется величиной потребности в ресурсе , где j = 1. M — номер потребителя
Описание решения
Предполагается, что транспортная задача сбалансированная, то есть запросы потребителей равны располагаемым ресурсам поставщиков:
. (2.5.1)
Требуется определить такие элементы матрицы перевозок (i = 1. M — номер потребителя; j = 1. N — номер поставщика), чтобы все потребности потребителей были обеспечены, все ресурсы поставщиков были потрачены, а общая стоимость затрат на перевозки W (целевая функция) была минимальной.
Таблица 2.5.2
Таблица объёмов перевозок
|
Объем перевозки товара от поставщика к потребителю |
Поставщики |
||||
|
1 |
2 |
3 |
4 |
5 |
Потребность |
|
Потребители |
А |
||||
|
Б |
|||||
|
В |
|||||
|
Объём располагаемого ресурса |
Целевая функция имеет вид
. (2.5.2)
Особенностью численного решения данной задачи является неотрицательность всех элементов матрицы объёмов перевозок: у программного пакета появляется «соблазн» уменьшения целевой функции за счёт выполнения некоторых перевозок в обратных направлениях, что математически соответствует получению прибыли от таких перевозок. Поэтому при решении транспортной задачи обязательным является ограничение на положительность объёмов перевозок
. (2.5.3)
Для сбалансированной задачи ограничениями при поиске целевой функции будут являться использование всех имеющихся ресурсов каждого поставщика (2.5.4) и обеспечение потребностей каждого покупателя (2.5.5):
для j = 1. M; (2.5.4)
для i = 1. N. (2.5.5)
Возможны два варианта несбалансированной задачи.
1. Суммарные потребности поставщиков превосходят общие потребности потребителей, т.е.
. (2.5.6)
Тогда все потребности потребителей должны быть выполнены, а некоторая часть ресурсов поставщиков окажется неизрасходованной, что приведёт к изменению знака в условии (2.5.4) с равенства на неравенство
2. Потребности потребителей превосходят имеющиеся ресурсы поставщиков, т.е.
. (2.5.7)
Тогда запросы потребителей будут обеспечены не полностью, что приведёт к изменению знака в условии (2.5.5) с равенства на неравенство.
В настоящей лабораторной работе транспортная задача будет решаться с помощью надстройки Поиск решения табличного процессора MS Excel.
Порядок решения задачи
1. Подготовка шаблона для решения задачи
По образцу фрагмента рабочего листа MS Excel, изображённого на рис.2.5.1, введите на новом листе матрицы объёмов и стоимостей перевозок. Транспортная задача пока не решена, поэтому матрица объёмов перевозок пока пуста. В рассчитываемые ячейки введите формулы, приведённые в табл.2.5.3
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
|
1 |
Таблица стоимостей перевозок |
||||||||
|
2 |
Оптовые базы |
||||||||
|
3 |
1 |
2 |
3 |
4 |
5 |
||||
|
4 |
Магазины |
А |
10 |
8 |
6 |
5 |
4 |
||
|
5 |
Б |
6 |
5 |
4 |
3 |
6 |
|||
|
6 |
В |
3 |
4 |
5 |
5 |
9 |
|||
|
7 |
|||||||||
|
8 |
Таблица объёмов перевозок |
||||||||
|
9 |
Оптовые базы |
||||||||
|
10 |
1 |
2 |
3 |
4 |
5 |
Всего |
Потребность |
||
|
11 |
Магазины |
А |
250 |
||||||
|
12 |
Б |
350 |
|||||||
|
13 |
В |
200 |
|||||||
|
14 |
Всего |
||||||||
|
15 |
Мощность |
120 |
200 |
190 |
210 |
80 |
|||
|
16 |
|||||||||
|
17 |
Целевая функция |
Рис. 2.5.1 Шаблон MS Excel для решения транспортной задачи
Таблица 2.5.3
Формулы Excel для решения транспортной задачи
|
Ячейка |
Формула |
Описание |
|
1 |
2 |
3 |
|
H11 |
=CУММ (С11: G11) |
Расчёт объёмов перевозок ресурса от всех оптовых баз (поставщиков) в каждый магазин (потребитель) |
|
H12 |
=CУММ (С12: G12) |
|
|
H13 |
=CУММ (С13: G13) |
|
|
С14 |
=СУММ (C11: C13) |
Расчёт объёмов перевозок ресурса от каждой оптовой базы (поставщика) всем магазинам (потребителям) |
|
D14 |
=СУММ (D11: D13) |
|
|
E14 |
=СУММ (E11: E13) |
|
|
F14 |
=СУММ (F11: F13) |
|
|
G14 |
=СУММ (G11: G13) |
|
|
C17 |
=СУММПРОИЗВ (C4: G6; C11: G13) |
Расчёт значения целевой функции — суммарной стоимости перевозок |
2. Настройка сервиса Поиск решения
Откройте окно Поиск решения, выполнив команду Сервис Поиск решения. Укажите в качестве целевой — ячейку С17, установите переключатель целевой ячейки в положение «минимальное значение». Введите в качестве изменяемых ячеек диапазон С11: G13.
Нажатием кнопки Добавить (условие) в окне Поиск решения последовательно введите ограничения поиска решения (2.5.3) — (2.5.5):
Таблица 2.5.4
Ограничения решения задачи для окна Поиск решения
|
Ссылка на ячейку |
Знак |
Ограничение |
|
$C$11: $G$13 |
>= |
0 |
|
$C$14: $G$14 |
= |
$C$15: $G$15 |
|
$H$11: $H$13 |
= |
$I$11: $I$13 |
Получившееся окно Поиска решения изображено на рис. 2.5.2.
Рис. 2.5.2 Настройки окна Поиск решения для сбалансированной транспортной задачи
После нажатия кнопки Выполнить в диалоговом окне Поиск решения откроется окно Результаты поиска решения с текстом «Решение найдено». Сохраните найденное решение и нажмите кнопку ОК. Результатом решения задачи оптимизации является таблица перевозок, соответствующая суммарной стоимости перевозок (целевой функции), равной 3330.
3. Решение несбалансированной транспортной задачи: запросы потребителей превосходят возможности отправителей
Решаемая в п.1 — 2 задача является сбалансированной, т.е. потребности получателей равны возможностям отправителей. В этом можно убедиться, введя функции =СУММ (I11: I13) и =СУММ (С15: G15) в ячейки I14 и С16 соответственно. Увеличьте потребность магазина Б до 550. При этом суммарная потребность всех магазинов будет равна 1000, а пропускная способность всех оптовых баз — 800. Естественно, что суммарный объём перевозок в этом случае не превысит 800, так как пропускная способность и потребителей, и поставщиков не может быть превышена исходя из требований здравого смысла. Для решения задачи в третьем ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) знак равенства замените на знак <=. После окончания процесса решения задачи суммарная стоимость перевозок (целевая функция) принимает значение 2990, т.е. уменьшится по сравнению со сбалансированной задачей. Однако магазины А и Б не обеспечивают свои потребности, так как возможности оптовых баз ограничены. Снижение общей стоимости перевозок при неизменном их объёме (800) стало возможным за счёт преобладания самых дешёвых маршрутов доставки: так, поставки в магазин Б увеличены с 350 до 520 единиц, а в магазин А — снижены с 250 до 80 единиц, так как в магазин Б доставлять товар в целом дешевле, чем в магазин А.
4. Решение несбалансированной транспортной задачи: предложение поставщиков превосходит потребности потребителей
Подобное соотношение на практике встречается чаще, чем в случае, рассмотренном в п.3. Восстановите потребность магазина Б до исходного значения 350, а пропускную способность (мощность) оптовой базы 5 увеличьте с 80 до 180 единиц. При этом суммарная потребность всех магазинов будет равна 800, а пропускная способность всех оптовых баз — 900. Суммарный объём перевозок в этом случае также не превысит 800 исходя из требований здравого смысла. Для решения задачи в третьем ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) восстановите знак равенства, а во втором ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) замените равенство на знак <=. После окончания процесса решения задачи суммарная стоимость перевозок (целевая функция) примет значение 3030, т.е. также уменьшится по сравнению со сбалансированной задачей. Однако на оптовой базе 2 образуется резерв пропускной способности 100 единиц, так как все потребности потребителей (магазинов) уже исполнены. Снижение общей стоимости перевозок при неизменном их объёме (800) также стало возможным за счёт выбора самых дешёвых маршрутов доставки.
5. Задача для самостоятельного решения
Имеется пять морских портов-отправителей грузов и четыре морских порта-получателя, между которыми необходимо оптимизировать перевозки. Таблица стоимостей перевозок, а также пропускные способности портов отправления и назначения по вариантам приведены в табл.2.5.5 и 2.5.6 Вариант задания выберите в соответствии с номером компьютера: первый вариант — для нечётных номеров, второй — для чётных.
Таблица 2.5.5
Исходные данные для самостоятельного решения транспортной задачи (вариант 1)
|
Исходные данные |
Порт-отправитель |
Пропускная способность получателя |
||||
|
1 |
2 |
3 |
4 |
|||
|
Порт — получатель |
А |
20 |
12 |
30 |
23 |
140 |
|
В |
47 |
14 |
38 |
18 |
160 |
|
|
С |
18 |
49 |
15 |
28 |
240 |
|
|
D |
23 |
34 |
22 |
30 |
180 |
|
|
E |
34 |
45 |
28 |
22 |
160 |
|
|
Пропускная способность отправителя |
200 |
350 |
180 |
150 |
Таблица 2.5.6
Исходные данные для самостоятельного решения транспортной задачи (вариант 2)
|
Исходные данные |
Порт-отправитель |
Пропускная способность получателя |
||||
|
1 |
2 |
3 |
4 |
|||
|
Порт — получатель |
А |
40 |
24 |
60 |
46 |
70 |
|
В |
94 |
28 |
76 |
36 |
80 |
|
|
С |
38 |
98 |
29 |
56 |
120 |
|
|
D |
46 |
68 |
90 |
60 |
90 |
|
|
E |
68 |
90 |
60 |
44 |
80 |
|
|
Пропускная способность отправителя |
100 |
175 |
90 |
75 |
5.1 Проверьте задачу на сбалансированность и решите её. Результаты решения сохраните на отдельном листе.
5.2 Решите несбалансированную задачу, аналогичную п.3. Для этого измените пропускную способность двух любых портов отправления на 20 единиц. Результаты решения сохраните на отдельном листе.
5.3 Решите несбалансированную задачу, аналогичную п.4. Для этого измените пропускную способность трёх любых портов назначения на 30 единиц. Результаты решения сохраните на отдельном листе.
Покажите полученную рабочую книгу MS Excel преподавателю.




 .
. .
.