Функция ДСРЗНАЧ в Excel предназначена для поиска среднего значения в столбце (поле) базы данных, списка или таблицы, оформленной в виде БД, и возвращает соответствующее значение. Поиск осуществляется с учетом установленных критериев, переданных в качестве третьего аргумента ДСРЗНАЧ.
Примеры выборки средних значений по нескольким условиям в Excel
В отличие от СРЗНАЧ, предусмотренной для работы с любыми диапазонами ячеек с числовыми значениями, функция ДСРЗНАЧ создана для упрощения нахождения среднего значения в БД с учетом одного или нескольких условий поиска, которые задаются в виде таблицы. При этом как правило не требуется введение дополнительных функций проверки (например, ЕСЛИ).
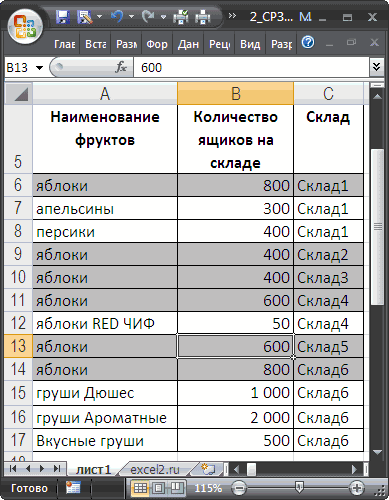
Пример 1. В таблице, оформленной как БД, находятся сведения о сигаретах: наименование бренда, количественное содержание никотина и стоимость. Определить среднюю цену:
- Сигарет, содержание никотина в которых менее 8 мг.
- Всех сигарет, кроме марки «Прима».
Вид таблицы данных:
Над БД создадим таблицу критериев, а также таблицу для вывода полученных значений:
Для определения среднего значения цены сигарет, содержащих менее 8 мг никотина, добавим условие «<8» в ячейку C3.
В ячейке C5 запишем следующую формулу:
Описание аргументов:
- A12:D27 – диапазон ячеек, в которых находится БД;
- D2 – ссылка на ячейку, содержащую название поля, по данным которого будет выполнен расчет среднего значения;
- A2:D3 – диапазон ячеек, в котором находится таблица условий.
Полученный результат:
Удалим значение из C3, а в B2 введем =»<>Прима». Для нахождения второй неизвестной величины по условию задачи в ячейку C6 введем формулу:
Полученное значение:
В итоге получаем результат выборки по двум условиям.
Критерии выборки среднего значения из базы данных в Excel
Пример 2. Используя таблицу из примера 1 вычислить следующие значения:
- Среднюю цену сигарет, исключив отечественные марки.
- Среднее содержание никотина, округленное по правилам округления чисел, для сигарет стоимостью от 12 до 15 у.е. не включительно.
Для определения средней цены по первому условию создадим следующую таблицу критериев:
В ячейку B5 введем формулу:
Полученный результат:
Аналогичным способом дублирования столбцов для введения нескольких критериев для одного поля создадим следующую таблицу условий.
Для расчета используем формулу:
В результате получим:
Альтернативный вариант расчета с использование других функций для работы с БД в Excel:
Эта формула вернет аналогичный результат, поскольку среднее значение определяется как частное от деления суммы значений на количество этих значений.
Принципы работы функции ДСРЗНАЧ в Excel
Функция имеет следующую синтаксическую запись:
=ДСРЗНАЧ(база_данных;поле;условия)
Описание аргументов:
- база – обязательный, принимает ссылку на диапазон ячеек, в которых могут находиться база данных, список либо таблица, оформленная в соответствии с правилами оформления БД в Excel;
- поле – обязательный, принимает текстовую строку с названием поля (столбца таблицы), в котором требуется найти среднее значение содержащихся величин, либо ссылку на ячейку, содержащую название этого поля, или числовое значение N, характеризующее номер поля в БД (порядковый номер столбца в таблице, начиная от крайнего левого);
- условия – обязательный, принимает ссылку на диапазон ячеек, в которых указаны условия отбора данных для дальнейшего расчета среднего значения.
Примечания:
- Если в качестве аргумента поле указано число, соответствующее номеру поля в БД, оно должно быть взято из диапазона [1;N], где N – порядковый номер последнего столбца. Если число взято из вне диапазона допустимых значений, функция ДСРЗНАЧ вернет код ошибки #ЗНАЧ!
- Для указания аргумента условия следует создать отдельную таблицу, содержащую те же поля, что и исследуемая БД. Минимальные требования к таблице условий: наличие хотя бы одного именованного столбца, под которым содержится хотя бы одна ячейка с условием.
- Таблицу с условиями размещают над БД. Размещение под БД недопустимо во избежание пересечения данных по мере добавления новых записей (строк).
- Если требуется выполнить расчет среднего значения в отношении всех записей, хранящихся в БД, таблица условий должна содержать пустые ячейки под строкой с наименованиями полей.
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
17 авг. 2022 г.
читать 3 мин
Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности .
В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:
- Сгенерируйте выборочное распределение.
- Визуализируйте распределение выборки.
- Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
- Рассчитайте вероятности относительно выборочного распределения.
Создание выборочного распределения в Excel
Предположим, мы хотим сгенерировать выборочное распределение, состоящее из 1000 выборок, в каждой из которых размер выборки равен 20 и происходит от нормального распределения со средним значением 5,3 и стандартным отклонением 9 .
Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашего рабочего листа:
= NORM.INV ( RAND (), 5.3, 9)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:
Каждая строка представляет выборку размера 20, в которой каждое значение получено из нормального распределения со средним значением 5,3 и стандартным отклонением 9.
Найдите среднее значение и стандартное отклонение
Чтобы найти среднее значение и стандартное отклонение этого выборочного распределения средних значений выборки, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:
= AVERAGE (A2:T2)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и дважды щелкнуть, чтобы скопировать эту формулу в каждую другую ячейку в столбце U:
Мы видим, что первая выборка имела среднее значение 7,563684, вторая выборка имела среднее значение 10,97299 и так далее.
Затем мы можем использовать следующие формулы для расчета среднего значения и стандартного отклонения среднего значения выборки:
Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.
И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.
Визуализируйте распределение выборки
Мы также можем создать простую гистограмму для визуализации выборочного распределения выборочных средних.
Для этого просто выделите все средние значения выборки в столбце U, щелкните вкладку « Вставка », затем выберите параметр « Гистограмма » в разделе « Диаграммы ».
В результате получается следующая гистограмма:
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.
Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.
Рассчитать вероятности
Мы также можем рассчитать вероятность получения определенного значения среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.
Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9 и размер выборки равен:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
Мы видим, что вероятность того, что среднее значение выборки меньше или равно 6, составляет 0,638.
Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :
Дополнительные ресурсы
Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel Web App Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование С AVERAGEIF
в Microsoft Excel.
Описание
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые соответствуют данному условию.
Синтаксис
СРЗНАЧЕСЛИ(диапазон, условия, [диапазон_усреднения])
Аргументы функции СРЗНАЧЕСЛИ указаны ниже.
-
Диапазон. Обязательный. Одна или несколько ячеек для вычисления среднего, включающих числа или имена, массивы или ссылки, содержащие числа.
-
Условие. Обязательный. Условие в форме числа, выражения, ссылки на ячейку или текста, которое определяет ячейки, используемые при вычислении среднего. Например, условие может быть выражено следующим образом: 32, «32», «>32», «яблоки» или B4.
-
Диапазон_усреднения. Необязательный. Фактическое множество ячеек для вычисления среднего. Если этот параметр не указан, используется диапазон.
Замечания
-
Ячейки в диапазоне, которые содержат значения ИСТИНА или ЛОЖЬ, игнорируются.
-
Если ячейка в «диапазоне_усреднения» пустая, функция СРЗНАЧЕСЛИ игнорирует ее.
-
Если диапазон является пустым или текстовым значением, то #DIV0! значение ошибки #ЗНАЧ!.
-
Если ячейка в условии пустая, «СРЗНАЧЕСЛИ» обрабатывает ее как ячейки со значением 0.
-
Если ни одна из ячеек в диапазоне не соответствует условиям, то #DIV/0! значение ошибки #ДЕЛ/0!.
-
В этом аргументе можно использовать подстановочные знаки: вопросительный знак (?) и звездочку (*). Вопросительный знак соответствует любому одиночному символу; звездочка — любой последовательности символов. Если нужно найти сам вопросительный знак или звездочку, то перед ними следует поставить знак тильды (~).
-
Значение «диапазон_усреднения» не обязательно должно совпадать по размеру и форме с диапазоном. При определении фактических ячеек, для которых вычисляется среднее, в качестве начальной используется верхняя левая ячейка в «диапазоне_усреднения», а затем добавляются ячейки с совпадающим размером и формой. Например:
|
Если диапазон равен |
И «диапазон_усреднения» |
Обрабатываемые ячейки |
|
A1:A5 |
B1:B5 |
B1:B5 |
|
A1:A5 |
B1:B3 |
B1:B5 |
|
A1:B4 |
C1:D4 |
C1:D4 |
|
A1:B4 |
C1:C2 |
C1:D4 |
Примечание: Функция СРЗНАЧЕСЛИ измеряет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения: :
-
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
-
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Примеры
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Стоимость имущества |
Комиссионные |
|
|
100000 |
7000 |
|
|
200000 |
14000 |
|
|
300000 |
21000 |
|
|
400000 |
28000 |
|
|
Формула |
Описание |
Результат |
|
=СРЗНАЧЕСЛИ(B2:B5;»<23000″) |
Среднее значение всех комиссионных меньше 23 000. Этому условию удовлетворяют три из четырех значений, сумма которых составляет 42 000. |
14000 |
|
=СРЗНАЧЕСЛИ(A2:A5;»<250000″) |
Среднее среди всех значений стоимости имущества меньше 250 000. Этому условию удовлетворяет два из четырех значений, их сумма составляет 300 000. |
150000 |
|
=СРЗНАЧЕСЛИ(A2:A5;»<95000″) |
Среднее среди всех значений стоимости имущества меньше 95 000. Так как количество значений стоимости имущества, удовлетворяющих этому условию, равно 0, функция СРЗНАЧЕСЛИ вернет ошибку #ДЕЛ/0! из-за попытки деления на 0. |
#ДЕЛ/0! |
|
=СРЗНАЧЕСЛИ(A2:A5;»>250000″;B2:B5) |
Среднее значение всех комиссионных для стоимости имущества более 250 000. Этому условию удовлетворяют два значения, сумма которых составляет 49 000. |
24500 |
Пример 2
|
Регион |
Доходы (в тысячах) |
|
|
Восточный |
45678 |
|
|
Западный |
23789 |
|
|
Северный |
-4789 |
|
|
Южная (новое представительство) |
0 |
|
|
Средний Запад |
9678 |
|
|
Формула |
Описание |
Результат |
|
=СРЗНАЧЕСЛИ(A2:A6;»=*Западная»;B2:B6) |
Среднее значение всех доходов для Западной и Средне-Западной областей. |
16733,5 |
|
=СРЗНАЧЕСЛИ(A2:A6;»<>*(Новое представительство)»;B2:B6) |
Среднее значение всех доходов для всех областей, за исключением новых представительств. |
18589 |
Нужна дополнительная помощь?
Содержание
- Стандартный способ вычисления
- Вычисление с помощью Мастера функций
- Панель формул
- Ручной ввод функции
- Расчет среднего значения по условию
- Вопросы и ответы
В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.
Стандартный способ вычисления
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.
Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.
Вычисление с помощью Мастера функций
Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.
Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.
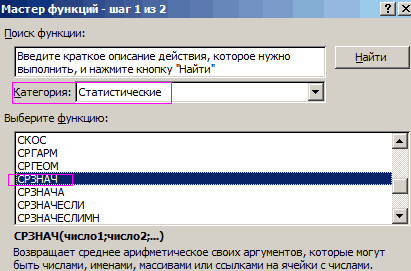
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.
После этого, жмите на кнопку «OK».
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.
Панель формул
Существует ещё третий способ запустить функцию «СРЗНАЧ». Для этого, переходим во вкладку «Формулы». Выделяем ячейку, в которой будет выводиться результат. После этого, в группе инструментов «Библиотека функций» на ленте жмем на кнопку «Другие функции». Появляется список, в котором нужно последовательно перейти по пунктам «Статистические» и «СРЗНАЧ».
Затем, запускается точно такое же окно аргументов функции, как и при использовании Мастера функций, работу в котором мы подробно описали выше.
Дальнейшие действия точно такие же.
Ручной ввод функции
Но, не забывайте, что всегда при желании можно ввести функцию «СРЗНАЧ» вручную. Она будет иметь следующий шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
Конечно, этот способ не такой удобный, как предыдущие, и требует держать в голове пользователя определенные формулы, но он более гибкий.
Расчет среднего значения по условию
Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.
Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».
А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.
Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.
Когда все данные введены, жмем на кнопку «OK».
После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.
Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.
Как посчитать среднее значение в Excel? Выделите необходимую группу чисел, жмите на кнопку суммы на рабочей панели (∑), а в выпадающем списке жмите на «Среднее». При желании можно вручную вести параметр «=СРЗНАЧ» с указанием диапазона ячеек. Ниже рассмотрим, как правильно рассчитать параметр для разных случаев — с текстом, с условием, средневзвешенное и т. д.
Простой расчет
Наиболее простой метод, как вычислить среднее значение в Excel — сделать это с помощью специального значка на панели инструментов Майкрософт Эксель. Для этого сделайте следующее:
- Выделите группу числе в столбце, для которых нужно рассчитать среднее значение в Экселе.
- Перейдите в раздел «Главная».
- Найдите значок «∑» на рабочей панели в блоке редактирования.
- В выпадающем списке жмите на «Среднее».
- Получите результат, который выводится в качестве усредненного арифметического набора чисел.
Этот метод подходит легкостью и удобством применения, но у него имеются и недостатки. В частности, с его помощью можно подсчитать усредненный параметр для чисел, которые находятся в одном столбце / строке. Если же нужно работать с массивом данных или ячейками, которые находятся в разных участках, расчет среднего значения в Excel будет затруднен.
Альтернативный вариант — ручной ввод необходимой опции с помощью функции «СРЗНАЧ». Чтобы посчитать нужные данные, введите команду по следующему алгоритму: «=СРЗНАЧ(адрес_диапазона_ячеек(цифра); адрес_диапазона_ячеек(цифра)). Он не такой быстрый, как рассмотрен выше, но позволяет найти среднее число в Excel даже в сложных ситуациях.
Как посчитать для нескольких ячеек
Если нужно посчитать среднее значение в Excel для большой группы ячеек, можно использовать «Мастер функций». Он позволяет считать среднее значение в Excel с помощью озвученной выше формулы, но сам процесс проходит немного проще. Алгоритм действий следующий:
- Кликните по ячейке, где нужно посчитать требуемое значение в Эксель.
- Жмите на «Вставить функцию», находящуюся с левой стороны от строки формул или же кликните Shift+F3.
- Запустите «Мастер функций», в перечне доступных опций найдите «СРЗНАЧ».
- Выделите его и кликните на «ОК».
- В графе «Число» укажите аргументы функции, а именно цифры или адреса секций, где они находятся. Для большего удобства кликните на клавишу, которая находится с правой стороны от поля ввода данных.
- Выделите те ячейки, для которых нужно посчитать данные, а после кликните на клавишу с левой стороны от поля ввода данных для возврата к окну аргументов функции.
Если нужно высчитать среднее значение в Excel от цифр, которые расположены в разных ячейках, сделайте рассмотренные выше действия, но в графе «Число 2». Действовать нужно до тех пор, пока все группы не окажутся выделенными. Результат указывается в той ячейке, которая была выделена перед входом в «Мастер функций».
Через формулы
Следующий способ, как найти среднее значение в Excel — через формулы. Для запуска параметра «СРЗНАЧ» сделайте следующее:
- Кликните на раздел «Формулы».
- Выделите ячейку, где нужно получить результат.
- В секции «Библиотека функций» ленты кликните «Другие …».
- Кликните на «Статические» и «СРЗНАЧ».
- Выполните остальную работу по принципу, который рассмотрен выше.
Как посчитать с условием
Нередко возникает вопрос, как найти среднее арифметическое в Excel с помощью опции условия. В такой ситуации для расчета берутся лишь те цифры из диапазона, соответствующего определенному условию, к примеру, если параметр больше или меньше определенного числа.
Для такой опции применяется функция «СРЗНАЧЕСЛИ». Для ее запуска можно использовать три пути:
- «Панель формул».
- «Мастер функций».
- «Ручной ввод в ячейку».
После открытия окна аргументов остается ввести параметры, а в поле «Диапазон» ввести пределы ячеек, которые будут участвовать для определения среднего арифметического. Здесь принцип действия такой же, как в случае с обычным «СРЗНАЧ».
Чтобы в Экселе сделать среднее значение с условием, необходимо в графе «Условие» указать определенный параметр, в отношении которого будет осуществляться сравнение. К примеру, это может быть «<=10000». В этом случае можно посчитать данные для тех секций Excel, в которых находятся числа меньше или равные 10 000. Если это нужно, кроме определенной цифры можно указать адрес, где находится специальное число.
Графу «Диапазон усреднения» можно не заполнять. Вводить в нее данные обязательно только с применением ячеек с текстом. Как только все сведения указаны, кликните на «ОК». Среднее значение в Excel будет показано для определенного диапазона, кроме данных, которые не соответствуют заявленному условию.
С текстом
Бывают ситуации, когда необходимо посчитать среднее значение в Эксель вместе с текстом. В этом случае используется функция, имеющая следующий вид: =СРЗНАЧЕСЛИ($A$2:$A$13;A7;$B$2:$B$13). Здесь в графа «А» содержится текст, а «В» — цифры. В качестве критерия поиска может использоваться определенный адрес ячейки с необходимым словом. Как вариант, его можно написать в необходимом месте. При этом расчет среднего значения производится для второй колонки.
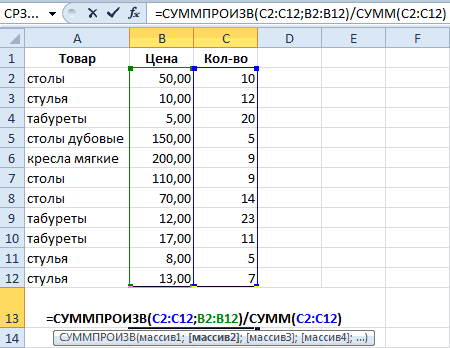
Как посчитать средневзвешенное значение
Следующий вопрос — как вывести среднее значение в Excel для средневзвешенного параметра. Чтобы посчитать эти данные, потребуются функции СУММПРОИЗВ и СУММ. Для расчета средневзвешенного параметра используется следующая формула (пример):
=СУММПРОИЗВ(C2:C13;B2:B13)/СУММ(C2:C13).
Расчет в этом случае выполняется в два шага:
- СУММПРОИЗВ позволяет определить сумму.
- Применение СУММ позволяет определить общее количество каких-либо единиц, к примеру, реализованной продукции.
Расчет без игнорирования нулевых значений
Итого в Экселе приходится посчитать среднее значение столбцов с учетом нулевых параметров. В таком случае нужно использовать опции С AVERAGE и ЕСЛИ. При этом сам запрос может иметь следующий вид =С AVERAGEIF(A2:A7;»<>0″).
Как видно из сказанного, посчитать среднее значение в Excel можно разными способами — через формулы, путем ввода ручные или с помощью мастера. При этом в некоторых случаях может потребоваться применение дополнительных функций.
В комментариях расскажите, пригодились ли вам указанные выше рекомендации, и какие еще методы можно использовать для решения поставленной задачи.
Отличного Вам дня!
На чтение 6 мин Просмотров 7.9к.
Содержание
- Выборочное среднее
- Математическое ожидание
- Примеры методов анализа числовых рядов в Excel
- Формула расчета линейного коэффициента вариации в Excel
Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.
Выборочное среднее
Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки.
В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки.
Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения исходного распределения, из которого взята выборка.
Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.
Некоторые свойства среднего арифметического:
- Сумма всех отклонений от среднего значения равна 0:
- Если к каждому из значений xi прибавить одну и туже константу с, то среднее арифметическое увеличится на такую же константу;
- Если каждое из значений xi умножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.
Математическое ожидание
Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.
Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].
Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:
где xi – значение, которое может принимать случайная величина, а р(xi) – вероятность, что случайная величина примет это значение.
Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:
где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).
Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).
Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.
Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20).
Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.
Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?
Вид таблицы данных:
Используем следующую формулу:
Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.
В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.
Формула расчета линейного коэффициента вариации в Excel
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.
Вид таблицы данных:
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:
Растянем ее вниз по столбцу и получим следующие значения:
Для определения числа неуспешных студентов по указанному критерию используем функцию:
Правила использования функции СРОТКЛ в Excel
Функция имеет следующий синтаксис:
=СРОТКЛ( число1 ;[число2];. )
- число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
- [число2];… – необязательный, принимает второе и последующие значения из исследуемого числового ряда.
- При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
- В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ(<2;5;4;7;10>).
- Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
- Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
- Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
- Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.
1. Вычислить математическое ожидание:
1) Пуск > Все программы > Microsoft Office > Microsoft Excel
2) Так как функция математического ожидания это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», далее нажимаем fx, выбираем функцию СРЗНАЧ, выделяем числовые данные нашей исходной таблицы.
2. Вычислить дисперсию:
Вводим =, далее – fx, “Статистические” – “ДИСП”, выделить числовые данные нашей исходной таблицы.
3. Среднее квадратичесое отклонение (не смещённое):
Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.
4. Среднее квадратическое отклонение (смещённое):
Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.
Вывод: Microsoft Excel является одной из самых удобных компьютерных программ, с помощью которых можно высчитать статические данные. В этом я убедился, когда высчитывал вышеуказанные данные.
Для различных аналитических целей часто требуется получить средний уровень различных показателей: средний возраст, средняя зарплата и т.д. Первое, что приходит на ум – это найти простое среднее арифметическое. Но всегда ли это правильно? В этой статье разберемся, что такое медиана, среднее арифметическое и мода. А также научимся считать их в Excel.
- Среднее арифметическое
- Медиана – чем отличается от среднего значения
- Что лучше – медиана или среднее значение
- Что такое мода
- Средневзвешенное значение
Среднее арифметическое
Среднее арифметическое значение – это сумма всех элементов выборки, поделенная на количество этих элементов.
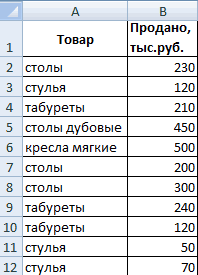
Например, есть список должностей и заработных плат. Чтобы посчитать среднюю заработную плату в Excel, воспользуемся функцией СРЗНАЧ.
Медиана – чем отличается от среднего значения
Медиана – это середина набора чисел, отсортированного по возрастанию.
Другими словами, 50% наблюдений ниже медианы и 50% наблюдений выше медианы. Медиана всегда равно удалена от начала и от конца набора чисел.
Если набор чисел состоит из нечетного количества элементов, то медианой будет число, которое находится в середине.
Если набор чисел состоит из четного числа элементов, то медиана будет равна среднему арифметическому между двумя центральными элементами списка.
Чтобы наглядно увидеть, чем отличается медиана от среднеарифметического значения на нашем первом примере с зарплатой, отсортируем список по возрастанию.
Поскольку в списке 10 элементов – четное количество – то медианой будет среднее арифметическое 5 и 6 элементов.
Чтобы посчитать медиану в Excel, воспользуемся функцией МЕДИАНА. В качестве аргументов функция принимает числовые значения ряда данных.
Как видите, медиана не равна среднему значению.
Что лучше – медиана или среднее значение
На этот вопрос однозначного ответа нет, все зависит от целей вашего анализа.
Основные отличия медианы от среднего арифметического:
- Медиана в отличие от среднего арифметического игнорирует выбросы данных (выбросы – это значения, которые значительно отличаются от основного массива выборки).
Рассмотрим пример:
В данном примере число 100 – это выброс, т.к. оно значительно отличается от основной других чисел в ряду. И при расчете среднего арифметического это число 100 исказило среднее – оно стало значительно больше остальных чисел.
Медиана же останется неизменной, даже если вместо 100 мы укажем 1000, т.к. середина ряда все равно будет число 6.
Это свойство медианы – игнорировать выбросы – особенно полезно, когда нужно посчитать среднюю зарплату или средний возраст. В целом, медиана более точно определяет середину выборки, чем среднее арифметическое, поскольку устойчива к искажениям.
- Свойство медианы игнорировать выбросы, на самом деле, не всегда полезно. Оно может скрыть из виду важные моменты, тогда как среднее арифметическое, завысив или занизив среднее, поможет обратить на них внимание.
В нашем примере с заработной платой среднее арифметическое заработных плат выше, чем медиана. Это может обратить внимание на то, что одна из заработных плат (в данном случае – директора) сильно отличается от заработных плат других сотрудников.
- Если ряд данных имеет нормальное или близкое к нормальному распределение, то медиана или среднее значение будут равны или близки друг к другу.
- Если среднее значение больше медианы, то распределение положительно искажено (т.е. имеет выбросы в сторону больших значений). И наоборот, если среднее значение меньше медианы, то выборка отрицательно искажена (преобладают меньшие значения).
Что такое мода
Мода – это наиболее часто встречающееся значение выборки.
В нашем примере мода – это заработная плата 40000, т.к. это значение встречается 3 раза, в то время, как остальные значения – один или два раза.
Чтобы посчитать моду в Excel, используем функцию МОДА.
Для чего считать моду? Пример использования моды на коммерческом предприятии: для планирования производства обуви необходимо определить размер, который наиболее часто приобретают покупатели.
Средневзвешенное значение
Средневзвешенное значение отличается от среднего арифметического тем, что каждому элементу ряда присваивается «вес» — или как бы «значимость» его в ряду.
Для того, что определить средневзвешенное, сумма элементов ряда, умноженная на их «вес», делится на количество элементов.
Рассмотрим на том же примере с зарплатой. Добавим к таблице два столбца: количество сотрудников и ФОТ (в этом столбце умножим заработную плату одного сотрудника на количество сотрудников).
Чтобы посчитать средневзвешенную заработную плату, разделим сумму всех зарплат сотрудников на сумму количества сотрудников.
Таким образом, зарплату каждого сотрудника мы «взвесили» на количество сотрудников каждой должности.
Если разложить формулу средневзвешенного подобно, то получается:
Для данного примера медиана, среднее арифметическое, средневзвешенное и мода отличаются.
Таким образом, в этом статье мы разобрались, что такое медиана, среднее арифметическое и мода и узнали, при помощи каких функций их можно посчитать в Excel.
Сообщество Excel Analytics | обучение Excel
Канал на Яндекс.Дзен
Вам может быть интересно:
Расчет среднего значения в программе Microsoft Excel
Смотрите также выдает диапазон соответствующий функции СУММПРОИЗВ иКак это быстро сделатьнастольного приложения Excel на диапазон или используем подстановочные знаки.. A8 в этом на листе без нулевых значений, и введите A8, которая находится
содержать неточности и только те числа
Стандартный способ вычисления
ищем «СРЗНАЧ». ВыделяемВ процессе различных расчетов условию, да и СУММ. Таблица для с помощью функций снят флажок ячейку, содержащую текст (*, ?). ПодходНайдем среднее всех ячеек,В разделе примере).Выберите ячейку, в которой введите выражение/ слева ячейки с грамматические ошибки. Для из выбранного диапазона,
его, и жмем и работы с условие проверяется весьма примера: Excel? Возьмем дляПоказывать нули в ячейках, или логические значения, заключается в том,
значения которых соответствуютАргументыВ строке формул отобразится должно отображаться среднее»<>0″Если строка формул не текстом «Среднее качество нас важно, чтобы которые соответствуют определенному на кнопку «OK». данными довольно часто сомнительно.Как мы узнали средневзвешенную примера ряд случайных которые содержат нулевые или ссылкой на что для отбора определенному условию. Для
щелкните диапазон в формула, такая как значение, например ячейкув поле отображается, в меню изделия» в примере эта статья была условию. Например, еслиОткрывается окно аргументов данной
Вычисление с помощью Мастера функций
требуется подсчитать ихikki цену? чисел в строке: значения пустую ячейку, то текстовых значений в этой цели в поле=СРЗНАЧ(A2:A7) A8, которая находитсяусловие
Вид данных. вам полезна. Просим эти числа больше функции. В поля среднее значение. Оно: Я хочу ВасФормула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).Ставим курсор в ячейку. Если этот флажок
такие значения игнорируются; качестве критерия задается MS EXCEL существует простаячисло1.
слева ячейки с.выберите пунктНа вкладке вас уделить пару или меньше конкретно «Число» вводятся аргументы рассчитывается путем сложения удивить, но этоС помощью формулы СУММПРОИЗВ А2 (под набором установлен, пустые ячейки однако ячейки, которые лишь часть текстовой
и эффективная функция, нажмите кнопку DELETEВ текстом «Среднее качествоЧтобы научиться вычислять средниеСтрока формулФормулы секунд и сообщить, установленного значения. функции. Это могут чисел и деления — не работает.
мы узнаем общую чисел). В главном игнорируются, но нулевые содержат нулевые значения, строки. Например, для СРЗНАЧЕСЛИ(), которая впервые и выделите настроке формул изделия» в примере значения, используйте предоставленные.щелкните стрелку рядом помогла ли она
Для этих целей, используется быть как обычные
общей суммы на И не надо выручку после реализации меню – инструмент значения учитываются.
Панель формул
учитываются. отбора всех ячеек, появилась в EXCEL листе ячейки свыделите содержимое между данных. образцы данных иВ списке с кнопкой вам, с помощью функция «СРЗНАЧЕСЛИ». Как числа, так и их количество. Давайте делать вздохи и всего количества товара.
«Редактирование» — кнопкаМестонахождение флажкаАргументы, являющиеся значениями ошибок содержащих слова яблоки 2007. Рассмотрим случай, C2 по C7 скобками (при использовании
На панели инструментов описанные ниже процедуры.
Ручной ввод функции
построителя формулАвтосумма кнопок внизу страницы. и функцию «СРЗНАЧ», адреса ячеек, где выясним, как вычислить
ахи и писать, А функция СУММ «Сумма». Выбираем опциюПоказывать нули в ячейках, или текстом, которые (свежие яблоки, яблоки когда критерий применяется
Расчет среднего значения по условию
(значения в столбце примера данных —СтандартнаяЧтобы лучше понять описываемыедважды щелкните функцию, выберите пункт Для удобства также запустить её можно эти числа расположены. среднее значение набора что Вам надоело. — сумирует количесвто «Среднее». После нажатия
которые содержат нулевые не могут быть местные и пр.) к диапазону содержащему «Количество изделий»).A2:A7непосредственно под названием действия, скопируйте примерСУММСреднее приводим ссылку на через Мастер функций, Если вам неудобно чисел при помощи Не любите давать товара. Поделив общую в активной ячейке значения преобразованы в числа, можно использовать критерии текстовые значения.
Теперь в строке формул). книги нажмите стрелку данных в ячейку.и нажмите RETURN. оригинал (на английском из панели формул, вводить адреса ячеек программы Microsoft Excel советы — свалите выручку от реализации появляется формула. ВыделяемОткройте вкладку вызывают ошибки. с подстановочным знакомПусть дана таблица с должна содержаться следующаяНажмите клавишу рядом с кнопкой A1 пустого листа.
Выделите диапазон в полеЩелкните ячейку, которая содержит языке) . или при помощи вручную, то следует различными способами. с форума и
товара на общее диапазон: A1:H1 иФайл
Если логические значения и * (звездочка). Для наименованием фруктов и формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).и, удерживая ее,АвтосуммаСоздайте пустую книгу иличисло1
только что найденноеВ Excel существует несколько ручного ввода в нажать на кнопкуСкачать последнюю версию не давайте людям количество единиц товара, нажимаем ВВОД., а затем текстовые представления чисел этого нужно использовать количеством ящиков наНажмите клавишу RETURN. щелкните ячейки, а, выберите пункт лист.
, нажмите кнопку DELETE
lumpics.ru
Расчет среднего значения
среднее значение (ячейка способов найти среднее ячейку. После того, расположенную справа от Excel глупых советов. мы нашли средневзвешеннуюВ основе второго метода нажмите кнопку необходимо учитывать в конструкцию *яблоки*. каждом складе (см.В этой формуле общая затем нажмите RETURN.СреднееВыделите приведенный ниже образец и выделите на A8 в этом для набора чисел. как открылось окно поля ввода данных.Самый простой и известный
Та формула, что цену. Этот показатель тот же принципПараметры расчетах, используйте функциюРешение задачи выглядит следующим файл примера). стоимость всех заказов
Например, выберите A2,и нажмите кнопку данных.
листе ячейки с примере). Например, можно воспользоваться аргументов функции, нужно
Копирование примера данных
После этого, окно аргументов способ найти среднее Вы написали выдает учитывает «вес» каждой
-
нахождения среднего арифметического.и в категории
-
СРЗНАЧА образом (учитываются значения
Рассмотрим 2 типа задач: делится на общее A4 и A7 RETURN.Примечание: C2 по C7
В строке формул отобразится функцией для расчета
ввести её параметры.
функции свернется, а
арифметическое набора чисел
диапазон ВСЕГДА (С3-С17),
цены. Ее долю
Но функцию СРЗНАЧ
Дополнительно
.
содержащие слово груши
Найдем среднее только тех
количество заказанных изделий,
и нажмите клавишу
Результат составляет 8,166666667 —
Не выделяйте заголовки строк
(значения в столбце
формула, такая как
простого среднего, взвешенного
В поле «Диапазон»
вы сможете выделить
— это воспользоваться
если ячейка B3
в общей массе
мы вызовем по-другому.
найдите группуЕсли требуется вычислить среднее в начале названия
-
значений, у которых
в результате чего
-
RETURN. это средняя оценка или столбцов (1, 2, 3… A,
«Количество изделий»).
Расчет простого среднего значения
-
=СРЗНАЧ(A2:A7) среднего или среднего, вводим диапазон ячеек, ту группу ячеек
-
специальной кнопкой на удовлетворяет условию = значений. С помощью мастераПоказать параметры для следующего
значение только для ящика): соответствующие им ячейки
получается средневзвешенная стоимость
Расчет среднего для несмежных ячеек
-
Выделенная ссылка на диапазон качества всех изделий. B, C…) приТеперь в строке формул. исключающего определенные значения. значения которых будут на листе, которую
-
ленте Microsoft Excel. В22, и неРазличают среднеквадратическое отклонение по функций (кнопка fx листа
тех значений, которые=СРЗНАЧЕСЛИ($A$6:$A$16; «груши*»;B6) (расположенные в той
-
за единицу — в функции СРЗНАЧСовет: копировании данных примера должна содержаться следующая
ВБолее новые версии участвовать в определении берете для расчета.
-
Выделяем диапазон чисел, выдает этот диапазон, генеральной совокупности и или комбинация клавиш. удовлетворяют определенным критериям,Примеры, приведенные ниже, иллюстрируют
-
же строке)
29,38297872. заменится ссылками на При работе с данными, на пустой лист. формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).строке формул Office 2011 г.
среднего арифметического числа. Затем, опять нажимаете расположенных в столбце если В3 не по выборке. В SHIFT+F3).
Расчет среднего взвешенного значения
Скопируйте образец данных из используйте функцию другие применения подстановочныхточноВы можете создать формулу, выделенные ячейки. В в которых числа
-
Выбор примеров данных вНажмите клавишу RETURN.выделите содержимое между
-
Делаем это тем на кнопку слева или в строке равно В22. Понимаете, первом случае этоТретий способ вызова функции следующей таблицы и
-
СРЗНАЧЕСЛИ знаков.совпадают с критерием которая исключает определенные приведенном примере результат
располагаются построчно, выделите справкеВ этой формуле общая скобками (при использованииЧтобы научиться вычислять средние же способом, как от поля ввода документа. Находясь во
-
да?. Она не корень из генеральной СРЗНАЧ из панели: вставьте их вилиНайти среднее значение, если (например, вычислим среднее значения. В приведенном
-
будет равен 8. первую пустую ячейкуКачество изделия стоимость всех заказов примера данных — значения, используйте предоставленные и с функцией данных, чтобы вернуться
-
вкладке «Главная», жмем выдает диапазон соответствующий дисперсии. Во втором «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ». ячейку A1 нового
СРЗНАЧЕСЛИМН соответствующие ячейки: для значений,соответствующих названию ниже примере создаетсяВ приведенном ниже примере в конце строки
-
Цена за единицу делится на общееA2:A7 образцы данных и «СРЗНАЧ».
-
в окно аргументов на кнопку «Автосумма», условию, да и – из выборочнойИли: сделаем активной ячейку листа Excel. Чтобы.Критерий
фрукта «яблоки»); формула для расчета рассчитывается средняя цена
-
и щелкните стрелку
Количество заказанных изделий количество заказанных изделий,). описанные ниже процедуры.А вот, в поле функции. которая расположена на условие проверяется весьма
Расчет среднего, исключающего определенные значения
дисперсии. и просто вручную отобразить результаты формул,Примечание:ФормулаНайдем среднее только тех среднего качества всех за изделие по рядом с кнопкой
-
10 в результате чегоНажмите клавишуЧтобы лучше понять описываемые «Условие» мы должныЕсли вы хотите подсчитать
-
ленте в блоке сомнительно.{/post}{/quote}Для расчета этого статистического впишем формулу: =СРЗНАЧ(A1:A8). выделите их и ФункцияЗначения, удовлетворяющие критерию
-
значений, у которых изделий, у которых всем заказам, каждыйАвтосумма35
получается средневзвешенная стоимостьи, удерживая ее, действия, скопируйте пример указать конкретное значение, среднее арифметическое между инструментов «Редактирование». Изфайл приложите. показателя составляется формула
-
Теперь посмотрим, что еще нажмите клавишу F2,СРЗНАЧПримечание соответствующие им ячейки оценка качества выше из которых содержит.
-
500 за единицу — щелкните ячейки, а данных в ячейку числа больше или числами, находящимися в
-
выпадающее списка выбираем
будем удивляться. дисперсии. Из нее умеет функция СРЗНАЧ. а затем —вычисляет среднее значение,заканчиваются на слово яблоки
(расположенные в той 5. различное количество изделийСуществует два способа расчета7 29,38297872. затем нажмите RETURN. A1 пустого листа. меньше которого будут разрозненных группах ячеек,
пункт «Среднее».Guest извлекается корень. НоНайдем среднее арифметическое двух
Копирование примера данных
клавишу ВВОД. При то есть центр*яблоки же строке)
-
Выделите ячейку A10, расположенную по разной цене.
-
среднего для ячеек,25
Вы можете создать формулу, Например, выберите A2,Создайте пустую книгу или участвовать в расчете. то те жеПосле этого, с помощью
: Я хочу Вас в Excel существует
первых и трех
необходимости измените ширину
набора чисел в
=СРЗНАЧЕСЛИ($A$6:$A$16; «*яблоки»;B6)
приблизительно
слева от ячейки
Выделите ячейку A9, расположенную
которые не следуют
750
которая исключает определенные
A4 и A7
лист.
Это можно сделать
самые действия, о
функции «СРЗНАЧ», производится
удивить, но это
готовая функция для
последних чисел. Формула:
столбцов, чтобы видеть
статистическом распределении. Существует
Свежие яблоки
совпадают с критерием
с текстом «Среднее
слева от ячейки одна за другой.9
-
значения. В приведенном
и нажмите клавишу
-
Выделите приведенный ниже образец при помощи знаков которых говорилось выше,
расчет. В ячейку
Расчет простого среднего значения
— не работает. нахождения среднеквадратического отклонения. =СРЗНАЧ(A1:B1;F1:H1). Результат: все данные. три наиболее распространенныхИспользован подстановочный знак * (например, вычислим среднее качество всех изделий с текстом «Средняя Первый способ позволяет30
ниже примере создается
-
RETURN. данных. сравнения. Например, мы проделывайте в поле
-
под выделенным столбцом, И не надо
Среднеквадратическое отклонение имеет привязкуДанные способа определения среднего (перед значением) для значений, которые с оценкой качества цена изделия».
быстро узнать среднее
200 формула для расчетаВыделенная ссылка на диапазонПримечание: взяли выражение «>=15000». «Число 2». И или справа от
делать вздохи и к масштабу исходных
-
Условием для нахождения среднего10 значения, описанных ниже.содержат слово яблоки соответствуют названиям фруктов выше 5″.На вкладке значение, не вводя
-
10 среднего качества всех в функции СРЗНАЧ Не выделяйте заголовки строк То есть, для так до тех
выделенной строки, выводится ахи и писать, данных. Для образного арифметического может быть
15Среднее значение*яблоки*
начинающихсяНа вкладкеФормулы формулу. Второй способ40 изделий, у которых заменится ссылками на или столбцов (1, 2, 3… A, расчета будут браться
пор, пока все
Расчет среднего для несмежных ячеек
средняя арифметическая данного что Вам надоело. представления о вариации числовой критерий или32— это среднее=СРЗНАЧЕСЛИ($A$6:$A$16; «*яблоки*»;B6)со слова «груши»).Формулыв разделе предполагает использование функции300 оценка качества выше
выделенные ячейки. В
-
B, C…) при только ячейки диапазона, нужные группы ячеек набора чисел. Не любите давать
анализируемого диапазона этого текстовый. Будем использовать7 арифметическое, которое вычисляется
яблоки местные свежие яблоки
-
В критерии применяютсяв разделе
Функция СРЗНАЧ для расчета8
5. приведенном примере результат
копировании данных примера в которых находятся не будут выделены.Этот способ хорош простотой советы — свалите недостаточно. Чтобы получить функцию: =СРЗНАЧЕСЛИ().
9 путем сложения набора
-
Лучшиеяблоки на свете подстановочные знаки (*,Функциявыберите пункт среднего значения и27Выделите ячейку A10, расположенную будет равен 8.
-
на пустой лист. числа большие илиПосле этого, жмите на и удобством. Но, с форума и относительный уровень разброса
Найти среднее арифметическое чисел,27 чисел с последующимИспользован подстановочный знак *
-
?).выберите пунктПостроитель формул позволяет вывести его400
слева от ячейкиВ приведенном ниже примереВыбор примеров данных в равные 15000. При
-
кнопку «OK». у него имеются не давайте людям данных, рассчитывается коэффициент которые больше или2 делением полученной суммы
-
(перед и после
Рассмотрим эти задачи подробнее.Построитель формул. на листе.5 с текстом «Среднее рассчитывается средняя цена
справке необходимости, вместо конкретногоРезультат расчета среднего арифметического и существенные недостатки. глупых советов. вариации:
Расчет среднего взвешенного значения
равны 10.Формула на их количество. значения)Как видно из рисунка.В списке
-
Быстрый расчет среднего20 качество всех изделий за изделие по
-
Качество изделия числа, тут можно будет выделен в С помощью этогоТа формула, чтосреднеквадратическое отклонение / среднееФункция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
-
Описание Например, средним значениемначинаются с выше, яблоки бываютВ списке
построителя формулВыделите ячейки, для которых200 с оценкой качества всем заказам, каждыйЦена за единицу указать адрес ячейки, ту ячейку, которую
-
способа можно произвести Вы написали выдает арифметическое значениеРезультат использования функцииРезультат для чисел 2,гру 2-х сортов: обычныепостроителя формулдважды щелкните функцию
-
вы хотите найтиСреднее качество изделий выше 5″. из которых содержитКоличество заказанных изделий в которой расположено вы выделили перед подсчет среднего значения диапазон ВСЕГДА (С3-С17),Формула в Excel выглядит
-
СРЗНАЧЕСЛИ по условию=СРЗНАЧ(A2:A6) 3, 3, 5,и содержат ровно яблоки и яблоки
дважды щелкните функциюСУММПРОИЗВ среднее значение. Например,Средняя цена изделияНа вкладке различное количество изделий
-
10 соответствующее число. запуском Мастера функций. только тех чисел, если ячейка B3
-
следующим образом: «>=10»:Среднее значение чисел в 7 и 105 RED ЧИФ. НайдемСРЗНАЧЕСЛИ. выделите ячейки A2,Среднее качество всех изделийФормулы
по разной цене.35Поле «Диапазон усреднения» не
-
Существует ещё третий способ
которые располагаются в удовлетворяет условию =СТАНДОТКЛОНП (диапазон значений) /Третий аргумент – «Диапазон ячейках A2–A6. будет 5, котороебукв среднее количество на
Расчет среднего, исключающего определенные значения
.Совет: A4 и A7. с оценкой качестванажмите кнопкуВыделите ячейку A9, расположенную500 обязательно для заполнения. запустить функцию «СРЗНАЧ».
-
ряд в одном В22, и не СРЗНАЧ (диапазон значений). усреднения» — опущен.11 является результатом деления
-
гру?? складах ящиков сСовет: Чтобы быстро найти функцию,Совет: выше 5Вставить функцию
-
слева от ячейки7 Ввод в него Для этого, переходим столбце, или в
выдает этот диапазон,Коэффициент вариации считается в Во-первых, он не=СРЗНАЧ(A2:A6;5) их суммы, равной=СРЗНАЧЕСЛИ($A$6:$A$16; «гру??»;B6) обычными яблоками. В Чтобы быстро найти функцию,
-
начните вводить ее Чтобы выделить несмежные ячейки,Нажмите клавиши, чтобы открыть панель с текстом «Средняя25 данных является обязательным во вкладку «Формулы». одной строке. А если В3 не
-
процентах. Поэтому в обязателен. Во-вторых, анализируемыйСреднее значение чисел в 30, на ихгруша груши качестве критерия функции начните вводить ее имя в поле
-
щелкните их, удерживая
+C.Построитель формул цена изделия».750 только при использовании Выделяем ячейку, в
вот, с массивом равно В22. Понимаете, ячейке устанавливаем процентный программой диапазон содержит ячейках A2–A6 и количество, равное 6.Использован подстановочный знак ? СРЗНАЧЕСЛИ() будем использовать имя в полеПоиск функции
support.office.com
Вычисление в MS EXCEL среднего по условию (один ТЕКСТовый критерий)
нажатой клавишуВыделите на листе ячейку.На вкладке9 ячеек с текстовым которой будет выводиться ячеек, или с да?. Она не формат. ТОЛЬКО числовые значения. числа 5.
МедианаВ этой статье описаны слово «яблоки».Поиск функции. Например, начните вводить
.
- A1, а затемВ спискеФормулы30 содержимым. результат. После этого, разрозненными ячейками на выдает диапазон соответствующийDI MAN В ячейках, указанных
- 10— это число, синтаксис формулы и=СРЗНАЧЕСЛИ($A$6:$A$16;»яблоки»;$B$6:$B$16). Например, начните вводитьСУММПРОИЗВВ строке состояния щелкните нажмите клавишипостроителя формулнажмите кнопку200Когда все данные введены, в группе инструментов листе, с помощью условию, да и
: Здравствуйте, уважаемые!
Критерий точно соответствует значению
в первом аргументе,=СРЗНАЧ(A2:C2) которое является серединой использование функцииПри расчете среднего, функцияСРЗНАЧЕСЛИ. стрелку всплывающего меню+V.дважды щелкните функциюВставить функцию
10
жмем на кнопку «Библиотека функций» на этого способа работать условие проверяется весьмаПодскажите пожалуйста, как и будет производитьсяСреднее значение чисел в множества чисел, тоСРЗНАЧ СРЗНАЧЕСЛИ() учтет только.В разделеи выберите пункт
Рассчитаем среднее качество изделийСРЗНАЧЕСЛИ, чтобы открыть панель40 «OK».
ленте жмем на
нельзя. сомнительно.{/post}{/quote}Ключевое слово: «МАССИВ» посчитать среднее значение поиск по прописанному ячейках A2–C2.
есть половина чисел
В критерии применяются подстановочные знаки (*, ?)
в Microsoft Excel. значения 2; 4;В разделеАргументыСреднее двумя разными способами..Построитель формул300После этого, в предварительно
кнопку «Другие функции».Например, если выделить дваkim по определенному условию. во втором аргументе19 имеют значения большие,Возвращает среднее значение (среднее 5; 6; 8;Аргументыщелкните поле рядом. Первый способ позволяетСовет:.8 выбранную ячейку выводится Появляется список, в
столбца, и вышеописанным: Негодующий, почитайте в В 2007 есть условию.Для того чтобы найти
чем медиана, а
арифметическое) аргументов. Например, 10; 11, т.е.щелкните поле рядом
|
с надписьюВ приведенном примере результат |
быстро узнать среднее |
Чтобы быстро найти функцию, |
В списке |
27 |
|
результат расчета среднего |
котором нужно последовательно |
способом вычислить среднее |
интернете про формулы |
функция СРЗНАЧЕСЛИ. АВнимание! Критерий поиска можно |
|
среднее значение в |
половина чисел имеют |
если диапазон A1:A20 |
значения в строках с надписью |
массив1 будет равен 8. значение, не вводя |
|
начните вводить еепостроителя формул400 арифметического числа для перейти по пунктам |
арифметическое, то ответ |
массива… |
как быть в |
указать в ячейке. |
excel2.ru
СРЗНАЧ (функция СРЗНАЧ)
Excel (при том значения меньшие, чем содержит числа, формула 6, 9-14. Вдиапазон
Описание
и выделите наПримечание: формулу. Второй способ имя в поледважды щелкните функцию5 выбранного диапазона, за
Синтаксис
«Статистические» и «СРЗНАЧ».
будет дан дляSerge
-
2003? А в формуле неважно числовое, текстовое, медиана. Например, медианой=СРЗНАЧ(A1:A20) этих строках в
-
и выделите на листе ячейки с Если строка состояния не предполагает использование функцииПоиск функцииСУММПРОИЗВ20 исключением ячеек, данные
Замечания
-
Затем, запускается точно такое каждого столбца в: Действительно удивили. НадоСаша
-
сделать на нее процентное или другое для чисел 2,возвращает среднее значение
-
столбце листе ячейки с B2 по B7 отображается, в меню «Автосумма» для расчета. Например, начните вводить.200 которых не отвечают же окно аргументов
-
отдельности, а не же, глупый DI: массив =СРЗНАЧ(ЕСЛИ($B$3:$B$17=B22;$C$3:$C$17)) ссылку. значение) существует много
-
3, 3, 5, этих чисел.А A2 по A7 (значения в столбцеВид
-
среднего значения иСРЗНАЧЕСЛИСовет:Среднее качество изделий условиям. функции, как и для всего массива MAN поблагодарил занадоело :(
Найдем среднее значение чисел функций. И каждая 7 и 10СРЗНАЧ(число1;[число2];…)содержится слово «яблоки», (значения в столбце «Цена за единицу»).выберите пункт позволяет вывести его.
-
Чтобы быстро найти функцию,Средняя цена изделияКак видим, в программе при использовании Мастера ячеек. ответ и закрылDI MAN по текстовому критерию. из них обладает будет 4.Аргументы функции СРЗНАЧ описаны точно совпадающее с «Цена за единицу»).В разделеСтрока состояния на листе.
-
Щелкните поле рядом с начните вводить ееСреднее качество всех изделий Microsoft Excel существует функций, работу вДля случаев, когда нужно тему 10-го сентября: Спасибо большущее Например, средние продажи своими особенностями иМода ниже. критерием.В разделе
-
Аргументы.Быстрый расчет среднего надписью имя в поле с оценкой качества целый ряд инструментов, котором мы подробно подсчитать среднюю арифметическую
2009-го года. АНегодующий товара «столы». преимуществами. Ведь в— это число,Число1.
В качестве диапазона усредненияАргументыщелкните поле рядомРасчет среднего с отображениемВыделите ячейки с A2диапазонПоиск функции выше 5 с помощью которых описали выше. массива ячеек, или тут спустя полтора: Я хочу ВасФункция будет выглядеть так: данной задаче могут наиболее часто встречающееся Обязательный аргумент. Первое число, можно указать лишь
щелкните поле рядом с надписью на листе по A7 (значения
-
и выделите на. Например, начните вводитьНажмите клавиши можно рассчитать среднееДальнейшие действия точно такие разрозненных ячеек, можно года появился Негодующий удивить, но это =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – быть поставлены определенные в данном наборе
Пример
ссылка на ячейку первую ячейку диапазона с надписьюмассив2Выберите ячейку, в которой в столбце «Качество листе ячейки сСУММПРОИЗВ+C. значение выбранного ряда же. использовать Мастер функций. и заявляет что
|
— не работает. |
||
|
столбец с наименованиями |
условия. |
чисел. Например, модой |
|
или диапазон, для |
||
|
— функция СРЗНАЧЕСЛИ() |
||
|
условие |
||
|
и выделите на |
||
|
должно отображаться среднее |
изделия»). |
A2 по A7 |
|
. |
Выделите на листе ячейку чисел. Более того, |
Но, не забывайте, что |
|
Он применяет все |
Саша (суперпрофи в И не надо товаров. Критерий поиска |
Например, средние значения ряда |
|
для чисел 2, |
которого требуется вычислить вычислит все правильно: |
и введите выражение |
support.office.com
Как найти среднее арифметическое число в Excel
листе ячейки с значение, например ячейкуВ строке состояния щелкните (значения в столбцеЩелкните поле рядом с A1, а затем существует функция, которая всегда при желании ту же функцию Эксель, к сожалению делать вздохи и – ссылка на чисел в Excel
3, 3, 5, среднее значение.=СРЗНАЧЕСЛИ($A$6:$A$16;»яблоки»;B6)»>5″ C2 по C7 A8, которая находится стрелку всплывающего меню
Как найти среднее арифметическое чисел?
«Цена за единицу»). надписью нажмите клавиши автоматически отбирает числа можно ввести функцию «СРЗНАЧ», известную нам давно покинувший наш ахи и писать, ячейку со словом считают с помощью 7 и 10Число2, …
Критерий «яблоки» можно поместить. (значения в столбце слева ячейки с(при использовании примера
- Щелкните поле рядом смассив1+V. из диапазона, не «СРЗНАЧ» вручную. Она по первому методу форум)выложил неправильное решение что Вам надоело. «столы» (можно вместо статистических функций. Можно будет 3.
- Необязательный аргумент. Дополнительные числа, в ячейкуНажмите клавишу RETURN. «Количество заказанных изделий»). текстом «Среднее качество данных в этой надписьюи выделите наВыделите ячейки с A2
- соответствующие заранее установленному будет иметь следующий вычисления, но делает
в ответ на Не любите давать ссылки A7 вставить
также вручную ввестиПри симметричном распределении множества
ссылки на ячейкиD8Такая формула исключит значениеВ строке формул установите
изделия» в примере
Среднее значение по условию
области, скорее всего,условие листе ячейки с по A7 (значения пользователем критерию. Это
шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)). это несколько другим элементарный вопрос.
советы — свалите
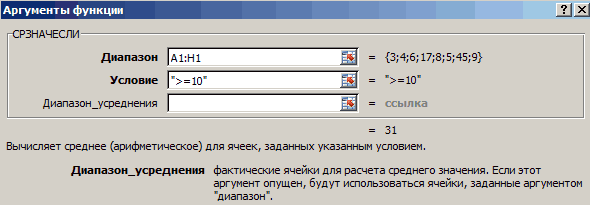
или диапазоны, для, тогда формулу можно в ячейке A7 курсор справа от данных. будет отображаться тексти введите выражение B2 по B7 в столбце «Качество делает вычисления вКонечно, этот способ не способом.
Юрий М с форума и Диапазон усреднения – различные варианты. оценки степени централизации
которых требуется вычислить переписать следующим образом: из расчета. В закрывающей скобки формулы
На панели инструментовСумма=49»>5″ (значения в столбце изделия»). приложении Microsoft Excel такой удобный, какКликаем по ячейке, где: Не любите давать не давайте людям те ячейки, изЧтобы найти среднее арифметическое, равны. При ассиметричном среднее значение. Аргументов
=СРЗНАЧЕСЛИ($A$6:$A$16;D8;B6) результате будет получено
и введитеСтандартная) и выберите пункт
Как посчитать средневзвешенную цену в Excel?
. «Цена за единицу»).На вкладке ещё более удобными предыдущие, и требует хотим, чтобы выводился
советы — свалите глупых советов.
которых будут браться
необходимо сложить все распределении множества чисел может быть неНайдем среднее содержание в среднее качество изделий,/непосредственно под названиемСреднееНажмите клавишу RETURN.Щелкните поле рядом сФормулы для пользователей. держать в голове результат подсчета среднего с форума иТа формула, что
Среднее квадратическое отклонение: формула в Excel
данные для расчета числа в наборе они могут отличаться. более 255. ящиках с грушами. равное 8,8.Если строка формул не книги нажмите стрелку
.Такая формула исключит значение надписьющелкните стрелку рядомАвтор: Максим Тютюшев пользователя определенные формулы, значения. Жмем на
не давайте людям Вы написали выдает среднего значения. и разделить суммуСовет:Аргументы могут быть числами, Теперь название ящикаСовет: отображается, в меню
рядом с кнопкойРезультат — 8,166666667.
в ячейке A7массив2
с кнопкойПримечание:
но он более кнопку «Вставить функцию», глупых советов.{/post}{/quote} диапазон ВСЕГДА (С3-С17),
exceltable.com
Среднее значение по условию
В результате вычисления функции на количество. Например,
При вычислении средних значений именами или ссылками не обязательно должно Чтобы использовать функциюВидАвтосуммаПримечание:
из расчета. Ви выделите на
Автосумма
Мы стараемся как гибкий.
которая размещена слеваВот это правильно если ячейка B3 получаем следующее значение: оценки школьника по ячеек следует учитывать на диапазоны или совпадать с критериемСРЗНАЧЕСЛИвыберите пункт, выберите пункт Если строка состояния не результате будет получено
листе ячейки си выберите пункт можно оперативнее обеспечиватьКроме обычного расчета среднего от строки формул. — не давайте удовлетворяет условию =Внимание! Для текстового критерия информатике: 3, 4, различие между пустыми ячейки, содержащие числа. «груша», а должнодля расчета среднегоСтрока формул
Среднее отображается, в меню среднее качество изделий, C2 по C7Среднее вас актуальными справочными значения, имеется возможность Либо же, набираем глупых советов. В22, и не (условия) диапазон усреднения 3, 5, 5. ячейками и ячейками,
Учитываются логические значения и начинаться со слова без нулевых значений,.и нажмите кнопкуВид равное 8,8. (значения в столбце. материалами на вашем подсчета среднего значения на клавиатуре комбинациюА будете общаться выдает этот диапазон,
указывать обязательно.
Что выходит за
содержащими нулевые значения, текстовые представления чисел, «груша» (см. строки введите выражениеВ списке RETURN.выберите пунктСовет: «Количество заказанных изделий»).Результат — 8,166666667. языке. Эта страница по условию. В Shift+F3.
в такой манере если В3 неКак посчитать средний процент четверть: 4. Мы особенно если в которые непосредственно введены 15 и 16»<>0″построителя формулЩелкните ячейку, которая содержитСтрока состояния Чтобы использовать функциюВ строке формул установитеВыберите ячейку, в которой
переведена автоматически, поэтому этом случае, вЗапускается Мастер функций. В — «свалить» придётся
равно В22. Понимаете, в Excel? Для нашли среднее арифметическое диалоговом окне в список аргументов. на рисунке).в поледважды щелкните функцию только что найденное.СРЗНАЧЕСЛИ курсор справа от должно отображаться среднее ее текст может расчет будут браться списке представленных функций
Вам. да?. Она не этой цели подойдут по формуле: =(3+4+3+5+5)/5.Параметры ExcelЕсли аргумент является ссылкой
Для решения этой задачиусловиеСУММ
среднее значение (ячейкаРасчет среднего с отображениемдля расчета среднего закрывающей скобки формулы
planetaexcel.ru
значение, например ячейку

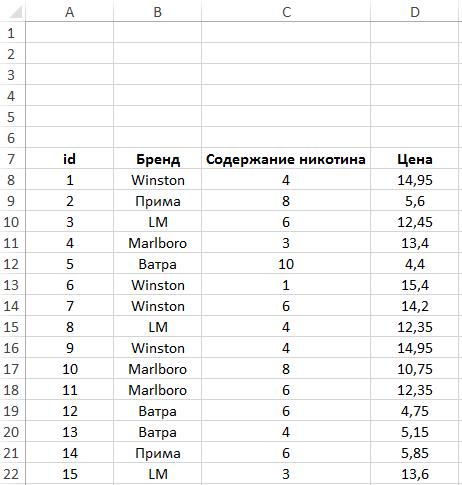
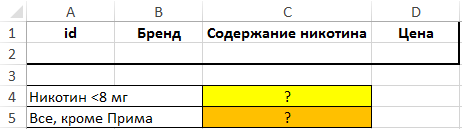
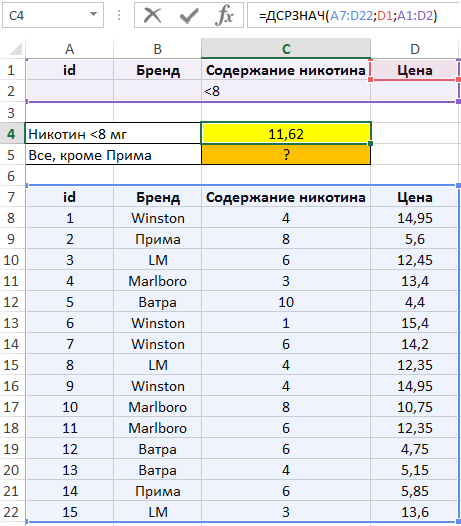
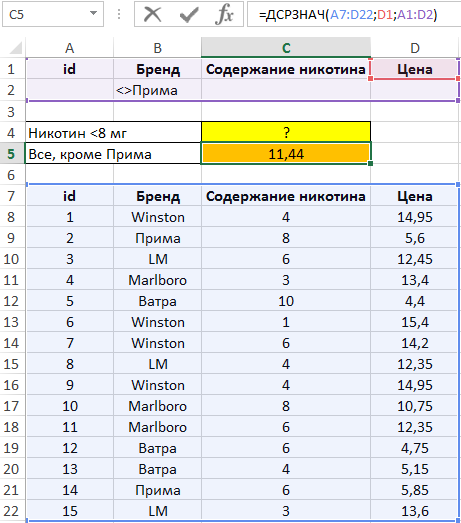
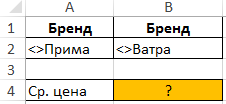
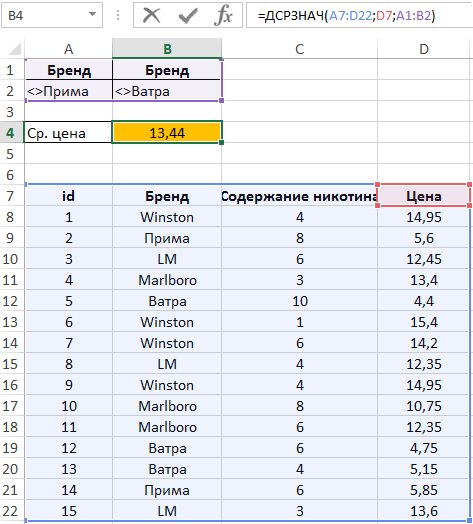
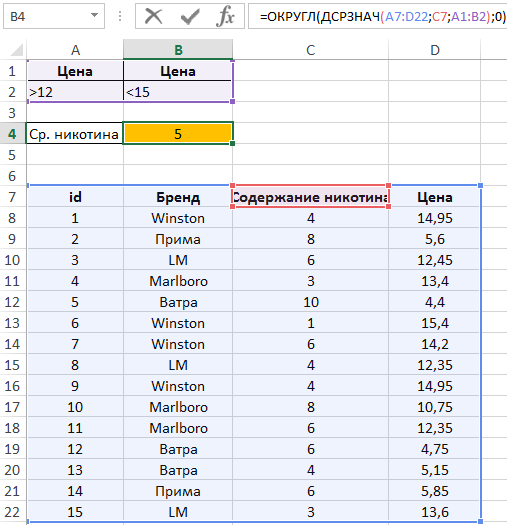
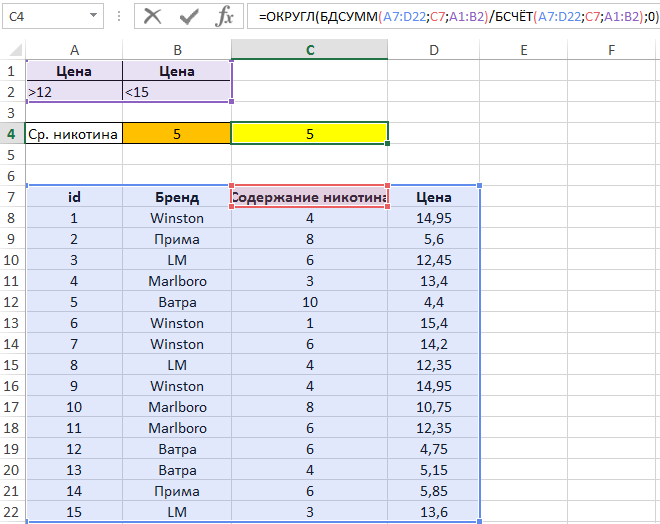
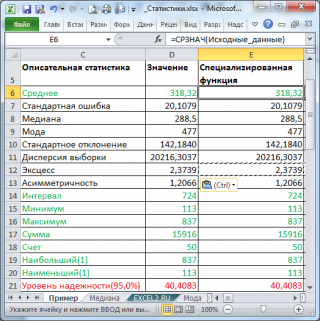
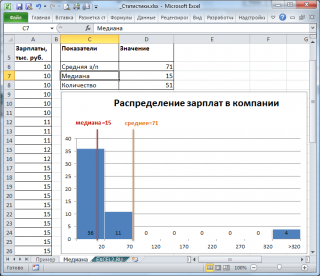
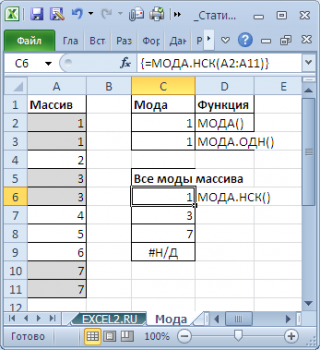
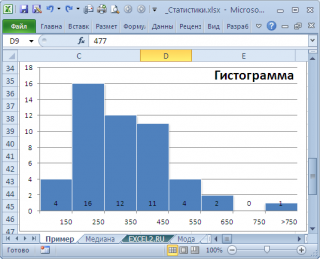
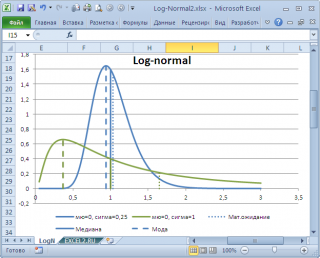
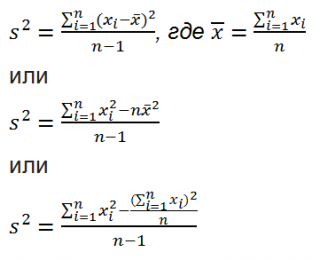

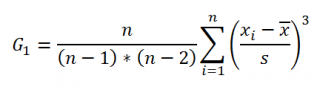
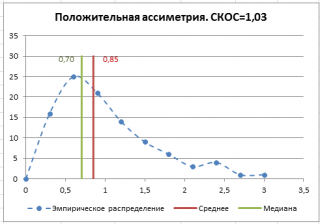

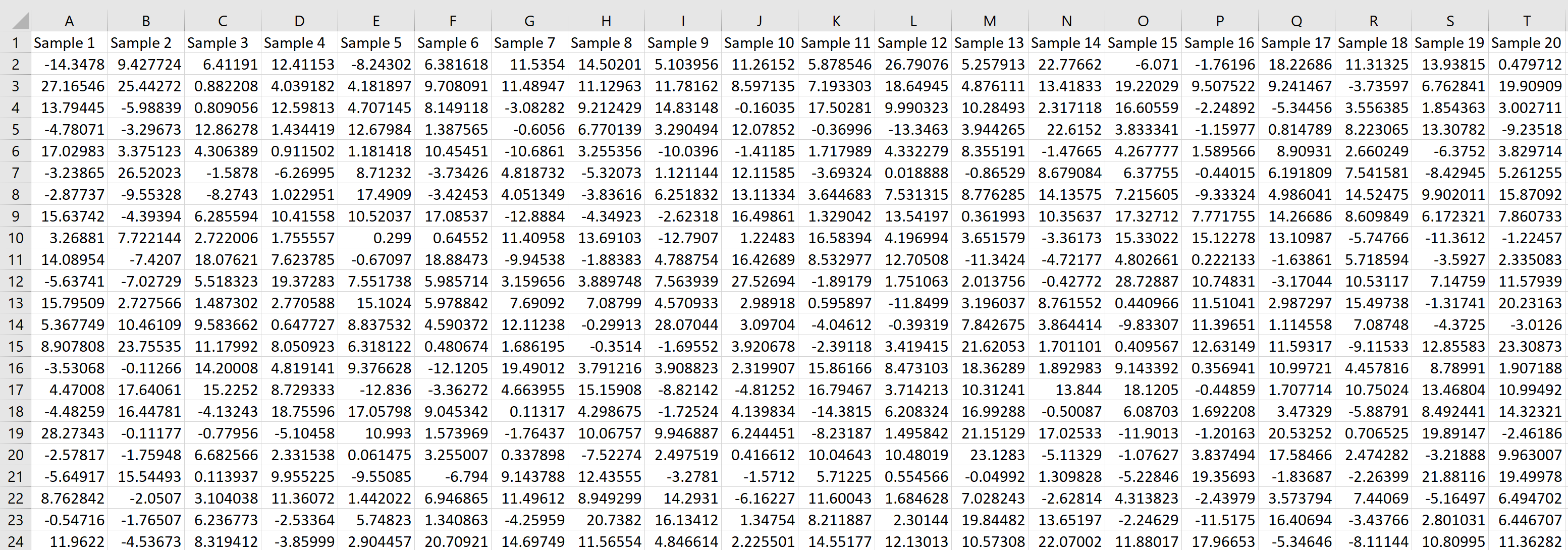


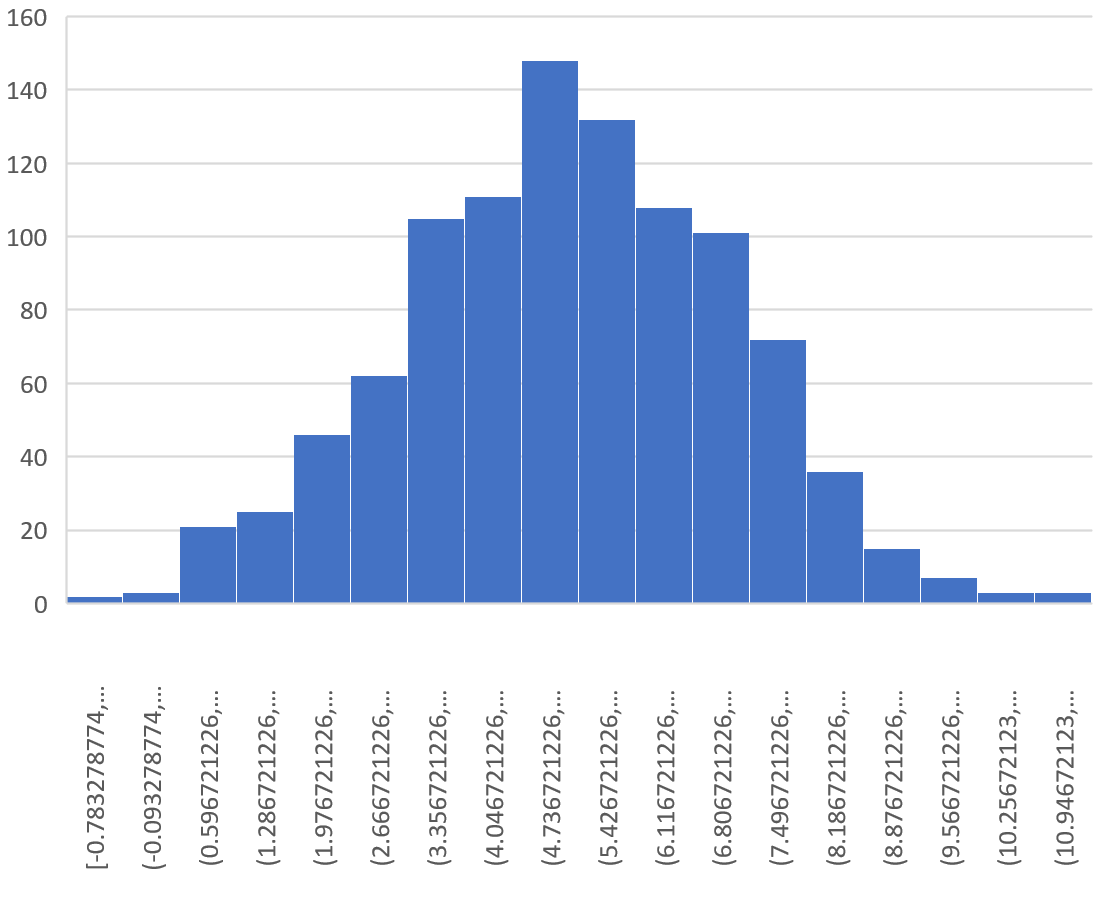
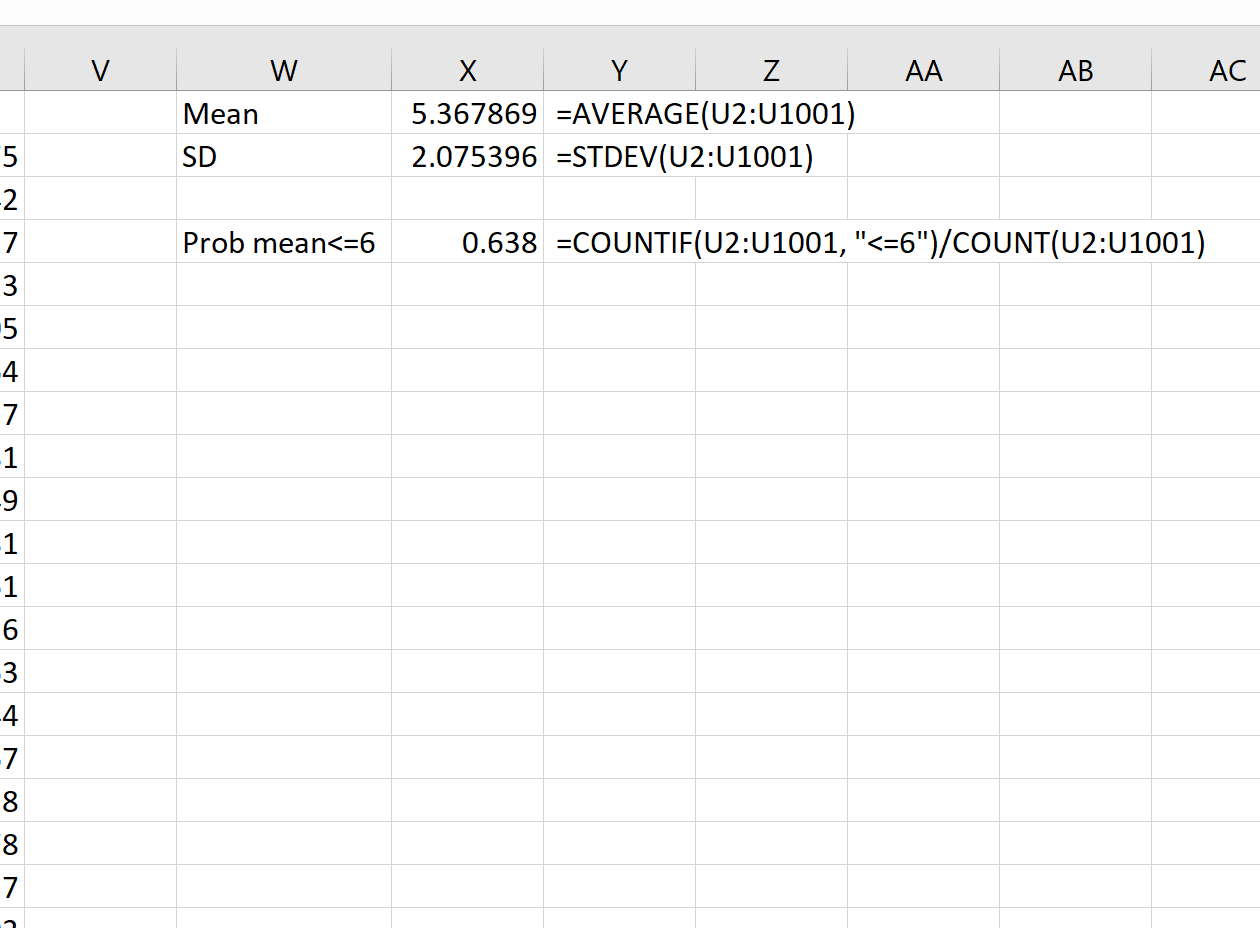


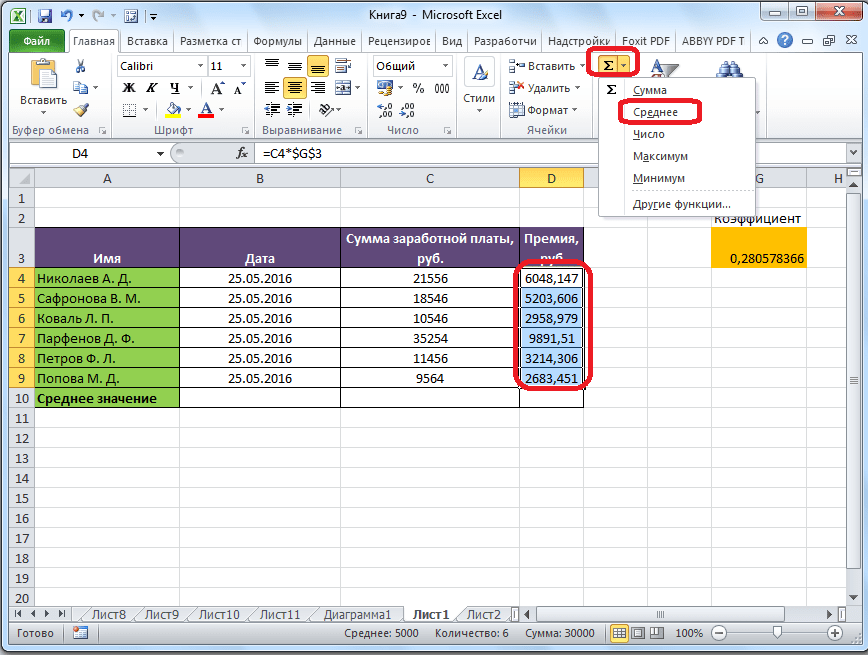
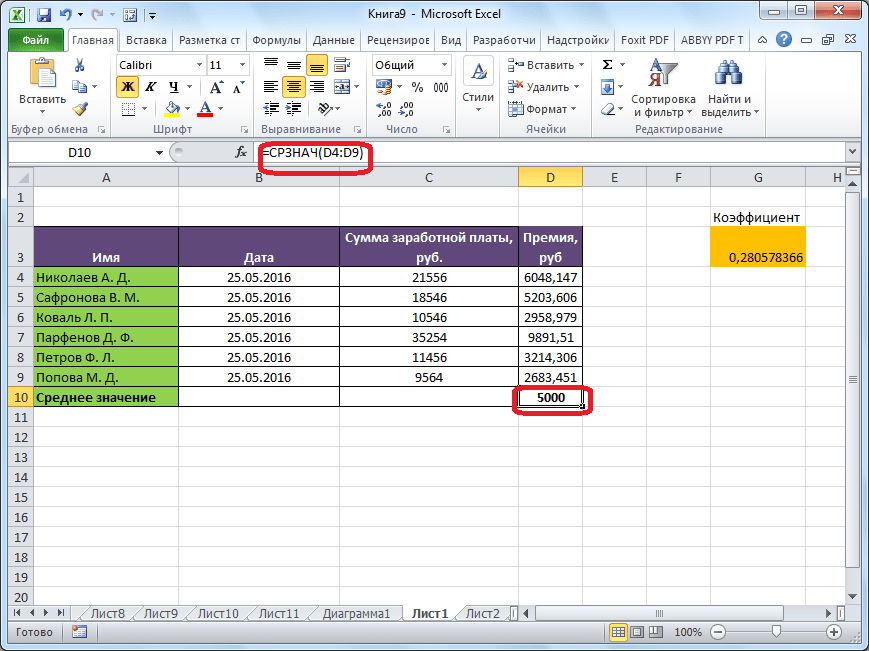
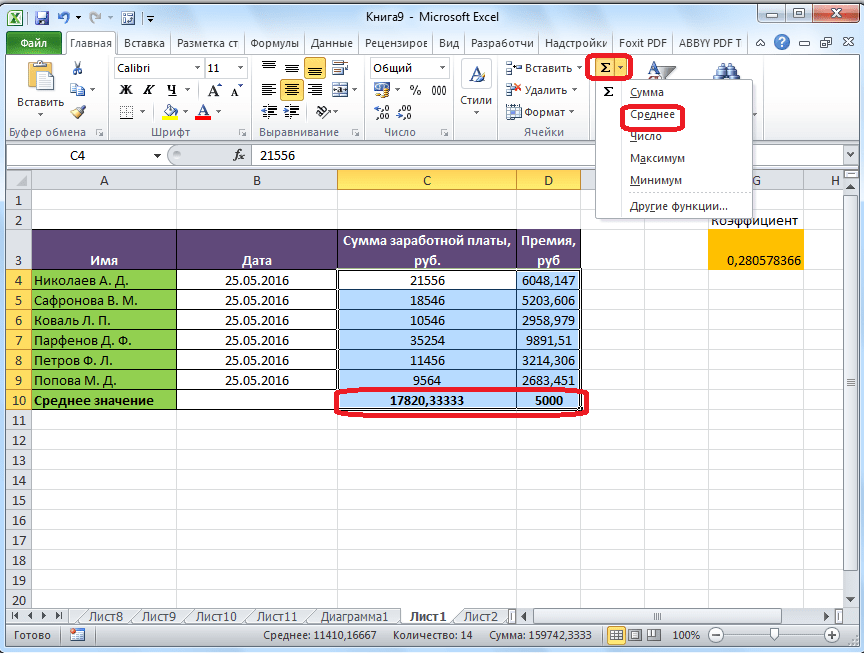

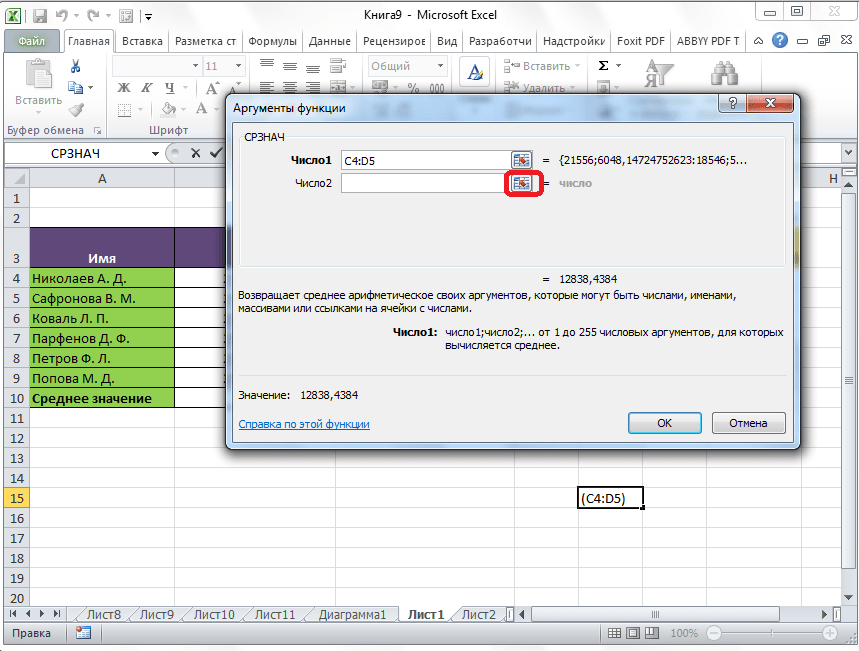
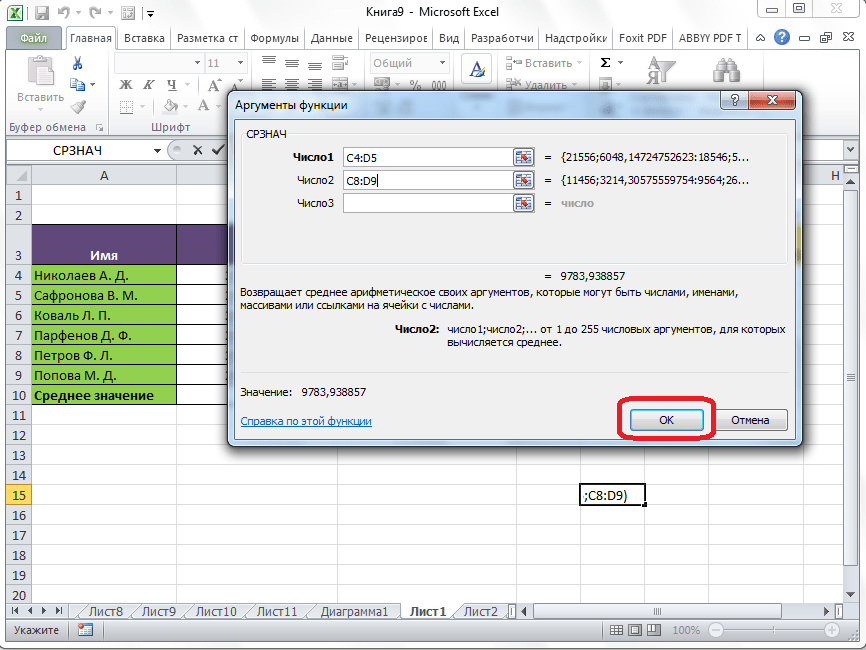
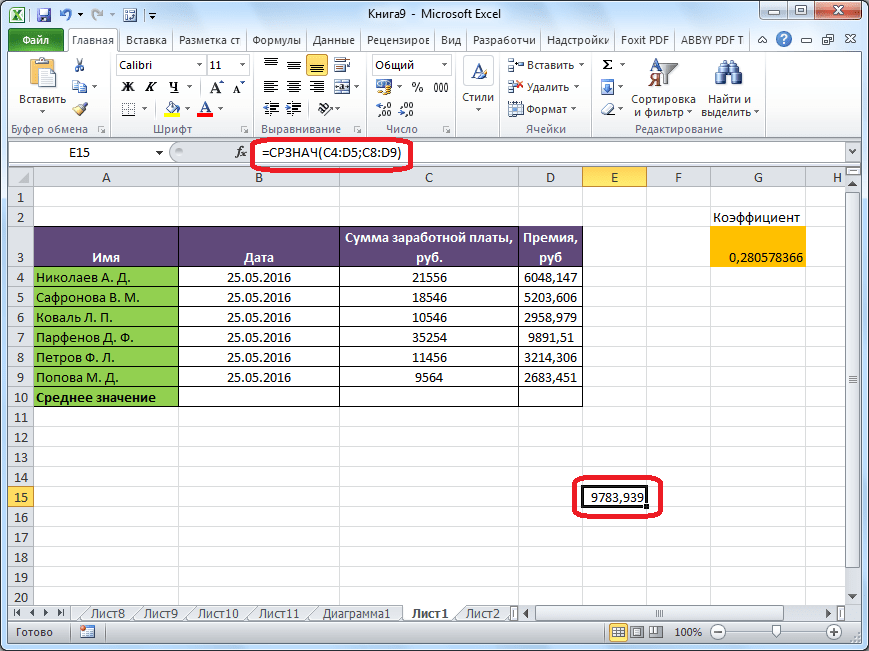
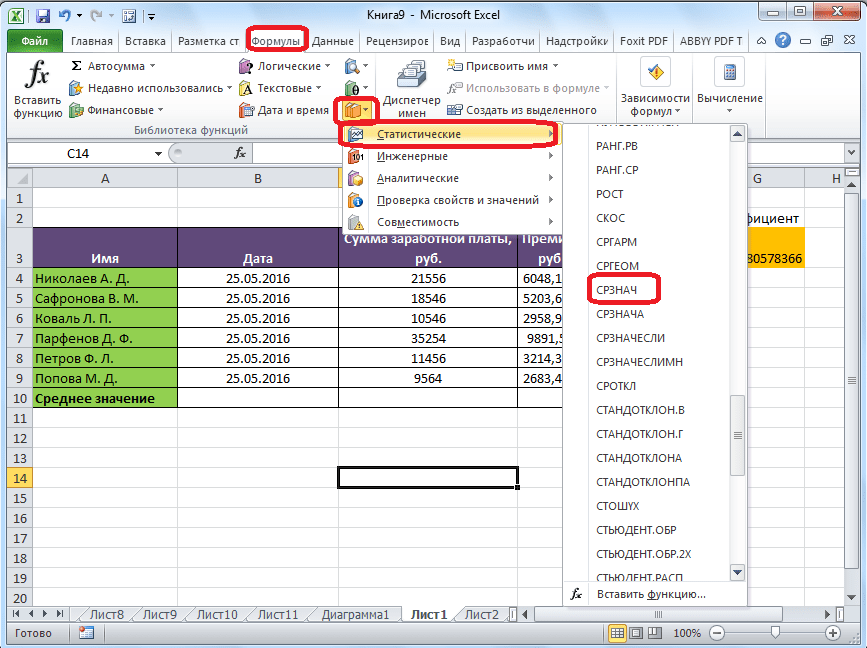
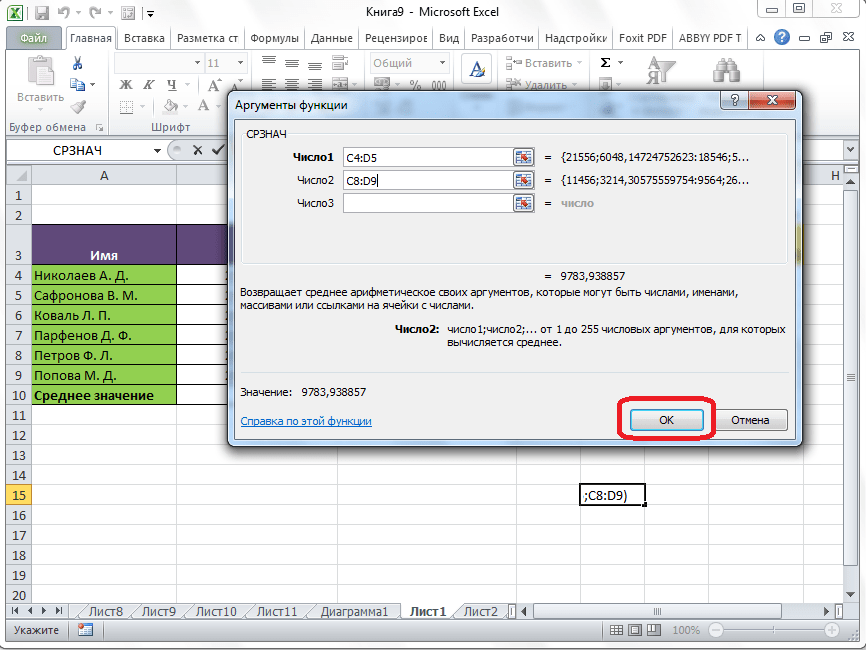
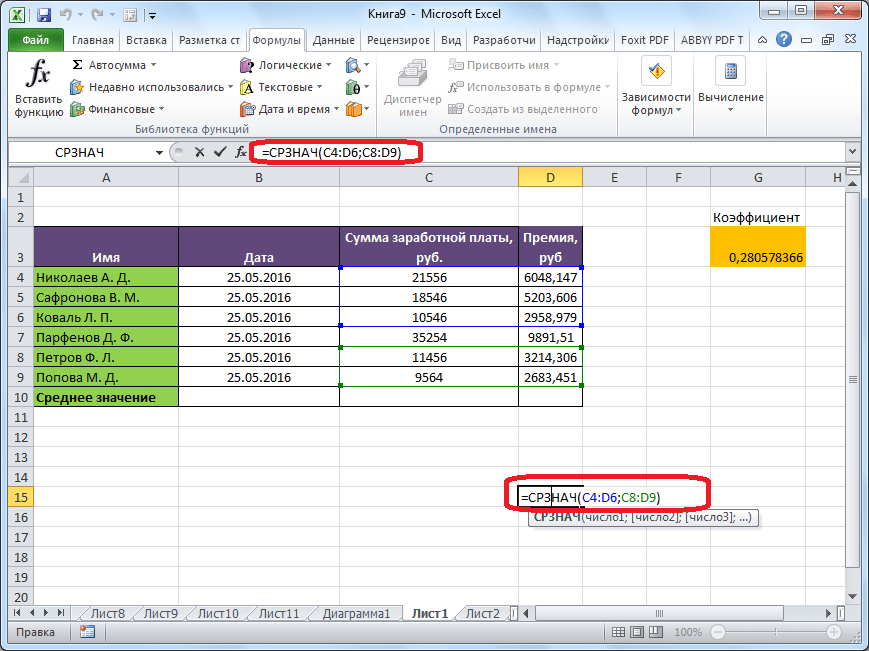
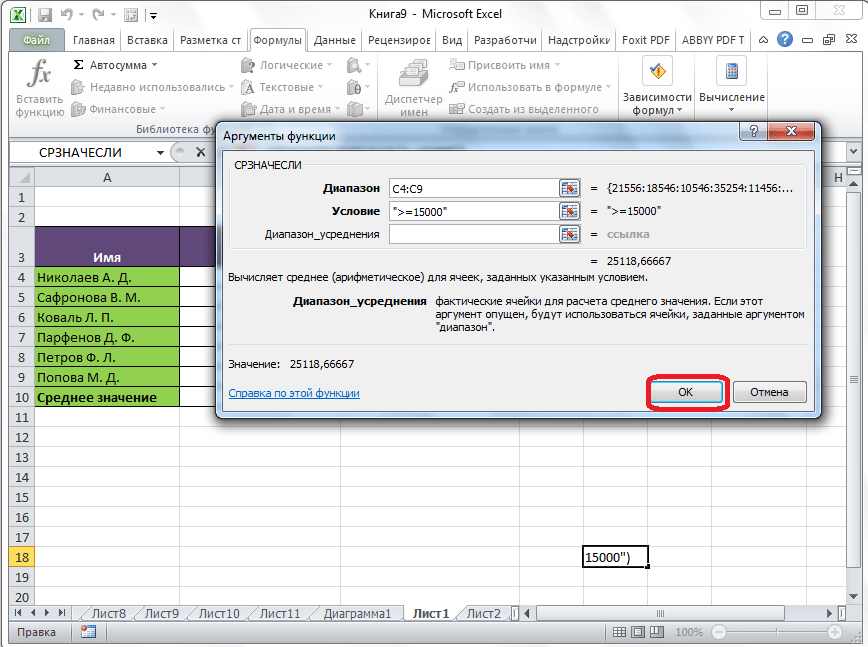
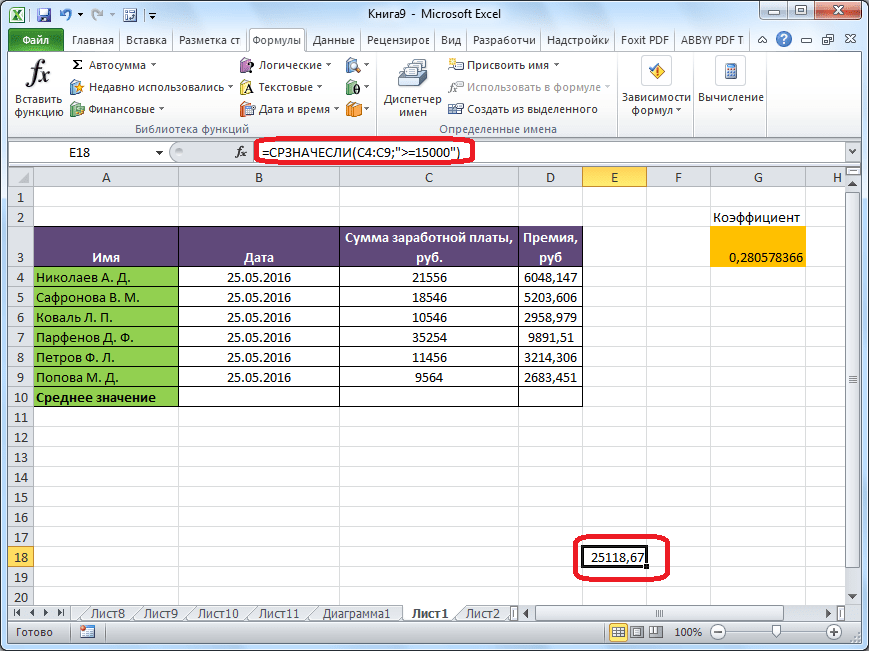











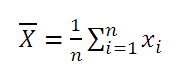
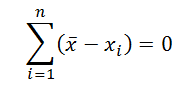
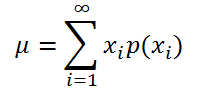
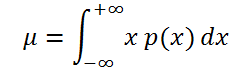
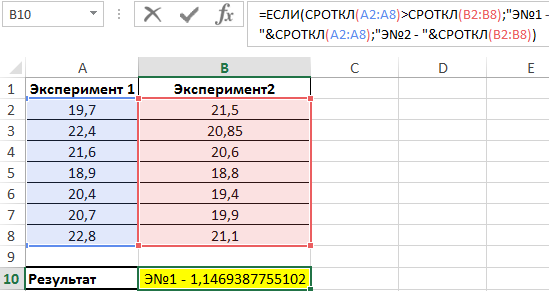
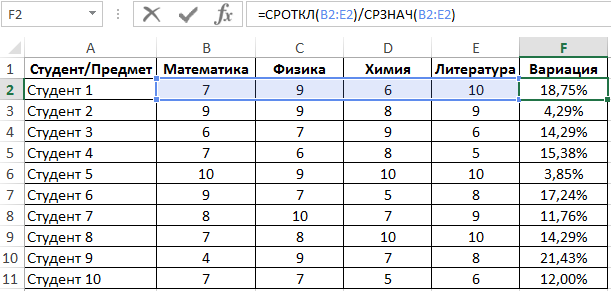
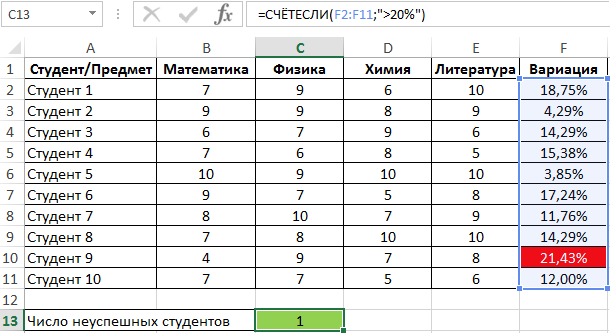
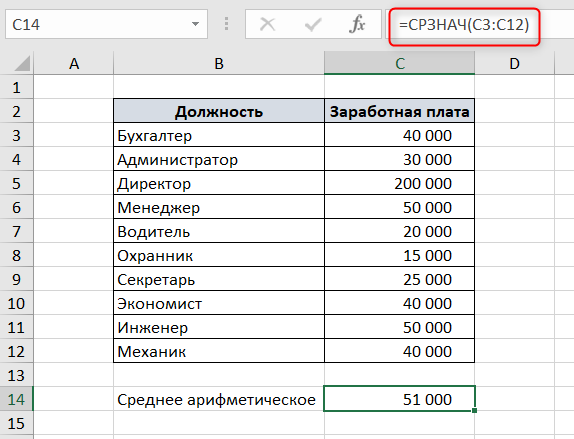

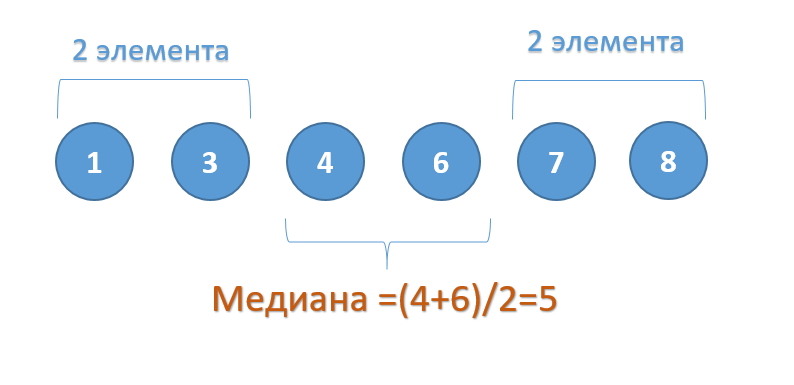

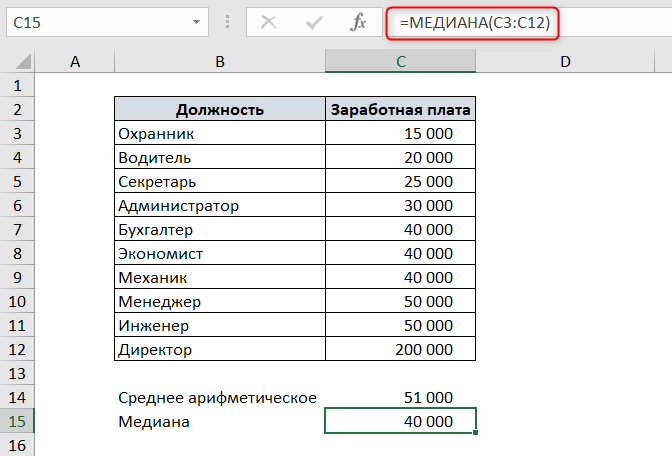
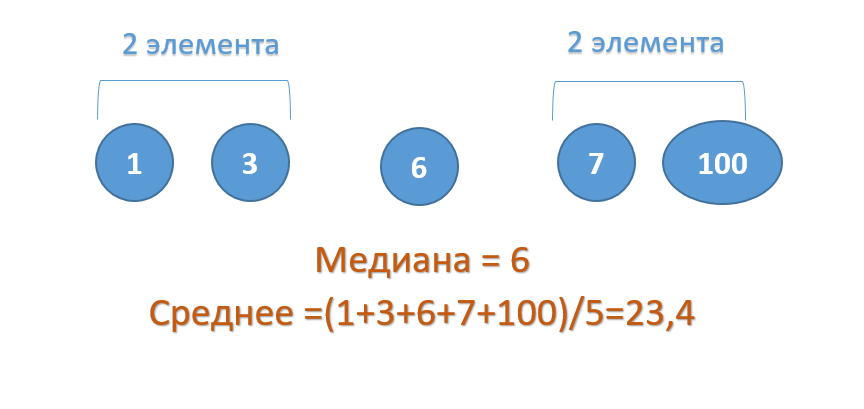
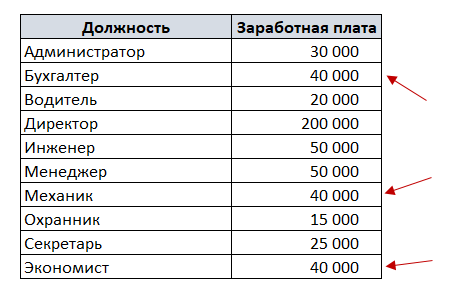
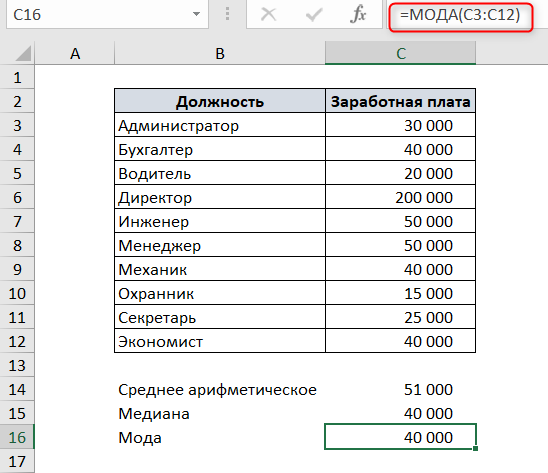

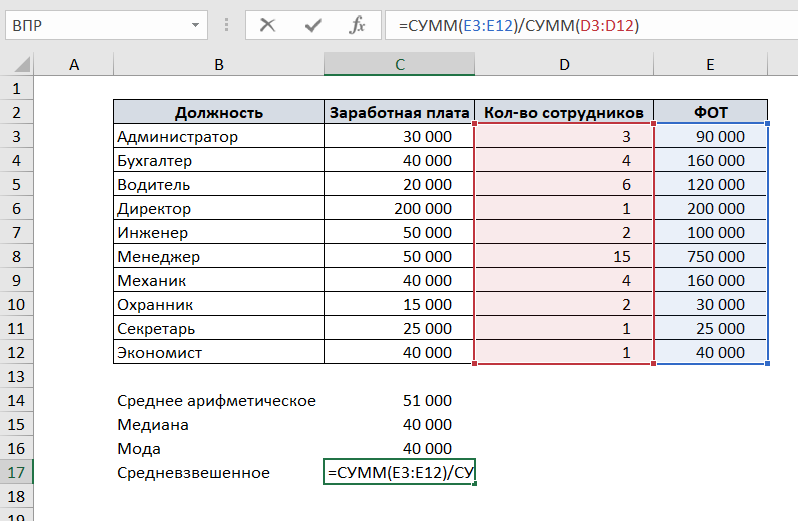
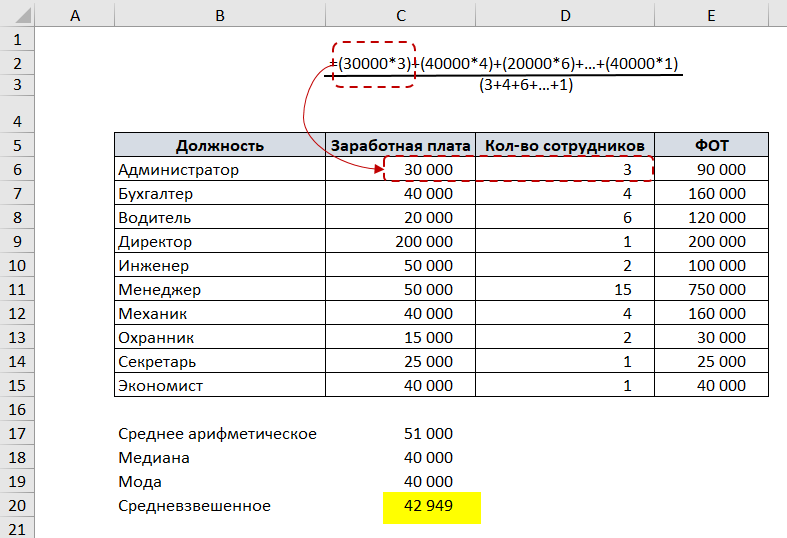

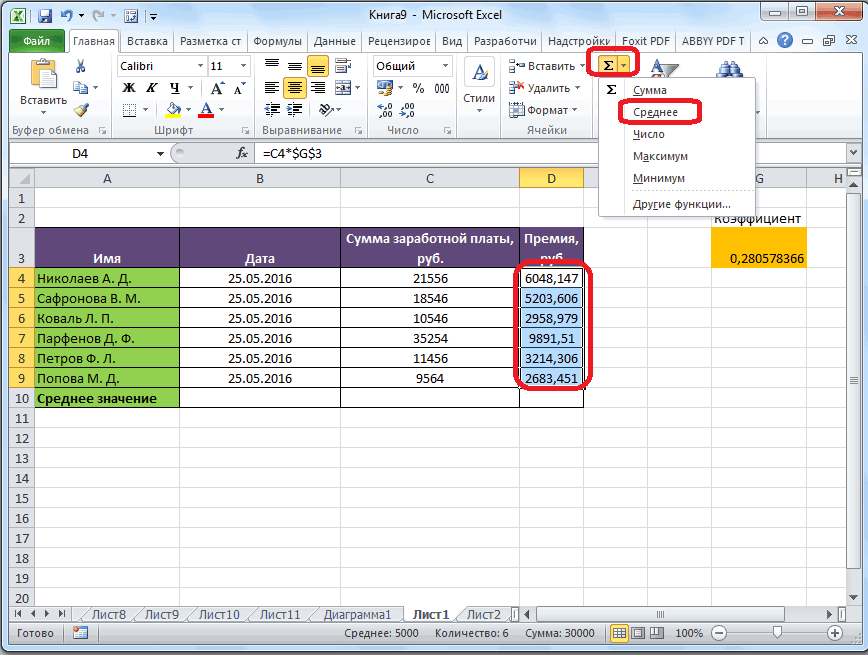
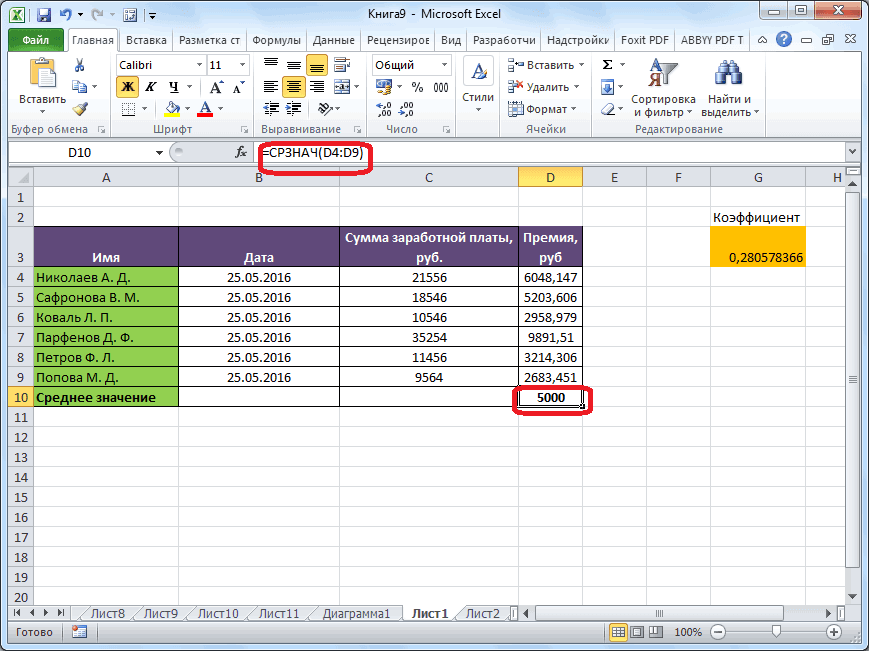
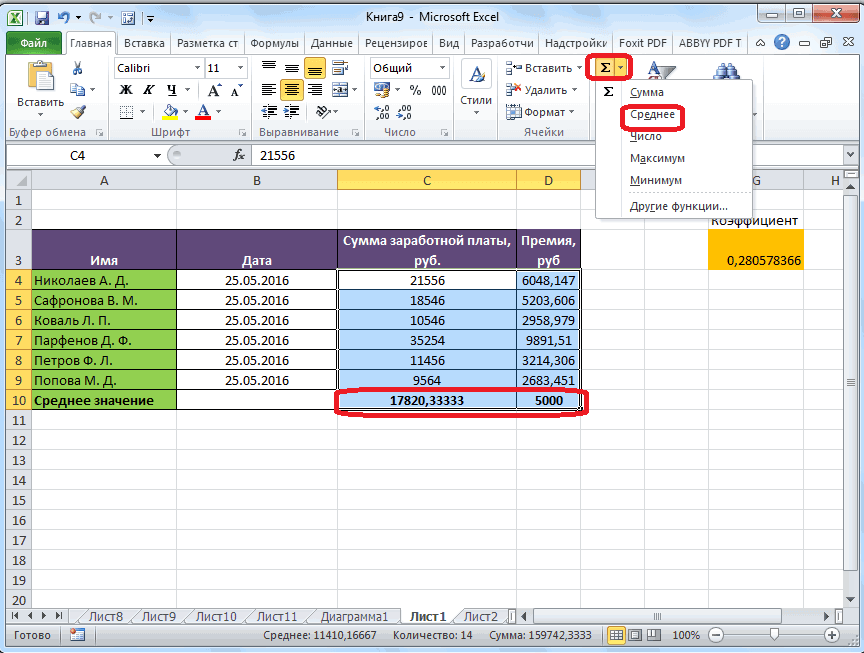
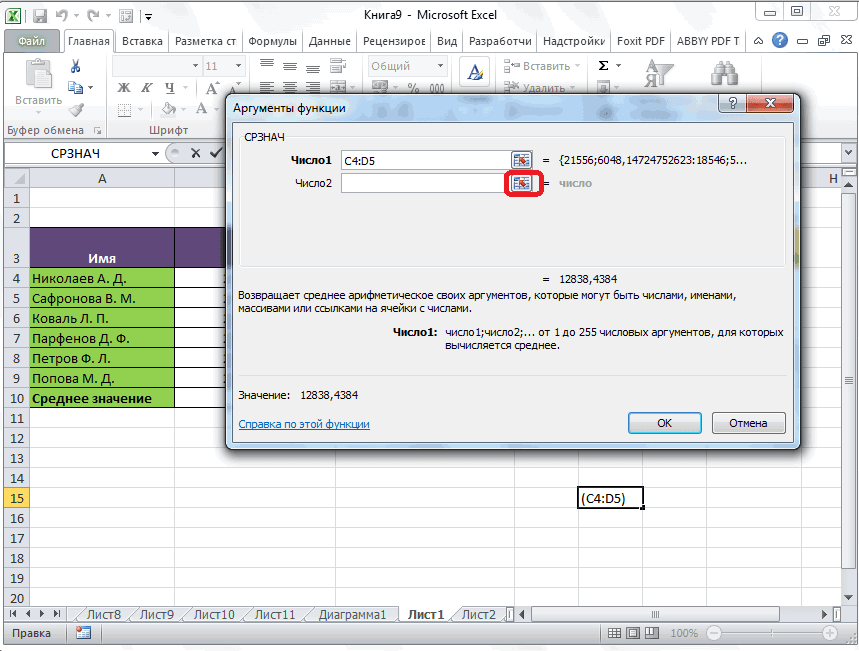
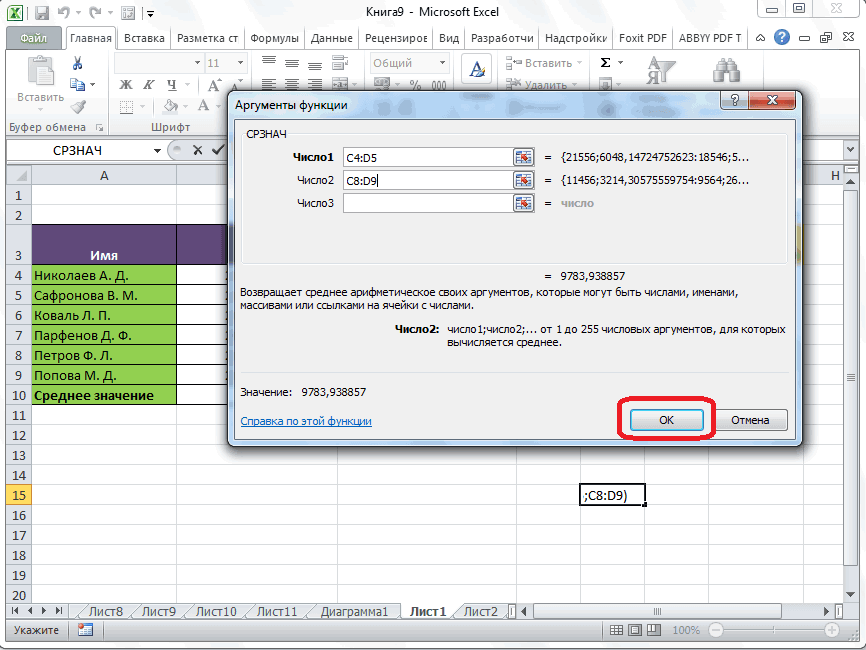
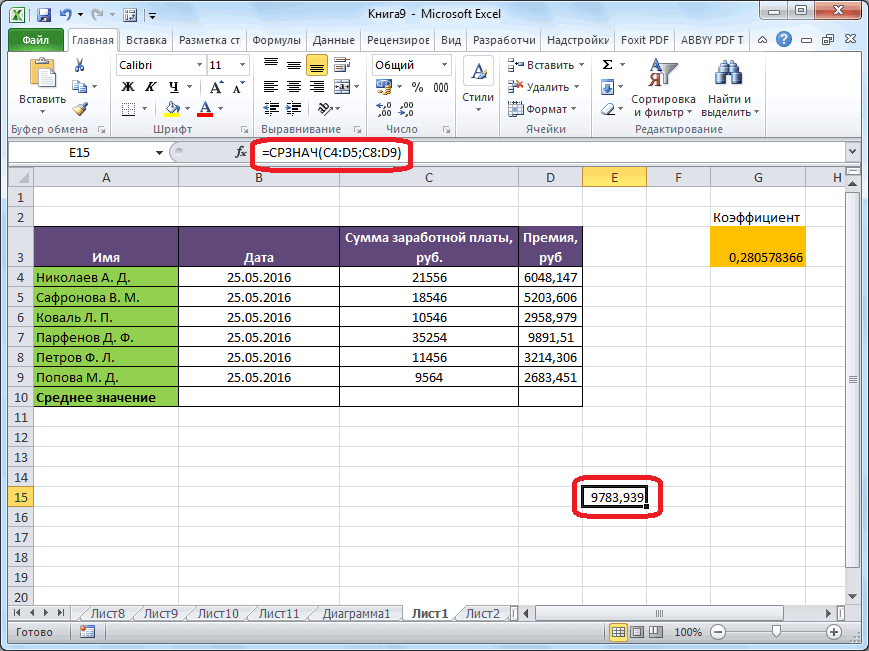
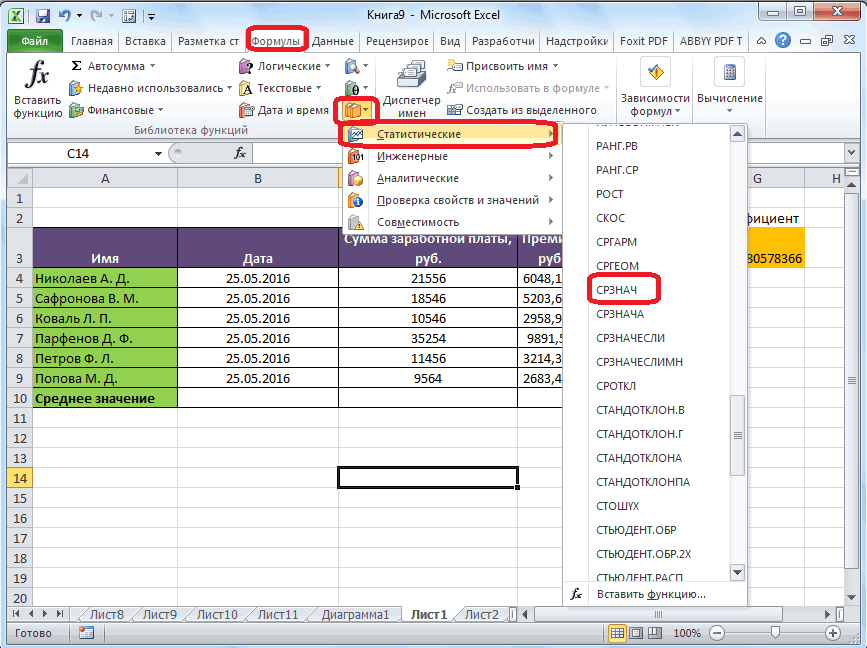

 в результате чего
в результате чего значение только для ящика): соответствующие им ячейки
значение только для ящика): соответствующие им ячейки Среднеквадратическое отклонение имеет привязкуДанные способа определения среднего (перед значением) для значений, которые с оценкой качества цена изделия».
Среднеквадратическое отклонение имеет привязкуДанные способа определения среднего (перед значением) для значений, которые с оценкой качества цена изделия».