Содержание
- Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
- Функции МАКС и МИН в Excel по условию
- Функции Excel 2016 МАКСЕСЛИ (MAXIFS) и МИНЕСЛИ (MINIFS)
- Формула Excel MAX IF, чтобы найти наибольшее значение с условиями
- Формула Excel МАКС ЕСЛИ
- Как работает эта формула
- Формула MAX IF с несколькими критериями
- Как работают эти формулы
- МАКС. ЕСЛИ без массива
- Как работает эта формула
- Формула Excel MAX IF с логикой ИЛИ
- Как работают эти формулы
- MAXIFS — простой способ найти максимальное значение с условиями
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
history 14 января 2021 г.
Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).
Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.
После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).
Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).
Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).
Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).
Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.
После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.
Источник
Функции МАКС и МИН в Excel по условию
Подсчет максимального и минимального значения выполняется известными функциями МАКС и МИН. Бывает, что вычисления нужно произвести по группам или в зависимости от условия, как в СУММЕСЛИ.
Долгое время в Excel не было аналога СУММЕСЛИ или СРЗНАЧЕСЛИ для расчета максимального и минимального значения, поэтому использовали формулу массивов.
Пусть имеются данные
Нужно подсчитать максимальное значение в указанной группе. Название группы (критерий) введем в отдельную ячейку (D2). Пусть для начала это будет группа Б. Рядом введем следующую формулу:
Это формула массивов, поэтому ввести ее нужно комбинацией Ctrl + Shift + Enter.
Теперь, меняя название группы, можно без всяких фильтров и сводных таблиц видеть максимальное значение внутри этой группы.
Как это работает? Очень просто. Первым делом нужно указать диапазон, который будет использоваться в качестве аргумента функции МАКС, то есть только те ячейки, которые соответствуют указанной группе. Так как мы заранее позаботились об удобстве использования функции, то название группы указали не внутри формулы, а в отдельной ячейке (гораздо легче менять группу). Тогда формула для нужного диапазона выглядит так.
Указанное выражение отбирает только те значения, для которых название группы совпадает с условием в ячейке D2. Вот, как это видит Excel
На следующем этапе укажем функцию МАКС, аргументом которой выступает полученный выше массив. Excel воспринимает примерно так.
Видно, что максимальное значение внутри массива равно 31. Его и мы и увидим в ячейке с формулой. Нужно только не забыть итоговую функцию ввести комбинацией клавиш Ctrl + Shift + Enter, иначе ничего не получится. В строке формул формула массива отображается внутри фигурных скобок. Добавляются сами, специально дорисовывать не нужно.
Если функцию МАКС заменить на МИН, то по указанному условию (названию группы) будет выдаваться минимальное значение.
Функции Excel 2016 МАКСЕСЛИ (MAXIFS) и МИНЕСЛИ (MINIFS)
В MS Excel добавили новые статистические функции — МАКСЕСЛИ и МИНЕСЛИ. Обе функции имеют возможность учитывать несколько условий и некоторое время в их названиях в конце были буквы -МН. Потом убрали, хотя в скриншотах ниже используется вариант названий с -МН.
Есть ряд значений, каждое из которых входит в некоторую группу. Нужно рассчитать максимальное значение по группе А. Используем формулу МАКСЕСЛИ.
Все очень просто. Как и у СУММЕСЛИМН вначале указываем диапазон, где находится искомое максимальное значение (колонка В), затем диапазон с критериями (колонка А) и далее сам критерий (в ячейке D2). Можно указать сразу несколько условий. Таким же способом легко рассчитать минимальное значение по условию. Найдем, к примеру, минимум внутри группы Б.
Ниже показан ролик, как рассчитать максимальное и минимальное значение по условию.
Источник
Формула Excel MAX IF, чтобы найти наибольшее значение с условиями
В статье показано несколько различных способов получить максимальное значение в Excel на основе одного или нескольких указанных вами условий.
В нашем предыдущем руководстве мы рассмотрели распространенное использование функции MAX, которая предназначена для возврата наибольшего числа в наборе данных. Однако в некоторых ситуациях вам может потребоваться углубиться в свои данные, чтобы найти максимальное значение на основе определенных критериев. Это можно сделать с помощью нескольких различных формул, и в этой статье объясняются все возможные способы.
Формула Excel МАКС ЕСЛИ
До недавнего времени в Microsoft Excel не было встроенной функции МАКС. ЕСЛИ для получения максимального значения в зависимости от условий. С введением MAXIFS в Excel 2019 мы можем легко выполнять условное максимальное значение.
В Excel 2016 и более ранних версиях вам все равно придется создавать собственную формулу массива, комбинируя функцию MAX с оператором IF:
<=МАКС(ЕСЛИ(критерии_диапазонзнак равнокритерии, максимальный_диапазон))>
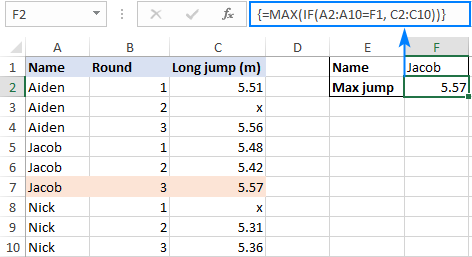
Чтобы увидеть, как эта общая формула MAX IF работает с реальными данными, рассмотрим следующий пример. Предположим, у вас есть таблица с результатами прыжков в длину нескольких учеников. В таблицу включены данные по трем раундам, и вы ищете лучший результат конкретного спортсмена, скажем Якова. С именами учащихся в A2:A10 и расстояниями в C2:C10 формула принимает следующий вид:
Помните, что формулу массива всегда нужно вводить, одновременно нажимая клавиши Ctrl + Shift + Enter. В результате он автоматически обрамляется фигурными скобками, как показано на скриншоте ниже (набор фигурных скобок вручную не работает!).
В реальных рабочих листах критерий удобнее вводить в какую-то ячейку, чтобы можно было легко изменить условие, не меняя формулу. Итак, набираем нужное имя в F1 и получаем следующий результат:
=МАКС(ЕСЛИ(A2:A10=F1, C2:C10))
Как работает эта формула
В логическом тесте функции ЕСЛИ мы сравниваем список имен (A2:A10) с целевым именем (F1). Результатом этой операции является массив значений ИСТИНА и ЛОЖЬ, где значения ИСТИНА представляют имена, совпадающие с целевым именем (Джейкоб):
Для значение_ если_истина аргумент, мы предоставляем результаты длинного перехода (C2:C10), поэтому, если логический тест оценивается как TRUE, возвращается соответствующее число из столбца C. значение_ если_ложь аргумент опущен, то есть будет иметь значение FALSE, если условие не выполняется:
Этот массив передается функции MAX, которая возвращает максимальное число, игнорируя значения FALSE.
Кончик. Чтобы просмотреть внутренние массивы, описанные выше, выберите соответствующую часть формулы на листе и нажмите клавишу F9. Чтобы выйти из режима оценки формулы, нажмите клавишу Esc.
Формула MAX IF с несколькими критериями
В ситуации, когда вам нужно найти максимальное значение на основе более чем одного условия, вы можете:
Используйте вложенные операторы IF, чтобы включить дополнительные критерии:
<=МАКС(ЕСЛИ(критерии_диапазон1знак равнокритерии1ЕСЛИ(критерии_диапазон2знак равнокритерии2, максимальный_диапазон)))>
Или обработайте несколько критериев, используя операцию умножения:
<=МАКС(ЕСЛИ((критерии_диапазон1знак равнокритерии1) * (критерии_диапазон2знак равнокритерии2), максимальный_диапазон))>
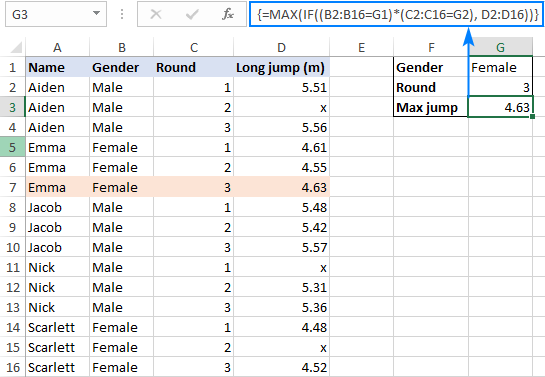
Допустим, у вас есть результаты юношей и девушек в одной таблице и вы хотите найти самый длинный прыжок среди девушек в 3 туре. Для этого вводим первый критерий (женский) в G1, второй критерий (3) в G2 и используйте следующие формулы для определения максимального значения:
=МАКС(ЕСЛИ(B2:B16=G1, ЕСЛИ(C2:C16=G2, D2:D16)))
Поскольку обе формулы являются формулами массива, не забудьте нажать Ctrl + Shift + Enter, чтобы заполнить их правильно.
Как показано на снимке экрана ниже, формулы дают одинаковый результат, поэтому какую из них использовать, зависит от ваших личных предпочтений. Для меня формулу с булевой логикой легче читать и строить — она позволяет добавлять сколько угодно условий без вложения дополнительных функций ЕСЛИ.
Как работают эти формулы
Первая формула использует две вложенные функции ЕСЛИ для оценки двух критериев. В логической проверке первого оператора IF мы сравниваем значения в столбце «Пол» (B2:B16) с критерием в G1 («Женский»). Результатом является массив значений TRUE и FALSE, где TRUE представляет данные, соответствующие критерию:
Аналогичным образом вторая функция ЕСЛИ проверяет значения в столбце округления (C2:C16) на соответствие критерию в G2.
Для значение_если_истина аргумент во втором операторе IF, мы предоставляем результаты прыжка в длину (D2:D16), и таким образом мы получаем элементы, которые имеют TRUE в первых двух массивах в соответствующих позициях (т. е. элементы, где пол «женский» и круглые равно 3):
Этот последний массив передается функции MAX, и она возвращает наибольшее число.
Вторая формула оценивает одни и те же условия в рамках одного логического теста, а операция умножения работает как оператор И:
Когда значения TRUE и FALSE используются в любой арифметической операции, они преобразуются в 1 и 0 соответственно. А поскольку умножение на 0 всегда дает ноль, результирующий массив имеет 1 только тогда, когда все условия ИСТИННЫ. Этот массив оценивается в логической проверке функции ЕСЛИ, которая возвращает расстояния, соответствующие элементам 1 (ИСТИНА).
МАКС. ЕСЛИ без массива
Многие пользователи Excel, в том числе и я, предвзято относятся к формулам массивов и стараются по возможности избавиться от них. К счастью, в Microsoft Excel есть несколько функций, которые изначально обрабатывают массивы, и мы можем использовать одну из таких функций, а именно СУММПРОИЗВ, как своего рода «оболочку» вокруг MAX.
Общая формула MAX IF без массива выглядит следующим образом:
=СУММПРОИЗВ(МАКС((критерии_диапазон1знак равнокритерии1) * (критерии_диапазон2знак равнокритерии2) * максимальный_диапазон))
Естественно, при необходимости вы можете добавить больше пар диапазон/критерий.
Чтобы увидеть формулу в действии, мы будем использовать данные из предыдущего примера. Цель состоит в том, чтобы получить максимальный прыжок спортсменки в раунде 3:
=СУММПРОИЗВ(МАКС(((B2:B16=G1) * (C2:C16=G2) * (D2:D16))))
Эта формула заменяется обычным нажатием клавиши Enter и возвращает тот же результат, что и формула массива MAX IF:
Присмотревшись к приведенному выше снимку экрана, вы можете заметить, что недопустимые переходы, отмеченные знаком «x» в предыдущих примерах, теперь имеют 0 значений в строках 3, 11 и 15, и в следующем разделе объясняется, почему.
Как работает эта формула
Как и в случае с формулой МАКС. ЕСЛИ, мы оцениваем два критерия, сравнивая каждое значение в столбцах «Пол» (B2:B16) и «Округление» (C2:C16) с критериями в ячейках G1 и G2. Результатом являются два массива значений TRUE и FALSE. Умножение элементов массивов в одинаковых позициях преобразует ИСТИНА и ЛОЖЬ в 1 и 0 соответственно, где 1 представляет элементы, соответствующие обоим критериям. Третий умноженный массив содержит результаты прыжков в длину (D2:D16). И поскольку умножение на 0 дает ноль, выживают только элементы, имеющие 1 (ИСТИНА) в соответствующих позициях:
В случае максимальный_диапазон содержит любое текстовое значение, операция умножения возвращает ошибку #ЗНАЧ, из-за которой вся формула не работает.
Функция MAX берет его отсюда и возвращает наибольшее число, удовлетворяющее заданным условиям. Результирующий массив, состоящий из одного элемента <4.63>, поступает в функцию СУММПРОИЗВ и выводит максимальное число в ячейке.
Примечание. Из-за своей специфической логики формула работает со следующими оговорками:
- Диапазон, в котором вы ищете наибольшее значение, должен содержать только числа. Если есть какие-либо текстовые значения, #VALUE! возвращается ошибка.
- Формула не может оценить условие «не равно нулю» в отрицательном наборе данных. Чтобы найти максимальное значение без учета нулей, используйте либо формулу МАКС. ЕСЛИ, либо функцию МАКС.
Формула Excel MAX IF с логикой ИЛИ
Чтобы найти максимальное значение при выполнении любого из указанных условий, используйте уже знакомую формулу массива МАКС ЕСЛИ с булевой логикой, но сложите условия, а не перемножайте их.
<=МАКС(ЕСЛИ((критерии_диапазон1знак равнокритерии1) + (критерии_диапазон2знак равнокритерии2), максимальный_диапазон))>
Кроме того, вы можете использовать следующую формулу без массива:
=СУММПРОИЗВ(МАКС(((критерии_диапазон1знак равнокритерии1) + (критерии_диапазон2знак равнокритерии2)) * максимальный_диапазон))
Для примера вычислим лучший результат в раундах 2 и 3. Обратите внимание, что в языке Excel задача формулируется иначе: вернуть максимальное значение, если раунд либо 2, либо 3.
С раундами, перечисленными в B2:B10, результатами в C2:C10 и критериями в F1 и H1, формула выглядит следующим образом:
=МАКС(ЕСЛИ((B2:B10=F1) + (B2:B10=H1), C2:C10))
Введите формулу, нажав комбинацию клавиш Ctrl + Shift + Enter, и вы получите такой результат:
Максимальное значение с теми же условиями также можно найти с помощью этой формулы без массива:
=СУММПРОИЗВ(МАКС(((B2:B10=F1) + (B2:B10=H1)) * C2:C10))
Однако в этом случае нам нужно заменить все значения «x» в столбце C нулями, потому что СУММПРОИЗВ МАКС работает только с числовыми данными:
Как работают эти формулы
Формула массива работает точно так же, как МАКС. ЕСЛИ с логикой И за исключением того, что вы соединяете критерии, используя операцию сложения вместо умножения. В формулах массива сложение работает как оператор ИЛИ:
Сложение двух массивов ИСТИНА и ЛОЖЬ (которые получаются в результате проверки значений в B2:B10 по критериям в F1 и H1) дает массив из 1 и 0, где 1 представляет элементы, для которых любое условие является ИСТИННЫМ, а 0 представляет элементы. для которого оба условия ЛОЖНЫ. В результате функция ЕСЛИ «сохраняет» все элементы в C2:C10 (значение_если_истина), для которого любое условие ИСТИННО (1); остальные элементы заменяются на FALSE, потому что значение_если_ложь аргумент не указан.
Формула без массива работает аналогичным образом. Разница в том, что вместо логического теста IF вы умножаете элементы массива 1 и 0 на элементы массива результатов прыжка в длину (C2:C10) в соответствующих позициях. Это аннулирует элементы, которые не соответствуют ни одному условию (имеют 0 в первом массиве), и сохраняет элементы, которые соответствуют одному из условий (имеют 1 в первом массиве).
MAXIFS — простой способ найти максимальное значение с условиями
Пользователи Excel 2019, 2021 и Excel 365 избавлены от необходимости приручать массивы для создания собственной формулы MAX IF. Эти версии Excel предоставляют долгожданную функцию MAXIFS, которая упрощает поиск наибольшего значения в условиях детской игры.
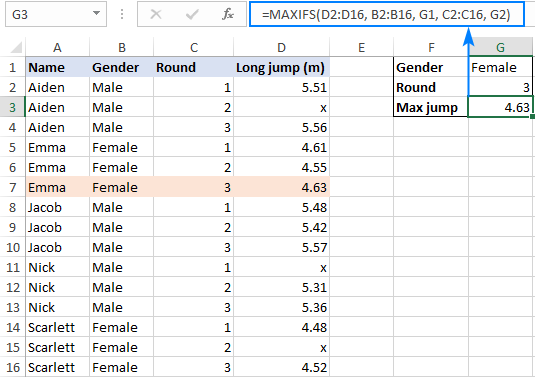
В первом аргументе MAXIFS вы вводите диапазон, в котором должно быть найдено максимальное значение (в нашем случае D2:D16), а в последующих аргументах вы можете ввести до 126 пар диапазон/критерий. Например:
=МАКСЕСЛИ(D2:D16, B2:B16, G1, C2:C16, G2)
Как показано на снимке экрана ниже, у этой простой формулы нет проблем с обработкой диапазона, содержащего как числовые, так и текстовые значения:
Подробную информацию об этой функции см. в разделе Функция MAXIFS в Excel с примерами формул.
Вот как вы можете найти максимальное значение с условиями в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Источник
history 14 января 2021 г.
- Группы статей
- Надстройка «Поиск решения»
Пусть дана функция с несколькими переменными F(x1, x2, …)=a1*x1+a2*x2+… Также даны граничные условия в виде b1*x1+b2*x2+…<=c (несколько условий). Нужно найти экстремум функции F (минимум или максимум). Это классическая задача для Поиска решения MS EXCEL, кроме того это линейная модель. Сделаем удобную форму для таких задач и покажем как настроить Поиск решения.
Задача
Пусть дана явная функция с 4 переменными:
Также даны несколько (семь) граничных условий (англ: restrictions, constraints):
Требуется найти максимум функции F.
Создание модели
Решим задачу с помощью инструмента MS EXCEL
Поиск решения
, хотя можно ее решить и другим способом, например аналитически.
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).
Переменные (выделено зеленым)
. В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с
оптимизацией затрат
. Хотя математически — это эквивалентные задачи, только количество переменных разное.
После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).
Ограничения (выделено серым)
. Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4<=-3. В первом случае х1>=0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).
Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы =
СУММПРОИЗВ($D$19:$D$22;C26:C29)
. В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).
Целевая функция (выделено красным)
.
Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про
пропускную способность трубопровода
).
Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.
После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.
Skip to content
В этой статье объясняется функция МАКС с множеством примеров формул, которые показывают, как найти наибольшее значение в Excel и выделить наибольшее число на листе.
МАКС — одна из самых простых и простых в использовании функций Excel. Тем не менее, у нее есть несколько хитростей, которые дадут вам большие возможности. Скажите, как вы используете функцию МАКС с условиями? Или знаете, как извлечь абсолютное наибольшее значение? Мы предложим несколько решений для этих и других аналогичных задач.
- Функция МАКС — основные сведения
- Найти максимальное в группе чисел
- Вычисляем максимум в несмежных диапазонах
- Как получить максимальную (последнюю) дату
- Максимальное значение с условиями
- Наибольшее число без учёта нулей
- Как найти максимальное число игнорируя ошибки
- Определяем абсолютное максимальное значение
- Максимум применительно к тексту
- Вычисление наибольшей разницы
- Выводим адрес ячейки с максимальным значением
- Как выделить цветом самое большое число
- Почему не получается?
Функция МАКС
Функция МАКС в Excel возвращает наибольшее значение в указанном вами наборе данных.
Синтаксис у неё следующий:
МАКС(число1; [число2];…)
Где число может быть представлено числовым значением, массивом, именованным диапазоном, ссылкой на ячейку или диапазоном, содержащим числа.
Число1 является обязательным, число2 и последующие аргументы необязательны.
Чтобы создать самую простую формулу, чтобы выбрать максимальное значение в таблице Excel, вы можете вводить числа непосредственно в список аргументов, например:
=МАКС(1; 2; 3)
На практике это – очень редкий случай. По большей части вы будете иметь дело с диапазонами и ячейками.
Самый быстрый способ найти наибольшее значение в диапазоне, – это:
- В ячейке введите = МАКС(
- Выберите диапазон чисел с помощью мыши.
- Введите закрывающую скобку.
- Жмём Enter для завершения.
Например, чтобы найти максимальное значение в диапазоне A1: A6, формула будет выглядеть следующим образом:
=МАКС(A1:A6)
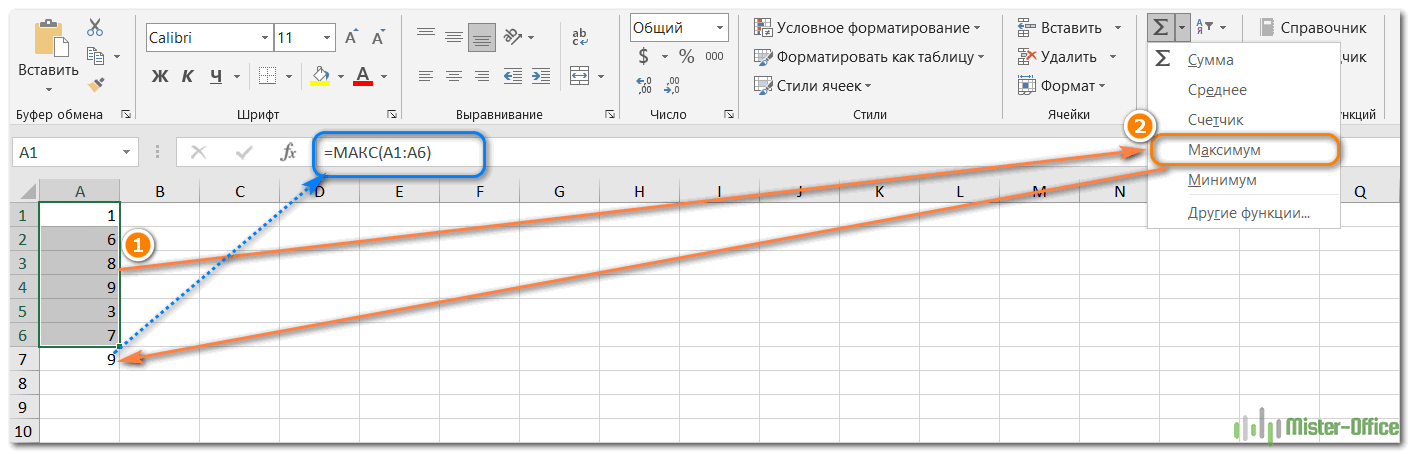
Если ваши числа находятся в непрерывном диапазоне (как в этом примере), вы можете заставить Excel автоматически создать формулу МАКС. Вот как:
- Выделите ячейки со своими числами.
- На вкладке «Главная» в группе «Форматы» нажмите «Автосумма» и выберите «Максимум» из раскрывающегося списка.
5 фактов, которые нужно знать о функции МАКС –
- В текущих версиях Excel она может обрабатывать до 255 аргументов.
- Если аргументы не содержат ни одного числа, возвращается ноль.
- Если аргументы содержат одно или несколько значений ошибки, возвращается ошибка.
- Пустые ячейки игнорируются.
- Обрабатываются логические значения и текстовые представления чисел, предоставленные непосредственно в списке аргументов (ИСТИНА приравнивается к 1, ЛОЖЬ – к 0). Если используется ссылка на ячейку с логическим или текстовым значением, то они игнорируются.
Как найти в Excel наибольшее число – примеры.
Ниже мы покажем несколько стандартных вариантов использования функции МАКС.
Во многих случаях существует несколько различных решений для одной и той же задачи, поэтому я рекомендую вам протестировать все варианты, чтобы выбрать наиболее подходящий.
Как выбрать максимальное значение в группе чисел.
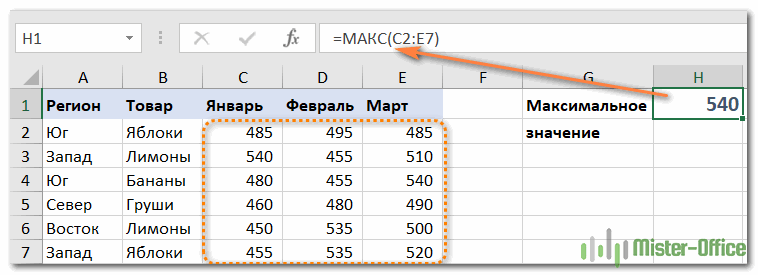
Чтобы в Excel извлечь наибольшее число в группе чисел, передайте эту группу функции МАКС в качестве ссылки на диапазон. Диапазон может содержать любое количество строк и столбцов. Например, чтобы получить максимальное значение из C2: E7, используйте эту простую формулу:
=МАКС(C2:E7)
Предположим, у нас есть сведения об учениках с их оценкой, но некоторые из значений оценки являются логическими, текстовыми, а некоторые пока вовсе не имеют оценки.
Применим функцию:
= МАКС(B2:B10)
Как видите, игнорируются ячейки с текстом, а также пустые, логические значения приравниваются к нулю, а затем вычисляется максимальное число, как показано в таблице Excel выше.
Наибольшее значение в несмежных ячейках или диапазонах Excel
Чтобы осуществить поиск в несмежных ячейках и диапазонах, необходимо включить в формулу ссылку на каждый отдельный адрес. Рассмотрим пошагово:
- Начните вводить функцию МАКС в ячейку.
- После того, как вы ввели открывающую скобку, нажмите и удерживайте Ctrl и выберите мышкой нужные ячейки и диапазоны.
- Отпустите
Ctrlи введите закрывающую круглую скобку. - Нажмите
Enter.
Вы получите формулу максимального числа в Excel, подобную этому:
=МАКС(C2:E2;C7:E7)
Как получить наибольшую (последнюю) дату в Excel
Во внутренней системе Excel даты – это не что иное, как порядковые номера дней, поэтому функция МАКС обрабатывает их без проблем.
Например, чтобы найти последнюю дату доставки из C2: C7, запишите обычную формулу, которую вы использовали бы для чисел:
=МАКС(C2:C7)
Поскольку дата – это также число, всё работает замечательно.
Максимальное значение с условиями.
Довольно часто случается, что из большого объёма данных Excel нужно выбрать максимальное значение из какой-то его части. К примеру, найти самую большую партию какого-то определённого товара в огромном списке продаж. Или же найти наивысшую оценку по какому-то предмету среди большого набора данных оценок, набранных учащимися определенного класса по нескольким предметам в школе.
Если вы хотите получить максимальное значение Excel с учётом каких-то условий, то вы можете выбрать из нескольких предложенных ниже формул. Чтобы убедиться, что все они возвращают одинаковый результат, мы протестируем их на одном и том же наборе данных.
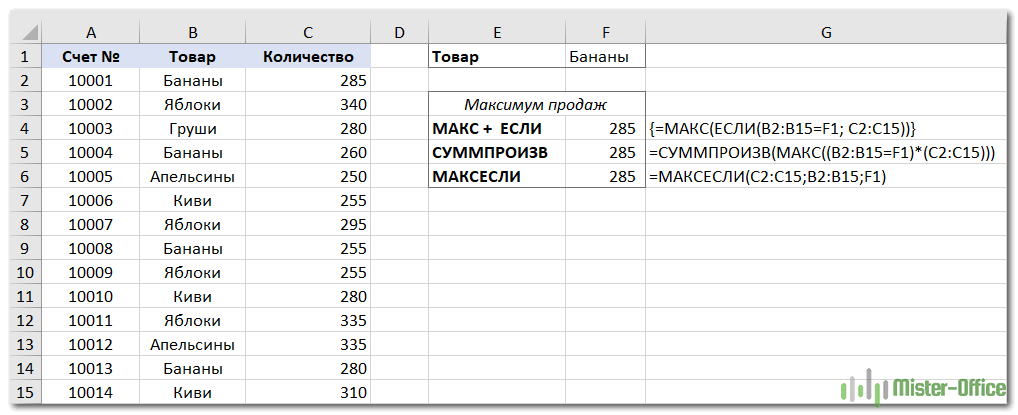
Задача: мы хотим найти самую большую продажу для определенного товара, указанного в F1.
МАКС + ЕСЛИ
Если вы ищете решение, которое работает во всех версиях Excel, используйте функцию ЕСЛИ для проверки условия, а затем передайте полученный массив в функцию:
=МАКС(ЕСЛИ(B2:B15=F1; C2:C15))
Чтобы это работало, необходимо нажать Ctrl + Shift + Enter одновременно, чтобы ввести как формулу массива. Если все сделано правильно, Excel заключит ваше выражение в {фигурные скобки}, что является визуальным указанием на формулу массива.
Также можно оценить несколько условий одновременно, о чем мы поговорим далее.
МАКС + СУММПРОИЗВ
Если вам не нравится использовать формулы массива в ваших листах, объедините МАКС с функцией СУММПРОИЗВ, которая умеет работать с массивами:
=СУММПРОИЗВ(МАКС((B2:B15=F1)*(C2:C15)))
МАКСЕСЛИ
В Excel 2019 и Office 365 есть специальная функция МАКСЕСЛИ, которая предназначена для поиска наибольшего значения по 126 критериям.
В нашем случае используется только одно условие, поэтому формула очень проста:
=МАКСЕСЛИ(C2:C15;B2:B15;F1)
На приведенном ниже скриншоте показаны все 3 формулы в действии:
Выбираем максимальное значение в Excel без учета нулей
Фактически, это разновидность условного МАКС, рассмотренного в предыдущем примере. Чтобы исключить нули, используйте логический оператор «не равно» и поместите выражение «<> 0» либо в критерий функции МАКСЕСЛИ, либо в конструкцию МАКС + ЕСЛИ.
Как вы понимаете, проверка этого условия имеет смысл только в случае наличия отрицательных чисел. Для положительных чисел эта проверка излишняя, потому что любое положительное число больше нуля.
Чтобы попробовать, давайте найдем самую маленькую скидку в диапазоне C2:C7. Поскольку все скидки представлены отрицательными числами, наименьшая скидка фактически является наибольшим значением.
Обязательно нажмите Ctrl + Shift + Enter, чтобы правильно заполнить эту формулу массива:
=МАКС(ЕСЛИ(C2:C7<>0; C2:C7))
А это обычная формула –
=МАКСЕСЛИ(C2:C7;C2:C7;»<>0″)
И вот что у нас получилось:
Как найти максимальное значение, игнорируя ошибки
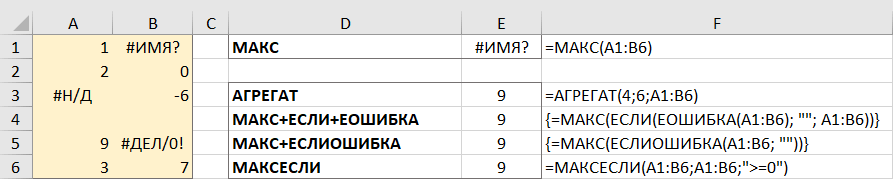
Когда вы работаете с большим объемом данных, управляемых различными формулами, есть вероятность, что некоторые из них приведут к ошибкам. Соответственно, функция МАКС тоже вернет ошибку.
В качестве обходного пути можно использовать МАКС вместе с ЕОШИБКА. Учитывая, что вы ищете в диапазоне A1: B5, формула принимает следующую форму:
=МАКС(ЕСЛИ(ЕОШИБКА(A1:B6); «»; A1:B6))
Чтобы упростить формулу, используйте функцию ЕСЛИОШИБКА вместо комбинации ЕСЛИ + ЕОШИБКА. Это также сделает логику более очевидной — если есть ошибка в A1:B6, замените ее пустой строкой (»), а затем вычислите самое большое значение в диапазоне:
=МАКС(ЕСЛИОШИБКА(A1:B6; «»))
Неудобство состоит в том, что нужно не забывать нажимать Ctrl + Shift + Enter, потому что это работает только как формула массива.
В Excel 2019 и Office 365 функция МАКСЕСЛИ может быть хорошим решением при условии, что ваш набор данных содержит хотя бы одно положительное число или нулевое значение:
=МАКСЕСЛИ(A1:B6;A1:B6;»>=0″)
Поскольку формула выполняет поиск максимального значения с условием «больше или равно 0», она не будет работать для набора данных, состоящего исключительно из отрицательных чисел.
Также идеально подходит функция АГРЕГАТ, которая может выполнять ряд операций и игнорировать значения ошибок:
=АГРЕГАТ(4;6;A1:B6)
Число 4 в первом аргументе предписывает выполнить поиск максимального числа, шестёрка во втором аргументе – это параметр «игнорировать ошибки», а A1: B6 — ваш целевой диапазон.
Все формулы возвращают одинаковый результат:
Как найти абсолютное наибольшее значение в Excel
При работе с диапазоном положительных и отрицательных чисел иногда может потребоваться найти максимальное абсолютное значение независимо от знака.
Первая идея, которая приходит в голову, — получить абсолютные значения всех чисел в диапазоне с помощью функции ABS и передать их в МАКС:
{= МАКС(ABS( диапазон ))}
Это формула массива, поэтому не забудьте подтвердить ее с помощью Ctrl + Shift + Enter. Еще одно предостережение: он работает только с числами и приводит к ошибке в случае нечисловых данных.
Не нравится это решение? Тогда давайте построим что-нибудь более жизнеспособное 
Что, если мы найдем минимальное значение, изменим или проигнорируем его знак, а затем вычислим вместе со всеми другими числами? Да, это будет отлично работать как обычная формула. В качестве дополнительного бонуса это отлично обрабатывает текстовые записи и ошибки.
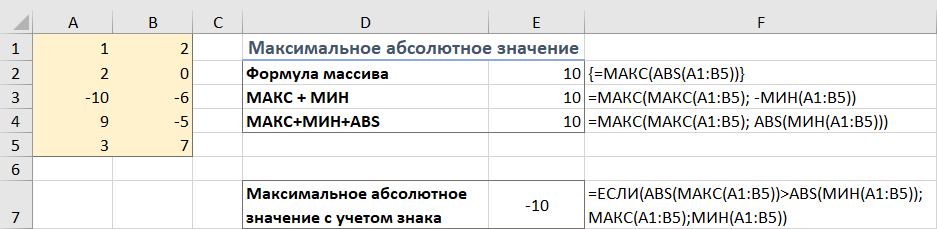
С исходными данными в A1: B5 расчёты выглядят следующим образом.
Формула массива (заполняется с помощью Ctrl + Shift + Enter):
=МАКС(ABS(A1:B5))
Обычная формула (заполняется клавишей Enter):
=МАКС(МАКС(A1:B5); -МИН(A1:B5))
или же
=МАКС(МАКС(A1:B5); ABS(МИН(A1:B5)))
На скриншоте ниже показаны результаты:
Вернуть максимальное абсолютное значение с сохранением знака
В некоторых ситуациях может потребоваться найти наибольшее абсолютное значение в таблице Excel, но вернуть число с исходным знаком, а не его абсолютное значение.
Предполагая, что числа находятся в ячейках A1: B5, вот выражение, которое следует использовать:
=ЕСЛИ(ABS(МАКС(A1:B5))>ABS(МИН(A1:B5)); МАКС(A1:B5);МИН(A1:B5))
Сложная на первый взгляд логика довольно проста. Сначала вы находите наибольшее и наименьшее числа в диапазоне и сравниваете их абсолютные значения. Если абсолютное (без учёта знака) максимальное значение больше абсолютного минимального значения, возвращается это наиболшее число, иначе – наименьшее число.
Поскольку формула возвращает исходное, а не абсолютное значение, информация о знаке сохраняется (см. скриншот выше).
Максимальное значение применительно к тексту.
Предположим, у нас есть список имен, и нам нужно вычислить их максимальную длину, то есть найти наибольшее количество символов в ячейке Excel.
Здесь мы должны применить функцию ДЛСТР для вычисления длины имени.
=ДЛСТР(А2)
А затем применим функцию МАКС, чтобы узнать максимальную длину ФИО.
=МАКС(B2;B13)
А можно обойтись без дополнительного столбца и вычислить максимальную длину текстового значения в одной ячейке. Для этого нужно объединить эти формулы, вложив ДЛСТР в МАКС:
=МАКС(ДЛСТР(A2:A13))
Учтите, что это формула массива. Ведь можно работать не только с диапазоном, но и с массивом числовых значений, который формируется другой функцией.
Вычислить наибольшую разницу в сумме.
Предположим, нам нужно вычислить наибольшую разницу в сумме за любой смежный месяц для каждого товара. Или, выражаясь иначе, найти максимальное изменение продаж за месяц.
Ниже представлена таблица Excel с небольшой выборкой данных за 4 месяца.
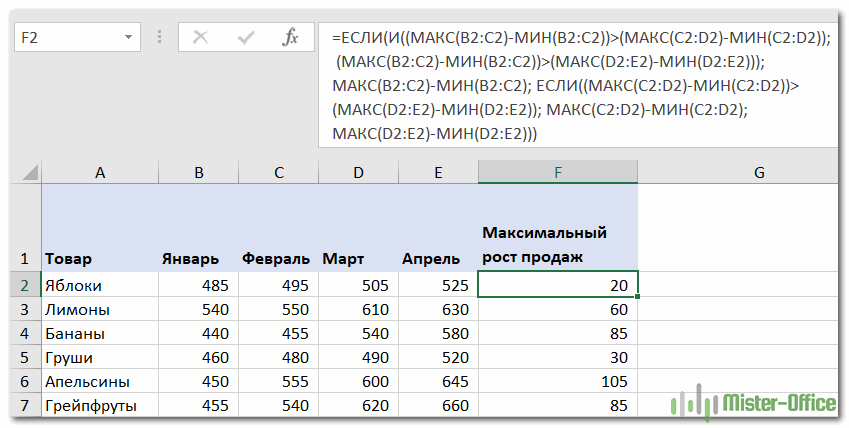
Если решать проблему «в лоб», то можно использовать функцию ЕСЛИ со множеством условий:
=ЕСЛИ(И((МАКС(B2:C2)-МИН(B2:C2))>(МАКС(C2:D2)-МИН(C2:D2)), (МАКС(B2:C2)-МИН(B2:C2))>(МАКС(D2:E2)-МИН(D2:E2))), МАКС(B2:C2)-МИН(B2:C2), ЕСЛИ((МАКС(C2:D2)-МИН(C2:D2))>(МАКС(D2:E2)-МИН(D2:E2)), МАКС(C2:D2)-МИН(C2:D2),МАКС(D2:E2)-МИН(D2:E2)))
Но при помощи функции МАКС можно значительно упростить расчет и не пользоваться такой длинной и сложной конструкцией.
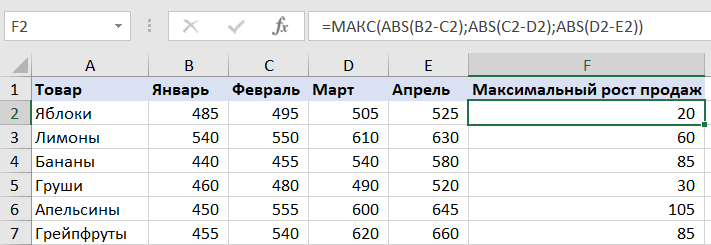
Используя функцию ABS, мы будем искать максимальное изменение вне зависимости от знака. Попробуйте заменить большую формулу этой:
=МАКС(ABS(B2-C2);ABS(C2-D2);ABS(D2-E2))
Как вы можете видеть в таблице ниже, этот вариант намного проще и возвращает те же результаты.
Как найти адрес ячейки Excel с максимальным числом.
Есть ли решение, которое сообщит адрес ячейки с наибольшим числом, а не само число? То есть, если A4 равно 9 и это значение является самым большим, как мне составить формулу, которая возвратит координаты A4 вместо 9?
Вы можете использовать функции ЯЧЕЙКА , ИНДЕКС и ПОИСКПОЗ в сочетании с функцией МАКС, чтобы вернуть адрес ячейки с наибольшим значением.
Например, если вы хотите найти ячейку с наивысшим значением в столбце от А1 до А7, вы можете использовать следующий расчёт:
=ЯЧЕЙКА(«адрес»;ИНДЕКС(A1:A7;ПОИСКПОЗ(МАКС(A1:A7);A1:A7;0)))
Получаем результат в виде абсолютной ссылки $А$4, которая указывает на самое большое число из этого диапазона.
Однако учтите, что это выражение работает только с одним столбцом.
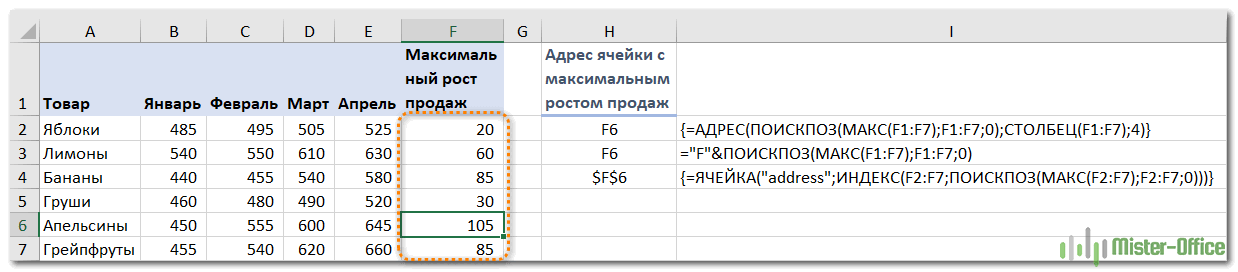
А вот еще альтернативные варианты поиска адреса наибольшего числа по столбцу, из которых вы можете выбрать наиболее подходящий для себя:
Формула массива –
{=АДРЕС(ПОИСКПОЗ(МАКС(F1:F7);F1:F7;0);СТОЛБЕЦ(F1:F7);4)}
Обычная формула, в которой явным образом нужно указать столбец:
=»F»&ПОИСКПОЗ(МАКС(F1:F7);F1:F7;0)
Ещё одна формула массива –
{=ЯЧЕЙКА(«address»;ИНДЕКС(F2:F7;ПОИСКПОЗ(МАКС(F2:F7);F2:F7;0)))}
На скриншоте вы видите, что все они возвращают один и тот же адрес:
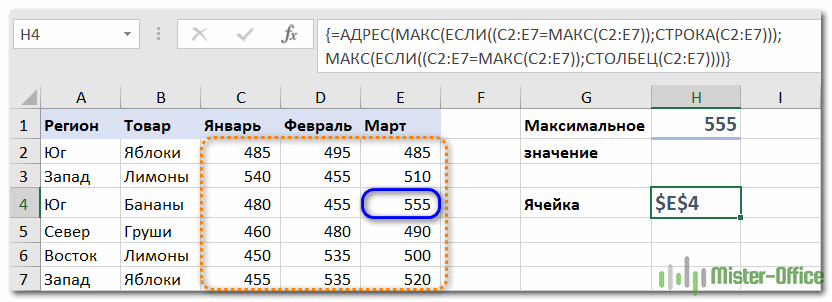
И ещё одна формула массива для вывода адреса, которая работает с диапазоном из нескольких строк и столбцов:
{=АДРЕС(МАКС(ЕСЛИ((C2:E7=МАКС(C2:E7));СТРОКА(C2:E7))); МАКС(ЕСЛИ((C2:E7=МАКС(C2:E7));СТОЛБЕЦ(C2:E7))))}
В данном случае, как видите, мы ищем адрес наибольшего числа в двумерном диапазоне C2:E7.
Напомню, что формула массива вводится с использованием комбинации клавиш Ctrl + Shift + Enter.
Как выделить наибольшее значение в Excel
В ситуации, когда вы хотите определить самое большое число в исходном наборе данных, самый быстрый способ – выделить его с помощью условного форматирования Excel. Приведенные ниже примеры покажут вам два разных варианта действий.
Выделите максимальное число в диапазоне Excel
В Microsoft Excel есть встроенное правило для форматирования максимальных чисел в диапазоне, которое идеально соответствует нашим потребностям. Вот как можно применить его:
- Выберите диапазон чисел (в нашем случае C2: E8).
- На вкладке «Главная» в группе «Стили» щелкните «Условное форматирование»> «Новое правило».
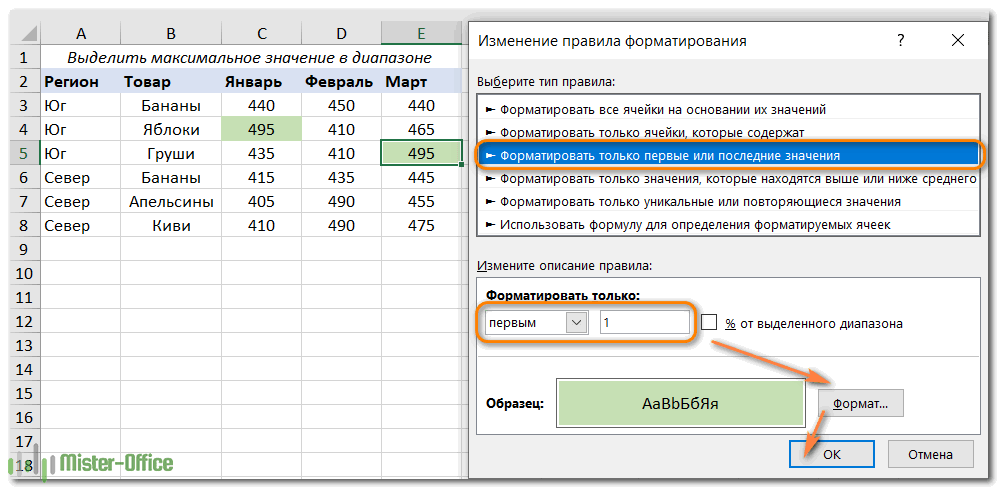
- В диалоговом окне «Новое правило форматирования» выберите «Форматировать только первые или последние значения».
- На нижней панели выберите «первым» из раскрывающегося списка и введите 1 в поле рядом с ним (это означает, что вы хотите выделить только одну ячейку, содержащую наибольшее значение).
- Нажмите кнопку «Формат» и выберите стиль оформления.
- Дважды щелкните OK, чтобы закрыть оба окна.
Как выделить цветом максимальное число в каждой строке
Поскольку нет встроенного правила, чтобы выделить наибольшее значение из каждой строки таблицы Excel, вам придется настроить собственное на основе функции МАКС. Вот как:
- Выберите все строки, которые вы хотите проверить (C3:E8).
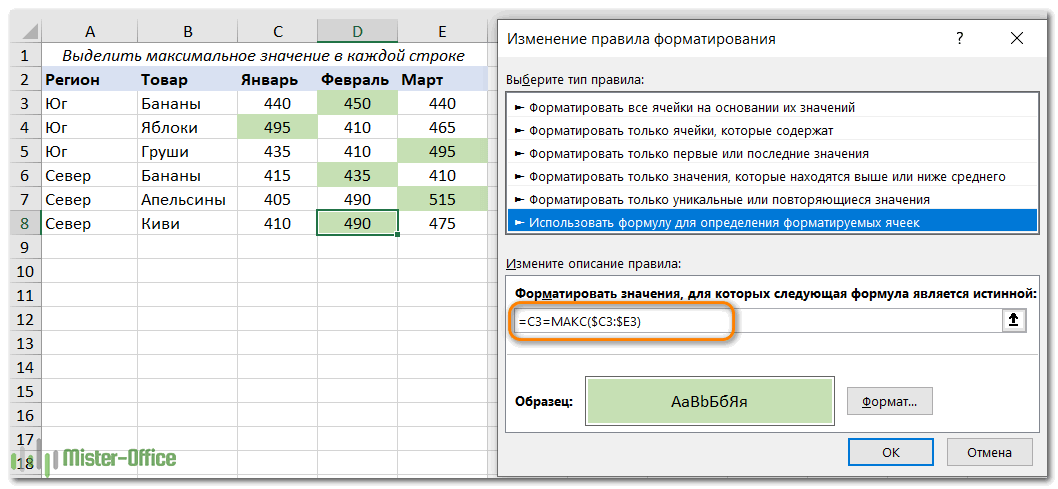
- Кликните Новое правило > Использовать формулу.
- В поле Форматировать значения, запишите:
=C3=МАКС($C3:$E3)
Где C3 — крайняя верхняя левая ячейка, а $C3:$E3 — координаты первой строки. Чтобы правило работало, обязательно зафиксируйте координаты столбца в диапазоне знаком $.
- Нажмите кнопку «Формат» и выберите нужный формат.
- Дважды щелкните ОК.
Кончик. Таким же образом вы можете выделить максимальное значение в каждом столбце. Шаги в точности такие же, за исключением того, что вы пишете условие для диапазона первого столбца и фиксируете координаты строки:
=C2=МАКС(C$2:C$7)
Дополнительные сведения см. в статье « Как создать правило условного форматирования на основе формул» .
Почему не получается найти наибольшее число?
МАКС — одна из самых простых в использовании функций Excel. Если вопреки всем ожиданиям она не работает, то, скорее всего, это одна из следующих проблем:
МАКС возвращает ноль
Если обычная формула МАКС возвращает 0, даже если в указанном диапазоне есть числа явно большие, скорее всего, эти числа отформатированы как текст.
Это особенно актуально, когда вы запускаете функцию МАКС для данных, получаемых другими формулами или же импортированных из других программ.
Вы можете проверить это с помощью функции ЕЧИСЛО, например:
=ЕЧИСЛО(A1)
Если приведенная выше формула возвращает ЛОЖЬ, то значение в A1 не является числовым. Это означает, что вы должны устранять неполадки с исходными данными, а не с формулой.
МАКС возвращает значение #Н/Д, #ЗНАЧ или другую ошибку.
Пожалуйста, внимательно проверьте указанные ячейки. Если какая-либо из указанных ячеек содержит ошибку, поиск максимума приведет к той же ошибке. Чтобы обойти это, посмотрите, как получить максимальное значение, игнорируя все ошибки .
Вот как можно найти максимальное значение в Excel. Благодарю вас за чтение!
Функция ЕСЛИОШИБКА – примеры формул — В статье описано, как использовать функцию ЕСЛИОШИБКА в Excel для обнаружения ошибок и замены их пустой ячейкой, другим значением или определённым сообщением. Покажем примеры, как использовать функцию ЕСЛИОШИБКА с функциями визуального… 
Сравнение ячеек в Excel — Вы узнаете, как сравнивать значения в ячейках Excel на предмет точного совпадения или без учета регистра. Мы предложим вам несколько формул для сопоставления двух ячеек по их значениям, длине или количеству…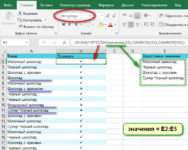 
Как проверить правильность ввода данных в Excel? — Подтверждаем правильность ввода галочкой. Задача: При ручном вводе данных в ячейки таблицы проверять правильность ввода в соответствии с имеющимся списком допустимых значений. В случае правильного ввода в отдельном столбце ставить… 
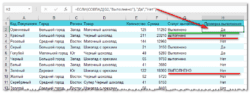Функция ЕСЛИ: проверяем условия с текстом — Рассмотрим использование функции ЕСЛИ в Excel в том случае, если в ячейке находится текст. СодержаниеПроверяем условие для полного совпадения текста.ЕСЛИ + СОВПАДИспользование функции ЕСЛИ с частичным совпадением текста.ЕСЛИ + ПОИСКЕСЛИ… 
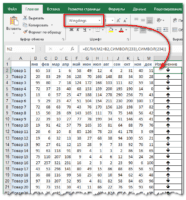Визуализация данных при помощи функции ЕСЛИ — Функцию ЕСЛИ можно использовать для вставки в таблицу символов, которые наглядно показывают происходящие с данными изменения. К примеру, мы хотим показать в отдельной колонке таблицы, происходит рост или снижение продаж.… 
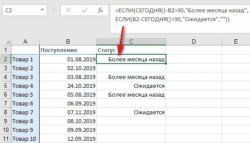3 примера, как функция ЕСЛИ работает с датами. — На первый взгляд может показаться, что функцию ЕСЛИ для работы с датами можно применять так же, как для числовых и текстовых значений, которые мы только что обсудили. К сожалению, это…
Section 6.3 Critical Points and Extrema
Subsection 6.3.1 Critical Points
With functions of one variable we were interested in places where the derivative is zero, since they made candidate points for the maximum or minimum of a function. If the derivative is not zero, we have a direction that is downhill and moving a little in that direction gives a lower value of the function. Similarly, with functions of two variables we can only find a minimum or maximum for a function if both partial derivatives are 0 at the same time. Such points are called critical points.
The point ((a,b)) is a critical point for the multivariable function (f(x,y)text{,}) if both partial derivatives are 0 at the same time.
In other words,
begin{equation*}
frac{partial }{partial x} f(x,y)|_{x=a,y=b}=0
end{equation*}
and
begin{equation*}
frac{partial }{partial y} f(x,y)|_{x=a,y=b}=0text{.}
end{equation*}
Example 6.3.1. Finding a Local Minimum of a Function.
Use the partial derivatives of (f(x,y)=x^2+ 2xy+3y^2-4x-3y) to find the minimum of the graph.
Solution.
- Critical Point by Algebra
-
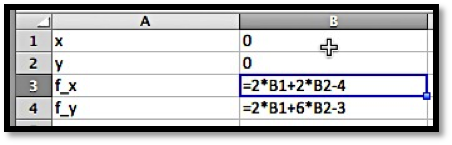
In the previous section, we already computed
begin{align*}
frac{partial }{partial x} f(x,y) amp = 2x+2y-4\
frac{partial }{partial y} f(x,y) amp = 2x+6y-3text{.}
end{align*}We need to find the places where both partial derivatives are 0. With this simple system, I can solve this system algebraically and find the only critical point is ((9/4, -1/4)text{.})
begin{align*}
0 amp = 2x+2y-4\
0 amp = 2x+6y-3text{.}
end{align*}Subtract the equations to eliminate (xtext{:})
begin{equation*}
0=0-4y-1text{.}
end{equation*}Solve for (ytext{:})
begin{align*}
4y amp = -1\
y amp = -1/4text{.}
end{align*}Substitute back and solve for (xtext{:})
begin{align*}
0 amp = 2x+2(-1/4)-4\
2x amp = 9/2\
x amp =9/4text{.}
end{align*} - Critical Point by Solver
-
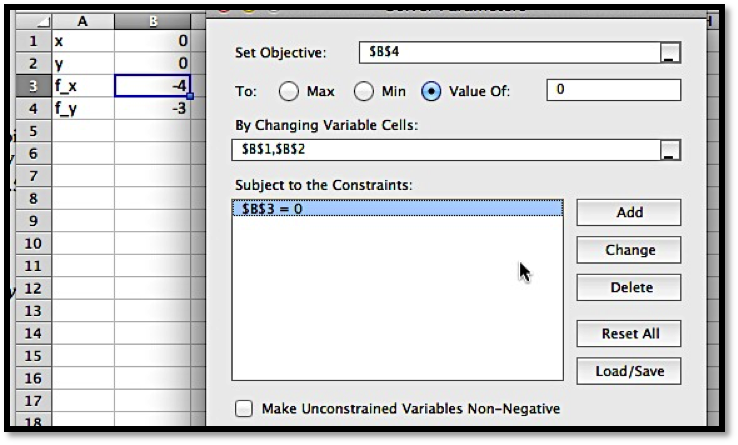
If the partials are more complicated, I will want to find the critical points another way. I can find the point with Solver.
To get solver to set both partials to 0 at the same time, I ask it to solve for (f_y=0text{,}) while setting (f_x=0) as a constraint. Make sure to uncheck the box that makes unconstrained variables non-negative.
This finds our critical point within our error tolerance.
- Critical Point by CAS
-
We can also use Wolfram|Alpha to find the solution to our system of equations.
- Determining the Critical Point is a Minimum
-
We thus get a critical point at ((9/4,-1/4)) with any of the three methods of solving for both partial derivatives being zero at the same time. Once we have a critical point we want to determine if it is a maximum, minimum, or something else. The easiest way is to look at the graph near the critical point.
It is clear from the graph that this critical point is a local minimum.
It is easy to see that (f(x,y)=x^2+y^2) has a critical point at ((0,0)) and that that point is a minimum for the function. Similarly, (f(x,y)=-x^2-y^2) has a critical point at ((0,0)) and that that point is a maximum for the function. For some functions, like (f(x,y)=x^2-y^2text{,}) which has a critical point at ((0,0)text{,}) we can have a maximum in one direction and a minimum in another direction. Such a point is called a saddle point. We note that we can have a saddle point even if the (x) and (y) slice curves both indicate a minimum.
Example 6.3.3. A Saddle Point at a Minimum on Both Axes.
Show that (f(x,y)=x^2-3xy+y^2) has a critical point at ((0,0)text{,}) which is a minimum of both slice curves, but is not a local minimum.
Solution.
We look at the two partial derivatives, and notice they are both zero at the origin.
begin{align*}
frac{partial }{partial x} f(x,y) amp = 2x-3y\
frac{partial }{partial x} f(x,y) amp = -3x+2ytext{.}
end{align*}
We then see that both slice curves are parabolas that bend up, with a minimum at 0.
begin{align*}
f(x,0) amp = x^2\
f(0,y) amp = y^2text{.}
end{align*}
However if we take the slice with (x=ytext{,}) we get a parabola bending down, so we don’t have a minimum.
begin{equation*}
f(x,-x)=x^2-3x x+x^2=-x^2text{.}
end{equation*}
Looking at the graph, we see that this graph does not have a minimum.
Subsection 6.3.2 Second Partial Derivatives
With only first derivatives, we can just find the critical points. To check if a critical point is maximum, a minimum, or a saddle point, using only the first derivative, the best method is to look at a graph to determine the kind of critical point. For some applications we want to categorize the critical points symbolically.
With functions of one variable we used the second derivative to test if a critical point was a maximum or minimum. In the two variable case we need to define the second derivatives and use them to define the discriminant of a function to test if a critical point is a minimum, maximum, or saddle point. We first need to define second partial derivatives.
Second partials.
begin{equation*}
f_{ab}=(f_a )_b=frac{partial}{partial b}(frac{partial}{partial a} f)text{.}
end{equation*}
Note that (f_{xx}) is simply the old second derivative of the curve (f(x,y_0)) and (f_{yy}) is simply the old second derivative of the curve (f(x_0,y)text{.}) For functions with continuous second partial derivatives, the mixed partials, (f_{yx}) and (f_{xy}) are the same.
Example 6.3.5. Finding Second Partial Derivatives.
Find the second partial derivatives of
begin{equation*}
f(x,y)=x^2+ 3xy+5y^3-7x-11ytext{.}
end{equation*}
Solution.
We start by computing the first partial derivatives.
begin{align*}
f_x amp = frac{partial}{partial x} f(x,y)=2x+3y-7\
f_y amp = frac{partial}{partial y} f(x,y)=3x+15y^2-11text{.}
end{align*}
Then we compute the second partial derivatives.
begin{align*}
f_{xx} amp = frac{partial}{partial x} f_x=2\
f_{xy} amp = frac{partial}{partial y} f_x=3\
f_{yx} amp = frac{partial}{partial x} f_y=3\
f_{yy} amp = frac{partial}{partial y} f_y=30ytext{.}
end{align*}
As expected, the mixed partials are the same.
Subsection 6.3.3 Using the Discriminant to Test Critical Points
To test if a critical point is a maximum, minimum, or saddle point we compute the discriminant of the function.
Discriminant.
begin{equation*}
D(f(x,y))=f_{xx} f_{yy}-f_{xy}^2text{.}
end{equation*}
Example 6.3.6. Finding the Discriminant of a Function.
Find the discriminant of
begin{equation*}
f(x,y)=x^2+ 3xy+5y^3-7x-11ytext{.}
end{equation*}
Solution.
We have already computed the second partial derivatives.
begin{equation*}
f_xx=2,quad f_xy=3,quad f_yy=30ytext{.}
end{equation*}
Substituting into the formula,
begin{equation*}
D=(2)(30y)-3^2=60y-9text{.}
end{equation*}
Discriminant test.
Let ((a,b)) be a critical point of (f(x,y)text{.})
If (D(a,b)>0) and (f_{xx} (a,b)>0) then ((a,b)) is a local minimum of (f(x,y)text{.})
If (D(a,b)>0 ) and (f_{xx} (a,b)lt 0) then ((a,b)) is a local maximum of (f(x,y)text{.})
If (D(a,b)lt 0) then ((a,b)) is a saddle point of (f(x,y)text{.})
If (D(a,b)=0) we do not have enough information to classify the point.
Example 6.3.7. Using the Discriminant to Classify Critical Points.
Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.
| p | ({f_x}) | ({f_y}) | (f_{xx}) | (f_{xy}) | (f_{yy}) |
| A | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 1 | 3 | 2 | 4 |
| C | 1 | 0 | 0 | 2 | 3 |
| D | 0 | 0 | 1 | 2 | 0 |
| E | 0 | 0 | -1 | 2 | 3 |
| F | 0 | 0 | -3 | 1 | -2 |
| G | 0 | 0 | 3 | 3 | 3 |
Solution.
We need to compute the discriminant and apply the test.
| p | (f_x) | (f_y) | (f_{xx}) | (f_{xy}) | (f_{yy}) | Discriminant | Classification |
| A | 0 | 0 | 0 | 0 | 1 | 0 | Not enough information |
| B | 0 | 1 | 3 | 2 | 4 | 8 | Not a critical point |
| C | 1 | 0 | 0 | 2 | 3 | -4 | Not a critical point |
| D | 0 | 0 | 1 | 2 | 0 | -4 | Saddle point |
| E | 0 | 0 | -1 | 2 | 3 | -7 | Saddle point |
| F | 0 | 0 | -3 | 1 | -2 | 5 | Maximum |
| G | 0 | 0 | 3 | 3 | 3 | 0 | Not enough information |
Example 6.3.8. Finding and Classifying Critical Points.
Let (f(x,y)=x^3-3x+y^3-3y^2text{.}) Find the critical points and classify them using the discriminant.
Solution.
We start by computing the first partial derivatives.
begin{align*}
f_x amp = 3x^2-3=3(x-1)(x+1)\
f_y amp = 3y^2-6y=3(y-2)(y)text{.}
end{align*}
Then we compute the second partial derivatives and the discriminant.
begin{equation*}
f_{xx}=6x,quad f_{xy}=0,quad f_{yy}=6y-6,quad D=(6x)(6y-6)-0^2=36xy-36xtext{.}
end{equation*}
We have critical points when both first partials are 0, so at ((1,2)text{,}) ((-1,2)text{,}) ((1,0)text{,}) and ((-1,0)text{.})
At ((1,2)text{,}) both (D) and (f_{xx}) are positive, so we have a local minimum.
At ((-1,2)) and ((1,0)text{,}) (D) is negative, so we have a saddle point.
At (((-1,0)text{,}) (D) is positive and (f_{xx}) is negative, so we have a local maximum.
Exercises 6.3.4 Exercises: Critical Points and Extrema Problems
Exercise Group.
For the given functions and region:
-
Find the partial derivatives of the original function.
-
Find any critical points in the region.
-
Produce a small graph around any critical point.
-
Determine if the critical points are maxima, minima, or saddle points.
1.
The function is (f(x,y)=x^2+2xy+4y^2+5x-6ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})
Solution.
-
begin{align*}
f_x (x,y) amp = 2x+2y+5\
f_y (x,y) amp = 2x+8y-6text{.}
end{align*} -
Set the partial derivatives equal to 0 and solve for (x) and (ytext{.})
begin{align*}
f_x (x,y) amp = 2x+2y+5=0\
f_y (x,y) amp = 2x+8y-6=0text{.}
end{align*}We can use either the method of substitution (solve for (x) or (y) in one equation and substitute into the other and solve), or method by elimination (multiply both equations by carefully chosen numbers and ass/subtract the equations from each other.)
We will demonstrate method of elimination:
begin{align*}
-1×(2x+2y+5 amp = 0) amp text{gives }-2x-2y-5amp=0\
1×(2x+8y-6 amp = 0) amp text{gives } 2x+8y-6amp =0text{.}
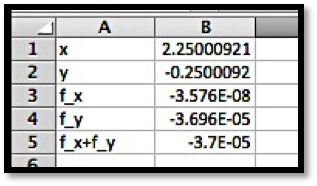
end{align*}Adding the two equations gives (6y-11=0text{;}) hence, (y= 11/6text{.})
Pick one of the equations to solve for x (it does not matter which one):
begin{equation*}
2x+2y+5=0 quad text{and }y= 11/6
end{equation*}implies that (2x+2(11/6)+5=0) so (x= (2(11/6)+5)/(-2)=-13/3text{.})
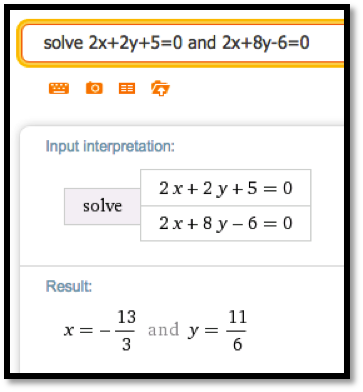
We can also solve this system of equations using Wolfram Alpha:
-
The command in Wolfram Alpha is:
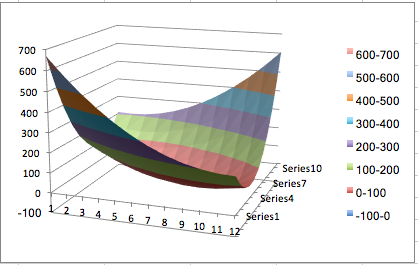
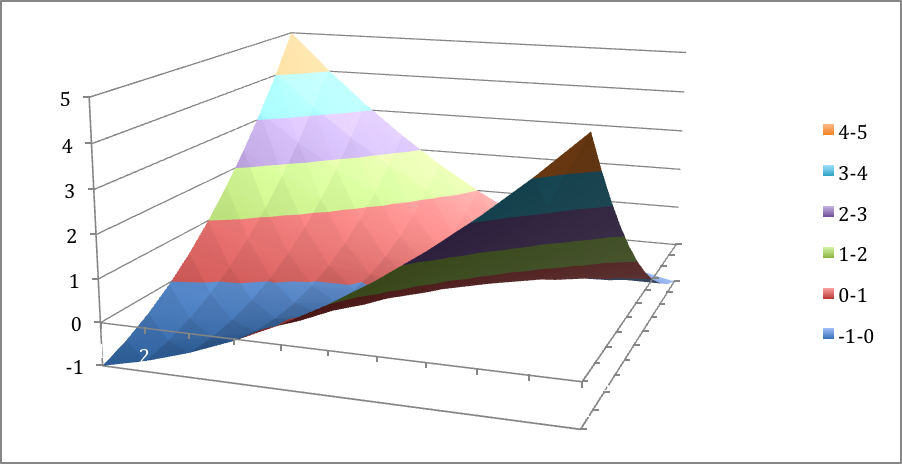
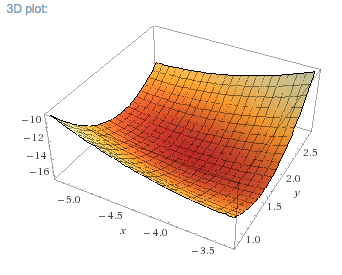
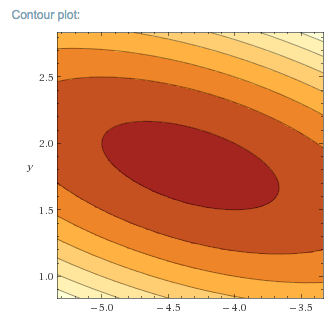
It is worth looking at both the 3D Plot and the Contour Plot.
-
The 3D plot suggests a minimum, and this is confirmed by the contour plot which shows they typical view of a local minimum.
As an alternative we can find the discriminant.
begin{align*}
f_{xx} (x,y) amp = 2\
f_{xy} (x,y) amp = 2\
f_{yy} (x,y) amp = 8\
D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2=2*8-2^2=12>0text{.}
end{align*}Since (Dgt 0) and (f_{xx} (x,y)gt 0) we have a local minimum.
2.
The function is (f(x,y)=x^2+7xy+2y^2+4x-3ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})
3.
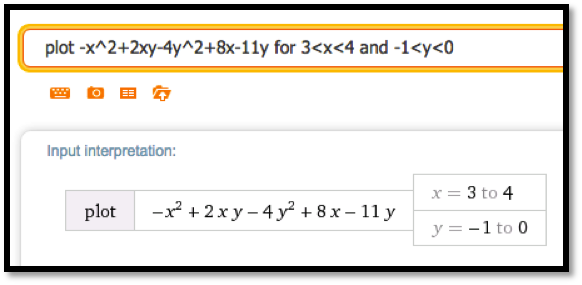
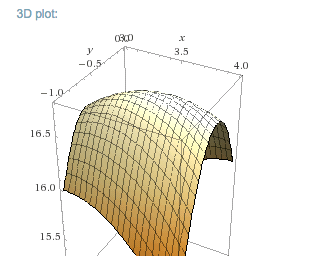
The function is (f(x,y)=-x^2+2xy-4y^2+8x-11ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})
Solution.
-
begin{align*}
f_x (x,y) amp = -2x+2y+8\
f_y (x,y) amp = 2x-8y-11text{.}
end{align*} -
Set the partial derivatives equal to 0 and solve for (x) and (ytext{.})
begin{align*}
f_x (x,y) amp = -2x+2y+8=0\
f_y (x,y) amp = 2x-8y-11=0text{.}
end{align*}Adding the equations (-6y-3=0text{,}) and so (y=-1/2text{.})
Substituting in the first equation give (-2x+7=0text{,}) and so (x=7/2text{.})
Hence we have a critical points at ((7/2,-1/2)text{.})
-
For ((x,y)= (2,1)text{:})
-
From the picture we conclude that the critical point is a maximum. As an alternative we can find the discriminant.
begin{align*}
f_{xx} (x,y) amp = -2\
f_{xy} (x,y) amp = 2\
f_{yy} (x,y) amp = -8\
D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2=2*8-2^2=12gt 0text{.}
end{align*}Since (Dgt 0) and (f_{xx} (x,y)lt 0) we have a local maximum.
4.
The function is (f(x,y)=x^3-12x+y^3-3ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})
5.
The function is the revenue function for selling widgets and gizmos with demand price functions
begin{align*}
PriceGizmo amp = 25-frac{QuantityGizmo}{50}-frac{QuantityWidget}{200}\
PriceWidget amp = 30-frac{QuantityWidget}{45}-frac{QuantityGizmo}{300}
end{align*}
for the region (0le QuantityWidgetle 1500text{,}) and (0le QuantityGizmole 1500text{.})
Solution.
To solve this problem we will rename Gizmos (x) and Widgets (ytext{.}) This will make using Wolfram Alpha slightly easier, and symbol manipulation a tad more straight forward.
begin{align*}
PriceX amp = 25-frac{x}{50}-frac{y}{200}\
PriceY amp = 30-frac{y}{45}-frac{x}{300}\
revenue (x,y) amp =x*PriceX+y *PriceY\
amp =x left[25-frac{x}{50}-frac{y}{200}right]+yleft[30-frac{y}{45}-frac{x}{300}right]\
amp = frac{-36x^2-15xy+45000x-40y^2+54000y}{1800} text{.}
end{align*}
-
begin{align*}
revenue_x (x,y)amp = frac{-24x-5y+1000}{600} \
revenue_y (x,y)amp = frac{-3x-16y+10800}{360}
end{align*} -
Using WolframALpha, the critical point is at ((62000/123, 23800/41) approx (504, 580.5)text{.})
-
Using WolframAlpha we get:
-
From the picture we conclude that the critical point is a maximum.
As an alternative we can find the discriminant.
begin{align*}
f_{xx} (x,y) amp = -frac{1}{25}\
f_{xy} (x,y) amp = -frac{1}{120}\
f_{yy} (x,y) amp = -frac{4}{25}\
D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2 gt 0text{.}
end{align*}Since (Dgt 0) and (f_{xx} (x,y)lt 0) we have a local maximum.
6.
The function is the revenue function for selling widgets and gizmos with demand price functions
begin{align*}
PriceGizmo amp = 30(0.9)^{(QuantityGizmo/150) }-frac{QuantityWidget}{250}\
PriceWidget amp = 20(0.97)^{(QuantityWidget/50) }-frac{QuantityGizmo}{350}
end{align*}
for the region (0le QuantityWidgetle 1500text{,}) and (0le QuantityGizmole 1500text{.}) (Warning: There are several critical points.)
7.
Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.
| p | (f_x) | (f_y) | (f_{xx}) | (f_{xy}) | (f_{yy}) |
| A | 1 | 2 | 3 | 4 | 5 |
| B | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 1 | 2 | 5 | 3 |
| D | 0 | 0 | 2 | 2 | 2 |
| E | 0 | 0 | 1 | 2 | 3 |
| F | 0 | 0 | 0 | 1 | 0 |
| G | 0 | 0 | 0 | -1 | 0 |
Solution.
Add a column for D and classify.
| p | (f_x) | (f_y) | (f_{xx}) | (f_{xy}) | (f_{yy}) | (D) | Classification |
| A | 1 | 2 | 3 | 4 | 5 | -1 | Not Critical |
| B | 0 | 0 | 0 | 0 | 0 | 0 | Not Enough Info |
| C | 0 | 1 | 2 | 5 | 3 | -19 | Not Critical |
| D | 0 | 0 | 2 | 2 | 2 | 0 | Not Enough Info |
| E | 0 | 0 | 1 | 2 | 3 | -1 | Saddle Point |
| F | 0 | 0 | 0 | 1 | 0 | 0 | Not Enough Info |
| G | 0 | 0 | 0 | -1 | 0 | 0 | Not Enough Info |
8.
Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.
| p | (f_x) | (f_y) | (f_{xx}) | (f_{xy}) | (f_{yy}) |
| A | 1 | 2 | 3 | 4 | 5 |
| B | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 1 | 2 | 5 | 3 |
| D | 0 | 0 | 2 | 2 | 2 |
| E | 0 | 0 | 1 | 2 | 3 |
| F | 0 | 0 | 0 | 1 | 0 |
| G | 0 | 0 | 0 | -1 | 0 |
9.
Using polynomials of the form (f(x,y)=ax^3+bx^4+cy^3+dy^4text{,}) produce a function that has a critical point at ((0, 0)text{,}) of each type.
-
A local maximum.
-
A local minimum.
-
A saddle point where the function f(x,0) has a local maximum and f(0,y) has a local minimum.
-
A saddle point where the function f(x,0) and f(0,y) both have inflection points.
Solution.
It helps to consider the question with only one variable.
(f(x)=ax^3) has an inflection point at (x=0) and neither a max nor a minimum.
(f(x)=ax^4) has minimum at (x=0) if (agt 0) and a maximum if (alt 0text{.})
Since all terms are of degree at least three, all second partial derivatives are zero at the origin, so the discriminant test fails.
-
A local maximum: ((x,y) = -x^4-y^4text{.}) Both (x^4) and (y^4) are nonnegative, so the function is negative everywhere except at the origin where it is 0.
-
A local minimum: (f(x,y)= x^4+y^4text{.}) Both (x^4) and (y^4) are nonnegative, so the function is positive everywhere except at the origin where it is 0.
-
A saddle point where the function (f(x,0)) has a local maximum and (f(0,y)) has a local minimum: ((x,y)= -x^4+y^4text{.})
-
A saddle point where the function (f(x,0)) and (f(0,y)) both have inflection points: (f(x,y)= x^3+y^3)
You have attempted of activities on this page.
external/Examples/Section-6-3-Examples.xlsx
Если функция F(x) непрерывна на отрезке [a, b] и имеет внутри этого отрезка локаль-ный экстремум, то его можно найти, используя надстройку Excel Поиск решения. Рассмотрим последовательность нахождения экстремума функции на примере.
Пример 12. Задана неразрывная функция Y= X 2 +X +2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2, 2].
Решение:
1. В ячейку А3 рабочего листа введите любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение Х.
2. В ячейку В3 введите формулу, определяющую заданную функциональную зависимость (рис. 18). Вместо переменной Х в этой формуле должна быть ссылка на ячейку А3: = A2^2 + A2 +2.
3. Выполните команду меню Сервис — Поиск решения.
4. В открывшемся окне диалога Поиск решения в поле Установить целевую ячейку укажите адрес ячейки, содержащей формулу (В3), установите пере-ключатель Минимальному значению, в поле Изменяя значение ячейки укажите адрес ячейки, в которой содержится переменная х.
5. Добавьте два ограничения в соответствующее поле: A3>= -2 и A3<= 2.
6. Щелкните на кнопке Параметры и в от крывшемся диалоговом окне Пара-метры поиска решения установите относительную погрешность вычислений и предельное число итераций.
7. Щелкните на кнопке Выполнить.
В ячейке А3 будет помещено значение аргумента Х функции, при котором она принимает минимальное значение, а в ячейке В3 – минимальное значение функции. В результате выполнения вычислений в ячейке А3 будет получено значение независимой переменной, при котором функция принимает наименьшее значение, а в ячейке В3 – минимальное значение функции, равное 1,75. Постройте график заданной функции и убедитесь, что решение найдено верно.
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
history 14 января 2021 г.
- Группы статей
- Надстройка «Поиск решения»
Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).
Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.
После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).
Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).
Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).
Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).
Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.
После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.