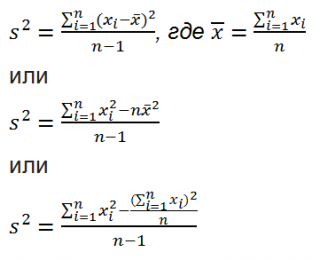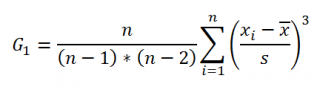Excel как статистический пакет - Word и Excel - помощь в работе с программами

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.

Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.

Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».

Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
- Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
- Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».

Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.

Однофакторный дисперсионный анализ

Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.

Двухфакторный дисперсионный анализ с повторениями

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:

Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.

Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.

Двухфакторный дисперсионный анализ без повторений

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).

Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.

Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.

Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).

Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».

Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.

Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).

Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.

Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.

Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.

С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».

Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.

Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.

Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.

Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:

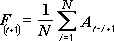
где

N — число предшествующих периодов, входящих в скользящее среднее;
A
j — фактическое значение в момент времени j;
F
j — прогнозируемое значение в момент времени j.

Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.

Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.

Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.

В средстве регрессии используется функция LINEST.

Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.

Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.

Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».

«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».

Парный двухвыборочный t-тест для средних

Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.

Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:

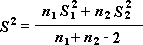
Двухвыборочный t-тест с одинаковыми дисперсиями

Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.

Двухвыборочный t-тест с различными дисперсиями

Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.

Для определения тестовой величины t используется следующая формула.

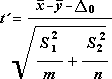
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.

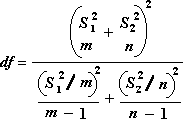
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.

При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Создание гистограммы в Excel 2016

Создание диаграммы Парето в Excel 2016

Загрузка средства анализа в Excel

Инженерные функции (справка)

Общие сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Поиск ошибок в формулах

Сочетания клавиш и горячие клавиши в Excel

Функции Excel (по алфавиту)

Функции Excel (по категориям)

Нужна дополнительная помощь?

Источник

Содержание

Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
Вопросы и ответы

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

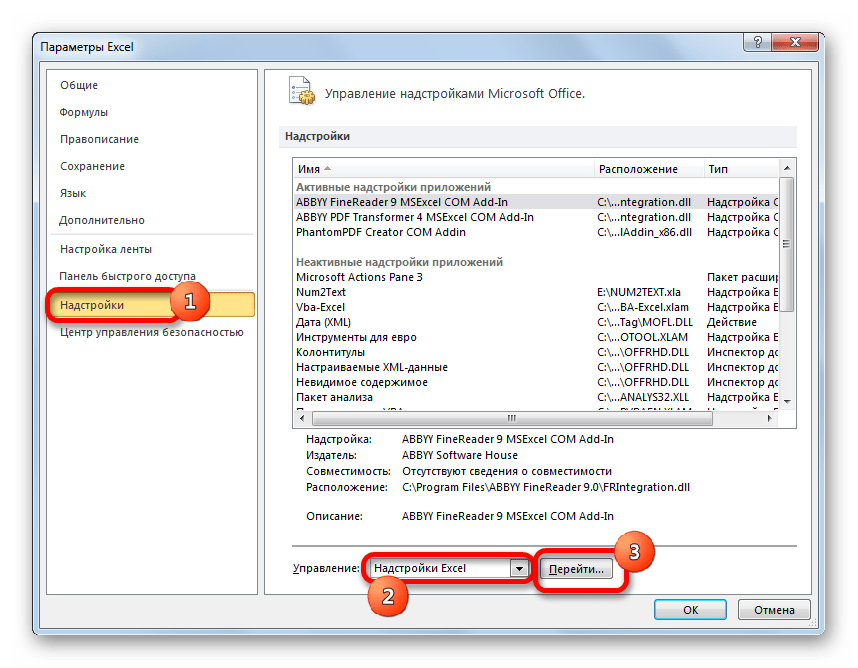
Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

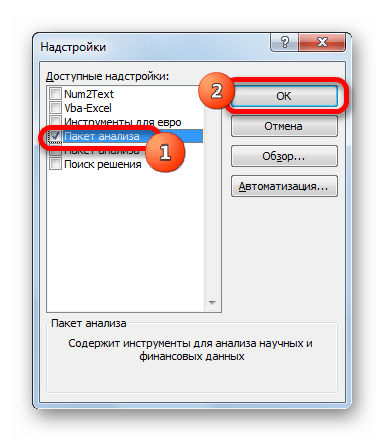
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

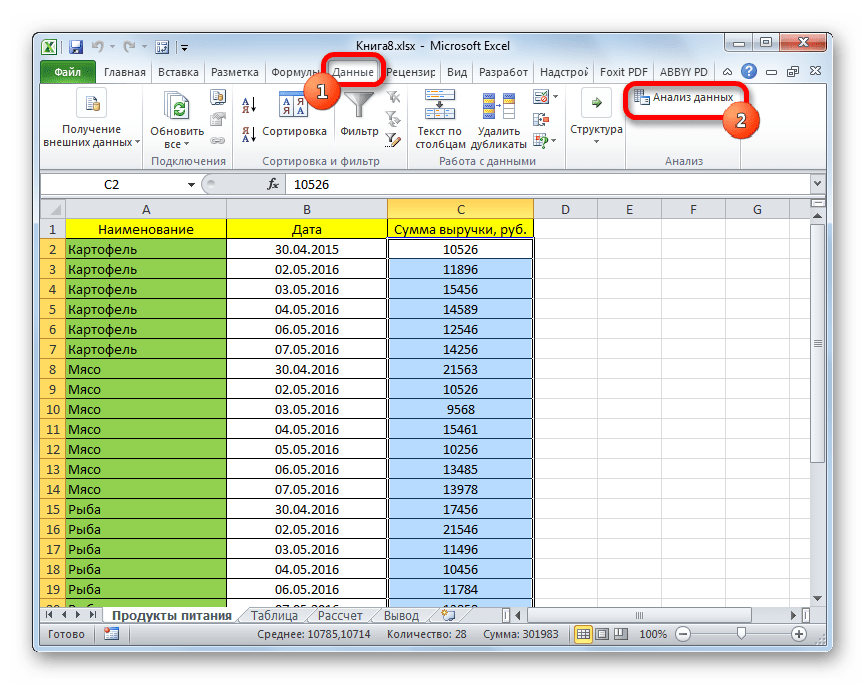
Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».

Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».

После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».

После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

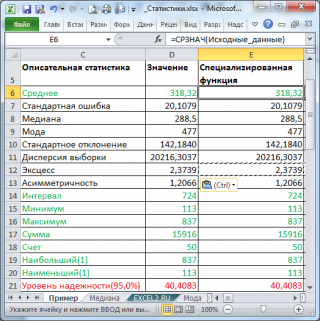
После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Содержание

Надстройка Пакет анализа EXCEL
Использование пакета анализа в MS Excel
Применение описательной статистики в Microsoft Excel
Использование описательной статистики
Подключение «Пакета анализа»
Применение инструмента «Описательная статистика»

Надстройка Пакет анализа EXCEL

history 13 октября 2016 г.

Использование надстройки «Пакет анализа», поможет упростить расчеты при проведении статистического или инженерного анали за.

Надстройка Пакет анализа ( Analysis ToolPak ) доступна из вкладки Данные , группа Анализ . Кнопка для вызова диалогового окна называется Анализ данных .

Если кнопка не отображается в указанной группе, то необходимо сначала включить надстройку (ниже дано пояснение для EXCEL 2010/2007):

на вкладке Файл выберите команду Параметры , а затем — категорию Надстройки .
в списке Управление (внизу окна) выберите пункт Надстройки Excel и нажмите кнопку Перейти .
в окне Доступные надстройки установите флажок Пакет анализа и нажмите кнопку ОК.

СОВЕТ : Если пункт Пакет анализа отсутствует в списке Доступные надстройки , нажмите кнопку Обзор , чтобы найти надстройку. Файл надстройки FUNCRES.xlam обычно хранится в папке MS OFFICE, например C : Program Files Microsoft Office Office 14 Library Analysis или его можно скачать с сайта MS.

После нажатия кнопки Анализ данных будет выведено диалоговое окно надстройки Пакет анализа .

Ниже описаны средства, включенные в Пакет анализа (по теме каждого средства написана соответствующая статья – кликайте по гиперссылкам).

Источник

Использование пакета анализа в MS Excel

Общие сведения. Пакет анализа, являющийся надстройкой, содержит коллекцию функций и инструментов, расширяющих встроенные аналитические возможности MS Excel. В частности, пакет анализа можно использовать для создания гистограмм, ранжирования данных, извлечения случайных или периодических выборок из множеств данных, проведения регрессионного анализа, получения основных статистических характеристик для выборки, генерации случайных чисел с различным распределением, а также применять преобразование Фурье и другие преобразования к своим данным.

Функции пакета анализа можно использовать точно так же, как и любые другие функции MS Excel, а чтобы получить доступ к инструментам пакета анализа, необходимо выполнить следующие действия:

1. Выбрать в меню Сервис команду Анализ данных. Затем на экране появится окно диалога, содержащее список инструментов анализа.

2. Чтобы использовать инструмент анализа, необходимо выбрать его имя в списке и нажмите кнопкуОК.

3. Заполнить открывшееся окно диалога. В большинстве случаев это означает задание входного диапазона с данными, которые вы собираетесь анализировать, задание выходного диапазона, в который должны быть помещены результаты, и выбор нужных параметров.

Если команда Анализ данных отсутствует в меню Сервис или если формула, которая использует функцию пакета анализа, возвращает ошибочное значение #ИМЯ?, выберите в меню Сервис команду Надстройки и затем — Пакет анализа -VBA в списке надстроек, после чего наж-мите кнопку ОК. При анализе данных часто возникает необходимость определения различных статистических характеристик или параметров распределения. С помощью MS Excel можно анали-зировать распределение, используя несколько инструментов: встроенные статистические функции, функции для оценки разброса данных, инструмент Описательная статистика, который предоставляет удобные сводные таблицы основных параметров распределения, инструменты Гистограмма и Ранг и персентиль.

Задание 1. Рассмотреть на практическом примере применение инструмента Описательная статистика пакета анализа.

1. Создать новый файл, на 1-м листе построить таблицу по приведенной ниже форме.

A	B	C	D
1	102,8396
2	102,0065
3	101,0474
4	98,5871
5	100,0231
6	102,5894
7	104,3369
8	101,2785
9	103,1233
10	97,2110
11	98,7534
12	100,2587
13	109,5468
14	105,1034
15	102,2587
16	101,6512
17	106,4527
18	102,5584
19	99,3213
20	100,0203

1. Инструмент Описательная статистика предлагает таблицу основных статистических характеристик для одного или нескольких множеств входных значений. Выходной диапазон этого инструмента содержит следующие статистические характеристики для каждой переменной из входного диапазона: среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия, коэффициент эксцесса, коэффициент асимметрии, интервал, минимальное значение, максимальное значение, сумма, число значений, k-e наибольшее и наименьшее значения (для любого заданного значения k) и уровень значимости для среднего.

2. Для использования инструмента Описательная статистика необходимо выбрать в меню Сервис команду Анализ данных, затем в окне диалога Анализ данных выбрать инструмент Описательная статистика и нажать кнопку ОК.

3. В открывшемся диалоговом окне установить следующие опции: Входной интервал: $A$1:$A$20, Группирование: по столбцам, Уровень надежности: флажок — 95%, К-ый наименьший: флажок – 20, К-ый наибольший – 20, Параметры вывода — Выходной интервал: $C$1, Итоговая статистика: флажок, Нажать кнопку ОК.

4. В результате в таблице будет отражен статистический анализ данного столбца (А1:А20).

5. Сохранить результаты на личном диске в файле под именем stat-2. xls.

Задание 2. Вычисление скользящего среднего. Скользящее среднее — это метод, позволяя-ющий упростить анализ тенденции за счет сглаживания колебаний измерений за некоторый период времени. Эти колебания могу возникать из-за случайного «шума», который часто является побочным эффектом техники измерения. Например, измерения высоты растущих детей будут зависеть и от точности линейки, и от того, насколько прямо стоит ребенок при измерении. Однако вы можете выполнить ряд измерений, затем сгладить их по отрезкам времени и построить окончательную кривую, которая будет более точно отражать фактическую скорость роста.

Колебания измерений и связанное с ними смещение данных могут быть результатом различных временных условий. Месячные продажи, например, могут изменяться в зависимости от количества рабочих дней в месяце или от количества продавцов, находящихся в отпуске.

1. Создать новый файл, на 1-м листе которого построить таблицу и двугодичную кривую спроса, показанные на рис. 1.

2. Для построения менее «шумной» линии тренда для этих данных можно использовать шестимесячное скользящее среднее. Первая точка в кривой скользящего среднего — это среднее за первые шесть месяцев (январь-июнь 2004 г.). Следующая точка — среднее со второго по седьмой месяцы (Февраль-Июль 2005 г.) и т.д. Инструмент Скользящее среднее может выполнить этот анализ вместо вас.

3. Чтобы использовать инструмент Скользящее среднее, выберите команду Анализ данных в меню Сервис, укажите инструмент Скользящее среднее в окне диалога Анализ данных и наж-мите кнопку ОК. Инструмент Скользящее среднее требует задания трех параметров: диапазона, который содержит анализируемые данные, диапазона для вычисляемых усредненных данных и интервала усреднения. Например, для определения трехмесячного скользящего среднего, задайте интервал 3.

4. На рис. 2. представлено шестимесячное скользящее среднее вместе с исходной кривой спроса из рис. 1. Инструмент Скользящее среднее возвращает выходные данные в столбце С, который использовался для построения сглаженной кривой в диаграмме. Обратите внимание, что первые пять ячеек выходного диапазона содержат ошибочное значение #Н/Д. Если интервал равен п, вы всегда будете иметь п-1 ошибочное значение #Н/Д в начале выходного диапазона. Включение этих значений в диаграмму не создает трудностей, так как Excel просто отставляет пустой начальную область сглаженной кривой.

1	Месяц	Спрос (руб.)
2	январь 2004	120325
3	февраль 2004	125600
4	март 2004	126000
5	апрель 2004	125400
6	май 2004	135200
7	июнь 2004	142000
8	июль 2004	145700
9	август 2004	148100
10	сентябрь 2004	152000
11	октябрь 2004	156000
12	ноябрь 2004	151000
13	декабрь 2004	152300
14	январь 2005	144400
15	февраль 2005	143900
16	март 2005	156200
17	апрель 2005	157500
18	май 2005	162000
19	июнь 2005	174800
20	июль 2005	176900
21	август 2005	184000
22	сентябрь 2005	197200
23	октябрь 2005	202600
24	ноябрь 2005	225000
25	декабрь 2005	255800

Рис. 1. Спрос в месяц

1	Месяц	Спрос (руб.)	Скользящее среднее по 6 месяцам
2	январь 2004	120325	#Н/Д
3	февраль 2004	125600	#Н/Д
4	март 2004	126000	#Н/Д
5	апрель 2004	125400	#Н/Д
6	май 2004	135200	#Н/Д
7	июнь 2004	142000	129087,5
8	июль 2004	145700	133316,7
9	август 2004	148100	137066,7
10	сентябрь 2004	152000	141400
11	октябрь 2004	156000	146500
12	ноябрь 2004	151000	149133,3
13	декабрь 2004	152300	150850
14	январь 2005	144400	150633,3
15	февраль 2005	143900	149933,3
16	март 2005	156200	150633,3
17	апрель 2005	157500	150883,3
18	май 2005	162000	152716,7
19	июнь 2005	174800	156466,7
20	июль 2005	176900	161883,3
21	август 2005	184000	168566,7
22	сентябрь 2005	197200	175400
23	октябрь 2005	202600	182916,7
24	ноябрь 2005	225000	193416,7
25	декабрь 2005	255800	206916,7

Рис. 2. Скользящее среднее по 6 месяцам

5. Сохранить результаты на личном диске в файле под именем stat-3.xls.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Применение описательной статистики в Microsoft Excel

Использование описательной статистики

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Подключение «Пакета анализа»

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

Применение инструмента «Описательная статистика»

Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
После выполнения данных действий непосредственно запускается окно «Описательная статистика».

В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:

В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».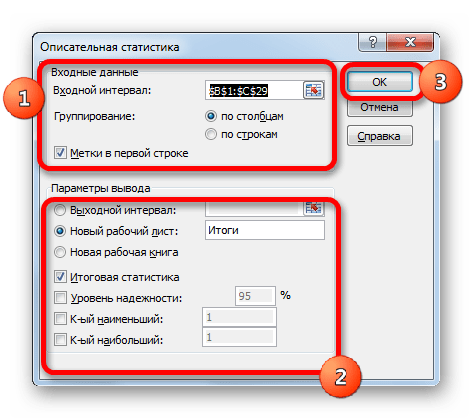

После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:

Асимметричность;
Интервал;
Минимум;
Стандартное отклонение;
Дисперсия выборки;
Максимум;
Сумма;
Эксцесс;
Среднее;
Стандартная ошибка;
Медиана;
Мода;
Счет.

Источник

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Если вы ищете работу и она хоть как-то связана с математикой/экономикой/финансами, то вы очень часто будете встречать такие требования к кандидату:
— Отличное знание статистики;
— Знание и умение Python/R, чтобы эту статистику применять.

Но что делать, если никаких знаний по языкам программирования у вас нет, а встречаться со статистическими моделями так или иначе придется? А работу-то найти нужно срочно…

К счастью, в версии Microsoft Excel выше 2010 вшит целый статистический пакет. О нем мало кто знает, а его реально можно использовать, если нет навыков программирования или доступного компилятора под рукой.

Для начала поговорим, где все эти формулы найти. Как обычно, переходим на вкладку «Формулы» на главной панели, выбираем «Другие функции» и пакет «Статистические». Перед Вами полный перечень статистических возможностей Excel.

Список статистических функций

Как вы можете видеть, формул в этом разделе представлено довольно много, как «ходовых», так и «узкоспециализированных». К сожалению, разобрать все в одной статье не получится, поэтому рассмотрим здесь самые часто встречающиеся. Если вы хотите познакомиться с математическими функциями Excel, то рекомендуем скачать наш бесплатный гайд.

На первый взгляд они могут показаться очень простыми. Однако, мы постарались раскрыть те моменты, которые обычно остаются без внимания и могут быть полезными.

СРЗНАЧ() и СРЗНАЧА()

Редко кто задумывался, а ведь вычисление среднего значения – сугубо статистическая процедура: именно поэтому это операция и помещена в статистический пакет.

Наверно, особо не стоит останавливаться на правилах использования формулы: функция СРЗНАЧ() принимает на вход массив аргументов и дает на выходе среднее значение по всем ячейкам, содержащим числа(!). Это очень важный момент, который далеко не все знают. Поясним на примере.

Пусть дан диапазон А1:С2 и мы ищем среднее значение по всем 6 ячейкам диапазона:

Применение функции СРЗНАЧ()

Однако, результат функции СРЗНАЧ(А1:С2) будет не 8,7, а 13. Почему? (4+15+11+22)/6 = 8,7 ведь?

Да, это правильно, но функция СРЗНАЧ() берет в расчет только те ячейки, где «встречает» числа. Текстовая информация и пустые ячейки просто игнорируются. Поэтому в данном примере СРЗНАЧ() усредняет по 4 ячейкам и выдает правильный ответ – 13.

А вот если нужно произвести усреднение по всему диапазону, вне зависимости от типа данных, нужно использовать функцию СРЗНАЧА().

Принцип работы такой же, как и у СРЗНАЧ(), только на вход будут поступать абсолютно все ячейки. Результат в нашем примере будет уже ожидаемый – 8,7.

Применение функции СРЗНАЧА()

Замечание

Выбор той или иной функции происходит в зависимости от задачи. В реальной жизни они могут понадобится в одинаковой мере.

Например, менеджеру нужно узнать среднедневную выручку за месяц на основании продаж за каждый день. Допустим, за несколько дней ячейки оставлены пустыми. Есть два варианта, почему так произошло:

1. В эти дни не было ни одной продажи. Тогда эти дни должны принимать участие в расчете среднего значения и менеджеру нужно использовать СРЗНАЧА() – так он исключит игнорирование пустых ячеек.

2. Эти дни были выходными. Тогда пропуски сами по себе никакой информации не несут и их надо игнорировать: фактически, эти дни не принимают участие в статистической выборке и функция СРЗНАЧ() поможет их пропустить.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

СРЗНАЧЕСЛИ()

Очевидно, что функция СРЗНАЧЕСЛИ() возвращает среднее тех значений, который удовлетворяют каким-то условиям. Помимо этого, условия можно накладывать не только на сами значения, но и на другие ячейки. Проиллюстрируем.

Например, вычислим среднее значение всех ячеек, которые больше нуля:

Применение функции СРЗНАЧЕСЛИ() с условием на аргумент

Мы выделили диапазон А1:С3 и наложили на него условие – «>0». А можно сделать по-другому.

Рассмотрим таблицу, в которую занесены продажи лекарств в городе. Посчитаем среднюю цену Анальгина по всему городу. Для этого наложим условие уже не на саму цену, а на название лекарства.

Формула записывается так:

=СРЗНАЧЕСЛИ(Диапазон_на_который_накладываем_условия; “Условие”; Диапазон_по_которому_считаем_среднее_значение)

В нашем случае это примет вид:

Применение функции СРЗНАЧЕСЛИ() с условием на другой диапазон

Кстати говоря, условия можно комбинировать с помощью функции СРЗНАЧЕСЛИМН().

Предположим, что в аптеке Зеленый Крест продается несколько видов Анальгина и в нашу таблицу они все занесены как Анальгин.

Тогда, чтобы усреднить цену всех Анальгинов в аптеке Зеленый Крест, нужно просто использовать формулу:

=СРЗНАЧЕСЛИМН(С2:С13; A2:A13; “зеленый крест”;B2:B13; “анальгин”)

Обратите внимание: диапазон усреднения указывается в конце только при использовании функции СРЗНАЧЕСЛИ() с дополнительным условием. В остальных случаях диапазон ячеек, по которым вычисляется среднее значение, стоит первым.

МИН()/МАКС() и НАИБОЛЬШИЙ()/НАИМЕНЬШИЙ()

На первый взгляд, разница между этими функциями не особо прослеживается, хотя зачем их используют – очевидно – найти самое большое или маленькое число. Однако, в работе этих функций есть небольшая, но очень полезная разница. Разберем подробней.

Функция МИН() просто принимает массив аргументов и находит самое маленькое число. МАКС() – самое большое. Все просто.

Функция НАИМЕНЬШИЙ() же находит n-ое наименьшее число в массиве. НАИБОЛЬШИЙ(), наоборот, находит n-ое наибольшее число.

Например, нужно найти пятое по величине число. Вводим:

=НАИБОЛЬШИЙ(диапазон; 5).

Фактически, получается, что результат работы НАИБОЛЬШИЙ(массив;1) и МАКС(массив) – одно и то же. Аналогичная ситуация с НАИМЕНЬШИЙ(массив;1) и МИН(массив).

Рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel», если вы хотите научиться выполнять рутинную работу быстрее.

МЕДИАНА() и МОДА()

Общеизвестные и достаточно важные статистические характеристики моды и медианы вычисляются по одноименным формулам.

Напомним, что медианой называется «середина» числового множества.

Например, если есть массив чисел от одного до десяти, то медианой будет число 5,5 (хотя оно само в массив не входит). Это из-за того, что количество элементов в массиве – четно и выбрать «центральное» просто невозможно.

Поиск медианы для «четного» массива

Вот если бы выборка начиналась не с единицы, а с двойки, то ответ был бы ровно 6.

Поиск медианы для «нечетного» массива

Теперь перейдем к моде. Мода – самое часто встречающееся число в выборке.

У функции нахождения моды есть целых три модификации в Excel старшее версии 2010 года: МОДА(), МОДА.ОДН() и МОДА.НСК().

Функция МОДА() оставлена для совместимости – ей, в целом, можно пользоваться: она работает совершенно аналогично функции МОДА.ОДН().

«ОДН» в названии функции значит, что, если в выборке несколько самых часто встречающихся элементов, то возвращено в качестве ответа будет только первое.

Применение функций МОДА() и МОДА.ОДН()

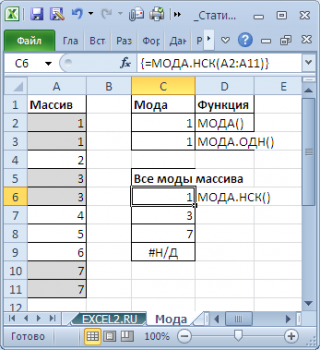
Для подсчета всех мод в выборке нужно использовать функцию МОДА.НСК().

Работает МОДА.НСК() следующим образом: выделяем побольше ячеек (если заранее не знаем, сколько мод у нас получится), в строке формул прописываем =МОДА.НСК(диапазон) и нажимаем Ctrl+Shift+Enter. Получили все моды в столбик.

«Слепой» метод применения функции МОДА.НСК()

Значения #Н/Д появляются, просто потому что мод у нас всего 2. Такой метод поиска мод называется «слепым» – мы просто берем побольше ячеек, чтобы наверняка хватило.

Если Вы не любите подобный «мусор» и Вам нравится, когда все красиво, можно сначала оценить: а сколько же у нас вообще будет мод? А потом просто выделить нужное количество ячеек.

Делается это так: сначала применяем функцию СЧЁТ() к нашей МОДА.НСК() – получили количество мод. А теперь выделяем только две ячейки и делаем все также, как написано выше.

Модификация применения МОДА.НСК()

Заключение

Статистический пакет Microsoft Excel содержит в себе еще огромное количество формул: проверку гипотез, принадлежность распределениям, доверительные интервалы, корреляцию и прочие инструменты, которые могут пригодиться при работе со статистикой даже на серьезном уровне.

Как мы и писали ранее, обозреть все в одной статье невозможно. Поэтому, если вы хотите узнать про менее известные, но не менее полезные статистические возможности Excel – пишите в комментариях, что вам было бы интересно и мы подготовим для вас новую статью из этого цикла.

Автор: Андрон Алексанян, СОО “Аптека-Центр”, эксперт SF Education

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

MS Office

5 примеров экономии времени в Excel

Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…

Как работать с датами в Excel?

Содержание статьи История о том, как я пропустил свидание с очаровательной блондинкой… Вы никогда не попадали впросак из-за того, что неправильно читали дату? «Да…

Источник

Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.

Задача

описательной статистики

(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений

выборки

к нескольким итоговым показателям, которые дают представление о

выборке

.В качестве таких статистических показателей используются:

среднее

медиана

мода

дисперсия, стандартное отклонение

и др.

Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные

статистические выводы о распределении

, из которого была взята

выборка

. Например, если у нас есть

выборка

значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой

выборки

мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.

Содержание статьи:

Надстройка Пакет анализа;
Среднее выборки

;
Медиана выборки

;
Мода выборки

;
Мода и среднее значение

;
Дисперсия выборки

;
Стандартное отклонение выборки

;
Стандартная ошибка

;
Ассиметричность

;
Эксцесс выборки

;
Уровень надежности

.

Надстройка Пакет анализа

Для вычисления статистических показателей одномерных

выборок

, используем

надстройку Пакет анализа

. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.

СОВЕТ

: Подробнее о других инструментах надстройки

Пакет анализа

и ее подключении – читайте в статье

Надстройка Пакет анализа MS EXCEL

Выборку

разместим на

листе

Пример

в файле примера

в диапазоне

А6:А55

(50 значений).

Примечание

: Для удобства написания формул для диапазона

А6:А55

создан

Именованный диапазон

Выборка.

В диалоговом окне

Анализ данных

выберите инструмент

Описательная статистика

.

После нажатия кнопки

ОК

будет выведено другое диалоговое окно,

в котором нужно указать:

входной интервал

(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле

Метки в первой строке (

Labels

in

first

row

).

В этом случае заголовок будет выведен в

Выходном интервале.

Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал

(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (

Summary

Statistics

)

. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:

среднее, медиана, мода, стандартное отклонение

и др.;
Также можно поставить галочки напротив полей

Уровень надежности (

Confidence

Level

for

Mean

)

,

К-й наименьший

(Kth Largest) и

К-й наибольший

(Kth Smallest).

В результате будут выведены следующие статистические показатели:

Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.

Если во

входном интервале

указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во

Входной интервал

и установите галочку в поле

Метки в первой строке

). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.

Зеленым цветом на картинке выше и в

файле примера

выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:

Интервал

(Range) — разница между максимальным и минимальным значениями;
Минимум

(Minimum) – минимальное значение в диапазоне ячеек, указанном во

Входном интервале

(см.

статью про функцию

МИН()

);
Максимум

(Maximum)– максимальное значение (см.

статью про функцию

МАКС()

);
Сумма

(Sum) – сумма всех значений (см.

статью про функцию

СУММ()

);
Счет

(Count) – количество значений во

Входном интервале

(пустые ячейки игнорируются, см.

статью про функцию

СЧЁТ()

);
Наибольший

(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.

статью про функцию

НАИБОЛЬШИЙ()

);
Наименьший

(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.

статью про функцию

НАИМЕНЬШИЙ()

).

Ниже даны подробные описания остальных показателей.

Среднее выборки

Среднее

(mean, average) или

выборочное среднее

или

среднее выборки

(sample average) представляет собой

арифметическое среднее

всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция

СРЗНАЧ()

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) оценкой

математического ожидания

случайной величины (подробнее см. статью

Среднее и Математическое ожидание в MS EXCEL

Медиана выборки

Медиана

(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

. Для определения

медианы

необходимо сначала

отсортировать множество чисел

. Например,

медианой

для чисел 2, 3, 3,

4

, 5, 7, 10 будет 4.

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для чисел 2, 3,

3

,

5

, 7, 10 будет 4, т.к. (3+5)/2.

Если имеется длинный хвост распределения, то

Медиана

лучше, чем

среднее значение

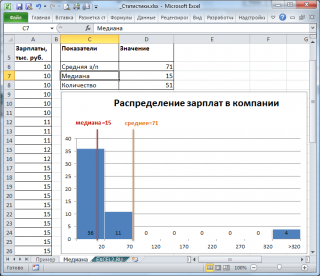
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у 50% сотрудников зарплата меньше или равна 15 тыс. руб.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант — MEDIAN().

Медиану

также можно вычислить с помощью формул

=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).

Подробнее о

медиане

см. специальную статью

Медиана в MS EXCEL

СОВЕТ

: Подробнее про

квартили

см. статью, про

перцентили (процентили)

см. статью.

Мода выборки

Мода

(Mode) – это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Например, в массиве (1; 1;

2

;

2

;

2

; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это

мода

. Для вычисления

моды

используется функция

МОДА()

, английский вариант MODE().

Примечание

: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье

Есть ли повторы в списке?

Начиная с

MS EXCEL 2010

вместо функции

МОДА()

рекомендуется использовать функцию

МОДА.ОДН()

, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция

МОДА.НСК()

, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.

Например, в массиве (1; 1;

2

;

2

;

2

; 3;

4

;

4

;

4

; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются

модами

. Функции

МОДА.ОДН()

и

МОДА()

вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.

файл примера

, лист

Мода

).

Чтобы исправить эту несправедливость и была введена функция

МОДА.НСК()

, которая выводит все

моды

. Для этого ее нужно ввести как

формулу массива

Как видно из картинки выше, функция

МОДА.НСК()

вернула все три

моды

из массива чисел в диапазоне

A2:A11

: 1; 3 и 7. Для этого, выделите диапазон

C6:C9

, в

Строку формул

введите формулу

=МОДА.НСК(A2:A11)

и нажмите

CTRL+SHIFT+ENTER

. Диапазон

C

6:

C

9

охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству

мод

. Если ячеек больше чем м

о

д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если

мода

только одна, то все выделенные ячейки будут заполнены значением этой

моды

.

Теперь вспомним, что мы определили

моду

для выборки, т.е. для конечного множества значений, взятых из

генеральной совокупности

. Для

непрерывных случайных величин

вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция

МОДА()

вернет ошибку.

Даже в нашем массиве с

модой

, которая была определена с помощью

надстройки Пакет анализа

, творится, что-то не то. Действительно,

модой

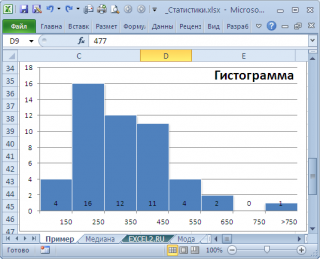
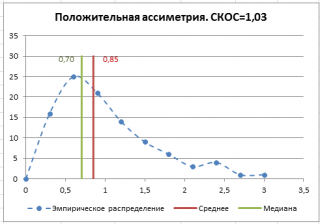
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на

гистограмму распределения

, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).

Проблема в том, что мы определили

моду

как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,

моду

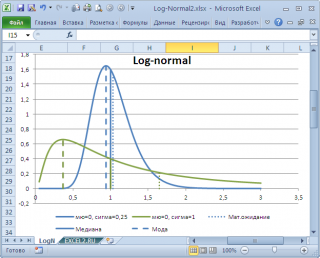
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для

логнормального распределения

мода

(наиболее вероятное значение непрерывной случайной величины х), вычисляется как

exp

(

m

—

s
²
)

, где m и s параметры этого распределения.

Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для

моды

распределения, из которого взята

выборка

(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).

Для того, чтобы получить оценку

моды

распределения, из

генеральной совокупности

которого взята

выборка

, можно, например, построить

гистограмму

. Оценкой для

моды

может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.

Вывод

: Значение

моды

для

выборки

, рассчитанное с помощью функции

МОДА()

, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер

выборки

существенно превышает количество этих значений.

Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),

модой

является число 15 (17 значений из 51, т.е. 33%). В этом случае функция

МОДА()

дает хорошую оценку «наиболее вероятного» значения зарплаты.

Примечание

: Строго говоря, в примере с зарплатой мы имеем дело скорее с

генеральной совокупностью

, чем с

выборкой

. Т.к. других зарплат в компании просто нет.

О вычислении

моды

для распределения

непрерывной случайной величины

читайте статью

Мода в MS EXCEL

Мода и среднее значение

Не смотря на то, что

мода

– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из

Генеральной совокупности

максимальна), не следует ожидать, что

среднее значение

обязательно будет близко к

моде

.

Примечание

:

Мода

и

среднее

симметричных распределений совпадает (имеется ввиду симметричность

плотности распределения

Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.

Модой

является 6, а среднее значение – 3,6666.

Другой пример. Для

Логнормального распределения

LnN(0;1)

мода

равна =EXP(m-s2)= EXP(0-1*1)=0,368, а

среднее значение

1,649.

Дисперсия выборки

Дисперсия выборки

или

выборочная дисперсия (

sample

variance

) характеризует разброс значений в массиве, отклонение от

среднего

.

Из формулы №1 видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии выборки

используется функция

ДИСП()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию

ДИСП.В()

.

Дисперсию

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)

–

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

.

Чем больше величина

дисперсии

, тем больше разброс значений в массиве относительно

среднего

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность

дисперсии

будет кг
²
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии – стандартное отклонение

.

Подробнее о

дисперсии

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартное отклонение выборки

Стандартное отклонение выборки

(Standard Deviation), как и

дисперсия

, — это мера того, насколько широко разбросаны значения в выборке

относительно их среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х

выборок

: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у

выборок

существенно отличается.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

СТАНДОТКЛОН()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

СТАНДОТКЛОН.В()

.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Подробнее о

стандартном отклонении

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартная ошибка

В

Пакете анализа

под термином

стандартная ошибка

имеется ввиду

Стандартная ошибка среднего

(Standard Error of the Mean, SEM).

Стандартная ошибка среднего

— это оценка

стандартного отклонения

распределения

выборочного среднего

Примечание

: Чтобы разобраться с понятием

Стандартная ошибка среднего

необходимо прочитать о

выборочном распределении

(см. статью

Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL

) и статью про

Центральную предельную теорему

.

Стандартное отклонение распределения выборочного среднего

вычисляется по формуле σ/√n, где n — объём

выборки, σ — стандартное отклонение исходного

распределения, из которого взята

выборка

. Т.к. обычно

стандартное отклонение

исходного распределения неизвестно, то в расчетах вместо

σ

используют ее оценку

s

—

стандартное отклонение выборки

. А соответствующая величина s/√n имеет специальное название —

Стандартная ошибка среднего.

Именно эта величина вычисляется в

Пакете анализа.

В MS EXCEL

стандартную ошибку среднего

можно также вычислить по формуле

=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))

Асимметричность

Асимметричность

или

коэффициент асимметрии

(skewness) характеризует степень несимметричности распределения (

плотности распределения

) относительно его

среднего

.

Положительное значение

коэффициента асимметрии

указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.

Коэффициент асимметрии

идеально симметричного распределения или выборки равно 0.

Примечание

:

Асимметрия выборки

может отличаться расчетного значения асимметрии теоретического распределения. Например,

Нормальное распределение

является симметричным распределением (

плотность его распределения

симметрична относительно

среднего

) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в

выборке

из соответствующей

генеральной совокупности

не обязательно должны располагаться совершенно симметрично относительно

среднего

. Поэтому,

асимметрия выборки

, являющейся оценкой

асимметрии распределения

, может отличаться от 0.

Функция

СКОС()

, английский вариант SKEW(), возвращает коэффициент

асимметрии выборки

, являющейся оценкой

асимметрии

соответствующего распределения, и определяется следующим образом:

где n – размер

выборки

, s –

стандартное отклонение выборки

.

В

файле примера на листе СКОС

приведен расчет коэффициента

асимметрии

на примере случайной выборки из

распределения Вейбулла

, которое имеет значительную положительную

асимметрию

при параметрах распределения W(1,5; 1).

Эксцесс выборки

Эксцесс

показывает относительный вес «хвостов» распределения относительно его центральной части.

Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-

σ

.

Примечание

: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение

Эксцесса

как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение

Эксцесса

ничего не говорит о форме пика распределения.

Согласно определения,

Эксцесс

равен четвертому

стандартизированному моменту:

Для

нормального распределения

четвертый момент равен 3*σ
⁴
, следовательно,

Эксцесс

равен 3. Многие компьютерные программы используют для расчетов не сам

Эксцесс

, а так называемый Kurtosis excess, который меньше на 3. Т.е. для

нормального распределения

Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.

Примечание

: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как

Эксцесс

(от англ. excess — «излишек»). Например, функция MS EXCEL

ЭКСЦЕСС()

на самом деле вычисляет Kurtosis excess.

Функция

ЭКСЦЕСС()

, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку

эксцесса распределения

случайной величины и определяется следующим образом:

Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из

нормального распределения

формула вернет близкое к 0 значение.

Если задано менее четырех точек данных, то функция

ЭКСЦЕСС()

возвращает значение ошибки #ДЕЛ/0!

Вернемся к

распределениям случайной величины

.

Эксцесс

(Kurtosis excess) для

нормального распределения

всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений

Эксцесс

зависит от параметров распределения: см., например,

распределение Вейбулла

или

распределение Пуассона

, для котрого

Эксцесс

= 1/λ.

Уровень надежности

Уровень

надежности

— означает вероятность того, что

доверительный интервал

содержит истинное значение оцениваемого параметра распределения.

Вместо термина

Уровень

надежности

часто используется термин

Уровень доверия

. Про

Уровень надежности

(Confidence Level for Mean) читайте статью

Уровень значимости и уровень надежности в MS EXCEL

Задав значение

Уровня

надежности

в окне

надстройки Пакет анализа

, MS EXCEL вычислит половину ширины

доверительного интервала для оценки среднего (дисперсия неизвестна)

Тот же результат можно получить по формуле (см.

файл примера

):

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)

s —

стандартное отклонение выборки

, n – объем

выборки

.

Подробнее см. статью про

построение доверительного интервала для оценки среднего (дисперсия неизвестна)

Источник