Excel как средство математической обработки

Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.

Применение математических функций

С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.

Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.

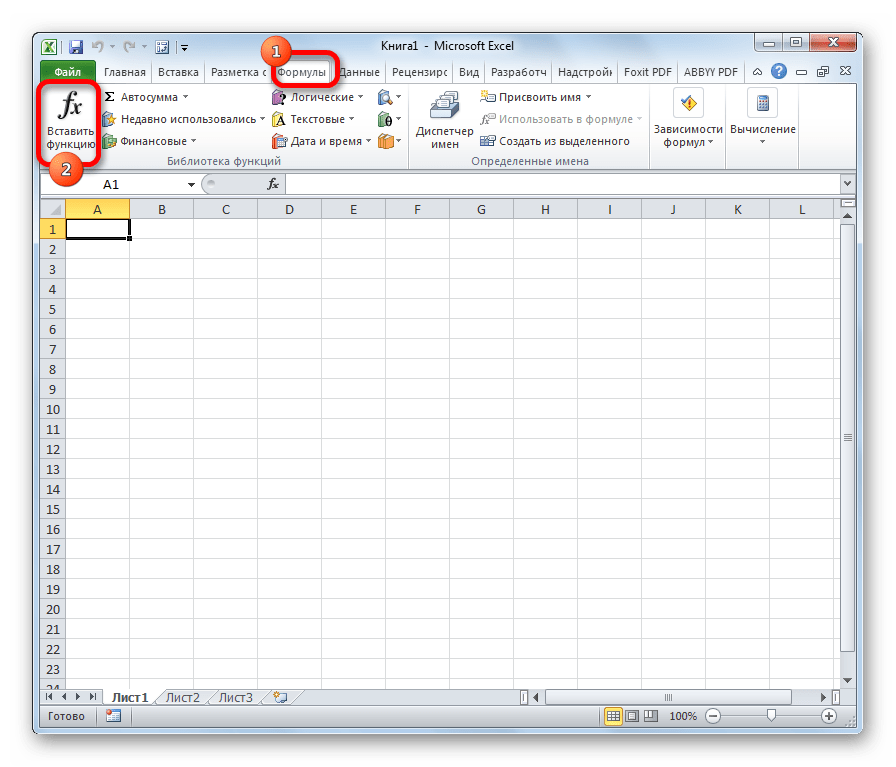
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».

Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.

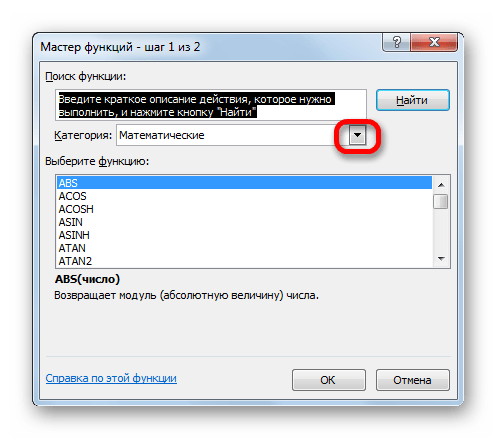
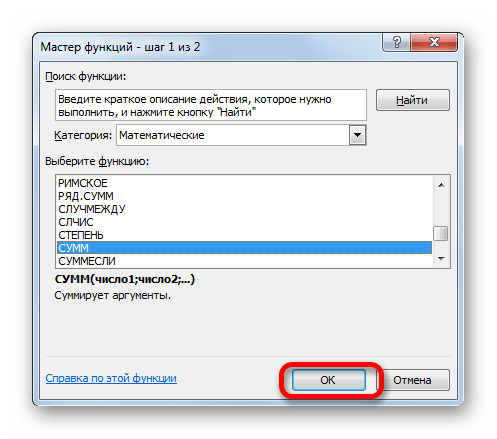
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».

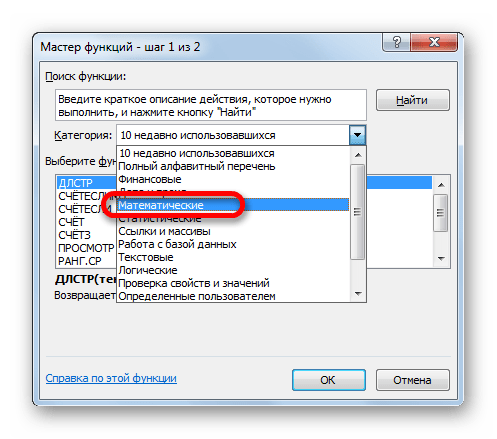
Открывается выпадающий список. Выбираем в нем позицию «Математические».

После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».

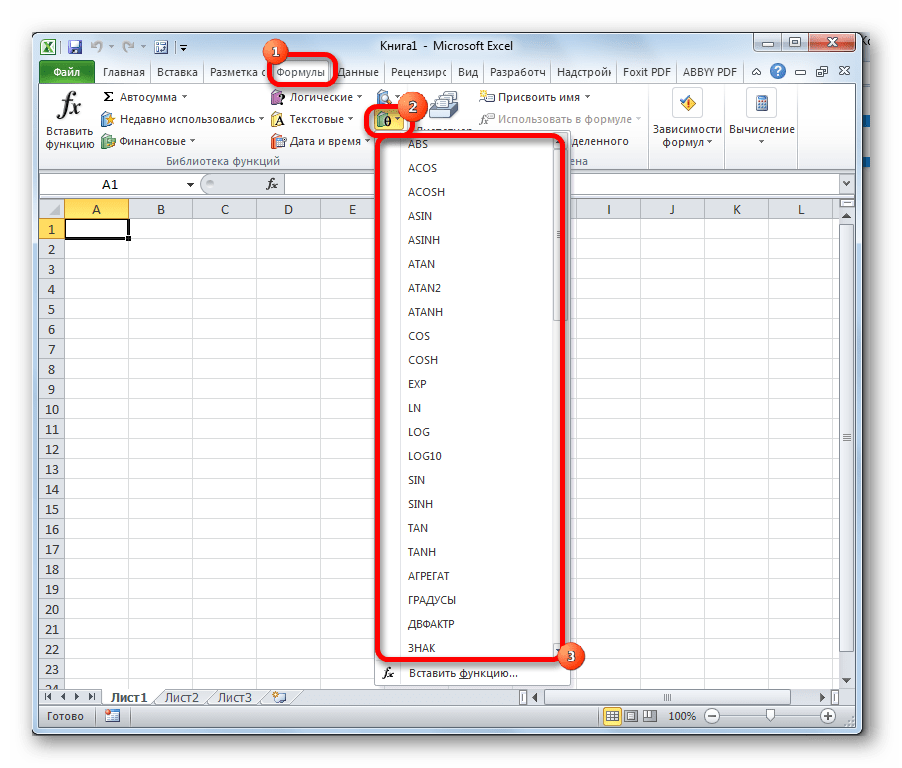
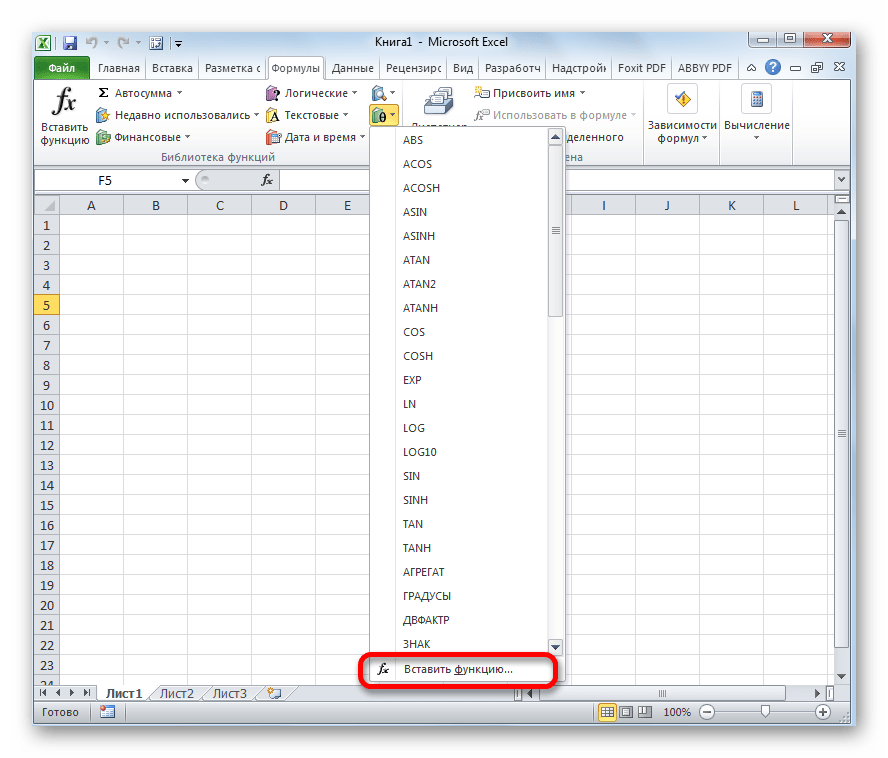
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.

Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.

Урок: Мастер функций в Excel

СУММ

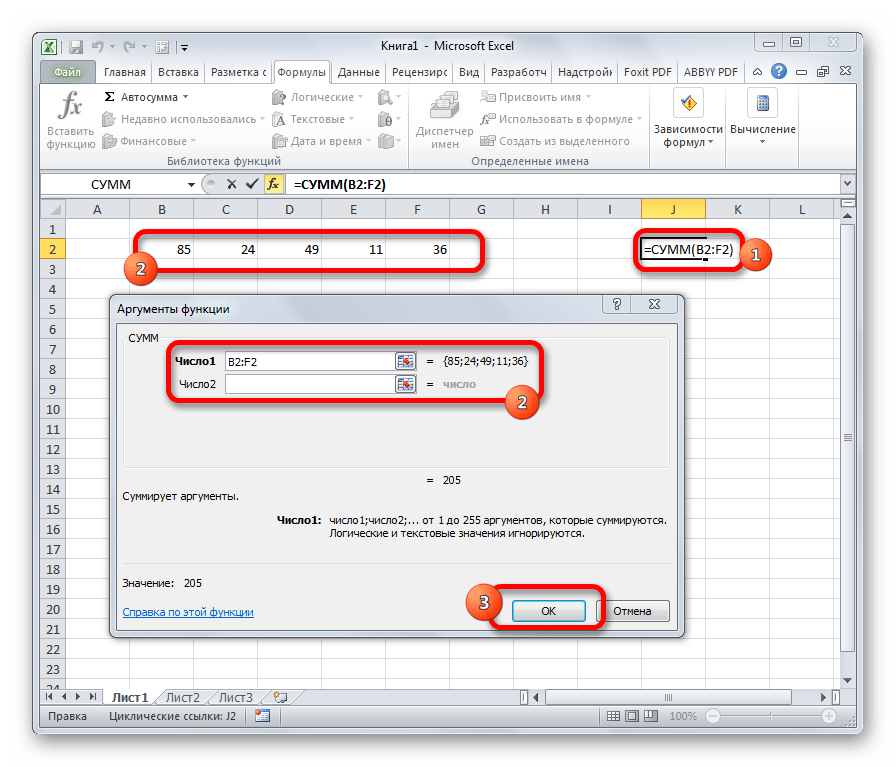
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:

=СУММ(число1;число2;…)

В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.

Урок: Как посчитать сумму в Экселе

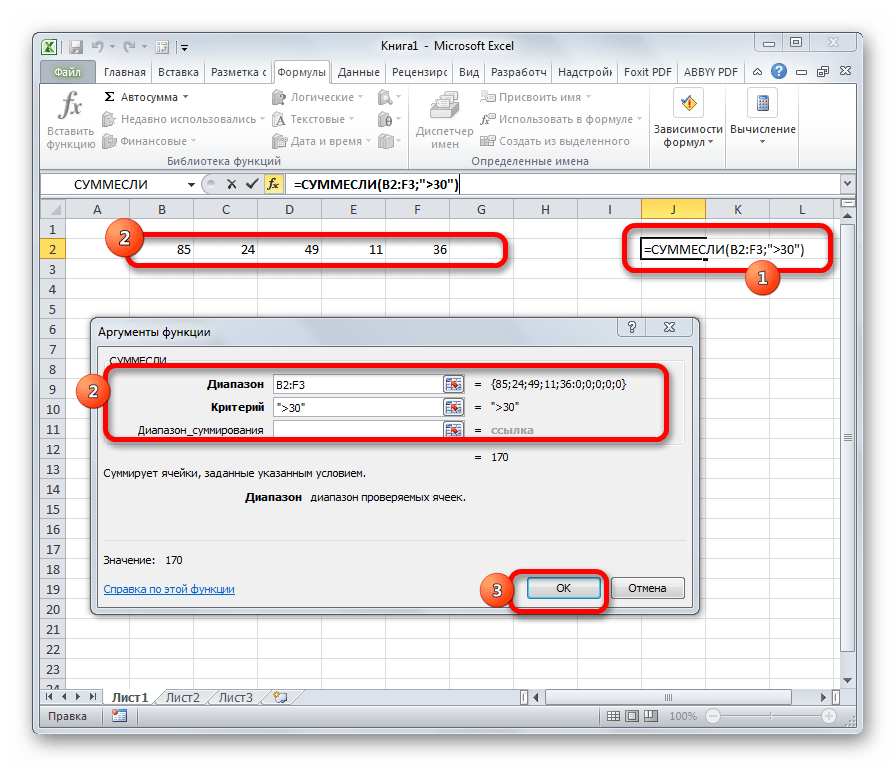
СУММЕСЛИ

Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

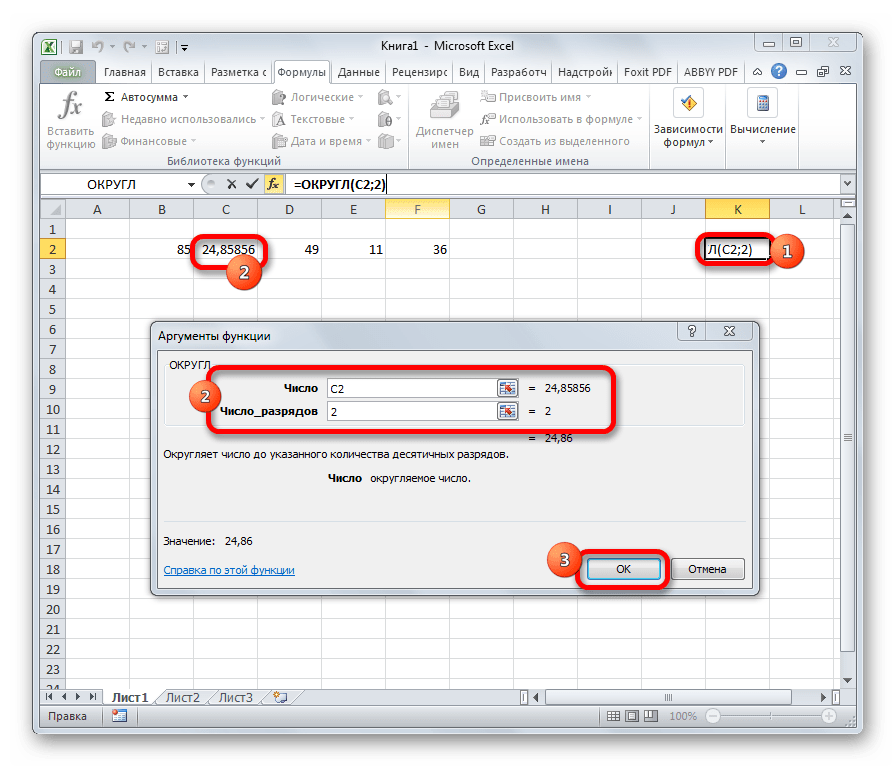
ОКРУГЛ

Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:

=ОКРУГЛ(число;число_разрядов)

Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.

Урок: Округление чисел в Excel

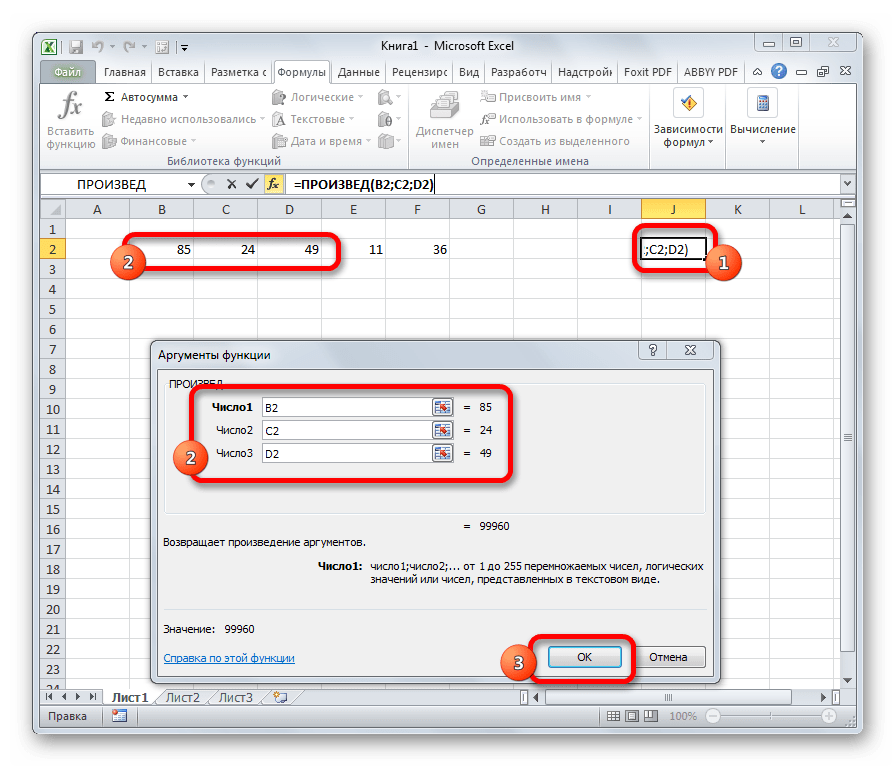
ПРОИЗВЕД

Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:

=ПРОИЗВЕД(число;число;…)

Урок: Как правильно умножать в Excel

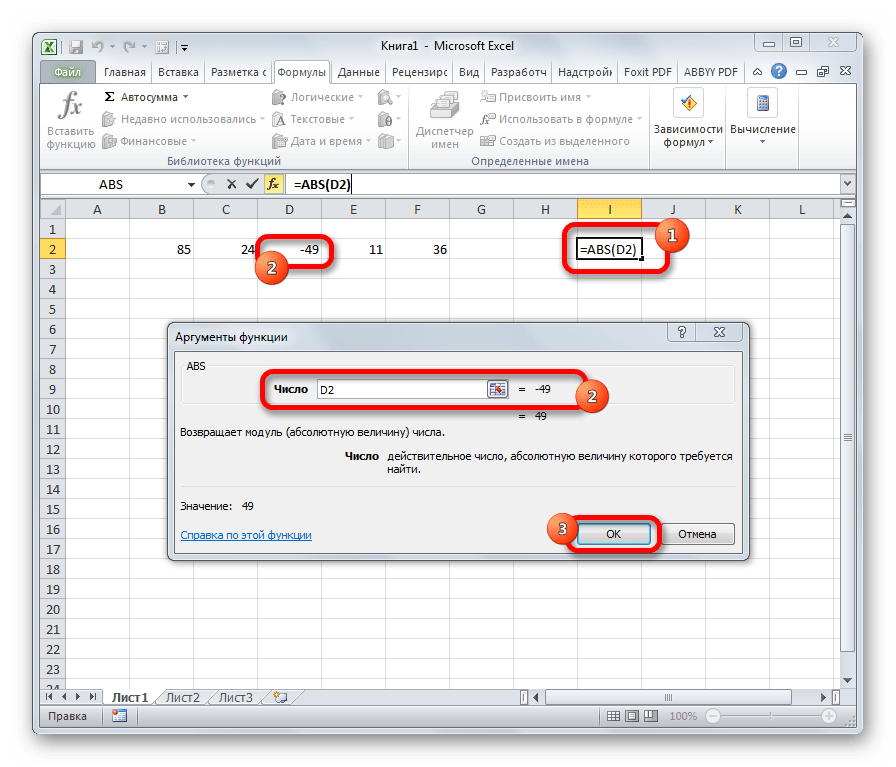
ABS

С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:

=ABS(число)

Урок: Функция модуля в Excel

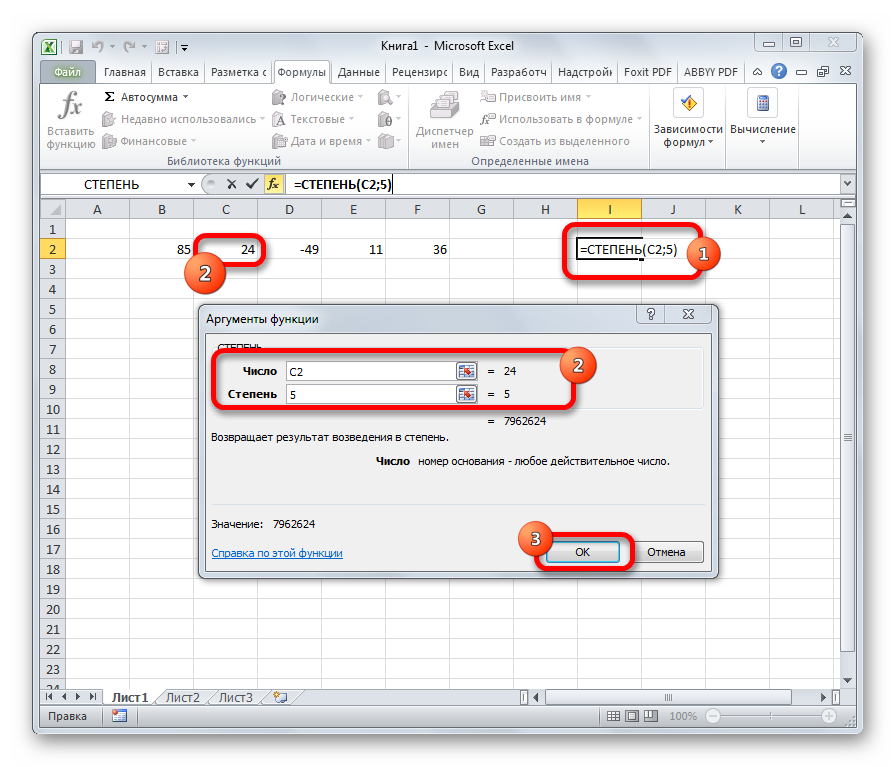
СТЕПЕНЬ

Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:

=СТЕПЕНЬ(число;степень)

Урок: Как возводить в степень в Экселе

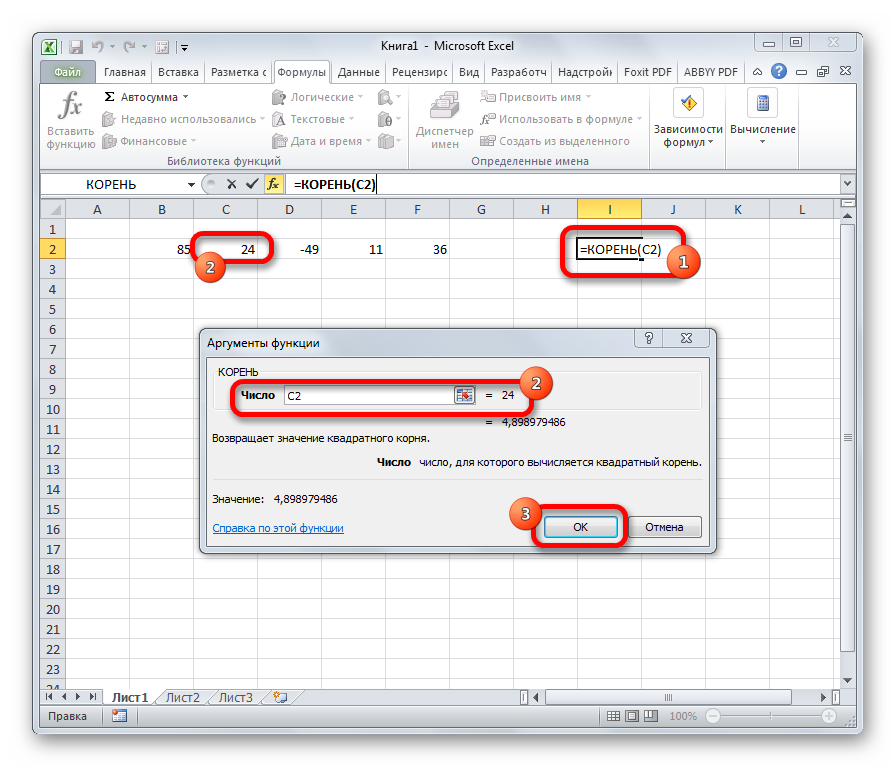
КОРЕНЬ

Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:

=КОРЕНЬ(число)

Урок: Как посчитать корень в Экселе

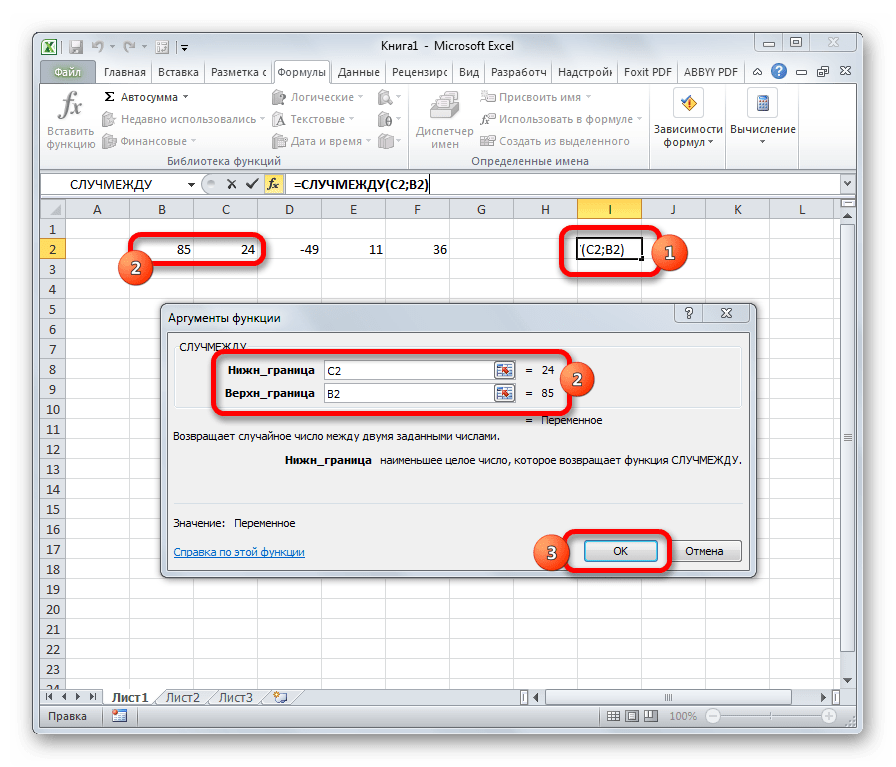
СЛУЧМЕЖДУ

Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:

=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)

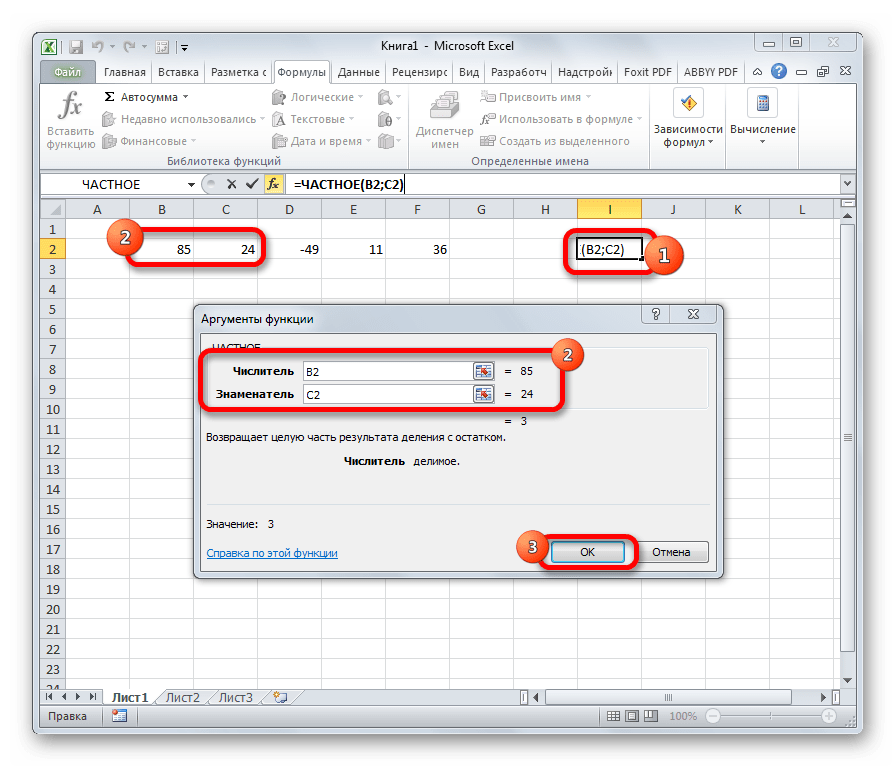
ЧАСТНОЕ

Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:

=ЧАСТНОЕ(Числитель;Знаменатель)

Урок: Формула деления в Экселе

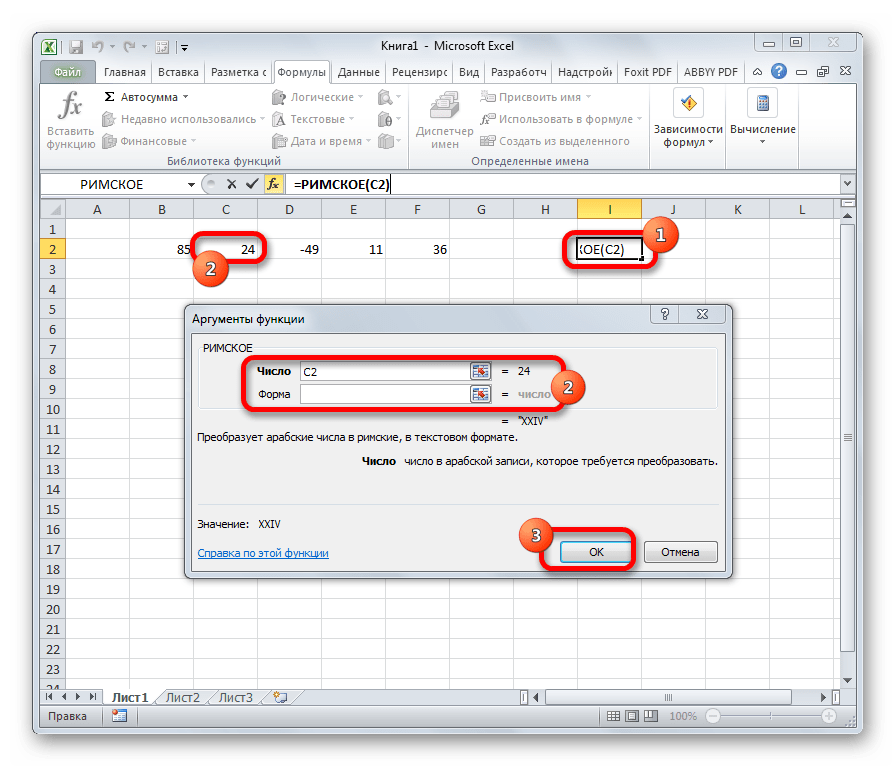
РИМСКОЕ

Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:

=РИМСКОЕ(Число;Форма)

Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.

Реферат на тему:

Использование табличного процессора MS Excel и математического моделирования для решения математических задач

                                                                                         
Выполнила: Миняева Анна

студентка группы МДИ-114

                                                                            
2012

                                                            Содержание:

1.     
Введение   ……………………………………………………………………………….3

2.     
Моделирование и решение математических задач……………………………………4

3.     
Моделирование и решение задач оптимизации……………………………………….8

4.     
Заключение………………………………………………………………………………26

5.     
Литература………………………………………………………………………………………………………..27

Введение

Microsoft Excel (также иногда называется Microsoft
Office Excel) — программа для работы с электронными таблицами, созданная
корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS.

Она предоставляет
возможности экономико-статистических расчетов, графические инструменты и язык
макропрограммирования VBA (Visual Basic for Application). Microsoft Excel
входит в состав Microsoft Office и на сегодняшний день Excel является одним из
наиболее популярных приложений в мире.

                          
Моделирование
и решение математических задач

С середины XX века в самых различных областях человеческой
деятельности стали широко применять математические методы и ЭВМ. Возникли такие
новые дисциплины, как «математическая экономика», «математическая химия»,
«математическая лингвистика» и т.д., изучающие математические модели
соответствующих объектов и явлений, а также методы исследования этих моделей.

Под моделью (от лат. modulus — мера, образец, норма)
понимают такой материальный или мысленно представляемый объект, который в
процессе познания (изучения) замещает объект — оригинал, сохраняя некоторые
важные для данного исследования типичные черты. Процесс построения и
использования модели, называется моделированием.

Во всех науках модели выступают как мощное орудие познания.

Например:
Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только
познавательный, но и сугубо практический, так как люди хотели научиться
предсказывать периодические явления, связанные с устройством Вселенной, такие,
как: затмение солнца и луны, наступление времен года.

Для решения этих задач, ученые строили свои представления о
Вселенной в виде схемы картины мира, в которой объекты (планеты, Солнце,
звезды, Земля и Луна) изображались точками, движущимся по каким-то кривым —
траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в
которых центральное место занимала наша Земля, или схема Коперника, в которой
центральное место занимало Солнце.

С
помощью этих схем ученые решали задачи предсказания отдельных астрономических
явлений. Эти схемы или картины мира — суть модели Вселенной, а метод
исследования Вселенной, нахождение законов и решения задач, связанных с помощью
этих моделей, является методом моделирования. В математике широко используется
метод моделирования при решении задач.

В процессе математического моделирования выделяют три
этапа:

1. Формализация —
перевод предложенной задачи (ситуации) на язык

математической
теории (построение математической модели задачи).

2. Решение задачи
в рамках математической теории (говорят: решение внутри модели).

    
3.Перевод результата математического решения задачи на тот язык, на котором
была   

    
сформулирована исходная задача (интерпретация решения).

Умение строить учебные модели и работать с ними является
одним из компонентов общего приема решения задач. С помощью модели словесно
заданный текст можно перевести на математический язык и увидеть структуру
математических отношений, скрытую в тексте. Использование одних и тех же
знаково-символических средств при построении модели для математических задач с
разными сюжетами и разных типов способствует формированию обобщенного способа
анализа задачи, выделению составляющих ее компонентов и нахождению путей
решения.

Моделирование числовых рядов и их применение при решении математических
задач

При решении некоторых задач часто возникает необходимость
использования последовательности чисел.

Числовые ряды, их моделирование и применение в математических задачах

Рядом
называется бесконечная последовательность чисел, элементы которой объединены
попарно арифметическими операциями сложения или вычитания.

Ряд
считается заданным, если известно выражение его общего элемента.

Сумма
конечного числа бесконечной последовательности ряда называется частичной суммой
ряда.

Для
вычисления частичной суммы нужно вычислить определенное число членов ряда и
затем найти их сумму. Для этого должны быть заданы: 1) количество суммируемых
элементов; 2) формула для вычисления элементов ряда.

Создание числовых последовательностей в табличном процессоре

В общем
случае для создания числовой последовательности в табличном процессоре нужно:

—
задать номера элементов последовательности в виде массива натуральных чисел,
расположенных либо в столбце, либо в строке таблицы в листе;

—
ввести в ячейку, соответствующую первому номеру элемента, формулу (выражение)
для его вычисления;

—
скопировать с помощью маркера автозаполнения в следующие ячейки столбца или
строки, где будет формироваться числовая последовательность.

Задание 1. Создать в листе табличного процессора
числовую последовательность, которая задана формулой общего элемента {n/(n+1)}.

Порядок реализации задания 1 в табличном процессоре

1)
Объединить ячейки А1:В1 и записать в них текст: Последовательность (n/(n+1));

2)
Отформатировать ячейки А2:В2 (перенос по словам) и записать в ячейке А2 текст «Номер
элемента», в ячейке В2 – «Значение элемента»;

3)
задать номера элементов последовательности в виде массива натуральных чисел в
ячейках столбца А, начиная с ячейки А3 (не менее 10);

4)
В ячейку В3 ввести формулу для вычисления первого элемента последовательности:
=А3/(А3+1);

5)
С помощью маркера автозаполнения скопировать формулу в следующие ячейки столбца
В, чтобы получить значения всех элементов последовательности.

Для
создания наиболее известных в математике последовательностей (арифметической,
геометрической и т.д.) в табличном процессоре имеет специальный инструмент Прогрессия,
который находится в процессоре на вкладке Главная в группе Редактирование,
где находится кнопка Заполнить. Данная кнопка открывает меню с выбором
метода заполнения. В списке вариантов есть вариант Прогрессия.
После его выбора откроется диалоговое окно, в котором требуется ввести тип и
параметры создаваемой последовательности. ( В Microsoft Excel 2003 – Правка, Заполнить,
Прогрессия)

При
исследовании последовательностей чисел требуется вычислить ее предел или
другие числовые характеристики.

Задание 2. Найти предел числовой 
последовательности .

Математическое решение

Порядок реализации в табличном процессоре

1)
В ячейку А1 внести текст: Предел последовательности n/(n+1);

2)
Полагая, что в ячейке А2 будет находиться число n,
в ячейку В2 введите формулу: =А2/(А2+1);

3)
В ячейку А2 введите достаточно большое число, примерно равное 1*10¹²;
если будет введено число, превышающее данную величину, то может наступить
переполнение ячейки и результат вычисления будет неправильным;

4)
После заполнения ячейки А2 в ячейке В2 появится приближенное значение предела
исследуемой числовой последовательности.

Функция – это модель, устанавливающая зависимость
какой-либо одной величины (переменной) от другой величины или нескольких
величин (аргументов).

Одни
из способов задания функции – табличный – имеет широкое распространение
в различных областях исследований: экспериментальных измерениях, таблицах
бухгалтерской отчетности, банковской деятельности, статистических исследованиях
и измерениях и т.д.

При
табличном задании функции один ряд данных представлен как значения
функции, другой (или другие) – как значения аргумента.

Каждому
значению аргумента соответствует значение функции, находящееся в той же строке
таблицы, что и аргумент.

Формула
функции даст также возможность найти значения функции, не отраженные в ее табличном
представлении. При выборе функции должны быть рассмотрены следующие вопросы:

1)
Выбор типа функции (линейная, показательная, логарифмическая и т.д.).

2)
Оценка погрешности приближения.

Виды функций, из которых производится
выбор зависимости, могут быть следующими:

 —
линейная у=ах+в; применяется в случае постоянного изменения данных на
определенную величину;

 —
полиномиальная – для данных, которые попеременно возрастают и убывают;

 —
логарифмическая y=a*lnx+b; применяется для описания данных, которые
вначале быстро убывают и возрастают, а затем стабилизируются;

 —
степенная у=в*х^а; используется для аппроксимации данных,
скорость изменения которых быстро увеличивается или уменьшается;

 —
экспоненциальная у=в*е^х; применяется для описания  данных,
которые быстро убывают и возрастают, а затем стабилизируются.

Мощным средством анализа данных Excel является
надстройка Solver (Поиск решения). С ее помощью можно определить, при
каких значениях указанных влияющих ячеек формула в целевой ячейке принимает
нужное значение (минимальное, максимальное или равное какой-либо величине). Для
процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы
при этом использовались те же влияющие ячейки. Для расчета заданного значения
применяются различные математические методы поиска по умолчанию в Excel
надстройка Поиск решения отключена. Чтобы активизировать ее в Excel 2007,
щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel,
а затем выберите категорию Надстройки. В поле Управление
выберите значение Надстройки Excel и нажмите кнопку Перейти.
В поле Доступные надстройки установите флажок рядом с пунктом Поиск
решения и нажмите кнопку ОК. В Excel 2003
и ниже выберите команду Сервис/Надстройки, в появившемся диалоговом
окне Надстройки установите флажок Поиск решения и щелкните на
кнопке ОК.

 Моделирование
и решение задач оптимизации

Оптимизацией
называется процесс выбора наилучшего варианта решения из множества возможных
решений.

При решении
оптимизационных задач с помощью надстройки «Поиск решения» целесообразно
различать линейные и нелинейные модели.

Под линейными
понимаются модели, в которых связь между входными значениями переменных и
результирующими значениями описывается линейными функциями.

Для использования
линейных методов следует установить параметр «Линейная модель» в окне «Параметры
поиска решения». Если этот параметр не установить, то даже для линейной
задачи будут использоваться общие более медленные методы.

Чтобы использовать надстройку «Поиск решения»
не обязательно знать методы программирования и исследования операций, но
необходимо определять, какие задачи можно решать этими методами.

Задание 3: Решите систему уравнений.

Математическое решение

Выразим
в каждом уравнении х относительно у, получим:

Можно
заметить, что все эти функции имеют общую точку (0;2). Это и есть их общее
решение.

Порядок реализации в табличном процессоре.

Для
реализации решения в табличном процессоре следует преобразовать систему
уравнений, выразив в каждом уравнении х относительно y.

 Получить
таблицу значений х в указанном диапазоне с  определенным шагом (инструмент
Прогрессия) в столбце А.

 Получить
таблицу значений функции у₁ для каждого значения х в столбце В.

 Получить
таблицу значений функции у₂ для кадого значения х в столбце С.

 Получить
таблицу значений функции у₃ для кадого значения х в столбце D.

 Построить
графики всех функций в одной области построения диаграммы (тип – ТОЧЕЧНАЯ, вид
– точки, соединенные линией).

 Задать
подписи рядов и заголовок диаграммы (в соответствии с темой задания).

Построение графиков и нахождение пары приближенных значений

При построении графиков функций  и нахождении их общей
точки – точки пересечения, наводим указатель мыши на точку пересечения, при
этом всплывает подсказка, что точка пересечения  с координатой (0; 2).

Уточним найденное решение, для этого ниже, например в ячейку
А25 внесем текст – уточнение решения, и ниже запишем неизвестные – х и у, в
ячейки А26, В26, С26. далее в ячейки А27-С27 внесем соответственно решение и
наши полученные ответы 0 и 2.

Еще ниже, например в ячейку А29  запишем текст- Формулы
уравнений, в ячейки А30-А32- тексты первое уравнение, второе уравнение, третье
уравнение. В ячейки В30-В32 внесем формулы наших функций с ссылками на ячейки
где у нас стоят наши ответы, это адреса ячеек В27 и С27. Следовательно, в
ячейке В30 будет стоять формула =-1,6*В27+2-С27, аналогично в ячейке  В31 будет
стоять формула =-2,5*В27+2-С27, и в ячейке В32 формула =-1,75*В27+2-С27.

Выбираем для уточнения Сервис, Поиск решения, в диалоговом
окне указываем целевую ячейку $B$30, равной значению 0.
Так как это разница левой и правой части функции. Указать, какие изменять
ячейки, мы проверяем ответы ячеек В27:С27, и указываем ограничения, что ячейки
с адресами В31=0 и В32=0. Выполняем поиск решения, сохраняем, получившиеся
значения.

                     Вычисление корней функции одной переменной.

Как известно из математики, корнями функции Y=f(x) называют такие значения
х, при которых функция принимает значение 0.

Процесс
нахождения корней функции осуществляется в два этапа.

Этап 1. Требуется определить, есть ли у
функции корни. Для этого нужно построить график функции для какого-то интервала
значений аргумента и визуально определить, имеет ли функция точки пересечения с
осью ОХ (осью абсцисс).

Этап 2. Требуется уточнить значения корней,
т.е. найти значения корней с заданной точностью.

При решении практических задач аргументом
функции обычно является значение какого-то ресурса, величина которого
ограничена и лежит в области допустимого диапазона значений. Поэтому при
решении задачи интерес представляют только те корни, которые находятся в
области возможных значений х.

Задача 4: Найти корни функции в диапазоне значений аргумента [-1;1] с
точностью 0,1.

Математическое решение

1.
Заданная функция представлена уравнением третьей степени, следовательно, она
может иметь не более трех корней.

2.
Функция непрерывна, поэтому достаточно найти отрезок длиной 0,2 на концах
которого функция имеет значения разных знаков. Имеем f(-1)=-0,1665
<0; f(-0,9)=0,035964 значит один корень уравнения
существует и он принадлежит отрезку [-1;-0,9], х ≈ -0,9
f(0)=0,139104>0; f(0,2)=0,005824>0;
f(0.3)=-0,04612<0; f(0,7)=-0,01588<0;
f(0,8)=0,081184>0, значит два других корня будут
принадлежать отрезкам [0,2;0,3] и [0,7;0.8], х ≈ 0,2 и х ≈ 0,7

2.
Для определения локализации корней функции требуется построить ее график на
указанном диапазоне значений аргумента. Для этого следует получить таблицу значений переменной х в
диапазоне [-1;1]. Для этого следует выбрать шаг изменения аргумента на
заданном отрезке, например, 0,1. Затем нужно вычислить все значения
аргумента на указанном отрезке с выбранным шагом изменения.

3.
Вычислить значения заданной функции для всех значений таблицы значений
аргумента. Таким образом, получится таблица
значений функции.

4.
По таблице значений аргумента и функции построить график и найти точки пересечения графика с осью абсцисс.
Так определяется количество и приближенное значение корней (интервалы,
содержащие корни функции).

5.
Интервалы, содержащие корни функции, дают возможность выбрать приближенное
значение каждого корня, далее требуется уточнить значение с заданной точностью.

Порядок реализации в табличном процессоре

1.
Объединить ячейки А1:С1 и внести в них текст:

2.
В ячейку А2 внести имя аргумента х, в ячейку В2 внести имя функции у.

3.
В ячейку А3 внести первое значение аргумента: -1.

4.
Выделить ячейку А3, затем вызвать команду Заполнить «Прогрессия…(вкладка Главная, группа Редактирование). В диалоговом окне
задать параметры прогрессии.

В
результате заполнения у вас должен появиться столбец значений аргумента.

5.
В ячейку В3 ввести выражение для вычисления значения функции для первого
значения аргумента:

6.
Выделив ячейку В3, за маркер автозаполнения скопировать формулу функции для
всех следующих значений аргумента. Получится столбец значений функции.

7.
По таблице значений аргумента и функции строим график функции. Для этого
выделяем два столбца значений (аргумент и функция), строим диаграмму (тип –
ТОЧЕЧНАЯ, вид – точки, соединенные линией). Подпись ряда – у=х^3-0,01*x^2-0,7044*x+0,139104, заголовок диаграммы – График функции.

Из
графика видно, что функция пересекает ось абсцисс на указанном отрезке три
раза. Следовательно, она имеет три корня.

8.
Чтобы определиться со значениями начальных приближений корней функции,
проанализируйте таблицу значений функции (столбец В). В ней нужно найти ячейки,
которые содержат значения, меняющие знак (например, с – на +, или наоборот).

            а)
функция меняет знак на отрезке [-1;-0,9];

            б)
функция меняет знак на отрезке [0,2;0,3];

            в)
функция меняет знак на отрезке [0,7;0,8].

Следовательно,
точные значения корней функции находятся внутри этих интервалов.

9.
В качестве начальных приближений корней функции нужно выбрать значения
аргумента в ячейках А4 (-0,9), А15 (0,2), А20 (0,7).

На
свободном участке листа, в ячейках А25:С25 (объединив их) разместить текст: .

10.
В ячейки А26:А28 ввести значения выбранных приближений Для каждого значения
ячеек А26:А28 в ячейки В26:В28 нужно ввести формулу функции из пункта 5.

11.
Нажмите на копку Файл.  В меню выберите пункт Параметры, в диалоговом
окне выберите пункт Формулы и в разделе Параметры вычислений
установите переключатель рядом с параметром Включить итеративные вычисления,
и укажите предельное число итераций 1000, а значение относительной погрешности
установите равным 0,000001.

(Или
 для версии 2003, Сервис Параметры, Вычисления, указать число итераций
1000, относительная погрешность 0,000001.

12.
После установки параметров вычислений выделите ячейку В26, нужно перейти на
вкладку Данные, в группе Работа с данными выбрать кнопку
Анализ «что если».

В
открывшемся списке вариантов выбрать Подбор параметра… Откроется
диалоговое окно, в котором требуется заполнить три поля. (Или Сервис, Подбор
параметра, в версии 2003)

В
поле Установить в ячейке нужно указать адрес ячейки, в которой будет
получено точное значение первого корня уравнения: В26.

В
поле Значение указывается значение функции для данного корня, т.е. 0.

В
поле Изменяя значений ячейки указывается адрес ячейки, содержащей
приближенное значение корня функции (ссылка на ячейку указывается в абсолютном
формате): $A$26.

После
нажатия на кнопку ОК в ячейке А26 появится точное значение корня
функции.

Нажмите
ОК в окне результата подбора параметра.

13.
Повторяя действия из п. 12 для каждого приближенного значения корня, нужно
получить точные значения второго и третьего корней функции.

Для решения практических задач часто требуется найти  экстремум.
Экстремумом является минимальное или максимальное значение функции.

Задача 3: Задана неразрывная функция . Требуется найти ее экстремум
(минимальное значение) на отрезке [-2;2].

Порядок реализации в табличном процессоре

1.
Объедините ячейки А1:С1 и введите текст задания: .

2.
В ячейку А2 введите имя аргумента х. В ячейку В2 введите имя функции у.

3.
В ячейку А3 введите любое значение аргумента, принадлежащее отрезку,
указанному в условии, например: -0,8.

4.
В ячейку В3 введите формулу для нахождения значения функции для значения
аргумента, заданного в ячейке А3: .

5.
Перейдите на вкладку Данные, в группе Анализ выберите кнопку Поиск
решения.

(Или в в версии 2003- Сервис, Поиск решения)

6.
В открывшемся диалоговом окне требуется задать все нужные параметры.

            а)
в поле Оптимизировать целевую функцию указана ссылка на ячейку В3 (в
абсолютном формате);

            б)
в строке До переключатель должент быть установлен рядом с параметром Минимум;

            в)
в поле Изменяя ячейки переменных должна быть указана ссылка на ячеку А3
(в абсолютном формате);

            г)
в области с названием В соответствии с ограничениями должны быть указаны
огранияения на значения переменной. Для этого нажмите справа на кнопку Добавить и
запишите первое условие:

Нажмите
кнопку Добавить в окне, указанном выше, и запишите второе условие:

После
чего нажмите кнопку ОК.

Окно
 Параметры поиска решения примет вид:

Нажмите
на кнопку Найти решение, после чего в ячейке А3 появится значение
аргумента, при котором функция (формула в ячейке В3) принимает минимальное
значение. Так же будет выведено диалоговое окно с дополнительными сведениями о
полученном результате.

Нажмите
в окне Результаты поиска решения кнопку ОК, чтобы сохранить найденное
решение.

7.
Проверим правильно ли найдено решение задания.

8.
Построим график функции.

С
помощью  Правка, Заполнить, Прогрессия , указать шаг, например 0,2, предельное
значение 2 (так как отрезок от -2 до 2) зададим значения х., в ячейке А7,

В
ячейку В7 внесем формулу =степень(А7;2)+А7+2 и скопировать формулу в ячейки
В8:В27

Построим
с помощью мастера диаграмм график функции

9.
Определите с помощью функции МИН минимум в столбце значений функции, и
определите значение аргумента для этого значения функции.

10.
В частном случае при нахождении экстремума на указанном отрезке,
найденное значение может быть не минимумом (максимумом) функции, а просто минимальным
(максимальным) значением на указанном отрезке, т.е. экстремумом являться
не будет. Чтобы проверить, является ли найденное решение экстремумом
функции, необходима дополнительная проверка с помощью вычисления производной
функции. Если производная функции для найденного решения равна нулю, то точка
является экстремумом, а не точкой перегиба функции.

Производная – это отношение малого приращения функции к
малому приращению аргумента. Для вычисления производной нашей функции , выполните следующие шаги:

1)     
В ячейку Е2 (лист с поиском экстремума, где
находится значение -0,5) введите значение переменной, отличающееся от
найденного на очень малую величину. Для этого введите в ячейку Е2
формулу: . В ячейку Е3 введите
формулу: . Задайте формат ячеек Е2:Е3
– числовой, число разрядов после запятой: 9.

2)     
В ячейку F2 введите формулу . Скопируйте формулу в ячейку F3. Отформатируйте ячейки F2:F3
аналогично тому, как отоформатированы ячейки Е2:Е3.

3)
В ячейку G2 записываем формулу для вычисления производной:

Отформатируйте
ячейку аналогично формату предыдущих: с количеством знаков после запятой 9.

Вывод: производная в указанной точке равна
0, следовательно, найденное значение является экстремальным.

Задача 4: Требуется найти значения аргумента в
диапазоне [-1;1], при которых функция имеет экстремумы.

Математическое решение

—                                         +

                     -0,5

Уَ(-0,6)=2*(-0,6)+1=-0,2

Уَ(0,5)=2*0,5+1=2

Производная
меняет знак с минуса на плюс, следовательно х=-0,5 у=1,75 – точка минимума

Порядок реализации в табличном процессоре.

.1.Получить
таблицу значений аргумента с шагом 0,1 с помощью Прогрессии .

В ячейки
А1 и В1 внести х и у. В ячейки А2:А22 с помощью Правка, Заполнить,
Прогрессия, с шагом 0,1 заполнить значения х.

2.
Получить таблицу значений функции для всех значений аргумента .

В
ячейку В2 внести формулу =СТЕПЕНЬ(A2;2)+A2+2. С помощью копирования формул
заполнить ячейки В3:В22

3.
Получить таблицу значений функции для всех значений (аргумент+dx) (dx = 0,00000001 – малое приращение
аргумента функции). Для этого в формуле функции вместо значения
аргумента записать аргумент+малое приращение.

В
ячейку С1 внесем обозначение у(х+∆х). В ячейку С2 внесем формулу нахождения
значения функции с приращением 0,00000001. Формула-
=степень(А2+1Е-8;2)+(А2+1Е-8)+2. Ячейки С3:С22 заполним  с помощью копирования
формул.

4.
Вычислить значения производной функции как отношение малого приращения
функции к малому приращению аргумента: =(второе значение
функции – первое значение функции)/приращение аргумента.

В
ячейку D1 введем обозначение уَ. В ячейку D2 введем формулу  =(C2-B2)/0,00000001- отношение малого приращения
функции к малому приращению аргумента.

5.Анализируя
полученные значения производной функции в точках сетки аргумента, определить, на
каком интервале функция меняет знак. В этом интервале может находиться
точка экстремума. Если производная меняет знак с минуса на плюс, то точка
экстремума является минимумом функции (и наоборот).

При
х=-0,5 и у=1,75 производная равна нулю, следовательно это критическая точка, а
производная меняет знак с “-“ на “+” , следовательно это минимум.

6.
Уточните значение аргумента, при котором производная равна 0, используя
интсрументы MS Excel  Подбор параметра или Поиск решения  В указанной точке функция принимает
минимальное значение (экстремальное значение).

Уточним
наш ответ с помощью Сервис, Поиск решения, для этого в ячейку А25 внесем любое
значение из отрезка [-1;1], например 0,2, а в ячейку В25 формулу нашей функции

 =
степень(А25;2)+А25+2. Выделим ячейку В25 и через Поиск решения установить
целевую ячейку В25, равной минимальному значению, изменяя ячейку А25, с
ограничениями ячека А25<=1 и А25>=1  и выполнить.

сохранить
полученный результат

Построим
график функции и график ее производной

                                                        
Заключение
            В настоящее время получило всеобщее признание то, что успех
развития многих областей науки и техники существенно зависит от развития многих
направлений математики. Математика становится средством решения проблем
организации производства, поисков оптимальных решений.                                       

            Программа

Microsoft Excel – одна из наиболее
практически значимых, востребованных.  Электронные таблицы не только позволяют
автоматизировать расчеты, но и являются эффективным средством моделирования
различных вариантов и ситуаций. Меняя значения исходных данных, можно
проследить за изменением получаемых результатов и из множества вариантов
решения задачи выбрать наиболее подходящий.

                                    Литература:
1. Мордкович А.Г . Алгебра и начала анализа 10-11.
М.: Просвещение, 2005

2.Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение,
1978

3. Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.:
Просвещение, 1985.

4. Информатика и информационные технологии, 10-11 класс. –
Бином Лаборатория знаний, 2005.

Цель работы: Исследовать возможность моделирования исследование математических функций, при помощи современных компьютерных средств. Методы проведенных исследований: математическое моделирование. Основные результаты научного исследования (научные, практические): разработана компьютерная модель для исследования  математических функций на основе программы Microsoft Excel .

актуальность темы работы – Microsoft Excel — одна из самых загадочных и интересных программ в пакете MS Office. Интересна она многочисленными средствами автоматизации работы, оформления документов и богатыми вычислительными возможностями. Загадочность ее состоит в том, что большинство пользователей применяют лишь малую толику того, что может дать им Excel. Это тем более удивительно, что спектр возможностей программы практически безграничен: от создания простых таблиц, построения диаграмм и графиков до решения сложных вычислительных задач и моделирования различных процессов.

постановка и формулировка проблемы – данная работа посвящена использованию электронных таблиц EXCEL в анализе функций. В ней, используя знания и навыки работы с мастером функций и диаграмм Excel, будет проведен анализ  функций с проведением расчетов по формулам и с построением графиков.
Для анализа элементарных функций необходимо уметь решать следующие задачи:

• определение возрастания или убывания функции на заданном интервале,
• определение максимума (минимума) данной функции на заданном интервале,
• нахождение точек пересечения функции с осью ОХ,
• нахождение производной функции

---

Статьи
Карта сайта
Главная страница

 

Ввод текста помогает оформлять заголовки таблиц, записывать
определенные пояснения. Допустим, нам надо рассчитать объем раствора по его
массе 10 г и плотности 1,25 г/мл, используя простейшую формулу V=m/d. Введем
в ячейки В5, С5, D5 заголовки столбцов будущей таблицы,
обозначения величин m, d и V, и приступим к вводу чисел. В
ячейку В6 введем численное значение массы 10. Заканчиваем ввод, нажимая Enter, и убеждаемся, что тест в ячейке, как правило, смещен к правой границе, а число к левой. Это удобно, так как позволяет замечать ошибки
ввода. В ячейку С6 введем дробное число 1,25. Здесь надо учесть, что в
зависимости от настройки конкретного компьютера для разделения целой и дробной
части числа может использоваться или запятая, или точка. При неправильном вводе
наши символы будут восприниматься как текст,  или даже как дата (янв.25).

Наконец, в ячейке D6 введем формулу, по
которой Excel будет проводить вычисления. Ввод формулы начинается со знака
равенства (=). Затем надо показать программе, где находится первое число в
нашей формуле, масса раствора, дать адрес этой ячейки  — В6. Конечно, можно
набрать этот адрес с клавиатуры, надо только учитывать, что В – это символ
английского алфавита. Поэтому, гораздо проще просто щелкнуть по нужной ячейке и
ее адрес будет введен автоматически (=В6). Далее надо ввести знак
арифметического действия. Эти знаки удобно вводить с правой части клавиатуры,
напоминающей клавиатуру калькулятора. Здесь есть клавиши со знаком сложения
(+), вычитания (-), умножения (*) и деления (/). И, наконец, надо показать
компьютеру, где находится делитель – щелкаем мышкой по ячейке С6 и получаем
окончательный вид формулы (=В6/С6). Нажимаем Enter, и,
если все было набрано правильно, получаем в ячейке D6 результат
(8). Таким образом, формулы возвращают в ячейку результат вычислений, число. Но
если щелкнуть по ячейке и посмотреть на строку формул, мы увидим, что на самом
деле находится в ней.

Иногда формула может возвращать и сообщение об ошибке. Щелкнем
по ячейке В6 и введем вместо числа 10 символы «10 г». В ячейке D6
тут же окажется сообщение #ЗНАЧ!, которое говорит о
неверном значении в одной из ячеек. Действительно, запись «10 г» воспринимается
уже как текст. Чтобы исправить ошибку надо снова вместо «10 г»  ввести число
10. (Для исправления неверных действий можно использовать и кнопку «Отменить»
на панели инструментов). Щелкнем теперь по ячейке С6 и нажмем клавишу “Del”. Этим мы удалим содержимое ячейки, и в соседней ячейке
тут же получим сообщение #ДЕЛ/0! (ошибка деления на 0). Действительно,
на ноль делить нельзя и ошибку надо исправить.

Итак, мы научились вводить числа и формулы, а значит и проводить
простейшие вычисления в Excel. Но как упростить эту процедуру, если таких
вычислений много? Здесь помогают приемы копирования, и автоматического
заполнения ячеек методом «протягивания». Пусть у нас 10 порций раствора массой 10 г, и в ячейки В6, В7 …, В16 надо ввести 10, 10, … и т.д. Щелкнем по ячейке В6, где число 10 уже
введено. В черной рамке выделенной ячейки, внизу справа, есть маленький черный
квадратик. При наведении на него указателя мышки, последний меняет форму. Если
в этот момент «взяться» (нажать левую кнопку мыши) и потянуть вниз, до ячейки
В16, то все десять ячеек окажутся автоматически заполнены нужным числом. Не
труднее заполнить и 100 ячеек!

А если массы растворов отличаются на некоторую постоянную
величину, например 10, 12,5, 15 г и т.д.? В этом случае достаточно ввести два
значения: число 10 в ячейку В6 и число 12,5 в ячейку В7. Теперь надо выделить
эти две ячейки. Для этого щелкаем по первой ячейке и, не отпуская кнопки, ведем
до второй. Теперь обе ячейки обведены жирной рамкой. Снова беремся за черный
квадратик и тянем вниз. Получаем ряд значений от 10 до 35.

Поскольку предполагается, что раствор у нас один и тот же,
оставим колонку С в покое и попробуем методом протягивания скопировать формулу,
которая у нас набрана в ячейке D6. Проделываем уже
описанную операцию: выделяем ячейку, беремся, протягиваем… и получаем во всех
ячейках, кроме первой, ошибку! Разберемся, почему это произошло, для чего
щелкнем по ячейке D7 и посмотрим на строку формул. В
ячейке D6 было написано «=В6/С6», а в ячейке D7 уже «=В7/С7»! То есть, при копировании формул Excel
автоматически меняет адреса ячеек, откуда он берет данные для расчетов. И это
совершенно правильно, когда речь идет о массе раствора. Но плотность раствора у
нас постоянная, как показать программе, что адрес этой ячейки менять не надо?

Для этого мы должны познакомиться с такими понятиями, как
относительный и абсолютный адрес. Те адреса, которые мы использовали,
называются относительными и меняются при копировании. Адрес в абсолютной форме
сопровождается знаками доллара и выглядит так: $C$6. Вот
эту поправку нам и надо внести в формулу в ячейке D6.

Исправлять записи в ячейках удобнее в строке формул. Щелкнем
сначала по ячейке D6, (формула появится в строке
формул), затем в нужном месте строки формул – там появится курсор. Конечно
знаки доллара можно ввести с клавиатуры, но проще, установив курсор на адресе
С6, нажать на клавиатуре клавишу F4. Понажимайте ее
несколько раз и посмотрите, как будет меняться адрес. Он может быть полностью
абсолютным, абсолютным по строчке, по колонке, и полностью относительным.
Добейтесь нужного вида и нажмите Enter. Формула
исправлена, теперь ее снова можно протянуть до ячейки D16.
Если все сделано правильно, вы получите ряд значений от 8 до 28 мл.

Итак, если Вы не только прочитали, но и проделали все, о чем шла
речь выше,  Вы научились многому. Вы умеете вводить текст, числа и формулы,
вносить исправления, устранять ошибки, копировать и заполнять ячейки рядами
данных. Не мешает сохранить результаты своей работы. Процедуры сохранения файла
и его открытия полностью совпадают с работой в Worde и не должны вызвать у Вас затруднений.

Формулы с
функциями.

Но в наших расчетах использовались только простейшие
арифметические действия. Для более сложных расчетов нужно научиться
использовать функции. Этим мы займемся на втором листе нашей книги.

Для перехода на нужный лист достаточно щелкнуть по его ярлычку.
Начнем работу с краткого повторения пройденного: дадим листу 2 имя «Ошибки», в
ячейку А3 введем текст «Данные эксперимента», в ячейки А5 и В5 — заголовки
новой таблицы «№» и «Х». Предполагается что мы проделали серию из 10 опытов,
измеряя некоторую величину Х (здесь не важно, что это, длина побега или объем
раствора). Номера опытов от 1 до 10 легко ввести протягиванием, а вот численные
значения Х надо последовательно ввести (табл.1).

Таблица 1. Примерный вид листа
«Ошибки»

Записи в колонках D и
Е – это подсказки, которые помогут разобраться с тем, какие характеристики мы
будем рассчитывать. Колонка F у
Вас должна быть пока пустой, в нее будем помещать наши формулы.

Обработку результатов начнем с расчета числа опытов n. Казалось бы это очевидное число, но в ходе работы, какой-то
результат мы можем отбросить, или провести еще пару опытов. Желательно, чтобы
нам не пришлось при этом переделывать все формулы. Для определения числа
значений используется специальная функция, которая называется СЧЕТ. Для ввода
формулы с функциями используется Мастер функций, который запускается командой
«Вставка функции» через меню «Вставка» – «Функция» или кнопкой на панели
инструментов с обозначением   f_x. Щелкнем мышкой по ячейке F6,
где должен находиться результат и запустим Мастер функций.

Первый шаг работы (рисунок 1) служит
для выбора нужной функции. Все функции разделены, в зависимости от своего
назначения на несколько категорий (математические, логические и др.). Для
обработки данных эксперимента используются в основном статистические функции.
Поэтому, прежде всего в списке категорий выбираем категорию «Статистические».
Во втором окне появляется список статистических функций. Если щелкнуть по любой
из них, внизу появляется краткое описание функции. Специальной ссылкой можно
вызвать систему помощи Excel, в которой данная функция будет разобрана
подробно, с примерами. Список функций упорядочен по алфавиту, что позволяет без
труда нужную нам функцию СЧЕТ («Подсчитывает количество чисел в списке
аргументов»). Выделив щелчком эту функцию, нажимаем кнопку Ok и переходим к шагу 2.

Второй шаг (рисунок 2) служит для задания аргументов функции. 
Функции СЧЕТ надо указать, какие числа ей надо пересчитывать, или в каких
ячейках находятся эти числа. Диапазон ячеек указывается адресами первой и
последней ячейки, записанными через двоеточие, в нашем случае данные находятся
в ячейках В6:В15. Как и в других случаях эти адреса лучше не вводить, а показать
мышкой. Для этого устанавливаем указатель мышки на первую ячейку, нажимаем
левую кнопку и ведем до последней. Обратите внимание, что окно аргументов можно
перемещать, если оно заслоняет нужную часть экрана. Кроме того, рядом с полем
для ввода есть маленькая кнопка с красной стрелочкой. При щелчке по ней окно
аргументов сворачивается до узкой полоски. Когда мы показываем в основном окне
диапазон ячеек, в окне аргументов появляется запись диапазона адресов, а рядом
с ним – значения чисел из первых ячеек. Предварительное значение функции тоже
показывается после ввода ее аргументов. Это помогает избегать ошибок. Помогает
работе с мастером функций и подсказка под полем для ввода аргументов, в которой
разъясняется их смысл и возможные значения. Заканчивается работа с мастером
функций нажатием кнопки “Ok” или клавиши “Enter”. Если все сделано правильно, в ячейке F6 появится нужное значение “10”.

Следующие два этапа обработки серии опытов проводятся
аналогично. В ячейке F7 c
помощью функции СРЗНАЧ рассчитывается
среднее значение выборки, в ячейке F8 – стандартное
отклонение выборки, с помощью функции СТАНДОТКЛОН.
. Будьте аккуратны при выборе функций
– среди них есть очень похожие по названию. Аргументами этих функций служит все
тот же диапазон ячеек.

Следующая формула сложная, частично она набирается как обычная
формула, начиная с символа ”=”. Указав, где находится делимое S и набрав знак операции (=F8/), вызываем
мастер функций. Функция КОРЕНЬ – математическая, поэтому на первом шаге
выбираем категорию математических функций. Аргументом этой функции служит число
опытов, которое мы рассчитали в ячейке F6. Окончательный
вид формулы “=F8/ КОРЕНЬ(F6)”.

Для расчета доверительного интервала необходимо определить
коэффициент Стьюдента. Он зависит от вероятности ошибки (при обычно задаваемой
надежности 95% вероятность ошибки составляет 5%), и от числа степеней свободы n-1). Для нахождения коэффициента Стьюдента используется
статистическая функция Excel СТЬЮДРАСПОБР (“Стьюдента распределение обратное“).
Особенностью этой функции является то, что первый аргумент, число 5% (или 0,05)
вводится в соответствующее окно с клавиатуры. Для второго указываем адрес
ячейки, где находится значение n,
затем дописываем в окне “-1”. Получаем запись “F6-1”.

Для нахождения
доверительного интервала используется обычная формула умножения. Конечно,
вместо букв там должны стоять адреса ячеек, где находятся коэффициент Стьюдента
и стандартное отклонение среднего. Как правило, значение доверительного
интервала округляется до одной значащей цифры, такой же порядок окружения
должен быть и у среднего. Поэтому окончательный результат можно записать так: с
95%-ной надежностью Х = 14,80±0,05. В заключение посчитаем относительную ошибку определения Х: d = ДИ / Х_ср (формула: “=F11/F7”).
Значение относительной ошибки обычно выражают в процентах, у нас 0,3%.

Если Вы впервые
работаете в Excel, описанная процедура обработки данных эксперимента может
показаться очень сложной.  Но на практике, вводить формулы, с помощью мастера
функций, ничуть не сложнее, чем обычные арифметические. К тому же, один раз
подготовив лист Excel для обработки данных, можно скопировать его, и ввести
результаты новой серии опытов в колонку В. Результаты будут тут же рассчитаны
автоматически.

Изучение
зависимостей.

Часто в исследованиях изучается зависимость некоторой величины
от другой. Характер этих зависимостей стремятся выразить математическими
формулами, коэффициенты которой могут иметь определенный физический смысл.
Наиболее употребительна и проста в обработке линейная зависимость, которую
можно выразить уравнением прямой у = kx + b. При этом коэффициент k показывает
степень влияния х на у, а b – некоторое
начальное значение у. Поскольку значения, полученные в ходе эксперимента,
всегда включают некоторую ошибку,  экспериментальные точки не лежат строго на
прямой. Как же провести по этим разбросанным точкам наилучшую линию. Для этого
используется статистический метод «наименьших квадратов» предлагающий
достаточно сложные функции для нахождения коэффициентов k и b, а также для оценки их
достоверности.

В Excel эта
задача решается при помощи статистических функций НАКЛОН (наклон прямой
относительно оси Х, коэффициент k) и ОТРЕЗОК  (отрезок
отсекаемый прямой на оси Y, коэффициент b). Кроме того, Excel позволяет
построить график зависимости, саму прямую, которая называется линией тренда, а
также вывести уравнение прямой на график.

Для знакомства с этим возможностями перейдем на Лист 3 нашей
книги, назовем его «Зависимость» и введем необходимые исходные данные (таблица
2).

Таблица 2. Примерный вид листа
«Зависимость»

В колонках В и С вводятся данные эксперимента по измерению
величин Х и У, записи в колонке Е играют роль подсказок, колонка F заполняется по мере обработки.
Начнем с ячейки F3.

Ввод формул проводится с помощью мастера функций так, как это
описывалось ранее. Маленькое отличие заключается в том, что у функций НАКЛОН и ОТРЕЗОК два
аргумента: диапазон ячеек со значениями Y и диапазон ячеек со значениями Х.
Щелкаем мышкой сначала по полю для ввода первого аргумента, показываем нужный
диапазон (С3:С13). Затем щелкаем по второму поля и повторяем ввод (В3:В13).
Также рассчитывается и значение функции ОТРЕЗОК в ячейке F4.

Для оценки достоверности можно использовать квадрат коэффициента
корреляции Пирсона (R²). Если он равен 1, то
имеет место полная корреляция с моделью, т.е. точки лежат строго на прямой. В
противоположном случае, если коэффициент  равен 0, то уравнение линейной
зависимости полностью неудачно. Для его нахождения используется статистическая
функция КВПИРСОН. Таким образом, данные
нашего эксперимента с достоверностью 0,98 описываются уравнением у = 1,42х+0,905.

Рассмотрим теперь второй метод обработки и представления
результатов эксперимента в виде графика. Для построения графиков и диаграмм в Excel’e используется
Мастер диаграмм, который можно запустить, используя меню Вставка – Диаграмма,
или кнопки на панели инструментов с условным изображением диаграммы.
Предварительно щелкнем мышкой по любой свободной ячейке нашего листа.

Рисунок 3. 

На первом шаге (рисунок 3) выбирается тип и вид диаграммы. Для
построения графика зависимости одной величины от другой используются точечные
диаграммы, причем лучше (из-за разброса точек) выбирать вид «Точки не
соединенные линиями». Заканчиваем выбор, щелкая по кнопке «Далее».

На втором шаге необходимо указать, где у нас находится
независимая величина Х и зависящая от нее Y (рисунок 4).
Для этого щелкаем по ярлычку вкладки «Ряд» и затем по кнопке «Добавить».

Рисунок 4.

Открываются поля для указания Х и Y. Ввод
значений адресов в эти поля не отличаются от работы с Мастером функций (только
при вводе Y предварительно
сотрите условное значение “={1}”. Если Вы правильно выполните эту часть работы,
на поле вверху уже появится примерный вид графика.

Следующие два шага имеют отношение к оформлению и размещению
графика. На первый раз можно, ничего не меняя, просто нажимать кнопки «Далее» и
«Готово». Полученный черновой вариант графика всегда можно редактировать,
изменять или удалять его отдельные элементы. Обычно для этого щелкают по
нужному элементу графика правой (!) кнопкой мышки. При этом открывается
контекстное меню, в котором выбирают подходящую команду.

Если правой кнопкой мышки щелкнуть по одной из точек графика, то
в контекстном меню можно увидеть команду «Добавить линию тренда». Это и есть
необходимая нам линия. Добавляется она тоже в два шага. На первом выбирается
тип (линейный), на втором – параметры. На вкладке Параметры нам важно поставить
галочки против слов: «показывать уравнение» и «поместить величину
достоверности». Если из теоретических предпосылок понятно, что прямая должна
проходить через начало координат (при нулевой концентрации скорость реакции,
очевидно, равна нулю) поставим галочку и в данном пункте. Примерный вид графика
после добавления линии тренда представлен на рисунке 5. Выведенное уравнение
прямой и величины достоверности совпадает с рассчитанными ранее.

Рисунок 5.

Итак, мы рассмотрели важнейшие приемы работы в Microsoft Excel, необходимые для качественной
обработки данных эксперимента. Разумеется эти приемы не исчерпывают всех
возможностей Excel, и могут развиваться в ходе работы.
Автор статьи с удовольствием ответит на все вопросы, связанные с работой в
данной программе. Желаю успеха!

Задать вопрос.

---

Excel представляет собой не просто удобное
средство для выполнения математических
и логических операций, а мощный и
универсальный инструмент по решению
достаточно серьезных задач, возникающих
в сфере экономики и финансов.

Среди типичных экономико-математических
приложений Excel могут быть названы:

• структуризация и первичная логическая
  обработка данных;

• статистическая обработка данных, анализ
  и прогнозирование;

• решение уравнений и оптимизационных
  задач;

• проведение финансово-экономических
  расчетов.

Excel позволяет организовывать работу
как с базами данных, созданными в
собственной среде (с помощью списков),
так и с внешними (с помощью средства
MicrosoftQuery).
Современные базы данных представляют
собой набор таблиц, имеющих сложные
связи. Но использование термина «база
данных» в рамках списков в Excel не
корректно, здесь имеется в виду работа
с «диапазоном данных», в котором могут
выполняться операции, характерные при
работе с базами данных, а именно, ввод,
удаление и редактирование записи,
сортировка и фильтрация. Кроме того, в
Excel существуют ограничения на количество
строк и столбцов. Поэтому Excel стоит
использовать только как средство анализа
содержимого диапазонов данных и
подготовки отчетов.

Excel предлагает мощный аппарат для анализа
данных.

1. Функции, реализующие статистические
методы обработки и анализа данных, в
Excel реализованы в виде специального
программного расширения – надстройки
Пакет анализа.

Целью статистического исследования
является обнаружение и исследование
соотношений между статистическими
(экономическими) данными и их использование
для изучения, прогнозирования и принятия
решений. Фундаментальными понятием
статистического анализа являются
понятия вероятности и случайной величины.

Конечно, Excel не предназначен для
комплексного статистического анализа
и обработки данных (в отличие от
специального статистического программного
обеспечения, такого как STATISTICA, Eviews, TSP,
SPSS, Microfit и др.). Однако и на базе электронных
таблиц можно провести некоторую
статистическую обработку данных. В
частности, в рамках Excel с помощью команд,
доступных из окна Анализ данных, можно
провести:

• описательный статистический анализ
  (Описательная статистика);

• ранжирование данных (Ранг и персентиль);

• графический анализ данных (Гистограмма);

• прогнозирование данных (Скользящее
  среднее, Экспоненциальное сглаживание);

• регрессионный анализ (Регрессия) и др.

2. Консолидация– обобщение однородных
данных из разных источников. При
консолидации на основе значений
нескольких ячеек формируется значение
результирующей ячейки путем суммирования,
нахождения среднего и т.д.

3. В Excel существует возможность, которая
позволяет осуществлять поиск данных
по определенным условиям. Это
реализовано тремя подходами:

• использование формул для поиска
  информации в таблице (функции просмотра);

• использование функции ветвления для
  принятия решений;

• работа с таблицей подстановок.

4. Cводная таблицаExcel (pivot table) представляет собой интерактивную
таблицу, применяемую для суммирования
или статистического анализа большого
количества исходных данных, обычно
содержащихся в одном из диапазонов
ячеек Excel либо являющихся результатом
запроса к какой-либо базе данных. Строки
и столбцы подобной интерактивной таблицы
базируются на данных из нескольких
столбцов исходной таблицы. Ячейки
сводной таблицы представляют собой
суммы значений одного из числовых полей
исходной таблицы. При этом суммирование
производится для тех строк исходной
таблицы, в которых значения столбцов,
образовавших столбцы и строки сводной
таблицы, совпадают с именами строки и
столбца сводной таблицы, на пересечении
которых находится данная ячейка.Cводные
таблицы иногда называют перекрестными
таблицами, или кросс-таблицами (crosstabs).

Инструмент Excel PivotTable Services позволяет
создавать сводные таблицы на основе
диапазонов Excel и запросов к базам данных.
Помимо этого сводные таблицы можно
создавать также на основе OLAP-кубов,
полученных с помощью OLAP-серверов.

On-Line Analytical Processing (OLAP) – это способ
организации больших коммерческих баз
данных. Базы данных OLAP позволяют получать
и анализировать данные, что облегчает
создание необходимых отчетов. Базы
данных OLAP спроектированы так, чтобы
ускорить загрузку данных.

В общем случае OLAP-куб представляет собой
структуру, содержащую многомерные
OLAP-данные, то есть измерения (dimensions)–
описательные данные, составляющие оси
многомерного куба, имеры (measures)–
суммируемые количественные величины.
Измерения могут содержать многоуровневые
иерархии значений, а меры являются
агрегатными данными (суммы, средние,
максимальные или минимальные значения,
количество записей) на основе полей
реляционной СУБД, представляющих интерес
с точки зрения статистического анализа.
Создавая OLAP-куб на основе базы данных
или запроса, мы преобразуем «плоские»
наборы данных в многомерные.

Следует отметить, что Excel и сам может
создавать локальные OLAP-кубы, сохраняемые
в файлах *.cub, либо описания кубов,
сохраняемые в файлах *.oqy и используемые
при пересчете куба на основе исходной
базы данных (такое описание содержит
сведения об источнике данных, запрос,
использовавшийся при создании куба, а
также сведения о его структуре).

В большинстве случаев OLAP-кубы создаются
в многомерных базах данных, управляемых
OLAP-серверами (такими как Microsoft SQL Server).
Однако иногда бывает удобно создать
локальное многомерное хранилище данных
в виде файла, в котором данные организованы
подобным способом. Это можно сделать с
помощью все тех же Microsoft PivotTable Services,
например, непосредственно из Excel либо
из другого приложения, применяющего
Microsoft PivotTable Services. Отметим, что OLAP-сервер
для создания или использования такого
OLAP-куба не требуется.

5. В Excel имеются мощные средства для
подбора и оптимизации параметров так
называемый «что-если» анализ (what-ifanalysis).Анализ «что-если»– процесс изменения значений ячеек и
анализа влияния этих изменений на
результат вычисления формул на листе,
например, изменение процентной ставки,
используемой в таблице амортизации для
определения сумм платежей. К средствам
анализа «что-если» относятсятаблицы
подстановок, средствоПодбор
параметра, надстройкаПоиск решения,сценарии.

Таблицей подстановок данныхназывается диапазон ячеек, показывающий,
как изменение значений подстановки
влияет на возвращаемый формулой
результат. Использование таблиц
подстановок вместе со статистическими
функциями позволяет быстро и эффективно
анализировать экономическую информацию.

Когда желаемый результат одиночной
формулы известен, но неизвестны значения,
которые требуется ввести для получения
этого результата, можно воспользоваться
средством «Подбор параметра» выбрав
команду Подбор параметрав менюСервис.Подбор параметра–
способ поиска определенного значения
ячейки путем изменения значения в другой
ячейке. При подборе параметра значение
в ячейке изменяется до тех пор, пока
формула, зависящая от этой ячейки, не
вернет требуемый результат.

Процедура поиска решенияпозволяет
найти оптимальное значение формулы,
содержащейся в ячейке, которая называется
целевой. Эта процедура работает с группой
ячеек, прямо или косвенно связанных с
формулой в целевой ячейке. Чтобы получить
по формуле, содержащейся в целевой
ячейке, заданный результат, процедура
изменяет значения во влияющих ячейках.
Чтобы сузить множество значений,
используемых в модели, применяются
ограничения. Эти ограничения могут
ссылаться на другие влияющие ячейки.
Процедуру поиска решения можно
использовать для определения значения
влияющей ячейки, которое соответствует
экстремуму зависимой ячейки, например
можно изменить объем планируемого
бюджета рекламы и увидеть, как это
повлияет на проектируемую сумму расходов.

Сценарий– это набор значений,
которые Excel сохраняет и может автоматически
подставлять на листе. Сценарии можно
использовать для прогноза результатов
моделей и систем расчетов. Существует
возможность создать и сохранить на
листе различные группы значений, а затем
переключаться на любой из этих новых
сценариев для просмотра различных
результатов.

Еще одна важная сфера приложения Excel
связана с осуществлением финансовых
расчетов. Финансовые вычисления включают
в себя всю совокупность методов и
расчетов, используемых при принятии
управленческих решений, – от элементарных
арифметических операций до сложных
алгоритмов построения многокритериальных
моделей, позволяющих получить оптимальные
характеристики коммерческих сделок в
зависимости от различных условий их
проведения. Проведение подобных
вычислений – трудоемкая процедура,
требующая определенной математической
подготовки, а также использования
большого количества справочных
материалов.

Широкий спектр встроенных финансовых
функций позволяет отказаться от ручного
ввода финансовых формул. Функции Excel
работают быстрее, чем введенные формулы,
и с меньшей вероятностью ошибок.

По типу решаемых задач все финансовые
функции Excel можно разделить на следующие
условные группы:

• функции для анализа аннуитетов и
  инвестиционных проектов;

• функции для анализа ценных бумаг;

• функции для расчета амортизационных
  платежей;

• вспомогательные функции.

Функции каждой группы имеют практически
одинаковый набор обязательных и
дополнительных (необязательных)
аргументов. Для получения более детальной
информации следует воспользоваться
справочной системой.

Соседние файлы в папке пособие_ЭИ

• #
• #
• #
• #
• #
• #
• #
• #
• #