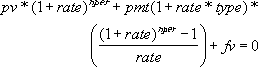Excel функция текущая стоимость

Рассчитаем

Приведенную (к текущему моменту) стоимость

инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.

Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и

Будущей стоимости

важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты:

простые проценты

,

сложные проценты

или

аннуитет

(в

файле примера

приведено решение задачи для каждого из методов).

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные  за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).

Примечание

. В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция

ПС()

используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить

ПС()

рассчитать Приведенную стоимость и по методу простых процентов (см.

файл примера

).

Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета

Будущей стоимости

(FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.

Из этой формулы получим, что:

PV = FV / (1+i*n)

Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).

Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.

Сложные проценты

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя

формулу наращения для сложных процентов

.

FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,

т.е. PV = FV / (1+i)^n

При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.

Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).

Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)

Сложные проценты (несколько сумм)

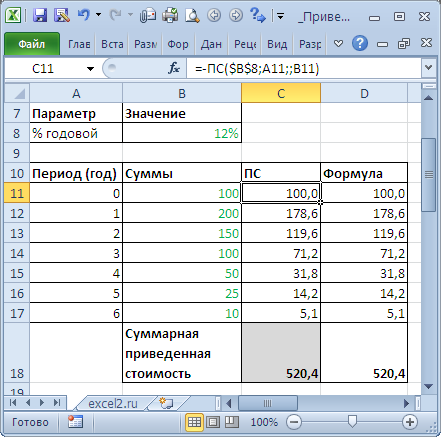
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции

ПС()

или альтернативной формулы PV = FV / (1+i)^n

Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см.

файл примера

).

Аннуитет

Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью

Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость

, где приведен расчет с помощью функции

ПС()

, а также вывод альтернативной формулы).

Здесь разберем другую задачу (см.

файл примера

):

Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?

Решение может быть найдено с помощью функции

ПС()

:

=ПС(12%/12;12;20000;-1000000;0)

= 662 347,68р.

Аргумент

Ставка

указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент

Кпер

– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент

Плт

— это 20000р., т.е. величина дополнительных взносов. Аргумент

Бс

— это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент

перечисляет

эти средства банку, а будущую сумму вклада клиент

получит

от банка. Это очень важное замечание касается всех

функций аннуитета

, т.к. в противном случае можно получить некорректный результат. Результат функции

ПС()

– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше

=ПС(12%/12;12;20000)

= -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость

= БС(12%/12;12;; 225 101,55+662 347,68)

= -1000000,0р., что и требовалось доказать.

Определение Приведенной стоимости в случае платежей произвольной величины

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция

ЧПС()

. Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция

ЧИСТНЗ()

. Об этих расчетах читайте в статье

Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL

.

Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.

Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel

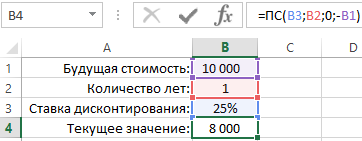
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?

Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:

Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.

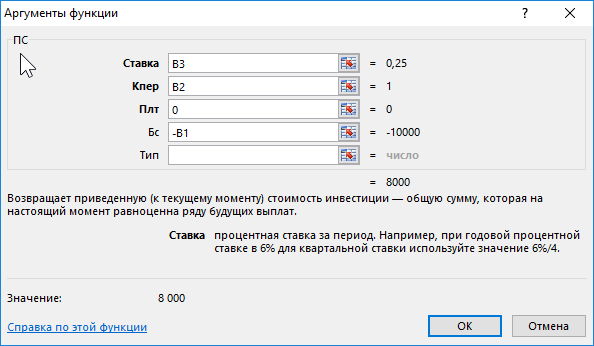
Функция ПС имеет 5 аргументов:

1. Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
2. Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
3. Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
4. Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
5. Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.



Формула расчета текущей стоимости денег с учетом инфляции в Excel

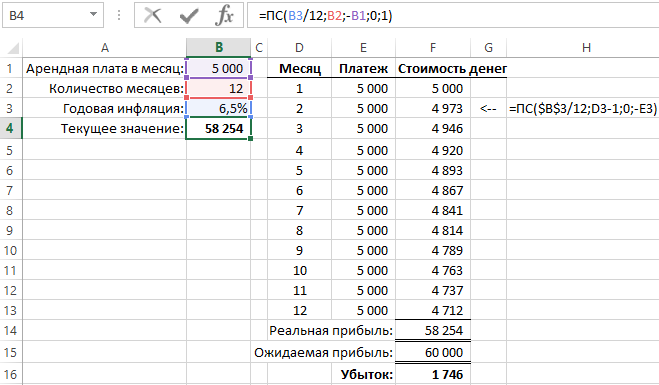
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:

В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.

В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.

Функция ПС возвращает приведенную к текущему моменту стоимость инвестиций. Очевидно, что деньги в будущем будут иметь ценность, отличную от настоящей. Функция ПС вычисляет сумму, которая на настоящий момент равноценна ряду будущих выплат. Вот ее синтаксис: ПС(ставка; кпер;плт;бс;тип ).

Аргументы финансовых функций

Пять основных финансовых функций Excel имеют много общих аргументов. Ниже перечислены типовые аргументы и их смысловое значение.

• Ставка. Процентная ставка, выплачиваемая по займу или используемая для дисконтирования будущих денежных потоков. Период, который охватывает процентная ставка, должен быть тем же, что и в параметрах Кпер и Плт.
• Кпер. Количество периодов. Это может быть количество платежей по займу или количество лет депозитного вклада. Количество периодов должно быть выражено в тех же единицах, которые используются в аргументах Ставка и Плт. К примеру, 30-летний заем с помесячными выплатами будет содержать 360 периодов. Именно это значение следует подставлять в параметр Кпер, а не 30.
• Плт. Размер одного платежа. В рассматриваемых финансовых функциях платежи должны иметь одинаковый размер во всех периодах, а периоды должны быть равнозначны. Величина платежа включает в себя как выплату по основному займу, так и выплату процентов.
• БС. Будущая стоимость инвестиции, рассчитанная на основе периодических постоянных (т.е. равных по величине) платежей и постоянной процентной ставки. Это последняя операция транзакции. Во многих случаях (например, при единовременном погашении займа) не существует будущей стоимости.
• ПС. Текущая приведенная стоимость инвестиции. Это первая операция транзакции, например, получение займа или вклад денег на депозит. Если транзакция состоит только из платежей, в ней может не существовать приведенной стоимости.
• Тип. Этот аргумент определяет время внесения платежей.
• Прбл. Приблизительное значение результата. При вычислении процентной ставки программе для получения результата может потребоваться выполнить множество итераций. Можно облегчить программе решение этой задачи, указав значение, близкое к ожидаемому результату.

Вычисление приведенной стоимости

В примере, приведенном ниже в этом разделе, вычисляется приведенное значение серии будущих выплат, иногда называемых ежегодной рентой. Если каждый год в течение десяти лет вносится платеж размером в 1200 долларов, то приведенная стоимость этих платежей составляет 6780,27 долларов: =ПС(,12;10;1200;0;0). Другими словами, если плательщик в настоящий момент предложит вам 6800 долларов, вам будет выгоднее их взять, чем получать в течение 10 лет по 1200 долларов. Если он предложит меньшую сумму, лучше подождать регулярных ежегодных платежей.

В приведенной выше формуле вы, наверное, заметили, что процентная ставка взята как бы ниоткуда. Функция ПС обычно используется для определения, сколько стоят на настоящий момент будущие выплаты. В этих ситуациях конкретная процентная ставка недоступна.
[stextbox id=»info»]Существует множество мнений относительно того, какую процентную ставку лучше использовать при определении приведенной стоимости. Выбор процентной ставки в значительной мере зависит от вас самих. Одни говорят, что нужно использовать текущую процентную ставку по банковским депозитам, другие утверждают, что нужно брать процентную ставку по инвестициям, не связанным с рисками, таким как казначейские облигации. В данном примере была использована процентная ставка по инвестициям в ценные бумаги.[/stextbox]
В приведенном выше примере была использована процентная ставка 12%. В результате получилось, что инвестиция размером в 6800 долларов принесет тот же доход, что и десятилетнее ожидание платежей по 1 200 долларов. Если плательщик предложит вам 7000 долларов немедленно, вы можете вложить их и получить лучший финансовый результат. Теперь давайте вернемся к таблицам и предположим, что у вас есть обязательства, по которым вы должны ежегодно выплачивать кому-то по 1200 долларов в течение 10 лет. Формула выглядит следующим образом: =ПС(,12;10;-1200;0;0).

Вместо входящего, в этой формуле использован исходящий денежный поток. Результат (-$6 780,27) также имеет знак, противоположный предыдущему примеру. В обоих примерах сумма платежей формирует всю транзакцию, поэтому будущей стоимости не существует. Также в примере использовано значение по умолчанию аргумента Тип. Аргументы БС и Тип не являются обязательными; они были включены в пример только для наглядности. На рис. 1 этот расчет показан в рабочей книге.

[stextbox id=»alert»]Из соображений простоты в формулах примеров, приведенных в тексте, используются только константы. На практике чаще всего в аргументы функций подставляются ссылки на ячейки.[/stextbox]

Приведенная стоимость единовременной будущей выплаты

В предыдущих примерах мы имели дело с сериями последовательных регулярных выплат, однако иногда существует всего одна будущая единовременная выплата. В качестве примера представим себе, что некоторый богатый родственник решил дать вам 100 тысяч долларов, но вы не можете получить их до своего сорокалетия. Если сейчас вам 25 лет, приведенная стоимость будущего платежа составит 31524,17 долларов. Эта сумма получена с помощью следующей формулы: =ПС(,08;15;0;100000).

Таким образом, это будет единовременный платеж ровно через 15 лет. Если бы у вас были сейчас какие-либо деньги, вы смогли бы инвестировать их под 8% годовых. Так как периодических платежей не будет, аргумент Тип в формуле опущен. Результат формулы свидетельствует о том, что если бы у вас было сейчас 31524,17 долларов и вы бы инвестировали их под 8%, то через 15 лет получили бы сотню тысяч долларов (рис. 2).

Приведенная стоимость периодических платежей с суммой погашения

В некоторых случаях периодические платежи идут в одной связке с большой суммой единовременной выплаты в конце периода займа. В качестве примера предположим, что ваш родственник попросил вас инвестировать в его бизнес. Он предложил следующие условия: если вы внесете инвестицию в 50 тысяч долларов сейчас, то он будет вам выплачивать ежемесячно по 200 долларов в течение пяти лет, после чего заплатит единовременным платежом еще 60 тысяч долларов. Чтобы определить, имеет ли такая инвестиция для вас смысл, найдите приведенную стоимость всех выплат: =ПС(,1/12;60;200;60000/1).

Давайте внимательно посмотрим на каждый из аргументов (рис. 3).

• Вы определили, что при любых обстоятельствах сможете получить прибыль в 10% годовых, используя свои деньги в течение пяти лет. По этой причине процентную ставку мы установили в 10%.
• Все аргументы должны охватывать один и тот же временной период. Так как выплаты будут осуществляться ежемесячно, все аргументы должны быть преобразованы соответствующим образом:
  • аргумент Ставка делим на 12 месяцев;
  • аргумент Кпер получаем, умножив 5 лет на 12 месяцев в году;
  • аргументы Плт и БС оставляем без изменений;
  • аргументу Тип присваиваем значение 1, так как предполагается, что первый платеж будет совершен немедленно.

Из этой формулы выходит, что приведенная стоимость всех будущих выплат составляет 46698,82 доллара. Следовательно, можно сделать вывод: лучше вложить свои пятьдесят тысяч долларов в какое-либо другое предприятие, чем на данных условиях отдать родственнику.

Подставляя в аргументы функции различные значения, можно найти нужное решение. Данный результат вы можете выставить в качестве контрпредложения. При этом вы даже можете воспользоваться функцией подбора параметра программы Excel. Для этого выберите команду Данные → Работа с данными → Анализ «что если’ → Подбор параметра. Эта функция поможет подобрать такие значения аргументов, при которых приведенная стоимость будущих выплат составит нужную вам сумму.