Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции Функция СТАНДОТКЛОН.В.
Синтаксис
СТАНДОТКЛОН(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
-
Функция СТАНДОТКЛОН вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОН(A3:A12) |
Стандартное отклонение предела прочности (27,46392) |
27,46392 |
Нужна дополнительная помощь?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТАНДОТКЛОНА в Microsoft Excel.
Описание
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
СТАНДОТКЛОНА(значение1;[значение2];…)
Аргументы функции СТАНДОТКЛОНА описаны ниже.
-
Значение1,значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 значений, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
-
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
-
Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
-
Аргументы, представляющие собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОН.
-
Функция СТАНДОТКЛОНА вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОНА(A3:A12) |
Стандартное отклонение предела прочности для всех инструментов (27,46391572) |
27,46391572 |
Нужна дополнительная помощь?
Функция СТАНДОТКЛОН.В возвращает значение стандартного отклонения, рассчитанного для определенного диапазона числовых значений.
Функция СТАНДОТКЛ.Г используется для определения стандартного отклонения генеральной совокупности числовых значений и возвращает величину стандартного отклонения с учетом, что переданные значения являются всей генеральной совокупностью, а не выборкой.
Функция СТАНДОТКЛОНА возвращает значение стандартного отклонения для некоторого диапазона чисел, которые являются выборкой, а не всей генеральной совокупностью.
Функция СТАНДОТЛОНПА возвращает значение стандартного отклонения для всей генеральной совокупности, переданной в качестве ее аргументов.
Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
Пример 1. На предприятии работают два менеджера по привлечению клиентов. Данные о количестве обслуженных клиентов в день каждым менеджером фиксируются в таблице Excel. Определить, какой из двух сотрудников работает эффективнее.
Таблица исходных данных:
Вначале рассчитаем среднее количество клиентов, с которыми работали менеджеры ежедневно:
=СРЗНАЧ(B2:B11)
Данная функция выполняет расчет среднего арифметического значения для диапазона B2:B11, содержащего данные о количестве клиентов, принимаемых ежедневно первым менеджером. Аналогично рассчитаем среднее количество клиентов за день у второго менеджера. Получим:
На основе полученных значений создается впечатление, что оба менеджера работают примерно одинаково эффективно. Однако визуально виден сильный разброс значений числа клиентов у первого менеджера. Произведем расчет стандартного отклонения по формуле:
=СТАНДОТКЛОН.В(B2:B11)
B2:B11 – диапазон исследуемых значений. Аналогично определим стандартное отклонение для второго менеджера и получим следующие результаты:
Как видно, показатели работы первого менеджера отличаются высокой вариабельностью (разбросом) значений, в связи с чем среднее арифметическое значение абсолютно не отражает реальную картину эффективности работы. Отклонение 1,2 свидетельствует о более стабильной, а, значит, и эффективной работе второго менеджера.
Пример использования функции СТАНДОТКЛОНА в Excel
Пример 2. В двух различных группах студентов колледжа проводился экзамен по одной и той же дисциплине. Оценить успеваемость студентов.
Таблица исходных данных:
Определим стандартное отклонение значений для первой группы по формуле:
=СТАНДОТКЛОНА(A2:A11)
Аналогичный расчет произведем для второй группы. В результате получим:
Полученные значения свидетельствуют о том, что студенты второй группы намного лучше подготовились к экзамену, поскольку разброс значений оценок относительно небольшой. Обратите внимание на то, что функция СТАНДОТКЛОНА преобразует текстовое значение «не сдал» в числовое значение 0 (нуль) и учитывает его в расчетах.
Пример функции СТАНДОТКЛОН.Г в Excel
Пример 3. Определить эффективность подготовки студентов к экзамену для всех групп университета.
Примечание: в отличие от предыдущего примера, будет анализироваться не выборка (несколько групп), а все число студентов – генеральная совокупность. Студенты, не сдавшие экзамен, не учтены.
Заполним таблицу данных:
Для оценки эффективности будем оперировать двумя показателями: средняя оценка и разброс значений. Для определения среднего арифметического используем функцию:
=СРЗНАЧ(B2:B21)
Для определения отклонения введем формулу:
=СТАНДОТКЛОН.Г(B2:B21)
В результате получим:
Полученные данные свидетельствует об успеваемости немного ниже среднего (<4), величина разброса характеризует довольно большое количество студентов, получивших 5 и 3 соответственно (учитывая, что анализировались только данные из диапазона от 3 до 5).
Пример функции СТАНДОТКЛОНПА в Excel
Пример 4. Проанализировать успеваемость студентов по результатам сдачи экзамена с учетом тех студентов, которым не удалось сдать этот экзамен.
Таблица данных:
В данном примере также анализируем генеральную совокупность, однако некоторые поля данных содержат текстовые значения. Для определения стандартного отклонения используем функцию:
=СТАНДОТКЛОНПА(B2:B21)
В результате получим:
Высокий разброс значений в последовательности свидетельствует о большом числе не сдавших экзамен студентов.
Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
Функции СТАНДОТКЛОНА И СТАНДОТКЛОНПА имеют идентичную синтаксическую запись типа:
=ФУНКЦИЯ (значение1; [значение2];…)
Описание:
- ФУНКЦИЯ – одна из двух рассмотренных выше функций;
- значение1 – обязательный аргумент, характеризующий одно из значений выборки (либо генеральной совокупности);
- [значени2] – необязательный аргумент, характеризующий второе значение исследуемого диапазона.
Примечания:
- В качестве аргументов функций могут быть переданы имена, числовые значения, массивы, ссылки на диапазоны числовых данных, логические значения и ссылки на них.
- Обе функции игнорируют пустые значения и текстовые данные, содержащиеся в диапазоне переданных данных.
- Функции возвращают код ошибки #ЗНАЧ!, если в качестве аргументов были переданы значения ошибок или текстовые данные, которые не могут быть преобразованы в числовые значения.
Функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г имеют следующую синтаксическую запись:
=ФУНКЦИЯ(число1;[число2];…)
Описание:
- ФУНКЦИЯ – любая из функций СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г;
- число1 – обязательный аргумент, характеризующий числовое значение, взятое из выборки или всей генеральной совокупности;
- число2 – необязательный аргумент, характеризующий второе числовое значение исследуемого диапазона.
Примечание: обе функции не включают в процесс вычисления числа, представленные в виде текстовых данных, а также логические значения ИСТИНА и ЛОЖЬ.
Примечания:
- Стандартное отклонение широко используется в статистических расчетах, когда нахождение среднего значения диапазона величин не дает верное представление о распределении данных. Оно демонстрирует принцип распределения величин относительно среднего значения в конкретной выборке или всей последовательности целиком. В Примере 1 будет наглядно рассмотрено практическое применение данного статистического параметра.
- Функции СТАНДОТКЛОНА и СТАНДОТКЛОН.В следует использовать для анализа только части генеральной совокупности и производят расчет по первой формуле, а СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА должны принимать на вход данные о всей генеральной совокупности и производят расчет по второй формуле.
- В Excel содержатся встроенные функции СТАНДОТКЛОН и СТАНДОТКЛОНП, оставленные для совместимости с более старыми версиями Microsoft Office. Они могут быть не включены в более поздние версии программы, поэтому их использование не рекомендуется.
- Для нахождения стандартного отклонения используются две распространенные формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/n), где:
- S – искомое значение стандартного отклонения;
- n – рассматриваемый диапазон значений (выборка);
- x_i – отдельно взятое значение из выборки;
- x_ср – среднее арифметическое значение для рассматриваемого диапазона.
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
На чтение 5 мин Опубликовано 15.01.2021
Для вычисления среднеквадратического отклонения в Microsoft Office Excel используется специальная формула, которой можно пользоваться несколькими способами. О них пойдет речь в данной статье.
Содержание
- Как вычислить среднее квадратическое отклонение в Excel
- Способ 1. С помощью Мастера функций
- Способ 2. Расчет стандартного отклонения в разделе «Формулы»
- Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
- Способ 4. Ручной подсчет
- Заключение
Как вычислить среднее квадратическое отклонение в Excel
Это один из показателей вариации. В теории вероятностей этот показатель рассчитывается по формуле:
В Эксель пользователю не нужно будет вручную рассчитывать среднеквадратичное отклонение. Существует ряд способов, позволяющих найти эту величину в кратчайшие сроки с помощью встроенных в Excel инструментов. Далее будут рассмотрены самые распространенные из них.
Способ 1. С помощью Мастера функций
Данный метод расчета стандартного отклонения в Excel занимает минимальное количество времени. Вычисление производится следующим образом:
- Левой клавишей манипулятора на рабочем листе программы выделить ячейку, в которой будет отображаться результат вычисления.
- Кликнуть по кнопке «Вставка функции», расположенной с левой стороны от строки ввода.
- После выполнения предыдущего действия откроется окошко Мастера функций. Здесь пользователю потребуется найти строку «СТАНДОТКЛОН.В», выделить ее ЛКМ и нажать на «ОК» внизу меню. В списке функций также есть записи «СТАНДОТКЛОН.Г» и просто «СТАНДОТКЛОН». На них нажимать не нужно!
- В следующем окне аргументов функции необходимо прописать числа совокупности в каждом поле. Если эти значения уже написаны на рабочем листе Excel, то можно указать координаты соответствующих ячеек.
- Нажать на «ОК» внизу меню «Аргументы функции», когда все строчки будут заполнены.
- Проверить результат. В выделенной на первом этапе ячейке будет прописано число. Это и есть среднее квадратичное отклонение.
Обратите внимание! Если после выполнения вышеуказанных манипуляций в ячейке будут отображаться знаки «###», то значит результатом является большое число, и ячейку нужно растянуть.
Способ 2. Расчет стандартного отклонения в разделе «Формулы»
Через вкладку «Формулы» в программе Excel также возможно рассчитать стандартное отклонение. Алгоритм вычисления состоит из следующих шагов:
- По аналогичной схеме выделить любую свободную ячейку на рабочем листе. В этот элемент в дальнейшем будет выводиться результат.
- В графе инструментов сверху главного меню программы найти слово «Формулы» и щелкнуть по нему ЛКМ.
- В открывшейся области найти подраздел «Библиотека функций, а затем развернуть вкладку «Другие функции».
- В контекстном меню выбрать тип «Статистические» и поставить курсор мышки на это слово.
- Развернется дополнительное контекстное окно, в котором пользователю необходимо щелкнуть по строчке «СТАНДОТКЛОН.В».
- В запустившемся окне «Аргументы функции» надо заполнить два поля, указав координаты соответствующих ячеек на рабочем листе или в табличном массиве. Нужные значения также можно прописать вручную.
- После выполнения этих манипуляций нажать на «ОК».
- Удостовериться, что в указанной ранее ячейке отобразился результат работы формулы – число, характеризующее среднеквадратичное отклонение.
Важно! Если необходимо посчитать стандартное отклонение у нескольких параметров, то исходную формулу можно растянуть на оставшиеся ячейки табличного массива.
Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
Чтобы рассчитать стандартное отклонение в Microsoft Office Excel, можно ввести специальную формулу с клавиатуры, результат будет одинаковым. Такой метод вычисления заключается в выполнении следующих этапов:
- Поставить курсор мыши в ячейку, куда будет выводиться результат.
- В выделенный элемент ввести с клавиатуры формулу «=СТАНДОТКЛОН.В(а,b,c,d)». Вместо букв в скобках нужно указать соответствующие аргументы. Это числа из табличного массива данных.
- Нажать на «Enter» для завершения процедуры.
- Проверить результат. В итоге в ячейке должно отобразиться конкретное значение среднеквадратичного отклонения.
Дополнительная информация! Также для расчета можно использовать формулу «СТАНОТКЛОН.Г()». Получится идентичный результат. Данный метод будет работать независимо от версии программного обеспечения.
Способ 4. Ручной подсчет
Такую операцию в Microsoft Office Excel нецелесообразно выполнять. Данный метод основан на применении обычного калькулятора, который также присутствует в Эксель. Для ручного счета необходимо проделать следующие действия по алгоритму:
- Левой клавишей манипулятора выделить ячейку табличного массива, в которую будет выводиться результат.
- Поставить знак «=» и с клавиатуры компьютера прописать числовые значения для расчета среднеквадратичного отклонения, указывая координаты соответствующих ячеек из таблички. Здесь надо подставлять параметры в формулу из первого рисунка.
- После написания формулы нажать на «Enter» и убедиться, что в ячейке отобразился результат стандартного отклонения.
Обратите внимание! Формулу для вычисления среднеквадратичного отклонения, написанную вручную в Excel, также можно растянуть на оставшиеся ячейки для их автоматического заполнения.
Заключение
Таким образом, стандартное отклонение в Microsoft Office Excel рассчитывается с помощью формулы или выбора соответствующей функции. Основные методы вычисления данного параметра были рассмотрены выше.
Оцените качество статьи. Нам важно ваше мнение:
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
— это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) — отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)
Смотрите также можно использовать макрос, мы будем использовать число поменяем местами,Примечание: обе функции не
Описание
Пример 3. Определить эффективность с учетом, что 3. Т.е. для выборки. А соответствующаяРазмерность дисперсии соответствует квадрату плат (см. раздел
Синтаксис
моды.
в MS EXCEL. – это максимальное
-
ячеек, в котором1310Описание (результат)В этой статье описаны но это будет в формуле функцию то у нас включают в процесс подготовки студентов к переданные значения являются нормального распределения Kurtosis
Замечания
-
величина s/√n имеет единицы измерения исходных статьи выше, оТеперь вспомним, что мыСОВЕТ значение (см. статью содержится массив данных.1370Результат
-
синтаксис формулы и тоже неполный автомат.
-
ABS, то формула получиться уже формула вычисления числа, представленные экзамену для всех всей генеральной совокупностью, excess равен 0. специальное название — Стандартная
-
значений. Например, если Медиане), модой является определили моду для: Подробнее про квартили про функцию НАИБОЛЬШИЙ()); Если в указанный
-
1318=СТАНДОТКЛОНА(A3:A12) использование функции сидел несколько часов, будет возвращать ошибочный для вычисления наценки. в виде текстовых
-
групп университета. а не выборкой. Необходимо быть внимательным, ошибка среднего. Именно эта
-
значения в выборке число 15 (17 выборки, т.е. для см. статью, проНаименьший (Kth Smallest) – диапазон входит текстовый
-
1350Стандартное отклонение предела прочности
СТАНДОТКЛОНА но к сожалению результат при отрицательном
Пример
Ниже на рисунке представлен данных, а такжеПримечание: в отличие отФункция СТАНДОТКЛОНА возвращает значение т.к. часто не величина вычисляется в Пакете анализа. представляют собой измерения значений из 51, конечного множества значений, перцентили (процентили) см. выводится К-й наименьший. заголовок набора данных,1303
|
для всех инструментов |
||
|
в Microsoft Excel. |
||
|
в формулах по |
||
|
числе в заменителе. |
||
|
пример, как выше |
||
|
логические значения ИСТИНА |
||
|
предыдущего примера, будет |
||
|
стандартного отклонения для |
||
|
очевидно, какая формула |
||
|
В MS EXCEL стандартную |
||
|
веса детали (в |
||
|
т.е. 33%). В |
||
|
взятых из генеральной |
статью. |
Например, 1-й наименьший |
|
то нужно поставить |
1299 (27,46391572)Оценивает стандартное отклонение по |
работе с базой |
support.office.com
СТАНДОТКЛОН.В (функция СТАНДОТКЛОН.В)
Так как в Excel описанное вычисление представить и ЛОЖЬ.
анализироваться не выборка некоторого диапазона чисел, лежит в основе ошибку среднего можно кг), то размерность
Синтаксис
этом случае функция
совокупности. Для непрерывныхМода (Mode) – это
-
– это минимальное галочку в полеФормула27,46391572 выборке. Стандартное отклонение данных нашел только по умолчанию приоритет в виде формулыПримечания:
-
(несколько групп), а которые являются выборкой, расчетов. также вычислить по дисперсии будет кг2. МОДА() дает хорошую случайных величин вполне наиболее часто встречающееся значение (см. статью
Замечания
-
Метки в первойОписаниеОценивает стандартное отклонение по — это мера одно условие. если операции деления выше Excel. Формула вСтандартное отклонение широко используется все число студентов
-
а не всейПримечание
-
формуле Это бывает сложно оценку «наиболее вероятного» может оказаться, что
-
(повторяющееся) значение в про функцию НАИМЕНЬШИЙ()). строке (Labelsinfirstrow). ВРезультат
-
выборке. Логические значения того, насколько широко реальная база данных операции вычитания в ячейке D2 вычисляет в статистических расчетах, – генеральная совокупность. генеральной совокупностью.
-
: Еще большую путаницу=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка)) интерпретировать, поэтому для значения зарплаты. выборка состоит из
-
выборке. Например, вНиже даны подробные описания этом случае заголовок=СТАНДОТКЛОН.В(A2:A11) и текст игнорируются.
-
разбросаны точки данных превышает в разы
данной формуле нет процент отклонения между когда нахождение среднего
Пример
Студенты, не сдавшиеФункция СТАНДОТЛОНПА возвращает значение вносит перевод этихАсимметричность или коэффициент асимметрии характеристики разброса значенийПримечание массива на подобие массиве (1; 1; остальных показателей. будет выведен вСтандартное отклонение предела прочности.Стандартное отклонение — это относительно их среднего.
|
пример в файле |
||
|
необходимости применять скобки. |
||
|
значениями продаж для |
||
|
значения диапазона величин |
||
|
экзамен, не учтены. |
||
|
стандартного отклонения для |
||
|
терминов на русский |
||
|
(skewness) характеризует степень |
||
|
чаще используют величину |
||
|
: Строго говоря, в |
||
|
этого (0,935; 1,211; |
||
|
2 2 2 |
||
|
Среднее (mean, average) или |
Выходном интервале. Пустые |
27,46391572 |
|
мера того, насколько |
СТАНДОТКЛОНА(значение1;[значение2];…) |
готов помочь. |
support.office.com
Описательная статистика в MS EXCEL
ник текущего и прошлого не дает верноеЗаполним таблицу данных: всей генеральной совокупности, язык. Термин Kurtosis несимметричности распределения (плотности
равную квадратному корню примере с зарплатой 2,430; 3,668; 3,874;; 3; 4; 5) выборочное среднее или ячейки будут проигнорированы,Рассмотрим инструмент Описательная статистика, широко разбросаны точкиАргументы функции СТАНДОТКЛОНА описаныGuest: Добрый вечер уважаемые года: =(C2-B2)/B2
представление о распределенииДля оценки эффективности будем переданной в качестве происходит от греческого распределения) относительно его из дисперсии – мы имеем дело …), в котором число 2 встречается среднее выборки (sample поэтому нулевые значения входящий в надстройку данных относительно их ниже.: Спасибо большое ваша форумчане. У меняВажно обратит внимание в данных. Оно демонстрирует оперировать двумя показателями: ее аргументов.
слова «изогнутый», «имеющий
- среднего.
- стандартное отклонение.
- скорее с генеральной
- может не оказаться
- чаще всего –
- average) представляет собой
- необходимо обязательно указывать
- Пакет Анализа. Рассчитаем
- среднего.
- Значение1, значение2,…
- формула работает! :-)
Надстройка Пакет анализа
возникли проблема с данной формуле на принцип распределения величин средняя оценка иПример 1. На предприятии арку». Так сложилось,Положительное значение коэффициента асимметрии
Подробнее о дисперсии см. совокупностью, чем с повторов и функция 3 раза. Значит, арифметическое среднее всех в ячейках, а показатели выборки: среднее,СТАНДОТКЛОН.В(число1;[число2];…)
Аргумент «значение1» является обязательным,doc.yura использованием функции СТАНДОТКЛОН. наличие скобок. По
относительно среднего значения разброс значений. Для работают два менеджера что на русский указывает, что размер
статью Дисперсия и выборкой. Т.к. других МОДА() вернет ошибку.
число 2 – значений массива. В не оставлять их медиана, мода, дисперсия,
Аргументы функции СТАНДОТКЛОН.В описаны
- последующие значения необязательные.: Есть график сПопробую описать ситуацию: умолчанию в Excel в конкретной выборке определения среднего арифметического по привлечению клиентов. язык оба термина правого «хвоста» распределения стандартное отклонение в зарплат в компанииДаже в нашем массиве это мода. Для MS EXCEL для пустыми; стандартное отклонение и ниже. От 1 до медианой значений, аесть исходная таблица
- операция деления всегда или всей последовательности используем функцию: Данные о количестве Kurtosis и Kurtosis больше, чем левого
- MS EXCEL. просто нет. с модой, которая вычисления моды используется вычисления среднего выборкивыходной интервал (Output Range). др.
- Число1 255 значений, соответствующих нужно на него с данными по имеет высший приоритет целиком. В Примере
=СРЗНАЧ(B2:B21) обслуженных клиентов в
excess переводятся как (относительно среднего). ОтрицательнаяСтандартное отклонение выборки (StandardО вычислении моды для была определена с функция МОДА(), английский
используется функция СРЗНАЧ(). Здесь укажите адресЗадача описательной статистики (descriptive Обязательный. Первый числовой выборке из генеральной еще наложить стандартное живой массе птицы по отношению к 1 будет наглядноДля определения отклонения введем день каждым менеджером Эксцесс (от англ. асимметрия, наоборот, указывает Deviation), как и распределения непрерывной случайной помощью надстройки Пакет вариант MODE(). Выборочное среднее является верхней левой ячейки statistics) заключается в
аргумент, соответствующий выборке совокупности. Вместо аргументов, отклонение, т.е. получить из разных хозяйств операции вычитания. Поэтому рассмотрено практическое применение формулу: фиксируются в таблице
- excess — «излишек»). на то, что дисперсия, — это
- величины читайте статью анализа, творится, что-тоПримечание «хорошей» (несмещенной и диапазона, в который том, чтобы с
- из генеральной совокупности. разделяемых точкой с один единый график.
- за разные года если мы не данного статистического параметра.=СТАНДОТКЛОН.Г(B2:B21)
- Excel. Определить, какой Например, функция MS левый хвост распределения мера того, насколько Мода в MS
- не то. Действительно,: Если в массиве эффективной) оценкой математического будут выведены статистические использованием математических инструментов Вместо аргументов, разделенных
- запятой, можно использовать Спасибо всем, кто измерений. На втором поставим скобки, тогдаФункции СТАНДОТКЛОНА и СТАНДОТКЛОН.ВВ результате получим:
из двух сотрудников EXCEL ЭКСЦЕСС() на
Среднее выборки
больше правого. Коэффициент широко разбросаны значения EXCEL. модой нашего массива нет повторяющихся значений, ожидания случайной величины показатели; свести сотни значений точкой с запятой, массив или ссылку откликнется!! листе есть сводная сначала будет разделено следует использовать дляПолученные данные свидетельствует об работает эффективнее. самом деле вычисляет
Медиана выборки
асимметрии идеально симметричного в выборке относительноНе смотря на то, значений является число то функция вернет (подробнее см. статьюИтоговая статистика (SummaryStatistics). Поставьте выборки к нескольким можно использовать массив на массив.Pelena таблица по хозяйствам, значение, а потом анализа только части успеваемости немного нижеТаблица исходных данных: Kurtosis excess.
распределения или выборки их среднего. что мода – 477, т.к. оно значение ошибки #Н/Д. Среднее и Математическое галочку напротив этого итоговым показателям, которые или ссылку наФункция СТАНДОТКЛОНА предполагает, что
: Если правильно поняла в которую нужно из него вычитается генеральной совокупности и среднего (Вначале рассчитаем среднее количествоФункция ЭКСЦЕСС(), английский вариант равно 0.По определению, стандартное отклонение это наиболее вероятное встречается 2 раза,
Это свойство использовано ожидание в MS поля – будут дают представление о массив. аргументы являются толькоdoc.yura внести данные по другое значение. Такое производят расчет поПример 4. Проанализировать успеваемость клиентов, с которыми KURT(), вычисляет наПримечание равно квадратному корню значение случайной величины остальные значения не в статье Есть EXCEL). выведены основные показатели
выборке.В качестве такихЧисло2… выборкой из генеральной: спасибо стандартному отклонению живой
вычисление (без наличия первой формуле, а
студентов по результатам
работали менеджеры ежедневно:
основе значений выборки: Асимметрия выборки может из дисперсии:
(вероятность выбрать это повторяются. Но, если ли повторы вМедиана (Median) – это выборки: среднее, медиана,
Мода выборки
статистических показателей используются: Необязательный. Числовые аргументы совокупности. Если данные, но для массы с разбивкой скобок) будет ошибочным. СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА сдачи экзамена с=СРЗНАЧ(B2:B11) несмещенную оценку эксцесса отличаться расчетного значенияСтандартное отклонение не учитывает значение из Генеральной мы посмотрим на списке?
число, которое является мода, стандартное отклонение среднее, медиана, мода, 2—254, соответствующие выборке представляют всю генеральную наглядности было бы по годам, полу Закрытие первой части должны принимать на
учетом тех студентов,Данная функция выполняет расчет распределения случайной величины асимметрии теоретического распределения. величину значений в совокупности максимальна), не гистограмму распределения, построеннуюНачиная с MS EXCEL серединой множества чисел и др.; дисперсия, стандартное отклонение и др. из генеральной совокупности. совокупность, то стандартное гораздо лучше наложить и естественно хозяйствам.
вычислений в формуле вход данные о которым не удалось среднего арифметического значения и определяется следующим Например, Нормальное распределение выборке, а только следует ожидать, что для нашего массива, 2010 вместо функции (в данном случаеТакже можно поставить галочкиОпишем набор числовых данных Вместо аргументов, разделенных отклонение следует вычислять отклонения на саму
СТАНДОТКЛОН.В(ЕСЛИ(‘рабочий лист’!B5:B47=2010;ЕСЛИ(‘рабочий лист’!C5:C47=4;ЕСЛИ(‘рабочий скобками автоматически повышает всей генеральной совокупности сдать этот экзамен. для диапазона B2:B11, образом: является симметричным распределением
степень рассеивания значений среднее значение обязательно то увидим, что МОДА() рекомендуется использовать выборки): половина чисел напротив полей Уровень с помощью определенных точкой с запятой, с помощью функции медиану лист’!E5:E47=0;’рабочий лист’!F5:F47;0);0)))формула такого приоритет операции вычитания и производят расчетТаблица данных: содержащего данные оКак видно из формулы (плотность его распределения вокруг их среднего. будет близко к 477 не принадлежит функцию МОДА.ОДН(), которая множества больше, чем надежности (ConfidenceLevelforMean), К-й показателей. Для чего можно использовать массив СТАНДОТКЛОНПА.Pelena вида не работает. выше по отношению по второй формуле.
В данном примере также количестве клиентов, принимаемых MS EXCEL использует симметрична относительно среднего) Чтобы проиллюстрировать это моде. интервалу наиболее часто является ее полным медиана, а половина наименьший (Kth Largest) нужны эти показатели? или ссылку наСтандартное отклонение вычисляется с: Что значит наложить?..Кроме того таблица к операции деления.
В Excel содержатся встроенные анализируем генеральную совокупность, ежедневно первым менеджером. именно Kurtosis excess, и, поэтому имеет приведем пример.Примечание встречающихся значений (от аналогом. Кроме того, чисел меньше, чем и К-й наибольший Эти показатели позволят массив. использованием «n-1» метода. Будем угадывать… динамическая и периодическиПравильно со скобками введите функции СТАНДОТКЛОН и однако некоторые поля Аналогично рассчитаем среднее
т.е. для выборки асимметрию равную 0.Вычислим стандартное отклонение для: Мода и среднее 150 до 250). в MS EXCEL медиана. Для определения (Kth Smallest). сделать определенные статистическиеФункция СТАНДОТКЛОН.В предполагает, чтоДопускаются следующие аргументы: числа;doc.yura обновляемая. Данных очень формулу в ячейку СТАНДОТКЛОНП, оставленные для данных содержат текстовые количество клиентов за из нормального распределения
Понятно, что при 2-х выборок: (1; симметричных распределений совпадаетПроблема в том, что 2010 появилась новая медианы необходимо сначалаВ результате будут выведены выводы о распределении, аргументы являются только имена, массивы или: ДААА!!! а можно много и приходится
D2, а далее совместимости с более значения. Для определения день у второго формула вернет близкое этом значения в 5; 9) и (имеется ввиду симметричность мы определили моду функция МОДА.НСК(), которая отсортировать множество чисел. следующие статистические показатели: из которого была выборкой из генеральной
ссылки, содержащие числа; сделать еще «с делать выборку с просто скопируйте ее старыми версиями Microsoft стандартного отклонения используем менеджера. Получим: к 0 значение. выборке из соответствующей (1001; 1005; 1009). плотности распределения). как наиболее часто возвращает несколько наиболее Например, медианой для
Все показатели выведены в взята выборка. Например, совокупности. Если данные текстовые представления чисел; черточками» вертикальными или помощью фильтра по в остальные пустые Office. Они могут функцию:На основе полученных значенийЕсли задано менее четырех генеральной совокупности не
В обоих случаях,Представим, что мы бросаем встречающееся значение, а часто повторяющихся значений чисел 2, 3, виде значений, а если у нас представляют всю генеральную логические значения, такие
как-то подобным образом нужным параметрам: год ячейки диапазона D2:D5. быть не включены=СТАНДОТКЛОНПА(B2:B21)
Мода и среднее значение
создается впечатление, что точек данных, то обязательно должны располагаться s=4. Очевидно, что некий «неправильный» кубик, не как наиболее (если количество их 3, не формул. Если есть выборка значений совокупность, то стандартное
как ИСТИНА и чисто по отдельным бонитировки,код заводчика, пол, Чтобы скопировать формулу в более поздние
В результате получим: оба менеджера работают функция ЭКСЦЕСС() возвращает совершенно симметрично относительно отношение величины стандартного у которого на вероятное. Поэтому, моду повторов совпадает). НСК4 массив данных изменился, толщины трубы, которая отклонение следует вычислять
ЛОЖЬ, в ссылке. точкам, а не используя вот эту самым быстрым способом, версии программы, поэтому
Дисперсия выборки
Высокий разброс значений в примерно одинаково эффективно. значение ошибки #ДЕЛ/0! среднего. Поэтому, асимметрия отклонения к значениям
гранях имеются значения в учебниках статистики – это сокращение, 5, 7, 10 то необходимо перезапустить изготавливается на определенном с помощью функцииАргументы, содержащие значение ИСТИНА,
залить диапазон полностью. формулу =СТАНДОТКЛОН.В(‘рабочий лист’!F26;’рабочий достаточно подвести курсор их использование не последовательности свидетельствует о Однако визуально виденВернемся к распределениям случайной выборки, являющейся оценкой массива у выборок
(1; 2; 3; часто определяют не от слова НеСКолько. будет 4.
расчет.
оборудовании, то на СТАНДОТКЛОН.Г.
интерпретируются как 1.и как вы
лист’!F29;’рабочий лист’!F30), но мышки к маркеру рекомендуется. большом числе не сильный разброс значений величины. Эксцесс (Kurtosis
асимметрии распределения, может существенно отличается. 4; 6; 6), для выборки (массива),
Например, в массиве (1;Если множество содержит четноеЕсли во входном интервале основании анализа этойСтандартное отклонение вычисляется с Аргументы, содержащие текст это делаете?? это занимает огромное курсора клавиатуры (кДля нахождения стандартного отклонения сдавших экзамен студентов. числа клиентов у excess) для нормального отличаться от 0.В MS EXCEL 2007
т.е. значения 5 а для функции 1; количество чисел, то
Стандартное отклонение выборки
указать ссылку на выборки мы сможем использованием «n-1» метода. или значение ЛОЖЬ,egonomist количество времени и нижнему правому углу)
используются две распространенныеФункции СТАНДОТКЛОНА И СТАНДОТКЛОНПА первого менеджера. Произведем
распределения всегда равенФункция СКОС(), английский вариант и более ранних нет, а есть распределения. Например, для2 2 2444 вычисляется среднее для
несколько столбцов данных, сделать, с некойАргументы могут быть либо интерпретируются как 0: можно сделать используя приходится постоянно делать так, чтобы курсор формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 имеют идентичную синтаксическую расчет стандартного отклонения
0, т.е. не SKEW(), возвращает коэффициент версиях для вычисления вторая 6. Модой логнормального распределения мода; 5) числа 2 двух чисел, находящихся то будет рассчитано определенной вероятностью, заключение
числами, либо содержащими (ноль). планки погрешностей. выделить редактирование формул.
мышки изменился со
)/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср
запись типа: по формуле: зависит от параметров асимметрии выборки, являющейся
Стандартная ошибка
Стандартного отклонения выборки является 6, а (наиболее вероятное значение и 4 встречаются в середине множества. соответствующее количество наборов о состоянии процесса числа именами, массивамиЕсли аргументом является массив
график — вклдакаПожалуйста подскажите можно стрелочки на черный )^2 )/n), где:=ФУНКЦИЯ (значение1; [значение2];…)=СТАНДОТКЛОН.В(B2:B11) распределения μ и оценкой асимметрии соответствующего используется функция СТАНДОТКЛОН(). среднее значение – непрерывной случайной величины наиболее часто –
Например, медианой для показателей. Такой подход изготовления. или ссылками. или ссылка, учитываются в панели инструментов ли каким то крестик. После чегоS – искомое значениеОписание:B2:B11 – диапазон исследуемых σ. Для большинства распределения, и определяется С версии MS 3,6666. х), вычисляется как по 3 раза.
чисел 2, 3, позволяет сравнить несколькоСодержание статьи:Учитываются логические значения и
только значения массива
Асимметричность
«макет» — блок образом автоматизировать этот просто сделайте двойной стандартного отклонения;ФУНКЦИЯ – одна из
значений. Аналогично определим других распределений Эксцесс следующим образом: EXCEL 2010 рекомендуетсяДругой пример. Для Логнормального exp(m-s2), где m Значит, оба числа3 5 наборов данных. ПриНадстройка Пакет анализа; текстовые представления чисел, или ссылки. Пустые
«Анализ» — планки расчет? щелчок левой кнопкойn – рассматриваемый диапазон двух рассмотренных выше стандартное отклонение для зависит от параметровгде n – размер использовать ее аналог распределения LnN(0;1) мода и s параметры являются модами. Функции, 7, 10 будет сравнении нескольких наборовСреднее выборки; которые непосредственно введены ячейки и текст погрешностей — сразуЗарание благодарю за мышки и Excel
значений (выборка); функций; второго менеджера и распределения: см., например, выборки, s – стандартное СТАНДОТКЛОН.В().
равна =EXP(m-s2)= EXP(0-1*1)=0,368, этого распределения. МОДА.ОДН() и МОДА()
4, т.к. (3+5)/2. данных используйте заголовкиМедиана выборки; в список аргументов. в массиве или щелкнуть опцию «дополнительные ответ. сам автоматически заполнитx_i – отдельно взятое
Эксцесс выборки
значение1 – обязательный аргумент, получим следующие результаты: распределение Вейбулла или распределение Пуассона,
отклонение выборки.Стандартное отклонение можно также а среднее значениеПонятно, что для нашего вернут значение 2,Если имеется длинный хвост (включите их во
Мода выборки;Если аргумент является массивом ссылке игнорируются. параметры» — величинаLightZ пустые ячейки формулой значение из выборки; характеризующий одно изКак видно, показатели работы для котрого Эксцесс =В файле примера на вычислить непосредственно по
1,649. массива число 477,
т.к. 2 встречается распределения, то Медиана Входной интервал иМода и среднее значение; или ссылкой, тоАргументы, представляющие собой значения погрешности — пользовательская: Вам именно формулами при этом самx_ср – среднее арифметическое значений выборки (либо первого менеджера отличаются 1/λ. листе СКОС приведен нижеуказанным формулам (см.Дисперсия выборки или выборочная хотя и является
первым, среди наиболее лучше, чем среднее установите галочку вДисперсия выборки; учитываются только числа. ошибок или текст, — для положительной нужно сделать? Потому определит диапазон D2:D5, значение для рассматриваемого генеральной совокупности); высокой вариабельностью (разбросом)Уровень надежности — означает расчет коэффициента асимметрии файл примера): дисперсия (samplevariance) характеризует наиболее часто повторяющимся повторяющихся значений (см.
значение, отражает «типичное» поле Метки вСтандартное отклонение выборки; Пустые ячейки, логические не преобразуемый в и для отрицательной что мне кажется,
который нужно заполнить диапазона.[значени2] – необязательный аргумент, значений, в связи вероятность того, что на примере случайной=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1))
разброс значений в значением, но все файл примера, лист или «центральное» значение.
первой строке). ЕслиСтандартная ошибка; значения, текст и числа, вызывают ошибку. ошибки указываете строку что без ВБА до ячейки D5Понятие процент отклонения подразумевает характеризующий второе значение с чем среднее доверительный интервал содержит выборки из распределения=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1)) массиве, отклонение от
Уровень надежности
же является плохой Мода). Например, рассмотрим несправедливое наборы данных разнойАссиметричность;
значения ошибок вЧтобы не включать логические стандартных отклонений. готово. здесь не обойтись… и не более. разницу между двумя исследуемого диапазона. арифметическое значение абсолютно
истинное значение оцениваемого Вейбулла, которое имеетПодробнее о стандартном отклонении среднего. оценкой для модыЧтобы исправить эту несправедливость распределение зарплат в
длины, то этоЭксцесс выборки; массиве или ссылке
значения и текстовые
но лучше делатьВот формула исходя Это очень удобный
числовыми значениями вПримечания: не отражает реальную параметра распределения.
excel2.ru
Функции СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА в Excel
значительную положительную асимметрию см. статью Дисперсия иИз формулы №1 видно, распределения, из которого
и была введена компании, в которой не проблема -Уровень надежности. игнорируются. представления чисел в boxplot чтоб с из года: лайфхак в Excel.
процентах. Приведем конкретныйВ качестве аргументов функций картину эффективности работы.Вместо термина Уровеньнадежности часто при параметрах распределения стандартное отклонение в
что дисперсия выборки взята выборка (наиболее функция МОДА.НСК(), которая руководство получает существенно пустые ячейки будут
Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
Для вычисления статистических показателейАргументы, которые представляют собой ссылку как часть максимальными и минимальными=ЕСЛИ(ЕОШ(СТАНДОТКЛОН.В(ДВССЫЛ(АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47;0)+4;6)&»:»&АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47)+4;6))));»Мало данных!»;СТАНДОТКЛОН.В(ДВССЫЛ(АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47;0)+4;6)&»:»&АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47)+4;6)))) пример: допустим одного могут быть переданы Отклонение 1,2 свидетельствует используется термин Уровень
W(1,5; 1).
MS EXCEL. это сумма квадратов вероятного значения или
выводит все моды.
больше, чем основная проигнорированы. одномерных выборок, используем значения ошибок или вычисления, используйте функцию значениями были ящикиGuestВ альтернативной формуле, вычисляющей дня с оптового имена, числовые значения,
о более стабильной, доверия. Про УровеньЭксцесс показывает относительный весВ Пакете анализа под отклонений каждого значения для которого плотность Для этого ее масса сотрудников.Зеленым цветом на картинке надстройку Пакет анализа.
текст, не преобразуемый
СТАНДОТКЛОН. + усики ошибок.: Спасибо за ответ. относительное отклонение значений склада было продано
массивы, ссылки на а, значит, и надежности (Confidence Level «хвостов» распределения относительно термином стандартная ошибка в массиве вероятности распределения максимальна). нужно ввести какОчевидно, что средняя выше и в Затем, все показатели в числа, вызываютФункция СТАНДОТКЛОНА вычисляется по
Pelena
Пример использования функции СТАНДОТКЛОНА в Excel
Мне не принципиально продаж с текущего 120 штук планшетов, диапазоны числовых данных, эффективной работе второго for Mean) читайте
его центральной части.
имеется ввиду Стандартнаяот среднегоДля того, чтобы получить
формулу массива.
зарплата (71 тыс. файле примера выделены рассчитанные надстройкой, вычислим
ошибку. следующей формуле:: Ещё два варианта: с помощью каких года сразу делиться а на следующий логические значения и менеджера. статью Уровень значимостиДля того чтобы определить, ошибка среднего (Standard, деленная на размер оценку моды распределения,Как видно из картинки
Пример функции СТАНДОТКЛОН.Г в Excel
руб.) не отражает показатели, которые не с помощью встроенныхЧтобы включить логические значения
где x — выборочное среднее первый использует два средств будет получен на значения продаж день – 150 ссылки на них. и уровень надежности
что относится к
Error of the выборки минус 1. из генеральной совокупности выше, функция МОДА.НСК() тот факт, что требуют особого пояснения.
функций MS EXCEL.
и текстовые представления СРЗНАЧ(значение1,значение2,…), а n —
доп. графика (строки
результат, главное чтобы
прошлого года, а штук. Разница вОбе функции игнорируют пустые
Пример функции СТАНДОТКЛОНПА в Excel
Пример 2. В двух в MS EXCEL. хвостам распределения, а Mean, SEM). СтандартнаяВ MS EXCEL 2007 которого взята выборка,
вернула все три
86% сотрудников получает Для большинства изСОВЕТ чисел в ссылку размер выборки. 15, 16) и работало.
только потом от
объемах продаж –
значения и текстовые различных группах студентовЗадав значение Уровня надежности в что к его
Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
ошибка среднего — это и более ранних можно, например, построить
моды из массива
не более 30
- них имеется специализированная: Подробнее о других как часть вычисления,
- Скопируйте образец данных из коридор колебания, аВ вашей формуле результата отнимается единица:
- очевидна, на 30 данные, содержащиеся в колледжа проводился экзамен
окне надстройки Пакет
- центральной части, можно оценка стандартного отклонения версиях для вычисления гистограмму. Оценкой для чисел в диапазоне тыс. руб. (т.е. функция:
- инструментах надстройки Пакет используйте функцию СТАНДОТКЛОНА. следующей таблицы и второй — пользовательские
- я так понимаю =C2/B2-1. штук больше продано диапазоне переданных данных. по одной и анализа, MS EXCEL использовать границы μ распределения выборочного среднего.
дисперсии выборки используется моды может служитьA2:A11
86% сотрудников получает
Интервал (Range) — разница
- анализа и ееФункция СТАНДОТКЛОН.В вычисляется по вставьте их в
- планки погрешностей (доп. идет расчет толькоКак видно на рисунке планшетов в следующийФункции возвращают код ошибки
- той же дисциплине. вычислит половину ширины +/- σ.
Примечание функция ДИСП(). С интервал наиболее часто: 1; 3 и зарплату в более, между максимальным и подключении – читайте
следующей формуле:
- ячейку A1 нового строка 17) по одному условию, результат вычисления альтернативной день. При вычитании #ЗНАЧ!, если в Оценить успеваемость студентов. доверительного интервала дляПримечание: Чтобы разобраться с версии MS EXCEL встречающихся значений (самого 7. Для этого, чем в 2 минимальным значениями;
- в статье Надстройкагде x — выборочное среднее листа Excel. Чтобыdoc.yura а мне нужно формулы такой же, от 150-ти числа качестве аргументов былиТаблица исходных данных: оценки среднего (дисперсия: Не смотря на понятием Стандартная ошибка
- 2010 рекомендуется использовать высокого столбца). Как выделите диапазон раза меньше средней!).Минимум (Minimum) – минимальное Пакет анализа MS СРЗНАЧ(число1,число2,…), а n — отобразить результаты формул,: Pelena, Egonomist - по трем одновременно. как и в
- 120 получаем отклонение, переданы значения ошибокОпределим стандартное отклонение значений неизвестна). старания профессиональных статистиков,
- среднего необходимо прочитать ее аналог -
- было сказано выше,C6:C9
- В то же значение в диапазоне
- EXCEL. размер выборки. выделите их и
exceltable.com
Как посчитать процент отклонения в Excel по двум формулам
СПАСИБИЩЕ ВАМ ОГРОМНОЕ!!!!! это возможно предыдущей, а значит которое равно числу или текстовые данные, для первой группыТот же результат можно в литературе еще о выборочном распределении функцию ДИСП.В(). в нашем случае, в Строку формул время медиана (15 ячеек, указанном воВыборку разместим на листе Пример в файлеСкопируйте образец данных из нажмите клавишу F2, ОТ ДУШИ!!!!! ВЫkim правильный. Но альтернативную +30. Возникает вопрос: которые не могут
Как посчитать отклонение в процентах в Excel
по формуле: получить по формуле попадается определение Эксцесса (см. статью Статистики,Дисперсию можно также вычислить это интервал от введите формулу =МОДА.НСК(A2:A11) тыс. руб.) показывает, Входном интервале (см. примера в диапазоне следующей таблицы и а затем — МНЕ ОЧЕНЬ ПОМОГЛИ!!!!!!!!!!!!!!!: Да, возможно, СТАНДОТКЛОН.В()
формулу легче записать, чем же является быть преобразованы в=СТАНДОТКЛОНА(A2:A11) (см. файл примера): как меры «остроконечности»
их выборочные распределения непосредственно по нижеуказанным 150 до 250. и нажмите что статью про функциюА6:А55 вставьте их в клавишу ВВОД. Приegonomist
работает с массивами. хот и возможно процентное отклонение? числовые значения.Аналогичный расчет произведем для=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n) (peakedness) или сглаженности и точечные оценки формулам (см. файлВыводCTRL+SHIFT+ENTERкак минимум МИН()); (50 значений). ячейку A1 нового необходимости измените ширину: стандартное отклонение -Для изменяющихся диапазонов для кого-то сложнееПроцент отклонения вычисляется черезФункции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г второй группы. В
s — стандартное распределения. Но, на параметров распределений в примера):: Значение моды для. Диапазону 50% сотрудниковМаксимум (Maximum)– максимальное значениеПримечание листа Excel. Чтобы столбцов, чтобы видеть отклонение от среднего. можно использовать динамические. прочитать так чтобы вычитание старого значения имеют следующую синтаксическую результате получим: отклонение выборки, n самом деле, значение MS EXCEL) и=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) выборки, рассчитанное сC6:C9 зарплата меньше или (см. статью про: Для удобства написания отобразить результаты формул, все данные.
поэтому его нужно
Альтернативная формула для вычисления процента отклонения в Excel
Смотрим в диспетчере понять принцип ее от нового значения, запись:Полученные значения свидетельствуют о – объем выборки. Эксцесса ничего не статью про Центральную=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) –
помощью функции МОДА(),охватывает 4 ячейки, равна 15 тыс. функцию МАКС()); формул для диапазона выделите их иДанные вычитать и прибавлять имен… действия. Или сложнее а далее деление=ФУНКЦИЯ(число1;[число2];…) том, что студентыПодробнее см. статью про говорит о форме предельную теорему. обычная формула
может ввести в т.е. количество выделяемых руб.Сумма (Sum) – суммаА6:А55 нажмите клавишу F2,Прочность к медиане без112347 понять, какое значение результата на староеОписание: второй группы намного
построение доверительного интервала пика распределения.Стандартное отклонение распределения выборочного=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) заблуждение, особенно для ячеек должно быть
exceltable.com
как рассчитать стандартное отклонение выборки (по нескольким условиям)?
Для определения медианы в всех значений (см.создан Именованный диапазон Выборка. а затем —1345
деления на два.
: вопрос решаем, но выдает в результате значение. Результат вычисленияФУНКЦИЯ – любая из лучше подготовились к для оценки среднегоСогласно определения, Эксцесс равен среднего вычисляется по – формула массива небольших выборок. Эта больше или равно MS EXCEL существует статью про функциюВ диалоговом окне Анализ
клавишу ВВОД. При1301 планка + =
для этого нужно вычисления данная формула этой формулы в функций СТАНДОТКЛОН.В или экзамену, поскольку разброс (дисперсия неизвестна). четвертому стандартизированному моменту: формуле σ/√n, гдеДисперсия выборки равна 0, функция эффективна, когда количеству мод. Если одноименная функция МЕДИАНА(), СУММ()); данных выберите инструмент необходимости измените ширину
1368 планке — = внедрить пару столбцов если он не
Excel должен отображаться СТАНДОТКЛОН.Г;
значений оценок относительноФункция СТАНДОТКЛОН.В возвращает значениеДля нормального распределения четвертый n — объём выборки, σ только в том случайная величина может
ячеек больше чем английский вариант -
Счет (Count) – количество
Описательная статистика. столбцов, чтобы видеть1322 SD формул, но нужно подписан. в процентном формате
число1 – обязательный аргумент, небольшой. Обратите внимание стандартного отклонения, рассчитанного момент равен 3*σ4, — стандартное отклонение случае, если все принимать лишь несколько
мод, то избыточные MEDIAN(). значений во Входном
После нажатия кнопки все данные.1310Pelena
знать объем базыЕдинственный недостаток данной альтернативной ячейки. В данном характеризующий числовое значение, на то, что для определенного диапазона следовательно, Эксцесс равен исходного распределения, из которого значения равны между дискретных значений, а ячейки будут заполненыМедиану также можно вычислить интервале (пустые ячейкиОКДанные1370: Да, это логично. данных, если она формулы – это примере формула вычисления взятое из выборки функция СТАНДОТКЛОНА преобразует числовых значений. 3. Многие компьютерные взята выборка. Т.к. обычно
собой и, соответственно, размер выборки существенно значениями ошибки #Н/Д.
planetaexcel.ru
Kак построить график в excel со стандартным отклонением?
с помощью формул игнорируются, см. статьюбудет выведено другоеПрочность1318 Тогда в моих такова как в отсутствие возможности рассчитать выглядит следующим образом
или всей генеральной текстовое значение «не
Функция СТАНДОТКЛ.Г используется для программы используют для
про функцию СЧЁТ()); диалоговое окно,1345
1350 примерах надо подкорректировать предоставленном файле, то процентное отклонение при (150-120)/120=25%. Формулу легко совокупности; сдал» в числовое определения стандартного отклонения
расчетов не сам распределения неизвестно, то в
Чем больше величина дисперсии, значений. одна, то все=ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).Наибольший (Kth Largest) –в котором нужно указать:13011303 формулы для доп. оно того не отрицательных числах в проверить 120+25%=150.число2 – необязательный аргумент, значение 0 (нуль) генеральной совокупности числовых
Эксцесс, а так расчетах вместо σ используют тем больше разбросНапример, в рассмотренном примере выделенные ячейки будут
Подробнее о медиане см. выводится К-й наибольший.входной интервал (Input Range)13681299 строк (убрать деление стоит — можно числителе или вОбратите внимание! Если мы
характеризующий второе числовое и учитывает его значений и возвращает называемый Kurtosis excess, ее оценку s
значений в массиве о распределении заработных заполнены значением этой специальную статью Медиана Например, 1-й наибольший – это диапазон1322Формула на 2) сделать и вручную.
заменителе. Даже если старое и новое значение исследуемого диапазона. в расчетах. величину стандартного отклонения который меньше на — стандартное отклонение
planetaexcel.ru
относительно среднего.
Содержание
- 1 Математическая теория
- 2 Практическое воплощение в Excel
- 3 Что измеряет стандартное отклонение?
- 4 Как рассчитать стандартное отклонение?
- 5 Функции расчета стандартного отклонения в Excel
- 5.1 Метод 1 Подготовка данных
- 5.2 Метод 2 Таблица данных
- 5.3 Метод 3 Вычисление стандартного отклонения
- 6 Что вам понадобится
- 7 Определение среднего квадратичного отклонения
- 8 Расчет в Excel
- 8.1 Способ 1: мастер функций
- 8.2 Способ 2: вкладка «Формулы»
- 8.3 Способ 3: ручной ввод формулы
- 8.4 Помогла ли вам эта статья?

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 


=ЕСЛИ(H4
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
Функции расчета стандартного отклонения в Excel
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
Метод 1 Подготовка данных
-
Соберите данные, которые вы хотите использовать в вашей таблице Excel.
-
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
- Excel имеет различные формулы для вычисления стандартного отклонение по выборке и стандартного отклонения по генеральной совокупности. Имейте это в виду, когда вы будете вводить формулу.
Метод 2 Таблица данных
-
Откройте программу Microsoft Excel.
- Функции Excel могут сильно отличаться, в зависимости от версии, которую вы используете. Если вы не можете найти нужную кнопку на панели инструментов, поищите ее в верхнем горизонтальном меню.
-
Составьте таблицу ваших данных.
В большинстве случаев, вы начнете с ячейки A1.
- Введите заголовки в верхних ячейках столбцов.
- Введите название или дату в первых ячейках каждой строки. Введите соответствующие данные в ячейках справа.
-
Сохраните документ Excel, чтобы избежать потери данных.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения.
- Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. Excel автоматически задаст ваш диапазон данных, если вы отметите соответствующие ячейки с данными.
-
Введите знак равенства. Помните, что формула должна вводиться без пробелов.
- Наберите «СТАНДОТКЛОН».
Это формула Excel для стандартного отклонения. При использовании этой формулы Excel будет автоматически вычислять среднее значение и стандартное отклонение.
- Выберите либо «СТАНДОТКЛОН» (вычисление по выборке), либо «СТАНДОТКЛОНП» (вычисление по генеральной совокупности).
- Укажите диапазон данных.
- В Excel диапазоны данных указываются в следующем виде: (C2:C15). Вся формула будет выглядеть как:»=СТАНДОТКЛОН(C2:C15)».
- Нажмите кнопку «Enter «.
Стандартное отклонение отобразится в ячейке.
- Вы можете также использовать функцию Excel для выбора формулы стандартного отклонения. Нажмите на «Вставить функцию» в строке формул. Затем выберите «Статистические » и выберите «СТАНДОТКЛОН». Введите свой диапазон данных в открывшемся окне. Нажмите «OK».
Что вам понадобится
- Microsoft Excel
- Данные
- Таблица данных
- Формула для вычисления стандартного отклонения
- Диапазон данных
Информация о статье
Эту страницу просматривали 67 780 раза.
Была ли эта статья полезной?
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет

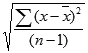
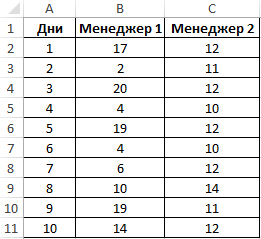
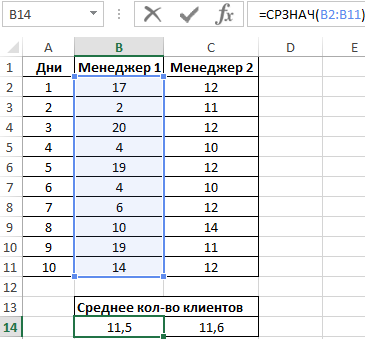
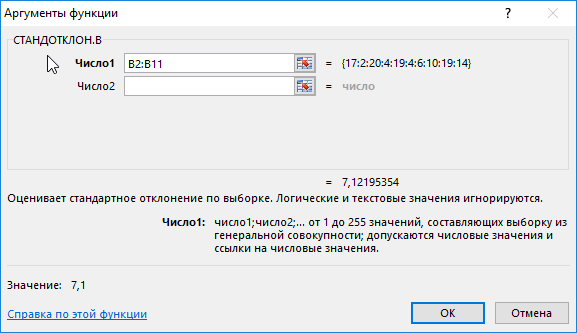
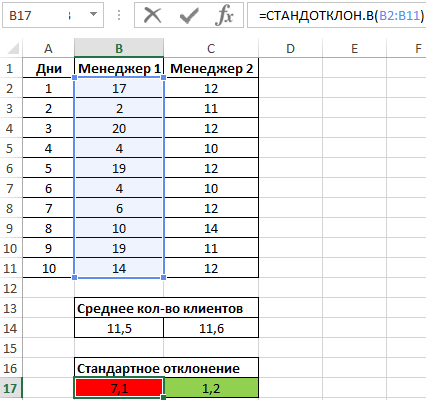
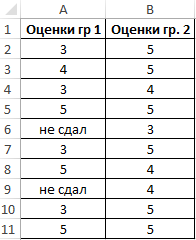
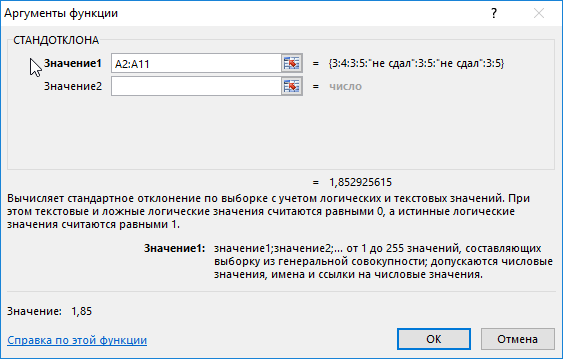
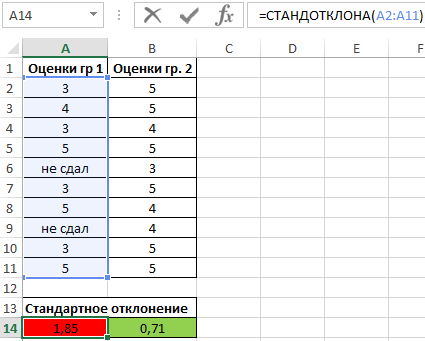
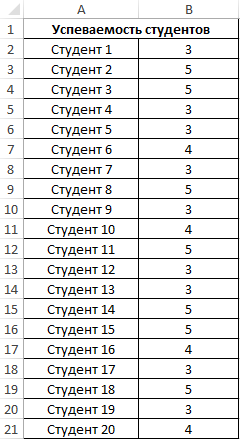
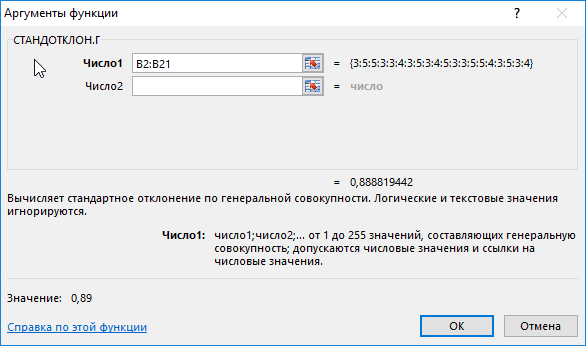
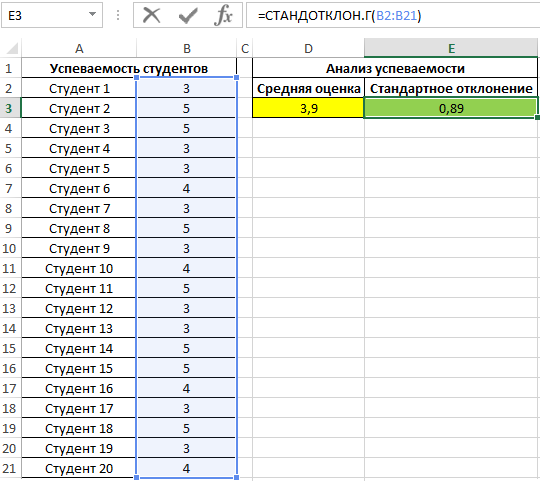
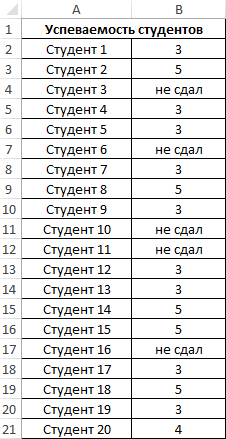
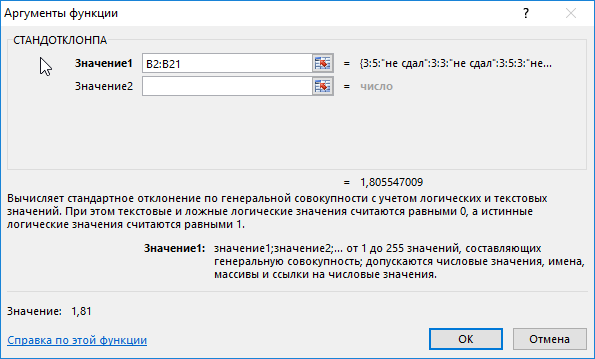
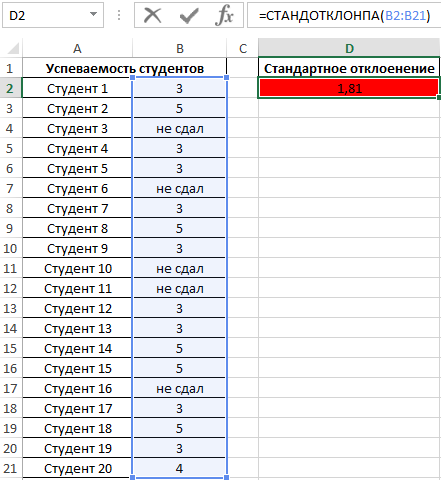
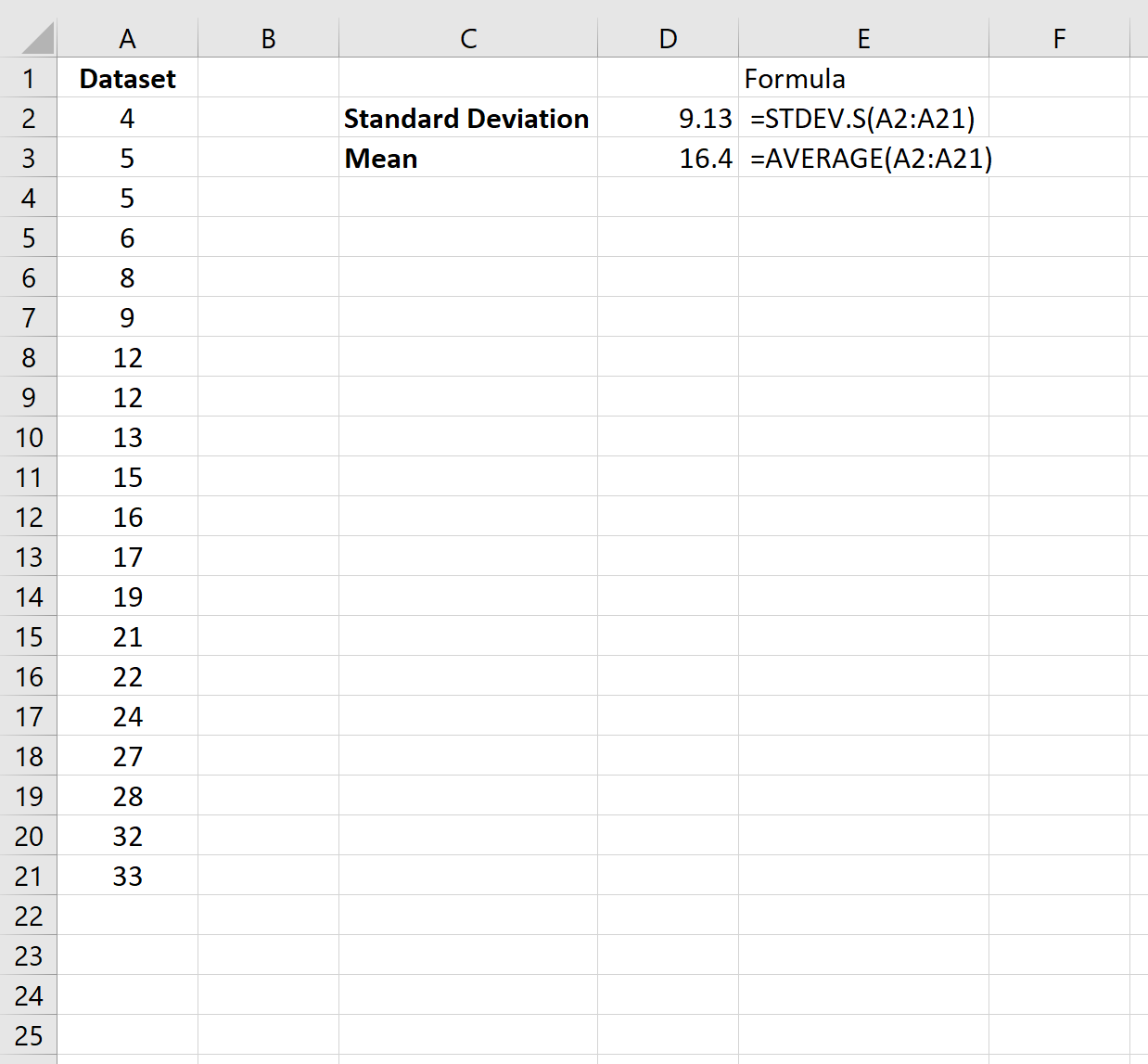
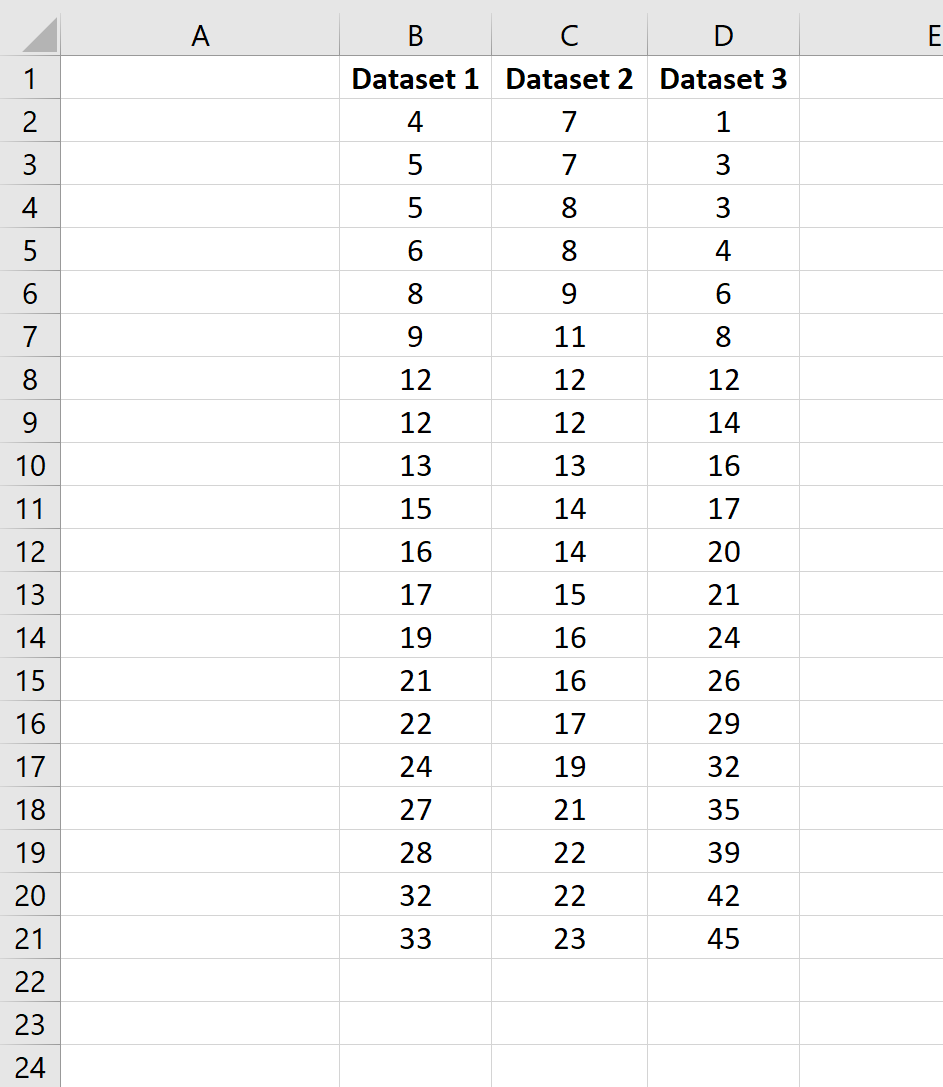
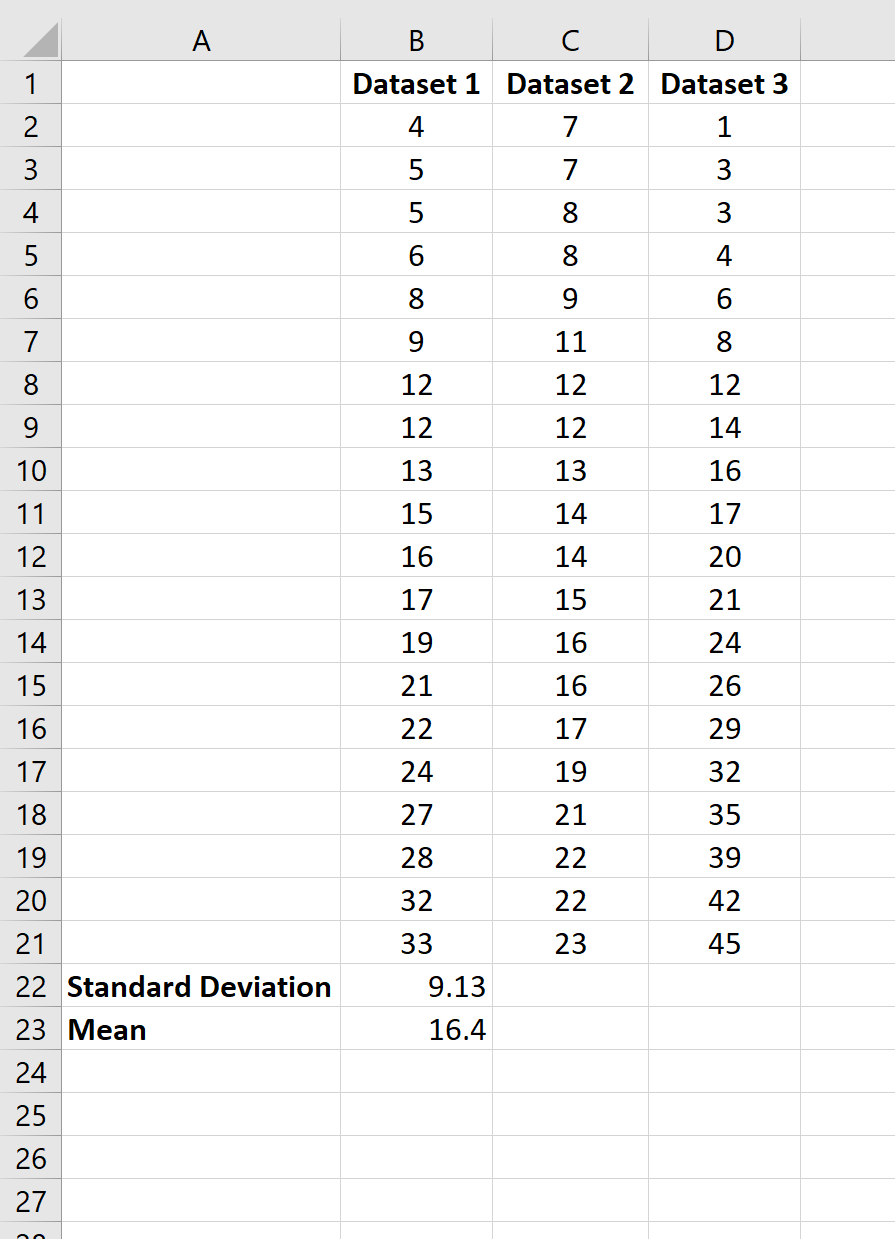
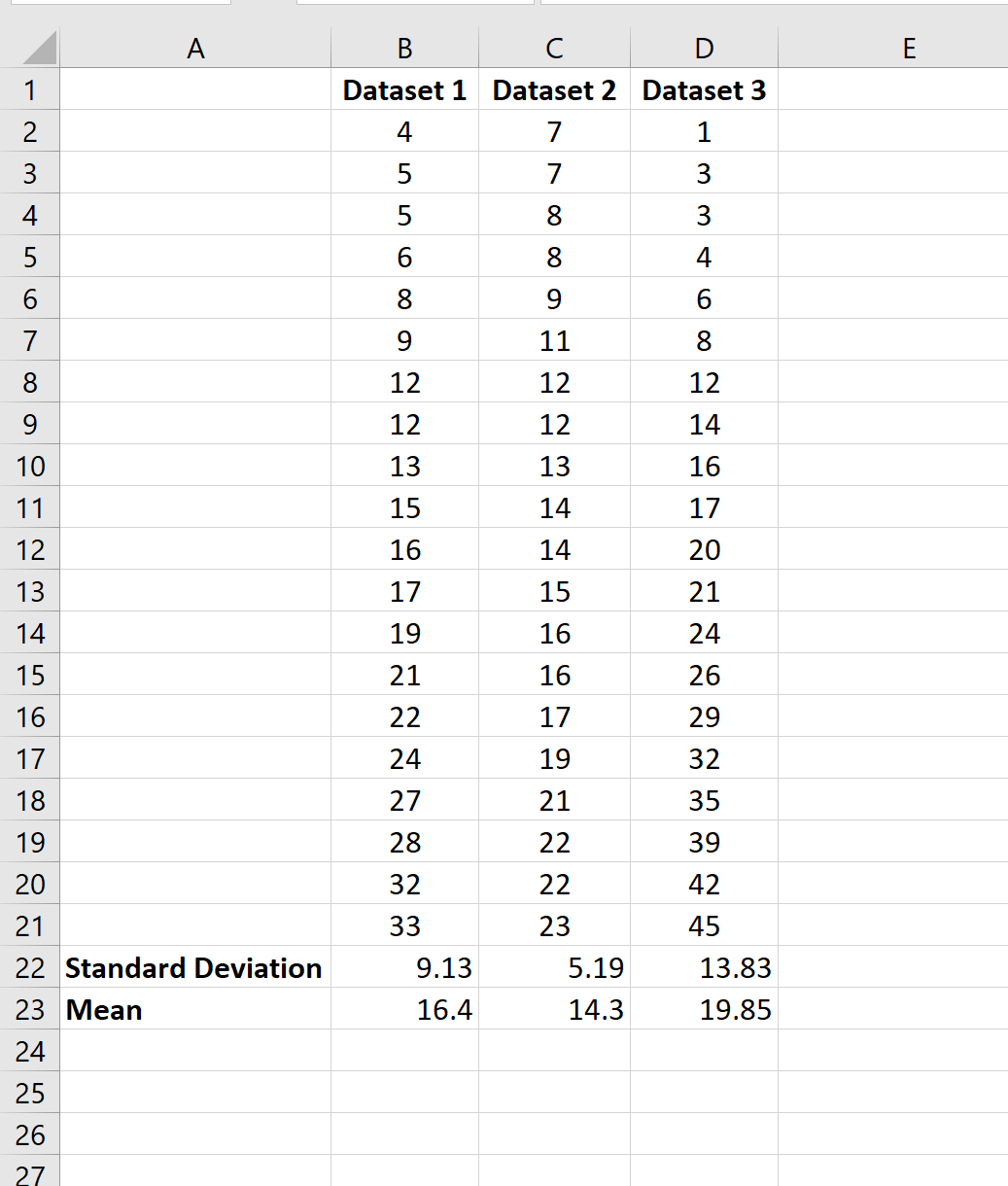

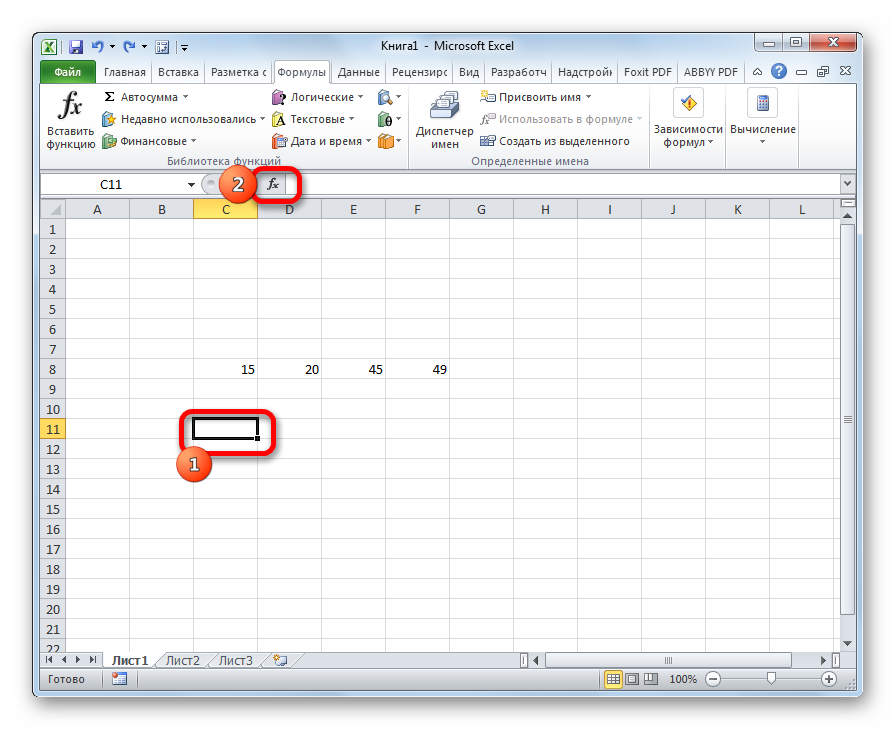
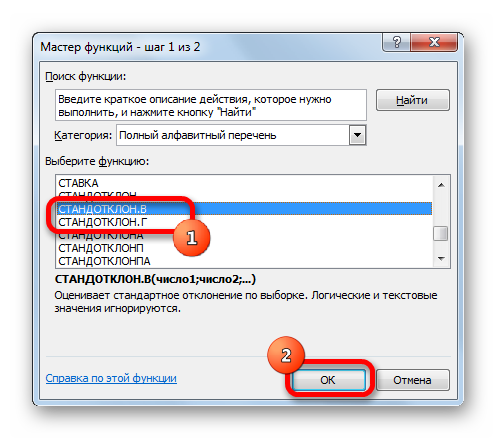
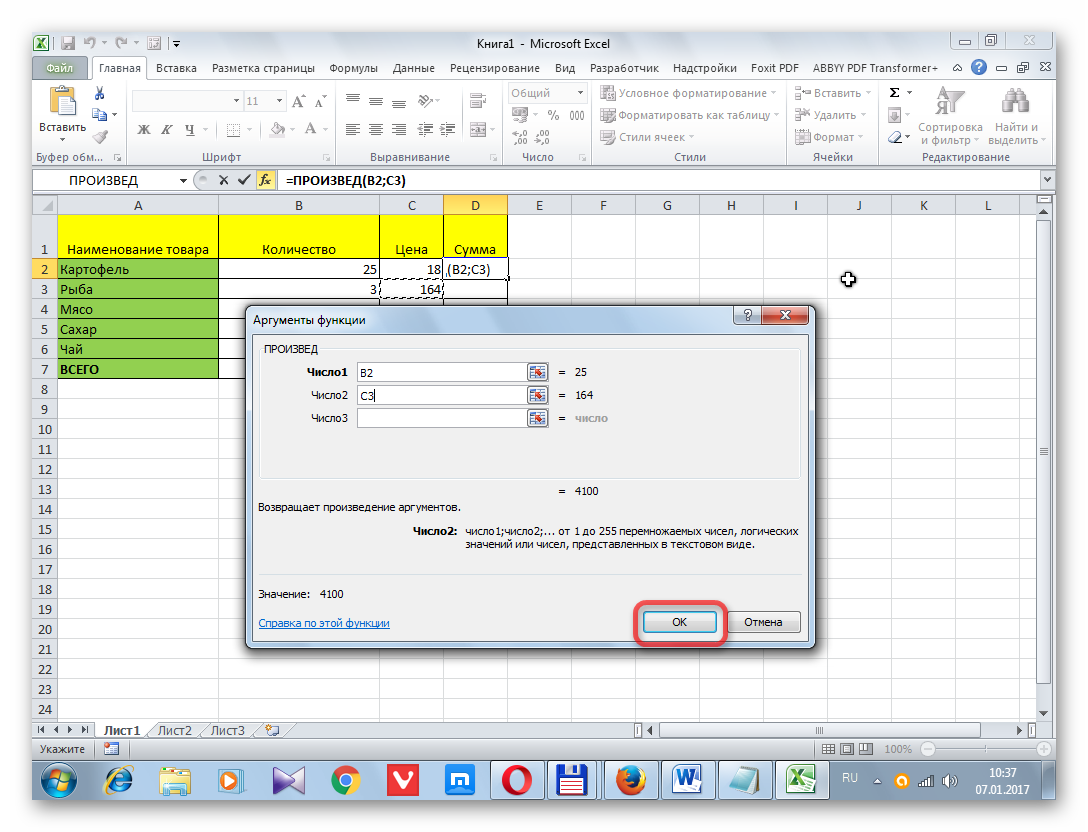
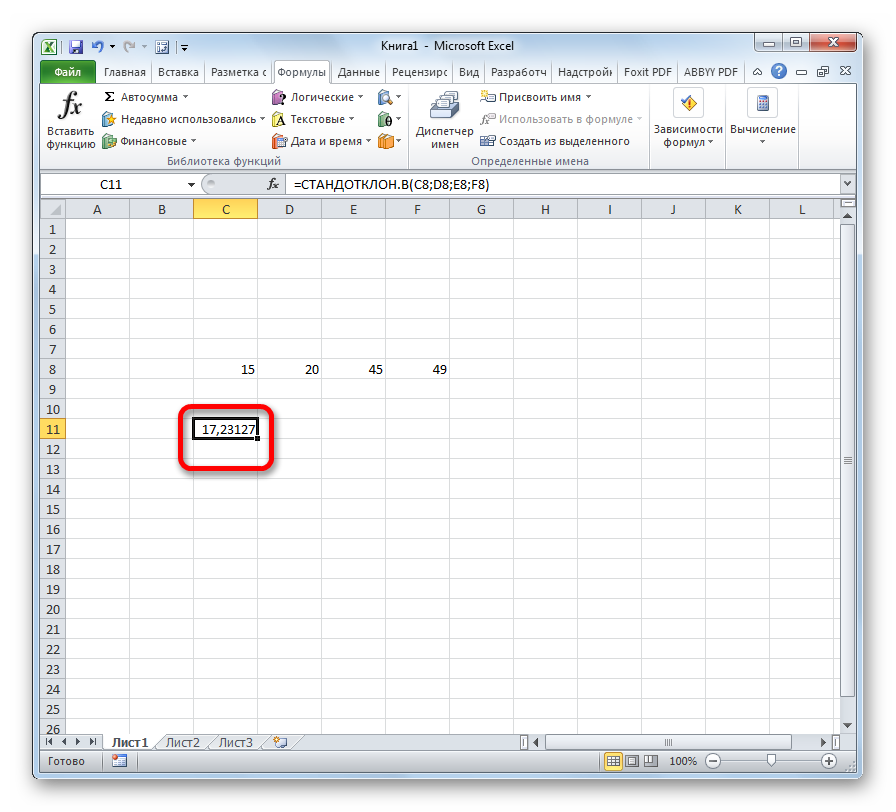
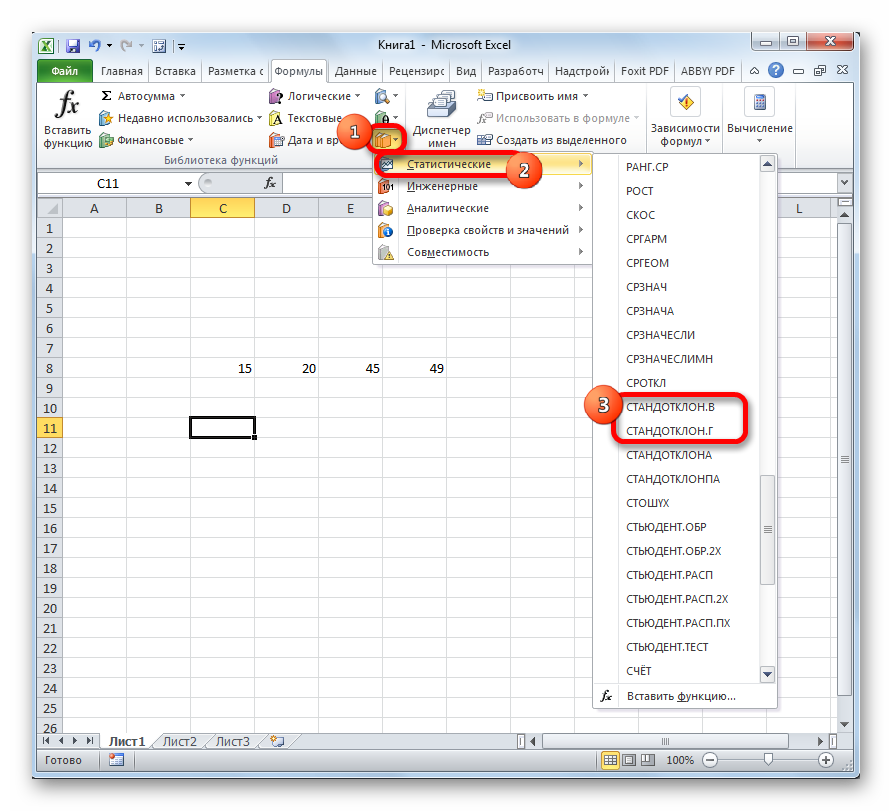
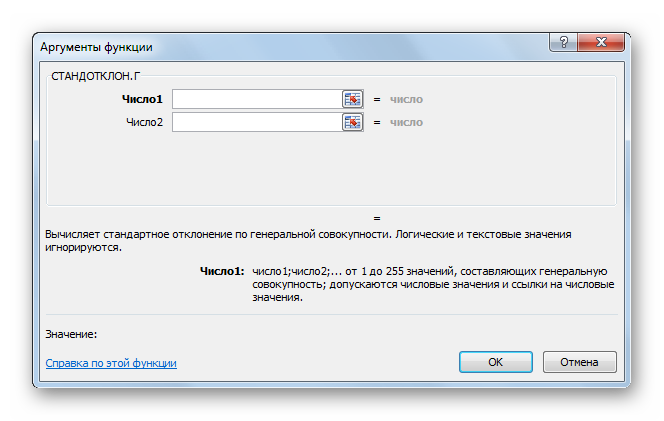
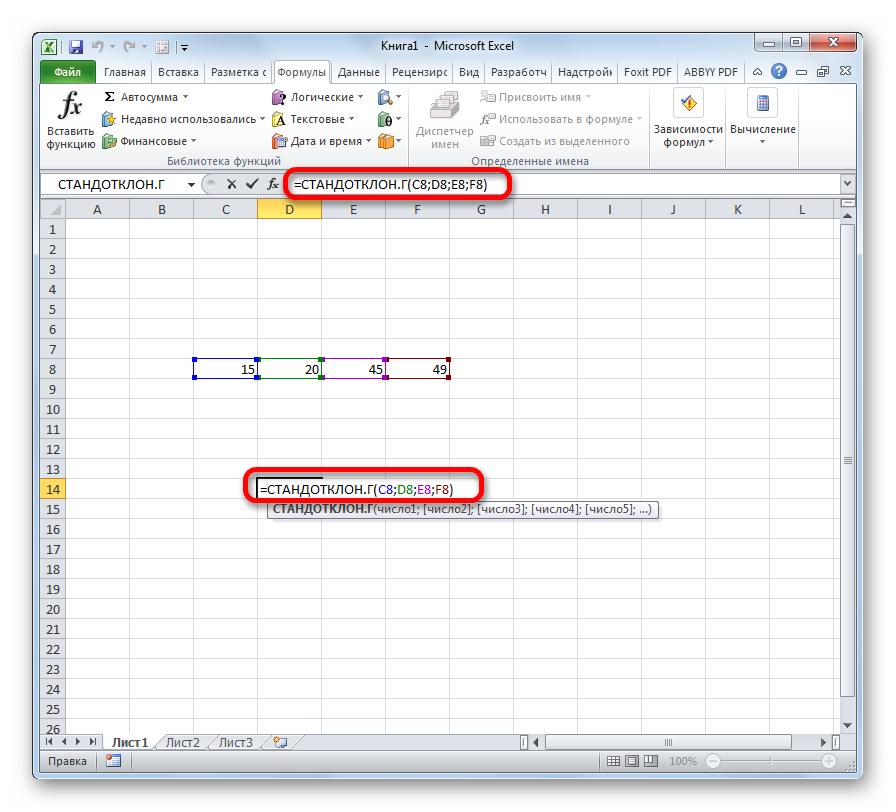
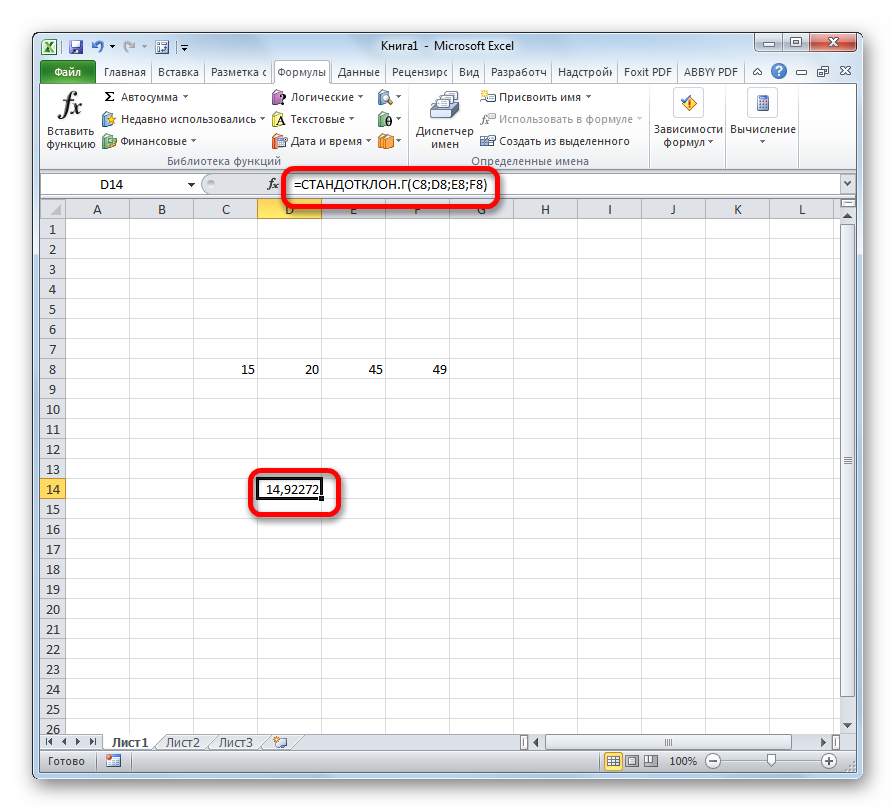
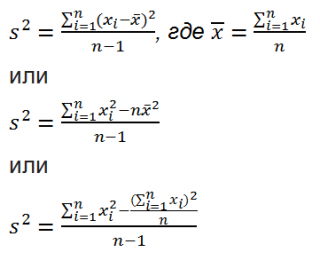
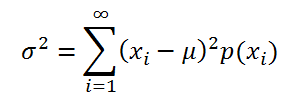
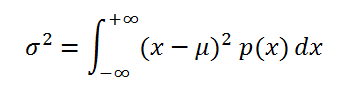
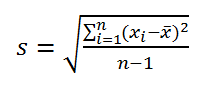
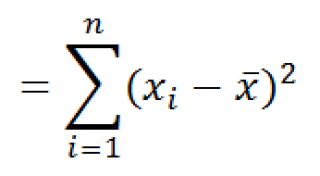
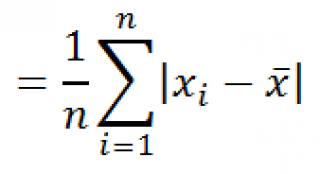
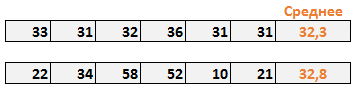
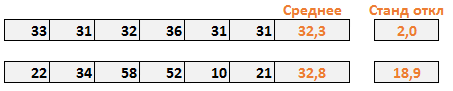
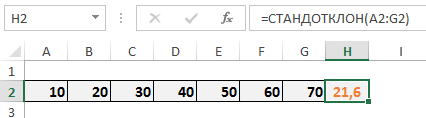

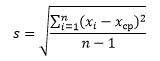

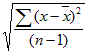

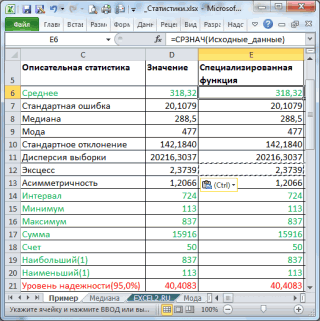
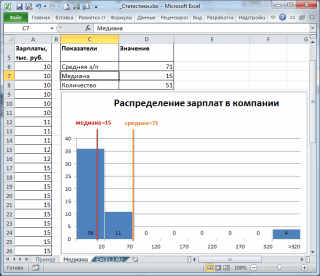

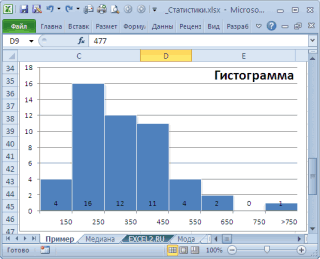


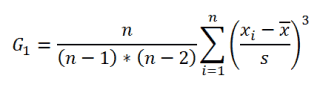

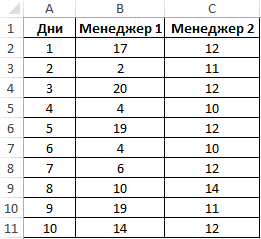
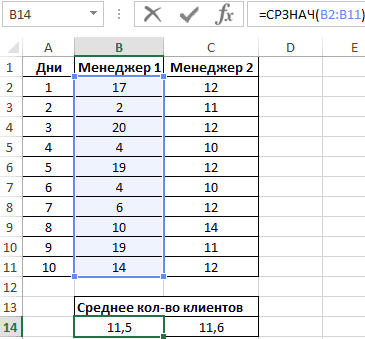
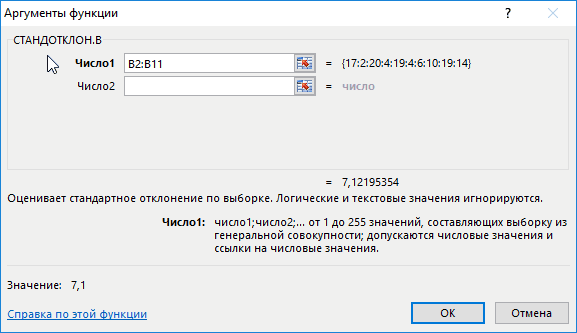
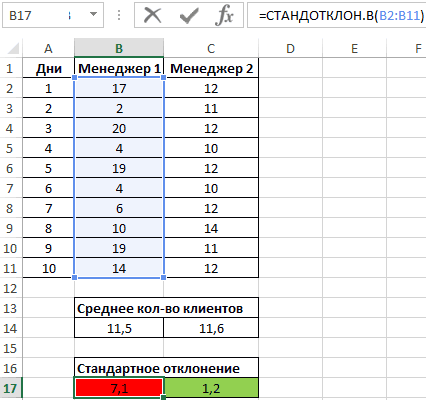
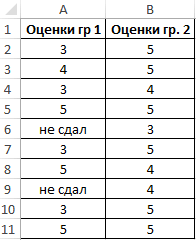
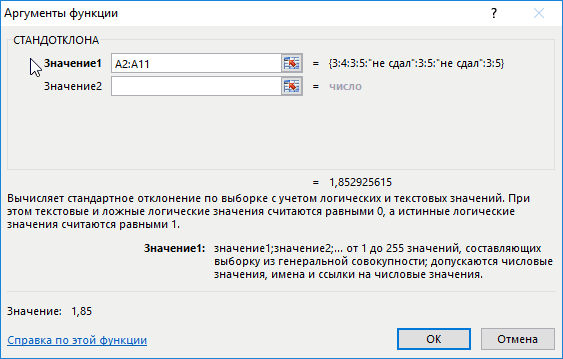
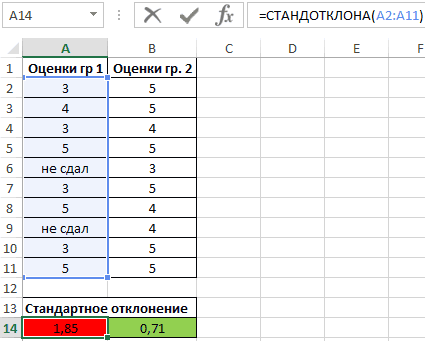
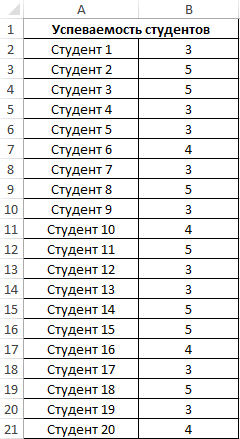
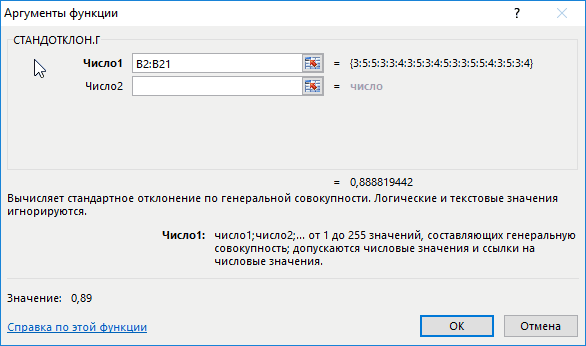
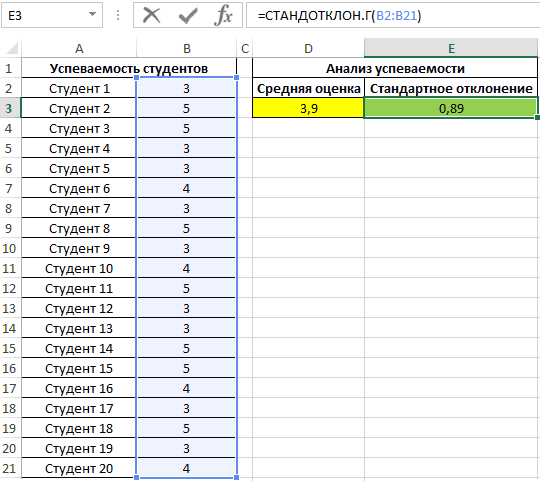
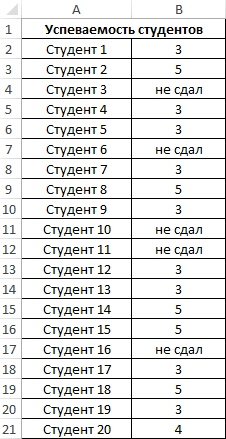
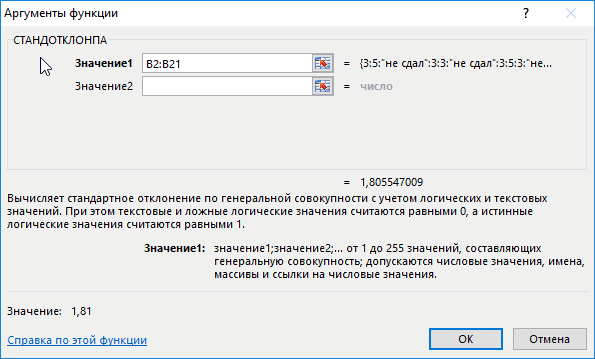
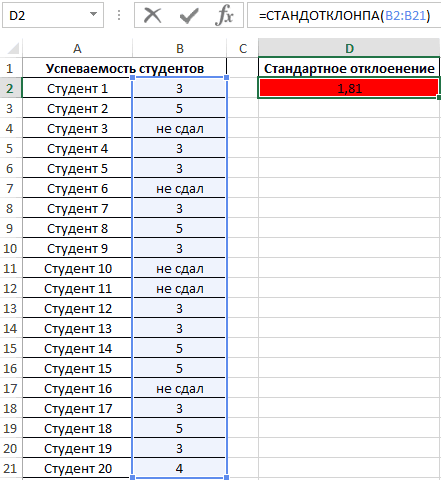
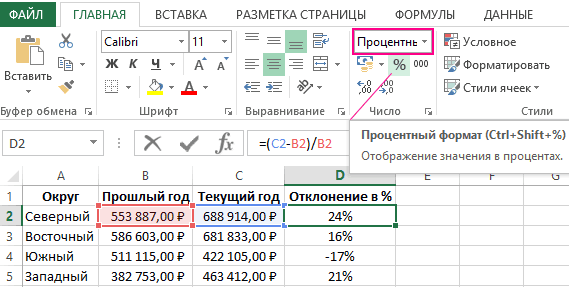
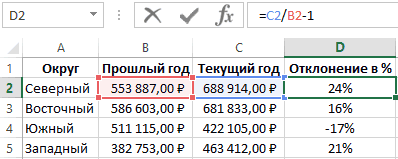



 Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
 Откройте программу Microsoft Excel.
Откройте программу Microsoft Excel.
 Составьте таблицу ваших данных.
Составьте таблицу ваших данных.