Функция ТЕНДЕНЦИЯ в Excel используется при расчетах последующих значений для рассматриваемого события и возвращает данные в соответствии с линейным трендом. Функция выполняет аппроксимацию (упрощение) прямой линией диапазона известных значений независимой и зависимой переменных с использованием метода наименьших квадратов и прогнозирует будущие значения зависимой переменной Y для указанных последующих значений независимой переменной X. Рассматриваемая функция не используется для получения статистической характеристики модели тренда и математического описания.
Линейным трендом называется распределение величин в изучаемой последовательности, которое может быть описано функцией типа y=ax+b. Поскольку функция ТЕНДЕНЦИЯ выполняет аппроксимацию прямой линией, точность результатов ее работы зависит от степени разброса значений в рассматриваемом диапазоне.
Примеры использования функции ТЕНДЕНЦИЯ в Excel
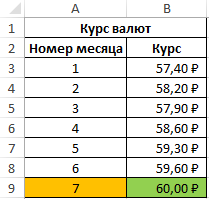
Пример 1. В таблице Excel содержатся средние значения данных о курсе доллара по отношению к рублю за последние 6 месяцев. Необходимо спрогнозировать средний курс на следующий месяц.
Вид исходной таблицы данных:
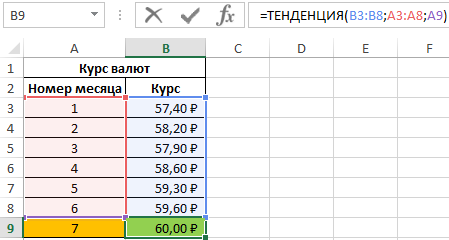
Для прогноза курса валют на 7-й месяц используем следующую функцию (обычная запись, Enter для вычислений):
=ТЕНДЕНЦИЯ(B3:B8;A3:A8;A9)
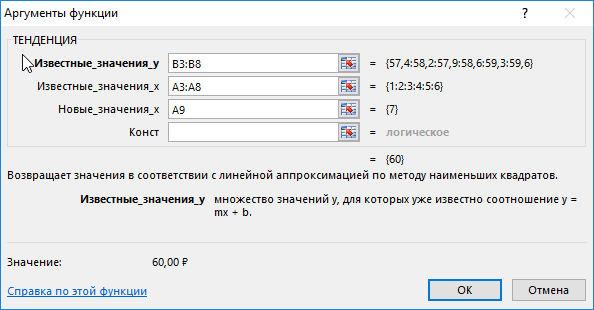
Описание аргументов:
- B3:B8 – диапазон известных значений курса валюты;
- A3:A8 – диапазон месяцев, для которых известны значения курса;
- A9 – значение, соответствующее номеру месяца, для которого необходимо выполнить расчет.
В результате получим:
Прогноз посещаемости с помощью функции ТЕНДЕНЦИЯ в Excel
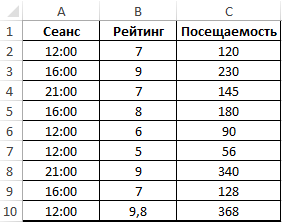
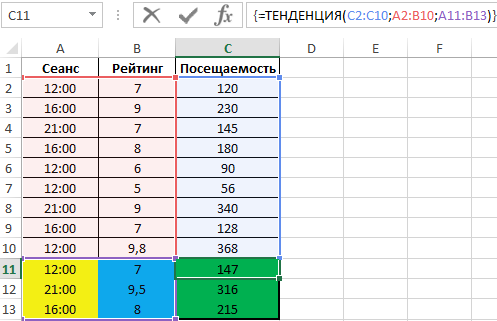
Пример 2. В кинотеатре фильмы показывают в различные сеансы, которые начинаются в 12:00, 16:00 и 21:00 соответственно. Каждый фильм имеет собственный рейтинг, в виде оценки от 1 до 10 баллов. Известны данные о посещаемости нескольких последних сеансов. Предположить, какой будет посещаемость для следующих фильмов:
- Рейтинг 7, сеанс 12:00;
- Рейтинг 9,5, сеанс 21:00;
- Рейтинг 8, сеанс 16:00.
Таблица исходных данных:
Для расчета используем функцию:
=ТЕНДЕНЦИЯ(C2:C10;A2:B10;A11:B13)
Примечания:
- Перед вводом функции необходимо выделить ячейки C11:C13;
- Расчет производим на основе диапазона значений A2:B10 (учитывается как время сеанса, так и рейтинг фильма)
В результате получим:
Не забывайте, что ТЕНДЕНЦИЯ является массивной функцией поэтому после ее ввода не забудьте выполнить ее в массиве. Для этого жмем не просто Enter, а комбинацию клавиш Ctrl+Shift+Enter. Если в строке формул по краям функции появились фигурные скобки {}, значит функция выполняется в массиве и все сделано правильно.
Прогнозирование производства продукции на графике Excel
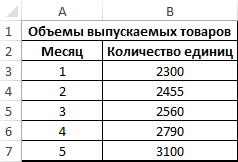
Пример 3. Предприятие постепенно наращивает производственные возможности, и ежемесячно увеличивает объемы выпускаемой продукции. Предположить, какое количество единиц продукции будет выпущено в следующие 3 месяца, проиллюстрировать на графике.
Исходная таблица:
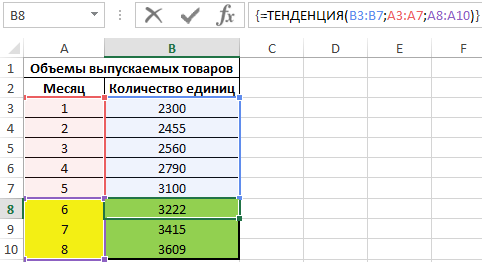
Для определения количества единиц продукции, которые будут выпущены на протяжении последующих 3-х месяцев используем функцию:
=ТЕНДЕНЦИЯ(B3:B7;A3:A7;A8:A10)
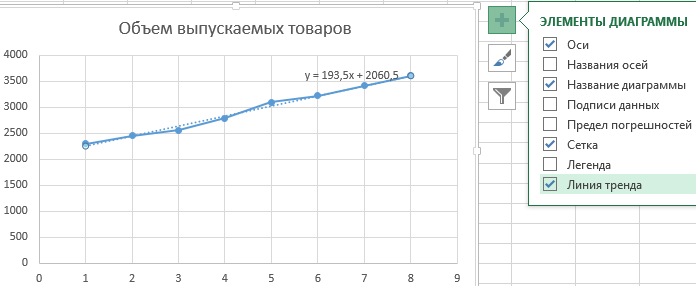
Построим график на основе имеющихся данных и отобразим линию тренда с уравнением:
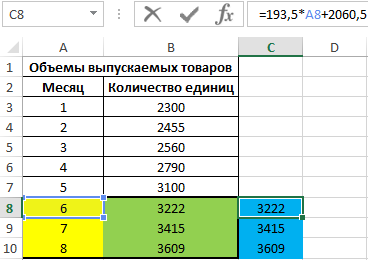
Введем в ячейке C8 формулу =193,5*A8+2060,5. В результате получим:
Аналогично с помощью подстановки значения независимой переменной в уравнение рассчитаем все остальные величины.
Данный пример наглядно демонстрирует принцип работы функции ТЕНДЕНЦИЯ.
Функция ТЕНДЕНЦИЯ в Excel и особенности ее использования
Функция ТЕНДЕНЦИЯ используется наряду с прочими функциями прогноза в Excel (ПРЕДСКАЗ, РОСТ) и имеет следующий синтаксис:
= ТЕНДЕНЦИЯ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])
Описание аргументов:
- известные_значения_y – обязательный аргумент, характеризующий диапазон исследуемых известных значений зависимой переменной y из уравнения y=ax+b.
- [известные_значения_x] – необязательный для заполнения аргумент, характеризующий диапазон известных значений независимой переменной x из уравнения y=ax+b.
- [новые_значения_x] – необязательный аргумент, характеризующий одно значение или диапазон данных, для которых необходимо определить соответствующие значения зависимой переменной y.
- [конст] – необязательный аргумент, принимающий на вход логические значения:
- ИСТИНА (значение по умолчанию, если явно не указано обратное) – функция ТЕНДЕНЦИЯ выполняет расчет коэффициента b из уравнения y=ax+b обычным методом.
- ЛОЖЬ – функция ТЕНДЕНЦИЯ использует упрощенный вариант уравнения – y=ax (коэффициент b = 0).
- Рассматриваемая функция интерпретирует каждый столбец или каждую строку из диапазона известных значений x в качестве отдельной переменной, если аргументом известное_y является диапазон ячеек из только одного столбца или только одной строки соответственно.
- Аргументы [известное_ x] и [новое_x] должны содержать одинаковое количество строк либо столбцов соответственно. Если новые значения независимой переменной явно не указаны, функция ТЕНДЕНЦИЯ выполняет расчет с условием, что аргументы [известное_ x] и [новое_ x] принимают одинаковые значения. Если оба эти аргумента явно не указаны, рассматриваемая функция использует массивы {1;2;3;…;n} с размерностью, соответствующей размерности известное_y.
- Данная функция может быть использована для аппроксимации полиномиальных кривых.
- ТЕНДЕНЦИЯ является формулой массива. Для определения нескольких последующих значений необходимо выделить диапазон соответствующего количества ячеек и для отображения результата использовать комбинацию клавиш Ctrl+Shift+Enter.
- В качестве аргумента [известное_ x] могут быть переданы:
- Только одна переменная, при этом два первых аргумента функции ТЕНДЕНЦИЯ могут являться диапазонами любой формы, но обязательным условием является одинаковая размерность (количество элементов).
- Несколько переменных, при этом в качестве аргумента известное_y должен быть передан вектор значений (диапазон из только одной строки или только одного столбца).
Примечания:
ТЕНДЕНЦИЯ (функция ТЕНДЕНЦИЯ)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция ТЕНДЕНЦИЯ возвращает значения по линейному тренду. Она помещается прямой линией (методом наименьших квадратов) known_y и known_x массива. Функции ТЕНДЕНЦИЯ возвращают значения y в этой строке для массива new_x, который вы указали.
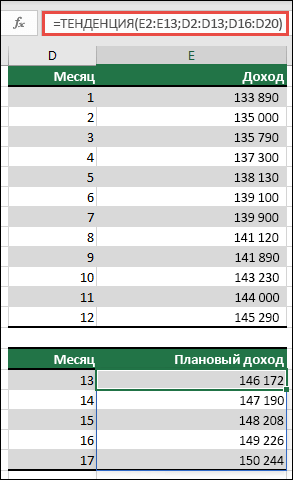
Примечание: Если у вас есть текущая версия Microsoft 365 ,вы можете ввести формулу в левую верхнюю ячейку диапазона вывода (в данном примере — ячейку E16), а затем нажать ввод, чтобы подтвердить формулу как формулу динамического массива. В противном случае формула должна быть введена как формула массива устаревшей: сначала выберем диапазон вывода (E16:E20), введите формулу в левую верхнюю ячейку диапазона выходных данных (E16), а затем нажмите CTRL+SHIFT+ВВОД, чтобы подтвердить ее. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
=ТЕНДЕНЦИЯ(known_y,[known_x]; [new_x]; [конст])
Аргументы функции ТЕНДЕНЦИЯ описаны ниже.
|
Аргумент |
Описание |
|---|---|
|
Известные_значения_y. Обязательно |
Набор значений y, которые уже известно в отношении y = mx + b
|
|
Известные_значения_x. Необязательно |
Необязательный набор значений x, которые уже известно в отношении y = mx + b
|
|
New_x Необязательно |
Новые значения x, для которых функции ТЕНДЕНЦИЯ нужно вернуть соответствующие значения y
|
|
Конст. Необязательно |
Логическое значение, указывав, нужно ли принудть константы b к значению 0.
|
-
Сведения о том, Microsoft Excel подстрок под данные, см. в этой теме.
-
Функцию ТЕНДЕНЦИЯ можно использовать для аппроксимации полиномиальной кривой, проводя регрессионный анализ для той же переменной, возведенной в различные степени. Например, пусть столбец A содержит значения y, а столбец B содержит значения x. Можно ввести значение x^2 в столбец C, x^3 в столбец D и т. д., а затем провести регрессионный анализ столбцов от B до D со столбцом A.
-
Формулы, возвращающая массивы, необходимо вводить как формулы массива с помощью CTRL+SHIFT+ВВОД, если только у вас не есть текущая версия Microsoft 365,а затем можно просто нажать ввод .
-
При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точки с запятой для разделения значений в одной строке и двоеточия для разделения строк.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
В
тех случаях, когда вас интересует прогноз
значений Y
на какой-то интервал времени (или другой
отрезок независимых переменных), Excel
предлагает использование функций
прогноза, основанных на линейном или
экспоненциальном приближении13.
Функция
ТЕНДЕНЦИЯ()
вычисляет значения в соответствии с
линейным
трендом.
Аппроксимирует прямой линией (по методу
наименьших квадратов) массивы известных
значений Y
и известных значений Х.
Возвращает значения Y,
в соответствии с этой прямой для заданного
массива новые значения Х.
Функция
ПРЕДСКАЗ()
вычисляет или предсказывает будущее
значение по существующим значениям.
Предсказываемое значение — это Y
-значение, соответствующее заданному
Х
— значению. Известные значения — это Х
— и Y
-значения, а новое значение предсказывается
с использованием линейной регрессии.
Эта функцию рассчитывает прогнозные
данные аналогично функции ТЕНДЕНЦИЯ().
Полученные значения одинаковы.
Функция
РОСТ()
рассчитывает
прогнозируемый экспоненциальный
рост на
основании имеющихся данных. Функция
РОСТ
возвращает значения Y
для последовательности новых значений
Х,
задаваемых с помощью существующих Х—
и Y-значений.
Функция рабочего листа РОСТ
может применяться также для аппроксимации
существующих Х—
и Y-значений
экспоненциальной кривой.
Синтаксис
функций ТЕНДЕНЦИЯ()
и РОСТ()
-
ТЕНДЕНЦИЯ
(Известные значения Y; Известные значения
Х; Новые значения Х; Константа).
Функция
возвращает значения Yв соответствии с линейным трендом.
-
РОСТ
(Известные значения Y; Известные значения
Х; Новые значения Х; Константа).
Функция возвращает значения Yв соответствии с экспоненциальным
трендом.
Аргументы
функций ТЕНДЕНЦИЯ()
и РОСТ()
«Известные
значения
Y»
— это
множество значений
Y, которые
уже известны для соотношения Y=m*x+b
(2.1) или Y=b*m^x
(2.40) — при экспоненциальном сглаживании.
«Известные
значения X»
— это необязательное множество значений
Х,
которые уже известны для соотношения
Y=m*x+b
(2.1) или Y=b*m^x
(2.40) — при экспоненциальном сглаживании.
«Новые
значения X»
— это новые значения X,
для которых должны быть определены
значения Y.
«Константа»
— это логическое выражение, которая при
значении равном «1» (истина)
указывает на необходимость вычисления
константы b.
Если константа равна «0»
(ложь),
то b
полагается равным «0»
или «1»
при экспоненциальном сглаживании.
Внимание.
Формулы, которые возвращают массивы,
должны вводится как формулы массивов,
после выделения подходящего числа
ячеек.
Задание 6. Прогнозирование с помощью функций тенденция() и рост()
Имеются
следующие данные
о товарообороте крупного магазина за
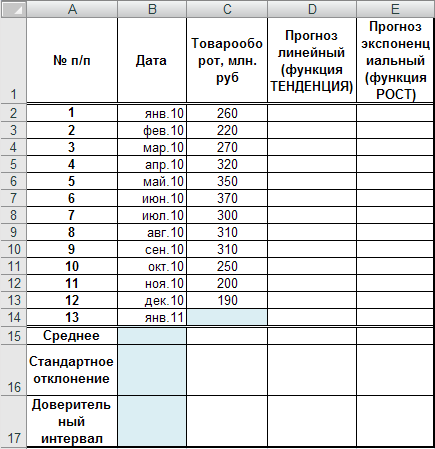
2010 год (рис. 3.6):
Для
прогнозирования значения Y
для нового значения Х
(значения, которое не содержится в
исследуемом ряде наблюдений) выполните
следующее (в нашем случае – это прогноз
на январь 2011 года):
Рис. 3. 6. Таблица с начальными данными
-
Курсор
установите в ячейку D14. -
Вызовите
функцию
ТЕНДЕНЦИЯ()
(категория функция «Статистические»). -
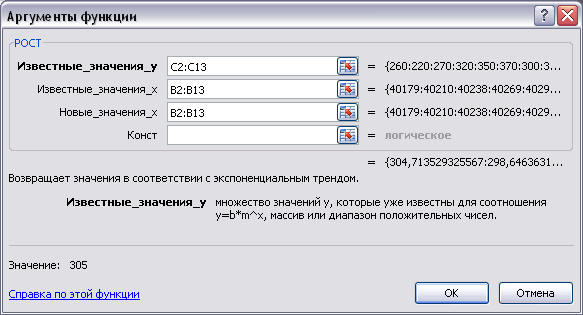
В
диалоговом окне Аргументы
функции
(рис. 3.7) введите необходимые адреса: -
В
окно «Известные
значения_Y»
введите адреса ячеек, содержащих
известные значения товарооборотов за
2010 год — Y
(С2:С13). -
В
окно «Известные
значения_Х»,
введите адреса ячеек известных дат — Х
(В2:В13) -
В
окно «Новые
значения_Х»
введите
адрес ячейки, содержащей новое значение
расчетного месяца (января 2011) — Х
(В14). -
Щелкните
на кнопке «ОК».
Примечание.
В предыдущих версиях Excel
даты не всегда корректно влияли на
конечный результат, поэтому вместо них
приходилось использовать
значения
номеров месяцев 2010 года (А2:А13).
Попробуйте пересчитать формулу с
использованием этих номеров, например,
в ячейке D15,
и вы увидите, что результат будет
аналогичным. Не забудьте, затем очистить
ячейку D15.
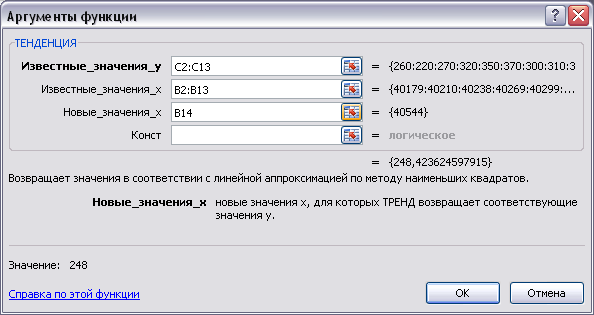
Рис. 3. 7. Окно для ввода аргументов функции
ТЕНДЕНЦИЯ() для
одного значения
-
Полученный
результат округлите до целых чисел
кнопкой
Уменьшить
разрядность.
Должно получиться число 249. -
Аналогично
выполните прогнозирование величины
товарооборота на январь 2011 года для
магазина, используя функцию РОСТ()
(ячейка
Е14).
Для
этого
последовательно
выполните вышеописанные действия,
заменив функцию ТЕНДЕНЦИЯ()
на
функцию
РОСТ().
В результате будет получено значение
—240.
Полученные значения
249 и 240 отличаются незначительно друг
от друга (на 3,6%), но довольно далеки от
величины товарооборота за декабрь 2011
года, равного 190.
Попробуйте
разобраться, почему это так. Для этого
рассчитайте с помощью функций ТЕНДЕНЦИЯ()
и РОСТ()
теоретические
значения товарооборота за весь 2004 год.
В
ячейки D2:D13
и E2:E13
введите функции ТЕНДЕНЦИЯ()
и РОСТ()
как формулы массива соответственно.
Рассмотрим этот процесс подробно на
функции ТЕНДЕНЦИЯ().
-
Выделите
интервал ячеек, куда должны быть
возвращены новые значения Y
— D2:D13.
-
Откройте
Мастер
функций
и в категории Статистические
выберите функцию ТЕНДЕНЦИЯ(). -
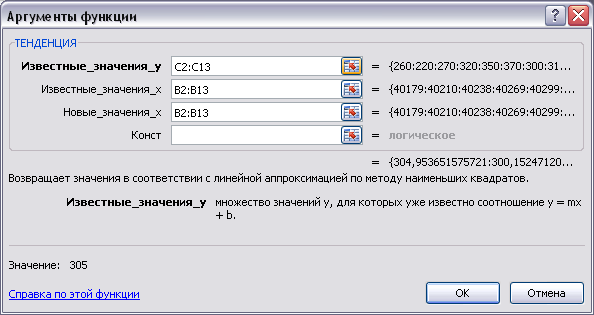
Введите
все необходимые данные, как показано
на рис. 3.8.
Рис. 3. 8. Окно для ввода аргументов функции
ТЕНДЕНЦИЯ()
-
Завершите
ввод данных одновременным
нажатием на клавиши CTRL
+ SHIFT
+ ENTER,
что позволит посчитать функцию
ТЕНДЕНЦИЯ()
как
формулу массива. -
Округлите
полученные данные до целых чисел. -
Аналогичные
действия выполните для ячеек E2:E13,
куда
будет введена функция РОСТ()
(рис.
3.9).
Рис. 3. 9. Окно для ввода аргументов функции
РОСТ()
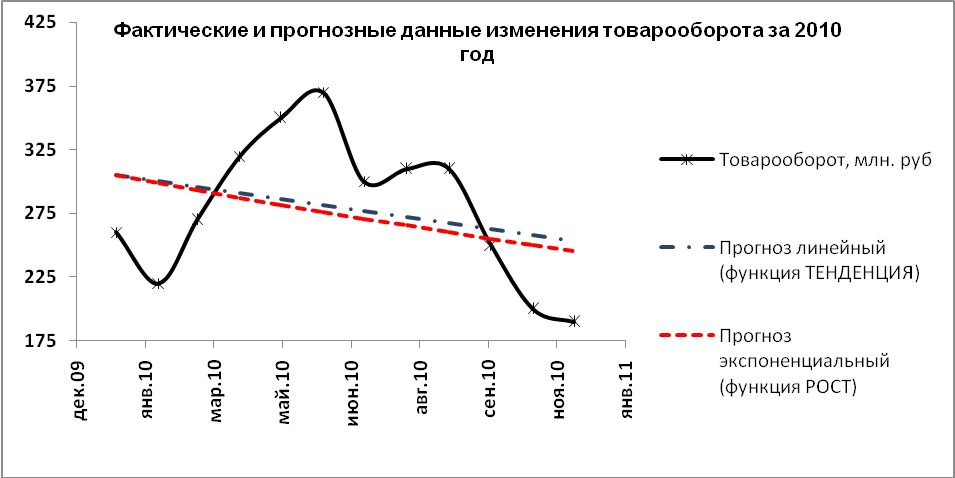
Как
видно из сравнения фактических и
прогнозных данных (рис. 3.14) между ними
существуют значительные отличия. Для
наглядности постройте Точечную
диаграмму продажи для фактических и
прогнозных данных. После соответствующей
корректировки она может иметь следующий
вид (рис. 3.10).
Рис. 3. 10.. Сравнение результатов
фактического товарооборота магазина
за 2010 год и рассчитанных по функциям
ТЕНДЕНЦИЯ() иРОСТ()
Из
графика видно, что применять функции
ТЕНДЕНЦИЯ()
и РОСТ()
надо достаточно осторожно, так как они
хорошо описывают только линейные
процессы.
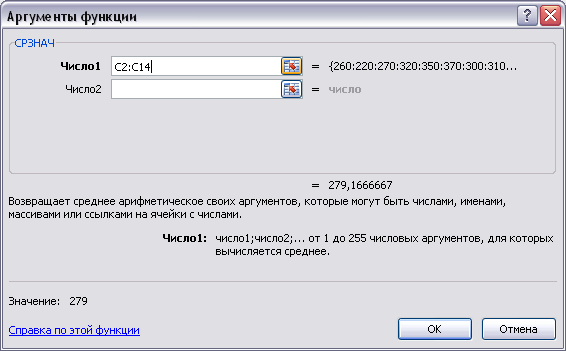
-
Самостоятельно
вычислите среднее значение СРЗНАЧ
в ячейках C15,
D15
и Е15.
Окно ввода аргументов функции для
ячейки С15
приведено на рис. 3.11, а полученные
значения – на рис. 3.14
Рис.
3. 11. Окно функции СРЗНАЧдля расчета среднего значения результатов,
полученных в блоке ячеекD2:D14
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
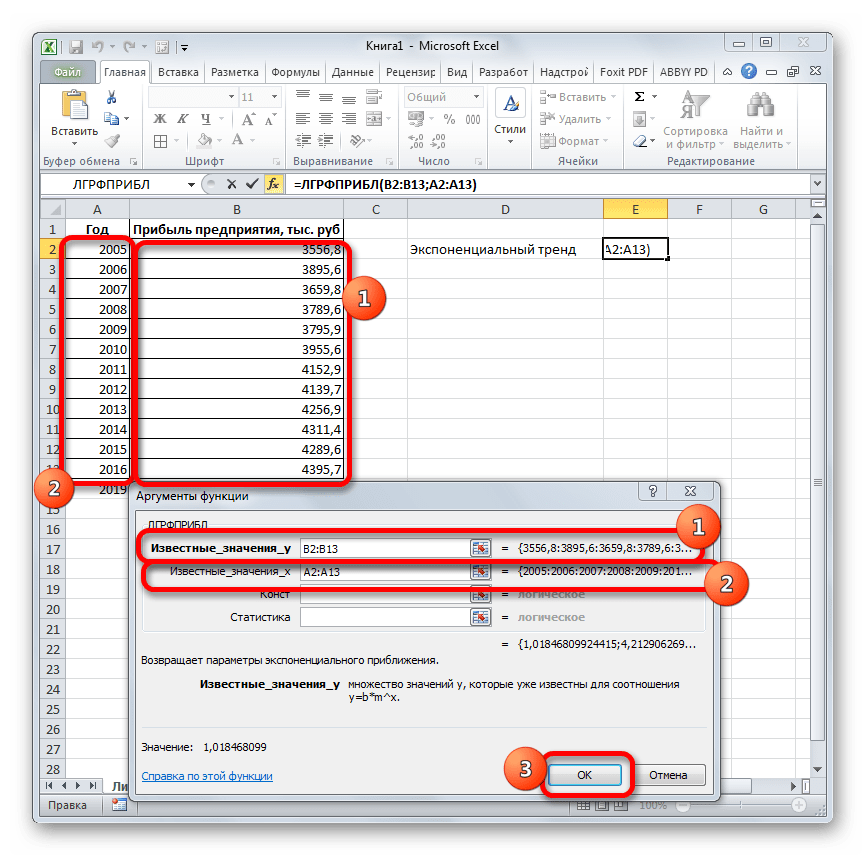
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
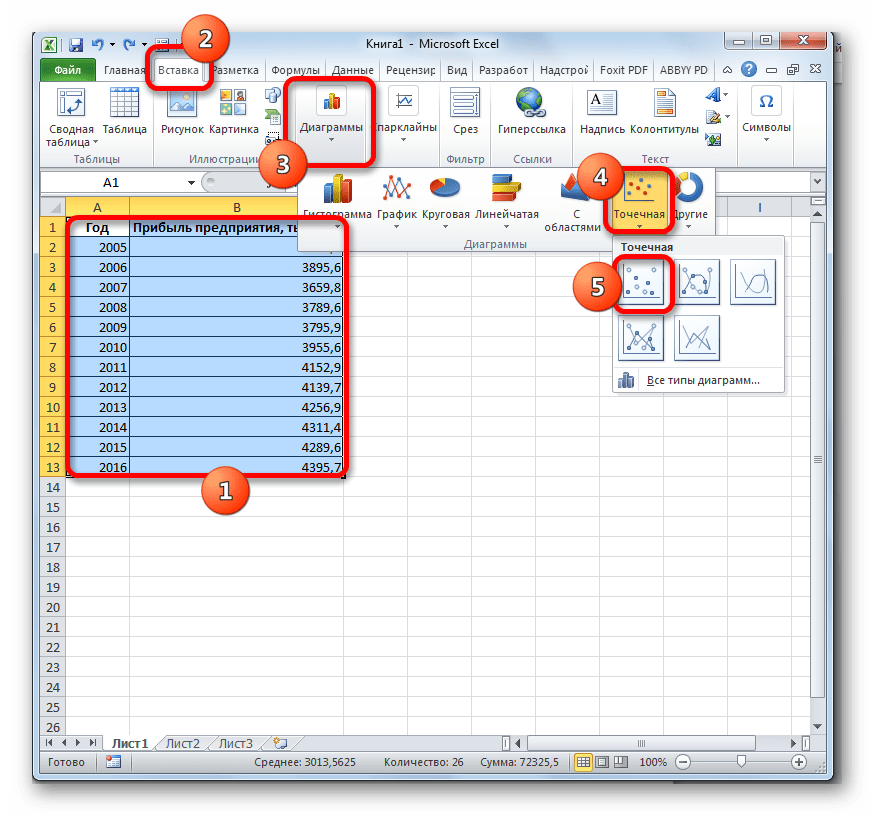
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
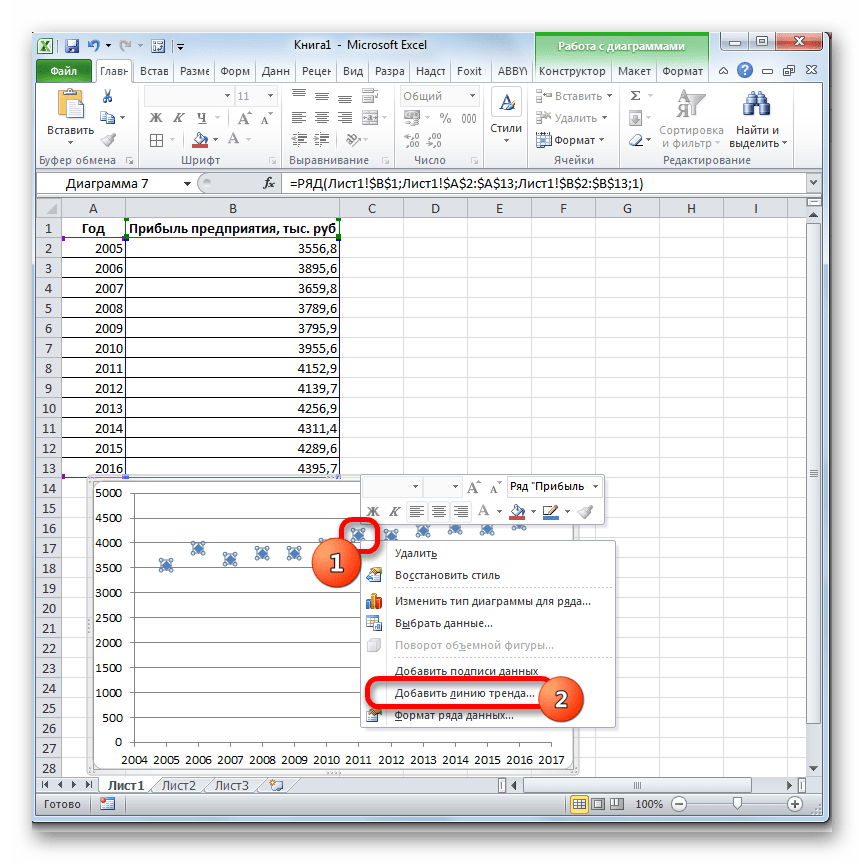
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
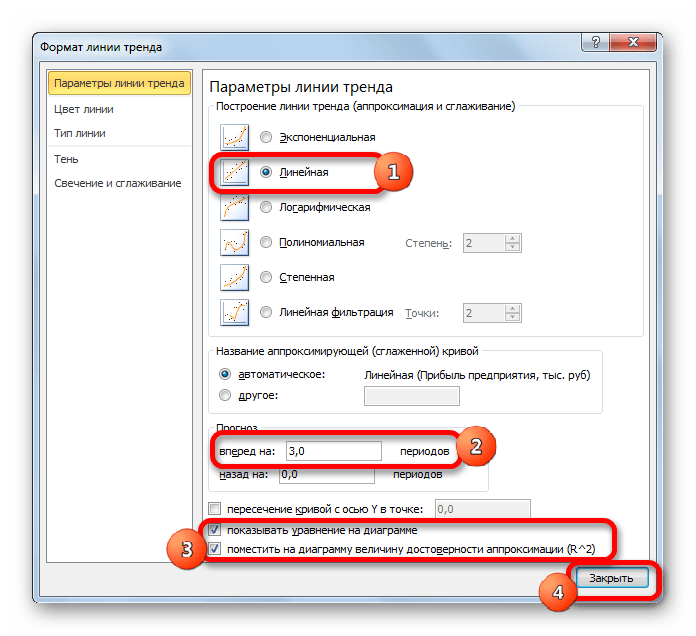
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
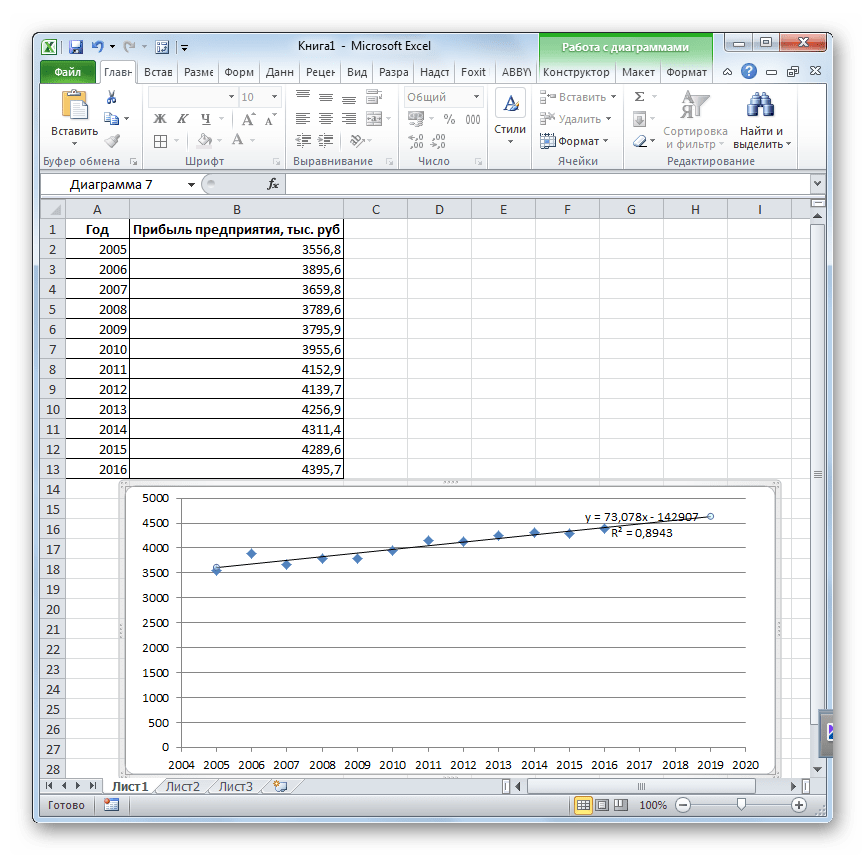
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
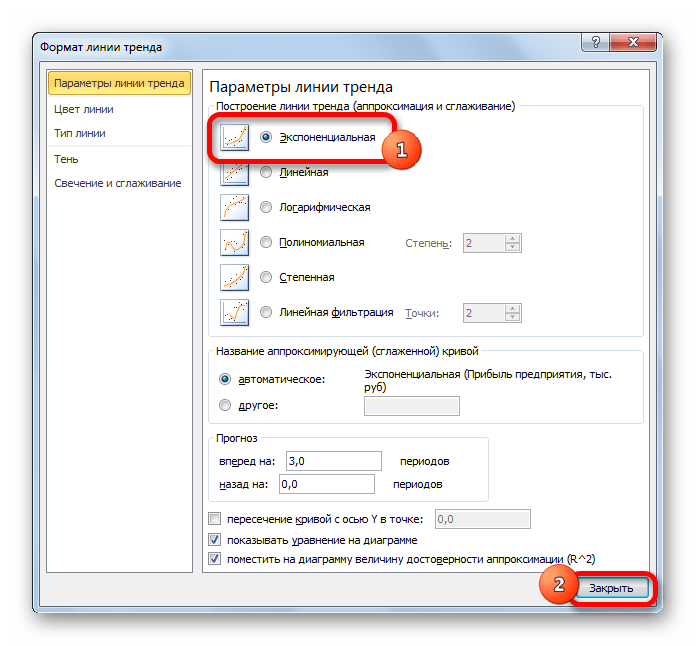
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
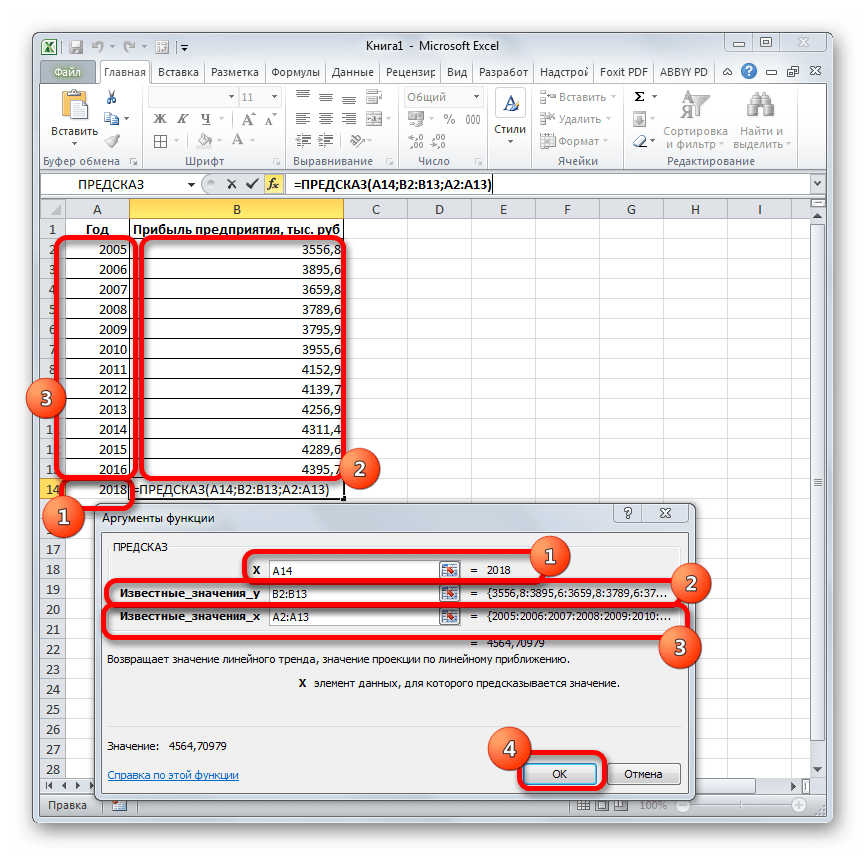
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
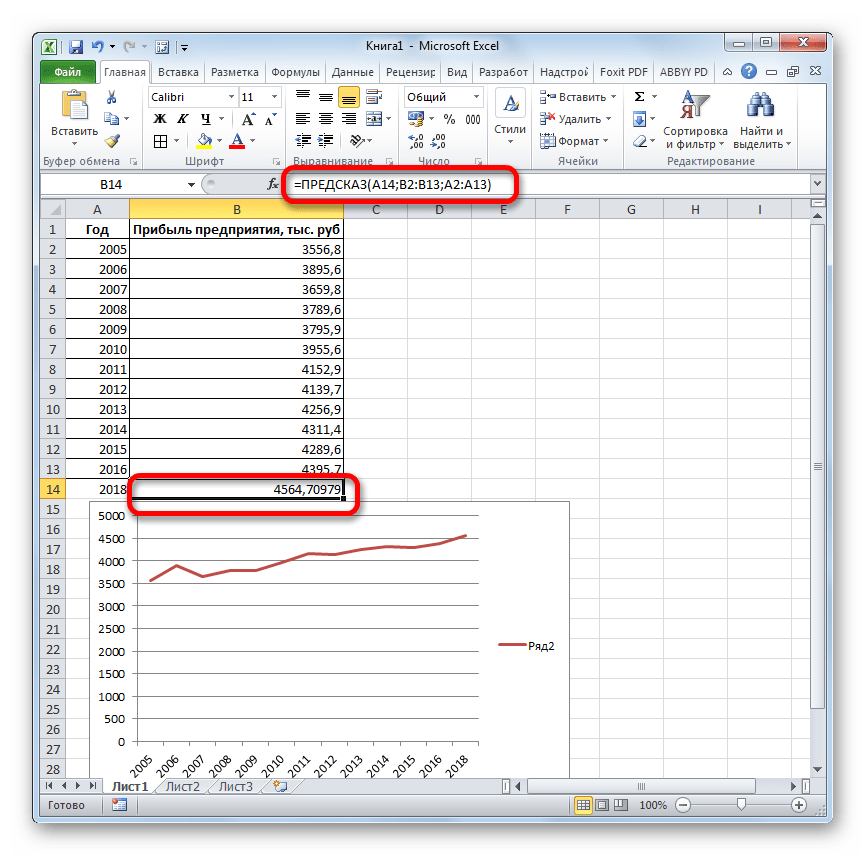
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
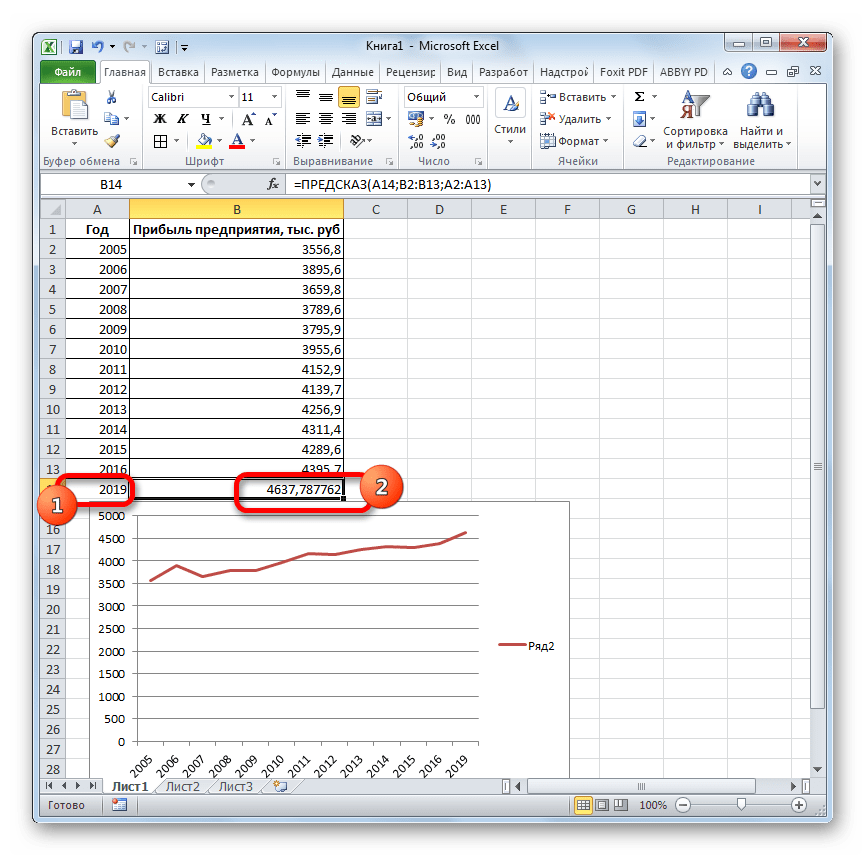
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
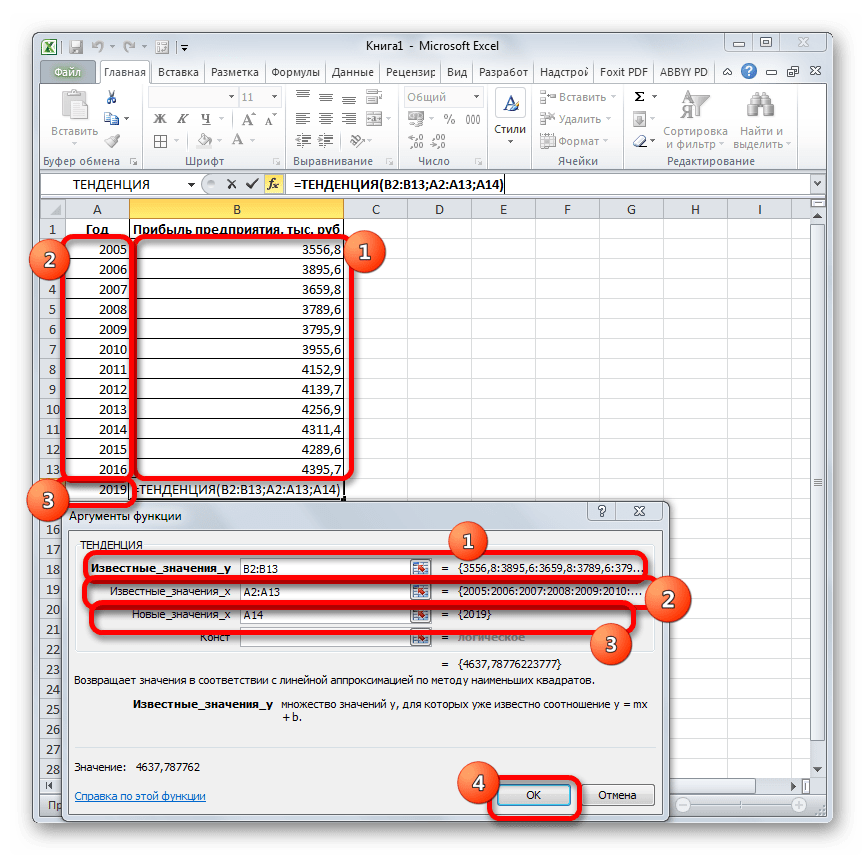
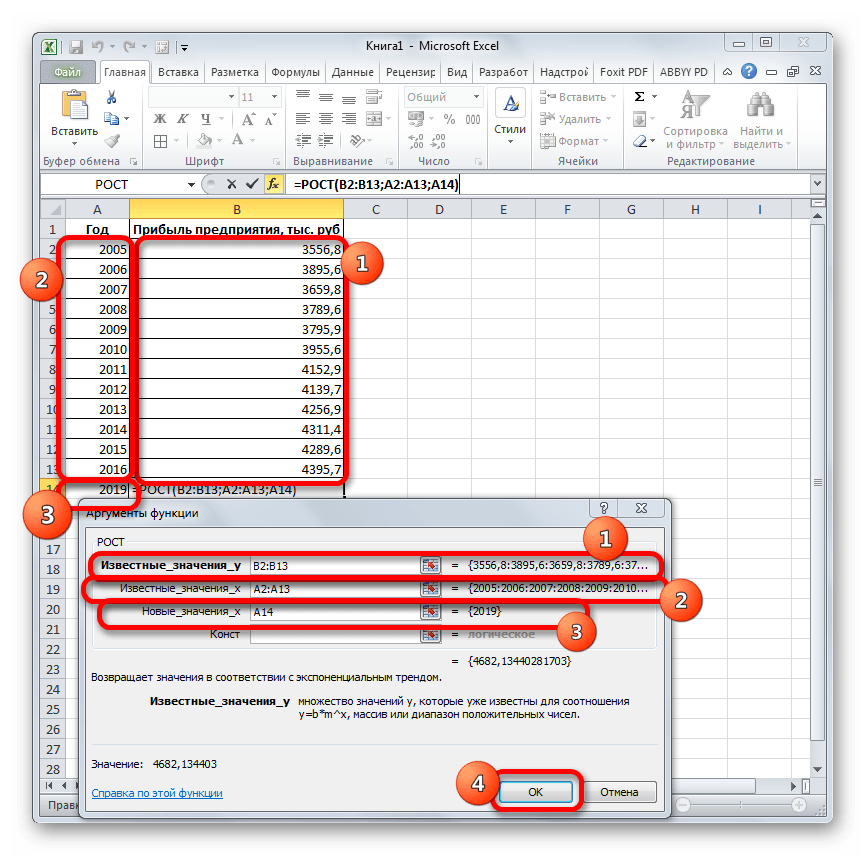
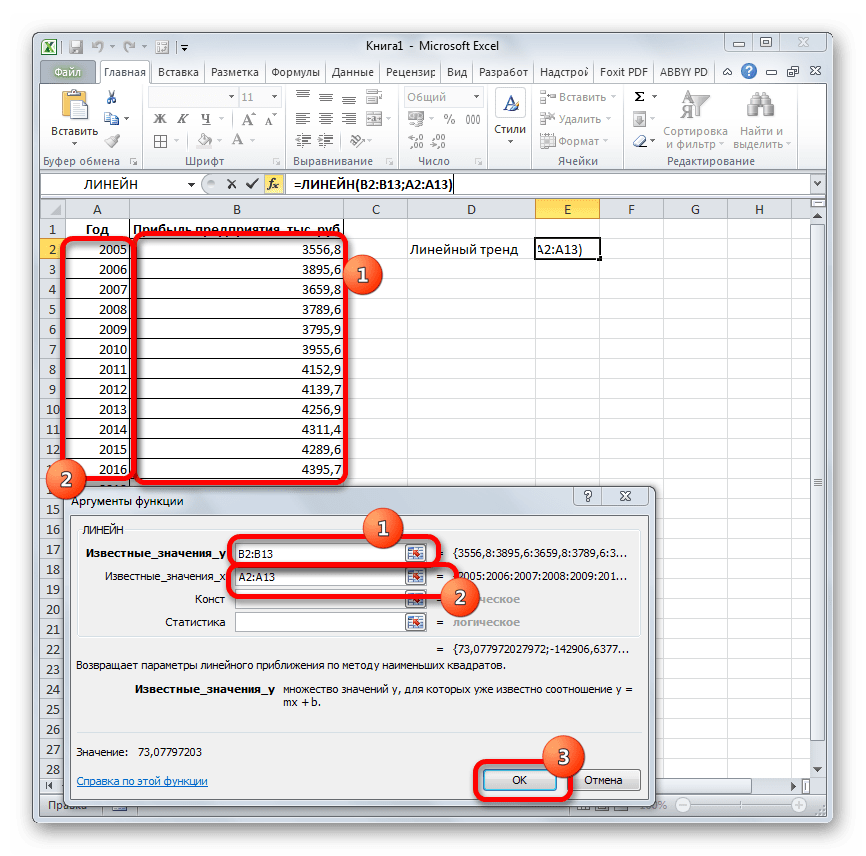
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
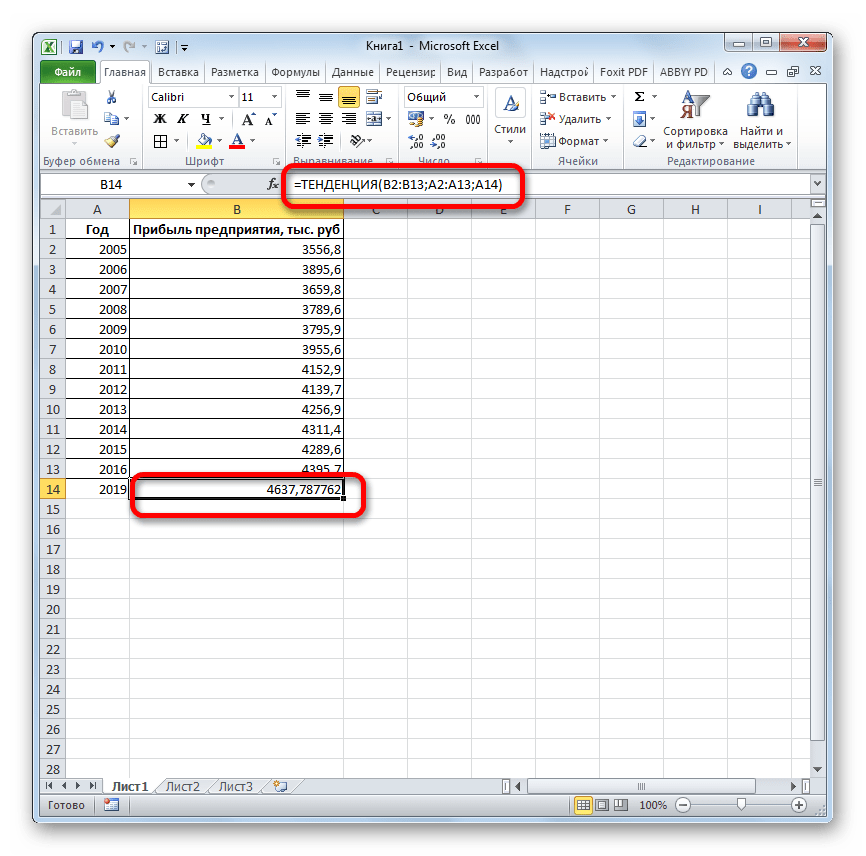
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
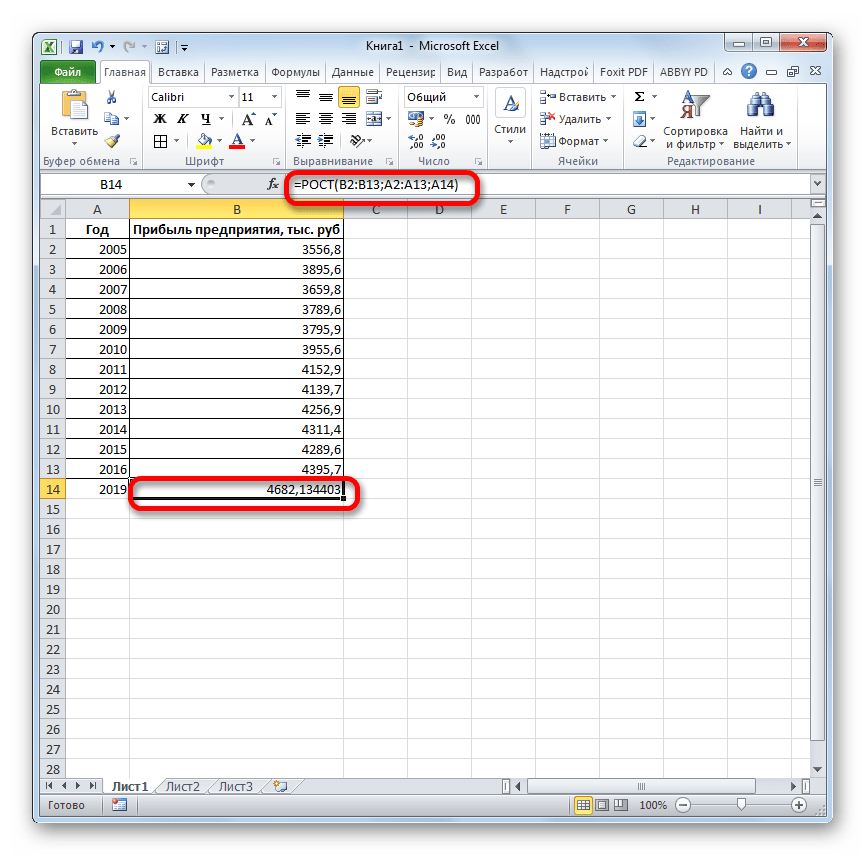
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
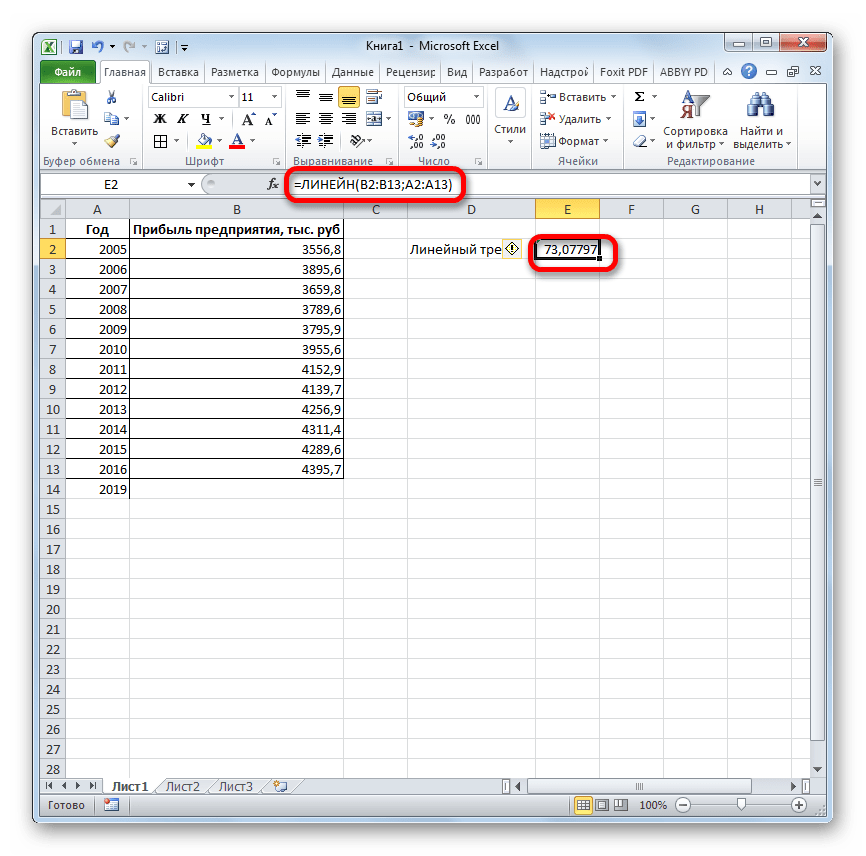
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
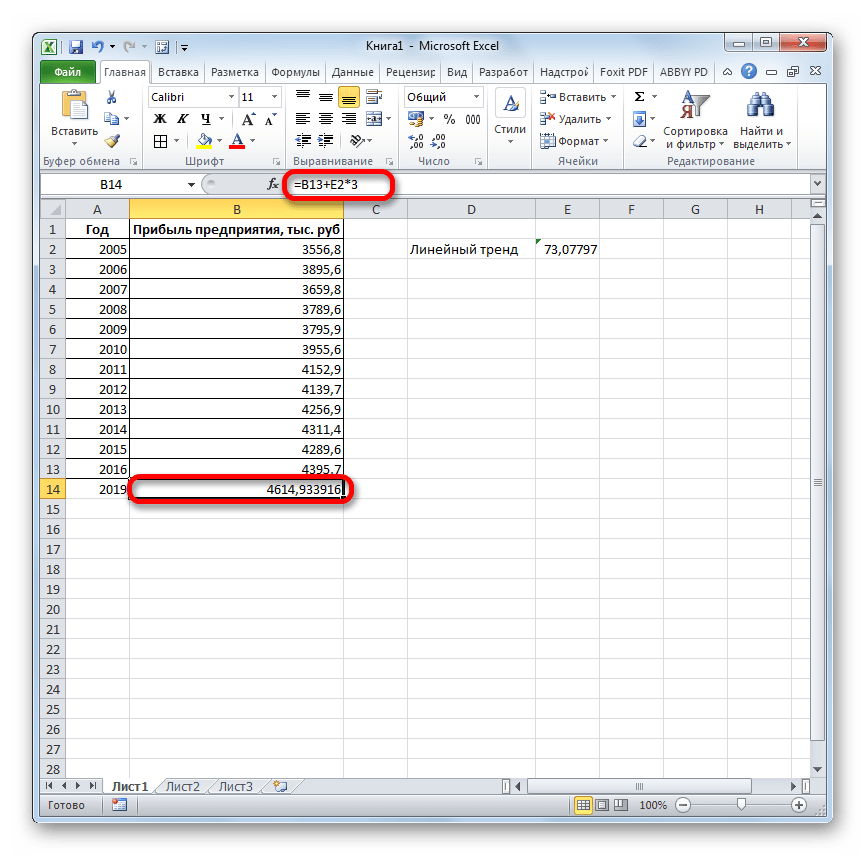
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
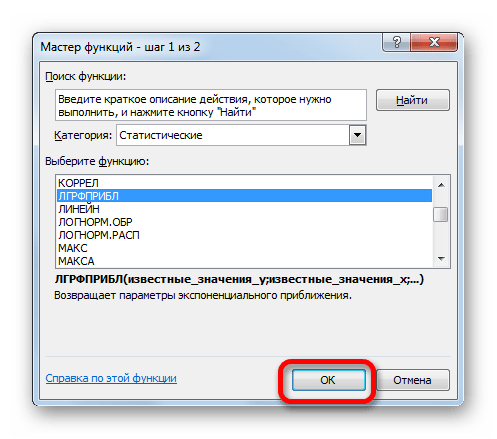
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
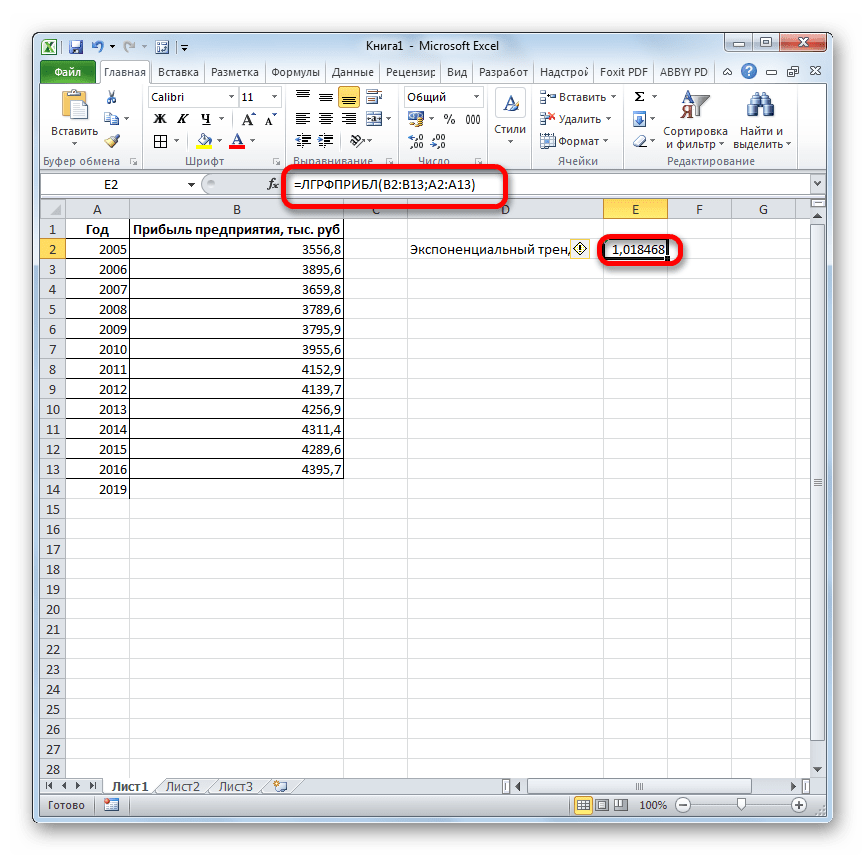
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
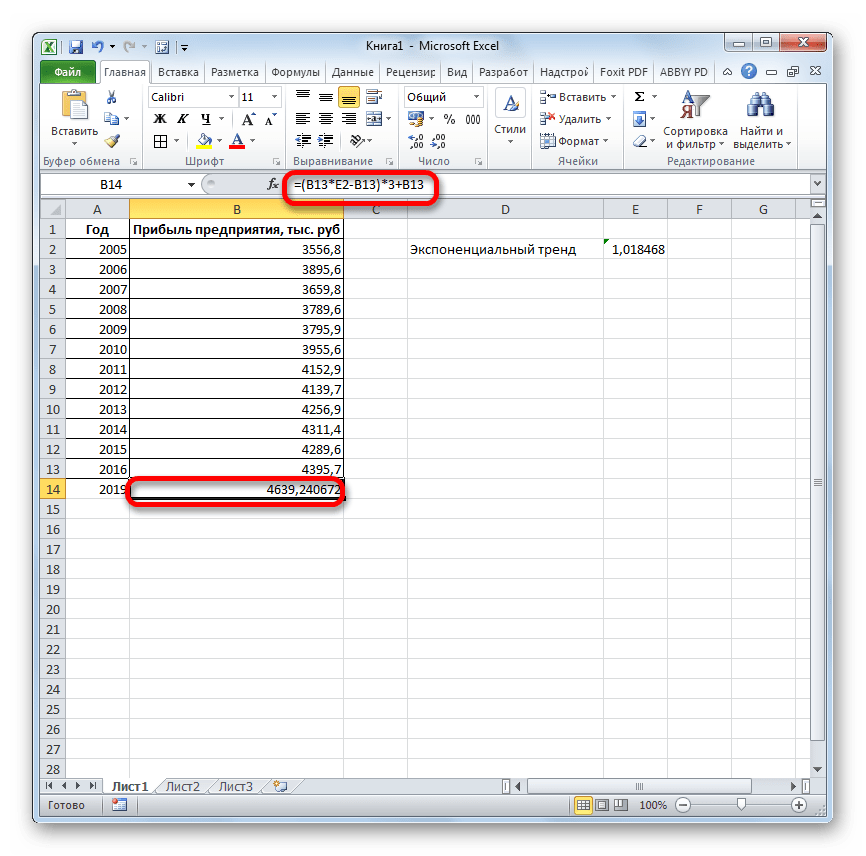
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)
Умение строить прогнозы, предсказывая (хотя бы примерно!) будущее развитие событий — неотъемлемая и очень важная часть любого современного бизнеса. Само-собой, это отдельная весьма сложная наука с кучей методов и подходов, но часто для грубой повседневной оценки ситуации достаточно простых техник. Одна из них — это функция ПРЕДСКАЗ (FORECAST) , которая умеет считать прогноз по линейному тренду.
Принцип работы этой функции несложен: мы предполагаем, что исходные данные можно интерполировать (сгладить) некой прямой с классическим линейным уравнением y=kx+b:
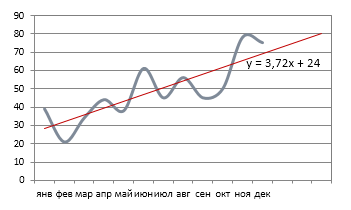
Построив эту прямую и продлив ее вправо за пределы известного временного диапазона — получим искомый прогноз.
Для построения этой прямой Excel использует известный метод наименьших квадратов. Если коротко, то суть этого метода в том, что наклон и положение линии тренда подбирается так, чтобы сумма квадратов отклонений исходных данных от построенной линии тренда была минимальной, т.е. линия тренда наилучшим образом сглаживала фактические данные.
Excel позволяет легко построить линию тренда прямо на диаграмме щелчком правой по ряду — Добавить линию тренда (Add Trendline), но часто для расчетов нам нужна не линия, а числовые значения прогноза, которые ей соответствуют. Вот, как раз, их и вычисляет функция ПРЕДСКАЗ (FORECAST) .
Синтаксис функции следующий
=ПРЕДСКАЗ( X ; Известные_значения_Y ; Известные_значения_X )
- Х — точка во времени, для которой мы делаем прогноз
- Известные_значения_Y — известные нам значения зависимой переменной (прибыль)
- Известные_значения_X — известные нам значения независимой переменной (даты или номера периодов)
Примеры функции ТЕНДЕНЦИЯ в Excel для прогнозирования данных
Функция ТЕНДЕНЦИЯ в Excel используется при расчетах последующих значений для рассматриваемого события и возвращает данные в соответствии с линейным трендом. Функция выполняет аппроксимацию (упрощение) прямой линией диапазона известных значений независимой и зависимой переменных с использованием метода наименьших квадратов и прогнозирует будущие значения зависимой переменной Y для указанных последующих значений независимой переменной X. Рассматриваемая функция не используется для получения статистической характеристики модели тренда и математического описания.
Линейным трендом называется распределение величин в изучаемой последовательности, которое может быть описано функцией типа y=ax+b. Поскольку функция ТЕНДЕНЦИЯ выполняет аппроксимацию прямой линией, точность результатов ее работы зависит от степени разброса значений в рассматриваемом диапазоне.
Примеры использования функции ТЕНДЕНЦИЯ в Excel
Пример 1. В таблице Excel содержатся средние значения данных о курсе доллара по отношению к рублю за последние 6 месяцев. Необходимо спрогнозировать средний курс на следующий месяц.
Вид исходной таблицы данных:
Для прогноза курса валют на 7-й месяц используем следующую функцию (обычная запись, Enter для вычислений):
- B3:B8 – диапазон известных значений курса валюты;
- A3:A8 – диапазон месяцев, для которых известны значения курса;
- A9 – значение, соответствующее номеру месяца, для которого необходимо выполнить расчет.
В результате получим:
Прогноз посещаемости с помощью функции ТЕНДЕНЦИЯ в Excel
Пример 2. В кинотеатре фильмы показывают в различные сеансы, которые начинаются в 12:00, 16:00 и 21:00 соответственно. Каждый фильм имеет собственный рейтинг, в виде оценки от 1 до 10 баллов. Известны данные о посещаемости нескольких последних сеансов. Предположить, какой будет посещаемость для следующих фильмов:
- Рейтинг 7, сеанс 12:00;
- Рейтинг 9,5, сеанс 21:00;
- Рейтинг 8, сеанс 16:00.
Таблица исходных данных:
Для расчета используем функцию:
- Перед вводом функции необходимо выделить ячейки C11:C13;
- Расчет производим на основе диапазона значений A2:B10 (учитывается как время сеанса, так и рейтинг фильма)
В результате получим:
Не забывайте, что ТЕНДЕНЦИЯ является массивной функцией поэтому после ее ввода не забудьте выполнить ее в массиве. Для этого жмем не просто Enter, а комбинацию клавиш Ctrl+Shift+Enter. Если в строке формул по краям функции появились фигурные скобки <>, значит функция выполняется в массиве и все сделано правильно.
Прогнозирование производства продукции на графике Excel
Пример 3. Предприятие постепенно наращивает производственные возможности, и ежемесячно увеличивает объемы выпускаемой продукции. Предположить, какое количество единиц продукции будет выпущено в следующие 3 месяца, проиллюстрировать на графике.
Для определения количества единиц продукции, которые будут выпущены на протяжении последующих 3-х месяцев используем функцию:
Построим график на основе имеющихся данных и отобразим линию тренда с уравнением:
Введем в ячейке C8 формулу =193,5*A8+2060,5. В результате получим:
Аналогично с помощью подстановки значения независимой переменной в уравнение рассчитаем все остальные величины.
Данный пример наглядно демонстрирует принцип работы функции ТЕНДЕНЦИЯ.
Функция ТЕНДЕНЦИЯ в Excel и особенности ее использования
Функция ТЕНДЕНЦИЯ используется наряду с прочими функциями прогноза в Excel (ПРЕДСКАЗ, РОСТ) и имеет следующий синтаксис:
= ТЕНДЕНЦИЯ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])
- известные_значения_y – обязательный аргумент, характеризующий диапазон исследуемых известных значений зависимой переменной y из уравнения y=ax+b.
- [известные_значения_x] – необязательный для заполнения аргумент, характеризующий диапазон известных значений независимой переменной x из уравнения y=ax+b.
- [новые_значения_x] – необязательный аргумент, характеризующий одно значение или диапазон данных, для которых необходимо определить соответствующие значения зависимой переменной y.
- [конст] – необязательный аргумент, принимающий на вход логические значения:
- ИСТИНА (значение по умолчанию, если явно не указано обратное) – функция ТЕНДЕНЦИЯ выполняет расчет коэффициента b из уравнения y=ax+b обычным методом.
- ЛОЖЬ – функция ТЕНДЕНЦИЯ использует упрощенный вариант уравнения – y=ax (коэффициент b = 0).
- Рассматриваемая функция интерпретирует каждый столбец или каждую строку из диапазона известных значений x в качестве отдельной переменной, если аргументом известное_y является диапазон ячеек из только одного столбца или только одной строки соответственно.
- Аргументы [известное_ x] и [новое_x] должны содержать одинаковое количество строк либо столбцов соответственно. Если новые значения независимой переменной явно не указаны, функция ТЕНДЕНЦИЯ выполняет расчет с условием, что аргументы [известное_ x] и [новое_ x] принимают одинаковые значения. Если оба эти аргумента явно не указаны, рассматриваемая функция использует массивы <1;2;3;…;n>с размерностью, соответствующей размерности известное_y.
- Данная функция может быть использована для аппроксимации полиномиальных кривых.
- ТЕНДЕНЦИЯ является формулой массива. Для определения нескольких последующих значений необходимо выделить диапазон соответствующего количества ячеек и для отображения результата использовать комбинацию клавиш Ctrl+Shift+Enter.
- В качестве аргумента [известное_ x] могут быть переданы:
- Только одна переменная, при этом два первых аргумента функции ТЕНДЕНЦИЯ могут являться диапазонами любой формы, но обязательным условием является одинаковая размерность (количество элементов).
- Несколько переменных, при этом в качестве аргумента известное_y должен быть передан вектор значений (диапазон из только одной строки или только одного столбца).
ПРЕДСКАЗ и ТЕНДЕНЦИЯ в Excel
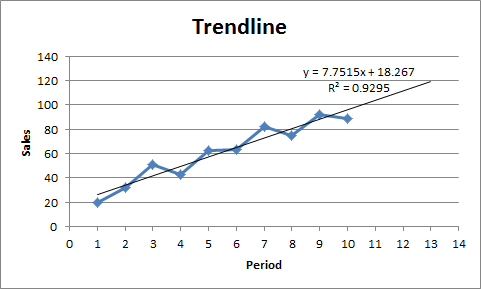
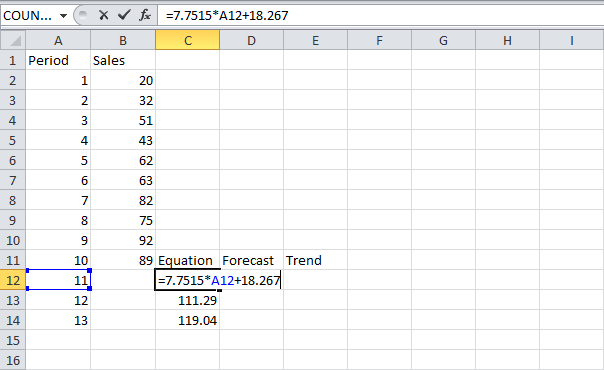
При добавлении линейного тренда на график Excel, программа может отображать уравнение прямо на графике (смотри рисунок ниже). Вы можете использовать это уравнение для расчета будущих продаж. Функции FORECAST (ПРЕДСКАЗ) и TREND (ТЕНДЕНЦИЯ) дают тот же результат.
Пояснение: Excel использует метод наименьших квадратов, чтобы найти линию, которая соответствует точкам наилучшим образом. Значение R 2 равно 0.9295, что является очень хорошим значением. Чем оно ближе к 1, тем лучше линия соответствует данным.
-
Используйте уравнение для расчета будущих продаж:
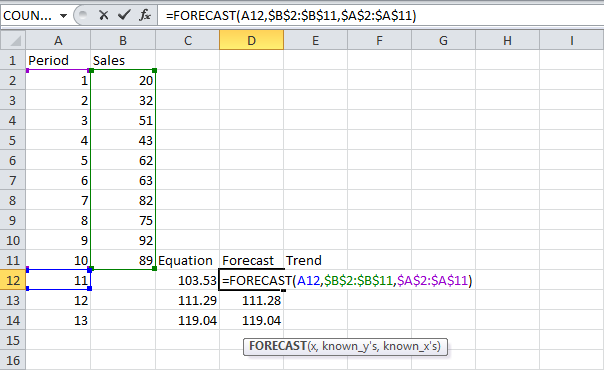
Используйте функцию FORECAST (ПРЕДСКАЗ), чтобы рассчитать будущие продажи:
Примечание: Когда мы протягиваем функцию FORECAST (ПРЕДСКАЗ) вниз, абсолютные ссылки ($B$2:$B$11 и $A$2:$A$11) остаются такими же, в то время как относительная ссылка (А12) изменяется на A13 и A14.
-
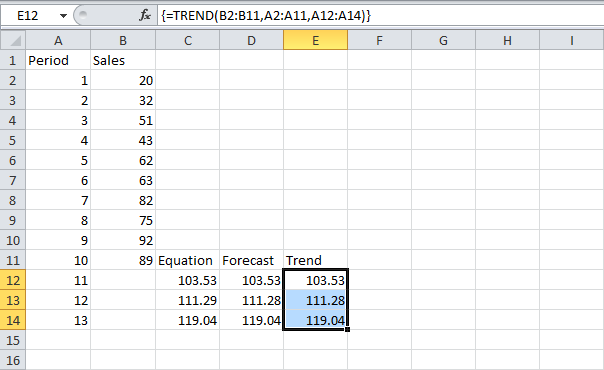
Если вам больше нравятся формулы массива, используйте функцию TREND (ТЕНДЕНЦИЯ) для расчета будущих продаж:
Примечание: Сначала выделите диапазон E12:E14. Затем введите формулу и нажмите Ctrl+Shift+Enter. Строка формул заключит ее в фигурные скобки, показывая, что это формула массива <>. Чтобы удалить формулу, выделите диапазон E12:E14 и нажмите клавишу Delete.
Пример функция тенденция в excel
Это первая статья из серии «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности», из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.
Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:
-
- Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
- Расчет сезонности;
- Расчет прогноза;
После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.
Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.
Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд продажи по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (минимальный уровень);
b – это значение, на которое увеличивается следующее значение временного ряда;
1-й способ расчета значений линейного тренда в Excel с помощью графика
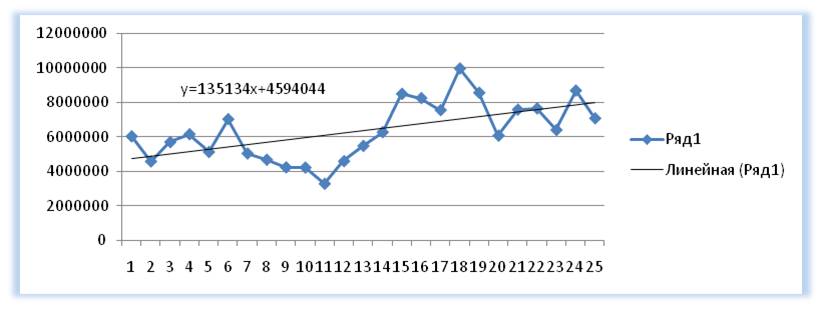
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
вместо константы ставим 1,
вместо статистики 0,
Получаем 135135 — значение (b) линейного тренда y=a+bx;
Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо
- установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;
- нажимаем клавишу F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых хотим рассчитать значения линейного тренда.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.
3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y — это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x — это номера периодов x для известных значений объёмов продаж y;
- новые значения x — это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа — ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в «новые значения x» вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Вместо X поставляем номер периода, для которого рассчитываем значение тренда.
Вместо «известные значения y» — объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
«известные значения x» — это номера периодов для каждого выделенного объёма продаж.
3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье «О линейном тренде».
5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
2. Заходим в меню программы и нажимаем «Start_Forecast». Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В следующих статье «Как самостоятельно сделать прогноз продаж с учетом роста и сезонности» мы:
О том, что еще важно знать о линейном тренде, вы можете узнать в статье «Что важно знать о линейном тренде».
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Комментарии
Сергей Иванович, добрый день!
С наступающим Новым Годом! Удачи и счастья в Новом Году!
По поводу формулы =ЛИНЕЙН()
Она очень гибкая в плане настроек и можно сделать все что хотите.
Посмотрите, пожалуйста. пример изменения формулы в этой статье:
https://4analytics.ru/trendi/3-sposoba-rascheta-polinoma-v-excel.html
Цитирую Сергей Иванович К.:
Анастасия, спасибо! Если будут вопросы, обращайтесь! Буду рад помочь!
Анастасия, спасибо! Если будут вопросы, обращайтесь! Буду рад помочь!
Использование встроенных функций Excel
В Excel имеется также инструмент регрессионного анализа для построения линий тренда вне области диаграммы. Для этой цели можно использовать ряд статистических функций рабочего листа, однако все они позволяют строить лишь линейные или экспоненциальные регрессии.
В Excel имеется несколько функций для построения линейной регрессии, в частности:
· НАКЛОН и ОТРЕЗОК.
А также несколько функций для построения экспоненциальной линии тренда, в частности:
Приемы построения регрессий с помощью функций ТЕНДЕНЦИЯ и РОСТ практически совпадают. То же самое можно сказать и о паре функций
ЛИНЕЙН и ЛГРФПРИБЛ. Для четырех этих функций при создании таблицы значений используются такие возможности Excel, как формулы массивов, что несколько загромождает процесс построения регрессий. Построение линейной регрессии легче всего осуществить с помощью функций НАКЛОН и ОТРЕЗОК, где первая из них определяет угловой коэффициент линейной регрессии, а вторая – отрезок, отсекаемый регрессией на оси ординат.
Задание. С таблицей данных о прибыли автотранспортного предприятия за 2000–2007 гг. (см. табл. 4.1) необходимо выполнить следующие действия:
1) получить ряды данных для линейной и экспоненциальной линии тренда с использованием функций ТЕНДЕНЦИЯ и РОСТ;
2) используя функции ТЕНДЕНЦИЯ и РОСТ, составить прогноз о прибыли предприятия на 2008 и 2009 гг.;
3) для исходных данных и полученных рядов данных построить диаграмму.
Методика выполнения. Воспользуемся исходной таблицей (см. рис. 4.4). Начнем с функции ТЕНДЕНЦИЯ.
1. Выделяем диапазон ячеек D4:D11, который следует заполнить значениями функции ТЕНДЕНЦИЯ, соответствующими известным данным о прибыли предприятия.
2. Вызываем команду Функция из меню Вставка. В появившемся диалоговом окне Мастер функций выделяем функцию ТЕНДЕНЦИЯ из категории Статистические, после чего щелкаем по кнопке ОК. Эту же операцию можно осуществить нажатием кнопки Вставка функции стандартной панели инструментов.
3. В появившемся диалоговом окне Аргументы функции вводим в поле Известные_значения_y диапазон ячеек C4:C11; в поле Известные_значения_х – диапазон ячеек B4:B11.
4. Чтобы вводимая формула стала формулой массива, используем комбинацию клавиш Ctrl + Shift + Enter.
Введенная нами формула в строке формул будет иметь следующий вид: =<ТЕНДЕНЦИЯ(C4:C11;B4:B11)>.
В результате диапазон ячеек D4:D11 заполняется соответствующими значениями функции ТЕНДЕНЦИЯ (рис. 4.7).
Рис. 4.7. Значения функций ТЕНДЕНЦИЯ и РОСТ
Для составления прогноза о прибыли предприятия на 2008 и 2009 гг. необходимо:
1) выделить диапазон ячеек D12:D13, куда будут заноситься значения, прогнозируемые функцией ТЕНДЕНЦИЯ;
2) вызвать функцию ТЕНДЕНЦИЯ и в появившемся диалоговом окне Аргументы функции ввести в поле Известные_значения_y – диапазон ячеек C4:C11; в поле Известные_значения_х – диапазон ячеек B4:B11; а в поле Новые_значения_х – диапазон ячеек B12:B13.
3) превратить эту формулу в формулу массива, используя комбинацию клавиш Ctrl + Shift + Enter.
Введенная формула будет иметь следующий вид:
а диапазон ячеек D12:D13 заполнится прогнозируемыми значениями функции ТЕНДЕНЦИЯ (см. рис. 4.7).
Аналогично заполняется ряд данных с помощью функции РОСТ, которая используется при анализе нелинейных зависимостей и работает точно так же, как ее линейный аналог ТЕНДЕНЦИЯ.
На рис. 4.8 представлена таблица в режиме показа формул.
Рис. 4.8. Таблица в режиме показа формул
Для исходных данных и полученных рядов данных построена диаграмма, изображенная на рис. 4.9.
Рис. 4.9. Графическое изображение линий тренда Прибыли
предприятия, функций ТЕНДЕНЦИЯ и РОСТ
Задание для самостоятельной работы. С таблицей данных о прибыли автотранспортного предприятия (см. табл. 4.1) необходимо выполнить следующие действия:
1) получить ряды данных для линейной регрессии, используя функции НАКЛОН и ОТРЕЗОК, в также используя функцию ЛИНЕЙН;
2) получить ряд данных для экспоненциальной регрессии с использованием функции ЛГРФПРИБЛ;
3) составить прогноз о прибыли за 2008–2009 гг., используя вышеназванные функции;
4) построить диаграмму для исходных и полученных рядов данных.
Отметим, что, в отличие от функций ТЕНДЕНЦИЯ и РОСТ, ни одна из перечисленных выше функций (НАКЛОН, ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ) не является регрессией. Эти функции играют лишь вспомогательную роль, определяя необходимые параметры регрессии.
Для линейной и экспоненциальной регрессий, построенных с помощью функций НАКЛОН, ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ, внешний вид их уравнений всегда известен, в отличие от линейной и экспоненциальной регрессий, соответствующих функциям ТЕНДЕНЦИЯ и РОСТ.

Лабораторная работа № 5
Модели линейной оптимизации в MS EXCEL
Цель: приобрести навыки в использовании настройки Поиск решения с условием максимизации или минимизации целевой функции.
Любую реальную проблему или ситуацию можно описать многими способами и на основе этого описания построить самые разнообразные формальные и математические модели. Этап разработки решения вытекает непосредственно из осознания наличия проблемы или ситуации, требующей принятия решения. На данном этапе необходимо просто четко сформулировать свою проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы, т. е. надо четко поставить проблему, а именно:
· сформулировать цели, которые должны быть достигнуты в результате реализации найденного решения;
· указать, что считать решением проблемы (решение должно гарантировать достижение целей);
· выявить и описать возможности достижения целей;
· выявить и описать факторы, от которых может зависеть решение проблемы;
· выявить и описать ограничения, препятствующие достижению целей;
· описать возможные альтернативные способы решения проблемы.
Эти пункты составляют формальную модель проблемы. Таким образом, формальная модель – это четкое описание вашей проблемы, в которой необходимо выделить перечисленные пункты.
Очень часто математическая постановка экономических задач, связанных с управлением, может быть сформулирована в общем виде следующим образом.
Пусть имеет место некоторая целевая функция z, которая зависит от параметров х = (х1, х2, …, хn),удовлетворяющих некоторым ограничениям α:
Требуется найти такие значения параметров или функций,которые обращают величину z в максимум или минимум. Такие задачи — отыскание значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, – носят общее название задач математического программирования и решаются методами теории исследования операций.
Среди задач математического программирования самыми простыми являются задачи линейного программирования (ЗЛП).
Основная задача линейного программирования (ОЗЛП) заключается в нахождении неотрицательных значений переменных, удовлетворяющих условиям – равенствам и обращающих в максимум линейную функцию этих переменных. Допустимое решение, максимизирующее целевую функцию, называется оптимальным решением (оптимальным планом).
Инструментом для решений задач оптимизации в MS Ехсеl служит надстройка Поиск решения. Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках.
Если данная надстройка установлена, то Поиск решения запускается из меню Сервис. Если такого пункта нет, следует выполнить команду Сервис → Надстройки. и выставить флажок против надстройки Поиск решения.
Решение поставленной задачи состоит из выполнения следующих действий:
1) анализа ситуации и формализации исходной проблемы (поставить проблему, четко определить цели, возможные решения и факторы, влияющие на решение проблемы);
2) построения математической модели (перевод формальной модели на четкий язык математических отношений);
3) анализа математической модели и получения математического решения проблемы (анализ построенной математической модели, построение компьютерной модели задачи);
4) анализа математического решения проблемы и формирование управленческого решения (на основе математического решения принимается управленческое решение).
При решении подобных задач используется термин «производственный план», который в общем смысле представляет собой план производства продукции, выпускаемой данным предприятием, расписанный по месяцам, неделям или дням (в зависимости от длительности производственного цикла предприятия).
Задание. Предприятие «Олимп» имеет месячный цикл производства. Необходимо определить, сколько в месяц необходимо производить краски типа А и типа Б. Производственная мощность позволяет выпускать в месяц суммарно 500 т краски всех типов. Тонна краски типа А приносит в среднем 2000 руб. прибыли, а одна тонна краски типа Б – 2500 руб. Заказ на краску типа А – не менее 200 т в месяц (по договорам на поставку), краски типа Б нельзя производить более 150 т, так как большее количество трудно реализовать. По рецептуре на изготовление краски типов А и Б тратится три вида сырья (табл. 5.1).