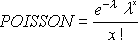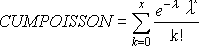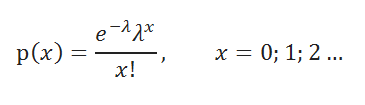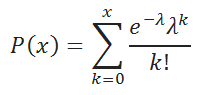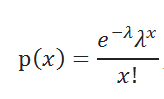Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает распределение Пуассона. Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например количества машин, появляющихся на площади за одну минуту.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ПУАССОН.РАСП.
Синтаксис
ПУАССОН(x;среднее;интегральная)
Аргументы функции ПУАССОН описаны ниже.
-
X Обязательный. Количество событий.
-
Среднее Обязательный. Ожидаемое числовое значение.
-
Интегральная — обязательный аргумент. Логическое значение, определя которое определяет форму возвращаемого распределения вероятности. Если значение «совокупное» имеет значение ИСТИНА, то пуассон возвращает совокупное значение вероятности того, что число случайных событий включительно будет от нуля до x. Если этот ложь, возвращается функция массовой вероятности Пуассона, которая вероятность того, что количество произошедших событий будет точно x.
Замечания
-
Если x не является целым числом, оно усекается.
-
Если x или «число» не является числом, то пуАССОН возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если x < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если в < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Функция ПУАССОН вычисляется следующим образом.
Если интегральная = ЛОЖЬ:
Если интегральная = ИСТИНА:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
2 |
Число событий |
|
|
5 |
Ожидаемое среднее |
|
|
Формула |
Описание (результат) |
Результат |
|
=ПУАССОН(A2;A3;ИСТИНА) |
Интегральное распределение Пуассона для приведенных выше условий (0,124652) |
0,124652 |
|
=ПУАССОН(A2;A3;ЛОЖЬ) |
Функция плотности распределения Пуассона для приведенных выше условий (0,084224) |
0,084224 |
Нужна дополнительная помощь?
Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL
ПУАССОН.РАСП()
построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и стандартного отклонения.
Сначала дадим сухое формальное определение распределения, затем приведем примеры ситуаций, когда
распределение Пуассона
(англ.
Poisson
distribution
) является адекватной моделью для описания случайной величины.
Если случайные события происходят в заданный период времени (или в определенном объеме вещества) со средней частотой λ(
лямбда
), то число событий
x
,
произошедших за этот период времени, будет иметь
распределение Пуассона
.
Плотность вероятности
распределения Пуассона
задается следующей формулой:
λ – единственный параметр
распределения Пуассона
.
СОВЕТ
: подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Применение распределения Пуассона
Примеры, когда
Распределение Пуассона
является адекватной моделью:
- число вызовов, поступивших на телефонную станцию за определенный период времени;
- число частиц, подвергнувшихся радиоактивному распаду за определенный период времени;
- число дефектов в куске ткани фиксированной длины.
Распределение Пуассона
является адекватной моделью, если выполняются следующие условия:
- события происходят независимо друг от друга, т.е. вероятность последующего события не зависит от предыдущего;
- средняя частота событий постоянна. Как следствие, вероятность события пропорциональна длине интервала наблюдения;
- два события не могут произойти одновременно;
- число событий должно принимать значения 0; 1; 2…
Примечание
: Хорошей подсказкой, что наблюдаемая случайная величина имеет
распределение Пуассона,
является тот факт, что
среднее значение выборки
приблизительно равно
дисперсии
(см. ниже).
Ниже представлены примеры ситуаций, когда
Распределение Пуассона
не может
быть применено:
- число студентов, которые выходят из университета в течение часа (т.к. средний поток студентов не постоянен: во время занятий студентов мало, а в перерыве между занятиями число студентов резко возрастает);
- число землетрясений амплитудой 5 баллов в год в Калифорнии (т.к. одно землетрясение может вызвать повторные толчки сходной амплитуды – события не независимы);
- число дней, которые пациенты проводят в отделении интенсивной терапии (т.к. число дней, которое пациенты проводят в отделении интенсивной терапии всегда больше 0).
Примечание
:
Распределение Пуассона
является приближением более точных дискретных распределений:
Гипергеометрического
и
Биномиального
.
Примечание
: О взаимосвязи
распределения Пуассона
и
Биномиального распределения
можно прочитать в статье
Взаимосвязь некоторых распределений в MS EXCEL
. О взаимосвязи
распределения Пуассона
и
Экспоненциального распределения
можно прочитать в статье про
Экспоненциальное распределение
.
Распределение Пуассона в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Распределения
Пуассона
имеется функция
ПУАССОН.РАСП()
, английское название — POISSON.DIST(), которая позволяет вычислить не только вероятность того, что за заданный период времени произойдет
х
событий (функцию
плотности вероятности
p(x), см. формулу выше), но и
интегральную функцию распределения
(вероятность того, что за заданный период времени произойдет не меньше
x
событий).
До MS EXCEL 2010 в EXCEL была функция
ПУАССОН()
, которая также позволяет вычислить
функцию распределения
и
плотность вероятности
p(x).
ПУАССОН()
оставлена в MS EXCEL 2010 для совместимости.
В
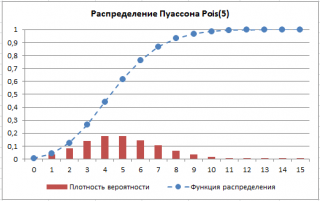
файле примера
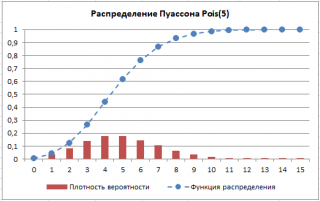
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Распределение Пуассона
имеет скошенную форму (длинный хвост справа у функции вероятности), но при увеличении параметра λ становится все более симметричным.
Примечание
: Для построения
интегральной функции распределения
идеально подходит диаграмма типа
График
, для
плотности распределения
–
Гистограмма с группировкой
. Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Примечание
:
Среднее
и
дисперсия
(квадрат
стандартного отклонения
) равны параметру
распределения Пуассона
– λ (см.
файл примера лист Пример
).
Задача
Типичным применением
Распределения Пуассона
в контроле качества является модель количества дефектов, которые могут появиться в приборе или устройстве.
Например, при среднем количестве дефектов в микросхеме λ (лямбда) равном 4, вероятность, что случайно выбранная микросхема будет иметь 2 или меньше дефектов, равна: =
ПУАССОН.РАСП(2;4;ИСТИНА)=0,2381
Третий параметр в функции установлен = ИСТИНА, поэтому функция вернет
интегральную функцию распределения
, то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до 4 включительно.
Вычисления в этом случае производятся по формуле:
Вероятность того, что случайно выбранная микросхема будет иметь ровно 2 дефекта, равна: =
ПУАССОН.РАСП(2;4;ЛОЖЬ)=0,1465
Третий параметр в функции установлен = ЛОЖЬ, поэтому функция вернет плотность вероятности.
Вероятность того, что случайно выбранная микросхема будет иметь больше 2-х дефектов, равна:
=1-ПУАССОН.РАСП(2;4;ИСТИНА) =0,8535
Примечание
: Если
x
не является целым числом, то при вычислении формулы
дробная часть числа отбрасывается
. Формулы
=ПУАССОН.РАСП(
2
; 4; ЛОЖЬ)
и
=ПУАССОН.РАСП(
2,9
; 4; ЛОЖЬ)
вернут одинаковый результат.
Генерация случайных чисел и оценка λ
С помощью надстройки
Пакет анализа
можно сгенерировать случайные числа, извлеченные из
распределения Пуассона
.
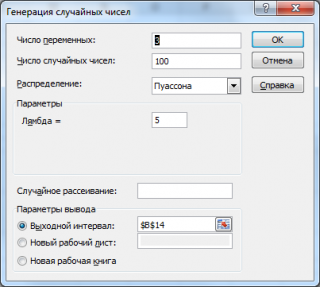
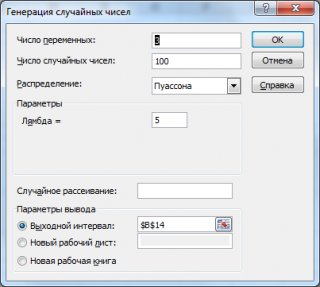
Сгенерируем 3 массива по 100 чисел с параметром λ=5. Для этого в окне
Генерация случайных чисел
установим следующие параметры:
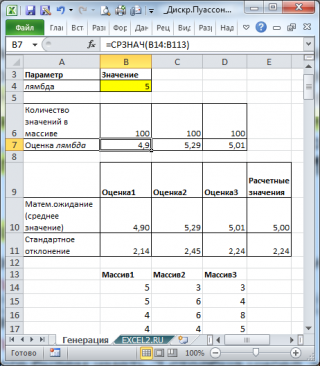
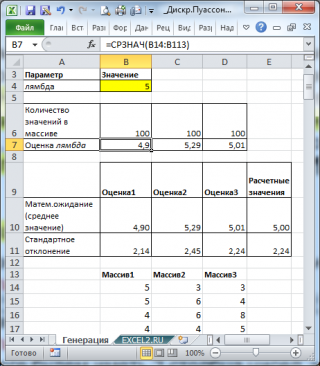
В итоге будем иметь 3 столбца чисел, на основании которых можно оценить параметр λ для каждого массива с помощью функции
СРЗНАЧ()
, см.
файл примера лист Генерация
.
Связь Распределения Пуассона с Биномиальным и Нормальным распределением
Распределение Пуассона
является предельным случаем
Биномиального распределения
, при условии, если параметр
n
Биномиального распределения
стремится к бесконечности, а
p
– к 0.
Можно сформулировать условия, когда приближение
распределением Пуассона
работает хорошо:
p
<0,1
(чем меньше p и больше n, тем приближение точнее);
p
>0,9
(учитывая, что
q
=1-
p
, вычисления в этом случае необходимо производить через
q
(а
х
нужно заменить на
n
—
x
). Следовательно, чем меньше
q
и больше
n
, тем приближение точнее).
Примечание
: Если 0,1<=p<=0,9, а n*p>10, то
Биномиальное распределение
можно аппроксимировать
Нормальным распределением
.
При значениях λ
>15
,
Распределение Пуассона
хорошо аппроксимируется
Нормальным распределением
со следующими параметрами: μ
=λ
, σ
2
=λ
.
Подробнее о связи этих распределений, можно прочитать в статье
Взаимосвязь некоторых распределений в MS EXCEL
. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Функция ПУАССОН.РАСП в Excel используется для получения распределения Пуассона для случайных событий, происходящих за определенный промежуток времени с известной средней частотой.
Закон Пуассона распределения вероятностей случайной величины в Excel
Функция ПУАССОН.РАСП возвращает два варианта значений (в зависимости от значения, переданного в качестве третьего аргумента):
- Интегральное распределение Пуассона – числовое значение вероятности того, что известное количество случайных событий принадлежит диапазону 0;[x] (то есть, от 0 до x включительно).
- Функция весовых коэффициентов – числовое значение вероятности того, что количество произошедших событий точно равно числу x.
Для расчета плотности вероятности используется следующая формула:
Здесь x находится в диапазоне от 0 до бесконечности со знаком плюс.
Примечания:
- Функция распределения вероятностей (в целом) – зависимость F(x), которая в точке x принимает значение, соответствующее вероятности того, что некоторая случайная величина X будет меньше значения x), то есть F(x)=P(X<x).
- Для понимания функций распределения вероятности рассмотрим пример о заводе по производству соков. При расфасовке тар емкостью 1000 г возможны отклонения от заявленного объема, поскольку дозирующее устройство работает с погрешностью. То есть, может быть емкость, содержащая 1000 г сока, и емкость с 980 г сока. Вероятность того, что в одной из тар будет 980 г напитка составляет 0, а 1000г – 1. Для нахождения промежуточных значений объемов используют функции распределения. К примеру, если настроить дозирующее устройство на наполнение емкостей по 990 г сока, вероятность нахождения тары с меньшим объемом напитка составляет 0,5.
- Функция ПУАССОН использовалась в более старых версиях Excel до 2010 года. Она была оставлена для обеспечения совместимости. В более новых версиях следует использовать функцию ПУАССОН.РАСП.
- Распределение Пуассона – один из видов функций распределения величин. Ее рационально использовать, если исследуемая математическая модель удовлетворяет следующим условиям:
- Вероятность каждого последующего события не связана с предыдущим, то есть каждое событие является независимым;
- События характеризуются средней частотой, которая является константой;
- Вероятность события и длина периода наблюдения являются пропорциональными величинами;
- Вероятность происхождения двух событий одновременна равна нулю;
- Отсчет количества событий начинается от 0 до бесконечности (0, 1, 2,…);
- Среднее значение выборки является величиной, близкой по значению к значению дисперсии.
Примечание: Распределение Пуассона неприменимо в следующих случаях:
- события являются зависимыми;
- непостоянство средней величины;
- минимальная величина превышает значение 0.
Решение задачи на распределение Пуассона в Excel
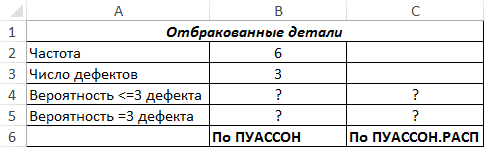
Пример 1. Отдел технического контроля определил, что среднее число не соблюденных допусков в размерах производимых деталей составляет 6. Определить вероятности следующих событий обеими рассматриваемыми функциями (для сравнения результатов вычислений):
- Вероятность наличия 3 и менее погрешностей в случайно отобранной детали.
- Вероятность наличия ровно 3 погрешностей в случайно выбранной детали.
Вид таблицы данных:
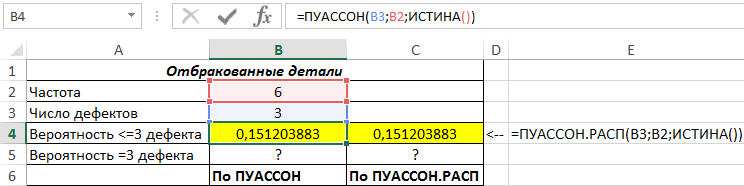
Рассчитаем вероятность наличия трех и менее дефектов с помощью функций:
=ПУАССОН(B3;B2;ИСТИНА())
=ПУАССОН.РАСП(B3;B2;ИСТИНА())
Описание аргументов:
- B3 – среднее значение;
- B2 – предполагаемое значение, для которого рассчитывается вероятность;
- ИСТИНА – указатель на интегральный тип функции.
Полученные результаты:
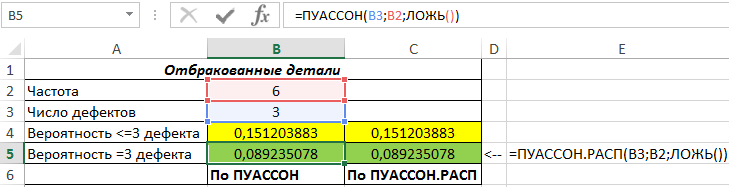
Для нахождения вероятности выбора детали с наличием ровно трех дефектов используем функции:
=ПУАССОН(B3;B2;ЛОЖЬ())
=ПУАССОН.РАСП(B3;B2;ЛОЖЬ())
Для расчета вероятности точного совпадения третий аргумент задан в качестве логического ЛОЖЬ.
Результаты вычислений:
Как видно, результаты вычислений обеих функций идентичны.
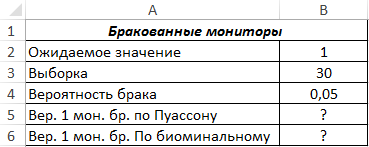
Биномиальное распределение Пуассона в Excel
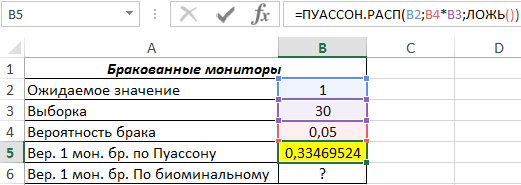
Пример 2. На заводе по производству мониторов ожидается, что 5% изделий будут бракованными. Была взята выборка из 30 мониторов. Определить вероятность того, что 1 монитор из 30 окажется бракованным. Для решения использовать распределение Пуассона и биномиальное распределение, полученные результаты сравнить.
Вид таблицы данных:
Для определения вероятности события, при котором в выборке будет найден один бракованный монитор с использованием распределения Пуассона запишем функцию:
=ПУАССОН.РАСП(B2;B4*B3;ЛОЖЬ())
Произведение B4*B3 соответствует среднему ожидаемому значению (1,5). Полученный результат:
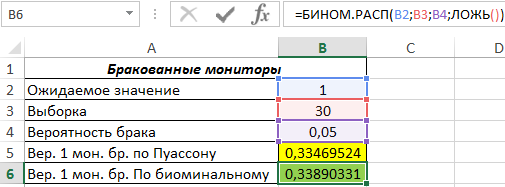
Для расчета с использованием биномиального распределения запишем функцию:
=БИНОМ.РАСП(B2;B3;B4;ЛОЖЬ())
Результат вычислений:
Как видно, для данной математической модели подходят оба метода определения вероятностей, поскольку полученные значения отличаются незначительно.
Распределение Пуассона является одним из наиболее часто используемых распределений в статистике.
В Excel мы можем использовать функцию ПУАССОН.РАСП() , чтобы найти вероятность того, что событие произойдет определенное количество раз в течение заданного интервала, на основе знания среднего количества раз, когда событие происходит в течение заданного интервала.
Синтаксис POISSON.DIST следующий:
ПУАССОНА.РАСП (x, среднее, кумулятивное)
- x: количество вхождений в течение заданного интервала
- среднее значение: среднее количество вхождений в течение заданного интервала
- кумулятивный: TRUE возвращает кумулятивную вероятность; FALSE возвращает точную вероятность
В следующих примерах показано, как решать вопросы вероятности Пуассона с помощью POISSON.DIST .
Пример 1
Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут 5 молотков в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество вхождений в течение заданного интервала (продажа 5 молотков)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 3 )
- кумулятивный: ЛОЖЬ (нам нужна точная вероятность, а не кумулятивная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(5, 3, ЛОЖЬ)
Вероятность того, что магазин продаст 5 молотков в данный день, равна 0,100819 .
Пример 2
Один магазин продает в среднем 15 банок тунца в день. Какова вероятность того, что этот магазин продаст более 20 банок тунца в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество вхождений в течение заданного интервала (продажа 20 банок)
- среднее: среднее количество вхождений в течение заданного интервала (в среднем они продают 15 банок)
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: 1 – ПУАССОН.РАСП(20, 15, ИСТИНА)
Вероятность того, что магазин продаст более 20 банок тунца в данный день, равна 0,082971 .
Примечание. В этом примере функция ПУАССОН.РАСП(20, 15, ИСТИНА) возвращает вероятность того, что магазин продаст 20 или менее банок тунца. Итак, чтобы найти вероятность того, что магазин продаст более 20 банок, мы просто используем 1 — ПУАССОН.РАСП(20, 15, ИСТИНА).
Пример 3
Один магазин спортивных товаров продает в среднем семь баскетбольных мячей в день. Какова вероятность того, что этот магазин продаст четыре или меньше баскетбольных мячей в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество событий в течение заданного интервала (продажа 4 баскетбольных мячей)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 7 )
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(4, 7, ИСТИНА)
Вероятность того, что магазин продаст 4 или меньше баскетбольных мячей в данный день, равна 0,172992 .
Пример 4
Один магазин продает в среднем двенадцать ананасов в день. Какова вероятность того, что в данном магазине в данный день продается от 12 до 14 ананасов?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество случаев в течение заданного интервала (продажа от 12 до 14 ананасов)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 12 )
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel:
ПУАССОНА.РАСП(14, 12, ИСТИНА) – ПУАССОНА.РАСП(11, 12, ИСТИНА)
Вероятность того, что магазин продаст от 12 до 14 ананасов в данный день, равна 0,310427 .
Примечание. В этом примере функция ПУАССОН.РАСП(14, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 14 или меньше ананасов, а ПУАССОН.РАСП(11, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 11 или меньше ананасов. Итак, чтобы найти вероятность того, что в магазине продается от 12 до 14 наименований, мы вычитаем разницу, так что мы фактически находим вероятность того, что в магазине продается 12, 13 или 14 ананасов.
Альтернативный способ решить эту задачу — просто найти отдельные вероятности продажи 12, 13 и 14 ананасов, а затем сложить эти вероятности:
Это дает нам ту же вероятность, что и предыдущий метод.
Содержание
- Как создать график распределения Пуассона в Excel
- Пример: график распределения Пуассона в Excel
- Как использовать распределение Пуассона в Excel
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Распределение Пуассона. Дискретные распределения в EXCEL
- Применение распределения Пуассона
- Распределение Пуассона в MS EXCEL
- Задача
- Генерация случайных чисел и оценка λ
- Связь Распределения Пуассона с Биномиальным и Нормальным распределением
Как создать график распределения Пуассона в Excel
Распределение Пуассона описывает вероятность получения k успехов за заданный интервал времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.
В следующем примере показано, как создать график распределения Пуассона в Excel.
Пример: график распределения Пуассона в Excel
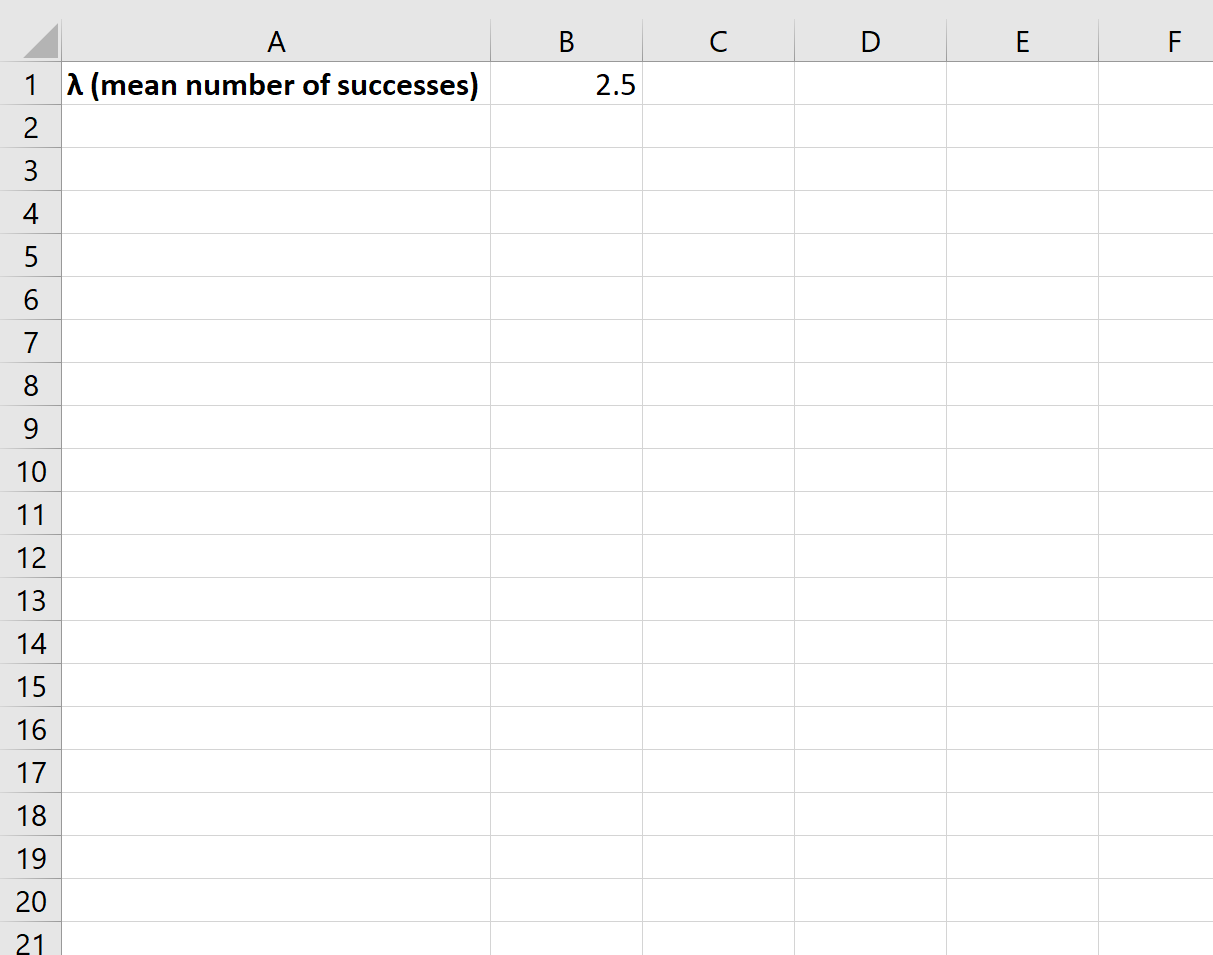
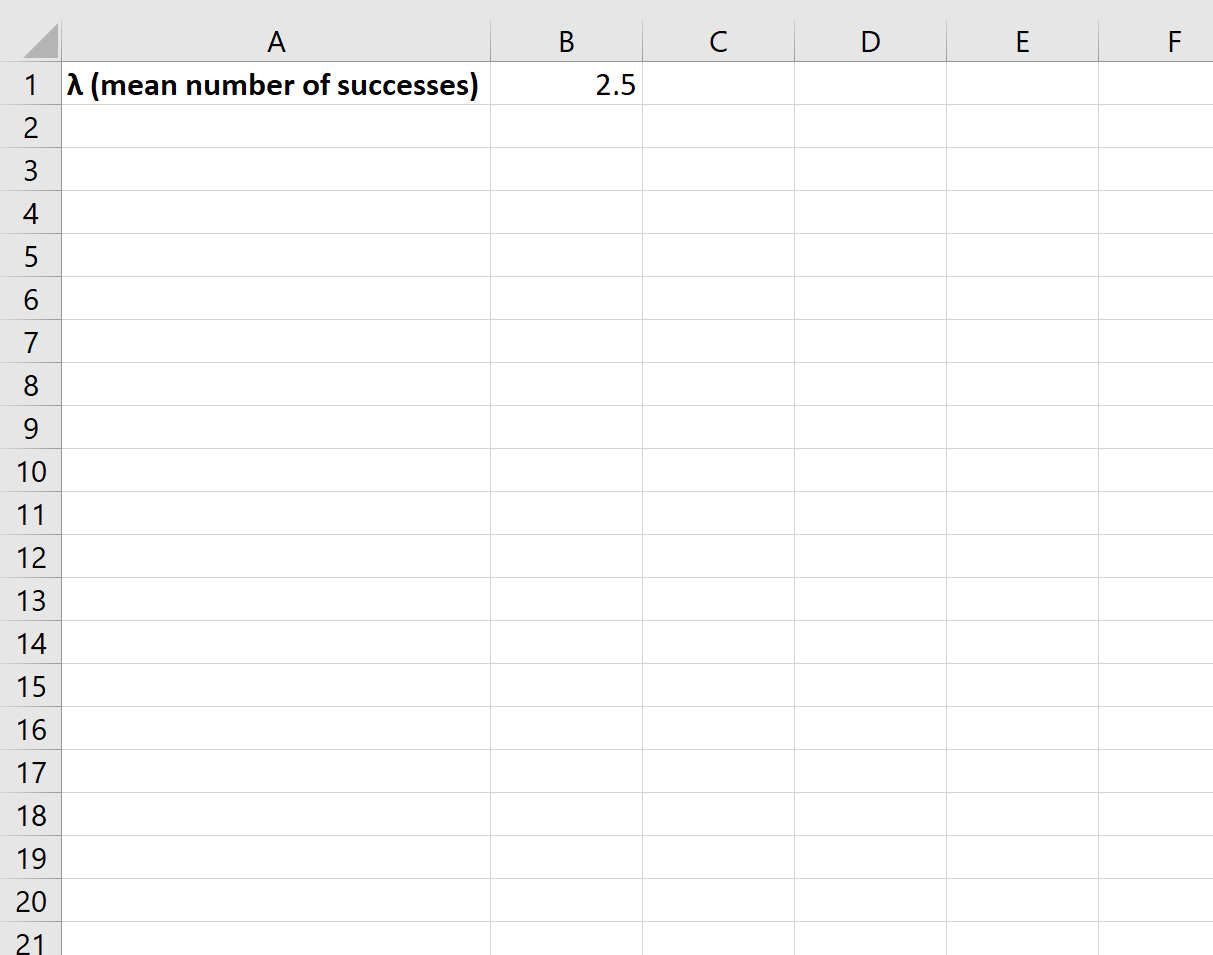
Чтобы создать график распределения Пуассона, нам нужно сначала определиться со значением λ (среднее количество успехов):
Далее нам нужно создать столбец для каждого возможного количества успехов:
Обратите внимание, что мы выбрали k = 10 возможных успехов. Мы могли бы выбрать больше, но вероятности становятся очень маленькими для значений больше 10, как мы увидим позже в этом посте.
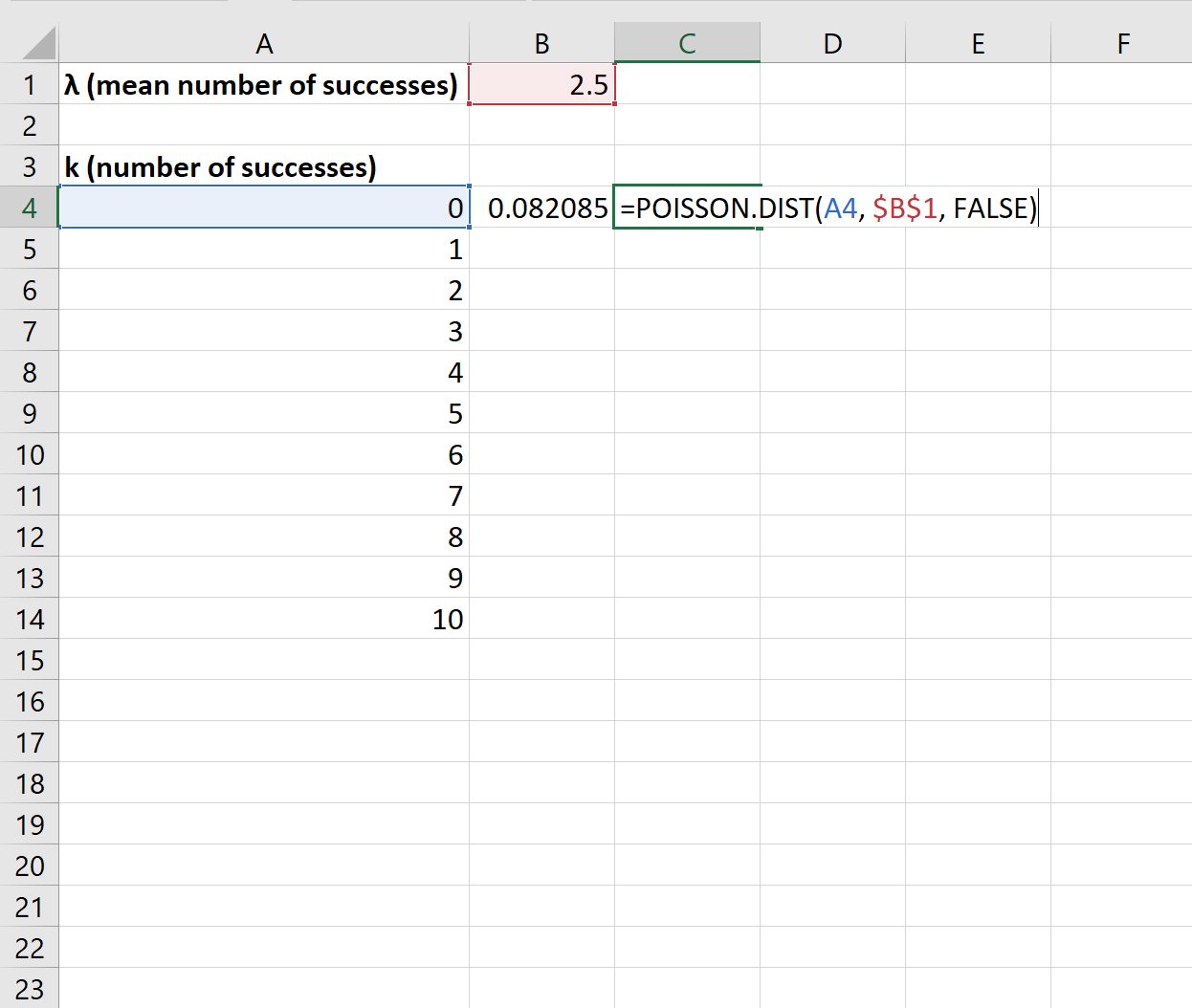
Затем мы можем использовать функцию POISSON.DIST() для вычисления вероятности Пуассона для первого числа успехов:
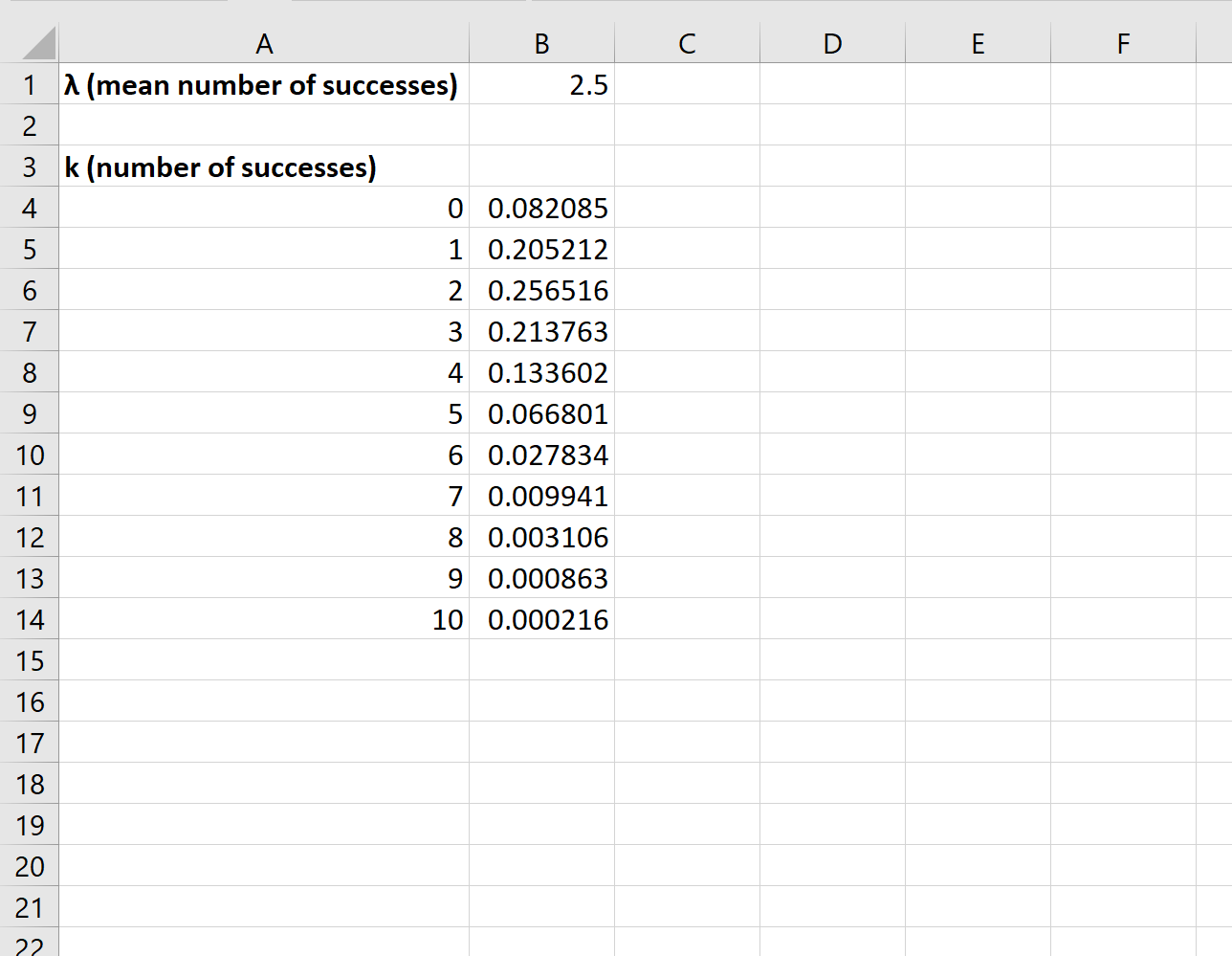
Затем мы можем скопировать и вставить эту формулу в оставшиеся ячейки столбца B:
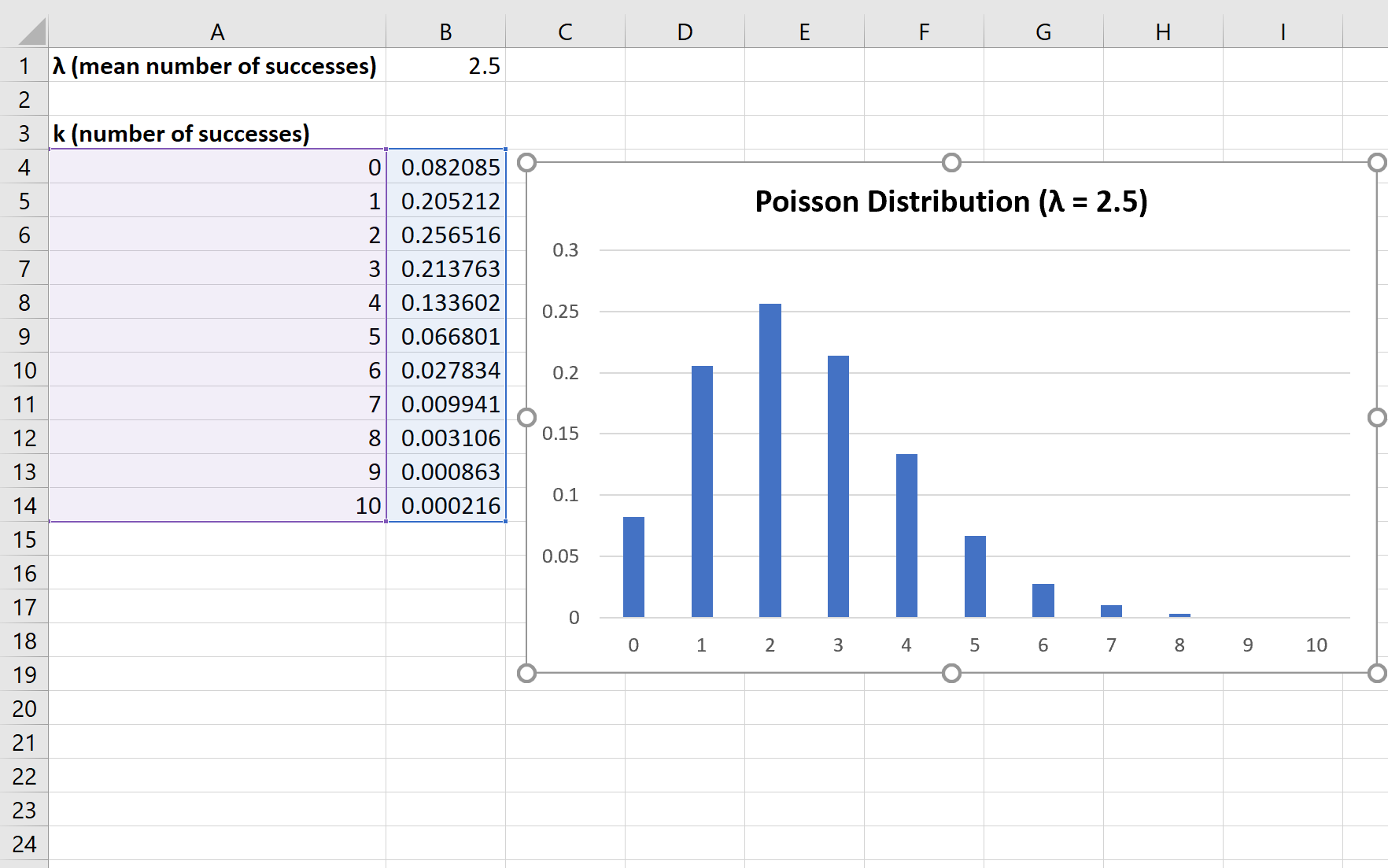
Наконец, мы можем выделить каждую из вероятностей Пуассона, затем щелкнуть вкладку « Вставка » на верхней ленте, затем щелкнуть значок « Вставить столбец или гистограмму» в группе « Диаграммы »:
Ось X графика показывает количество успехов, а ось Y показывает соответствующую вероятность этого количества успехов.
Обратите внимание, что если вы измените значение λ (среднее количество успехов), график автоматически изменится, чтобы отразить новые вероятности.
Например, если мы изменим значение λ на 4, вероятности Пуассона и график автоматически обновятся:
Источник
Как использовать распределение Пуассона в Excel
Распределение Пуассона является одним из наиболее часто используемых распределений в статистике.
В Excel мы можем использовать функцию ПУАССОН.РАСП() , чтобы найти вероятность того, что событие произойдет определенное количество раз в течение заданного интервала, на основе знания среднего количества раз, когда событие происходит в течение заданного интервала.
Синтаксис POISSON.DIST следующий:
ПУАССОНА.РАСП (x, среднее, кумулятивное)
- x: количество вхождений в течение заданного интервала
- среднее значение: среднее количество вхождений в течение заданного интервала
- кумулятивный: TRUE возвращает кумулятивную вероятность; FALSE возвращает точную вероятность
В следующих примерах показано, как решать вопросы вероятности Пуассона с помощью POISSON.DIST .
Пример 1
Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут 5 молотков в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество вхождений в течение заданного интервала (продажа 5 молотков)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 3 )
- кумулятивный: ЛОЖЬ (нам нужна точная вероятность, а не кумулятивная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(5, 3, ЛОЖЬ)
Вероятность того, что магазин продаст 5 молотков в данный день, равна 0,100819 .
Пример 2
Один магазин продает в среднем 15 банок тунца в день. Какова вероятность того, что этот магазин продаст более 20 банок тунца в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество вхождений в течение заданного интервала (продажа 20 банок)
- среднее: среднее количество вхождений в течение заданного интервала (в среднем они продают 15 банок)
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: 1 – ПУАССОН.РАСП(20, 15, ИСТИНА)
Вероятность того, что магазин продаст более 20 банок тунца в данный день, равна 0,082971 .
Примечание. В этом примере функция ПУАССОН.РАСП(20, 15, ИСТИНА) возвращает вероятность того, что магазин продаст 20 или менее банок тунца. Итак, чтобы найти вероятность того, что магазин продаст более 20 банок, мы просто используем 1 — ПУАССОН.РАСП(20, 15, ИСТИНА).
Пример 3
Один магазин спортивных товаров продает в среднем семь баскетбольных мячей в день. Какова вероятность того, что этот магазин продаст четыре или меньше баскетбольных мячей в данный день?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество событий в течение заданного интервала (продажа 4 баскетбольных мячей)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 7 )
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(4, 7, ИСТИНА)
Вероятность того, что магазин продаст 4 или меньше баскетбольных мячей в данный день, равна 0,172992 .
Пример 4
Один магазин продает в среднем двенадцать ананасов в день. Какова вероятность того, что в данном магазине в данный день продается от 12 до 14 ананасов?
В этом примере мы можем подключить следующие числа к функции POISSON.DIST :
- x: количество случаев в течение заданного интервала (продажа от 12 до 14 ананасов)
- среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 12 )
- кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel:
ПУАССОНА.РАСП(14, 12, ИСТИНА) – ПУАССОНА.РАСП(11, 12, ИСТИНА)
Вероятность того, что магазин продаст от 12 до 14 ананасов в данный день, равна 0,310427 .
Примечание. В этом примере функция ПУАССОН.РАСП(14, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 14 или меньше ананасов, а ПУАССОН.РАСП(11, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 11 или меньше ананасов. Итак, чтобы найти вероятность того, что в магазине продается от 12 до 14 наименований, мы вычитаем разницу, так что мы фактически находим вероятность того, что в магазине продается 12, 13 или 14 ананасов.
Альтернативный способ решить эту задачу — просто найти отдельные вероятности продажи 12, 13 и 14 ананасов, а затем сложить эти вероятности:
Это дает нам ту же вероятность, что и предыдущий метод.
Источник
Распределение Пуассона. Дискретные распределения в EXCEL
history 6 ноября 2016 г.
Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ПУАССОН.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и стандартного отклонения.
Сначала дадим сухое формальное определение распределения, затем приведем примеры ситуаций, когда распределение Пуассона (англ. Poisson distribution ) является адекватной моделью для описания случайной величины.
Если случайные события происходят в заданный период времени (или в определенном объеме вещества) со средней частотой λ( лямбда ), то число событий x , произошедших за этот период времени, будет иметь распределение Пуассона .
Плотность вероятности распределения Пуассона задается следующей формулой:
λ – единственный параметр распределения Пуассона .
Применение распределения Пуассона
Примеры, когда Распределение Пуассона является адекватной моделью:
- число вызовов, поступивших на телефонную станцию за определенный период времени;
- число частиц, подвергнувшихся радиоактивному распаду за определенный период времени;
- число дефектов в куске ткани фиксированной длины.
Распределение Пуассона является адекватной моделью, если выполняются следующие условия:
- события происходят независимо друг от друга, т.е. вероятность последующего события не зависит от предыдущего;
- средняя частота событий постоянна. Как следствие, вероятность события пропорциональна длине интервала наблюдения;
- два события не могут произойти одновременно;
- число событий должно принимать значения 0; 1; 2…
Примечание : Хорошей подсказкой, что наблюдаемая случайная величина имеет распределение Пуассона, является тот факт, что среднее значение выборки приблизительно равно дисперсии (см. ниже).
Ниже представлены примеры ситуаций, когда Распределение Пуассона не может быть применено:
- число студентов, которые выходят из университета в течение часа (т.к. средний поток студентов не постоянен: во время занятий студентов мало, а в перерыве между занятиями число студентов резко возрастает);
- число землетрясений амплитудой 5 баллов в год в Калифорнии (т.к. одно землетрясение может вызвать повторные толчки сходной амплитуды – события не независимы);
- число дней, которые пациенты проводят в отделении интенсивной терапии (т.к. число дней, которое пациенты проводят в отделении интенсивной терапии всегда больше 0).
Примечание : Распределение Пуассона является приближением более точных дискретных распределений: Гипергеометрического и Биномиального .
Примечание : О взаимосвязи распределения Пуассона и Биномиального распределения можно прочитать в статье Взаимосвязь некоторых распределений в MS EXCEL . О взаимосвязи распределения Пуассона и Экспоненциального распределения можно прочитать в статье про Экспоненциальное распределение .
Распределение Пуассона в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Распределения Пуассона имеется функция ПУАССОН.РАСП() , английское название — POISSON.DIST(), которая позволяет вычислить не только вероятность того, что за заданный период времени произойдет х событий (функцию плотности вероятности p(x), см. формулу выше), но и интегральную функцию распределения (вероятность того, что за заданный период времени произойдет не меньше x событий).
До MS EXCEL 2010 в EXCEL была функция ПУАССОН() , которая также позволяет вычислить функцию распределения и плотность вероятности p(x). ПУАССОН() оставлена в MS EXCEL 2010 для совместимости.
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Распределение Пуассона имеет скошенную форму (длинный хвост справа у функции вероятности), но при увеличении параметра λ становится все более симметричным.
Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Примечание : Среднее и дисперсия (квадрат стандартного отклонения ) равны параметру распределения Пуассона – λ (см. файл примера лист Пример ).
Задача
Типичным применением Распределения Пуассона в контроле качества является модель количества дефектов, которые могут появиться в приборе или устройстве.
Например, при среднем количестве дефектов в микросхеме λ (лямбда) равном 4, вероятность, что случайно выбранная микросхема будет иметь 2 или меньше дефектов, равна: = ПУАССОН.РАСП(2;4;ИСТИНА)=0,2381
Третий параметр в функции установлен = ИСТИНА, поэтому функция вернет интегральную функцию распределения , то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до 4 включительно.
Вычисления в этом случае производятся по формуле:
Вероятность того, что случайно выбранная микросхема будет иметь ровно 2 дефекта, равна: = ПУАССОН.РАСП(2;4;ЛОЖЬ)=0,1465
Третий параметр в функции установлен = ЛОЖЬ, поэтому функция вернет плотность вероятности.
Вероятность того, что случайно выбранная микросхема будет иметь больше 2-х дефектов, равна: =1-ПУАССОН.РАСП(2;4;ИСТИНА) =0,8535
Примечание : Если x не является целым числом, то при вычислении формулы дробная часть числа отбрасывается . Формулы =ПУАССОН.РАСП( 2 ; 4; ЛОЖЬ) и =ПУАССОН.РАСП( 2,9 ; 4; ЛОЖЬ) вернут одинаковый результат.
Генерация случайных чисел и оценка λ
С помощью надстройки Пакет анализа можно сгенерировать случайные числа, извлеченные из распределения Пуассона .
Сгенерируем 3 массива по 100 чисел с параметром λ=5. Для этого в окне Генерация случайных чисел установим следующие параметры:
В итоге будем иметь 3 столбца чисел, на основании которых можно оценить параметр λ для каждого массива с помощью функции СРЗНАЧ() , см. файл примера лист Генерация .
Связь Распределения Пуассона с Биномиальным и Нормальным распределением
Распределение Пуассона является предельным случаем Биномиального распределения , при условии, если параметр n Биномиального распределения стремится к бесконечности, а p – к 0.
Можно сформулировать условия, когда приближение распределением Пуассона работает хорошо:
- p0,9 (учитывая, что q=1-p , вычисления в этом случае необходимо производить через q (а х нужно заменить на n—x ). Следовательно, чем меньше q и больше n , тем приближение точнее).
Примечание : Если 0,1 10, то Биномиальное распределение можно аппроксимировать Нормальным распределением .
При значениях λ >15 , Распределение Пуассона хорошо аппроксимируется Нормальным распределением со следующими параметрами: μ =λ , σ 2 =λ .
Подробнее о связи этих распределений, можно прочитать в статье Взаимосвязь некоторых распределений в MS EXCEL . Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник