Excel функция линейн полином

полиномЕсть 3 способа расчета значений полинома в Excel:

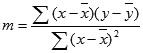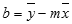
  • 1-й способ с помощью графика;
  • 2-й способ с помощью функции Excel =ЛИНЕЙН();
  • 3-й способ с помощью Forecast4AC PRO;

Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.

Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).

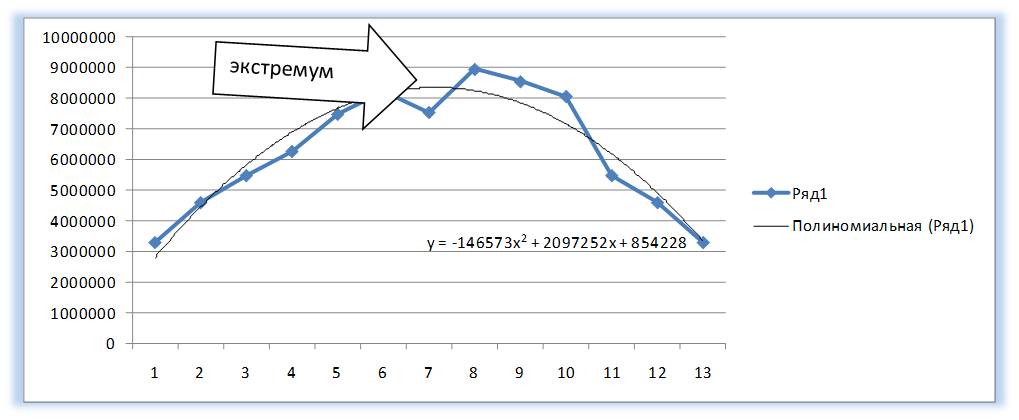
Что такое полином? Полином — это степенная функция y=ax2+bx+c (полином второй степени) и y=ax3+bx2+cx+d (полином третей степени) и т.д.  Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.

У полинома второй степени y=ax2+bx+c один экстремум (на графике ниже 1 максимум).

один экстремум

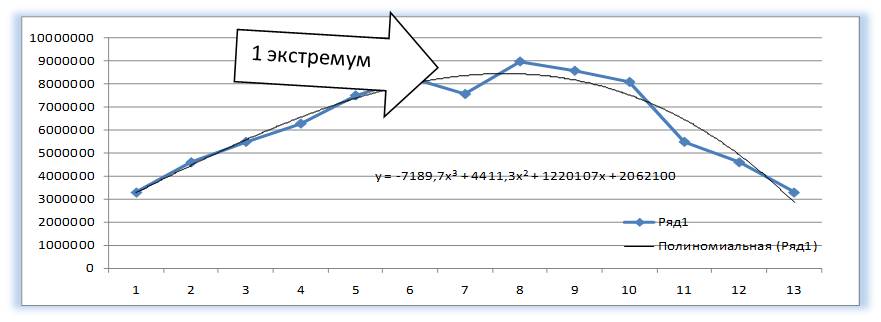
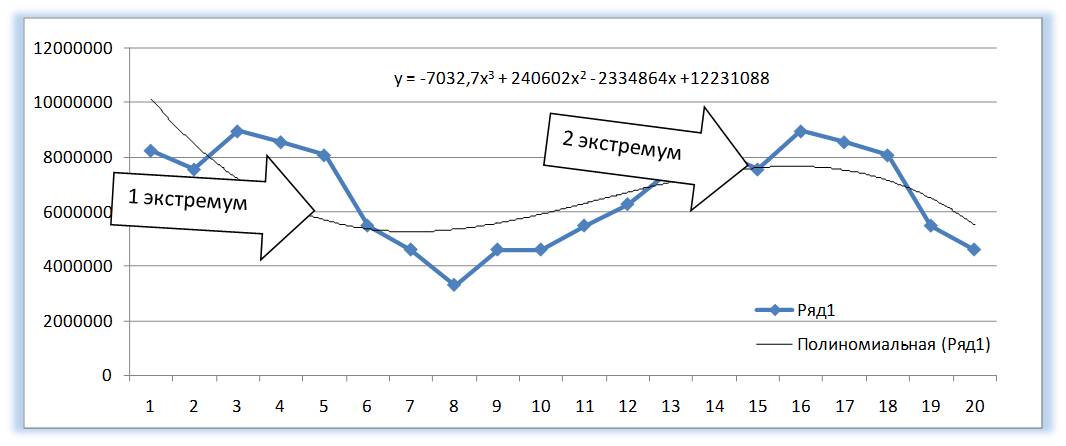
У Полинома третьей степени y=ax3+bx2+cx+d может быть один или два экстремума.

Один экстремум

один экстремум полинома

Два экстремума

2 экстремума полинома третьей степени

У Полинома четвертой степени не более трех экстремумов и т.д.

Как рассчитать значения полинома в Excel?

Есть 3 способа расчета значений полинома в Excel:

  • 1-й способ с помощью графика;
  • 2-й способ с помощью функции Excel =ЛИНЕЙН;
  • 3-й способ с помощью Forecast4AC PRO;

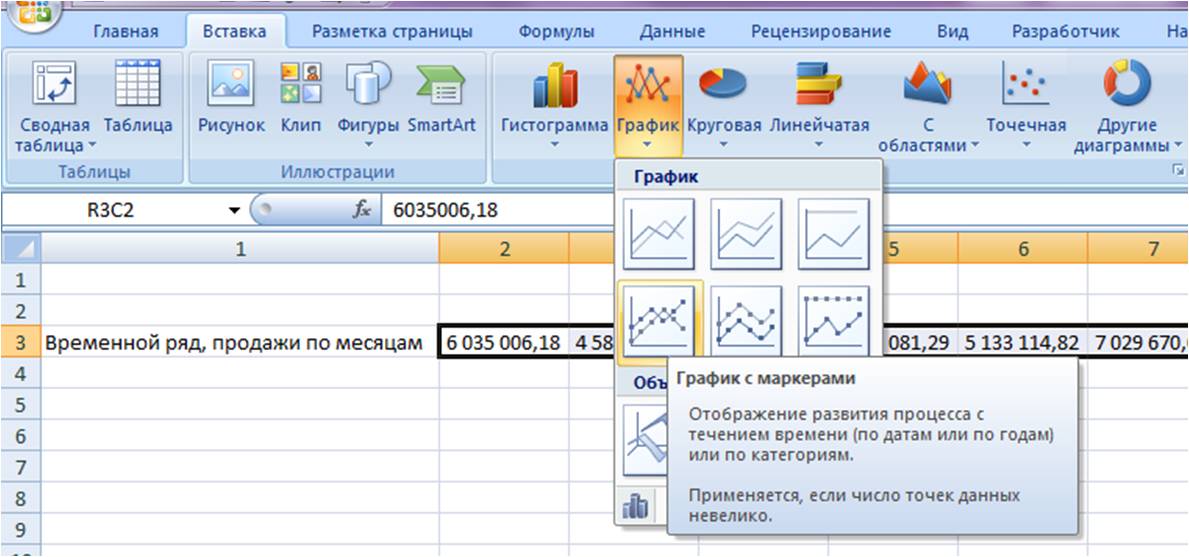
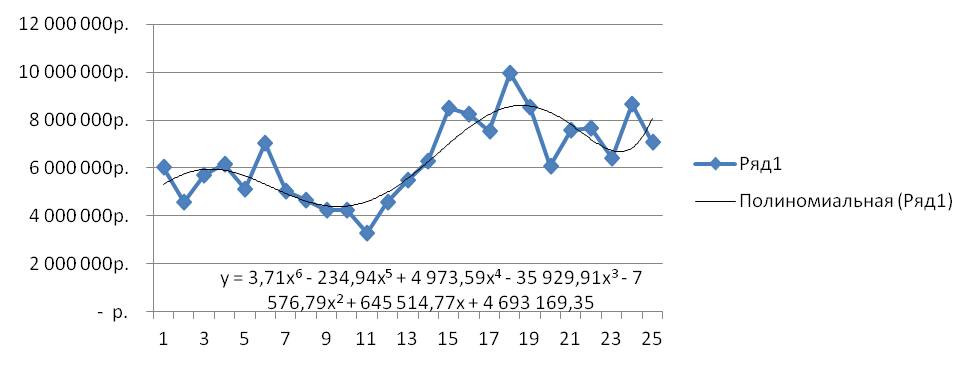
1-й способ расчета полинома — с помощью графика

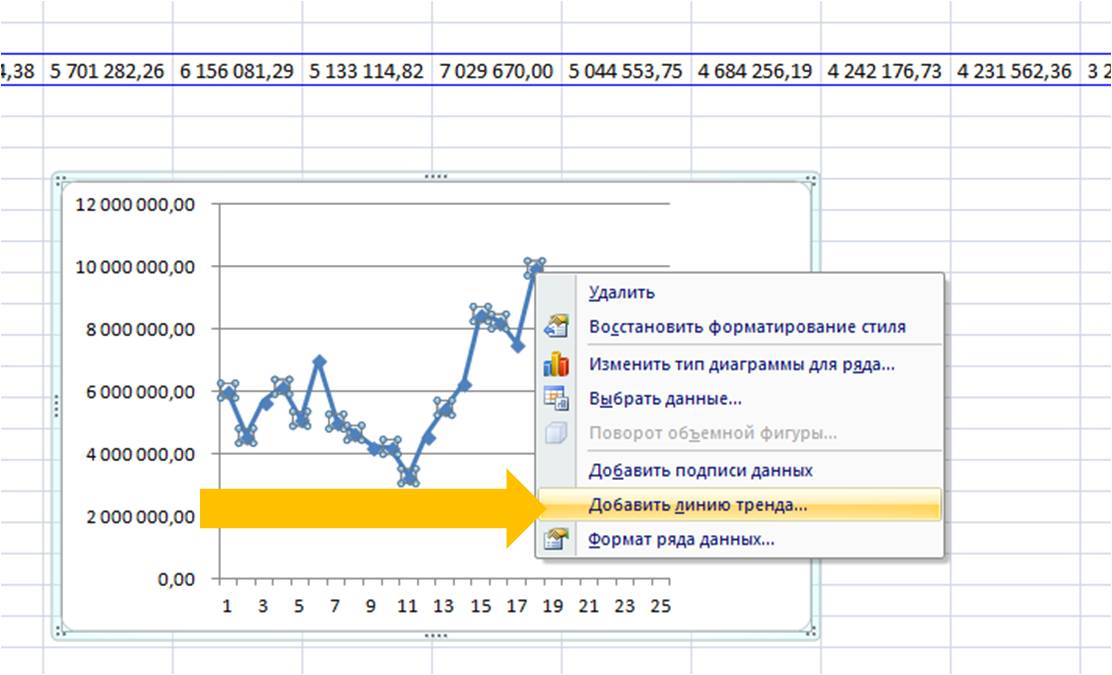
Выделяем ряд со значениями и строим график временного ряда.

график полинома

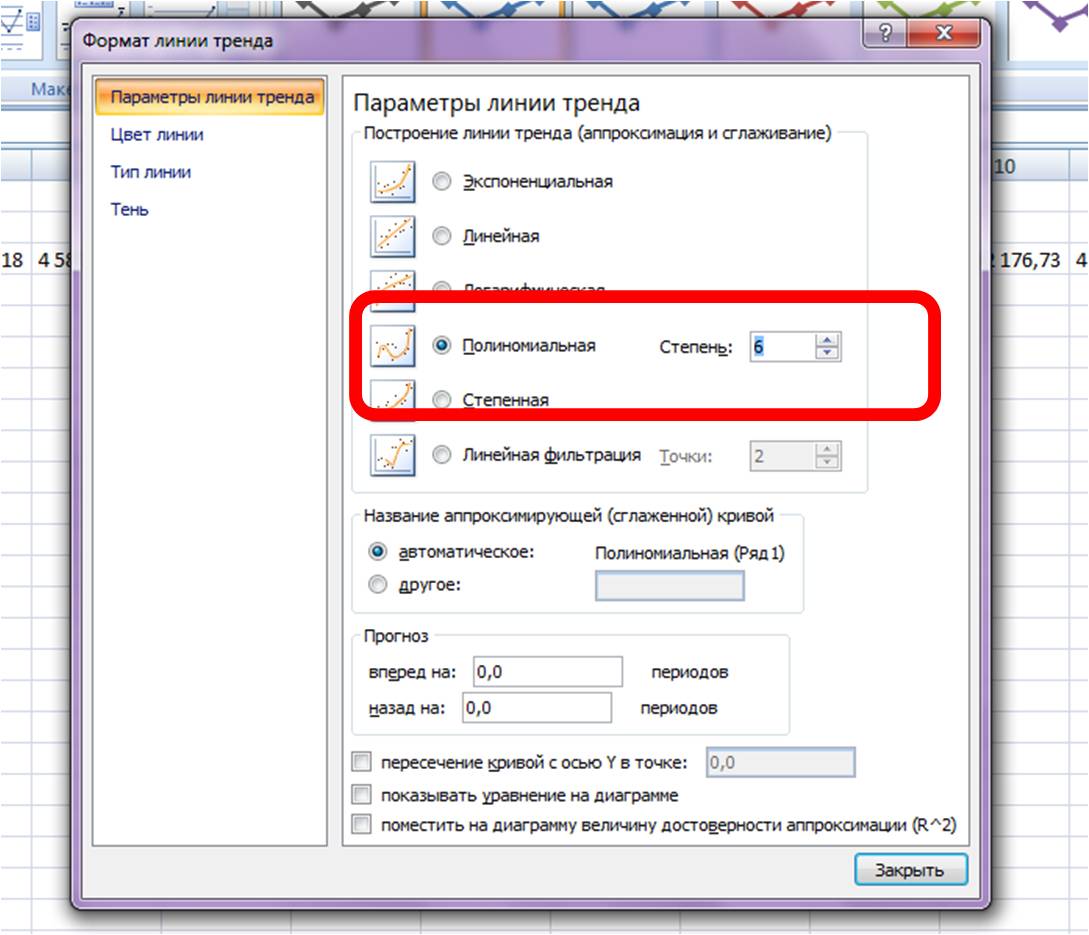
На график добавляем полином 6-й степени.

добавляем линию тренда в Excel

polinom 6 stepeni

Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»

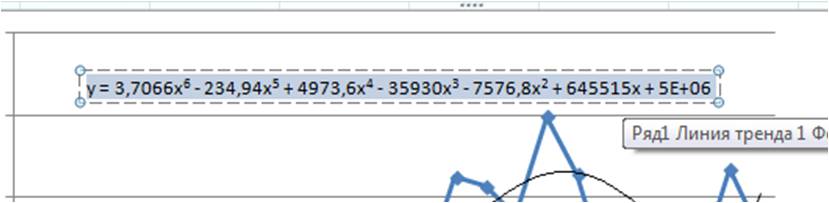
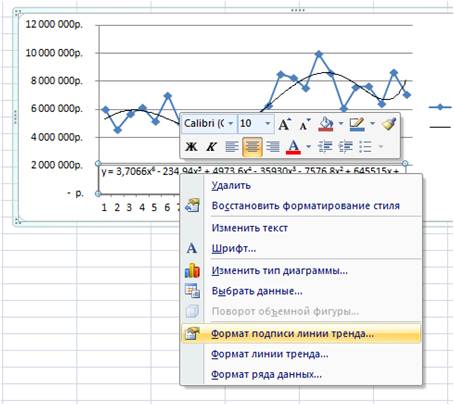
После этого уравнение выводится на график y = 3,7066x6 — 234,94x5 + 4973,6x4 — 35930x3 — 7576,8x2 + 645515x + 5E+06. Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома

выделяем уравнение тренда

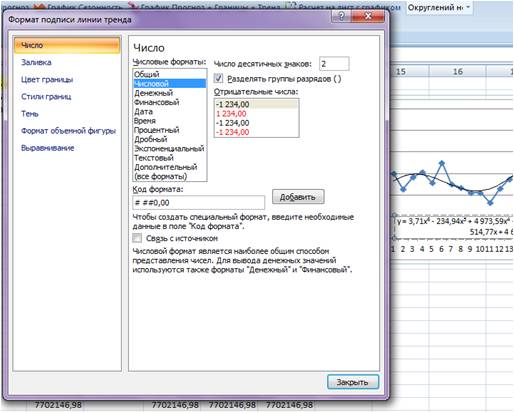
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»

формат подписи полинома

В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».

 формат подписи полинома

Получаем уравнение полинома в читаемом формате:

 y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35

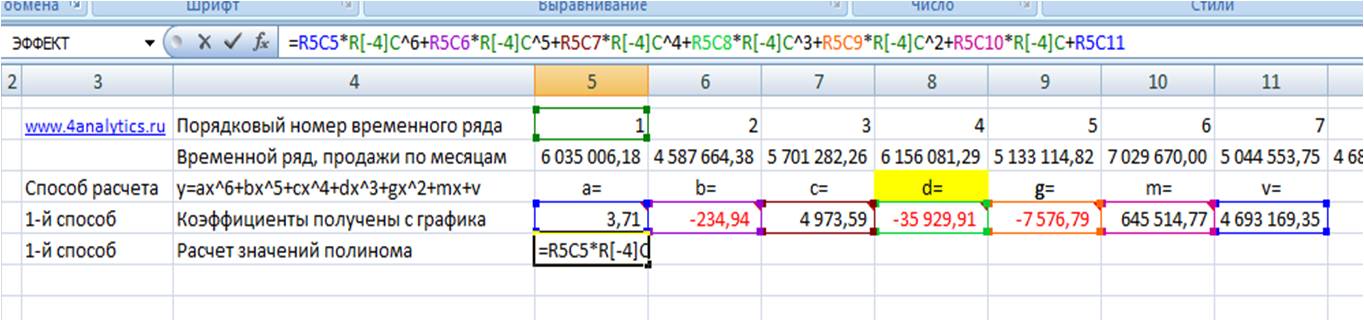
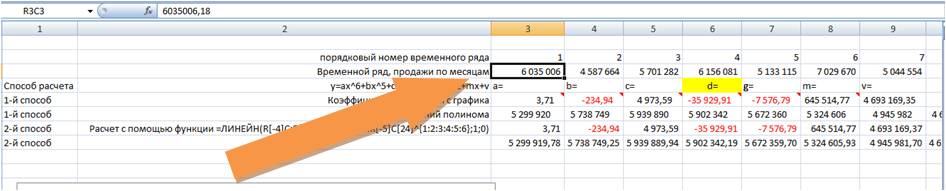
уравнение полинома

Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel

коэффициенты полинома

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.

номер временного ряда для полинома

Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

вводим формулу полинома в ячейку

Получаем формулу следующего вида:

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8 

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода. 

Скачать файл с примером расчета значений полинома.

2-й способ расчета полинома в Excel — функция ЛИНЕЙН()

 Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()

Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:

  • «известные значения y» (объёмы продаж за периоды),
  • «известные значения x» (порядковый номер временного ряда),
  • в константу ставим «1»,
  • в статистику «0»

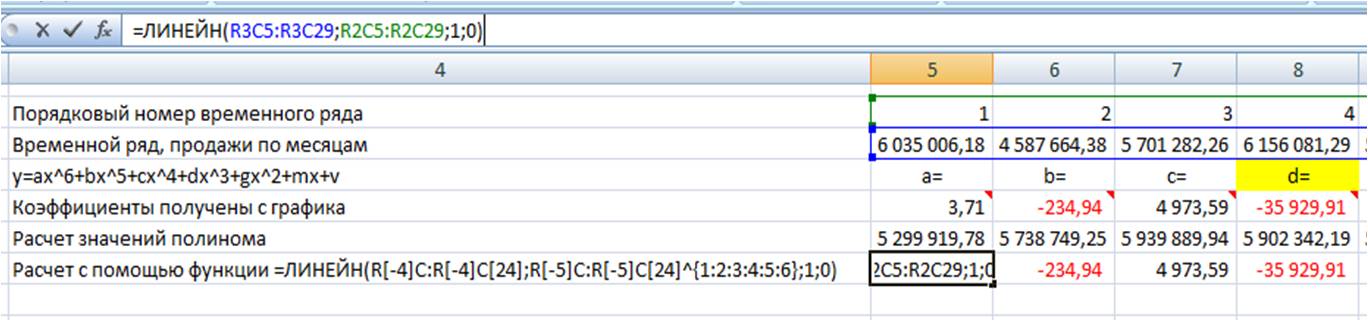
Получаем следующего вида формулу:

Линейн формула Excel

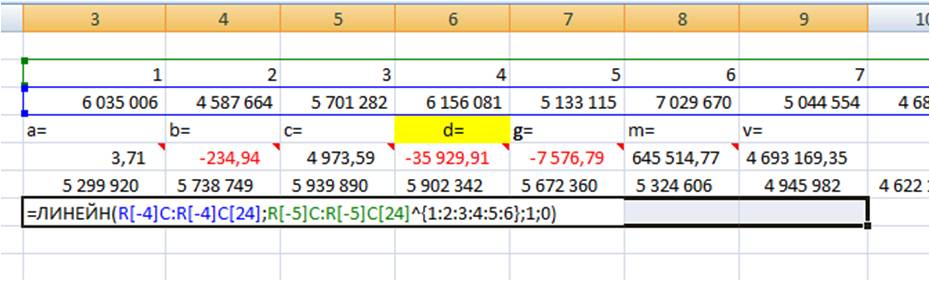
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),

Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.

Для этого в часть формулы с «известными значениями x» вписываем степень полинома:

  • ^{1:2:3:4:5:6} — для расчета коэффициентов полинома 6-й степени
  • ^{1:2:3:4:5} — для расчета коэффициентов полинома 5-й степени
  • ^{1:2} — для расчета коэффициентов полинома 2-й степени

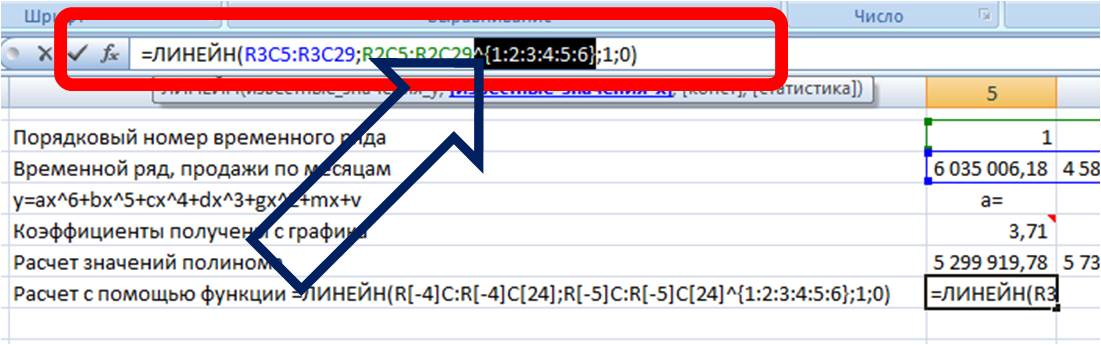
вводим степень полинома

Получаем формулу следующего вида:

=ЛИНЕЙН(R[-4]C:R[-4]C[24]; R[-5]C:R[-5]C[24]^{1:2:3:4:5:6}; 1; 0)

Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v

Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:

1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:

ustanovit kursor

2. Нажать на клавишу F2

uravnenie polinoma 6stepeni 2sposob

 3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)

uravnenie polinoma 6stepeni 2sposob

Получаем 7 коэффициентов полиномиального тренда 6-й степени.

Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.

номер временного ряда для полинома

Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

вводим формулу полинома в ячейку

Получаем формулу следующего вида:

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8 

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода. 

Скачать файл с примером расчета значений полинома.

2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.

3-й способ расчета значений полиномиальных трендов  — Forecast4AC PRO

Устанавливаем курсор в начало временного ряда

уравнение полинома

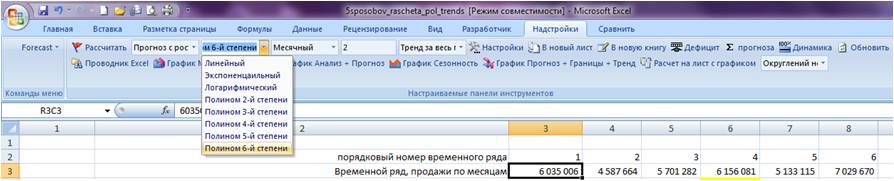
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».

функция полинома

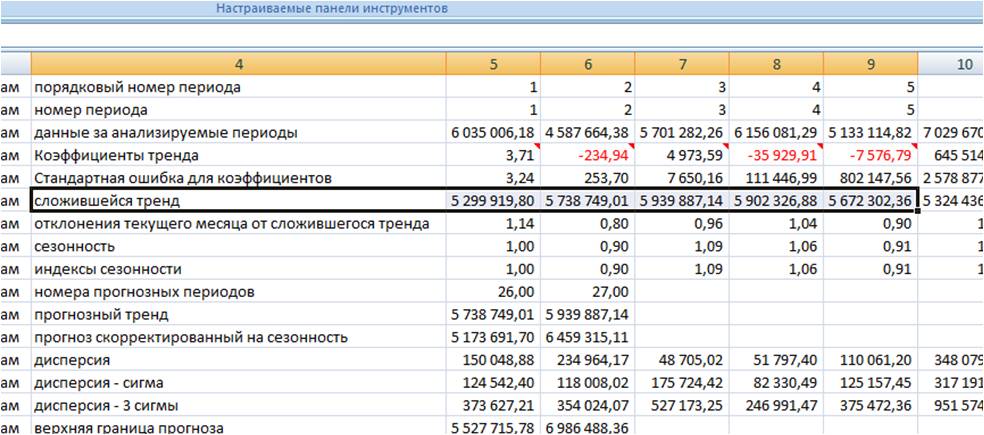
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:

копируем полином

Копируем значения в наш лист.

Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:

Скачать файл с примером расчета значений полинома.

  1. Коэффициентов полиномиального тренда выведенных на график;
  2. Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
  3. и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

Novo Forecast - прогноз в Excel - точно, легко и быстро!

  • Novo Forecast Lite — автоматический расчет прогноза в Excel.
  • 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
  • Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

  • Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Зарегистрируйтесь и скачайте решения

Статья полезная? Поделитесь с друзьями

Источник

В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.

Описание

Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.

Уравнение для прямой линии имеет следующий вид:

y = mx + b

или

y = m1x1 + m2x2 +… + b

если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

Синтаксис

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Аргументы функции ЛИНЕЙН описаны ниже.

Синтаксис

  • Известные_значения_y.    Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.

    • Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

    • Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

  • Известные_значения_x.    Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.

    • Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

    • Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.

  • Конст.    Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

    • Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.

    • Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

  • Статистика.    Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.

    • Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.

    • Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

      Дополнительная регрессионная статистика.

Величина

Описание

se1,se2,…,sen

Стандартные значения ошибок для коэффициентов m1,m2,…,mn.

seb

Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).

r2

Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе «Замечания» далее в этой теме.

sey

Стандартная ошибка для оценки y.

F

F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.

df

Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.

ssreg

Регрессионная сумма квадратов.

ssresid

Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.

На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Лист

Замечания

  • Любую прямую можно описать ее наклоном и пересечением с осью y:

    Наклон (m):
    Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).

    Y-перехват (b):
    Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.

    Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.

  • Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:

    Наклон:
    =ИНДЕКС( LINEST(known_y,known_x’s);1)

    Y-перехват:
    =ИНДЕКС( LINEST(known_y,known_x),2)

  • Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:

    Уравнение

    Уравнение

    где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).

  • Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.

  • Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.

  • В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.

  • Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.

  • При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.

  • Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.

  • Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:

    • Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.

    • Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.

  • Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:

    =ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))

    работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:

    y = m1*x + m2*x^2 + m3*x^3 + b

    Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.

  • Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.

Примеры

Пример 1. Наклон и Y-пересечение

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Известные значения y

Известные значения x

1

0

9

4

5

2

7

3

Результат (наклон)

Результат (y-пересечение)

2

1

Формула (формула массива в ячейках A7:B7)

=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ)

Пример 2. Простая линейная регрессия

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Месяц

Продажи

1

3 100 ₽

2

4 500 ₽

3

4 400 ₽

4

5 400 ₽

5

7 500 ₽

6

8 100 ₽

Формула

Результат

=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1})

11 000 ₽

Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы.

Пример 3. Множественная линейная регрессия

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Общая площадь (x1)

Количество офисов (x2)

Количество входов (x3)

Время эксплуатации (x4)

Оценочная цена (y)

2310

2

2

20

142 000 ₽

2333

2

2

12

144 000 ₽

2356

3

1,5

33

151 000 ₽

2379

3

2

43

150 000 ₽

2402

2

3

53

139 000 ₽

2425

4

2

23

169 000 ₽

2448

2

1,5

99

126 000 ₽

2471

2

2

34

142 900 ₽

2494

3

3

23

163 000 ₽

2517

4

4

55

169 000 ₽

2540

2

3

22

149 000 ₽

-234,2371645

13,26801148

0,996747993

459,7536742

1732393319

Формула (формула динамического массива, введенная в A19)

=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА)

Пример 4. Использование статистики F и r2

В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.

Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.

Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).

Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение «Альфа» = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.

Пример 5. Вычисление t-статистики

Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:

t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7

Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.

Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.

Переменная

t-наблюдаемое значение

Общая площадь

5,1

Количество офисов

31,3

Количество входов

4,8

Возраст

17,7

Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.

Источник

  • Редакция Кодкампа

17 авг. 2022 г.
читать 1 мин

Вы можете использовать функцию ЛИНЕЙН() в Excel, чтобы подобрать полиномиальную кривую с определенной степенью.

Например, вы можете использовать следующий базовый синтаксис, чтобы подогнать полиномиальную кривую со степенью 3:

=LINEST( known_ys , known_xs ^{1, 2, 3})

Функция возвращает массив коэффициентов, описывающих полиномиальную подгонку.

В следующем пошаговом примере показано, как использовать эту функцию для подбора полиномиальной кривой в Excel.

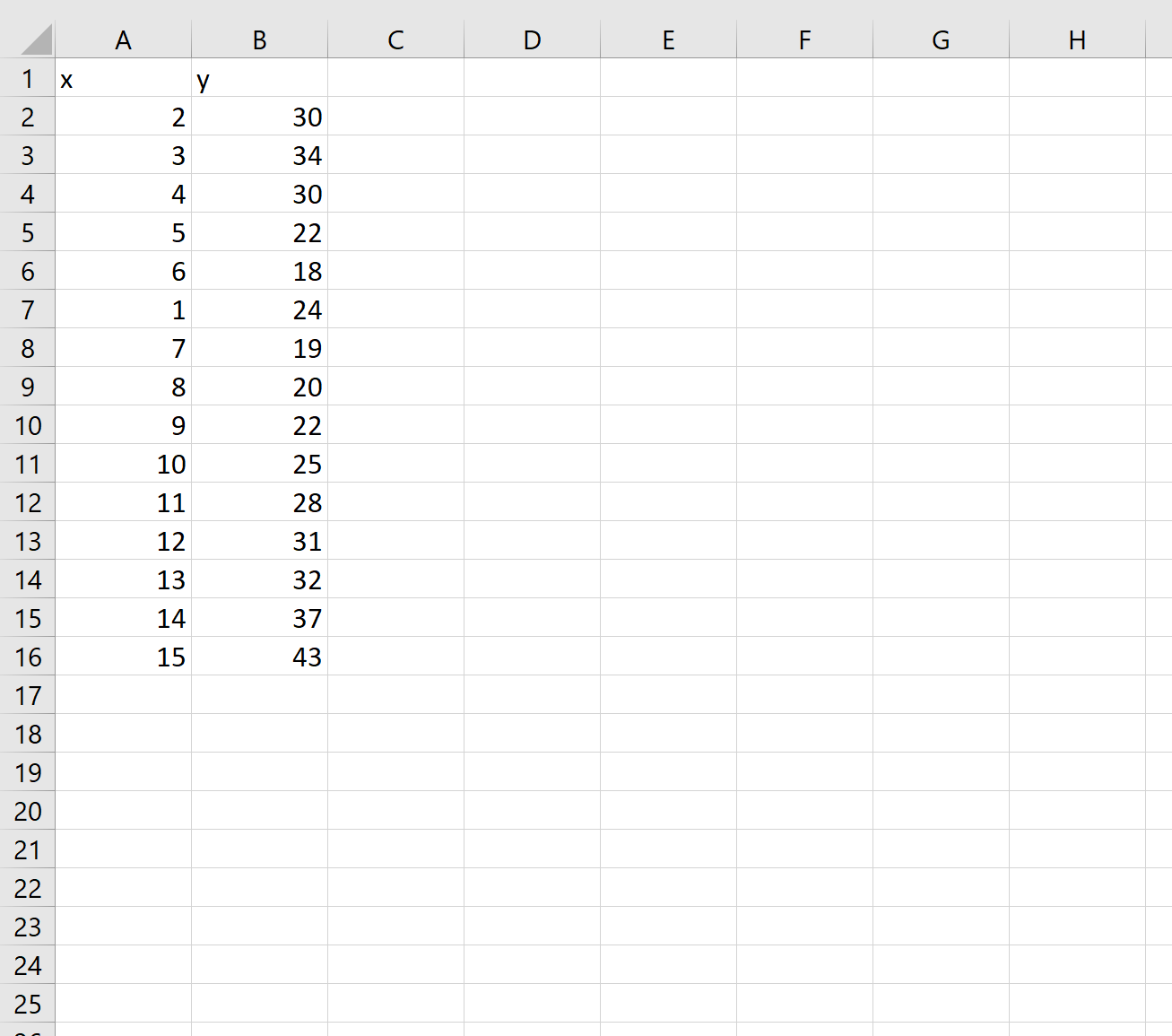
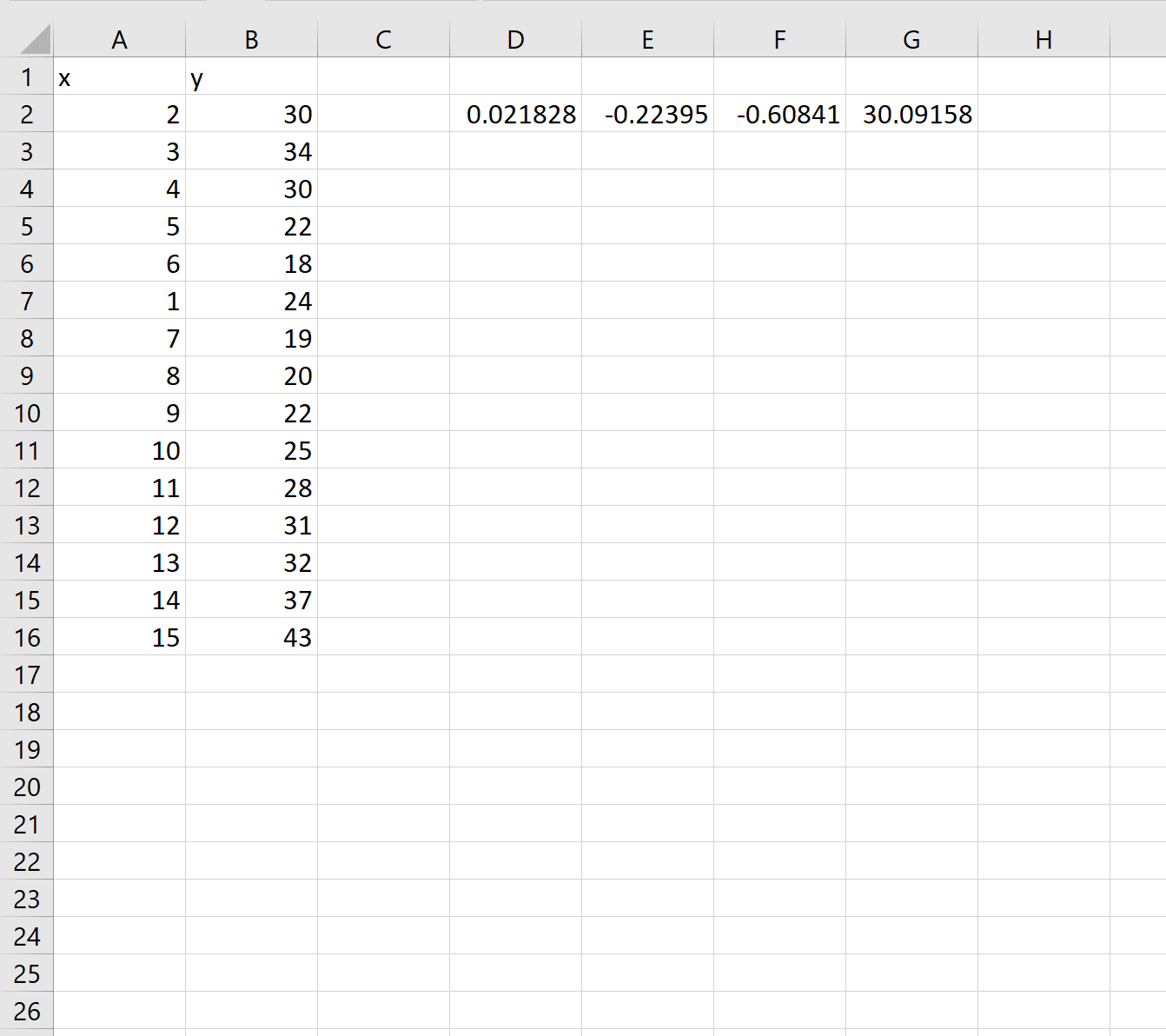
Шаг 1: Создайте данные

Во-первых, давайте создадим некоторые данные для работы:

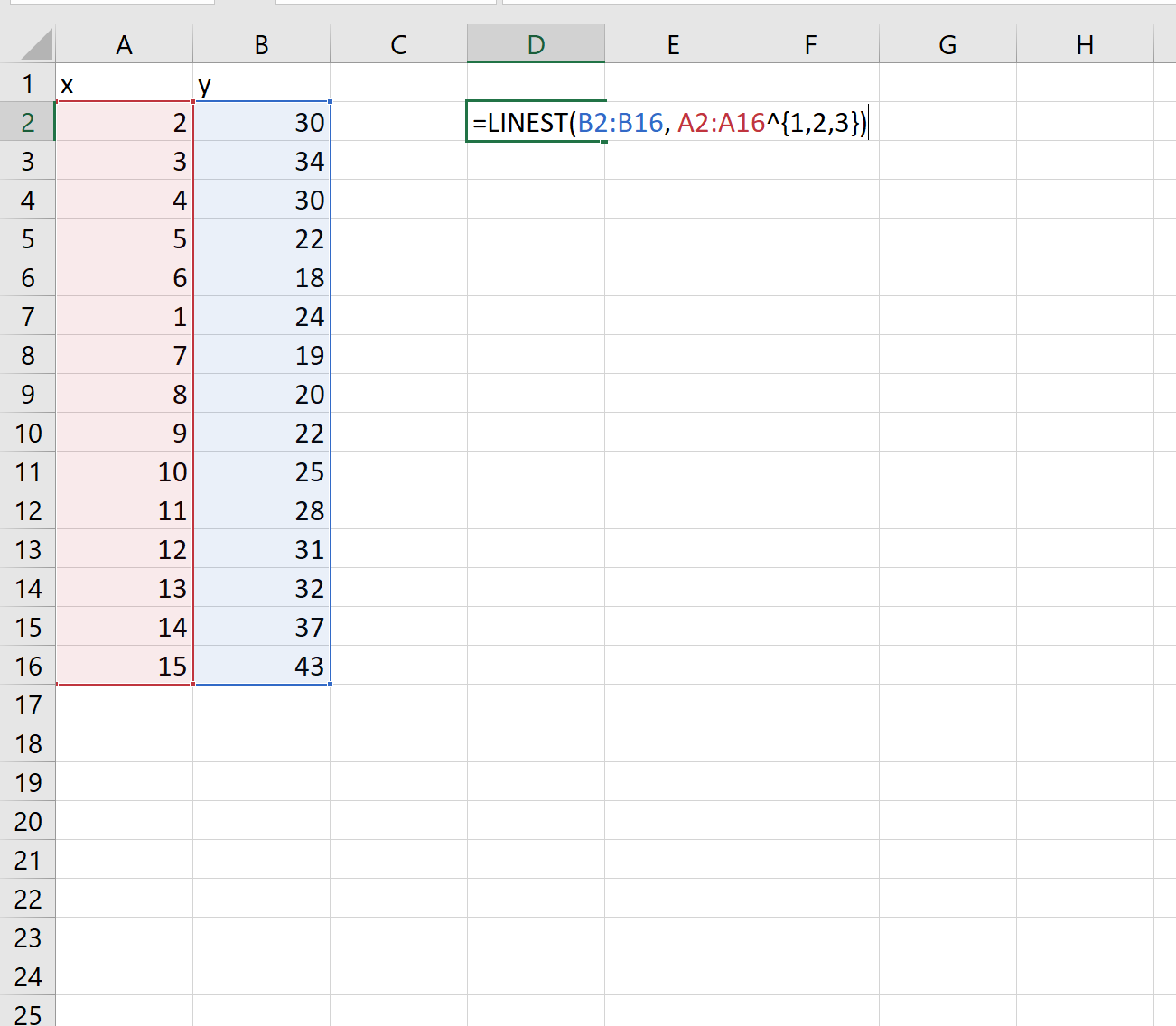
Шаг 2: Подберите полиномиальную кривую

Далее воспользуемся функцией ЛИНЕЙН() , чтобы подобрать полиномиальную кривую степени 3 к набору данных:

Полиномиальная подгонка Excel

Шаг 3: Интерпретация полиномиальной кривой

Как только мы нажмем ENTER , появится массив коэффициентов:

Используя эти коэффициенты, мы можем построить следующее уравнение, описывающее взаимосвязь между x и y:

у = 0,0218x 3 – 0,2239x 2 – 0,6084x + 30,0915

Мы также можем использовать это уравнение для вычисления ожидаемого значения y на основе значения x.

Например, предположим, что x = 4. Ожидаемое значение y будет следующим:

у = 0,0218(4) 3 – 0,2239(4) 2 – 0,6084(4) + 30,0915 = 25,47

Дополнительные ресурсы

Как выполнить полиномиальную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как добавить квадратную линию тренда в Excel

Источник

Задача отыскания функциональной зависимости очень важна, поэтому для ее решения в MS Excel введен набор функций, основанных на методе наименьших квадратов. В качестве результата выдаются не только коэффициенты функции, приближающей данные, но и статистические характеристики полученных результатов.

Смысл выходной статистической информации функции ЛИНЕЙН

Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, вычисляя прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую.

Общий синтаксис вызова функции ЛИНЕЙН имеет следующий вид:

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

Для работы с функцией необходимо заполнить как минимум 1 обязательный и при необходимости 3 необязательных аргумента:

аргументы.

  1. Известные_значения_y − это множество значений y, которые уже известны для соотношения y=mx+b.
  2. Известные_значения_x − это множество известных значений x. Если этот аргумент опущен, то предполагается, что это массив {1; 2; 3; …} такого же размера, как и известные_значения_y.
  3. Конст − это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если в функции ЛИНЕЙН аргумент константа имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.
  4. Статистика − это логическое значение, которое указывает, требуется ли выдать дополнительную статистику по регрессии.



Примеры использования функции ЛИНЕЙН в Excel

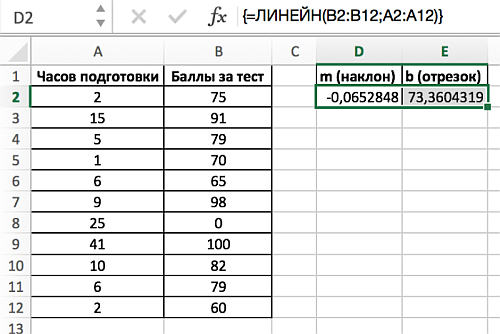
Для решения первой задачи – о соотношении часов подготовки студентов к тесту и результатов теста, как х и у соответственно, – необходимо применить следующий порядок действий (в связи с тем, что ЛИНЕЙН является функцией, которая возвращает массив):

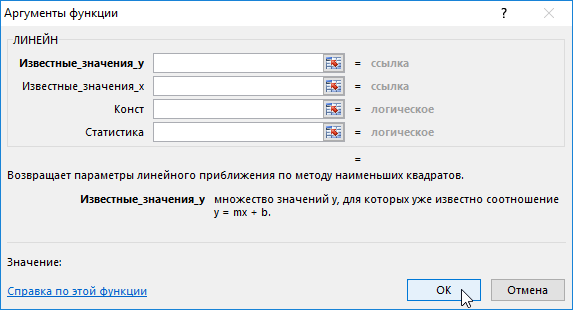
  1. Выделите диапазон D2:Е2, так как функция ЛИНЕЙН возвращает массив из двух значений, расположенных по горизонтали, но не по вертикали.
  2. Введите известные значения y – баллы, которые студенты заработали на последнем тестировании (диапазон ячеек В2:В12).
  3. Затем введите известные значения х – количество часов, которые студенты потратили на подготовку к тестам (диапазон А2:А12).
  4. Опустите аргумент [конст].
  5. Опустите аргумент [статистика].
  6. Введите формулу с помощью Ctrl+Shift+Enter.

Результатом применения функции становится:

Результат применения функции.

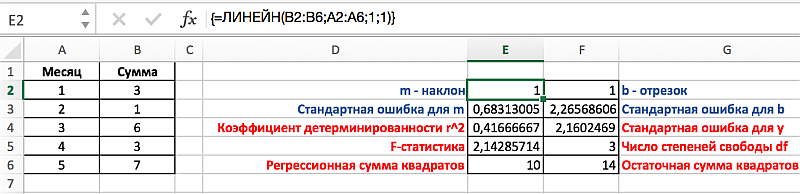
Теперь, на примере решения второй задачи, разберем необходимость в отображении не только наклона и отрезка, но и дополнительной статистики. Для примера, на диапазоне А1:В6 выстроим таблицу с соотношением у и х соответствующих сумме заработка студентом денежных средств за период в 5 месяцев. Так как мы имеем лишь одну переменную х, то необходимо выделить диапазон состоящий из двух столбцов и пяти строк. Важно отметить, что в том случае, если переменных х будет больше, то количество столбцов может изменяться соответственно их количеству, однако строк будет всегда 5.

Применительно к решаемой нами задаче, выделим диапазон Е2:F6, затем введем формулу аналогично предыдущей задаче, но в данном случае третьему и четвертому аргументу присвоим значение 1 соответствующее ИСТИНЕ. Для вывода параметров статистики функции ЛИНЕЙН необходимо нажат Ctrl+Shift+Enter, результат должен соответствовать следующему рисунку, на котором представлено обозначение дополнительных статистик:

введем формулу.

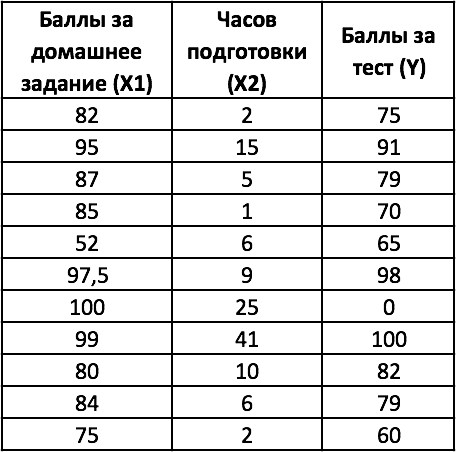
Вернемся к примеру № 1, касающемуся зависимости между часами подготовки студентов к тесту и баллов за тест. Добавим к условию задачи данные о баллах за домашнее задание — представляющие дополнительную переменную х, что свидетельствует о необходимости применения множественной регрессии.

В случае множественной регрессии, когда значения «y» зависят от двух переменных «х», функция ЛИНЕЙН возвращает 12 статистик. На рисунке с модифицированной таблицей от 1 примера, представленном ниже используются следующие обозначения:

  • y = зависимая переменная;
  • x1 = независимая переменная 1 = баллы за домашнее задание;
  • x2 = независимая переменная 2 = часы подготовки к тесту.

функция ЛИНЕЙН.

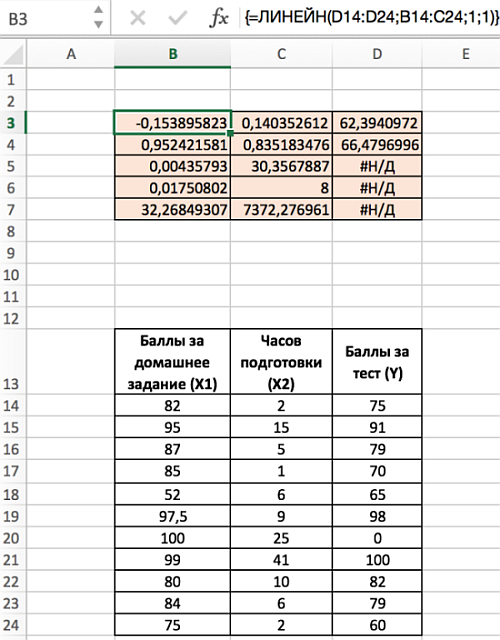
Чтобы выполнить множественную регрессию:

  1. Выделите диапазон В3:D7 (число столбцов = число переменных +1; число строк всегда равно 5).
  2. Наберите формулу =ЛИНЕЙН(D14:D24;B14:C24;1;1). Для аргумента известные_значения_х, выделите оба столбца значений x из диапазона В14:С24.
  3. Введите функцию с помощью клавиш Ctrl+Shift+Enter.
  4. Обратите внимание, что несмотря на то, что значения х1 указаны в диапазоне В14:С24 до значений х2, наклон сначала указан для х2.

выполнить множественную регрессию.

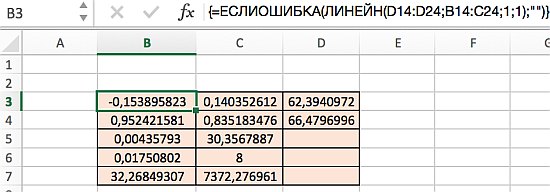
Диапазон D5:D7 содержит ошибку #Н/Д – значащую, что формула не может обнаружить значения для данных ячеек. Визуально наличие ошибки отвлекает от сути решения, поэтому далее предложим вариант избавления от нее. Так, если дополнить формулу содержащую функцию ЛИНЕЙН функцией ЕСЛИОШИБКА, то можно значительно улучшить вид таблицы, результат которой представлен ниже:

ЕСЛИОШИБКА.

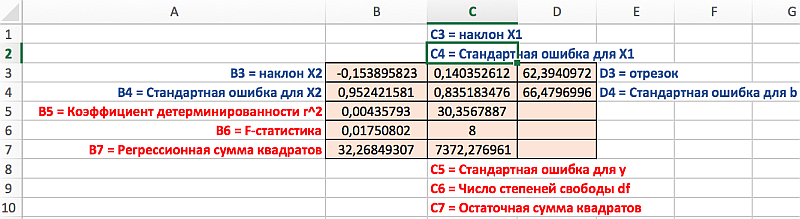
Распределение статистик в таблице их значение представлено на следующем рисунке:

Распределение статистик в таблице.

Скачать примеры функции ЛИНЕЙН в Excel

В результате мы получили всю необходимую выходную статистическую информацию, которая нас интересует.

Источник

Excel: как построить степенной полином функцией ЛИНЕЙН

Мы уже строили аналогичный интерполирующий полином в Excel, и в Mathcad «вручную», и стандартными функциями Mathcad тоже можно это сделать.

Сейчас мы хотим, во-первых, построить в Excel интерполирующий полином тоже стандартной функцией, во-вторых, не вдаваясь в детали теории, понять смысл этой простой задачи — как построить кривую, проходящую через несколько известных точек на плоскости.

Итак, по известному набору из N значений функции f(xi)=yi, заданному парой векторов xi, yi=f(xi), i=1, 2, ..., N, нужно построить кривую, проходящую через все точки.

Через N различных между собой по оси x точек всегда можно построить кривую, зависящую от xN-1, её уравнение будет иметь общий вид

f(x)=c0+c1*x+c2*x2+…+сN-1*xN-1 (1)

В этом уравнении нам неизвестны коэффициенты сi. Из условия, что кривая проходит через все заданные в постановке задачи точки, можно записать систему линейных алгебраических уравнений:

c0 +c1x1 +c2x12 +...+cN-1x1N-1 =y1

c0 +c1x2 +c2x22 +...+cN-1x2N-1 =y2

...

c0 +c1xN +c2xN2 +...+cN-1xNN-1 =yN

или, в матричном виде

Система линейных алгебраических уравнений, записанная в матричном виде

Система линейных алгебраических уравнений, записанная в матричном виде

Решив эту систему уравнений, то есть, найдя обратную к матрице Вандермонда матрицу и умножив её на вектор y, найдём коэффициенты сi. Теперь, подставив их в уравнение (1), мы можем аналитически оценить значение функции в произвольной точке x.

Ниже показано «ручное» решение в Excel и решение с помощью стандартной функции ЛИНЕЙН.

Скриншот файла Excel с решением

Скриншот файла Excel с решением

Вот пояснения к формулам:

  • C2 — формируем матрицу из степеней значений x; избегаем при этом возведения нуля в нулевую степень, заменяя любое число, возводимое в нулевую степень, единицей; ввести формулу в ячейку C2; затем растягиваем формулу на ячейки C2:C5, отпускаем левую кнопку мыши и, не снимая выделения, растягиваем на столбцы D:F (см. Пояснение 1 ниже);
  • G2:G5 — вычисляем коэффициенты полинома ci «вручную», обратив матрицу и умножив её на вектор значений yi; выделить диапазон G2:G5; не снимая выделения, ввести формулу в ячейку G2; не снимая выделения, нажать комбинацию клавиш Crl+Shift+Enter (см. Пояснение 2 ниже);
  • I2 — вычисляем полином третьей степени в точках, не обязательно совпадающих с исходными; по выделенным жирным шрифтом значениям полинома видно, что он прошёл через исходные точки; ввести формулу в ячейку I2, растянуть за уголок до I8;
  • J2:J5 — вычисляем коэффициенты полинома ci с помощью функции ЛИНЕЙН, пример в справке (пример 2), к сожалению, прямо ошибочен, плюс не показывает вычисление нескольких коэффициентов полинома; выделить диапазон J2:J5; не снимая выделения, ввести формулу в ячейку G2; не снимая выделения, нажать комбинацию клавиш Crl+Shift+Enter; коэффициенты возвращаются в «перевёрнутом» по отношению к нашему ручному расчёту виде;
  • K2 — для единообразия расчёта переворачиваем массив коэффициентов, готовой функции для этого нет, показан образец, как перевернуть диапазон в Excel; ввести формулу в ячейку K2, растянуть за уголок до K5;
  • L2 — вычисляем полином третьей степени в тех же точках H2:H8, в которых вычисляли его значения первым способом; ввести формулу в ячейку L2, растянуть за уголок до L8; видно, что кривая также прошла через исходные точки данных.

 Скачать файл Excel (2007 и выше, делался в Excel 2016) в архиве .zip (13 Кб)

Пояснение 1. Как растянуть формулу на матрицу значений

1. Введите требуемую формулу и нажмите Enter, на рисунке показан вид экрана перед нажатием:

Ввод "матричной" формулы со смешанными ссылками

Ввод «матричной» формулы со смешанными ссылками

2. Подведите курсор мыши к нижнему правому уголку ячейки C2, уголок превратился в чёрный крестик, зажмите левую кнопку мыши и растяните формулу вниз до ячейки C5.

Курсор для растягивания в Excel, "чёрный крестик"

Курсор для растягивания в Excel, «чёрный крестик»

Формула растянута вниз

Формула растянута вниз

3. Отпустите кнопку мыши, снова так же подведите курсор к уголку ячейки C5 (опять чёрный крестик) и при зажатой левой кнопке мыши растяните выделение вправо до столбца F.

Заполнение таблицы формулой в Excel

Заполнение таблицы формулой в Excel

Пояснение 2. Как ввести формулу массива

1. Выделить диапазон ячеек, в которые будет помещён результат матричной или векторной операции (мышкой при зажатой левой кнопке за любое место, на котором курсор имеет вид по умолчанию или при зажатой Shift клавишами со стрелками):

Вид курсора по умолчанию в Excel

Вид курсора по умолчанию в Excel

Мы сами отвечаем за правильность выделения ячеек диапазона результата, например, Excel не обязан знать, что в результате обращения матрицы размерностью 3x3 получится тоже матрица размерностью 3x3:

Выделение диапазона ячеек результата в Excel

Выделение диапазона ячеек результата в Excel

2. Не снимая выделения, ввести формулу массива в первую ячейку выделенного диапазона, это можно сделать «вручную», просто нажав клавишу F2 и начав набирать формулу со знака «=«, или с помощью Мастера Функций (см. п.3 документа по Excel здесь).

Ввод формулы массива в первую ячейку выделенного диапазона

Ввод формулы массива в первую ячейку выделенного диапазона

3. При зажатых клавишах Ctrl и Shift, нажать клавишу Enter, то есть, ввести комбинацию клавиш Ctrl+Shift+Enter.

22.02.2020, 18:58 [4248 просмотров]

К этой статье пока нет комментариев, Ваш будет первым

Источник

Понравилась статья? Поделить с друзьями:
  • Excel функция линейн как пользоваться
  • Excel функция кпер пример
  • Excel функция корня в степени
  • Excel функция корень кубический
  • Excel функция копировать ячейки