С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( , т.е. означает надежности );
станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома произведем обработку данной серии экспериментальных данных.
| Используемуе формулы |
 |
| Результат расчета |
 |
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Формула погрешности
- Формула погрешности
Формула погрешности (оглавление)
- Формула погрешности
- Примеры формулы допустимой погрешности (с шаблоном Excel)
- Калькулятор формулы ошибки поля
Формула погрешности
В статистике мы рассчитываем доверительный интервал, чтобы увидеть, куда упадет значение данных выборочной статистики. Диапазон значений, которые находятся ниже и выше выборочной статистики в доверительном интервале, называется границей ошибки. Другими словами, это в основном степень ошибки в статистике выборки. Чем выше погрешность, тем меньше будет достоверность результатов, поскольку степень отклонения в этих результатах очень высока. Как следует из названия, погрешность — это диапазон значений выше и ниже фактических результатов. Например, если мы получаем ответ в опросе, в котором 70% людей ответили «хорошо», а допустимая погрешность составляет 5%, это означает, что в целом от 65% до 75% населения считают, что ответ «хороший»,
Margin of Error = Z * S / √n
- Z — Z счет
- S — стандартное отклонение населения
- n — Размер выборки
Другая формула для расчета погрешности:
Margin of Error = Z * √((p * (1 – p)) / n)
- p — доля образца (доля образца, которая является успешной)
Теперь, чтобы найти желаемую оценку z, вам нужно знать доверительный интервал выборки, потому что оценка Z зависит от этого. Ниже приведена таблица, чтобы увидеть отношение доверительного интервала и z балла:
| Доверительный интервал | Z — Оценка |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Как только вы знаете доверительный интервал, вы можете использовать соответствующее значение z и рассчитать предел погрешности оттуда.
Примеры формулы допустимой погрешности (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчёт Margin of Error.
Вы можете скачать этот шаблон Margin of Error здесь — Шаблон Margin of Error
Формула погрешности — пример № 1
Допустим, мы проводим опрос, чтобы увидеть, каков балл, который получают студенты университетов. Мы выбрали 500 учеников случайным образом и задали их оценку. Среднее значение составляет 2, 4 из 4, а стандартное отклонение составляет, скажем, 30%. Предположим, что доверительный интервал составляет 99%. Рассчитайте погрешность.
Решение:
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * S / √n
- Погрешность = 2, 58 * 30% / √ (500)
- Погрешность = 3, 46%
Это означает, что с вероятностью 99% средний балл учащихся составляет 2, 4 плюс или минус 3, 46%.
Формула погрешности — пример № 2
Допустим, вы запускаете новый продукт для здоровья на рынке, но вы не знаете, какой вкус понравится людям. Вы путаетесь между ароматом банана и ванили и решили провести опрос. Для вас это 500 000 человек, что является вашим целевым рынком, и из этого вы решили спросить мнение 1000 человек, и это будет образец. Предположим, что доверительный интервал составляет 90%. Рассчитайте погрешность.
Решение:
Как только опрос закончен, вы узнали, что банану понравился 470 человек, а 530 попросили аромат ванили.
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * √ ((p * (1 — p)) / n)
- Погрешность = 1, 65 * √ ((0, 47 * (1 — 0, 47)) / 1000)
- Погрешность = 2, 60%
Таким образом, мы можем сказать, что с 90% уверенностью, что 47% всех людей любили банановый аромат плюс или минус 2, 60%.
объяснение
Как обсуждалось выше, предел погрешности помогает нам понять, подходит ли размер выборки для вашего опроса или нет. В случае, если погрешность слишком велика, возможно, размер нашей выборки слишком мал, и нам нужно его увеличить, чтобы результаты выборки более точно соответствовали результатам совокупности.
Существуют некоторые сценарии, в которых предел погрешности не будет иметь большого значения и не поможет нам в отслеживании ошибки:
- Если вопросы опроса не разработаны и не помогают получить требуемый ответ
- Если люди, отвечающие на опрос, имеют некоторую предвзятость в отношении продукта, для которого проводится опрос, то и результат будет не очень точным
- Если выбранная выборка является надлежащим представителем населения, в этом случае также результаты будут далеко.
Кроме того, одно большое предположение здесь состоит в том, что население обычно распределено. Таким образом, если размер выборки слишком мал и распределение населения не является нормальным, z-оценка не может быть рассчитана, и мы не сможем найти предел погрешности.
Актуальность и использование формулы ошибки
Всякий раз, когда мы используем выборочные данные, чтобы найти какой-то релевантный ответ для набора населения, возникает некоторая неопределенность и вероятность того, что результат может отличаться от фактического результата. Допустимая погрешность скажет нам, что каков уровень отклонения, это образец выборки. Нам необходимо минимизировать погрешность, чтобы результаты наших выборок отражали реальную историю данных о населении. Поэтому, чем ниже погрешность, тем лучше будут результаты. Запас погрешности дополняет и дополняет имеющуюся у нас статистическую информацию. Например, если опрос показал, что 48% людей предпочитают проводить время дома в выходные дни, мы не можем быть настолько точными, и в этой информации отсутствуют некоторые элементы. Когда мы ввели здесь предел погрешности, скажем, 5%, то результат будет интерпретирован как 43-53% людей, которым понравилась идея быть дома в выходные дни, что имеет полный смысл.
Калькулятор формулы ошибки поля
Вы можете использовать следующий калькулятор Margin of Error
Рекомендуемые статьи
Это было руководство по формуле ошибки. Здесь мы обсудим, как рассчитать погрешность, а также на практических примерах. Мы также предоставляем калькулятор Margin of Error с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Руководство по формуле амортизации прямой линии
- Примеры формулы удвоения времени
- Как рассчитать амортизацию?
- Формула для центральной предельной теоремы
- Альтман Z Оценка | Определение | Примеры
- Формула амортизации | Примеры с шаблоном Excel
Для эффективного использования формул необходимо ознакомиться с тремя ключевыми понятиями.
Вычисление — это процесс расчета по формулам и последующего отображения значений результатов в ячейках, содержащих формулы. Во избежание ненужных вычислений, которые забрать время и замедлить работу компьютера, Microsoft Office Excel автоматически пересчитывает формулы только при изменении влияющих на формулу ячеек. Это является стандартной процедурой при первом открытии книги и ее редактировании. Однако тем, как и когда Excel будет пересчитывать формулы, можно управлять.
Итерация — это повторный пересчет на отдельном числовом условии. Excel не может автоматически вычислить формулу, которая ссылается (прямо или косвенно) на ячейку, содержаную эту формулу. Это называется циклской ссылкой. Если формула ссылается на одну из собственных ячеек, необходимо определить, сколько раз она должна пересчитываться. Цикловые ссылки могут итерироваться бесконечно. Тем не менее, вы можете сами задать предельное число итераций и относительную погрешность.
Точность — это показатель степени сходимости вычислений. Excel хранит и выполняет вычисления с точностью 15 значащих цифр. Однако существует возможность изменить точность вычислений, так что Excel при пересчете формул будет использовать для вычислений не хранимое, а отображаемое значение.
Во время вычислений можно выбирать команды и выполнять ввод чисел или формул. Для выполнения команд или других действий вычисления прерываются, а затем возобновляются снова. Если книга содержит большое число формул либо листы содержат таблицы данных или функции, автоматически пересчитываемые при каждом пересчете книги, процесс вычислений может занять значительное время. Он также может быть длительным, если листы содержат связи с другими листами или книгами. Можно изменить способ выполнения вычислений, установив параметр пересчета вручную.
Важно: Изменение любого из этих параметров влияет на все открытые книги.
-
На вкладке Файл нажмите кнопку Параметры и выберите категорию Формулы.
В Excel 2007 нажмите кнопку «Microsoft Office»,выберите «Параметры Excel»и щелкните категорию «Формулы».
-
Выполните одно из указанных ниже действий.
-
Для пересчета всех зависимых формул при каждом изменении значения, формулы или имени в разделе Параметры вычислений в группе Вычисления в книге выберите пункт Автоматически. Это — способ вычислений по умолчанию.
-
Чтобы пересчитать все зависимые формулы, кроме таблиц данных, при каждом изменении значения, формулы или имени в разделе «Параметры вычислений» в разделе «Вычисления книги» выберите значение «Автоматически» за исключением таблиц данных.
-
Для отключения автоматического пересчета и выполнения пересчета открытых книг только при явном требовании (с помощью клавиши F9) в разделе Параметры вычислений в группе Вычисления в книге выберите параметр Вручную.
Примечание: При выборе параметра Вручную Excel автоматически устанавливает флажок Пересчитывать книгу перед сохранением. Если сохранение книги занимает много времени, для его экономии снимите флажок Пересчитывать книгу перед сохранением.
-
Для ручного пересчета всех открытых книг, включая таблицы данных, и обновления всех открытых листов диаграмм на вкладке Формулы в группе Вычисление нажмите кнопку Пересчет.
-
Для ручного пересчета активного листа, всех диаграмм и листов диаграмм, связанных с этим листом, на вкладке Формулы в группе Вычисление нажмите кнопку Произвести вычисления.
-
Совет: Многие из этих параметров можно изменять и вне диалогового окна Параметры Excel. Откройте вкладку Формулы и в группе Вычисления щелкните элемент Параметры вычислений, а затем — Выполнять автоматически.
Примечание: Если лист содержит формулу, связанную с непересчитанным листом, и эта связь обновляется, появится сообщение о том, что исходный лист полностью не пересчитан. Для обновления связи с текущим значением, записанном в исходном листе, даже если оно неверно, нажмите кнопку ОК. Для прекращения обновления связи и использования предыдущего значения, полученного из исходного листа, нажмите кнопку Отмена.
|
Действие |
Клавиши |
|
Пересчет измененных после последнего вычисления формул и формул, зависящих от них, во всех открытых книгах. Если задан автоматический пересчет книги, нажимать клавишу F9 для пересчета не требуется. |
F9 |
|
Пересчет измененных после последнего вычисления формул и формул, зависящих от них, в активном листе. |
SHIFT+F9 |
|
Пересчет всех формул во всех открытых книгах независимо от того, были ли они изменены после прошлого пересчета. |
CTRL+ALT+F9 |
|
Проверка зависимых формул, а затем пересчет всех формул во всех открытых книгах независимо от того, были ли они изменены после прошлого пересчета. |
CTRL+SHIFT+ALT+F9 |
-
На вкладке Файл нажмите кнопку Параметры и выберите категорию Формулы.
В Excel 2007 нажмите кнопку «Microsoft Office»,выберите «Параметры Excel»и щелкните категорию «Формулы».
-
В разделе Параметры вычислений установите флажок Включить итеративные вычисления.
-
Чтобы установить максимальное число пересчетов, введите в поле Предельное число итераций число итераций. Чем больше число итераций, тем больше времени потребуется для пересчета листа.
-
Для установки максимальной разности между результатами пересчетов введите ее в поле Относительная погрешность. Чем меньше это число, тем точнее результат, и тем больше времени требуется на пересчет листа.
Примечание: «Поиск решения» и «Поиск цели» — это часть набора команд, иногда называемых инструментами анализ «что если» средств. Обе команды используют итерацию контролируемым способом для получения нужных результатов. С помощью функции «Поиск решения» можно найти оптимальное значение для определенной ячейки, настроив значения в нескольких ячейках или применив определенные ограничения к одному или нескольким значениям в вычислениях. Если вы знаете нужный результат одной формулы, но не входные значения, необходимые для его определения, можно использовать средству поиска целью.
Изменяя точность вычислений в книге, необходимо учитывать важные факторы, указанные ниже.
По умолчанию в вычислениях используются хранимые, а не отображаемые значения
Отображаемые и печатаемые значения зависят от выбора формата и отображения хранимых значений. Например, ячейка, в которой отображается дата «22.06.2008», также содержит порядковый номер, который является хранимым значением даты в этой ячейке. Можно изменить отображение даты на другой формат (например, «22-июнь-2008»), но хранимое в ячейке значение не изменится.
С осторожностью изменяйте точность вычислений
При пересчете формулы Excel обычно использует значения, хранящиеся в ячейках, на которые она ссылается. Например, если в двух ячейках содержится значение 10,005, а формат ячеек предполагает отображение значений в виде денежных единиц, в каждой из ячеек будет отображаться значение 10,01 ₽. При сложении этих значений результат будет равен 20,01 ₽, поскольку Excel складывает хранимые значения 10,005 и 10,005, а не отображаемые значения.
При изменении точности вычислений в книге путем использования отображаемых (форматированных) значений Excel безвозвратно меняет точность хранимых в ячейках значений от полной (15 цифр) до любого другого числа десятичных знаков отображаемого формата. После такого изменения возврат к исходной точности невозможен.
-
На вкладке Файл нажмите кнопку Параметры и выберите категорию Дополнительно.
В Excel 2007 нажмите кнопку «Microsoft Office»,выберите «Параметры Excel»и щелкните категорию «Дополнительные параметры».
-
В разделе При пересчете этой книги выберите нужную книгу и установите флажок Задать указанную точность.
Хотя Excel ограничивает точность до 15 десятичных разрядов, это не означает, что максимальное число, которое можно хранить в Excel, ограничено 15 разрядами. Для положительных чисел предельное значение равно 9,99999999999999E+307, а для отрицательных значений — –9.99999999999999E+307. Эти числа приблизительно равны 1 или –1 с 308 нулями.
Точность в Excel означает, что любое число с разрядностью более 15 хранится и отображается только с точностью в 15 десятичных разрядов. Десятичная запятая может стоять перед любым из этих разрядов. Все разряды справа от 15-го обнуляются. Например, у числа 1234567,890123456 16 разрядов (7 до запятой и 9 после). В Excel это число хранится и отображается как 1234567,89012345 (в строке формулы и ячейке). Если установить для ячейки формат, отображающий все разряды (вместо экспоненциального формата, такого как 1,23457E+06), вы увидите, что число показывается как 1234567,890123450. 6 в конце (16-й разряд) отбрасывается и заменяется на 0. Последним является 15-й разряд, а все последующие равны нулю.
Компьютер может содержать более одного процессора (несколько физических процессоров) или поддерживать многопоточность (несколько логических процессоров). На таких компьютерах можно уменьшить или контролировать время, требуемое для пересчета книг, содержащих множество формул, путем определения числа процессоров, используемых для пересчета. Во многих случаях пересчет может выполняться частями одновременно. Распределение нагрузки между несколькими процессорами может уменьшить общее время пересчета.
-
На вкладке Файл нажмите кнопку Параметры и выберите категорию Дополнительно.
В Excel 2007 нажмите кнопку «Microsoft Office»,выберите «Параметры Excel»и щелкните категорию «Дополнительные параметры».
-
Для включения или отключения возможности использования для вычислений нескольких процессоров в разделе Формулы установите или снимите флажок Включить многопоточные вычисления.
Заметка Этот флажок по умолчанию установлен, и для вычислений используются все процессоры. Число процессоров на компьютере определяется автоматически и отображается рядом с параметром использовать все процессоры данного компьютера.
-
Дополнительно при выборе параметра Включить многопоточные вычисления можно задавать число используемых процессоров компьютера. Например, можно ограничить число процессоров, используемых для пересчета, если нужно выделить процессорное время другим выполняемым на компьютере программам.
-
Чтобы управлять числом процессоров, в области «Число потоковвычислений» выберите «Вручную». Введите число процессоров (максимальное число — 1024).
Чтобы гарантировать правильность пересчета старых книг, приложение Excel при первом открытии книги, сохраненной в более старой версии Excel, и книги, созданной в текущей версии, ведет себя по-разному.
-
При открытии книги, созданной в текущей версии, в Excel пересчитываются только формулы, зависящие от измененных ячеек.
-
При открытии книги, созданной в более ранней версии Excel, пересчитываются все формулы в книге. Это гарантирует полную оптимизацию книги для использования в текущей версии Excel. Исключением является ситуация, когда книга находится в другом режиме вычислений, например ручном.
-
Поскольку полный пересчет требует больше времени, чем частичный, открытие книги, которая не была сохранена в формате текущей версии Microsoft Excel, может потребовать больше времени. После сохранения книги в формате текущей версии Microsoft Excel книга будет открываться быстрее.
В Excel в Интернете результаты формулы автоматически пересчитываются при изменении данных в ячейках, которые используются в этой формуле. Этот автоматический пересчет можно отключить и вычислить результаты формулы вручную. Вот как это сделать:
Примечание: Изменение параметра вычисления влияет только на текущую книгу, а не на другие открытые книги в браузере.
-
В Excel в Интернете щелкните вкладку «Формулы».
-
Рядом с параметрами вычисленийвыберите один из следующих параметров в этом меню:
-
Чтобы пересчитать все зависимые формулы при каждом изменении значения, формулы или имени, выберите значение «Автоматически». Этот параметр установлен по умолчанию.
-
Чтобы пересчитать все зависимые формулы, кроме таблиц данных, при каждом изменении значения, формулы или имени нажимайте кнопку «Автоматически, кроме таблиц данных».
-
Чтобы отключить автоматический пересчет и пересчет открытых книг только явным образом, нажмите кнопку «Вручную».
-
Чтобы пересчитать книгу вручную (включая таблицы данных), нажмите кнопку «Вычислить книгу».
-
Примечание: В Excel в Интернете нельзя изменить количество пересчетов формулы до тех пор, пока не будет выполнены определенное числовый условие, а также изменить точность вычислений с помощью отображаемого значения, а не хранимого значения при пересчете формул. Однако это можно сделать в приложении Excel для настольных систем. Чтобы задать параметры вычислений и изменить пересчет, итерацию или точность формулы, откройте книгу с помощью кнопки «Открыть в Excel».
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Содержание
- Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
- Вопросы и ответы
Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.
Расчет ошибки средней арифметической
Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.
В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.
Способ 1: расчет с помощью комбинации функций
Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.
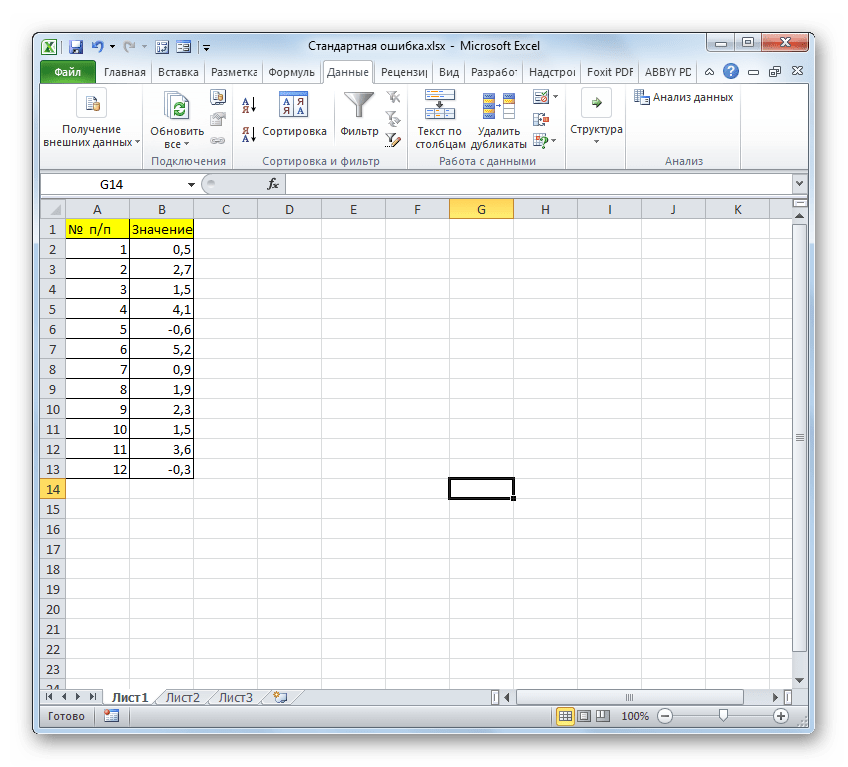
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.
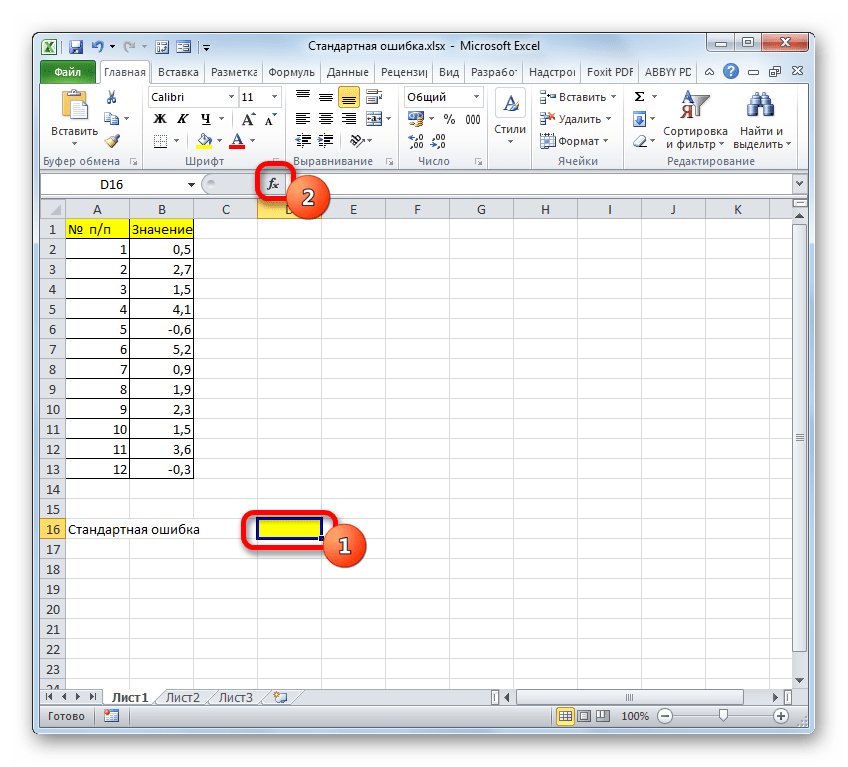
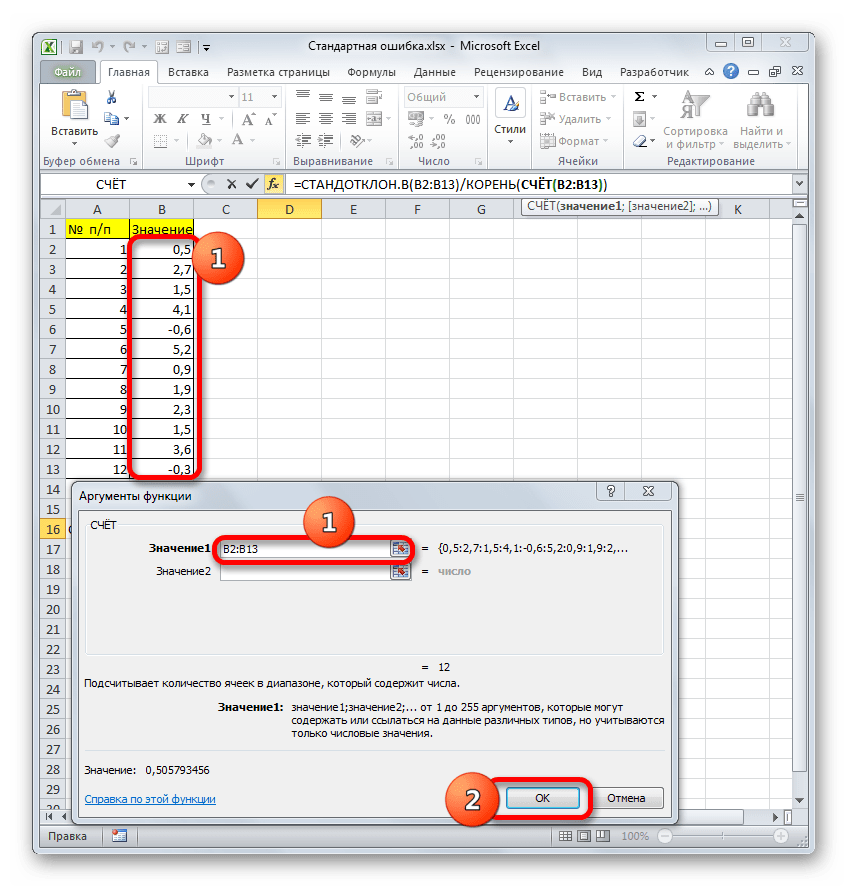
- Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».
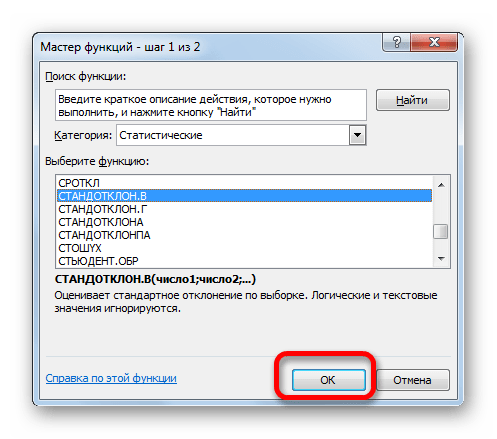
- Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».
- Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
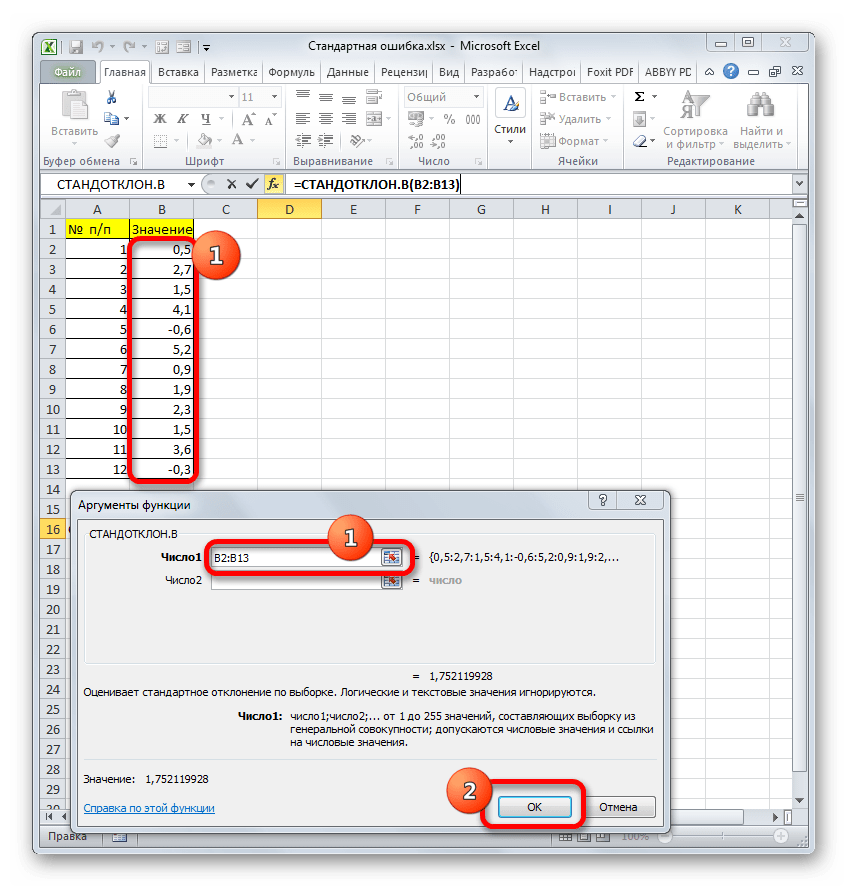
=СТАНДОТКЛОН.В(число1;число2;…)«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.
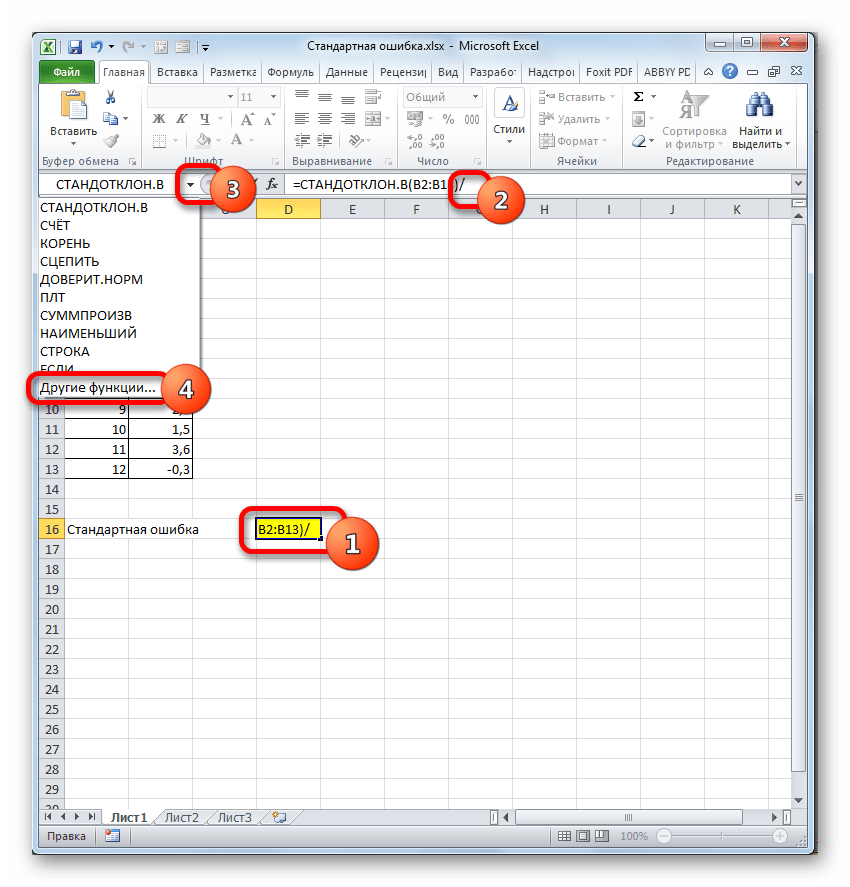
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».
- В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».
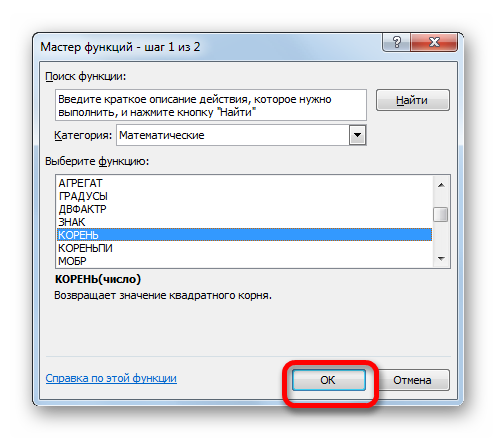
- Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».
- Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.
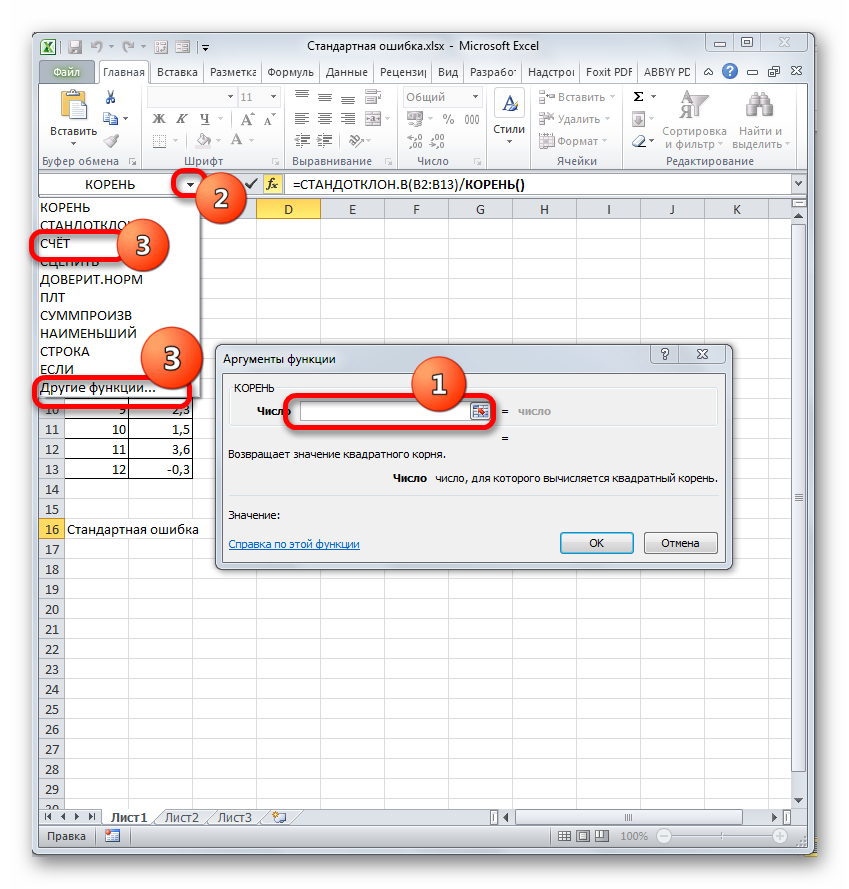
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».
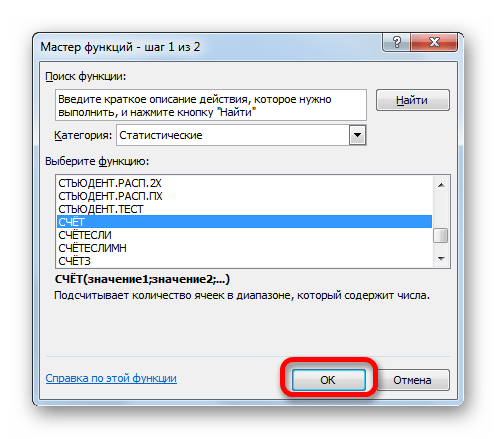
- В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».
- Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».
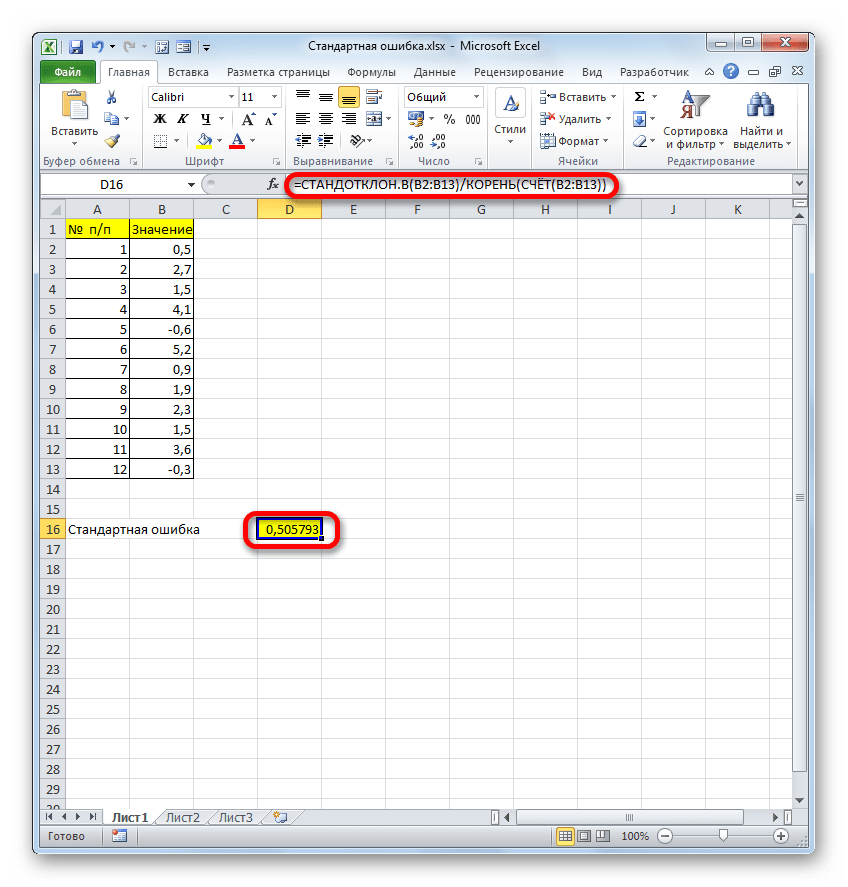
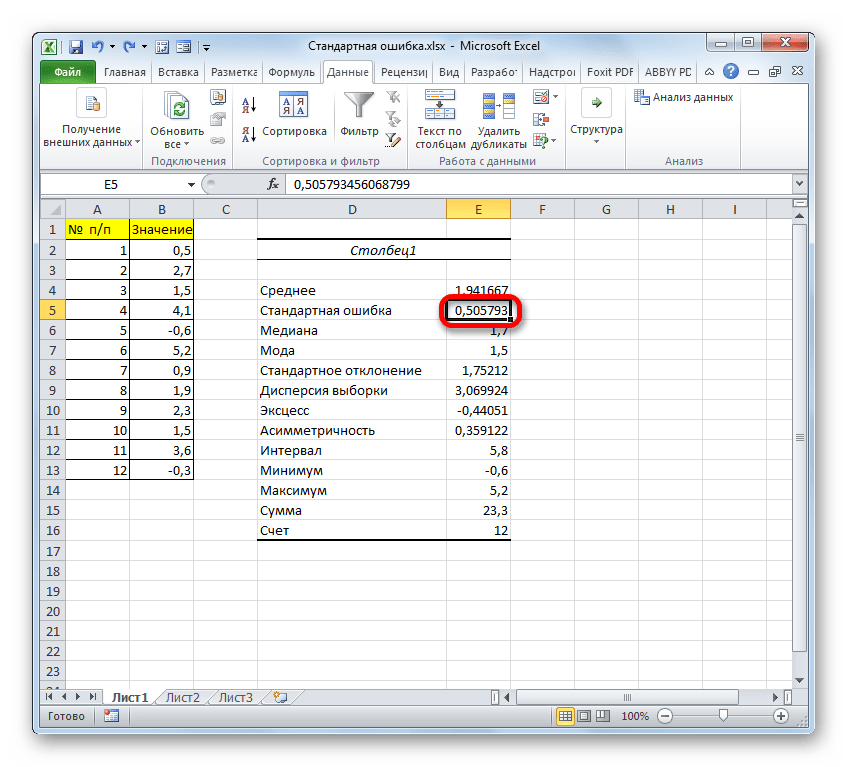
- После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.
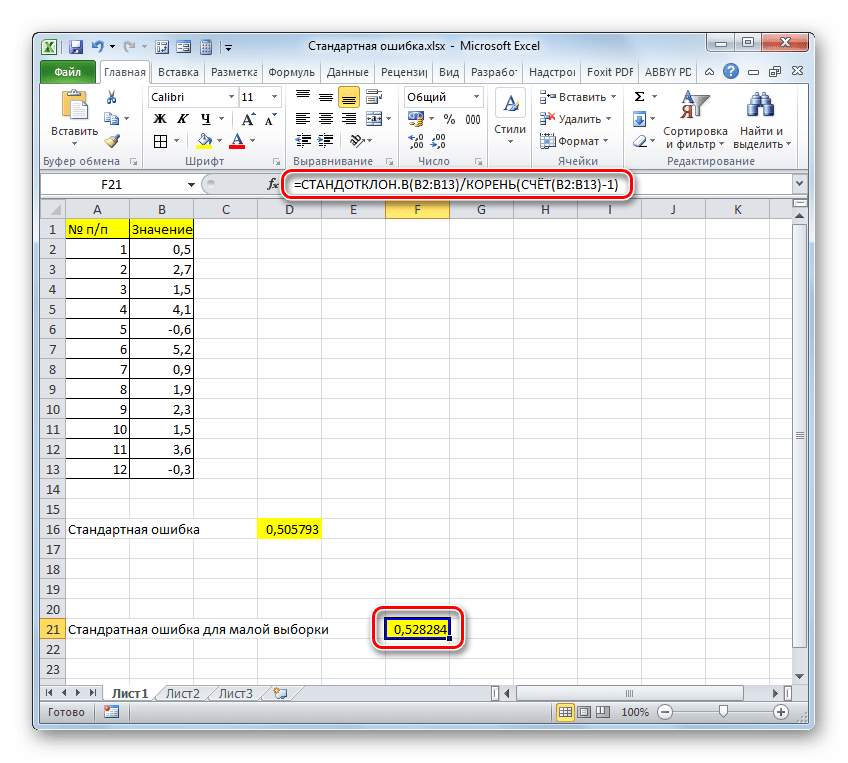
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)
Урок: Статистические функции в Экселе
Способ 2: применение инструмента «Описательная статистика»
Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.
Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.
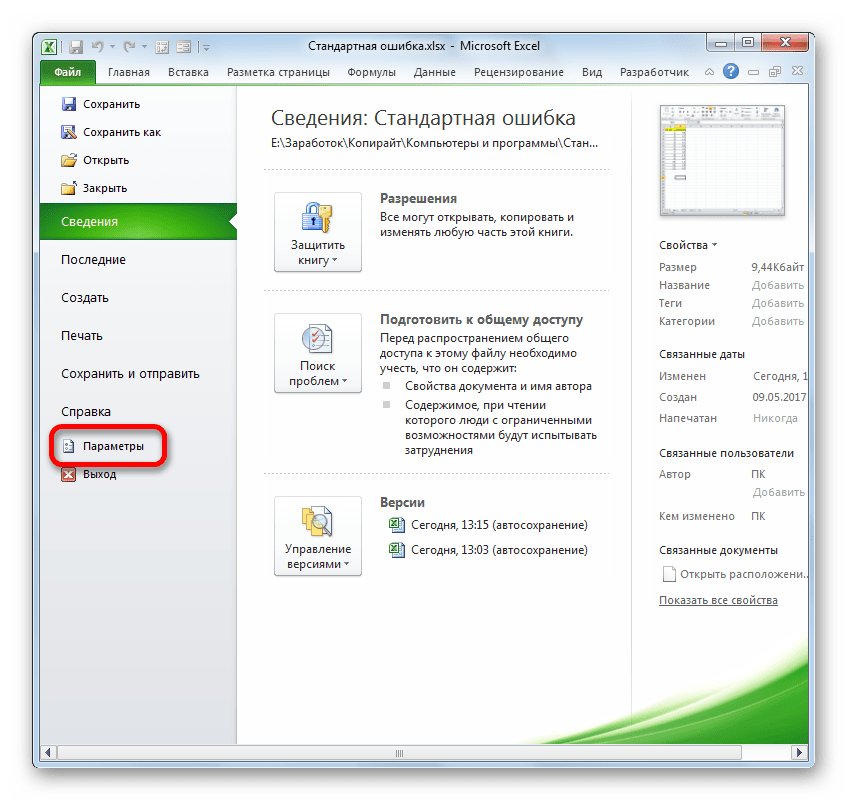
- После того, как открыт документ с выборкой, переходим во вкладку «Файл».
- Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».
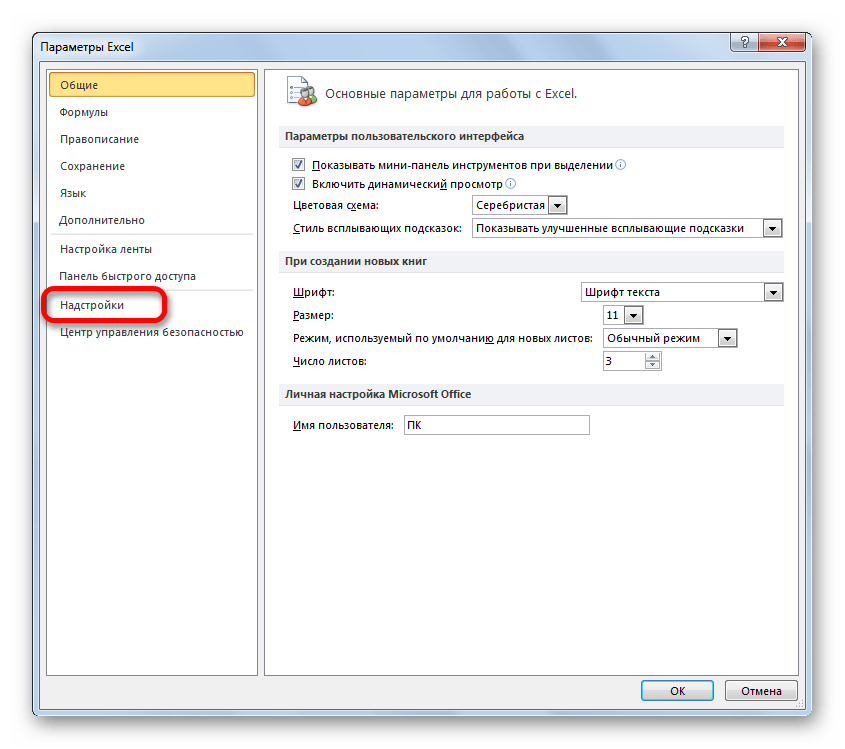
- Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».
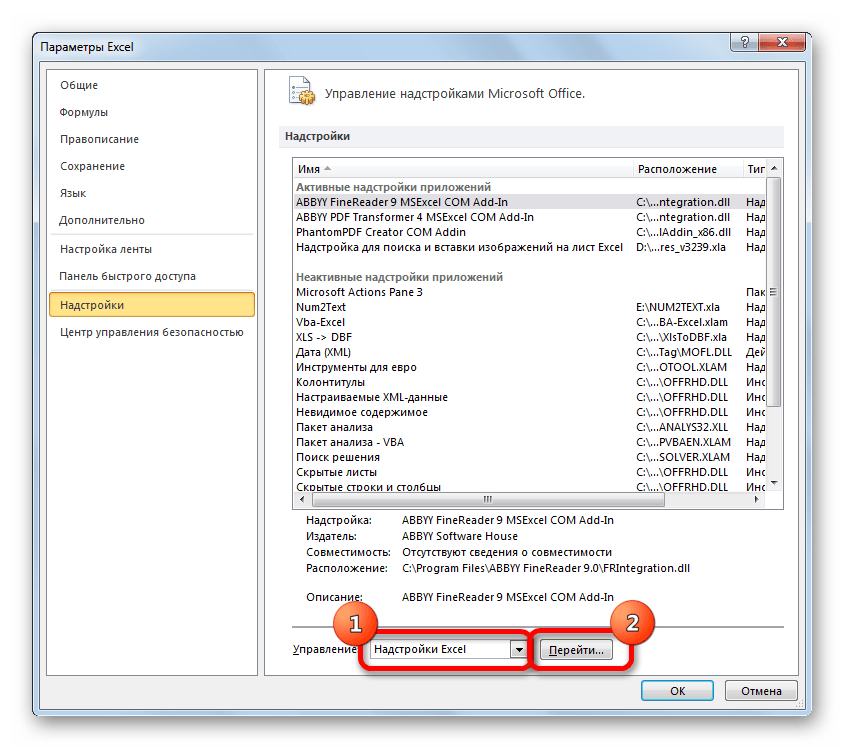
- В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.
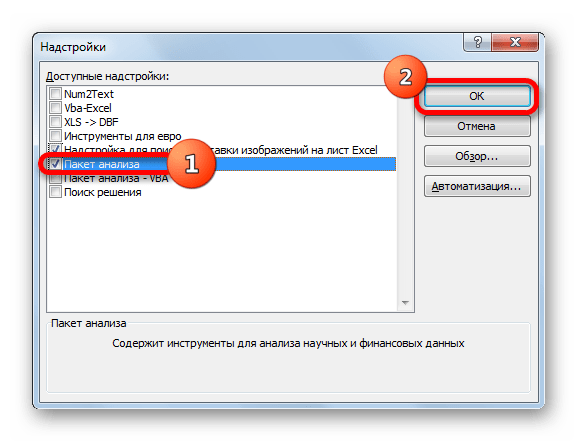
- Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.
- После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».
- После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.
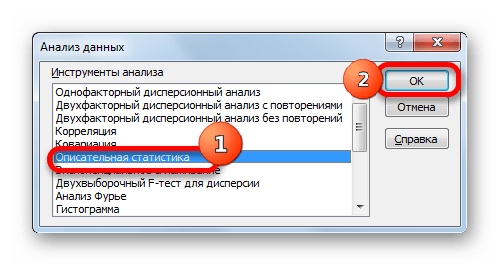
- Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.
- Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
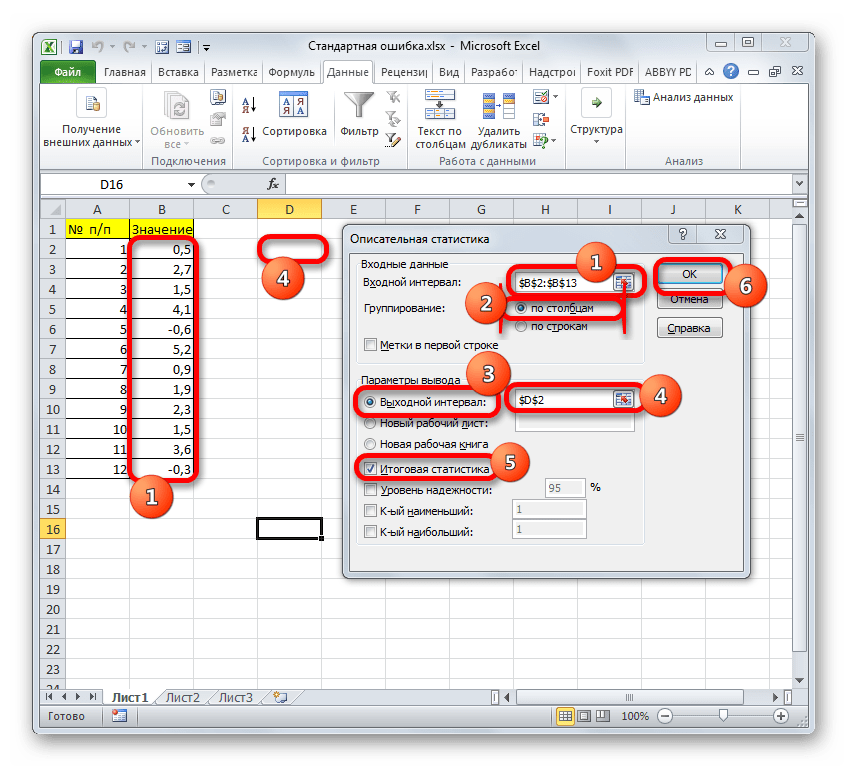
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.
В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.
Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.
Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.
Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.
После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.
- После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.
Урок: Описательная статистика в Экселе
Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.
С использованием встроенных функций
Excel расчет доверительного
интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа —
уровень значимости используемый для
вычисления уровня надежности.
(,
т.е.
означает надежности);
станд_откл
— стандартное отклонение, предполагается
известным;
размер — размер выборки.
Лабораторная работа
1
Тема: Обработка прямых
измерений в Excel (2 часа ).
Задание:
Обработать заданный набор экспериментальных
данных методом Стьюдента, построить
экспериментальные кривые методом
наименьших квадратов.
|
Пример |
Используемуе |
|
|
|
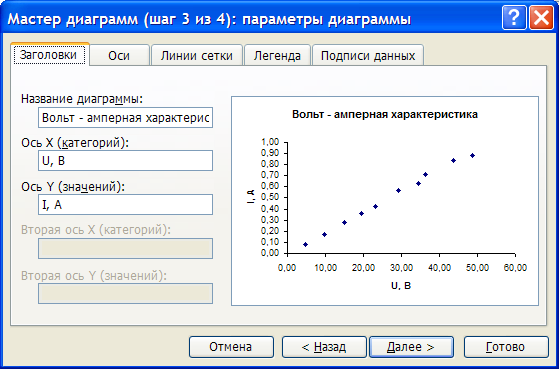
Для построения графика используем
мастер диаграмм.
Расчет
погрешности при косвенных измерениях
При измерении
величины косвенным методом предполагается,
что известна математическая модель
связывающая искомую
величину
с величинами
,
измеряемыми непосредственно. Далее
предполагается, выполнена обработка
всех прямых измерений, т. е. определены
доверительные интервалы для величин
:
Погрешность величины у
определяется по формуле:
где
.
Расчет косвенной
погрешности в Maple
Рассмотрим расчет погрешности на примере
функции одной переменной
,
где
Таким образом, найден доверительный
интервал величины
.
В случае, если определяемая в косвенном
измерении величина, является функцией
нескольких переменных, рекомендуем:
-
вычисление погрешности оформить в виде
процедуры
>dy:=proc(y, dx) ……код
процедуры
…… end proc
Код процедуры учащийся должен составить
самостоятельно на основе примера,
рассмотренного выше.
-
параметр dx считать массивом из N
переменных -
для определения списка аргументов и
их количества величины y
можно использовать операторы op() и
nops():
-
Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).
Задание:
Написать программу нахождения погрешности
косвенного измерения в среде Maple.
Выполнение задания
1. Ввести выборку значений измеряемых
величин в матричном виде
2. Определить размерность выборки
3. Задать уровень значимости и определить
степень доверия:
4. Вычислить среднее значение выборки
измеряемой величины:
a) с помощью операций
суммирования
б) с помощью встроенных функций
5. Вычислить значения среднеквадратичного
отклонения.
а) с помощью операций суммирования
,
в) с помощью встроенных функций
6. Вычислить доверительный интервал:
а) Задать коэффициент Стьюдента для
данных размерности выборки и степени
доверия:
.
б) Вычислить абсолютную случайную
погрешность
.
в) Вычислить верхнюю и нижнюю границы
доверительного интервала.
.
7. Учесть приборные погрешности:
а) Задать приборные погрешности
.
б) Вычислить абсолютную случайную
погрешность с учетом приборных
погрешностей
.
8. Представить результат:
а) Абсолютная погрешность:
,
б) Относительная погрешность:
,
в) Верхняя и нижняя границы доверительного
интервала.
.
Примечание. Вычисления провести:
а) в обычном виде,
(См. Дов_инт_01)
б) с помощью операций суммирования,
(См. Дов_инт_02)
в) с помощью встроенных функций.
(См. Дов_инт_03)
2. Вычисление косвенных погрешностей
Выполнение задания
1. Провести аналитические вычисления:
а) Ввести выражение для исследуемой
функции:
,
б) Получить выражение для среднего
значения величины исследуемой функции:
,
в) Получить выражение косвенной
погрешности исследуемой функции в общем
виде и для значения :
,
,
1. Провести численные вычисления:
а) Ввести численные значения постоянных,
б) Ввести средние значения и доверительные
интервалы переменных,
в) Вычислить относительные погрешности
переменных,
г) Вычислить среднее значение исследуемой
функции:
,
г) Вычислить косвенную погрешность
(абсолютную погрешность) исследуемой
функции
,
г) Вычислить относительную погрешность
исследуемой функции
,
в) Вычислить верхнюю и нижнюю границы
доверительного интервала исследуемой
функции:
.
(См. Косв_погр).
3. Построение графиков. Полиномиальная
регрессия
Выполнение задания
1. Ввод выборок значений величин :
2. Вычислить верхнюю и нижнюю границы
доверительного величины Y:
.
3. Полиномиальная регрессия:
а) Задать степень полинома k:
б) Задать число точек данных:
.
в) Задать регрессионную зависимость:
.
г) Определить коэффициенты уравнения
регрессии
:
,
.
4. Построить графики:
а) точечных график данных,
б) кривую регрессии,
в) доверительные интервалы величины Y.
(См. Постр_граф).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как посчитать погрешность в excel
Пусть – точное значение, – приближенное значение некоторого числа.
Абсолютная погрешность приближенного числа равна модулю разности между его точным и приближенным значениями:
Довольно часто точное значение неизвестно, поэтому вместо абсолютной погрешности используют понятие границы абсолютной погрешности:
Число называется предельной абсолютной погрешностью, оно равно или превышает значение абсолютной погрешности.
Основной характеристикой точности числа является относительная погрешность.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
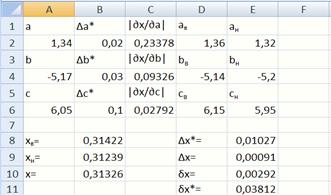
Общая формула для оценки предельной абсолютной погрешности функции нескольких переменных имеет вид:
где –предельная абсолютная погрешность числа .
Пример: Известно, что где
Для оценки предельной абсолютной погрешности воспользуемся формулой:
Рис. 1. Вид экрана для вычисления абсолютной и относительной погрешностей
Исходные данные вводятся в блок А1:B6 (рис. 1). В ячейки С1:С6вводятся формулы для вычисления частных производных искомой функции. В ячейку Е8записывается формула . Модуль вводится с использованием функции =abs().
В ячейках D1:E6рассчитываются верхние и нижние оценки значений переменных по формулам (аналогично для других переменных).
В ячейках B8:B10вычисляются верхняя и нижняя оценки значений функции и само значение функции отличие вычисляемых функций в используемом наборе аргументов.
В ячейку Е9записывается формула для вычисления абсолютной погрешности Найденная абсолютная погрешность не должна превышать значение предельной абсолютной погрешности, т.е.
В ячейку Е10записывается формула для вычисления относительной погрешности
Предельную относительную погрешность заданной функции вычислим следующим образом:
Полученную формулу записывают в ячейку Е11. Найденная относительная погрешность не должна превышать значение предельной относительной погрешности, т.е.
Задания для самостоятельного выполнения.
Из таблицы 1 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Вычислить частные производные, верхнюю и нижнюю оценки значений функции и само значение функции, изменить формулу вычисления предельной относительной погрешности. Все остальные ячейки пересчитаются автоматически.
Контрольные вопросы
1. Как записать основные математические функции в Excel.
2. Сформулируйте определение абсолютной и относительной погрешностей.
3. Запишите формулы для вычисления предельной абсолютной и предельной относительной погрешностей.
4. Основные правила вычисления абсолютной и относительной погрешностей.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8833 — | 7547 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( , т.е. означает надежности );
станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
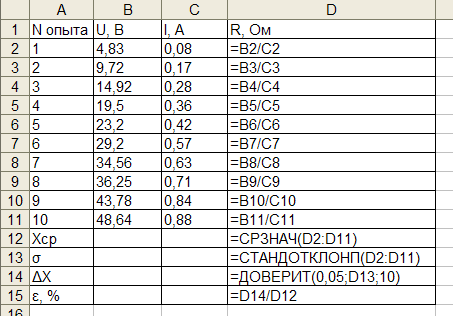
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома произведем обработку данной серии экспериментальных данных.
| Используемуе формулы |
 |
| Результат расчета |
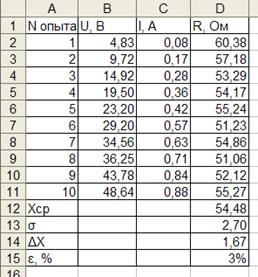 |
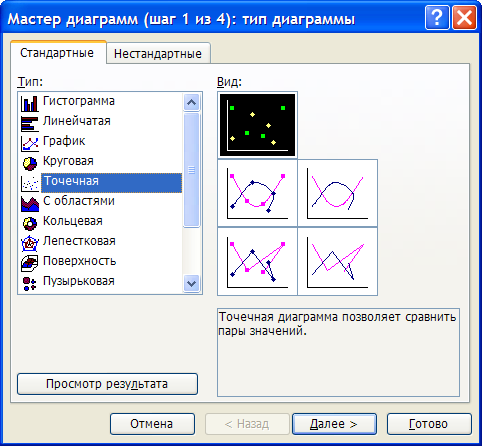
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Доброго дня, друзья.
Так как в после прошлого поста несколько человек заинтересовались моей таблицей, решил поделиться с вами еще одной своей таблицей.
Есть у нас лаборатория, и мы постоянно сверяем результаты наших исследований с результатами контрагентов. По нормативным документам нужно придерживаться определенных пределов расхождений в результатах.
Чтобы постоянно не открывать таблицу с значениями пределов воспроизведения, селал себе такую таблчку.
Чтобы было понятно, Результаты испытаний записываются в виде X±Δ
где X – результат анализа;
±Δ – погрешность результатов анализа, в нашем случае воспроизводимость..
То есть для первого испытания на медь для Пробы 1 результат у нас (H7) 1,30±0,12, а у контрагентов (ячейка C7) 4,81±0,12. А разница между результатами 4,81-1,30=3,51
Мы не входим в предел воспроизведения, ячейка M7 окрасилась в красный и сразу видим, что и один из нас хочет другого немного обмануть)) Если бы ячейка стала зеленой, то все норм.
Вот чтобы такие расчеты постоянно не делать, была создана данная таблица.
Данные вычисления могут быть полезны чтобы узнать и в других областях, где нужно узнать, вписываемся мы в пределы или нет.
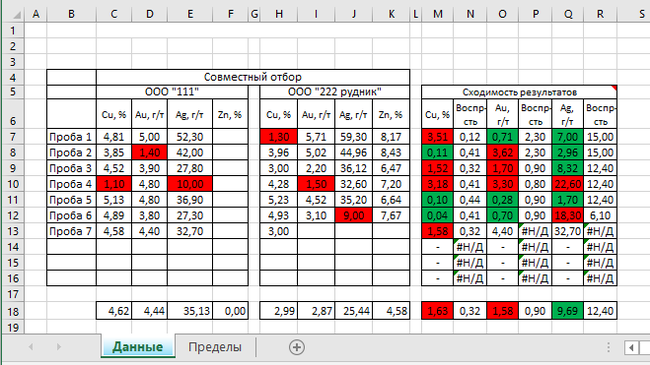
Вот так выглядит рабочая таблица на странице Данные:
Левая табличка разделена на две чати — наши данные при отгрузке продукта и данные контрагента при приемке продкта. В правой табличке, соответственно производятся все вычисления и ячейка окрашивается в определенный цвет при выполнении и невыполнении условий.
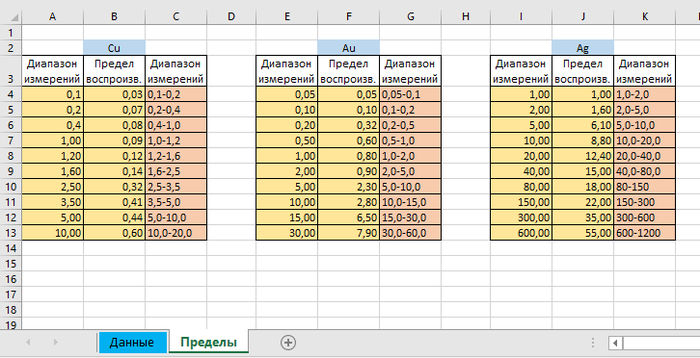
Также имеется вторая табличка на странице Пределы, где расписаны пределы по диапазонам:
Вычисления производятся по желтым ячейкам, а розовые для информации. Первый и третий столбци по сути одно и то же.
Итак погнали. Что тут творится вообще ))
Буду объяснять для пробы 1, результаты Cu, ячейки M7 и N7. Остальное аналогично
Сперва вычислим раницу между нашими результатами испытаний. Нам нужны только абсолютные значения, так как разность может быть отрицательной. В M7 ввоим формулу:
В N7 вводим следующую формулу:
Тут остановимся, разберем формулу по частям:
Берем значение из ячейки H7 (это наш результат) и ищем на странице Пределы в массиве для Cu пределы значений, куда входит наш результат. Находим, что походит диапазон 1,2-1,6
Ищем номер строки значениея из ячейки H7 в таблице на листе Пределы. В предыдущей формуле мы нашли, что значение относится к пределам 1,2-1,6 и теперь легком можем найти номер строки, где он находится.
Так, номер строки нашли, и нам надо узнать значение погрешности или воспроизведения. Тут нам поможет функция ИНДЕКС, который возвращает значение на пересечении указанных номеров строки и столбца в массиве.Номер строки мы узнали из предыдущей формулы, номер столбца, где нужно искать результат укажем вручную:
Тут Пределы!$B$4:$C$13 это массив где мы делаем поиск
ПОИСКПОЗ(ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА);Пределы!$C$4:$C$13;0) — номер строки.
И единичка в конце — номер столбца.
Теперь мы узнали, что наш результат должен быть 1,30±0,12
А разница результатов двух предприятий 3,51. Это означает, что мы не входим в предел воспроизведения.
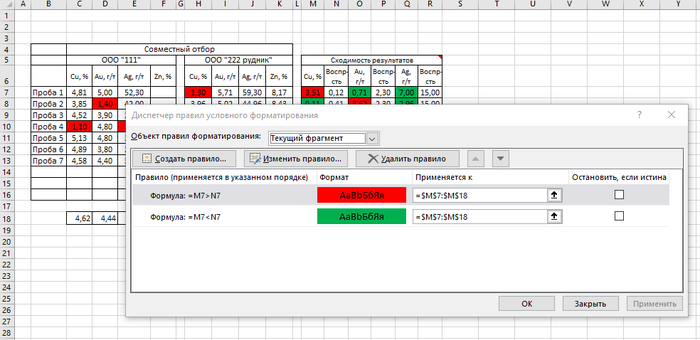
Чтобы визуально сразу увидеть это, окрасим эту ячейку в красный. Делается это через меню Условное форматирование
Выбираем в меню Условное форматирование — Правила выделения ячеек — Больше (Меньше) и задаем форматирование — окрасить ячейку в красный или зеленый цвет.
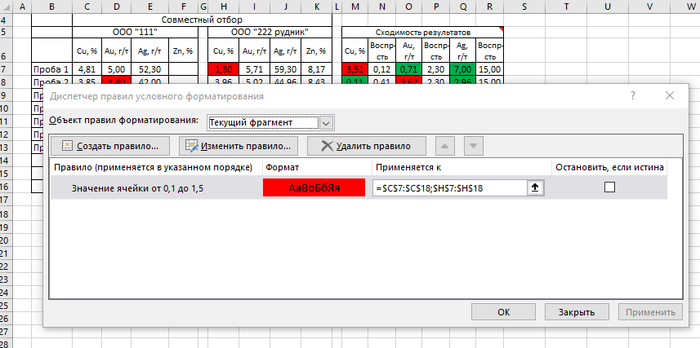
Также у нас есть ограничение в поставке продукта. Качество должно быть не менее определенного значения. Чтобы тоже сразу наглядно это увидеть, я через Условное форматирование выбрал пункт Между.. и задал нужные значения
Если отгрузим товар с качеством по меди меньше 1,5%, то ячейка окрашивается в красный цвет.
Спасибо что дочитали, надеюсь кому-нибудь пригодится данная таблица или формулы.
Как нанести погрешности на графике в Excel
Как построить график в Excel с учетом погрешностей? Подобная задача нередко возникает у студента при обработке результатов лабораторных работ. Результаты представляют собой, как правило, два массива данных (в общем случае Х и Y). Пусть, для примера, имеется следующая экспериментальная зависимость:
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| У | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
Требуется представить эту зависимость Y от Х графически. Получится примерно то, что представлено на рисунке.
Например, в ходе лабораторной работы студент измерял зависимость силы тока в одной из ветвей электрической цепи (в Амперах) от напряжения на том или ином ее элементе (в Вольтах). Необходимо отложить данные на графике с учетом погрешностей.
Надо сказать, что сделать построение вручную, как ни парадоксально, в данном случае даже немного проще, чем с использованием, казалось бы, такой мощной и удобной программы, как Excel . Дело в том, что, на самом деле, график, приведенный на предыдущем рисунке… построен неверно.
Почему? Ведь, вроде бы, ничего сложного нет. Нажимаем в Excel кнопку « Мастер диаграмм », Выбираем тип диаграммы – точечная . Затем нажимаем « Далее », задаем массивы для X и Y, затем опять « Далее »… — и вскоре получится то, что приведено на предыдущем рисунке.
Вроде бы, все правильно. Да только график построен строго по точкам. Видно, что зависимость немонотонная, с достаточно острым максимумом – что не всегда имеет место в реальности. Ибо в реальности подавляющее большинство зависимостей могут быть более плавными.
Конечно, здесь надо смотреть, какие конкретно показатели анализируются. Если это, к примеру, динамика биржевого курса ценных бумаг; или – динамика поступления платежей от покупателей, равно как и другой аналогичный экономический показатель, то, конечно, можно с уверенностью сказать, что график вовсе не обязан быть плавным. В самом деле, очень многие экономические показатели меняются, как правило, скачкообразно.
А вот если анализировать данные, скажем, из области психологии, физики, биологии (отчасти), а также из ряда иных отраслей, то там графики экспериментальных зависимостей, за немногим исключением, зачастую являются достаточно плавными (хотя, все относительно, конечно) .
Но, вроде бы, и здесь нет никаких проблем: следует провести линию тренда, которых Excel предлагает несколько типов. Так, можно выбрать линейный, степенной, экспоненциальный и т.д. тренд.
Можно… На примере выбранных нами данных, выбор показал, что наиболее близким для выбранной совокупности данных является параболический тренд. Отобразим его на рисунке.
Вроде бы, то, что проведено черной линией (тренд), уже гораздо ближе к истине. Правда, совсем ненамного. Фактически, проведенный тренд достаточно хорошо соответствует исходным данным только для 3, 4 и 7-й точек. Для остальных точек имеются существенные расхождения, причем ошибка доходит до 80%.
Ясно, что построенный тренд, в силу его высокой погрешности, в данном случае никак нельзя принять в качестве качественного графика, отражающего ход зависимости, выявленной экспериментально. Однако, и первоначально построенную (синюю) линию, вероятно, также нельзя принять в качестве такового, ибо, повторимся, она вообще не учитывает погрешностей.
Как же быть?
Конечно, есть возможность провести интерполяцию и уже с ее учетом определить функцию, которая будет наиболее плавной (с учетом погрешностей) и построить ее в качестве графика. Однако, это – задача достаточно сложная, представляющая собой предмет отдельного разговора. Скажем, в том же MatLab , конечно, существуют подобные функции, при помощи которых можно это реализовать.
Однако, тогда, в любом случае, придется писать программу (в MatLab это будет проще, в Excel – посложнее, ибо там придется программировать вручную готовые функции, которые уже имеются в MatLab ). А для студента, которому требуется обработать данные лабораторной или (реже) контрольной работы, это может являться сложной, отдельной задачей. В самом деле, вместо анализа результатов он вынужден вначале думать, каким образом построить эти результаты, а потом программировать. Добро, если лабораторная работа проходит на старшем курсе. Однако, зачастую, студент делает их, начиная с самого начала своего обучения, т.е. когда опыта математической обработки, не говоря уже об умении строить интерполяционные многочлены, нет вообще.
Какими бывают погрешности
Погрешности бывают, в общем случае, относительные (в процентах) и абсолютные (выраженные в единицах измеряемой величины). Кроме того, они могут иметь постоянное значение или переменное.
Надо сказать, что старые версии программы Excel не позволяют просто так нанести погрешность на график. А вот, начиная, по крайней мере, с версии Excel 2007 , это можно сделать достаточно просто. Вот пример, как наносятся погрешности в Excel.
Да, все вроде бы, замечательно. Но только график, приведенный на сайте (по указанной ссылке), также построен, строго говоря, неверно. Дело в том, следует повторить, что график должен представлять собой, по возможности, плавную линию. Которая где-то пройдет через середину интервала погрешности, а где-то, быть может, через один из его краев. Так вот, стандартные средства Excel даже самых новых версий не позволяют построить такой график автоматически. Тем более, если идет речь о том, что каждая экспериментальная точка может иметь, вообще говоря, разную погрешность.
Когда это бывает?
Например, в случае, когда разные экспериментальные точки были получены на базе исследований, проведенных разными методами.
Например, взять эксперименты по измерению зависимости внутреннего трения (т.е. степени перехода механической энергии в тепловую при упругих деформациях) материалов от частоты упругой деформации.
- Если частота равна нулю (т.е. происходит равномерная деформация материала), то необходимо применять установки для растяжения/сжатия, способные измерить работу, затраченную на нагрев материала в процессе деформации.
- Если говорить о частоте, когда ее значения лежат в пределах 10 Гц… 1000 Гц, то такие измерения проводятся при помощи совсем других установок, например, с использованием так называемых крутильных маятников (т.е. когда образец совершает вынужденные крутильные колебания заданной частоты).
- Если вести речь о диапазоне частот 20 кГц… 200 кГц то здесь необходимо применять ультразвуковые установки.
- Наконец, исследования при гиперзвуковых частотах (более 10 9 Гц) проводятся при помощи оптических, пьезоэлектрических методов.
Таким образом, даже ориентировочное рассмотрение выявило, что существуют, как минимум, четыре основных диапазона частот, для каждого из которых может быть применен какой-либо свой метод исследования, кардинально отличающийся от других. Соответственно, у каждого из методов может быть свое значение погрешности (относительной или абсолютной).
Как построить плавный график в Excel с учетом погрешностей?
Итак, как построить нормальный, правильный график? Который, с одной стороны, был бы, по возможности, плавным (т.е. содержал бы поменьше нестабильных, немонотонных участков — в пределах погрешности, конечно), а с другой – лежал бы в рамках допустимых погрешностей.
Рассмотрим самый сложный, общий случай – разных погрешностей для каждой из экспериментальных точек и покажем, как можно применить Excel для того, чтобы построить корректный график зависимости.
Пусть погрешности экспериментальных точек равны следующим значениям:
Ясно, что как относительная, так и абсолютная погрешности данных будут разными для каждой из экспериментальных точек. Однако, для каждой из них можно определить минимальное и максимальное значения (через интервал которых и должен пройти график). Проведем такой расчет (благо, при помощи Excel это сделать очень легко и быстро):
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| Y | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
| Относительная погрешность (для Y), % | 10 | 7 | 5 | 12 | 20 | 17 | 23 |
| Минимальное значение Y | 2,9 | 3,9 | 8,6 | 13,0 | 18,4 | 12,6 | 9,9 |
| Максимальное значение Y | 3,5 | 4,5 | 9,5 | 16,5 | 27,6 | 17,8 | 15,8 |
Минимальные и максимальные значения Y образуют допустимый интервал (диапазон), в котором может находиться график. Отложим этот диапазон на рисунке.
Нижняя граница диапазона показана зеленой линией, верхняя – черной. Толстая черная линия – это ранее нанесенные тренд. Четко видно, что тренд (даже, повторимся, оптимальный, выбранный из предлагаемого программой Excel перечня) только в двух (из семи) экспериментальных точках проходит в пределах допустимой области. Следовательно, необходимо отказаться от него. Удалим его с рисунка.
Итак, построена допустимая область. Искомый график зависимости должен лежать внутри нее, при этом имея, по возможности, наиболее плавный вид.
Его построение (если расчет оптимального интерполяционного многочлена вызывает сложность) проще провести вручную. Т.е. распечатать на бумаге полученный рисунок и уже на нем нанести график. Но, вполне возможно это сделать и при помощи компьютера – чтобы вообще не возиться с пишущими принадлежностями, причем сделать это можно очень быстро.
Для этого удобнее всего использовать программу Inkscape. Она является совершенно бесплатной, если у Вас она еще не установлена, можете скачать ее с официального сервера. https://inkscape.org/ru/download/
Устанавливаем ее, затем открываем. Копируем рисунок (отметим, лучше это сделать не из Word, а из первоисточника, т.е. из Excel).
Затем, как обычно, нажимаем кнопку «Вставить», размещаем рисунок примерно по центру рабочей области. Если ее размеры не совпадают с рисунком, нужно ее настроить, для чего нажимаем « Файл », « Свойства документа » и там устанавливаем альбомную ориентацию и указываем требуемые размеры (параметры «Ширина» и « Высота »). Примерно вот что должно получиться в итоге.
Так как Excel создает диаграммы в векторном виде, они без проблем редактируются в Incscape. Таким образом, наша задача – вручную таким образом исправить синюю линию, чтобы она стала как можно более плавной.
Нажав клавишу F2 , затем, удерживая « Shift », кликаем мышкой по элементам синей кривой так, чтобы на ней появились серые узлы. Когда они появятся на каждом из ее участков, это означает, что мы выделили ее ВСЮ в режиме редактирования узлов.
Затем нажимаем в меню пункт « Контур », « Упростить ». Число узлов значительно снизится, останутся лишь основные. Кстати, если кликнуть по каждому узлу в отдельности, его можно будет стереть путем нажатия клавиши « Delete ». Но, это будет достаточно долго, поэтому проще использовать команду » Упростить «.
Затем, удерживая левую кнопку мыши на соответствующем узле, двигаем его в ту или иную сторону. Так повторяем с другими узлами (при необходимости скорректировать кривизну линии в конкретном узле, можно также двигать рычаги каждого из них).
В итоге линия принимает вид, показанный на рисунке.
Для наглядности (чтобы можно было помнить, где проходила линия графика, построенная в Excel), экспериментальные точки, в виде синих ромбиков, оставлены.
Вставить рисунок из Incscape в Word достаточно просто – как обычно: нажимаем « Правка », « Выделить все » (как уже говорилось, рабочая область должна быть подогнана к размерам рисунка; впрочем, можно и рисунок, путем его деформаций, подогнать к размерам рабочей области программы Inkscape) , затем – « Скопировать ».
Проверяем, что рисунок выделился, как полагается. Тогда переходим в Word и выполняем вставку из буфера обмена, как обычно, путем нажатия кнопки « Вставить » на панели инструментов. Но, учтите, что, к сожалению, исправить в Excel измененную диаграмму уже не получится (она вставится, как рисунок) . Поэтому все, что необходимо сделать на диаграмме в Excel, надо делать заранее, ДО ТОГО, т.е. до преобразования ее в Inkscape. Вместе с тем, при желании, полученный рисунок можно вновь скопировать в Inkscape провести, если нужно, дальнейшее его редактирование.
Таким образом, мы получили сглаженный, более плавный график, чем тот, который был построен автоматически в Excel. Даже не взяв в руки карандаш или иной пишущий инструмент: использовались лишь некоторые клавиши и мышь.
Наносим линии погрешностей
Что же касается линий погрешностей, то их можно провести, используя соответствующие возможности Excel (если он у Вас, как минимум, версии 2007 г.) . Правда, так как величина погрешности в нашем примере для каждой из точек – разная, то возможности Excel по построению погрешностей здесь помогут мало.
Так что, в данном случае, можно начертить их вручную (т.е. нарисовать мышкой соответствующие вертикальные линии, проходящие через каждую экспериментальную точку).
Однако, это, на наш взгляд, утомительно. Поэтому, если совсем не хочется возиться с ручным рисованием, выход вполне есть – их можно выполнить, нарисовав соответствующее (в данном случае 7) дополнительных графиков. Повторимся, это следует сделать ДО того, как преобразовывать диаграмму в Inkscape.
Итак, заходим на вкладку « Диаграмма ». Нажимаем в панели инструментов « Диаграмма », « Исходные данные ». Выбираем вкладку « Ряд », затем нажимаем «Добавить».
Далее, жмем кнопку с красной стрелочкой – там, где значения Х. Переходим на Лист, на котором находятся данные, по которым построена эта диаграмма и указываем, к примеру, четвертое значение Х (равное 7). Затем (внимание!), удерживая клавишу « Ctrl », кликаем вновь мышкой по тому же самому значению Х (т.е. по Х, равном 7). В итоге в строке, где задается адрес диапазона значений Х, адрес ячейки, в которой расположена цифра 7, должен присутствовать ДВАЖДЫ , через точку с запятой. Убедившись в этом, нажимаем, как обычно, красную стрелочку.
Теперь выбираем значения Y. После нажатия красной стрелочки, перейдя на нужный Лист, кликаем на минимальное значения Y, соответствующее Х, равному 7. Затем, удерживая клавишу « Ctrl », кликаем максимальное значение Y. В итоге, через точку с запятой в адресной строке должны появиться адреса двух ячеек, соответствующие минимальному и максимальному значению Y (для Х=7).
Наконец, переходим на диаграмму, дважды кликаем мышкой на получившемся вертикальном отрезке с маркерами, зайдя, тем самым, в свойства только что построенного отрезка. Там устанавливаем вид маркера в виде знака минус (« — »). Потом устанавливаем, к примеру, черные цвета линий и маркера и нажимаем « ОК ». Результат наших действий приведен на рисунке.
Видим, что для точки Х=7 появилась линия погрешности. Кстати, ширину этой линии можно, при желании, изменять — путем изменения размера маркера.
Поступая таким же образом со всеми остальными точками, можно вскоре построить линии погрешностей для каждой из них (кому не хочется выполнять эту нудную работу, если точек много, можно написать несложный макрос — пишется один раз; правда, некоторым студентам, например, учашимся на младших курсах, это, возможно, будет затруднительно, поэтому проще будет сделать так, как говориось выше) . А линии, ограничивающие диапазоны минимальных и максимальных значений (зеленую и черную, соответственно) можно, кстати, потом удалить, если они не нужны. Тогда график примет полностью стандартный вид.
Его можно потом перенести в Inkscape и придать графику (синяя линия) более плавный вид.
Excel в помощь для определения пределов погрешности
Так как в после прошлого поста несколько человек заинтересовались моей таблицей, решил поделиться с вами еще одной своей таблицей.
Есть у нас лаборатория, и мы постоянно сверяем результаты наших исследований с результатами контрагентов. По нормативным документам нужно придерживаться определенных пределов расхождений в результатах.
Чтобы постоянно не открывать таблицу с значениями пределов воспроизведения, селал себе такую таблчку.
То есть для первого испытания на медь для Пробы 1 результат у нас (H7) 1,30±0,12, а у контрагентов (ячейка C7) 4,81±0,12. А разница между результатами 4,81-1,30=3,51
Мы не входим в предел воспроизведения, ячейка M7 окрасилась в красный и сразу видим, что и один из нас хочет другого немного обмануть)) Если бы ячейка стала зеленой, то все норм.
Вот чтобы такие расчеты постоянно не делать, была создана данная таблица.
Данные вычисления могут быть полезны чтобы узнать и в других областях, где нужно узнать, вписываемся мы в пределы или нет.
Вот так выглядит рабочая таблица на странице Данные:
Левая табличка разделена на две чати — наши данные при отгрузке продукта и данные контрагента при приемке продкта. В правой табличке, соответственно производятся все вычисления и ячейка окрашивается в определенный цвет при выполнении и невыполнении условий.
Также имеется вторая табличка на странице Пределы, где расписаны пределы по диапазонам:
Вычисления производятся по желтым ячейкам, а розовые для информации. Первый и третий столбци по сути одно и то же.
Итак погнали. Что тут творится вообще ))
Буду объяснять для пробы 1, результаты Cu, ячейки M7 и N7. Остальное аналогично
Сперва вычислим раницу между нашими результатами испытаний. Нам нужны только абсолютные значения, так как разность может быть отрицательной. В M7 ввоим формулу:
В N7 вводим следующую формулу:
Тут остановимся, разберем формулу по частям:
ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА)
Берем значение из ячейки H7 (это наш результат) и ищем на странице Пределы в массиве для Cu пределы значений, куда входит наш результат. Находим, что походит диапазон 1,2-1,6
ПОИСКПОЗ(ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА);Пределы!$C$4:$C$13;0)
Ищем номер строки значениея из ячейки H7 в таблице на листе Пределы. В предыдущей формуле мы нашли, что значение относится к пределам 1,2-1,6 и теперь легком можем найти номер строки, где он находится.
Так, номер строки нашли, и нам надо узнать значение погрешности или воспроизведения. Тут нам поможет функция ИНДЕКС, который возвращает значение на пересечении указанных номеров строки и столбца в массиве.Номер строки мы узнали из предыдущей формулы, номер столбца, где нужно искать результат укажем вручную:
ИНДЕКС(Пределы!$B$4:$C$13;ПОИСКПОЗ(ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА);Пределы!$C$4:$C$13;0);1)
Тут Пределы!$B$4:$C$13 это массив где мы делаем поиск
ПОИСКПОЗ(ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА);Пределы!$C$4:$C$13;0) — номер строки.
И единичка в конце — номер столбца.
Теперь мы узнали, что наш результат должен быть 1,30±0,12
А разница результатов двух предприятий 3,51. Это означает, что мы не входим в предел воспроизведения.
Чтобы визуально сразу увидеть это, окрасим эту ячейку в красный. Делается это через меню Условное форматирование
Выбираем в меню Условное форматирование — Правила выделения ячеек — Больше (Меньше) и задаем форматирование — окрасить ячейку в красный или зеленый цвет.
Также у нас есть ограничение в поставке продукта. Качество должно быть не менее определенного значения. Чтобы тоже сразу наглядно это увидеть, я через Условное форматирование выбрал пункт Между.. и задал нужные значения
Если отгрузим товар с качеством по меди меньше 1,5%, то ячейка окрашивается в красный цвет.
Спасибо что дочитали, надеюсь кому-нибудь пригодится данная таблица или формулы.