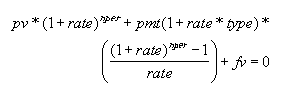Excel calculator for compounding interest

“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it”. – Albert Einstein

What is Compound Interest?

Let me take a simple example to explain it.

Suppose you invest USD 1000 in a bank account that promises to give you 10% return at the end of the year.

So at the end of year 1, you get USD 1100 (1000+100).

Now since you didn’t have any immediate use of the money, you let it stay in the account. And the bank did its part and added 10% at the end of the year.

Since now you had USD 1100 in the account, the bank pays you 10% interest on 1100 (which includes the USD 1000 you invested at the beginning and the USD 100 interest you earned at the end of the first year). So you end up with USD 1210.

The benefit of compounding is that even your interest would earn interest.

What is the difference between Simple Interest and Compound Interest?

Simple Interest simply calculates the interest amount based on the initial investment, total number of years, and the rate of interest, For example, if you invest USD 1000 for 20 years at 10% rate, you will get USD 3000 a the end of 20 years (that is USD 100o of your initial investment and 2000 of the simple interest).

Compound Interest, on the other hand, calculates interest on the interest amount as well. So if you invest USD 1000 for 20 years at 10% rate, the first year your investment grows to USD 1100. In the second year, your investment grows to USD 1210 (this happens as in the second year, you earn interest on 1100 and not 1000). At the end of 20 years, compound interest will make your investment grow to USD 6727.5.

As you can note, the investment with compound interest grew twice as compared with the one with simple interest.

‘Simple interest is calculated on the principal, or original, amount of a loan. Compound interest is calculated on the principal amount and also on the accumulated interest of previous periods, and can thus be regarded as “interest on interest.’ (Source: Investopedia).

Calculating Compound Interest in Excel

Let’s see how investment grows year-on-year when calculating compound interest is Excel.

Suppose you invest USD 1000 at a 10% interest rate.

By the end of Year 1, your investment grows to USD 1100.

Now in the second year, the interest is paid on USD 1100. So the investment grows to 1210.

At the end of five years, the investment grows to 1610.51.

The formula for compound interest at the end of five years is: =B1 * 1.1 * 1.1 * 1.1 * 1.1 * 1.1

Or =B1*(1.1)^5

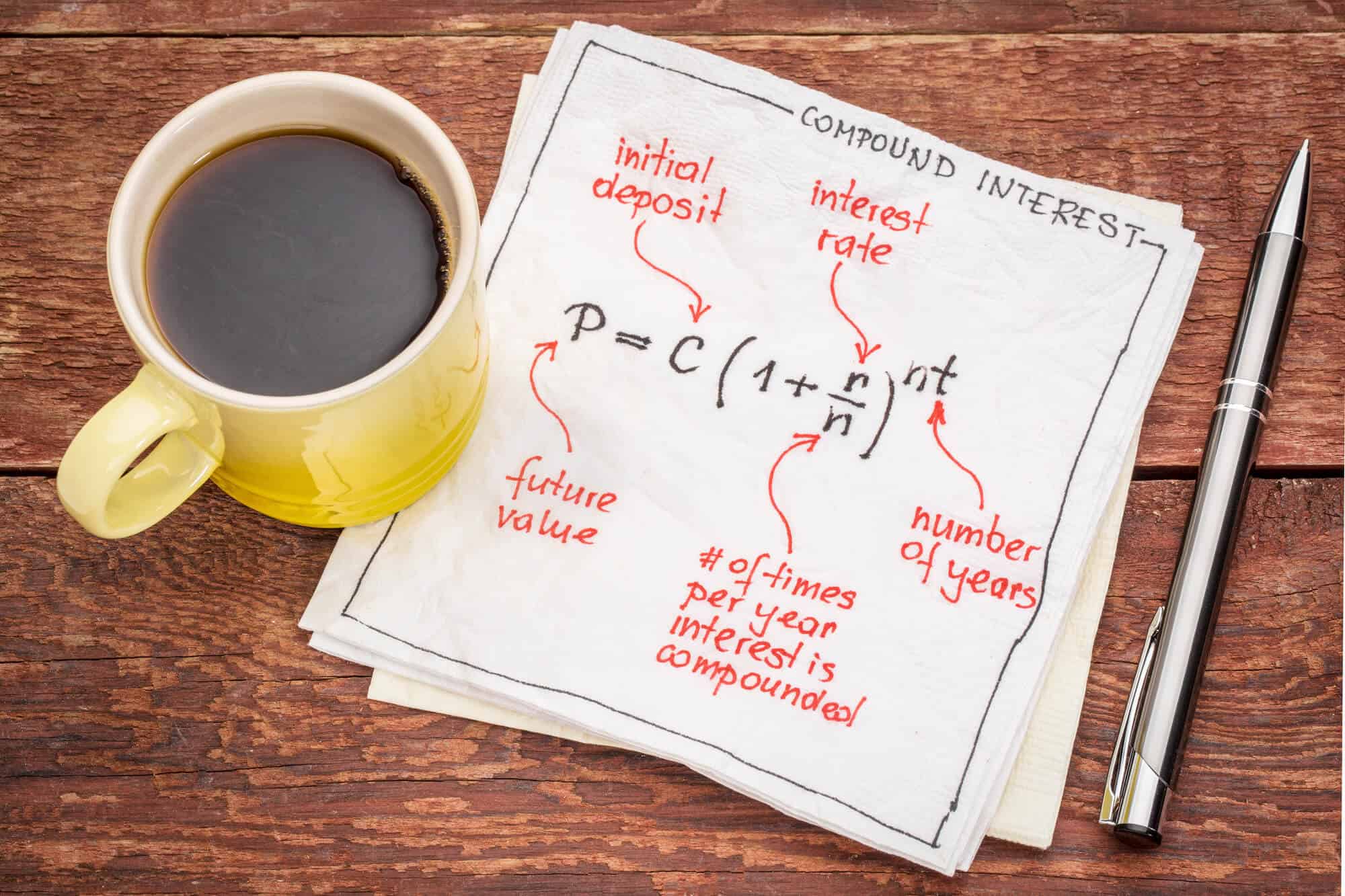
So here is the formula for calculating the value of your investment when compound interest in used:

Future Value of Investment = P*(1+ R/N)^(T*N)

• P – This is the principal amount or the initial investment.
• R – the annual interest rate. Note that the rate needs to be in percentage in Excel. For example, when the compound interest is 10%, use 10% or .1, or 10/100 as R.
• T – the number of years.
• N – Number of time interest is compounded in a year. In the case where the interest is compounded annually, N is taken as 1. In the case of quarterly compounding, N is 4. In the case of monthly compounding, N is 12.

Now let’s have a look at different examples of calculating compound interest in Excel.

Yearly Compounding

In the case of yearly compounding, compound interest can be calculated using the below formula:

Compound Interest = P *R^T

The future value of the investment can be calculated using the following formula:

Future Value of Investment = P*(1+R)^T

Note that you need to specify the rate as 10% or 0.1.

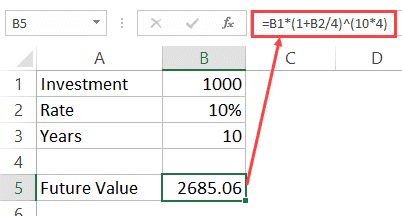
Quarterly Compounding

In the case of quarterly compounding, compound interest can be calculated using the below formula:

Compound Interest = P *(R/4)^(T*4)

The future value of the investment can be calculated using the following formula:

Future Value of Investment = P*(1+R/4)^(T*4)

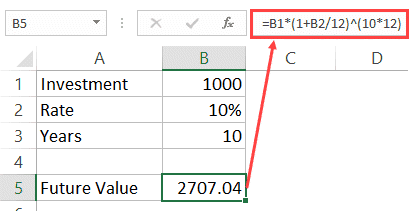
Monthly Compounding

In the case of quarterly compounding, compound interest can be calculated using the below formula:

Compound Interest = P *(R/12)^(T*12)

The future value of the investment can be calculated using the following formula:

Future Value of Investment = P*(1+R/12)^(T*12)

Note that the as the number of period increase, the value of your future investment grows. In the examples shown above, the value in monthly compounding is highest.

Similarly, you can calculate the investment value with weekly compounding (use Ns 52) or daily compounding (use N as 365).

Using Excel FV Function to Calculate Compound Interest

Apart from the formulas shown above, you can also use the FV function to calculate compound interest in Excel.

FV is a financial function in Excel that is used to calculate the future values of the investments.

Here is the formula that will give you the future value of the investments:

=FV(R/N,R*N,,-P)

• R – the annual rate of interest.
• N – Number of time interest is compounded in a year. In the case where the interest is compounded annually, N is taken as 1. In the case of quarterly compounding, N is 4. In the case of monthly compounding, N is 12.
• P – the initial investment. Note that this is used with a negative sign as this is an outflow.

Compound Interest Calculator Template

Here is a simple compound interest calculator template you can use to calculate the value of investments.

From the drop-down, select the number of times the interest is to be compounded. The result will automatically update in cell E2.

Click here to download the compound interest calculator template.

You May Also Find the Following Excel Tutorials Useful:

• Calculating Weighted Average in Excel.
• Age Calculation Template.
• Calculating Standard Deviation in Excel.
• Calculating CAGR in Excel.
• Using PMT Function in Excel.
• Calculating Moving Average in Excel
• How to Calculate IRR in Excel
• Calculating NPV in Excel

Compound Interest refers to earning or paying interest on interest. Although it can apply to both savings and loans, it is easiest to understand when thinking about savings. After each compound period, the interest earned over that period is added to the principal so that the next calculation of interest includes the original principal plus the previously earned interest.

With Simple Interest (the opposite of compound interest), interest is only calculated from the principal, and interest is not added to the principal.

This page includes a basic online compound interest calculator that you can use for simple future value problems. You can download the spreadsheet to see how compounding works from month to month.

Advertisement

Compound interest is used for both savings and loans, but this calculator is based on its use in calculating the future value of savings.

This calculator uses the following formulas and definitions:

F = P*(1+rate)^nper + A*( ((1+rate)^nper - 1)/rate )
rate = ((1+r/n)^(n/p))-1
nper = p * t
Total Payments = A*nper
Total Interest = F - P - Total Payments

• r = nominal annual interest rate (decimal)
• n = number of compounding periods per year
• p = number of payment periods per year
• rate = rate per payment period
• nper = total number of payment periods
• A = an amount added to the principal at the end of each payment period

When the Payment (A) is zero, a little algebra will show that the above formula simplifies down to the basic compound interest formula:

F = P*(1+r/n)^(n*t)

* Caution This calculator lets you choose Payment and Compounding combinations that don’t necessarily make sense. For example, a compound frequency of Monthly and a payment frequency of Weekly don’t match up (there isn’t an exact number of weeks in a month). The math still gives a result, but it probably would not match what is going on from week to week in an actual savings account.

Description

This spreadsheet was designed as an educational tool — to help show how compound interest works for both savings and loans. The table is based on the payment frequency and shows the amount of interest added each period. The graph compares the total (cumulative) principal and payments to the balance over time.

One of the worksheets in this file is nearly identical to the online calculator above, and was used to help verify the calculations.

BETA (7/29/2019) — This spreadsheet is currently a BETA version because I haven’t tested every possible input combination. Plus, people tend to use spreadsheets in ways I haven’t thought of.

Update 10/30/2022 — Fixed the Daily compounding option to reference «Daily (365)»

Compound Interest Formula

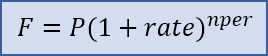
The basic compound interest formula for calculating a future value is F = P*(1+rate)^nper where

• F = the future accumulated value
• P = the principal (starting) amount
• rate = the interest rate per compounding period
• nper = the total number of compounding periods

Formula for Compounding Yearly, Monthly, Weekly

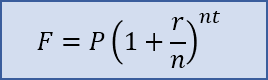
The formula is often written as F = P*(1+r/n)^(n*t) with the following variables definitions:

• P = the principal amount (the initial savings or the starting loan amount)
• r = the nominal annual interest rate in decimal form. (e.g. 5% means r=0.05)
• n = the number of compound periods per year (e.g. for monthly, n=12)
• t = the time in years

This is the same as the basic formula where rate = r/n and nper = n*t. Although the math can handle a decimal value for nper, it should usually be a whole number. For example, with monthly compounding for a total of 18 months, n=12 and t=1.5 resulting in nper=12*1.5=18.

Formula for Daily Compounding

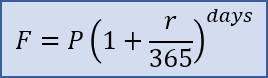
For daily compounding, the value for n (number of compound periods per year) is typically 365 and you use total number of days in place of n*t like this: F = P*(1+r/365)^days. For day count conventions other than n=365, see the wikipedia article.

How to Calculate Compound Interest in Excel

In Excel and Google Sheets, you can use the FV function to calculate a future value using the compound interest formula. The following three examples show how the FV function is related to the basic compound interest formula.

F = P*(1+rate)^nper
F = -FV(rate,nper,,P)
F = FV(rate,nper,,-P)

Example 1: What is the future value of an initial investment of $5,000 that earns 5% compounded annually for 10 years? Answer: F = 5000*(1+0.05)^10 = 8144.47. The Excel formula would be F = -FV(0.05,10,,5000) or F = FV(5%,10,,-5000). In Excel, when you add a percent sign after a number, the number is divided by 100.

Example 2: What is the future value of an initial investment of $5,000 that earns 5% compounded monthly for 10 years? Answer: F = 5000*(1+0.05/12)^(12*10) = 8235.05. The Excel formula would be F = -FV(0.05/12,12*10,,5000) or F = FV(5%/12,12*10,,-5000).

Note For savings calculations, the FV function in Excel can be a bit confusing because if you enter the present value as a positive number, you need to negate the final result. That is because with annuity functions like FV and PV, Excel assumes that cash you pay out, such as your initial savings and deposits to savings, is represented as negative numbers.

The syntax for the FV function in Excel is FV(rate,nper,pmt,[pv],[type]). Excel solves for FV using the following equation (for rate≠0):

Fig 1: Formula relating pv, rate, nper, pmt, fv in Excel.

When pmt=0, fv=—pv*(1+rate)^nper, so the variable P used in the standard compound interest formula relates to the Excel formula as P=—pv. Likewise, the variable A (defined below as positive for deposits to savings) relates to pmt as A=—pmt.

Compound Interest Formula for a Series of Payments

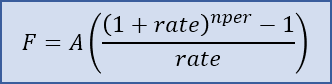
For both loans and savings, we typically want to include a series of payments or deposits in our calculation, such as depositing 100 each month for 3 years. The formula for the future value of a uniform series of deposits or payments is F=A(((1+rate)^nper-1)/rate) where

• A = the payment amount, added to the principal at the end of each period
• rate = the rate per payment period
• nper = the number of payments

When the payment period matches the compound period, rate=r/n and nper=n*t.

This formula can be derived from the compound interest formula, based on the fact that the total future value is the sum of each individual payment compounded over the time remaining. If you are interested in the derivation, see Reference [2] at the bottom of this page.

In Excel and Google Sheets, we can use the FV function again. The formulas below show how the FV function relates to the standard formula. Note that for now we aren’t including a principal amount.

F = A*(((1+rate)^nper-1)/rate)
F = -FV(rate,nper,A)
F = FV(rate,nper,-A)

Example 3: If I deposit $1000 at the end of each year, and my investment earns 4% annually, what is the future value at the end of 5 years? Answer: =1000*(((1+0.04)^5-1)/0.04) = 5416.32. The Excel formula would be F = -FV(0.04,5,1000) or F = FV(4%,5,-1000).

Note These formulas assume that the deposits (payments) are made at the end of each compound period. According to Figure 1, this means that type=0 (the default for the FV function). If I wanted to deposit $1000 at the beginning of each year for 5 years, the FV function in Excel allows me to calculate the result as =FV(4%,5,-1000,,1) where type=1. Just remember that the type argument has to do with the timing of the deposits (A), not the principal (P).

Future Value for both Principal and a Series of Payments

When you start with a non-zero principal amount and you make a series of payments, the resulting formula is just the sum of the two formulas described above. The FV function lets you include both the payment amount and the principal as follows:

F = P*(1+rate)^nper + A*(((1+rate)^nper-1)/rate)
F = -FV(rate,nper,A,P)
F = FV(rate,nper,-A,-P)

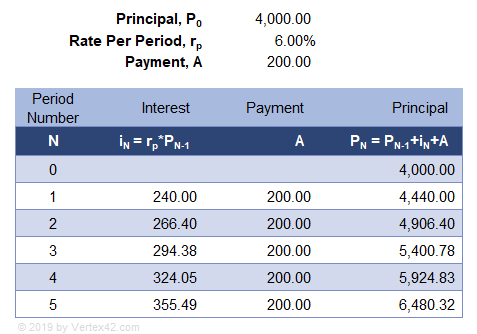
Example 4: If my starting savings is $4000 and I earn a whopping 6% compounded annually and I deposit $200 at the end of each year, what is the future value at the end of 5 years? Answer: =4000*(1+0.06)^5 + 200*(((1+0.06)^5-1)/0.06) = 6480.32. The Excel formula would be F = -FV(0.06,5,200,4000).

The table below shows how the calculations work each compound period. The table starts with an initial principal of P₀=4000. The next rows shows that at the end of the first year, the interest is calculated a i₁=rate*P₀. The new principal is P₁=P₀+i₁+A. This process continues until the end of year 5, where P₅=6480.32 (the same value we calculated with the compound interest formula).

Formula for Rate per Payment Period (when Compound Period ≠ Payment Period)

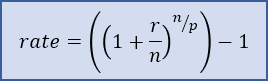
The calculator at the top of the page allows you to choose a compound frequency that is different from the payment frequency. The Rate Per Payment Period is calculated using the formula rate = ((1+r/n)^(n/p))-1 and the total number of periods is nper = p*t where

• r = the nominal annual interest rate in decimal form
• n = the number of compound periods per year
• p = the number of payment periods per year
• t = the time in years

These values for rate and nper can then be used in the compound interest formulas mentioned above.

A common example where this formula is needed is for a savings account where the interest is compounded daily but deposits are only made monthly. To approximate what the bank is doing, you can use n=365 (Compound Frequency = Daily) and p=12 (Payment Frequency = Monthly).

Another real-world example is the Canadian mortgage where the compounding is semi-annual (2 times per year) and the payments are monthly (12 per year).

Compound Interest Formula for Loans

Traditional amortized loans use the same formulas as those defined above for savings, except that the loan amount is represented as a negative value for the starting principal, P. Payment amounts (A) are still positive values.

How to Calculate the Loan Payment

For fully amortized loans, you typically need to calculate the payment amount (A) that will make the Future Value zero (F=0) after a specific number of years. The formula for the payment amount is found by solving for A using the formula from Figure 1. In Excel, you can use the PMT function. Note that if the loan is for $3000, P=—3000).

AF=0 = (-P*(1+rate)^nper) / (((1+rate)^nper - 1)/rate)
AF=0 = PMT(rate,nper,P))

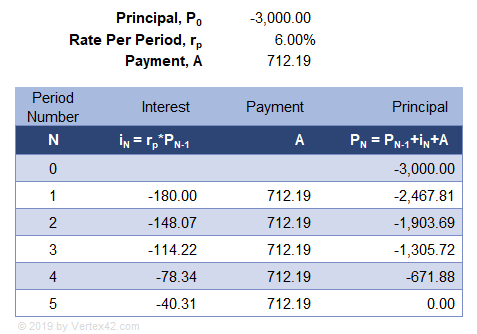
Example 5: If I apply for a loan for $3000 with a rate of 6% compounded annually, what is my payment if I want to pay it off completely in 5 years? Answer: A = (-(-3000)*(1+0.06)^5) / (((1+0.06)^5-1)/0.06) = 712.1892. The Excel formula is A = PMT(0.06,5,-3000).

The table below uses the exact same equations as the savings example, except that the principal is P₀=-3000 and the payment, A, was calculated so that the future value is zero after year.

Am I paying «Interest on Interest» if my loan payments are on time?

That is an interesting debate. Here are the two competing arguments.

Argument #1: Yes. The table in Example 5 clearly shows that the new principal is calculated by adding the interest and the payment to the previous principal. The formulas are exactly the same as the savings example, except that you are starting with a negative principal. The formulas show that interest IS added to the principal, which satisfies the definition of compound interest, and that explains why you can use the compound interest formulas in traditional loan calculations.

Argument #2: No. For an amortized loan, the payment isn’t actually 100% principal. Instead, you must first pay the amount of interest that you are charged, and the rest of your payment is applied to the principal. (This is how almost all amortized loans are worded). You are paying the interest first, so no interest is added to the principal. Therefore, you are not paying interest on interest if your payments are enough to completely pay the interest charged each period.

I was in the camp of Argument #2 for many years, and it wasn’t until creating these compound interest calculators that I realized Argument #2 is just legal jargon — a way to claim you aren’t paying interest on interest. Saying that the payment is only partially principal because the interest is first subtracted from the payment means that the formula for the new principal, P_N, would just be written with parentheses as P_N=P_N-1+(i_N+A). The parentheses tell us to first add the interest (a negative value in this case) to the loan payment. Then, the result is added to the principal. Does that actually change the final value? Of course not.

Argument #2 then says «Yeah, but your payment is enough to completely pay the amount of interest charged, so no interest is actually added to the principal. Therefore, you aren’t paying interest on interest.»

Argument #1 replies with «Yeah, but without affecting the result, the math allows me to consider my payment to be applied to the original principal, with the interest added afterward. Thus, I AM paying interest on interest.»

Argument #2 would then say «Our definition of the loan payment means that you are forced to add the amounts in parentheses first, so we are allowed to say we aren’t adding interest to the principal.»

Which argument is correct? Or, could they both be correct? Ultimately, the fact is that the compound interest formulas calculate the same result for Example 5, regardless.

What does this mean for the borrower?

Ultimately, the take away is that part of your regular loan payment is being used to pay off interest. To take advantage of the compound interest formula, the borrower should make additional principal-only payments. Learn how debt payoff is similar to an investment.

Note Even a so-called Simple Interest Loan requires the payments to be applied first to the accrued interest before they can be applied to the principal. So, even though the daily interest accrual is based on simple interest, the amortization is still based on the compound interest formula.

Disclaimer: This information on this page is for educational purposes only. We do not guarantee the results or the applicability to your unique financial situation. You should seek the advice of qualified professionals regarding financial decisions.

Compound Interest Calculator is a ready-to-use excel template that helps to calculate compound interest with multiple compounding periods.

In addition to that, the template also provides a complete schedule of payments and interests accumulating each payment period.

What is Compound Interest?

Compound interest is the method of calculating interest any given amount assuming that the interest earned each period is added to the principal. Hence, you receive not only interest on your principal amount but also the added interest each year.

While calculating compound interest the compounding periods matter the most and have a significant difference. For example, the amount of 10% compound interest compounded annually will be lower than 5% compound interest compounded semi-annually over the same time period.

Formula To Calculate Compound Interest

Compound Interest (A) = P [(1 + i)ⁿ – 1] 

Where: P = Principal Amount,  i = interest rate, n = compounding periods.

To simplify the process, we have created a simple and easy Compound Interest Calculator Excel Template with predefined formulas.

Just enter a few data and the template will calculate the compound interest for a particular investment. Additionally, the template also provides a schedule of payments and accumulated interests in each period.

Click here to download the Compound Interest Calculator Excel Template.

Additionally, you can also download other financial analysis templates like NPV and XIRR Calculator, CAGR Calculator, ROCE Calculator, Income Tax Calculator FY 2018-19 and Loan Amortization Template from our website.

Let us understand the content of the templates in detail and how to use it.

Contents of Compound Interest Calculator Excel Template

This template consists of 3 sheets: Basic Calculator, Advanced Calculator, and Cumulative Interest & Payment Schedule.

Basic Calculator

The basic calculator consists of 2 sections: Input and Output. Those cells having light-blue color is the input section and cells with dark blue are the output section.

The input section consists of the following heads:

Principal Amount
Annual Interests Rate
Compounding Frequency
Years of Growth
Additional Deposit
Additional Deposit Frequency

The Output section is auto-populated based on the above-entered data. It consists of the following heads:

NPER
Rate: Rate per payment period.
Future Value: Future value is derived using the FV Function in Excel
Total Payments
Total Interest

Applying the compound interest formula the template calculates everything.

Advanced Calculator

This sheet also consists of 2 sections: Input and Cumulative Income Report.

The input section is the same as the above. Additionally, it consists of a start date that will help to make the cumulative interest & payment schedule.

Compounding frequency and deposit frequency both have a drop-down list. Select the desired option fro the list where:

1 = Annually
2 = Semi-Annually
4 = Quarterly
6 = Bi-Monthly
12 = Monthly
24 = Semi-Monthly
26 = Bi-Weekly
52 = Weekly
365 = Daily

The payment frequency doesn’t have the “365” option in the dropdown of periods as it is not excepted daily basis.

Cumulative Income Report consists of the following heads:

Rate/Period: Rate per payment period.

Total Additional Payments: It is the total additional payments made. Payments multiplied by pay periods.

Total Payments: Principal Amount + Total Additional Payments.

Total Interest: Future Value – Total Payments.

Cumulative Interest and Payment Schedule

The template creates a payment and interest schedule based on the data input in the Advanced Compound Interest Calculator. No entry is to be made on this sheet. It is auto-populated.

The Schedule sheet consists of the following columns:

Sr. No: Serial Number of the payments. O is for the principal amount.

Date: Considering the start date and payment schedule it fetches the dates.

Interim Payment: Additional payments made at payment periods.

Net Payment: Principal amount + Interim Payment + Interest Amount.

Interest: The template uses the rates of Interest depending on compounding periods.

Cumulative Interest: Previous Interest + Current Interest.

Balance: This column has the final balance depending on the tenure. Furthermore, It displays the value at the end of each period as well as at the completion of the period.

Thus, this template can be helpful to individuals planning to invest in fixed deposits in banks and for loan purposes.

We thank our readers for liking, sharing and following us on different social media platforms.

If you have any queries please share in the comment section below. We will be more than happy to assist you.

Compound Interest refers to earning or paying interest on interest. Although it can apply to both savings and loans, it is easiest to understand when thinking about savings. Download this compound interest calculator excel template and get started.

After each compound period, the interest earned over that period is added to the principal so that the next calculation of interest includes the original principal plus the previously earned interest.

With Simple Interest (the opposite of compound interest), interest is only calculated from the principal, and interest is not added to the principal.

Features and Functionality of this Compound Interest Excel Calculator

This spreadsheet and excel template/ calculator was designed as an educational tool – to help show how compound interest works for both savings and loans.

The table is based on the payment frequency and shows the amount of interest added each period. The graph compares the total (cumulative) principal and payments to the balance over time.

One of the worksheets in this file is nearly identical to the online calculator above, and was used to help verify the calculations.

Compound Interest Formula

The basic compound interest formula for calculating a future value is F = P*(1+rate)^nper where

• F = the future accumulated value
• P = the principal (starting) amount
• rate = the interest rate per compounding period
• nper = the total number of compounding periods

Formula for Compounding Yearly, Monthly, Weekly

The formula is often written as F = P*(1+r/n)^(n*t) with the following variables definitions:

• P = the principal amount (the initial savings or the starting loan amount)
• r = the nominal annual interest rate in decimal form. (e.g. 5% means r=0.05)
• n = the number of compound periods per year (e.g. for monthly, n=12)
• t = the time in years

This is the same as the basic formula where rate = r/n and nper = n*t. Although the math can handle a decimal value for nper, it should usually be a whole number. For example, with monthly compounding for a total of 18 months, n=12 and t=1.5 resulting in nper=12*1.5=18.

Formula for Daily Compounding

For daily compounding, the value for n (number of compound periods per year) is typically 365 and you use total number of days in place of n*t like this: F = P*(1+r/365)^days. For day count conventions other than n=365, see the Wikipedia article.

If you want to study more about this template, you can visit tutorial on compound interest calculation as well.

Download and use Compound Interest Calculator Excel template

To use this free compound interest calculator excel template, you should have Microsoft Office/ Microsoft Excel installed in your system.

After installing Excel or Spreadsheet, download the zip file of this template, extract the template using WinRAR or 7Zip decompressing software. Once extracted, you can open the file using Excel and start entering data or customizing the template.

If the excel templates can not be downloaded, Leave us a message in the Comment Section. We will solve the related problems for you as soon as possible. All Excel templates and dashboards and tools are sole property of exceldownloads.com.
As a User, you can download and use the excel templates, dashboards and calculators for personal and business use with no payment i.e. for free, but without permission, you can not distribute it on the Internet website or CD/DVD channels !

---

Without permission granted from us/ management team of ExcelDownloads.com, use of these excel templates and dashboards is not allowed. However, if you want to share this templates and dashboards with your friends and peers, we have provided sharing option in various social media and platform via which you can share our content.

---

We hope that you can get our help in making your personal and business activities easier with the use of free excel templates and dashboards, and at the same time, support the construction of our website by considering our efforts and aforesaid instructions.