Excel 2007 что такое solver - Word и Excel - помощь в работе с программами

Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.

Включение функции

Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.

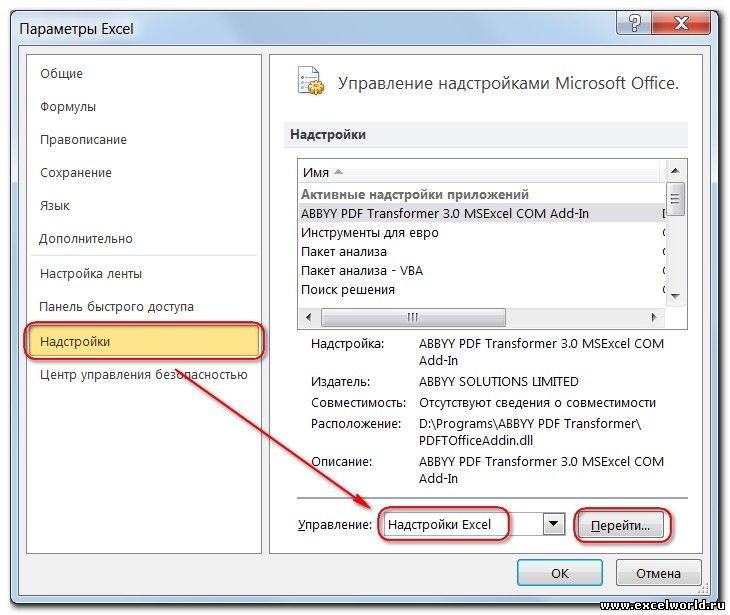
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».

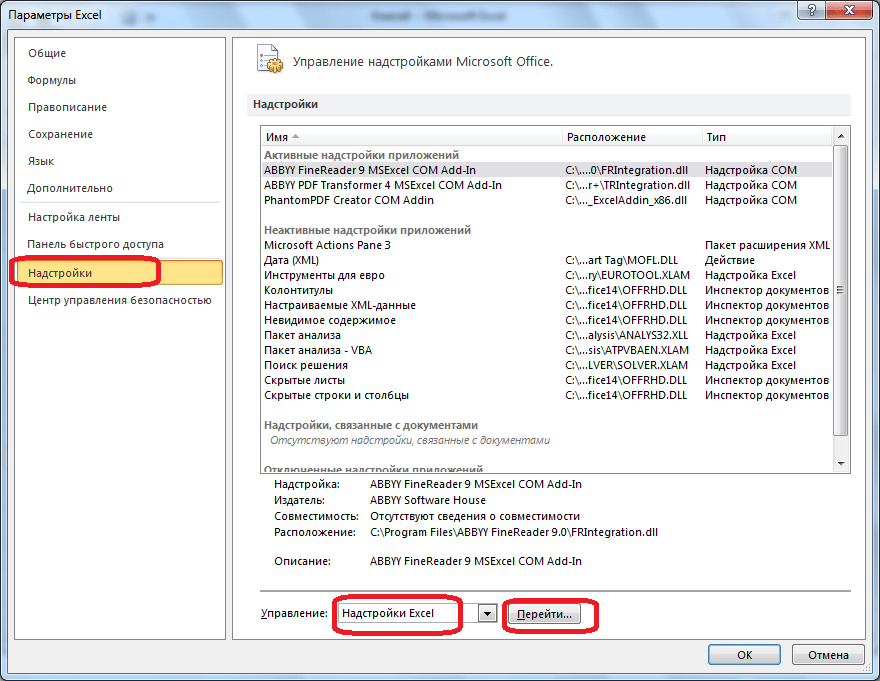
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».

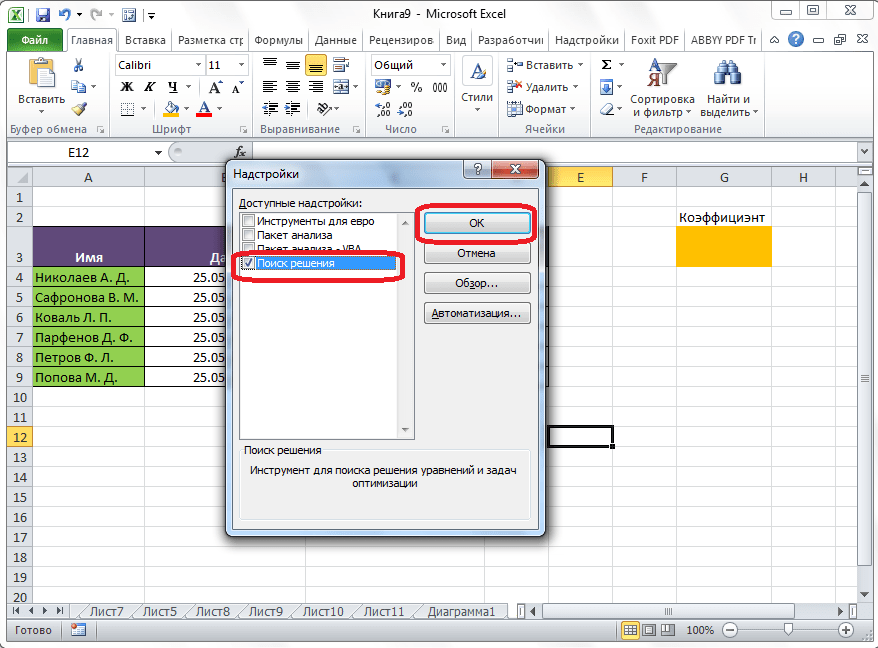
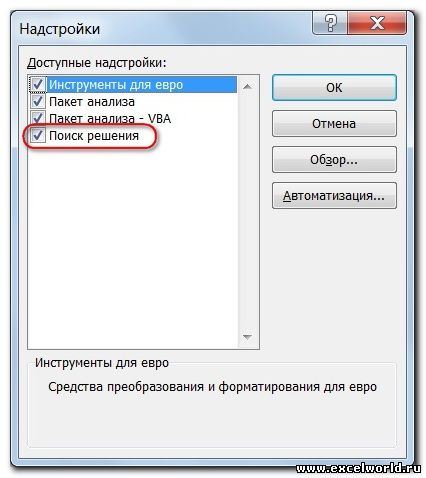
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».

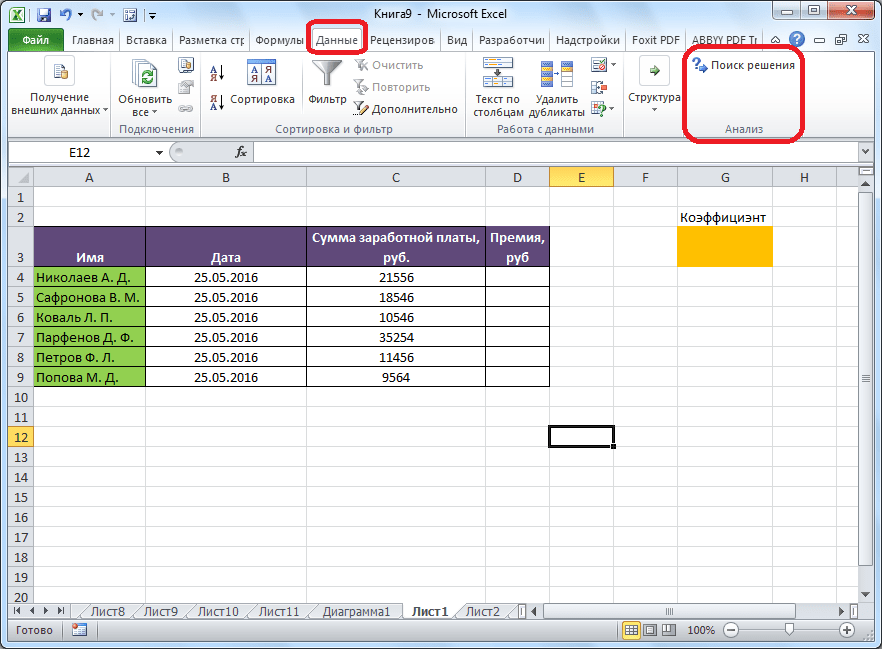
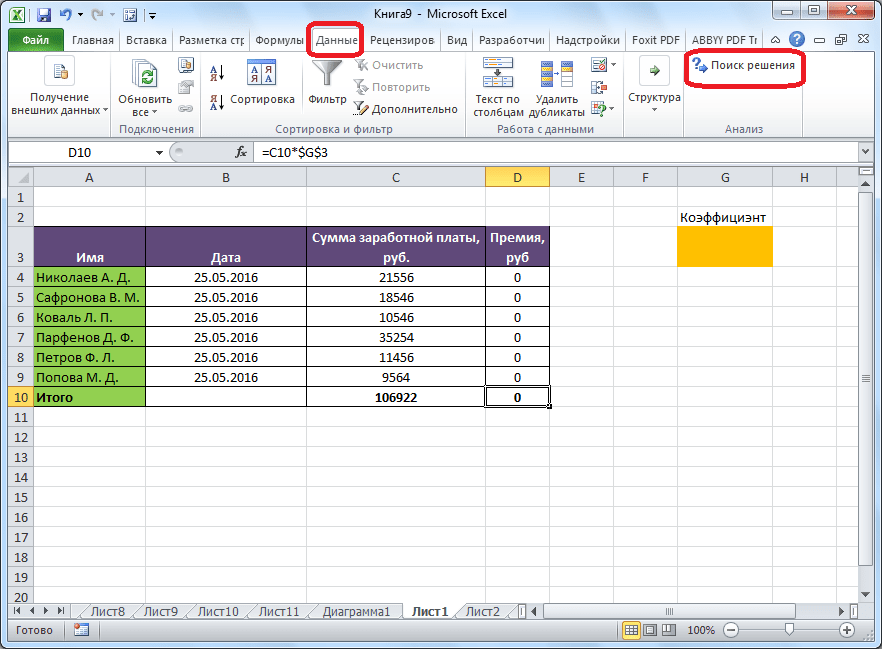
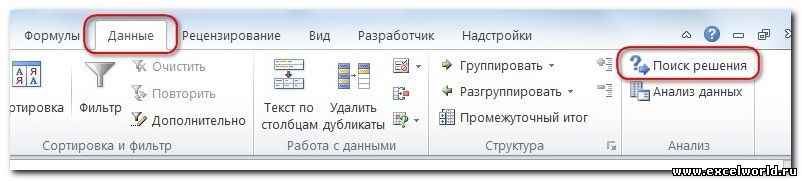
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».

Подготовка таблицы

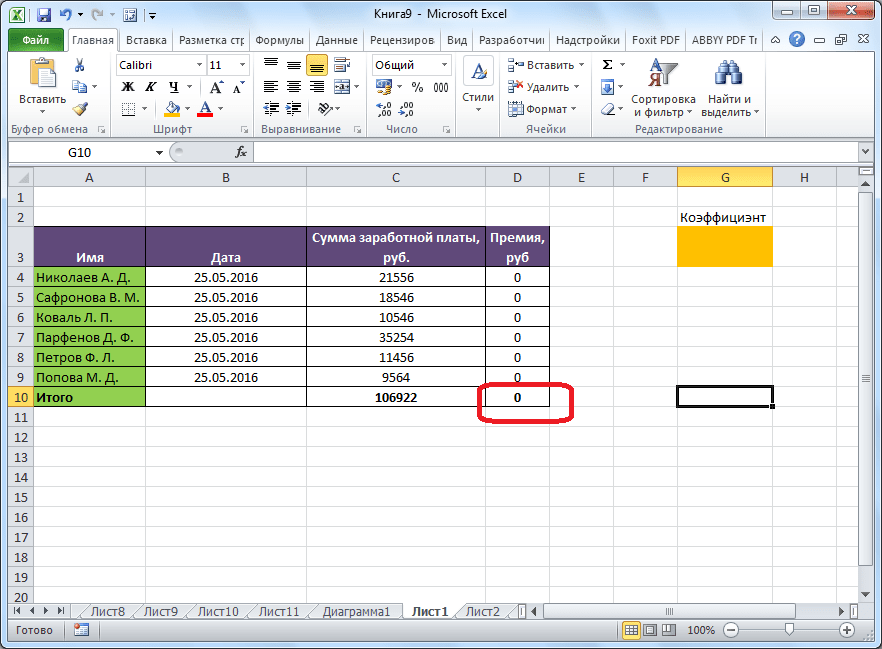
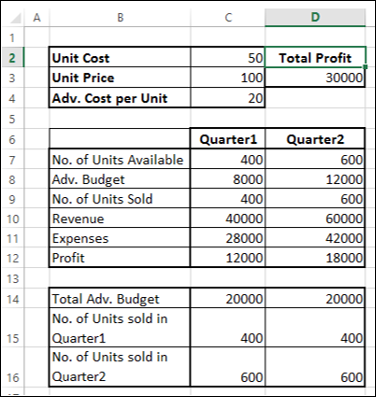
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

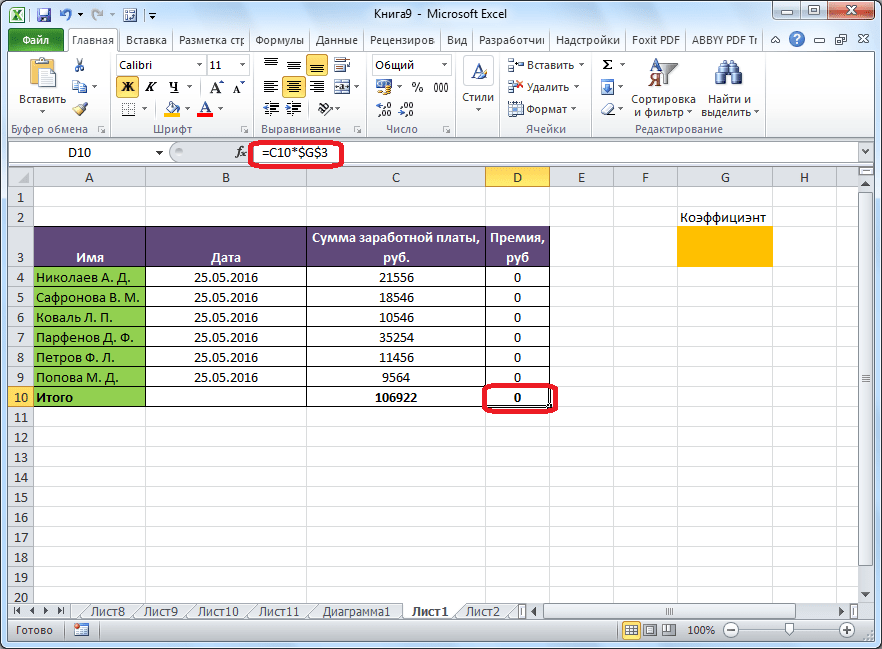
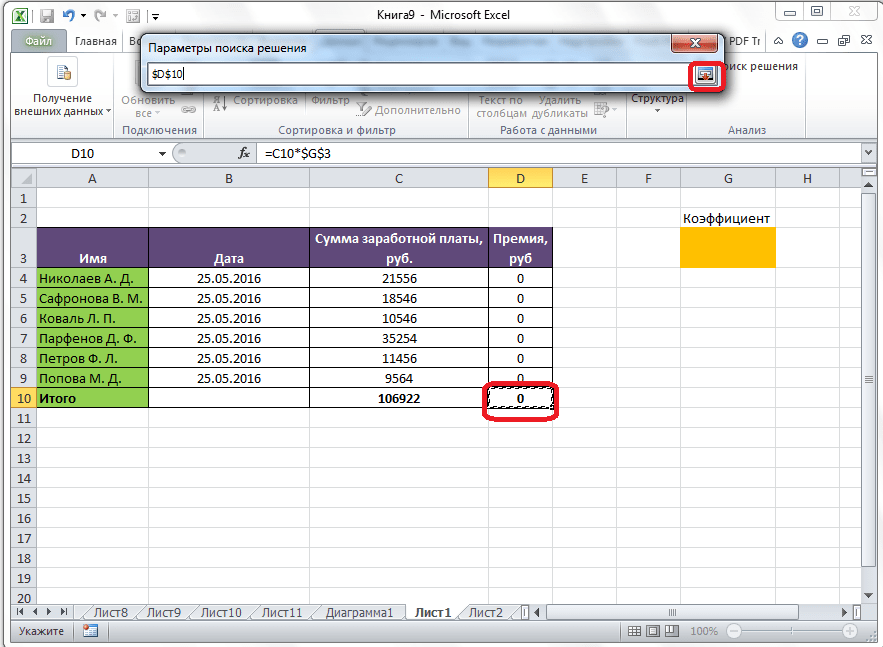
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

Запуск инструмента Поиск решения

После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».

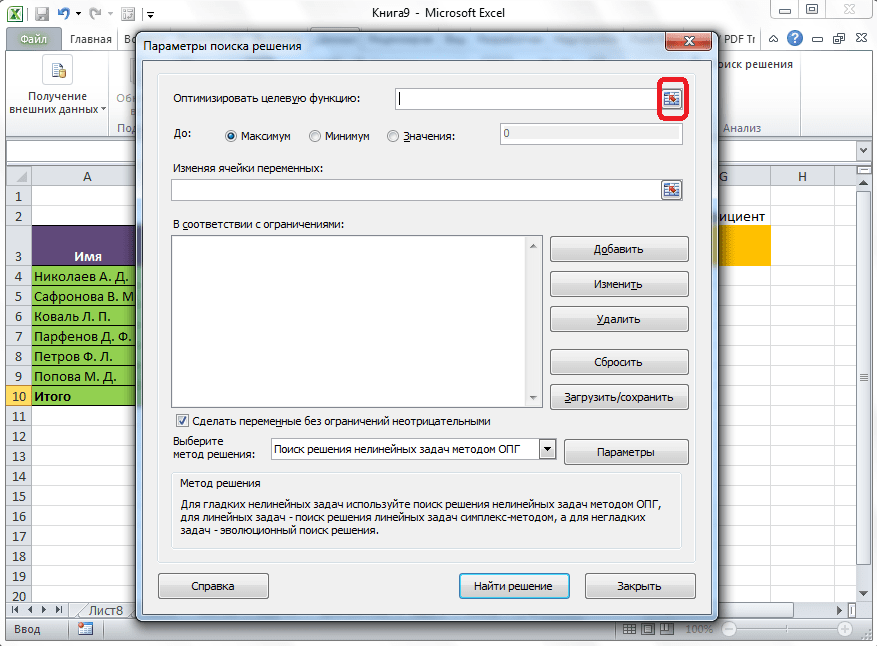
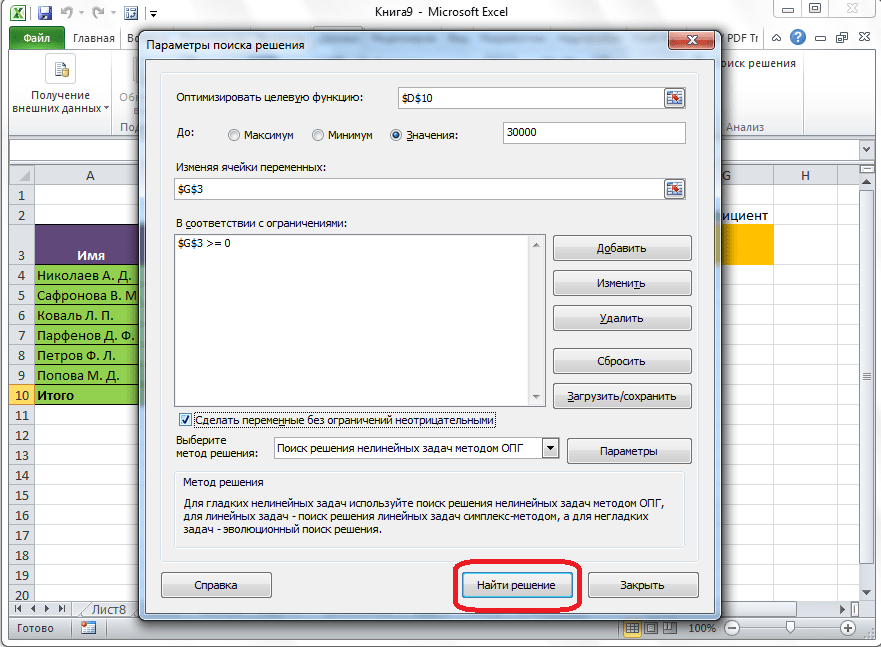
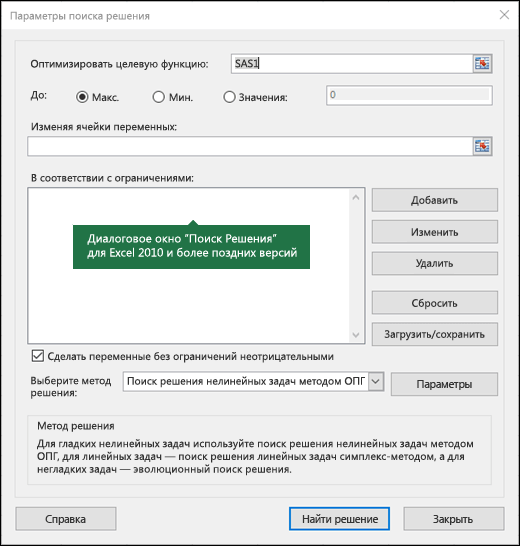
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.

После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.

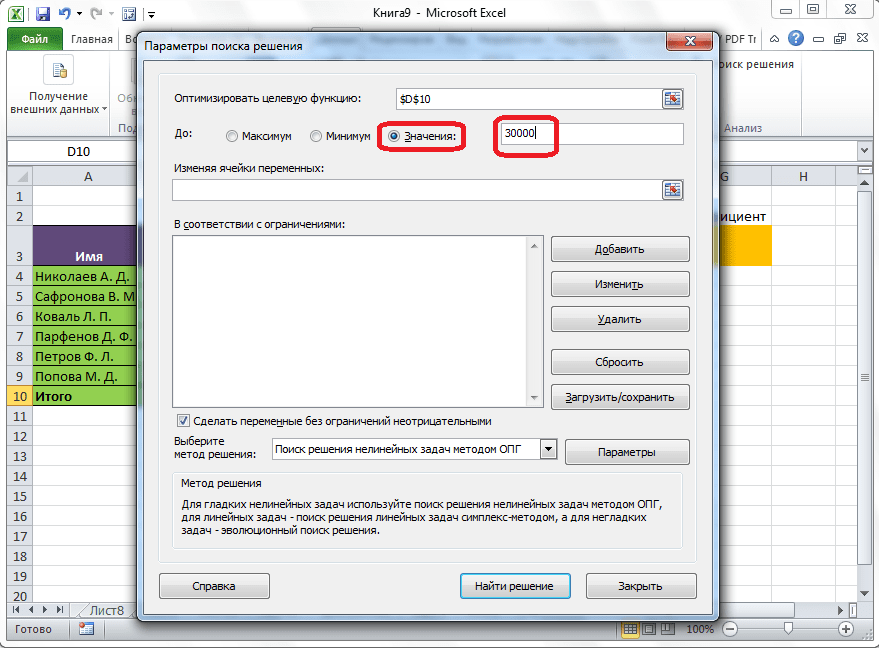
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.

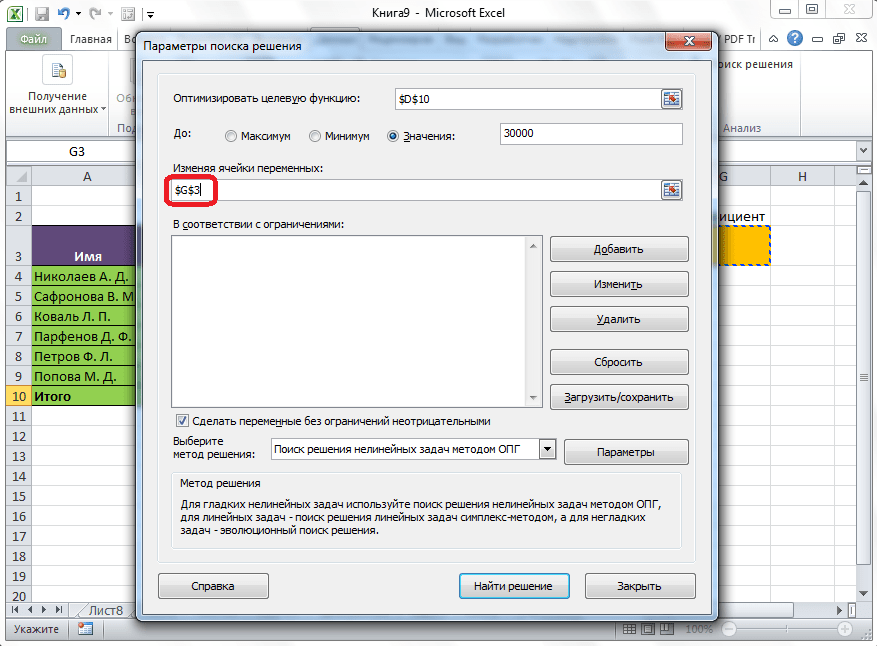
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.

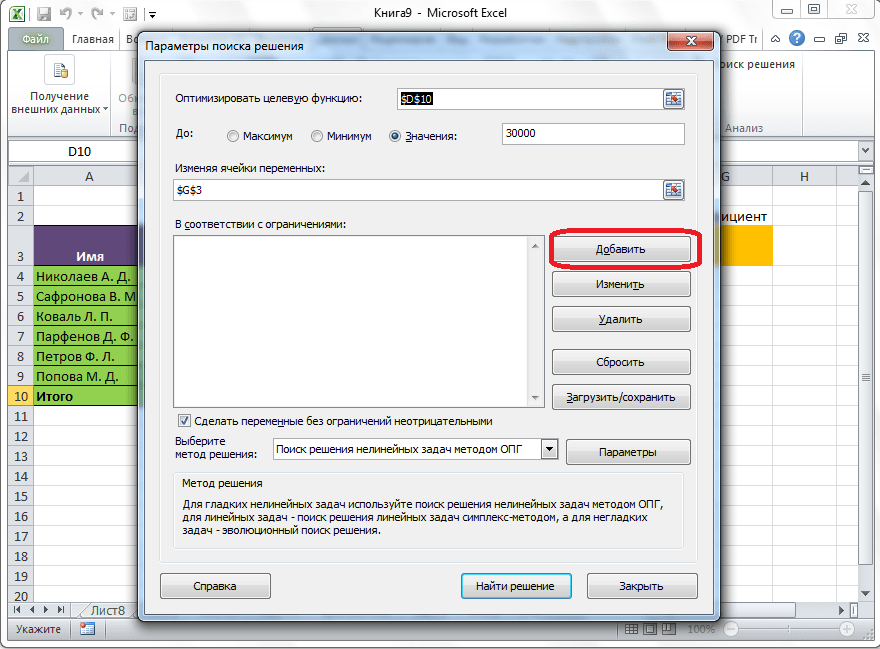
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».

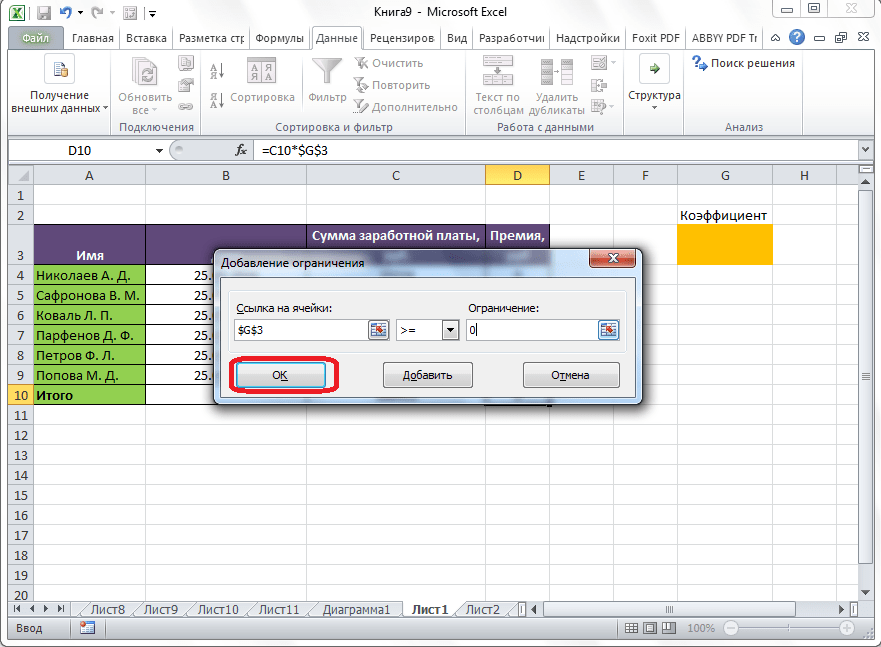
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.

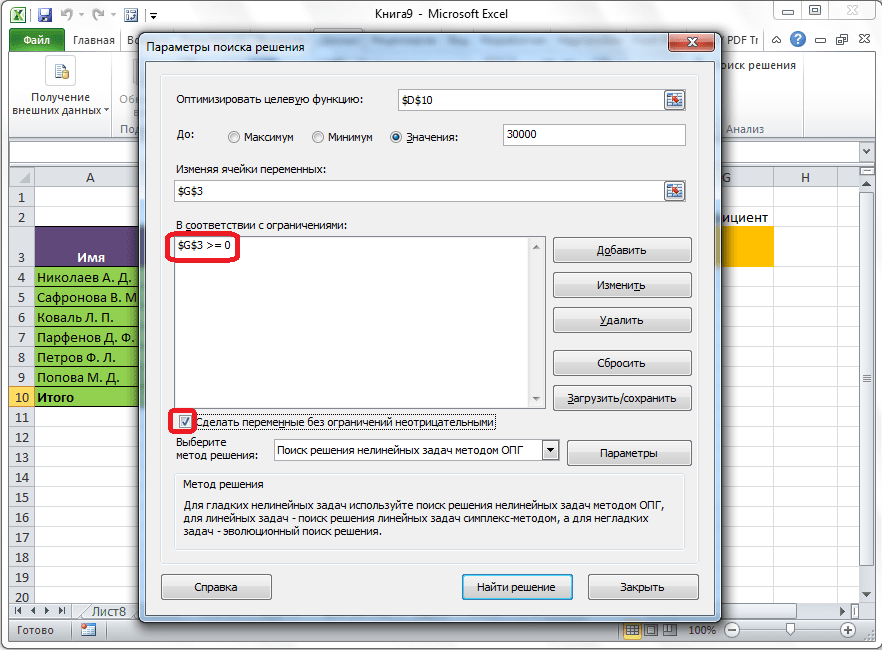
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.

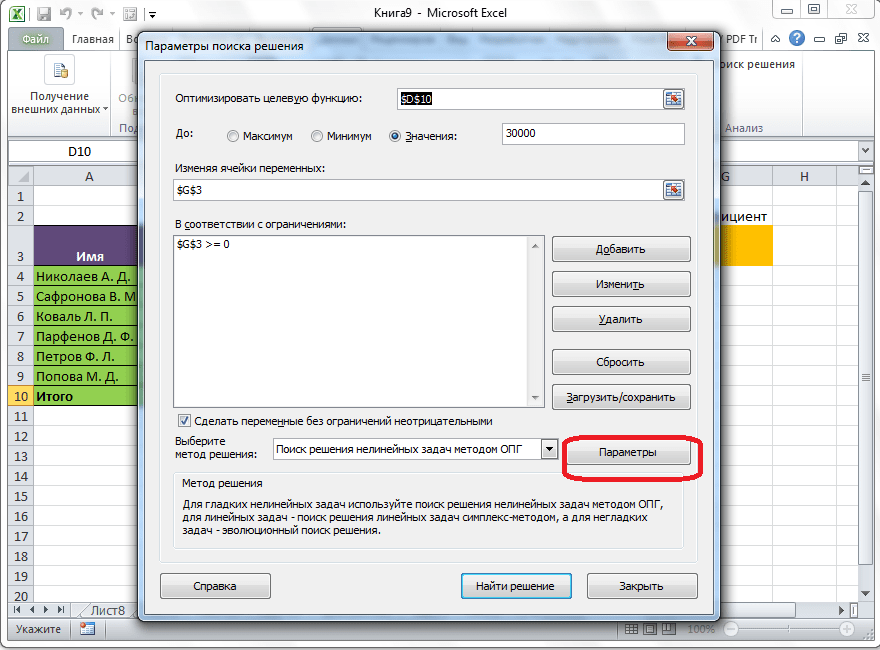
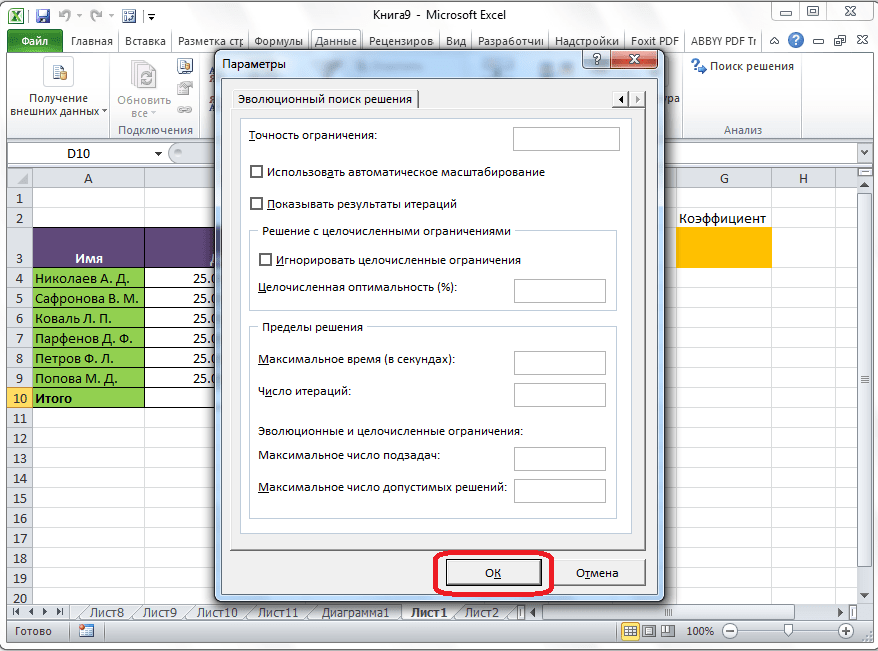
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».

Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.

После того, как все настройки установлены, жмем на кнопку «Найти решение».

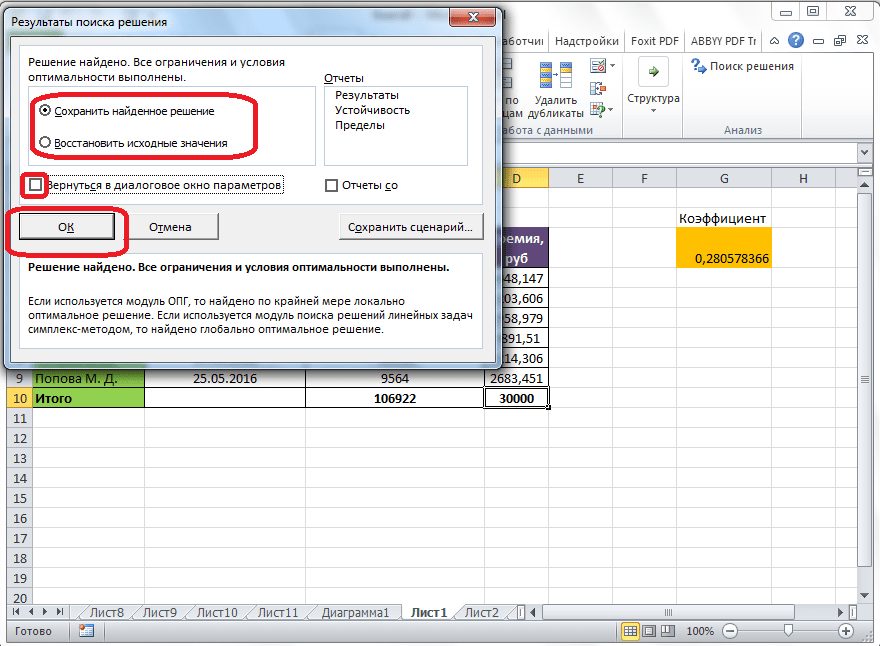
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».

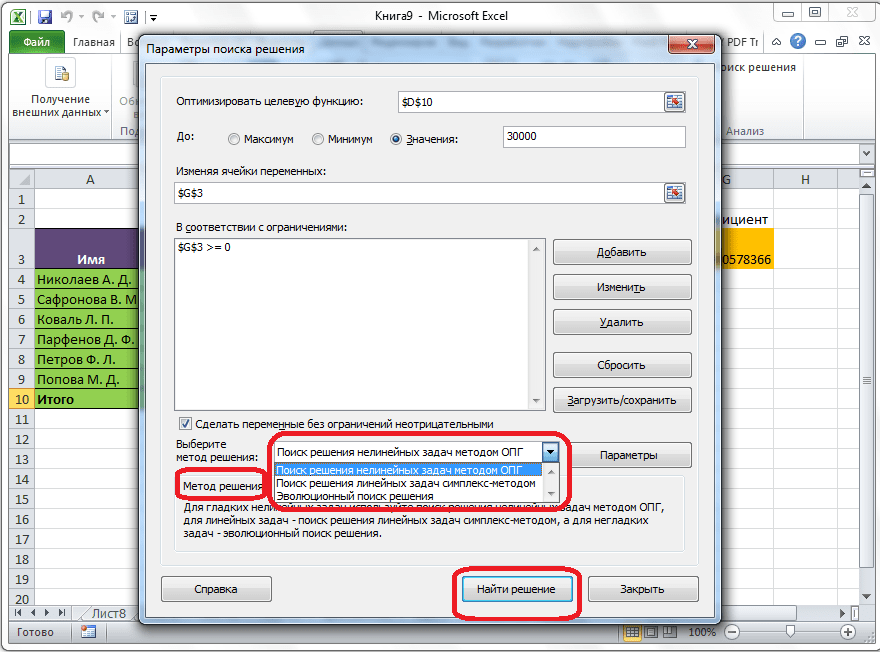
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.

Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.

Источник

«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.

Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.

Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.

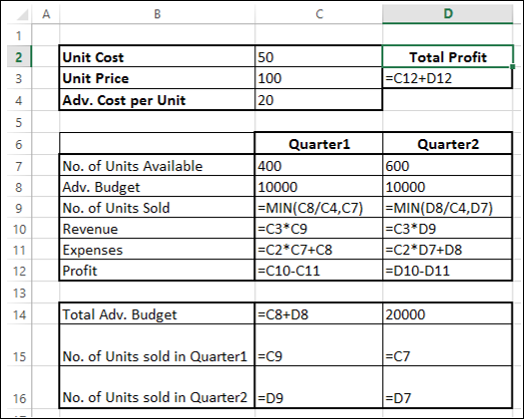
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).

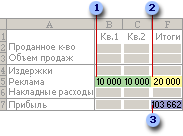
1. Ячейки переменных

2. Ячейка с ограничениями

3. Целевая ячейка

После выполнения процедуры получены следующие значения.

На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
Выполните одно из следующих действий.
- Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
- Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
- Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
- В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
1. В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
2. В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
3. Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
4. Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
5. Выполните одно из указанных ниже действий.
  - Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
  - Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
    Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.
    
    Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
6. В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
7. Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
- Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
- Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
- Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
- Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
- Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.

После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
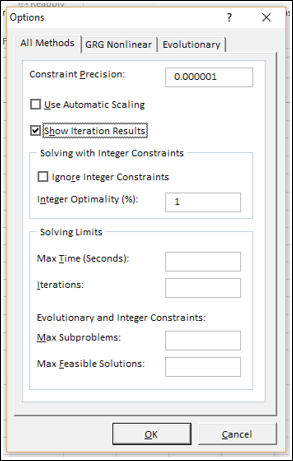
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
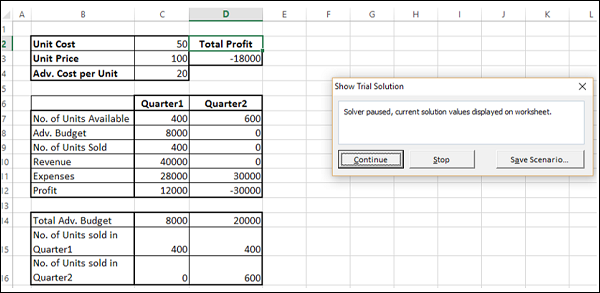
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
- Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
- Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.

В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.

В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.

При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.

Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.

В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.

Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
Симплекс-метод. Используется для линейных задач.
Эволюционный метод Используется для негладких задач.

В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).

переменных

с ограничениями

цель

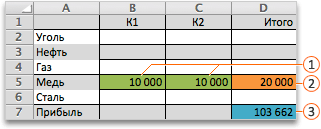
В результате выполнения получены следующие значения:

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.

Примечание: Целевая ячейка должна содержать формулу.

Выполните одно из следующих действий.

Задача	Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных	Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных	Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение	Щелкните Значение, а затем введите нужное значение в поле.

В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.

Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.

В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.

Для этого выполните следующие действия:

В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.

Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
Выполните одно из указанных ниже действий.

Задача	Необходимые действия
Принять ограничение и добавить другое	Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения	Нажмите кнопку ОК.

Нажмите кнопку Найти решение и выполните одно из следующих действий:

Задача	Необходимые действия
Сохранить значения решения на листе	В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения	Щелкните Восстановить исходные значения.

Примечания:

Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.

В диалоговом окне Показать предварительное решение выполните одно из следующих действий:

Задача	Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения	Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение	Нажмите кнопку Продолжить.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:

Задача	Необходимые действия
Настроить время решения и число итераций	На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить. Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность	На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости	На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.

Задача

Необходимые действия

Настроить время решения и число итераций

На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.

Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.

Задать точность

На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.

Задать степень сходимости

На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.

Нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.

При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.

Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:

Метод решения	Описание
Нелинейный метод обобщенного понижающего градиента (ОПГ)	Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции.
Поиск решения линейных задач симплекс-методом	Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *.
Эволюционный поиск решения	Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных.

Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.

Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.

Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».

Дополнительная справка по надстройке «Поиск решения»

За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:

Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.

Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Использование «Решения» для бюджетов с использованием средств на счете вех

Использование «Решение» для определения оптимального сочетания продуктов

Введение в анализ гипотетических вариантов

Полные сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Обнаружение ошибок в формулах

Сочетания клавиш в Excel

Функции Excel (по алфавиту)

Функции Excel (по категориям)

Источник

What Is Excel Solver?

Solve your programming woes with this popular Excel add-in

Updated on December 2, 2020

The Excel Solver add-in performs mathematical optimization. This is typically used to fit complex models to data or find iterative solutions to problems. For example, you might want to fit a curve through some data points, using an equation. Solver can find the constants in the equation that give the best fit to the data. Another application is where it is difficult to rearrange a model to make the required output the subject of an equation.

Where Is Solver in Excel?

The Solver add-in is included with Excel but it isn’t always loaded as part of a default installation. To check if it’s loaded, select the DATA tab and look for the Solver icon in the Analysis section.

If you can’t find Solver under the DATA tab then you will need to load the add-in:

Select the FILE tab and then select Options.
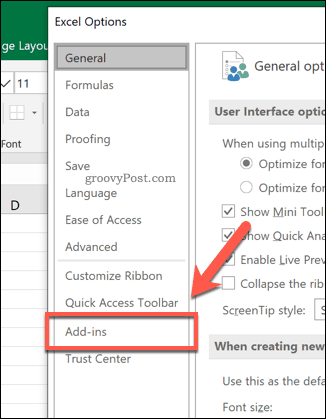
In the Options dialogue box select Add-Ins from the tabs on the left-hand side.
At the bottom of the window, select Excel Add-ins from the Manage dropdown and select Go…
Check the check-box next to Solver Add-in and select OK.
The Solver command should now appear on the DATA tab. You’re ready to use Solver.

Using Solver in Excel

Let’s start with a simple example to understand what the Solver does. Imagine that we want to know what radius will give a circle with an area of 50 square units. We know the equation for the area of a circle (A=pi r²). We could, of course, rearrange this equation to give the radius required for a given area, but for the sake of example let’s pretend we don’t know how to do that.

Create a spreadsheet with the radius in B1 and calculate the area in B2 using the equation =pi()*B1^2.

We could manually adjust the value in B1 until B2 shows a value that is close enough to 50. Depending on how accurate we need to be, this might be a practical approach. However, if we need to be very exact, it will take a long time to make the required adjustments. Actually, this is essentially what Solver does. It makes adjustments to values in certain cells, and checks the value in a target cell:

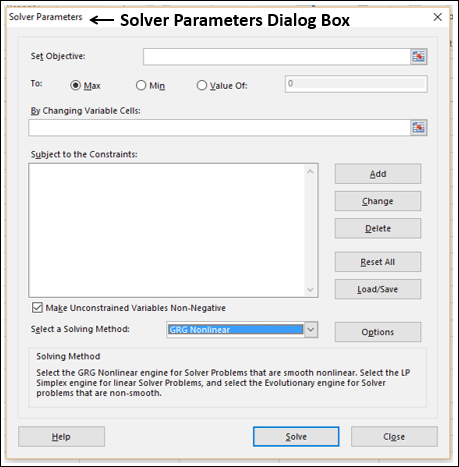
Select DATA tab and Solver, to load the Solver Parameters dialogue box
Set Objective cell to be the Area, B2. This is the value that will be checked, adjusting other cells until this one reaches the correct value.
Select the button for Value of: and set a value of 50. This is the value that B2 should achieve.
In the box titled By Changing Variable Cells: enter the cell containing the radius, B1.
Leave the other options as they are by default and select Solve. The optimization is carried out, the value of B1 is adjusted until B2 is 50 and the Solver Results dialogue is displayed.
Select OK to keep the solution.

This simple example showed how the solver works. In this case, we could have more easily got the solution in other ways. Next we will look at some examples where Solver gives solutions that would be difficult to find any other way.

Fitting a Complex Model Using the Excel Solver Add-In

Excel has a built-in function to perform linear regression, fitting a straight line through a set of data. Many common non-linear functions can be linearized meaning that linear regression can be used to fit functions such as exponentials. For more complex functions the Solver can be used to perform a ‘least squares minimization’. In this example, we will consider fitting an equation of the form ax^b+cx^d to the data shown below.

This involves the following steps:

Arrange the dataset with the x values in column A and the y-values in column B.
Create the 4 coefficient values (a, b, c, and d) somewhere on the spreadsheet, these can be given arbitrary starting values.
Create a column of fitted Y values, using an equation of form ax^b+cx^d which references the coefficients created in step 2 and the x values in column A. Note that in order to copy the formula down the column, the references to the coefficients must be absolute while the references to x values must be relative.
Although not essential, you can get a visual indication of how good a fit the equation is by plotting both y columns against the x values on a single XY scatter chart. It makes sense to use markers for the original data points, since these are discrete values with noise, and to use a line for the fitted equation.
Next, we need a way of quantifying the difference between the data and our fitted equation. The standard way to do this is to calculate the sum of the squared differences. In a third column, for each row, the original data value for Y is subtracted from the fitted equation value, and the result is squared. So, in D2, the value is given by =(C2-B2)^2. The sum of all these squared values is then calculated. Since the values are squared they can only be positive.
You are now ready to perform the optimization using Solver. There are four coefficients that need to be adjusted (a, b, c and d). You also have a single objective value to minimize, the sum of the squared differences. Launch the solver, as above, and set the solver parameters to reference these values, as shown below.
Uncheck the option to Make Unconstrained Variables Non-Negative, this would force all coefficients to take positive values.
Select Solve and review the results. The chart will update giving a good indication of the goodness of fit. If the solver doesn’t produce a good fit on the first attempt you could try running it again. If the fit has improved, try resolving from the current values. Otherwise, you could try manually improving the fit before resolving.
Once a good fit has been obtained you can exit the solver.

Solving a Model Iteratively

Sometimes there is a relatively simple equation which gives an output in terms of some input. However, when we try to invert the problem it is not possible to find a simple solution. For example, the power consumed by a vehicle is approximately given by P = av + bv^3 where v is the velocity, a is a coefficient for the rolling resistance and b is a coefficient for aerodynamic drag. Although this is quite a simple equation, it is not easy to rearrange to give an equation of the velocity the vehicle will reach for a given power input. We can, however, use Solver to iteratively find this velocity. For example, find the velocity attained with a power input of 740 W.

Set up a simple spreadsheet with the velocity, the coefficients a and b, and the power calculated from them.
Launch the Solver and enter the power, B5, as the objective. Set an objective value of 740 and select the velocity, B2, as the variable cells to change. Select solve to start the solution.
The solver adjusts the value of the velocity until the power is very close to 740, providing the velocity we require.
Solving models in this way can often be faster and less error-prone than inverting complex models.

Understanding the different options available in the solver can be quite difficult. If you’re having difficulty obtaining a sensible solution then it’s often useful to apply boundary conditions to the changeable cells. These are limiting values beyond which they should not be adjusted. For example, in the previous example, the velocity should not be less than zero and it would also be possible to set an upper bound. This would be a speed you’re pretty sure the vehicle cannot go faster than. If you are able to set bounds for the changeable variable cells, then it also makes other more advanced options work better, such as multistart. This will run a number of different solutions, starting at different initial values for variables.

Choosing the Solving Method can also be difficult. Simplex LP is only suitable for linear models, if the problem isn’t linear it will fail with a message that this condition was not met. The other two methods are both suited to non-linear methods. GRG Nonlinear is the fastest but it’s solution can be highly dependent on the initial starting conditions. It does have the flexibility that it doesn’t require variables to have bounds set. The Evolutionary solver is often the most reliable but it requires all variables to have both upper and lower bounds, which may be difficult to work out in advance.

The Excel Solver add-in is a very powerful tool which can be applied to many practical problems. To fully access the power of Excel, try combining Solver with Excel macros.

Thanks for letting us know!

Get the Latest Tech News Delivered Every Day

Источник

Плагин Excel Solver позволяет найти минимальные и максимальные значения для потенциального расчета. Вот как это установить и использовать.

Существует не так много математических проблем, которые не могут быть решены с помощью Microsoft Excel. Его можно использовать, например, для решения сложных аналитических расчетов «что если» с использованием таких инструментов, как поиск цели, но при этом доступны более эффективные инструменты.

Если вы хотите найти минимальные и максимальные числа, возможные для решения математической задачи, вам необходимо установить и использовать надстройку Solver. Вот как установить и использовать Солвер в Microsoft Excel.

Solver — сторонняя надстройка, но Microsoft включает ее в Excel (хотя по умолчанию она отключена). Он предлагает анализ «что если», чтобы помочь вам определить переменные, необходимые для решения математической задачи.

Например, какое минимальное количество продаж вам нужно совершить, чтобы покрыть стоимость дорогостоящего бизнес-оборудования?

Эта проблема состоит из трех частей: целевого значения, переменных, которые оно может изменить, чтобы достичь этого значения, и ограничений, с которыми должен работать Solver. Эти три элемента используются надстройкой Solver для расчета продаж, которые вы бы хотели выполнить. необходимо покрыть стоимость этого оборудования.

Это делает Solver более продвинутым инструментом, чем собственная функция поиска цели в Excel.

Как включить Солвер в Excel

Как мы уже упоминали, Solver включен в Excel как сторонняя надстройка, но сначала вам нужно включить его, чтобы использовать.

Для этого откройте Excel и нажмите Файл> Параметры открыть меню параметров Excel.

Открытие меню параметров в Excel

в Параметры Excel окно, нажмите Надстройки вкладка для просмотра настроек для надстроек Excel.

Вкладка надстроек Excel

в Надстройки На вкладке вы увидите список доступных надстроек Excel.

Выбрать Надстройки Excel от управлять раскрывающееся меню внизу окна, затем нажмите Идти кнопка.

Управление надстройками Excel

в Надстройки установите флажок рядом с Надстройка Солвера вариант, затем нажмите Хорошо подтвердить.

Включение Excel Solver добавить в

Как только вы нажмете Хорошо, надстройка Solver будет включена, и вы сможете начать ее использовать.

Использование Солвера в Microsoft Excel

Надстройка Solver будет доступна для использования, как только она будет включена. Для начала вам понадобится электронная таблица Excel с соответствующими данными, чтобы вы могли использовать Солвер. Чтобы показать вам, как использовать Солвер, мы будем использовать пример математической задачи.

Исходя из нашего предыдущего предложения, существует электронная таблица, показывающая стоимость дорогостоящего оборудования. Чтобы заплатить за это оборудование, бизнес должен продать определенное количество продуктов, чтобы заплатить за оборудование.

Для этого запроса несколько переменных могут измениться для достижения цели. Вы можете использовать Solver для определения стоимости продукта для оплаты оборудования на основе заданного количества продуктов.

В качестве альтернативы, если вы установили цену, вы могли бы определить количество продаж, которое вам нужно было бы достичь безубыточности — это проблема, которую мы попытаемся решить с помощью Солвера.

Запуск Солвера в Excel

Чтобы использовать Solver для решения этого типа запроса, нажмите Данные вкладка на панели ленты Excel.

Вкладка «Данные» на ленточной панели Excel

в анализировать раздел нажмите решающее устройство вариант.

Кнопка Солвер в Excel

Это загрузит Параметры решателя окно. Отсюда вы можете настроить запрос Солвера.

Выбор параметров решателя

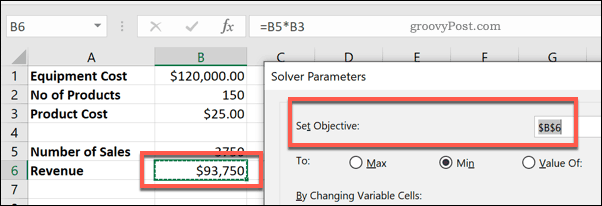
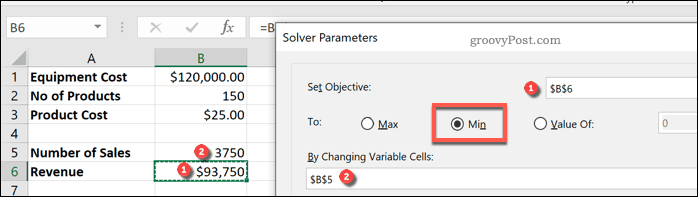
Во-первых, вам нужно выбрать Установить цель клетка. Для этого сценария мы хотим, чтобы доход в ячейке B6 соответствовал стоимости оборудования в ячейке B1, чтобы достичь безубыточности. Исходя из этого, мы можем определить количество продаж, которое нам нужно сделать.

Ячейка Задать цель в Солвере для Excel

к цифра позволяет найти минимум (Min) или максимум (Максимум) возможное значение для достижения цели, или вы можете установить ручную цифру в Значение коробка.

Лучшим вариантом для нашего тестового запроса будет Min вариант. Это потому, что мы хотим найти минимальное количество продаж, чтобы достичь нашей цели безубыточности. Если вы хотите добиться большего, чем это (например, чтобы получить прибыль), вы можете установить целевой показатель дохода в Значение коробка вместо.

Цена остается неизменной, поэтому количество продаж в ячейке B5 является переменная ячейка, Это значение, которое необходимо увеличить.

Вам нужно будет выбрать это в Изменяя переменные ячейки коробка выбора.

Установка переменных Excel Solver

Вы должны будете установить ограничения дальше. Это тесты, которые Solver будет использовать для определения окончательного значения. Если у вас сложные критерии, вы можете установить несколько ограничений для работы Солвера.

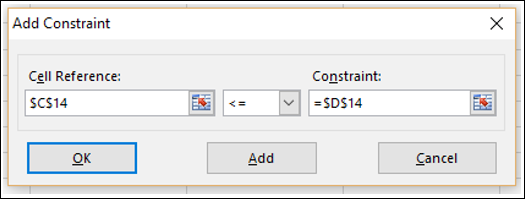
Для этого запроса мы ищем номер дохода, который больше или равен первоначальной стоимости оборудования. Чтобы добавить ограничение, нажмите Добавить кнопка.

Добавление ограничения Excel Solver

Использовать Добавить ограничение окно для определения ваших критериев. В этом примере ячейка B6 (показатель целевого дохода) должна быть больше или равна стоимости оборудования в ячейке B1.

После того, как вы выбрали критерии ограничения, нажмите Хорошо или Добавить кнопок.

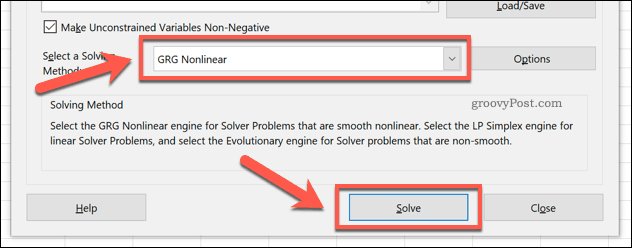
Добавление ограничения к запросу Excel Solver

Прежде чем вы сможете выполнить свой запрос Solver, вам необходимо подтвердить метод решения, который будет использовать Solver.

По умолчанию это установлено на GRG нелинейный вариант, но есть другие доступные методы решения, Когда вы будете готовы выполнить запрос Солвера, нажмите Решать кнопка.

Окончательные варианты Excel Solver

Запуск Solver Query

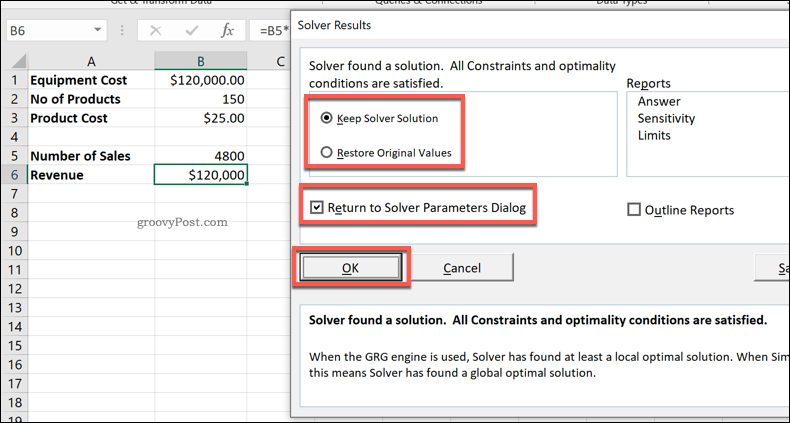
Как только вы нажмете РешатьExcel попытается выполнить ваш запрос Солвера. Появится окно результатов, показывающее, был ли запрос успешным.

В нашем примере Solver обнаружил, что минимальное количество продаж, необходимое для соответствия стоимости оборудования (и, следовательно, безубыточности), составило 4800.

Вы можете выбрать Keep Solver Solution вариант, если вы довольны изменениями, внесенными Солвером, или Восстановить исходные значения если нет

Чтобы вернуться в окно «Параметры решателя» и внести изменения в свой запрос, нажмите Вернуться к диалогу параметров решателя флажок.

Окно результатов Excel Solver

щелчок Хорошо чтобы закрыть окно результатов, чтобы закончить.

Работа с данными Excel

Надстройка Excel Solver берет сложную идею и делает ее возможной для миллионов пользователей Excel. Однако это нишевая функция, и вы можете использовать Excel для более простых расчетов.

Вы можете использовать Excel для расчета процентных изменений или, если вы работаете с большим количеством данных, вы можете делать перекрестные ссылки на ячейки в нескольких листах Excel. Вы даже можете вставить данные Excel в PowerPoint, если вы ищете другие способы использования ваших данных.

Источник

Содержание

Загрузка надстройки «Поиск решения» в Excel
Дополнительные сведения
Как установить и использовать Солвер в Excel
Что такое Солвер для Excel?
Как включить Солвер в Excel
Использование Солвера в Microsoft Excel
Запуск Солвера в Excel
Выбор параметров решателя
Запуск Solver Query
Работа с данными Excel
Excel solver по русски

Загрузка надстройки «Поиск решения» в Excel

«Поиск решения» — это программная надстройка для Microsoft Office Excel, которая доступна при установке Microsoft Office или приложения Excel.

Чтобы можно было работать с надстройкой «Поиск решения», ее нужно сначала загрузить в Excel.

В Excel 2010 и более поздних версий выберите Файл > Параметры.

Примечание: В Excel 2007 нажмите кнопку Microsoft Office кнопку и выберите Excel параметры.

Выберите команду Надстройки, а затем в поле Управление выберите пункт Надстройки Excel.

Нажмите кнопку Перейти.

В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.

Если надстройка Поиск решения отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы найти ее.

Если появится сообщение о том, что надстройка «Поиск решения» не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.

После загрузки надстройки для поиска решения в группе Анализ на вкладки Данные становится доступна команда Поиск решения.

В меню Сервис выберите Надстройки Excel.

В поле Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.

Если надстройка Поиск решения отсутствует в списке поля Доступные надстройкинажмите кнопку Обзор, чтобы найти ее.

Если появится сообщение о том, что надстройка «Поиск решения» не установлена на компьютере, нажмите в диалоговом окне кнопку Да, чтобы ее установить.

После загрузки надстройки «Поиск решения» на вкладке Данные станет доступна кнопка Поиск решения.

В настоящее время надстройка «Поиск решения», предоставляемая компанией Frontline Systems, недоступна для Excel на мобильных устройствах.

«Поиск решения» — это бесплатная надстройка для Excel 2013 с пакетом обновления 1 (SP1) и более поздних версий. Для получения дополнительной информации найдите надстройку «Поиск решения» в Магазине Office.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Источник

Как установить и использовать Солвер в Excel

Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)

Что такое Солвер для Excel?

Это делает Solver более продвинутым инструментом, чем собственная функция поиска цели в Excel.

Как включить Солвер в Excel

Для этого откройте Excel и нажмите Файл> Параметры открыть меню параметров Excel.

в Параметры Excel окно, нажмите Надстройки вкладка для просмотра настроек для надстроек Excel.

в Надстройки На вкладке вы увидите список доступных надстроек Excel.

Выбрать Надстройки Excel от управлять раскрывающееся меню внизу окна, затем нажмите Идти кнопка.

в Надстройки установите флажок рядом с Надстройка Солвера вариант, затем нажмите Хорошо подтвердить.

Как только вы нажмете Хорошо, надстройка Solver будет включена, и вы сможете начать ее использовать.

Использование Солвера в Microsoft Excel

Запуск Солвера в Excel

Чтобы использовать Solver для решения этого типа запроса, нажмите Данные вкладка на панели ленты Excel.

в анализировать раздел нажмите решающее устройство вариант.

Это загрузит Параметры решателя окно. Отсюда вы можете настроить запрос Солвера.

Выбор параметров решателя

Вам нужно будет выбрать это в Изменяя переменные ячейки коробка выбора.

После того, как вы выбрали критерии ограничения, нажмите Хорошо или Добавить кнопок.

Запуск Solver Query

щелчок Хорошо чтобы закрыть окно результатов, чтобы закончить.

Работа с данными Excel

Источник

Excel solver по русски

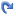
Информация о сайте

Инструменты и настройки

Excel Windows
и
Excel Macintosh

Вопросы и решения

Работа и общение

Работа форума и сайта

Функции листа Excel

= Мир MS Excel/Статьи об Excel

Приёмы работы с книгами, листами, диапазонами, ячейками [6]

Приёмы работы с формулами [13]

Настройки Excel [3]

Инструменты Excel [4]

Интеграция Excel с другими приложениями [4]

Форматирование [1]

Выпадающие списки [2]

Примечания [1]

Сводные таблицы [1]

Гиперссылки [1]

Excel и интернет [1]

Excel для Windows и Excel для Mac OS [2]

Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения , который особенно удобен для решения так называемых «задач оптимизации».

Пример 1. Распределение премии

Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=,
Кнопка, включающая итеративные вычисления с заданными параметрами.

Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Целевая ячейка B12 содержит формулу для расчёта прибыли
Параметр оптимизации — максимум
Изменяемые ячейки B9:C9
Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

Пример 3. Транспортная задача (минимизация затрат)

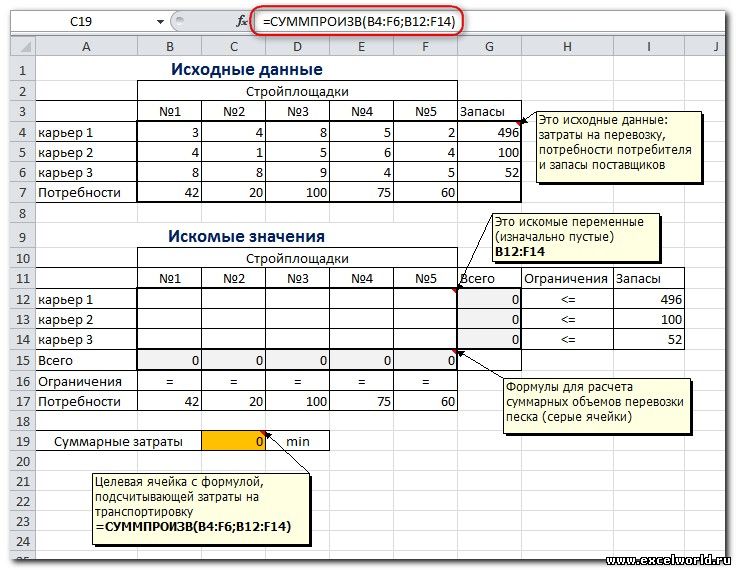
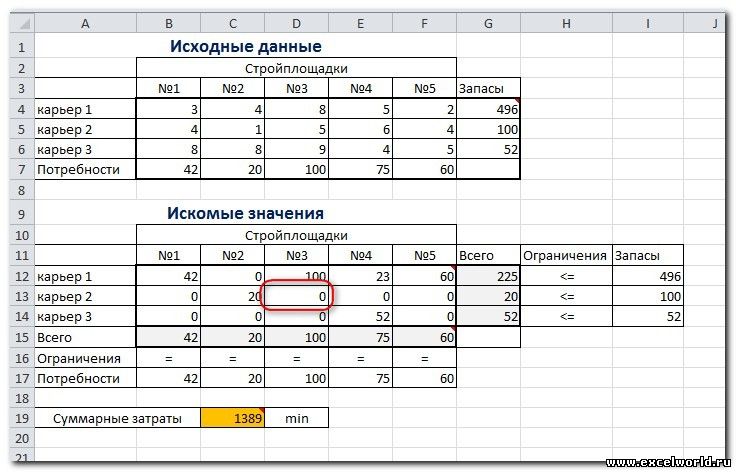
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.

Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку .

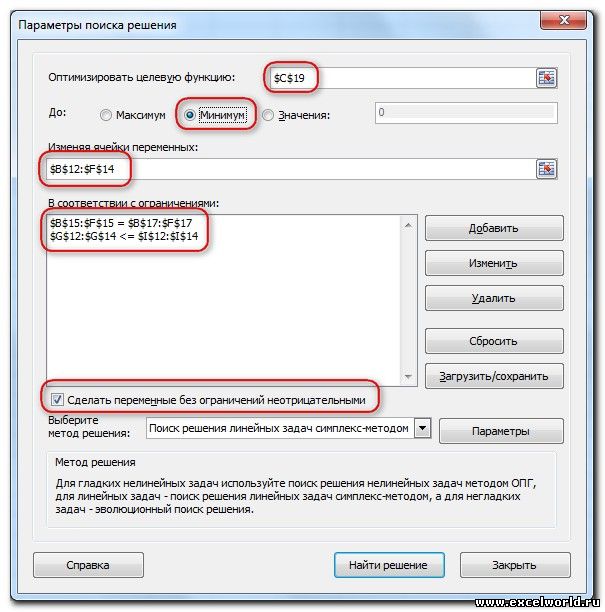
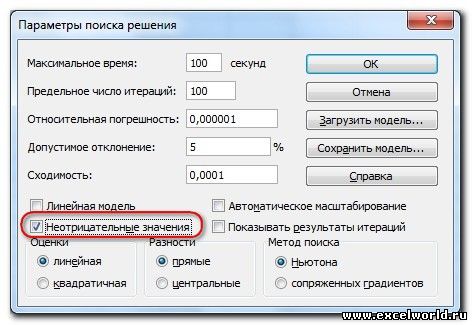
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

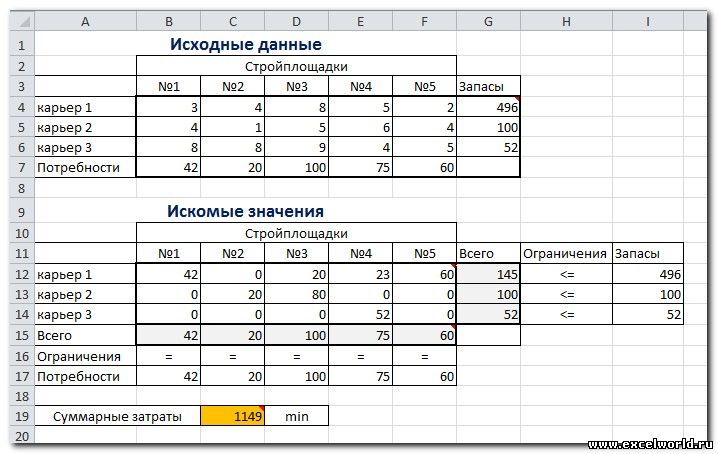
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

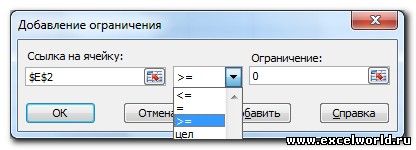
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат

Источник

Поиск решений

Мощным
средством анализа данных Excel
является надстройка Solver
(Поиск решения).
С ее помощью можно определить, при каких
значениях указанных влияющих ячеек
формула в целевой ячейке принимает
нужное значение (минимальное, максимальное
или равное какой-либо величине). Для
процедуры поиска решения можно задать
ограничения, причем не обязательно,
чтобы при этом использовались те же
влияющие ячейки. Для расчета заданного
значения применяются различные
математические методы поиска. Вы можете
установить режим, в котором полученные
значения переменных автоматически
заносятся в таблицу. Кроме того, результаты
работы программы могут быть оформлены
в виде отчета.

Программа Поиск решений
(в оригинале Excel Solver) – дополнительная
надстройка табличного процессора MS
Excel, которая предназначена для решения
определенных систем уравнений, линейных
и нелинейных задач оптимизации,

По
умолчанию в Excel надстройка Поиск решения
отключена. Чтобы активизировать ее в
Excel
2007,
щелкните значок Кнопка
Microsoft Office
, щелкните Параметры
Excel,
а затем выберите категорию Надстройки.
В поле Управление
выберите значение Надстройки
Excel
и нажмите кнопку Перейти.
В поле Доступные
надстройки
установите флажок рядом с пунктом Поиск
решения
и нажмите кнопку ОК.

Процедура поиска решения

1.
Создайте таблицу с формулами, которые
устанавливают связи между ячейками.

2.
Выделите целевую ячейку, которая должна
принять необходимое значение, и выберите
команду:

В
Excel 2007
Данные/Анализ/Поиск
решения;

Поле
Set Target Cell (Установить целевую ячейку)
открывшегося диалогового окна надстройки
Solver (Поиск решения) будет содержать
адрес целевой ячейки.

3.
Установите переключатели Equal To (Равной),
задающие значение целевой ячейки, —
Мах (максимальному значению), Min
(минимальному значению) или Value of
(значению). В последнем случае введите
значение в поле справа.

4.
Укажите в поле By Changing Cells (Изменяя ячейки),
в каких ячейках программа должна изменять
значения в поисках оптимального
результата.

5.
Создайте ограничения в списке Subject to
the Constraints (Ограничения). Для этого щелкните
на кнопке Add (Добавить) и в диалоговом
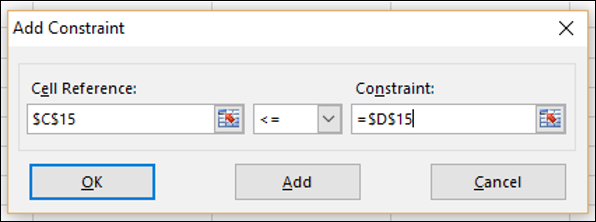
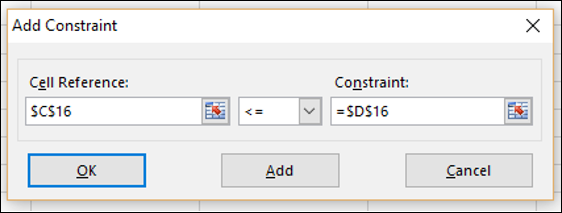
окне Add Constraint (Добавление ограничения)
определите ограничение.

6.
Щелкните на кнопке на кнопке Options
(Параметры), и в появившемся окне
установите переключатель Неотрицательные
значения (если переменные должны быть
позитивными числами), Линейная модель
(если задача, которую вы решаете, относится
к линейным моделям)

7.
Щелкнув на кнопке Solver (Выполнить),
запустите процесс поиска решения.

8.
Когда появится диалоговое окно Solver
Results (Результаты поиска решения), выберите
переключатель Keep Solve Solution (Сохранить
найденное решение) или Restore Original Values
(Восстановить исходные значения).

9.
Щелкните на кнопке ОК.

Параметры средства Поиск решения

Максимальное
время —
служит для ограничения времени,
отпущенного на поиск решения задачи. В
этом поле можно ввести время в секундах,
не превышающее 32 767 (примерно девять
часов); значение 100, используемое по
умолчанию, вполне приемлемо для решения
большинства простых задач.

Предельное
число итераций
— управляет временем решения задачи
путем ограничения числа вычислительных
циклов (итераций).

Относительная
погрешност
— определяет точность вычислений. Чем
меньше значение этого параметра, тем
выше точность вычислений.

Допустимое
отклонение
— предназначен для задания допуска на
отклонение от оптимального решения,
если множество значений влияющей ячейки
ограничено множеством целых чисел. Чем
больше значение допуска, тем меньше
времени требуется на поиск решения.

Сходимость
— применяется только к нелинейным
задачам. Когда относительное изменение
значения в целевой ячейке за последние
пять итераций становится меньше числа,
указанного в поле Сходимость, поиск
прекращается.

Линейная
модель —
служит для ускорения поиска решения
путем применения к задаче оптимизации
линейной модели. Нелинейные модели
предполагают использование нелинейных
функций, фактора роста и экспоненциального
сглаживания, что замедляет
вычисления.

Неотрицательные
значения —
позволяет установить нулевую нижнюю
границу для тех влияющих ячеек, для
которых не было задано соответствующее
ограничение в диалоговом окне Добавить
ограничение.

Автоматическое
масштабирование
— используется, когда числа в изменяемых
ячейках и в целевой ячейке существенно
различаются.

Показывать
результаты итераций
— приостанавливает поиск решения для
просмотра результатов отдельных
итераций.

Загрузить
модель —
после щелчка на этой кнопке отрывается
одноименное диалоговое окно, в котором
можно ввести ссылку на диапазон ячеек,
содержащих модель оптимизации.

Сохранить
модель —
служит для отображения на экране
одноименного диалогового окна, в

котором
можно ввести ссылку на диапазон ячеек,
предназначенный для хранения модели
оптимизации.

Оценка
линейная —
выберите этот переключатель для работы
с линейной моделью.

Оценка
квадратичная
— выберите этот переключатель для работы
с нелинейной моделью.

Разности
прямые —
используется в большинстве задач, где
скорость изменения ограничений
относительно невысока. Увеличивает
скорость работы средства Поиск
решения.

Разности
центральные
— используется для функций, имеющих
разрывную производную. Данный способ
требует больше вычислений, однако его
применение может быть оправданным, если
выдано сообщение о том, что получить
более точное решение не удается.

Метод
поиска Ньютона —
требует больше памяти, но выполняет
меньше итераций, чем в методе сопряженных
градиентов.

Метод
поиска сопряженных градиентов
— реализует метод сопряженных градиентов,
для которого требуется меньше памяти,
но выполняется больше итераций, чем в
методе Ньютона. Данный метод следует
использовать, если задача достаточно
большая и необходимо экономить память
или если итерации дают слишком малое
отличие в последовательных приближениях.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».

Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.

Сделать это можно так:

для версий старше Excel 2007 через команду меню Сервис —> Надстройки;

начиная с Excel 2007 через диалоговое окно Параметры Excel

Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.

В версиях до Excel 2007 аналогичная команда появится в меню Сервис

Разберём порядок работы Поиска решения на простом примере.

Пример 1. Распределение премии

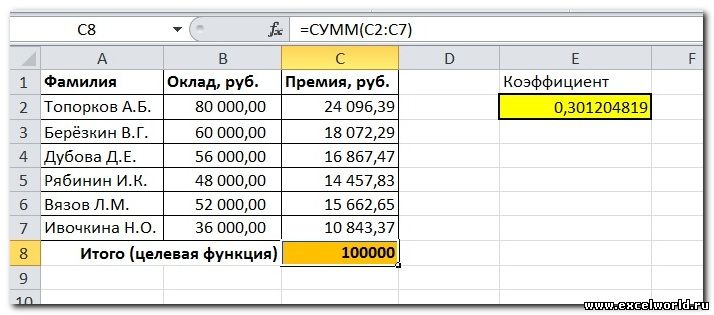
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.

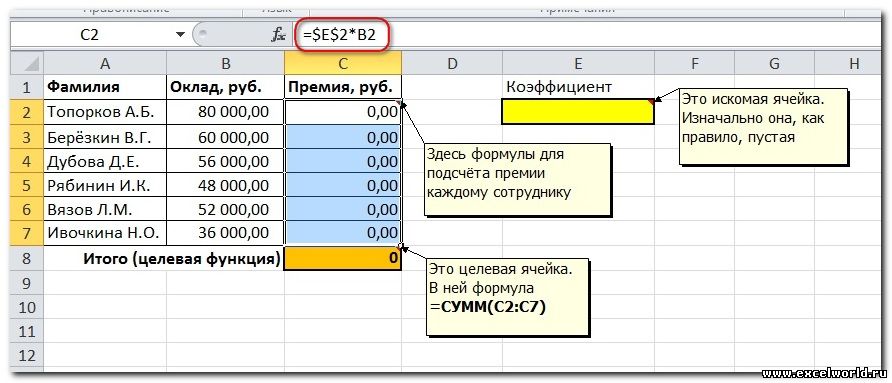
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).

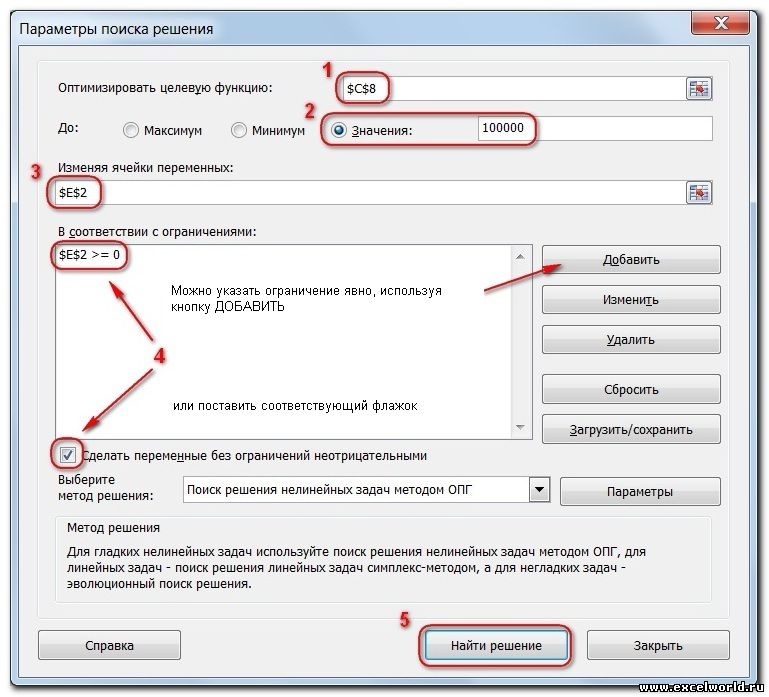
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:

Начиная с Excel 2010

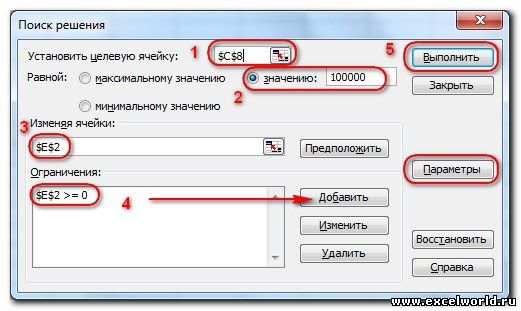
До Excel 2010

Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
Кнопка, включающая итеративные вычисления с заданными параметрами.

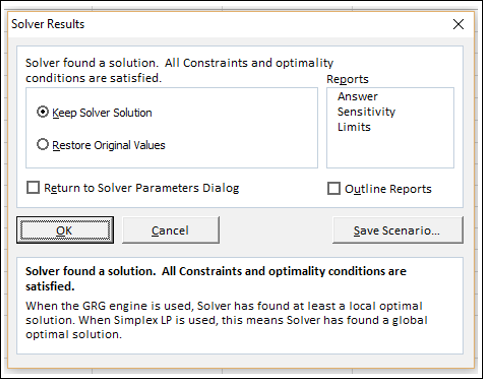
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.

Начиная с Excel 2010

До Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

Разберём еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных книжных полок.

Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?

Порядок действий нам уже известен.

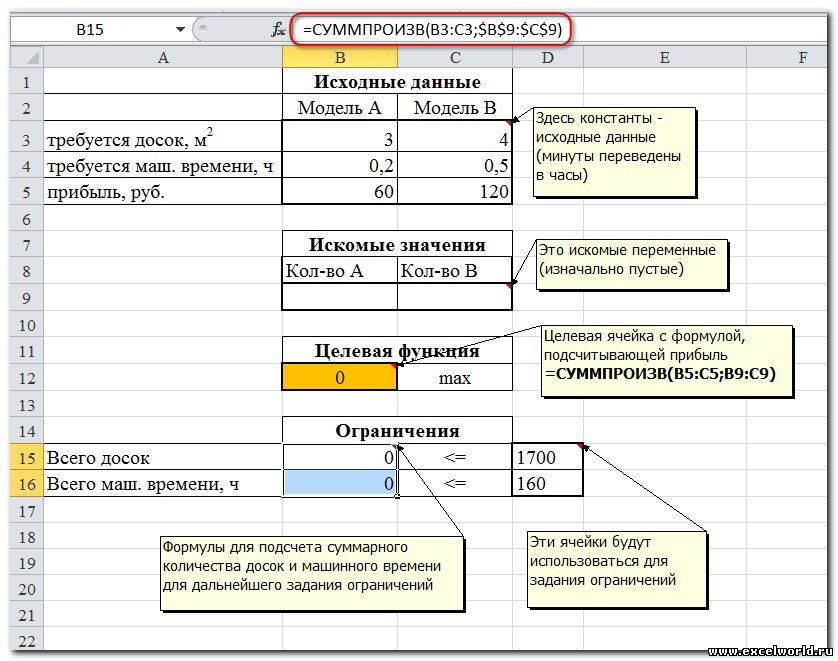
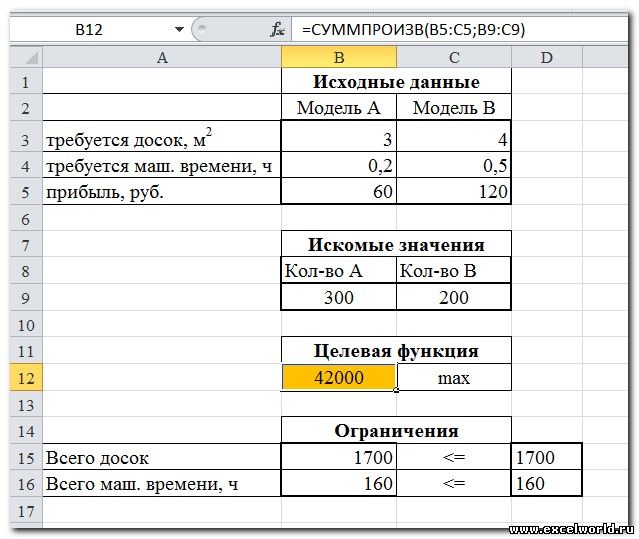
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке

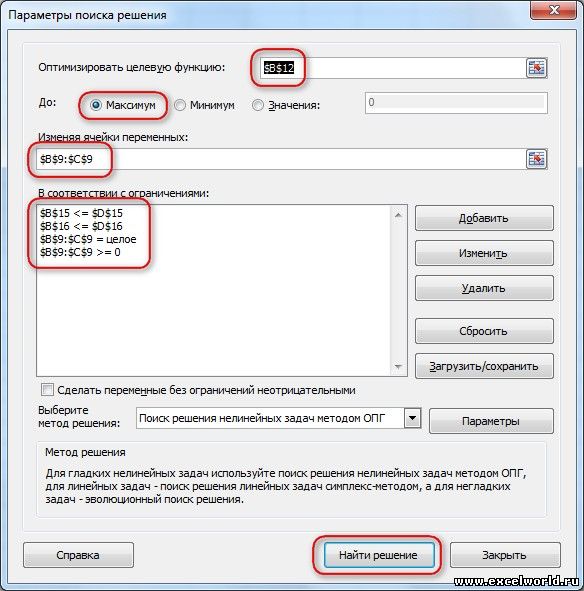
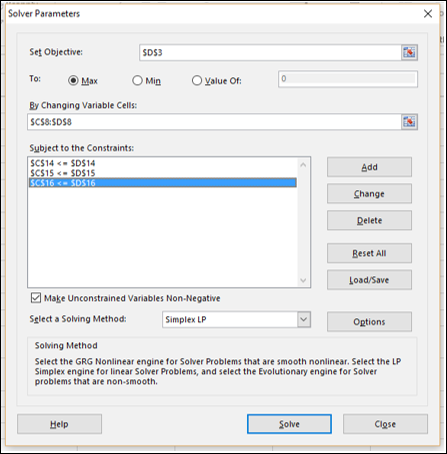
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры

Целевая ячейка B12 содержит формулу для расчёта прибыли
Параметр оптимизации — максимум
Изменяемые ячейки B9:C9
Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

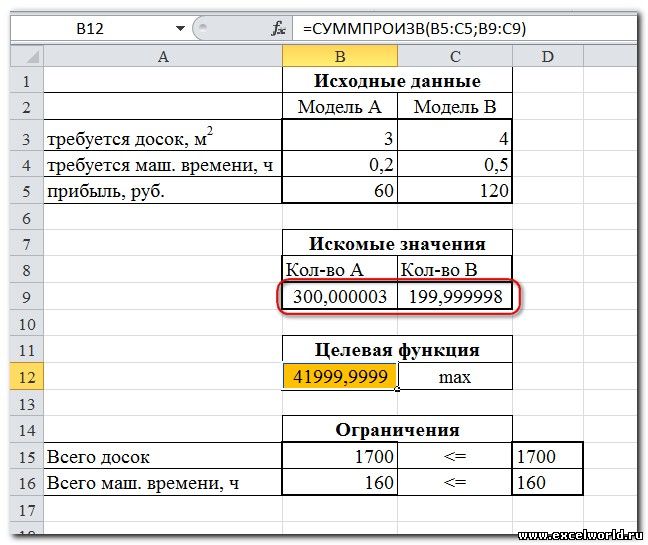
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:

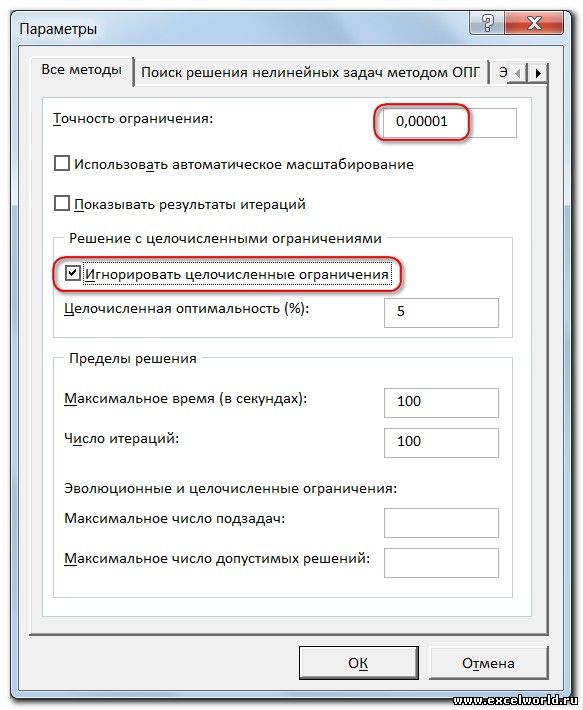
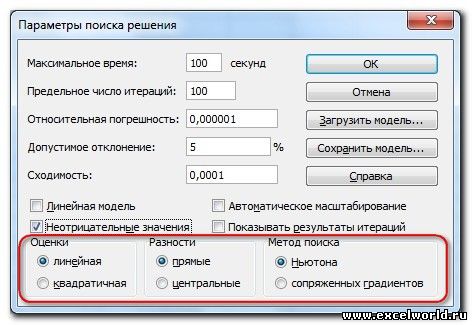
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно

Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.

Пример 3. Транспортная задача (минимизация затрат)

Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

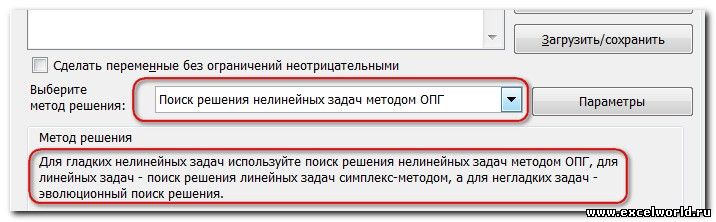
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения

Начиная с Excel 2010

До Excel 2010

В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:

Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?

Источник

Solver – это надстройка Microsoft Excel, которую можно использовать для оптимизации в анализе «что, если».

По мнению О’Брайена и Маракаса, оптимизационный анализ является более сложным расширением целенаправленного анализа. Вместо того, чтобы устанавливать конкретное целевое значение для переменной, цель состоит в том, чтобы найти оптимальное значение для одной или нескольких целевых переменных при определенных ограничениях. Затем одна или несколько других переменных меняются неоднократно, с учетом указанных ограничений, пока вы не найдете лучшие значения для целевых переменных.

В Excel вы можете использовать Solver, чтобы найти оптимальное значение (максимальное или минимальное или определенное значение) для формулы в одной ячейке, называемой целевой ячейкой, при условии соблюдения определенных ограничений или ограничений для значений других ячеек формулы на рабочем листе. ,

Это означает, что Солвер работает с группой ячеек, называемых переменными решения, которые используются при вычислении формул в ячейках цели и ограничения. Солвер корректирует значения в ячейках переменных решения, чтобы удовлетворить ограничения на ячейки ограничений и получить желаемый результат для целевой ячейки.

Вы можете использовать Solver, чтобы найти оптимальные решения для различных проблем, таких как –

Определение ежемесячного ассортимента продукции для подразделения по производству лекарств, которое максимизирует прибыльность.
Планирование рабочей силы в организации.
Решение транспортных проблем.
Финансовое планирование и бюджетирование.

Определение ежемесячного ассортимента продукции для подразделения по производству лекарств, которое максимизирует прибыльность.

Планирование рабочей силы в организации.

Решение транспортных проблем.

Финансовое планирование и бюджетирование.

Активация Solver надстройки

Прежде чем приступить к поиску решения проблемы с Solver, убедитесь, что надстройка Solver активирована в Excel следующим образом:

Нажмите вкладку ДАННЫЕ на ленте. Команда Solver должна появиться в группе «Анализ», как показано ниже.

Если вы не можете найти команду Солвера, активируйте ее следующим образом:

Нажмите вкладку ФАЙЛ.
Нажмите Опции на левой панели. Откроется диалоговое окно «Параметры Excel».
Нажмите Надстройки на левой панели.
Выберите Надстройки Excel в поле «Управление» и нажмите «Перейти».

Откроется диалоговое окно «Надстройки». Проверьте Надстройку Solver и нажмите Ok. Теперь вы можете найти команду Solver на ленте под вкладкой DATA.

Методы решения, используемые Solver

Вы можете выбрать один из следующих трех методов решения, которые поддерживает Excel Solver, в зависимости от типа проблемы:

LP Simplex

Используется для линейных задач. Модель Солвера является линейной при следующих условиях:

Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка) * (постоянная).
Каждое ограничение удовлетворяет требованию линейной модели. Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющейся ячейки) * (константы) и сравнения сумм с константой.

Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка) * (постоянная).

Каждое ограничение удовлетворяет требованию линейной модели. Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющейся ячейки) * (константы) и сравнения сумм с константой.

Обобщенный редуцированный градиент (GRG) нелинейный

Используется для гладких нелинейных задач. Если ваша целевая ячейка, любое из ваших ограничений или оба содержат ссылки на изменяющиеся ячейки, которые не имеют (изменяющейся ячейки) * (постоянной) формы, у вас есть нелинейная модель.

эволюционный

Понимание оценки Солвера

Для Солвера требуются следующие параметры –

Ячейки с переменными решениями
Клетки ограничения
Объективные Клетки
Метод решения

Оценка решателя основана на следующем:

Значения в ячейках переменных решения ограничены значениями в ячейках ограничений.
Вычисление значения в целевой ячейке включает значения в ячейках переменных решения.
Солвер использует выбранный метод решения, чтобы получить оптимальное значение в целевой ячейке.

Значения в ячейках переменных решения ограничены значениями в ячейках ограничений.

Вычисление значения в целевой ячейке включает значения в ячейках переменных решения.

Солвер использует выбранный метод решения, чтобы получить оптимальное значение в целевой ячейке.

Определение проблемы

Предположим, вы анализируете прибыль, полученную компанией, которая производит и продает определенный продукт. Вас просят найти сумму, которая может быть потрачена на рекламу в следующие два квартала, но не более 20 000. Уровень рекламы в каждом квартале влияет на следующее –

Количество проданных единиц, косвенно определяющих сумму выручки от продаж.
Сопутствующие расходы и
Прибыль

Вы можете приступить к определению проблемы как –

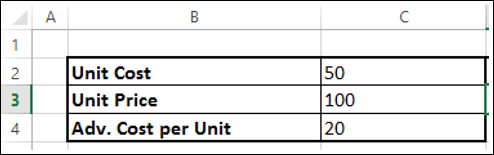
Найти стоимость единицы.
Найти стоимость рекламы на единицу.
Найти цену за единицу.

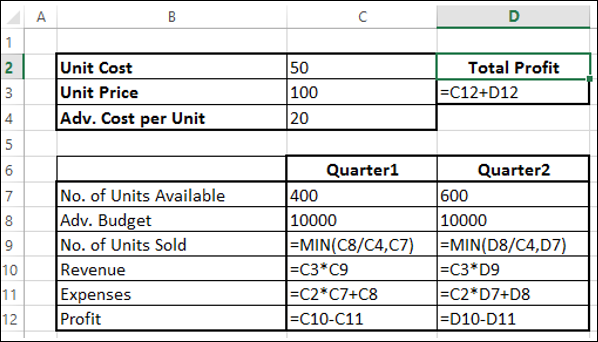
Затем установите ячейки для необходимых расчетов, как указано ниже.

Как вы можете заметить, расчеты сделаны для квартала 1 и квартала 2, которые рассматриваются:

Количество единиц, доступных для продажи в квартале 1, составляет 400, а в квартале 2 – 600 (ячейки – C7 и D7).
Начальные значения для рекламного бюджета установлены как 10000 за квартал (ячейки – C8 и D8).
Количество проданных единиц зависит от стоимости рекламы на единицу и, следовательно, является бюджетом на квартал / Adv. Стоимость за единицу. Обратите внимание, что мы использовали функцию Min, чтобы убедиться, что нет. единиц, проданных в <= нет. из доступных единиц. (Клетки – C9 и D9).
Выручка рассчитывается как цена за единицу * Количество проданных единиц (ячейки – C10 и D10).
Расходы рассчитываются как стоимость единицы * Количество доступных единиц + Adv. Стоимость за этот квартал (Клетки – C11 и D12).
Прибыль – это доход – расходы (ячейки C12 и D12).
Общая прибыль – это прибыль за квартал 1 + прибыль за квартал 2 (ячейка – D3).

Количество единиц, доступных для продажи в квартале 1, составляет 400, а в квартале 2 – 600 (ячейки – C7 и D7).

Начальные значения для рекламного бюджета установлены как 10000 за квартал (ячейки – C8 и D8).

Количество проданных единиц зависит от стоимости рекламы на единицу и, следовательно, является бюджетом на квартал / Adv. Стоимость за единицу. Обратите внимание, что мы использовали функцию Min, чтобы убедиться, что нет. единиц, проданных в <= нет. из доступных единиц. (Клетки – C9 и D9).

Выручка рассчитывается как цена за единицу * Количество проданных единиц (ячейки – C10 и D10).

Расходы рассчитываются как стоимость единицы * Количество доступных единиц + Adv. Стоимость за этот квартал (Клетки – C11 и D12).

Прибыль – это доход – расходы (ячейки C12 и D12).

Общая прибыль – это прибыль за квартал 1 + прибыль за квартал 2 (ячейка – D3).

Далее вы можете установить параметры для Солвера, как указано ниже –

Как вы можете заметить, параметры Солвера –

Объективная ячейка – D3, в которой содержится общая прибыль, которую вы хотите максимизировать.
Ячейки с переменными решениями – это C8 и D8, которые содержат бюджеты на два квартала – квартал 1 и квартал 2.
Есть три ячейки ограничения – C14, C15 и C16.
- Ячейка C14, которая содержит общий бюджет, должна установить ограничение 20000 (ячейка D14).
- Ячейка C15, которая содержит номер единиц, проданных в первом квартале, – установить ограничение <= нет. единиц, доступных в Quarter1 (ячейка D15).
- Ячейка C16, которая содержит номер единиц, проданных в Quarter2, это установить ограничение <= нет. единиц, доступных в квартале 2 (ячейка D16).

Объективная ячейка – D3, в которой содержится общая прибыль, которую вы хотите максимизировать.

Ячейки с переменными решениями – это C8 и D8, которые содержат бюджеты на два квартала – квартал 1 и квартал 2.

Есть три ячейки ограничения – C14, C15 и C16.

Ячейка C14, которая содержит общий бюджет, должна установить ограничение 20000 (ячейка D14).

Ячейка C15, которая содержит номер единиц, проданных в первом квартале, – установить ограничение <= нет. единиц, доступных в Quarter1 (ячейка D15).

Ячейка C16, которая содержит номер единиц, проданных в Quarter2, это установить ограничение <= нет. единиц, доступных в квартале 2 (ячейка D16).

Решение проблемы

Следующим шагом является использование Солвера, чтобы найти решение следующим образом:

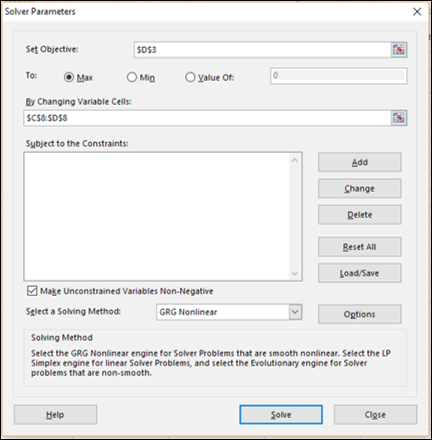
Шаг 1 – Перейдите в ДАННЫЕ> Анализ> Решатель на ленте. Откроется диалоговое окно «Параметры решателя».

Шаг 2 – В поле «Установить цель» выберите ячейку D3.

Шаг 3 – Выберите Макс.

Шаг 4 – Выберите диапазон C8: D8 в поле « Изменение переменных ячеек» .

Шаг 5 – Затем нажмите кнопку Добавить, чтобы добавить три ограничения, которые вы определили.

Шаг 6 – Откроется диалоговое окно Add Constraint. Установите ограничение для общего бюджета, как указано ниже, и нажмите «Добавить».

Шаг 7 – Установите ограничение для общего номера. единиц, проданных в квартале 1, как указано ниже, и нажмите кнопку Добавить.

Шаг 8 – Установите ограничение для общего номера. единиц, проданных в квартале 2, как указано ниже, и нажмите кнопку ОК.

Появится диалоговое окно «Параметры решателя» с тремя ограничениями, добавленными в поле «Подчинить ограничениям».

Шаг 9 – В поле « Выбрать метод решения» выберите Simplex LP.

Шаг 10 – Нажмите кнопку Решить. Откроется диалоговое окно «Результаты решателя». Выберите Keep Solver Solution и нажмите ОК.

Результаты появятся в вашем рабочем листе.

Как вы можете заметить, оптимальное решение, которое дает максимальную общую прибыль с учетом данных ограничений, оказывается следующим:

Общая прибыль – 30000.
Adv. Бюджет на 1 квартал – 8000.
Adv. Бюджет на Квартал2 – 12000.

Пошаговое решение Solver Trial Solutions

Вы можете просмотреть пробные решения Solver, посмотрев результаты итерации.

Шаг 1 – Нажмите кнопку «Параметры» в диалоговом окне «Параметры решателя».

Откроется диалоговое окно « Параметры ».

Шаг 2 – Установите флажок «Показать результаты итерации» и нажмите «ОК».

Шаг 3 – Откроется диалоговое окно « Параметры решателя». Нажмите Решить .

Шаг 4 – Появится диалоговое окно « Показать пробное решение », в котором будет отображено сообщение « Солвер остановлен», а текущие значения решения будут отображены на листе .

Как вы можете видеть, текущие значения итерации отображаются в ваших рабочих ячейках. Вы можете либо остановить Солвер, принимая текущие результаты, либо продолжить, пока Солвер не найдет решение на следующих шагах.

Шаг 5 – Нажмите Продолжить.

Диалоговое окно « Показать пробное решение » появляется на каждом этапе, и, наконец, после нахождения оптимального решения открывается диалоговое окно «Результаты решения». Ваш рабочий лист обновляется на каждом шаге, и, наконец, отображаются значения результатов.

Сохранение выбора Солвера

У вас есть следующие варианты сохранения для задач, которые вы решаете с помощью Солвера –

Вы можете сохранить последние выбранные значения в диалоговом окне «Параметры решателя» вместе с рабочим листом, сохранив рабочую книгу.

Каждый лист в книге может иметь свои собственные варианты Солвера, и все они будут сохранены при сохранении книги.

Вы также можете определить более одной проблемы на рабочем листе, каждый из которых имеет свой собственный выбор Солвера. В таком случае вы можете загружать и сохранять проблемы по отдельности с помощью диалогового окна «Параметры решателя» «Загрузить / сохранить».

Нажмите кнопку Загрузить / Сохранить . Откроется диалоговое окно загрузки / сохранения.

Чтобы сохранить модель проблемы, введите ссылку для первой ячейки вертикального диапазона пустых ячеек, в который вы хотите поместить модель проблемы. Нажмите Сохранить.

Модель проблемы (набор параметров решателя) появляется начиная с ячейки, которую вы указали в качестве справочной.

Чтобы загрузить модель проблемы, введите ссылку для всего диапазона ячеек, которые содержат модель проблемы. Затем нажмите на кнопку «Загрузить».

Источник